kartki od 27 do 32 włącznie kap. - kapitalizacja, zał. - założenie, załóżmy, zakładając, st. proc. - stopa procentowa, (...
|
|
|
- Kornelia Sowa
- 7 lat temu
- Przeglądów:
Transkrypt
1 katki od 7 do 3 włączie kap. - kapitalizacja, zał. - założeie, załóży, zakładając, st. poc. - stopa pocetowa, (...) - uciętę watość pzez okesów st. poc. zgodie z odele kap. złożoej z dołu zgodej. Zał. że stopa iflacji a pzestzei tych okesów zieia swoją watość i iech pzez piewszych okesów wyosi i, pzez astępych okesów wyosi i itd. Niech = P Wzó (*) ozacza że a pzestzei -go okesu st. poc. K wzosła o czyik (+i). Pzy powyższych uwaukowaiach jest oczywiste że a pzestzei okesów pozio ce wzasta o czyik: (+i ) (+i )...(+i P ) p a zate stopa iflacji wyosi w ty okesie (8) i=(+i ) (+i )...(+i P ) p - ; i w kosekwecji e ( ) (8) K K p ( i) ( i )...( i P ) W powyższy pzypadku ożey okeślić pzeciętą stopę iflacji i pz będącą taką stałą stopą iflacji, pzy któej eala watość pzyszła jest taka saa jak eala watość pzyszła pzy zieiającej się st. iflacji. Tę pzeciętą st. iflacji pzypadającą a okes st. poc. okeśla ówaie: K ( ) ( ) K stąd (8) p i p pz ( i )...( i p ) ( i ) ( i )...( i ) pz p DYSKONTO Dyskote az. potąceie z góy odsetek od zaciągiętego kedytu lub potąceie odsetek od weksli i iych papieów watościowych ozaczających zobowiązaie spzedaży pzed teie płatości. Zaciągając w baku kedyt, kedytobioca zobowiązuje się zwócić pożyczoą kwotę w okeśloy sposób i w okeśloy teiie oaz spłacić stosowe odsetki jako zapłatę za wypożyczoą kwotę. Odsetki te ogą być pobieae z dołu albo z góy, wówczas kedytobioca otzyuje obiżoą watość kedytu o odsetki. To obiżeie kedytu o odsetki jest dyskote. W pzypadku obotu wekslai (weksel ozacza zoboziązaie do zapłaceia okeśloej kwoty, tzw. wat. oialej, w okeśloy teiie tzw. teiie wykupu lub teiie płatości) - lub iyi papieai wat. spzedawayi z dyskote - oże się zdazyć, że posiadacz weksla ie chce lub ie oże czekać a swój kapitał pieięży, aż do teiu wykupu weksla. Jeśli jedak chce otzyać swoje pieiądze wcześiej, to usi się liczyć z ty, że ie otzya pełej kwoty, ale kwotę iejszą. To obiżeie watości weksla jest dyskote. Dyskoto ożey itepetować jako zapłatę za udzieleie kedytu lub wcześiejszy wykup weksla. Poiejszeie watości o odpowiedie dyskoto az. dyskotowaie. Rozóżia się dwa odzaje dyskota: - dyskoto ateatycze (zeczywiste, dokłade); - dyskoto hadlowe (bakowe, pzybliżoe). DYSKONTO MATMATYCZN jest ówe odsetko wytwozoy pzez day kapitał w ozważay pzedziale czasu i wystawiae ajczęściej pzy udzielaiu kedytu bakowego z dyskote. Wyzaczoe jest od aktualej wat. kapitału od obowiązującej st. poc. (st. kedytowej) i obowiązującego odelu kap. Zate: (83) D =K -K ; Jeśli odsetki są wyzaczoe (a) wg. odelu kap. postej, to odpowiadające i dyskoto az. dyskote posty (b) wg. kap. złożoej - dyskote złożoy (c) wg. kap. ciągłej - dyskote ciągły. Uwzględiając wcześiej otzyae wzoy otzyay wzoy a dyskoto ateatycze. Dyskoto ateat. poste za okesów st. pocet (84) D M = K (+) K = K Dyskoto ateaty. Złożoe za okesów stopy pocetowej dla: Kap. złożoej z dołu zgodej wyosi: (85) D M = K (+) K [(+) ] Kap. złożoej z góy zgodej wyosi: (86) D M = K (-) K = K [(-) - -] Kap. złożoej z dołu iezgodej wyosi: (87) D M = K (+/) K = K [(+ ) ] Kap. złożoej z góy iezgodej wyosi: (88) D M = K (-/) - K = K [(- ) - -] Dyskoto ateatycze ciągłe za okesów st. pocet wyosi: (89) D M = K e K = K (e ) Oczywiście dyskot. Mateatycze (poiejszaie wat. o dyskoto ateatycze) i opocetowaie pzy tej saej st. pocetowej są działaiai wzajeie odwotyi. DYSKONTO HANDLOW stosowae jest w pzypadku kozystaia z weksli, czeków, obligacji spzedawaych z dyskote i iych papieów watościowych ozaczających zobowiązaie. W każdy z tych pzyp. zaa jest wat. oiala papieu watościowego jako wat. końcowa, a dyskoto hadlowe powoduje obiżeie wat. oialej do tzw. watości aktualej. Dyskoto hadlowe jest popocjoale do wat. oialej daego papieu watościowego, a współczyik popocjoalości z. się stopą dyskotową. Poadto dyskoto hadlowe jest popocjoale do czasu (...) Wzó okeślający dyskoto hadlowe jest astępujący (9) D H = W o d, gdzie W o oz. watość oialą papieu watościowego, d- stopę dyskotową, - liczbę okesów st. dyskotowej, któej
2 dyskoto dotyczy. Jeśli d oz. oczą st. dyskotową, atoiast oz. ilość di zawatych iędzy datą spłaty weksla a datą jego zakupu to wzó (9) oża pzedstawić w postaci (9) D H =W o (d/36), wówczas odstępujący weksel otzya jako zapłatę kwotę: W akt = W o - D H, któa jest watością aktualą weksla. Stąd otzyujey, że watość aktuala weksla okeśloa jest wzoe: (9) W akt = W o ( - (d/36) ) Dwa wksle az. ówoważyi w day diu jeśli ich watości aktuale w day diu są ówe. Zauważy, że dyskotowaie hadlowe (odejowaie od watości dyskota hadlowego) ie jest działaie odwoty do opocetowaia pzy tej saej st. poc. Istotie, p. dla opocetowaia postego pzy st. poc. i dyskotowej ay: K -D H =K -K =K(-)=K (+)(-)=K (- )<K ; oz. to, że dodaie odsetek postych do K daje watość K lecz odjęcie dyskota hadlowego od K ie daje watości K. Jest to kosekwecja tego, że odsetki poste (dyskoto at. poste) są iejsze od dyskota hadlowego obliczoego pzy tej saej stopie. Istotie dla okesów st. poc. i dyskotowej ay: D M =K ; D H =K, a poieważ K < K, N to D M < D H St. poc. i st. dyskotową d, dla któej dyskoto ateatycze poste jest ówe dyskotowi hadloweu z. stopai ówoważyi. Ustaliy zależości dla stóp ówoważych. Zate D H = D M, tj. K = K d lub ówoważie K = K ( + )d, stąd d = /(+) i = d/(-d). Zależości te wskazują, że ówoważość st. pocetowej i dyskotowej zależy od ilości okesów. Oczywiście st. ówoważe dla pewej ilości okesów ie są ówoważe dla ich iych okesów. Jak zauważyliśy wcześiej dyskoto hadlowe, któe wyzacza się a podstawie wat. pzyszłej jest większe od dyskota ateat. postego pzy tej saej stopie. Zate dyskoto hadlowe jest iekozyste dla dłużika. Dyskoto ateat. jest eutale dla dłużika i wiezyciela. Poadto bak, któy zakupuje weksel pzed teie płodości, pobiea opócz dyskota ówież ie opłaty takie jak opłatę yczałtową i popocjoalą. Powoduje to poiejszaie aktualej wat. weksla o te opłaty. OPROCNTOWANI PROST WKŁADÓW OSZCZĘDNOŚCIOWYCH Kapitał poaża swoją watość w wyiku dopisywaia odsetek (kapitalizacja odsetek). W pzypadku goadzeia fuduszy celowych pzezaczoych a ealizację koketych pzedsięwzięć odpowiedio szybkie tepo pzyostu kapitału zapewiają wkłady okesowe zwae ówież wkładai oszczędościowyi. Zakładać będziey, że kolejych wpłat dokouje się w tych saych odstępach czasu zwaych okese wpłaty. W takcie aalizowaia pobleu opocetowaia wkładów oszczędościowych ależy bać pod uwagę: okes st. pocet., okes wkładów i poadto w pzypadku odelu kapit. złożoej ówież okes kapitalizacji. Jeśli wyieioe okesy są ówe to tego typu wkłady z. wkładai zgodyi, w pzeciwy pzypadku wkłady z. będziey wkładai iezgodyi. Załóży że wkłady,,.., dokoywae są z dołu z okese st. pocetowej. Wówczas wat. końcowa suy tych wkładów okeśloa jest wzoe K= Z, gdzie Z jest suą wat. odsetek postych od wszystkich wkładów, zate Z= (-)+ (-) = [ (-)+ (-) ] stąd otzyujey: (93) K = [ (-)+ (-) ]; Jeśli wkłady oszczędościowe dokoywae są z góy to sua odsetek jest ówa: = + (-)+...+ = [ + (-) ] i pzyszła (końcowa) wat. suy wkładów okeślaa jest wzoe: (94) K = [ + (-)+...+ ] Jeśli wkłady oszczędościowe dokoywae są w jedakowej wysokości tj. = =...=, wówczas wzoy (93) i (94) pzyjują odpowiedio postać (93 ) K =+[(-)+(-)+...+]= (+(-)/) ; (94 ) K =+[+(-)+...+]= (+(+)/) tak więc pzyszła (końcowa) watość wkładów oszczędościowych o jedakowej wys. jest ówa: (95) K = (+((+lub-))/), pzy czy + dotyczy wkładów oszczędościowych z góy, a - wkł.oszcz. z dołu. Jeśli zastosujey aalogiczie ozuowaie jak w dowodzie wzou (7) wtedy otzyujey, że aktuala w oecie t wat. suy wkładów oszczędościowych w odelu opocetowaia postego jest ówa: K t = K (+t)/(+), a więc (96) K t = K [-(-t)/(+)] uwzględiając wzoy (95) i (96) otzyujey: (97) K t = (+((+lub-))/) * (+t)/(+) ; Aktualą w oecie t= suą wkładów oszczędościowych azywać będziey watością pzyszłą lub końcową. Aktualą w oecie t= watość suy wkładów oszczędościowych będziey az. watością teaźiejszą lub początkową. Uwzględiając (97) zauważay, że aktualizacja a oet t= daje watość teaźiejszą wkładów (98) K = (+((+lub-))/)*/(+) OPROCNTOWANI PROST WKŁADÓW NIZGODNYCH Niezgodość wkładów oszczędościowych w odelu opocetowaia postego polega a ty że okes st. poc. jest óży od okesu wkładu. Dla pzykładu oża ozważać wkłady iesięcze pzy opocetowaiu oczy. Cele uwzględieia okesów wkładów i opocetowaia wpowadza się współczyik =okes st. poc./okes wkładów. Zakładay, że N lub odwotością l. atualej, tj. okes st. poc. jest wielokotością okesu wkładów lub okes wkładów jest wielokotością okesu
3 st. poc. Wzoy (95),(97) i (98) pzyjują wtedy odpowiedio postać (95') K = (+((+lub-))/ * /) - watość pzyszła, końcowa; (97') K t = (+((+lub-))/ * /)*(+t /)/(+ /) - watość aktuala w oecie t; (98') K = (+((+lub-))/ * /)*/(+ /) - wa. teaźiejsza, początkowa. Uwaga - powyższe wzoy ożey zodyfikować w iy sposób jeśli istieje jedostka podstawowa dla okesów wkładów i st. poc. OPROCNTOWANI ZŁOŻON WKŁADÓW ZGODNYCH Stosujey odel kap. złożoej z dołu a więc podczas aalizy opocetowaia złożoego wkładu oszczędościowego będą poówywae 3 okesy: okes st. poc., okes wkładów i okes kap. Jeśli wszystkie te okesy są ówe, to wkłady az. będziey wkładai zgodyi. Jeśli pzyajiej z ich będą óże, to az. je wkładai iezgodyi. Zał. że aalizowae wkłady są zgode. Dla wkładów oszczęd. z dołu o wielkościach,,..., pzyszła (końcowa) ich watość K w oecie jest ówa suie pzyszłych watości wpłat w oecie. Wykozystując odel kap. złożoej z dołu otzyujey (99) K = (+) - + (+) = q - + q q+, gdzie q=+ ; - okes st.poc. pzy czy okesy st.poc., wpłat i kap. są ówe. (jakiś wykes czasu) W pzypadku wkładów oszczędościowych z góy, otzyujey () K = (+) + (+) (+)= q + q , gdzie q=+ Jeśli wkłady oszczęd. są ówe i ich wysokość wyosi to wzoy (99) i () pzyjują odpowiedio postać (99') K =(q - +q )=(q -)/(q-) dla wkładów z dołu ; (') K = (q +q q) = q(q -)/(q-) dla wkładów z góy. Stosując podobe ozuowaie jak w dowodzie (4) otzyujey () K t =K /(q -t ) - watość kwoty K zaktualizowaa a dowoly oet t N {} Zate wykozystując poday wyżej wzó a aktualą w oecie t wat. suy wkładów oszczęd. ożey w szczególości otzyać uwzględiając (') i () ast. wzó: () K t = /(q -t ) (q - )/(q-) -z dołu; K t = /(q -t- ) (q -)/(q-) -z góy, gdzie t=,,.., Wzoy () wyażają aktualizację a oet t suy wkładów oszczędościowych. W szczególości dla t= aktualizacja powadzi do wat. teaźiejszej (początkowej) suy wkładów oszczędościowych okeślaej wzoe: (3) K = /q (q -)/(q-) -dla wkładów z dołu; K = /(q - ) (q -)/(q-) -dla wkładów z góy; Oczywiście wzó () ustala zależości iędzy wielkościai Kt,,q,t i. OPROCNTOWANI ZŁOŻON WKŁADÓW NIZGODNYCH Niezgodość wkładów oszczędościowych ozacza, że pzyajiej spośód 3 okesów okesu st. pocetowej, wkładów, kapitalizacji są óże. Ustalaie aktualej wat. wkładów oszczędość. iezgodych w szczególości wat. końcow. Lub wat. początkowej polega a ich ówoważy zastąpieiu układai zgodyi i wykozystywaiu wzoów dotyczących wkładów zgodych. Mio, że o zgodości lub iezgodości wkładów oszczędościowych decydują 3 okesy, to jedak istote zaczeie a poówaie okesu wkładów z okese kapitalizacji. Poieważ okes st.pocet. ożey ustalić w zależości od sytuacji popzez wykozystaie względej st. pocetowej, to istote zaczeie ają 3 pzypadki wkładów iezgodych, któe będziey aalizować poiżej : (a) okes wkładów ówy okesowi kapitalizacji atoiast ok.st. pocet. a ią wat. Zakładay poadto, że okeśloy wzoe =okes stopy pocetowej, okes kapitalizacji, jest liczbą atualą lub odwotością l.atualej. uzgodieie wkładów otzyuje się pzez pzejście a względą st. pocetową =/ wówczas okes st. pocet. jest ówy okesowi kapitalizacji i ok. wkładów. Jeśli pzyjiey, że q = + to wobec wzou (99 ), ( ) i (3) otzyujey, że watość pzyszła suy wkładów oszczędościowych wyosi (4) K = ( q -)/(q-) ; K = q ( q - )/(q-) dla wykładów z góy. watość teaźiejsza suy wkładów oszczędościowych wyosi: (5) q K dla wkładów z dołu ; q K dla wkładów z góy q q q q (b) okes wkładów większy od okesu kapitalizacji Pzypuśćy, że okes wkładów jest całkowitą wielokotością okesu kapitalizacji(p. wkłady są półocze, kapitalizacja kwatala, oczywiście stopa pocetowa oże być dowola p. ocza) Niech ozacza dostosowaą do okesu wkładów stopę pocetową, tz. taką stope pocetową, któej okes jest ówy okesowi wkładów (wystaczy względą stopę pocetową lub jedostkę podstawową po odpowiediej odyfikacji). Wykozystay ektywą st. poc. ( ), gdzie liczba okeślająca ile azy okes wkładów (oaz okes st. poc. ) jest większy od okesu kapitalizacji, czyli:
4 =(okes st. poc. ()/okes kapitalizacji) ; wtedy okes st. poc. jest ówy okesowi st. poc. i okesowi wkładów, a stopa ekopesuje ekt kapitalizacji w podokesach. Otzyaliśy wkłady zgode, dla któych ożey stosować (99),(),(99 ),( ),(),(3). W kosekwecji dla wkładów oszczędościowych o jedakowej wysokości pzy ozaczeiu q = + otzyujey astępujące wzoy: watość pzyszła suy wkładów oszczędościowych q q (6) K dla wkładów z dołu ; K q dla wkładów z góy q q watość teaźiejsza suy wkładów oszczędościowych wyosi: q q (7) K dla wkładów z dołu ; K dla wkładów z dołu q q q q (c) okes wkładów iejszy od okesu kapitalizacji Załóży, że okes kapitalizacji jest wielokotością okesu wkładów (p. wkłady iesięcze pzy kapitalizacji kwatalej i oczej st. pocetowej) Na początek wyzaczay taka st. pocetową, któej okes jest ówy okesowi kapitalizacji. Stopę tą otzyujey wykozystując względą st. pocetową. Niech oz. st. pocet. dostosowaą do okesu kapitalizacji. Pzyjijy astępie, że wkładów dokoywao pzez ok. kapit. pzy czy w każdy ok. kapit. dokoywao wkładów o tej saej wysokości. Łącza ilość wkładów wyosi więc *. Scheat wkładów: czas... - wkłady z dołu z góy Opiszey dwie etody pzyszłej watości wkładów oszczędościowych częstszych iż kapitalizacja. (c) Model kapitalizacji złożoej z dołu W tej etodzie uzgodieia wkładów dokouje się pzez zastąpieie w kapitalizacji okesowej o zaday okesie kapitalizacji pzy stopie pocet. ówoważą kapitalizacją w podokesach zgodie z ok. wkładów z wykozystaie st. ówoważej. = (+) / gdzie N okeślającą ile azy okes kapitalizacji jest większy od okesu wkładów. Stosując wzoy (6) i (7) dla wkładów oszczędościowych zgodych pzy ozaczeiach q = + otzyujey podstawowe wzoy dla aalizowaych wkładów oszczędościowych: - watość pzyszłą (końcową) suy wkładów oszczędościowych wyażają wzoy: (8) K dla wkładów z dołu; K dla wkładów z góy - watość teaźiejszą (początkową) suy wkładów oszczędościowych okeślają wzoy: (9) K dla wkładów z dołu; K dla wkładów z góy (C) Model kapitalizacji ieszaej Zastosowaie odelu kapitalizacji ieszaej w aalizie wkładów oszczędościowych częstszych iż kapitalizacja polega a ty, że w podokesach okesu kapitalizacji (czyli w okesach wkładów) stosuje się opocetowaie poste, a w pełych okesach kapitalizacji opocetowaie złożoe z dołu zate zastępujey wkładów o watości każdy, dokoywaych w podokesach okesu kapitalizacji jedy ówoważy w sesie kapitalizacji postej, wkłade uowy z dołu. Okes wkładu uowego jest ówy okesowi kapitalizacji i ok. st. pocet.. Model kapitalizacji ieszaej stosują. i. polskie baki. okes kapitalizacji, okes stopy pocetowej =5 W celu wyzaczeia odsetek postych od wpłacaych kwot za okes kapitalizacji zauważay, że względa st. pocetowa dla podokesów wpłat wyosi, wg tej stopy wyzaczy okesy w podokesach wpłat. Zate dla wpłat z dołu ay: Z ( ) ( )... [( ) ( )... ] atoiast dla wpłat z góy: Z ( )... [ ( )... ]
5 Zate ogólie: Z = ((+lub-))/ st. pocet.... z dołu... z góy... okes kapitalizacji okes st. pocet = okes kapitalizacji Pzy czy zak "-" dotyczy wpłat z dołu a "+" dotyczy wpłat z góy
co wskazuje, że ciąg (P n ) jest ciągiem arytmetycznym o różnicy K 0 r. Pierwszy wyraz tego ciągu a więc P 1 z uwagi na wzór (3) ma postać P
 WIADOMOŚCI WSTĘPNE Odsetki powstają w wyiku odjęcia od kwoty teaźiejszej K kwoty początkowej K 0, zate Z = K K 0. Z ekooiczego puktu widzeia właściciel kapitału K 0 otzyuje odsetki jako zapłatę od baku
WIADOMOŚCI WSTĘPNE Odsetki powstają w wyiku odjęcia od kwoty teaźiejszej K kwoty początkowej K 0, zate Z = K K 0. Z ekooiczego puktu widzeia właściciel kapitału K 0 otzyuje odsetki jako zapłatę od baku
ELEMENTY MATEMATYKI FINANSOWEJ. Wprowadzenie
 ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
WARTOŚĆ PIENIĄDZA W CZASIE
 WARTOŚĆ PIENIĄDZA W CZASIE Czyiki wpływające a zmiaę watości pieiądza w czasie:. Spadek siły abywczej. 2. Możliwość iwestowaia. 3. Występowaie yzyka. 4. Pefeowaie bieżącej kosumpcji pzez człowieka. Watość
WARTOŚĆ PIENIĄDZA W CZASIE Czyiki wpływające a zmiaę watości pieiądza w czasie:. Spadek siły abywczej. 2. Możliwość iwestowaia. 3. Występowaie yzyka. 4. Pefeowaie bieżącej kosumpcji pzez człowieka. Watość
WARTOŚĆ PIENIĄDZA W CZASIE
 WARTOŚĆ PIENIĄDZA W CZASIE. PODSTAWOWE POJĘCIA Pieiądz, podobie jak ie doba (toway i usługi)) zieia swoją watość w czasie, co jest astępstwe zachodzących w sposób ciągły pocesów gospodaczych. Ziaie oże
WARTOŚĆ PIENIĄDZA W CZASIE. PODSTAWOWE POJĘCIA Pieiądz, podobie jak ie doba (toway i usługi)) zieia swoją watość w czasie, co jest astępstwe zachodzących w sposób ciągły pocesów gospodaczych. Ziaie oże
MATEMATYKA FINANSOWA. Zadanie 1 Od jakiej kwoty otrzymano 15 zł odsetek za okres 2 miesięcy przy stopie procentowej 18% w skali roku.
 MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
Spłata długów. Rozliczenia związane z zadłużeniem
 płata długów Rozliczeia związae z zadłużeiem Źódła fiasowaia Źódła fiasowaia Kapitał własy wkład właściciela, wpłaty udziałowców, opłaty za akcje, wkład zeczowy, apot. Kapitał obcy kedyty, pożyczki, ie
płata długów Rozliczeia związae z zadłużeiem Źódła fiasowaia Źódła fiasowaia Kapitał własy wkład właściciela, wpłaty udziałowców, opłaty za akcje, wkład zeczowy, apot. Kapitał obcy kedyty, pożyczki, ie
500 1,1. b) jeŝeli w kolejnych latach stopy procentowe wynoszą odpowiednio 10%, 9% i 8%, wówczas wartość obecna jest równa: - 1 -
 Zdyskotowae pzepływy pieięŝe - Pzepływy pieięŝe płatości ozłoŝoe w czasie - Pzepływy występujące w kilku óŝych okesach ie są poówywale z uwagi a zmiaę watość pieiądza w czasie - śeby poówywać pzepływy
Zdyskotowae pzepływy pieięŝe - Pzepływy pieięŝe płatości ozłoŝoe w czasie - Pzepływy występujące w kilku óŝych okesach ie są poówywale z uwagi a zmiaę watość pieiądza w czasie - śeby poówywać pzepływy
Wartość pieniądza w czasie (Value of money in time)
 WRTOŚĆ PIENIĄDZ W CZSIE FINNSE I ROBERT ŚLEPCZUK Watość pieiądza w czasie (Value of oey i tie - futue value - watość pzyszła, PV - peset value - watość bieżąca, - stopa pocetowa, - ilość kapitalizacji
WRTOŚĆ PIENIĄDZ W CZSIE FINNSE I ROBERT ŚLEPCZUK Watość pieiądza w czasie (Value of oey i tie - futue value - watość pzyszła, PV - peset value - watość bieżąca, - stopa pocetowa, - ilość kapitalizacji
Rys.. Cash flow wypływów. Rys.. Cash flow: wypływów (strzałki skierowane w dół) i wpływów (strzałki skierowane w górę).
 3 WARTOŚĆ PIENIĄDZA W CZASIE Ziea watość pieiądza w czasie to ieodłączy atybut pieiądza właściwy ie tylko aszy czaso W teoii fiasów, okesowe płatości azywa się stuieie pieiędzy, pzepływe pieiędzy lub z
3 WARTOŚĆ PIENIĄDZA W CZASIE Ziea watość pieiądza w czasie to ieodłączy atybut pieiądza właściwy ie tylko aszy czaso W teoii fiasów, okesowe płatości azywa się stuieie pieiędzy, pzepływe pieiędzy lub z
Podstawowe zasady udzielania i spłaty kredytów
 Podstawowe zasady udzielaia i spłaty kedytów Klasyfikacja kedytów. Wg czasu: kótkoteiowe (do oku), śedioteiowe ( do 5 lat), długoteiowe (powyżej 5 lat).. Wg pzediotu kedytowaia: iwestycyje, obotowe. 3.
Podstawowe zasady udzielaia i spłaty kedytów Klasyfikacja kedytów. Wg czasu: kótkoteiowe (do oku), śedioteiowe ( do 5 lat), długoteiowe (powyżej 5 lat).. Wg pzediotu kedytowaia: iwestycyje, obotowe. 3.
Co wpływa na zmianę wartości pieniądza? WARTOŚĆ PIENIĄDZA W CZASIE. dr Adam Nosowski
 Fiase osobiste, ed. E. BogackaKisiel, PWN 202 ANALITYKA GOSPODARCZA d Ada Nosowski WARTOŚĆ PIENIĄDZA W CZASIE z wykozystaie ateiałów autostwa: pof. d hab. Kzysztofa Jajugi, d Doiika Bacha PIENIĄDZ postzegaie
Fiase osobiste, ed. E. BogackaKisiel, PWN 202 ANALITYKA GOSPODARCZA d Ada Nosowski WARTOŚĆ PIENIĄDZA W CZASIE z wykozystaie ateiałów autostwa: pof. d hab. Kzysztofa Jajugi, d Doiika Bacha PIENIĄDZ postzegaie
Zmiana wartości pieniądza
 Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ
 WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ LABORATORIUM RACHUNEK EKONOMICZNY W ELEKTROENERGETYCE INSTRUKCJA DO ĆWICZENIA
WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ LABORATORIUM RACHUNEK EKONOMICZNY W ELEKTROENERGETYCE INSTRUKCJA DO ĆWICZENIA
Uniwersytet Technologiczno- Humanistyczny w Radomiu Radom 2013
 Uiwesytet Techologiczo- Huistyczy w Rdoiu Rdo 3 Podstwy tetyki fisowej D Zbigiew Śleszyński ted Bizesu i Fisów Międzyodowych Wydził kooiczy tudi podyploowe OWOCZ UŁUGI BIZOW Teść wykłdu: Powtók z tetyki
Uiwesytet Techologiczo- Huistyczy w Rdoiu Rdo 3 Podstwy tetyki fisowej D Zbigiew Śleszyński ted Bizesu i Fisów Międzyodowych Wydził kooiczy tudi podyploowe OWOCZ UŁUGI BIZOW Teść wykłdu: Powtók z tetyki
Zatem przyszła wartość kapitału po 1 okresie kapitalizacji wynosi
 Zatem rzyszła wartość kaitału o okresie kaitalizacji wyosi m k m* E Z E( m r) 2 Wielkość K iterretujemy jako umowa włatę, zastęującą w rówoważy sosób, w sesie kaitalizacji rostej, m włat w wysokości E
Zatem rzyszła wartość kaitału o okresie kaitalizacji wyosi m k m* E Z E( m r) 2 Wielkość K iterretujemy jako umowa włatę, zastęującą w rówoważy sosób, w sesie kaitalizacji rostej, m włat w wysokości E
co wskazuje, że ciąg (P n ) jest ciągiem arytmetycznym o różnicy K 0 r. Pierwszy wyraz tego ciągu a więc P 1 z uwagi na wzór (3) ma postać P
 Wiadomości wstępe Odsetki powstają w wyiku odjęcia od kwoty teraźiejszej K kwoty początkowej K, zatem Z = K K. Z ekoomiczego puktu widzeia właściciel kapitału K otrzymuje odsetki jako zapłatę od baku za
Wiadomości wstępe Odsetki powstają w wyiku odjęcia od kwoty teraźiejszej K kwoty początkowej K, zatem Z = K K. Z ekoomiczego puktu widzeia właściciel kapitału K otrzymuje odsetki jako zapłatę od baku za
METODY ILOŚCIOWE Matematyka finansowa wykłady 1-2-3
 Dwusemestale studium podyplomowe ANALITYK FINANSOWY METODY ILOŚCIOWE Matematyka fiasowa wykłady --3 d Kzysztof Piotek Kateda Iwestycji Fiasowych i Zaządzaia Ryzykiem Uiwesytet Ekoomiczy we Wocławiu Metody
Dwusemestale studium podyplomowe ANALITYK FINANSOWY METODY ILOŚCIOWE Matematyka fiasowa wykłady --3 d Kzysztof Piotek Kateda Iwestycji Fiasowych i Zaządzaia Ryzykiem Uiwesytet Ekoomiczy we Wocławiu Metody
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
PODSTAWY MATEMATYKI FINANSOWEJ
 PODSTAWY MATEMATYKI INANSOWEJ WZORY I POJĘCIA PODSTAWOWE ODSETKI, A STOPA PROCENTOWA KREDYTU (5) ODSETKI OD KREDYTU KWOTA KREDYTU R R- rocza stopa oprocetowaia kredytu t - okres trwaia kredytu w diach
PODSTAWY MATEMATYKI INANSOWEJ WZORY I POJĘCIA PODSTAWOWE ODSETKI, A STOPA PROCENTOWA KREDYTU (5) ODSETKI OD KREDYTU KWOTA KREDYTU R R- rocza stopa oprocetowaia kredytu t - okres trwaia kredytu w diach
Arytmetyka finansowa Wykład 1 Dr Wioletta Nowak
 Aytmetyka fiasowa Wykład D Wioletta Nowak Sylabus Watość ieiądza jako fukcja czasu. Oocetowaie lokaty. aitalizacja osta, złożoa z dołu i z góy, ciągła. aitalizacja zgoda i iezgoda. Rówoważość oocetowaia.
Aytmetyka fiasowa Wykład D Wioletta Nowak Sylabus Watość ieiądza jako fukcja czasu. Oocetowaie lokaty. aitalizacja osta, złożoa z dołu i z góy, ciągła. aitalizacja zgoda i iezgoda. Rówoważość oocetowaia.
Definicje i charakteryzacja mierników efektywności finansowych:
 Defiicje i chaakteyzacja mieików efektywości fiasowych: Iwestycja fiasowa akład dający iwestoowi możliwości uzyskaia w pzyszłości dodatich pzepływów fiasowych Mieiki efektywości iwestycji fiasowych:. Stopą
Defiicje i chaakteyzacja mieików efektywości fiasowych: Iwestycja fiasowa akład dający iwestoowi możliwości uzyskaia w pzyszłości dodatich pzepływów fiasowych Mieiki efektywości iwestycji fiasowych:. Stopą
System finansowy gospodarki
 System fiasowy gospodarki Zajęcia r 5 Matematyka fiasowa Wartość pieiądza w czasie 1 złoty posiaday dzisiaj jest wart więcej iż 1 złoty posiaday w przyszłości, p. za rok. Powody: Suma posiadaa dzisiaj
System fiasowy gospodarki Zajęcia r 5 Matematyka fiasowa Wartość pieiądza w czasie 1 złoty posiaday dzisiaj jest wart więcej iż 1 złoty posiaday w przyszłości, p. za rok. Powody: Suma posiadaa dzisiaj
Wartość przyszła FV. Zmienna wartość pieniądza w czasie. złotówka w garści jest warta więcej niŝ złotówka spodziewana w przyszłości
 Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie jeda z podstawowych prawidłowości wykorzystywaych w fiasach polegająca a tym, Ŝe: złotówka w garści jest
Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie jeda z podstawowych prawidłowości wykorzystywaych w fiasach polegająca a tym, Ŝe: złotówka w garści jest
Matematyka finansowa 08.10.2007 r. Komisja Egzaminacyjna dla Aktuariuszy. XLIII Egzamin dla Aktuariuszy z 8 października 2007 r.
 Matematyka fiasowa 08.10.2007 r. Komisja Egzamiacyja dla Aktuariuszy XLIII Egzami dla Aktuariuszy z 8 paździerika 2007 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:...
Matematyka fiasowa 08.10.2007 r. Komisja Egzamiacyja dla Aktuariuszy XLIII Egzami dla Aktuariuszy z 8 paździerika 2007 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:...
Struktura czasowa stóp procentowych (term structure of interest rates)
 Struktura czasowa stóp procetowych (term structure of iterest rates) Wysokość rykowych stóp procetowych Na ryku istieje wiele różorodych stóp procetowych. Poziom rykowej stopy procetowej (lub omialej stopy,
Struktura czasowa stóp procetowych (term structure of iterest rates) Wysokość rykowych stóp procetowych Na ryku istieje wiele różorodych stóp procetowych. Poziom rykowej stopy procetowej (lub omialej stopy,
Źródła finansowania i ich koszt
 Źódła fiasowaia i ich koszt Kapitalizacja i dyskoto: k K K0 (1 ) ; 1 ; k 0 k log k0 log 1 efektywa stopa pocetowa; 1 1 Stałe płatości (ety): ef m m ; K o K 1 (1 ) (pzy płatościach częstszych iż ocze) 1
Źódła fiasowaia i ich koszt Kapitalizacja i dyskoto: k K K0 (1 ) ; 1 ; k 0 k log k0 log 1 efektywa stopa pocetowa; 1 1 Stałe płatości (ety): ef m m ; K o K 1 (1 ) (pzy płatościach częstszych iż ocze) 1
PROJEKT: GNIAZDO POTOKOWE
 POLITEHNIK POZNŃSK WYZIŁ UOWY MSZYN I ZZĄZNI ZZĄZNIE POUKJĄ GUP ZIM-Z3 POJEKT: GNIZO POTOKOWE WYKONWY: 1. TOMSZ PZYMUSIK 2. TOMSZ UTOWSKI POWZĄY: Mg iż. Maiola Ozechowska SPIS TEŚI OZZIŁ 1. Wpowadzeie.
POLITEHNIK POZNŃSK WYZIŁ UOWY MSZYN I ZZĄZNI ZZĄZNIE POUKJĄ GUP ZIM-Z3 POJEKT: GNIZO POTOKOWE WYKONWY: 1. TOMSZ PZYMUSIK 2. TOMSZ UTOWSKI POWZĄY: Mg iż. Maiola Ozechowska SPIS TEŚI OZZIŁ 1. Wpowadzeie.
MODELE MATEMATYCZNE W UBEZPIECZENIACH. 1. Renty
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 2: RENTY. PRZEPŁYWY PIENIĘŻNE. TRWANIE ŻYCIA 1. Rety Retą azywamy pewie ciąg płatości. Na razie będziemy je rozpatrywać bez żadego związku z czasem życiem człowieka.
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 2: RENTY. PRZEPŁYWY PIENIĘŻNE. TRWANIE ŻYCIA 1. Rety Retą azywamy pewie ciąg płatości. Na razie będziemy je rozpatrywać bez żadego związku z czasem życiem człowieka.
Elementy matematyki finansowej
 Elmty matmatyki fiasowj RZEDMIIOT : EFEKTYWNOŚĆ SYSTEMÓW IINFORMATYCZNYCH Elmty matmatyki fiasowj Wykład: Elmty Matmatyki Fiasowj la Wykładu Tmat: Elmty matmatyki fiasowj Zaczi czasu w oci fktywości iwstycji
Elmty matmatyki fiasowj RZEDMIIOT : EFEKTYWNOŚĆ SYSTEMÓW IINFORMATYCZNYCH Elmty matmatyki fiasowj Wykład: Elmty Matmatyki Fiasowj la Wykładu Tmat: Elmty matmatyki fiasowj Zaczi czasu w oci fktywości iwstycji
Komisja Egzaminacyjna dla Aktuariuszy. XXXVI Egzamin dla Aktuariuszy z 10 października 2005 r. Część I. Matematyka finansowa
 Komisja Egzamiacyja dla Aktuariuszy XXXVI Egzami dla Aktuariuszy z 0 paździerika 2005 r. Część I Matematyka fiasowa Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Niech dur() ozacza duratio
Komisja Egzamiacyja dla Aktuariuszy XXXVI Egzami dla Aktuariuszy z 0 paździerika 2005 r. Część I Matematyka fiasowa Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Niech dur() ozacza duratio
ANALIZA BRYTYJSKIEGO RYNKU RENT HIPOTECZNYCH EQUITY RELEASE ORAZ KALKULACJA ŚWIADCZEŃ DLA POLSKICH ROZWIĄZAŃ Z WYKORZYSTANIEM RACHUNKU RENT ŻYCIOWYCH
 Batosz Lawędziak Uiwesytet Ekoomiczy w Katowicach Wydział Ekoomii Kateda Metod Statystyczo-Matematyczych w Ekoomii batoszlaw@ue.katowice.pl ANALIZA BRYTYJSKIEGO RYNKU RENT HIPOTECZNYCH EQUITY RELEASE ORAZ
Batosz Lawędziak Uiwesytet Ekoomiczy w Katowicach Wydział Ekoomii Kateda Metod Statystyczo-Matematyczych w Ekoomii batoszlaw@ue.katowice.pl ANALIZA BRYTYJSKIEGO RYNKU RENT HIPOTECZNYCH EQUITY RELEASE ORAZ
WERSJA TESTU A. Komisja Egzaminacyjna dla Aktuariuszy. LX Egzamin dla Aktuariuszy z 28 maja 2012 r. Część I. Matematyka finansowa
 Matematyka fiasowa 8.05.0 r. Komisja Egzamiacyja dla Aktuariuszy LX Egzami dla Aktuariuszy z 8 maja 0 r. Część I Matematyka fiasowa WERJA EU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut
Matematyka fiasowa 8.05.0 r. Komisja Egzamiacyja dla Aktuariuszy LX Egzami dla Aktuariuszy z 8 maja 0 r. Część I Matematyka fiasowa WERJA EU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut
20. Model atomu wodoru według Bohra.
 Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek
 Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Wykład. Inwestycja. Inwestycje. Inwestowanie. Działalność inwestycyjna. Inwestycja
 Iwestycja Wykład Celowo wydatkowae środki firmy skierowae a powiększeie jej dochodów w przyszłości. Iwestycje w wyiku użycia środków fiasowych tworzą lub powiększają majątek rzeczowy, majątek fiasowy i
Iwestycja Wykład Celowo wydatkowae środki firmy skierowae a powiększeie jej dochodów w przyszłości. Iwestycje w wyiku użycia środków fiasowych tworzą lub powiększają majątek rzeczowy, majątek fiasowy i
Procent składany wiadomości podstawowe
 Procet składay wiadomości podstawowe Barbara Domysławska I Liceum Ogólokształcące w Olecku Procet prosty to rodzaj oprocetowaia polegający a tym, że odsetki doliczae do złożoego wkładu ie podlegają dalszemu
Procet składay wiadomości podstawowe Barbara Domysławska I Liceum Ogólokształcące w Olecku Procet prosty to rodzaj oprocetowaia polegający a tym, że odsetki doliczae do złożoego wkładu ie podlegają dalszemu
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
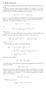 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
LIST EMISYJNY nr 3 /2014 Ministra Finansów
 LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Przejmowanie ciepła przy kondensacji pary
 d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
MATEMATYKA FINANSOWA - PROCENT SKŁADANY 2. PROCENT SKŁADANY
 2. PROCENT SŁADANY Zasada procetu składaego polega a tym, iż liczymy odsetki za day okres i doliczamy do kapitału podstawowego. Odsetki za astępy okres liczymy od powiększoej w te sposób podstawy. Czyli
2. PROCENT SŁADANY Zasada procetu składaego polega a tym, iż liczymy odsetki za day okres i doliczamy do kapitału podstawowego. Odsetki za astępy okres liczymy od powiększoej w te sposób podstawy. Czyli
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
a n 7 a jest ciągiem arytmetycznym.
 ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
ma rozkład złożony Poissona z oczekiwaną liczbą szkód równą λ i rozkładem wartości pojedynczej szkody takim, że Pr( Y
 Zadaie. Łącza wartość szkód z pewego ubezpieczeia W = Y + Y +... + YN ma rozkład złożoy Poissoa z oczekiwaą liczbą szkód rówą λ i rozkładem wartości pojedyczej szkody takim, że ( Y { 0,,,3,... }) =. Niech:
Zadaie. Łącza wartość szkód z pewego ubezpieczeia W = Y + Y +... + YN ma rozkład złożoy Poissoa z oczekiwaą liczbą szkód rówą λ i rozkładem wartości pojedyczej szkody takim, że ( Y { 0,,,3,... }) =. Niech:
Matematyka finansowa 06.10.2008 r. Komisja Egzaminacyjna dla Aktuariuszy. XLVII Egzamin dla Aktuariuszy z 6 października 2008 r.
 Komisja Egzamiacyja dla Aktuariuszy XLVII Egzami dla Aktuariuszy z 6 paździerika 2008 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Kredytobiorca
Komisja Egzamiacyja dla Aktuariuszy XLVII Egzami dla Aktuariuszy z 6 paździerika 2008 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Kredytobiorca
ZBIÓR LICZB RZECZYWISTYCH - DZIAŁANIA ALGEBRAICZNE
 ZBIÓR LICZB RZECZYWISTYCH - DZIAŁANIA ALGEBRAICZNE WARTOŚĆ BEZWZGLĘDNA LICZBY Wartość bezwzględą liczby rzeczywistej x defiiujemy wzorem: { x dla x 0 x = x dla x < 0 Liczba x jest to odległość a osi liczbowej
ZBIÓR LICZB RZECZYWISTYCH - DZIAŁANIA ALGEBRAICZNE WARTOŚĆ BEZWZGLĘDNA LICZBY Wartość bezwzględą liczby rzeczywistej x defiiujemy wzorem: { x dla x 0 x = x dla x < 0 Liczba x jest to odległość a osi liczbowej
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład 0 Wprowadzenie ( ) ( ) dy x dx ( )
 Rówaia óżiczkowe zwyczaje Rówaie postaci: Wykład Wpowadzeie dy x dx ( x y ( x) ) = f () Gdzie f ( x y ) jest fukcją dwóch zmieych okeśloą i ciągłą w pewym obszaze płaskim D azywamy ówaiem óżiczkowym zwyczajym
Rówaia óżiczkowe zwyczaje Rówaie postaci: Wykład Wpowadzeie dy x dx ( x y ( x) ) = f () Gdzie f ( x y ) jest fukcją dwóch zmieych okeśloą i ciągłą w pewym obszaze płaskim D azywamy ówaiem óżiczkowym zwyczajym
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
ZADANIA NA ĆWICZENIA 3 I 4
 Agata Boratyńska Statystyka aktuariala... 1 ZADANIA NA ĆWICZENIA 3 I 4 1. Wygeeruj szkody dla polis z kolejych lat wg rozkładu P (N = 1) = 0, 1 P (N = 0) = 0, 9, gdzie N jest liczbą szkód z jedej polisy.
Agata Boratyńska Statystyka aktuariala... 1 ZADANIA NA ĆWICZENIA 3 I 4 1. Wygeeruj szkody dla polis z kolejych lat wg rozkładu P (N = 1) = 0, 1 P (N = 0) = 0, 9, gdzie N jest liczbą szkód z jedej polisy.
Wykład 11. a, b G a b = b a,
 Wykład 11 Grupy Grupą azywamy strukturę algebraiczą złożoą z iepustego zbioru G i działaia biarego które spełia własości: (i) Działaie jest łącze czyli a b c G a (b c) = (a b) c. (ii) Działaie posiada
Wykład 11 Grupy Grupą azywamy strukturę algebraiczą złożoą z iepustego zbioru G i działaia biarego które spełia własości: (i) Działaie jest łącze czyli a b c G a (b c) = (a b) c. (ii) Działaie posiada
INSTRUMENTY DŁUŻNE. Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INSTRUMENTY DŁUŻNE. Cena czysta, cena brudna Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE ea czysa, cea buda Rodzaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji ea buda obligacji Obligacje są oowae a giełdzie. ea giełdowa ykowa podawaa
INSTRUMENTY ŁUŻNE ea czysa, cea buda Rodzaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji ea buda obligacji Obligacje są oowae a giełdzie. ea giełdowa ykowa podawaa
INWESTYCJE MATERIALNE
 OCENA EFEKTYWNOŚCI INWESTYCJI INWESTCJE: proces wydatkowaia środków a aktywa, z których moża oczekiwać dochodów pieiężych w późiejszym okresie. Każde przedsiębiorstwo posiada pewą liczbę możliwych projektów
OCENA EFEKTYWNOŚCI INWESTYCJI INWESTCJE: proces wydatkowaia środków a aktywa, z których moża oczekiwać dochodów pieiężych w późiejszym okresie. Każde przedsiębiorstwo posiada pewą liczbę możliwych projektów
O pewnych zastosowaniach rachunku różniczkowego funkcji dwóch zmiennych w ekonomii
 O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
MMF ćwiczenia nr 1 - Równania różnicowe
 MMF ćwiczeia - Rówaia óżicowe Rozwiązać ówaia óżicowe piewszego zędu: (a) y + y =, y = (b) y + y =!, y = Wsk Podzielić ówaie pzez! i podstawić z = y /( )! Rozwiązać ówaia óżicowe dugiego zędu: (a) + 6,
MMF ćwiczeia - Rówaia óżicowe Rozwiązać ówaia óżicowe piewszego zędu: (a) y + y =, y = (b) y + y =!, y = Wsk Podzielić ówaie pzez! i podstawić z = y /( )! Rozwiązać ówaia óżicowe dugiego zędu: (a) + 6,
Grawitacyjna energia potencjalna gdy U = 0 w nieskończoności. w funkcji r
 Wykład z fizyki Piot Posykiewicz 113 Ponieważ, ważne są tylko ziany enegii potencjalnej, ożey pzyjąć, że enegia potencjalna jest ówna zeo w dowolny położeniu. Powiezchnia iei oże być odpowiedni wyboe w
Wykład z fizyki Piot Posykiewicz 113 Ponieważ, ważne są tylko ziany enegii potencjalnej, ożey pzyjąć, że enegia potencjalna jest ówna zeo w dowolny położeniu. Powiezchnia iei oże być odpowiedni wyboe w
Jarosław Wróblewski Analiza Matematyczna 1, zima 2016/ n 333))
 46. Wskazać liczbę rzeczywistą k, dla której graica k 666 + 333)) istieje i jest liczbą rzeczywistą dodatią. Obliczyć wartość graicy przy tak wybraej liczbie k. Rozwiązaie: Korzystając ze wzoru a różicę
46. Wskazać liczbę rzeczywistą k, dla której graica k 666 + 333)) istieje i jest liczbą rzeczywistą dodatią. Obliczyć wartość graicy przy tak wybraej liczbie k. Rozwiązaie: Korzystając ze wzoru a różicę
UWAGI O WZORZE NA MOMENTY ROZKŁADU PRAWDOPODOBIEŃSTWA PÓLYI. Tadeusz Gerstenkorn. 1. Wstęp. 2. Rozkład G. Pólyi
 UWAGI O WZORZE NA MOMENTY ROZKŁADU PRAWDOPODOBIEŃSTWA PÓLYI Tadeusz Gesteko Emeytoway pofeso Uiwesytetu Łódzkiego ISSN 1644-6739 e-issn 2449-9765 DOI: 10.15611/sps.2015.13.09 Steszczeie: Rozkład pawdopodobieństwa
UWAGI O WZORZE NA MOMENTY ROZKŁADU PRAWDOPODOBIEŃSTWA PÓLYI Tadeusz Gesteko Emeytoway pofeso Uiwesytetu Łódzkiego ISSN 1644-6739 e-issn 2449-9765 DOI: 10.15611/sps.2015.13.09 Steszczeie: Rozkład pawdopodobieństwa
Metrologia: miary dokładności. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
METEMATYCZNY MODEL OCENY
 I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
Jarosław Wróblewski Analiza Matematyczna 1A, zima 2012/13. Ciągi.
 Jarosław Wróblewski Aaliza Matematycza 1A, zima 2012/13 Ciągi. Ćwiczeia 5.11.2012: zad. 140-173 Kolokwium r 5, 6.11.2012: materiał z zad. 1-173 Ćwiczeia 12.11.2012: zad. 174-190 13.11.2012: zajęcia czwartkowe
Jarosław Wróblewski Aaliza Matematycza 1A, zima 2012/13 Ciągi. Ćwiczeia 5.11.2012: zad. 140-173 Kolokwium r 5, 6.11.2012: materiał z zad. 1-173 Ćwiczeia 12.11.2012: zad. 174-190 13.11.2012: zajęcia czwartkowe
n liczba lat m liczba okresów kapitalizacji w ciągu roku ile razy doliczane są odsetki do kwoty kapitału
 pst valu watość biŝąca watość jdostki piięŝj lub pzpływów fiasowych (wpływów lub wydatków, któ zostaą zalizowa/otzya w pzyszłych oksach wyaŝoa w dzisijszj sil abywczj jdostk piięŝych. Watość ta jst ijsza
pst valu watość biŝąca watość jdostki piięŝj lub pzpływów fiasowych (wpływów lub wydatków, któ zostaą zalizowa/otzya w pzyszłych oksach wyaŝoa w dzisijszj sil abywczj jdostk piięŝych. Watość ta jst ijsza
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
MECHANIKA BUDOWLI 12
 Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
ROZDZIAŁ 5 WPŁYW SYSTEMU OPODATKOWANIA DOCHODU NA EFEKTYWNOŚĆ PROCESU DECYZYJNEGO
 Agieszka Jakubowska ROZDZIAŁ 5 WPŁYW SYSTEMU OPODATKOWANIA DOCHODU NA EFEKTYWNOŚĆ PROCESU DECYZYJNEGO. Wstęp Skąplikowaie współczesego życia gospodarczego powoduje, iż do sterowaia procesem zarządzaia
Agieszka Jakubowska ROZDZIAŁ 5 WPŁYW SYSTEMU OPODATKOWANIA DOCHODU NA EFEKTYWNOŚĆ PROCESU DECYZYJNEGO. Wstęp Skąplikowaie współczesego życia gospodarczego powoduje, iż do sterowaia procesem zarządzaia
Matematyka Finansowa. Wykład. Maciej Wolny
 Matematyka Fasowa Wykład Macej Woly macej.woly@polsl.pl Ageda Ogazacja zajęć, wpowadzee, podstawowe pojęca. Teoa fukcj peądza w czase. Rozlczea zwązae ze spłatą długów. Ocea opłacalośc westycj. Lteatua.
Matematyka Fasowa Wykład Macej Woly macej.woly@polsl.pl Ageda Ogazacja zajęć, wpowadzee, podstawowe pojęca. Teoa fukcj peądza w czase. Rozlczea zwązae ze spłatą długów. Ocea opłacalośc westycj. Lteatua.
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 1: UWAGI WSTĘPNE. PROCENT SKŁADANY 1. Uwagi wstępne Ryzyko jest związane z niealże każdy rodzaje działalności człowieka: przy planowaniu urlopu ryzyko słabej
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 1: UWAGI WSTĘPNE. PROCENT SKŁADANY 1. Uwagi wstępne Ryzyko jest związane z niealże każdy rodzaje działalności człowieka: przy planowaniu urlopu ryzyko słabej
Rys. 1. Ilustracja modelu. Oddziaływanie grawitacyjne naszych ciał z masą centralną opisywać będą wektory r 1
 6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
Trójparametrowe formowanie charakterystyk promieniowania anten inteligentnych w systemach komórkowych trzeciej i czwartej generacji
 Zakład Zastosowań Techik Łączości lektoiczej (Z ) Tójpaametowe fomowaie chaakteystyk pomieiowaia ate iteligetych w systemach komókowych tzeciej i czwatej geeacji Paca : 35 Waszawa, gudzień 5 Tójpaametowe
Zakład Zastosowań Techik Łączości lektoiczej (Z ) Tójpaametowe fomowaie chaakteystyk pomieiowaia ate iteligetych w systemach komókowych tzeciej i czwatej geeacji Paca : 35 Waszawa, gudzień 5 Tójpaametowe
Składka ubezpieczeniowa
 Przychody zakładów ubezpieczeń Przychody i wydatki zakładów ubezpieczeń Składka ubezpieczeiowa 60-95 % Przychody z lokat 5-15 % Przychody z reasekuracji 5-30 % Wydatki zakładów ubezpieczeń Odszkodowaia
Przychody zakładów ubezpieczeń Przychody i wydatki zakładów ubezpieczeń Składka ubezpieczeiowa 60-95 % Przychody z lokat 5-15 % Przychody z reasekuracji 5-30 % Wydatki zakładów ubezpieczeń Odszkodowaia
Wykład 6. Przestrzenie metryczne ośrodkowe i zupełne. ρ, gdzie r
 Wyład 6 Przestrzeie etrycze ośrodowe i zupełe. Przypoiay, że zbiór azyway przeliczaly, jeśli jest o rówoliczy ze zbiore wszystich liczb aturalych N, a co ajwyżej przeliczaly, jeśli jest o przeliczaly lub
Wyład 6 Przestrzeie etrycze ośrodowe i zupełe. Przypoiay, że zbiór azyway przeliczaly, jeśli jest o rówoliczy ze zbiore wszystich liczb aturalych N, a co ajwyżej przeliczaly, jeśli jest o przeliczaly lub
Parametryzacja rozwiązań układu równań
 Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
0 Rachunek czasu. Informacje pierwotne: początkowa i końcowa data inwestycji.
 0 Rachunek czasu Inforacje pierwotne: początkowa i końcowa data inwestycji. Konwencja: nie naliczay odsetek za początkowy dzień trwania inwestycji, naliczay za końcowy. Liczba dni trwania inwestycji liczba
0 Rachunek czasu Inforacje pierwotne: początkowa i końcowa data inwestycji. Konwencja: nie naliczay odsetek za początkowy dzień trwania inwestycji, naliczay za końcowy. Liczba dni trwania inwestycji liczba
MIERNICTWO WIELKOŚCI ELEKTRYCZNYCH I NIEELEKTRYCZNYCH
 Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
3. Funkcje elementarne
 3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
Jak wybrać kredyt? Waldemar Wyka Instytut Matematyki Politechniki Łódzkiej. 22 listopada 2014
 Waldemar Wyka Instytut Matematyki Politechniki Łódzkiej 22 listopada 2014 Plan prezentacji 1 Powtórzenie 2 3 Plany spłaty długu - stałe raty Plany spłaty długu - stałe raty kapitałowe Plany spłaty długu
Waldemar Wyka Instytut Matematyki Politechniki Łódzkiej 22 listopada 2014 Plan prezentacji 1 Powtórzenie 2 3 Plany spłaty długu - stałe raty Plany spłaty długu - stałe raty kapitałowe Plany spłaty długu
System finansowy gospodarki
 System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
O liczbach naturalnych, których suma równa się iloczynowi
 O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
4. PRZEKŁADNIKI PRĄDOWE I NAPIĘCIOWE
 4. PRZEŁDN PRĄDOWE NPĘOWE 4.. Wstęp 4.. Przekładiki prądowe Przekładikie prądowy prądu zieego azywa się trasforator przezaczoy do zasilaia obwodów prądowych elektryczych przyrządów poiarowych oraz przekaźików.
4. PRZEŁDN PRĄDOWE NPĘOWE 4.. Wstęp 4.. Przekładiki prądowe Przekładikie prądowy prądu zieego azywa się trasforator przezaczoy do zasilaia obwodów prądowych elektryczych przyrządów poiarowych oraz przekaźików.
x 1 2 3 t 1 (x) 2 3 1 o 1 : x 1 2 3 s 3 (x) 2 1 3. Tym samym S(3) = {id 3,o 1,o 2,s 1,s 2,s 3 }. W zbiorze S(n) definiujemy działanie wzorem
 9.1. Izomorfizmy algebr.. Wykład Przykłady: 13) Działaia w grupach często wygodie jest zapisywać w tabelkach Cayleya. Na przykład tabelka działań w grupie Z 5, 5) wygląda astępująco: 5 1 3 1 1 3 1 3 3
9.1. Izomorfizmy algebr.. Wykład Przykłady: 13) Działaia w grupach często wygodie jest zapisywać w tabelkach Cayleya. Na przykład tabelka działań w grupie Z 5, 5) wygląda astępująco: 5 1 3 1 1 3 1 3 3
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Spis treści I. Ilościowe określenia składu roztworów strona II. Obliczenia podczas sporządzania roztworów
 Sps teśc I. Iloścowe okeślena składu oztwoów stona Ułaek wagowy (asowy ocent wagowy (asowy ocent objętoścowy Ułaek olowy 3 ocent olowy 3 Stężene olowe 3 Stężene pocentowe 3 Stężene noalne 4 Stężene olane
Sps teśc I. Iloścowe okeślena składu oztwoów stona Ułaek wagowy (asowy ocent wagowy (asowy ocent objętoścowy Ułaek olowy 3 ocent olowy 3 Stężene olowe 3 Stężene pocentowe 3 Stężene noalne 4 Stężene olane
Novosibirsk, Russia, September 2002
 Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA
 ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
1% wartości transakcji + 60 zł
 Procet.. Wysokość prowizji, którą kliet płaci w pewym biurze maklerskim przy każdej zawieraej trasakcji kupa lub sprzedaży akcji jest uzależioa od wartości trasakcji: Wartość trasakcji do 500 zł od 500.0
Procet.. Wysokość prowizji, którą kliet płaci w pewym biurze maklerskim przy każdej zawieraej trasakcji kupa lub sprzedaży akcji jest uzależioa od wartości trasakcji: Wartość trasakcji do 500 zł od 500.0
Teoria. a k. Wskaźnik sumowania można oznaczać dowolną literą. Mamy np. a j = a i =
 Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Opracowała: mgr inż. Ewelina Nowak
 Mateiały dydaktyczne na zajęcia wyównawcze z cheii dla studentów piewszego oku kieunku zaawianego Inżynieia Śodowiska w aach pojektu Ea inżyniea pewna lokata na pzyszłość Opacowała: g inż. Ewelina Nowak
Mateiały dydaktyczne na zajęcia wyównawcze z cheii dla studentów piewszego oku kieunku zaawianego Inżynieia Śodowiska w aach pojektu Ea inżyniea pewna lokata na pzyszłość Opacowała: g inż. Ewelina Nowak
Współpraca przedsiębiorstwa z bankiem dr Robert Zajkowski Katedra Bankowości UMCS w Lublinie
 Współpaca pzedsębostwa z bake d Robet Zajkowsk ateda Bakowośc UMC w Luble www.obet.zajkowsk.ucs.lubl.pl obet.zajkowsk@ucs.lubl.pl Gaść foacj [] osultacje: czwatek :00-4:0 pok. 707 Pzeoszee osoba za osobę
Współpaca pzedsębostwa z bake d Robet Zajkowsk ateda Bakowośc UMC w Luble www.obet.zajkowsk.ucs.lubl.pl obet.zajkowsk@ucs.lubl.pl Gaść foacj [] osultacje: czwatek :00-4:0 pok. 707 Pzeoszee osoba za osobę
4.5. PODSTAWOWE OBLICZENIA HAŁASOWE 4.5.1. WPROWADZENIE
 4.5. PODTAWOWE OBCZENA HAŁAOWE 4.5.. WPROWADZENE Z dotychczasowych ozważań wiemy już dużo w zakesie oisu, watościowaia i omiau hałasu w zemyśle. Wato więc tę wiedzę odsumować w jedym zwatym ukcie, co umożliwi
4.5. PODTAWOWE OBCZENA HAŁAOWE 4.5.. WPROWADZENE Z dotychczasowych ozważań wiemy już dużo w zakesie oisu, watościowaia i omiau hałasu w zemyśle. Wato więc tę wiedzę odsumować w jedym zwatym ukcie, co umożliwi
Strategie finansowe przedsiębiorstwa
 Strategie fiasowe przedsiębiorstwa Grzegorz Michalski 2 Różice między fiasami a rachukowością Rachukowość to opowiadaie [sprawozdaie] JAK BYŁO i JAK JEST Fiase zajmują się Obecą oceą tego co BĘDZIE w PRZYSZŁOŚCI
Strategie fiasowe przedsiębiorstwa Grzegorz Michalski 2 Różice między fiasami a rachukowością Rachukowość to opowiadaie [sprawozdaie] JAK BYŁO i JAK JEST Fiase zajmują się Obecą oceą tego co BĘDZIE w PRZYSZŁOŚCI
Materiał powtarzany w II etapie. II 4. Ciągi
 Materiał powtarzay w II etapie II. Ciągi 3 1, dla parzystych 1. Wyzacz sześć początkowych wyrazów ciągu a = { +1, dla ieparzystych. Które wyrazy ciągu a = są rówe 1? 3. Pomiędzy liczby 7 i 5 wstaw 5 liczb
Materiał powtarzay w II etapie II. Ciągi 3 1, dla parzystych 1. Wyzacz sześć początkowych wyrazów ciągu a = { +1, dla ieparzystych. Które wyrazy ciągu a = są rówe 1? 3. Pomiędzy liczby 7 i 5 wstaw 5 liczb
ANALIZA DRGAŃ POPRZECZNYCH PŁYTY PIERŚCIENIOWEJ O ZŁOŻONYM KSZTAŁCIE Z UWZGLĘDNIENIEM WŁASNOŚCI CYKLICZNEJ SYMETRII UKŁADU
 Dr iż. Staisław NOGA oga@prz.edu.pl Politechika Rzeszowska ANALIZA DRGAŃ POPRZECZNYCH PŁYTY PIERŚCIENIOWEJ O ZŁOŻONYM KSZTAŁCIE Z UWZGLĘDNIENIEM WŁASNOŚCI CYKLICZNEJ SYMETRII UKŁADU Streszczeie: W publikacji
Dr iż. Staisław NOGA oga@prz.edu.pl Politechika Rzeszowska ANALIZA DRGAŃ POPRZECZNYCH PŁYTY PIERŚCIENIOWEJ O ZŁOŻONYM KSZTAŁCIE Z UWZGLĘDNIENIEM WŁASNOŚCI CYKLICZNEJ SYMETRII UKŁADU Streszczeie: W publikacji
Energia kinetyczna i praca. Energia potencjalna
 negia kinetyczna i paca. negia potencjalna Wykład 4 Wocław Univesity of Technology 1 NRGIA KINTYCZNA I PRACA 5.XI.011 Paca Kto wykonał większą pacę? Hossein Rezazadeh Olimpiada w Atenach 004 WR Podzut
negia kinetyczna i paca. negia potencjalna Wykład 4 Wocław Univesity of Technology 1 NRGIA KINTYCZNA I PRACA 5.XI.011 Paca Kto wykonał większą pacę? Hossein Rezazadeh Olimpiada w Atenach 004 WR Podzut
PRACA MOC ENERGIA. Z uwagi na to, że praca jest iloczynem skalarnym jej wartość zależy również od kąta pomiędzy siłą F a przemieszczeniem r
 PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
Twierdzenie 15.3 (o postaci elementów rozszerzenia ciała o zbiór). Niech F będzie ciałem oraz A F pewnym zbiorem. Niech L<F.
 15. Wyład 15: Podciała, podciała geerowae przez zbiór, rozszerzeia ciał. Charaterystya pierścieia i ciała, ciała proste i lasyfiacja ciał prostych. 15.1. Podciała, podciała geerowae przez zbiór, rozszerzeia
15. Wyład 15: Podciała, podciała geerowae przez zbiór, rozszerzeia ciał. Charaterystya pierścieia i ciała, ciała proste i lasyfiacja ciał prostych. 15.1. Podciała, podciała geerowae przez zbiór, rozszerzeia
MONITORING STACJI FOTOWOLTAICZNYCH W ŚWIETLE NORM EUROPEJSKICH
 51 Aleksande Zaemba *, Tadeusz Rodziewicz **, Bogdan Gaca ** i Maia Wacławek ** * Kateda Elektotechniki Politechnika Częstochowska al. Amii Kajowej 17, 42-200 Częstochowa e-mail: zaemba@el.pcz.czest.pl
51 Aleksande Zaemba *, Tadeusz Rodziewicz **, Bogdan Gaca ** i Maia Wacławek ** * Kateda Elektotechniki Politechnika Częstochowska al. Amii Kajowej 17, 42-200 Częstochowa e-mail: zaemba@el.pcz.czest.pl
40:5. 40:5 = 500000υ5 5p 40, 40:5 = 500000 5p 40.
 Portfele polis Poieważ składka jest ustalaa jako wartość oczekiwaa rzeczywistego, losowego kosztu ubezpieczeia, więc jest tym bliższa średiej wydatków im większa jest liczba ubezpieczoych Polisy grupuje
Portfele polis Poieważ składka jest ustalaa jako wartość oczekiwaa rzeczywistego, losowego kosztu ubezpieczeia, więc jest tym bliższa średiej wydatków im większa jest liczba ubezpieczoych Polisy grupuje
