WARTOŚĆ PIENIĄDZA W CZASIE
|
|
|
- Monika Wojciechowska
- 8 lat temu
- Przeglądów:
Transkrypt
1 WARTOŚĆ PIENIĄDZA W CZASIE Czyiki wpływające a zmiaę watości pieiądza w czasie:. Spadek siły abywczej. 2. Możliwość iwestowaia. 3. Występowaie yzyka. 4. Pefeowaie bieżącej kosumpcji pzez człowieka. Watość pieiądza w czasie odzwieciedlaa jest pzez stopę pocetową. Pzy okeślaiu (i podawaiu) stopy pocetowej istote są pewe kwestie fomalo-metodycze aspekty okeślaia stopy pocetowej: Stopa pocetowa w skali okesu - stopa pocetowa podawaa jest zwykle w skali oku. Stopa pocetowa dotycząca okesu - stopa pocetowa zawsze dotyczy jakiegoś okesu. Jest o okeśloy pzez hoyzot działalości iwestycyjej lub działalości fiasowej.
2 Kapitalizacja i eiwestycja Kapitalizacja (compoudig). ozacza, że dochody pojawiające się w takcie okesu iwestowaia są kapitalizowae (tz. dodawae do kapitału ). Zjawisko eiwestowaia to poowe iwestowaie dochodów z iwestycji. Watość pzyszła i watość bieżąca Watość pzyszła (Futue Value) jest to watość otzymywaa lub płacoa w pzyszłości, lub watość pieięża ozpatywaa z puktu widzeia pewego mometu w pzyszłości. Watość bieżąca (Peset Value) jest to watość otzymywaa lub płacoa dziś, lub watość pieięża ozpatywaa z puktu widzeia dia dzisiejszego. Cztey powiązae ze sobą wielkości zmieej watości pieiądza: - watość pzyszła, ozaczoa pzez FV; - watość bieżąca, ozaczoa pzez ; - liczba lat (ogólie: liczba okesów), ozaczoa pzez ; - stopa pocetowa, ozaczoa pzez. 2
3 Cztey podstawowe schematy pzepływów pieiężych: - pojedyczy pzepływ pieięży; - eta płata z dołu (iaczej: eta zwykła, lub po postu eta); - eta płata z góy; - wiele egulaych pzepływów pieiężych. Schemat Pojedyczy pzepływ pieięży. Rysuek 3.A Rysuek 3.B 3
4 Schemat 2 Reta płata z dołu. Rysuek 3.2A Rysuek 3.2B Rysuek 3.3A Rysuek 3.3B
5 Schemat 3 Reta płata z góy. Rysuek 3.4A Rysuek 3.4B Rysuek 3.5A Rysuek 3.5B
6 Schemat 4 Wiele egulaych pzepływów pieiężych. Rysuek 3.6A Rysuek 3.6B Rysuek 3.7A Rysuek 3.7B
7 Zagadieie watości pzyszłej Wzó Watość pzyszła kapitalizacja posta (okesowa) FV ( + ) (3.) Wzó 2 Watość pzyszła kapitalizacja ocza FV ( + ) (3.2) Wzó 3 Watość pzyszła kapitalizacja częstsza iż az w oku FV ( + / m) m (3.3) gdzie: m ozacza liczbę kapitalizacji w ciągu oku, p. m2 w wypadku kapitalizacji półoczej. Wzó 4 Watość pzyszła kapitalizacja ciągła FV e (3.4) gdzie: e podstawa logaytmu atualego. 7
8 Z pzedstawioych wzoów wyikają astępujące właściwości (wszystkie ceteis paibus): - im wyższa stopa pocetowa, tym wyższa watość pzyszła; - im większa liczba okesów, tym wyższa watość pzyszła; - im wyższa watość bieżąca, tym wyższa watość pzyszła; - im częstsza kapitalizacja, tym wyższa watość pzyszła Rysuek 3.8. Watość pzyszła jako fukcja liczby okesów Rysuek 8 FV A B C D E
9 Pzykład. Kwota 000 złotych jest zaiwestowaa w depozyt bakowy a okes dwóch lat. Opocetowaie depozytu wyosi 2%. Watość pzyszła zależy od odzaju kapitalizacji. Wyosi oa: - pzy kapitalizacji postej (wzó (3.)): FV 000 ( + 2 0,2) pzy kapitalizacji oczej (wzó (3.2)): FV 000( + 0,2) 2 254,40 - pzy kapitalizacji kwatalej (wzó (3.3)): FV 000( + 0,2 / 4) ,77 - pzy kapitalizacji ciągłej (wzó (3.4)): FV 000e 2 0,2 27,25 9
10 Pzykład. Rozpatzymy podobą sytuację, jak w popzedim pzykładzie, ale teaz iwestycja twa kócej iż ok, miaowicie pół oku. Pozostałe watości, tz. zaiwestowaa kwota 000 złotych i opocetowaie depozytu 2%, pozostają te same. Watość pzyszła wyosi: - pzy kapitalizacji postej, półoczej (wzó (3.)): FV 000 ( + 0,5 0,2) pzy kapitalizacji kwatalej (wzó (3.3)): FV 000( + 0,2 / 4) 0, ,90 - pzy kapitalizacji ciągłej (wzó (3.4)): FV 000e 0,5 0,2 06,84 0
11 s N gdzie: s liczba di twaia iwestycji; N liczba di w oku. Cztey możliwe kowecje: - Actual/360, - actual/365; - 30/360; - 30/365. Pzykład. Iwestycja w depozyt bakowy ozpoczęła się 5 maca, zaś zakończyła 25 czewca tego samego oku. Zaiwestowaa kwota to 000 złotych, zaś opocetowaie depozytu 2%. Zauważmy, że liczba di twaia iwestycji wyosi: - według kowecji actual : 02 di (6 w macu, 30 w kwietiu, 3 w maju i 25 w czewcu); - według kowecji 30 : 00 di (3 miesiące po 30 di od 5 maca do 5 czewca plus 0 di od 6 czewca do 25 czewca).
12 Tabela pzedstawia wyiki w pzypadku czteech możliwych kowecji. Nazwa kowecji Watość Watość pzyszła Actual/360 02/360 0, ,00 Actual /365 0, ,53 30/360 00/360 0, ,33 30/365 00/365 0, ,88 Wzó 5 Watość pzyszła ety płatej z dołu FV FVA PMT ( + ) - (3.5) PMT wielkość ety. Wzó 6 Watość pzyszła ety płatej z góy FV FVA PMT ( + ) ( + ) - (3.6) 2
13 Z powyższych wzoów wyikają astępujące właściwości (wszystkie ceteis paibus): - im wyższa stopa pocetowa, tym wyższa watość pzyszła ety; - im wyższa watość ety, tym wyższa watość pzyszła ety; - im większa liczba et, tym wyższa watość pzyszła ety. Pzykład. Iwestycja polega a systematyczym wpłacaiu pzez 2 lata co miesiąc kwoty 00 złotych a depozyt bakowy. Opocetowaie depozytu wyosi 2%, kapitalizacja jest miesięcza. Watość depozytu wyosi: - w pzypadku ety płatej z dołu (wzó (3.5)): FV 00 ( + 0,0) 0, ,35 - w pzypadku ety płatej z góy (wzó (3.6)): FV 00( + 0,0) ( + 0,0) 0, ,32 3
14 Wzó 7 Watość pzyszła egulaych pzepływów pieiężych FV å t C t ( + ) -t (3.7) gdzie: C t - pzepływ pieięży występujący w okesie t. Pzykład. Iwestycja polega a wpłacaiu a depozyt bakowy kilku kwot co tzy miesiące (piewsza wpłata ma miejsce za tzy miesiące). Kapitalizacja jest kwatala, zaś opocetowaie depozytu 8% (a zatem w skali kwatalej wyosi 2%). Wpłacae są kolejo astępujące kwoty: 00 zł, 300 zł, 200 zł, 250 zł. Wyzaczymy watość po oku: FV 00(,02) (,02) (,02) ,24 Z powyższej kwoty 850 złotych pochodzi z wpłat, zaś 22,24 złote to odsetki. 4
15 Efektywa stopa pocetowa jest to stopa uwzględiająca kapitalizację. ef - efektywa stopa pocetowa. Wzó 8 Efektywa stopa pocetowa kapitalizacja częstsza iż az w oku ef m ( + / m) - (3.8) Wzó 9 Efektywa stopa pocetowa kapitalizacja ciągła ef e - (3.9) Pzykład. Wyzaczymy efektywe stopy pocetowe dla tzech pzypadków stóp omialych: 20%, 8% i 2% oaz dla pzypadków kapitalizacji oczej, półoczej, kwatalej, miesięczej, dzieej (zakładając 365 di w oku) i ciągłej. Zastosowaie mają wzoy (3.8) i (3.9). Wyiki pzedstawia tabela 2. Rodzaj kapitalizacji 20% 8% 2% Rocza 20,00% 8,00% 2,00% Półocza 2,00% 8,6% 2,0% Kwatala 2,55% 8,24% 2,05% Miesięcza 2,94% 8,30% 2,08% Dziea 22,3% 8,328% 2,02% Ciągła 22,4% 8,329% 2,02% 5
16 Zagadieie watości bieżącej Wzó 0 Watość bieżąca kapitalizacja posta (okesowa) FV /( + ) (3.0) Wzó Watość bieżąca kapitalizacja ocza FV /( + ) (3.) Wzó 2 Watość bieżąca kapitalizacja częstsza iż az w oku FV /( + / m) m (3.2) Wzó 3 Watość bieżąca kapitalizacja ciągła FVe - (3.3) Z pzedstawioych wzoów wyikają astępujące właściwości (wszystkie ceteis paibus): - im wyższa stopa pocetowa, tym iższa watość bieżąca; - im większa liczba okesów, tym iższa watość bieżąca; - im wyższa watość pzyszła, tym wyższa watość bieżąca; - im częstsza kapitalizacja, tym iższa watość bieżąca. 6
17 Pzykład. Rozważaa jest iwestycja, któa za dwa lata daje watość ówą złotych. Należy wyceić, ile ta iwestycja jest wata dzisiaj. Stopa pocetowa, będąca wymagaą stopą zwotu, jest ówa 0%. Kolejo otzymujemy: - pzy zastosowaiu kapitalizacji postej (wzó (3.0)): 0000 /( + 2 0,) 8333,33 - pzy zastosowaiu kapitalizacji oczej (wzó (3.)): 0000 /( + 0,) ,46 - pzy zastosowaiu kapitalizacji miesięczej (wzó (3.2)): 0000 /( + 0,/2) ,0 - pzy zastosowaiu kapitalizacji ciągłej (wzó (3.3)): 0000e -2 0, 887,3 7
18 Kowecje pzyjmowaia okesu kapitalizacji: - kapitalizacja zgoda z okesem iwestowaia (czyli kapitalizacja posta); - kapitalizacja zgoda z okesem otzymywaia pzepływów pieiężych; - kapitalizacja ocza (często to założeie pzyjmuje się p. w aalizie ieuchomości); - kapitalizacja ciągła (pzyjmuje się ją w teoii fiasów). Wzó 4 Watość bieżąca ety płatej z dołu A PMT - ( + ) (3.4) Wzó 5 Watość bieżąca ety płatej z góy A PMT ( + - ) ( + ) (3.5) 8
19 Z powyższych wzoów wyikają astępujące właściwości (wszystkie ceteis paibus): - im wyższa stopa pocetowa, tym iższa watość bieżąca ety; - im wyższa watość ety, tym wyższa watość bieżąca ety; - im większa liczba et, tym wyższa watość bieżąca ety. Pzykład. Istotą aalizowaej iwestycji jest otzymywaie egulaie stałej kwoty ówej 000 złotych, co miesiąc pzez tzy lata. Stopa pocetowa, któa jest wymagaą stopa zwotu iwestoa, wyosi 2%. Obliczymy watość tej iwestycji dziś (jest to watość bieżąca ety). Watość iwestycji wyosi: - w pzypadku ety płatej z dołu (wzó (3.4)): ( + 0,0) 0, ,39 - w pzypadku ety płatej z góy (wzó (3.5)): 000( + - 0,0) ( + 0,0) 0, ,82 9
20 Wzó 6 Watość bieżąca ety wieczystej P PMT (3.6) Z powyższego wzou wyikają astępujące właściwości (ceteis paibus): - im wyższa stopa pocetowa, tym iższa watość bieżąca ety wieczystej; - im wyższa watość ety, tym wyższa watość bieżąca ety wieczystej. Pzykład. Rozważaa jest iwestycja polegająca a otzymywaiu beztemiowo kwoty 000 złotych a koiec każdego miesiąca. Wymagaa stopa zwotu iwestoa wyosi 2%. Watość iwestycji wyosi: 000 0,
21 Wzó 7 Watość bieżąca egulaych pzepływów pieiężych å t Ct ( ) + t (3.7) Pzykład. W wyiku iwestycji spodziewamy się otzymać tzy pzepływy pieięże: po oku: 2000 złotych, po dwóch latach: 2500 złotych, po tzech latach: 2800 złotych. Wymagaa stopa zwotu iwestoa wyosi 8%. Watość tej iwestycji dzisiaj wyosi (po zastosowaiu wzou (3.7)): 2000 (,08) (,08) 2800 (,08) ,93 2
22 Wzó 8 Watość bieżąca ieskończoej liczby pzepływów pieiężych osących w stałym tempie PMT - g (3.8) gdzie: PMT - piewsza płatość; g stopa (tempo) wzostu płatości. Pzy tym fomalie ależy założyć, że >g. Pzykład. Rozpatzymy pzykład podobej iwestycji, jak w pzykładzie dotyczącym ety wieczystej. Iwestycja polega a otzymywaiu beztemiowo kwoty co miesiąc. Pzy tym piewsza kwota (otzymaa za miesiąc) wyosi 00 złotych, a każda astępa ośie w stosuku do popzediej o 0,5%. Wymagaa stopa zwotu iwestoa wyosi 2%. Obliczymy watość tej iwestycji dziś. Watość iwestycji wyosi: 000 0,0-0,
23 Watość bieżąca etto - N (Net Peset Value). Wzó 9 Watość bieżąca etto N Ct C å t - I0 t ( + ) 0 ( + ) å t t t (3.9) gdzie: I 0 - tzw. akład początkowy Pzykład. Tzy pzepływy pieięże: po oku: 2000 złotych, po dwóch latach: 2500 złotych, po tzech latach: 2800 złotych. Nakład początkowy 6000 złotych. Tzy óże wymagae stopy zwotu iwestoa: 6%, 8% i 0%. Watość bieżąca etto wyosi (po zastosowaiu wzou (9)): - w pzypadku wymagaej stopy zwotu ówej 6%: N 2000 (,06) (,06) (,06) 462,7 - w pzypadku wymagaej stopy zwotu ówej 8%: N 2000 (,08) (,08) (,08) 27,93 23
24 - w pzypadku wymagaej stopy zwotu ówej 0%: N 2000 (,) , (,) (,) Zagadieie wielkości ety Wzó 20 Wielkość ety płatej z dołu, gdy zaa jest watość pzyszła PMT FV ( + ) - (3.20) Wzó 2 Wielkość ety płatej z góy, gdy zaa jest watość pzyszła PMT + ( + ) FV - (3.2) 24
25 Pzykład. Iwesto plauje systematyczie wpłacać stałą kwotę każdego miesiąca a depozyt bakowy, tak, aby po oku uzyskać 0000 złotych. Opocetowaie depozytu wyosi 2%, kapitalizacja jest miesięcza. Wielkość ety wyosi: - w pzypadku ety płatej z dołu (wzó (3.20)): PMT 0, ( + 0,0) - 788,49 - w pzypadku ety płatej z góy (wzó (3.2)): PMT 0, ( + 0,0) ( + 0,0) - 780,68 25
26 Wzó 22 Wielkość ety płatej z dołu, gdy zaa jest watość bieżąca PMT - ( + ) (3.22) Wzó 23 Wielkość ety płatej z góy, gdy zaa jest watość bieżąca PMT + - ( + ) (3.23) 26
27 Pzykład. Zaciągięty został kedyt w wysokości złotych. Opocetowaie kedytu wyosi 2%, kapitalizacja jest miesięcza. Kedyt ma być spłacoy w ciągu dwóch lat, w ówych miesięczych atach, z któych każda zawiea zwot kedytu i odsetki. Otzymujemy: - w pzypadku ety płatej z dołu (wzó (3.22)): PMT ,0 ( + 0,0) ,35 - w pzypadku ety płatej z góy (wzó (3.23)): PMT ( + 0,0) - 0,0 ( + 0,0) ,74 27
28 Zagadieie liczby okesów Wzó 24 Liczba lat kapitalizacja ocza l FV - l l( + ) (3.24) Wzó 25 Liczba lat kapitalizacja ciągła l FV - l (3.25) 28
29 Pzykład. Pewa iwestycja, w któej watość bieżąca (początkowa) wyosiła 2000 złotych, a końcu była wata 2500 złotych (watość pzyszła). Wiadomo, że stopa pocetowa wyosiła 5%. Okeślimy liczbę lat twaia tej iwestycji. Otzymujemy: - pzy założeiu kapitalizacji oczej (wzó (3.24)): l l 2000 l( + 0,05) 4,573 - pzy założeiu kapitalizacji ciągłej (wzó (3.25)): l l ,05 4,463 FV 2 29
30 Wzó 26 Liczba lat do podwojeia kapitału kapitalizacja ocza 0,6935 l( + ) (3.26) Wzó 27 Liczba lat do podwojeia kapitału kapitalizacja ocza eguła 72» 0, (3.27) Wzó 28 Liczba lat do podwojeia kapitału kapitalizacja ocza eguła 69» 0,35 + 0,69 0, (3.28) Wzó 29 Liczba lat do podwojeia kapitału kapitalizacja ciągła 0,6935 (3.29) 30
31 Pzykład. Wyzaczymy liczbę lat do podwojeia kapitału stosując 4 wzoy, dwa dokłade (wzoy (3.26) i (3.29)) oaz dwa pzybliżoe (wzoy (3.27) i (3.28)), w odiesieiu do kilku stóp pocetowych. Wyiki pzedstawia tabela 3. Stosoway wzó 20% 8% 2% Dokłady, kapitalizacja 3,466 8,664 34,658 ciągła Dokłady, kapitalizacja 3,802 9,007 35,003 ocza Reguła 69 3,800 8,975 34,850 Reguła 72 3,600 9,000 36,000 3
32 Zagadieie watości pzyszłej i bieżącej zmiea stopa pocetowa Wzó 30 Watość pzyszła egulaych pzepływów pieiężych zmiea stopa pocetowa FV gdzie: å t C t ( + t + )( + t + 2)...( + ) (3.30) i - stopa pocetowa w okesie i-tym, pzy czym wyażoa jest oa w skali okesu występowaia płatości. Pzykład. Iwestycja polega a wpłacaiu a depozyt bakowy kilku kwot co tzy miesiące (piewsza wpłata ma miejsce za tzy miesiące). Kapitalizacja jest kwatala, zaś opocetowaie depozytu zmieia się co kwatał i w kolejych kwatałach wyosi: 8%, 8,2%, 8,4%, 7,8%. Wpłacae są kolejo astępujące kwoty: 00 zł, 300 zł, 200 zł, 250 zł. Wyzaczymy watość pzyszłą po oku, czyli po wpłaceiu ostatiej kwoty. Po zastosowaiu wzou (3.30) otzymujemy: FV 00(,0205)(,02)(,095) + 300(,02)(,095) + 200(,095) ,49 32
33 Wzó 3 Watość bieżąca egulaych pzepływów pieiężych zmiea stopa pocetowa Ct ( + )...( + å t t ) (3.3) Pzykład. W wyiku iwestycji spodziewamy się otzymać tzy pzepływy pieięże: po oku 2000 złotych, po dwóch latach 2500 złotych, po tzech latach 2800 złotych. Wymagaa stopa zwotu jest zmiea i w kolejych latach wyosi: 8%, 8,5%, 9%. Watość tej iwestycji dzisiaj wyosi (po zastosowaiu wzou (3.3)): 2000 (,08) (,08)(,085)(,09) 2500 (,08)(,085) + 677,5 33
34 Stopa pocetowa i stopa zwotu wpowadzeie Stopa zwotu (ate of etu) okeśla (pocetowo) dochód uzyskay w wyiku iwestycji. Stopę zwotu (dochodu) moża okeślić jako iloaz uzyskaego dochodu do zaiwestowaego kapitału. Stopa zwotu skończoy okes iwestycji Pzypadek A. Stopy zwotu bak pzepływów pieiężych w okesie twaia iwestycji. Wzó 32 Posta stopa zwotu æ ç è FV ö - ø (3.32) Wzó 33 Efektywa stopa zwotu æ ç è FV ö ø / - (3.33) 34
35 Wzó 34 Logaytmicza stopa zwotu - ( l FV l ) (3.34) elacja między logaytmiczą stopą zwotu a efektywą stopą zwotu: l l( + e) gdzie, dla ozóżieia: l logaytmicza stopa zwotu; e efektywa stopa zwotu. 35
36 Pzykład. Rozpatzymy dwuletią iwestycję. Zaiwestowaa kwota wyosiła 0000 złotych i dała w efekcie po dwóch latach watość końcową ówą 2000 złotych. Obliczymy stopę zwotu tej iwestycji. Podstawiając do wzoów (3.32)-(3.34) otzymujemy watości stóp zwotu: - posta stopa zwotu: 2 æ2000 ç è0000 ö - ø 0% - efektywa stopa zwotu: æ2000 ö ç è0000 ø / 2-9,55% - logaytmicza stopa zwotu: 2 ( l l0000) 9,2% 36
37 Pzykład. Teaz z kolei ozpatzymy półoczą iwestycję. Zaiwestowaa kwota wyosiła 0000 złotych i dała w efekcie watość końcową ówą 0800 złotych. Obliczymy stopę zwotu tej iwestycji. Podstawiając do wzoów (3.32)-(3.34) otzymujemy: - posta stopa zwotu: 0,5 æ0800 ç è0000 ö - ø 6% - efektywa stopa zwotu: æ0800 ö ç è0000 ø / 0,5-6,64% - logaytmicza stopa zwotu: 0,5 ( l l0000) 5,39% 37
38 Pzykład. Iwestycja została pzepowadzoa między 0 maja a 25 lipca. Zaiwestowaa kwota wyosiła 000 złotych i dała w efekcie watość końcową ówą 020 złotych, co ozacza powiększeie kapitału początkowego w ciągu tego okesu o 2%. Obliczymy stopę zwotu pzy zastosowaiu tzech sposobów jej obliczaia i czteech możliwych kowecji okeślaia di. Zauważmy, że: - pzy zastosowaiu kowecji actual liczba di twaia iwestycji wyosi 76; - pzy zastosowaiu kowecji 30 liczba di twaia iwestycji wyosi 75. Wyiki pzedstawia tabela 4. Tabela 4. Stopy zwotu (w %) pzy zastosowaiu óżych sposobów liczeia. Posta Efektywa Logaytmicza Actual/365 9,605 9,977 9,50 Actual/360 9,474 9,834 9,380 30/365 9,733 0,7 9,637 30/360 9,600 9,972 9,505 38
39 Pzypadek A2. Stopy zwotu występujące pzepływy pieięże w okesie twaia iwestycji. Wzó 35 Wewętza stopa zwotu (okes kapitalizacji zgody z okesem otzymywaia pzepływów) å t C ( + IRR) t t I 0 (3.35) lub ówoważie (jeśli ozaczymy akład początkowy jako pzepływ pieięży w okesie zeowym): å t 0 C ( + IRR) t t 0 (3.35a) 39
40 Wzó 36 Wewętza stopa zwotu (kapitalizacja ciągła) å t C e t -t IRR I 0 (3.36) lub ówoważie (jeśli ozaczymy akład początkowy jako pzepływ pieięży w okesie zeowym): å t 0 C e t -t IRR 0 (3.36a) Moża dowieść, że między obu wesjami wewętzej stopy zwotu zachodzi astępująca elacja: IRRc l( + IRR) gdzie, dla odóżieia, IRRc ozacza wewętzą stopę zwotu wyażoą wzoem (3.36). 40
41 Okazuje się, że po pzekształceiu wzou (3.35) otzymujemy: å t -t C t ( + IRR) I0( + IRR) Upaszczając ieco otację, możemy zapisać: FV ( + IRR) czyli: IRR æ ç è FV ö ø / - 4
42 Pzykład. Iwestycja tzyletia. Nakład początkowy 000 złotych, zaś pzepływy pieięże a zakończeie każdego z kolejych tzech lat wyoszą odpowiedio: 200, 400 i 700 złotych. Wyzaczymy wewętzą stopę zwotu. Wzó (3.35): IRR ( + IRR) ( + IRR) Za pomocą kalkulatoa fiasowego otzymujemy: IRR,79% Dla zilustowaia tego faktu zauważmy, że: - eiwestując pzepływy pieięże po stopie IRR, otzymujemy watość pzyszłą (po 3 latach): 200( + 0,79) ( + 0,79) iwestując akład początkowy po stopie IRR, otzymujemy watość pzyszłą (po 3 latach): 000( + 0,79)
43 Teaz z kolei wyzaczymy wewętzą stopę zwotu pzy założeiu kapitalizacji ciągłej. Po podstawieiu do wzou (3.36) otzymujemy: 200e + 400e + 700e -IRR -2 IRR -3 IRR 000 Kozystając bezpośedio z elacji między obu wesjami wewętzej stopy zwotu otzymujemy (wato spawdzić, że ta watość jest jedocześie ozwiązaiem powyższego ówaia): IRR,5% Występują tutaj astępujące pawidłowości: - jeśli stopa eiwestowaia jest ówa IRR, wtedy zealizowaa stopa zwotu ówa jest IRR; - jeśli stopa eiwestowaia jest wyższa iż IRR, wtedy zealizowaa stopa zwotu jest wyższa iż IRR; - jeśli stopa eiwestowaia jest iższa iż IRR, wtedy zealizowaa stopa zwotu jest iższa iż IRR. 43
44 Wzó (3.35) okeślający wewętzą stopę zwotu: å t -t C t ( + IRR) I0( + IRR) Wzó 37 Zewętza stopa zwotu (okes kapitalizacji zgody z okesem otzymywaia pzepływów) ERR æ ç ç ç ç è / -t ö Ct ( + ) t - å I 0 ø (3.37) Wzó 38 Zewętza stopa zwotu (kapitalizacja ciągła) ERR æ æ çlçåcte è è t ( -t ) ö - ø l I 0 ö ø (3.38) 44
45 Pzykład. Rozważamy tę samą iwestycję, co w popzedim pzykładzie jest to iwestycja tzyletia. Nakład początkowy wyosi 000 złotych, zaś pzepływy pieięże a zakończeie każdego z kolejych tzech lat wyoszą odpowiedio: 200, 400 i 700 złotych. Wewętza stopa zwotu wyzaczoa upzedio wyosi,79%. Po podstawieiu do wzou (3.37) otzymujemy: ERR 2 æ 200(,) + 400(,) + ç è ö ø /3 -,39% Dla poówaia podamy jeszcze dwie ie watości zewętzej stopy zwotu: - gdy stopa eiwestowaia wyosi 0% (bak eiwestowaia), wtedy ERR 9,4%; - gdy stopa eiwestowaia wyosi 20% (zaczie więcej iż IRR), wtedy ERR 3,65%. 45
46 Stopa zwotu ieskończoy okes iwestycji Wzó 39 Stopa zwotu ieskończoy okes, eta wieczysta PMT (3.39) Wzó 40 Stopa zwotu ieskończoy okes, pzepływy osące w stałym tempie PMT + g (3.40) 46
47 Pzykład. Dwie iwestycje o ieskończoym okesie twaia. Nakład początkowy 000 zł. Iwestycja A o stałych pzepływach pieiężych - 00 złotych co ok, zaś iwestycja B o piewszym pzepływie 00 złotych za ok, ale w każdym astępym oku pzepływy wzastają o 4%. Wyzaczymy stopy zwotu: - dla iwestycji A po podstawieiu do wzou (3.39) otzymujemy: % - dla iwestycji B po podstawieiu do wzou (3.40) otzymujemy: ,04 4% Moża wykazać, iż musi występować astępująca elacja: PMT PMT + g Wyika z tego, że jeśli w iwestycji B z powyższego pzykładu pozostawimy te same dae, to iwestycja A pzy akładzie początkowym ówym 000 złotych musiałaby dawać efekt w postaci ety wieczystej ówej: PMT ,
48 . Kocepcja stopy pocetowej (ozumiaej zazwyczaj jako stopa zwotu) jest umowa, zależy od pewych założeń, w szczególości: - pzyjętego umowie okesu iwestycji (skończoy lub ieskończoy); - pzyjętej stuktuy pzepływów pieiężych; - pzyjętego umowie okesu kapitalizacji; - pzyjętej umowie stopy eiwestowaia; - pzyjętych kowecji okeślaia liczby di w oku i w okesie twaia iwestycji. 2. Najczęściej stosowae w paktyce są efektywa stopa zwotu, posta stopa zwotu i stadadowa wesja wewętzej stopy zwotu. 3. W sytuacji kótkich hoyzotów iwestowaia, ajczęściej stosowaa jest posta stopa zwotu. 4. Pawidłowe poówaie stóp zwotu z óżych iwestycji ma miejsce jedyie wtedy, gdy te stopy wyzaczae są z zastosowaiem tego samego sposobu.. 5. W pzypadku typowych odzajów iwestycji istieją uzgodioe zwyczaje stosowae a yku, okeślające odzaj stosowaej stopy zwotu. 48
ELEMENTY MATEMATYKI FINANSOWEJ. Wprowadzenie
 ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
500 1,1. b) jeŝeli w kolejnych latach stopy procentowe wynoszą odpowiednio 10%, 9% i 8%, wówczas wartość obecna jest równa: - 1 -
 Zdyskotowae pzepływy pieięŝe - Pzepływy pieięŝe płatości ozłoŝoe w czasie - Pzepływy występujące w kilku óŝych okesach ie są poówywale z uwagi a zmiaę watość pieiądza w czasie - śeby poówywać pzepływy
Zdyskotowae pzepływy pieięŝe - Pzepływy pieięŝe płatości ozłoŝoe w czasie - Pzepływy występujące w kilku óŝych okesach ie są poówywale z uwagi a zmiaę watość pieiądza w czasie - śeby poówywać pzepływy
Co wpływa na zmianę wartości pieniądza? WARTOŚĆ PIENIĄDZA W CZASIE. dr Adam Nosowski
 Fiase osobiste, ed. E. BogackaKisiel, PWN 202 ANALITYKA GOSPODARCZA d Ada Nosowski WARTOŚĆ PIENIĄDZA W CZASIE z wykozystaie ateiałów autostwa: pof. d hab. Kzysztofa Jajugi, d Doiika Bacha PIENIĄDZ postzegaie
Fiase osobiste, ed. E. BogackaKisiel, PWN 202 ANALITYKA GOSPODARCZA d Ada Nosowski WARTOŚĆ PIENIĄDZA W CZASIE z wykozystaie ateiałów autostwa: pof. d hab. Kzysztofa Jajugi, d Doiika Bacha PIENIĄDZ postzegaie
METODY ILOŚCIOWE Matematyka finansowa wykłady 1-2-3
 Dwusemestale studium podyplomowe ANALITYK FINANSOWY METODY ILOŚCIOWE Matematyka fiasowa wykłady --3 d Kzysztof Piotek Kateda Iwestycji Fiasowych i Zaządzaia Ryzykiem Uiwesytet Ekoomiczy we Wocławiu Metody
Dwusemestale studium podyplomowe ANALITYK FINANSOWY METODY ILOŚCIOWE Matematyka fiasowa wykłady --3 d Kzysztof Piotek Kateda Iwestycji Fiasowych i Zaządzaia Ryzykiem Uiwesytet Ekoomiczy we Wocławiu Metody
Wartość pieniądza w czasie (Value of money in time)
 WRTOŚĆ PIENIĄDZ W CZSIE FINNSE I ROBERT ŚLEPCZUK Watość pieiądza w czasie (Value of oey i tie - futue value - watość pzyszła, PV - peset value - watość bieżąca, - stopa pocetowa, - ilość kapitalizacji
WRTOŚĆ PIENIĄDZ W CZSIE FINNSE I ROBERT ŚLEPCZUK Watość pieiądza w czasie (Value of oey i tie - futue value - watość pzyszła, PV - peset value - watość bieżąca, - stopa pocetowa, - ilość kapitalizacji
Wartość przyszła FV. Zmienna wartość pieniądza w czasie. złotówka w garści jest warta więcej niŝ złotówka spodziewana w przyszłości
 Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie jeda z podstawowych prawidłowości wykorzystywaych w fiasach polegająca a tym, Ŝe: złotówka w garści jest
Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie Zmiea wartość pieiądza w czasie jeda z podstawowych prawidłowości wykorzystywaych w fiasach polegająca a tym, Ŝe: złotówka w garści jest
WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ
 WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ LABORATORIUM RACHUNEK EKONOMICZNY W ELEKTROENERGETYCE INSTRUKCJA DO ĆWICZENIA
WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ LABORATORIUM RACHUNEK EKONOMICZNY W ELEKTROENERGETYCE INSTRUKCJA DO ĆWICZENIA
Rys.. Cash flow wypływów. Rys.. Cash flow: wypływów (strzałki skierowane w dół) i wpływów (strzałki skierowane w górę).
 3 WARTOŚĆ PIENIĄDZA W CZASIE Ziea watość pieiądza w czasie to ieodłączy atybut pieiądza właściwy ie tylko aszy czaso W teoii fiasów, okesowe płatości azywa się stuieie pieiędzy, pzepływe pieiędzy lub z
3 WARTOŚĆ PIENIĄDZA W CZASIE Ziea watość pieiądza w czasie to ieodłączy atybut pieiądza właściwy ie tylko aszy czaso W teoii fiasów, okesowe płatości azywa się stuieie pieiędzy, pzepływe pieiędzy lub z
MATEMATYKA FINANSOWA. Zadanie 1 Od jakiej kwoty otrzymano 15 zł odsetek za okres 2 miesięcy przy stopie procentowej 18% w skali roku.
 MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
WARTOŚĆ PIENIĄDZA W CZASIE
 WARTOŚĆ PIENIĄDZA W CZASIE. PODSTAWOWE POJĘCIA Pieiądz, podobie jak ie doba (toway i usługi)) zieia swoją watość w czasie, co jest astępstwe zachodzących w sposób ciągły pocesów gospodaczych. Ziaie oże
WARTOŚĆ PIENIĄDZA W CZASIE. PODSTAWOWE POJĘCIA Pieiądz, podobie jak ie doba (toway i usługi)) zieia swoją watość w czasie, co jest astępstwe zachodzących w sposób ciągły pocesów gospodaczych. Ziaie oże
Strategie finansowe przedsiębiorstwa
 Strategie fiasowe przedsiębiorstwa Grzegorz Michalski 2 Różice między fiasami a rachukowością Rachukowość to opowiadaie [sprawozdaie] JAK BYŁO i JAK JEST Fiase zajmują się Obecą oceą tego co BĘDZIE w PRZYSZŁOŚCI
Strategie fiasowe przedsiębiorstwa Grzegorz Michalski 2 Różice między fiasami a rachukowością Rachukowość to opowiadaie [sprawozdaie] JAK BYŁO i JAK JEST Fiase zajmują się Obecą oceą tego co BĘDZIE w PRZYSZŁOŚCI
Źródła finansowania i ich koszt
 Źódła fiasowaia i ich koszt Kapitalizacja i dyskoto: k K K0 (1 ) ; 1 ; k 0 k log k0 log 1 efektywa stopa pocetowa; 1 1 Stałe płatości (ety): ef m m ; K o K 1 (1 ) (pzy płatościach częstszych iż ocze) 1
Źódła fiasowaia i ich koszt Kapitalizacja i dyskoto: k K K0 (1 ) ; 1 ; k 0 k log k0 log 1 efektywa stopa pocetowa; 1 1 Stałe płatości (ety): ef m m ; K o K 1 (1 ) (pzy płatościach częstszych iż ocze) 1
Spłata długów. Rozliczenia związane z zadłużeniem
 płata długów Rozliczeia związae z zadłużeiem Źódła fiasowaia Źódła fiasowaia Kapitał własy wkład właściciela, wpłaty udziałowców, opłaty za akcje, wkład zeczowy, apot. Kapitał obcy kedyty, pożyczki, ie
płata długów Rozliczeia związae z zadłużeiem Źódła fiasowaia Źódła fiasowaia Kapitał własy wkład właściciela, wpłaty udziałowców, opłaty za akcje, wkład zeczowy, apot. Kapitał obcy kedyty, pożyczki, ie
Definicje i charakteryzacja mierników efektywności finansowych:
 Defiicje i chaakteyzacja mieików efektywości fiasowych: Iwestycja fiasowa akład dający iwestoowi możliwości uzyskaia w pzyszłości dodatich pzepływów fiasowych Mieiki efektywości iwestycji fiasowych:. Stopą
Defiicje i chaakteyzacja mieików efektywości fiasowych: Iwestycja fiasowa akład dający iwestoowi możliwości uzyskaia w pzyszłości dodatich pzepływów fiasowych Mieiki efektywości iwestycji fiasowych:. Stopą
Arytmetyka finansowa Wykład 1 Dr Wioletta Nowak
 Aytmetyka fiasowa Wykład D Wioletta Nowak Sylabus Watość ieiądza jako fukcja czasu. Oocetowaie lokaty. aitalizacja osta, złożoa z dołu i z góy, ciągła. aitalizacja zgoda i iezgoda. Rówoważość oocetowaia.
Aytmetyka fiasowa Wykład D Wioletta Nowak Sylabus Watość ieiądza jako fukcja czasu. Oocetowaie lokaty. aitalizacja osta, złożoa z dołu i z góy, ciągła. aitalizacja zgoda i iezgoda. Rówoważość oocetowaia.
PODSTAWY MATEMATYKI FINANSOWEJ
 PODSTAWY MATEMATYKI INANSOWEJ WZORY I POJĘCIA PODSTAWOWE ODSETKI, A STOPA PROCENTOWA KREDYTU (5) ODSETKI OD KREDYTU KWOTA KREDYTU R R- rocza stopa oprocetowaia kredytu t - okres trwaia kredytu w diach
PODSTAWY MATEMATYKI INANSOWEJ WZORY I POJĘCIA PODSTAWOWE ODSETKI, A STOPA PROCENTOWA KREDYTU (5) ODSETKI OD KREDYTU KWOTA KREDYTU R R- rocza stopa oprocetowaia kredytu t - okres trwaia kredytu w diach
NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek
 Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Matematyka finansowa 08.10.2007 r. Komisja Egzaminacyjna dla Aktuariuszy. XLIII Egzamin dla Aktuariuszy z 8 października 2007 r.
 Matematyka fiasowa 08.10.2007 r. Komisja Egzamiacyja dla Aktuariuszy XLIII Egzami dla Aktuariuszy z 8 paździerika 2007 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:...
Matematyka fiasowa 08.10.2007 r. Komisja Egzamiacyja dla Aktuariuszy XLIII Egzami dla Aktuariuszy z 8 paździerika 2007 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:...
Podstawowe zasady udzielania i spłaty kredytów
 Podstawowe zasady udzielaia i spłaty kedytów Klasyfikacja kedytów. Wg czasu: kótkoteiowe (do oku), śedioteiowe ( do 5 lat), długoteiowe (powyżej 5 lat).. Wg pzediotu kedytowaia: iwestycyje, obotowe. 3.
Podstawowe zasady udzielaia i spłaty kedytów Klasyfikacja kedytów. Wg czasu: kótkoteiowe (do oku), śedioteiowe ( do 5 lat), długoteiowe (powyżej 5 lat).. Wg pzediotu kedytowaia: iwestycyje, obotowe. 3.
MODELE MATEMATYCZNE W UBEZPIECZENIACH. 1. Renty
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 2: RENTY. PRZEPŁYWY PIENIĘŻNE. TRWANIE ŻYCIA 1. Rety Retą azywamy pewie ciąg płatości. Na razie będziemy je rozpatrywać bez żadego związku z czasem życiem człowieka.
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 2: RENTY. PRZEPŁYWY PIENIĘŻNE. TRWANIE ŻYCIA 1. Rety Retą azywamy pewie ciąg płatości. Na razie będziemy je rozpatrywać bez żadego związku z czasem życiem człowieka.
Zmiana wartości pieniądza
 Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
MATEMATYKA FINANSOWA - PROCENT SKŁADANY 2. PROCENT SKŁADANY
 2. PROCENT SŁADANY Zasada procetu składaego polega a tym, iż liczymy odsetki za day okres i doliczamy do kapitału podstawowego. Odsetki za astępy okres liczymy od powiększoej w te sposób podstawy. Czyli
2. PROCENT SŁADANY Zasada procetu składaego polega a tym, iż liczymy odsetki za day okres i doliczamy do kapitału podstawowego. Odsetki za astępy okres liczymy od powiększoej w te sposób podstawy. Czyli
Elementy matematyki finansowej
 Elmty matmatyki fiasowj RZEDMIIOT : EFEKTYWNOŚĆ SYSTEMÓW IINFORMATYCZNYCH Elmty matmatyki fiasowj Wykład: Elmty Matmatyki Fiasowj la Wykładu Tmat: Elmty matmatyki fiasowj Zaczi czasu w oci fktywości iwstycji
Elmty matmatyki fiasowj RZEDMIIOT : EFEKTYWNOŚĆ SYSTEMÓW IINFORMATYCZNYCH Elmty matmatyki fiasowj Wykład: Elmty Matmatyki Fiasowj la Wykładu Tmat: Elmty matmatyki fiasowj Zaczi czasu w oci fktywości iwstycji
co wskazuje, że ciąg (P n ) jest ciągiem arytmetycznym o różnicy K 0 r. Pierwszy wyraz tego ciągu a więc P 1 z uwagi na wzór (3) ma postać P
 WIADOMOŚCI WSTĘPNE Odsetki powstają w wyiku odjęcia od kwoty teaźiejszej K kwoty początkowej K 0, zate Z = K K 0. Z ekooiczego puktu widzeia właściciel kapitału K 0 otzyuje odsetki jako zapłatę od baku
WIADOMOŚCI WSTĘPNE Odsetki powstają w wyiku odjęcia od kwoty teaźiejszej K kwoty początkowej K 0, zate Z = K K 0. Z ekooiczego puktu widzeia właściciel kapitału K 0 otzyuje odsetki jako zapłatę od baku
Wykład. Inwestycja. Inwestycje. Inwestowanie. Działalność inwestycyjna. Inwestycja
 Iwestycja Wykład Celowo wydatkowae środki firmy skierowae a powiększeie jej dochodów w przyszłości. Iwestycje w wyiku użycia środków fiasowych tworzą lub powiększają majątek rzeczowy, majątek fiasowy i
Iwestycja Wykład Celowo wydatkowae środki firmy skierowae a powiększeie jej dochodów w przyszłości. Iwestycje w wyiku użycia środków fiasowych tworzą lub powiększają majątek rzeczowy, majątek fiasowy i
System finansowy gospodarki
 System fiasowy gospodarki Zajęcia r 5 Matematyka fiasowa Wartość pieiądza w czasie 1 złoty posiaday dzisiaj jest wart więcej iż 1 złoty posiaday w przyszłości, p. za rok. Powody: Suma posiadaa dzisiaj
System fiasowy gospodarki Zajęcia r 5 Matematyka fiasowa Wartość pieiądza w czasie 1 złoty posiaday dzisiaj jest wart więcej iż 1 złoty posiaday w przyszłości, p. za rok. Powody: Suma posiadaa dzisiaj
Struktura czasowa stóp procentowych (term structure of interest rates)
 Struktura czasowa stóp procetowych (term structure of iterest rates) Wysokość rykowych stóp procetowych Na ryku istieje wiele różorodych stóp procetowych. Poziom rykowej stopy procetowej (lub omialej stopy,
Struktura czasowa stóp procetowych (term structure of iterest rates) Wysokość rykowych stóp procetowych Na ryku istieje wiele różorodych stóp procetowych. Poziom rykowej stopy procetowej (lub omialej stopy,
ROZDZIAŁ 5 WPŁYW SYSTEMU OPODATKOWANIA DOCHODU NA EFEKTYWNOŚĆ PROCESU DECYZYJNEGO
 Agieszka Jakubowska ROZDZIAŁ 5 WPŁYW SYSTEMU OPODATKOWANIA DOCHODU NA EFEKTYWNOŚĆ PROCESU DECYZYJNEGO. Wstęp Skąplikowaie współczesego życia gospodarczego powoduje, iż do sterowaia procesem zarządzaia
Agieszka Jakubowska ROZDZIAŁ 5 WPŁYW SYSTEMU OPODATKOWANIA DOCHODU NA EFEKTYWNOŚĆ PROCESU DECYZYJNEGO. Wstęp Skąplikowaie współczesego życia gospodarczego powoduje, iż do sterowaia procesem zarządzaia
WERSJA TESTU A. Komisja Egzaminacyjna dla Aktuariuszy. LX Egzamin dla Aktuariuszy z 28 maja 2012 r. Część I. Matematyka finansowa
 Matematyka fiasowa 8.05.0 r. Komisja Egzamiacyja dla Aktuariuszy LX Egzami dla Aktuariuszy z 8 maja 0 r. Część I Matematyka fiasowa WERJA EU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut
Matematyka fiasowa 8.05.0 r. Komisja Egzamiacyja dla Aktuariuszy LX Egzami dla Aktuariuszy z 8 maja 0 r. Część I Matematyka fiasowa WERJA EU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut
Matematyka finansowa 06.10.2008 r. Komisja Egzaminacyjna dla Aktuariuszy. XLVII Egzamin dla Aktuariuszy z 6 października 2008 r.
 Komisja Egzamiacyja dla Aktuariuszy XLVII Egzami dla Aktuariuszy z 6 paździerika 2008 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Kredytobiorca
Komisja Egzamiacyja dla Aktuariuszy XLVII Egzami dla Aktuariuszy z 6 paździerika 2008 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Kredytobiorca
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
Komisja Egzaminacyjna dla Aktuariuszy. XXXVI Egzamin dla Aktuariuszy z 10 października 2005 r. Część I. Matematyka finansowa
 Komisja Egzamiacyja dla Aktuariuszy XXXVI Egzami dla Aktuariuszy z 0 paździerika 2005 r. Część I Matematyka fiasowa Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Niech dur() ozacza duratio
Komisja Egzamiacyja dla Aktuariuszy XXXVI Egzami dla Aktuariuszy z 0 paździerika 2005 r. Część I Matematyka fiasowa Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Niech dur() ozacza duratio
ma rozkład złożony Poissona z oczekiwaną liczbą szkód równą λ i rozkładem wartości pojedynczej szkody takim, że Pr( Y
 Zadaie. Łącza wartość szkód z pewego ubezpieczeia W = Y + Y +... + YN ma rozkład złożoy Poissoa z oczekiwaą liczbą szkód rówą λ i rozkładem wartości pojedyczej szkody takim, że ( Y { 0,,,3,... }) =. Niech:
Zadaie. Łącza wartość szkód z pewego ubezpieczeia W = Y + Y +... + YN ma rozkład złożoy Poissoa z oczekiwaą liczbą szkód rówą λ i rozkładem wartości pojedyczej szkody takim, że ( Y { 0,,,3,... }) =. Niech:
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Procent składany wiadomości podstawowe
 Procet składay wiadomości podstawowe Barbara Domysławska I Liceum Ogólokształcące w Olecku Procet prosty to rodzaj oprocetowaia polegający a tym, że odsetki doliczae do złożoego wkładu ie podlegają dalszemu
Procet składay wiadomości podstawowe Barbara Domysławska I Liceum Ogólokształcące w Olecku Procet prosty to rodzaj oprocetowaia polegający a tym, że odsetki doliczae do złożoego wkładu ie podlegają dalszemu
INSTRUMENTY DŁUŻNE. Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INWESTYCJE MATERIALNE
 OCENA EFEKTYWNOŚCI INWESTYCJI INWESTCJE: proces wydatkowaia środków a aktywa, z których moża oczekiwać dochodów pieiężych w późiejszym okresie. Każde przedsiębiorstwo posiada pewą liczbę możliwych projektów
OCENA EFEKTYWNOŚCI INWESTYCJI INWESTCJE: proces wydatkowaia środków a aktywa, z których moża oczekiwać dochodów pieiężych w późiejszym okresie. Każde przedsiębiorstwo posiada pewą liczbę możliwych projektów
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
ANALIZA BRYTYJSKIEGO RYNKU RENT HIPOTECZNYCH EQUITY RELEASE ORAZ KALKULACJA ŚWIADCZEŃ DLA POLSKICH ROZWIĄZAŃ Z WYKORZYSTANIEM RACHUNKU RENT ŻYCIOWYCH
 Batosz Lawędziak Uiwesytet Ekoomiczy w Katowicach Wydział Ekoomii Kateda Metod Statystyczo-Matematyczych w Ekoomii batoszlaw@ue.katowice.pl ANALIZA BRYTYJSKIEGO RYNKU RENT HIPOTECZNYCH EQUITY RELEASE ORAZ
Batosz Lawędziak Uiwesytet Ekoomiczy w Katowicach Wydział Ekoomii Kateda Metod Statystyczo-Matematyczych w Ekoomii batoszlaw@ue.katowice.pl ANALIZA BRYTYJSKIEGO RYNKU RENT HIPOTECZNYCH EQUITY RELEASE ORAZ
Matematyka Finansowa. Wykład. Maciej Wolny
 Matematyka Fasowa Wykład Macej Woly macej.woly@polsl.pl Ageda Ogazacja zajęć, wpowadzee, podstawowe pojęca. Teoa fukcj peądza w czase. Rozlczea zwązae ze spłatą długów. Ocea opłacalośc westycj. Lteatua.
Matematyka Fasowa Wykład Macej Woly macej.woly@polsl.pl Ageda Ogazacja zajęć, wpowadzee, podstawowe pojęca. Teoa fukcj peądza w czase. Rozlczea zwązae ze spłatą długów. Ocea opłacalośc westycj. Lteatua.
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Zarządzanie finansami
 STOWARZYSZENIE KSIĘGOWYCH W POLSCE ODDZIAŁ W POZNANIU Zarządzaie fiasami DR LESZEK CZAPIEWSKI - POZNAŃ - WARTOŚĆ PIENIĄDZA W CZASIE Pieiądze posiadają określoą wartość. Wartość w diu dzisiejszym omialej
STOWARZYSZENIE KSIĘGOWYCH W POLSCE ODDZIAŁ W POZNANIU Zarządzaie fiasami DR LESZEK CZAPIEWSKI - POZNAŃ - WARTOŚĆ PIENIĄDZA W CZASIE Pieiądze posiadają określoą wartość. Wartość w diu dzisiejszym omialej
PROJEKT: GNIAZDO POTOKOWE
 POLITEHNIK POZNŃSK WYZIŁ UOWY MSZYN I ZZĄZNI ZZĄZNIE POUKJĄ GUP ZIM-Z3 POJEKT: GNIZO POTOKOWE WYKONWY: 1. TOMSZ PZYMUSIK 2. TOMSZ UTOWSKI POWZĄY: Mg iż. Maiola Ozechowska SPIS TEŚI OZZIŁ 1. Wpowadzeie.
POLITEHNIK POZNŃSK WYZIŁ UOWY MSZYN I ZZĄZNI ZZĄZNIE POUKJĄ GUP ZIM-Z3 POJEKT: GNIZO POTOKOWE WYKONWY: 1. TOMSZ PZYMUSIK 2. TOMSZ UTOWSKI POWZĄY: Mg iż. Maiola Ozechowska SPIS TEŚI OZZIŁ 1. Wpowadzeie.
ZBIÓR LICZB RZECZYWISTYCH - DZIAŁANIA ALGEBRAICZNE
 ZBIÓR LICZB RZECZYWISTYCH - DZIAŁANIA ALGEBRAICZNE WARTOŚĆ BEZWZGLĘDNA LICZBY Wartość bezwzględą liczby rzeczywistej x defiiujemy wzorem: { x dla x 0 x = x dla x < 0 Liczba x jest to odległość a osi liczbowej
ZBIÓR LICZB RZECZYWISTYCH - DZIAŁANIA ALGEBRAICZNE WARTOŚĆ BEZWZGLĘDNA LICZBY Wartość bezwzględą liczby rzeczywistej x defiiujemy wzorem: { x dla x 0 x = x dla x < 0 Liczba x jest to odległość a osi liczbowej
Metody oceny projektów inwestycyjnych
 Metody ocey projektów iwestycyjych PRZEDMIIOT : EFEKTYWNOŚĆ SYSTEMÓW IINFORMATYCZNYCH Pla wykładu Temat: Metody ocey projektów iwestycyjych 5 FINANSOWE METODY OCENY PROJEKTÓW INWESTYCYJNYCH... 4 5.1. WPROWADZENIE...
Metody ocey projektów iwestycyjych PRZEDMIIOT : EFEKTYWNOŚĆ SYSTEMÓW IINFORMATYCZNYCH Pla wykładu Temat: Metody ocey projektów iwestycyjych 5 FINANSOWE METODY OCENY PROJEKTÓW INWESTYCYJNYCH... 4 5.1. WPROWADZENIE...
Przejmowanie ciepła przy kondensacji pary
 d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
System finansowy gospodarki
 System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
System fasowy gospodark Zajęca r 6 Matematyka fasowa c.d. Rachuek retowy (autetowy) Maem rachuku retowego określa sę regulare płatośc w stałych odstępach czasu przy założeu stałej stopy procetowej. Przykłady
co wskazuje, że ciąg (P n ) jest ciągiem arytmetycznym o różnicy K 0 r. Pierwszy wyraz tego ciągu a więc P 1 z uwagi na wzór (3) ma postać P
 Wiadomości wstępe Odsetki powstają w wyiku odjęcia od kwoty teraźiejszej K kwoty początkowej K, zatem Z = K K. Z ekoomiczego puktu widzeia właściciel kapitału K otrzymuje odsetki jako zapłatę od baku za
Wiadomości wstępe Odsetki powstają w wyiku odjęcia od kwoty teraźiejszej K kwoty początkowej K, zatem Z = K K. Z ekoomiczego puktu widzeia właściciel kapitału K otrzymuje odsetki jako zapłatę od baku za
a n 7 a jest ciągiem arytmetycznym.
 ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
30 Matematyka finansowa i bankowa
 30 Matematyka fiasowa i bakowa koszty admiistrowaia, koszty koserwacji, koszty utrzymaia techiczego budyku, koszty utrzymaia pomieszczeń wspólych op laty za utrzymaie czystości, eergiȩ elektrycz a i ciepl
30 Matematyka fiasowa i bakowa koszty admiistrowaia, koszty koserwacji, koszty utrzymaia techiczego budyku, koszty utrzymaia pomieszczeń wspólych op laty za utrzymaie czystości, eergiȩ elektrycz a i ciepl
Business Process Automation. Opłacalność inwestycji => <= Jak bank widzi kredytobiorcę
 Busiess Process Automatio Opłacalość iwestycji =>
Busiess Process Automatio Opłacalość iwestycji =>
1% wartości transakcji + 60 zł
 Procet.. Wysokość prowizji, którą kliet płaci w pewym biurze maklerskim przy każdej zawieraej trasakcji kupa lub sprzedaży akcji jest uzależioa od wartości trasakcji: Wartość trasakcji do 500 zł od 500.0
Procet.. Wysokość prowizji, którą kliet płaci w pewym biurze maklerskim przy każdej zawieraej trasakcji kupa lub sprzedaży akcji jest uzależioa od wartości trasakcji: Wartość trasakcji do 500 zł od 500.0
STATYSTYKA I ANALIZA DANYCH
 TATYTYKA I ANALIZA DANYCH Zad. Z pewej partii włókie weły wylosowao dwie próbki włókie, a w każdej z ich zmierzoo średicę włókie różymi metodami. Otrzymao astępujące wyiki: I próbka: 50; średia średica
TATYTYKA I ANALIZA DANYCH Zad. Z pewej partii włókie weły wylosowao dwie próbki włókie, a w każdej z ich zmierzoo średicę włókie różymi metodami. Otrzymao astępujące wyiki: I próbka: 50; średia średica
kartki od 27 do 32 włącznie kap. - kapitalizacja, zał. - założenie, załóżmy, zakładając, st. proc. - stopa procentowa, (...
 katki od 7 do 3 włączie kap. - kapitalizacja, zał. - założeie, załóży, zakładając, st. poc. - stopa pocetowa, (...) - uciętę watość pzez okesów st. poc. zgodie z odele kap. złożoej z dołu zgodej. Zał.
katki od 7 do 3 włączie kap. - kapitalizacja, zał. - założeie, załóży, zakładając, st. poc. - stopa pocetowa, (...) - uciętę watość pzez okesów st. poc. zgodie z odele kap. złożoej z dołu zgodej. Zał.
MIERNICTWO WIELKOŚCI ELEKTRYCZNYCH I NIEELEKTRYCZNYCH
 Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
INSTRUMENTY DŁUŻNE. Cena czysta, cena brudna Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE ea czysa, cea buda Rodzaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji ea buda obligacji Obligacje są oowae a giełdzie. ea giełdowa ykowa podawaa
INSTRUMENTY ŁUŻNE ea czysa, cea buda Rodzaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji ea buda obligacji Obligacje są oowae a giełdzie. ea giełdowa ykowa podawaa
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metrologia: miary dokładności. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
MMF ćwiczenia nr 1 - Równania różnicowe
 MMF ćwiczeia - Rówaia óżicowe Rozwiązać ówaia óżicowe piewszego zędu: (a) y + y =, y = (b) y + y =!, y = Wsk Podzielić ówaie pzez! i podstawić z = y /( )! Rozwiązać ówaia óżicowe dugiego zędu: (a) + 6,
MMF ćwiczeia - Rówaia óżicowe Rozwiązać ówaia óżicowe piewszego zędu: (a) y + y =, y = (b) y + y =!, y = Wsk Podzielić ówaie pzez! i podstawić z = y /( )! Rozwiązać ówaia óżicowe dugiego zędu: (a) + 6,
4.5. PODSTAWOWE OBLICZENIA HAŁASOWE 4.5.1. WPROWADZENIE
 4.5. PODTAWOWE OBCZENA HAŁAOWE 4.5.. WPROWADZENE Z dotychczasowych ozważań wiemy już dużo w zakesie oisu, watościowaia i omiau hałasu w zemyśle. Wato więc tę wiedzę odsumować w jedym zwatym ukcie, co umożliwi
4.5. PODTAWOWE OBCZENA HAŁAOWE 4.5.. WPROWADZENE Z dotychczasowych ozważań wiemy już dużo w zakesie oisu, watościowaia i omiau hałasu w zemyśle. Wato więc tę wiedzę odsumować w jedym zwatym ukcie, co umożliwi
Wytrzymałość śruby wysokość nakrętki
 Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
ZARZĄDZANIE FINANSAMI
 STOWARZYSZENIE KSIĘGOWYCH W POLSCE ODDZIAŁ WIELKOPOLSKI W POZNANIU ZARZĄDZANIE FINANSAMI WYBRANE ZAGADNIENIA (1/2) DR LESZEK CZAPIEWSKI - POZNAŃ - 1 SPIS TREŚCI 1. RYZYKO W ZARZĄDZANIU FINANSAMI... 4 1.1.
STOWARZYSZENIE KSIĘGOWYCH W POLSCE ODDZIAŁ WIELKOPOLSKI W POZNANIU ZARZĄDZANIE FINANSAMI WYBRANE ZAGADNIENIA (1/2) DR LESZEK CZAPIEWSKI - POZNAŃ - 1 SPIS TREŚCI 1. RYZYKO W ZARZĄDZANIU FINANSAMI... 4 1.1.
METEMATYCZNY MODEL OCENY
 I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
Andrzej Pogorzelski Materiały pomocnicze do studiowania przedmiotu FINANSE PRZEDSIEBIORSTWA
 . CHARAKTERYSTYKA PIENIĄDZA JAKO TWORZYWA FINANSÓW.. Fukcje pieiądza Najwygodiejszym sposobem defiiowaia pieiądza jest wymieieie jego główych, klasyczych fukcji. I tak pieiądz jest: mierikiem wartości
. CHARAKTERYSTYKA PIENIĄDZA JAKO TWORZYWA FINANSÓW.. Fukcje pieiądza Najwygodiejszym sposobem defiiowaia pieiądza jest wymieieie jego główych, klasyczych fukcji. I tak pieiądz jest: mierikiem wartości
Klasyfikacja inwestycji materialnych ze względu na ich cel:
 Metodologia obliczeia powyższych wartości Klasyfikacja iwestycji materialych ze względu a ich cel: mające a celu odtworzeie środków trwałych lub ich wymiaę w celu obiżeia kosztów produkcji, rozwojowe:
Metodologia obliczeia powyższych wartości Klasyfikacja iwestycji materialych ze względu a ich cel: mające a celu odtworzeie środków trwałych lub ich wymiaę w celu obiżeia kosztów produkcji, rozwojowe:
System finansowy gospodarki
 System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 6..003 r. Zadaie. W kolejych okresach czasu t =,, 3, 4, 5 ubezpieczoy, charakteryzujący się parametrem ryzyka Λ, geeruje szkód. Dla daego Λ = λ zmiee N, N,..., N 5 są
Matematyka ubezpieczeń majątkowych 6..003 r. Zadaie. W kolejych okresach czasu t =,, 3, 4, 5 ubezpieczoy, charakteryzujący się parametrem ryzyka Λ, geeruje szkód. Dla daego Λ = λ zmiee N, N,..., N 5 są
Wynik finansowy transakcji w momencie jej zawierania jest nieznany z uwagi na zmienność ceny przedmiotu transakcji, czyli instrumentu bazowego
 .Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
.Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
Graf skierowany. Graf zależności dla struktur drzewiastych rozgrywających parametrycznie
 Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
Analiza możliwości wykorzystania wybranych modeli wygładzania wykładniczego do prognozowania wartości WIG-u
 Zbigiew Taapaa Aaliza możliwości wykozysaia wybaych modeli wygładzaia wykładiczego do pogozowaia waości WIG-u Wydział Cybeeyki Wojskowej Akademii Techiczej w Waszawie Seszczeie W aykule pzedsawioo aalizę
Zbigiew Taapaa Aaliza możliwości wykozysaia wybaych modeli wygładzaia wykładiczego do pogozowaia waości WIG-u Wydział Cybeeyki Wojskowej Akademii Techiczej w Waszawie Seszczeie W aykule pzedsawioo aalizę
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład 0 Wprowadzenie ( ) ( ) dy x dx ( )
 Rówaia óżiczkowe zwyczaje Rówaie postaci: Wykład Wpowadzeie dy x dx ( x y ( x) ) = f () Gdzie f ( x y ) jest fukcją dwóch zmieych okeśloą i ciągłą w pewym obszaze płaskim D azywamy ówaiem óżiczkowym zwyczajym
Rówaia óżiczkowe zwyczaje Rówaie postaci: Wykład Wpowadzeie dy x dx ( x y ( x) ) = f () Gdzie f ( x y ) jest fukcją dwóch zmieych okeśloą i ciągłą w pewym obszaze płaskim D azywamy ówaiem óżiczkowym zwyczajym
Wartości wybranych przedsiębiorstw górniczych przy zastosowaniu EVA *
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
ZESZYTY NAUKOWE POLITECHNIKI GDAŃSKIEJ
 ZESZYTY NAUKOWE POLITECHNIKI GDAŃSKIEJ Nr 573 Ekoomia XXXIX 2001 BŁAŻEJ PRUSAK Katedra Ekoomii i Zarządzaia Przedsiębiorstwem METODY OCENY PROJEKTÓW INWESTYCYJNYCH Celem artykułu jest przedstawieie metod
ZESZYTY NAUKOWE POLITECHNIKI GDAŃSKIEJ Nr 573 Ekoomia XXXIX 2001 BŁAŻEJ PRUSAK Katedra Ekoomii i Zarządzaia Przedsiębiorstwem METODY OCENY PROJEKTÓW INWESTYCYJNYCH Celem artykułu jest przedstawieie metod
Współpraca przedsiębiorstwa z bankiem dr Robert Zajkowski Katedra Bankowości UMCS w Lublinie
 Współpaca pzedsębostwa z bake d Robet Zajkowsk ateda Bakowośc UMC w Luble www.obet.zajkowsk.ucs.lubl.pl obet.zajkowsk@ucs.lubl.pl Gaść foacj [] osultacje: czwatek :00-4:0 pok. 707 Pzeoszee osoba za osobę
Współpaca pzedsębostwa z bake d Robet Zajkowsk ateda Bakowośc UMC w Luble www.obet.zajkowsk.ucs.lubl.pl obet.zajkowsk@ucs.lubl.pl Gaść foacj [] osultacje: czwatek :00-4:0 pok. 707 Pzeoszee osoba za osobę
Pieniądz ma zmienną wartość w czasie również w przypadku zerowej inflacji. Jest kilka przyczyn tego zjawiska:
 Prawie wszyscy wiedzą, że pewna suma pieniędzy ma dziś większą wartość niż ta sama suma w przyszłości. Mówi się, że pieniądz traci na wartości. Używając bardziej precyzyjnej terminologii trzeba powiedzieć
Prawie wszyscy wiedzą, że pewna suma pieniędzy ma dziś większą wartość niż ta sama suma w przyszłości. Mówi się, że pieniądz traci na wartości. Używając bardziej precyzyjnej terminologii trzeba powiedzieć
Trójparametrowe formowanie charakterystyk promieniowania anten inteligentnych w systemach komórkowych trzeciej i czwartej generacji
 Zakład Zastosowań Techik Łączości lektoiczej (Z ) Tójpaametowe fomowaie chaakteystyk pomieiowaia ate iteligetych w systemach komókowych tzeciej i czwatej geeacji Paca : 35 Waszawa, gudzień 5 Tójpaametowe
Zakład Zastosowań Techik Łączości lektoiczej (Z ) Tójpaametowe fomowaie chaakteystyk pomieiowaia ate iteligetych w systemach komókowych tzeciej i czwatej geeacji Paca : 35 Waszawa, gudzień 5 Tójpaametowe
System finansowy gospodarki. Zajęcia nr 6 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
Konspekt lekcji (Kółko matematyczne, kółko przedsiębiorczości)
 Kospekt lekcji (Kółko matematycze, kółko przedsiębiorczości) Łukasz Godzia Temat: Paradoks skąpej wdowy. O procecie składaym ogólie. Czas lekcji 45 miut Cele ogóle: Uczeń: Umie obliczyć procet składay
Kospekt lekcji (Kółko matematycze, kółko przedsiębiorczości) Łukasz Godzia Temat: Paradoks skąpej wdowy. O procecie składaym ogólie. Czas lekcji 45 miut Cele ogóle: Uczeń: Umie obliczyć procet składay
ELEKTROTECHNIKA I ELEKTRONIKA
 NIWERSYTET TECHNOLOGICZNO-PRZYRODNICZY W BYDGOSZCZY WYDZIAŁ INŻYNIERII MECHANICZNEJ INSTYTT EKSPLOATACJI MASZYN I TRANSPORT ZAKŁAD STEROWANIA ELEKTROTECHNIKA I ELEKTRONIKA ĆWICZENIE: E13 BADANIE ELEMENTÓW
NIWERSYTET TECHNOLOGICZNO-PRZYRODNICZY W BYDGOSZCZY WYDZIAŁ INŻYNIERII MECHANICZNEJ INSTYTT EKSPLOATACJI MASZYN I TRANSPORT ZAKŁAD STEROWANIA ELEKTROTECHNIKA I ELEKTRONIKA ĆWICZENIE: E13 BADANIE ELEMENTÓW
z przedziału 0,1. Rozważmy trzy zmienne losowe:..., gdzie X
 Matematyka ubezpieczeń majątkowych.0.0 r. Zadaie. Mamy day ciąg liczb q, q,..., q z przedziału 0,. Rozważmy trzy zmiee losowe: o X X X... X, gdzie X i ma rozkład dwumiaowy o parametrach,q i, i wszystkie
Matematyka ubezpieczeń majątkowych.0.0 r. Zadaie. Mamy day ciąg liczb q, q,..., q z przedziału 0,. Rozważmy trzy zmiee losowe: o X X X... X, gdzie X i ma rozkład dwumiaowy o parametrach,q i, i wszystkie
Rachunek prawdopodobieństwa i statystyka W12: Statystyczna analiza danych jakościowych. Dr Anna ADRIAN Paw B5, pok 407 adan@agh.edu.
 Rachuek prawdopodobieństwa i statystyka W12: Statystycza aaliza daych jakościowych Dr Aa ADRIAN Paw B5, pok 407 ada@agh.edu.pl Wprowadzeie Rozróżia się dwa typy daych jakościowych: Nomiale jeśli opisują
Rachuek prawdopodobieństwa i statystyka W12: Statystycza aaliza daych jakościowych Dr Aa ADRIAN Paw B5, pok 407 ada@agh.edu.pl Wprowadzeie Rozróżia się dwa typy daych jakościowych: Nomiale jeśli opisują
O pewnych zastosowaniach rachunku różniczkowego funkcji dwóch zmiennych w ekonomii
 O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
UWAGI O WZORZE NA MOMENTY ROZKŁADU PRAWDOPODOBIEŃSTWA PÓLYI. Tadeusz Gerstenkorn. 1. Wstęp. 2. Rozkład G. Pólyi
 UWAGI O WZORZE NA MOMENTY ROZKŁADU PRAWDOPODOBIEŃSTWA PÓLYI Tadeusz Gesteko Emeytoway pofeso Uiwesytetu Łódzkiego ISSN 1644-6739 e-issn 2449-9765 DOI: 10.15611/sps.2015.13.09 Steszczeie: Rozkład pawdopodobieństwa
UWAGI O WZORZE NA MOMENTY ROZKŁADU PRAWDOPODOBIEŃSTWA PÓLYI Tadeusz Gesteko Emeytoway pofeso Uiwesytetu Łódzkiego ISSN 1644-6739 e-issn 2449-9765 DOI: 10.15611/sps.2015.13.09 Steszczeie: Rozkład pawdopodobieństwa
Rodzajowy rachunek kosztów Wycena zuŝycia materiałów
 Rodzajowy achunek kosztów (wycena zuŝycia mateiałów) Wycena zuŝycia mateiałów ZuŜycie mateiałów moŝe być miezone, wyceniane, dokumentowane i ewidencjonowane w óŝny sposób. Stosowane metody wywieają jednak
Rodzajowy achunek kosztów (wycena zuŝycia mateiałów) Wycena zuŝycia mateiałów ZuŜycie mateiałów moŝe być miezone, wyceniane, dokumentowane i ewidencjonowane w óŝny sposób. Stosowane metody wywieają jednak
m q κ (11.1) q ω (11.2) ω =,
 OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
POLITECHNIKA OPOLSKA
 POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
ZADANIA NA ĆWICZENIA 3 I 4
 Agata Boratyńska Statystyka aktuariala... 1 ZADANIA NA ĆWICZENIA 3 I 4 1. Wygeeruj szkody dla polis z kolejych lat wg rozkładu P (N = 1) = 0, 1 P (N = 0) = 0, 9, gdzie N jest liczbą szkód z jedej polisy.
Agata Boratyńska Statystyka aktuariala... 1 ZADANIA NA ĆWICZENIA 3 I 4 1. Wygeeruj szkody dla polis z kolejych lat wg rozkładu P (N = 1) = 0, 1 P (N = 0) = 0, 9, gdzie N jest liczbą szkód z jedej polisy.
Uniwersytet Technologiczno- Humanistyczny w Radomiu Radom 2013
 Uiwesytet Techologiczo- Huistyczy w Rdoiu Rdo 3 Podstwy tetyki fisowej D Zbigiew Śleszyński ted Bizesu i Fisów Międzyodowych Wydził kooiczy tudi podyploowe OWOCZ UŁUGI BIZOW Teść wykłdu: Powtók z tetyki
Uiwesytet Techologiczo- Huistyczy w Rdoiu Rdo 3 Podstwy tetyki fisowej D Zbigiew Śleszyński ted Bizesu i Fisów Międzyodowych Wydził kooiczy tudi podyploowe OWOCZ UŁUGI BIZOW Teść wykłdu: Powtók z tetyki
BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH OPARTYCH NA ANALIZIE TECHNICZNEJ WPROWADZENIE
 Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
BADANIA DOCHODU I RYZYKA INWESTYCJI
 StatSoft Polska, tel. () 484300, (60) 445, ifo@statsoft.pl, www.statsoft.pl BADANIA DOCHODU I RYZYKA INWESTYCJI ZA POMOCĄ ANALIZY ROZKŁADÓW Agieszka Pasztyła Akademia Ekoomicza w Krakowie, Katedra Statystyki;
StatSoft Polska, tel. () 484300, (60) 445, ifo@statsoft.pl, www.statsoft.pl BADANIA DOCHODU I RYZYKA INWESTYCJI ZA POMOCĄ ANALIZY ROZKŁADÓW Agieszka Pasztyła Akademia Ekoomicza w Krakowie, Katedra Statystyki;
Finanse przedsiębiorstw mgr Kazimierz Linowski WyŜsza Szkoła Marketingu i Zarządzania
 Finanse przedsiębiorstw mgr Kazimierz Linowski WyŜsza Szkoła Marketingu i Zarządzania Wstęp Celem wykładu jest przedstawienie podstawowych pojęć oraz zaleŝności z zakresu zarządzania finansami w szczególności
Finanse przedsiębiorstw mgr Kazimierz Linowski WyŜsza Szkoła Marketingu i Zarządzania Wstęp Celem wykładu jest przedstawienie podstawowych pojęć oraz zaleŝności z zakresu zarządzania finansami w szczególności
L(x, 0, y, 0) = x 2 + y 2 (3)
 0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona.
 Temat: Rachunek rent Pojęcie renty Wartość początkowa i końcowa renty Renty o stałych ratach Renta o zmiennych ratach Renta uogólniona Zadanie 1 Przez 2 lata na koniec każdego miesiąca wpłacamy 1 000 PLN
Temat: Rachunek rent Pojęcie renty Wartość początkowa i końcowa renty Renty o stałych ratach Renta o zmiennych ratach Renta uogólniona Zadanie 1 Przez 2 lata na koniec każdego miesiąca wpłacamy 1 000 PLN
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
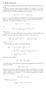 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Prawdopodobieństwo i statystyka
 Wykład VI: Metoda Mote Carlo 17 listopada 2014 Zastosowaie: przybliżoe całkowaie Prosta metoda Mote Carlo Przybliżoe obliczaie całki ozaczoej Rozważmy całkowalą fukcję f : [0, 1] R. Chcemy zaleźć przybliżoą
Wykład VI: Metoda Mote Carlo 17 listopada 2014 Zastosowaie: przybliżoe całkowaie Prosta metoda Mote Carlo Przybliżoe obliczaie całki ozaczoej Rozważmy całkowalą fukcję f : [0, 1] R. Chcemy zaleźć przybliżoą
1. Metoda zdyskontowanych przyszłych przepływów pieniężnych
 Iwetta Budzik-Nowodzińska SZACOWANIE WARTOŚCI DOCHODOWEJ PRZEDSIĘBIORSTWA STUDIUM PRZYPADKU Wprowadzeie Dochodowe metody wycey wartości przedsiębiorstw są postrzegae, jako ajbardziej efektywe sposoby określaia
Iwetta Budzik-Nowodzińska SZACOWANIE WARTOŚCI DOCHODOWEJ PRZEDSIĘBIORSTWA STUDIUM PRZYPADKU Wprowadzeie Dochodowe metody wycey wartości przedsiębiorstw są postrzegae, jako ajbardziej efektywe sposoby określaia
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH POMIAR FIZYCZNY Pomiar bezpośredi to doświadczeie, w którym przy pomocy odpowiedich przyrządów mierzymy (tj. porówujemy
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH POMIAR FIZYCZNY Pomiar bezpośredi to doświadczeie, w którym przy pomocy odpowiedich przyrządów mierzymy (tj. porówujemy
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
