G:\WYKLAD IIIBC 2001\FIN2001\Ruch falowy2001.doc. Drgania i fale II rok Fizyki BC
|
|
|
- Krzysztof Krawczyk
- 7 lat temu
- Przeglądów:
Transkrypt
1 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Ruh falow: Fala rohodąe się w presreni aburenie lub odsałenie (pole). - impuls lub drgania. Jeśli rohodi się prędośią o po asie : ( r) - funja falowa równanie fali
2 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Dla usalonego r punie r : Drgania i fale II ro Fii BC r ( r ) - drgania w Dla usalonego roład whleń: ( ) - presrenn r
3 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Ogólniej: aburenie pola opisująego własność finą pole eleromagnene deformaja iśnienie emperaura pole grawiajne W ależnośi od geomerii wbudenia fale salarne lub weorowe. Dla fali salarnej: ( r) (np. fale dźwięowe). Dla fali weorowej: ( r) (np. fale elasne fale eleromagnene). 3
4 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Fala powaranie opóźnieniem. W uładie porusająm się wdłuż osi wra abureniem sał jes dan pre ( ) mienia się (pr brau dspersji). Po asie i nie ( - w laboraorjnm) : ( ) [ ( ) ] ( ) - sał jes ahowan! Dla ruhu w lewo ( ) : ( ) ( m ) Równanie falowe: m 4
5 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC 5 d d d d d d d d Równanie dla fali jednowmiarowej Fale liniowe: Zasada superpoji: jeżeli funje ( ) ( ) ( ) n... są rowiąaniami równania falowego o ih ombinaja liniowa: ( ) ( ) C n n i i spełnia o równanie. Jeśli dwie fale i : ( ) ( )
6 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Rohodenie się liniowh wbudeń lub pól weorowh nie jes ałóane pre inne wbudenia i pola weorowe. Fala harmonina: funja falowa ma posać ( ) Asin ( m ) lub ( ) Aos ( m ) Asin ( m ) [ Asin ( m ) ] Dla () Asin( m ) m Asin - drgania harmonine sin π sin T Dla ( ) A A π T - aburenie ma w presreni sał harmoninej funji - oresowość presrenna! 6
7 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC ( m nt ) Asin ( m nt ) π Asin T π T m n π T λ - długość fali Asin π T π - liba długośi fali w długośi π λ - liba falowa ( ) Masima i minima presuwają się prędośią - λ poosaje a sama. Fala harmonina presuwa się o λ w iągu oresu. Prędość faowa: Faa ϕ m ϕ f ( ) Dla ϕ m Dla ϕ 7
8 Dla 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do ϕ Drgania i fale II ro Fii BC ϕ m ϕ Ogólnie Dla ϕ ( ) Asin m ϕ i Asin m ; ϕ ϕ ϕ ϕ ± π λ λ ± prędość faowa λ ν T π T ( ) ( ) ( ) Aos Aos Aosπ λ T Aos Bp os C ep Re{ D ( ) Bq sin( ) [ i( ) ] C ep[ i( ) ] ep[ i( ) ] π λ 8
9 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Fala nieharmonina: Bło: dowoln ruh periodn można predsawić jao superpoję ruhów harmoninh o ęsośiah 3... Nieh f ( ) - ruh falow periodn - w danm punie powara się dla f Dla danego T T... nt ( ) f [ ( ± T )] f ( m T ) maleje o nt ( nλ) powara się gd rośnie lub Ruh falow periodn w asie jes periodn w presreni. 9
10 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Nieh f ( ) oresem λ f ( ) f ( λ) Drgania i fale II ro Fii BC - funja periodna w presreni Z wierdenia Fouriera: ( ) gdie drgań) f a a a os a os... an os n... b sin b sin... b sin n... π (odpowiada gd pisaliśm dla λ ( ) a a os( ) a os( )... b sin ( ) b sin ( )... a b a n sin os n n π π f T υ λ υ T f ( ) a os ( )... ( )... b sin( ) ( )... b sin n( )... os Każd periodn ruh falow może bć predsawion jao superpoja harmoninh ruhów falowh o ęsośiah... n i długośiah fali λ λ...
11 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Fala płasa: Równanie powierhni sałej fa: ϕ ± ϕ ons - jeśli płasna fala płasa. Fala płasa haraeruje się jednm ieruniem propagaji opisanm pre wersor u ; u. salarna: ( r ) ( r u ) weorowa: ( r ) ( r u ) Powierhnia falowa fali płasiej: r u C ons Nieh ierune propagaji : salarna: ( r ) ( ) weorowa: ( r ) ( ) u bo [ ] r u [ ( ) ( ) ( ) ] powierhnie falowe równoległe do płasn.
12 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Fala podłużna: Fala poprena: T Drgania i fale II ro Fii BC ( r ) L ( ) ( ) ro L ( r ) [ ] L L T ( r ) T ( ) [ ( ) ( ) ] diυ T ( r ) Polaraja liniowa fali poprenej sała orienaja ależ od asu i położenia. T nie Można opisać jednosowm weorem polaraji p; p ( r ) T ( ) ( )p T T T [ osγ sinγ ] ons p γ - ą w płasźnie faowej wględem pionu (). Równoważność fal salarnh i weorowh: Fala salarna ( r) jes równoważna podłużnej fali weorowej L ( r ) : L ( r ) grad ( r ) fala salarna poenjał fali weorowej ( r ) ro{ grad ( r ) } ro L
13 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Prład: r ( r ) L ( r ) d r r weorowa podłużna salarna Dźwię w gaie lub ie: falę salarną iśnienia (gęsośi) można predsawić jao weorową falę podłużną whlenia. Dla A ( u r ) sin - harmonina fala płasa u - weor propagaji Asin i( r ± Ae ) ( r m ) Asin ( r ) harmonina fala płasa Coło fali powierhnia faowa oddielająa obsar presreni aburon pre rohodąą się falę od obsaru ór jese nie osał aburon. Coło fali jes powierhnią sałej fa. Coło fali płasiej jes płasną r ons. 3
14 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC 4 Fala rójwmiarowa: ( ) ( ) ± i Ae - prędość faowa Rowiąanie harmonine: ( ) ( ) r i Ae r ± ( ) ( ) r r A Ae r r i m sin ±
ρ - gęstość ładunku j - gęstość prądu FALE ELEKTROMAGNETYCZNE W PRÓŻNI: Równania Maxwella: -przenikalność elektryczna próżni=8,8542x10-12 F/m
 -- G:\AA_Wklad \FIN\DOC\em.do Drgania i fale III rok Fiki C FAL LKTROMAGNTYCZN W PRÓŻNI: Równania Mawella: di ρ ε ρ di j ρ - gęsość ładunku j - gęsość prądu ro di ro j ε ε -prenikalność elekrna próżni8854
-- G:\AA_Wklad \FIN\DOC\em.do Drgania i fale III rok Fiki C FAL LKTROMAGNTYCZN W PRÓŻNI: Równania Mawella: di ρ ε ρ di j ρ - gęsość ładunku j - gęsość prądu ro di ro j ε ε -prenikalność elekrna próżni8854
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
5. Równania Maxwella. 5.1 Równania Maxwella 5.2 Transformacja pól 5.3 Fala elektromagnetyczna
 5 Równania Maxwella 5 Równania Maxwella 5 Transformaja pól 53 ala eleromagnezna 86 5 Równania Maxwella Wśród poazanh uprzednio równań Maxwella znajduje się prawo Ampere a j Jedna można pozać, że posać
5 Równania Maxwella 5 Równania Maxwella 5 Transformaja pól 53 ala eleromagnezna 86 5 Równania Maxwella Wśród poazanh uprzednio równań Maxwella znajduje się prawo Ampere a j Jedna można pozać, że posać
Fale biegnące. y t=0 vt. y = f(x), t = 0 y = f(x - vt), t ogólne równanie fali biegnącej w prawo
 ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
ver b drgania harmoniczne
 ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ANEMOMETRIA LASEROWA
 1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Pochodna kierunkowa i gradient Równania parametryczne prostej przechodzącej przez punkt i skierowanej wzdłuż jednostkowego wektora mają postać:
 ochodna kierunkowa i gradient Równania parametrcne prostej prechodącej pre punkt i skierowanej wdłuż jednostkowego wektora mają postać: Oblicam pochodną kierunkową u ( u, u ) 1 + su + su 1 (, ) d d d ˆ
ochodna kierunkowa i gradient Równania parametrcne prostej prechodącej pre punkt i skierowanej wdłuż jednostkowego wektora mają postać: Oblicam pochodną kierunkową u ( u, u ) 1 + su + su 1 (, ) d d d ˆ
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
drgania h armoniczne harmoniczne
 ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
= sin. = 2Rsin. R = E m. = sin
 Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Studia magisterskie ENERGETYKA. Jan A. Szantyr. Wybrane zagadnienia z mechaniki płynów. Ćwiczenia 6. Wyznaczanie przepływu przez rurociągi II
 Sia maiserskie ENERGETYKA Jan A. Sanyr Wyrane aanienia meaniki płynów Ćwienia 6 Wynaanie prepływ pre rroiąi II Prykła W owarym iornik najje się prosokąny owór o serokośi i wysokośi, amykany aswą. Olełość
Sia maiserskie ENERGETYKA Jan A. Sanyr Wyrane aanienia meaniki płynów Ćwienia 6 Wynaanie prepływ pre rroiąi II Prykła W owarym iornik najje się prosokąny owór o serokośi i wysokośi, amykany aswą. Olełość
Wykład I Krzysztof Golec-Biernat Optyka 1 / 16
 Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
G:\AA_Wyklad 2000\FIN\DOC\Fale wodnem.doc. Drgania i fale III rok Fizyki BC. Model: - długi kanał o prostokątnym przekroju i głębokości h,
 13-1-00 G:\AA_Wklad 000\FIN\DOC\Fale Fale wodne: Drgania i fale III rok Fiki BC Model: - długi kanał o prostokątnm prekroju i głębokości h, - ruch fali wdłuż, nieależn od x, wchlenia wdłuż, - woda nieściśliwa
13-1-00 G:\AA_Wklad 000\FIN\DOC\Fale Fale wodne: Drgania i fale III rok Fiki BC Model: - długi kanał o prostokątnm prekroju i głębokości h, - ruch fali wdłuż, nieależn od x, wchlenia wdłuż, - woda nieściśliwa
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Arkusz 6. Elementy geometrii analitycznej w przestrzeni
 Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Dualizm korpuskularno falowy
 Dualizm korpuskularno falowy Fala elektromagnetyczna o długości λ w pewnych zjawiskach zachowuje się jak cząstka (foton) o pędzie p=h/λ i energii E = h = h. c/λ p Cząstki niosą pęd p Cząstce o pędzie p
Dualizm korpuskularno falowy Fala elektromagnetyczna o długości λ w pewnych zjawiskach zachowuje się jak cząstka (foton) o pędzie p=h/λ i energii E = h = h. c/λ p Cząstki niosą pęd p Cząstce o pędzie p
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Wykład 21: Studnie i bariery cz.1.
 Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Podstawy fizyki wykład 7
 Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki sezon 1 VIII. Ruch falowy
 Podstawy fizyki sezon 1 VIII. Ruch falowy Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Gdzie szukać fal? W potocznym
Podstawy fizyki sezon 1 VIII. Ruch falowy Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Gdzie szukać fal? W potocznym
Równania Maxwella. roth t
 , H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
FALE MATERII. De Broglie, na podstawie analogii optycznych, w roku 1924 wysunął hipotezę, że
 FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
Zestaw zadań 12: Przekształcenia liniowe. Macierze przekształceń liniowych. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t
 Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące
 Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Powierzchnie stopnia drugiego
 Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy
 Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
Ψ(x, t) punkt zamocowania liny zmienna t, rozkład zaburzeń w czasie. x (lub t)
 RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
obszary o większej wartości zaburzenia mają ciemny odcień, a
 Co to jest fala? Falę stanowi rozchodzące się w ośrodku zaburzenie, zmiany jakiejś wielkości (powtarzające się wielokrotnie i cyklicznie zmieniające swoje wychylenie). Fala pojawia się w ośrodkach, których
Co to jest fala? Falę stanowi rozchodzące się w ośrodku zaburzenie, zmiany jakiejś wielkości (powtarzające się wielokrotnie i cyklicznie zmieniające swoje wychylenie). Fala pojawia się w ośrodkach, których
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 18, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
2. Rodzaje fal. Fale te mogą rozchodzić się tylko w jakimś ośrodku materialnym i podlegają prawom Newtona.
 . Rodzaje fal Wykład 9 Fale mechaniczne, których przykładem są fale wzbudzone w długiej sprężynie, fale akustyczne, fale na wodzie. Fale te mogą rozchodzić się tylko w jakimś ośrodku materialnym i podlegają
. Rodzaje fal Wykład 9 Fale mechaniczne, których przykładem są fale wzbudzone w długiej sprężynie, fale akustyczne, fale na wodzie. Fale te mogą rozchodzić się tylko w jakimś ośrodku materialnym i podlegają
W siła działająca na bryłę zredukowana do środka masy ( = 0
 Popęd i popęd bryły Bryła w ruchu posępowym. Zasada pędu i popędu ma posać: p p S gdie: p m v pęd bryły w ruchu posępowym S c W d popęd siły diałającej na bryłę w ruchu posępowym aś: v c prędkość środka
Popęd i popęd bryły Bryła w ruchu posępowym. Zasada pędu i popędu ma posać: p p S gdie: p m v pęd bryły w ruchu posępowym S c W d popęd siły diałającej na bryłę w ruchu posępowym aś: v c prędkość środka
Aby nie uszkodzić głowicy dźwiękowej, nie wolno stosować amplitudy większej niż 2000 mv.
 Tematy powiązane Fale poprzeczne i podłużne, długość fali, amplituda, częstotliwość, przesunięcie fazowe, interferencja, prędkość dźwięku w powietrzu, głośność, prawo Webera-Fechnera. Podstawy Jeśli fala
Tematy powiązane Fale poprzeczne i podłużne, długość fali, amplituda, częstotliwość, przesunięcie fazowe, interferencja, prędkość dźwięku w powietrzu, głośność, prawo Webera-Fechnera. Podstawy Jeśli fala
Interferometr Macha-Zehndera. Zapis sinusoidalnej siatki dyfrakcyjnej i pomiar jej okresu przestrzennego.
 Ćwiczenie 6 Interferometr Macha-Zehndera. Zapis sinusoidalnej siatki dyfrakcyjnej i pomiar jej okresu przestrzennego. Interferometr Macha-Zehndera Interferometr Macha-Zehndera jest często wykorzystywany
Ćwiczenie 6 Interferometr Macha-Zehndera. Zapis sinusoidalnej siatki dyfrakcyjnej i pomiar jej okresu przestrzennego. Interferometr Macha-Zehndera Interferometr Macha-Zehndera jest często wykorzystywany
Zasada nieoznaczoności Heisenberga
 Fale materii paczki falowe o różnej szerokości Dwa gaussowskie rozkład amplitud fal armonicznc o różnc szerokościac σ p i różnc wartościac średnic pędu p. Części rzeczwista ReΨ i urojona mψ funkcji falowc
Fale materii paczki falowe o różnej szerokości Dwa gaussowskie rozkład amplitud fal armonicznc o różnc szerokościac σ p i różnc wartościac średnic pędu p. Części rzeczwista ReΨ i urojona mψ funkcji falowc
Fale mechaniczne i akustyka
 Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
WSTĘP DO OPTYKI FOURIEROWSKIEJ
 1100-4BW1, rok akademicki 018/19 WSTĘP DO OPTYKI FOURIEROWSKIEJ dr hab. Rafał Kasztelanic Wykład 4 Przestrzeń swobodna jako filtr częstości przestrzennych Załóżmy, że znamy rozkład pola na fale monochromatyczne
1100-4BW1, rok akademicki 018/19 WSTĘP DO OPTYKI FOURIEROWSKIEJ dr hab. Rafał Kasztelanic Wykład 4 Przestrzeń swobodna jako filtr częstości przestrzennych Załóżmy, że znamy rozkład pola na fale monochromatyczne
WYKŁAD FIZYKAIIIB 2000 Drgania tłumione
 YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 18, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Elektrodynamika. Część 9. Potencjały i pola źródeł zmiennych w czasie. Ryszard Tanaś
 Elektrodynamika Część 9 Potencjały i pola źródeł zmiennych w czasie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 10 Potencjały i pola źródeł zmiennych w
Elektrodynamika Część 9 Potencjały i pola źródeł zmiennych w czasie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 10 Potencjały i pola źródeł zmiennych w
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Moment pędu fali elektromagnetycznej
 napisał Michał Wierzbicki Moment pędu fali elektromagnetycznej Definicja momentu pędu pola elektromagnetycznego Gęstość momentu pędu pola J w elektrodynamice definuje się za pomocą wzoru: J = r P = ɛ 0
napisał Michał Wierzbicki Moment pędu fali elektromagnetycznej Definicja momentu pędu pola elektromagnetycznego Gęstość momentu pędu pola J w elektrodynamice definuje się za pomocą wzoru: J = r P = ɛ 0
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku.
 Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na okres drgań
 KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
Zestaw zadań 12: Przekształcenia liniowe. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t. x y + 2t 2x 3y + 5z t x z t
 Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
Wykład 9. Fizyka 1 (Informatyka - EEIiA 2006/07)
 Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
gęstością prawdopodobieństwa
 Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
OPTYKA FALOWA. W zjawiskach takich jak interferencja, dyfrakcja i polaryzacja światło wykazuje naturę
 OPTYKA FALOWA W zjawiskach takich jak interferencja, dyfrakcja i polaryzacja światło wykazuje naturę falową. W roku 8 Thomas Young wykonał doświadczenie, które pozwoliło wyznaczyć długość fali światła.
OPTYKA FALOWA W zjawiskach takich jak interferencja, dyfrakcja i polaryzacja światło wykazuje naturę falową. W roku 8 Thomas Young wykonał doświadczenie, które pozwoliło wyznaczyć długość fali światła.
ZADANIA Z FUNKCJI ANALITYCZNYCH LICZBY ZESPOLONE
 . Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
. Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
Fizyka Elementarna rozwiązania zadań. Część 20, 21 i 22 Przygotowanie: Grzegorz Brona,
 Fizyka Elementarna rozwiązania zadań. Część 0, 1 i Przygotowanie: Grzegorz Brona, 0.1.008 Seria 0 Zadanie 1 Punkt Q porusza się w płaszczyźnie XOY po okręgu o promieniu A ze stałą prędkością kątową ω.
Fizyka Elementarna rozwiązania zadań. Część 0, 1 i Przygotowanie: Grzegorz Brona, 0.1.008 Seria 0 Zadanie 1 Punkt Q porusza się w płaszczyźnie XOY po okręgu o promieniu A ze stałą prędkością kątową ω.
Promieniowanie dipolowe
 Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Powtórzenie na kolokwium nr 4. Dynamika punktu materialnego
 Powtórzenie na olowiu nr 4 Dynaia puntu aterialnego 1 zadanie dynaii: znany jest ruh, szuay siły go wywołująej. Znane funje opisująe trajetorię ruhu różnizujey i podstawiay do równań ruhu. 2 zadanie dynaii:
Powtórzenie na olowiu nr 4 Dynaia puntu aterialnego 1 zadanie dynaii: znany jest ruh, szuay siły go wywołująej. Znane funje opisująe trajetorię ruhu różnizujey i podstawiay do równań ruhu. 2 zadanie dynaii:
Podwaliny szczególnej teorii względności
 W-6 (Jarosewi) 7 slajdów Na podsawie preenaji prof. J. Rukowskiego Podwalin sególnej eorii wględnośi asada wględnośi Galileusa ekspermen Mihelsona i Morle a ransformaja Lorena pierwsa spreność współesnej
W-6 (Jarosewi) 7 slajdów Na podsawie preenaji prof. J. Rukowskiego Podwalin sególnej eorii wględnośi asada wględnośi Galileusa ekspermen Mihelsona i Morle a ransformaja Lorena pierwsa spreność współesnej
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Solitony i zjawiska nieliniowe we włóknach optycznych
 Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Początek XX wieku. Dualizm korpuskularno - falowy
 Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu
 Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Podstawy fizyki sezon 2 8. Fale elektromagnetyczne
 Podstawy fizyki sezon 8. Fale elektromagnetyczne Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Przenoszenie
Podstawy fizyki sezon 8. Fale elektromagnetyczne Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Przenoszenie
 Ą ń ń ć Ę Ę ć ć ń ń Ż ń ń Ą Ą ń Ż Ń Ż ć Ą ń ŚĆ ć Ę Ę Ą ń Ś ń ć Ę Ą ń Ę ń ń ń ń ć ń ń Ś Ź ń ć ć ń ć ń Ś Ż Ę Ń ń ń ń ń ń ć Ń Ę Ę Ę Ę Ę ńń ź ĄĘ Ę ź ń Ąń Ę Ę Ę Ź Ę Ę Ą Ś Ę Ę ć Ś Ą Ń ć ń ń ć Ś ć Ń Ó ń ń ć
Ą ń ń ć Ę Ę ć ć ń ń Ż ń ń Ą Ą ń Ż Ń Ż ć Ą ń ŚĆ ć Ę Ę Ą ń Ś ń ć Ę Ą ń Ę ń ń ń ń ć ń ń Ś Ź ń ć ć ń ć ń Ś Ż Ę Ń ń ń ń ń ń ć Ń Ę Ę Ę Ę Ę ńń ź ĄĘ Ę ź ń Ąń Ę Ę Ę Ź Ę Ę Ą Ś Ę Ę ć Ś Ą Ń ć ń ń ć Ś ć Ń Ó ń ń ć
4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)
 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 5, Radosław Chrapkiewicz, Filip Ozimek
 Podstaw Fizki IV Optka z elementami fizki współczesnej wkład 5, 27.02.2012 wkład: pokaz: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wkład 4 - przpomnienie dielektrki
Podstaw Fizki IV Optka z elementami fizki współczesnej wkład 5, 27.02.2012 wkład: pokaz: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wkład 4 - przpomnienie dielektrki
Fizyka dla Informatyki Stosowanej
 Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
podsumowanie (E) E l Eds 0 V jds
 e-8.6.7 fale podsumowanie () Γ dl 1 ds ρ d S ε V D ds ρ d S ( ϕ ) 1 ρ ε D ρ D ρ V D ( D εε ) εε S jds V ρ d t j ρ t j σ podsumowanie (H) Bdl Γ μ S jds B μ j S Bds B ( B A) Hdl Γ S jds H j ( B μμ H ) ε
e-8.6.7 fale podsumowanie () Γ dl 1 ds ρ d S ε V D ds ρ d S ( ϕ ) 1 ρ ε D ρ D ρ V D ( D εε ) εε S jds V ρ d t j ρ t j σ podsumowanie (H) Bdl Γ μ S jds B μ j S Bds B ( B A) Hdl Γ S jds H j ( B μμ H ) ε
Widmo fal elektromagnetycznych
 Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
WŁASNOŚCI FAL (c.d.)
 RUCH FALOWY Własności i rodzaje fal. Prędkość rozchodzenia się fal. Fala harmoniczna płaska. Fala stojąca. Zasada Huygensa. Dyfrakcja fal. Obraz dyfrakcyjny. Kryterium Rayleigha. Interferencja fal. Doświadczenie
RUCH FALOWY Własności i rodzaje fal. Prędkość rozchodzenia się fal. Fala harmoniczna płaska. Fala stojąca. Zasada Huygensa. Dyfrakcja fal. Obraz dyfrakcyjny. Kryterium Rayleigha. Interferencja fal. Doświadczenie
Zjawisko interferencji fal
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natężenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natężenia fal) w którym zachodzi stabilne w czasie ich
MECHANIKA RELATYWISTYCZNA TRANFORMACJA LORENTZA
 Wdiał EAIiE Kierunek: ELEKTRONIKA I TELEKOMUNIKACJA Predmio: Fika II MECHANIKA RELATYWISTYCZNA TRANFORMACJA LORENTZA 0/0, lao SZCZEGÓLNA TEORIA WZGLĘDNOŚCI Fika relawisna jes wiąana pomiarem miejsa i asu
Wdiał EAIiE Kierunek: ELEKTRONIKA I TELEKOMUNIKACJA Predmio: Fika II MECHANIKA RELATYWISTYCZNA TRANFORMACJA LORENTZA 0/0, lao SZCZEGÓLNA TEORIA WZGLĘDNOŚCI Fika relawisna jes wiąana pomiarem miejsa i asu
PRZYKŁADY RUCHU HARMONICZNEGO. = kx
 RUCH HARMONICZNY; FALE PRZYKŁADY RUCHU HARMONICZNEGO F d k F s k Gdowski F k Każdy ruch w którym siła starająca się przywrócić położenie równowagi jest proporcjonalna do wychylenia od stanu równowagi jest
RUCH HARMONICZNY; FALE PRZYKŁADY RUCHU HARMONICZNEGO F d k F s k Gdowski F k Każdy ruch w którym siła starająca się przywrócić położenie równowagi jest proporcjonalna do wychylenia od stanu równowagi jest
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE
 LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
18 K A T E D R A F I ZYKI STOSOWAN E J
 18 K A T E D R A F I ZYKI STOSOWAN E J P R A C O W N I A F I Z Y K I Ćw. 18. Wyznaczanie długości fal świetlnych diody laserowej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło jest promieniowaniem
18 K A T E D R A F I ZYKI STOSOWAN E J P R A C O W N I A F I Z Y K I Ćw. 18. Wyznaczanie długości fal świetlnych diody laserowej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło jest promieniowaniem
Wykład FIZYKA I. 11. Fale mechaniczne. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
x od położenia równowagi
 RUCH HARMONICZNY Ruch powtarając się w regularnch odstępach casu nawa ruche okresow. Jeżeli w taki ruchu seroko rouiane odchlenie od stanu równowagi ( np. odchlenie as podcepionej do sprężn, wartość wektora
RUCH HARMONICZNY Ruch powtarając się w regularnch odstępach casu nawa ruche okresow. Jeżeli w taki ruchu seroko rouiane odchlenie od stanu równowagi ( np. odchlenie as podcepionej do sprężn, wartość wektora
Fizyka dla Informatyki Stosowanej
 Fia dla Inforai Sosowanej Jae Gola Seesr iow 16/17 Wład nr Na pierws władie podane osał wielośi służąe do opisu ruhu ora prład ruhów. Tera asanowi się nad prawai rądąi ruhe na raie dla prpadu punu aerialnego.
Fia dla Inforai Sosowanej Jae Gola Seesr iow 16/17 Wład nr Na pierws władie podane osał wielośi służąe do opisu ruhu ora prład ruhów. Tera asanowi się nad prawai rądąi ruhe na raie dla prpadu punu aerialnego.
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 19, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 19, 27.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 18 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 19, 27.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 18 - przypomnienie
Światło jako fala Fala elektromagnetyczna widmo promieniowania Czułość oka ludzkiego w zakresie widzialnym
 Światło jako fala Fala elektromagnetyczna widmo promieniowania ν = c λ Czułość oka ludzkiego w zakresie widzialnym Wytwarzanie fali elektromagnetycznej o częstościach radiowych E(x, t) = Em sin (kx ωt)
Światło jako fala Fala elektromagnetyczna widmo promieniowania ν = c λ Czułość oka ludzkiego w zakresie widzialnym Wytwarzanie fali elektromagnetycznej o częstościach radiowych E(x, t) = Em sin (kx ωt)
Fale elektromagnetyczne
 Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
KATEDRA TELEKOMUNIKACJI I FOTONIKI
 ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
Energia w ruchu harmonicznym
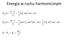 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 5 Temat: Interferometr Michelsona 7.. Cel i zakres ćwiczenia 7 INTERFEROMETR MICHELSONA Celem ćwiczenia jest zapoznanie się z budową i
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 5 Temat: Interferometr Michelsona 7.. Cel i zakres ćwiczenia 7 INTERFEROMETR MICHELSONA Celem ćwiczenia jest zapoznanie się z budową i
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 12, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład, 0..07 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład - przypomnienie superpozycja
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład, 0..07 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład - przypomnienie superpozycja
Światło Światł jako fala
 Światło jako fala 1 Fala elektromagnetczna widmo promieniowania ν c Czułość oka ludzkiego w zakresie widzialnm Wtwarzanie fali elektromagnetcznej o częstościach radiowch E(x, B(x, t) t) E B m m sin (kx
Światło jako fala 1 Fala elektromagnetczna widmo promieniowania ν c Czułość oka ludzkiego w zakresie widzialnm Wtwarzanie fali elektromagnetcznej o częstościach radiowch E(x, B(x, t) t) E B m m sin (kx
Równania Maxwella i równanie falowe
 Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
13. Optyka Polaryzacja przez odbicie.
 13. Optyka 13.8. Polaryzaja przz odbii. x y z Fala lktromagntyzna, to fala poprzzna. Wktory E i są prostopadł do kirunku rozhodznia się fali. W wszystkih punktah wktory E (podobni jak ) są do sibi równolgł.
13. Optyka 13.8. Polaryzaja przz odbii. x y z Fala lktromagntyzna, to fala poprzzna. Wktory E i są prostopadł do kirunku rozhodznia się fali. W wszystkih punktah wktory E (podobni jak ) są do sibi równolgł.
h 2 h p Mechanika falowa podstawy pˆ 2
 Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 11, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 11, 19.03.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 10 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 11, 19.03.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 10 - przypomnienie
1. Rezonans w obwodach elektrycznych 2. Filtry częstotliwościowe 3. Sprzężenia magnetyczne 4. Sygnały odkształcone
 Wyład 6 - wersja srócona. ezonans w obwodach elerycznych. Filry częsoliwościowe. Sprzężenia magneyczne 4. Sygnały odszałcone AMD ezonans w obwodach elerycznych Zależności impedancji dwójnia C od pulsacji
Wyład 6 - wersja srócona. ezonans w obwodach elerycznych. Filry częsoliwościowe. Sprzężenia magneyczne 4. Sygnały odszałcone AMD ezonans w obwodach elerycznych Zależności impedancji dwójnia C od pulsacji
Ośrodki dielektryczne optycznie nieliniowe
 Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 13, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 13, 16.11.017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 1 - przypomnienie
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 13, 16.11.017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 1 - przypomnienie
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
