W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące
|
|
|
- Damian Kot
- 5 lat temu
- Przeglądów:
Transkrypt
1 Jucaan, Meico, Februar 005
2 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę Składanie fal fale sojące
3 3/ L.R. Jaroszewicz Pojęcie ruchu falowego Ośrodek sprężs cechuje ożliwość wzajenego oddziałwania na siebie cząsek wchodzącch w jego skład i przekazwania w en sposób energii. Jeżeli w pewneu obszarowi ośrodka sprężsego dosarcz energii nadając jego cząskoą ruch np. drgając o dziękię sprężs ę własnościo ośrodka energia a będzie ransporowana z prędkością zależną od ch własności. Ruch związan z ranspore energii przez ośrodek sprężs, bez ransporu as, nazwa ruchai falowi lub po prosu falai. Ruch osclacjne albo inaczej drgania, oówione w rakcie poprzedniego p wkładu, sąą również związaneą z ruche falow wośrodkach sprężsch.
4 4/ L.R. Jaroszewicz Rodzaje fal Kierunek rozchodzenia się zaburzenia ośrodka, w ruchu falow, nazwa proienie i fali. Zbiór punków, w kórch zaburzenie a ę saą fazę drgania w danej chwili czasu sanowi powierzchnię falową. Powierzchnię falową najdalej odsunięa od źródła nazwa czołe fali. Ze względu na fizkę oddziałwania: #fale sprężse # fale elekroagneczne. -Ze względu na kierunek drgań cząsek w odniesieniu do kierunku rozchodzenia się fali: # poprzeczne # podłużne. Ze względu na kszał ł powierzchni i falowej: # płaskie # kulise # walcowe. Ze względu na obszar zaburzenia: # powierzchniowe # objęościowe
5 5/ L.R. Jaroszewicz Równanie fali płaskiej ( ) [ ] τ p j 0 ( ) [ ] τ 0 τ τ ( ) [ ] τ (0 ϕ0 ) Wchlenia i będą równe gd arguen funkcji us będą różnić się o n dla n0,,,... Dla n - > długość fali ) (
6 6/ L.R. Jaroszewicz Wchlenie w dowoln punkcie oddalon o od punku 0 wnosi Wchlenie w dowoln punkcie oddalon o od punku 0 wnosi ) ( k i Oznaczając /k ( ) k ( ) + k Równanie fali: Ψ Ψ Ψ r k j r k r ep Re cos ), ( Paraer fali li d ść ( li ść) f dł ść f li ( k d apliuda, częsość (częsoliwość), faza, długość fali (wekor falow), prędkość: f k d d ( ) cons k
7 7/ L.R. Jaroszewicz Równanie falowe ( ) ) ( ( ) ) ) ( ( Ψ Ψ + Ψ + Ψ z Ψ ΔΨ
8 8/ L.R. Jaroszewicz Prędkość propagacji fali S F Δl FΔ Δ ΔlΔ l l σ ε E F σ S εes ES Wczasie Δ zaburzenie dorze w ruchu falow na odległość l od czoła pręa ę asa objęa zaburzenie ls Prędkość rozchodzenia się zaburzenia Δl Δl ESΔ ls E/ l ΔΔ l Δ W wniku naprężenia σ prędkość cząsek wzrośnie od zero do E/ Jeżeli działanie sił wwołuje, nie zian długości pręa, lecz odkszałcenie objęościowe lub posaciowe o G E Δ K Δl Δ W ośrodkach gazowch, w sałej eperaurze, oduł sprężsości objęościowej jes równ ciśnieniu Kp. Jeśli brak jes wian ciepła z ooczenie (przeian adiabaczne) wówczas K κp gdzie κc P /C V. W powierzu κ.4,.93 kg/ 3 prz ciśnieniu p03 hpa 33.5 /s.
9 9/ L.R. Jaroszewicz Energia i pęd przenoszone przez falęę Gęsość energii zgroadzonej w jednosce obję- ( k ) ościś ośrodka ś sprężsego ż przenoszącego fale d e spr V a V cos( k) V a cos( k) V a e d spr Naężenie fali jes sruienie energii przez jednoskową powierzchnię prosopadłą do proienia fali I e spr Va V cos( + ϕ ) a e spr ( ) pęd przenoszon przez falę dp d p d
10 0/ L.R. Jaroszewicz Składanie fal fale sojące i ( k ), i, w + cos [( + k) ( - k) ] [( + k) + ( - k) ] Gd cos k B cos 0 B 0 B cos k cos Cał sprężs ośrodek liniow podzieli się na przedział o długości /. Wszskie punk każdej akiej części będą drgać w zgodnch fazach, naoias faz części sąsiednich będą różnić się o Gd cos B B węzeł srzałka a 0 L 0 L 0 L L / /4
11 Jucaan, Meico, Februar 005
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
Fale biegnące. y t=0 vt. y = f(x), t = 0 y = f(x - vt), t ogólne równanie fali biegnącej w prawo
 ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
Energia w ruchu harmonicznym
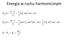 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku.
 Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
ę ę ż ż ć ć ę ć ę ż ć ć ę Ś ę ę ę Ź Ź ż Ś ę ć ć ę ę ę ę ę ę ż ć ż ć ę ę ę Ź ę ż ę ę ę
 ę Ł ć ż ć ż ć ę ę ę ż ć ż ć ę ż ż ć ę ę ę ę ę ę ę ę ę ż ę ę ę Ź ę ż ę ć ż ę ę ę Ź ć Ź ę ę ż ż ć ć ę ć ę ż ć ć ę Ś ę ę ę Ź Ź ż Ś ę ć ć ę ę ę ę ę ę ż ć ż ć ę ę ę Ź ę ż ę ę ę ć ę ę ż ę ż ć ć Ść ć ę ć ć ż
ę Ł ć ż ć ż ć ę ę ę ż ć ż ć ę ż ż ć ę ę ę ę ę ę ę ę ę ż ę ę ę Ź ę ż ę ć ż ę ę ę Ź ć Ź ę ę ż ż ć ć ę ć ę ż ć ć ę Ś ę ę ę Ź Ź ż Ś ę ć ć ę ę ę ę ę ę ż ć ż ć ę ę ę Ź ę ż ę ę ę ć ę ę ż ę ż ć ć Ść ć ę ć ć ż
Ł ż ż Ł ż ż ż ż ż ż ż ż Ś ż ż ż ż ż ż ż ż ż ź ż ż ż ż ż ć ż ż ż ż ż ć ż
 Ś Ż Ś ć ż Ś ż ź ż ż ż ć ż ć Ł ż ż Ł ż ż ż ż ż ż ż ż Ś ż ż ż ż ż ż ż ż ż ź ż ż ż ż ż ć ż ż ż ż ż ć ż ż ż ż ż ć ż ć ź ż ż ć ć ż ć ż ż ż ć ż ż ć ć ż ż ż ż ć ż ż ż ż ż ż ć ż ż ż ż ż ć ż ć ć ż ć ż ż ż ć ć ć
Ś Ż Ś ć ż Ś ż ź ż ż ż ć ż ć Ł ż ż Ł ż ż ż ż ż ż ż ż Ś ż ż ż ż ż ż ż ż ż ź ż ż ż ż ż ć ż ż ż ż ż ć ż ż ż ż ż ć ż ć ź ż ż ć ć ż ć ż ż ż ć ż ż ć ć ż ż ż ż ć ż ż ż ż ż ż ć ż ż ż ż ż ć ż ć ć ż ć ż ż ż ć ć ć
Ł Ł ż Ś ż Ś Ź ć
 Ł Ę Ł Ł ż Ś ż Ś Ź ć ć Ść Ż ż ż ż Ś Ś Ć ć Ś Ę ĘĆ Ł Ł ŚĆ ŚĆ Ą ż ć ĘŚ Ą Ą Ę ż Ć Ś ć Ż Ż ć Ś Ą ż ż Ż Ą Ą Ś Ż ż ż Ś Ś Ę ż Ś Ś ż Ś Ż Ść Ś ż ć ż Ł ż ż ż Ł ż Ł Ż ż Ą Ą Ą ć Ś ż ż ż Ż Ś ż Ł Ś ź ż ż ź Ź ź ź Ź Ź Ę
Ł Ę Ł Ł ż Ś ż Ś Ź ć ć Ść Ż ż ż ż Ś Ś Ć ć Ś Ę ĘĆ Ł Ł ŚĆ ŚĆ Ą ż ć ĘŚ Ą Ą Ę ż Ć Ś ć Ż Ż ć Ś Ą ż ż Ż Ą Ą Ś Ż ż ż Ś Ś Ę ż Ś Ś ż Ś Ż Ść Ś ż ć ż Ł ż ż ż Ł ż Ł Ż ż Ą Ą Ą ć Ś ż ż ż Ż Ś ż Ł Ś ź ż ż ź Ź ź ź Ź Ź Ę
ń ń ć ń Ź ć ń ć Ź ń Ź ź ć Ę ć Ź ć ź ń ń ź
 ń ń Ę Ó Ń Ł ń Ł Ó Ł Ść ń ć Ś Ó ń ń ń ń Ź ć ć ń ń ć ń Ź ć ń ć Ź ń Ź ź ć Ę ć Ź ć ź ń ń ź ć ć ń ń ń ń ń ć ć ń Ź ń Ź ń ń ź ń Ł ć ź ź ź ź ń ć Ź ć ń ń ń ń ź ń ć ń ń ń ń ń ć ń ń ń ć ź ń ć ź Ź ń ń Ę ź Ć ź ć ć
ń ń Ę Ó Ń Ł ń Ł Ó Ł Ść ń ć Ś Ó ń ń ń ń Ź ć ć ń ń ć ń Ź ć ń ć Ź ń Ź ź ć Ę ć Ź ć ź ń ń ź ć ć ń ń ń ń ń ć ć ń Ź ń Ź ń ń ź ń Ł ć ź ź ź ź ń ć Ź ć ń ń ń ń ź ń ć ń ń ń ń ń ć ń ń ń ć ź ń ć ź Ź ń ń Ę ź Ć ź ć ć
ś ę ę Ś Ż Ś ę ę ść ś ś ę Ś Ś Ś Ś ś Ś ż Ż ę ż Ś Ź Ś Ś ś Ś Ś Ż Ś ś ęść ę ę Ś ę ę
 ż ęś ę ż Ł ś ż ś ęś ę Ż ę ę ś Ś Ś ś ś Ś ś Ś ę ę ś ę ę Ś Ż Ś ę ę ść ś ś ę Ś Ś Ś Ś ś Ś ż Ż ę ż Ś Ź Ś Ś ś Ś Ś Ż Ś ś ęść ę ę Ś ę ę ś ż ż ż Ż ęść ę Łę ś ś Ź ż Ż ę Ś ś ż Ż Ź Ż ś ś ż ż ż Ż Ż Ź Ś ś Ż Ż Ł ś ś ż
ż ęś ę ż Ł ś ż ś ęś ę Ż ę ę ś Ś Ś ś ś Ś ś Ś ę ę ś ę ę Ś Ż Ś ę ę ść ś ś ę Ś Ś Ś Ś ś Ś ż Ż ę ż Ś Ź Ś Ś ś Ś Ś Ż Ś ś ęść ę ę Ś ę ę ś ż ż ż Ż ęść ę Łę ś ś Ź ż Ż ę Ś ś ż Ż Ź Ż ś ś ż ż ż Ż Ż Ź Ś ś Ż Ż Ł ś ś ż
ś ść ść ś ść ść ś ś ś ś ść ś ś ś ść ść
 Ą Ł Ł Ł Ę Ł ś ś ś ś ść ść ść ść Ś ść ŚĆ ś ŚĆ ś ś ść ść ś ść ść ś ś ś ś ść ś ś ś ść ść ś ś ś Ż ś Ś ś Ś ść ś ś ś ś ś ś ś ś Ś ś ś ś ś Ł Ś ś ś ś Ś ś ś ź Ś ŚĆ ś ś ś ś ś ś Ś ś Ś ś ś ś ś ś ś ś Ś Ś ść ś ś ś ś
Ą Ł Ł Ł Ę Ł ś ś ś ś ść ść ść ść Ś ść ŚĆ ś ŚĆ ś ś ść ść ś ść ść ś ś ś ś ść ś ś ś ść ść ś ś ś Ż ś Ś ś Ś ść ś ś ś ś ś ś ś ś Ś ś ś ś ś Ł Ś ś ś ś Ś ś ś ź Ś ŚĆ ś ś ś ś ś ś Ś ś Ś ś ś ś ś ś ś ś Ś Ś ść ś ś ś ś
ź Ź Ź ć ć ć ź ć ć ć ć ć Ź
 ź Ź Ź ć ć ć ź ć ć ć ć ć Ź ć ć ć ć ć ć ć ć Ż ć ć ć ć ć ć ć ć ć ć ć Ż Ż ć ć ć ć ć ć ć ć Ż ć ć ć ź ć Ź ć ć ć ć ć ć ć ć ć ź ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ż ć ć ć ć Ż ć ć ć ć ć ć ć ć Ż ć Ł Ś Ś ć Ą Ę ć Ę ć Ż ć
ź Ź Ź ć ć ć ź ć ć ć ć ć Ź ć ć ć ć ć ć ć ć Ż ć ć ć ć ć ć ć ć ć ć ć Ż Ż ć ć ć ć ć ć ć ć Ż ć ć ć ź ć Ź ć ć ć ć ć ć ć ć ć ź ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ż ć ć ć ć Ż ć ć ć ć ć ć ć ć Ż ć Ł Ś Ś ć Ą Ę ć Ę ć Ż ć
Fale mechaniczne i akustyka
 Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Ą ŚĆ Ś Ś Ę ć
 Ą Ę Ą Ą ŚĆ Ś Ś Ę ć ć ć ć ź ć ć ć ć ć ć ć ć Ą ć ć ć Ą Ś ć Ś ć ć Ą ć Ś Ś Ą Ś Ą ć ć Ą ź ź ć ć Ą ć ź ć Ą ć Ą ć ć ć ć ć ć ć ć ć ć ć ć ć ź ć ć Ś ć ć ć Ę Ą ć Ą ć ć ć ć ć ć Ł ź ź ź Ł Ł ć Ą ć ć ć ć ć Ą ć Ą ć Ą
Ą Ę Ą Ą ŚĆ Ś Ś Ę ć ć ć ć ź ć ć ć ć ć ć ć ć Ą ć ć ć Ą Ś ć Ś ć ć Ą ć Ś Ś Ą Ś Ą ć ć Ą ź ź ć ć Ą ć ź ć Ą ć Ą ć ć ć ć ć ć ć ć ć ć ć ć ć ź ć ć Ś ć ć ć Ę Ą ć Ą ć ć ć ć ć ć Ł ź ź ź Ł Ł ć Ą ć ć ć ć ć Ą ć Ą ć Ą
Ż ń ń ź ć Ż Ł ć ż ć ż ć Ś Ć ć ż ń ż ń ń ż Ć ż ć ż ń
 Ż ż ż ń Ł Ż ż ń ń ż ń Ę ń ń ż Ż ż Ż ń ń ź ć Ż Ł ć ż ć ż ć Ś Ć ć ż ń ż ń ń ż Ć ż ć ż ń Ę ń ń Ź Ż ć ń ń ń ń ż ż ć Ź ń ń Ź Ś Ś ń ć Ź ń Ę Ę ń ć ż ć Ś Ę Ź ż ń ż Ż Ż Ś ż Ć ż ń Ć ż ż ń ć Ż ż ż ć Ć Ż ż Ś ż ć Ź
Ż ż ż ń Ł Ż ż ń ń ż ń Ę ń ń ż Ż ż Ż ń ń ź ć Ż Ł ć ż ć ż ć Ś Ć ć ż ń ż ń ń ż Ć ż ć ż ń Ę ń ń Ź Ż ć ń ń ń ń ż ż ć Ź ń ń Ź Ś Ś ń ć Ź ń Ę Ę ń ć ż ć Ś Ę Ź ż ń ż Ż Ż Ś ż Ć ż ń Ć ż ż ń ć Ż ż ż ć Ć Ż ż Ś ż ć Ź
ż ń ż ć ń ż ść ś ż ć ś ś Ż ść ść ś ść ść ść ść ć ń ć ń ć ń ś ś ś ż ć ź ś ś ś ń ż ś ż ż ż ś ś ż ć
 ż ń ż ć ń ż ść ś ż ć ś ś Ż ść ść ś ść ść ść ść ć ń ć ń ć ń ś ś ś ż ć ź ś ś ś ń ż ś ż ż ż ś ś ż ć ż ż ż ś ś ść ż ść ś ść ś ż ś ś ś ś ś ż ś ś ś ś ż ś ś ś ś ż ś Ź ś ś ś ś ż ń ś ż ż ż ć ż ź ż ż ć ż Ż ś ć ś
ż ń ż ć ń ż ść ś ż ć ś ś Ż ść ść ś ść ść ść ść ć ń ć ń ć ń ś ś ś ż ć ź ś ś ś ń ż ś ż ż ż ś ś ż ć ż ż ż ś ś ść ż ść ś ść ś ż ś ś ś ś ś ż ś ś ś ś ż ś ś ś ś ż ś Ź ś ś ś ś ż ń ś ż ż ż ć ż ź ż ż ć ż Ż ś ć ś
Ż Ę ź Ó
 ź ź Ę Ą Ż Ę ź Ó Ź Ó ź Ę ź Ę Ę Ą Ź Ą Ń Ź Ź Ź Ź ź Ą ź Ę Ą Ć ź ź ź Ę ź Ź ź ź Ę Ł ź Ź Ź Ź ź ź Ź Ź ź ź Ą Ł Ó Ó Ą Ą Ś Ę Ę Ą Ą Ś Ś Ł Ę Ę ź ź Ó Ą Ą Ą Ł Ą Ę Ź Ę ź ź Ę Ą Ź Ź ź Ł Ą Ł Ą ź Ą ź Ł Ą Ó ĘŚ Ą Ę Ę ź Ź Ę
ź ź Ę Ą Ż Ę ź Ó Ź Ó ź Ę ź Ę Ę Ą Ź Ą Ń Ź Ź Ź Ź ź Ą ź Ę Ą Ć ź ź ź Ę ź Ź ź ź Ę Ł ź Ź Ź Ź ź ź Ź Ź ź ź Ą Ł Ó Ó Ą Ą Ś Ę Ę Ą Ą Ś Ś Ł Ę Ę ź ź Ó Ą Ą Ą Ł Ą Ę Ź Ę ź ź Ę Ą Ź Ź ź Ł Ą Ł Ą ź Ą ź Ł Ą Ó ĘŚ Ą Ę Ę ź Ź Ę
Wstęp teoretyczny. Więcej na: dział laboratoria
 Więcej na: www.treolo.prv.pl, www.treolo.eu dział laboratoria Wstęp teoretyczny Sprężystość, własność polegająca na powrocie odkształconego ciała do jego pierwotnej fory po zniknięciu sił wywołujących
Więcej na: www.treolo.prv.pl, www.treolo.eu dział laboratoria Wstęp teoretyczny Sprężystość, własność polegająca na powrocie odkształconego ciała do jego pierwotnej fory po zniknięciu sił wywołujących
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Ł ś ś ń ń ś
 Ę ń Ł ś ś ń ń ś ść ę ę ś ż ś ś ś ę ę ś ę ś ę ć ź ż ś ęś ż ę ś ś ś ć ź ę ę ś ś ść ć ę ę ś ś ę ę ę ę ś Ł Ł Ł Ł Ł ś ć ę ę ę ę ń Ą Ą ż ę ę Ł Ś ę Ł Ł ę ę ę ś Ą ę ę ę Ł Ł ń ń ś Ą Ń ś Ł Ó Ł ść ń ń ą ę ść ń
Ę ń Ł ś ś ń ń ś ść ę ę ś ż ś ś ś ę ę ś ę ś ę ć ź ż ś ęś ż ę ś ś ś ć ź ę ę ś ś ść ć ę ę ś ś ę ę ę ę ś Ł Ł Ł Ł Ł ś ć ę ę ę ę ń Ą Ą ż ę ę Ł Ś ę Ł Ł ę ę ę ś Ą ę ę ę Ł Ł ń ń ś Ą Ń ś Ł Ó Ł ść ń ń ą ę ść ń
ć ć Ł ć Ź ć Ł ź ć Ś ć ć Ż Ł Ż ć ż ć
 Ł Ź Ł Ł ź ź Ż Ż ż Ż ć Ś ż ć ć Ę ć ć Ł ć Ź ć Ł ź ć Ś ć ć Ż Ł Ż ć ż ć Ł ć ć ć ć Ł Ż ć Ł ź ć Ś Ż Ż Ż ż Ż Ż ż Ż Ś Ż Ą Ł Ż ź Ż Ż Ż Ż Ż Ż Ś Ż Ż ż Ż Ż ż ż Ł Ż Ś Ż Ż Ż Ż Ż Ż Ś Ż Ę Ł Ź Ó ż Ę Ł ź Ł Ź Ż ż Ł Ż Ż ż
Ł Ź Ł Ł ź ź Ż Ż ż Ż ć Ś ż ć ć Ę ć ć Ł ć Ź ć Ł ź ć Ś ć ć Ż Ł Ż ć ż ć Ł ć ć ć ć Ł Ż ć Ł ź ć Ś Ż Ż Ż ż Ż Ż ż Ż Ś Ż Ą Ł Ż ź Ż Ż Ż Ż Ż Ż Ś Ż Ż ż Ż Ż ż ż Ł Ż Ś Ż Ż Ż Ż Ż Ż Ś Ż Ę Ł Ź Ó ż Ę Ł ź Ł Ź Ż ż Ł Ż Ż ż
ć
 Ł Ę Ę Ą ć Ś ć ć ź ź ć ć ź ź ź ć ć ź Ś ć ć ć ć ć Ś ć Ż ć ŚĆ Ć Ż Ś Ż Ś Ż ć Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ć ć Ć ć Ć ć Ś Ś Ś ć Ć Ż Ć ć ć Ś Ż Ż Ś Ć Ż ć ć ć ć ć Ś Ś Ś ć Ż Ż ć ć Ś Ś ć Ś Ż ć Ś ć ć ć Ż Ć ć ć Ż Ś Ż Ć
Ł Ę Ę Ą ć Ś ć ć ź ź ć ć ź ź ź ć ć ź Ś ć ć ć ć ć Ś ć Ż ć ŚĆ Ć Ż Ś Ż Ś Ż ć Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ć ć Ć ć Ć ć Ś Ś Ś ć Ć Ż Ć ć ć Ś Ż Ż Ś Ć Ż ć ć ć ć ć Ś Ś Ś ć Ż Ż ć ć Ś Ś ć Ś Ż ć Ś ć ć ć Ż Ć ć ć Ż Ś Ż Ć
Ę ś
 ć Ę Ł ś Ę ś ś ż Ź ż ż ż ż ż ś ż ż Ż Ę ś ść ść ś Ć ś ś Ć ść Ź ć Ż ć ś ż ś ść ś ś ś ś ć Ć ś Ć ś ś Ź ś ś Ź ś ź ś ż ż ś ś ś ź ś ś Ź Ł ż ś ż Ę Ź ś Ę Ę ż Ę Ź Ę ś ś ś ć ź ś ś ś ś ś ś ś Ź ś ż ż ć ć ć ś Ę ż ś ć
ć Ę Ł ś Ę ś ś ż Ź ż ż ż ż ż ś ż ż Ż Ę ś ść ść ś Ć ś ś Ć ść Ź ć Ż ć ś ż ś ść ś ś ś ś ć Ć ś Ć ś ś Ź ś ś Ź ś ź ś ż ż ś ś ś ź ś ś Ź Ł ż ś ż Ę Ź ś Ę Ę ż Ę Ź Ę ś ś ś ć ź ś ś ś ś ś ś ś Ź ś ż ż ć ć ć ś Ę ż ś ć
Ę Ę ĘŚ Ą Ł Ę ś ą ź ż ź ą ż ć ąż ą ś ą ń
 ż ć Ę Ę ś ą ą ż ą ą ń ś ą ą Ą Ę Ą ą ą ą Ź ć ą ą ś ą ą ą Ą Ę Ą Ł ą ą ą ą Ę Ę ĘŚ Ą Ł Ę ś ą ź ż ź ą ż ć ąż ą ś ą ń Ą ą ż ż ą ą ż ś ż ź Ę ż ż ń Ę Ś Ę ś ż ą ą ą ż ś ś ś ż ż ą ą ż ą ż ś ą ą ż ś ś ą ą ś ż ś
ż ć Ę Ę ś ą ą ż ą ą ń ś ą ą Ą Ę Ą ą ą ą Ź ć ą ą ś ą ą ą Ą Ę Ą Ł ą ą ą ą Ę Ę ĘŚ Ą Ł Ę ś ą ź ż ź ą ż ć ąż ą ś ą ń Ą ą ż ż ą ą ż ś ż ź Ę ż ż ń Ę Ś Ę ś ż ą ą ą ż ś ś ś ż ż ą ą ż ą ż ś ą ą ż ś ś ą ą ś ż ś
Fizyka dla Informatyki Stosowanej
 Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Ś Ę Ą Ł Ś Ł Ł Ł Ł Ł Ś Ś Ł Ł Ł Ą Ł Ł Ł Ł Ł Ą Ą Ł
 ę Ą Ł Ł Ś Ę Ą Ł Ś Ł Ł Ł Ł Ł Ś Ś Ł Ł Ł Ą Ł Ł Ł Ł Ł Ą Ą Ł Ł ś ś ś ś ę ś ę ę ś ść ść ść ę ę ę ść ę ś Ą Ą ś Ż ść Ź Ś Ą ę ść ść ść Ą ś Ż ę Ż Ń Ą Ł ś ę ś ę ś ś ę ś ś ść Ę Ś ś Ś ś Ś ś Ś ź ę ź ę ść ś ę Ę ś Ł ść
ę Ą Ł Ł Ś Ę Ą Ł Ś Ł Ł Ł Ł Ł Ś Ś Ł Ł Ł Ą Ł Ł Ł Ł Ł Ą Ą Ł Ł ś ś ś ś ę ś ę ę ś ść ść ść ę ę ę ść ę ś Ą Ą ś Ż ść Ź Ś Ą ę ść ść ść Ą ś Ż ę Ż Ń Ą Ł ś ę ś ę ś ś ę ś ś ść Ę Ś ś Ś ś Ś ś Ś ź ę ź ę ść ś ę Ę ś Ł ść
Ć ć ć Ś ć
 ź Ę Ę Ę ź ć ć ć Ć ć ć Ś ć ź ć ć ć Ć Ś ź Ś Ć ć Ż ź ć Ż Ś Ł ŚĆ ć ć ć Ć ć Ść ć Ż ć ć ć ć ć ć ć ć Ą ć ć Ś ć Ś ć Ż Ś ć Ó ć Ś ć Ś ć ć ć ć Ś ć ć Ś ć Ć Ż ć Ć ć ć ć ć Ę ć ź ć ć ć ć ć ź ć ć ć Ć ź ć Ż ć ć ć Ś ć Ć
ź Ę Ę Ę ź ć ć ć Ć ć ć Ś ć ź ć ć ć Ć Ś ź Ś Ć ć Ż ź ć Ż Ś Ł ŚĆ ć ć ć Ć ć Ść ć Ż ć ć ć ć ć ć ć ć Ą ć ć Ś ć Ś ć Ż Ś ć Ó ć Ś ć Ś ć ć ć ć Ś ć ć Ś ć Ć Ż ć Ć ć ć ć ć Ę ć ź ć ć ć ć ć ź ć ć ć Ć ź ć Ż ć ć ć Ś ć Ć
Ś ć Ś Ę Ś Ś Ś Ś Ę Ę
 Ł Ś Ę ź Ż Ż ź ź Ż Ś Ż Ś Ł Ś ć Ś Ę Ś Ś Ś Ś Ę Ę Ś Ę Ń Ę ć ć Ę Ś Ę Ś Ę Ś Ś Ś ŚĘ ć Ś Ś Ś Ś ŚĘ Ł Ś Ł ź Ę ź ź ź ź Ń Ś Ś Ń ź ć ź ź ź ź ź ź Ś ź Ż ź Ń ź Ś ź ź ć Ę ź Ę Ę Ś Ę Ę Ł ź ź Ę ć Ś Ś Ł Ś Ę Ś Ł Ł Ś ć Ł ź Ł
Ł Ś Ę ź Ż Ż ź ź Ż Ś Ż Ś Ł Ś ć Ś Ę Ś Ś Ś Ś Ę Ę Ś Ę Ń Ę ć ć Ę Ś Ę Ś Ę Ś Ś Ś ŚĘ ć Ś Ś Ś Ś ŚĘ Ł Ś Ł ź Ę ź ź ź ź Ń Ś Ś Ń ź ć ź ź ź ź ź ź Ś ź Ż ź Ń ź Ś ź ź ć Ę ź Ę Ę Ś Ę Ę Ł ź ź Ę ć Ś Ś Ł Ś Ę Ś Ł Ł Ś ć Ł ź Ł
Prędkośd rozchodzenia się sprężystych fal podłużnych w ciałach stałych, cieczach i
 1 S t r o n a 6. Prędkośd rozchodzenia się sprężystych fal podłużnych w ciałach stałych, cieczach i gazach. Prawo Hooke a: Siła sprężystości: F Xsp = k. 0) Co do wartości bezwzględnej jest ona równa (lub
1 S t r o n a 6. Prędkośd rozchodzenia się sprężystych fal podłużnych w ciałach stałych, cieczach i gazach. Prawo Hooke a: Siła sprężystości: F Xsp = k. 0) Co do wartości bezwzględnej jest ona równa (lub
Ę Ż Ż Ż ś ż Ż
 Ż ż ż ś ś ż ż ż ś ż Ż Ź ś Ź Ź ś ś ż ż ś ś ś ś Ż ś Ż Ę Ż Ż Ż ś ż Ż ś ś ś Ż Ą ż ś ś ź Ż ż ż ś ś ż Ł Ż ź ż ż ś ś Ę ż ż ż ż Ę ś ż ć ś Ę ż ś ż ś Ż ż ś ż ś ść ść Ę ż ż ż ś ż Ą Ż Ś ś Ą Ż ż ż ś Ę ś Ż ś Ń ś ż Ą
Ż ż ż ś ś ż ż ż ś ż Ż Ź ś Ź Ź ś ś ż ż ś ś ś ś Ż ś Ż Ę Ż Ż Ż ś ż Ż ś ś ś Ż Ą ż ś ś ź Ż ż ż ś ś ż Ł Ż ź ż ż ś ś Ę ż ż ż ż Ę ś ż ć ś Ę ż ś ż ś Ż ż ś ż ś ść ść Ę ż ż ż ś ż Ą Ż Ś ś Ą Ż ż ż ś Ę ś Ż ś Ń ś ż Ą
ś ś ź ć ć ż ż ść ź ś Ę ś ż ś ź ś Ę ż ż ć ś ś ź
 ż Ś Ż ś ś ś ćż ć ś ś ż ż ż ś ś ź ć ć ż ż ść ź ś Ę ś ż ś ź ś Ę ż ż ć ś ś ź ś ż ż ż ż ść Ź ś ż ż ś ś ś ść ć Ń ż ś ś ś Ł ś ś ś Ź ż ś ż ż ś ść ś ść ś Ż ś ż ż ś ś Ń ś ś ś ż ś ś ś ś ś Ń ś ś ś ś ś ś ś ś Ń ś ż
ż Ś Ż ś ś ś ćż ć ś ś ż ż ż ś ś ź ć ć ż ż ść ź ś Ę ś ż ś ź ś Ę ż ż ć ś ś ź ś ż ż ż ż ść Ź ś ż ż ś ś ś ść ć Ń ż ś ś ś Ł ś ś ś Ź ż ś ż ż ś ść ś ść ś Ż ś ż ż ś ś Ń ś ś ś ż ś ś ś ś ś Ń ś ś ś ś ś ś ś ś Ń ś ż
ć ć ż ć ź ż ż ź ź ŚĆ Ź ź ć Ź ź ź ź ź Ś Ą Ć Ć ć Ź ź
 Ł Ł ć ć Ś Ź Ć Ś ć ć ż ć ź ż ż ź ź ŚĆ Ź ź ć Ź ź ź ź ź Ś Ą Ć Ć ć Ź ź Ś Ć Ć Ś ź Ć ż ż ź ż Ć ć ż Ć Ć ż ż ź Ć Ś Ś ż ż ć ż ż Ć ż Ć Ś Ś Ź Ć Ę ż Ś Ć ć ć ź ź Ś Ć Ś Ć Ł Ś Ź Ś ć ż Ś Ć ć Ś ż ÓŹ Ś Ś Ź Ś Ś Ć ż ż Ś ż
Ł Ł ć ć Ś Ź Ć Ś ć ć ż ć ź ż ż ź ź ŚĆ Ź ź ć Ź ź ź ź ź Ś Ą Ć Ć ć Ź ź Ś Ć Ć Ś ź Ć ż ż ź ż Ć ć ż Ć Ć ż ż ź Ć Ś Ś ż ż ć ż ż Ć ż Ć Ś Ś Ź Ć Ę ż Ś Ć ć ć ź ź Ś Ć Ś Ć Ł Ś Ź Ś ć ż Ś Ć ć Ś ż ÓŹ Ś Ś Ź Ś Ś Ć ż ż Ś ż
ć Ą Ą Ł Ą
 ź ź ź ć ć Ą Ą Ł Ą ź ź Ę Ą ź Ą ć Ł Ł Ą Ś Ę ź ź Ą Ą ź ć ć Ł Ę ć ź ć ć Ą Ć ź ź ź ć ć ć ć ć ź ź ć ć ź ć Ś Ę ć ć ć ć Ł ź ź ź ź ć Ę Ż ć ć ć ć Ę Ę ć Ę Ę ć ć Ę ć ć Ł ć Ć ć Ł Ł Ę Ę ć Ę ć ź ć Ń Ł Ł Ł Ś ć ć ć Ę Ś
ź ź ź ć ć Ą Ą Ł Ą ź ź Ę Ą ź Ą ć Ł Ł Ą Ś Ę ź ź Ą Ą ź ć ć Ł Ę ć ź ć ć Ą Ć ź ź ź ć ć ć ć ć ź ź ć ć ź ć Ś Ę ć ć ć ć Ł ź ź ź ź ć Ę Ż ć ć ć ć Ę Ę ć Ę Ę ć ć Ę ć ć Ł ć Ć ć Ł Ł Ę Ę ć Ę ć ź ć Ń Ł Ł Ł Ś ć ć ć Ę Ś
ż ć
 Ł Ł ż ć ć ż ć Ą Ł ó ó ć ż ć ć ż ć Ę ć Ę ć ć Ę ć ć ć Ę ż ć ć ć Ś ć Ę Ę ż ż ć ż Ę ć ć Ę ż ż Ę Ł ć ć Ą Ę Ł ć ć ć ż ć Ę Ł Ść Ą Ę Ł ć ć ć ć Ę Ł Ść Ą Ę Ł ć ć ć Ł ć Ę Ę ć ć ć ć Ł Ść ć ć Ę Ę Ł Ś Ą Ś Ś Ł Ą Ą ż
Ł Ł ż ć ć ż ć Ą Ł ó ó ć ż ć ć ż ć Ę ć Ę ć ć Ę ć ć ć Ę ż ć ć ć Ś ć Ę Ę ż ż ć ż Ę ć ć Ę ż ż Ę Ł ć ć Ą Ę Ł ć ć ć ż ć Ę Ł Ść Ą Ę Ł ć ć ć ć Ę Ł Ść Ą Ę Ł ć ć ć Ł ć Ę Ę ć ć ć ć Ł Ść ć ć Ę Ę Ł Ś Ą Ś Ś Ł Ą Ą ż
ć Ś Ś Ść
 ć Ś Ś Ść Ś Ł Ź Ść ć ć ć Ść ć Ść Ś Ść ć ć Ś Ó Ś Ś ć ć Ś Ś Ó Ś Ś ć Ą ć Ś Ś Ł ć Ś Ś Ł ć Ą Ść ć Ś Ó Ź ć ć Ś Ś ć ć ć Ś Ść Ść Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ą Ś Ą Ś Ś Ź Ź ć ć Ś Ę Ź Ł ź Ę Ę Ś Ś Ś Ę Ą Ź ć Ł Ś Ś Ś Ś ć Ś
ć Ś Ś Ść Ś Ł Ź Ść ć ć ć Ść ć Ść Ś Ść ć ć Ś Ó Ś Ś ć ć Ś Ś Ó Ś Ś ć Ą ć Ś Ś Ł ć Ś Ś Ł ć Ą Ść ć Ś Ó Ź ć ć Ś Ś ć ć ć Ś Ść Ść Ś Ś Ś Ś Ś Ś Ś Ś Ś Ś ć Ą Ś Ą Ś Ś Ź Ź ć ć Ś Ę Ź Ł ź Ę Ę Ś Ś Ś Ę Ą Ź ć Ł Ś Ś Ś Ś ć Ś
 ż Ę Ł Ą ż ż ż ź Ł ć Ł ż ć ć Ść ć ź ż ż Ź ć ć ć ć ć ć ć ż ż Ś Ś ż Ś ć ż ć ć Ł Ść ż Ś ż Ś ż ć ż ć ć ć ż ć ż ć ż ż ż ż ć ż ż Ł ć ż ć Ł ż Ź Ę ż ż Ś ć ż ż ć Ź Ś ż Ą ż ć Ś ć ć ż ć ć Ś ż Ź Ł ć ć ć Ć ć ć Ś ć ż
ż Ę Ł Ą ż ż ż ź Ł ć Ł ż ć ć Ść ć ź ż ż Ź ć ć ć ć ć ć ć ż ż Ś Ś ż Ś ć ż ć ć Ł Ść ż Ś ż Ś ż ć ż ć ć ć ż ć ż ć ż ż ż ż ć ż ż Ł ć ż ć Ł ż Ź Ę ż ż Ś ć ż ż ć Ź Ś ż Ą ż ć Ś ć ć ż ć ć Ś ż Ź Ł ć ć ć Ć ć ć Ś ć ż
C e l e m c z ę ś c i d y s k u s y j n e j j e s t u ś w i a d o m i e n i e s o b i e, w o p a r c i u o r o z w a ż a n i a P i s m a Ś w.
 1. C e l s p o t k a n i a. C e l e m c z ę ś c i d y s k u s y j n e j j e s t u ś w i a d o m i e n i e s o b i e, w o p a r c i u o r o z w a ż a n i a P i s m a Ś w., ż e : B y d z b a w i o n y m
1. C e l s p o t k a n i a. C e l e m c z ę ś c i d y s k u s y j n e j j e s t u ś w i a d o m i e n i e s o b i e, w o p a r c i u o r o z w a ż a n i a P i s m a Ś w., ż e : B y d z b a w i o n y m
ć ż ż ć Ą ż ż Ł ć Ż ż Ż Ż Ż Ż
 Ł Ę Ł ż Ż ć ż ż ć ż ż ć Ą ż ż Ł ć Ż ż Ż Ż Ż Ż ż ż Ł ż Ż Ł Ż Ż Ż Ż ż ż Ż Ż Ż ć ć ż ć ż ż ŻĄ ć ć ż Ż Ż ż Ż Ż ć Ż ź ć ż Ę Ż Ę Ż ć Ż Ż ć Ż ć ż Ż Ż ż Ż Ą Ż ć ż ć Ś Ą ż Ż Ż Ż ż Ż Ż Ż Ż Ż Ż Ż Ż ż ż Ż ż ż Ż Ż
Ł Ę Ł ż Ż ć ż ż ć ż ż ć Ą ż ż Ł ć Ż ż Ż Ż Ż Ż ż ż Ł ż Ż Ł Ż Ż Ż Ż ż ż Ż Ż Ż ć ć ż ć ż ż ŻĄ ć ć ż Ż Ż ż Ż Ż ć Ż ź ć ż Ę Ż Ę Ż ć Ż Ż ć Ż ć ż Ż Ż ż Ż Ą Ż ć ż ć Ś Ą ż Ż Ż Ż ż Ż Ż Ż Ż Ż Ż Ż Ż ż ż Ż ż ż Ż Ż
ó ń ó
 Ł ź ó ń ó ó ń ó ó ń ż ó ó Ł ń ó ó ń Ą ó ń ó ó ź Ł ó ó ó Ż ż Ł ó Ż ó ó ż Ś ż ó Ś ż Ż Ą Ź Ę Ó ó ó ó ń Ć ó ó ż ż Ż ó ó ń ó ż ż ó Ł ó Ż ó ż ŚÓ ż Ś ń ń Ś ż Ż ó ó Ę ó Ł ó ó ó Ą ż Ż Ó ó Ł ó Ę Ż ó ó ń ó Ż Ż ń
Ł ź ó ń ó ó ń ó ó ń ż ó ó Ł ń ó ó ń Ą ó ń ó ó ź Ł ó ó ó Ż ż Ł ó Ż ó ó ż Ś ż ó Ś ż Ż Ą Ź Ę Ó ó ó ó ń Ć ó ó ż ż Ż ó ó ń ó ż ż ó Ł ó Ż ó ż ŚÓ ż Ś ń ń Ś ż Ż ó ó Ę ó Ł ó ó ó Ą ż Ż Ó ó Ł ó Ę Ż ó ó ń ó Ż Ż ń
Ż Ź Ż ż Ś Ś Ź Ż Ż Ż Ż Ż ć ć Ż
 ż Ż Ź Ż ż Ś Ś Ź Ż Ż Ż Ż Ż ć ć Ż ć Ż Ę ż Ż Ź Ź ż Ż Ż ć Ż ż ć ż ć Ż Ż Ż ż Ż Ń ż Ż Ż ż ż ż ć ć Ż ć Ź ż ż Ź ż ć ż ć Ę ć ż Ł Ż ż ż ć ć Ż Ż ż Ż ż Ż ć Ż Ż ć Ż ż Ż Ż ć ć ć ć Ę ż ż ż Ę ź ż Ź Ź ż Ż Ń ć Ż Ź Ż Ż
ż Ż Ź Ż ż Ś Ś Ź Ż Ż Ż Ż Ż ć ć Ż ć Ż Ę ż Ż Ź Ź ż Ż Ż ć Ż ż ć ż ć Ż Ż Ż ż Ż Ń ż Ż Ż ż ż ż ć ć Ż ć Ź ż ż Ź ż ć ż ć Ę ć ż Ł Ż ż ż ć ć Ż Ż ż Ż ż Ż ć Ż Ż ć Ż ż Ż Ż ć ć ć ć Ę ż ż ż Ę ź ż Ź Ź ż Ż Ń ć Ż Ź Ż Ż
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.

























































