Dodawanie fal: Dla fal zapisanych jako fale o zespolonych amplitudach i takich samych wykładnikach jest to łatwe: Dodawanie fal:
|
|
|
- Joanna Murawska
- 7 lat temu
- Przeglądów:
Transkrypt
1 7. Inerferenca: fale soące, dudnienia i prędkość rupowa Fale soące: suma fal o przeciwnych kierunkach Dudnienia: suma fal o róŝnych częsoliwościach Prędkość fazowa (eszcze raz) Zarzymać świało Ruch z prędkością większą niŝ świało Dodawanie fal: Dla fal zapisanych ako fale o zespolonych ampliudach i akich samych wykładnikach es o ławe: ( x, ) E exp i( kx ) + E exp i( kx ) + E3 exp i( kx ) % % % % ( E + E + E3)exp i( kx ) % % % dzie zespolone fazy począkowe zaware są w E. ~, E ~ i E ~ 3 Ale zespolone eksponensy moą być róŝne! Na przykłąd: Zwróć uwaę na znak! ( x, ) E exp i( kx ) + E exp i( kx ) + E3 exp i( k3x + 3) % % % %? Zasada superpozyci: (układy liniowe) Zasadzie superpozyci podleaą fale (rozwiązania równania faloweo), w ym harmoniczna fala elekromaneyczna. Dwie fale kołowe zmarszczek na powierzchni wody przechodzą edna przez druą. W przeciwieńswie do przedmioów maerialnych, fale moą się przenikać. Moą nakładać się na siebie w przesrzeni i dy o zachodzi, wychylenia dodaą się. Pole elekromaneyczne pochodzące od kilku źródeł es sumą pól, akie wywarza kaŝde z ych źródeł. Ale uŝ naęŝenie świała pochodząceo od kilku źródeł nie spełnia zasady superpozyci, poniewaŝ es proporconalne do kwadrau sumy pól elekrycznych: Konsekwencą zasady superpozyci fal es inerferenca fal. Dodawanie fal: 4
2 Dodawanie fal o róŝnych ampliudach: Fala soąca - Wynik dodawania fal o e same dłuości fali, ale róŝnych kierunkach: Dla fal zapisanych ako fale o zespolonych ampliudach i akich samych wykładnikach es o ławe: ( x, ) E exp i( kx ) + E exp i( kx ) + E3 exp i( kx ) % % % % ( E + E + E3)exp i( kx ) % % % dzie zespolone fazy począkowe zaware są w E. ~, E ~ i E ~ 3 Ale zespolone eksponensy moą być róŝne! Na przykłąd: Zwróć uwaę na znak! ( x, ) E exp i( kx ) + E exp i( kx ) + E3 exp i( k3x + 3) % % % %? ( x, ) E exp i( kx ) + E exp i( kx + ) % % % E exp( ikx)[exp( i) + exp( i)] % E exp( ikx)cos( ) % PoniewaŜ musimy wziąć część rzeczywisą pól, orzymuemy: E ( x, ) E cos( kx)cos( ) o (E es rzeczywisa) Fale soące powsaą na przykład we wnękach laserowych, dzie odbiane są one am i z powroem między zwierciadłami. Fala soąca Fala soąca - Wynik dodawania fal o e same dłuości fali, ale róŝnych kierunkach: ( x, ) E exp i( kx ) + E exp i( kx + ) % % % E exp( ikx)[exp( i) + exp( i)] % E exp( ikx)cos( ) % E ( x, ) E cos( kx)cos( ) o Miesca, dzie ampliuda es zawsze równa zero o węzły fali. Miesca, dzie oscylace ampliudy są maksymalne o srzałki Węzły srzałki 3 4
3 Fala soąca Dudnienia świała: prędkość rupowa Mamy więc: E ( x, ) E cos( kx)cos( ) o E o (x,) E cos(k x ) cos( kx ) To es szybko oscyluąca fala: [cos(k x )] z wolnozmienną ampliudą: [E cos( kx )] fala nośna obwiednia Miesca, dzie ampliuda es zawsze równa zero o węzły fali. Miesca, dzie oscylace ampliudy są maksymalne o srzałki węzeł srzałka Prędkość fazowa wynika z części szybkozmienne: p / k A co z druą prędkością - prędkością ampliudy? Zdefiniumy prędkość rupową : / k W oólności prędkość rupowa o: d /dk Dudnienia świała: prędkość rupowa wynik dodawania fal elekromaneycznych o róŝnych częsoliwościach E ( x, ) Re{ E exp i ( k x ) + E exp i ( k x )} o o Niech E będzie rzeczywise k + k k k Wprowadźmy: Le k and i k Podobnie: Similiarly, + and i So: Tak więc: k k E ( x, ) Re{ E exp i ( k x + kx ) + E exp i ( k x kx + )} [ ] Re{ E exp i ( k x ) exp i ( kx ) + exp[ i ( kx )] } Re{ E exp i ( k x )cos( kx )} Prędkość rupowa i prędkość fazowa róŝnią się w ośrodkach z dyspersą (n()). Jeśli: Dla dwóch fal o róŝnych częsościach: k nck nck ck ck n n k k n n, nn( k k) n n c nck nck n n ( k k ) p (prędkość fazowa) E cos( k x )cos( kx ) Jeśli: n n, p szybko-zmienny wolno-zmienny 5 6
4 Prędkość rupowa es prędkością impulsu świelneo PoniewaŜ wyprowadziliśmy prędkość rupową uŝywaąc dwóch częsości, myślmy o nie ako o prędkości doyczące pewne (dane) częsości (częsość nośna) z obwiednią, kóre cenrum przesuwa się z prędkością fazową (prędkością impulsu) Kiedy φ, impuls przemieszcza się z ą samą prędkością co fala nośna (czyli ak, ak frony falowe): Dudnienia świała: prędkość rupowa d /dk E( ) E ( )exp[ ( )] ~ x ik x p ~ Obwiednia rozchodzi się z prędkością rupową. Fala nośna rozchodzi się z prędkością fazową p / k z I < S r > cε [W/m ] Zdarza się o rzadko. Dudnienia świała: prędkość rupowa d /dk E( ) E ( )exp[ ( )] ~ x ik x p ~ Obwiednia rozchodzi się z prędkością rupową. Fala nośna rozchodzi się z prędkością fazową p / k Inacze: E( ) I( z ) exp[ ik( z )] φ Dudnienia świała: prędkość rupowa Dla dwóch fal o róŝnych częsościach: E o (x,) E cos(k x ) cos( kx ) d /dk υ υ p Zazwycza, eneria propaue się z prędkością rupową A co z prędkością rozchodzenia się enerii? 7 8
5 Dudnienia świała: prędkość rupowa Poszczeólne fale: Suma: W ośrodku dyspersynym: fale harmoniczne o róŝnych częsościach rozchodzą się z róŝnymi prędkościami. Fala będąca paczką fal zawieraących częsości z pewneo przedziału będzie więc zmieniać swó kszał. KaŜda ze składowych harmonicznych rozchodzi się ze zwykłą prędkością fazową (falową): p / k, Obwiednia: NaęŜenie (irradianca): 7 naomias paczka fal ako całość przesuwa się z prędkością p. Falę aką opisać moŝemy ako falę harmoniczną o zmieniaące się (modulowane) ampliudzie; prędkość rozchodzenia się rzbieów modulaci o prędkość rupowa: d/dk. 9 Podsumowanie (przypomnienie) Prędkość rupowa a dyspersa ośrodka: n() d /dk Częsość fali harmoniczne es aka sama w rozwaŝanym ośrodku, ak i poza nim, ale k k n, Tak więc wyodnie es pomyśleć o ako o zmienne niezaleŝne: PoniewaŜ: k n() / c, [ dk d] / pochodna k: dk /d ( n + dn/d ) / c c / ( n + dn/d) (c /n) / ( + /n dn/d ) φ / k c /n, dn Osaecznie: φ / + c / (n + dn/d) n d Tak więc prędkość rupowa równa es prędkości fazowe, ylko wedy, dy dn/d, (brak dyspersi, ak ak np. w próŝni). 9
6 Dyspersa prędkości rupowe a impulsy świała Impuls świała zawiera wiele częsości. Prędkość rupowa będzie róŝna dla róŝnych dłuości świała. czasowy począek impulsu r (Ŝóła) < r (czerwona) czasowy koniec impulsu Dyspersa powodue zmianę kszału impulsu! Dielekryki liniowe: funkca dielekryczna w modelu Lorenza Gdy ośrodek posiada wiele częsości rezonansowych : Prawie wszędzie: dn/d >, Ne f ε r ( ) + ε m ( iγ ) κ n e Rezonanse: oscylacyne i roacyne podczerień widzialne UV X czesoliwość (Hz) prześcia elekronowe am eŝ: p c /n Dyspersa: funkca dielekryczna i współczynnik załamania w modelu Lorenza Ne ε r ( ) + ε me ( iγ) ε + i ε n ~ ( ) ε ( ) n ( ) Re n ~ ( ) κ ( ) Im n ~ ( ) współczynnik załamania i współczynnik eksynkci (absorpci) Prędkość rupowa a dyspersa ośrodka A co się dziee w obszarze anomalne dyspersi? c / (n + dn/d) dn/d es uemne. Tak więc moŝe przewyŝszyć c dla ych częsości! Współczynnik załamania n Obszary dyspersi anomalne < c < c < c Dyspersa Dyspersa Dyspersa normalna normalna normalna Prędkość rupowa moŝe przekroczyć c w ośrodku w obszarze anomalne dyspersi
7 Prędkość rupowa a dyspersa ośrodka A co się dziee w obszarze anomalne dyspersi? κ n Rezonanse: oscylacyne i roacyne c / (n + dn/d) dn/d es uemne. Tak więc moŝe przewyŝszyć c dla ych częsości! Ale: prześcia elekronowe Obszary dyspersi anomalne są: spekralnie wąskie sowarzyszone z rezonansową absorpcą Prędkość rupowa a dyspersa ośrodka A co się dziee w obszarze anomalne dyspersi? c / (n + dn/d)? podczerień widzialne UV X Prędkość rupowa moŝe przekroczyć c w ośrodku w obszarze 5 czesoliwość (Hz) anomalne dyspersi 7 Prędkość rupowa a dyspersa ośrodka A co się dziee w obszarze anomalne dyspersi? κ n Rezonanse: oscylacyne i roacyne c / (n + dn/d) dn/d es uemne. Tak więc moŝe przewyŝszyć c dla ych częsości! Ale: prześcia elekronowe Obszary dyspersi anomalne są: spekralnie wąskie sowarzyszone z rezonansową absorpcą Czy moŝna: zarzymać świało? przyspieszyć świało?!? podczerień widzialne UV X A moŝe prędkość rupowa nie ma sensu w obszarze 6 czesoliwość (Hz) anomalne dyspersi? 3 4
8 Propaaca impulsu w ośrodku dyspersynym, Szybcie niŝ świało Power (µw) "slow-lih medium Vacuum - 4 Time (ns) del 67.5 ns Delayed ośrodek dyspersyny Wyniki obserwaci doświadczalnych: Power (µw) power (µw) "fas-lih medium adanced ime (ns) ad 7.4 ns acuum power (µw) c 3 km s - - prędkość świała w próŝni (w kosmosie) es edną z napowszechnie znanych sałych fizycznych Obieky posiadaące masę wymaaą nieskończenie duŝe enerii by ą osiąnąć, Cząseczki bezmasowe akie ak foon w próŝni przenoszą (swoą) enerię dokładnie z prędkością c, Relaywisyczne poęcie ednoczesności prowadzi do wniosku, Ŝe informaca nie moŝe wędrować szybcie niŝ świało (eśli nie chcemy zrezynować z sysemu poęć i loiki, kórymi się doąd posłuiwaliśmy). Niemnie ednak prędkości większe niŝ c są obserwowane! Zarzymać świało Szybcie niŝ świało W obszarze anomalne dyspersi, eśli: Kompuery opyczne? Złapanie świała w kryszałach silikonowych umoŝliwiłoby konsrukce kompuerów na nowych zasadach Podziurkowana warswa silikonu: spowalniaący świało świałowód skonsruowany z myślą o uŝyciu do buforowania synałów opycznych ako elemen kompuera opyczneo (fooniczneo) lub rouera siecioweo. impuls es dosaecznie wąski spekralnie obszar, przez kóry wędrue es dosaecznie króki, ładki fron falowy impulsu es modyfikowany przez ośrodek i: moŝliwa es obserwaca propaaci prędkości rupowe impulsu z prędkością większą niŝ c (~(3 x c)), ale prędkość ransmiowane enerii impulsu o zmodyfikowanym kszałcie wiąŝe się nie z prędkością rupową impulsu,, ale doyczy prędkości, z aką porusza się wiodąca krawędź (fron) impulsu w ośrodku. Prędkość a nie przekracza prędkości c. Wniosek: rzeba przemyśleć definicę prędkości przenoszenia enerii i określić ą na nowo! 5 6
9 Jak przekazywana es informaca? Z aką prędkością się ona porusza? Brak dobre odpowiedzi!!! Manipulaca świałem Nowe narzędzia Uemny współczynnik załamania (meamaeriały) Anomalna dyspersa ze zminimalizowaną absorpcą (pompowanie opyczne, kryszały fooniczne) Szybcie niŝ świało Wniosek: rzeba przemyśleć definicę prędkości przenoszenia enerii i informaci określić ą na nowo! Ani prędkość rupowa, ani prędkość fazowa nie są dobrymi poęciami, by opisać prędkość przenoszenia informaci impulsu w warunkach wykonanych doświadczeń. Jes nią prędkość synału, zdefiniowana ako prędkość wędrówki fronu faloweo impulsu. Zodnie z Teorią Wzlędności, prędkość a nidy nie moŝe przekroczyć prędkości świała w próŝni, poniewaŝ, dyby ak się sało, oznaczałoby o synał cofaący się w czasie (sprzeczność z zasadą przyczynowości). Zadanie domowe: Sellmeier wyprowadził nasępuące wyraŝenie na zaleŝność współczynnika załamania od dłuości fali: n A + ( λ λ PokaŜ, Ŝe wyraŝenie o odpowiada wyraŝeniu: Ne ε r ) + ε m w obszarach przezroczysości z dala od linni absorpcynych. Określ wynikaące warości A i λ. λ ( e ) f ( iγ ) 7 8
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Wykład FIZYKA I. 11. Fale mechaniczne. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
WYKŁAD FIZYKAIIIB 2000 Drgania tłumione
 YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
WSTĘP DO ELEKTRONIKI
 WSTĘP DO ELEKTRONIKI Część I Napięcie, naężenie i moc prądu elekrycznego Sygnały elekryczne i ich klasyfikacja Rodzaje układów elekronicznych Janusz Brzychczyk IF UJ Elekronika Dziedzina nauki i echniki
WSTĘP DO ELEKTRONIKI Część I Napięcie, naężenie i moc prądu elekrycznego Sygnały elekryczne i ich klasyfikacja Rodzaje układów elekronicznych Janusz Brzychczyk IF UJ Elekronika Dziedzina nauki i echniki
Związek między ruchem harmonicznym a ruchem jednostajnym po okręgu
 Związek międz ruchem harmonicznm a ruchem jednosajnm po okręgu Rozważm rzu Q i R punku P na osie i : Q cos v r R sin R Q P δ Q cos ( δ ) R sin ( δ ) Jeżeli punk P porusza się ruchem jednosajnm po okręgu,
Związek międz ruchem harmonicznm a ruchem jednosajnm po okręgu Rozważm rzu Q i R punku P na osie i : Q cos v r R sin R Q P δ Q cos ( δ ) R sin ( δ ) Jeżeli punk P porusza się ruchem jednosajnm po okręgu,
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)
 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Fale biegnące. y t=0 vt. y = f(x), t = 0 y = f(x - vt), t ogólne równanie fali biegnącej w prawo
 ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
Zjawisko interferencji fal
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Przykład: Fale anharmoniczne będące sumami oscylacji sinusoidalnych: Fourierowska reprezentacja fali prostokątnej: Analiza Fouriera 1/18/2010
 Wykład 3 Wprowadzenie do opyki ulraszybkiej Przykład: Fale anharmoniczne będące sumami oscylacji sinusoidalnych: RozwaŜmy sumę fal sinusoidalnych (o jes harmonicznych) o róŝnych częsościach: O analizie
Wykład 3 Wprowadzenie do opyki ulraszybkiej Przykład: Fale anharmoniczne będące sumami oscylacji sinusoidalnych: RozwaŜmy sumę fal sinusoidalnych (o jes harmonicznych) o róŝnych częsościach: O analizie
falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Ćwiczenie 133. Interferencja fal akustycznych - dudnienia. Wyznaczanie częstotliwości dudnień. Teoretyczna częstotliwość dudnienia dla danego pomiaru
 Kaedra Fizyki SGGW Nazwisko... Daa... Nr na liście... Imię... Wydział... Dzień yg.... Godzina... Ćwiczenie 33 Inererencja al akusycznych - dudnienia Tabela I. Wyznaczanie częsoliwości dudnień Pomiar Czas,
Kaedra Fizyki SGGW Nazwisko... Daa... Nr na liście... Imię... Wydział... Dzień yg.... Godzina... Ćwiczenie 33 Inererencja al akusycznych - dudnienia Tabela I. Wyznaczanie częsoliwości dudnień Pomiar Czas,
Równanie falowe. Fale podłużne a fale. poprzeczne : Indeks terminów i nazw dotychczas omówionych:
 Indeks terminów i nazw dotychczas omówionych: Fale podłużne a fale poprzeczne zaburzenie, które się rozprzestrzenia się w czasie i przestrzeni. doświadczenie Michelsona- Morleya, doświadczenie Younga,
Indeks terminów i nazw dotychczas omówionych: Fale podłużne a fale poprzeczne zaburzenie, które się rozprzestrzenia się w czasie i przestrzeni. doświadczenie Michelsona- Morleya, doświadczenie Younga,
Fizyka dla Informatyki Stosowanej
 Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Statystyka nieoddziaływujących gazów Bosego i Fermiego
 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
drgania h armoniczne harmoniczne
 ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
Zjawisko interferencji fal
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natężenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natężenia fal) w którym zachodzi stabilne w czasie ich
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
( ) ( ) ( τ) ( t) = 0
 Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera
 Jucatan, Mexico, February 005 W-10 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka
Jucatan, Mexico, February 005 W-10 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
POMIAR PARAMETRÓW SYGNAŁOW NAPIĘCIOWYCH METODĄ PRÓKOWANIA I CYFROWEGO PRZETWARZANIA SYGNAŁU
 Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
Szeregi Fouriera. Powyższe współczynniki można wyznaczyć analitycznie z następujących zależności:
 Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
ver b drgania harmoniczne
 ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
Laseryimpulsowe-cotojest?
 Laseryimpulsowe-coojes? Pior Migdał marca5 Laseryciągłe Prawie każdy widział laser, choćby w posaci breloczka z odpowiednią diodą LED. Co jes charakerysyczne dla promienia emiowanego z akiego urządzenia?
Laseryimpulsowe-coojes? Pior Migdał marca5 Laseryciągłe Prawie każdy widział laser, choćby w posaci breloczka z odpowiednią diodą LED. Co jes charakerysyczne dla promienia emiowanego z akiego urządzenia?
Fale mechaniczne i akustyka
 Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Ośrodki dielektryczne optycznie nieliniowe
 Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu
 Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
IV. Transmisja. /~bezet
 Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Solitony i zjawiska nieliniowe we włóknach optycznych
 Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
Wydział EAIiE Kierunek: Elektrotechnika. Wykład 12: Fale. Przedmiot: Fizyka. RUCH FALOWY -cd. Wykład /2009, zima 1
 RUCH FALOWY -cd Wykład 9 2008/2009, zima 1 Energia i moc (a) dla y=y m, E k =0, E p =0 (b) dla y=0 drgający element liny uzyskuje maksymalną energię kinetyczną i potencjalną sprężystości (jest maksymalnie
RUCH FALOWY -cd Wykład 9 2008/2009, zima 1 Energia i moc (a) dla y=y m, E k =0, E p =0 (b) dla y=0 drgający element liny uzyskuje maksymalną energię kinetyczną i potencjalną sprężystości (jest maksymalnie
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
LINIA DŁUGA Konspekt do ćwiczeń laboratoryjnych z przedmiotu TECHNIKA CYFROWA
 LINIA DŁUGA Z Z, τ e u u Z L l Konspek do ćwiczeń laboraoryjnych z przedmiou TECHNIKA CYFOWA SPIS TEŚCI. Definicja linii dłuiej... 3. Schema zasępczy linii dłuiej przedsawiony za pomocą elemenów o sałych
LINIA DŁUGA Z Z, τ e u u Z L l Konspek do ćwiczeń laboraoryjnych z przedmiou TECHNIKA CYFOWA SPIS TEŚCI. Definicja linii dłuiej... 3. Schema zasępczy linii dłuiej przedsawiony za pomocą elemenów o sałych
Drgania i fale II rok Fizyk BC
 00--07 5:34 00\FIN00\Drgzlo00.doc Drgania złożone Zasada superpozycji: wychylenie jest sumą wychyleń wywołanych przez poszczególne czynniki osobno. Zasada wynika z liniowości związku między wychyleniem
00--07 5:34 00\FIN00\Drgzlo00.doc Drgania złożone Zasada superpozycji: wychylenie jest sumą wychyleń wywołanych przez poszczególne czynniki osobno. Zasada wynika z liniowości związku między wychyleniem
Wymagania edukacyjne z fizyki dla klasy III
 edukacyjne z fizyki dla klasy III edukacyjne z fizyki dla klasy III gimnazjum opare na programie nauczania Świa fizyki, auorswa B. Sagnowskiej (wersja 2), wydawnicwa Zamkor, 10. Prąd Tema według 10.1.
edukacyjne z fizyki dla klasy III edukacyjne z fizyki dla klasy III gimnazjum opare na programie nauczania Świa fizyki, auorswa B. Sagnowskiej (wersja 2), wydawnicwa Zamkor, 10. Prąd Tema według 10.1.
RUCH HARMONICZNY. sin. (r.j.o) sin
 RUCH DRGJĄCY Ruch harmoniczny Rodzaje drgań Oscylaor harmoniczny Energia oscylaora harmonicznego Wahadło maemayczne i fizyczne Drgania łumione Drgania wymuszone i zjawisko rezonansu RUCH HRMONICZNY Ruch
RUCH DRGJĄCY Ruch harmoniczny Rodzaje drgań Oscylaor harmoniczny Energia oscylaora harmonicznego Wahadło maemayczne i fizyczne Drgania łumione Drgania wymuszone i zjawisko rezonansu RUCH HRMONICZNY Ruch
Optyczna spektroskopia oscylacyjna. w badaniach powierzchni
 Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku.
 Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące
 Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Energia w ruchu harmonicznym
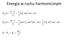 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Fale mechaniczne i akustyczne
 Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
Podstawy fizyki wykład 7
 Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni. Dla próżni równania Maxwella w tzw. postaci różniczkowej są następujące:
 Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
Drgania. W Y K Ł A D X Ruch harmoniczny prosty. k m
 Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
Aby nie uszkodzić głowicy dźwiękowej, nie wolno stosować amplitudy większej niż 2000 mv.
 Tematy powiązane Fale poprzeczne i podłużne, długość fali, amplituda, częstotliwość, przesunięcie fazowe, interferencja, prędkość dźwięku w powietrzu, głośność, prawo Webera-Fechnera. Podstawy Jeśli fala
Tematy powiązane Fale poprzeczne i podłużne, długość fali, amplituda, częstotliwość, przesunięcie fazowe, interferencja, prędkość dźwięku w powietrzu, głośność, prawo Webera-Fechnera. Podstawy Jeśli fala
Podstawy fizyki sezon 1 VII. Ruch drgający
 Podstawy fizyki sezon 1 VII. Ruch drgający Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Ruch skutkiem działania
Podstawy fizyki sezon 1 VII. Ruch drgający Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Ruch skutkiem działania
Fotonika. Plan: Wykład 9: Interferencja w układach warstwowych
 Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Rys.1. Podstawowa klasyfikacja sygnałów
 Kaedra Podsaw Sysemów echnicznych - Podsawy merologii - Ćwiczenie 1. Podsawowe rodzaje i ocena sygnałów Srona: 1 1. CEL ĆWICZENIA Celem ćwiczenia jes zapoznanie się z podsawowymi rodzajami sygnałów, ich
Kaedra Podsaw Sysemów echnicznych - Podsawy merologii - Ćwiczenie 1. Podsawowe rodzaje i ocena sygnałów Srona: 1 1. CEL ĆWICZENIA Celem ćwiczenia jes zapoznanie się z podsawowymi rodzajami sygnałów, ich
(1.1) gdzie: - f = f 2 f 1 - bezwzględna szerokość pasma, f śr = (f 2 + f 1 )/2 częstotliwość środkowa.
 MODULACJE ANALOGOWE 1. Wstęp Do przesyłania sygnału drogą radiową stosuje się modulację. Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej.
MODULACJE ANALOGOWE 1. Wstęp Do przesyłania sygnału drogą radiową stosuje się modulację. Modulacja polega na odzwierciedleniu przebiegu sygnału oryginalnego przez zmianę jednego z parametrów fali nośnej.
2.6.3 Interferencja fal.
 RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Zjawisko interferencji fal
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natężenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natężenia fal) w którym zachodzi stabilne w czasie ich
Metody Optyczne w Technice. Wykład 5 Interferometria laserowa
 Metody Optyczne w Technice Wykład 5 nterferometria laserowa Promieniowanie laserowe Wiązka monochromatyczna Duża koherencja przestrzenna i czasowa Niewielka rozbieżność wiązki Duża moc Największa możliwa
Metody Optyczne w Technice Wykład 5 nterferometria laserowa Promieniowanie laserowe Wiązka monochromatyczna Duża koherencja przestrzenna i czasowa Niewielka rozbieżność wiązki Duża moc Największa możliwa
Dynamiczne formy pełzania i relaksacji (odprężenia) górotworu
 Henryk FILCEK Akademia Górniczo-Hunicza, Kraków Dynamiczne formy pełzania i relaksacji (odprężenia) góroworu Sreszczenie W pracy podano rozważania na ema możliwości wzbogacenia reologicznego równania konsyuywnego
Henryk FILCEK Akademia Górniczo-Hunicza, Kraków Dynamiczne formy pełzania i relaksacji (odprężenia) góroworu Sreszczenie W pracy podano rozważania na ema możliwości wzbogacenia reologicznego równania konsyuywnego
Kinematyka W Y K Ł A D I. Ruch jednowymiarowy. 2-1 Przemieszczenie, prędkość. x = x 2 - x x t
 Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
POMIARY CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH. Cel ćwiczenia. Program ćwiczenia
 Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSOLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Poznanie podsawowych meod pomiaru częsoliwości i przesunięcia
Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSOLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Poznanie podsawowych meod pomiaru częsoliwości i przesunięcia
Wykład FIZYKA I. 2. Kinematyka punktu materialnego. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
I. KINEMATYKA I DYNAMIKA
 piagoras.d.pl I. KINEMATYKA I DYNAMIKA KINEMATYKA: Położenie ciała w przesrzeni można określić jedynie względem jakiegoś innego ciała lub układu ciał zwanego układem odniesienia. Ruch i spoczynek są względne
piagoras.d.pl I. KINEMATYKA I DYNAMIKA KINEMATYKA: Położenie ciała w przesrzeni można określić jedynie względem jakiegoś innego ciała lub układu ciał zwanego układem odniesienia. Ruch i spoczynek są względne
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 320 3201
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 320 3201
Przemieszczeniem ciała nazywamy zmianę jego położenia
 1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU
 X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
ĆWICZENIE 7 WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA. Wprowadzenie
 ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
Interferencja. Dyfrakcja.
 Interferencja. Dyfrakcja. Wykład 8 Wrocław University of Technology 05-05-0 Światło jako fala Zasada Huygensa: Wszystkie punkty czoła fali zachowują się jak punktowe źródła elementarnych kulistych fal
Interferencja. Dyfrakcja. Wykład 8 Wrocław University of Technology 05-05-0 Światło jako fala Zasada Huygensa: Wszystkie punkty czoła fali zachowują się jak punktowe źródła elementarnych kulistych fal
Równania Maxwella. roth t
 , H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
Matematyka ubezpieczeń majątkowych r. ma złożony rozkład Poissona. W tabeli poniżej podano rozkład prawdopodobieństwa ( )
 Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
- Strumień mocy, który wpływa do obszaru ograniczonego powierzchnią A ( z minusem wpływa z plusem wypływa)
 37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
(Plan wynikowy) - zakładane osiągnięcia ucznia Fizyka klasa II
 (Plan wynikowy) - zakładane osiągnięcia ucznia Fizyka klasa II 1 Zapoznanie z wymaganiami edukacyjnymi i kryeriami oceniania. Regulamin pracowni i przepisy BHP. 1. Jak opisujemy ruch? (1.1, 1., 1.5, 1.6,
(Plan wynikowy) - zakładane osiągnięcia ucznia Fizyka klasa II 1 Zapoznanie z wymaganiami edukacyjnymi i kryeriami oceniania. Regulamin pracowni i przepisy BHP. 1. Jak opisujemy ruch? (1.1, 1., 1.5, 1.6,
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Wykład I Krzysztof Golec-Biernat Optyka 1 / 16
 Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
Rozkład i Wymagania KLASA III
 Rozkład i Wymagania KLASA III 10. Prąd Lp. Tema lekcji Wymagania konieczne 87 Prąd w mealach. Napięcie elekryczne opisuje przepływ w przewodnikach, jako ruch elekronów swobodnych posługuje się inuicyjnie
Rozkład i Wymagania KLASA III 10. Prąd Lp. Tema lekcji Wymagania konieczne 87 Prąd w mealach. Napięcie elekryczne opisuje przepływ w przewodnikach, jako ruch elekronów swobodnych posługuje się inuicyjnie
POMIAR PRĘDKOŚCI DŹWIĘKU METODĄ REZONANSU I METODĄ SKŁADANIA DRGAŃ WZAJEMNIE PROSTOPADŁYCH
 Ćwiczenie 5 POMIR PRĘDKOŚCI DŹWIĘKU METODĄ REZONNSU I METODĄ SKŁDNI DRGŃ WZJEMNIE PROSTOPDŁYCH 5.. Wiadomości ogólne 5... Pomiar prędkości dźwięku metodą rezonansu Wyznaczanie prędkości dźwięku metodą
Ćwiczenie 5 POMIR PRĘDKOŚCI DŹWIĘKU METODĄ REZONNSU I METODĄ SKŁDNI DRGŃ WZJEMNIE PROSTOPDŁYCH 5.. Wiadomości ogólne 5... Pomiar prędkości dźwięku metodą rezonansu Wyznaczanie prędkości dźwięku metodą
Wymagania przedmiotowe z fizyki - klasa III (obowiązujące w roku szkolnym 2013/2014)
 Wymagania przedmioowe z izyki - klasa III (obowiązujące w roku szkolnym 013/014) 8. Drgania i ale sprężyse!wskazuje w ooczeniu przykłady ciał wykonujących ruch drgający!podaje znaczenie pojęć: położenie
Wymagania przedmioowe z izyki - klasa III (obowiązujące w roku szkolnym 013/014) 8. Drgania i ale sprężyse!wskazuje w ooczeniu przykłady ciał wykonujących ruch drgający!podaje znaczenie pojęć: położenie
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
LABORATORIUM ELEKTROAKUSTYKI. ĆWICZENIE NR 1 Drgania układów mechanicznych
 LABORATORIUM ELEKTROAKUSTYKI ĆWICZENIE NR Drgania układów mechanicznych Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z właściwościami układów drgających oraz metodami pomiaru i analizy drgań. W ramach
LABORATORIUM ELEKTROAKUSTYKI ĆWICZENIE NR Drgania układów mechanicznych Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z właściwościami układów drgających oraz metodami pomiaru i analizy drgań. W ramach
Wykład 9: Fale cz. 2. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Energia i natężenie fali Średnia energia ruchu drgającego elementu ośrodka o masie m, objętości V
Wykład 9: Fale cz. dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Energia i natężenie fali Średnia energia ruchu drgającego elementu ośrodka o masie m, objętości V
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Szkoła z przyszłością. szkolenie współfinansowane przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Szkoła z przyszłośią szkolenie współfinansowane przez Unię Europejską w ramah Europejskiego Funduszu Społeznego Narodowe Cenrum Badań Jądrowyh, ul. Andrzeja Sołana 7, 05-400 Owok-Świerk ĆWICZENIE a L A
Szkoła z przyszłośią szkolenie współfinansowane przez Unię Europejską w ramah Europejskiego Funduszu Społeznego Narodowe Cenrum Badań Jądrowyh, ul. Andrzeja Sołana 7, 05-400 Owok-Świerk ĆWICZENIE a L A
PODSTAWY CHEMII KWANTOWEJ. Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoretycznej Zespół Chemii Kwantowej Grupa Teorii Reaktywności Chemicznej
 PODSTWY CHEMII KWTOWEJ Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
PODSTWY CHEMII KWTOWEJ Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
Ćwiczenie nr 25: Interferencja fal akustycznych
 Wydział PRACOWNIA FIZYCZNA WFiIS AGH Imię i nazwisko 1. 2. Temat: Rok Grupa Zespół Nr ćwiczenia Data wykonania Data oddania Zwrot do popr. Data oddania Data zaliczenia OCENA Ćwiczenie nr 25: Interferencja
Wydział PRACOWNIA FIZYCZNA WFiIS AGH Imię i nazwisko 1. 2. Temat: Rok Grupa Zespół Nr ćwiczenia Data wykonania Data oddania Zwrot do popr. Data oddania Data zaliczenia OCENA Ćwiczenie nr 25: Interferencja
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
1.UKŁADY RÓWNAŃ LINIOWYCH
 UKŁADY RÓWNAŃ 1.UKŁADY RÓWNAŃ LINIOWYCH Układ: a1x + b1y = c1 a x + by = c nazywamy układem równań liniowych. Rozwiązaniem układu jest kaŝda para liczb spełniająca kaŝde z równań. Przy rozwiązywaniu układów
UKŁADY RÓWNAŃ 1.UKŁADY RÓWNAŃ LINIOWYCH Układ: a1x + b1y = c1 a x + by = c nazywamy układem równań liniowych. Rozwiązaniem układu jest kaŝda para liczb spełniająca kaŝde z równań. Przy rozwiązywaniu układów
Fizyka II (Elektryczność i magnetyzm) Fizyka II (dla ZFBM-FM i -NI)
 1 Fizyka II (lekryczność i magneyzm) Fizyka II (dla ZFBM-FM i -NI) Wykład 13, 9 maja 19 Szeregowy obwód RLC R C L g 1 1 I C L R 1 C L R I Szeregowy obwód RLC X L L 1 X C C reakancja indukcyjna reakancja
1 Fizyka II (lekryczność i magneyzm) Fizyka II (dla ZFBM-FM i -NI) Wykład 13, 9 maja 19 Szeregowy obwód RLC R C L g 1 1 I C L R 1 C L R I Szeregowy obwód RLC X L L 1 X C C reakancja indukcyjna reakancja
Temat VIII. Drgania harmoniczne
 Tema VIII Drgania harmoniczne Równanie ruchu F k Siła k m Równanie ruchu sin cos Położenie równowagi w ruchu drgającym Położenie równowagi o akie położenie, w kórym siły wymuszające ruch równoważą się
Tema VIII Drgania harmoniczne Równanie ruchu F k Siła k m Równanie ruchu sin cos Położenie równowagi w ruchu drgającym Położenie równowagi o akie położenie, w kórym siły wymuszające ruch równoważą się
Fale elektromagnetyczne. Obrazy.
 Fale elektroagnetyczne. Obrazy. Wykład 7 1 Wrocław University of Technology 28-4-212 Tęcza Maxwella 2 1 Tęcza Maxwella 3 ( kx t) ( kx t) E = E sin ω = sin ω Prędkość rozchodzenia się fali: 1 8 c = = 3.
Fale elektroagnetyczne. Obrazy. Wykład 7 1 Wrocław University of Technology 28-4-212 Tęcza Maxwella 2 1 Tęcza Maxwella 3 ( kx t) ( kx t) E = E sin ω = sin ω Prędkość rozchodzenia się fali: 1 8 c = = 3.
WYMAGANIA EDUKACYJNE
 GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z FIZYKI w klasie III gimnazjum sr. 1 7. Przemiany energii w zjawiskach
GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z FIZYKI w klasie III gimnazjum sr. 1 7. Przemiany energii w zjawiskach
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 18, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE
 LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.
![Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość. Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.](/thumbs/102/155632743.jpg) Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
