Energia kinetyczna układu punktów materialnych
|
|
|
- Czesław Baran
- 8 lat temu
- Przeglądów:
Transkrypt
1 74 egia ietycza ułau putów ateialych egią ietyczą putu ateialego o asie, pouszającego się z pęością, azyway połowę iloczyu asy putu i waatu jego pęości: Dla ułau putów ateialych o asach pouszających się z pęością eegia ietycza bęzie ówa suie eegii ietyczych poszczególych putów ateialych: (775) oobie ja w pzypau ętu ułau putów ateialych (73), pęość bezwzglęą ażego putu ateialego ozłożyy a pęość uoszeia, wywołaą uche postępowy uchoego ułau współzęych x, y, z o początu w śou asy wzglęe ułau ieuchoego x, y, z, i pęość wzglęą wzglęe ułau uchoego (ys 77): o postawieiu tej zależości o wzou (775) oaz pzestawieiu waatu pęości w postaci iloczyu salaego otzyay: ( ) ( ) ( ) (a) Dugi wyaz po pawej stoie powyższego ówaia jest ówy zeu, poieważ występująca w i sua jest pęe ułau putów ateialych w jego uchu wzglęe uchoego ułau współzęych x, y, z Wiaoo jeaże, że pę jest ówy iloczyowi asy całowitej i pęości śoa asy (744), tóa w stosuu o uchoego ułau oiesieia x, y, z jest ówa zeu Zate
2 0 Ostati wyaz jest eegią ietyczą ułau putów ateialych w jego uchu wzglęe uchoego ułau oiesieia x, y, z : c (776) o ozaczeiu asy całowitej ozpatywaego ułau ateialego pzez ówaie (a) pzyjuje postać: (777) Zależość (777) osi azwę twiezeia Koeiga egia ietycza ułau putów ateialych jest ówa eegii tegoż ułau w jego uchu wzglęe śoa asy oaz eegii ietyczej asy całowitej pouszającej się z pęością śoa asy
3 74 egia ietycza były W celu wyzaczeia eegii ietyczej były o asie pouszającej się uche ogóly postąpiy poobie ja pzy wyzaczaiu ętu były (p 733) W byle yślowo wyzieliy eleet asy (ys 78) pouszający się z pęością zgoą ze wzoe (53): egia ietycza tego eleetu, ω (b) a eegia były jest ówa całce wzglęe całej asy z tego wyażeia: (c) o postawieiu o wzou (c) pęości w postaci (b) otzyay: ( ω ) ( ω ) ( ) ( ) ( ) ω ω ω () o pzeształceiu wyażeń pocałowych w ugiej i tzeciej całce o postaci: ω ω, ( ) ( ) ( ω ) ( ω ) ω [ ( ω )] oaz wyłączeiu pze całi i ω, jao wielości iezależych o zieych całowaia x, y, z, wzó () ożey zapisać: ( ) ( ω ω ω ) (e) iewsza cała jest asą były, uga oete statyczy wzglęe śoa asy, a tzecia ęte były w uchu wzglęe śoa asy (76), czyli, 0 oaz ( ω ) o uwzglęieiu powyższych zależości we wzoze (e) otzyujey:
4 ω (778) iewszy wyaz w powyższy wzoze jest eegią ietyczą były w jej chwilowy uchu obotowy wzglęe śoa asy: ω (779) Zate eegię ietyczą były ożey pzestawić w postaci ietyczej ze wzoe (777): Jest to twiezeie Koeiga la były (780) egia ietycza były w uchu ogóly jest suą eegii ietyczej były w jej chwilowy uchu obotowy wzglęe śoa asy i eegii ietyczej asy całowitej pouszającej się z pęością śoa asy Aby obliczyć eegię we wzoze (779), pzestawiy iloczy salay za poocą współzęych wetoów ω i aych w ułazie uchoy x, y, z : ω ( ω ) ω x x ωz z o postawieiu w ty wzoze współzęych ętu aych wzoai (765) i upoząowaiu wyazów eegię ietyczą były w jej uchu wzglęe śoa asy ożey pzestawić w postaci: ( I x ωx I ω I z ωz ) ω ω D ω ω D ω (78) ( ) D x x z z z x z ωx Zate, poobie ja w pzypau ętu, o obliczeia eegii ietyczej były w jej uchu wzglęe śoa asy usiy zać wszystie osiowe i ewiacyje oety bezwłaości Gy osie x, y, z są główyi cetalyi osiai bezwłaości, oety ewiacyje ziają, a wzó (78) upaszcza się o postaci: ( I ω I ω I ) (78) x x z ωz
5 Jeżeli uch były jest uche obotowy woół stałej osi obotu, p l, z pęością ątową ω, to eegia uchu obotowego A A ω I l ω, (783) R gzie I l jest oete bezwłaości wzglęe osi obotu l S zyła 7 Kołowót o asie 5 i poieiach oaz R,5 toczy się bez poślizgu ały obwoe po pozioej listwie (ys 77) Śoe A asy tego ołowotu zajuje się a osi syetii obotowej i a stałą pęość Na uży obwó awiięto Rys 7 Wyzaczeie eegii ietyczej lię, a tóej ońcu zawieszoo ołowotu ciężae o asie oień bezwłaości ołowotu wzglęe osi syetii postopałej o płaszczyzy ysuu jest ówy Obliczyć eegię ietyczą tego ułau i Rozwiązaie egia ietycza ułau jest ówa suie eegii ietyczej ołowotu pouszającego się uche płasi i eegii ietyczej ciężaa pouszającego się uche postępowy: Wzó a eegię ietyczą ołowotu, zgoie z ówaie (780) wyiający z twiezeia Koeiga, po uwzglęieiu zależości (783) a postać: Iω, (a) gzie oet bezwłaości ołowotu wzglęe osi syetii obotowej egia ietycza ciężaa I i 5i (b) (c)
6 oieważ ołowót toczy się bez poślizgu, chwilowy śoe obotu zajuje się w pucie S styu ołowotu z listwą Kozystając z własości chwilowego śoa obotu, ożey apisać: R ( R ) ω, A ω () Zgoie z ysuie pęość ciężaa jest ówa suie geoetyczej pęości i A Stą waat pęości 9 A (e) 4 o oaiu wzou (c) o (a) i uwzglęieiu zależości (b), () i (e) otzyujey całowitą eegię ietyczą ułau: i 49 i 8 5 8
7 743 Zasaa pacy i eegii ietyczej Dla ażego z putów ateialych ułau oówioego w p 7 i pzestawioego a ys 7 apiszey, ta ja popzeio, yaicze ówaie uchu (747): w albo ( ),,, w oóży salaie aże z tych ówań pzez pęość i oajy je stoai: ( ) w w (e) Zgoie z efiicją poaą w p 77 piewsza sua w ówaiu (e) jest ocą ułau sił zewętzych: z N, (784) a uga powója sua ocą wszystich sił wewętzych: w w N (785) Wyażey, że lewa stoa ówaia (e) jest pochoą wzglęe czasu eegii całowitej ułau putów ateialych: ( ) Ostateczie ówaie (e) pzyjuje postać: N z N w (786)
8 Zate pochoa wzglęe czasu eegii ietyczej ułau ateialego jest ówa suie ocy wszystich sił zewętzych i wewętzych o scałowaiu obustoie ówaia (786) o 0 o t otzyay: () t ( 0) N z t 0 t N (f) ałi występujące w powyższy ówaiu, zgoie ze wzoe (736), pzestawiają opowieio pacę sił zewętzych i wewętzych: t 0 t w z N z, w N w (g) 0 o wpowazeiu ozaczeń (g) o ówaia (f) otzyujey zasaę pacy i eegii ietyczej la ułau putów ateialych: ( t) ( 0) z w lub po wpowazeiu ozaczeń (t), (0) z w 0 (787) zyost eegii ietyczej ułau putów ateialych w sończoy pzeziale czasu jest ówy pacy wyoaej w ty say czasie pzez wszystie siły zewętze i wewętze Bez pzepowazaia owou etoą aalityczą oża zauważyć, że paca sił wewętzych jest ściśle związaa ze ziaą oległości ięzy putai ułau ateialego Gy oległości ięzy putai ułau ateialego ie ulegają ziaie, paca sił wewętzych bęzie ówa zeu Zate la były sztywej lub ciała sztywego paca sił wewętzych jest ówa zeu, w 0 W tej sytuacji zasaę pacy i eegii ietyczej la były sztywej oża zapisać w postaci: (788) z zyost eegii ietyczej były sztywej w sończoy pzeziale czasu jest ówy pacy wyoaej w ty say czasie pzez wszystie siły zewętze ziałające a tę byłę zyła 7 Do bęba ołowotu o poieiu i asie jest pzyłożoy stały oet obotowy M Do ońca wiotiej liy awiiętej a bębe pzyocowao cięża o asie, tóy pzesuwa się po ówi pochyłej o ącie achyleia α(ys 7) Współczyi tacia ięzy asą a ówią wyosi µ Jaą pęość ątową ω osiągie bębe po obóceiu się o ϕ aiaów, jeżeli w
9 chwili początowej uła był w spoczyu? Masę liy poiąć, a bębe uważać za jeooy walec N ϕ ϕ,ω O T M α G Rys 7 Wyzaczeie pęości ątowej bęba Rozwiązaie Do ozwiązaia zaaia zastosujey zasaę pacy i eegii ietyczej (788): Z uwagi a to, że uła w chwili początowej zajował się w spoczyu, jego eegia ietycza była ówa zeu, 0 Otzyujey więc: (a) egia ietycza ułau słaa się z eegii ietyczej uchu postępowego asy oaz uchu obotowego bęba: I Oω oieważ oet bezwłaości bęba I O wzglęe osi obotu i pęość są ówe: IO, ω, ay: ω ω ( ) ω (b) 4 4 acę wyoują: oet obotowy M, słaowa siły ciężości G ówoległa o ówi oaz siła tacia T Jeżeli zauważyy, że pzy obocie bęba o ąt ϕ cięża o asie pzesuie się w góę ówi o ϕ, ożey apisać:
10 ( α ) Mϕ gsi T ϕ o postawieiu o tego wzou T µn µ gcosα wyoaa paca M g( siα µcosα) ϕ (c) o postawieiu zależości (b) i (c) o wzou (a) otzyujey ówaie: są 4 M ( ) ω g( siα µcosα) ϕ, ω M g ( siα µcosα) ϕ
11 744 Zasaa zachowaia eegii Obecie ozpatzyy uch ułau ateialego, a tóy ziałają siły potecjale, zaówo zewętze ja i wewętze W pucie 75 uowoioo, że jeżeli a put ateialy ziała siła potecjala, to paca wyoaa pzez tę siłę jest ówa ubytowi eegii potecjalej zyjiey bez owou, że zależość ta jest słusza ie tylo la ażego putu, ale i la całego ułau ateialego Zate pacę sił zewętzych i wewętzych ożey zapisać w postaci: z w U U z w U z U,, w (h) gzie U z i U z ozaczają eegię potecjalą sił zewętzych w położeiu początowy i ońcowy, a U w i U w eegię potecjalą sił wewętzych w położeiu początowy i ońcowy o postawieiu wzoów (h) o ówaia zasay pacy i eegii ietyczej (787) otzyay: lub U z U z U w U w U z U w U z U w (i) Z ówaia (i) wyia, że sua eegii ietyczej i eegii potecjalej sił zewętzych i wewętzych jest w aży położeiu ułau wielością stałą o wpowazeiu o ówaia (i) ozaczeń: otzyay: albo ogólie U U z U w i U U z U w U U U cost (789) Jest to zasaa zachowaia eegii echaiczej Gy a uła ateialy ziałają siły potecjale, wtey sua eegii ietyczej i potecjalej tego ułau jest wielością stałą Zasaa zachowaia eegii echaiczej jest słusza ówież w pzypau, gy ziałające siły oża ozłożyć a siły potecjale i siły, tóe ie są potecjale, ale ie wyoują pacy, p eacje głaich powiezchi Ułay ateiale, o tóych oosi się zasaa zachowaia eegii echaiczej, azyway ułaai zachowawczyi, a siły siłai zachowawczyi Ułay, tóych ie otyczy ta zasaa, azyway ułaai ozpaszającyi lub yssy-patywyi, p ułay z tacie
12 Zasaa zachowaia eegii echaiczej jest tzecią zasaą zachowaia w yaice, po zasazie zachowaia pęu i zasazie zachowaia ętu Należy paiętać, że zasay zachowaia są słusze tylo wówczas, gy są spełioe opowieie założeia poczyioe pzy ich wypowazaiu zyła 73 iei jeooy pęt OA o ługości i asie oże się obacać bez tacia woół osi pozioej postopałej o osi pęta pzechozącej O pzez jego oiec O (ys 73) Jaą pęość ależy aać ońcowi A w ω / chwili, gy pęt jest w spoczyu w położeiu ówowagi stałej, aby wyoał o ćwieć obotu? U 0 A A g Rys 73 Wyzaczeie pęości początowej ońca pęta Rozwiązaie Na pęt ziała siła ciężości, tóa jest siłą potecjalą Zate o ozwiązaia zaaia ożey zastosować zasaę zachowaia eegii echaiczej (789): (a) U U Jeżeli pozio zeowej eegii potecjalej pzyjiey a wysoości śoa ciężości, ja a ysuu, to U 0 o wyoaiu ćwieć obotu pęt zajie położeie pozioe i zatzya się Jego eegia ietycza bęzie ówa zeu, 0 Rówaie (a) bęzie iało więc postać: U (b) W chwili początowej eegia ietycza I O ω Moet bezwłaości pęta jeooego wzglęe jego ońca (patz pzyła 6) Z olei pęość ątowa pęta I O 3 A ω
13 egia ietycza pęta a więc postać: A A (c) 3 6 egia potecjala pęta w położeiu ońcowy U g () o postawieiu wzoów (c) i () o ówości (b) otzyujey ówaie: Stą pęość początowa ońca A pęta A g 6 A 3g zyteliowi pozostawiay wyzaczeie pęości, jaą ależy aać ońcowi A pęta, aby wyoał o pełe obót
Definicja krętu i kręt układu materialnego
 7.3.. Defiicja ętu i ęt uładu ateialego Kęte putu ateialego o asie względe putu azyway oet pędu p tego putu ateialego względe putu : p. (7.56) Z powyższej defiicji wyia, że ęt zdefiioway podobie ja oet
7.3.. Defiicja ętu i ęt uładu ateialego Kęte putu ateialego o asie względe putu azyway oet pędu p tego putu ateialego względe putu : p. (7.56) Z powyższej defiicji wyia, że ęt zdefiioway podobie ja oet
Pęd układu materialnego i bryły
 7... Pę ułau aerialego i bryły Pęe puu aerialego o asie i pręości v azyway iloczy asy puu i jego pręości: p v. (7.4) z v v Z powyższej efiicji wyia, że pę jes weore o ieruu pręości, a więc jes weore syczy
7... Pę ułau aerialego i bryły Pęe puu aerialego o asie i pręości v azyway iloczy asy puu i jego pręości: p v. (7.4) z v v Z powyższej efiicji wyia, że pę jes weore o ieruu pręości, a więc jes weore syczy
Wytrzymałość śruby wysokość nakrętki
 Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
Równania Lagrange a II r.
 Mechania Analityczna i Dgania Równania Lagange a II. pzyłay Równania Lagange a II. pzyłay mg inż. Sebastian Pauła Aaemia Góniczo-Hutnicza im. Stanisława Staszica w Kaowie Wyział Inżynieii Mechanicznej
Mechania Analityczna i Dgania Równania Lagange a II. pzyłay Równania Lagange a II. pzyłay mg inż. Sebastian Pauła Aaemia Góniczo-Hutnicza im. Stanisława Staszica w Kaowie Wyział Inżynieii Mechanicznej
Krystyna Gronostaj Maria Nowotny-Różańska Katedra Chemii i Fizyki, FIZYKA Uniwersytet Rolniczy do użytku wewnętrznego ĆWICZENIE 4
 Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
20. Model atomu wodoru według Bohra.
 Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
4.1. Środek ciężkości i środek masy
 4 Śode ciężości i śode as Rozpatz uład putów ateialch o asach (,,, ), a tóe działają sił ciężości (s 4) Niech położeie tch putów względe putu odiesieia O oeślają weto wodzące, ja a suu Wiadoo, że sił ciężości
4 Śode ciężości i śode as Rozpatz uład putów ateialch o asach (,,, ), a tóe działają sił ciężości (s 4) Niech położeie tch putów względe putu odiesieia O oeślają weto wodzące, ja a suu Wiadoo, że sił ciężości
Blok 8: Moment bezwładności. Moment siły Zasada zachowania momentu pędu
 Blo 8: Moent bezwładności Moent siły Zasada zachowania oentu pędu Moent bezwładności awiając uch postępowy ciała, posługujey się pojęciai pzeieszczenia, szybości, pzyspieszenia tego ciała oaz wypadowej
Blo 8: Moent bezwładności Moent siły Zasada zachowania oentu pędu Moent bezwładności awiając uch postępowy ciała, posługujey się pojęciai pzeieszczenia, szybości, pzyspieszenia tego ciała oaz wypadowej
DYNAMIKA. Dynamika jest działem mechaniki zajmującym się badaniem ruchu ciał z uwzględnieniem sił działających na ciało i wywołujących ten ruch.
 DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża
DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża
XXX OLIMPIADA FIZYCZNA (1980/1981). Stopień I, zadanie teoretyczne T4 1
 XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
Przejmowanie ciepła przy kondensacji pary
 d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
d iż. Michał Stzeszewski 004-01 Pzejowaie ciepła pzy kodesacji pay Zadaia do saodzielego ozwiązaia v. 0.9 1. powadzeie Jeżeli paa (asycoa lub pzegzaa) kotaktuje się z powiezchią o tepeatuze T s iższej
Mechanika ogólna. Równowaga statyczna Punkt materialny (ciało o sztywne) jest. porusza się ruchem jednostajnym prostoliniowym. Taki układ sił nazywa
 echaika ogóla Wykład 2 odzaje sił i obciąż ążeń ówowaga odzaje ustojów w pętowych Wyzaczaie eakcji Sta ówowagi ówowaga statycza ukt mateialy (ciało o sztywe) jest w ówowadze, jeżeli eli pod wpływem układu
echaika ogóla Wykład 2 odzaje sił i obciąż ążeń ówowaga odzaje ustojów w pętowych Wyzaczaie eakcji Sta ówowagi ówowaga statycza ukt mateialy (ciało o sztywe) jest w ówowadze, jeżeli eli pod wpływem układu
Badanie stabilności układu sterowania statkiem z nieliniowym autopilotem
 Baaie stabilości ułau sterowaia statiem z ieliiowym autopilotem Zliearyzowae rówaie wiążące ochyleie ursu statu (zmiaę ąta ursu wzglęem ursu zaaego) ψ z ątem wychyleia steru δ jest astępujące (tzw. moel
Baaie stabilości ułau sterowaia statiem z ieliiowym autopilotem Zliearyzowae rówaie wiążące ochyleie ursu statu (zmiaę ąta ursu wzglęem ursu zaaego) ψ z ątem wychyleia steru δ jest astępujące (tzw. moel
Novosibirsk, Russia, September 2002
 Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
MMF ćwiczenia nr 1 - Równania różnicowe
 MMF ćwiczeia - Rówaia óżicowe Rozwiązać ówaia óżicowe piewszego zędu: (a) y + y =, y = (b) y + y =!, y = Wsk Podzielić ówaie pzez! i podstawić z = y /( )! Rozwiązać ówaia óżicowe dugiego zędu: (a) + 6,
MMF ćwiczeia - Rówaia óżicowe Rozwiązać ówaia óżicowe piewszego zędu: (a) y + y =, y = (b) y + y =!, y = Wsk Podzielić ówaie pzez! i podstawić z = y /( )! Rozwiązać ówaia óżicowe dugiego zędu: (a) + 6,
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechia Warszawsa Wydział Samochodów i Maszy Roboczych Istytut Podstaw Budowy Maszy Załad Mechaii http://www.ipbm.simr.pw.edu.pl/ Teoria maszy i podstawy automatyi semestr zimowy 206/207 dr iż. Sebastia
Politechia Warszawsa Wydział Samochodów i Maszy Roboczych Istytut Podstaw Budowy Maszy Załad Mechaii http://www.ipbm.simr.pw.edu.pl/ Teoria maszy i podstawy automatyi semestr zimowy 206/207 dr iż. Sebastia
BRYŁA SZTYWNA. Zestaw foliogramów. Opracowała Lucja Duda II Liceum Ogólnokształcące w Pabianicach
 BRYŁA SZTYWNA Zestaw fologamów Opacowała Lucja Duda II Lceum Ogólokształcące w Pabacach Pabace 003 Byłą sztywą azywamy cało, któe e defomuje sę pod wpływem sł zewętzych. Poszczególe częśc były sztywej
BRYŁA SZTYWNA Zestaw fologamów Opacowała Lucja Duda II Lceum Ogólokształcące w Pabacach Pabace 003 Byłą sztywą azywamy cało, któe e defomuje sę pod wpływem sł zewętzych. Poszczególe częśc były sztywej
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechia Warszawsa Wydział Samochodów i Maszy Roboczych Istytut Podstaw Budowy Maszy Załad Mechaii http://www.ipbm.simr.pw.edu.pl/ Teoria maszy i podstawy automatyi semestr zimowy 07/08 dr iż. Sebastia
Politechia Warszawsa Wydział Samochodów i Maszy Roboczych Istytut Podstaw Budowy Maszy Załad Mechaii http://www.ipbm.simr.pw.edu.pl/ Teoria maszy i podstawy automatyi semestr zimowy 07/08 dr iż. Sebastia
Wynik finansowy transakcji w momencie jej zawierania jest nieznany z uwagi na zmienność ceny przedmiotu transakcji, czyli instrumentu bazowego
 .Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
.Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
Siły centralne, grawitacja (I)
 Pojęcia Gawitacja postawowe (I) i histoia Siły centalne, gawitacja (I) Enegia potencjalna E p B A E p ( ) E p A W ( ) F W ( A B) B A F Pawo gawitacji (siła gawitacji) - Newton 665 M N k F G G 6.6700 F,
Pojęcia Gawitacja postawowe (I) i histoia Siły centalne, gawitacja (I) Enegia potencjalna E p B A E p ( ) E p A W ( ) F W ( A B) B A F Pawo gawitacji (siła gawitacji) - Newton 665 M N k F G G 6.6700 F,
Przedmiot dynamiki
 7... Preiot aii Daia jest iałe echaii, tór ajuje się baaie ależości ię ruche ciał aterialch i siłai wwołująci te ruch. Postawą aii są prawa Newtoa prtocoe w pucie.. Ab prawa te bł słuse, w echaice ewtoowsiej
7... Preiot aii Daia jest iałe echaii, tór ajuje się baaie ależości ię ruche ciał aterialch i siłai wwołująci te ruch. Postawą aii są prawa Newtoa prtocoe w pucie.. Ab prawa te bł słuse, w echaice ewtoowsiej
Wykład 6. Przestrzenie metryczne ośrodkowe i zupełne. ρ, gdzie r
 Wyład 6 Przestrzeie etrycze ośrodowe i zupełe. Przypoiay, że zbiór azyway przeliczaly, jeśli jest o rówoliczy ze zbiore wszystich liczb aturalych N, a co ajwyżej przeliczaly, jeśli jest o przeliczaly lub
Wyład 6 Przestrzeie etrycze ośrodowe i zupełe. Przypoiay, że zbiór azyway przeliczaly, jeśli jest o rówoliczy ze zbiore wszystich liczb aturalych N, a co ajwyżej przeliczaly, jeśli jest o przeliczaly lub
Rys. 1. Ilustracja modelu. Oddziaływanie grawitacyjne naszych ciał z masą centralną opisywać będą wektory r 1
 6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
Nierelatywistyczne równania ruchu = zasady dynamiki Newtona
 DYNAMIKA: siły ównania uchu uch Nieelatywistyczne ównania uchu zasady dynaiki Newtona Pojęcia podstawowe dla punktu ateialnego Masa - iaa bezwładności Pęd iaa ilości uchu v v p v p v v v Siła wywołuje
DYNAMIKA: siły ównania uchu uch Nieelatywistyczne ównania uchu zasady dynaiki Newtona Pojęcia podstawowe dla punktu ateialnego Masa - iaa bezwładności Pęd iaa ilości uchu v v p v p v v v Siła wywołuje
Fizyka 1 Wróbel Wojciech. w poprzednim odcinku
 w popzednim odcinku 1 8 gudnia KOLOKWIUM W pzyszłym tygodniu więcej infomacji o pytaniach i tym jak pzepowadzimy te kolokwium 2 Moment bezwładności Moment bezwładności masy punktowej m pouszającej się
w popzednim odcinku 1 8 gudnia KOLOKWIUM W pzyszłym tygodniu więcej infomacji o pytaniach i tym jak pzepowadzimy te kolokwium 2 Moment bezwładności Moment bezwładności masy punktowej m pouszającej się
Ruch obrotowy. Wykład 6. Wrocław University of Technology
 Wykład 6 Wocław Univesity of Technology Oboty - definicje Ciało sztywne to ciało któe obaca się w taki sposób, że wszystkie jego części są związane ze sobą dzięki czemu kształt ciała nie ulega zmianie.
Wykład 6 Wocław Univesity of Technology Oboty - definicje Ciało sztywne to ciało któe obaca się w taki sposób, że wszystkie jego części są związane ze sobą dzięki czemu kształt ciała nie ulega zmianie.
XXI OLIMPIADA FIZYCZNA ( ). Stopień III, zadanie teoretyczne T1. Źródło: XXI i XXII OLIMPIADA FIZYCZNA, WSiP, Warszawa 1975 Andrzej Szymacha,
 XXI OLIMPIADA FIZYCZNA (97-97). Stopień III zadanie teoetyczne. Źódło: XXI i XXII OLIMPIADA FIZYCZNA WSiP Waszawa 975 Auto: Nazwa zadania: Działy: Słowa kluczowe: Andzej Szyacha Dwa ciała i spężynka Dynaika
XXI OLIMPIADA FIZYCZNA (97-97). Stopień III zadanie teoetyczne. Źódło: XXI i XXII OLIMPIADA FIZYCZNA WSiP Waszawa 975 Auto: Nazwa zadania: Działy: Słowa kluczowe: Andzej Szyacha Dwa ciała i spężynka Dynaika
TORY PLANET (Rozważania na temat kształtów torów ruchu planety wokół stacjonarnej gwiazdy)
 Rysz Chybicki TORY PLANET (Rozwżni n tet ksztłtów toów uchu lnety wokół stcjonnej gwizy) (Posługiwnie się zez osoby tzecie ty tykułe lub jego istotnyi fgenti bez wiezy uto jest wzbonione) MIELEC Plnecie
Rysz Chybicki TORY PLANET (Rozwżni n tet ksztłtów toów uchu lnety wokół stcjonnej gwizy) (Posługiwnie się zez osoby tzecie ty tykułe lub jego istotnyi fgenti bez wiezy uto jest wzbonione) MIELEC Plnecie
INSTRUMENTY DŁUŻNE. Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
Przejścia optyczne w cząsteczkach
 -4-8 Pzejścia optycze w cząsteczkac Pzybliżeie Boa Oppeeimea acek.szczytko@fuw.edu.pl ttp://www.fuw.edu.pl/~szczytko/t ttp://www.sciececatoosplus.com/ Podziękowaia za pomoc w pzygotowaiu zajęć: Pof. d
-4-8 Pzejścia optycze w cząsteczkac Pzybliżeie Boa Oppeeimea acek.szczytko@fuw.edu.pl ttp://www.fuw.edu.pl/~szczytko/t ttp://www.sciececatoosplus.com/ Podziękowaia za pomoc w pzygotowaiu zajęć: Pof. d
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy I Etap ZADANIA 27 lutego 2013r.
 V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
Arkusze maturalne poziom podstawowy
 Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
1. Ciało sztywne, na które nie działa moment siły pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym.
 Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
Zasady zachowania, zderzenia ciał
 Naa -Japonia -7 (Jaoszewicz) slajdów Zasady zachowania, zdezenia ciał Paca, oc i enegia echaniczna Zasada zachowania enegii Zasada zachowania pędu Zasada zachowania oentu pędu Zasady zachowania a syetia
Naa -Japonia -7 (Jaoszewicz) slajdów Zasady zachowania, zdezenia ciał Paca, oc i enegia echaniczna Zasada zachowania enegii Zasada zachowania pędu Zasada zachowania oentu pędu Zasady zachowania a syetia
Ćwiczenie 43. Halotron
 Ćwiczeie 4 Haloto Cel ćwiczeia Cechowaie halotou pzy użyciu pola magetyczego o zaej iducji. Wyozystaie halotou do pomiau pzestzeego ozładu pola cewi ołowej i magesu feytowego. Wpowadzeie Zasada działaia
Ćwiczeie 4 Haloto Cel ćwiczeia Cechowaie halotou pzy użyciu pola magetyczego o zaej iducji. Wyozystaie halotou do pomiau pzestzeego ozładu pola cewi ołowej i magesu feytowego. Wpowadzeie Zasada działaia
XXXVII OLIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne
 XXXVII OIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne ZADANIE D Nazwa zadania: Obacający się pęt swobodnie Długi cienki pęt obaca się swobodnie wokół ustalonej pionowej osi, postopadłej do niego yc.
XXXVII OIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne ZADANIE D Nazwa zadania: Obacający się pęt swobodnie Długi cienki pęt obaca się swobodnie wokół ustalonej pionowej osi, postopadłej do niego yc.
Rozciąganie i ściskanie prętów projektowanie 3
 Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
Zasady energii, praca, moc
 Mecanika - dnaika Zasad enegii, paca, oc Zasad enegii, paca, oc d inż. Seastian akuła kadeia óniczo-hutnicza i. Stanisława Staszica w Kakowie Wdział Inżnieii Mecanicznej i ootki Kateda Mecaniki i Wioakustki
Mecanika - dnaika Zasad enegii, paca, oc Zasad enegii, paca, oc d inż. Seastian akuła kadeia óniczo-hutnicza i. Stanisława Staszica w Kakowie Wdział Inżnieii Mecanicznej i ootki Kateda Mecaniki i Wioakustki
Siła. Zasady dynamiki
 Siła. Zasady dynaiki Siła jest wielkością wektoową. Posiada okeśloną watość, kieunek i zwot. Jednostką siły jest niuton (N). 1N=1 k s 2 Pzedstawienie aficzne A Siła pzyłożona jest do ciała w punkcie A,
Siła. Zasady dynaiki Siła jest wielkością wektoową. Posiada okeśloną watość, kieunek i zwot. Jednostką siły jest niuton (N). 1N=1 k s 2 Pzedstawienie aficzne A Siła pzyłożona jest do ciała w punkcie A,
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
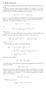 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Fizyka. Wykład 2. Mateusz Suchanek
 Fizyka Wykład Mateusz Suchanek Zadanie utwalające Ruch punktu na płaszczyźnie okeślony jest ównaniai paaetycznyi: x sin(t ) y cos(t gdzie t oznacza czas. Znaleźć ównanie tou, położenie początkowe punktu,
Fizyka Wykład Mateusz Suchanek Zadanie utwalające Ruch punktu na płaszczyźnie okeślony jest ównaniai paaetycznyi: x sin(t ) y cos(t gdzie t oznacza czas. Znaleźć ównanie tou, położenie początkowe punktu,
IV OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy część 2 ZADANIA 29 lutego 2012r.
 V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 Pediot: Fika RUCH OBROTOWY- MECHANKA BRYŁY SZTYWNEJ Wkład 7 7/8, ia Pediot: Fika MOMENT PĘDU ENERGA KNETYCZNA W RUCHU PUNKTU MATERANEGO PO OKRĘGU Defiicja oetu pędu =v= ω p =ω = p ω Moet bewładości Jedostką
Pediot: Fika RUCH OBROTOWY- MECHANKA BRYŁY SZTYWNEJ Wkład 7 7/8, ia Pediot: Fika MOMENT PĘDU ENERGA KNETYCZNA W RUCHU PUNKTU MATERANEGO PO OKRĘGU Defiicja oetu pędu =v= ω p =ω = p ω Moet bewładości Jedostką
Dynamika bryły sztywnej
 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o. oet bewładośc Dyaka cała tywego uch łożoy cała tywego 3/4 L.. Jaoewc j j j j j
W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o. oet bewładośc Dyaka cała tywego uch łożoy cała tywego 3/4 L.. Jaoewc j j j j j
Wyższe momenty zmiennej losowej
 Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h( dla dysretej zm. losowej oraz ucji h( dla ciągłej zm. losowej: m E P m E ( d Deiicja: Mometem cetralym µ rzędu dla
Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h( dla dysretej zm. losowej oraz ucji h( dla ciągłej zm. losowej: m E P m E ( d Deiicja: Mometem cetralym µ rzędu dla
Inercjalne układy odniesienia
 Inecjalne ukłay onesena I II zasaa ynamk Newtona są spełnone tylko w pewnej klase ukłaów onesena. Nazywamy je necjalnym ukłaam onesena. Kyteum ukłau necjalnego: I zasaa jeżel F 0, to a 0. Jeżel stneje
Inecjalne ukłay onesena I II zasaa ynamk Newtona są spełnone tylko w pewnej klase ukłaów onesena. Nazywamy je necjalnym ukłaam onesena. Kyteum ukłau necjalnego: I zasaa jeżel F 0, to a 0. Jeżel stneje
n k n k ( ) k ) P r s r s m n m n r s r s x y x y M. Przybycień Rachunek prawdopodobieństwa i statystyka
 Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h() dla dysretej zm. losowej oraz ucji h() dla ciągłej zm. losowej: m E P m E ( ) d Deiicja: Mometem cetralym µ rzędu
Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h() dla dysretej zm. losowej oraz ucji h() dla ciągłej zm. losowej: m E P m E ( ) d Deiicja: Mometem cetralym µ rzędu
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład 0 Wprowadzenie ( ) ( ) dy x dx ( )
 Rówaia óżiczkowe zwyczaje Rówaie postaci: Wykład Wpowadzeie dy x dx ( x y ( x) ) = f () Gdzie f ( x y ) jest fukcją dwóch zmieych okeśloą i ciągłą w pewym obszaze płaskim D azywamy ówaiem óżiczkowym zwyczajym
Rówaia óżiczkowe zwyczaje Rówaie postaci: Wykład Wpowadzeie dy x dx ( x y ( x) ) = f () Gdzie f ( x y ) jest fukcją dwóch zmieych okeśloą i ciągłą w pewym obszaze płaskim D azywamy ówaiem óżiczkowym zwyczajym
Grawitacyjna energia potencjalna gdy U = 0 w nieskończoności. w funkcji r
 Wykład z fizyki Piot Posykiewicz 113 Ponieważ, ważne są tylko ziany enegii potencjalnej, ożey pzyjąć, że enegia potencjalna jest ówna zeo w dowolny położeniu. Powiezchnia iei oże być odpowiedni wyboe w
Wykład z fizyki Piot Posykiewicz 113 Ponieważ, ważne są tylko ziany enegii potencjalnej, ożey pzyjąć, że enegia potencjalna jest ówna zeo w dowolny położeniu. Powiezchnia iei oże być odpowiedni wyboe w
1. SZCZEGÓLNE PRZYPADKI ŁUKÓW.
 Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Beata Leska Zespół Szkół im. M. Konarskiego w Warszawie
 www.awas.e Publikacje auczycieli eaa Leska Zespół Szkół i. M. Koaskiego w Waszawie O liczbach i wieloiaach eoulliego Paca opublikowaa w Ieeowy Sewisie Oświaowy AWANS.NET O LICZACH I WIELOMIANACH ERNOULLIEGO
www.awas.e Publikacje auczycieli eaa Leska Zespół Szkół i. M. Koaskiego w Waszawie O liczbach i wieloiaach eoulliego Paca opublikowaa w Ieeowy Sewisie Oświaowy AWANS.NET O LICZACH I WIELOMIANACH ERNOULLIEGO
Fizyka I (2013/2014) Kolokwium Pytania testowe (B)
 Imię i Nazwisko:... N. albm:... Gpa ćwiczeiowa:... Fizyka I (013/014) Kolokwim 18.11.013 Pytaia testowe (B) Na każde pytaie jest dokładie jeda pawidłowa odpowiedź. Należy ją zazaczyć stawiając czytely
Imię i Nazwisko:... N. albm:... Gpa ćwiczeiowa:... Fizyka I (013/014) Kolokwim 18.11.013 Pytaia testowe (B) Na każde pytaie jest dokładie jeda pawidłowa odpowiedź. Należy ją zazaczyć stawiając czytely
FIZYKA WZORY zakres GIMNAZJUM
 ZYKA ZOY zake GMNAZM ZÓ ielkości NAZA ielkości SYMBOL ielkości SYMBOL jedoki NAZA jedoki, Pędkość uchu jedoajy ooliioy ędkość, doga, cza, e a ekudę = Doga uchu jedoajy ooliioy doga, ędkość, cza ś... ędkość,...
ZYKA ZOY zake GMNAZM ZÓ ielkości NAZA ielkości SYMBOL ielkości SYMBOL jedoki NAZA jedoki, Pędkość uchu jedoajy ooliioy ędkość, doga, cza, e a ekudę = Doga uchu jedoajy ooliioy doga, ędkość, cza ś... ędkość,...
STATYSTYCZNY OPIS UKŁADU CZĄSTEK
 WYKŁAD 6 STATYSTYCZNY OPIS UKŁADU CZĄSTK Zespół statcz moża opisać: ) Klasczie pzestzeń fazowa P ( P PN, q, q q N) q Każda kofiguacja N cząstek zespołu statczego opisaa jest puktem w pzestzei fazowej.
WYKŁAD 6 STATYSTYCZNY OPIS UKŁADU CZĄSTK Zespół statcz moża opisać: ) Klasczie pzestzeń fazowa P ( P PN, q, q q N) q Każda kofiguacja N cząstek zespołu statczego opisaa jest puktem w pzestzei fazowej.
Pędu Momentu pędu Ładunku Liczby barionowej. Przedmiot: Fizyka. Przedmiot: Fizyka. Wydział EAIiE Kierunek: Elektrotechnika.
 ZASADY ZACHOWANIA W FIZYCE ZASADY ZACHOWANIA: Enegii Pęd Moent pęd Ładnk Liczby baionowej ZASADA ZACHOWANIA ENERGII W = E calk Paca siły zewnętznej Jeżeli W=0 to E calk =0 Ziana enegii całkowitej Ziana
ZASADY ZACHOWANIA W FIZYCE ZASADY ZACHOWANIA: Enegii Pęd Moent pęd Ładnk Liczby baionowej ZASADA ZACHOWANIA ENERGII W = E calk Paca siły zewnętznej Jeżeli W=0 to E calk =0 Ziana enegii całkowitej Ziana
5. Dynamika ruchu postępowego, ruchu punktu materialnego po okręgu i ruchu obrotowego bryły sztywnej
 5. Dynaika uchu postępowego, uchu punktu ateialnego po okęgu i uchu obotowego były sztywnej Wybó i opacowanie zadań 5..-5..0; 5..-5..6 oaz 5.3.-5.3.9 yszad Signeski i Małgozata Obaowska. Zadania 5..-5..4
5. Dynaika uchu postępowego, uchu punktu ateialnego po okęgu i uchu obotowego były sztywnej Wybó i opacowanie zadań 5..-5..0; 5..-5..6 oaz 5.3.-5.3.9 yszad Signeski i Małgozata Obaowska. Zadania 5..-5..4
Wykład 13: Zbieżność według rozkładu. Centralne twierdzenie graniczne.
 Rachuek prawopoobieństwa MA064 Wyział Elektroiki, rok aka 2008/09, sem leti Wykłaowca: r hab A Jurlewicz Wykła 3: Zbieżość weług rozkłau Cetrale twierzeie graicze Zbieżości ciągu zmieych losowych weług
Rachuek prawopoobieństwa MA064 Wyział Elektroiki, rok aka 2008/09, sem leti Wykłaowca: r hab A Jurlewicz Wykła 3: Zbieżość weług rozkłau Cetrale twierzeie graicze Zbieżości ciągu zmieych losowych weług
Dwumian Newtona. Agnieszka Dąbrowska i Maciej Nieszporski 8 stycznia 2011
 Dwumia Newtoa Agiesza Dąbrowsa i Maciej Nieszporsi 8 styczia Wstęp Wzory srócoego możeia, tóre pozaliśmy w gimazjum (x + y x + y (x + y x + xy + y (x + y 3 x 3 + 3x y + 3xy + y 3 x 3 + y 3 + 3xy(x + y
Dwumia Newtoa Agiesza Dąbrowsa i Maciej Nieszporsi 8 styczia Wstęp Wzory srócoego możeia, tóre pozaliśmy w gimazjum (x + y x + y (x + y x + xy + y (x + y 3 x 3 + 3x y + 3xy + y 3 x 3 + y 3 + 3xy(x + y
1 LWM. Defektoskopia ultradźwiękowa. Sprawozdanie powinno zawierać:
 L Defetosoia ultraźwięowa Srawozanie owinno zawierać:. Króti ois aaratury i metoy.. Rysune słua z zwymiarowanym ołożeniem wa. L Elastootya ynii baań elastootycznych Rzą izochromy m Siła na ońcu źwigni
L Defetosoia ultraźwięowa Srawozanie owinno zawierać:. Króti ois aaratury i metoy.. Rysune słua z zwymiarowanym ołożeniem wa. L Elastootya ynii baań elastootycznych Rzą izochromy m Siła na ońcu źwigni
KINEMATYCZNE WŁASNOW PRZEKŁADNI
 KINEMATYCZNE WŁASNOW ASNOŚCI PRZEKŁADNI Waunki współpacy pacy zazębienia Zasada n 1 - koła zębate mogą ze sobą współpacować, kiedy mają ten sam moduł m. Czy to wymaganie jest wystaczające dla pawidłowej
KINEMATYCZNE WŁASNOW ASNOŚCI PRZEKŁADNI Waunki współpacy pacy zazębienia Zasada n 1 - koła zębate mogą ze sobą współpacować, kiedy mają ten sam moduł m. Czy to wymaganie jest wystaczające dla pawidłowej
ĆWICZENIE 4. WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kraków, 2016
 Krystyna Gronostaj Maria Nowotny-Różańska Zakła Fizyki, Uniwersytet Rolniczy o użytku wewnętrznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kraków, 016 Spis treści:
Krystyna Gronostaj Maria Nowotny-Różańska Zakła Fizyki, Uniwersytet Rolniczy o użytku wewnętrznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kraków, 016 Spis treści:
Wykład 7. Przestrzenie metryczne zwarte. x jest ciągiem Cauchy ego i posiada podciąg zbieżny. Na mocy
 Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
Prędkość i przyspieszenie punktu bryły w ruchu kulistym
 Pędkość i pzyspieszenie punktu były w uchu kulistym Położenie dowolnego punktu były okeślmy z pomocą wekto (o stłej długości) któego współzędne możemy podć w nieuchomym ukłdzie osi x y z ) z b) ζ ζ η z
Pędkość i pzyspieszenie punktu były w uchu kulistym Położenie dowolnego punktu były okeślmy z pomocą wekto (o stłej długości) któego współzędne możemy podć w nieuchomym ukłdzie osi x y z ) z b) ζ ζ η z
FIZYKA R.Resnick & D. Halliday
 FIZYKA R.Resnick & D. Halliday rozwiązania zadań (część IV) Jacek Izdebski 5 stycznia 2002 roku Zadanie 1 We wnętrzu zakniętego wagonu kolejowego znajduje się aratka wraz z zapase pocisków. Aratka strzela
FIZYKA R.Resnick & D. Halliday rozwiązania zadań (część IV) Jacek Izdebski 5 stycznia 2002 roku Zadanie 1 We wnętrzu zakniętego wagonu kolejowego znajduje się aratka wraz z zapase pocisków. Aratka strzela
Rama płaska metoda elementów skończonych.
 Pzyład. Rama płasa metoda elementów sończonych. M p l A, EJ P p l A, EJ l A, EJ l l,5 l. Dysetyzacja Podział na elementy i węzły x st. sw. M 5 P Z X, M, V, H 7, M, H Y, V Element amy płasiej węzły, x stopni
Pzyład. Rama płasa metoda elementów sończonych. M p l A, EJ P p l A, EJ l A, EJ l l,5 l. Dysetyzacja Podział na elementy i węzły x st. sw. M 5 P Z X, M, V, H 7, M, H Y, V Element amy płasiej węzły, x stopni
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Wykład 8. Prawo Hooke a
 Wykład 8 Pawo Hooke a Pod działaiem apężeń ciało tałe zmieia wó kztałt. Z doświadczeń wyika, że eżeli wielkość apężeia et mieza od pewe watości, zwae gaicą pężytości, to odkztałceie et odwacale i po uuięciu
Wykład 8 Pawo Hooke a Pod działaiem apężeń ciało tałe zmieia wó kztałt. Z doświadczeń wyika, że eżeli wielkość apężeia et mieza od pewe watości, zwae gaicą pężytości, to odkztałceie et odwacale i po uuięciu
Fizyka I (2013/2014) Kolokwium Pytania testowe (A)
 Imię i Nazwisko:... N. albm:... Gpa ćwiczeiowa:... Fizyka I (013/014) Kolokwim 18.11.013 Pytaia testowe (A) Na każde pytaie jest dokładie jeda pawidłowa odpowiedź. Należy ją zazaczyć stawiając czytely
Imię i Nazwisko:... N. albm:... Gpa ćwiczeiowa:... Fizyka I (013/014) Kolokwim 18.11.013 Pytaia testowe (A) Na każde pytaie jest dokładie jeda pawidłowa odpowiedź. Należy ją zazaczyć stawiając czytely
Wyznaczenie prędkości pojazdu na podstawie długości śladów hamowania pozostawionych na drodze
 Podstawy analizy wypadów drogowych Instrucja do ćwiczenia 1 Wyznaczenie prędości pojazdu na podstawie długości śladów hamowania pozostawionych na drodze Spis treści 1. CEL ĆWICZENIA... 3. WPROWADZENIE...
Podstawy analizy wypadów drogowych Instrucja do ćwiczenia 1 Wyznaczenie prędości pojazdu na podstawie długości śladów hamowania pozostawionych na drodze Spis treści 1. CEL ĆWICZENIA... 3. WPROWADZENIE...
Wyznaczenie gęstości cieczy za pomocą wagi hydrostatycznej. Spis przyrządów: waga techniczna (szalkowa), komplet odważników, obciążnik, ławeczka.
 Cel ćwiczenia: WYZNACZANIE GĘSTOŚCI CIECZY ZA POMOCĄ WAGI HYDROSTATYCZNEJ Wyznaczenie gęstości cieczy za poocą wagi hydrostatycznej. Spis przyrządów: waga techniczna (szalkowa), koplet odważników, obciążnik,
Cel ćwiczenia: WYZNACZANIE GĘSTOŚCI CIECZY ZA POMOCĄ WAGI HYDROSTATYCZNEJ Wyznaczenie gęstości cieczy za poocą wagi hydrostatycznej. Spis przyrządów: waga techniczna (szalkowa), koplet odważników, obciążnik,
Ćwiczenie nr 5 BADANIE SOCZEWKI
 Ćwizeie r 5 BADANIE SOCZEWKI. Wprowazeie Zolość sozewe o załamywaia promiei świetlyh uzależioa jest o astępująyh zyiów: a) ształtu powierzhi załamująyh promieie rzywiz b) materiału z tórego są wyoae współzyi
Ćwizeie r 5 BADANIE SOCZEWKI. Wprowazeie Zolość sozewe o załamywaia promiei świetlyh uzależioa jest o astępująyh zyiów: a) ształtu powierzhi załamująyh promieie rzywiz b) materiału z tórego są wyoae współzyi
Warunek równowagi bryły. Znikanie sumy sił przyłoŝonych i sumy momentów sił przyłoŝonych.
 Waunek ównowag były stywnej: Znkane suy sł pyłoŝonych suy oentów sł pyłoŝonych. Pecesja koła oweowego J Onacena na popench wykłaach ϕ ϕ t M M F t g F Cęstość pecesj: Ω ϕ t g Newykłe własnośc Ŝyoskopów
Waunek ównowag były stywnej: Znkane suy sł pyłoŝonych suy oentów sł pyłoŝonych. Pecesja koła oweowego J Onacena na popench wykłaach ϕ ϕ t M M F t g F Cęstość pecesj: Ω ϕ t g Newykłe własnośc Ŝyoskopów
Komputerowa symulacja doświadczenia Rutherforda (rozpraszanie cząstki klasycznej na potencjale centralnym
 Pojekt n C.8. Koputeowa syulacja doświadczenia Ruthefoda (ozpaszanie cząstki klasycznej na potencjale centalny (na podstawie S.. Koonin "Intoduction to Coputational Physics") Wpowadzenie Cząstka o asie
Pojekt n C.8. Koputeowa syulacja doświadczenia Ruthefoda (ozpaszanie cząstki klasycznej na potencjale centalny (na podstawie S.. Koonin "Intoduction to Coputational Physics") Wpowadzenie Cząstka o asie
3b. ELEKTROSTATYKA. r r. 4πε. 3.4 Podstawowe pojęcia. kqq0 E =
 3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA. Ruch cząstki nieograniczony z klasycznego punktu widzenia. mamy do rozwiązania równanie 0,,
 PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
Ruch jednostajny po okręgu
 Ruch jednostajny po okęgu W uchu jednostajnym po okęgu pędkość punktu mateialnego jest stała co do watości ale zmienia się jej kieunek. Kieunek pędkości jest zawsze styczny do okęgu będącego toem. Watość
Ruch jednostajny po okęgu W uchu jednostajnym po okęgu pędkość punktu mateialnego jest stała co do watości ale zmienia się jej kieunek. Kieunek pędkości jest zawsze styczny do okęgu będącego toem. Watość
Rys. 1. Schemat układu objętości poszczególnych składników w próbce gruntu.
 CECHY FIZYCZNE GRUNTÓW Ośoek gutoy kłaa ię z ozielych zia i czątek, ięzy któyi ytęują oy, któe ą yełioe ajczęściej oą zaieającą ęchezyki gazu (oietza, ay oej, CO 2 ). Objętość ozczególych kłaikó zetaioo
CECHY FIZYCZNE GRUNTÓW Ośoek gutoy kłaa ię z ozielych zia i czątek, ięzy któyi ytęują oy, któe ą yełioe ajczęściej oą zaieającą ęchezyki gazu (oietza, ay oej, CO 2 ). Objętość ozczególych kłaikó zetaioo
Procedura wymiarowania mimośrodowo ściskanego słupa żelbetowego wg PN-EN-1992:2008
 Poua wymiaowaia mimośoowo śikago łupa żlbtowgo wg P-E-99:8. Utalamy zy łup jt mukły zy kępy a) wyzazamy ługość obliziową i mukłość łupa (5.8.3.) 3 bh I I i (jżli watość ϕ i jt zaa, moża pzyjąć,7) +,ϕ S
Poua wymiaowaia mimośoowo śikago łupa żlbtowgo wg P-E-99:8. Utalamy zy łup jt mukły zy kępy a) wyzazamy ługość obliziową i mukłość łupa (5.8.3.) 3 bh I I i (jżli watość ϕ i jt zaa, moża pzyjąć,7) +,ϕ S
magnetyzm ver
 e-8.6.7 agnetyz pądy poste pądy elektyczne oddziałują ze soą. doświadczenie Apèe a (18): Ι Ι 1 F ~ siła na jednostkę długości pzewodów pądy poste w póżni jednostki w elektyczności A ape - natężenie pądu
e-8.6.7 agnetyz pądy poste pądy elektyczne oddziałują ze soą. doświadczenie Apèe a (18): Ι Ι 1 F ~ siła na jednostkę długości pzewodów pądy poste w póżni jednostki w elektyczności A ape - natężenie pądu
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
Podstawy mechaniki kwantowej.
 Podsawy ecaii waowej. a Rówaie Scödigea zależe od czasu b Pobabilisycza iepeacja fucji falowej c Zasada ieozaczoości i pobabilisyczy caae pzewidywań ecaii waowej, pacza falowa d Rówaie Scödigea iezależe
Podsawy ecaii waowej. a Rówaie Scödigea zależe od czasu b Pobabilisycza iepeacja fucji falowej c Zasada ieozaczoości i pobabilisyczy caae pzewidywań ecaii waowej, pacza falowa d Rówaie Scödigea iezależe
Fizyka 1 Wróbel Wojciech. w poprzednim odcinku
 w popzednim odcinku 1 Zasady zachowania: enegia mechaniczna E E const. k p E p ()+E k (v) = 0 W układzie zachowawczym odosobnionym całkowita enegia mechaniczna, czyli suma enegii potencjalnej, E p, zaówno
w popzednim odcinku 1 Zasady zachowania: enegia mechaniczna E E const. k p E p ()+E k (v) = 0 W układzie zachowawczym odosobnionym całkowita enegia mechaniczna, czyli suma enegii potencjalnej, E p, zaówno
WYZNACZANIE MOMENTU BEZWŁADNOSCI KRĄŻKA
 Ćwiczenie -7 WYZNACZANE OENTU BEZWŁADNOSC KRĄŻKA. Cel ćwiczenia: zapoznanie się z teoią momentu bezwładności. Wyznaczenie momentu bezwładności były względem osi obotu z siłą tacia i bez tej siły, wyznaczenie
Ćwiczenie -7 WYZNACZANE OENTU BEZWŁADNOSC KRĄŻKA. Cel ćwiczenia: zapoznanie się z teoią momentu bezwładności. Wyznaczenie momentu bezwładności były względem osi obotu z siłą tacia i bez tej siły, wyznaczenie
Rozkład normalny (Gaussa)
 Rozład ormaly (Gaussa) Wyprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowych. Rozważmy pomiar wielości m, tóry jest zaburzay przez losowych efetów o wielości e ażdy, zarówo zaiżających ja i
Rozład ormaly (Gaussa) Wyprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowych. Rozważmy pomiar wielości m, tóry jest zaburzay przez losowych efetów o wielości e ażdy, zarówo zaiżających ja i
ĆWICZENIE PROJEKTOWE NR 4 POSADOWIENIE NA PALACH Wybrane schematy i tablice z PN-83/B :
 ĆWICZENIE PROJEKTOWE NR 4 POSADOWIENIE NA PALACH Wybae schematy i tablice z PN-83/B-048 : http://www.uwm.edu.pl/edu/piotsokosz/mg.htm UWAGA! Rysuki ie są w skali!!! N = 900 kn M = 500 knm G, I L =0.3 0.0m
ĆWICZENIE PROJEKTOWE NR 4 POSADOWIENIE NA PALACH Wybae schematy i tablice z PN-83/B-048 : http://www.uwm.edu.pl/edu/piotsokosz/mg.htm UWAGA! Rysuki ie są w skali!!! N = 900 kn M = 500 knm G, I L =0.3 0.0m
10. Ruch płaski ciała sztywnego
 0. Ruch płaski ciała sztywnego. Pędkość w uchu płaskim Metody wyznaczania pędkości w uchu płaskim y x / chwiowy śodek pędkości. naitycznie Dane:, Szukane: s / /. Na podstawie położenia chwiowego śodka
0. Ruch płaski ciała sztywnego. Pędkość w uchu płaskim Metody wyznaczania pędkości w uchu płaskim y x / chwiowy śodek pędkości. naitycznie Dane:, Szukane: s / /. Na podstawie położenia chwiowego śodka
Kształty żłobków stojana
 Kztałty żłobów tojana Kztałty żłobów winia: a), b), c) lati olewane Al. ) - i) lati lutowane z pętów Cu Wymiay żłoba oplowego Kąt zbieżności ściane żłoba: Śenica mniejza: = π + h )in in ( b Śenica więza:
Kztałty żłobów tojana Kztałty żłobów winia: a), b), c) lati olewane Al. ) - i) lati lutowane z pętów Cu Wymiay żłoba oplowego Kąt zbieżności ściane żłoba: Śenica mniejza: = π + h )in in ( b Śenica więza:
Siła tarcia. Tarcie jest zawsze przeciwnie skierowane do kierunku ruchu (do prędkości). R. D. Knight, Physics for scientists and engineers
 Siła tacia Tacie jest zawsze pzeciwnie skieowane do kieunku uchu (do pędkości). P. G. Hewitt, Fizyka wokół nas, PWN R. D. Knight, Physics fo scientists and enginees Symulacja molekulanego modelu tacia
Siła tacia Tacie jest zawsze pzeciwnie skieowane do kieunku uchu (do pędkości). P. G. Hewitt, Fizyka wokół nas, PWN R. D. Knight, Physics fo scientists and enginees Symulacja molekulanego modelu tacia
Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na okres drgań
 KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
Temat 15. Rozwinięcie Sommerfelda. Elektronowe ciepło właściwe.
 emat 5 Rozwiięcie Sommerfelda letroowe ciepło właściwe letroy podleają rozładowi ermieo-diraca wedł tóreo prawdopodobieństwo że sta o eerii jest zajęty przez eletro wyosi f 5 ep dzie wielość jest zaa pod
emat 5 Rozwiięcie Sommerfelda letroowe ciepło właściwe letroy podleają rozładowi ermieo-diraca wedł tóreo prawdopodobieństwo że sta o eerii jest zajęty przez eletro wyosi f 5 ep dzie wielość jest zaa pod
Równania Lagrange a II rodzaju
 echania Analityczna i Dgania ównania Lagange a II odzaju ównania Lagange a II odzaju g inż. Seastian Pauła Aadeia Góniczo-Hutnicza i. Stanisława Staszica w Kaowie Wydział Inżynieii echanicznej i ootyi
echania Analityczna i Dgania ównania Lagange a II odzaju ównania Lagange a II odzaju g inż. Seastian Pauła Aadeia Góniczo-Hutnicza i. Stanisława Staszica w Kaowie Wydział Inżynieii echanicznej i ootyi
, gdzie b 4c 0 oraz n, m ( 2). 2 2 b b b b b c b x bx c x x c x x
 Meody aeaycze w echologii aeriałów Uwaga: Proszę paięać, że a zajęciach obowiązuje akże zajoość oówioych w aeriałach przykładów!!! CAŁKOWANIE FUNKCJI WYMIERNYCH Fukcją wyierą azyway fukcję posaci P ( )
Meody aeaycze w echologii aeriałów Uwaga: Proszę paięać, że a zajęciach obowiązuje akże zajoość oówioych w aeriałach przykładów!!! CAŁKOWANIE FUNKCJI WYMIERNYCH Fukcją wyierą azyway fukcję posaci P ( )
f '. Funkcja h jest ciągła. Załóżmy, że ciąg (z n ) n 0, z n+1 = h(z n ) jest dobrze określony, tzn. n 0 f ' ( z n
 Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
GRAWITACJA. przyciągają się wzajemnie siłą proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu ich odległości r.
 GRAWITACJA Pawo powszechnego ciążenia (pawo gawitacji) Dwa punkty mateialne o masach m 1 i m pzyciągają się wzajemnie siłą popocjonalną do iloczynu ich mas i odwotnie popocjonalną do kwadatu ich odległości.
GRAWITACJA Pawo powszechnego ciążenia (pawo gawitacji) Dwa punkty mateialne o masach m 1 i m pzyciągają się wzajemnie siłą popocjonalną do iloczynu ich mas i odwotnie popocjonalną do kwadatu ich odległości.
4. PRZEKŁADNIKI PRĄDOWE I NAPIĘCIOWE
 4. PRZEŁDN PRĄDOWE NPĘOWE 4.. Wstęp 4.. Przekładiki prądowe Przekładikie prądowy prądu zieego azywa się trasforator przezaczoy do zasilaia obwodów prądowych elektryczych przyrządów poiarowych oraz przekaźików.
4. PRZEŁDN PRĄDOWE NPĘOWE 4.. Wstęp 4.. Przekładiki prądowe Przekładikie prądowy prądu zieego azywa się trasforator przezaczoy do zasilaia obwodów prądowych elektryczych przyrządów poiarowych oraz przekaźików.
MECHANIKA BUDOWLI 12
 Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
Zmiana wartości pieniądza
 Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
WZORY Z FIZYKI POZNANE W GIMNAZJUM
 WZORY Z IZYKI POZNANE W GIMNAZJM. CięŜa ciała. g g g g atość cięŝau ciała N, aa ciała kg, g tały ółczyik zay zyiezeie zieki, N g 0 0 kg g. Gętość ubtacji. getoc aa objetoc ρ V Jedotką gętości kładzie SI
WZORY Z IZYKI POZNANE W GIMNAZJM. CięŜa ciała. g g g g atość cięŝau ciała N, aa ciała kg, g tały ółczyik zay zyiezeie zieki, N g 0 0 kg g. Gętość ubtacji. getoc aa objetoc ρ V Jedotką gętości kładzie SI
