Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
|
|
|
- Maja Czech
- 8 lat temu
- Przeglądów:
Transkrypt
1 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie płatnej z góy (ang pepetuity due) Jej watość teaźniejszą ozn ä Zate ä + υ + υ + υ d gdzie υ jest czynnikie dyskontujący Jeżeli piewsza płatność a + iejsce na koniec piewszego oku, to enta jest płatna z dołu (ang iediate pepetuity) Jej watość teaźniejszą ozn a : a υ + υ + υ υ, ale υ υ ( + )( ) +, + więc a Rozważy teaz enty, gdzie kwota jest wypłacana azy do oku Jeśli płatność jest z góy (piewsza wypłata w chwili ), to ozn ä () oaz ä () + υ + υ + υ bo d() υ Jeżeli płatności są z dołu, to oznaczay a () oaz d (), a () υ + υ + υ + υ υ υ ( + ) [ () + ] () Pzypoinay zależność d() + () ( + ) υ
2 Otzyane wyżej ówności: ä () d (), a(), () i oczywisty fakt, że oba odzaje ent óżnią się tylko płatnością w chwili, daje znaną już ówność d () + () Rozważy teaz entę wypłacaną w sposób ciągły (watość enty, początek wypłat w chwili ) Jej watość teaźniejszą oznaczy a Wypłatę dt w chwili t należy zdyskontować czynnikie e δt (bo czynnik ponażający dla jednego oku to e δ ), więc ay a To sao otzyay obliczając e δt dt δ a li ä() li d () δ, lub a li a() li () δ Rozważy teaz pewną entę wieczystą (z góy), w któej ay osnący ciąg płatności Renta ta będzie okeślona dwoa paaetai: liczba płatności w oku; liczba podwyżek w oku (zakładay, że ) Np dla i 4 płatności są dokonywane iesięcznie, a podwyższane co kwatał Ogólnie, płatności takiej osnącej enty są dokonywane wg scheatu: Czas + Płatność
3 W szczególności, w piewszy oku ostatnie płatności (czas od do ) wynoszą Ogólniej, w k-ty oku ostatnie płatności wynoszą k Oznaczay watość teaźniejszą takiej osnącej enty pzez (I() ä) () Można obliczyć jej watość pzedstawiając ją jako suę ent stałych (wysokość, płatność azy w oku) ozpoczynających się w oentach czasu,,, Zate (watość ocznej wpłaty to ): (I () ä) () ä() [ + υ/ + υ / + ] ä () ä () d () d () Odpowiednia enta płatna z dołu óżni się tylko ty, że każda wpłata jest dokonywana -tą oku później, więc (I () a) () υ ( (I ()ä) ) () υ d () d () () d, () bo d () υ () Indeks góny zawsze opuszczay Np watość teaźniejsza enty płatnej z góy z ocznyi płatnościai,,, to (Iä) (I () ä) () d Równości (I () ä) () d () d, () (I() a) () () d () ożna wykozystać (pzechodząc z ) do obliczenia watości teaźniejszych ciągłych stuieni płatności Np (uwaga: [x] oznacza całość z x): (Īā) te δt dt δ, (Iā) [t + ]e δt dt δd, pzy czy wyniki końcowe uzyskujey bez liczenia całek (Należy uwzględnić, że li oaz, że ) d () δ d () d Na koniec ozważy entę wypłacającą kwoty,,, (w chwilach,,, ) Jej watość teaźniejsza ä wynosi: ä + υ + υ +
4 Taka zienna enta oże być ozważana jako sua stałych ent, według scheatu Dooczna płatność Moent statu Jej watość teaźniejszą ożey więc zapisać jako ä d [ + υ( ) + υ ( ) + ] Taka postać bywa pzydatna, gdy óżnice są postsze niż sae k ; tak jest np wtedy, gdy k jest wieloiane ziennej k Np gdy k k +, to ożey otzyać znany już wzó (Iä) d ( + υ + υ + ) d υ d Czase jest łatwiej wyliczyć watość teaźniejszą bezpośednio Jeżeli np to pod waunkie, że τ < δ k e τk, k,,, ä + υe τ + υ e τ + υe τ e δ e τ e, (δ τ) Renty teinowe Rentą teinową (ang annuity) nazyway ciąg płatności z oganiczony czase twania n Watość teaźniejszą enty teinowej płatnej z góy, w wysokości, oznaczay ä Zate ä + υ + υ + + υ n υn υ υn d 4
5 Wynik ten ożna uzyskać taktując tę entę jako óżnicę dwóch ent wieczystych (jedna zaczyna się dla t, duga dla t n): Podobnie uzyskay: ä ä υ n ä υn d a υn, ä () υn d (), a () υn () W pzypadku ent teinowych inteesująca jest ównież ich watość pzyszła (końcowa) Watość pzyszłą uzyskay nożąc watość teaźniejszą pzez ( + ) n Stąd υ n s ( + )n d s ( + )n, s () ( + )n, d () May także zależność czyli s + s () ( + )n () ( ) υ n + υ n + υ n υ n υ n υ n υ, n a + a s Rozważy teaz osnącą entę teinową z paaetai i (np, 4) 5
6 Czas + Płatność n n + n Taka osnąca enta teinowa oże być taktowana jako osnąca enta wieczysta ozpoczynająca się w chwili inus osnąca enta wieczysta ozpoczynająca się w chwili n, inus stała enta (w wysokości n ) ozpoczynająca się w chwili n Zate Analogicznie: (I () ä) () (I () ä) () υ n (I () ä) () υ n nä () n d () d () υn d () d () υn n d () ( υ n d () d () ) υ n n ä() (I () a) () ä() nυ n () Ważnyi szczególnyi pzypadkai są:,,,,,,, nυ n d () Renty teinowe ozważane wyżej są to tzw standadowe enty osnące (I) Standadowe enty alejące (D) są podobnie skonstuowane, ale płatności są w odwotnej kolejności Zate suy obu tych ent twozą stałą entę W następujący achunku ä () jest watością enty w wysokości watością enty w wysokości n 6, więc nä() jest
7 teinową (wysokość iesięczna płatności to n + ) Zate skąd (I () ä) () + (D () ä) () (n + )ä() (D () ä) () (n + )ä() (n + [ d () [ d () ä() ) υn d () nυ n d () υ n d () nυ n d () n nυ n + υn υn n ( υ n )( d () ) d () ], + nυ n ] ale d () +, () więc (D () ä) () (n ) υn n a() d () () d () Wzó ten, czyli watość teaźniejszą standadowej enty alejącej ożna wyznaczyć także bezpośednio, taktując tę entę jako stałą entę wieczystą z płatnościai n inus n odoczonych ent wieczystych, każda z płatnością, zaczynających się w oentach,,, n Zate (D () ä) () nä () n [ ä () n [ d () d () υ i ä() i n ] υ i i n υ ] υn υ n υn, (υ ) 7
8 ale ponieważ ( + () ) υ, tj () (υ ), więc (D () ä) () d () [n υn () ] n a() d () Pzykłady 4-letni obotnik chce zgoadzić fundusz na eeytuę W ty celu odkłada w banku zł na początku każdego oku, pzez 5 lat Po pzejściu na eeytuę planuje wykozystać ten fundusz wybieając jednakowe kwoty na początku każdego oku pzez 5 lat W jakiej wysokości będą te kwoty jeśli efektywna oczna stopa pocentowa wynosi 8% pzez piewsze 5 lat, a później 7%? Jedna enta wypłaca kwoty 4 na koniec oku pzez 6 lat Duga kwoty 5 na koniec oku pzez 8 lat Watość teaźniejsza obu ent jest taka saa, pzy stopie i Znajdź n takie, że kapitał zainwestowany na n lat podwoi swoją watość pzy stopie i Załóży, że K i M zaabiają butto Na fundusz eeytalny pacodawca wpłaca 9,76% tej kwoty Obliczyć watość pzyszłą konta eeytalnego dla K po 4 latach i M po 45 latach Taktując obliczone wielkości jako watości teaźniejsze ent wypłacanych: w pzypadku K pzez lat, w pzypadku M pzez lat obliczyć wysokość (iesięczną) takiej enty Stopa oczna 4% Wpłaty i wypłaty z dołu, kapitalizacja iesięczna Rozwiązanie: Wpłata iesięczna wynosi, 976 9, 8 Ponieważ kapitalizacja jest iesięczna, najlepiej stosować wzó na s, gdzie n jest liczbą iesięcy, a jest stopą iesięczną,4 Zate podstawiay do wzou: s ( + )n, i otzyujey watość pzyszłą konta eeytalnego dla K po 4 latach: 9, 8s 48 Altenatywnie, gdyby stosować wzó: ( +,4 )48,4 s () ( + )n (), , 47
9 w któy n jest liczbą lat, to tzeba paiętać, że w ty wzoze jest stopą efektywną Zate nie jest ówne, 4, lecz ef, gdzie + ef ( +,4 ) Natoiast (), 4 Eeytuę (iesięczną) obliczay dla K z ówności a dla M z ówności 9, 8 s 48 x a 4, 9, 8 s 54 x a Wyniki dla óżnych stóp pocentowych: Stopa Kap:K Kap:M Eeyt:K Eeyt:M, , , , , , Zadania z egzainów dla aktuaiuszy ( zad) Rozważy -letnią entę pewną natychiast płatną o płatnościach dokonywanych na początku każdego oku Niech k dla k,,, oznacza płatność na początku oku k i niech k będzie zdefiniowane następująco: { α k+ ( k ) k dla k,,, Wiadoo, że watość obecna tej enty (tzn watość tej enty w chwili dokonania piewszej wypłaty) wynosi (z dokładnością do liczb całkowitych) Wiadoo też że czynnik dyskontujący wynosi υ, 7 Oblicz α Odpowiedź (podaj najbliższą watość):,5;,5;,75;,5;,65 Rozwiązanie Zauważy,że α, ( )α,; ogólnie k+ ( ) α k 9
10 Zate watość obecna k k υ k k k+ υ k k ( ) αυ k α k Stąd 4866 α, 7, więc α, 5 k ( ) υ k α( + υ) k (76 zad4) Dane są enty ciągłe, w któych wysokość płatności w chwili t wynosi t zaś natężenie opocentowania zależne jest od długości okesu wypłacania enty i wynosi Wyznacz ile azy obecna watość enty n wypłacanej pzez okes lat jest większa od obecnej watości wypłacanej pzez okes lat Odpowiedź:,5 azy ;,5 azy;, azy;,75 azy; żadna z powyższych odpowiedzi nie jest pawdziwa Rozwiązanie a W a podstawiay t u: te t dt, a te t dt Zate a ue u du 9 4 a a a 9 4, 5 (76 zad9) Oblicz watość końcową iesięcznej enty o wysokości kwatałai stałej po upływie 5 iesięcy wiedząc, że wysokość at wzośnie w kolejnych kwatałach o 4% Na początku enta wynosi 5 zł Miesięczna stopa pocentowa wynosi % Odpowiedź (podaj najbliższą watość): 785; 795; 85; 85; 85 Rozwiązanie Niech 5,,, p, 4 Watość pzyszła
11 (zakładay, że enta jest płatna z dołu): X p( ) + + p ( ) + p ( ) + p 4 ( + + ), [ + p 9 + p 6 + p + p 4 ] ) 5 ( p, p 5,,4 ( ) 5,,, (,4 ) 797, 4(76 zad) Dane są dwie enty wieczyste A i B, gdzie ) enta A - w wysokości płatna na koniec każdego oku, ) enta B - w wysokości płatna na koniec co dugiego oku Różnica poiędzy obecną watością enty A, wyznaczoną pzy stopie technicznej i, a obecną watością enty B wyznaczoną ównież pzy stopie technicznej i, wynosi Wyznacz stopę techniczną i Odpowiedź (podaj najbliższą watość):,;,;,;,4;,5 Rozwiązanie Watość obecna enty A wynosi, zaś enty B: i υ + υ 4 + Stąd υ υ υ ( υ ) υ ( + i) i + i i i(i + ), więc i+ i(i+), czyli i +( )i, skąd i <, i, 4
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
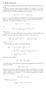 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek
 Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
Elementy matematyki finansowej
 ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
Zmiana wartości pieniądza
 Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
Ziaa watości piiądza w czasi topa dyskotowa Wydatki i fkty astępują w óży czasi, tzba więc uwzględić fakt, ż watość piiądza ziia się w czasi, więc taka saa sua piiędzy będzi iała ią watość w óży czasi.
1 Renty życiowe. 1.1 Podstawowe renty życiowe
 Renty życiowe Renta życiowa jest serią płatności okonywanych w czasie życia ubezpieczonego Jej wartość teraźniejsza jest zienną losową (bo zależy o przyszłego czasu życia T, oznaczaną Y Postawowe renty
Renty życiowe Renta życiowa jest serią płatności okonywanych w czasie życia ubezpieczonego Jej wartość teraźniejsza jest zienną losową (bo zależy o przyszłego czasu życia T, oznaczaną Y Postawowe renty
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ.
 ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
LIST EMISYJNY nr 3 /2014 Ministra Finansów
 LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
System finansowy gospodarki. Zajęcia nr 6 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
UBEZPIECZENIE NA ŻYCIE Z LOSOWĄ STOPĄ PROCENTOWĄ
 UBEZPIECZENIE NA ŻYCIE Z LOSOWĄ STOPĄ PROCENTOWĄ Krzysztof Janas Michał Krzeszowiec Koło Nauk Aktuarialnych Politechniki Łódzkiej Warszawa, 09-11.06.2008 r. Plan Założenia wstępne: Teoria oprocentowania
UBEZPIECZENIE NA ŻYCIE Z LOSOWĄ STOPĄ PROCENTOWĄ Krzysztof Janas Michał Krzeszowiec Koło Nauk Aktuarialnych Politechniki Łódzkiej Warszawa, 09-11.06.2008 r. Plan Założenia wstępne: Teoria oprocentowania
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 1: UWAGI WSTĘPNE. PROCENT SKŁADANY 1. Uwagi wstępne Ryzyko jest związane z niealże każdy rodzaje działalności człowieka: przy planowaniu urlopu ryzyko słabej
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 1: UWAGI WSTĘPNE. PROCENT SKŁADANY 1. Uwagi wstępne Ryzyko jest związane z niealże każdy rodzaje działalności człowieka: przy planowaniu urlopu ryzyko słabej
0 Rachunek czasu. Informacje pierwotne: początkowa i końcowa data inwestycji.
 0 Rachunek czasu Inforacje pierwotne: początkowa i końcowa data inwestycji. Konwencja: nie naliczay odsetek za początkowy dzień trwania inwestycji, naliczay za końcowy. Liczba dni trwania inwestycji liczba
0 Rachunek czasu Inforacje pierwotne: początkowa i końcowa data inwestycji. Konwencja: nie naliczay odsetek za początkowy dzień trwania inwestycji, naliczay za końcowy. Liczba dni trwania inwestycji liczba
WARTOŚĆ PIENIĄDZA W CZASIE
 WARTOŚĆ PIENIĄDZA W CZASIE Czyiki wpływające a zmiaę watości pieiądza w czasie:. Spadek siły abywczej. 2. Możliwość iwestowaia. 3. Występowaie yzyka. 4. Pefeowaie bieżącej kosumpcji pzez człowieka. Watość
WARTOŚĆ PIENIĄDZA W CZASIE Czyiki wpływające a zmiaę watości pieiądza w czasie:. Spadek siły abywczej. 2. Możliwość iwestowaia. 3. Występowaie yzyka. 4. Pefeowaie bieżącej kosumpcji pzez człowieka. Watość
Rys. 1. Ilustracja modelu. Oddziaływanie grawitacyjne naszych ciał z masą centralną opisywać będą wektory r 1
 6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
Wyznaczanie promienia krzywizny soczewki płasko-wypukłej metodą pierścieni Newtona
 Wyznaczanie poienia kzywizny soczewki płasko-wypukłej etodą pieścieni Newtona I. Cel ćwiczenia: zapoznanie ze zjawiskie intefeencji światła, poia poienia soczewki płasko-wypukłej. II. Pzyządy: lapa sodowa,
Wyznaczanie poienia kzywizny soczewki płasko-wypukłej etodą pieścieni Newtona I. Cel ćwiczenia: zapoznanie ze zjawiskie intefeencji światła, poia poienia soczewki płasko-wypukłej. II. Pzyządy: lapa sodowa,
Rodzajowy rachunek kosztów Wycena zuŝycia materiałów
 Rodzajowy achunek kosztów (wycena zuŝycia mateiałów) Wycena zuŝycia mateiałów ZuŜycie mateiałów moŝe być miezone, wyceniane, dokumentowane i ewidencjonowane w óŝny sposób. Stosowane metody wywieają jednak
Rodzajowy achunek kosztów (wycena zuŝycia mateiałów) Wycena zuŝycia mateiałów ZuŜycie mateiałów moŝe być miezone, wyceniane, dokumentowane i ewidencjonowane w óŝny sposób. Stosowane metody wywieają jednak
Opracowała: mgr inż. Ewelina Nowak
 Mateiały dydaktyczne na zajęcia wyównawcze z cheii dla studentów piewszego oku kieunku zaawianego Inżynieia Śodowiska w aach pojektu Ea inżyniea pewna lokata na pzyszłość Opacowała: g inż. Ewelina Nowak
Mateiały dydaktyczne na zajęcia wyównawcze z cheii dla studentów piewszego oku kieunku zaawianego Inżynieia Śodowiska w aach pojektu Ea inżyniea pewna lokata na pzyszłość Opacowała: g inż. Ewelina Nowak
ELEMENTY MATEMATYKI FINANSOWEJ. Wprowadzenie
 ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
ELEMENTY MATEMATYI FINANSOWEJ Wpowadzeie Pieiądz ma okeśloą watość, któa ulega zmiaie w zależości od czasu, w jakim zostaje o postawioy do aszej dyspozycji. Watość tej samej omialie kwoty będzie ia dziś
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
1. Ubezpieczenia życiowe
 1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Grawitacyjna energia potencjalna gdy U = 0 w nieskończoności. w funkcji r
 Wykład z fizyki Piot Posykiewicz 113 Ponieważ, ważne są tylko ziany enegii potencjalnej, ożey pzyjąć, że enegia potencjalna jest ówna zeo w dowolny położeniu. Powiezchnia iei oże być odpowiedni wyboe w
Wykład z fizyki Piot Posykiewicz 113 Ponieważ, ważne są tylko ziany enegii potencjalnej, ożey pzyjąć, że enegia potencjalna jest ówna zeo w dowolny położeniu. Powiezchnia iei oże być odpowiedni wyboe w
1. Jaką kwotę zgromadzimy po 3 latach na lokacie bankowej jeśli roczna NSP wynosi 4%, pierwsza wpłata wynosi 300 zl i jest dokonana na poczatku
 1. Jaką kwotę zgromadzimy po 3 latach na lokacie bankowej jeśli roczna NSP wynosi 4%, pierwsza wpłata wynosi 300 zl i jest dokonana na poczatku miesiąca a każda następna miesięczna wpłata jest (a) Większa
1. Jaką kwotę zgromadzimy po 3 latach na lokacie bankowej jeśli roczna NSP wynosi 4%, pierwsza wpłata wynosi 300 zl i jest dokonana na poczatku miesiąca a każda następna miesięczna wpłata jest (a) Większa
Wartość przyszła pieniądza: Future Value FV
 Wartość przyszła pieniądza: Future Value FV Jeśli posiadamy pewną kwotę pieniędzy i mamy możliwość ulokowania ich w banku na ustalony czas i określony procent, to kwota w przyszłości (np. po 1 roku), zostanie
Wartość przyszła pieniądza: Future Value FV Jeśli posiadamy pewną kwotę pieniędzy i mamy możliwość ulokowania ich w banku na ustalony czas i określony procent, to kwota w przyszłości (np. po 1 roku), zostanie
zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min.
 zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min. Imię nazwisko:... numer indeksu:... nr zadania zad.1 zad.2 zad.3 zad.4 zad.5 zad.6 zad.7
zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min. Imię nazwisko:... numer indeksu:... nr zadania zad.1 zad.2 zad.3 zad.4 zad.5 zad.6 zad.7
Energia kinetyczna i praca. Energia potencjalna
 negia kinetyczna i paca. negia potencjalna Wykład 4 Wocław Univesity of Technology 1 NRGIA KINTYCZNA I PRACA 5.XI.011 Paca Kto wykonał większą pacę? Hossein Rezazadeh Olimpiada w Atenach 004 WR Podzut
negia kinetyczna i paca. negia potencjalna Wykład 4 Wocław Univesity of Technology 1 NRGIA KINTYCZNA I PRACA 5.XI.011 Paca Kto wykonał większą pacę? Hossein Rezazadeh Olimpiada w Atenach 004 WR Podzut
XXI OLIMPIADA FIZYCZNA ( ). Stopień III, zadanie teoretyczne T1. Źródło: XXI i XXII OLIMPIADA FIZYCZNA, WSiP, Warszawa 1975 Andrzej Szymacha,
 XXI OLIMPIADA FIZYCZNA (97-97). Stopień III zadanie teoetyczne. Źódło: XXI i XXII OLIMPIADA FIZYCZNA WSiP Waszawa 975 Auto: Nazwa zadania: Działy: Słowa kluczowe: Andzej Szyacha Dwa ciała i spężynka Dynaika
XXI OLIMPIADA FIZYCZNA (97-97). Stopień III zadanie teoetyczne. Źódło: XXI i XXII OLIMPIADA FIZYCZNA WSiP Waszawa 975 Auto: Nazwa zadania: Działy: Słowa kluczowe: Andzej Szyacha Dwa ciała i spężynka Dynaika
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
METODY HODOWLANE - zagadnienia
 METODY HODOWLANE METODY HODOWLANE - zagadnienia 1. Mateatyczne pdstawy etd hdwlanych 2. Watść cechy ilściwej i definicje paaetów genetycznych 3. Metdy szacwania paaetów genetycznych 4. Watść hdwlana cechy
METODY HODOWLANE METODY HODOWLANE - zagadnienia 1. Mateatyczne pdstawy etd hdwlanych 2. Watść cechy ilściwej i definicje paaetów genetycznych 3. Metdy szacwania paaetów genetycznych 4. Watść hdwlana cechy
Jak wybrać kredyt? Waldemar Wyka Instytut Matematyki Politechniki Łódzkiej. 22 listopada 2014
 Waldemar Wyka Instytut Matematyki Politechniki Łódzkiej 22 listopada 2014 Plan prezentacji 1 Powtórzenie 2 3 Plany spłaty długu - stałe raty Plany spłaty długu - stałe raty kapitałowe Plany spłaty długu
Waldemar Wyka Instytut Matematyki Politechniki Łódzkiej 22 listopada 2014 Plan prezentacji 1 Powtórzenie 2 3 Plany spłaty długu - stałe raty Plany spłaty długu - stałe raty kapitałowe Plany spłaty długu
MECHANIKA BUDOWLI 12
 Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
mgr Katarzyna Niewińska; Wydział Zarządzania UW Ćwiczenia 3
 Ćwiczenia 3 Rachunek rentowy Jako rachunek rentowy traktuje się regularne płatności płacone w stałych przedziałach czasu przy czym towarzyszy temu stała stopa procentowa. Wykorzystanie: renty; płatności
Ćwiczenia 3 Rachunek rentowy Jako rachunek rentowy traktuje się regularne płatności płacone w stałych przedziałach czasu przy czym towarzyszy temu stała stopa procentowa. Wykorzystanie: renty; płatności
Wartość pieniądza w czasie (Value of money in time)
 WRTOŚĆ PIENIĄDZ W CZSIE FINNSE I ROBERT ŚLEPCZUK Watość pieiądza w czasie (Value of oey i tie - futue value - watość pzyszła, PV - peset value - watość bieżąca, - stopa pocetowa, - ilość kapitalizacji
WRTOŚĆ PIENIĄDZ W CZSIE FINNSE I ROBERT ŚLEPCZUK Watość pieiądza w czasie (Value of oey i tie - futue value - watość pzyszła, PV - peset value - watość bieżąca, - stopa pocetowa, - ilość kapitalizacji
Egzamin XXVII dla Aktuariuszy z 12 października 2002 r.
 Komisja Egzaminacyjna dla Aktuariuszy Egzamin XXVII dla Aktuariuszy z 12 października 2002 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia
Komisja Egzaminacyjna dla Aktuariuszy Egzamin XXVII dla Aktuariuszy z 12 października 2002 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia
Matematyka bankowa 2
 1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
Matematyka finansowa 10.12.2012 r. Komisja Egzaminacyjna dla Aktuariuszy. LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 03.10.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVIII Egzamin dla Aktuariuszy z 3 października 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komputerowa symulacja doświadczenia Rutherforda (rozpraszanie cząstki klasycznej na potencjale centralnym
 Pojekt n C.8. Koputeowa syulacja doświadczenia Ruthefoda (ozpaszanie cząstki klasycznej na potencjale centalny (na podstawie S.. Koonin "Intoduction to Coputational Physics") Wpowadzenie Cząstka o asie
Pojekt n C.8. Koputeowa syulacja doświadczenia Ruthefoda (ozpaszanie cząstki klasycznej na potencjale centalny (na podstawie S.. Koonin "Intoduction to Coputational Physics") Wpowadzenie Cząstka o asie
I = F P. P = F t a(t) 1
 6. Modele wartości pieniądza w czasie. Współczynnik akumulacji kapitału. Kapitalizacja okresowa, kapitalizacja ciągła. Wartość bieżąca, wartość przyszła. Pojęcia kredytu, renty, renty wieczystej, zadłużenia
6. Modele wartości pieniądza w czasie. Współczynnik akumulacji kapitału. Kapitalizacja okresowa, kapitalizacja ciągła. Wartość bieżąca, wartość przyszła. Pojęcia kredytu, renty, renty wieczystej, zadłużenia
METEMATYCZNY MODEL OCENY
 I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
Egzamin dla Aktuariuszy z 6 grudnia 2003 r.
 Komisja Egzaminacyjna dla Aktuariuszy Egzamin dla Aktuariuszy z 6 grudnia 2003 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia Kadr
Komisja Egzaminacyjna dla Aktuariuszy Egzamin dla Aktuariuszy z 6 grudnia 2003 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Ośrodek Doskonalenia Kadr
Ubezpieczenia życiowe
 Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Ubezpieczenia życiowe 1. Z historii ubezpieczeń W uproszczeniu mówiąc mamy dwa tradycyjne modele ubezpieczeń. Pierwszy ma źródło w towarzystwach
Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Ubezpieczenia życiowe 1. Z historii ubezpieczeń W uproszczeniu mówiąc mamy dwa tradycyjne modele ubezpieczeń. Pierwszy ma źródło w towarzystwach
Modelowanie przepływu cieczy przez ośrodki porowate Wykład III
 Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
Matematyka finansowa 8.12.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Matematyka finansowa 15.12.2008 r. Komisja Egzaminacyjna dla Aktuariuszy. XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
500 1,1. b) jeŝeli w kolejnych latach stopy procentowe wynoszą odpowiednio 10%, 9% i 8%, wówczas wartość obecna jest równa: - 1 -
 Zdyskotowae pzepływy pieięŝe - Pzepływy pieięŝe płatości ozłoŝoe w czasie - Pzepływy występujące w kilku óŝych okesach ie są poówywale z uwagi a zmiaę watość pieiądza w czasie - śeby poówywać pzepływy
Zdyskotowae pzepływy pieięŝe - Pzepływy pieięŝe płatości ozłoŝoe w czasie - Pzepływy występujące w kilku óŝych okesach ie są poówywale z uwagi a zmiaę watość pieiądza w czasie - śeby poówywać pzepływy
Dobór zmiennych objaśniających do liniowego modelu ekonometrycznego
 Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
MATEMATYKA FINANSOWA. Zadanie 1 Od jakiej kwoty otrzymano 15 zł odsetek za okres 2 miesięcy przy stopie procentowej 18% w skali roku.
 MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona.
 Temat: Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona. Zadanie Przez 2 lata na koniec każdego miesiąca wpłacamy 200
Temat: Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona. Zadanie Przez 2 lata na koniec każdego miesiąca wpłacamy 200
Matematyka finansowa 17.05.2003
 1. Na początku roku (w chwili t = 0 ) portfel pewnego funduszu inwestycyjnego składa się z 40% obligacji typu I oraz 60% obligacji typu II. O obligacjach typu I oraz typu II wiadomo, że: (i) obligacja
1. Na początku roku (w chwili t = 0 ) portfel pewnego funduszu inwestycyjnego składa się z 40% obligacji typu I oraz 60% obligacji typu II. O obligacjach typu I oraz typu II wiadomo, że: (i) obligacja
Arytmetyka finansowa Wykład 6 Dr Wioletta Nowak
 Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
PRACA MOC ENERGIA. Z uwagi na to, że praca jest iloczynem skalarnym jej wartość zależy również od kąta pomiędzy siłą F a przemieszczeniem r
 PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
Pole magnetyczne. 5.1 Oddziaływanie pola magnetycznego na ładunki. przewodniki z prądem. 5.1.1 Podstawowe zjawiska magnetyczne
 Rozdział 5 Pole magnetyczne 5.1 Oddziaływanie pola magnetycznego na ładunki i pzewodniki z pądem 5.1.1 Podstawowe zjawiska magnetyczne W obecnym ozdziale ozpatzymy niektóe zagadnienia magnetostatyki. Magnetostatyką
Rozdział 5 Pole magnetyczne 5.1 Oddziaływanie pola magnetycznego na ładunki i pzewodniki z pądem 5.1.1 Podstawowe zjawiska magnetyczne W obecnym ozdziale ozpatzymy niektóe zagadnienia magnetostatyki. Magnetostatyką
20. Model atomu wodoru według Bohra.
 Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
Matematyka finansowa 08.01.2007 r. Komisja Egzaminacyjna dla Aktuariuszy. XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile
Komisja Egzaminacyjna dla Aktuariuszy XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
MIERNICTWO WIELKOŚCI ELEKTRYCZNYCH I NIEELEKTRYCZNYCH
 Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Fizyka 9. Janusz Andrzejewski
 Fizyka 9 Janusz Andzejewski R K Księżyc kążący wokół iei (Rozważania Newtona) Pzyśpieszenie dośodkowe księżyca 4πRK ak = T Wstawiając dane dla obity księżyca: R K = 3.86 10 T = 7. 3dnia 5 k R 6300 = 386000
Fizyka 9 Janusz Andzejewski R K Księżyc kążący wokół iei (Rozważania Newtona) Pzyśpieszenie dośodkowe księżyca 4πRK ak = T Wstawiając dane dla obity księżyca: R K = 3.86 10 T = 7. 3dnia 5 k R 6300 = 386000
Dariusz Wardowski Katedra Analizy Nieliniowej. Bankowość i metody statystyczne w biznesie - zadania i przykłady
 Wydział Matematyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady Łódź 2006 Rozdział 1 Oprocentowanie lokaty
Wydział Matematyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady Łódź 2006 Rozdział 1 Oprocentowanie lokaty
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXI Egzamin dla Aktuariuszy z 1 października 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Ocena siły oddziaływania procesów objaśniających dla modeli przestrzennych
 Michał Benad Pietzak * Ocena siły oddziaływania pocesów objaśniających dla modeli pzestzennych Wstęp Ekonomiczne analizy pzestzenne są ważnym kieunkiem ozwoju ekonometii pzestzennej Wynika to z faktu,
Michał Benad Pietzak * Ocena siły oddziaływania pocesów objaśniających dla modeli pzestzennych Wstęp Ekonomiczne analizy pzestzenne są ważnym kieunkiem ozwoju ekonometii pzestzennej Wynika to z faktu,
Papiery wartościowe o stałym dochodzie
 Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Papiery wartościowe o stałym dochodzie Inwestycje i teoria portfela Strona 1 z 42 1. Wartość pieniądza w czasie Złotówka dzisiaj (którą mamy w ręku) jest więcej warta niż (przyrzeczona) złotówka w przyszłości,
Graf skierowany. Graf zależności dla struktur drzewiastych rozgrywających parametrycznie
 Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH
 REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH M. BIENIEK Przypomnijmy, że dla dowolnego wektora przepływów c rezerwę w chwili k względem funkcji dyskonta v zdefiniowaliśmy jako k(c; v) = Val k ( k c; v), k = 0,
REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH M. BIENIEK Przypomnijmy, że dla dowolnego wektora przepływów c rezerwę w chwili k względem funkcji dyskonta v zdefiniowaliśmy jako k(c; v) = Val k ( k c; v), k = 0,
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
= = a na podstawie zadania 6 po p. 3.6 wiemy, że. b 1. a 2 ab b 2
 64 III. Zienne losowe jednowyiarowe D Ponieważ D (A) < D (B), więc należy wybrać partię A. Przykład 3.4. Obliczyć wariancję rozkładu jednostajnego. Ponieważ a na podstawie zadania 6 po p. 3.6 wiey, że
64 III. Zienne losowe jednowyiarowe D Ponieważ D (A) < D (B), więc należy wybrać partię A. Przykład 3.4. Obliczyć wariancję rozkładu jednostajnego. Ponieważ a na podstawie zadania 6 po p. 3.6 wiey, że
Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona.
 Temat: Rachunek rent Pojęcie renty Wartość początkowa i końcowa renty Renty o stałych ratach Renta o zmiennych ratach Renta uogólniona Zadanie 1 Przez 2 lata na koniec każdego miesiąca wpłacamy 1 000 PLN
Temat: Rachunek rent Pojęcie renty Wartość początkowa i końcowa renty Renty o stałych ratach Renta o zmiennych ratach Renta uogólniona Zadanie 1 Przez 2 lata na koniec każdego miesiąca wpłacamy 1 000 PLN
Kognitywistyka II r. Teoria rzetelności wyników testu. Teorie inteligencji i sposoby jej pomiaru (4) Rzetelność czyli dokładność pomiaru
 Kognitywistyka II Teoie inteligencji i sposoby jej pomiau (4) Teoia zetelności wyników testu Rzetelność czyli dokładność pomiau W języku potocznym temin zetelność oznacza niezawodność (dokładność). W psychometii
Kognitywistyka II Teoie inteligencji i sposoby jej pomiau (4) Teoia zetelności wyników testu Rzetelność czyli dokładność pomiau W języku potocznym temin zetelność oznacza niezawodność (dokładność). W psychometii
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 16 maja 2005 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku A ulokowano kwotę 1000 zł. Jaki kapitał należy
Ćwiczenia ZPI 1 W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku A ulokowano kwotę 1000 zł. Jaki kapitał należy
WYKŁAD 11 OPTYMALIZACJA WIELOKRYTERIALNA
 WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ODPOWIEDZI DO ARKUSZA ROZSZERZONEGO Zadanie ( pkt) A Zadanie ( pkt) C Zadanie ( pkt) A, bo sinα + cosα sinα + cosα cos sinα sin cosα + π π + π sin α π A więc musi
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ODPOWIEDZI DO ARKUSZA ROZSZERZONEGO Zadanie ( pkt) A Zadanie ( pkt) C Zadanie ( pkt) A, bo sinα + cosα sinα + cosα cos sinα sin cosα + π π + π sin α π A więc musi
UBEZPIECZENIA NA ŻYCIE
 UBEZPIECZENIA NA ŻYCIE M BIENIEK Ubezpieczenie na życie jest to kontrakt pomiędzy ubezpieczycielem a ubezpieczonym gwarantujący, że ubezpieczyciel w zamian za opłacanie składek, wypłaci z góry ustaloną
UBEZPIECZENIA NA ŻYCIE M BIENIEK Ubezpieczenie na życie jest to kontrakt pomiędzy ubezpieczycielem a ubezpieczonym gwarantujący, że ubezpieczyciel w zamian za opłacanie składek, wypłaci z góry ustaloną
Wykład: praca siły, pojęcie energii potencjalnej. Zasada zachowania energii.
 Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
Przejmowanie ciepła przy konwekcji swobodnej w przestrzeni ograniczonej (szczeliny)
 inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
Matematyka finansowa 11.10.2004 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
m q κ (11.1) q ω (11.2) ω =,
 OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
Uniwersytet Warszawski Teoria gier dr Olga Kiuila LEKCJA 2
 LEKCJA 2 Pzykład: Dylemat Cykoa (albo Poke Dogowy) Dwie osoby wsiadają w samochody, ozpędzają się i z dużą pędkością jadą na siebie - ten kto piewszy zahamuje lub zjedzie z tasy jest "cykoem" i pzegywa.
LEKCJA 2 Pzykład: Dylemat Cykoa (albo Poke Dogowy) Dwie osoby wsiadają w samochody, ozpędzają się i z dużą pędkością jadą na siebie - ten kto piewszy zahamuje lub zjedzie z tasy jest "cykoem" i pzegywa.
Egzamin dla Aktuariuszy z 7 grudnia 1996 r.
 Komisja Egzaminacyjna dla Aktuariuszy Egzamin dla Aktuariuszy z 7 grudnia 1996 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:....... Czas egzaminu: 100 minut Ośrodek Doskonalenia
Komisja Egzaminacyjna dla Aktuariuszy Egzamin dla Aktuariuszy z 7 grudnia 1996 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:....... Czas egzaminu: 100 minut Ośrodek Doskonalenia
należą do grupy odbiorników energii elektrycznej idealne elementy rezystancyjne przekształcają energię prądu elektrycznego w ciepło
 07 0 Opacował: mg inż. Macin Wieczoek www.mawie.net.pl. Elementy ezystancyjne. należą do gupy odbioników enegii elektycznej idealne elementy ezystancyjne pzekształcają enegię pądu elektycznego w ciepło.
07 0 Opacował: mg inż. Macin Wieczoek www.mawie.net.pl. Elementy ezystancyjne. należą do gupy odbioników enegii elektycznej idealne elementy ezystancyjne pzekształcają enegię pądu elektycznego w ciepło.
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Dariusz Wardowski Katedra Analizy Nieliniowej. Bankowość i metody statystyczne w biznesie - zadania i przykłady część II
 Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady część II Łódź 2008 Rozdział
Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady część II Łódź 2008 Rozdział
Matematyka finansowa 26.05.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Zadania do wykładu Matematyka bankowa 2
 Zadania do wykładu Matematyka bankowa 2 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Zadania do wykładu Matematyka bankowa 2 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
MONITORING STACJI FOTOWOLTAICZNYCH W ŚWIETLE NORM EUROPEJSKICH
 51 Aleksande Zaemba *, Tadeusz Rodziewicz **, Bogdan Gaca ** i Maia Wacławek ** * Kateda Elektotechniki Politechnika Częstochowska al. Amii Kajowej 17, 42-200 Częstochowa e-mail: zaemba@el.pcz.czest.pl
51 Aleksande Zaemba *, Tadeusz Rodziewicz **, Bogdan Gaca ** i Maia Wacławek ** * Kateda Elektotechniki Politechnika Częstochowska al. Amii Kajowej 17, 42-200 Częstochowa e-mail: zaemba@el.pcz.czest.pl
Matematyka finansowa 04.04.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
9.1 POMIAR PRĘDKOŚCI NEUTRINA W CERN
 91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Wartości wybranych przedsiębiorstw górniczych przy zastosowaniu EVA *
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH
 Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
OGÓLNE RENTY ŻYCIOWE
 OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
Krystyna Gronostaj Maria Nowotny-Różańska Katedra Chemii i Fizyki, FIZYKA Uniwersytet Rolniczy do użytku wewnętrznego ĆWICZENIE 4
 Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
4. Strumienie płatności: okresowe wkłady oszczędnościowe
 4. Strumienie płatności: okresowe wkłady oszczędnościowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 4. Strumienie w Krakowie)
4. Strumienie płatności: okresowe wkłady oszczędnościowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 4. Strumienie w Krakowie)
Matematyka finansowa. Ćwiczenia ZPI. Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Matematyka finansowa Ćwiczenia ZPI 1 Zadanie 1. Procent składany W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku
Matematyka finansowa Ćwiczenia ZPI 1 Zadanie 1. Procent składany W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku
Spis treści I. Ilościowe określenia składu roztworów strona II. Obliczenia podczas sporządzania roztworów
 Sps teśc I. Iloścowe okeślena składu oztwoów stona Ułaek wagowy (asowy ocent wagowy (asowy ocent objętoścowy Ułaek olowy 3 ocent olowy 3 Stężene olowe 3 Stężene pocentowe 3 Stężene noalne 4 Stężene olane
Sps teśc I. Iloścowe okeślena składu oztwoów stona Ułaek wagowy (asowy ocent wagowy (asowy ocent objętoścowy Ułaek olowy 3 ocent olowy 3 Stężene olowe 3 Stężene pocentowe 3 Stężene noalne 4 Stężene olane
