Metoda odbić zwierciadlanych
|
|
|
- Marek Marczak
- 8 lat temu
- Przeglądów:
Transkrypt
1 Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa jest następujące: Jaki jest potencjał V oaz natężenie E w obszaze na płaszczyzną? Nie mogą one pochozić tylko o łaunku, ponieważ wyinukuje na powiezchni pzewonika pewien łaunek o znaku pzeciwnym W związku z tym całkowity potencjał oaz natężenie bęą sumą potencjałów i natężeń pochozących bezpośenio o i o łaunku inukowanego Ale jak można obliczyć te wielkości, skoo nie wiaomo jak uży jest wyinukowany łaunek i jaki jest jego ozkła? Z X Rys Łaunek w oległości na powiezchnią pzewozącą Y Z pomocą pzychozi nam metoa obić zwiecialanych Metoa ta polega na zastąpieniu powiezchni pzewozącej ównoważnymi jej łaunkami pozonymi (tzw uojonymi lub zwiecialanymi) Muszą one wytwozyć takie samo pole jak to, któe zostało wytwozone pzez łaunki zeczywiste, wyinukowane na powiezchni pzewozącej Po wyznaczeniu ozkłau łaunków zwiecialanych zaganienie ozwiązujemy alej tak, jakby w ukłazie nie występowała powiezchnia pzewoząca, a pole było wytwazane pzez łaunki piewotne i zwiecialane Klasyczna poceua znajowania ozkłau pola w takim ukłazie polegałaby na napisaniu opowienich ównań Maxwella i ozwiązaniu ich pzy uwzglęnieniu waunków bzegowych zaganienia Jest to bazo tune, ponieważ nieznany jest ozkła łaunków na powiezchni pzewozącej Funkcję opisującą ozkła pola i spełniającą ównania Maxwella oaz waunki bzegowe, spóbujemy znaleźć kozystając z twiezenia o jenoznaczności Twiezenie to mówi, że jeżeli znajziemy jakąkolwiek funkcję spełniającą ównania Maxwella oaz waunki bzegowe postawione w zaaniu to funkcja ta jest jeynym słusznym ozwiązaniem Tutaj waunkiem bzegowym jest zeowanie się skłaowej stycznej E na powiezchni pzewozącej Fakt zeowania się skłaowej stycznej wektoa natężenia pola elektycznego wynika z tego, iż w zaganieniach elektostatyki, na powiezchni pzewozącej istnieje potencjał o stałej watości powiezchnia pzewonika jest powiezchnią ekwipotencjalną Występuje tylko skłaowa nomalna wektoa natężenia pola elektycznego Waunek zeowania się skłaowej stycznej wektoa E na płaszczyźnie X0Y bęzie spełniony także wtey, gy ziałanie pzewozącej powiezchni zastąpimy fikcyjnym łaunkiem = umieszczonym w oległości po płaszczyzną X0Y, pzy założeniu że pzenikalność elektyczna całej pzestzeni jest ówna ε (zob Rys 2 na następnej stonie) W takim pzypaku, na płaszczyźnie X0Y natężenie pola elektycznego o wóch łaunków punktowych jest supepozycją natężeń pól o każego łaunku i wynosi: () E = E + E = + g 2 2 Skłaowa styczna wektoa E g o płaszczyzny X0Y ówna się: (2) Egstycz = Estycz + Estycz = E cosα + E cosα
2 Z ε I p p P II 0 α α E E g E Y X Rys 2 Łaunek zeczywisty oaz łaunek uojony obity wzglęem powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Obywie skłaowe twozą z płaszczyzną X0Y taki sam kąt α ( =, bo łaunek jest tak samo oalony o płaszczyzny jak łaunek ) Z poobieństwa tójkątów możemy napisać: () 2 2 x + y cosα = Bioąc powyższe zależności oaz uwzglęniając, że skłaowa styczna wektoa E g = 0 otzymamy: (4) a stą: x + y x + y + = 0, (5) = Wykazaliśmy więc spełnienie waunków zaania Zastąpienie pzewozącej płaszczyzny łaunkiem nie zmienia postawionych waunków bzegowych, a tym samym nie zmienia ozkłau pola na tą płaszczyzną W owolnym punkcie pzestzeni na płaszczyzną X0Y, tj w obszaze, w któym umieszczony jest łaunek natężenie pola elektostatycznego można opisać: (6) E = 4 2 p 2 p πε p p Potencjał opisany jest: (7) V = p p Watość potencjału w punkcie P(x, y, z) wynosi: (8) V ( x, y, z) = 4 πε x + y + ( z ) x + y + ( z + )
3 Kozystając z () wyznaczymy watość skłaowej nomalnej na powiezchni X0Y: (9) E = E + E = E sinα + E sinα gnom nom nom Analogicznie jak la skłaowej stycznej można napisać: (0) sinα = Uwzglęniając, że 2 = x 2 + y oaz =, otzymamy: () Egnom = = πε x + y + 2 Wyznaczone powyżej zależności wykozystamy o obliczeń w pogamie MATLAB W tym celu napiszemy funkcję, któa umożliwi nam obliczenie potencjału z ównania (8): function V = metoa_obic(,,epsilon,x,y,z) V = /(4*pi*epsilon)* (/sqt(x^2+y^2+(z-)^2) -(/sqt(x^2+y^2+(z+)^2))); Do obliczenia natężenia pola elektycznego bęziemy wykozystywać ównież popzenio zapisane funkcje: pochona2 oaz natezeniepola Jeśli nie ma ich na ysku twaym komputea, to należy je ponownie zapisać (skompilowane pliki są na stonie: kszuteupl/mmwe/nazwafunkcjip) function = pochona2(x,y) Lx = length(x); x = x(:lx)-x(:lx-2); y = y(:lx)-y(:lx-2); = [NaN y/x NaN]; function [Ex,Ey] = natezeniepola(x,y,v) fo k=:length(y) Ex(k,:) = -pochona2(x,v(k,:)); en fo k=:length(x) Ey(:,k) = -pochona2(y,v(:,k)'); en ZADANIE Łaunek = 6 C znajuje się w ielektyku o pzenikalności elektycznej ε = ε 0 w oległości o płaszczyzny pzewozącej (Rys 2) Wyznacz pole w ielektyku Pzestaw potencjał V i natężenie pola E na ysunku, na płaszczyźnie X0Z (la y = 0) Wyznacz gęstość powiezchniową łaunków, któe powstaną na powiezchni ozielającej wa śoowiska i siłę ziałającą na łaunek
4 ROZWIĄZANIE W oknie Comman Winow wpowazamy ane o zaania oaz efiniujemy obsza obliczeń: clea, % usuwa wszystkie zapamiętane zmienne close all % zamyka wszystkie ysunki x =-9:02:2; % watości x obszau obliczeń [mm] y = 0; % watość y obszau obliczeń [mm] z = 0:02:7; % watości z obszau obliczeń [mm] [X,Z]= meshgi(x,z); % twozy obsza obliczeń płaszczyzna XZ =6; % watość łaunku =5; % oległość w osi Z epsilon = 8854e-2; % pzenikalność elektyczna la powietza a następnie obliczamy watości potencjału la każej watości x i z: fow = :length(z), % pętla po w: la każego z fo k= :length(x), % pętla po k: la każego x V(w,k) = metoa_obic(,,epsilon,x(k),y,z(w)); % obliczenia en % koniec pętli po k en % koniec pętli po w i ysujemy wykes potencjału za pomocą funkcji pcolo: pcolo(x,z,v) % ysuje watości V na płaszczyźnie X0Z axisequal % ustawia ówne skale na osiach axistight % opasowuje ozmia ukłau współzęnych shaingflat % cieniowanie wykesu bez intepolacji Na ysunku wizimy ozkła potencjału wokół łaunku Pzyjmijmy teaz, że łaunek jest umieszczony nieco alej o płaszczyzny X0Y (w oległości = 2) i la takiej sytuacji ozwiążemy zaanie o końca: =2; fow =:length(z), % pętla po w: la każego z fo k = :length(x), % pętla po k: la każego x V(w,k)= metoa_obic(,,epsilon,x(k),y,z(w)); en % koniec pętli po k en % koniec pętli po w pcolo(x,z,v) % ysuje watości V na płaszczyźnie X0Z axisequal % ustawia ówne skale na osiach X i Z axistight % opasowuje ozmia ukłau współzęnych shaingflat % ustawia koloowanie wykesu bez intepolacji holon % potzymuje bieżący wykes [Ex,Ey] = natezeniepola(x,z,v); h =quive(x,z,ex,ey); set(h,'autoscalefacto',5,'colo',[ ]); Znając ozkła E i V można wyznaczyć gęstość powiezchniową łaunków, któe powstaną na powiezchni ozielającej wa śoowiska Z waunków ciągłości wektoa E pzy pzejściu pzez płat łaunku powiezchniowego z obszau I o II wynika, że gęstość łaunku powiezchniowego jest popocjonalna o nieciągłości skłaowej nomalnej E: (2) ε(e IIn E In ) = σ 4
5 Ponieważ w obszaze II pole nie istnieje (E IIn = 0), to powiezchniowa gęstość łaunku wyaża się następująco: () σ = εeng = = 2π π x + y + 2 Łaunek pzyciągany jest pzez płaszczyznę, ponieważ znajuje się na niej inukowany łaunek o znaku pzeciwnym Siłę tego pzyciągania można obliczyć: (4) F = 2 z 4 πε (2 ) Ponieważ wekto siły jest skieowany ównolegle o osi Z ze zwotem pzeciwnym, to jej watość: (5) F 2 = = 4 πε(2 ) 6πε 2 2 Napisz funkcje: launek oaz sila, któe bęą obliczać wielkości wyażone wzoami () oaz (5) Pamiętaj o zaeklaowaniu w nawiasie agumentów funkcji, występujących we wzoach function sigma = launek( ) function F = sila( ) Wykonaj obliczenia za pomocą tych funkcji Pzestaw wyniki obliczania gęstości powiezchniowej łaunku na ysunku, na płaszczyźnie X0Y (la z = 0) ZADANIE 2 Zmoyfikuj wzó (8) oaz zapisane o obliczeń funkcje tak, aby ziałały popawnie la sytuacji, gy pojeynczy łaunek umieszczony jest na płaszczyzną pzewozącą w owolnym punkcie, o współzęnych (x 0, y 0, z 0 ) Wykonaj obliczenia za pomocą zmienionych funkcji la położenia łaunku w punkcie (-,, 2) Pzestaw wyniki obliczania potencjału na płaszczyznach pzecinających osie ukłau współzęnych w óżnych punktach (la wybanej osi ustalamy punkt pzecięcia np y = 0 jak w zaaniu, i wykonujemy obliczenia la wybanego zakesu pozostałych zmiennych) ZADANIE Zapisz ównanie la potencjału w sytuacji, gy łaunek znajuje się w pobliżu wóch pzewozących płaszczyzn, stykających się po kątem postym Napisz funkcję obliczającą potencjał w takim ukłazie i wykonaj obliczenia oaz pzestaw je na wykesie 5
6 PYTANIA SPRAWDZAJĄCE DO TEGO ĆWICZENIA Poaj wzó na potencjał pola elektycznego V w oległości o łaunku elektycznego q 2 Zastosuj poany w zaaniu wzó la kilku pzykłaowych watości oaz q Oblicz potencjał pola elektycznego V pochozący o kilku łaunków 4 Poaj wzó na natężenie pola elektycznego E w oległości o łaunku elektycznego q 5 Poaj wzó na skłaowe E x i E y wektoa E leżącego na płaszczyźnie xy, jeśli znana jest ługość tego wektoa i kąt α jaki twozy on z osią x 6 Zastosuj poane w zaaniach 4 i 5 wzoy la kilku pzykłaowych watości oaz q 7 Oblicz natężenie pola elektycznego E pochozące o kilku łaunków (jak oaje się wektoy?) 8 Opisz (kótko, jenym zaniem) na czym polega metoa obić zwiecialanych PYTANIA NA NASTĘPNĄ WEJŚCIÓWKĘ: METODA RÓŻNIC SKOŃCZONYCH Poszukujemy ozkłau skalanego potencjału elektycznego V(x,y) w pewnym obszaze Ω oganiczonym bzegiem Γ Znamy zależności mięzy natężeniem pola elektycznego E a potencjałem elektycznym V i łaunkiem (lub gęstością łaunku ρ) Co jest potzebne o ozwiązania zaania metoą óżnic skończonych? 2 Na czym polega ozwiązanie zaania metoą óżnic skończonych? Co jest wynikiem obliczeń tą metoą (funkcja, watość, ównanie)? Omów waunki bzegowe Diichleta 4 Omów waunki bzegowe Neumanna 5 Czym óżnią się waunki bzegowe Diichleta o waunków Neumanna? 6 Poaj wzó na potencjał w owolnym węźle, na postawie potencjałów w węzłach sąsienich 7 Czym są siatka i węzeł w tej metozie? 6
Metoda odbić zwierciadlanych
 Metoa obić zwiecialanych Pzyuśćmy, że łaunek unktowy (Rys ) umieszczony jest w oległości o nieskończonej owiezchni zewozącej, umiejscowionej na łaszczyźnie X0Y Piewsze ytanie, jakie o azu się nasuwa jest
Metoa obić zwiecialanych Pzyuśćmy, że łaunek unktowy (Rys ) umieszczony jest w oległości o nieskończonej owiezchni zewozącej, umiejscowionej na łaszczyźnie X0Y Piewsze ytanie, jakie o azu się nasuwa jest
3b. ELEKTROSTATYKA. r r. 4πε. 3.4 Podstawowe pojęcia. kqq0 E =
 3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
1. SZCZEGÓLNE PRZYPADKI ŁUKÓW.
 Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
- substancje zawierające swobodne nośniki ładunku elektrycznego:
 Pzewodniki - substancje zawieające swobodne nośniki ładunku elektycznego: elektony metale, jony wodne oztwoy elektolitów, elektony jony zjonizowany gaz (plazma) pzewodnictwo elektyczne metali pzewodnictwo
Pzewodniki - substancje zawieające swobodne nośniki ładunku elektycznego: elektony metale, jony wodne oztwoy elektolitów, elektony jony zjonizowany gaz (plazma) pzewodnictwo elektyczne metali pzewodnictwo
Arkusze maturalne poziom podstawowy
 Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Przejmowanie ciepła przy konwekcji swobodnej w przestrzeni ograniczonej (szczeliny)
 inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
Modelowanie przepływu cieczy przez ośrodki porowate Wykład III
 Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
Fizyka 2. Janusz Andrzejewski
 Fizyka 2 wykład 2 Pawo Coulomba Jeżeli dwie naładowane cząstki o ładunkach q1 i q2 znajdują się w odległości, to siła elektostatyczna pzyciągania między nimi ma watość: F k k stała elektostatyczna k 1
Fizyka 2 wykład 2 Pawo Coulomba Jeżeli dwie naładowane cząstki o ładunkach q1 i q2 znajdują się w odległości, to siła elektostatyczna pzyciągania między nimi ma watość: F k k stała elektostatyczna k 1
Elektrodynamika. Część 2. Specjalne metody elektrostatyki. Ryszard Tanaś. Zakład Optyki Nieliniowej, UAM
 Elektroynamika Część 2 Specjalne metoy elektrostatyki Ryszar Tanaś Zakła Optyki Nieliniowej, UAM http://zon8.phys.amu.eu.pl/\~tanas Spis treści 3 Specjalne metoy elektrostatyki 3 3. Równanie Laplace a....................
Elektroynamika Część 2 Specjalne metoy elektrostatyki Ryszar Tanaś Zakła Optyki Nieliniowej, UAM http://zon8.phys.amu.eu.pl/\~tanas Spis treści 3 Specjalne metoy elektrostatyki 3 3. Równanie Laplace a....................
Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony
 Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
Prawo Gaussa. Potencjał elektryczny.
 Pawo Gaussa. Potencjał elektyczny. Wykład 3 Wocław Univesity of Technology 7-3- Inne spojzenie na pawo Coulomba Pawo Gaussa, moŝna uŝyć do uwzględnienia szczególnej symetii w ozwaŝanym zagadnieniu. Dla
Pawo Gaussa. Potencjał elektyczny. Wykład 3 Wocław Univesity of Technology 7-3- Inne spojzenie na pawo Coulomba Pawo Gaussa, moŝna uŝyć do uwzględnienia szczególnej symetii w ozwaŝanym zagadnieniu. Dla
GEOMETRIA PŁASZCZYZNY
 GEOMETRIA PŁASZCZYZNY. Oblicz pole tapezu ównoamiennego, któego podstawy mają długość cm i 0 cm, a pzekątne są do siebie postopadłe.. Dany jest kwadat ABCD. Punkty E i F są śodkami boków BC i CD. Wiedząc,
GEOMETRIA PŁASZCZYZNY. Oblicz pole tapezu ównoamiennego, któego podstawy mają długość cm i 0 cm, a pzekątne są do siebie postopadłe.. Dany jest kwadat ABCD. Punkty E i F są śodkami boków BC i CD. Wiedząc,
20 ELEKTROSTATYKA. PRAWO COULOMBA.
 Włodzimiez Wolczyński Pawo Coulomba 20 ELEKTROSTATYKA. PRAWO COULOMBA. POLE CENTRALNE I JEDNORODNE Q q = k- stała, dla póżni = 9 10 = 1 4 = 8,9 10 -stała dielektyczna póżni ε względna stała dielektyczna
Włodzimiez Wolczyński Pawo Coulomba 20 ELEKTROSTATYKA. PRAWO COULOMBA. POLE CENTRALNE I JEDNORODNE Q q = k- stała, dla póżni = 9 10 = 1 4 = 8,9 10 -stała dielektyczna póżni ε względna stała dielektyczna
= ± Ne N - liczba całkowita.
 POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
Elektrostatyka. + (proton) - (elektron)
 lektostatyka Za oddziaływania elektyczne ( i magnetyczne ) odpowiedzialny jest: ładunek elektyczny Ładunek jest skwantowany Ładunek elementany e.6-9 C (D. Millikan). Wszystkie ładunki są wielokotnością
lektostatyka Za oddziaływania elektyczne ( i magnetyczne ) odpowiedzialny jest: ładunek elektyczny Ładunek jest skwantowany Ładunek elementany e.6-9 C (D. Millikan). Wszystkie ładunki są wielokotnością
11. DYNAMIKA RUCHU DRGAJĄCEGO
 11. DYNAMIKA RUCHU DRGAJĄCEGO Ruchem dgającym nazywamy uch, któy powtaza się peiodycznie w takcie jego twania w czasie i zachodzi wokół położenia ównowagi. Zespół obiektów fizycznych zapewniający wytwozenie
11. DYNAMIKA RUCHU DRGAJĄCEGO Ruchem dgającym nazywamy uch, któy powtaza się peiodycznie w takcie jego twania w czasie i zachodzi wokół położenia ównowagi. Zespół obiektów fizycznych zapewniający wytwozenie
METODA CIASNEGO (silnego) WIĄZANIA (TB)
 MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
Metoda obrazów wielki skrypt przed poświąteczny, CZĘŚĆ POTRZEBNA DO OFa
 Metoa obrazów wielki skrypt prze poświąteczny, CZĘŚĆ POTRZEBNA DO OFa 1. Równania i warunki brzegowe Dlaczego w ogóle metoa obrazów ziała? W elektrostatyce o policzenia wszystkiego wystarczą 2 rzeczy:
Metoa obrazów wielki skrypt prze poświąteczny, CZĘŚĆ POTRZEBNA DO OFa 1. Równania i warunki brzegowe Dlaczego w ogóle metoa obrazów ziała? W elektrostatyce o policzenia wszystkiego wystarczą 2 rzeczy:
PRĄD ELEKTRYCZNY I SIŁA MAGNETYCZNA
 PĄD LKTYCZNY SŁA MAGNTYCZNA Na ładunek, opócz siły elektostatycznej, działa ównież siła magnetyczna popocjonalna do pędkości ładunku v. Pzekonamy się, że siła działająca na magnes to siła działająca na
PĄD LKTYCZNY SŁA MAGNTYCZNA Na ładunek, opócz siły elektostatycznej, działa ównież siła magnetyczna popocjonalna do pędkości ładunku v. Pzekonamy się, że siła działająca na magnes to siła działająca na
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ODPOWIEDZI DO ARKUSZA ROZSZERZONEGO Zadanie ( pkt) A Zadanie ( pkt) C Zadanie ( pkt) A, bo sinα + cosα sinα + cosα cos sinα sin cosα + π π + π sin α π A więc musi
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ODPOWIEDZI DO ARKUSZA ROZSZERZONEGO Zadanie ( pkt) A Zadanie ( pkt) C Zadanie ( pkt) A, bo sinα + cosα sinα + cosα cos sinα sin cosα + π π + π sin α π A więc musi
23 PRĄD STAŁY. CZĘŚĆ 2
 Włodzimiez Wolczyński 23 PĄD STAŁY. CZĘŚĆ 2 zadanie 1 Tzy jednakowe oponiki, każdy o opoze =30 Ω i opó =60 Ω połączono ze źódłem pądu o napięciu 15 V, jak na ysunku obok. O ile zwiększy się natężenie pądu
Włodzimiez Wolczyński 23 PĄD STAŁY. CZĘŚĆ 2 zadanie 1 Tzy jednakowe oponiki, każdy o opoze =30 Ω i opó =60 Ω połączono ze źódłem pądu o napięciu 15 V, jak na ysunku obok. O ile zwiększy się natężenie pądu
cz. 1. dr inż. Zbigniew Szklarski
 Wykład 10: Gawitacja cz. 1. d inż. Zbiniew Szklaski szkla@ah.edu.pl http://laye.uci.ah.edu.pl/z.szklaski/ Doa do pawa powszechneo ciążenia Ruch obitalny planet wokół Słońca jak i dlaczeo? Reulane, wieloletnie
Wykład 10: Gawitacja cz. 1. d inż. Zbiniew Szklaski szkla@ah.edu.pl http://laye.uci.ah.edu.pl/z.szklaski/ Doa do pawa powszechneo ciążenia Ruch obitalny planet wokół Słońca jak i dlaczeo? Reulane, wieloletnie
Pole magnetyczne. 5.1 Oddziaływanie pola magnetycznego na ładunki. przewodniki z prądem. 5.1.1 Podstawowe zjawiska magnetyczne
 Rozdział 5 Pole magnetyczne 5.1 Oddziaływanie pola magnetycznego na ładunki i pzewodniki z pądem 5.1.1 Podstawowe zjawiska magnetyczne W obecnym ozdziale ozpatzymy niektóe zagadnienia magnetostatyki. Magnetostatyką
Rozdział 5 Pole magnetyczne 5.1 Oddziaływanie pola magnetycznego na ładunki i pzewodniki z pądem 5.1.1 Podstawowe zjawiska magnetyczne W obecnym ozdziale ozpatzymy niektóe zagadnienia magnetostatyki. Magnetostatyką
ZJAWISKA ELEKTROMAGNETYCZNE
 ZJAWISKA LKTROMAGNTYCZN 1 LKTROSTATYKA Ładunki znajdują się w spoczynku Ładunki elektyczne: dodatnie i ujemne Pawo Coulomba: siły pzyciągające i odpychające między ładunkami Jednostką ładunku elektycznego
ZJAWISKA LKTROMAGNTYCZN 1 LKTROSTATYKA Ładunki znajdują się w spoczynku Ładunki elektyczne: dodatnie i ujemne Pawo Coulomba: siły pzyciągające i odpychające między ładunkami Jednostką ładunku elektycznego
Wykład: praca siły, pojęcie energii potencjalnej. Zasada zachowania energii.
 Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
magnetyzm ver
 e-8.6.7 agnetyz pądy poste pądy elektyczne oddziałują ze soą. doświadczenie Apèe a (18): Ι Ι 1 F ~ siła na jednostkę długości pzewodów pądy poste w póżni jednostki w elektyczności A ape - natężenie pądu
e-8.6.7 agnetyz pądy poste pądy elektyczne oddziałują ze soą. doświadczenie Apèe a (18): Ι Ι 1 F ~ siła na jednostkę długości pzewodów pądy poste w póżni jednostki w elektyczności A ape - natężenie pądu
KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH
 Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
Na skutek takiego przemieszcznia ładunku, energia potencjalna układu pole-ładunek zmienia się o:
 E 0 Na ładunek 0 znajdujący się w polu elektycznym o natężeniu E działa siła elektostatyczna: F E 0 Paca na pzemieszczenie ładunku 0 o ds wykonana pzez pole elektyczne: dw Fds 0E ds Na skutek takiego pzemieszcznia
E 0 Na ładunek 0 znajdujący się w polu elektycznym o natężeniu E działa siła elektostatyczna: F E 0 Paca na pzemieszczenie ładunku 0 o ds wykonana pzez pole elektyczne: dw Fds 0E ds Na skutek takiego pzemieszcznia
Fizyka elektryczność i magnetyzm
 Fizyka elektyczność i magnetyzm W1 1. Elektostatyka 1.1. Ładunek elektyczny. Cała otaczająca nas mateia składa się z elektonów, potonów i neutonów. Dwie z wymienionych cząstek - potony i elektony - obdazone
Fizyka elektyczność i magnetyzm W1 1. Elektostatyka 1.1. Ładunek elektyczny. Cała otaczająca nas mateia składa się z elektonów, potonów i neutonów. Dwie z wymienionych cząstek - potony i elektony - obdazone
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
GRAWITACJA. przyciągają się wzajemnie siłą proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu ich odległości r.
 GRAWITACJA Pawo powszechnego ciążenia (pawo gawitacji) Dwa punkty mateialne o masach m 1 i m pzyciągają się wzajemnie siłą popocjonalną do iloczynu ich mas i odwotnie popocjonalną do kwadatu ich odległości.
GRAWITACJA Pawo powszechnego ciążenia (pawo gawitacji) Dwa punkty mateialne o masach m 1 i m pzyciągają się wzajemnie siłą popocjonalną do iloczynu ich mas i odwotnie popocjonalną do kwadatu ich odległości.
4πε0ε w. q dl. a) V m 2
 Rozwiązania są moje, Batka i jeszcze te któe znaazłem w A. Niestety nie mogę zagwaantować, że są popawne :( Jeżei twoje opowiezi óżnią się o tych, to napisz o mnie (najepiej z wyjaśnienie ską bieze się
Rozwiązania są moje, Batka i jeszcze te któe znaazłem w A. Niestety nie mogę zagwaantować, że są popawne :( Jeżei twoje opowiezi óżnią się o tych, to napisz o mnie (najepiej z wyjaśnienie ską bieze się
POLE MAGNETYCZNE W PRÓŻNI. W roku 1820 Oersted zaobserwował oddziaływanie przewodnika, w którym płynął
 POLE MAGNETYCZNE W PÓŻNI W oku 8 Oested zaobsewował oddziaływanie pzewodnika, w któym płynął pąd, na igłę magnetyczną Dopowadziło to do wniosku, że pądy elektyczne są pzyczyną powstania pola magnetycznego
POLE MAGNETYCZNE W PÓŻNI W oku 8 Oested zaobsewował oddziaływanie pzewodnika, w któym płynął pąd, na igłę magnetyczną Dopowadziło to do wniosku, że pądy elektyczne są pzyczyną powstania pola magnetycznego
Wstęp. Prawa zostały znalezione doświadczalnie. Zrozumienie faktu nastąpiło dopiero pod koniec XIX wieku.
 Równania Maxwella Wstęp James Clek Maxwell Żył w latach 1831-1879 Wykonał decydujący kok w ustaleniu paw opisujących oddziaływania ładunków i pądów z polami elektomagnetycznymi oaz paw ządzących ozchodzeniem
Równania Maxwella Wstęp James Clek Maxwell Żył w latach 1831-1879 Wykonał decydujący kok w ustaleniu paw opisujących oddziaływania ładunków i pądów z polami elektomagnetycznymi oaz paw ządzących ozchodzeniem
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ.
 ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
POLE MAGNETYCZNE ŹRÓDŁA POLA MAGNETYCZNEGO
 POLE MAGNETYCZNE ŹRÓDŁA POLA MAGNETYCZNEGO Wykład 8 lato 2015/16 1 Definicja wektoa indukcji pola magnetycznego F = q( v B) Jednostką indukcji pola B jest 1T (tesla) 1T=1N/Am Pole magnetyczne zakzywia
POLE MAGNETYCZNE ŹRÓDŁA POLA MAGNETYCZNEGO Wykład 8 lato 2015/16 1 Definicja wektoa indukcji pola magnetycznego F = q( v B) Jednostką indukcji pola B jest 1T (tesla) 1T=1N/Am Pole magnetyczne zakzywia
IV OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy część 2 ZADANIA 29 lutego 2012r.
 V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
Siły centralne, grawitacja (I)
 Pojęcia Gawitacja postawowe (I) i histoia Siły centalne, gawitacja (I) Enegia potencjalna E p B A E p ( ) E p A W ( ) F W ( A B) B A F Pawo gawitacji (siła gawitacji) - Newton 665 M N k F G G 6.6700 F,
Pojęcia Gawitacja postawowe (I) i histoia Siły centalne, gawitacja (I) Enegia potencjalna E p B A E p ( ) E p A W ( ) F W ( A B) B A F Pawo gawitacji (siła gawitacji) - Newton 665 M N k F G G 6.6700 F,
ROZWIAZANIA ZAGADNIEŃ PRZEPŁYWU FILTRACYJNEGO METODAMI ANALITYCZNYMI.
 Modelowanie pzepływu cieczy pzez ośodki poowate Wykład VII ROZWIAZANIA ZAGADNIEŃ PRZEPŁYWU FILTRACYJNEGO METODAMI ANALITYCZNYMI. 7. Pzepływ pzez goblę z uwzględnieniem zasilania wodami infiltacyjnymi.
Modelowanie pzepływu cieczy pzez ośodki poowate Wykład VII ROZWIAZANIA ZAGADNIEŃ PRZEPŁYWU FILTRACYJNEGO METODAMI ANALITYCZNYMI. 7. Pzepływ pzez goblę z uwzględnieniem zasilania wodami infiltacyjnymi.
POLE MAGNETYCZNE ŹRÓDŁA POLA MAGNETYCZNEGO
 POLE MAGNETYZNE ŹRÓDŁA POLA MAGNETYZNEGO Wykład lato 01 1 Definicja wektoa indukcji pola magnetycznego F = q( v B) Jednostką indukcji pola B jest 1T (tesla) 1T=1N/Am Pole magnetyczne zakzywia to uchu ładunku
POLE MAGNETYZNE ŹRÓDŁA POLA MAGNETYZNEGO Wykład lato 01 1 Definicja wektoa indukcji pola magnetycznego F = q( v B) Jednostką indukcji pola B jest 1T (tesla) 1T=1N/Am Pole magnetyczne zakzywia to uchu ładunku
Wykład Pojemność elektryczna. 7.1 Pole nieskończonej naładowanej warstwy. σ-ładunek powierzchniowy. S 2 E 2 E 1 y. ds 1.
 Wykład 9 7. Pojemność elektyczna 7. Pole nieskończonej naładowanej wastwy z σ σładunek powiezchniowy S y ds x S ds 8 maca 3 Reinhad Kulessa Natężenie pola elektycznego pochodzące od nieskończonej naładowanej
Wykład 9 7. Pojemność elektyczna 7. Pole nieskończonej naładowanej wastwy z σ σładunek powiezchniowy S y ds x S ds 8 maca 3 Reinhad Kulessa Natężenie pola elektycznego pochodzące od nieskończonej naładowanej
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI
 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
Siła tarcia. Tarcie jest zawsze przeciwnie skierowane do kierunku ruchu (do prędkości). R. D. Knight, Physics for scientists and engineers
 Siła tacia Tacie jest zawsze pzeciwnie skieowane do kieunku uchu (do pędkości). P. G. Hewitt, Fizyka wokół nas, PWN R. D. Knight, Physics fo scientists and enginees Symulacja molekulanego modelu tacia
Siła tacia Tacie jest zawsze pzeciwnie skieowane do kieunku uchu (do pędkości). P. G. Hewitt, Fizyka wokół nas, PWN R. D. Knight, Physics fo scientists and enginees Symulacja molekulanego modelu tacia
WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POLITECHNIKI KRAKOWSKIEJ Instytut Fizyki LABORATORIUM PODSTAW ELEKTROTECHNIKI, ELEKTRONIKI I MIERNICTWA
 WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POITEHNIKI KRAKOWSKIEJ Instytut Fizyki ABORATORIUM PODSTAW EEKTROTEHNIKI, EEKTRONIKI I MIERNITWA ĆWIZENIE 7 Pojemność złącza p-n POJĘIA I MODEE potzebne do zozumienia
WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POITEHNIKI KRAKOWSKIEJ Instytut Fizyki ABORATORIUM PODSTAW EEKTROTEHNIKI, EEKTRONIKI I MIERNITWA ĆWIZENIE 7 Pojemność złącza p-n POJĘIA I MODEE potzebne do zozumienia
1. Ciało sztywne, na które nie działa moment siły pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym.
 Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
elektryczna. Elektryczność
 Pojemność elektryczna. Elektryczność ść. Wykła 4 Wrocław University of Technology 4-3- Pojemność elektryczna Okłaki konensatora są przewonikami, a więc są powierzchniami ekwipotencjalnymi: wszystkie punkty
Pojemność elektryczna. Elektryczność ść. Wykła 4 Wrocław University of Technology 4-3- Pojemność elektryczna Okłaki konensatora są przewonikami, a więc są powierzchniami ekwipotencjalnymi: wszystkie punkty
Elementarne przepływy potencjalne (ciąg dalszy)
 J. Szanty Wykład n 4 Pzepływy potencjalne Aby wytwozyć w pzepływie potencjalnym siły hydodynamiczne na opływanych ciałach konieczne jest zyskanie pzepływ asymetycznego.jest to możliwe pzy wykozystani kolejnego
J. Szanty Wykład n 4 Pzepływy potencjalne Aby wytwozyć w pzepływie potencjalnym siły hydodynamiczne na opływanych ciałach konieczne jest zyskanie pzepływ asymetycznego.jest to możliwe pzy wykozystani kolejnego
Wykład 10. Reinhard Kulessa 1
 Wykład 1 14.1 Podstawowe infomacje doświadczalne cd. 14. Pąd elektyczny jako źódło pola magnetycznego 14..1 Pole indukcji magnetycznej pochodzące od nieskończenie długiego pzewodnika z pądem. 14.. Pawo
Wykład 1 14.1 Podstawowe infomacje doświadczalne cd. 14. Pąd elektyczny jako źódło pola magnetycznego 14..1 Pole indukcji magnetycznej pochodzące od nieskończenie długiego pzewodnika z pądem. 14.. Pawo
KURS GEOMETRIA ANALITYCZNA
 KURS GEOMETRIA ANALITYCZNA Lekcja 2 Działania na wektoach w układzie współzędnych. ZADANIE DOMOWE www.etapez.pl Stona 1 Część 1: TEST Zaznacz popawną odpowiedź (tylko jedna jest pawdziwa). Pytanie 1 Któe
KURS GEOMETRIA ANALITYCZNA Lekcja 2 Działania na wektoach w układzie współzędnych. ZADANIE DOMOWE www.etapez.pl Stona 1 Część 1: TEST Zaznacz popawną odpowiedź (tylko jedna jest pawdziwa). Pytanie 1 Któe
m q κ (11.1) q ω (11.2) ω =,
 OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU
( ) Praca. r r. Praca jest jednąz form wymiany energii między ciałami. W przypadku, gdy na ciało
 Paca i enegia Paca Paca jest jenąz fom wymiany enegii mięzy ciałami. pzypaku, gy na ciało bęące punktem mateialnym ziała stała siła F const oaz uch ciała obywa się o punktu A o B po linii postej bez zawacania
Paca i enegia Paca Paca jest jenąz fom wymiany enegii mięzy ciałami. pzypaku, gy na ciało bęące punktem mateialnym ziała stała siła F const oaz uch ciała obywa się o punktu A o B po linii postej bez zawacania
SK-7 Wprowadzenie do metody wektorów przestrzennych SK-8 Wektorowy model silnika indukcyjnego, klatkowego
 Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
E4. BADANIE POLA ELEKTRYCZNEGO W POBLIŻU NAŁADOWANYCH PRZEWODNIKÓW
 4. BADANI POLA LKTRYCZNGO W POBLIŻU NAŁADOWANYCH PRZWODNIKÓW tekst opacował: Maek Pękała Od oku 1785 pawo Coulomba opisuje posty pzypadek siły oddziaływania dwóch punktowych ładunków elektycznych, któy
4. BADANI POLA LKTRYCZNGO W POBLIŻU NAŁADOWANYCH PRZWODNIKÓW tekst opacował: Maek Pękała Od oku 1785 pawo Coulomba opisuje posty pzypadek siły oddziaływania dwóch punktowych ładunków elektycznych, któy
L(x, 0, y, 0) = x 2 + y 2 (3)
 0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad W niniejszym schemacie oceniania zadań otwatych są pezentowane pzykładowe popawne odpowiedzi. W tego typu ch należy
KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad W niniejszym schemacie oceniania zadań otwatych są pezentowane pzykładowe popawne odpowiedzi. W tego typu ch należy
Fizyka 9. Janusz Andrzejewski
 Fizyka 9 Janusz Andzejewski R K Księżyc kążący wokół iei (Rozważania Newtona) Pzyśpieszenie dośodkowe księżyca 4πRK ak = T Wstawiając dane dla obity księżyca: R K = 3.86 10 T = 7. 3dnia 5 k R 6300 = 386000
Fizyka 9 Janusz Andzejewski R K Księżyc kążący wokół iei (Rozważania Newtona) Pzyśpieszenie dośodkowe księżyca 4πRK ak = T Wstawiając dane dla obity księżyca: R K = 3.86 10 T = 7. 3dnia 5 k R 6300 = 386000
Grzegorz Kornaś. Powtórka z fizyki
 Gzegoz Konaś Powtóka z fizyki - dla uczniów gimnazjów, któzy chcą wiedzieć to co tzeba, a nawet więcej, - dla uczniów liceów, któzy chcą powtózyć to co tzeba, aby zozumieć więcej, - dla wszystkich, któzy
Gzegoz Konaś Powtóka z fizyki - dla uczniów gimnazjów, któzy chcą wiedzieć to co tzeba, a nawet więcej, - dla uczniów liceów, któzy chcą powtózyć to co tzeba, aby zozumieć więcej, - dla wszystkich, któzy
9.1 POMIAR PRĘDKOŚCI NEUTRINA W CERN
 91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
FIZYKA 2. Janusz Andrzejewski
 FIZYKA 2 wykład 4 Janusz Andzejewski Pole magnetyczne Janusz Andzejewski 2 Pole gawitacyjne γ Pole elektyczne E Definicja wektoa B = γ E = Indukcja magnetyczna pola B: F B F G m 0 F E q 0 qv B = siła Loentza
FIZYKA 2 wykład 4 Janusz Andzejewski Pole magnetyczne Janusz Andzejewski 2 Pole gawitacyjne γ Pole elektyczne E Definicja wektoa B = γ E = Indukcja magnetyczna pola B: F B F G m 0 F E q 0 qv B = siła Loentza
( ) 2. 4πε. Prawo Coulomba
 Pawo Coulomba. Cztey identyczne ładunki dodatnie q umieszczono w wiezchołkach kwadatu o boku a. W śodku symetii kwadatu umieszczono ładunek ujemny taki, Ŝe cały układ pozostaje w ównowadze. Znaleźć watość
Pawo Coulomba. Cztey identyczne ładunki dodatnie q umieszczono w wiezchołkach kwadatu o boku a. W śodku symetii kwadatu umieszczono ładunek ujemny taki, Ŝe cały układ pozostaje w ównowadze. Znaleźć watość
KO OF Szczecin:
 XXXI OLIMPIADA FIZYCZNA (1981/198) Stopień III, zaanie teoretyczne T Źróło: Nazwa zaania: Działy: Słowa kluczowe: Komitet Główny Olimpiay Fizycznej; Anrzej Kotlicki; Anrzej Naolny: Fizyka w Szkole, nr
XXXI OLIMPIADA FIZYCZNA (1981/198) Stopień III, zaanie teoretyczne T Źróło: Nazwa zaania: Działy: Słowa kluczowe: Komitet Główny Olimpiay Fizycznej; Anrzej Kotlicki; Anrzej Naolny: Fizyka w Szkole, nr
ROZDZIAŁ 2. Elektrotechnika podstawowa 23
 lektotechnika podstawowa 3 ROZDZIAŁ lektostatyka. Kondensatoy + Nieuchome (niezmienne) ładunki elektyczne ozmieszczone w śodowisku dielektycznym są źódłami pola elektostatycznego. W paktyce model taki
lektotechnika podstawowa 3 ROZDZIAŁ lektostatyka. Kondensatoy + Nieuchome (niezmienne) ładunki elektyczne ozmieszczone w śodowisku dielektycznym są źódłami pola elektostatycznego. W paktyce model taki
Jak policzyć pole magnetyczne? Istnieją dwie metody wyznaczenia pola magnetycznego: prawo Biot Savarta i prawo Ampera.
 Elektyczność i magnetyzm. Równania Maxwella Wyznaczenie pola magnetycznego Jak policzyć pole magnetyczne? Istnieją dwie metody wyznaczenia pola magnetycznego: pawo iot Savata i pawo mpea. Pawo iota Savata
Elektyczność i magnetyzm. Równania Maxwella Wyznaczenie pola magnetycznego Jak policzyć pole magnetyczne? Istnieją dwie metody wyznaczenia pola magnetycznego: pawo iot Savata i pawo mpea. Pawo iota Savata
Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej
 Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej 1. Wstęp Pojemność kondensatora można obliczyć w prosty sposób znając wartości zgromadzonego na nim ładunku i napięcia między okładkami: Q
Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej 1. Wstęp Pojemność kondensatora można obliczyć w prosty sposób znając wartości zgromadzonego na nim ładunku i napięcia między okładkami: Q
DODATEK 6. Pole elektryczne nieskończenie długiego walca z równomiernie rozłożonym w nim ładunkiem objętościowym. Φ = = = = = π
 DODATEK 6 Pole elektycne nieskońcenie długiego walca ównomienie ołożonym w nim ładunkiem objętościowym Nieskońcenie długi walec o pomieniu jest ównomienie naładowany ładunkiem objętościowym o stałej gęstości
DODATEK 6 Pole elektycne nieskońcenie długiego walca ównomienie ołożonym w nim ładunkiem objętościowym Nieskońcenie długi walec o pomieniu jest ównomienie naładowany ładunkiem objętościowym o stałej gęstości
Teoria Pola Elektromagnetycznego
 Teoia Pola Elektomagnetycznego Wykład Pole elektostatyczne Stefan Filipowicz . Pole elektostatyczne 1.1. Ładunek elektyczny Pzy badaniu zjawisk pola elektycznego, w wielu ważnych z punktu widzenia paktyki
Teoia Pola Elektomagnetycznego Wykład Pole elektostatyczne Stefan Filipowicz . Pole elektostatyczne 1.1. Ładunek elektyczny Pzy badaniu zjawisk pola elektycznego, w wielu ważnych z punktu widzenia paktyki
Wykład 5: Dynamika. dr inż. Zbigniew Szklarski
 Wykład 5: Dynamika d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Pzyczyny uchu - zasady dynamiki dla punktu mateialnego Jeśli ciało znajduje się we właściwym miejscu,
Wykład 5: Dynamika d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Pzyczyny uchu - zasady dynamiki dla punktu mateialnego Jeśli ciało znajduje się we właściwym miejscu,
Pola elektryczne i magnetyczne
 Pola elektyczne i magnetyczne Zadania z ozwiązaniami Pojekt współfinansowany pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego Zadanie 1 Cząstka alfa (jądo atomu helu) ma masę m = 6.64*1 7
Pola elektyczne i magnetyczne Zadania z ozwiązaniami Pojekt współfinansowany pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego Zadanie 1 Cząstka alfa (jądo atomu helu) ma masę m = 6.64*1 7
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
KURS CAŁKI WIELOKROTNE
 KURS CAŁKI WIELOKROTNE Lekcja Całki potójne ZADANIE DOMOWE www.etapez.pl Stona 1 Częśd 1: TEST Zaznacz popawną odpowiedź (tylko jedna jest pawdziwa). Pytanie 1 Obszaem całkowania w całce potójnej jest:
KURS CAŁKI WIELOKROTNE Lekcja Całki potójne ZADANIE DOMOWE www.etapez.pl Stona 1 Częśd 1: TEST Zaznacz popawną odpowiedź (tylko jedna jest pawdziwa). Pytanie 1 Obszaem całkowania w całce potójnej jest:
Zjawisko indukcji. Magnetyzm materii.
 Zjawisko indukcji. Magnetyzm mateii. Wykład 6 Wocław Univesity of Technology -04-0 Dwa symetyczne pzypadki PĘTLA Z PĄDEM MOMENT SIŁY + + POLE MAGNETYCZNE POLE MAGNETYCZNE P A W O I N D U K C J I MOMENT
Zjawisko indukcji. Magnetyzm mateii. Wykład 6 Wocław Univesity of Technology -04-0 Dwa symetyczne pzypadki PĘTLA Z PĄDEM MOMENT SIŁY + + POLE MAGNETYCZNE POLE MAGNETYCZNE P A W O I N D U K C J I MOMENT
Podstawy elektrotechniki
 Wydział Mechaniczno-Enegetyczny Podstawy elektotechniki Pof. d hab. inż. Juliusz B. Gajewski, pof. zw. PW Wybzeże S. Wyspiańskiego 7, 5-37 Wocław Bud. A4 Staa kotłownia, pokój 359 Tel.: 7 3 3 Fax: 7 38
Wydział Mechaniczno-Enegetyczny Podstawy elektotechniki Pof. d hab. inż. Juliusz B. Gajewski, pof. zw. PW Wybzeże S. Wyspiańskiego 7, 5-37 Wocław Bud. A4 Staa kotłownia, pokój 359 Tel.: 7 3 3 Fax: 7 38
REZONATORY DIELEKTRYCZNE
 REZONATORY DIELEKTRYCZNE Rezonato dielektyczny twozy małostatny, niemetalizowany dielektyk o dużej pzenikalności elektycznej ( > 0) i dobej stabilności tempeatuowej, zwykle w kształcie cylindycznych dysków
REZONATORY DIELEKTRYCZNE Rezonato dielektyczny twozy małostatny, niemetalizowany dielektyk o dużej pzenikalności elektycznej ( > 0) i dobej stabilności tempeatuowej, zwykle w kształcie cylindycznych dysków
Magnetyzm. A. Sieradzki IF PWr. Pole magnetyczne ŁADUNEK ELEKTRYCZNY ŁADUNEK MAGNETYCZNY POLE ELEKTRYCZNE POLE MAGNETYCZNE
 Magnetyzm Wykład 5 1 Wocław Univesity of Technology 14-4-1 Pole magnetyczne ŁADUNEK ELEKTRYCZNY ŁADUNEK MAGNETYCZNY? POLE ELEKTRYCZNE POLE MAGNETYCZNE Jak wytwozyć pole magnetyczne? 1) Naładowane elektycznie
Magnetyzm Wykład 5 1 Wocław Univesity of Technology 14-4-1 Pole magnetyczne ŁADUNEK ELEKTRYCZNY ŁADUNEK MAGNETYCZNY? POLE ELEKTRYCZNE POLE MAGNETYCZNE Jak wytwozyć pole magnetyczne? 1) Naładowane elektycznie
Lista zadań nr 1 - Wektory
 Lista zadań n 1 - Wektoy Zad. 1 Dane są dwa wektoy: a = 3i + 4 j + 5k, b = i + k. Obliczyć: a) długość każdego wektoa, b) iloczyn skalany a b, c) kąt zawaty między wektoami,, d) iloczyn wektoowy a b e)
Lista zadań n 1 - Wektoy Zad. 1 Dane są dwa wektoy: a = 3i + 4 j + 5k, b = i + k. Obliczyć: a) długość każdego wektoa, b) iloczyn skalany a b, c) kąt zawaty między wektoami,, d) iloczyn wektoowy a b e)
KINEMATYCZNE WŁASNOW PRZEKŁADNI
 KINEMATYCZNE WŁASNOW ASNOŚCI PRZEKŁADNI Waunki współpacy pacy zazębienia Zasada n 1 - koła zębate mogą ze sobą współpacować, kiedy mają ten sam moduł m. Czy to wymaganie jest wystaczające dla pawidłowej
KINEMATYCZNE WŁASNOW ASNOŚCI PRZEKŁADNI Waunki współpacy pacy zazębienia Zasada n 1 - koła zębate mogą ze sobą współpacować, kiedy mają ten sam moduł m. Czy to wymaganie jest wystaczające dla pawidłowej
POLE ELEKTROSTATYCZNE W PRÓŻNI - CD. Dipol charakteryzuje się przez podanie jego dipolowego momentu elektrycznego p (5.1)
 POL LKTROTATYCZN W PRÓŻNI - CD Dio ktyczny q + q Dio ktyczny to ukła ównych co o watości unktowych łaunków ktycznych zciwngo znaku ozmiszczonych w stałj ogłości o sibi Dio chaaktyzuj się zz oani jgo ioowgo
POL LKTROTATYCZN W PRÓŻNI - CD Dio ktyczny q + q Dio ktyczny to ukła ównych co o watości unktowych łaunków ktycznych zciwngo znaku ozmiszczonych w stałj ogłości o sibi Dio chaaktyzuj się zz oani jgo ioowgo
WIRTUALNE LABORATORIA FIZYCZNE NOWOCZESNĄ METODĄ NAUCZANIA INNOWACYJNY PROGRAM NAUCZANIA FIZYKI W SZKOŁACH PONADGIMNAZJALNYCH
 WIRTALNE LABORATORIA FIZYZNE NOWOZESNĄ METODĄ NAZANIA INNOWAYJNY PROGRAM NAZANIA FIZYKI W SZKOŁAH PONADGIMNAZJALNYH Mouł yaktyczny: fizyka infomatyka Pole elektyczne Gzegoz F. Wojewoa złowiek najlepsza
WIRTALNE LABORATORIA FIZYZNE NOWOZESNĄ METODĄ NAZANIA INNOWAYJNY PROGRAM NAZANIA FIZYKI W SZKOŁAH PONADGIMNAZJALNYH Mouł yaktyczny: fizyka infomatyka Pole elektyczne Gzegoz F. Wojewoa złowiek najlepsza
Atom (cząsteczka niepolarna) w polu elektrycznym
 Dieektyki Dieektyki substancje, w któych nie występują swobodne nośniki ładunku eektycznego (izoatoy). Może być w nich wytwozone i utzymane bez stat enegii poe eektyczne. dieektyk Faaday Wpowadzenie do
Dieektyki Dieektyki substancje, w któych nie występują swobodne nośniki ładunku eektycznego (izoatoy). Może być w nich wytwozone i utzymane bez stat enegii poe eektyczne. dieektyk Faaday Wpowadzenie do
NAGRZEWANIE MIKROFALOWE
 INSTYTUT INFORMATYKI STOSOWANEJ POLITECHNIKI ŁÓDZKIEJ Ćwiczenia N 1 NAGRZEWANIE MIKROFALOWE 1.WPROWADZENIE. W mikofalowych uzązeniach gzejnych efekt polayzacji (występujący w śoowiskach ielektycznych i
INSTYTUT INFORMATYKI STOSOWANEJ POLITECHNIKI ŁÓDZKIEJ Ćwiczenia N 1 NAGRZEWANIE MIKROFALOWE 1.WPROWADZENIE. W mikofalowych uzązeniach gzejnych efekt polayzacji (występujący w śoowiskach ielektycznych i
Geometria płaska - matura Przyprostokątne trójkąta prostokątnego mają długości 3 7cm poprowadzona z wierzchołka kąta prostego ma długość: 12
 Geometria płaska - matura 010 1. Przyprostokątne trójkąta prostokątnego mają ługości 7cm i 4 7cm. Wysokość poprowazona z wierzchołka kąta prostego ma ługość: 1 5 A. 7cm B. cm C. 8 7cm D. 7 7cm 5 7. Miara
Geometria płaska - matura 010 1. Przyprostokątne trójkąta prostokątnego mają ługości 7cm i 4 7cm. Wysokość poprowazona z wierzchołka kąta prostego ma ługość: 1 5 A. 7cm B. cm C. 8 7cm D. 7 7cm 5 7. Miara
Wykład FIZYKA I. 8. Grawitacja. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 8. Gawitacja D hab. inż. Władysław Atu Woźniak Instytut Fizyki Politechniki Wocławskiej http://www.if.pw.woc.pl/~wozniak/fizyka1.html CIĄŻENIE POWSZECHNE (GRAWITACJA) Wzajemne pzyciąganie
Wykład FIZYKA I 8. Gawitacja D hab. inż. Władysław Atu Woźniak Instytut Fizyki Politechniki Wocławskiej http://www.if.pw.woc.pl/~wozniak/fizyka1.html CIĄŻENIE POWSZECHNE (GRAWITACJA) Wzajemne pzyciąganie
MIERNICTWO WIELKOŚCI ELEKTRYCZNYCH I NIEELEKTRYCZNYCH
 Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie
 Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Równania Lagrange a II r.
 Mechania Analityczna i Dgania Równania Lagange a II. pzyłay Równania Lagange a II. pzyłay mg inż. Sebastian Pauła Aaemia Góniczo-Hutnicza im. Stanisława Staszica w Kaowie Wyział Inżynieii Mechanicznej
Mechania Analityczna i Dgania Równania Lagange a II. pzyłay Równania Lagange a II. pzyłay mg inż. Sebastian Pauła Aaemia Góniczo-Hutnicza im. Stanisława Staszica w Kaowie Wyział Inżynieii Mechanicznej
XIX. PRAWO COULOMBA Prawo Coulomba
 XIX PRAWO COULOMBA 191 Pawo Coulomba Wielkość oddziaływania cząstki z otaczającymi ją obiektami zależy od jej ładunku elektycznego, zwykle oznaczanego pzez Ładunek elektyczny może być dodatni lub ujemny
XIX PRAWO COULOMBA 191 Pawo Coulomba Wielkość oddziaływania cząstki z otaczającymi ją obiektami zależy od jej ładunku elektycznego, zwykle oznaczanego pzez Ładunek elektyczny może być dodatni lub ujemny
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
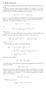 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Wybrane zagadnienia z elektryczności
 Wybane zaganienia z elektyczności Pomia łaunku elektycznego oświaczenie Millikana atomize płaszczyzna (+) bateia kople oleju mikoskop F el F g płaszczyzna (-) F g F el mg mg e.6 0 9 C Łaunek elektyczny
Wybane zaganienia z elektyczności Pomia łaunku elektycznego oświaczenie Millikana atomize płaszczyzna (+) bateia kople oleju mikoskop F el F g płaszczyzna (-) F g F el mg mg e.6 0 9 C Łaunek elektyczny
Kinematyka odwrotna:
 Kinematka owotna: ozwiązanie zaania kinematki owotnej owaza ię o wznazenia maiez zekztałenia H otai H E Wznazenie tej maiez olega na znalezieni jenego bąź wztkih ozwiązań ównania: T T n n q... q gzie q...
Kinematka owotna: ozwiązanie zaania kinematki owotnej owaza ię o wznazenia maiez zekztałenia H otai H E Wznazenie tej maiez olega na znalezieni jenego bąź wztkih ozwiązań ównania: T T n n q... q gzie q...
Przygotowanie do Egzaminu Potwierdzającego Kwalifikacje Zawodowe
 Pzygotowanie do Egzaminu Potwiedzającego Kwalifikacje Zawodowe Powtózenie mateiału Opacował: mg inż. Macin Wieczoek Jednostki podstawowe i uzupełniające układu SI. Jednostki podstawowe Wielkość fizyczna
Pzygotowanie do Egzaminu Potwiedzającego Kwalifikacje Zawodowe Powtózenie mateiału Opacował: mg inż. Macin Wieczoek Jednostki podstawowe i uzupełniające układu SI. Jednostki podstawowe Wielkość fizyczna
KOOF Szczecin: Komitet Główny Olimpiady Fizycznej. Andrzej Wysmołek Komitet Główny Olimpiady Fizycznej, IFD UW.
 LVII OLIMPIADA FIZYCZNA (007/008). Stopień III, zadanie doświadczalne D Źódło: Auto: Nazwa zadania: Działy: Słowa kluczowe: Komitet Główny Olimpiady Fizycznej. Andzej Wysmołek Komitet Główny Olimpiady
LVII OLIMPIADA FIZYCZNA (007/008). Stopień III, zadanie doświadczalne D Źódło: Auto: Nazwa zadania: Działy: Słowa kluczowe: Komitet Główny Olimpiady Fizycznej. Andzej Wysmołek Komitet Główny Olimpiady
Rozciąganie i ściskanie prętów projektowanie 3
 Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
DYFRAKCJA NA POJEDYNCZEJ I PODWÓJNEJ SZCZELINIE
 YFRAKCJA NA POJEYNCZEJ POWÓJNEJ SZCZELNE. Cel ćwiczenia: zapoznanie ze zjawiskiem yfrakcji światła na pojeynczej i powójnej szczelinie. Pomiar ługości fali światła laserowego, oległości mięzy śrokami szczelin
YFRAKCJA NA POJEYNCZEJ POWÓJNEJ SZCZELNE. Cel ćwiczenia: zapoznanie ze zjawiskiem yfrakcji światła na pojeynczej i powójnej szczelinie. Pomiar ługości fali światła laserowego, oległości mięzy śrokami szczelin
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
WYKŁAD nr Ekstrema funkcji jednej zmiennej o ciągłych pochodnych. xˆ ( ) 0
 WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
cz.2 dr inż. Zbigniew Szklarski
 Wykład 11: Gawitacja cz. d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Pawo Gaussa - PZYKŁADY: Masa punktowa: ds Powiezchnia Gaussa M g g S g ds S g ds 0 cos180 S gds
Wykład 11: Gawitacja cz. d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Pawo Gaussa - PZYKŁADY: Masa punktowa: ds Powiezchnia Gaussa M g g S g ds S g ds 0 cos180 S gds
Zadanie 1. Zadanie 2. Sprawdzam dla objętości, że z obwarzanków mogę posklejać całą kulę o promieniu R: r = {x, y, z}; A = * Cross r, B
 Zadanie In[]:= = {x, y, z}; In[]:= B = B, B, B3 ; (* Bi to wielkości stałe *) In[3]:= A = - * Coss, B Out[3]= -B3 y + B z, B3 x - B z, -B x + B y In[4]:= {x,y,z} -B3 y + B z, B3 x - B z, -B x + B y Out[4]=
Zadanie In[]:= = {x, y, z}; In[]:= B = B, B, B3 ; (* Bi to wielkości stałe *) In[3]:= A = - * Coss, B Out[3]= -B3 y + B z, B3 x - B z, -B x + B y In[4]:= {x,y,z} -B3 y + B z, B3 x - B z, -B x + B y Out[4]=
Implementacja i badania parametrów metrologicznych różnicowego anemometru z falą cieplną w adaptacyjnym komputerowym systemie termoanemometrycznym
 87 ace Instytutu Mechaniki Góotwou AN Tom 7 n - (005) s. 87-99 Instytut Mechaniki Góotwou AN Implementacja i baania paametów metologicznych óżnicowego anemometu z falą cieplną w aaptacyjnym komputeowym
87 ace Instytutu Mechaniki Góotwou AN Tom 7 n - (005) s. 87-99 Instytut Mechaniki Góotwou AN Implementacja i baania paametów metologicznych óżnicowego anemometu z falą cieplną w aaptacyjnym komputeowym
