Kinematyka odwrotna:

Plan wykładu 6. Hanna Pawłowska Elementy termodynamiki atmosfery i fizyki chmur Wykład 6

Plan wykłau 6 emoynamika związana z uhem ionowym Poe euo-aiabatyzny emeatua ekwiwalentna, temeatua ekwiwalentno-otenjalna, liqui wate otential temeatue Gaient wilgotno-aiabatyzny Hanna Pawłowka Elementy

Zastosowanie algorytmu Euklidesa

Zatoowanie algoytmu Euklidea Pzelewanie wody Dyonujez dwoma czeakami o ojemnościach 4 i 6 litów, utym ojemnikiem o nieoganiczonej objętości i nieoganiczoną ilością wody Podaj oób naełnienia ojemnika 14

ÓŁ Ą Ś Ą Ł Ś Ó Ą Ł ź ź Ą ż ż ż ż ż Ę Ę ź Ą ż Ę Ń Ę ż ż ź ż ż Ń ż Ą ż ć ż ć ć ć ć ż ć ć ć ć ż Ł Ę Ą ć ć ć ć ć ć ć ć ć ź ć ź Ę ć ź ć ż ć ć ć ż ź ć ć ć ć ż ź ż ż ć ż ż ć ż Ę Ą ć Ł ź ż ż Ł Ó ÓŁ ć Ą ć Ą ż ż

ć ź ź Ł ź ź ź Ś ć ć Ę ÓŁ ź Ń ź ź ź ć ć Ń ć ć ć Ń ź Ę Ś Ń ć ć ć ź ć ć ć ć ć ć ź Ś Ę ź ź Ż ć ź ź ć ź Ń ź ć ć ć ź ź Ł Ń ć Ń Ń ź Ś Ń Ę Ę Ę ź ć ć Ę ź Ń Ł Ę ź ź Ń Ę Ę Ł Ł Ś Ś ć ć Ł ź ć ć Ł Ó Ż Ś Ł Ó ź Ę Ń

Ł ś Ł Ą ś Ź Ł ś Ł ś ź ś ę ÓŁ ÓŁ ź ź ś ś ę ę ź ć ś ś ę ć ę ś ę ś ź ę ś ę ś ś ś ę ę ć ę ś Ł ę ę ę Ę Ą ś ś ś Ł ś ę ś Ł Ń Ł Ń ę ś ś ę Ż Ż ś Ż ś ś Ż ś ź ś ś ź ś ę ś ę Ń ę ę ę ś ę ś ę ś ź ś Ł ś ś ś ś ę ś ś

Ń ÓŁ Ł Ś Ł Ł Ś ÓŁ Ł Ś Ń ÓŁ Ł Ń Ź ę Ą ę ę ę ę ę ę Ź ę ć ć ę ę ę ę ę Ź ć ę ę ę ć ć ę ę ę Ł ę ę ę Ł Ł ę ę ę ę ę ź ę ę ę ę ź ę ć ę ć ć ę ę ź ź ę ć ę ę ź Ź ę ź ę ę ć Ź Ą ć ć ć ę ę ę ę ę Ź ź ę ć Ł ź ę ę Ź Ę

Ł ÓŁ Ł Ą Ś Ą Ą Ś Ś ć ć ć ć ć ć ć ć ć ć ć Ę ć ń ć ć ć ć ć ć ć ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ą ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ń ń ć Ś ń ć ń ć ń ć ć Ś ć Ż Ś Ś ń Ł Ń ń ć ć ć ć Ś ń

Ł Ń Ś ś ę ę ś ś ś ś ę ę ę ę ś ś ę ś ę ś ę ś ś ć Ą ś ę ś ś ę ś ę ś ś Ń ś ś ś ś ś ś ę ę ę ę ś ś ę ć ś ś ę ś ę ś ę ę ś ę ś Ą ę ś ę ś ś ś ś ę ś ś ę ę ś ś ę ś ś ś ę ę ę ś ś ś ę ś ę ś ę ć ś ś ę ś ę ę Ą ę ę ę

Ą Ą Ł Ś ÓŁ Ł ć ć ź ÓŁ ć ć Ś ć ć Ą ć ć ć ź ć ć ć ć ć Ą Ó ÓŁ ć ć Ł Ł ź Ś ć ć ć ć Ł Ł ć ć Ł Ł Ł ć Ó ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ź Ż ź Ł ć Ż Ć Ż Ś Ż ć ć ć ć Ł Ż Ś ć Ś ź ć ź ć ć ć ź ć Ś Ź ŚĆ ź ć ć Ś Ś

Ą Ł Ł Ł Ś ż ź ź Ł Ś Ą Ł Ś Ś Ł Ó ż Ł Ś Ą ć ć ż ż Ą ż ć ż ż ć ć ć Ś ć ż Ś ż ż Ą ć ż ż ć ć ć ć ż ż Ś ć ż ż ÓŁ ż ż ż Ł Ł Ś Ó ć ż Ł ż ż ż ż ż Ć Ó Ó ż ż Ó Ł Ł ż Ą ż ż ż ż ż ż ż ż ż ć ż ż ć ż ż ż ć ż ż ż Ł ć

Wynik finansowy transakcji w momencie jej zawierania jest nieznany z uwagi na zmienność ceny przedmiotu transakcji, czyli instrumentu bazowego

.Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je

Teoria i metody optymalizacji

eoia dualności dla zadania pogamowania liniowego PL EORIA I MEODY OPYMALIZACJI Zadanie liniowego pogamowania całkowitoliczbowego PCL Wdział Elektoniki Kie. Automatka i Robotka Studia II t. NZ d inż. Ewa

Modelowanie przepływu cieczy przez ośrodki porowate Wykład III

Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości

MECHANIKA OGÓLNA (II)

MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla

ĆWICZENIE 5. Badanie przekaźnikowych układów sterowania

ĆWICZENIE 5 Badanie zekaźnikowych układów steowania 5. Cel ćwiczenia Celem ćwiczenia jest badanie zekaźnikowych układów steowania obiektem całkującoinecyjnym. Ćwiczenie dotyczy zekaźników dwu- i tójołożeniowych

IV OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy część 2 ZADANIA 29 lutego 2012r.

V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich

PLAN WYKŁADU. Opis pary wodnej w atmosferze Opis wilgotnego, nienasyconego powietrza 1 /22

PLAN WYKŁADU Oi ay wonj w atofz Oi wilgotngo, ninayongo owitza /22 Poęzniki Salby, Chat 4 C&W, Chat 4 &Y, Chat 2 2 /22 OPIS PAY WODNEJ W AOSFEZE 3 /22 aua.naa.go 4 /22 Dla tatu i iśniń otykanyh w atofz,

II.6. Wahadło proste.

II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia

Model klasyczny gospodarki otwartej

Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli

Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie

Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego

m q κ (11.1) q ω (11.2) ω =,

OPIS RUCHU, DRGANIA WŁASNE TŁUMIONE Oga Kopacz, Adam Łodygowski, Kzysztof Tymbe, Michał Płotkowiak, Wojciech Pawłowski Konsutacje naukowe: pof. d hab. Jezy Rakowski Poznań 00/00.. Opis uchu OPIS RUCHU

Metoda odbić zwierciadlanych

Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa

Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony

Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej

SCENARIUSZ LEKCJI MATEMATYKI Temat: Zadania na dowodzenie w trygonometrii. Cel: Uczeń tworzy łańcuch argumentów i uzasadnia jego poprawność.

SCENAIUSZ LEKCJI MATEMATYKI Temat: Zadania na dowodzenie w tygonometii Cel: Uczeń twozy łańcuch agumentów i uzasadnia jego popawność Czas: godzina lekcyjna Cele zajęć: Uczeń po zajęciach: wykozystuje definicje

23. CAŁKA POWIERZCHNIOWA NIEZORIENTOWANA

. CAŁKA POWIERZCHNIOWA NIEZORIENTOWANA Płat powiechniow o ównaniach paametcnch: ( ) ( ) ( ) () gdie oba jet obaem eglanm nawam płatem gładkim (płatem eglanm) gd w każdm pnkcie tego płata itnieje płacna

Metoda odbić zwierciadlanych

Metoa obić zwiecialanych Pzyuśćmy, że łaunek unktowy (Rys ) umieszczony jest w oległości o nieskończonej owiezchni zewozącej, umiejscowionej na łaszczyźnie X0Y Piewsze ytanie, jakie o azu się nasuwa jest

1. Ciało sztywne, na które nie działa moment siły pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym.

Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,

LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH

LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH ĆWICZENIE 3 NEURONOWE STEROWANIE ROBOTEM Neuonowe steowanie ynamiką obota. Cel ćwiczenia należy zestawić ukła steowania amionami obota z wykozystaniem metoy owotnego

Rozciąganie i ściskanie prętów projektowanie 3

Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku

Zastosowanie teorii pierścieni w praktyce

Upozczenie wyażeń 2x+(y x) = x+y Spotkania z Matematyka Zatoowanie teoii pieścieni w paktyce Alekande Deniiuk denijuk@matman.uwm.edu.pl Uniweytet Wamińko-Mazuki w Olztynie Wydział Matematyki i Infomatyki

Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.

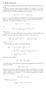Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie

PRĘDKOŚCI KOSMICZNE OPRACOWANIE

PRĘDKOŚCI KOSMICZNE OPRACOWANIE I, II, III pędkość komiczna www.iwiedza.net Obecnie, żyjąc w XXI wieku, wydaje ię nomalne, że człowiek potafi polecieć w komo, opuścić Ziemię oaz wylądować na Kiężycu. Poza

1. SZCZEGÓLNE PRZYPADKI ŁUKÓW.

Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak

Ł Ą Ą Ą ÓŁ Ą ć ć ń ń ń Ą ć ń ń ć ń Ę ń ń Ę ń ń ń ń ń ń Ą ń Ć ń ń ń ń ż ń ń ń ź Ś ń ń ń ż ż ż ń ń Ę ć Ś ć ć ż ń ń ń Ł ń ń ń ń ń ż Ł ÓŁ ÓŁ Ą Ś Ę Ą Ą Ą Ł Ł Ą Ą Ś ż ÓŁ ż Ł Ą Ę ć ż Ł ż Ż ż ń Ś Ó Ś Ś Ó ń Ą ż

29 Rozpraszanie na potencjale sferycznie symetrycznym - fale kuliste

9 Rozpaszanie na potencjae sfeycznie symetycznym - fae kuiste W ozdziae tym zajmiemy się ozpaszaniem na potencjae sfeycznie symettycznym V ). Da uchu o dodatniej enegii E = k /m adiane ównanie Schödingea

Wyznaczanie współczynnika sztywności drutu metodą dynamiczną.

Ćwiczenie M- Wyznaczanie współczynnika sztywności dutu metodą dynamiczną.. Ce ćwiczenia: pomia współczynnika sztywności da stai metodą dgań skętnych.. Pzyządy: dwa kążki metaowe, statyw, dut staowy, stope,

KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony

KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie

MECHANIKA BUDOWLI 12

Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE

ź ź Ż ź ź ź ć ć ÓŁ ź ćź ć ć ć ć Ó Ó ć ź ć ć ć ć ć ć ź ź ź Ś Ó ć ć ć Ć ć ź ć Ę ź Ś ć Ś ć Ź ć ć ź ź ć ć ć ć ć ć ć ź ź ć ć Ś ź Ś Ś ź ź Ś Ś Ś ć ć ć ć ć ć ć ć ć ć ź ć ź Ć ź Ś Ś Ś ź Ś Ż ć ź ź ź ź ć ć ź ź ć ć

Ł ÓŁ Ó Ó Ó ć Ź Ó Ą ć Ź Ó Ś ć Ś Ó Ó ć Ó Ź Ó Ś ć Ź ć Ę Ó Ó Ą Ł ć Ą Ą Ą Ó ć Ó Ó Ó ć Ó ć ć ć Ó Ą Ź Ó Ą ć Ś Ó Ą Ź Ó Ź Ś Ó Ó Ź Ó Ó Ź Ź Ó Ó ć Ó Ą Ć Ó Ó Ź Ź Ź Ę Ó ć ć Ł Ó Ó Ó ć ć Ó ź ć ć Ó Ś Ó ć ź Ź ź ć Ś Ó ć

ÓŁ Ł Ó ź Ł Ą Ł ń ń Ą ń ź Ą ń ż ć Ę Ę Ę ż ć ń ć ń ż ń ć ń Ę ż ć ź ć ź ć Ę ż ż Ę Ę Ą ż ź ń ź ź ż ć ż ń Ę ć ć ć ń Ę ń ć Ę ć ń ń ż ń ń ń ń ń ń ń ż Ę ń ń ń Ę ń ć ż Ż Ż ćę Ę Ę ż ć Ą ż Ę ż Ę ż Ę Ę ć Ę ć ż ż ć

Wyznaczanie temperatury i ciśnienia gazu z oddziaływaniem Lennarda Jonesa metodami dynamiki molekularnej

Pojekt n C.4. Wyznazanie tempeatuy i iśnienia gazu z oddziaływaniem Lennada Jonesa metodami dynamiki molekulanej Wpowadzenie Fizyka Rozważamy model gazu zezywistego zyli zbió atomów oddziaływująyh z sobą

Przejmowanie ciepła przy konwekcji swobodnej w przestrzeni ograniczonej (szczeliny)

inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska

SK-7 Wprowadzenie do metody wektorów przestrzennych SK-8 Wektorowy model silnika indukcyjnego, klatkowego

Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,

Ą ć ź ć Ą ć Ą Ą Ł Ź Ą Ź ć ć Ź Ą Ą Ą ź Ł ć Ź Ą ć ź ć Ą Ź ć ź Ą Ą Ą Ł Ą Ł Ź ć Ś Ń ć Ł Ź Ó ć ć ć Ą ÓŁ ź Ą Ą Ź ć Ź Ź Ą Ł Ł ć ć ć ć ź ć ź ć Ą Ą Ź Ź Ą ć Ą Ź Ś Ą Ó Ź Ó Ą Ź Ą Ł Ł Ź ć Ś ć Ą Ą ć Ź Ó Ś Ś Ź ź ź Ś

METEMATYCZNY MODEL OCENY

I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień

XXX OLIMPIADA FIZYCZNA (1980/1981). Stopień I, zadanie teoretyczne T4 1

XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:

Ł ć ź ź Ą Ń ź ź ź Ę Ą Ń ć Ł Ł ć ć ć ć ć ć ć ć ć ź ź ć ć Ł ć ć ć Ł ć Ł ć ź Ś Ś ć ź ć ź ź ć Ł Ę Ę Ń ź ź ć ć Ł Ł Ą Ą ź Ą Ę ź ź Ś Ł ŚĆ ć ć ć Ń Ą Ę ź Ę Ł Ę Ą ź Ń ć ć ź ź Ą ź ź ć ć ŚĆ ć Ś Ś Ś ć Ę ć ć ć Ś

ś ŁĄ ŁĄ Ą Ą Ż Ą Ł ŁĄ Ł Ł Ą Ł Ą Ą Ó Ł Ó ś Ł Ł Ł Ą Ą ŁĄ Ą ŁĄ ÓŁ Ł ć Ż ś Ź ÓŁ Ą Ą ŁĄ Ą Ł Ź ć ź ś ś ś ŁĄ ÓŁ Ą Ć Ź Ź ś Ź ś Ź ś Ź ś ś Ł Ł Ą ś Ź ś ś ś Ł Ł Ą Ą Ź ś Ł Ł Ł Ą Ą ŁĄ Ź ś ś ś ść Ą Ł ź ść Ź ź ś Ł Ł ź

11. DYNAMIKA RUCHU DRGAJĄCEGO

11. DYNAMIKA RUCHU DRGAJĄCEGO Ruchem dgającym nazywamy uch, któy powtaza się peiodycznie w takcie jego twania w czasie i zachodzi wokół położenia ównowagi. Zespół obiektów fizycznych zapewniający wytwozenie

Ruch kulisty bryły. Kinematyka

Ruch kulist bł. Kinematka Ruchem kulistm nawam uch, w casie któego jeden punktów bł jest stale nieuchom. Ruch kulist jest obotem dookoła chwilowej osi obotu (oś ta mienia swoje położenie w casie). a) b)

Ą ÓŁ Ź ÓŹ Ó Ź Ź Ó Ź Ź Ś Ś Ó Ź Ó Ś Ó ć ć ć Ś Ó ć Ó Ó ź Ó Ó Ó Ó Ó Ó Ó Ó Ó Ó ć Ó Ź Ź Ó Ó Ó Ź Ź ć Ó Ó Ó Ó Ó Ź Ź ć Ź Ó Ź ć Ó Ó Ó ć Ą Ś ć Ź Ś Ź ć Ó ź Ś Ł Ś Ś Ź Ś Ó Ź Ź Ź Ś Ś Ę Ź Ó Ś Ź Ó ć Ź Ź Ó ź Ó ć Ę Ó Ź ć

WZORY Z FIZYKI POZNANE W GIMNAZJUM

WZORY Z IZYKI POZNANE W GIMNAZJM. CięŜa ciała. g g g g atość cięŝau ciała N, aa ciała kg, g tały ółczyik zay zyiezeie zieki, N g 0 0 kg g. Gętość ubtacji. getoc aa objetoc ρ V Jedotką gętości kładzie SI

Ś Ę ź Ę Ą Ł Ż Ą ć Ł Ż ŁĄ Ł Ł Ż Ż ŁĄ Ś Ą ć Ś Ś Ó Ę ć ć ź ć Ś Ę ć ć Ę Ę Ę Ę ć Ę Ę Ę ć ć Ę ź Ę Ę Ę Ł Ł Ł Ę Ę Ó Ó Ń Ó Ę Ł Ę Ę Ł Ę Ę Ó Ż Ę Ę Ę Ó Ś Ż ź Ę ź ź Ę Ż Ś Ś Ś Ż ć ź Ę Ę Ę Ż Ą Ę Ś Ę Ę Ę ÓŁ Ę Ą ć Ę Ą

D.4 VHM. ATIGarryson. High-performance tools. Ready for action. Pilniki obrotowe z węglika spiekanego firmy Garryson. Allegheny Technologies

High-performane tool. Reay for ation. D.4 VHM Pilnii obrotowe z węglia pieanego firmy Garryon TIGarryon llegheny Tehnologie iepowleane p i l n i i o b r o t o w e z w ę g l i a p i e a n e g o niepowleane

KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH

Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź

Pole magnetyczne. 5.1 Oddziaływanie pola magnetycznego na ładunki. przewodniki z prądem. 5.1.1 Podstawowe zjawiska magnetyczne

Rozdział 5 Pole magnetyczne 5.1 Oddziaływanie pola magnetycznego na ładunki i pzewodniki z pądem 5.1.1 Podstawowe zjawiska magnetyczne W obecnym ozdziale ozpatzymy niektóe zagadnienia magnetostatyki. Magnetostatyką

Instrukcja do ćwiczeń laboratoryjnych. Sterowanie dławieniowe-równoległe prędkością ruchu odbiornika hydraulicznego

Intrukcja o ćwiczeń laboratoryjnych Sterowanie ławieniowe-równoległe rękością ruchu obiornika hyraulicznego Wtę teoretyczny Niniejza intrukcja oświęcona jet terowaniu ławieniowemu równoległemu jenemu ze

Wykład 9. Model ISLM: część I

Makoekonomia 1 Wykład 9 Model ISLM: część I Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Model ISLM Równowaga gaficzna Równowaga algebaiczna Skutki zmian paametów egzogenicznych

CHARAKTERYSTYKI UŻYTKOWE I WZORCOWANIE SZEROKOPASMOWYCH MIERNIKÓW NADFIOLETU

Jezy PIETRZYKOWSKI CHARAKTERYSTYKI UŻYTKOWE I WZORCOWANIE SZEROKOPASMOWYCH MIERNIKÓW NADFIOLETU STRESZCZENIE Okeślono haakteystyki użytkowe szeokopasmowyh mieników nadfioletu oaz ih klasyfikaję. Podano

TERMODYNAMIKA PROCESOWA. Wykład V

ERMODYNAMIKA PROCESOWA Wykład V Równania stanu substancji czystych Równanie stanu gazu doskonałego eoia stanów odpowiadających sobie Równania wiialne Pof. Antoni Kozioł, Wydział Chemiczny Politechniki

GEOMETRIA PŁASZCZYZNY

GEOMETRIA PŁASZCZYZNY. Oblicz pole tapezu ównoamiennego, któego podstawy mają długość cm i 0 cm, a pzekątne są do siebie postopadłe.. Dany jest kwadat ABCD. Punkty E i F są śodkami boków BC i CD. Wiedząc,

Arkusze maturalne poziom podstawowy

Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że

Wykład 15. Reinhard Kulessa 1

Wykład 5 9.8 Najpostsze obwody elektyczne A. Dzielnik napięcia. B. Mostek Wheatstone a C. Kompensacyjna metoda pomiau siły elektomotoycznej D. Posty układ C. Pąd elektyczny w cieczach. Dysocjacja elektolityczna.

Krystyna Gronostaj Maria Nowotny-Różańska Katedra Chemii i Fizyki, FIZYKA Uniwersytet Rolniczy do użytku wewnętrznego ĆWICZENIE 4

Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012

Optyka 2. Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego

Optka Projekt współinansowan przez Unię Europejską w ramach Europejskiego Funuszu Społecznego Optka II Promień świetln paając na powierzchnię zwierciała obija się zgonie z prawem obicia omówionm w poprzeniej

Siła. Zasady dynamiki

Siła. Zasady dynaiki Siła jest wielkością wektoową. Posiada okeśloną watość, kieunek i zwot. Jednostką siły jest niuton (N). 1N=1 k s 2 Pzedstawienie aficzne A Siła pzyłożona jest do ciała w punkcie A,

Zadanie 1. Zadanie 2. Sprawdzam dla objętości, że z obwarzanków mogę posklejać całą kulę o promieniu R: r = {x, y, z}; A = * Cross r, B

Zadanie In[]:= = {x, y, z}; In[]:= B = B, B, B3 ; (* Bi to wielkości stałe *) In[3]:= A = - * Coss, B Out[3]= -B3 y + B z, B3 x - B z, -B x + B y In[4]:= {x,y,z} -B3 y + B z, B3 x - B z, -B x + B y Out[4]=

Maria Dems. T. Koter, E. Jezierski, W. Paszek

Sany niesalone masyn synchonicnych Maia Dems. Koe, E. Jeieski, W. Pasek Zwacie aowe pąnicy synchonicnej San wacia salonego, wany akże waciem nomalnym lb pomiaowym yskje się pe wacie acisków wonika (j (sojana

Studia magisterskie ENERGETYKA. Jan A. Szantyr. Wybrane zagadnienia z mechaniki płynów. Ćwiczenia 2. Wyznaczanie reakcji hydrodynamicznych I

Studia magisteskie ENERGETYK Jan. Szanty Wybane zagadnienia z mehaniki płynów Ćwizenia Wyznazanie eakji hydodynamiznyh I Pzykład 1 Z dyszy o śedniah =80 [mm] i d=0 [mm] wypływa woda ze śednią pędkośią

WYZNACZANIE MODUŁU SPRĘŻYSTOŚCI PRZY POMOCY WAHADŁA TORSYJNEGO

Mehk WYZNACZANIE MOUŁU SPĘŻYSTOŚCI PZY POMOCY WAHAŁA TOSYJNEO. Ops teoetz o ćwze zeszzo jest stoe www.wt.wt.e.p w ze YAKTYKA FIZYKA ĆWICZENIA LABOATOYJNE.. Ops kł poowego Oekte ń jest pęt o łgoś śe któego

J. Szantyr Wykład 11 Równanie Naviera-Stokesa

J. Sant Wkład Równanie Naviea-Stokesa Podstawienie ależności wnikającch model łn Newtona do ównania achowania ęd daje ównanie nane jako ównanie Naviea-Stokesa. Geoge Stokes 89 903 Clade Navie 785-836 Naviea-Stokesa.

OSCYLATOR HARMONICZNY

OSCYLTOR HRMONICZNY Dgania swobone oscylaoa haonicznego negia oencjalna sęŝysości Dgania łuione oscylaoa haonicznego Dgania wyuszone oscylaoa haonicznego Rezonans aliuowy Rezonans ocy Doboć ukłau gającego

KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Chemia Poziom rozszerzony

KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Chemia Poziom ozszezony Listopad W niniejszym schemacie oceniania zadań otwatych są pezentowane pzykładowe popawne odpowiedzi. W tego typu ch należy

ź ć Ń Ę Ś Ę ź Ś Ę ć ŚĆ Ó ÓŁ Ł ć ź ź ź ź Ń ć Ę Ę ź ć ć ź ć ć Ł ć Ę Ń ć Ę Ę ć Ł ć ź ź ć ź ć ć ć ź ć ź ź Ó Ń Ó Ż ź ć Ó ź ź ć ź ź Ś ć ć ź ć ć Ę Ł ź ź Ę Ę Ę Ę Ń Ę Ł Ę Ń Ń Ń ź Ń Ń ź ź Ń Ł ź ź ź Ę ź ź Ę Ń Ń

Sterowanie prędkością silnika krokowego z zastosowaniem mikrokontrolera ATmega8

mg inż. ŁUKASZ BĄCZEK d hab. inż. ZYGFRYD GŁOWACZ pof. ndzw. w AGH Akademia Góniczo-Hutnicza Wydział Elektotechniki, Automatyki, Infomatyki i Elektoniki Kateda Mazyn Elektycznych Steowanie pędkością ilnika

16. Pole magnetyczne, indukcja. Wybór i opracowanie Marek Chmielewski

6. Poe magnetczne, nukcja Wbó opacowane Maek meewsk 6.. Znaeźć nukcje poa magnetcznego w oegłośc o neskończone ługego pzewonka wacowego o pomenu pzekoju popzecznego a w któm płne pą I. 6.. Wznaczć nukcję

METODA CIASNEGO (silnego) WIĄZANIA (TB)

MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi

11. 3.BRYŁY OBROTOWE. Walec bryła obrotowa powstała w wyniku obrotu prostokąta dokoła prostej zawierającej jeden z jego boków

..BRYŁY OBROTOWE Wae była obotowa powstała w wyniku obotu postokąta dokoła postej zawieająej jeden z jego boków pomień podstawy waa wysokość waa twoząa waa Pzekój osiowy waa postokąt o boka i Podstawa

Aerotriangulacja metodą niezaleŝnych wiązek

KP FC - aeo 27 Dwa zasanize etap pomiaow pomia wkonuje się na autogaie owm lub analitznm wkonuje się oientaję wewnętzną la kaŝego zjęia miez się współzęne tłowe otopunktów i punktów wiąŝąh oblizeniow blizenie

= ± Ne N - liczba całkowita.

POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9

8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI

8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,

NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek

Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa

Dobór zmiennych objaśniających do liniowego modelu ekonometrycznego

Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość

Wyznaczanie współczynnika wnikania ciepła dla konwekcji swobodnej

Kateda Silników Salinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie wsółczynnika wnikania cieła dla konwekcji swobodnej - - Pojęcia odstawowe Konwekcja- zjawisko wymiany cieła między owiezchnią

5.1 Połączenia gwintowe

5.0 Połączenia Połączenia służą o pzenoszenia obciążeń mięzy elementami konstukcyjnymi uniemożliwiając ich wzajemne pzemieszczenia. POŁĄCZENIA NIEROZŁĄCZNE ROZŁĄCZNE PLASTYCZNE - nitowe - zawijane - zaginane

Zrobotyzowany system docierania powierzchni płaskich z zastosowaniem plików CL Data

MECHANIK NR 8-9/2015 25 Zobotyzowany system docieania powiezcni płaskic z zastosowaniem plików CL Data Robotic system fo flat sufaces lapping using CLData ADAM BARYLSKI NORBERT PIOTROWSKI * DOI: 10.17814/mecanik.2015.8-9.335