Algorytm określania symetrii czasteczek
|
|
|
- Kamila Janiszewska
- 8 lat temu
- Przeglądów:
Transkrypt
1 O czym to b Podzi 21 września 2007
2 O czym to b O czym to b Podzi 1 2 3
3 O czym to b Podzi W lasności symetrii hamiltonianu: zmniejszenie z lożoności obliczeń i wymagań pami eciowych, utrzymanie tożsamościowych (wynikajacych z symetrii) relacji, u latwienie interpretacji obliczeń.
4 O czym to b Podzi Czasteczka a Jakie informacje bed a nam potrzebne? grupa punktowa, wspó lrz edne po symetryzacji, transformacja z orientacji wejściowej (wspó lrz edne podane przez użytkownika) do standardowej (wyznaczonej przez program).
5 O czym to b Podzi Ustawienie wst epne Czasteczka a Jeśli liczba atomów == 1, to obliczenia atomowe (K h ). Wyznacz środek masy i umieść go w OXYZ. Wyznacz g lówne osie tensora momentu bezw ladności.
6 O czym to b Podzi Czasteczka a Wartości w lasne momentu bezw ladności 3 równe: bak, 2 równe: wszystkie niezerowe: bak, przynajmniej jedna zerowa: czasteczka, 3 różne wartości w lasne: bak a.
7 Czasteczka O czym to b Podzi Czasteczka a Ustaw oś odpowiadajac a momentowi == 0 równolegle do osi Z, Jeśli czasteczka i jej odbicie wzgledem p laszczyzny OZ (czyli XY) sa takie same, to D h, wpp C v.
8 a O czym to b Podzi Czasteczka a Zorientuj osie momentu bezw ladności zgodnie z osiami OXYZ, Sprawdź, które osie sa osiami dwukrotnymi (moga być 3, 1, lub brak),
9 O czym to b Podzi Czasteczka a a (3 osie dwukrotne) Jeśli wszystkie osie X, Y i Z sa osiami dwukrotnymi, to D 2 lub D 2h jeśli oprócz osi C 2 jest dodatkowo środek inwersji, a C 2 oraz i generuja p laszczyzne symetrii prostopad l a do OZ, to jest D 2h, wpp jest D 2.
10 O czym to b Podzi a (1 oś dwukrotna) Czasteczka a Jeśli jest 1 oś dwukrotna (pokrywajaca sie z OX, OY lub OZ), to ustaw ja do OZ. Może być C 2h, C 2v lub C 2 jeśli jest p laszczyzna symetrii, to C 2h wpp, jeśli jest p laszczyzna osi Z, to grupa C 2v, wpp. grupa C 2.
11 O czym to b Podzi Czasteczka a a (brak osi dwukrotnych) Jeśli nie ma osi dwukrotnych, to C s, C i lub C 1. jeśli jest p laszczyzna symetrii, to jest C s, a p laszczyzna symetrii ma być p laszczyzna XY. jeśli jest środek inwersji, to grupa C i, wpp. grupa C 1.
12 O czym to b Podzi Czasteczka a Trójkrotna degeneracja bak. Możliwe sa grupy: kubiczne T, T d, T h, O, O h, I lub I h, oraz D 2d, D 2h lub D 2. Może sie zdarzyć, że bak jest przypadkowo. Jeśli sa 3 prostopad le 2-krotne osie, to grupy: D 2d, D 2h lub D 2, wpp przypadek najtrudniejszy (omówiony przy okazji baka symetrycznego).
13 O czym to b Podzi Czasteczka a : Ustalenie orientacji standardowej 1 Znajdź oś g lówna, 2 ustaw czasteczk e tak, aby oś g lówna by la OZ, 3 znajdź g lówna p laszczyzne, czyli p laszczyzne symetrii zawierajac a oś g lówna, 4 obróć czasteczk e, aby g lówna p laszczyzna by la p laszczyzna XZ (czyli OY),
14 O czym to b Podzi Czasteczka a : Pozosta le elementy symetrii po pierwsze znajdź osie C 2, znajdź p laszczyzny (korzystajac z wygenerowanych par) sprawdź, czy p laszczyzna zawiera OXYZ (tanie) jeśli tak, to sprawdź, czy jest to p laszczyzna symetrii teraz sprawdź osie C 6,..., C 3, S 6 (= C 6 ),..., S 2 (= C 2 = i),
15 O czym to b Podzi Czasteczka a 1 Dwie wartości w lasne momentu ladunku sa równe i różne od trzeciej (bak ): może być dowolna grupa aksjalna, czyli każda oprócz kubicznych. 2 Z wyjatkiem rzadkich przypadków, jedyna osia jest oś o krotności >= 3 (pokrywajaca sie z niezdegenerowana osia tensora momentu bezw ladności).
16 O czym to b Podzi Czasteczka a : orientacja osi g lównej 1 Ustaw niezdegenerowana oś OZ (g lówna oś), 2 określ jej krotność, czyli dla n (8, 7, 6, 5, 4, 3, 2) rób: jeśli geometria obrócona o 2π/n jest równoważna danej, to dopisz oś C n do zbioru osi, jeśli geometria obrócona o 2π/2n i odbita w p laszczyźnie do osi jest równoważna danej, to dopisz oś S 2n do zbioru osi, jeśli geometria obrócona o 2π/n i odbita w p laszczyźnie do osi jest równoważna danej, to dopisz oś S n do zbioru osi.
17 O czym to b Podzi Czasteczka a : orientacja pozosta lych elementów symetrii 1 Poszukaj ewentualnej osi C 2 OZ (bierzemy pierwsza znaleziona). 2 Jeśli jest, to zorientuj ja osi OX. Orientacja standardowa jest osiagni eta. pozostaje znaleźć pozosta le osie C 2 wraz z S 4 oraz p laszczyzny (σ v lub/i σ h ) i środek inwersji. 3 wpp, poszukaj σ v. Jeśli istnieje, to ustaw ja w p laszczyźnie XZ. wpp, poszukaj σ h. Jeśli istnieje, to ustaw ja w p laszczyźnie XY.
18 O czym to b Podzi Czasteczka a : określanie pozosta lych elementów symetrii 1 Teraz czasteczka znajduje sie w orientacji standardowej (zarówno przy obecności jak i nieobecności osi C 2 ). Jeszcze raz wyznacz osie C 2 i p laszczyzny. 2 Jeśli czasteczka jest p laska, to dodaj p laszczyzne symetrii do zbioru, 3 Sprawdź istnienie środka symetrii.
19 O czym to b Podzi Czasteczka a i symetryzacja 1 Majac wyznaczone elementy symetrii przeglada sie tablice zawierajac a elementy symetrii każdej grupy jeśli któraś grupa pasuje, to BINGO! wpp, znajdź grupe, która ma najwiecej elementów spośród znalezionych; wypisz ostrzeżenie, gdyż możliwe, że po niewielkiej zmianie kryterium ε zostanie znaleziona wyższa grupa symetrii. Zmiana kryterium należy do użytkownika.
20 Symetryzacja O czym to b Podzi Czasteczka a 1 Stwórz liste flag odpowiadajac a liście atomów, a nastepnie dla każdego atomu rób: Sprawdź, czy po zastosowaniu kolejno wszystkich znalezionych elementów symetrii któryś inny atom jest do niego równoważny. jeśli tak, to ustaw flage odpowiadajac a temu równoważnemu atomowi. 2 Teraz atomy, dla których flaga nie zosta la ustawiona, sa nierównoważne przez symetrie.
21 Symetryzacja O czym to b Podzi Czasteczka a 1 Weź list e nierównoważnych atomów oraz list e dok ladnych elementów symetrii. 2 Dla każdego atomu rób: dla każdego elementu symetrii zastosuj ten element do wspó lrz ednych atomu. jeśli nie ma atomu o takich (nowych) wspó lrz ednych, to dodaj ten atom (wspó lrz edne). 3 Teraz lista zawiera symetryzowane wspó lrz edne atomów.
22 Czynności końcowe O czym to b Podzi Czasteczka a Ponieważ każda operacja symetrii jest rejestrowana, to można latwo wyznaczyć macierz transformacji z orientacji wejściowej do orientacji standardowej.
23 O czym to b Podzi Algorytm znajdywania osi C 2 i p laszczyzn symetrii Algorytm znajdywania osi C n i S n (n > 2) Algorytm obrotu wzgledem dowolnej osi o dowolny kat Algorytm znajdywania osi C 2 i p laszczyzn symetrii 1 Dla i = 1,... liczba atomów rób: Dla j = i + 1,... liczba atomów rób: weź atom i ty i j ty. Znajdź v środek odcinka ij. Jeśli odleg lość v od OXYZ (czyli v ) jest > ε, to znormalizuj v. wpp v = i, znormalizuj v. obróć wspó lrzedne wokó l v o kat π. Jeśli wspó lrzedne sie pokrywaja, to dodaj oś C 2 do zbioru, obróć wspó lrzedne wokó l v o kat π/2 oraz odbij w p laszczyźnie do v. Jeśli wspó lrzedne sie pokrywaja, to dodaj oś S 4 do zbioru. P laszczyzny P: dla n P, v P równanie p laszczyzny P = (n 1, n 2, n 3): D = n v. D < ε P OXYZ. Jeśli p laszczyzna jest p laszczyzna symetrii, to dopisz ja do puli. Dla k = j + 1,... liczba atomów weź atom i, j, k i zastosuj algorytm znajdywania osi C n i S n (n > 2) (nastepna plansza). 2 Sprawdź wystepowanie środka symetrii.
24 O czym to b Podzi Algorytm znajdywania osi C 2 i p laszczyzn symetrii Algorytm znajdywania osi C n i S n (n > 2) Algorytm obrotu wzgledem dowolnej osi o dowolny kat Algorytm znajdywania osi C n i S n (n > 2) 1 Sprawdź, czy trójka jest wpó l. Jeśli tak, to weź nastepn a, wpp: oblicz wspó lczynniki p laszczyzny zawierajacej te trójke, a stad wektor normalny, przechodzacy przez OXYZ. Sprawdź, czy to jest oś C n lub S n. Jeśli znaleziono oś, to dopisz ja do zbioru.
25 O czym to b Podzi Algorytm znajdywania osi C 2 i p laszczyzn symetrii Algorytm znajdywania osi C n i S n (n > 2) Algorytm obrotu wzgledem dowolnej osi o dowolny kat Algorytm obrotu wzgledem dowolnej osi o dowolny kat 1 unormuj oś 2 oblicz ( kwaternion: cos(k at/2), sin(kat/2) oś[1], sin(kat/2) oś[2], sin(kat/2) oś[3] ) 3 znormalizuj kwaternion 4 W = kwaternion[0]; X = kwaternion[1]; Y = kwaternion[2]; Z = kwaternion[3] macierz obrotu: mat = 1 2(Y 2 + Z 2 ) 2(XY ZW ) 2(XZ + YW ) 2(XY + ZW ) 1 2(X 2 + Z 2 ) 2(YZ XW ) 2(XZ YW ) 2(YZ + XW ) 1 2(X 2 + Y 2 )
26 O czym to b Podzi Dzi ekuj e za uwag e i zapraszam do dyskusji.
Symetria w obliczeniach molekularnych
 Zak lad Metod Obliczeniowych Chemii UJ 15 marca 2005 1 2 Możliwości przyspieszenia obliczeń 3 GAMESS 2004 4 Zastosowania symetrii Zmniejszenie zapotrzebowania na zasoby (procesor, pami eć, dysk) Utrzymanie
Zak lad Metod Obliczeniowych Chemii UJ 15 marca 2005 1 2 Możliwości przyspieszenia obliczeń 3 GAMESS 2004 4 Zastosowania symetrii Zmniejszenie zapotrzebowania na zasoby (procesor, pami eć, dysk) Utrzymanie
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3
 WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
Rotacje i drgania czasteczek
 Rotacje i drgania czasteczek wieloatomowych Gdy znamy powierzchnie energii potencjalnej V( R 1, R 2,..., R N ) to możemy obliczyć poziomy energetyczne czasteczki. Poziomy te sa w ogólności efektem: rotacji
Rotacje i drgania czasteczek wieloatomowych Gdy znamy powierzchnie energii potencjalnej V( R 1, R 2,..., R N ) to możemy obliczyć poziomy energetyczne czasteczki. Poziomy te sa w ogólności efektem: rotacji
ELEMENTY I OPERACJE SYMETRII Symbol Element symetrii Operacja symetrii
 ELEMENTY I OPERACJE SYMETRII Symbol Element symetrii Operacja symetrii C n oś symetrii n-krotna (oś główna - oś o obrót wokół osi symetrii o kąt równy 360 0 /n najwyższej krotności) σ płaszczyzna symetrii
ELEMENTY I OPERACJE SYMETRII Symbol Element symetrii Operacja symetrii C n oś symetrii n-krotna (oś główna - oś o obrót wokół osi symetrii o kąt równy 360 0 /n najwyższej krotności) σ płaszczyzna symetrii
Struktura elektronowa czasteczek. przybliżenie Borna-Oppenheimera. równania Schrödingera dla elektronów przy ustalonym po lożeniu jader
 Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Indeks odwzorowania zmiennej zespolonej wzgl. krzywej zamknietej
 Indeks odwzorowania zmiennej zespolonej wzgl edem krzywej zamkni etej 1. Liczby zespolone - konstrukcja Hamiltona 2. Homotopia odwzorowań na okr egu 3. Indeks odwzorowania ciag lego wzgledem krzywej zamknietej
Indeks odwzorowania zmiennej zespolonej wzgl edem krzywej zamkni etej 1. Liczby zespolone - konstrukcja Hamiltona 2. Homotopia odwzorowań na okr egu 3. Indeks odwzorowania ciag lego wzgledem krzywej zamknietej
Matematyka A, klasówka, 24 maja zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le. rozwia
 Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
i elektronów w czasteczkach (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra 2M b a i b; m -masa elektronu e 2 r ij
 Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
Prosta i płaszczyzna w przestrzeni
 Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
Arkusz 6. Elementy geometrii analitycznej w przestrzeni
 Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Funkcje wielu zmiennych
 Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Uklady modelowe III - rotator, atom wodoru
 Wyk lad 5 Uklady modelowe III - rotator, atom wodoru Model Separacja ruchu środka masy R = m 1r 1 + m 2 r 2 m 1 + m 2 Ĥ = Ĥ tr (R) + Ĥ rot (r) Ĥ tr 2 (R) = 2(m 1 + m 2 ) R [ Ψ E tr (R; t) = exp i (k R
Wyk lad 5 Uklady modelowe III - rotator, atom wodoru Model Separacja ruchu środka masy R = m 1r 1 + m 2 r 2 m 1 + m 2 Ĥ = Ĥ tr (R) + Ĥ rot (r) Ĥ tr 2 (R) = 2(m 1 + m 2 ) R [ Ψ E tr (R; t) = exp i (k R
WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych
 WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych Prof. dr hab. Halina Abramczyk Dr inż. Beata Brożek-Płuska POLITECHNIKA ŁÓDZKA Wydział Chemiczny, Instytut Techniki Radiacyjnej Laboratorium
WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych Prof. dr hab. Halina Abramczyk Dr inż. Beata Brożek-Płuska POLITECHNIKA ŁÓDZKA Wydział Chemiczny, Instytut Techniki Radiacyjnej Laboratorium
Zastosowanie Robotów. Ćwiczenie 6. Mariusz Janusz-Bielecki. laboratorium
 Zastosowanie Robotów laboratorium Ćwiczenie 6 Mariusz Janusz-Bielecki Zak lad Informatyki i Robotyki Wersja 0.002.01, 7 Listopada, 2005 Wst ep Do zadań inżynierów robotyków należa wszelkie dzia lania
Zastosowanie Robotów laboratorium Ćwiczenie 6 Mariusz Janusz-Bielecki Zak lad Informatyki i Robotyki Wersja 0.002.01, 7 Listopada, 2005 Wst ep Do zadań inżynierów robotyków należa wszelkie dzia lania
Wyk lad 8 macierzy i twierdzenie Kroneckera-Capellego
 Wyk lad 8 Rzad macierzy i twierdzenie Kroneckera-Capellego 1 Określenie rz edu macierzy Niech A bedzie m n - macierza Wówczas wiersze macierzy A możemy w naturalny sposób traktować jako wektory przestrzeni
Wyk lad 8 Rzad macierzy i twierdzenie Kroneckera-Capellego 1 Określenie rz edu macierzy Niech A bedzie m n - macierza Wówczas wiersze macierzy A możemy w naturalny sposób traktować jako wektory przestrzeni
JEDNOSTKI ATOMOWE =1, m e =1, e=1, ; 1 E 2 h = 4, J. Energia atomu wodoru lub jonu wodoropodobnego w jednostkach atomowych:
 do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
Uk lady modelowe II - oscylator
 Wyk lad 4 Uk lady modelowe II - oscylator Model Prawo Hooke a F = m d 2 x = kx = dv dt2 dx Potencja l Równanie ruchu V = 1 2 kx2 d 2 x dt 2 + k m x = 0 Obraz klasyczny Rozwiazania k x = A sin t = A sin
Wyk lad 4 Uk lady modelowe II - oscylator Model Prawo Hooke a F = m d 2 x = kx = dv dt2 dx Potencja l Równanie ruchu V = 1 2 kx2 d 2 x dt 2 + k m x = 0 Obraz klasyczny Rozwiazania k x = A sin t = A sin
Elementy symetrii makroskopowej.
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Elementy symetrii makroskopowej. 2 godz. Cel ćwiczenia: zapoznanie się z działaniem elementów symetrii makroskopowej
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Elementy symetrii makroskopowej. 2 godz. Cel ćwiczenia: zapoznanie się z działaniem elementów symetrii makroskopowej
Wykład 5. Komórka elementarna. Sieci Bravais go
 Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
Wyk lad 7 Baza i wymiar przestrzeni liniowej
 Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
x a 1, podając założenia, przy jakich jest ono wykonywalne. x a 1 = x a 2 ( a 1) = x 1 = 1 x.
 Zestaw. Funkcja potęgowa, wykładnicza i logarytmiczna. Elementarne równania i nierówności. Przykład 1. Wykonać działanie x a x a 1, podając założenia, przy jakich jest ono wykonywalne. Rozwiązanie. Niech
Zestaw. Funkcja potęgowa, wykładnicza i logarytmiczna. Elementarne równania i nierówności. Przykład 1. Wykonać działanie x a x a 1, podając założenia, przy jakich jest ono wykonywalne. Rozwiązanie. Niech
Sterowalność liniowych uk ladów sterowania
 Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Funkcje wielu zmiennych
 Funkcje wielu zmiennych 13 Zbiory w przestrzeni Definicja Przestrzeni a trójwymiarow a (przestrzeni a) nazywamy zbiór wszystkich trójek uporz adkowanych (x y z) gdzie x y z R. Przestrzeń tȩ oznaczamy symbolem
Funkcje wielu zmiennych 13 Zbiory w przestrzeni Definicja Przestrzeni a trójwymiarow a (przestrzeni a) nazywamy zbiór wszystkich trójek uporz adkowanych (x y z) gdzie x y z R. Przestrzeń tȩ oznaczamy symbolem
Iloczyn wektorowy. Autorzy: Michał Góra
 Iloczyn wektorowy Autorzy: Michał Góra 019 Iloczyn wektorowy Autor: Michał Góra DEFINICJA Definicja 1: Iloczyn wektorowy Iloczynem wektorowym wektorów v = ( v x, v y, v z ) R 3 oraz w = ( w x, w y, w z
Iloczyn wektorowy Autorzy: Michał Góra 019 Iloczyn wektorowy Autor: Michał Góra DEFINICJA Definicja 1: Iloczyn wektorowy Iloczynem wektorowym wektorów v = ( v x, v y, v z ) R 3 oraz w = ( w x, w y, w z
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Geometria analityczna
 Wydział Matematyki Stosowanej Zestaw zadań nr 10 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus maja 018r. 1 Działania na wektorach Zadanie 1. Oblicz długość wektorów: Geometria
Wydział Matematyki Stosowanej Zestaw zadań nr 10 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus maja 018r. 1 Działania na wektorach Zadanie 1. Oblicz długość wektorów: Geometria
Geometria analityczna
 Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Wykład 1. Symetria Budowy Kryształów
 Wykład Symetria Budowy Kryształów Ciała krystaliczne i amorficzne Każda substancja ciekła (z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe. Jednakże proces
Wykład Symetria Budowy Kryształów Ciała krystaliczne i amorficzne Każda substancja ciekła (z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe. Jednakże proces
Przekształcenia geometryczne w grafice komputerowej. Marek Badura
 Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Elementy geometrii analitycznej w R 3
 Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Elementy symetrii. obiekt geometryczny taki jak linia, płaszczyzna lub punkt, względem którego dokonuje się operacji symetrii.
 ELEMENTY SYMETRII Element symetrii obiekt geometryczny taki jak linia, płaszczyzna lub punkt, względem którego dokonuje się operacji symetrii. ELEMENTY SYMETRII Elementy symetrii PŁASZZYZNA peracje symetrii
ELEMENTY SYMETRII Element symetrii obiekt geometryczny taki jak linia, płaszczyzna lub punkt, względem którego dokonuje się operacji symetrii. ELEMENTY SYMETRII Elementy symetrii PŁASZZYZNA peracje symetrii
Chemiateoretyczna. Monika Musiał. Elementy teorii grup
 Chemiateoretyczna Monika Musiał Elementy teorii grup Grup a G nazywamy zbiór elementów {A,B,C,...} o nastȩpuja cych własnościach: zdefiniowane jest działanie przyporza dkowuja ce każdej parze elementów
Chemiateoretyczna Monika Musiał Elementy teorii grup Grup a G nazywamy zbiór elementów {A,B,C,...} o nastȩpuja cych własnościach: zdefiniowane jest działanie przyporza dkowuja ce każdej parze elementów
c) prawdopodobieństwo znalezienia cząstki między x=1.0 a x=1.5 jest równe
 TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
3. Operacje symetrii, macierze operacji symetrii. Grupy punktowe. Przypisywanie grupy punktowej dla zadanych obiektów
 3. Operacje symetrii, macierze operacji symetrii. Grupy punktowe. Przypisywanie grupy punktowej dla zadanych obiektów Opracowanie: dr hab. inż. Jarosław Chojnacki, Politechnika Gdańska, Gdańsk 207 Każda
3. Operacje symetrii, macierze operacji symetrii. Grupy punktowe. Przypisywanie grupy punktowej dla zadanych obiektów Opracowanie: dr hab. inż. Jarosław Chojnacki, Politechnika Gdańska, Gdańsk 207 Każda
Wyk lad 7 Metoda eliminacji Gaussa. Wzory Cramera
 Wyk lad 7 Metoda eliminacji Gaussa Wzory Cramera Metoda eliminacji Gaussa Metoda eliminacji Gaussa polega na znalezieniu dla danego uk ladu a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
Wyk lad 7 Metoda eliminacji Gaussa Wzory Cramera Metoda eliminacji Gaussa Metoda eliminacji Gaussa polega na znalezieniu dla danego uk ladu a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Symetria w fizyce materii
 Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
Symbol termu: edu (sumy ca lkowitego orbitalnego momentu edu i ca lkowitego spinu) Przyk lad: 2 P 3. kwantowa
 Notatki do wyk ladu VI (z 18.11.2013) Symbol termu: 2S+1 L (1) L -liczba kwantowa ca lkowitego orbitalnego momentu pedu Duże litery S, P, D, F, itd. dla L=0, 1, 2, 3, itd. 2S+1 - multipletowość; S - liczba
Notatki do wyk ladu VI (z 18.11.2013) Symbol termu: 2S+1 L (1) L -liczba kwantowa ca lkowitego orbitalnego momentu pedu Duże litery S, P, D, F, itd. dla L=0, 1, 2, 3, itd. 2S+1 - multipletowość; S - liczba
1) 2) 3) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25)
 1) Wykresem funkcji kwadratowej f jest parabola o wierzchołku w początku układu współrzędnych i przechodząca przez punkt. Wobec tego funkcja f określona wzorem 2) Punkt należy do paraboli o równaniu. Wobec
1) Wykresem funkcji kwadratowej f jest parabola o wierzchołku w początku układu współrzędnych i przechodząca przez punkt. Wobec tego funkcja f określona wzorem 2) Punkt należy do paraboli o równaniu. Wobec
c ze wzoru dwumianowego Newtona obliczyć sumy: a) 3 2 obliczyć wartości wyrazów będa cych liczbami ca lkowitymi,
 3 Korzystaja c ze wzoru dwumianowego Newtona obliczyć sumy: a) n ( n n k) ; b) 4 W rozwinie ciu dwumianowym: ( 4 a) ) 1, 3 2 obliczyć wartości wyrazów będa cych liczbami ca lkowitymi, ( ) b) 3 13, 5 +
3 Korzystaja c ze wzoru dwumianowego Newtona obliczyć sumy: a) n ( n n k) ; b) 4 W rozwinie ciu dwumianowym: ( 4 a) ) 1, 3 2 obliczyć wartości wyrazów będa cych liczbami ca lkowitymi, ( ) b) 3 13, 5 +
Zadania z z matematyki dla studentów gospodarki przestrzennej UŠ. Marek Majewski Aktualizacja: 31 pa¹dziernika 2006
 Zadania z z matematyki dla studentów gospodarki przestrzennej UŠ Marek Majewski Aktualizacja: 1 pa¹dziernika 006 Spis tre±ci 1 Macierze dziaªania na macierzach. Wyznaczniki 1 Macierz odwrotna. Rz d macierzy
Zadania z z matematyki dla studentów gospodarki przestrzennej UŠ Marek Majewski Aktualizacja: 1 pa¹dziernika 006 Spis tre±ci 1 Macierze dziaªania na macierzach. Wyznaczniki 1 Macierz odwrotna. Rz d macierzy
Przekształcenia liniowe
 ALGEBRA LINIOWA 2 Wydział Mechaniczny / AIR, MTR Semestr letni 2009/2010 Prowadzący: dr Teresa Jurlewicz Przekształcenia liniowe Uwaga. W nawiasach kwadratowych podane są numery zadań znajdujących się
ALGEBRA LINIOWA 2 Wydział Mechaniczny / AIR, MTR Semestr letni 2009/2010 Prowadzący: dr Teresa Jurlewicz Przekształcenia liniowe Uwaga. W nawiasach kwadratowych podane są numery zadań znajdujących się
Geometria odwzorowań inżynierskich rzut środkowy 06A
 Scriptiones Geometrica Volumen I (2014), No. 6A, 1 10. Geometria odwzorowań inżynierskich rzut środkowy 06A Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Rzut środkowy i jego niezmienniki Przyjmijmy
Scriptiones Geometrica Volumen I (2014), No. 6A, 1 10. Geometria odwzorowań inżynierskich rzut środkowy 06A Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Rzut środkowy i jego niezmienniki Przyjmijmy
Wyk lad 11 1 Wektory i wartości w lasne
 Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Oddzia lywania miedzycz. jony molekularne lub atomy. edzy A i B:
 Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
Geometria odwzorowań inżynierskich. 1. Perspektywa odbić w zwierciad lach p laskich 06F
 Scriptiones Geometrica Volumen I (2014), No. 6F, 1 10. Geometria odwzorowań inżynierskich Perspektywa odbić w zwierciad lach p laskich 06F Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Perspektywa
Scriptiones Geometrica Volumen I (2014), No. 6F, 1 10. Geometria odwzorowań inżynierskich Perspektywa odbić w zwierciad lach p laskich 06F Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Perspektywa
Arkusz 4. Elementy geometrii analitycznej w przestrzeni
 Arkusz 4. Elementy geometrii analitycznej w przestrzeni Zadanie 4.1. Obliczy dªugo±ci podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Arkusz 4. Elementy geometrii analitycznej w przestrzeni Zadanie 4.1. Obliczy dªugo±ci podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
MiNI Akademia Matematyki na Politechnice Warszawskiej
 MiNI Akademia Matematyki na Politechnice Warszawskiej Krzysztof Che lmiński Okr egi i styczne MiNI PW, 14.10.2017 Podstawowe twierdzenia wykorzystywane w zadaniach z ćwiczeń Twierdzenie 1 (najmocniesze
MiNI Akademia Matematyki na Politechnice Warszawskiej Krzysztof Che lmiński Okr egi i styczne MiNI PW, 14.10.2017 Podstawowe twierdzenia wykorzystywane w zadaniach z ćwiczeń Twierdzenie 1 (najmocniesze
1. Elementy (abstrakcyjnej) teorii grup
 1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
Matematyka A, egzamin, 17 czerwca 2005 rozwia zania
 Matematyka A, egzamin, 7 czerwca 00 rozwia zania Mam nadzieje, że nie ma tu b le dów poza jakimiś literówkami, od których uwolnić sie trudno. Zache cam do obejrzenia rozwia zań zadań z egzaminu dla matematyki
Matematyka A, egzamin, 7 czerwca 00 rozwia zania Mam nadzieje, że nie ma tu b le dów poza jakimiś literówkami, od których uwolnić sie trudno. Zache cam do obejrzenia rozwia zań zadań z egzaminu dla matematyki
Krystalochemia białek 2016/2017
 Zestaw zadań 4. Grupy punktowe. Składanie elementów symetrii. Translacyjne elementy symetrii grupy punktowe, składanie elementów symetrii, translacyjne elementy symetrii: osie śrubowe, płaszczyzny ślizgowe
Zestaw zadań 4. Grupy punktowe. Składanie elementów symetrii. Translacyjne elementy symetrii grupy punktowe, składanie elementów symetrii, translacyjne elementy symetrii: osie śrubowe, płaszczyzny ślizgowe
stosunek przyrostu funkcji y do odpowiadajacego dy dx = lim y wielkości fizycznej x, y = f(x), to pochodna dy v = ds edkości wzgl edem czasu, a = dv
 Matematyka Pochodna Pochodna funkcji y = f(x) w punkcie x nazywamy granice, do której daży stosunek przyrostu funkcji y do odpowiadajacego mu przyrostu zmiennej niezaleźnej x, g przyrost zmiennej daży
Matematyka Pochodna Pochodna funkcji y = f(x) w punkcie x nazywamy granice, do której daży stosunek przyrostu funkcji y do odpowiadajacego mu przyrostu zmiennej niezaleźnej x, g przyrost zmiennej daży
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Czastka swobodna Bariera potencja lu Pud lo jednowymiarowe FEMO Pud la wielowymiarowe. Wyk lad 3. Uk lady modelowe I
 Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Pisemny egzamin dyplomowy. na Uniwersytecie Wroc lawskim. na kierunku matematyka. zadania testowe. 22czerwca2009r. 60 HS-8-8
 EGZAMIN DYPLOMOWY, cze ść I (testowa) 22.06.2009 INSTRUKCJE DOTYCZA CE WYPE LNIANIA TESTU 1. Nie wolno korzystać z kalkulatorów. 2. Sprawdzić, czy wersja testu podana na treści zadań jest zgodna z wersja
EGZAMIN DYPLOMOWY, cze ść I (testowa) 22.06.2009 INSTRUKCJE DOTYCZA CE WYPE LNIANIA TESTU 1. Nie wolno korzystać z kalkulatorów. 2. Sprawdzić, czy wersja testu podana na treści zadań jest zgodna z wersja
Pojȩcie przestrzeni metrycznej
 ROZDZIA l 1 Pojȩcie przestrzeni metrycznej Definicja 1.1. Dowolny niepusty zbiór X z funkcja ρ : X X [0, ), spe lniaja ca naste puja ce trzy warunki M1: ρ(x, y) = 0 x = y, M2: ρ(x, y) = ρ(y, x), M3: ρ(x,
ROZDZIA l 1 Pojȩcie przestrzeni metrycznej Definicja 1.1. Dowolny niepusty zbiór X z funkcja ρ : X X [0, ), spe lniaja ca naste puja ce trzy warunki M1: ρ(x, y) = 0 x = y, M2: ρ(x, y) = ρ(y, x), M3: ρ(x,
Po lożenie punktu w przestrzenie w chwili czasowej t może być opisane jako wektor x(t), reprezentujacy
 1. Bry la sztywna Symulacja komputerowa ruchu bry ly sztywnej jest ważnym zagadnieniem podczas modelowania i weryfikacji różnych systemów fizycznych. Mówiac bry la sztywna, mamy na myśli bry l e, która
1. Bry la sztywna Symulacja komputerowa ruchu bry ly sztywnej jest ważnym zagadnieniem podczas modelowania i weryfikacji różnych systemów fizycznych. Mówiac bry la sztywna, mamy na myśli bry l e, która
Wyk lad 3 Wyznaczniki
 1 Określenie wyznacznika Wyk lad 3 Wyznaczniki Niech A bedzie macierza kwadratowa stopnia n > 1 i niech i, j bed a liczbami naturalnymi n Symbolem A ij oznaczać bedziemy macierz kwadratowa stopnia n 1
1 Określenie wyznacznika Wyk lad 3 Wyznaczniki Niech A bedzie macierza kwadratowa stopnia n > 1 i niech i, j bed a liczbami naturalnymi n Symbolem A ij oznaczać bedziemy macierz kwadratowa stopnia n 1
edzi (local edge detectors) Lokalne operatory wykrywania kraw
 Lokalne operatory wykrywania kraw edzi (local edge detectors) Jeśli dwie reprezentacje sa zbyt odleg le, by można by lo latwo określić transformacje miedzy nimi, to u latwić zadanie można przez wprowadzenie
Lokalne operatory wykrywania kraw edzi (local edge detectors) Jeśli dwie reprezentacje sa zbyt odleg le, by można by lo latwo określić transformacje miedzy nimi, to u latwić zadanie można przez wprowadzenie
Statystyka w analizie i planowaniu eksperymentu
 29 marca 2011 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
29 marca 2011 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
Statystyka w analizie i planowaniu eksperymentu
 31 marca 2014 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
31 marca 2014 Przestrzeń statystyczna - podstawowe zadania statystyki Zdarzeniom losowym określonym na pewnej przestrzeni zdarzeń elementarnych Ω można zazwyczaj na wiele różnych sposobów przypisać jakieś
KURS FUNKCJE. LEKCJA 2 PODSTAWOWA Przekształcenia wykresu funkcji ZADANIE DOMOWE. Strona 1
 KURS FUNKCJE LEKCJA PODSTAWOWA Przekształcenia wykresu unkcji ZADANIE DOMOWE www.etrapez.pl Strona Część : TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie Wykres unkcji ( x) q otrzymujemy
KURS FUNKCJE LEKCJA PODSTAWOWA Przekształcenia wykresu unkcji ZADANIE DOMOWE www.etrapez.pl Strona Część : TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie Wykres unkcji ( x) q otrzymujemy
po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x)
 Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
cie uk ladu równań liniowych i podaliśmy sposoby rozwia
 8. UK LADY RÓWNAŃ LINIOWYCH. DIAGONALIZACJA MACIERZY. W porzednim paragrafie zdefiniowaliśmy poje cie uk ladu równań liniowych i podaliśmy sposoby rozwia zania go, w przypadku, gdy uk lad jest uk ladem
8. UK LADY RÓWNAŃ LINIOWYCH. DIAGONALIZACJA MACIERZY. W porzednim paragrafie zdefiniowaliśmy poje cie uk ladu równań liniowych i podaliśmy sposoby rozwia zania go, w przypadku, gdy uk lad jest uk ladem
SZKO LA PODSTAWOWA HELIANTUS WARSZAWA ul. BAŻANCIA 16. Szeṡcian w uk ladzie wspȯ lrzȩdnych x, y, z GEOMETRIA PRZESTRZENNA STEREOMETRIA
 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 z y 0 x Szeṡcian w uk ladzie wspȯ lrzȩdnych x, y, z GEOMETRIA PRZESTRZENNA STEREOMETRIA Prof. dr. Tadeusz STYŠ Warszawa 2018 1 1 Projekt trzynasty
SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 z y 0 x Szeṡcian w uk ladzie wspȯ lrzȩdnych x, y, z GEOMETRIA PRZESTRZENNA STEREOMETRIA Prof. dr. Tadeusz STYŠ Warszawa 2018 1 1 Projekt trzynasty
Zajęcia nr 1 (1h) Dwumian Newtona. Indukcja. Zajęcia nr 2 i 3 (4h) Trygonometria
 Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Wyk lad 5 W lasności wyznaczników. Macierz odwrotna
 Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
1 Wartości własne oraz wektory własne macierzy
 Rozwiązania zadania umieszczonego na końcu poniższych notatek proszę przynieść na kartkach Proszę o staranne i formalne uzasadnienie odpowiedzi Za zadanie można uzyskać do 6 punktów (jeżeli przyniesione
Rozwiązania zadania umieszczonego na końcu poniższych notatek proszę przynieść na kartkach Proszę o staranne i formalne uzasadnienie odpowiedzi Za zadanie można uzyskać do 6 punktów (jeżeli przyniesione
Bryła sztywna. Wstęp do Fizyki I (B+C) Wykład XXI:
 Bryła sztywna Wstęp do Fizyki I (B+C) Wykład XXI: Porównanie ruchu obrotowego z ruchem postępowym Ogólne wyrażenie na moment pędu Tensor momentu bezwładności Osie główne Równania Eulera Bak swobodny Porównanie
Bryła sztywna Wstęp do Fizyki I (B+C) Wykład XXI: Porównanie ruchu obrotowego z ruchem postępowym Ogólne wyrażenie na moment pędu Tensor momentu bezwładności Osie główne Równania Eulera Bak swobodny Porównanie
Wyk lad 1 Podstawowe struktury algebraiczne
 Wyk lad 1 Podstawowe struktury algebraiczne 1 Dzia lanie w zbiorze Majac dane dowolne dwa przedmioty a b możemy z nich utworzyć pare uporzadkowan a (a b) o poprzedniku a i nastepniku b. Warunek na równość
Wyk lad 1 Podstawowe struktury algebraiczne 1 Dzia lanie w zbiorze Majac dane dowolne dwa przedmioty a b możemy z nich utworzyć pare uporzadkowan a (a b) o poprzedniku a i nastepniku b. Warunek na równość
g liczb rzeczywistych (a n ) spe lnia warunek
 . Czy jest prawda, że a) R y R z R y + yz + = 0 ; b) R y R z R y + yz + 0 ; c) R y R z R y + yz + = 0 ; d) R y R z R y + yz + 0? 2. Czy jest prawdziwa nierówność a) ctg > ; b) tg < cos ; c) cos < sin ;
. Czy jest prawda, że a) R y R z R y + yz + = 0 ; b) R y R z R y + yz + 0 ; c) R y R z R y + yz + = 0 ; d) R y R z R y + yz + 0? 2. Czy jest prawdziwa nierówność a) ctg > ; b) tg < cos ; c) cos < sin ;
A. Strojnowski - Twierdzenie Jordana 1
 A Strojnowski - Twierdzenie Jordana 1 Zadanie 1 Niech f b edzie endomorfizmem skończenie wymiarowej przestrzeni V nad cia lem charakterystyki różnej od 2 takim, że M(f) nie jest diagonalizowalna ale M(f
A Strojnowski - Twierdzenie Jordana 1 Zadanie 1 Niech f b edzie endomorfizmem skończenie wymiarowej przestrzeni V nad cia lem charakterystyki różnej od 2 takim, że M(f) nie jest diagonalizowalna ale M(f
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW NR 78353 WYGENEROWANY AUTOMATYCZNIE W SERWISIE WWW.ZADANIA.INFO POZIOM PODSTAWOWY CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 5 4 jest
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW NR 78353 WYGENEROWANY AUTOMATYCZNIE W SERWISIE WWW.ZADANIA.INFO POZIOM PODSTAWOWY CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 5 4 jest
Bryła sztywna. Fizyka I (B+C) Wykład XXIII: Tensor momentu bezwładności i osie główne Równania Eulera Bak swobodny. Podsumowanie wykładu Egzamin
 Bryła sztywna Wykład XXIII: Fizyka I (BC) Tensor momentu bezwładności i osie główne Równania Eulera Bak swobodny Podsumowanie wykładu Egzamin Tensor momentu bezwładności Tensor momentu bezwładności pozwala
Bryła sztywna Wykład XXIII: Fizyka I (BC) Tensor momentu bezwładności i osie główne Równania Eulera Bak swobodny Podsumowanie wykładu Egzamin Tensor momentu bezwładności Tensor momentu bezwładności pozwala
Wyk lad 4 Dzia lania na macierzach. Określenie wyznacznika
 Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Wyk lad 14 Formy kwadratowe I
 Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
Wyk lad 9 Baza i wymiar przestrzeni liniowej
 Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
VII.1 Pojęcia podstawowe.
 II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
że w wyniku pomiaru zmiennej dynamicznej A, której odpowiada operator αˆ otrzymana zostanie wartość 2.41?
 TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
Transformacja Lorentza - Wyprowadzenie
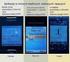 Transformacja Lorentza - Wyprowadzenie Rozważmy obserwatorów zwiazanych z różnymi inercjalnymi uk ladami odniesienia, S i S. Odpowiednie osie uk ladów S i S sa równoleg le, przy czym uk lad S porusza sie
Transformacja Lorentza - Wyprowadzenie Rozważmy obserwatorów zwiazanych z różnymi inercjalnymi uk ladami odniesienia, S i S. Odpowiednie osie uk ladów S i S sa równoleg le, przy czym uk lad S porusza sie
Literatura: Oznaczenia:
 Literatura: 1. R.R.Andruszkiewicz,,,Wyk lady z algebry ogólnej I, Wydawnictwo UwB, Bia lystok 2005. 2. Cz. Bagiński,,,Wst ep do teorii grup, Wydawnictwo Script, Warszawa 2002. 3. M. Bryński i J. Jurkiewicz,,,Zbiór
Literatura: 1. R.R.Andruszkiewicz,,,Wyk lady z algebry ogólnej I, Wydawnictwo UwB, Bia lystok 2005. 2. Cz. Bagiński,,,Wst ep do teorii grup, Wydawnictwo Script, Warszawa 2002. 3. M. Bryński i J. Jurkiewicz,,,Zbiór
Grupy przestrzenne i ich symbolika
 Grupy przestrzenne i ich symbolika Po co mi (chemikowi) znajomość symboli grup przestrzennych? Informacje zawarte w symbolu układ krystalograficzny obecność operacji symetrii punktowej (spektroskopia)
Grupy przestrzenne i ich symbolika Po co mi (chemikowi) znajomość symboli grup przestrzennych? Informacje zawarte w symbolu układ krystalograficzny obecność operacji symetrii punktowej (spektroskopia)
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Wyk lad 9 Baza i wymiar przestrzeni liniowej
 Wyk lad 9 Baza i wymiar liniowej Baza liniowej Niech V bedzie nad cia lem K Powiemy, że zbiór wektorów {α,, α n } jest baza V, jeżeli wektory α,, α n sa liniowo niezależne oraz generuja V tzn V = L(α,,
Wyk lad 9 Baza i wymiar liniowej Baza liniowej Niech V bedzie nad cia lem K Powiemy, że zbiór wektorów {α,, α n } jest baza V, jeżeli wektory α,, α n sa liniowo niezależne oraz generuja V tzn V = L(α,,
Zestaw Obliczyć objętość równoległościanu zbudowanego na wektorach m, n, p jeśli wiadomo, że objętość równoległościanu zbudowanego na wektorach:
 Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Algebra i jej zastosowania ćwiczenia
 Algebra i jej zastosowania ćwiczenia 14 stycznia 2013 1 Kraty 1. Pokazać, że każda klasa kongruencji kraty (K, +, ) jest podkrata kraty (K, +, ). 2. Znaleźć wszystkie kongruencje kraty 2 3, gdzie 2 jest
Algebra i jej zastosowania ćwiczenia 14 stycznia 2013 1 Kraty 1. Pokazać, że każda klasa kongruencji kraty (K, +, ) jest podkrata kraty (K, +, ). 2. Znaleźć wszystkie kongruencje kraty 2 3, gdzie 2 jest
KONKURS ZOSTAŃ PITAGORASEM MUM. Podstawowe własności figur geometrycznych na płaszczyźnie
 KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
GAL z aweber/zadania/gal2017gw/ Wersja
 Przestrzenie rzutowe GAL z 27 http://wwwmimuwedupl/ aweber/zadania/gal27gw/ Wersja 2627 Patrz osobny plik http://wwwmimuwedupl/ aweber/zadania/gal27gw/przestrzenie rzutowe-zadaniapdf Do zrobienia na ćwiczeniach:
Przestrzenie rzutowe GAL z 27 http://wwwmimuwedupl/ aweber/zadania/gal27gw/ Wersja 2627 Patrz osobny plik http://wwwmimuwedupl/ aweber/zadania/gal27gw/przestrzenie rzutowe-zadaniapdf Do zrobienia na ćwiczeniach:
Geometria odwzorowań inżynierskich cienie w rzucie środkowym 06D
 Scriptiones Geometrica Volumen I (2014), No. 6D, 1 9. Geometria odwzorowań inżynierskich cienie w rzucie środkowym 06D Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Cienie w perspektywie i perspektywie
Scriptiones Geometrica Volumen I (2014), No. 6D, 1 9. Geometria odwzorowań inżynierskich cienie w rzucie środkowym 06D Edwin Koźniewski Zak lad Informacji Przestrzennej 1. Cienie w perspektywie i perspektywie
Geometria odwzorowań inżynierskich Zadania 02
 Scriptiones Geometrica Volumen I (2007), No. Z2, 1 3. Geometria odwzorowań inżynierskich Zadania 02 1. Odwzorowania w rzucie równoleg lym. Przekroje cd. Konstrukcje p laskie 1.1. Przekszat lcenia na p
Scriptiones Geometrica Volumen I (2007), No. Z2, 1 3. Geometria odwzorowań inżynierskich Zadania 02 1. Odwzorowania w rzucie równoleg lym. Przekroje cd. Konstrukcje p laskie 1.1. Przekszat lcenia na p
Wzory Viete a i ich zastosowanie do uk ladów równań wielomianów symetrycznych dwóch i trzech zmiennych
 Wzory Viete a i ich zastosowanie do uk ladów równań wielomianów symetrycznych dwóch i trzech zmiennych Pawe l Józiak 007-- Poje cia wste pne Wielomianem zmiennej rzeczywistej t nazywamy funkcje postaci:
Wzory Viete a i ich zastosowanie do uk ladów równań wielomianów symetrycznych dwóch i trzech zmiennych Pawe l Józiak 007-- Poje cia wste pne Wielomianem zmiennej rzeczywistej t nazywamy funkcje postaci:
FUNKCJE LICZBOWE. x 1
 FUNKCJE LICZBOWE Zbiory postaci {x R: x a}, {x R: x a}, {x R: x < a}, {x R: x > a} oznaczane sa symbolami (,a], [a, ), (,a) i (a, ). Nazywamy pó lprostymi domknie tymi lub otwartymi o końcu a. Symbol odczytujemy
FUNKCJE LICZBOWE Zbiory postaci {x R: x a}, {x R: x a}, {x R: x < a}, {x R: x > a} oznaczane sa symbolami (,a], [a, ), (,a) i (a, ). Nazywamy pó lprostymi domknie tymi lub otwartymi o końcu a. Symbol odczytujemy
Podstawowe metody i przybliżenia: metoda wariacyjna, rachunek zaburzeń
 Wyk lad 6 Podstawowe metody i przybliżenia: metoda wariacyjna, rachunek zaburzeń Uk lady modelowe czastka swobodna czastka na barierze potencja lu czastka w pudle oscylator harmoniczny oscylator Morse
Wyk lad 6 Podstawowe metody i przybliżenia: metoda wariacyjna, rachunek zaburzeń Uk lady modelowe czastka swobodna czastka na barierze potencja lu czastka w pudle oscylator harmoniczny oscylator Morse
Rachunek różniczkowy i całkowy w przestrzeniach R n
 Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
Baza w jądrze i baza obrazu ( )
 Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
ALGEBRA z GEOMETRIA, ANALITYCZNA,
 ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
TENSOMETRIA ZARYS TEORETYCZNY
 TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
Aproksymacja kraw. Od wielu lokalnych cech (edge elements) do spójnej, jednowymiarowej. epnej aproksymacji
 Aproksymacja kraw edzi Od wielu lokalnych cech (edge elements) do spójnej, jednowymiarowej cechy (edge). Różne podejścia: szukanie w pobliżu wst epnej aproksymacji transformacja Hough a. Wiedza o obiektach:
Aproksymacja kraw edzi Od wielu lokalnych cech (edge elements) do spójnej, jednowymiarowej cechy (edge). Różne podejścia: szukanie w pobliżu wst epnej aproksymacji transformacja Hough a. Wiedza o obiektach:
