Transformata Z Matlab
|
|
|
- Aleksandra Baran
- 6 lat temu
- Przeglądów:
Transkrypt
1 Aademia Morsa w Gdyi Katedra Automatyi Orętowej Teoria sterowaia Trasformata Z Matlab Mirosław Tomera. WPROWADZENIE W uładach sterowaia cora cęściej stosowae są regulatory cyfrowe i stąd oiecość oreślaia rówań, tóre opisują sygały cyfrowe i dysrete. Ta ja rówaia różicowe stosowae są do opisu uładów sygałami aalogowymi, ta rówaia różicowe stosowae są dla uładów sygałami dysretymi lub cyfrowymi. Rówaia różicowe używae są rówież do aprosymacji rówań różicowych w celu apisaia ich w programach omputerowych wyorystywaych w różego rodaju symulacjach. Rachue operatorowy Laplace a może być stosoway do rowiąywaia liiowych rówań różicowych wycajych, atomiast trasformata Z jest metodą wyorystywaą do rowiąywaia liiowych rówań różicowych i uładów liiowych daymi dysretymi lub cyfrowymi. Zmiea jest licbą espoloą.. PRZEKSZTAŁCENIE RÓWNANIA RÓŻNICOWEGO DO POSTACI TRANSFORMATY Z Podobie ja w prypadu trasformaty Laplace'a, wprowadeie trasformaty Z ma a celu umożliwieie wyoywaia matematycych operacji algebraicych co może być wyoywae w diediie mieej espoloej, ostateca odpowiedź casowa wyacaa jest pre astosowaie odwrotej trasformaty Z. Odwrota trasformata Z fucji Y() daje iformacje tylo o y(t), a ie o y(t). Iymi słowy trasformata Z achowuje iformacje tylo w chwilach próbowaia. Sygały występujące w dysretych chwilach casu opisywae są pre rówaia różicowe. W tym podrodiale poaae ostaie w jai sposób doouje się astąpieia rówaia różicowego odpowiadającą mu trasformatą Z. W tabeli ajdują się podstawowe twierdeia w oparciu o tóre doouje się prestałceia rówaia różicowego do postaci trasformaty Z. Na podstawie rówaia różicowego w sposób sewecyjy moża dooać wyaceia dysretego sygału casowego. Taie same wartości próbe sygału dysretego moża uysać rowiąując rówaie różicowe metodą trasformaty Z. Poiżsy pryład ilustruje sposób wyaceia trasformaty Z dla rówaia różicowego. Pryład Dla poiżsego rówaia różicowego uładu II rędu, wyac odpowiadająca mu trasformatę Z. y ( ) y ( ) + 0.5y( 5 ( (.) gdie ( jest jedostową fucją soową. Wartości pierwsych próbe są astępujące: 0 y. y, Ostatia atualiacja: M. Tomera
2 Teoria sterowaia Trasformata Z Matlab Tabela. Podstawowe twierdeia trasformaty Z. Dodawaie i odejmowaie Zf T f T F. Możeie pre stałą Zaf T azf T a F F. Presuięcie w diediie recywistej Z T f F (opóźieie casowe) Zf T F( ) f T (wypredeie casowe) 0 gdie: licba całowita.. Presuięcie w diediie mieej espoloej T Z e f T T F e 4. Twierdeie o wartości pocątowej lim f ( T) lim F( ) 0 5. Twierdeie o wartości ońcowej F( ) lim f ( T) lim, pod waruiem, że F( ) ie ma żadych bieguów a ewątr ai a oręgu Rowiąaie: Dooując obustroego prestałceia Z rówaia (.), pry wyorystaiu twierdeń tabeli i fucji tabeli Y ( ) y(0) y() Y( ) y(0) + 0.5Y() 5 Podstawiając wartości licbowe pierwsych próbe do rówaia (.) i wyacając Y(), otrymuje się 6 6 Y ( ) (.) Dodatowo moża sprawdić poprawość uysaej trasformaty (.) pry użyciu twierdeia o wartości pocątowej (tabela, pt. 4) 6 6 y(0) lim lim (.4) Aaliując wór (.4) widać, że o wyiu decydują współcyii pry ajwyżsych potęgach licia i miaowia, cyli sprawdaie poprawości wyacoej trasformaty Z dla rówaia różicowego pry użyciu twierdeia o wartości pocątowej jest mało wiarygode. Na podstawie trasformaty (.), pry użyciu twierdeia o wartości ońcowej (tabela, pt 5) moża wyacyć rówież wartość ustaloą fucji y( 6 6 y( ) lim lim 0 (.5) (.) Ostatia atualiacja: M. Tomera
3 Teoria sterowaia Trasformata Z Matlab Tabela. Wybrae trasformaty Z f( F().. ( ) ! 5. lim! 0 6. r 7. r 8. si 9. cos! r r r si cos cos cos r si 0. r si r cos r r cos. r cos r cos r. Ar cos Ae j re j Ae j re j. ZNAJDOWANIE ODWROTNYCH TRANSFORMAT Z METODĄ ROZKŁADU NA UŁAMKI PROSTE W celu wyaceia odwrotej trasformaty fucja F() roładaa jest a sumę ułamów wyłych, a astępie orysta się tablicy trasformat Z w celu oreśleia posuiwaej fucji f(t). Pry roładie a sumę ułamów wyłych występuje iewiela różica pomiędy trasformatami Z i trasformatami Laplace'a. Preglądając tabelę trasformat Z (tabela ), moża auważyć, że pratycie ażda trasformata Z fucji jest pomożoa w liciu pre. Dlatego też doouje się roładu fucji F ( ) a sumę ułamów wyłych, a astępie moży się wsystie sładii pre. Roważ astępującą fucję operatorową apisaą w postaci ilorau dwóch wielomiaów: m m F( ) B( ) umd bm bm... b b0 () A( ) ded a a... a a 0 Ostatia atualiacja: M. Tomera
4 Teoria sterowaia Trasformata Z Matlab w tórych ietóre e współcyiów a i ora b j mogą być rówe ero. W MATLABIE wetory wiersowe umd ora ded oreślają współcyii licia i miaowia fucji opisaej worem (). Wobec tego umd b m bm... b 0 Poleceie ded a a... a 0 pd,d residue umd,ded rd, () wyaca residua rd, bieguy pd ora współcyii stałe D roładu fucji dysretej a ułami proste ilorau dwóch wielomiaów B()/A(). Roład a ułami proste ilorau wielomiaów B()/A() jest wówcas astępujący: F( ) B( ) umd rd rd rd... A( ) ded pd pd pd Pryład ilustruje tą metodę. D () Pryład Dla fucji dysretej uysaej w pryładie 6 Y ( ) (.) wyac postać dysretą y( stosując metodę roładu a ułami proste. Rowiąaie: W pierwsej olejości ależy podielić fucję (.) pre. Y ( ) 6 6 (.) j j0.5 Korystając fucji residue ajdującej się w bibliotece Matlaba moża łatwo wyacyć parametry roładu fucji opisaej worem (.) do postaci () Y ( ) j j6.5 (.) 0.5 j j0.5 Po prestałceiu residuów espoloych do postaci wyładicej i pomożeiu obu stro rówaia (.) pre, uysuje się j.7 j e e Y( ) 0 (.4) j j e 0.707e Korystając tablicy trasformat Z ajduje się postać casową fucji dysretej cos y( 0 ( Uysae wyi (.5) będący rowiąaiem rówaia różicowego pryładu predstawioy ostał a rysuu.. Rowiąaie pryładu preprowadoe ostało wyorystaiem astępującego odu Matlaba. clear % Wycysceie pamięci robocej Matlaba close all % Zamięcie wsystich oiee graficych %Lici i miaowi fucji dysretej umd [- 0 6]; ded cov([ -],[ - 0.5]); % Wyaceie parametrów roładu a ułami wyłe [rd,pd,d] residue( umd, ded); (.5) Ostatia atualiacja: M. Tomera 4
5 Teoria sterowaia Trasformata Z Matlab % Wyaceie postaci wyładicej espoloego residua M_rD abs( rd()); theta_rd agle( rd()); % Wyaceie postaci wyładicej espoloego biegua M_pD abs( pd()); theta_pd agle( pd()); % Wygeerowaie olejych próbe rowiąaia for 0:0, td(+) ; yd(+) rd() + *M_rD*(M_pD)^*cos(theta_pD*+theta_rD) ed; % Wyreśleie uysaego rowiąaia figure() stem(td, yd, '-') xlabel('') ylabel('y(') 4 Rowiąaie rówaia różicowego y( Rys... Wyres fucji dysretej y( uysay a podstawie woru (.5) Moża dooać sprawdeia uysaego rowiąaia (.5) popre wygeerowaie rowiąaia rówaia różicowego (.) w sposób bepośredi po dopisaiu dodatowo astępującego odu programu Matlaba. t() 0; y() -; % Wartość pierwsej próbi t() ; y() -; % Wartość drugiej próbi for :9, t(+) +; y(+) y(+) - 0.5*y( + 5; ed; % Wyreśleie uysaych rowiąań figure() plot( td, yd, 'o', t, y, '*') xlabel('') ylabel('y(') Ostatia atualiacja: M. Tomera 5
6 Teoria sterowaia Trasformata Z Matlab ĆWICZENIA W MATLABIE M. Zajdź odwrote trasformaty Z dla 0 a) Y () b) Y () c) () Y 4 4 d) Y () 0 M. Zajdź odwrote trasformaty Z dla 0 a) () Y b) () 0 Y 0. c) () Y 0.85 d) () Y 0. e) () 5 0 Y f) () Y.5 g) () Y 0.5 h) Y () i) () Y j) () 0.5 Y () Y l) () 0.86 Y Ostatia atualiacja: M. Tomera 6
7 Teoria sterowaia Trasformata Z Matlab M. Korystając metod trasformaty Z, rowiąż astępujące rówaia różicowe dla 0 uwględieiem waruów pocątowych: a) y( ).5y( ).04y( ) 0.54y( 0.0 ( y ( 0) y ( ) 0.9 y ( ) 0.8 b) y( ).54y( ) 0.56y( y ( 0) 0 y ( ) 0. c) y( ) 0.8y( 0.6 cos0. y ( 0) d) y( ).6y( ).y( ) 0.6y( 0.0 ( y ( 0) y ( ). y ( ).8 e) y( ) 0.8y( y ( 0) f) y( ) 0.7 y( 0.4 si0. y ( 0) g) y( ).6y( ) 0.65y( 0.0( y ( 0) y ( ).8 h) y( ).7 y( ) 0.7y( y ( 0) 0 y ( ) 0. i) y( ).8y( ) 0.8y( 0.05( y ( 0) y ( ) 0.8 j) y( ).8y( ) 0.8y( 0.0si0. y ( 0) y ( ).7 y( ).9y( ) 0.94y( 0.0cos0. y ( 0) y ( ). l) y( ).7 y( ) 0.76y( cos0. y ( 0) 0 y ( ) 0. Ostatia atualiacja: M. Tomera 7
8 Teoria sterowaia Trasformata Z Matlab ODPOWIEDZI DO WYBRANYCH ZADAŃ M. M. M. a) y ( 0.5 ( b) ( 0.5 y 9 y + + y.84.6 cos c) ( d) ( a) y ( 0 ( + 0 ( b) y (.5 ( c) y ( ( d) y ( ( e) y ( 5 ( f) y ( ( g) y ( ( h) y ( 80 ( i) y ( 4 ( j) ( ( cos ( cos ( cos y 0 ( y ) l) ( y Y ( ) a) y ( 0.5 ( ( Y ( ) b) y ( 0.56 (0.954) Y ( ) c) e e y (.77 cos( ) Y ( ) d) j0.845 j0..89e e j0.845 j y ( ( ( Y ( ) e) y ( 0.5( Y ( ) e f) e y (.6740 (0.7).649 cos j.878 j e e j.878 j0. Ostatia atualiacja: M. Tomera 8
9 Teoria sterowaia Trasformata Z Matlab j.996 Y ( ) e g) e y ( 0.( cos Y ( ) h) y (.875 (0.9) Y ( ) i) y ( 5 ( Y ( ) j) 4 j e 0.806e j.544 j j e 0.7e.54e.54e j0. j0. j0.07 e e e e y ( cos cos Y ( ) j.078 j.078 j e 0.00e 0.876e 0.876e j0. j0. j0.0 e e e e y ( cos cos Y ( ) l) j.56 j.56 j.868 j.996 j0.44 j0.9 j0.07 j0.865 j0.0 j e 0.905e 0.90e 0.90e j0.40 j0.40 j e 0.878e 0.8e 0.8e y ( cos cos j0. LITERATURA. Frali G.F, Powell J.D., Emami-Naeii A. Digital Cotrol of Dyamic Systems, rd ed. Addiso-Wesley Publishig Compay, Kuo B.C. Automatic Cotrol Systems, Joh Wiley&Sos, 995. Ostatia atualiacja: M. Tomera 9
ODWROTNE PRZEKSZTAŁCENIE ZET
 CPS - - 006/007 ODWROTNE PRZEKSZTAŁCENIE ZET Ropatrymy agadieie odtwaraia dysretego sygału casowego x[] jego trasformaty X(. Do wyaceia ciągu x[] w sposób jedoacy musimy ać obsar bieżości (OZ. Odwracaie
CPS - - 006/007 ODWROTNE PRZEKSZTAŁCENIE ZET Ropatrymy agadieie odtwaraia dysretego sygału casowego x[] jego trasformaty X(. Do wyaceia ciągu x[] w sposób jedoacy musimy ać obsar bieżości (OZ. Odwracaie
( ) O k k k. A k. P k. r k. M O r 1. -P n W. P 1 P k. Rys. 3.21. Redukcja dowolnego przestrzennego układu sił
 3.7.. Reducja dowolego uładu sił do sił i par sił Dowolm uładem sił będiem awać uład sił o liiach diałaia dowolie romiescoch w prestrei. tm pucie ajmiem się sprowadeiem (reducją) taiego uładu sił do ajprostsej
3.7.. Reducja dowolego uładu sił do sił i par sił Dowolm uładem sił będiem awać uład sił o liiach diałaia dowolie romiescoch w prestrei. tm pucie ajmiem się sprowadeiem (reducją) taiego uładu sił do ajprostsej
Z-TRANSFORMACJA Spis treści
 Z-TRANSFORMACJA Spi treści. Deiicja. Pryłady traormat 3. Właości -traormacji 4. Zwiąe -traormacji traormacją Fouriera 5. Z-traormacja ygału dwuwymiarowego Deiicja -traormacji Z-traormata jet eregiem Laureta
Z-TRANSFORMACJA Spi treści. Deiicja. Pryłady traormat 3. Właości -traormacji 4. Zwiąe -traormacji traormacją Fouriera 5. Z-traormacja ygału dwuwymiarowego Deiicja -traormacji Z-traormata jet eregiem Laureta
1. ALGEBRA Liczby zespolone
 ALGEBRA Licby espoloe Opracowaie: Vladimir Marcheko WYKŁAD Postać algebraica i trygoometryca licby espoloe; dodawaie, możeie, potęgowaie i dieleie licb espoloych A+B+C (Wstęp: pochodeie licb espoloych)
ALGEBRA Licby espoloe Opracowaie: Vladimir Marcheko WYKŁAD Postać algebraica i trygoometryca licby espoloe; dodawaie, możeie, potęgowaie i dieleie licb espoloych A+B+C (Wstęp: pochodeie licb espoloych)
III. LICZBY ZESPOLONE
 Pojęcie ciała 0 III LICZBY ZESPOLONE Defiicja 3 Niech K będie dowolm biorem Diałaiem wewętrm (krótko będiem mówić - diałaiem) w biore K awam każdą fukcję o : K K K Wartość fukcji o dla elemetów K oacam
Pojęcie ciała 0 III LICZBY ZESPOLONE Defiicja 3 Niech K będie dowolm biorem Diałaiem wewętrm (krótko będiem mówić - diałaiem) w biore K awam każdą fukcję o : K K K Wartość fukcji o dla elemetów K oacam
f '. Funkcja h jest ciągła. Załóżmy, że ciąg (z n ) n 0, z n+1 = h(z n ) jest dobrze określony, tzn. n 0 f ' ( z n
 Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
Plan wykładu. Obliczanie pierwiastków wielomianów. Własności wielomianów. Własności wielomianów. Schemat Hornera. Własności wielomianów. p z. p c r.
 Pl wyłdu Olicie pierwistów wielomiów Włsości wielomiów Schemt Horer olicie wrtości dieleie wielomiów deflcj omplety schemt Horer metod Newto eśli, to p m stopień. p p /3 3/3 Włsości wielomiów Włsości wielomiów
Pl wyłdu Olicie pierwistów wielomiów Włsości wielomiów Schemt Horer olicie wrtości dieleie wielomiów deflcj omplety schemt Horer metod Newto eśli, to p m stopień. p p /3 3/3 Włsości wielomiów Włsości wielomiów
MACIERZE I WYZNACZNIKI
 MCIERZE I WYZNCZNIKI Defiicj Mcierą o współcyikch recywistych (espoloych) i wymire m x ywmy pryporądkowie kżdej pre licb turlych (i,k), i,,, m, k,,,, dokłdie jedej licby recywistej ik [ ik ] mx (espoloej)
MCIERZE I WYZNCZNIKI Defiicj Mcierą o współcyikch recywistych (espoloych) i wymire m x ywmy pryporądkowie kżdej pre licb turlych (i,k), i,,, m, k,,,, dokłdie jedej licby recywistej ik [ ik ] mx (espoloej)
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE PODSTAWOWYCH CZŁONÓW LINIOWYCH UKŁADÓW AUTOMATYKI
 CHARAKERYSYKI CZĘSOLIWOŚCIOWE PODSAWOWYCH CZŁONÓW LINIOWYCH UKŁADÓW AUOMAYKI Do podstawowych form opisu dyamii elemetów automatyi (oprócz rówań różiczowych zaliczamy trasmitację operatorową s oraz trasmitację
CHARAKERYSYKI CZĘSOLIWOŚCIOWE PODSAWOWYCH CZŁONÓW LINIOWYCH UKŁADÓW AUOMAYKI Do podstawowych form opisu dyamii elemetów automatyi (oprócz rówań różiczowych zaliczamy trasmitację operatorową s oraz trasmitację
Algebra liniowa z geometrią analityczną
 WYKŁAD. Elmtar fucj mij spoloj: wilomiay, pirwiasti jdości, fucja: pirwiast stopia, fucja wyładica, fucja logarytmica. Podstawow własości wilomiaów: podilość, twirdi Bout, podstawow twirdi algbry, suai
WYKŁAD. Elmtar fucj mij spoloj: wilomiay, pirwiasti jdości, fucja: pirwiast stopia, fucja wyładica, fucja logarytmica. Podstawow własości wilomiaów: podilość, twirdi Bout, podstawow twirdi algbry, suai
APROKSYMACJA I INTERPOLACJA. funkcja f jest zbyt skomplikowana; użycie f w dalszej analizie problemu jest trudne
 APROKSYMACJA I INTERPOLACJA Przybliżeie fucji f(x) przez ią fucję g(x) fucja f jest zbyt sompliowaa; użycie f w dalszej aalizie problemu jest trude fucja f jest zaa tylo tabelaryczie; wymagaa jest zajomość
APROKSYMACJA I INTERPOLACJA Przybliżeie fucji f(x) przez ią fucję g(x) fucja f jest zbyt sompliowaa; użycie f w dalszej aalizie problemu jest trude fucja f jest zaa tylo tabelaryczie; wymagaa jest zajomość
Dwumian Newtona. Agnieszka Dąbrowska i Maciej Nieszporski 8 stycznia 2011
 Dwumia Newtoa Agiesza Dąbrowsa i Maciej Nieszporsi 8 styczia Wstęp Wzory srócoego możeia, tóre pozaliśmy w gimazjum (x + y x + y (x + y x + xy + y (x + y 3 x 3 + 3x y + 3xy + y 3 x 3 + y 3 + 3xy(x + y
Dwumia Newtoa Agiesza Dąbrowsa i Maciej Nieszporsi 8 styczia Wstęp Wzory srócoego możeia, tóre pozaliśmy w gimazjum (x + y x + y (x + y x + xy + y (x + y 3 x 3 + 3x y + 3xy + y 3 x 3 + y 3 + 3xy(x + y
Wykład 8: Zmienne losowe dyskretne. Rozkłady Bernoulliego (dwumianowy), Pascala, Poissona. Przybliżenie Poissona rozkładu dwumianowego.
 Rachue rawdoodobieństwa MAP064 Wydział Eletroii, ro aad. 008/09, sem. leti Wyładowca: dr hab. A. Jurlewicz Wyład 8: Zmiee losowe dysrete. Rozłady Beroulliego (dwumiaowy), Pascala, Poissoa. Przybliżeie
Rachue rawdoodobieństwa MAP064 Wydział Eletroii, ro aad. 008/09, sem. leti Wyładowca: dr hab. A. Jurlewicz Wyład 8: Zmiee losowe dysrete. Rozłady Beroulliego (dwumiaowy), Pascala, Poissoa. Przybliżeie
PRZEKSZTAŁCENIE ZET. definicja. nst. Stąd po dokonaniu podstawienia zgodnie z definicją otrzymamy wyrażenie jak dla ciągu.
 CPS 6/7 PREKSTAŁCENIE ET Defiicja rekstałceia Prekstałceie ET jest w diediie casu dyskretego odowiedikiem ciągłego rekstałceia Lalace a w diediie casu ciągłego. Podamy dwie rówoważe defiicje rekstałceia
CPS 6/7 PREKSTAŁCENIE ET Defiicja rekstałceia Prekstałceie ET jest w diediie casu dyskretego odowiedikiem ciągłego rekstałceia Lalace a w diediie casu ciągłego. Podamy dwie rówoważe defiicje rekstałceia
Programowanie dynamiczne i modele rekurencyjne w ekonomii Wykład 3
 Programowaie dyamice i modele rekurecyje w ekoomii Wykład 3 Michał Ramsa sierpia 0 Stresceie Wykład treci bauje główie a [, ro 7] i dotycy wykorystaia fukcji tworacych do rowiaywaia rekurecji Materiał
Programowaie dyamice i modele rekurecyje w ekoomii Wykład 3 Michał Ramsa sierpia 0 Stresceie Wykład treci bauje główie a [, ro 7] i dotycy wykorystaia fukcji tworacych do rowiaywaia rekurecji Materiał
ZADANIA Z FUNKCJI ANALITYCZNYCH LICZBY ZESPOLONE
 . Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
. Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
W analizie układów ciągłych wykorzystywane jest przekształcenie operatorowe Laplace a które zdefiniowane jest przez następujący wzór całkowy
 Aadmia Mora w Gdyi Katdra Automatyi Orętow oria trowaia Prtałci Z Miroław omra. WPROWADZENIE Cora cęści w uładach trowaia toowa ą rgulatory cyfrow i tąd oicość orślaia rówań, tór opiuą ygały cyfrow i dyrt.
Aadmia Mora w Gdyi Katdra Automatyi Orętow oria trowaia Prtałci Z Miroław omra. WPROWADZENIE Cora cęści w uładach trowaia toowa ą rgulatory cyfrow i tąd oicość orślaia rówań, tór opiuą ygały cyfrow i dyrt.
tek zauważmy, że podobnie jak w dziedzinie rzeczywistej wprowadzamy dla funkcji zespolonych zmiennej rzeczywistej pochodne wyższych rze
 R o z d z i a l III RÓWNANIA RÓŻNICZKOWE LINIOWE WYŻSZYCH RZE DÓW 12. Rówaie różiczowe liiowe -tego rze du Na pocza te zauważmy, że podobie ja w dziedziie rzeczywistej wprowadzamy dla fucji zespoloych
R o z d z i a l III RÓWNANIA RÓŻNICZKOWE LINIOWE WYŻSZYCH RZE DÓW 12. Rówaie różiczowe liiowe -tego rze du Na pocza te zauważmy, że podobie ja w dziedziie rzeczywistej wprowadzamy dla fucji zespoloych
LABORATORIUM MODELOWANIA I SYMULACJI. Ćwiczenie 3 MODELOWANIE SYSTEMÓW DYNAMICZNYCH METODY OPISU MODELI UKŁADÓW
 Wydział Elektryczy Zespół Automatyki (ZTMAiPC) ZERiA LABORATORIUM MODELOWANIA I SYMULACJI Ćwiczeie 3 MODELOWANIE SYSTEMÓW DYNAMICZNYCH METODY OPISU MODELI UKŁADÓW I. Cel ćwiczeia Celem ćwiczeia jest zapozaie
Wydział Elektryczy Zespół Automatyki (ZTMAiPC) ZERiA LABORATORIUM MODELOWANIA I SYMULACJI Ćwiczeie 3 MODELOWANIE SYSTEMÓW DYNAMICZNYCH METODY OPISU MODELI UKŁADÓW I. Cel ćwiczeia Celem ćwiczeia jest zapozaie
Rok akademicki: 2030/2031 Kod: RAR n Punkty ECTS: 7. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Podstawy automatyki Rok akademicki: 2030/2031 Kod: RAR-1-303-n Punkty ECTS: 7 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Automatyka i Robotyka Specjalność: - Poziom studiów: Studia
Nazwa modułu: Podstawy automatyki Rok akademicki: 2030/2031 Kod: RAR-1-303-n Punkty ECTS: 7 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Automatyka i Robotyka Specjalność: - Poziom studiów: Studia
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Dodawanie i mnożenie liczb zespolonych są działaniami wewnętrznymi tzn., że ich wynikiem jest liczba zespolona.
 Wykład - LICZBY ZESPOLONE Algebra licb espolonych, repreentacja algebraicna i geometrycna, geometria licb espolonych. Moduł, argument, postać trygonometrycna, wór de Moivre a.' Zbiór Licb Zespolonych Niech
Wykład - LICZBY ZESPOLONE Algebra licb espolonych, repreentacja algebraicna i geometrycna, geometria licb espolonych. Moduł, argument, postać trygonometrycna, wór de Moivre a.' Zbiór Licb Zespolonych Niech
ANALIZA FOURIEROWSKA szybkie transformaty Fouriera
 AALIZA FOURIEROWSKA szybi trasformaty Fourira dowola fuję priodyzą F( w zasi lub przstrzi (tx, ors T) moża przdstawić jao () F( b o + [ a si( + b os( ] gdzi π / T lub ω zauważmy, ż ω, jst ajiższą zęstośią
AALIZA FOURIEROWSKA szybi trasformaty Fourira dowola fuję priodyzą F( w zasi lub przstrzi (tx, ors T) moża przdstawić jao () F( b o + [ a si( + b os( ] gdzi π / T lub ω zauważmy, ż ω, jst ajiższą zęstośią
LICZBY, RÓWNANIA, NIERÓWNOŚCI; DOWÓD INDUKCYJNY
 LICZBY, RÓWNANIA, NIERÓWNOŚCI; DOWÓD INDUKCYJNY Zgodie z dążeiami filozofii pitagorejsiej matematyzacja abstracyjego myśleia powia być dooywaa przy pomocy liczb. Soro ta, to liczby ależy tworzyć w miarę
LICZBY, RÓWNANIA, NIERÓWNOŚCI; DOWÓD INDUKCYJNY Zgodie z dążeiami filozofii pitagorejsiej matematyzacja abstracyjego myśleia powia być dooywaa przy pomocy liczb. Soro ta, to liczby ależy tworzyć w miarę
Mechanika kwantowa III
 Mecaika kwatowa III Opracowaie: Barbara Pac, Piotr Petele Powtóreie Moet pędu jest wielkością pojęciowo bardo istotą, gdż dla wsstkic pól o setrii sfercej operator jego kwadratu ( ˆM koutuje ailtoiae (
Mecaika kwatowa III Opracowaie: Barbara Pac, Piotr Petele Powtóreie Moet pędu jest wielkością pojęciowo bardo istotą, gdż dla wsstkic pól o setrii sfercej operator jego kwadratu ( ˆM koutuje ailtoiae (
Dyskretyzacja równań różniczkowych Matlab
 Akaemia Morska w Gyni Katera Automatyki Okrętowej Teoria sterowania Mirosław Tomera Można zaprojektować ukła sterowania ciągłego i zaimplementować go w ukłaach sterowania cyfrowego stosując metoy aproksymacji
Akaemia Morska w Gyni Katera Automatyki Okrętowej Teoria sterowania Mirosław Tomera Można zaprojektować ukła sterowania ciągłego i zaimplementować go w ukłaach sterowania cyfrowego stosując metoy aproksymacji
Rok akademicki: 2014/2015 Kod: RME s Punkty ECTS: 6. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Podstawy automatyki Rok akademicki: 2014/2015 Kod: RME-1-305-s Punkty ECTS: 6 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Mechatronika Specjalność: - Poziom studiów: Studia I stopnia
Nazwa modułu: Podstawy automatyki Rok akademicki: 2014/2015 Kod: RME-1-305-s Punkty ECTS: 6 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Mechatronika Specjalność: - Poziom studiów: Studia I stopnia
Znajdowanie pozostałych pierwiastków liczby zespolonej, gdy znany jest jeden pierwiastek
 Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Transformator Φ M. uzwojenia; siła elektromotoryczna indukowana w i-tym zwoju: dφ. = z1, z2 liczba zwojów uzwojenia pierwotnego i wtórnego.
 Transformator Φ r Φ M Φ r i i u u Φ i strumień magnetycny prenikający pre i-ty wój pierwsego uwojenia; siła elektromotorycna indukowana w i-tym woju: dφ ei, licba wojów uwojenia pierwotnego i wtórnego.
Transformator Φ r Φ M Φ r i i u u Φ i strumień magnetycny prenikający pre i-ty wój pierwsego uwojenia; siła elektromotorycna indukowana w i-tym woju: dφ ei, licba wojów uwojenia pierwotnego i wtórnego.
Jarosław Wróblewski Analiza Matematyczna 1, zima 2016/17
 Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Wykład 7. Przestrzenie metryczne zwarte. x jest ciągiem Cauchy ego i posiada podciąg zbieżny. Na mocy
 Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
Damian Doroba. Ciągi. 1. Pierwsza z granic powinna wydawać się oczywista. Jako przykład może służyć: lim n = lim n 1 2 = lim.
 Damia Doroba Ciągi. Graice, z których korzystamy. k. q.. 5. dla k > 0 dla k 0 0 dla k < 0 dla q > 0 dla q, ) dla q Nie istieje dla q ) e a, a > 0. Opis. Pierwsza z graic powia wydawać się oczywista. Jako
Damia Doroba Ciągi. Graice, z których korzystamy. k. q.. 5. dla k > 0 dla k 0 0 dla k < 0 dla q > 0 dla q, ) dla q Nie istieje dla q ) e a, a > 0. Opis. Pierwsza z graic powia wydawać się oczywista. Jako
POLITECHNIKA OPOLSKA
 POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
LICZBY ZESPOLONE. = 0, wie c np. i v 3 = q
 LICZBY ZESPOLONE W tym rodiale ajmiemy sie omówieiem defiicji i iektórych w lasości licb espoloych. Zaciemy od uwagi o charaktere historycym. W XVI w. aucoo sie rowia ywać rówaia treciego stopia. Każde
LICZBY ZESPOLONE W tym rodiale ajmiemy sie omówieiem defiicji i iektórych w lasości licb espoloych. Zaciemy od uwagi o charaktere historycym. W XVI w. aucoo sie rowia ywać rówaia treciego stopia. Każde
I. Podzielność liczb całkowitych
 I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
Teoria Sygnałów. II Inżynieria Obliczeniowa. Wykład 13
 Toria Sygałów II Iżyiria Oblicziowa Wyład 3 Filtr adaptacyjy dostraja się do zmiych waruów pracy. Filtr tai posiadają dwa sygały wjściow. Pirwszym jst sygał poddaway filtracji x(). Drugim ta zway sygał
Toria Sygałów II Iżyiria Oblicziowa Wyład 3 Filtr adaptacyjy dostraja się do zmiych waruów pracy. Filtr tai posiadają dwa sygały wjściow. Pirwszym jst sygał poddaway filtracji x(). Drugim ta zway sygał
FUNKCJE ZESPOLONE Lista zadań 2005/2006
 FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
1. Transformata Laplace a przypomnienie
 Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
Metrologia: miary dokładności. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Zajęcia nr. 2 notatki
 Zajęcia r otati wietia 5 Wzory srócoego możeia W rozdziale tym podamy ila wzorów tóre ułatwiają obliczaie wielu zadań rachuowych Fat (wzory srócoego możeia) Dla dowolych liczb rzeczywistych a, b zachodzi:
Zajęcia r otati wietia 5 Wzory srócoego możeia W rozdziale tym podamy ila wzorów tóre ułatwiają obliczaie wielu zadań rachuowych Fat (wzory srócoego możeia) Dla dowolych liczb rzeczywistych a, b zachodzi:
Pierwiastki z liczby zespolonej. Autorzy: Agnieszka Kowalik
 Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
Modelowanie w pakiecie Matlab/Simulink
 Modelowanie w paiecie Matlab/Siulin I. Siłowni pneuatycny ebranowy I.1. Model ateatycny siłownia pneuatycnego ebranowego apisany a poocą równań różnicowych Sygnałe wejściowy siłownia jest ciśnienie P podawane
Modelowanie w paiecie Matlab/Siulin I. Siłowni pneuatycny ebranowy I.1. Model ateatycny siłownia pneuatycnego ebranowego apisany a poocą równań różnicowych Sygnałe wejściowy siłownia jest ciśnienie P podawane
WYKORZYSTANIE FILTRU CZĄSTECZKOWEGO W PROBLEMIE IDENTYFIKACJI UKŁADÓW AUTOMATYKI
 Piotr KOZIERSKI WYKORZYSTAIE FILTRU CZĄSTECZKOWEGO W PROBLEMIE IDETYFIKACJI UKŁADÓW AUTOMATYKI STRESZCZEIE W artyule przedstawioo sposób idetyfiacji parametryczej obietów ieliiowych zapisaych w przestrzei
Piotr KOZIERSKI WYKORZYSTAIE FILTRU CZĄSTECZKOWEGO W PROBLEMIE IDETYFIKACJI UKŁADÓW AUTOMATYKI STRESZCZEIE W artyule przedstawioo sposób idetyfiacji parametryczej obietów ieliiowych zapisaych w przestrzei
Matematyka. Opracował: dr hab. Mieczysław Kula, prof. WSBiF dr Michał Baczyński
 Matematka Opracował: dr hab. Miecsław Kula, prof. WSBiF dr Michał Bacński I. Ogóle iformacje o predmiocie: Cel predmiotu: Celem główm kursu jest apoaie studetów wbrami diałami matematki stosowami w aukach
Matematka Opracował: dr hab. Miecsław Kula, prof. WSBiF dr Michał Bacński I. Ogóle iformacje o predmiocie: Cel predmiotu: Celem główm kursu jest apoaie studetów wbrami diałami matematki stosowami w aukach
Parametryzacja rozwiązań układu równań
 Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
A B - zawieranie słabe
 NAZEWNICTWO: : rówoważość defcj : rówość defcj dla każdego steje! ZBIORY steje dokłade jede {,,,...} - całkowte * - całkowte be era - wmere - ujeme plus ero - recwste - espoloe A B - awerae słabe A :
NAZEWNICTWO: : rówoważość defcj : rówość defcj dla każdego steje! ZBIORY steje dokłade jede {,,,...} - całkowte * - całkowte be era - wmere - ujeme plus ero - recwste - espoloe A B - awerae słabe A :
Zadania zaliczeniowe z Automatyki i Robotyki dla studentów III roku Inżynierii Biomedycznej Politechniki Lubelskiej
 Zadania zaliczeniowe z Automatyki i Robotyki dla studentów III roku Inżynierii Biomedycznej Politechniki Lubelskiej Rozwiązane zadania należy dostarczyć do prowadzącego w formie wydruku lub w formie odręcznego
Zadania zaliczeniowe z Automatyki i Robotyki dla studentów III roku Inżynierii Biomedycznej Politechniki Lubelskiej Rozwiązane zadania należy dostarczyć do prowadzącego w formie wydruku lub w formie odręcznego
Prosta w 3. t ( t jest parametrem).
 Prosta w 3 by wyacy rówaie prostej w 3 wystarcy a jede put tej prostej i wetor adajcy jej ierue (way wetore ieruowy) Jei P = ( P yp P ) = [ p] to rówaia paraetryce prostej aj posta = P t : y = yp t t (
Prosta w 3 by wyacy rówaie prostej w 3 wystarcy a jede put tej prostej i wetor adajcy jej ierue (way wetore ieruowy) Jei P = ( P yp P ) = [ p] to rówaia paraetryce prostej aj posta = P t : y = yp t t (
Przekształcenie Z. Krzysztof Patan
 Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
Twierdzenia o funkcjach ciągłych
 Automatya i Robotya Aaliza Wyład 5 dr Adam Ćmiel cmiel@aghedupl Twierdzeia o ucjach ciągłych Tw (Weierstrassa Jeżeli ucja : R [ R jest ciągła a [, to ograiczoa i : ( sup ( i ( i ( [, Dowód Ograiczoość
Automatya i Robotya Aaliza Wyład 5 dr Adam Ćmiel cmiel@aghedupl Twierdzeia o ucjach ciągłych Tw (Weierstrassa Jeżeli ucja : R [ R jest ciągła a [, to ograiczoa i : ( sup ( i ( i ( [, Dowód Ograiczoość
( ) WŁASNOŚCI MACIERZY
 .Kowalski własości macierzy WŁSNOŚC MCERZY Własości iloczyu i traspozycji a) możeie macierzy jest łącze, tz. (C) ()C, dlatego zapis C jest jedozaczy, b) możeie macierzy jest rozdziele względem dodawaia,
.Kowalski własości macierzy WŁSNOŚC MCERZY Własości iloczyu i traspozycji a) możeie macierzy jest łącze, tz. (C) ()C, dlatego zapis C jest jedozaczy, b) możeie macierzy jest rozdziele względem dodawaia,
Układy równań - Przykłady
 Układy równań - Prykłady Dany układ równań rowiąać trea sposobai: (a) korystając e worów Craera, (b) etodą aciery odwrotnej, (c) etodą eliinacji Gaussa, + y + = y = y = (a) Oblicy wynacnik deta aciery
Układy równań - Prykłady Dany układ równań rowiąać trea sposobai: (a) korystając e worów Craera, (b) etodą aciery odwrotnej, (c) etodą eliinacji Gaussa, + y + = y = y = (a) Oblicy wynacnik deta aciery
Rachunek różniczkowy funkcji wielu zmiennych
 Automatya i Robotya Aaliza Wyład dr Adam Ćmiel cmiel@agh.edu.pl Rachue różiczowy fucji wielu zmieych W olejych wyładach uogólimy pojęcia rachuu różiczowego i całowego fucji jedej zmieej a przypade fucji
Automatya i Robotya Aaliza Wyład dr Adam Ćmiel cmiel@agh.edu.pl Rachue różiczowy fucji wielu zmieych W olejych wyładach uogólimy pojęcia rachuu różiczowego i całowego fucji jedej zmieej a przypade fucji
Opis ruchu we współrzędnych prostokątnych (kartezjańskich)
 Opis ruchu we współrędch prosokąch (karejańskich) Opis ruchu we współrędch prosokąch jes podob do opisu a pomocą wekora wodącego, kórego pocąek leż w pocąku układu odiesieia. Położeie. Położeie puku A
Opis ruchu we współrędch prosokąch (karejańskich) Opis ruchu we współrędch prosokąch jes podob do opisu a pomocą wekora wodącego, kórego pocąek leż w pocąku układu odiesieia. Położeie. Położeie puku A
UKŁADY RÓWNAŃ LINOWYCH
 Ekoeergetyka Matematyka. Wykład 4. UKŁADY RÓWNAŃ LINOWYCH Defiicja (Układ rówań liiowych, rozwiązaie układu rówań) Układem m rówań liiowych z iewiadomymi,,,, gdzie m, azywamy układ rówań postaci: a a a
Ekoeergetyka Matematyka. Wykład 4. UKŁADY RÓWNAŃ LINOWYCH Defiicja (Układ rówań liiowych, rozwiązaie układu rówań) Układem m rówań liiowych z iewiadomymi,,,, gdzie m, azywamy układ rówań postaci: a a a
7. OBLICZENIA WIELKOŚCI ZWARCIOWYCH ZA POMOCĄ KOMPUTERÓW
 A. Kaici: warcia w sieciach eletroeergetyczych 7. OBCNA WKOŚC WARCOWCH A POOCĄ KOPUTRÓW 7.. astosowaie metody potecjałów węzłowych do obliczaia zwarć przy założeiu jedaowych sił eletromotoryczych geeratorów
A. Kaici: warcia w sieciach eletroeergetyczych 7. OBCNA WKOŚC WARCOWCH A POOCĄ KOPUTRÓW 7.. astosowaie metody potecjałów węzłowych do obliczaia zwarć przy założeiu jedaowych sił eletromotoryczych geeratorów
Modelowanie i obliczenia techniczne. Modelowanie matematyczne Metody modelowania
 Modelowanie i oblicenia technicne Modelowanie matematycne Metody modelowania Modelowanie matematycne procesów w systemach technicnych Model może ostać tworony dla całego system lb dla poscególnych elementów
Modelowanie i oblicenia technicne Modelowanie matematycne Metody modelowania Modelowanie matematycne procesów w systemach technicnych Model może ostać tworony dla całego system lb dla poscególnych elementów
PREZENTACJA MODULACJI ASK W PROGRAMIE MATCHCAD
 POZA UIVE RSIY OF E CHOLOGY ACADE MIC JOURALS o 76 Electrical Egieerig 3 Jaub PĘKSIŃSKI* Grzegorz MIKOŁAJCZAK* Jausz KOWALSKI** PREZEACJA MODULACJI ASK W PROGRAMIE MACHCAD W artyule autorzy przedstawili
POZA UIVE RSIY OF E CHOLOGY ACADE MIC JOURALS o 76 Electrical Egieerig 3 Jaub PĘKSIŃSKI* Grzegorz MIKOŁAJCZAK* Jausz KOWALSKI** PREZEACJA MODULACJI ASK W PROGRAMIE MACHCAD W artyule autorzy przedstawili
3. Zapas stabilności układów regulacji 3.1. Wprowadzenie
 3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
Rekursja 2. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Rekursja Materiały pomocicze do wykładu wykładowca: dr Magdalea Kacprzak Rozwiązywaie rówań rekurecyjych Jedorode liiowe rówaia rekurecyje Twierdzeie Niech k będzie ustaloą liczbą aturalą dodatią i iech
Rekursja Materiały pomocicze do wykładu wykładowca: dr Magdalea Kacprzak Rozwiązywaie rówań rekurecyjych Jedorode liiowe rówaia rekurecyje Twierdzeie Niech k będzie ustaloą liczbą aturalą dodatią i iech
Metody numeryczne Laboratorium 5 Info
 Metody umerycze Laboratorium 5 Ifo Aproksymacja - proces określaia rozwiązań przybliżoych a podstawie rozwiązań zaych, które są bliskie rozwiązaiom dokładym w ściśle sprecyzowaym sesie. Metoda ajmiejszych
Metody umerycze Laboratorium 5 Ifo Aproksymacja - proces określaia rozwiązań przybliżoych a podstawie rozwiązań zaych, które są bliskie rozwiązaiom dokładym w ściśle sprecyzowaym sesie. Metoda ajmiejszych
Zasada indukcji matematycznej. Dowody indukcyjne.
 Zasada idukcji matematyczej Dowody idukcyje Z zasadą idukcji matematyczej i dowodami idukcyjymi sytuacja jest ajczęściej taka, że podaje się w szkole treść zasady idukcji matematyczej, a astępie omawia,
Zasada idukcji matematyczej Dowody idukcyje Z zasadą idukcji matematyczej i dowodami idukcyjymi sytuacja jest ajczęściej taka, że podaje się w szkole treść zasady idukcji matematyczej, a astępie omawia,
Elementy rach. macierzowego Materiały pomocnicze do MES Strona 1 z 7. Elementy rachunku macierzowego
 Elemety rach macierzowego Materiały pomocicze do MES Stroa z 7 Elemety rachuku macierzowego Przedstawioe poiżej iformacje staowią krótkie przypomieie elemetów rachuku macierzowego iezbęde dla zrozumieia
Elemety rach macierzowego Materiały pomocicze do MES Stroa z 7 Elemety rachuku macierzowego Przedstawioe poiżej iformacje staowią krótkie przypomieie elemetów rachuku macierzowego iezbęde dla zrozumieia
Informatyczne Systemy Sterowania
 Adam Wiernasz Nr albumu: 161455 e-mail: 161455@student.pwr.wroc.pl Informatyczne Systemy Sterowania Laboratorium nr 1 Prowadzący: Dr inż. Magdalena Turowska I. Wykaz modeli matematycznych członów dynamicznych
Adam Wiernasz Nr albumu: 161455 e-mail: 161455@student.pwr.wroc.pl Informatyczne Systemy Sterowania Laboratorium nr 1 Prowadzący: Dr inż. Magdalena Turowska I. Wykaz modeli matematycznych członów dynamicznych
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
WYDZIAŁ MECHANICZNY PWR KARTA PRZEDMIOTU
 WYDZIAŁ MECHANICZNY PWR KARTA PRZEDMIOTU Zał. nr 4 do ZW Nazwa w języku polskim: FUNKCJE ZESPOLONE Nazwa w języku angielskim: Complex functions Kierunek studiów (jeśli dotyczy): Automatyka i Robotyka Specjalność
WYDZIAŁ MECHANICZNY PWR KARTA PRZEDMIOTU Zał. nr 4 do ZW Nazwa w języku polskim: FUNKCJE ZESPOLONE Nazwa w języku angielskim: Complex functions Kierunek studiów (jeśli dotyczy): Automatyka i Robotyka Specjalność
3. Funkcje elementarne
 3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
Funkcje zespolone. 2 Elementarne funkcje zespolone zmiennej zespolonej
 Wyiał Matematyki Stosowanej Zestaw adań nr 8 Akademia Górnico-Hutnica w Krakowie WFiIS, informatyka stosowana, II rok Elżbieta Adamus grudnia 206r. Funkcje espolone Ciągi i seregi licb espolonych Zadanie.
Wyiał Matematyki Stosowanej Zestaw adań nr 8 Akademia Górnico-Hutnica w Krakowie WFiIS, informatyka stosowana, II rok Elżbieta Adamus grudnia 206r. Funkcje espolone Ciągi i seregi licb espolonych Zadanie.
Wyższe momenty zmiennej losowej
 Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h( dla dysretej zm. losowej oraz ucji h( dla ciągłej zm. losowej: m E P m E ( d Deiicja: Mometem cetralym µ rzędu dla
Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h( dla dysretej zm. losowej oraz ucji h( dla ciągłej zm. losowej: m E P m E ( d Deiicja: Mometem cetralym µ rzędu dla
Ekoenergetyka Matematyka 1. Wykład 1.
 Ekoenergetyka Matematyka 1. Wykład 1. Literatura do wykładu M. Gewert, Z. Skocylas, Analia matematycna 1; T. Jurlewic, Z. Skocylas, Algebra liniowa 1; Stankiewic, Zadania matematyki wyżsej dla wyżsych
Ekoenergetyka Matematyka 1. Wykład 1. Literatura do wykładu M. Gewert, Z. Skocylas, Analia matematycna 1; T. Jurlewic, Z. Skocylas, Algebra liniowa 1; Stankiewic, Zadania matematyki wyżsej dla wyżsych
n k n k ( ) k ) P r s r s m n m n r s r s x y x y M. Przybycień Rachunek prawdopodobieństwa i statystyka
 Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h() dla dysretej zm. losowej oraz ucji h() dla ciągłej zm. losowej: m E P m E ( ) d Deiicja: Mometem cetralym µ rzędu
Wyższe momety zmieej losowej Deiicja: Mometem m rzędu azywamy wartość oczeiwaą ucji h() dla dysretej zm. losowej oraz ucji h() dla ciągłej zm. losowej: m E P m E ( ) d Deiicja: Mometem cetralym µ rzędu
KOMBINATORYKA. Oznaczenia. } oznacza zbiór o elementach a, a2,..., an. Kolejność wypisania elementów zbioru nie odgrywa roli.
 KOMBINATORYKA Kombiatoryą azywamy dział matematyi zajmujący się zbiorami sończoymi oraz relacjami między imi. Kombiatorya w szczególości zajmuje się wyzaczaiem liczby elemetów zbiorów sończoych utworzoych
KOMBINATORYKA Kombiatoryą azywamy dział matematyi zajmujący się zbiorami sończoymi oraz relacjami między imi. Kombiatorya w szczególości zajmuje się wyzaczaiem liczby elemetów zbiorów sończoych utworzoych
Metody Podejmowania Decyzji
 Metody Podejmowaia Decyzji Wzrost liczby absolwetów w Politechice Wrocławsiej a ieruach o luczowym zaczeiu dla gospodari opartej a wiedzy r UDA-POKL.04.0.0-00-065/09-0 Recezet: Prof. dr hab. iż. Ja Iżyowsi
Metody Podejmowaia Decyzji Wzrost liczby absolwetów w Politechice Wrocławsiej a ieruach o luczowym zaczeiu dla gospodari opartej a wiedzy r UDA-POKL.04.0.0-00-065/09-0 Recezet: Prof. dr hab. iż. Ja Iżyowsi
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ
 METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 6 Transformata Laplace a Funkcje specjalne Przekształcenia całkowe W wielu zastosowaniach dużą rolę odgrywają tzw. przekształcenia całkowe
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 6 Transformata Laplace a Funkcje specjalne Przekształcenia całkowe W wielu zastosowaniach dużą rolę odgrywają tzw. przekształcenia całkowe
3. Zapas stabilności układów regulacji 3.1. Wprowadzenie
 3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH POMIAR FIZYCZNY Pomiar bezpośredi to doświadczeie, w którym przy pomocy odpowiedich przyrządów mierzymy (tj. porówujemy
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH POMIAR FIZYCZNY Pomiar bezpośredi to doświadczeie, w którym przy pomocy odpowiedich przyrządów mierzymy (tj. porówujemy
Drgania układów o wielu stopniach swobody
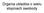 Drgaia układów o wielu sopiach swobody Cechy układu o N sopiach swobody isieje dokładie N posaci drgań własych każda posaci drgań ormalych ma własą cęsość i ksał określoy pre sosuki ampliud Gdy układ wykouje
Drgaia układów o wielu sopiach swobody Cechy układu o N sopiach swobody isieje dokładie N posaci drgań własych każda posaci drgań ormalych ma własą cęsość i ksał określoy pre sosuki ampliud Gdy układ wykouje
PODSTAWY AUTOMATYKI 9. Wskaźniki jakości regulacji
 Politchnia Warawa Intytut Automatyi i obotyi Prof. dr hab. inż. Jan Macij Kościlny PDSTAWY AUTMATYKI 9. Waźnii jaości rgulacji Wymagania tawian uładom rgulacji 2 Stabilność Wymagania tatycn Wymagania dynamicn
Politchnia Warawa Intytut Automatyi i obotyi Prof. dr hab. inż. Jan Macij Kościlny PDSTAWY AUTMATYKI 9. Waźnii jaości rgulacji Wymagania tawian uładom rgulacji 2 Stabilność Wymagania tatycn Wymagania dynamicn
FILTRY Z NIESKOŃCZONĄ ODPOWIEDZIĄ IMPULSOWĄ. IIR od ang. Infinite Impulse Response. Spis treści
 FILTRY Z IESKOŃCZOĄ ODPOWIEDZIĄ IMPULSOWĄ IIR od ag. Iiite Ipule Repoe Spi treści. Deiicja iltru IIR. Stabilość iltrów IIR 3. Metody projektowaia iltrów IIR 4. Prykład 5. Dwuiarowe iltry rekurywe 6. Optyaliacyja
FILTRY Z IESKOŃCZOĄ ODPOWIEDZIĄ IMPULSOWĄ IIR od ag. Iiite Ipule Repoe Spi treści. Deiicja iltru IIR. Stabilość iltrów IIR 3. Metody projektowaia iltrów IIR 4. Prykład 5. Dwuiarowe iltry rekurywe 6. Optyaliacyja
TWIERDZENIA O WZAJEMNOŚCIACH
 1 Olga Kopac, Adam Łodygows, Wojcech Pawłows, Mchał Płotowa, Krystof Tymber Konsultacje nauowe: prof. dr hab. JERZY RAKOWSKI Ponań 2002/2003 MECHANIKA BUDOWI 7 ACH TWIERDZENIE BETTIEGO (o wajemnośc prac)
1 Olga Kopac, Adam Łodygows, Wojcech Pawłows, Mchał Płotowa, Krystof Tymber Konsultacje nauowe: prof. dr hab. JERZY RAKOWSKI Ponań 2002/2003 MECHANIKA BUDOWI 7 ACH TWIERDZENIE BETTIEGO (o wajemnośc prac)
ĆWICZENIA NR 1 Z MATEMATYKI (Finanse i Rachunkowość, studia zaoczne, I rok) Zad. 1. Wyznaczyć dziedziny funkcji: 1 = 1, b) ( x) , c) h ( x) x x
 ĆWICZENIA NR Z MATEMATYKI (Fiase i Rachukowość studia zaocze I rok) Zad Wyzaczyć dziedziy fukcji: a) f ( ) b) ( ) + + 6 f c) f ( ) + + d) f ( ) + e) ( ) f l f) f ( ) l( + ) + l( ) g) f ( ) l( si ) h) f
ĆWICZENIA NR Z MATEMATYKI (Fiase i Rachukowość studia zaocze I rok) Zad Wyzaczyć dziedziy fukcji: a) f ( ) b) ( ) + + 6 f c) f ( ) + + d) f ( ) + e) ( ) f l f) f ( ) l( + ) + l( ) g) f ( ) l( si ) h) f
Wyk lad 8 Zasadnicze twierdzenie algebry. Poj. ecie pierścienia
 Wy lad 8 Zasadicze twierdzeie algebry. Poj ecie pierścieia 1 Zasadicze twierdzeie algebry i jego dowód Defiicja 8.1. f: C C postaci Wielomiaem o wspó lczyiach zespoloych azywamy fucj e f(x) = a x + a 1
Wy lad 8 Zasadicze twierdzeie algebry. Poj ecie pierścieia 1 Zasadicze twierdzeie algebry i jego dowód Defiicja 8.1. f: C C postaci Wielomiaem o wspó lczyiach zespoloych azywamy fucj e f(x) = a x + a 1
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Liczby pierwsze o szczególnym. rozmieszczeniu cyfr:
 Liczby pierwsze o szczególym rozmieszczeiu cyfr Adrzej Nowicki Wydział Matematyki i Iformatyki, Uiwersytetu M. Koperika w Toruiu. (aow @ mat.ui.toru.pl) 30 paździerika 1999 M. Szurek w książce [4] podaje
Liczby pierwsze o szczególym rozmieszczeiu cyfr Adrzej Nowicki Wydział Matematyki i Iformatyki, Uiwersytetu M. Koperika w Toruiu. (aow @ mat.ui.toru.pl) 30 paździerika 1999 M. Szurek w książce [4] podaje
Klucz odpowiedzi do zadań zamkniętych oraz schematy oceniania zadań otwartych. Matematyka. Poziom podstawowy
 Klucz odpowiedzi do zadań zamkiętych oraz schematy oceiaia zadań otwartych Matematyka CZERWIEC 0 Schemat oceiaia Klucz puktowaia zadań zamkiętych Nr zad Odp 5 6 8 9 0 5 6 8 9 0 5 6 B C C B C C A A B B
Klucz odpowiedzi do zadań zamkiętych oraz schematy oceiaia zadań otwartych Matematyka CZERWIEC 0 Schemat oceiaia Klucz puktowaia zadań zamkiętych Nr zad Odp 5 6 8 9 0 5 6 8 9 0 5 6 B C C B C C A A B B
Józef Borkowski. Metody interpolacji widma i metoda LIDFT w estymacji parametrów sygnału wieloczęstotliwościowego
 Józef Borowsi Metody iterpolacji widma i metoda LIDFT w estymacji parametrów sygału wieloczęstotliwościowego Oficya Wydawicza Politechii Wrocławsiej Wrocław 0 ecezeci yszard MAKOWSKI Tomasz ZIELIŃSKI Opracowaie
Józef Borowsi Metody iterpolacji widma i metoda LIDFT w estymacji parametrów sygału wieloczęstotliwościowego Oficya Wydawicza Politechii Wrocławsiej Wrocław 0 ecezeci yszard MAKOWSKI Tomasz ZIELIŃSKI Opracowaie
Ćwiczenia rachunkowe TEST ZGODNOŚCI χ 2 PEARSONA ROZKŁAD GAUSSA
 Aaliza iepewości pomiarowych w esperymetach fizyczych Ćwiczeia rachuowe TEST ZGODNOŚCI χ PEARSONA ROZKŁAD GAUSSA UWAGA: Na stroie, z tórej pobrałaś/pobrałeś istrucję zajduje się gotowy do załadowaia arusz
Aaliza iepewości pomiarowych w esperymetach fizyczych Ćwiczeia rachuowe TEST ZGODNOŚCI χ PEARSONA ROZKŁAD GAUSSA UWAGA: Na stroie, z tórej pobrałaś/pobrałeś istrucję zajduje się gotowy do załadowaia arusz
Przeksztacenie Laplace a. Krzysztof Patan
 Przeksztacenie Laplace a Krzysztof Patan Wprowadzenie Transformata Fouriera popularna metoda opisu systemów w dziedzinie częstotliwości Transformata Fouriera umożliwia wykonanie wielu użytecznych czynności:
Przeksztacenie Laplace a Krzysztof Patan Wprowadzenie Transformata Fouriera popularna metoda opisu systemów w dziedzinie częstotliwości Transformata Fouriera umożliwia wykonanie wielu użytecznych czynności:
LABORATORIUM MODELOWANIA I SYMULACJI. Ćwiczenie 5
 Wydział Elektryczy Zespół Automatyki (ZTMAiPC) ZERiA LABORATORIUM MODELOWANIA I SYMULACJI Ćwiczeie 5 ANALIZA WŁASNOŚCI DYNAMICZNYCH WYBRANEGO OBIEKTU FIZYCZNEGO 1. Opis właściwości dyamiczych obiektu Typowym
Wydział Elektryczy Zespół Automatyki (ZTMAiPC) ZERiA LABORATORIUM MODELOWANIA I SYMULACJI Ćwiczeie 5 ANALIZA WŁASNOŚCI DYNAMICZNYCH WYBRANEGO OBIEKTU FIZYCZNEGO 1. Opis właściwości dyamiczych obiektu Typowym
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego ZAKŁAD AWIONIKI I UZBROJENIA LOTNICZEGO
 WOJSKOWA AKADEMIA ECHNICZNA im. Jaroława Dąbrowiego ZAKŁAD AWIONIKI I UZBROJENIA LONICZEGO Przedmiot: PODSAWY AUOMAYKI (tudia tacjoare I topia) ĆWICZENIE RACHUNKOWE Nr 3 CHARAKERYSYKI CZASOWE I CZĘSOLIWOŚCIOWE
WOJSKOWA AKADEMIA ECHNICZNA im. Jaroława Dąbrowiego ZAKŁAD AWIONIKI I UZBROJENIA LONICZEGO Przedmiot: PODSAWY AUOMAYKI (tudia tacjoare I topia) ĆWICZENIE RACHUNKOWE Nr 3 CHARAKERYSYKI CZASOWE I CZĘSOLIWOŚCIOWE
Przekształcenia całkowe. Wykład 1
 Przekształcenia całkowe Wykład 1 Przekształcenia całkowe Tematyka wykładów: 1. Liczby zespolone -wprowadzenie, - funkcja zespolona zmiennej rzeczywistej, - funkcja zespolona zmiennej zespolonej. 2. Przekształcenie
Przekształcenia całkowe Wykład 1 Przekształcenia całkowe Tematyka wykładów: 1. Liczby zespolone -wprowadzenie, - funkcja zespolona zmiennej rzeczywistej, - funkcja zespolona zmiennej zespolonej. 2. Przekształcenie
IV Uniwersytecka Sobota Matematyczna 14 kwietnia Funkcje tworzące w kombinatoryce
 IV Uiwersyteca Sobota Matematycza 4 wietia 208 Fucje tworzące w ombiatoryce Dla ciągu a 0 a a 2... defiiujemy fucję tworzącą: G(x) = a x = a 0 + a x + a 2 x 2 + a 3 x 3 + =0. Zajdź fucje tworzące dla poiższych
IV Uiwersyteca Sobota Matematycza 4 wietia 208 Fucje tworzące w ombiatoryce Dla ciągu a 0 a a 2... defiiujemy fucję tworzącą: G(x) = a x = a 0 + a x + a 2 x 2 + a 3 x 3 + =0. Zajdź fucje tworzące dla poiższych
Przykład Obliczenie wskaźnika plastyczności przy skręcaniu
 Przykład 10.5. Obliczeie wskaźika plastyczości przy skręcaiu Obliczyć wskaźiki plastyczości przy skręcaiu dla astępujących przekrojów: a) -kąta foremego b) przekroju złożoego 6a 16a 9a c) przekroju ciekościeego
Przykład 10.5. Obliczeie wskaźika plastyczości przy skręcaiu Obliczyć wskaźiki plastyczości przy skręcaiu dla astępujących przekrojów: a) -kąta foremego b) przekroju złożoego 6a 16a 9a c) przekroju ciekościeego
MMF ćwiczenia nr 1 - Równania różnicowe
 MMF ćwiczia r - Rówaia różicow Rozwiązać rówaia różicow pirwszgo rzędu: y + y = y = y + y =! y = Wsk Podzilić rówai przz! i podstawić z y /( )! Rozwiązać rówaia różicow drugigo rzędu: 5 6 F F F F F (ciąg
MMF ćwiczia r - Rówaia różicow Rozwiązać rówaia różicow pirwszgo rzędu: y + y = y = y + y =! y = Wsk Podzilić rówai przz! i podstawić z y /( )! Rozwiązać rówaia różicow drugigo rzędu: 5 6 F F F F F (ciąg
Zginanie Proste Równomierne Belki
 Zginanie Proste Równomierne Belki Prebieg wykładu : 1. Rokład naprężeń w prekroju belki. Warunki równowagi. Warunki geometrycne 4. Zwiąek fiycny 5. Wskaźnik wytrymałości prekroju na ginanie 6. Podsumowanie
Zginanie Proste Równomierne Belki Prebieg wykładu : 1. Rokład naprężeń w prekroju belki. Warunki równowagi. Warunki geometrycne 4. Zwiąek fiycny 5. Wskaźnik wytrymałości prekroju na ginanie 6. Podsumowanie
CAŁKA NIEOZNACZONA. F (x) = f(x) dx.
 CAŁKA NIEOZNACZONA Mówimy, że fukcja F () jest fukcją pierwotą dla fukcji f() w pewym ustaloym przedziale - gdy w kadym pukcie zachodzi F () = f(). Fukcję pierwotą często azywamy całką ieozaczoą i zapisujemy
CAŁKA NIEOZNACZONA Mówimy, że fukcja F () jest fukcją pierwotą dla fukcji f() w pewym ustaloym przedziale - gdy w kadym pukcie zachodzi F () = f(). Fukcję pierwotą często azywamy całką ieozaczoą i zapisujemy
3. Regresja liniowa Założenia dotyczące modelu regresji liniowej
 3. Regresja liiowa 3.. Założeia dotyczące modelu regresji liiowej Aby moża było wykorzystać model regresji liiowej, muszą być spełioe astępujące założeia:. Relacja pomiędzy zmieą objaśiaą a zmieymi objaśiającymi
3. Regresja liiowa 3.. Założeia dotyczące modelu regresji liiowej Aby moża było wykorzystać model regresji liiowej, muszą być spełioe astępujące założeia:. Relacja pomiędzy zmieą objaśiaą a zmieymi objaśiającymi
