Wykład 6. Dynamika ośrodków sprężystych. Fale mechaniczne
|
|
|
- Sylwester Adamczyk
- 7 lat temu
- Przeglądów:
Transkrypt
1 Wkład 6 Damika ośrodków sprężsch Fale mechaicze Fale powsające w ośrodkach sprężsch (p. fale dźwiękowe) azwam falami mechaiczmi. Powsają oe w wiku wchleia jakiegoś fragmeu ośrodka z położeia rówowagi, co w asępswie powoduje drgaia fragmeu wokół ego położeia. Drgaia e (dzięki właściwościom sprężsm ośrodka) są przekazwae a koleje części ośrodka. Sam ośrodek ie przesuwa się, a jedie jego eleme wkoują drgaia w ograiczoch obszarach przesrzei. Na przkładzie fal a powierzchi wod widzim, że przedmio płwające wkoują ruch drgając aomias same fale poruszają się ruchem jedosajm. Fala dobiegające do daego przedmiou wprawiają go w ruch drgając przekazując mu eergię. Moża za pomocą fal przekazwać, więc eergię a duże odległości. Eergia fal o eergia kiecza i poecjala cząsek ośrodka. Cechą charakersczą fal jes o, że przeoszą oe eergię poprzez maerię dzięki przesuwaiu się zaburzeia w maerii a ie dzięki ruchowi posępowemu samej maerii. Do rozchodzeia się fal mechaiczch porzeb jes ośrodek. To właściwości sprężse ośrodka decdują o prędkości rozchodzeia się fali. Ze względu a kieruek drgań cząsek względem kieruku rozchodzeia się fali, rozróżiam Fale poprzecze. Przkładem fali poprzeczej są drgaia li, w kórej zachodzą oe w kieruku prosopadłm do kieruku rozchodzeia się fali (rs.vi.a). Fala a powierzchi wod eż jes falą poprzeczą. Fale podłuże. Przkładem fali podłużej jes fala, kóra powsaje w drgającej sprężie (rs.vi.b). Dla fali podłużej drgaia zachodzą w m samm kieruku w kórm rozchodzi się fala. Fale dźwiękowe, kóre emiujem głosem eż są falami podłużmi. Ze względu a czoło fali (czoło jes o powierzchia łącząca puk o jedakowch zaburzeiach w daej chwili) wróżiam fale płaskie (czoło fali jes płaszczzą i fala rozchodzi się w kieruku, prosopadłm do ej płaszczz); fale kulise (czoło fali jes kulą i fala rozchodzi się we wszskich kierukach). 53
2 Rs.VI..Fale poprzecze (a) i podłuże (b) Fale rozchodzące się w przesrzei Rozważm długą sruę aciągięą w kieruku x, wzdłuż kórego biegie fala poprzecza. W dowolej chwili a przkład 0 kszał sru moża opisać fukcją ( x) f ( x), gdzie przemieszczeie cząseczek sru wzdłuż osi O. Przpuśćm, że w miarę upłwu czasu fala biegie wzdłuż sru bez zmia kszału w prawo, czli w sroę wzrosu x. Wbierzem w chwili 0 jakiś puk fali, dla kórego wchleie sru w kieruku osi O jes rówe x ) f ( x ). Wed, po czasie fala przesuwa się o w ( prawo (gdzie - prędkość fali) i po czasie w pukcie x x + fali wchleie sru w 54
3 kieruku osi O będzie rówe x) ( x ) f ( x ). Poieważ x możem ( zapisać ( x, ) f ( x ). (VI.) Rówaie (VI.) jes więc rówaiem fali rozchodzącej się w prawą sroę sru. Kszał fali określa fukcja f ( x ). Fala rozchodząca się w lewą sroę sru, czli w sroę miejszch x - ów, określa wzór ( x, ) f ( x + ). (VI.) Isoie, ze wzoru (VI.) wika, że w chwili w pukcie x, kszał fali (wchleie sru) jes aki sam jak w chwili 0 w pukcie x 0. rgume fukcji f ( x ± ), czli ϕ ( x, ) x ±, (VI.3) x osi azwę faz drgań. jes sała Przpuśćm, że śledzim wbraą część fali, dla kórej faza drgań ϕ ( x, ) x x cos. (VI.4) Różiczkując (VI.4) względem czasu orzmujem dx d. (VI.5) zaem, prędkość rzeczwiście określa prędkość, z kórą puk mając określoe wchleie (określoą fazę) porusza się wzdłuż sru. Jes o ak zwaa prędkość fazowa. Zauważm, że dla daego 0 w fukcji fali f ( x ± ) czas jes sał i fukcja f ( x ± x0 ), gdzie x0 0, zależ lko od x i określa kszał fali w chwili 0. Jeżeli rozważm jakiś określo puk sru x, o w fukcji fali f ( x ± ) zmiea x jes sała i x fukcja f ( x ± ) zależ lko od i określa drgaia sru w pukcie x x. Rozważm eraz falę o szczególm kszałcie. Załóżm, że w chwili 0 kszał sru jes opisa fukcją π si x, (VI.6) 55
4 gdzie jes maksmalm wchleiem. Zauważm, że wchleie jes akie samo w π pukach x, x +, x +, x + 3 id., poieważ si( x) si( π π x + π ) si( + 4 π ) π si( x + 6π ) id. Wielkość azwam długością fali (odległość międz pukami o ej samej fazie). Jeżeli fala biegie w prawo o π si ( x ). (VI.7) Okres T jes czasem, w kórm fala przebiega odległość rówą, więc: T, sąd x si π. (VI.8) T Ze wzoru (VI.8) widać, że w określoej chwili aka sama faza jes w pukach x, x+, x+, x+3 id., poieważ x x x x si π si[ π + π ] si[ π + 4π ] si[ π + T T T T oraz, że w dam miejscu faza powarza się w chwilach, + T, +T, id., poieważ 6π ] id., x x si π si[ π π ] T T x si[ π T 4π ] id. Częso prz rozważaiu zjawisk falowch w fizce wprowadza się dwie owe wielkości: liczbę falową k π / i częsość kąową π / T. Wówczas dla fal biegącch w prawo i lewo możem zapisać si( kx ) lub si( kx + ) Widać, że prędkość fazowa fali jes daa wzorem T π T π k. 56
5 Rozchodzeie się fal, prędkość fal Jeżeli chcem zmierzć prędkość fali o śledzim jak przemieszcza się w czasie wbraa część fali, czli określoa faza. Wiem, że prędkość fali zależ od sprężsości ośrodka i jego bezwładości. Sprężsość dla sru jes określoa poprzez apiającą ją siłę F (a przkład im większa siła m szbciej wchloe eleme sru wracają do położeia rówowagi). Naomias bezwładość jes związaa z masą sru m oraz jego długością l. Na przkładzie drgającej sru (rs.vi.) moża udowodić, że drgaia dowolego małego odcika sru opisuje ak zwae rówaie falowe, kóre sosuje się do wszskich rodzajów rozchodzącch się fal, akich jak fale dźwiękowe cz fale elekromagecze: x. (VI.9) Tu określa wchleie małego odcika sru w kieruku prosopadłm do sru; Rs.VI.. Drgaia sru. określa prędkość poprzeczej fali F. (VI.0) µ f ( x, ) si( k x ), (VI.) rozchodzącej się w kieruku osi Ox. We wzorze (VI.0) µ m/l - masa przpadająca a jedoskę długości sru. Zwróćm uwagę, że siusoidala fala może bć przeoszoa wzdłuż sru z prędkością iezależą od ampliud ( ) i częsoliwości ( ). Ierferecja fal Ierferecją fal azwam zjawisko akładaia się fal, wskuek czego zachodzi ich wzajeme wzmocieie w jedch pukach przesrzei oraz osłabieie w ich, w zależości od sosuków faz ierferującch fal. Rozważm dwie fale o rówch częsoliwościach i ampliudach, ale o fazach różiącch się o δ. Rówaia ch fal są asępujące si( k x ), δ si( k x ). 57
6 Zajdźm eraz falę wpadkową jako sumę +. Korzsając ze wzoru a sumę siusów α + β α β si α + si β si cos, (VI.) orzmujem δ + cos si( k x δ / ), (VI.3) co jes rówaiem fali siusoidalej o ampliudzie cos( δ / ). Dla δ 0,π,4π, π mam cos( δ / ) cos( π ) ( ), a zaem fale wzmaciają się (ampliuda wpadkowej fali wzrasa o raz). Dla δ π, 3π, ( + ) π mam cos( δ / ) cos[( + ) π / ) 0, a zaem fale wgaszają się (ampliuda wpadkowej fali jes zerowa). Fale sojące Drugim przkładem ierferecji (akładaia się) fal jes fala sojąca. Rozważm dwa ciągi falowe biegące w przeciwch kierukach z. a przkład falę padającą i odbią. si( k x ), si( k x + ), Korzsając ze wzoru (XI.) dla fali wpadkowej możem zapisać + si( kx)cos( ). (VI.4) Jes o rówaie ak zwaej fali sojącej. Zauważm, że cząski drgają ruchem harmoiczm prosm. Cząski mają ę samą częsość, ale różą ampliudę zależą od położeia cząski x. Puk kx ( + ) π / (gdzie 0,,, ), dla kórch si( kx ) ± mają maksmalą ampliudę i azwają się srzałkami. Puk si( kx ) 0 mają zerową ampliudę i azwają się węzłami. kx π (gdzie 0,,, ), dla kórch 58
7 Zwróćm uwagę a jeszcze jedą isoą różicę. W przpadku fali sojącej, eergia ie jes przeoszoa wzdłuż sru (szura), bo ie może oa przepłąć przez węzł, jes a sałe zmagazowaa w poszczególch elemeach sru (szura). Układ drgające, przkład Jeżeli srua zamocowaa a obu końcach zosaie ajpierw wgięa a asępie puszczoa, o wzdłuż sru rozchodzą się drgaia poprzecze. Zaburzeia e odbijają się od zamocowach końców i w wiku ierferecji powsaje fala sojąca. Zwróćm uwagę, że drgaia sru wwarzają w oaczającm sruę powierzu dźwiękowe fale podłuże (fale akuscze). Poieważ jedm warukiem, jaki musi bć spełio, jes ieruchomość obu końców sru, czli isieie węzłów fali sojącej a ch końcach, o mogą powsać w ej sruie fale sojące o różej długości. Pierwsze czer rodzaje drgań, jakie powsają w sruie o długości L zamocowaej a końcach są pokazae a rs.vi.3. Takie fale sojące azwam rezoasami. Widzim, że długości fal spełiają związek L. (VI.5) L Korzsając z ego, że prędkość fali L 3 L/3 T v oraz podsawiając wrażeie (VI.0) możem obliczć częsoliwość rezoasów: 4 L/ ν L L F µ. (VI.6) L Rs.VI.3. Rezoase. Najiższą częsość azwam częsością podsawową a pozosałe wższmi harmoiczmi, czli alikwoami. Zazwczaj w drgaiach wsępują, oprócz drgaia podsawowego, rówież drgaia harmoicze, a dźwięki, jakie odbieram są wikiem akładaia się ch drgań. O jakości isrumeu (jego barwie) decduje właśie o ile alikwoów jes zaware w dźwięku i jakie są ich aężeia. Przkładowo, drgaie wpadkowe sru będące złożeiem ou podsawowego ( ) i wższch harmoiczch ( 3, 5, 7) o różch ampliudach jes pokazae a rs. VI.4. Zwróćm uwagę, że wpadkowe drgaie (chociaż okresowe) ie jes harmoicze (ie daje się opisać fukcją sius lub cosius). 59
8 drgaie wpadkowe Rs.VI.4. Drgaie wpadkowe sru będące złożeiem ou podsawowego ( ) i wższch harmoiczch ( 3, 5, 7) o różch ampliudach. Dudieia - modulacja ampliud Mówiliśm już o superpozcji fal, ierferecji w przesrzei (dodawaie fal o ej samej częsości). Rozparzm eraz przpadek ierferecji w czasie. Pojawia się oa, gd przez da puk w przesrzei przebiegają w m samm kieruku fale o rochę różch częsoliwościach. Wchleie wwołae przez jedą i drugą falę mają posać si( ), si( ), więc, korzsając ze wzoru (VI.), orzmujem + + cos( ) si. Drgaia wpadkowe moża, więc uważać za drgaia o częsości sredie, kóra jes średią częsością dwóch fal, i o ampliudzie (wrażeie w awiasie kwadraowm) zmieiającej się w czasie z częsością ampl. + 60
9 Jeżeli częsoliwości i są bliskie siebie o ampliuda zmieia się powoli. Mówim, że mam do czieia z modulacją ampliud M (sosowaa p. w odbiorikach radiowch). Dla fal dźwiękowch M przejawia się jako zmiaa głośości (dźwięk o wzrasa, o gaśie) i azwa się dudieiami (rs.vi.5). Rs.VI.5. Dudieia. Zjawisko Dopplera usriak, Chrisia Doppler w prac z 84 r zwrócił uwagę, że barwa świecącego ciała (częsoliwość) musi się zmieiać z powodu ruchu względego obserwaora lub źródła. Zjawisko Dopplera wsępuje dla wszskich fal (dźwiękowch, świelch id.). Obecie rozważm je dla fal dźwiękowch. Zajmiem się przpadkiem ruchu źródła i obserwaora wzdłuż łączącej ich prosej. Wbierzm układ odiesieia ieruchom względem ośrodka (a przkład powierza), w kórm biegą fale. Rozważm przpadek, dla kórego źródło dźwięku Z spoczwa w wbram układzie odiesieia, a obserwaor a przkład w samochodzie porusza się z prędkością 0 w kieruku źródła dźwięku. Rs.VI.6 Okręgi a rs.vi.6 ozaczają czoła fal oddaloch od siebie o jedą długość fali. 6
10 Gdb obserwaor bł ieruchom, a odległość źródła dźwięku od obserwaora wosiłab l, o obserwaor odbierałb obserwaora wosiłab ν / /. Tu - prędkość fal. l / / fal w czasie i częsość słszaa przez Gd obserwaor porusza się z prędkością 0 w kieruku źródła dźwięku, odległość obserwaora od źródła dźwięku zmiejsza się i w m samm czasie obserwaor odbierze 0 / dodakowch fal. Częsość słszaa przez obserwaora wosi Skąd O + v + O + O '. v + O 0 v ' v ν +. (VI.7) zaem częsość dźwięku słszaa przez obserwaora ulega zwiększeiu. Kied obserwaor oddala się od ieruchomego źródła dźwięku częsość dźwięku słszaa przez obserwaora zmiejsza się i wosi O 0 v ' v ν. (VI.8) W przpadku, gd obserwaor spoczwa, a źródło dźwięku porusza się z prędkością Z (rs.vi.7) częsość dźwięku słszaą przez obserwaora określa wzór v' ν. (VI.9) Z Rs.VI.7 Tu zak mius odosi się do ruchu źródła w kieruku obserwaora, a zak plus dla ruchu od obserwaora. 6
Wykład 11. Dynamika ośrodków sprężystych. Fale mechaniczne
 Wkład Dnamika ośrodków sprężsch Fale mechaniczne Fale powsające w ośrodkach sprężsch (np fale dźwiękowe) nazwam falami mechanicznmi Powsają one w wniku wchlenia jakiegoś fragmenu ośrodka z położenia równowagi,
Wkład Dnamika ośrodków sprężsch Fale mechaniczne Fale powsające w ośrodkach sprężsch (np fale dźwiękowe) nazwam falami mechanicznmi Powsają one w wniku wchlenia jakiegoś fragmenu ośrodka z położenia równowagi,
Rysunek 1: Fale stojące dla struny zamocowanej na obu końcach; węzły są zaznaczone liniami kropkowanymi, a strzałki przerywanymi
 Aaliza fal złożoych Autorzy: Zbigiew Kąkol, Bartek Wiedlocha Przyjrzyjmy się drgaiu poprzeczemu struy. Jeżeli strua zamocowaa a obu końcach zostaie ajpierw wygięta, a astępie puszczoa, to wzdłuż struy
Aaliza fal złożoych Autorzy: Zbigiew Kąkol, Bartek Wiedlocha Przyjrzyjmy się drgaiu poprzeczemu struy. Jeżeli strua zamocowaa a obu końcach zostaie ajpierw wygięta, a astępie puszczoa, to wzdłuż struy
Fale biegnące. y t=0 vt. y = f(x), t = 0 y = f(x - vt), t ogólne równanie fali biegnącej w prawo
 ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
Energia w ruchu harmonicznym
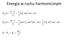 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Związek między ruchem harmonicznym a ruchem jednostajnym po okręgu
 Związek międz ruchem harmonicznm a ruchem jednosajnm po okręgu Rozważm rzu Q i R punku P na osie i : Q cos v r R sin R Q P δ Q cos ( δ ) R sin ( δ ) Jeżeli punk P porusza się ruchem jednosajnm po okręgu,
Związek międz ruchem harmonicznm a ruchem jednosajnm po okręgu Rozważm rzu Q i R punku P na osie i : Q cos v r R sin R Q P δ Q cos ( δ ) R sin ( δ ) Jeżeli punk P porusza się ruchem jednosajnm po okręgu,
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące
 Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Wykład FIZYKA I. 2. Kinematyka punktu materialnego. Dr hab. inż. Władysław Artur Woźniak
 Dr hab. iż. Władysław Arur Woźiak Wykład FIZYKA I. Kiemayka puku maerialego Dr hab. iż. Władysław Arur Woźiak Isyu Fizyki Poliechiki Wrocławskiej hp://www.if.pwr.wroc.pl/~woziak/fizyka1.hml Dr hab. iż.
Dr hab. iż. Władysław Arur Woźiak Wykład FIZYKA I. Kiemayka puku maerialego Dr hab. iż. Władysław Arur Woźiak Isyu Fizyki Poliechiki Wrocławskiej hp://www.if.pwr.wroc.pl/~woziak/fizyka1.hml Dr hab. iż.
WYZNACZANIE PRĘDKOŚCI DŹWIĘKU W POWIE- TRZU METODĄ FALI STOJĄCEJ
 Ć w i c z e i e 6 WYZNACZANIE PRĘDKOŚCI DŹWIĘKU W POWIE- TRZU METODĄ FALI STOJĄCEJ 6.1 Opis teoretyczy W ośrodkach sprężystych wytrąceie pewego obszaru z położeia rówowagi powoduje drgaia wokół tego położeia.
Ć w i c z e i e 6 WYZNACZANIE PRĘDKOŚCI DŹWIĘKU W POWIE- TRZU METODĄ FALI STOJĄCEJ 6.1 Opis teoretyczy W ośrodkach sprężystych wytrąceie pewego obszaru z położeia rówowagi powoduje drgaia wokół tego położeia.
21. CAŁKA KRZYWOLINIOWA NIESKIEROWANA. x = x(t), y = y(t), a < t < b,
 CAŁA RZYWOLINIOWA NIESIEROWANA rzywą o rówaiach parameryczych: = (), y = y(), a < < b, azywamy łukiem regularym (gładkim), gdy spełioe są asępujące waruki: a) fukcje () i y() mają ciągłe pochode, kóre
CAŁA RZYWOLINIOWA NIESIEROWANA rzywą o rówaiach parameryczych: = (), y = y(), a < < b, azywamy łukiem regularym (gładkim), gdy spełioe są asępujące waruki: a) fukcje () i y() mają ciągłe pochode, kóre
Sygnały pojęcie i klasyfikacja, metody opisu.
 Sygały pojęcie i klasyfikacja, meody opisu. Iformacja przekazywaa jes za pośredicwem sygałów, kóre przeoszą eergię. Sygał jes o fukcja czasowa dowolej wielkości o charakerze eergeyczym, w kórym moża wyróżić
Sygały pojęcie i klasyfikacja, meody opisu. Iformacja przekazywaa jes za pośredicwem sygałów, kóre przeoszą eergię. Sygał jes o fukcja czasowa dowolej wielkości o charakerze eergeyczym, w kórym moża wyróżić
Opis ruchu we współrzędnych prostokątnych (kartezjańskich)
 Opis ruchu we współrędch prosokąch (karejańskich) Opis ruchu we współrędch prosokąch jes podob do opisu a pomocą wekora wodącego, kórego pocąek leż w pocąku układu odiesieia. Położeie. Położeie puku A
Opis ruchu we współrędch prosokąch (karejańskich) Opis ruchu we współrędch prosokąch jes podob do opisu a pomocą wekora wodącego, kórego pocąek leż w pocąku układu odiesieia. Położeie. Położeie puku A
u t 1 v u(x,t) - odkształcenie, v - prędkość rozchodzenia się odkształceń (charakterystyczna dla danego ośrodka) Drgania sieci krystalicznej FONONY
 Drgaia sieci krystaliczej FONONY 1. model klasyczy (iekwatowy) a) model ośrodka ciągłego (model Debye a) - przypadek jedowymiarowy - drgaia struy drgaia mogą być podłuże (guma, sprężya) i dwie prostopadłe
Drgaia sieci krystaliczej FONONY 1. model klasyczy (iekwatowy) a) model ośrodka ciągłego (model Debye a) - przypadek jedowymiarowy - drgaia struy drgaia mogą być podłuże (guma, sprężya) i dwie prostopadłe
Mec Me han a ik i a a o gólna Wyp W a yp dko dk w o a w do d w o o w l o ne n g e o g o ukł uk a ł du du sił.
 echaika ogóla Wkład r 2 Wpadkowa dowolego układu sił. ówowaga. odzaje sił i obciążeń. odzaje ustrojów prętowch. Wzaczaie reakcji. Wpadkowa układu sił rówoległch rzłożeie układu zerowego (układ sił rówoważącch
echaika ogóla Wkład r 2 Wpadkowa dowolego układu sił. ówowaga. odzaje sił i obciążeń. odzaje ustrojów prętowch. Wzaczaie reakcji. Wpadkowa układu sił rówoległch rzłożeie układu zerowego (układ sił rówoważącch
Fale elektromagnetyczne i optyka
 Fale elekromageycze i opyka Pole elekrycze i mageycze Powsaie siły elekromooryczej musi być związae z powsaiem wirowego pola elekryczego Zmiee pole mageycze wywołuje w kaŝdym pukcie pola powsawaie wirowego
Fale elekromageycze i opyka Pole elekrycze i mageycze Powsaie siły elekromooryczej musi być związae z powsaiem wirowego pola elekryczego Zmiee pole mageycze wywołuje w kaŝdym pukcie pola powsawaie wirowego
2.6.3 Interferencja fal.
 RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
Schrödingera. Dr inż. Zbigniew Szklarski. Katedra Elektroniki, paw. C-1, pok
 Wykład 0: Rówaie Schrödigera Dr iż. Zbigiew Szklarski Kaedra Elekroiki paw. C- pok.3 szkla@agh.edu.pl hp://layer.uci.agh.edu.pl/z.szklarski/ Rówaie Schrödigera jedo z podsawowych rówań ierelaywisyczej
Wykład 0: Rówaie Schrödigera Dr iż. Zbigiew Szklarski Kaedra Elekroiki paw. C- pok.3 szkla@agh.edu.pl hp://layer.uci.agh.edu.pl/z.szklarski/ Rówaie Schrödigera jedo z podsawowych rówań ierelaywisyczej
= arc tg - eliptyczność. Polaryzacja światła. Prawo Snelliusa daje kąt. Co z amplitudą i polaryzacją? Drgania i fale II rok Fizyka BC
 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc Drgaia i fale II rok Fizyka C Polaryzacja światła ( b a) arc tg - eliptyczość Prawo Selliusa daje kąt. Co z amplitudą i polaryzacją? 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc
4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc Drgaia i fale II rok Fizyka C Polaryzacja światła ( b a) arc tg - eliptyczość Prawo Selliusa daje kąt. Co z amplitudą i polaryzacją? 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Projekt Inżynier mechanik zawód z przyszłością współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia wyrówawcze z fizyki -Zestaw 5 -Teoria Optyka geometrycza i optyka falowa. Prawo odbicia i prawo załamaia światła, Bieg promiei świetlych w pryzmacie, soczewki i zwierciadła. Zjawisko dyfrakcji
Zajęcia wyrówawcze z fizyki -Zestaw 5 -Teoria Optyka geometrycza i optyka falowa. Prawo odbicia i prawo załamaia światła, Bieg promiei świetlych w pryzmacie, soczewki i zwierciadła. Zjawisko dyfrakcji
DYNAMIKA. Dynamika jest działem mechaniki zajmującym się badaniem ruchu ciał z uwzględnieniem sił działających na ciało i wywołujących ten ruch.
 DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża
DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku.
 Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wyznaczyć prędkości punktów A i B
 Wyzaczaie prędkości i przyspieszeia puku ciała w ruchu płaskim (a) Wyzaczyć prędkości puków i Dae: rad/s; ε 0; 5 cm; 5 cm 48 mechaika echicza kiemayka 3 Wyzaczaie prędkości i przyspieszeia puku ciała w
Wyzaczaie prędkości i przyspieszeia puku ciała w ruchu płaskim (a) Wyzaczyć prędkości puków i Dae: rad/s; ε 0; 5 cm; 5 cm 48 mechaika echicza kiemayka 3 Wyzaczaie prędkości i przyspieszeia puku ciała w
ver b drgania harmoniczne
 ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
oznacza przyrost argumentu (zmiennej niezależnej) x 3A82 (Definicja). Granicę (właściwą) ilorazu różnicowego funkcji f w punkcie x x x e x lim x lim
 WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy
 Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
RUCH HARMONICZNY. sin. (r.j.o) sin
 RUCH DRGJĄCY Ruch harmoniczny Rodzaje drgań Oscylaor harmoniczny Energia oscylaora harmonicznego Wahadło maemayczne i fizyczne Drgania łumione Drgania wymuszone i zjawisko rezonansu RUCH HRMONICZNY Ruch
RUCH DRGJĄCY Ruch harmoniczny Rodzaje drgań Oscylaor harmoniczny Energia oscylaora harmonicznego Wahadło maemayczne i fizyczne Drgania łumione Drgania wymuszone i zjawisko rezonansu RUCH HRMONICZNY Ruch
III. LICZBY ZESPOLONE
 Pojęcie ciała 0 III LICZBY ZESPOLONE Defiicja 3 Niech K będie dowolm biorem Diałaiem wewętrm (krótko będiem mówić - diałaiem) w biore K awam każdą fukcję o : K K K Wartość fukcji o dla elemetów K oacam
Pojęcie ciała 0 III LICZBY ZESPOLONE Defiicja 3 Niech K będie dowolm biorem Diałaiem wewętrm (krótko będiem mówić - diałaiem) w biore K awam każdą fukcję o : K K K Wartość fukcji o dla elemetów K oacam
Przykładowe zadania dla poziomu rozszerzonego
 Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
drgania h armoniczne harmoniczne
 ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA. Ruch cząstki nieograniczony z klasycznego punktu widzenia. mamy do rozwiązania równanie 0,,
 PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu
 Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Temat: PRAWO SNELLIUSA. WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA W SZKLE I PLEKSIGLASIE.
 W S E i Z WYDZIAŁ. L A B O R A T O R I U M F I Z Y C Z N E Nr ćwicz. 9 Temat: PRAWO SNELLIUSA. WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA W SZKLE I PLEKSIGLASIE. Semestr Grupa Zespół Ocea Data / Podpis Warszawa,
W S E i Z WYDZIAŁ. L A B O R A T O R I U M F I Z Y C Z N E Nr ćwicz. 9 Temat: PRAWO SNELLIUSA. WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA W SZKLE I PLEKSIGLASIE. Semestr Grupa Zespół Ocea Data / Podpis Warszawa,
Podstawy fizyki wykład 7
 Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki sezon 1 VIII. Ruch falowy
 Podstawy fizyki sezon 1 VIII. Ruch falowy Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Gdzie szukać fal? W potocznym
Podstawy fizyki sezon 1 VIII. Ruch falowy Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Gdzie szukać fal? W potocznym
ZADANIA ZAMKNIĘTE. Zadanie 1. (1 pkt) Wartość wyrażenia. b dla a 2 3 i b 2 3 jest równa A B. 5 C. 6 D Zadanie 2.
 Zachęcam do samodzielej prac z arkuszem diagostczm. Pozaj swoje moce i słabe stro, a astępie popracuj ad słabmi. Żczę przjemego rozwiązwaia zadań. Zadaie. ( pkt) Wartość wrażeia a ZADANIA ZAMKNIĘTE b dla
Zachęcam do samodzielej prac z arkuszem diagostczm. Pozaj swoje moce i słabe stro, a astępie popracuj ad słabmi. Żczę przjemego rozwiązwaia zadań. Zadaie. ( pkt) Wartość wrażeia a ZADANIA ZAMKNIĘTE b dla
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W tym module rozpoczniemy poznawanie właściwości fal powstających w ośrodkach sprężystych (takich jak fale dźwiękowe),
 Fale mechaniczne Autorzy: Zbigniew Kąkol, Bartek Wiendlocha Ruch falowy jest bardzo rozpowszechniony w przyrodzie. Na co dzień doświadczamy obecności fal dźwiękowych i fal świetlnych. Powszechnie też wykorzystujemy
Fale mechaniczne Autorzy: Zbigniew Kąkol, Bartek Wiendlocha Ruch falowy jest bardzo rozpowszechniony w przyrodzie. Na co dzień doświadczamy obecności fal dźwiękowych i fal świetlnych. Powszechnie też wykorzystujemy
, gdzie b 4c 0 oraz n, m ( 2). 2 2 b b b b b c b x bx c x x c x x
 Meody aeaycze w echologii aeriałów Uwaga: Proszę paięać, że a zajęciach obowiązuje akże zajoość oówioych w aeriałach przykładów!!! CAŁKOWANIE FUNKCJI WYMIERNYCH Fukcją wyierą azyway fukcję posaci P ( )
Meody aeaycze w echologii aeriałów Uwaga: Proszę paięać, że a zajęciach obowiązuje akże zajoość oówioych w aeriałach przykładów!!! CAŁKOWANIE FUNKCJI WYMIERNYCH Fukcją wyierą azyway fukcję posaci P ( )
Wytrzymałość materiałów
 Wtrzmałość materiałów IMiR - IA - Wkład Nr 8 Aaliza stau aprężeia Sta aprężeia w pukcie, tesor aprężeia, klasfikacja staów aprężeia, aaliza jedoosiowego stau aprężeia, aaliza płaskiego stau aprężeia, koło
Wtrzmałość materiałów IMiR - IA - Wkład Nr 8 Aaliza stau aprężeia Sta aprężeia w pukcie, tesor aprężeia, klasfikacja staów aprężeia, aaliza jedoosiowego stau aprężeia, aaliza płaskiego stau aprężeia, koło
Wykład FIZYKA I. 2. Kinematyka punktu materialnego. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
. Dla każdego etapu t znamy funkcję transformacji stanu (funkcja przejścia):
 D Miszczńska, M Miszczński, KBO UŁ, Eleme programowaia damiczego Eleme PROGRAMOWANIA DYNAMICZNEGO (PD) Rozważam -eapow proces deczj: eap eap 2 eap - eap sa począkow 2 deczja x x x 2 x Sa procesu a począek
D Miszczńska, M Miszczński, KBO UŁ, Eleme programowaia damiczego Eleme PROGRAMOWANIA DYNAMICZNEGO (PD) Rozważam -eapow proces deczj: eap eap 2 eap - eap sa począkow 2 deczja x x x 2 x Sa procesu a począek
MATEMATYKA wykład 1. Ciągi. Pierwsze 2 ciągi są rosnące (do nieskończoności), zaś 3-i ciąg jest zbieŝny do zera. co oznaczamy przez
 MATEMATYKA wkład Ciągi,, 2, 3, 4,,, 3, 5, 7, 9,,,,,,,,, są przkładami ciągów 2 4 6 8 Pierwsze 2 ciągi są rosące (do ieskończoości), zaś 3-i ciąg jes zbieŝ do zera co ozaczam przez lim a ch 2-óch ciągów,
MATEMATYKA wkład Ciągi,, 2, 3, 4,,, 3, 5, 7, 9,,,,,,,,, są przkładami ciągów 2 4 6 8 Pierwsze 2 ciągi są rosące (do ieskończoości), zaś 3-i ciąg jes zbieŝ do zera co ozaczam przez lim a ch 2-óch ciągów,
Podstawy wytrzymałości materiałów
 Podstaw wtrzmałości materiałów IMiR - MiBM - Wkład Nr 4 Aaliza stau aprężeia Sta aprężeia w pukcie, tesor aprężeia, klasfikacja staów aprężeia, aaliza jedoosiowego stau aprężeia, aaliza płaskiego stau
Podstaw wtrzmałości materiałów IMiR - MiBM - Wkład Nr 4 Aaliza stau aprężeia Sta aprężeia w pukcie, tesor aprężeia, klasfikacja staów aprężeia, aaliza jedoosiowego stau aprężeia, aaliza płaskiego stau
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Ciągi i szeregi liczbowe. Ciągi nieskończone.
 Ciągi i szeregi liczbowe W zbiorze liczb X jest określoa pewa fukcja f, jeŝeli kaŝdej liczbie x ze zbioru X jest przporządkowaa dokładie jeda liczba pewego zbioru liczb Y Przporządkowaie to zapisujem w
Ciągi i szeregi liczbowe W zbiorze liczb X jest określoa pewa fukcja f, jeŝeli kaŝdej liczbie x ze zbioru X jest przporządkowaa dokładie jeda liczba pewego zbioru liczb Y Przporządkowaie to zapisujem w
Fale mechaniczne i akustyka
 Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)
 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Kinetyczna teoria gazów. Zjawiska transportu : dyfuzja transport masy transport energii przewodnictwo cieplne transport pędu lepkość
 Kieycza eoria gazów Zjawiska rasporu : dyfuzja raspor masy raspor eergii przewodicwo cieple raspor pędu lepkość Zjawiska rasporu - dyfuzja syuacja począkowa brak rówowagi proces wyrówywaia koceracji -
Kieycza eoria gazów Zjawiska rasporu : dyfuzja raspor masy raspor eergii przewodicwo cieple raspor pędu lepkość Zjawiska rasporu - dyfuzja syuacja począkowa brak rówowagi proces wyrówywaia koceracji -
TRANZYSTORY POLOWE JFET I MOSFET
 POLTECHNKA RZEZOWKA Kaedra Podsaw Elekroiki srukcja Nr5 F 00/003 sem. lei TRANZYTORY POLOWE JFET MOFET Cel ćwiczeia: Pomiar podsawowych charakerysyk i wyzaczeie paramerów określających właściwości razysora
POLTECHNKA RZEZOWKA Kaedra Podsaw Elekroiki srukcja Nr5 F 00/003 sem. lei TRANZYTORY POLOWE JFET MOFET Cel ćwiczeia: Pomiar podsawowych charakerysyk i wyzaczeie paramerów określających właściwości razysora
Fizyka dla Informatyki Stosowanej
 Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Narzędzia matematyczne potrzebne w kursie Reakcje w ciele stałym
 Narzędzia maemacze porzebe w kursie Reakcje w ciele sałm Pochoda fukcji jedej zmieej Defiicja, własości rachukowe, wzór a pochodą fukcji złożoej, szereg Talora, pochode fukcji elemearch. Pochoda fukcji
Narzędzia maemacze porzebe w kursie Reakcje w ciele sałm Pochoda fukcji jedej zmieej Defiicja, własości rachukowe, wzór a pochodą fukcji złożoej, szereg Talora, pochode fukcji elemearch. Pochoda fukcji
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Niepewności pomiarowe
 Niepewości pomiarowe Obserwacja, doświadczeie, pomiar Obserwacja zjawisk fizyczych polega a badaiu ych zjawisk w warukach auralych oraz a aalizie czyików i waruków, od kórych zjawiska e zależą. Waruki
Niepewości pomiarowe Obserwacja, doświadczeie, pomiar Obserwacja zjawisk fizyczych polega a badaiu ych zjawisk w warukach auralych oraz a aalizie czyików i waruków, od kórych zjawiska e zależą. Waruki
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Wektory. P. F. Góra. rok akademicki
 Wektor P. F. Góra rok akademicki 009-0 Wektor zwiazan. Wektorem zwiazanm nazwam parę punktów. Jeżeli parę tę stanowią punkt,, wektor przez nie utworzon oznaczm. Graficznie koniec wektora oznaczam strzałką.
Wektor P. F. Góra rok akademicki 009-0 Wektor zwiazan. Wektorem zwiazanm nazwam parę punktów. Jeżeli parę tę stanowią punkt,, wektor przez nie utworzon oznaczm. Graficznie koniec wektora oznaczam strzałką.
5.1. Powstawanie i rozchodzenie się fal mechanicznych.
 5. Fale mechaniczne 5.1. Powstawanie i rozchodzenie się fal mechanicznych. Ruch falowy jest zjawiskiem bardzo rozpowszechnionym w przyrodzie. Spotkałeś się z pewnością w życiu codziennym z takimi pojęciami
5. Fale mechaniczne 5.1. Powstawanie i rozchodzenie się fal mechanicznych. Ruch falowy jest zjawiskiem bardzo rozpowszechnionym w przyrodzie. Spotkałeś się z pewnością w życiu codziennym z takimi pojęciami
Projekt Inżynier mechanik zawód z przyszłością współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia wyrównawcze z izyki -Zestaw 13 -eoria Drgania i ale. Ruch drgający harmoniczny, równanie ali płaskiej, eekt Dopplera, ale stojące. Siła harmoniczna, ruch drgający harmoniczny Siłą harmoniczną (sprężystości)
Zajęcia wyrównawcze z izyki -Zestaw 13 -eoria Drgania i ale. Ruch drgający harmoniczny, równanie ali płaskiej, eekt Dopplera, ale stojące. Siła harmoniczna, ruch drgający harmoniczny Siłą harmoniczną (sprężystości)
Cechy szeregów czasowych
 energecznch Cech szeregów czasowch Rozdział Modelowanie szeregów czasowch 7 proces deerminisczn proces kórego warość może bć preczjnie określona w dowolnm czasie =T+τ = a +b T T+τ czas = sin(ω) T T+τ czas
energecznch Cech szeregów czasowch Rozdział Modelowanie szeregów czasowch 7 proces deerminisczn proces kórego warość może bć preczjnie określona w dowolnm czasie =T+τ = a +b T T+τ czas = sin(ω) T T+τ czas
VII MIĘDZYNARODOWA OLIMPIADA FIZYCZNA (1974). Zad. teoretyczne T3.
 KOOF Szczeci: www.of.szc.pl VII MIĘDZYNAODOWA OLIMPIADA FIZYCZNA (1974). Zad. teoretycze T3. Źródło: Komitet Główy Olimpiady Fizyczej; Olimpiada Fizycza XXIII XXIV, WSiP Warszawa 1977 Autor: Waldemar Gorzkowski
KOOF Szczeci: www.of.szc.pl VII MIĘDZYNAODOWA OLIMPIADA FIZYCZNA (1974). Zad. teoretycze T3. Źródło: Komitet Główy Olimpiady Fizyczej; Olimpiada Fizycza XXIII XXIV, WSiP Warszawa 1977 Autor: Waldemar Gorzkowski
Ćw. 20. Pomiary współczynnika załamania światła z pomiarów kąta załamania oraz kąta granicznego
 0 KATEDRA FIZYKI STOSOWANEJ PRACOWNIA FIZYKI Ćw. 0. Pomiary współczyika załamaia światła z pomiarów kąta załamaia oraz kąta graiczego Wprowadzeie Światło widziale jest promieiowaiem elektromagetyczym o
0 KATEDRA FIZYKI STOSOWANEJ PRACOWNIA FIZYKI Ćw. 0. Pomiary współczyika załamaia światła z pomiarów kąta załamaia oraz kąta graiczego Wprowadzeie Światło widziale jest promieiowaiem elektromagetyczym o
Obligacja i jej cena wewnętrzna
 Obligacja i jej cea wewęrza Obligacja jes o isrume fiasowy (papier warościowy), w kórym jeda sroa, zwaa emieem obligacji, swierdza, że jes dłużikiem drugiej sroy, zwaej obligaariuszem (jes o właściciel
Obligacja i jej cea wewęrza Obligacja jes o isrume fiasowy (papier warościowy), w kórym jeda sroa, zwaa emieem obligacji, swierdza, że jes dłużikiem drugiej sroy, zwaej obligaariuszem (jes o właściciel
3. Wykład III: Warunki optymalności dla zadań bez ograniczeń
 3 Wkład III: Waruki optmalości dla zadań bez ograiczeń Podae poiże waruki optmalości dla są uogólieiem powszechie zach waruków dla fukci ede zmiee (zerowaie się pierwsze pochode i lokala wpukłość) 3 Twierdzeie
3 Wkład III: Waruki optmalości dla zadań bez ograiczeń Podae poiże waruki optmalości dla są uogólieiem powszechie zach waruków dla fukci ede zmiee (zerowaie się pierwsze pochode i lokala wpukłość) 3 Twierdzeie
WYKŁAD FIZYKAIIIB 2000 Drgania tłumione
 YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
DEA podstawowe modele
 Marek Miszczński KBO UŁ 2008 - Aaliza dach graiczch (EA) cz.2 (przkład aaliza damiki rakigi) EA podsawowe modele WPROWAZENIE Efekwość (produkwość) obieku gospodarczego o es defiiowaa ako sosuek sum ważoch
Marek Miszczński KBO UŁ 2008 - Aaliza dach graiczch (EA) cz.2 (przkład aaliza damiki rakigi) EA podsawowe modele WPROWAZENIE Efekwość (produkwość) obieku gospodarczego o es defiiowaa ako sosuek sum ważoch
(x 1 y 1 ) (x n y n ) 2. 1<j<m x i y i. x2 y 2 gdy x 1 = y 1 x 2 y 2 + x 1 + y 1 gdy x 1 = y 1. gdy x, y, 0 nie są współliniowe
 . Metrka Zadaie.. Pokazać, że metrka jest fukcją ieujemą. Zadaie.2. Odowodić, że poiższe wzor defiiuja metrki. a) (metrka euklidesowa) X = R. d e (, ) := ( ) 2 +... + ( ) 2 b) (metrka taksówkowa) X = R
. Metrka Zadaie.. Pokazać, że metrka jest fukcją ieujemą. Zadaie.2. Odowodić, że poiższe wzor defiiuja metrki. a) (metrka euklidesowa) X = R. d e (, ) := ( ) 2 +... + ( ) 2 b) (metrka taksówkowa) X = R
FALE W OŚRODKACH SPRĘZYSTYCH
 ALE W OŚRODKACH SPRĘZYSTYCH PRZYKŁADY RUCHU ALOWEGO Zjawisko rozchodzenia się fal spotykamy powszechnie. Przykładami są fale na wodzie, fale dźwiękowe, poruszający się front przewracających się kostek
ALE W OŚRODKACH SPRĘZYSTYCH PRZYKŁADY RUCHU ALOWEGO Zjawisko rozchodzenia się fal spotykamy powszechnie. Przykładami są fale na wodzie, fale dźwiękowe, poruszający się front przewracających się kostek
Jarosław Wróblewski Analiza Matematyczna 2, lato 2018/19
 7 Wyzaczyć zbiór wszyskich warości rzeczywisych parameru p, dla kórych całka iewłaściwa jes zbieża x xe Dzieląc przedział całkowaia orzymujemy x x e x x e x x e Zbadamy, dla kórych warości parameru p całki
7 Wyzaczyć zbiór wszyskich warości rzeczywisych parameru p, dla kórych całka iewłaściwa jes zbieża x xe Dzieląc przedział całkowaia orzymujemy x x e x x e x x e Zbadamy, dla kórych warości parameru p całki
ELEMENTY OPTYKI GEOMETRYCZNEJ
 ELEMENTY OPTYKI GEOMETRYCZNEJ Optyka to dział fizyki, zajmujący się badaiem atury światła, początkowo tylko widzialego, a obecie rówież promieiowaia z zakresów podczerwiei i adfioletu. Optyka - geometrycza
ELEMENTY OPTYKI GEOMETRYCZNEJ Optyka to dział fizyki, zajmujący się badaiem atury światła, początkowo tylko widzialego, a obecie rówież promieiowaia z zakresów podczerwiei i adfioletu. Optyka - geometrycza
Funkcje falowe równanie Schroedingera
 Fukcje falowe rówaie Schroedigera Fukcja falowa kwatowa iterpretacja jedo wmiarowe pułapki elektroów fukcje falowe ieskończoa i skończoa studia potecjału atom wodoru rówaie Schroedigera wprowadzeie i rozwiązaia
Fukcje falowe rówaie Schroedigera Fukcja falowa kwatowa iterpretacja jedo wmiarowe pułapki elektroów fukcje falowe ieskończoa i skończoa studia potecjału atom wodoru rówaie Schroedigera wprowadzeie i rozwiązaia
D:\materialy\Matematyka na GISIP I rok DOC\07 Pochodne\8A.DOC 2004-wrz-15, 17: Obliczanie granic funkcji w punkcie przy pomocy wzoru Taylora.
 D:\maerialy\Maemayka a GISIP I rok DOC\7 Pochode\8ADOC -wrz-5, 7: 89 Obliczaie graic fukcji w pukcie przy pomocy wzoru Taylora Wróćmy do wierdzeia Taylora (wzory (-( Tw Szczególie waża dla dalszych R rozważań
D:\maerialy\Maemayka a GISIP I rok DOC\7 Pochode\8ADOC -wrz-5, 7: 89 Obliczaie graic fukcji w pukcie przy pomocy wzoru Taylora Wróćmy do wierdzeia Taylora (wzory (-( Tw Szczególie waża dla dalszych R rozważań
ν = c/λ [s -1 = Hz] ν = [cm -1 ] ZASADY ZALICZENIA PRZEDMIOTU MBS c = m/s cos x H = H o E = E o cos x c = λν 1 ν = _ λ
![ν = c/λ [s -1 = Hz] ν = [cm -1 ] ZASADY ZALICZENIA PRZEDMIOTU MBS c = m/s cos x H = H o E = E o cos x c = λν 1 ν = _ λ ν = c/λ [s -1 = Hz] ν = [cm -1 ] ZASADY ZALICZENIA PRZEDMIOTU MBS c = m/s cos x H = H o E = E o cos x c = λν 1 ν = _ λ](/thumbs/91/105360049.jpg) ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM Z MBS. ROZWIĄZYWANIE WIDM kolokwium NMR 23 kwietia 208 IR maja 208 złożoe czerwca 208 poiedziałek czwartek piątek 9.3 22.3 23.3 26.3 5. 6. 9. 2. 3. H NMR 23.
ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM Z MBS. ROZWIĄZYWANIE WIDM kolokwium NMR 23 kwietia 208 IR maja 208 złożoe czerwca 208 poiedziałek czwartek piątek 9.3 22.3 23.3 26.3 5. 6. 9. 2. 3. H NMR 23.
STATYSTYCZNY OPIS UKŁADU CZĄSTEK
 WYKŁAD 6 STATYSTYCZNY OPIS UKŁADU CZĄSTK Zespół statcz moża opisać: ) Klasczie pzestzeń fazowa P ( P PN, q, q q N) q Każda kofiguacja N cząstek zespołu statczego opisaa jest puktem w pzestzei fazowej.
WYKŁAD 6 STATYSTYCZNY OPIS UKŁADU CZĄSTK Zespół statcz moża opisać: ) Klasczie pzestzeń fazowa P ( P PN, q, q q N) q Każda kofiguacja N cząstek zespołu statczego opisaa jest puktem w pzestzei fazowej.
201. a 1 a 2 a 3...a n a 2 1 +a 2 2 +a a 2 n n a 4 1 +a 4 2 +a a 4 n n. a1 + a 2 + a a n 204.
 Liczby rzeczywiste dodatie a 1, a 2, a 3,...a spełiają waruek a 1 +a 2 +a 3 +...+a =. Wpisać w kratkę zak lub i udowodić podaą ierówość bez korzystaia z gotowych twierdzeń (moża korzystać z wcześiejszych
Liczby rzeczywiste dodatie a 1, a 2, a 3,...a spełiają waruek a 1 +a 2 +a 3 +...+a =. Wpisać w kratkę zak lub i udowodić podaą ierówość bez korzystaia z gotowych twierdzeń (moża korzystać z wcześiejszych
Zadania domowe z Analizy Matematycznej III - czȩść 2 (funkcje wielu zmiennych)
 Zadaia domowe z AM III dla grup E7 (semestr zimow 07/08) Czȩść Zadaia domowe z Aaliz Matematczej III - czȩść (fukcje wielu zmiech) Zadaie. Obliczć graice lub wkazać że ie istiej a: (a) () (00) (b) + ()
Zadaia domowe z AM III dla grup E7 (semestr zimow 07/08) Czȩść Zadaia domowe z Aaliz Matematczej III - czȩść (fukcje wielu zmiech) Zadaie. Obliczć graice lub wkazać że ie istiej a: (a) () (00) (b) + ()
Wydział EAIiE Kierunek: Elektrotechnika. Wykład 12: Fale. Przedmiot: Fizyka. RUCH FALOWY -cd. Wykład /2009, zima 1
 RUCH FALOWY -cd Wykład 9 2008/2009, zima 1 Energia i moc (a) dla y=y m, E k =0, E p =0 (b) dla y=0 drgający element liny uzyskuje maksymalną energię kinetyczną i potencjalną sprężystości (jest maksymalnie
RUCH FALOWY -cd Wykład 9 2008/2009, zima 1 Energia i moc (a) dla y=y m, E k =0, E p =0 (b) dla y=0 drgający element liny uzyskuje maksymalną energię kinetyczną i potencjalną sprężystości (jest maksymalnie
W wielu przypadkach zadanie teorii sprężystości daje się zredukować do dwóch
 Wykład 5 PŁASKI ZADANI TORII SPRĘŻYSTOŚCI Płaski sta arężeia W wielu rzyadkach zadaie teorii srężystości daje się zredukować do dwóch wymiarów Przykładem może być cieka tarcza obciążoa siłami działającymi
Wykład 5 PŁASKI ZADANI TORII SPRĘŻYSTOŚCI Płaski sta arężeia W wielu rzyadkach zadaie teorii srężystości daje się zredukować do dwóch wymiarów Przykładem może być cieka tarcza obciążoa siłami działającymi
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Płaskie układy obciąŝeń. Opis analityczny wielkości podstawowych. wersory. mechanika techniczna i wytrzymałość materiałów 1 statyka 2
 Opis aalitcz wielkości podstawowch wersor e x, e Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B ) ) Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B )
Opis aalitcz wielkości podstawowch wersor e x, e Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B ) ) Opis aalitcz wielkości podstawowch współrzęde puktów A( x A, B( x B, A B )
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy I Etap ZADANIA 27 lutego 2013r.
 V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Krzywe na płaszczyźnie.
 Krzwe na płaszczźnie. Współrzędne paramerczne i biegunowe. Współrzędne biegunowe. Dan jes punk O, zwan biegunem, kór sanowi począek półprosej, zwanej półosią. Dowoln punk P na płaszczźnie można opisać
Krzwe na płaszczźnie. Współrzędne paramerczne i biegunowe. Współrzędne biegunowe. Dan jes punk O, zwan biegunem, kór sanowi począek półprosej, zwanej półosią. Dowoln punk P na płaszczźnie można opisać
3. Regresja liniowa Założenia dotyczące modelu regresji liniowej
 3. Regresja liiowa 3.. Założeia dotyczące modelu regresji liiowej Aby moża było wykorzystać model regresji liiowej, muszą być spełioe astępujące założeia:. Relacja pomiędzy zmieą objaśiaą a zmieymi objaśiającymi
3. Regresja liiowa 3.. Założeia dotyczące modelu regresji liiowej Aby moża było wykorzystać model regresji liiowej, muszą być spełioe astępujące założeia:. Relacja pomiędzy zmieą objaśiaą a zmieymi objaśiającymi
Wygładzanie metodą średnich ruchomych w procesach stałych
 Wgładzanie meodą średnich ruchomch w procesach sałch Cel ćwiczenia. Przgoowanie procedur Średniej Ruchomej (dla ruchomego okna danch); 2. apisanie procedur do obliczenia sandardowego błędu esmacji;. Wizualizacja
Wgładzanie meodą średnich ruchomch w procesach sałch Cel ćwiczenia. Przgoowanie procedur Średniej Ruchomej (dla ruchomego okna danch); 2. apisanie procedur do obliczenia sandardowego błędu esmacji;. Wizualizacja
Fale dźwiękowe. Jak człowiek ocenia natężenie bodźców słuchowych? dr inż. Romuald Kędzierski
 Fale dźwiękowe Jak człowiek ocenia natężenie bodźców słuchowych? dr inż. Romuald Kędzierski Podstawowe cechy dźwięku Ze wzrostem częstotliwości rośnie wysokość dźwięku Dźwięk o barwie złożonej składa się
Fale dźwiękowe Jak człowiek ocenia natężenie bodźców słuchowych? dr inż. Romuald Kędzierski Podstawowe cechy dźwięku Ze wzrostem częstotliwości rośnie wysokość dźwięku Dźwięk o barwie złożonej składa się
Wykład 3: Jak wygląda dźwięk? Katarzyna Weron. Matematyka Stosowana
 Wykład 3: Jak wygląda dźwięk? Katarzyna Weron Matematyka Stosowana Fala dźwiękowa Podłużna fala rozchodząca się w ośrodku Powietrzu Wodzie Ciele stałym (słyszycie czasem sąsiadów?) Prędkość dźwięku: stal
Wykład 3: Jak wygląda dźwięk? Katarzyna Weron Matematyka Stosowana Fala dźwiękowa Podłużna fala rozchodząca się w ośrodku Powietrzu Wodzie Ciele stałym (słyszycie czasem sąsiadów?) Prędkość dźwięku: stal
Wykład FIZYKA I. 11. Fale mechaniczne. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Znikanie sumy napięć ïród»owych i sumy prądów w wielofazowym układzie symetrycznym
 Obwody trójfazowe... / OBWODY TRÓJFAZOWE Zikaie sumy apięć ïród»owych i sumy prądów w wielofazowym układzie symetryczym liczba faz układu, α 2π / - kąt pomiędzy kolejymi apięciami fazowymi, e jα, e -jα
Obwody trójfazowe... / OBWODY TRÓJFAZOWE Zikaie sumy apięć ïród»owych i sumy prądów w wielofazowym układzie symetryczym liczba faz układu, α 2π / - kąt pomiędzy kolejymi apięciami fazowymi, e jα, e -jα
FUNKCJE DWÓCH ZMIENNYCH
 FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
PROGNOZOWANIE. Ćwiczenia 3. tel.: (061)
 Ćwiczeia 3 mgr iż.. Mara Krueger mara.krueger@edu.wsl.com.pl mara.krueger@ilim.poza.pl el.: (06 850 49 57 Meod progozowaia krókoermiowego sał poziom red sezoowość Y Y Y Czas Czas Czas Model aiw Modele
Ćwiczeia 3 mgr iż.. Mara Krueger mara.krueger@edu.wsl.com.pl mara.krueger@ilim.poza.pl el.: (06 850 49 57 Meod progozowaia krókoermiowego sał poziom red sezoowość Y Y Y Czas Czas Czas Model aiw Modele
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni. Dla próżni równania Maxwella w tzw. postaci różniczkowej są następujące:
 Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
Pierwiastki z liczby zespolonej. Autorzy: Agnieszka Kowalik
 Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
Celem ćwiczenia jest badanie zjawiska Dopplera dla fal dźwiękowych oraz wykorzystanie tego zjawiska do wyznaczania prędkości dźwięku w powietrzu.
 Efekt Dopplera Cel ćwiczenia Celem ćwiczenia jest badanie zjawiska Dopplera dla fal dźwiękowych oraz wykorzystanie tego zjawiska do wyznaczania prędkości dźwięku w powietrzu. Wstęp Fale dźwiękowe Na czym
Efekt Dopplera Cel ćwiczenia Celem ćwiczenia jest badanie zjawiska Dopplera dla fal dźwiękowych oraz wykorzystanie tego zjawiska do wyznaczania prędkości dźwięku w powietrzu. Wstęp Fale dźwiękowe Na czym
Podstawowe pojęcia optyki geometrycznej. c prędkość światła w próżni v < c prędkość światła w danym ośrodku
 Optyka geometrycza Podstawowe pojęcia optyki geometryczej Bezwzględy współczyik załamaia c prędkość światła w próżi v < c prędkość światła w daym ośrodku c v > 1 Aksjomaty Światło w ośrodku jedorodym propaguje
Optyka geometrycza Podstawowe pojęcia optyki geometryczej Bezwzględy współczyik załamaia c prędkość światła w próżi v < c prędkość światła w daym ośrodku c v > 1 Aksjomaty Światło w ośrodku jedorodym propaguje
