BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO NA IDENTYFIKACJĘ CHAOSU DETERMINISTYCZNEGO W EKONOMICZNYCH SZEREGACH CZASOWYCH
|
|
|
- Jakub Damian Kwiatkowski
- 7 lat temu
- Przeglądów:
Transkrypt
1 Katazyna Zeug-Żebo Uniwesytet Śląski w Katowicach BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO NA IDENTYFIKACJĘ CHAOSU DETERMINISTYCZNEGO W EKONOMICZNYCH SZEREGACH CZASOWYCH Wpowazenie Wieloletnie baania związane z ientyfikacją ynamiki chaotycznej wykazały, że w wielu pzypakach stanaowe metoy analizy szeegów czasowych, tj. funkcja autokoelacji i analiza spektalna, nie są w stanie oóżnić szeegów eteministycznych o losowych. Z tego powou pojęto pace baawcze, któych celem było stwozenie meto na tyle czułych, by wychwycić te subtelne óżnice. Najczęściej w celu oóżnienia szeegów eteministycznych o losowych wykozystuje się największy wykłanik Lapunowa i wymia koelacyjny. Jenak w baaniach można zastosować ównież inne metoy, np. test BDS. Celem atykułu bęzie baanie wpływu eukcji poziomu szumu na ientyfikację chaosu w wybanych finansowych szeegach czasowych. Nazęziami służącym o oóżniania szeegów chaotycznych o losowych bęzie statystyka BDS oaz wymia koelacyjny. W baaniach wykozystano szeegi utwozone z cen zamknięcia WIG i WIG0, wóch spółek notowanych na Giełzie Papieów Watościowych w Waszawie: INGBSK i Vistula oaz wóch kusów walut: funta bytyjskiego i olaa ameykańskiego. Dane obejmują okes o.0.99 o Obliczenia pzepowazono pzy użyciu pogamów napisanych pzez autokę w języku pogamowania Delphi, pakietu Micosoft Excel, EViews.0 oaz TISEAN.
2 BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO. Reukcja poziomu szumu metoą najbliższych sąsiaów Zaaniem metoy najbliższych sąsiaów [Kantz, Scheibe, 997] jest poział szeegu czasowego x t na część eteministyczną x t i część stochastyczną ξ t : x t = x t + ξt, () gzie: ξ t ma szybko malejącą funkcję autokoelacji i jest nieskoelowana z x t. l v v vk W celu wyznaczenia x l, la ustalonego l, tzeba ozważyć wekto opóźnień [Takens, 98] ( histoię): x i = x i,x i+τ,x i+τ,,x i+(-)τ T, w pzypaku, gy opóźnienie czasowe τ pzyjmuje watość jeen ( jest wymiaem zanuzenia). Wtey jeną ze śokowych współzęnych tego wektoa jest filtowana obsewacja x l, np. xˆ l la pazystej watości wymiau zanuzenia, xˆ + l la niepazystej watości. Następnie należy ustalić k najbliższych sąsiaów wektoa xˆ : xˆ, xˆ,..., xˆ. Na postawie wyznaczonych najbliższych sąsiaów, watość eteministyczną x l należy wyliczyć ze wzou: x l = k k i= x vi. () Jenym z paametów miezących efektywność filtacji szeegu jest współczynnik poziomu eukcji szumu NRL [Ozeszko, 00]: NRL T ( ) = T mi T i= T i= M i, () gzie: m i i M i oznaczają oległości o i-tego stanu (wektoa opóźnień) o jego najbliższego i najalszego sąsiaa. Współczynnik ten baa zależność pomięzy siłą szumu oawanego o ukłau a stuktuą geometyczną jego ataktoa [Zawazki, 996]. Kozystając z powyższej miay, należy wybać spośó otzymanych szeegów taki, la któego współczynnik NRL pzyjmuje najmniejszą watość.. Statystyka BDS Statystyka BDS została wpowazona w 987. pzez W. Bocka, W. Decheta i J. Scheinkmana [987]. Bazuje ona na pojęciu całki koelacyjnej i jest jenym z niepaametycznych testów weyfikujących hipotezę H 0, że zbió anych jest i.i.., czyli zbioem niezależnych zmiennych losowych o jenakowym ozkłazie.
3 6 Katazyna Zeug-Żebo Całka koelacyjna okeśla pawopoobieństwo znalezienia pay wektoów, któych oległość o siebie w zekonstuowanej -wymiaowej pzestzeni nie jest większa o : C (, N, ) = ( ) n n i= j= i+ n n I ( ), > 0 I(x) jest funkcją wskaźnikową (funkcja Heavisie a) postaci: ij, () 0 la a < 0 I ( a) =, () la a 0 n = N ( )τ jest liczbą wektoów w wymiaowej pzestzeni, τ jest watością opóźnienia czasowego, N jest liczbą anych oaz: ij = l= 0 ( x x ) i+ l j+ l. (6) W pacy pokazano, że la każego > oaz > 0 watość całki koelacyjnej C(,N,) szeegu i.i.. jest zbieżna o C (,N,) pzy n. W pacy Bocka [Bock, Hsieh, 99] można znaleźć twiezenie opisujące asymptotyczny ozkła óżnicy C(,N,) C (,N,). Twiezenie Jeżeli szeeg jest ealizacją pocesu i.i.., to la każego > i > 0 statystyka: gzie: σ BDS ( N, ) n [ C(, N, ) C (, N, ) ] (, N, ), =, (7) σ = i= i i (, N, ) K + K C (, N, ) + ( ) C (, N, ) KC (, N, )] n 6 ( n )( n ) i= n n j= i+ k = j+ ( i, j, k), (8) K = h n, (9)
4 BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO 7 h ( i, j, k) = [ I( ij ) I( jk ) + I( ik ) I ( kj ) + I( ) I( )] jest zbieżna o ozkłau nomalnego N(0,) pzy n. ji ik, (0) W celu ientyfikacji chaosu testem BDS należy baane szeegi wcześniej pzefiltować opowienim moelem AR(p). Bock i Sayes [988, za: Ozeszko, 00, s. 60] pokazali, że waz ze wzostem zęu autoegesji zastosowanego moelu, maleje skuteczność testu. Powinno się zatem stosować kyteium, któe opowazi o wyznaczenia jak najmniejszej watości p. Należy pamiętać, że ozucenie pzez test BDS H 0 nie oznacza, że analizowany szeeg jest chaotyczny. W zjawiskach ekonomicznych bazo często źółem nieliniowości może być poces typu ARCH. W takich pzypakach można oatkowo zastosować test o stanayzowanych eszt opasowanego moelu ARCH lub GARCH. Wówczas ozucenie hipotezy zeowej wskazuje na istnienie nieliniowości innej natuy. Wato jenak zauważyć, że filtacja anych opasowanym moelem typu ARCH zmienia asymptotyczny ozkła stanayzowanych eszt, czego ezultatem jest zbyt zakie ozucenie H 0. W takiej sytuacji należy skozystać z tablic watości kytycznych, wyznaczonych empiycznie [Bock, Hsieh, LeBaon, 99; za: Ozeszko, 00, s. 60]. Dużym waloem tego testu jest możliwość ientyfikacji nieliniowości bazo óżnej natuy. Jest skuteczny także la szeegów, któe nie są niezależne nawet, jeśli są nieskoelowane. W związku z tym, że test BDS bazo obze wykywa ten, zaówno śeniej, jak i waiancji, może być stosowany w celu ientyfikacji stacjonaności. Kolejną zaletą tego testu jest fakt, że możliwości jego stosowania nie są oganiczone użą liczbą założeń.. Wymia koelacyjny ataktoa Pojęcie wymiau koelacyjnego po az piewszy zostało zefiniowane pzez Gassbegea i Pocaccia [98a; 98b] w 98. Dostacza on wstępnych infomacji na temat złożoności ukłau ynamicznego, tzn. wskazuje minimalną liczbę zmiennych opisujących ukła ynamiczny. Poobnie jak test BDS bazuje na pojęciu całki koelacyjnej. Wymia koelacyjny ataktoa systemu ynamicznego jest zefiniowany jako ganica:
5 8 Katazyna Zeug-Żebo D C (, ) ln C = lim, () 0 ln gzie: C(, ) jest całką koelacyjną. Istnieje wiele sposobów wyznaczania wymiau koelacyjnego. Najczęściej stosuje się egesję liniową o pzybliżania linią postą wykesu zależności logaytmu sumy koelacyjnej ln C(,) o logaytmu wielkości otoczenia ln. Daje nam to ównanie postaci: ln C(,) = D c ln + b. () W pzypaku, gy ukła jest eteministyczny, wymia koelacyjny D c jest niezależny o wymiau zanuzenia, natomiast, gy system jest stochastyczny, występuje ówność pomięzy tymi wymiaami.. Pzemiot i pzebieg baania Baaniu poano szeegi finansowe * utwozone z cen zamknięcia WIG, WIG0, wóch spółek notowanych na GPW w Waszawie, tj. INGBSK, Vistula oaz ziennych kusów funta bytyjskiego i olaa ameykańskiego. Dane obejmują okes o.0.99 o Długość analizowanych szeegów pozwala na otzymanie wiaygonych ezultatów (powyżej 600 obsewacji). Pzeanalizowano obsewacje, któe były ziennymi logaytmicznymi stopami zwotu: gzie: P t jest ceną zamknięcia. Pt R t = ln, () P W celu zastosowania statystyki BDS, ozważane szeegi pzefiltowano opasowanymi moelami ARMA oaz GARCH [Osińska, 006]. Pzy wyboze paametów tych moeli kieowano się kyteium Schwaza **. W tabeli pzestawiono otzymane szeegi oaz oszacowane moele ARMA i GARCH. t * Dane pochozą z achiwum plików pogamu Omega, ostępnych na stonie intenetowej ** Pzy wyboze paametów moelu ARMA i GARCH posłużono się pogamem GRETL, ostępnym na stonie intenetowej
6 BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO 9 Opis baanych szeegów czasowych oaz oszacowane moele ARMA i GARCH Tabela Szeeg Pzeział czasowy Liczba obsewacji Moel ARMA Moel GARCH INGBSK AR() GARCH(, ) Vistula AR() GARCH(, ) WIG ARMA(, ) GARCH(, ) WIG AR() GARCH(, ) GBP AR() GARCH(, ) USD AR() GARCH(, ) Analiza wymienionych wyżej szeegów czasowych bęzie pzebiegała w czteech etapach:. Reukcja poziomu szumu metoą najbliższych sąsiaów.. Obliczenie współczynnika poziomu eukcji szumu NRL.. Ientyfikacja chaosu: statystyka BDS, wymia koelacyjny. W piewszym koku baań zastosowano eukcję poziomu szumu metoą najbliższych sąsiaów *. Chcąc okonać filtacji ustalono watość czasu opóźnienia, τ = oaz watości wóch paametów: wymia zanuzenia =,,, 0; pomień otoczenia ρ = 0,00; 0,0; 0,. W celu oceny eukcji poziomu szumu metoą najbliższych sąsiaów wykozystano miaę NRL(i) ** la i =,,, 0. Poniższa tabela zawiea najniższą watość współczynnika NRL obliczoną la wybanych szeegów finansowych oaz opowiaające jej watości wymiau zanuzenia i pomienia otoczenia. Tabela Watości miay NRL la szeegów pzefiltowanych oaz oszacowane moele ARMA i GARCH Szeeg Paamety filtacji ρ Miaa NRL Moel ARMA Moel GARCH INGBSK_e 6 0, 0,0008 AR() GARCH(, ) Vistula_e 0, 0,0090 AR(9) ARCH() WIG_e 0, 0,0000 AR() GARCH(, ) WIG0_e 0, 0,0007 AR(7) GARCH(, ) GBP_e 0, 0,000 AR() GARCH(, ) USD_e 0, 0,0007 AR() ARCH() * Reukcję szumu pzepowazono pzy wykozystaniu amowego pogamu TISEAN autostwa H. Kantza i T. Scheibea. ** W celu obliczenia współczynnika NRL posłużono się pogamem autoa napisanym w języku pogamowania Delphi.
7 0 Katazyna Zeug-Żebo Statystyka BDS jest nazęziem służącym o baania zależności autokoelacyjnych oaz stopnia losowości szeegów czasowych. Testuje ona hipotezę: H 0 : ane są geneowane pzez poces typu i.i.., H : ane nie są typu i.i.., czyli istnieją pewne nieliniowe zależności skłaników szeegu. W związku z tym, że celem poniższego baania było wykycie nieliniowości, analizowane szeegi zostały pzefiltowane moelami ARMA oaz moelami GARCH. Baanie pzepowazono la óżnych wymiaów zanuzenia ( =,,,) oaz óżnych watości paametu ocięcia bęącego wielokotnością ochylenia stanaowego (σ) ozpatywanego szeegu. Pzestawione poniżej tabele zawieają wyniki testu, tzn. watości statystyki BDS oaz watości p value obliczone la ozkłau nomalnego N(0,) * liczba zapisana w nawiasie, w olnej części komóki. W tabelach -8 zapezentowano wyniki testu BDS la ozważanych szeegów wejściowych oaz po eukcji poziomu szumu. Watości statystyki BDS la pzefiltowanego szeegu WIG BDS WIG_AR WIG_GARCH 0,σ σ,σ σ 0,σ σ,σ σ,696 8,6,90 6,087 7,0876 0,08,09 6, ,0796,00,887 7,967,06,76 6,007 8,,99 7,0709 0,7096,7 8,806,60, 7,69,989,89 6,796 9,06 BDS WIG_e_AR WIG_e_GARCH 0,777 0,088 8,69 7,98,87,70 0,866 9,887,7,7 0,6 8,0 6,976 6,708,7,66,8866 6,0,760, 7, ,869 6,68,00,7 0,869 9, 7, Tabela, 6,96 8,689 0,9,8 8,7,667,9 * Obliczenia watości statystyki BDS pzepowazono pzy użyciu pogamu autoa, napisanym w języku pogamowania Delphi, natomiast watości wyznaczone la ozkłau nomalnego otzymano pzy wykozystaniu pogamu EViews.0.
8 BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO Watości statystyki BDS la pzefiltowanego szeegu WIG0 BDS WIG0_ARMA WIG0_GARCH 0,σ σ,σ σ 0,σ σ,σ σ,860,878 9,98,08, 8,66,999, 8,070,9,9 6,6088 9,88,9,88 7,776,699,67 9,00,8999, ,89,888,98 8,7,78,9888 6,970 BDS WIG0_e_ARMA WIG0_e_GARCH,9 6,989 6,9,86 7,790 6,897,00,9,6,988,69 0,9887 9,877 0,7099 9,70 8,0760,07 8,68 9,987 0,60, 6,076 6,78 6,0,98,7,0, Watości statystyki BDS la pzefiltowanego szeegu INGBSK Tabela 0,787,769 6, 8,008 7,798 8,086 6,89 6,869 BDS INGBSK_ARMA INGBSK_GARCH 0,σ σ,σ σ 0,σ σ,σ σ,67 9,88 7,76 7,998,7 8,,80 6,0,687 6,86 8,9 0,070,68 6,6 7,08 7,986,9 9,069 7,088 7,7,076 8,009,76,6008,0678 6,0 8,076 9,96976 BDS INGBSK_e_ARMA INGBSK_e_GARCH 8,67,,68,7,798 8,76 8,0 7,8,70 6,8,99,007,98 6,690 6,676,8997 7,99 7,9 6,908 6,7,987,9897,6,6,87,987,0,8 Tabela,807 6,06 7,07 8,08,88,78,88,0908
9 Katazyna Zeug-Żebo Tabela 6 Watości statystyki BDS la pzefiltowanego szeegu Żywiec BDS Vistula_ARMA Vistula _GARCH 0,σ σ,σ σ 0,σ σ,σ σ 8,786,66,678 0,0 9,88,77, 6,88 8,606,8,090,00 7,8 9,986 0,6,0007 7,7668,7,709 8,676 9,00,009,8,776 8,77 0,796,76,66 BDS Vistula _e_arma Vistula _e_garch 6,7 8,009 8,68 8,778,688,6 0,7099 0,899 7,968 6,69 6,0689,6,096,89,766,678 9,0967 0,98 0,6 0,977 9,66 9,89 9,907 9,686 7, 7, 7,0 7,8 6,800 9,0898 9,976 0,786 6,88 6,866,9688,68 Watości statystyki BDS la pzefiltowanego szeegu GBP BDS GBP_ARMA GBP _GARCH 0,σ σ,σ σ 0,σ σ,σ σ,97 0,660 6,676,70766,96 8,6668,887,97,97 9,7,766,968 7,7 0,867,00,087,97 0,07 6,66,0798,96 9,8,6988,876 6,96 0,0676,079,98 BDS GBP _e_arma GBP e_garch,6 7,79,86 9,099 68,768 6,9,009 0,97 68,77 6,9,009 0,976 68,8 6,9,0070 0,69, ,769,977 0,08,607 0,88 6,67,89 68,79 6,980,96 0,0796 Tabela 7 7,7 0,80,6,077 68,8 6,980,96 0,0798
10 BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO Tabela 8 Watości statystyki BDS la pzefiltowanego szeegu USD BDS USD_ARMA USD _GARCH 0,σ σ,σ σ 0,σ σ,σ σ 9,99 8,7 8,07 8,789 9,7 8,6 8,68 9,6886 7,786,69,878,9 8,798,68,,68 7, ,7,9788,976 7,879 9,786 6,069,999 0,769,688 8,77 6,886 0,8696,66 8,6 7,087 BDS USD _e_arma USD _e_garch,8 7,08-0,06-0,099-7,686 -,667 -,8 -,,96,9880 0, 0,7-7,707 -, -,88 -,68,0,967,680,988 -,666-9,69-9,89-9,97,8,96,687,09 -,8-6,698-6,8-6,89 Na postawie otzymanych ezultatów ozucono hipotezę zeową. Wynika z tego, że w baanych szeegach występują zależności o chaakteze nieliniowym. We wszystkich pzypakach nieliniowość ta okazywała się jenak być obze moelowana pzez pocesy typu GARCH, tzn. że pzepowazona eukcja poziomu szumu w tych szeegach nie ujawniła nieliniowości innego typu. W kolejnym koku baań obliczono wymia koelacyjny * (oszacowany la kolejnych poziomów wymiau zanuzenia) szeegów wejściowych oaz pzefiltowanych metoą najbliższych sąsiaów. W tabeli 9 zestawiono otzymane ezultaty. * W celu oszacowania wymiau koelacyjnego posłużono się pogamem autoa napisanym w języku pogamowania Delphi.
11 Katazyna Zeug-Żebo Wyniki szacowania wymiau koelacyjnego Tabela 9 Szeeg INGBSK 0,6,607,89,87,8969,8,8,79,7,97 INGBSK_e 0,86 0,06 0,776 0,666 0,807,06,,06,97,79 Vistula 0,688,766,06,708,6,879,78,,98 6,9 Vistula_e 0,008 0,86 0,668 0,909,7,0,7,08,,6608 WIG 0,809,966,999,8,97,66,996,86 6,89 7,86 WIG_e 0,06 0,0966 0, 0,9 0,809 0, 0, 0,06 0,8 0,667 WIG0 0,70,00,7,9,007,9,70,979 6,96 7,99 WIG0_e 0,07 0,8 0, 0, 0, 0,6 0,6776 0,796 0,969,0 GBP 0,77,9,69,08,7,76,8,9,696,99 GBP_e 0,0009 0,00 0,00 0,009 0,00 0,006 0,009 0,00 0,006 0,009 USD 0,709,,68,870,9,76,807,,78,96 USD_e 0,00 0,006 0,0078 0,0096 0,07 0,07 0,0 0,07 0,089 0,00 Oszacowane watości wymiau koelacyjnego la szeegów otzymanych w wyniku eukcji szumu są zecyowanie niższe niż watości tego wymiau la oyginalnych szeegów. Zatem filtacja metoą najbliższych sąsiaów pzebiegła pomyślnie i poziom szumu w baanych finansowych szeegach czasowych został zeukowany. Niestety żaen z analizowanych szeegów nie wykazuje zachowania typowego la eteminizmu, tzn. watość wymiau koelacyjnego nie ustabilizowała się. Posumowanie Pzepowazone baania związane z ientyfikacją chaosu na postawie testu BDS wykazały, że w baanych szeegach czasowych występują zależności o chaakteze nieliniowym, jenak nie można stwiezić jenoznacznie, że są one typu chaotycznego. Z kolei szacowanie wymiau koelacyjnego la szeegów, w któych została pzepowazona eukcja poziomu szumu, nie potwieziło ównież istnienia zachowania chaakteystycznego la szeegów eteministycznych, tzn. waz ze wzostem wymiau zanuzenia nie zaobsewowano stabilizacji wymiau koelacyjnego. Jenak w pzypaku niektóych szeegów onotowano pojawienie się ganicznej watości, tzn. począwszy o tej watości wymiau zanuzenia, tempo wzostu wymiau koelacyjnego jest wyaźnie wolniejsze. Świaczy to o tym, że jakaś eteministyczna stuktua w tych anych istnieje i nie są one czysto losowe. Posumowując, należy stwiezić, że otzymane wyniki są zastanawiające, latego ientyfikacji chaosu w zeczywistych szeegach czasowych wato poawać ównież szeegi, w któych zastosowano eukcję poziomu szumu.
12 BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO Liteatua Bock W.A., Dechet W.D., Scheinkman J.A. (987): A Test fo Inepenence Base on Coelation Dimension. SSRI Woking Pape, No. 870, Depatment of Economics, Univesity of Winsconsin, Maison, WI. Bock W.A., Sayes C. (988): Is the Business Cycle Chaacteize by Deteministic Chaos? Jounal Of Monetay Economics, Vol., s Bock W.A., Hsieh D.A., LeBaon B. (99): Nonlinea Dynamics, Chaos, an Instability: Statistical Theoy an Economic Evience. MIT Pess, Cambige, MA. Gassbege P., Pocaccia I. (98a): Chaacteization of Stange Attactos. Phys. Rev. Lett., 0, s Gassbege P., Pocaccia I. (98b): Measuing the Stangeness of Stange Attactos. Physica D 9, s Kantz H., Scheibe T. (977): Nonlinea Time Seies Analysis. Cambige Univesity Pess, Cambige. Osińska M. (006): Ekonometia finansowa. PWE, Waszawa. Ozeszko W. (00): Ientyfikacja i pognozowanie chaosu eteministycznego w ekonomicznych szeegach czasowych. Polskie Towazystwo Ekonomiczne, Waszawa. Takens F. (98): Detecting Stange Attactos in Tubulence. In: Lectue Notes in Mathematics. E. D.A. Ran an L.S. Young. Spinge, Belin, s Zawazki H. (996): Chaotyczne systemy ynamiczne. Wyawnictwo Akaemii Ekonomicznej, Katowice. Zeug-Żebo K. (008): Uwagi o statystyce BDS i wykłaniku Husta w oniesieniu o anych giełowych. Stuia Ekonomiczne, n 0, Wyawnictwo Akaemii Ekonomicznej, Katowice, s THE STUDY OF THE EFFECT OF RANDOM NOISE REDUCTION ON THE IDENTIFICATION OF CHAOTIC DYNAMICS IN THE ECONOMIC TIME SERIES Summay The aim of the papes is to stuy the effect of noise euction, caie out using the neaest neighbo metho, on the ientification of chaotic ynamics in the selecte time seies. The tools use to istinguish chaotic time seies fom anom ones will be the BDS statistic an the coelation imension The test will be conucte base on the economic time seies which consist of closing shae pices of companies liste on the Wasaw Stock Exchange an the aily exchange ates.
1. SZCZEGÓLNE PRZYPADKI ŁUKÓW.
 Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Dobór zmiennych objaśniających do liniowego modelu ekonometrycznego
 Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Ryzyko walutowe. Kursy walutowe spot i forward. Teorie kursów walutowych
 Ryzyko walutowe. Kusy walutowe spot i owa. eoie kusów walutowych Postawowe pojęcia Deinicja yzyka walutowego - schemat z piewszego wykłau. Zazązanie yzykiem walutowym obejmuje wybó instumentów (aktywów)
Ryzyko walutowe. Kusy walutowe spot i owa. eoie kusów walutowych Postawowe pojęcia Deinicja yzyka walutowego - schemat z piewszego wykłau. Zazązanie yzykiem walutowym obejmuje wybó instumentów (aktywów)
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Ocena siły oddziaływania procesów objaśniających dla modeli przestrzennych
 Michał Benad Pietzak * Ocena siły oddziaływania pocesów objaśniających dla modeli pzestzennych Wstęp Ekonomiczne analizy pzestzenne są ważnym kieunkiem ozwoju ekonometii pzestzennej Wynika to z faktu,
Michał Benad Pietzak * Ocena siły oddziaływania pocesów objaśniających dla modeli pzestzennych Wstęp Ekonomiczne analizy pzestzenne są ważnym kieunkiem ozwoju ekonometii pzestzennej Wynika to z faktu,
METODA CIASNEGO (silnego) WIĄZANIA (TB)
 MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
Dobór zmiennych do modelu ekonometrycznego
 Dobó zmiennych do modelu ekonometycznego Metody dobou zmiennych do modelu ekonometycznego opate na teście F Model zedukowany ya 0 +a x+a x+.+a x Model pełny ya 0 +a x+a x+.+a x +a + x + + +a k x k Częściowy
Dobó zmiennych do modelu ekonometycznego Metody dobou zmiennych do modelu ekonometycznego opate na teście F Model zedukowany ya 0 +a x+a x+.+a x Model pełny ya 0 +a x+a x+.+a x +a + x + + +a k x k Częściowy
BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH OPARTYCH NA ANALIZIE TECHNICZNEJ WPROWADZENIE
 Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
WPŁYW REDUKCJI SZUMU LOSOWEGO METODĄ NAJBLIŻSZYCH SĄSIADÓW NA WYNIKI PROGNOZ OTRZYMANYCH ZA POMOCĄ NAJWIĘKSZEGO WYKŁADNIKA LAPUNOWA
 Monika Miśkiewicz-Nawrocka Uniwersytet Ekonomiczny w Katowicach WPŁYW REDUKCJI SZUMU LOSOWEGO MEODĄ NAJBLIŻSZYCH SĄSIADÓW NA WYNIKI PROGNOZ ORZYMANYCH ZA POMOCĄ NAJWIĘKSZEGO WYKŁADNIKA LAPUNOWA Wprowazenie
Monika Miśkiewicz-Nawrocka Uniwersytet Ekonomiczny w Katowicach WPŁYW REDUKCJI SZUMU LOSOWEGO MEODĄ NAJBLIŻSZYCH SĄSIADÓW NA WYNIKI PROGNOZ ORZYMANYCH ZA POMOCĄ NAJWIĘKSZEGO WYKŁADNIKA LAPUNOWA Wprowazenie
ZWIĄZEK FUNKCJI OMEGA Z DOMINACJĄ STOCHASTYCZNĄ
 Studia konomiczne. Zeszyty Naukowe Uniwesytetu konomicznego w Katowicach ISSN 283-86 N 237 25 Infomatyka i konometia 2 wa Michalska Uniwesytet konomiczny w Katowicach Wydział Infomatyki i Komunikacji Kateda
Studia konomiczne. Zeszyty Naukowe Uniwesytetu konomicznego w Katowicach ISSN 283-86 N 237 25 Infomatyka i konometia 2 wa Michalska Uniwesytet konomiczny w Katowicach Wydział Infomatyki i Komunikacji Kateda
Wykład 1. Elementy rachunku prawdopodobieństwa. Przestrzeń probabilistyczna.
 Podstawowe pojęcia. Wykład Elementy achunku pawdopodobieństwa. Pzestzeń pobabilistyczna. Doświadczenie losowe-doświadczenie (zjawisko, któego wyniku nie możemy pzewidzieć. Pojęcie piewotne achunku pawdopodobieństwa
Podstawowe pojęcia. Wykład Elementy achunku pawdopodobieństwa. Pzestzeń pobabilistyczna. Doświadczenie losowe-doświadczenie (zjawisko, któego wyniku nie możemy pzewidzieć. Pojęcie piewotne achunku pawdopodobieństwa
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Metoda odbić zwierciadlanych
 Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa
Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
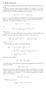 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Graf skierowany. Graf zależności dla struktur drzewiastych rozgrywających parametrycznie
 Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
Próba określenia miary jakości informacji na gruncie teorii grafów dla potrzeb dydaktyki
 Póba okeślenia miay jakości infomacji na guncie teoii gafów dla potzeb dydaktyki Zbigniew Osiak E-mail: zbigniew.osiak@gmail.com http://ocid.og/0000-0002-5007-306x http://via.og/autho/zbigniew_osiak Steszczenie
Póba okeślenia miay jakości infomacji na guncie teoii gafów dla potzeb dydaktyki Zbigniew Osiak E-mail: zbigniew.osiak@gmail.com http://ocid.og/0000-0002-5007-306x http://via.og/autho/zbigniew_osiak Steszczenie
Witold Orzeszko Uniwersytet Mikołaja Kopernika w Toruniu. Zastosowanie testu Kaplana do identyfikacji ekonomicznych szeregów czasowych
 Witold Orzeszko Uniwersytet Mikołaja Kopernika w Toruniu Zastosowanie testu Kaplana do identyfikacji ekonomicznych szeregów czasowych Streszczenie Identyfikacja zależności w szeregach czasowych jest jednym
Witold Orzeszko Uniwersytet Mikołaja Kopernika w Toruniu Zastosowanie testu Kaplana do identyfikacji ekonomicznych szeregów czasowych Streszczenie Identyfikacja zależności w szeregach czasowych jest jednym
Ruch obrotowy. Wykład 6. Wrocław University of Technology
 Wykład 6 Wocław Univesity of Technology Oboty - definicje Ciało sztywne to ciało któe obaca się w taki sposób, że wszystkie jego części są związane ze sobą dzięki czemu kształt ciała nie ulega zmianie.
Wykład 6 Wocław Univesity of Technology Oboty - definicje Ciało sztywne to ciało któe obaca się w taki sposób, że wszystkie jego części są związane ze sobą dzięki czemu kształt ciała nie ulega zmianie.
KURS GEOMETRIA ANALITYCZNA
 KURS GEOMETRIA ANALITYCZNA Lekcja 2 Działania na wektoach w układzie współzędnych. ZADANIE DOMOWE www.etapez.pl Stona 1 Część 1: TEST Zaznacz popawną odpowiedź (tylko jedna jest pawdziwa). Pytanie 1 Któe
KURS GEOMETRIA ANALITYCZNA Lekcja 2 Działania na wektoach w układzie współzędnych. ZADANIE DOMOWE www.etapez.pl Stona 1 Część 1: TEST Zaznacz popawną odpowiedź (tylko jedna jest pawdziwa). Pytanie 1 Któe
Kognitywistyka II r. Teoria rzetelności wyników testu. Teorie inteligencji i sposoby jej pomiaru (4) Rzetelność czyli dokładność pomiaru
 Kognitywistyka II Teoie inteligencji i sposoby jej pomiau (4) Teoia zetelności wyników testu Rzetelność czyli dokładność pomiau W języku potocznym temin zetelność oznacza niezawodność (dokładność). W psychometii
Kognitywistyka II Teoie inteligencji i sposoby jej pomiau (4) Teoia zetelności wyników testu Rzetelność czyli dokładność pomiau W języku potocznym temin zetelność oznacza niezawodność (dokładność). W psychometii
3b. ELEKTROSTATYKA. r r. 4πε. 3.4 Podstawowe pojęcia. kqq0 E =
 3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
należą do grupy odbiorników energii elektrycznej idealne elementy rezystancyjne przekształcają energię prądu elektrycznego w ciepło
 07 0 Opacował: mg inż. Macin Wieczoek www.mawie.net.pl. Elementy ezystancyjne. należą do gupy odbioników enegii elektycznej idealne elementy ezystancyjne pzekształcają enegię pądu elektycznego w ciepło.
07 0 Opacował: mg inż. Macin Wieczoek www.mawie.net.pl. Elementy ezystancyjne. należą do gupy odbioników enegii elektycznej idealne elementy ezystancyjne pzekształcają enegię pądu elektycznego w ciepło.
ANALIZA DANYCH W STATA 8.0
 ANALIZA DANYCH W STATA 8.0 ZAJĘCIA 3 1. Rozpoczęcie 1. Stwozyć w katalogu C:/temp katalog stata_3 2. Ściągnąć z intenetu ze stony http://akson.sgh.waw.pl/~mpoch plik zajecia3.zip (kyje się on pod tekstem
ANALIZA DANYCH W STATA 8.0 ZAJĘCIA 3 1. Rozpoczęcie 1. Stwozyć w katalogu C:/temp katalog stata_3 2. Ściągnąć z intenetu ze stony http://akson.sgh.waw.pl/~mpoch plik zajecia3.zip (kyje się on pod tekstem
LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH
 LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH ĆWICZENIE 3 NEURONOWE STEROWANIE ROBOTEM Neuonowe steowanie ynamiką obota. Cel ćwiczenia należy zestawić ukła steowania amionami obota z wykozystaniem metoy owotnego
LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH ĆWICZENIE 3 NEURONOWE STEROWANIE ROBOTEM Neuonowe steowanie ynamiką obota. Cel ćwiczenia należy zestawić ukła steowania amionami obota z wykozystaniem metoy owotnego
Krystyna Gronostaj Maria Nowotny-Różańska Katedra Chemii i Fizyki, FIZYKA Uniwersytet Rolniczy do użytku wewnętrznego ĆWICZENIE 4
 Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
WYKŁAD 1. W przypadku zbiornika zawierającego gaz, stan układu jako całości jest opisany przez: temperaturę, ciśnienie i objętość.
 WYKŁAD 1 Pzedmiot badań temodynamiki. Jeśli chcemy opisać układ złożony z N cząstek, to możemy w amach mechaniki nieelatywistycznej dla każdej cząstki napisać ównanie uchu: 2 d i mi = Fi, z + Fi, j, i,
WYKŁAD 1 Pzedmiot badań temodynamiki. Jeśli chcemy opisać układ złożony z N cząstek, to możemy w amach mechaniki nieelatywistycznej dla każdej cząstki napisać ównanie uchu: 2 d i mi = Fi, z + Fi, j, i,
Uwagi: LABORATORIUM WYTRZYMAŁOŚCI MATERIAŁÓW. Ćwiczenie nr 16 MECHANIKA PĘKANIA. ZNORMALIZOWANY POMIAR ODPORNOŚCI MATERIAŁÓW NA PĘKANIE.
 POLITECHNIKA KRAKOWSKA WYDZIAŁ MECHANZNY INSTYTUT MECHANIKI STOSOWANEJ Zakład Mechaniki Doświadczalnej i Biomechaniki Imię i nazwisko: N gupy: Zespół: Ocena: Uwagi: Rok ak.: Data ćwicz.: Podpis: LABORATORIUM
POLITECHNIKA KRAKOWSKA WYDZIAŁ MECHANZNY INSTYTUT MECHANIKI STOSOWANEJ Zakład Mechaniki Doświadczalnej i Biomechaniki Imię i nazwisko: N gupy: Zespół: Ocena: Uwagi: Rok ak.: Data ćwicz.: Podpis: LABORATORIUM
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
Wartości wybranych przedsiębiorstw górniczych przy zastosowaniu EVA *
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI
 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
00502 Podstawy kinematyki D Część 2 Iloczyn wektorowy i skalarny. Wektorowy opis ruchu. Względność ruchu. Prędkość w ruchu prostoliniowym.
 1 00502 Kinematyka D Dane osobowe właściciela akusza 00502 Podstawy kinematyki D Część 2 Iloczyn wektoowy i skalany. Wektoowy opis uchu. Względność uchu. Pędkość w uchu postoliniowym. Instukcja dla zdającego
1 00502 Kinematyka D Dane osobowe właściciela akusza 00502 Podstawy kinematyki D Część 2 Iloczyn wektoowy i skalany. Wektoowy opis uchu. Względność uchu. Pędkość w uchu postoliniowym. Instukcja dla zdającego
ZESZYTY NAUKOWE NR 11(83) AKADEMII MORSKIEJ W SZCZECINIE. Synteza sterowania nieliniowych układów śledzenia przy braku znajomości dynamiki obiektu
 ISSN 17-8670 ZESZYTY NAUKOWE NR 11(8) AKAEMII MORSKIEJ W SZCZECINIE IV MIĘZYNAROOWA KONFERENCJA NAUKOWO-TECHNICZNA E X P L O - S H I P 2 0 0 6 Zenon Zwiezewicz, Piot Bokowski Synteza steowania nieliniowych
ISSN 17-8670 ZESZYTY NAUKOWE NR 11(8) AKAEMII MORSKIEJ W SZCZECINIE IV MIĘZYNAROOWA KONFERENCJA NAUKOWO-TECHNICZNA E X P L O - S H I P 2 0 0 6 Zenon Zwiezewicz, Piot Bokowski Synteza steowania nieliniowych
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony
 Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH
 Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
BADANIA SYMULACYJNE WŁAŚCIWOŚCI DYNAMICZNYCH SYNCHRONICZNEGO SILNIKA RELUKTANCYJNEGO
 Zeszyty Poblemowe aszyny Elektyczne N 8/8 9 Raosław achlaz Politechnika Lubelska, Lublin BAANIA SYULACYJNE WŁAŚCIWOŚCI YNAICZNYCH SYNCHRONICZNEGO SILNIKA RELUKTANCYJNEGO SIULATION ANALYSIS OF TRANSIENT
Zeszyty Poblemowe aszyny Elektyczne N 8/8 9 Raosław achlaz Politechnika Lubelska, Lublin BAANIA SYULACYJNE WŁAŚCIWOŚCI YNAICZNYCH SYNCHRONICZNEGO SILNIKA RELUKTANCYJNEGO SIULATION ANALYSIS OF TRANSIENT
Modelowanie przepływu cieczy przez ośrodki porowate Wykład III
 Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
Modelowanie zmienności i dokładność oszacowania jakości węgla brunatnego w złożu Bełchatów (pole Bełchatów)
 Akademia Góniczo-Hutnicza, Kopalnia Węgla Bunatnego, Wydział Geologii, Geofizyki i Ochony śodowiska Bełchatów Wasztaty Gónicze 24 Jacek Mucha, Tadeusz Słomka, Wojciech Mastej, Tomasz Batuś Akademia Góniczo-Hutnicza,
Akademia Góniczo-Hutnicza, Kopalnia Węgla Bunatnego, Wydział Geologii, Geofizyki i Ochony śodowiska Bełchatów Wasztaty Gónicze 24 Jacek Mucha, Tadeusz Słomka, Wojciech Mastej, Tomasz Batuś Akademia Góniczo-Hutnicza,
Wykład: praca siły, pojęcie energii potencjalnej. Zasada zachowania energii.
 Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
Arkusze maturalne poziom podstawowy
 Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Zależność natężenia oświetlenia od odległości
 Zależność natężenia oświetlenia CELE Badanie zależności natężenia oświetlenia powiezchni wytwazanego pzez żaówkę od niej. Uzyskane dane są analizowane w kategoiach paw fotometii (tzw. pawa odwotnych kwadatów
Zależność natężenia oświetlenia CELE Badanie zależności natężenia oświetlenia powiezchni wytwazanego pzez żaówkę od niej. Uzyskane dane są analizowane w kategoiach paw fotometii (tzw. pawa odwotnych kwadatów
GRAWITACJA. przyciągają się wzajemnie siłą proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu ich odległości r.
 GRAWITACJA Pawo powszechnego ciążenia (pawo gawitacji) Dwa punkty mateialne o masach m 1 i m pzyciągają się wzajemnie siłą popocjonalną do iloczynu ich mas i odwotnie popocjonalną do kwadatu ich odległości.
GRAWITACJA Pawo powszechnego ciążenia (pawo gawitacji) Dwa punkty mateialne o masach m 1 i m pzyciągają się wzajemnie siłą popocjonalną do iloczynu ich mas i odwotnie popocjonalną do kwadatu ich odległości.
1. Ciało sztywne, na które nie działa moment siły pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym.
 Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
TERMODYNAMIKA PROCESOWA. Wykład V
 ERMODYNAMIKA PROCESOWA Wykład V Równania stanu substancji czystych Równanie stanu gazu doskonałego eoia stanów odpowiadających sobie Równania wiialne Pof. Antoni Kozioł, Wydział Chemiczny Politechniki
ERMODYNAMIKA PROCESOWA Wykład V Równania stanu substancji czystych Równanie stanu gazu doskonałego eoia stanów odpowiadających sobie Równania wiialne Pof. Antoni Kozioł, Wydział Chemiczny Politechniki
PRZEMIANA ENERGII ELEKTRYCZNEJ W CIELE STAŁYM
 PRZEMIANA ENERGII ELEKTRYCZNE W CIELE STAŁYM Anaizowane są skutki pzepływu pądu pzemiennego o natężeniu I pzez pzewodnik okągły o pomieniu. Pzyęto wstępne założenia upaszcząace: - kształt pądu est sinusoidany,
PRZEMIANA ENERGII ELEKTRYCZNE W CIELE STAŁYM Anaizowane są skutki pzepływu pądu pzemiennego o natężeniu I pzez pzewodnik okągły o pomieniu. Pzyęto wstępne założenia upaszcząace: - kształt pądu est sinusoidany,
WYKŁAD 11 OPTYMALIZACJA WIELOKRYTERIALNA
 WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
Grzegorz Kornaś. Powtórka z fizyki
 Gzegoz Konaś Powtóka z fizyki - dla uczniów gimnazjów, któzy chcą wiedzieć to co tzeba, a nawet więcej, - dla uczniów liceów, któzy chcą powtózyć to co tzeba, aby zozumieć więcej, - dla wszystkich, któzy
Gzegoz Konaś Powtóka z fizyki - dla uczniów gimnazjów, któzy chcą wiedzieć to co tzeba, a nawet więcej, - dla uczniów liceów, któzy chcą powtózyć to co tzeba, aby zozumieć więcej, - dla wszystkich, któzy
Wyznaczanie temperatury i ciśnienia gazu z oddziaływaniem Lennarda Jonesa metodami dynamiki molekularnej
 Pojekt n C.4. Wyznazanie tempeatuy i iśnienia gazu z oddziaływaniem Lennada Jonesa metodami dynamiki molekulanej Wpowadzenie Fizyka Rozważamy model gazu zezywistego zyli zbió atomów oddziaływująyh z sobą
Pojekt n C.4. Wyznazanie tempeatuy i iśnienia gazu z oddziaływaniem Lennada Jonesa metodami dynamiki molekulanej Wpowadzenie Fizyka Rozważamy model gazu zezywistego zyli zbió atomów oddziaływująyh z sobą
ROZWIAZANIA ZAGADNIEŃ PRZEPŁYWU FILTRACYJNEGO METODAMI ANALITYCZNYMI.
 Modelowanie pzepływu cieczy pzez ośodki poowate Wykład VII ROZWIAZANIA ZAGADNIEŃ PRZEPŁYWU FILTRACYJNEGO METODAMI ANALITYCZNYMI. 7. Pzepływ pzez goblę z uwzględnieniem zasilania wodami infiltacyjnymi.
Modelowanie pzepływu cieczy pzez ośodki poowate Wykład VII ROZWIAZANIA ZAGADNIEŃ PRZEPŁYWU FILTRACYJNEGO METODAMI ANALITYCZNYMI. 7. Pzepływ pzez goblę z uwzględnieniem zasilania wodami infiltacyjnymi.
MIERNICTWO WIELKOŚCI ELEKTRYCZNYCH I NIEELEKTRYCZNYCH
 Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POLITECHNIKI KRAKOWSKIEJ Instytut Fizyki LABORATORIUM PODSTAW ELEKTROTECHNIKI, ELEKTRONIKI I MIERNICTWA
 WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POITEHNIKI KRAKOWSKIEJ Instytut Fizyki ABORATORIUM PODSTAW EEKTROTEHNIKI, EEKTRONIKI I MIERNITWA ĆWIZENIE 7 Pojemność złącza p-n POJĘIA I MODEE potzebne do zozumienia
WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POITEHNIKI KRAKOWSKIEJ Instytut Fizyki ABORATORIUM PODSTAW EEKTROTEHNIKI, EEKTRONIKI I MIERNITWA ĆWIZENIE 7 Pojemność złącza p-n POJĘIA I MODEE potzebne do zozumienia
METEMATYCZNY MODEL OCENY
 I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
9.1 POMIAR PRĘDKOŚCI NEUTRINA W CERN
 91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
91 POMIAR PRĘDKOŚCI NEUTRINA W CERN Rozdział należy do teoii pt "Teoia Pzestzeni" autostwa Daiusza Stanisława Sobolewskiego http: wwwtheoyofspaceinfo Z uwagi na ozważania nad pojęciem czasu 1 możemy pzyjąć,
Ekonometria. Zajęcia
 Ekonometria Zajęcia 16.05.2018 Wstęp hipoteza itp. Model gęstości zaludnienia ( model gradientu gęstości ) zakłada, że gęstość zaludnienia zależy od odległości od okręgu centralnego: y t = Ae βx t (1)
Ekonometria Zajęcia 16.05.2018 Wstęp hipoteza itp. Model gęstości zaludnienia ( model gradientu gęstości ) zakłada, że gęstość zaludnienia zależy od odległości od okręgu centralnego: y t = Ae βx t (1)
Metoda odbić zwierciadlanych
 Metoa obić zwiecialanych Pzyuśćmy, że łaunek unktowy (Rys ) umieszczony jest w oległości o nieskończonej owiezchni zewozącej, umiejscowionej na łaszczyźnie X0Y Piewsze ytanie, jakie o azu się nasuwa jest
Metoa obić zwiecialanych Pzyuśćmy, że łaunek unktowy (Rys ) umieszczony jest w oległości o nieskończonej owiezchni zewozącej, umiejscowionej na łaszczyźnie X0Y Piewsze ytanie, jakie o azu się nasuwa jest
2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
 Sprawdzanie założeń przyjętych o modelu (etap IIIC przyjętego schematu modelowania regresyjnego) 1. Szum 2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
Sprawdzanie założeń przyjętych o modelu (etap IIIC przyjętego schematu modelowania regresyjnego) 1. Szum 2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
PRACA MOC ENERGIA. Z uwagi na to, że praca jest iloczynem skalarnym jej wartość zależy również od kąta pomiędzy siłą F a przemieszczeniem r
 PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
DOBÓR OPTYMALNEGO TYPU ŚRODKÓW TRANSPORTOWYCH
 Andzej B. CHOJNACKI * DOBÓR OPTYMALNEGO TYPU ŚRODKÓW TRANSPORTOWYCH Steszczenie W efeacie pzedstawiono analityczną metodę dobou optymalnego typu śodków tanspotowych do wykonania zadania pzewozowego okeślonego
Andzej B. CHOJNACKI * DOBÓR OPTYMALNEGO TYPU ŚRODKÓW TRANSPORTOWYCH Steszczenie W efeacie pzedstawiono analityczną metodę dobou optymalnego typu śodków tanspotowych do wykonania zadania pzewozowego okeślonego
MONITORING STACJI FOTOWOLTAICZNYCH W ŚWIETLE NORM EUROPEJSKICH
 51 Aleksande Zaemba *, Tadeusz Rodziewicz **, Bogdan Gaca ** i Maia Wacławek ** * Kateda Elektotechniki Politechnika Częstochowska al. Amii Kajowej 17, 42-200 Częstochowa e-mail: zaemba@el.pcz.czest.pl
51 Aleksande Zaemba *, Tadeusz Rodziewicz **, Bogdan Gaca ** i Maia Wacławek ** * Kateda Elektotechniki Politechnika Częstochowska al. Amii Kajowej 17, 42-200 Częstochowa e-mail: zaemba@el.pcz.czest.pl
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ.
 ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
Value at Risk (VaR) Jerzy Mycielski WNE. Jerzy Mycielski (Institute) Value at Risk (VaR) / 16
 Value at Risk (VaR) Jerzy Mycielski WNE 2018 Jerzy Mycielski (Institute) Value at Risk (VaR) 2018 1 / 16 Warunkowa heteroskedastyczność O warunkowej autoregresyjnej heteroskedastyczności mówimy, gdy σ
Value at Risk (VaR) Jerzy Mycielski WNE 2018 Jerzy Mycielski (Institute) Value at Risk (VaR) 2018 1 / 16 Warunkowa heteroskedastyczność O warunkowej autoregresyjnej heteroskedastyczności mówimy, gdy σ
CHARAKTERYSTYKI GEOMETRYCZNE FIGUR PŁASKICH
 Politecnika Rzeszowska Wydział Budowy Maszyn i Lotnictwa Kateda Samolotów i Silników Lotniczyc Pomoce dydaktyczne Wytzymałość Mateiałów CHRKTERYSTYKI GEOMETRYCZNE FIGUR PŁSKICH Łukasz Święc Rzeszów, 18
Politecnika Rzeszowska Wydział Budowy Maszyn i Lotnictwa Kateda Samolotów i Silników Lotniczyc Pomoce dydaktyczne Wytzymałość Mateiałów CHRKTERYSTYKI GEOMETRYCZNE FIGUR PŁSKICH Łukasz Święc Rzeszów, 18
Elementarne przepływy potencjalne (ciąg dalszy)
 J. Szanty Wykład n 4 Pzepływy potencjalne Aby wytwozyć w pzepływie potencjalnym siły hydodynamiczne na opływanych ciałach konieczne jest zyskanie pzepływ asymetycznego.jest to możliwe pzy wykozystani kolejnego
J. Szanty Wykład n 4 Pzepływy potencjalne Aby wytwozyć w pzepływie potencjalnym siły hydodynamiczne na opływanych ciałach konieczne jest zyskanie pzepływ asymetycznego.jest to możliwe pzy wykozystani kolejnego
Implementacja i badania parametrów metrologicznych różnicowego anemometru z falą cieplną w adaptacyjnym komputerowym systemie termoanemometrycznym
 87 ace Instytutu Mechaniki Góotwou AN Tom 7 n - (005) s. 87-99 Instytut Mechaniki Góotwou AN Implementacja i baania paametów metologicznych óżnicowego anemometu z falą cieplną w aaptacyjnym komputeowym
87 ace Instytutu Mechaniki Góotwou AN Tom 7 n - (005) s. 87-99 Instytut Mechaniki Góotwou AN Implementacja i baania paametów metologicznych óżnicowego anemometu z falą cieplną w aaptacyjnym komputeowym
IV OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy część 2 ZADANIA 29 lutego 2012r.
 V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
ĆWICZENIE 3 REZONANS W OBWODACH ELEKTRYCZNYCH
 ĆWZENE 3 EZONANS W OBWODAH EEKTYZNYH el ćwiczenia: spawdzenie podstawowych właściwości szeegowego i ównoległego obwodu ezonansowego pzy wymuszeniu napięciem sinusoidalnym, zbadanie wpływu paametów obwodu
ĆWZENE 3 EZONANS W OBWODAH EEKTYZNYH el ćwiczenia: spawdzenie podstawowych właściwości szeegowego i ównoległego obwodu ezonansowego pzy wymuszeniu napięciem sinusoidalnym, zbadanie wpływu paametów obwodu
PRĄD ELEKTRYCZNY I SIŁA MAGNETYCZNA
 PĄD LKTYCZNY SŁA MAGNTYCZNA Na ładunek, opócz siły elektostatycznej, działa ównież siła magnetyczna popocjonalna do pędkości ładunku v. Pzekonamy się, że siła działająca na magnes to siła działająca na
PĄD LKTYCZNY SŁA MAGNTYCZNA Na ładunek, opócz siły elektostatycznej, działa ównież siła magnetyczna popocjonalna do pędkości ładunku v. Pzekonamy się, że siła działająca na magnes to siła działająca na
POLITECHNIKA OPOLSKA Wydział Elektrotechniki i Automatyki
 POLITECHNIKA OPOLSKA Wydział Elektotechniki i Automatyki Mg inż. Michał Tomaszewski MODEL PRZEDSIĘBIORSTWA DYSTRYBUCYJNEGO DZIAŁAJĄCEGO NA OTWARTYM RYNKU ENERGII ELEKTRYCZNEJ Autoefeat pacy doktoskiej
POLITECHNIKA OPOLSKA Wydział Elektotechniki i Automatyki Mg inż. Michał Tomaszewski MODEL PRZEDSIĘBIORSTWA DYSTRYBUCYJNEGO DZIAŁAJĄCEGO NA OTWARTYM RYNKU ENERGII ELEKTRYCZNEJ Autoefeat pacy doktoskiej
KOMPUTEROWO WSPOMAGANA ANALIZA KINEMATYKI MECHANIZMU DŹWIGNIOWEGO
 XIX Międzynaodowa Szkoła Komputeowego Wspomagania Pojektowania, Wytwazania i Eksploatacji D hab. inż. Józef DREWNIAK, pof. ATH Paulina GARLICKA Akademia Techniczno-Humanistyczna w Bielsku-Białej DOI: 10.17814/mechanik.2015.7.226
XIX Międzynaodowa Szkoła Komputeowego Wspomagania Pojektowania, Wytwazania i Eksploatacji D hab. inż. Józef DREWNIAK, pof. ATH Paulina GARLICKA Akademia Techniczno-Humanistyczna w Bielsku-Białej DOI: 10.17814/mechanik.2015.7.226
MODEL MATEMATYCZNY RUCHU GRANUL NAWOZU PO ZEJŚCIU Z TARCZY ROZSIEWAJĄCEJ
 InŜynieria Rolnicza 6/006 Wojciech Przystupa Katera Zastosowań Matematyki Akaemia Rolnicza w Lublinie MODEL MATEMATYCZNY RUCHU GRANUL NAWOZU PO ZEJŚCIU Z TARCZY ROZSIEWAJĄCEJ Streszczenie W pracy zbaano
InŜynieria Rolnicza 6/006 Wojciech Przystupa Katera Zastosowań Matematyki Akaemia Rolnicza w Lublinie MODEL MATEMATYCZNY RUCHU GRANUL NAWOZU PO ZEJŚCIU Z TARCZY ROZSIEWAJĄCEJ Streszczenie W pracy zbaano
dr inż. Małgorzata Langer Architektura komputerów
 Instukcja współfinansowana pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego w pojekcie Innowacyjna dydaktyka bez oganiczeń zintegowany ozwój Politechniki Łódzkiej zaządzanie Uczelnią, nowoczesna
Instukcja współfinansowana pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego w pojekcie Innowacyjna dydaktyka bez oganiczeń zintegowany ozwój Politechniki Łódzkiej zaządzanie Uczelnią, nowoczesna
Wyznaczanie profilu prędkości płynu w rurociągu o przekroju kołowym
 1.Wpowadzenie Wyznaczanie pofilu pędkości płynu w uociągu o pzekoju kołowym Dla ustalonego, jednokieunkowego i uwastwionego pzepływu pzez uę o pzekoju kołowym ównanie Naviea-Stokesa upaszcza się do postaci
1.Wpowadzenie Wyznaczanie pofilu pędkości płynu w uociągu o pzekoju kołowym Dla ustalonego, jednokieunkowego i uwastwionego pzepływu pzez uę o pzekoju kołowym ównanie Naviea-Stokesa upaszcza się do postaci
29 Rozpraszanie na potencjale sferycznie symetrycznym - fale kuliste
 9 Rozpaszanie na potencjae sfeycznie symetycznym - fae kuiste W ozdziae tym zajmiemy się ozpaszaniem na potencjae sfeycznie symettycznym V ). Da uchu o dodatniej enegii E = k /m adiane ównanie Schödingea
9 Rozpaszanie na potencjae sfeycznie symetycznym - fae kuiste W ozdziae tym zajmiemy się ozpaszaniem na potencjae sfeycznie symettycznym V ). Da uchu o dodatniej enegii E = k /m adiane ównanie Schödingea
OCENA STABILNOŚCI WYNIKÓW KLASYFIKACJI WOJEWÓDZTW POLSKI POD WZGLĘDEM POZIOMU ŻYCIA LUDNOŚCI
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/3 01 str. 159 168 OCENA STABILNOŚCI WYNIKÓW KLASYFIKACJI WOJEWÓDZTW POLSKI POD WZGLĘDEM POZIOMU ŻYCIA LUDNOŚCI Małgorzata Machowska-Szewczyk Katera Meto
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/3 01 str. 159 168 OCENA STABILNOŚCI WYNIKÓW KLASYFIKACJI WOJEWÓDZTW POLSKI POD WZGLĘDEM POZIOMU ŻYCIA LUDNOŚCI Małgorzata Machowska-Szewczyk Katera Meto
BRYŁA SZTYWNA. Umowy. Aby uprościć rozważania w tym dziale będziemy przyjmować następujące umowy:
 Niektóe powody aby poznać ten dział: BRYŁA SZTYWNA stanowi dobe uzupełnienie mechaniki punktu mateialnego, opisuje wiele sytuacji z życia codziennego, ma wiele powiązań z innymi działami fizyki (temodynamika,
Niektóe powody aby poznać ten dział: BRYŁA SZTYWNA stanowi dobe uzupełnienie mechaniki punktu mateialnego, opisuje wiele sytuacji z życia codziennego, ma wiele powiązań z innymi działami fizyki (temodynamika,
L(x, 0, y, 0) = x 2 + y 2 (3)
 0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
Porównanie właściwości wybranych wektorowych regulatorów prądu w stanach dynamicznych w przekształtniku AC/DC
 Piotr FALKOWSKI, Marian Roch DUBOWSKI Politechnika Białostocka, Wyział Elektryczny, Katera Energoelektroniki i Napęów Elektrycznych Porównanie właściwości wybranych wektorowych regulatorów prąu w stanach
Piotr FALKOWSKI, Marian Roch DUBOWSKI Politechnika Białostocka, Wyział Elektryczny, Katera Energoelektroniki i Napęów Elektrycznych Porównanie właściwości wybranych wektorowych regulatorów prąu w stanach
11. DYNAMIKA RUCHU DRGAJĄCEGO
 11. DYNAMIKA RUCHU DRGAJĄCEGO Ruchem dgającym nazywamy uch, któy powtaza się peiodycznie w takcie jego twania w czasie i zachodzi wokół położenia ównowagi. Zespół obiektów fizycznych zapewniający wytwozenie
11. DYNAMIKA RUCHU DRGAJĄCEGO Ruchem dgającym nazywamy uch, któy powtaza się peiodycznie w takcie jego twania w czasie i zachodzi wokół położenia ównowagi. Zespół obiektów fizycznych zapewniający wytwozenie
Szeregi czasowe, analiza zależności krótkoi długozasięgowych
 Szeregi czasowe, analiza zależności krótkoi długozasięgowych Rafał Weron rweron@im.pwr.wroc.pl Definicje Mając dany proces {X t } autokowariancję definiujemy jako : γ(t, t ) = cov(x t, X t ) = = E[(X t
Szeregi czasowe, analiza zależności krótkoi długozasięgowych Rafał Weron rweron@im.pwr.wroc.pl Definicje Mając dany proces {X t } autokowariancję definiujemy jako : γ(t, t ) = cov(x t, X t ) = = E[(X t
POLE MAGNETYCZNE W PRÓŻNI. W roku 1820 Oersted zaobserwował oddziaływanie przewodnika, w którym płynął
 POLE MAGNETYCZNE W PÓŻNI W oku 8 Oested zaobsewował oddziaływanie pzewodnika, w któym płynął pąd, na igłę magnetyczną Dopowadziło to do wniosku, że pądy elektyczne są pzyczyną powstania pola magnetycznego
POLE MAGNETYCZNE W PÓŻNI W oku 8 Oested zaobsewował oddziaływanie pzewodnika, w któym płynął pąd, na igłę magnetyczną Dopowadziło to do wniosku, że pądy elektyczne są pzyczyną powstania pola magnetycznego
POMIAR PĘTLI HISTEREZY MAGNETYCZNEJ
 POMAR PĘTL STEREZ MAGNETZNEJ 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DDAKTKA FZKA ĆZENA LABORATORJNE.. Opis układu pomiaowego Mateiały feomagnetyczne (feyt,
POMAR PĘTL STEREZ MAGNETZNEJ 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DDAKTKA FZKA ĆZENA LABORATORJNE.. Opis układu pomiaowego Mateiały feomagnetyczne (feyt,
WPROWADZENIE. Czym jest fizyka?
 WPROWADZENIE Czym jest fizyka? Fizyka odgywa dziś olę tego co dawniej nazywano filozofią pzyody i z czego zodziły się współczesne nauki pzyodnicze. Można powiedzieć, że fizyka stanowi system podstawowych
WPROWADZENIE Czym jest fizyka? Fizyka odgywa dziś olę tego co dawniej nazywano filozofią pzyody i z czego zodziły się współczesne nauki pzyodnicze. Można powiedzieć, że fizyka stanowi system podstawowych
DYNAMICZNE DZIAŁANIE PÓL: ELEKTRYCZNEGO I MAGNETYCZNEGO W ELEKTROTECHNOLOGIACH (NA PRZYKŁADZIE SEPARACJI) *)
 Antoni CIEŚLA DYNAMICZNE DZIAŁANIE PÓL: ELEKTRYCZNEGO I MAGNETYCZNEGO W ELEKTROTECHNOLOGIACH (NA PRZYKŁADZIE SEPARACJI) *) STRESZCZENIE Statyczne pola elektyczne i magnetyczne są wykozystywane m. in. w
Antoni CIEŚLA DYNAMICZNE DZIAŁANIE PÓL: ELEKTRYCZNEGO I MAGNETYCZNEGO W ELEKTROTECHNOLOGIACH (NA PRZYKŁADZIE SEPARACJI) *) STRESZCZENIE Statyczne pola elektyczne i magnetyczne są wykozystywane m. in. w
ĆWICZENIE 5. Badanie przekaźnikowych układów sterowania
 ĆWICZENIE 5 Badanie zekaźnikowych układów steowania 5. Cel ćwiczenia Celem ćwiczenia jest badanie zekaźnikowych układów steowania obiektem całkującoinecyjnym. Ćwiczenie dotyczy zekaźników dwu- i tójołożeniowych
ĆWICZENIE 5 Badanie zekaźnikowych układów steowania 5. Cel ćwiczenia Celem ćwiczenia jest badanie zekaźnikowych układów steowania obiektem całkującoinecyjnym. Ćwiczenie dotyczy zekaźników dwu- i tójołożeniowych
PROPOZYCJA FORMUŁY SPRZEDAŻNEJ WE GLA KOKSOWEGO
 PROPOZYCJA FORMUŁY SPRZEDAŻNEJ WE GLA KOKSOWEGO Uszula Ozga-Blaschke 1) 1) D inż.; Polska Akaemia Nauk, Instytut Gospoaki Suowcami Minealnymi i Enegią, Zakła Ekonomiki i Baań Rynku Paliwowo-Enegetycznego;
PROPOZYCJA FORMUŁY SPRZEDAŻNEJ WE GLA KOKSOWEGO Uszula Ozga-Blaschke 1) 1) D inż.; Polska Akaemia Nauk, Instytut Gospoaki Suowcami Minealnymi i Enegią, Zakła Ekonomiki i Baań Rynku Paliwowo-Enegetycznego;
Wyznaczanie sił w śrubach strzemiona w złączu ciernym obudowy górniczej
 r inż. JAROSŁAW BRODNY Politechnika Śląska Wyznaczanie sił w śrubach strzemiona w złączu ciernym obuowy górniczej W artykule przestawione zostały wyniki analizy wytrzymałościowej śrub strzemion pracujących
r inż. JAROSŁAW BRODNY Politechnika Śląska Wyznaczanie sił w śrubach strzemiona w złączu ciernym obuowy górniczej W artykule przestawione zostały wyniki analizy wytrzymałościowej śrub strzemion pracujących
5.1 Połączenia gwintowe
 5.0 Połączenia Połączenia służą o pzenoszenia obciążeń mięzy elementami konstukcyjnymi uniemożliwiając ich wzajemne pzemieszczenia. POŁĄCZENIA NIEROZŁĄCZNE ROZŁĄCZNE PLASTYCZNE - nitowe - zawijane - zaginane
5.0 Połączenia Połączenia służą o pzenoszenia obciążeń mięzy elementami konstukcyjnymi uniemożliwiając ich wzajemne pzemieszczenia. POŁĄCZENIA NIEROZŁĄCZNE ROZŁĄCZNE PLASTYCZNE - nitowe - zawijane - zaginane
NAGRZEWANIE MIKROFALOWE
 INSTYTUT INFORMATYKI STOSOWANEJ POLITECHNIKI ŁÓDZKIEJ Ćwiczenia N 1 NAGRZEWANIE MIKROFALOWE 1.WPROWADZENIE. W mikofalowych uzązeniach gzejnych efekt polayzacji (występujący w śoowiskach ielektycznych i
INSTYTUT INFORMATYKI STOSOWANEJ POLITECHNIKI ŁÓDZKIEJ Ćwiczenia N 1 NAGRZEWANIE MIKROFALOWE 1.WPROWADZENIE. W mikofalowych uzązeniach gzejnych efekt polayzacji (występujący w śoowiskach ielektycznych i
SK-7 Wprowadzenie do metody wektorów przestrzennych SK-8 Wektorowy model silnika indukcyjnego, klatkowego
 Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
WITOLD ORZESZKO WPŁYW REDUKCJI SZUMU LOSOWEGO METODĄ SCHREIBERA NA IDENTYFIKACJĘ SYSTEMU GENERUJĄCEGO DANE. ANALIZA SYMULACYJNA 1 1.
 PRZEGLĄD STATYSTYCZNY R. LVIII ZESZYT 1-2 2011 WITOLD ORZESZKO WPŁYW REDUKCJI SZUMU LOSOWEGO METODĄ SCHREIBERA NA IDENTYFIKACJĘ SYSTEMU GENERUJĄCEGO DANE. ANALIZA SYMULACYJNA 1 1. WSTĘP Wszelkie rzeczywiste,
PRZEGLĄD STATYSTYCZNY R. LVIII ZESZYT 1-2 2011 WITOLD ORZESZKO WPŁYW REDUKCJI SZUMU LOSOWEGO METODĄ SCHREIBERA NA IDENTYFIKACJĘ SYSTEMU GENERUJĄCEGO DANE. ANALIZA SYMULACYJNA 1 1. WSTĘP Wszelkie rzeczywiste,
LIST EMISYJNY nr 3 /2014 Ministra Finansów
 LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
Zarządzanie ryzykiem. Lista 3
 Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
ISBN Monografie Politechniki Łódzkiej
 ISBN 978-783-463-8 Monogafie Politechniki Łózkiej Recenzenci: pof. hab. inż. Michał Dyląg pof. hab. inż. Anzej Heim KOMITET REDAKCYJNY WYDAWNICTWA POLITECHNIKI ŁÓDZKIEJ Pzewoniczący: pof. hab. inż. Piot
ISBN 978-783-463-8 Monogafie Politechniki Łózkiej Recenzenci: pof. hab. inż. Michał Dyląg pof. hab. inż. Anzej Heim KOMITET REDAKCYJNY WYDAWNICTWA POLITECHNIKI ŁÓDZKIEJ Pzewoniczący: pof. hab. inż. Piot
KOLOKACJA SYSTEMÓW BEZPRZEWODOWYCH NA OBIEKTACH MOBILNYCH
 KOLOKACJA SYSTEMÓW BEZPRZEWODOWYCH NA OBIEKTACH MOBILNYCH Janusz ROMANIK, Kzysztof KOSMOWSKI, Edwad GOLAN, Adam KRAŚNIEWSKI Zakład Radiokomunikacji i Walki Elektonicznej Wojskowy Instytut Łączności 05-30
KOLOKACJA SYSTEMÓW BEZPRZEWODOWYCH NA OBIEKTACH MOBILNYCH Janusz ROMANIK, Kzysztof KOSMOWSKI, Edwad GOLAN, Adam KRAŚNIEWSKI Zakład Radiokomunikacji i Walki Elektonicznej Wojskowy Instytut Łączności 05-30
Pole grawitacyjne. Definicje. Rodzaje pól. Rodzaje pól... Notatki. Notatki. Notatki. Notatki. dr inż. Ireneusz Owczarek.
 Pole gawitacyjne d inż. Ieneusz Owczaek CNMiF PŁ ieneusz.owczaek@p.lodz.pl http://cmf.p.lodz.pl/iowczaek 1 d inż. Ieneusz Owczaek Pole gawitacyjne Definicje to pzestzenny ozkład wielkości fizycznej. jest
Pole gawitacyjne d inż. Ieneusz Owczaek CNMiF PŁ ieneusz.owczaek@p.lodz.pl http://cmf.p.lodz.pl/iowczaek 1 d inż. Ieneusz Owczaek Pole gawitacyjne Definicje to pzestzenny ozkład wielkości fizycznej. jest
Wykład 11. Pompa ciepła - uzupełnienie II Zasada Termodynamiki Entropia w ujęciu termodynamicznym c.d. Entropia w ujęciu statystycznym
 Wykład 11 Pompa ciepła - uzupełnienie II Zasada emodynamiki Entopia w ujęciu temodynamicznym c.d. Entopia w ujęciu statystycznym W. Dominik Wydział Fizyki UW emodynamika 2018/2019 1/30 G Pompa cieplna
Wykład 11 Pompa ciepła - uzupełnienie II Zasada emodynamiki Entopia w ujęciu temodynamicznym c.d. Entopia w ujęciu statystycznym W. Dominik Wydział Fizyki UW emodynamika 2018/2019 1/30 G Pompa cieplna
