Ryzyko walutowe. Kursy walutowe spot i forward. Teorie kursów walutowych
|
|
|
- Laura Cieślik
- 6 lat temu
- Przeglądów:
Transkrypt
1 Ryzyko walutowe. Kusy walutowe spot i owa. eoie kusów walutowych Postawowe pojęcia Deinicja yzyka walutowego - schemat z piewszego wykłau. Zazązanie yzykiem walutowym obejmuje wybó instumentów (aktywów) zaganicznych, stuktuy aktywów zaganicznych oaz walut. ystemy kusów walutowych - system kusów stałych - system kusów zmiennych Mięzynaoowy ynek walutowy Mięzynaoowy ynek walutowy jest w 95% ynkiem "hutowych" tansakcji (najczęściej 1 mln UD) pomięzy bankami centalnymi, największymi bankami, oaz użymi pzesiębiostwami. otowania kusów - bezpośenie - pośenie Koszt tansakcyjny kus spzeaży - kus kupna (1) spea 1 kus spzeaży topy apecjacji, epecjacji, ewaluacji, ewaluacji topa zmiany watości la waluty obcej (apecjacji bąź epecjacji): (2) gzie: t t1 t1 t t1 1 t1 t1 - stopa zmiany watości waluty obcej, t - kus spot waluty obcej w notowaniu bezpośenim, t-1 - popzeni kus waluty obcej, t - zmiana absolutna kusu waluty obcej. topa apecjacji bąź epecjacji (zależnie o znaku) waluty kajowej wynosi: (3) 1 t 1 t1 1 t1 t
2 Zazązanie yzykiem inansowym i instumenty pochone [ ] topy logaytmiczne (4) * t ln ln(1 ) t1 (5) 1 * ln t ln(1 ) 1 t1 (6) e e * * 1 1 Pzykła 1. topy apecjacji i epecjacji Kus spot wynosi 4, UD/PL. Polecenia: 1. Wyznaczyć stopę apecjacji olaa, gy kus spot osiągnie poziom 4,2 UD/PL. 2. Jaka bęzie w tej sytuacji stopa epecjacji złotego. 3. Ile wynosi stopa apecjacji olaa pzy zastosowaniu kapitalizacji ciągłej? 4. Ile wynosi stopa epecjacji złotego pzy zastosowaniu kapitalizacji ciągłej? Rozwiązanie A 1. 4 UD/PL 1 4,2 UD/PL topa apecjacji olaa wynosi: 5% A 2. 1/,25 PL/UD 1/1,2381 PL/UD topa epecjacji złotego wynosi: 1-4,8% A 3. topa apecjacji olaa pzy zastosowaniu kapitalizacji ciągłej wynosi: ln(4,2 : 4,) 4,879% A 4. topa epecjacji złotego pzy zastosowaniu kapitalizacji ciągłej wynosi: ln(,2381 :,25) -4,879% Paaoks iegela Watość oczekiwana kusu waluty obcej nie jest ówna owotności watości oczekiwanej kusu waluty kajowej. Zapis matematyczny jest nazywany także nieównością Jensena. 2
3 Zazązanie yzykiem inansowym i instumenty pochone [ ] Pzykła 2. Paaoks iegela Pognozowane kusy wynoszą 3, UD/PL z pawopoobieństwem,5 oaz 5, UD/PL z pawopoobieństwem,5. Polecenia: 1. Wyznaczyć opowienie kusy złotówki (UD/zł). 2. Wyznaczyć watość oczekiwaną kusu waluty obcej i watość oczekiwaną kusu waluty kajowej. 3. Wyznaczyć kus waluty kajowej (obcej) na postawie watości oczekiwanej kusu waluty obcej (kajowej). Poównać ten kus z watością oczekiwaną kusu kusu waluty kajowej. Rozwiązanie A 1. Pawopoobieństwo Kus waluty obcej Kus waluty kajowej,5 1 3, UD/PL 1/ 1,3333 PL/UD,5 2 5, UD/PL 1/ 2,2 PL/UD A 2. Kus waluty obcej Kus waluty kajowej Watość oczekiwana 4 UD/PL,2667 PL/UD A 3. Kus waluty obcej Kus waluty kajowej Owotność watości oczekiwanej kusu 3,75 UD/PL,25 PL/UD Kusy spot i owa 1+ i (7) F 1+ i Pemia owa F F (8) 1 * * * (9) ln(1 ) ln1+ i ln1+ i i i Pognozowanie kusów metoami analizy technicznej 3
4 Zazązanie yzykiem inansowym i instumenty pochone [ ] Śenia uchoma Śenia uchoma ługoteminowa Śenia uchoma kótkoteminowa Kup pzeaj Czas Rys. 1. ygnał kupna / spzeaży w metozie śenich uchomych Źóło: Opacowanie własne. eoie kusów walutowych 1. eoia paytetu siły kupna Absolutny paytet siły kupna P (1) P gzie: - kus spot, P - poziom cen w kaju, P - poziom cen za ganicą. Wzglęny paytet siły kupna (11) E() 1+ π 1+ π 2. eoia Fishea R (12) 1 i 1 i 1 π gzie: - stopa inlacji, i - nominalna stopa pocentowa w skali ocznej, i R - ealna stopa pocentowa w skali ocznej. Mięzynaoowy eekt Fishea 1+ i 1+ π (13) 1+ i 1+ π gzie: i - nominalna stopa pocentowa w skali ocznej w kaju, i - nominalna stopa pocentowa w skali ocznej za ganicą. 4
5 Zazązanie yzykiem inansowym i instumenty pochone [ ] iepokyty paytet pocentowy (14) E() 1+ i 1+ i Pokyty paytet pocentowy 1+ i (15) F lub 1+ i i F e * i * 3. eoia bilansu płatniczego 4. eoie monetane - moel elastycznych cen (Fenkel, Koui i Mussa) - moel sztywnych cen (Donbusch) 5. eoia ynku aktywów (moele ynamiki kusów) 5
6 Zazązanie yzykiem inansowym i instumenty pochone [ ] Pzykła 3. Abitaż pzy wykozystaniu owa bąź utues Dane są: zakup spzeaż kus walutowy spot 4,5 4,6 stopa pocentowa w walucie kajowej 17,% 18,% stopa pocentowa w walucie zaganicznej 5,% 6,% Polecenia: 1. Pzestawić seię opeacji abitażowych związanych z zakupem waluty na temin jenego oku, wyznaczyć ganiczny kus owa, ustalić wynik pzy kusie niższym o 1 pkb. Kwota pożyczki wynosi 1 UD. 2. Pzestawić seię opeacji abitażowych związanych z spzaażą waluty na temin jenego oku, wyznaczyć ganiczny kus owa, ustalić wynik pzy kusie wyższym o 1 pkb. Kwota pożyczki wynosi 46 zł. Dane: pożyczka UD 1 UD pożyczka zł 46 zł pkb 1 Rozwiązanie A 1. Dziś Rok później UD zł UD zł pożyczka UD ,% st. poc. ask spzeaż UD 45 4,5 kus spot bi epozyt w zł ,% st. poc. bi zakup UD na temin 16 4,967 ganiczny kus owa wynik Ganiczny kus owa (bi): 4,5*(1+17%)/(1+6%)4,967 Pzy niższym kusie owa wystąpią kozyści abitażowe: zakup UD na temin kus 4, wynik 2 A 2. Dziś Rok później zł UD zł UD pożyczka zł ,% st. poc. ask zakup UD 1 4,6 kus spot ask epozyt w UD ,% st. poc. bi spzeaż UD na temin ,1695 ganiczny kus owa wynik wynik Ganiczny kus owa (ask): 4,6*(1+18%)/(1+5%)5,1695 Pzy wyższym kusie owa wystąpią kozyści abitażowe: spzeaż UD na temin kus 5, wynik 11 6
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Spis treści. Rozdział 1 Charakterystyka i klasyfikacja instrumentów finansowych. Ryzyko w działalności przedsiębiorstwa
 Spis teści Wstęp.......................................... 7 Rozdział 1 Chaakteystyka i klasyfikacja instumentów finansowych. Ryzyko w działalności pzedsiębiostwa 1.1. Istota instumentów finansowych........................
Spis teści Wstęp.......................................... 7 Rozdział 1 Chaakteystyka i klasyfikacja instumentów finansowych. Ryzyko w działalności pzedsiębiostwa 1.1. Istota instumentów finansowych........................
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
Wykład 9. Model ISLM: część I
 Makoekonomia 1 Wykład 9 Model ISLM: część I Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Model ISLM Równowaga gaficzna Równowaga algebaiczna Skutki zmian paametów egzogenicznych
Makoekonomia 1 Wykład 9 Model ISLM: część I Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Model ISLM Równowaga gaficzna Równowaga algebaiczna Skutki zmian paametów egzogenicznych
Makroekonomia 1 Wykład 8: Wprowadzenie do modelu ISLM: krzywa LM oraz krzywa IS
 Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Deteminanty popytu na pieniądz Równowaga na ynku
Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Deteminanty popytu na pieniądz Równowaga na ynku
Arytmetyka finansowa Wykład 6 Dr Wioletta Nowak
 Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
Zarządzanie ryzykiem. Lista 3
 Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
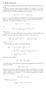 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Makroekonomia 1 Wykład 8: Wprowadzenie do modelu ISLM: krzywa LM oraz krzywa IS
 Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS D hab. Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Nasz mapa dogowa Kzyż keynesowski Teoia pefeencji płynności
Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS D hab. Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Nasz mapa dogowa Kzyż keynesowski Teoia pefeencji płynności
UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI. Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH
 UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH WPROWADZENIE Opcje są instrumentem pochonym, zatem takim, którego cena zależy o ceny instrumentu
UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH WPROWADZENIE Opcje są instrumentem pochonym, zatem takim, którego cena zależy o ceny instrumentu
Temat 3 - Pieniądz i system bankowy
 Temat 3 - Pieniądz i system bankowy Pieniądz pewien powszechnie akceptowany towa, któy w zależności od sytuacji pełni funkcję: śodka wymiany jednostki ozachunkowej (umożliwia wyażanie cen i powadzenie
Temat 3 - Pieniądz i system bankowy Pieniądz pewien powszechnie akceptowany towa, któy w zależności od sytuacji pełni funkcję: śodka wymiany jednostki ozachunkowej (umożliwia wyażanie cen i powadzenie
Makroekonomia 1 dla MSEMen. Gabriela Grotkowska
 Makoekonomia 1 dla MSEMen Gabiela Gotkowska Rozszezamy analizę pzyczyn wahao koniunktualnych W czasie dwóch ostatnich zajęd zajmowaliśmy się analizą deteminantów wielkości PKB w kótkim okesie Analiza ta
Makoekonomia 1 dla MSEMen Gabiela Gotkowska Rozszezamy analizę pzyczyn wahao koniunktualnych W czasie dwóch ostatnich zajęd zajmowaliśmy się analizą deteminantów wielkości PKB w kótkim okesie Analiza ta
NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek
 Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem. Temat wykładu: Wycena kontraktów swap
 Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem Temat wykładu: Wycena kontraktów swap Podstawowe zagadnienia: 1. Wycena swapa procentowego metodą wyceny obligacji 2.
Materiały do samodzielnego kształcenia Inżynieria finansowa i zarządzanie ryzykiem Temat wykładu: Wycena kontraktów swap Podstawowe zagadnienia: 1. Wycena swapa procentowego metodą wyceny obligacji 2.
Matematyka I dla DSM zbiór zadań
 I Sumowanie skończone W zadaniach -4 obliczyć podaną sumę. Matematyka I dla DSM zbiór zadań do użytku wewnętrznego dr Leszek Rudak Uniwersytet Warszawski Wydział Zarządzania. 5 i. i= 4 i 3. i= 5 ( ) i
I Sumowanie skończone W zadaniach -4 obliczyć podaną sumę. Matematyka I dla DSM zbiór zadań do użytku wewnętrznego dr Leszek Rudak Uniwersytet Warszawski Wydział Zarządzania. 5 i. i= 4 i 3. i= 5 ( ) i
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
OPCJE. Wycena w modelach dyskretnych Parytet kupna - sprzedaży Ograniczenia na cenę opcji
 OPJE Wycena w moelach ysetnych Paytet na - szeaży Oganiczenia na cenę ocji Zaganienia wycena ocji Fncja wyłaty, fncja zys Ryne osonały - założenia Wzoy na wycenę ocji zy założeni oesowej aitalizacji osete
OPJE Wycena w moelach ysetnych Paytet na - szeaży Oganiczenia na cenę ocji Zaganienia wycena ocji Fncja wyłaty, fncja zys Ryne osonały - założenia Wzoy na wycenę ocji zy założeni oesowej aitalizacji osete
Czy opcje walutowe mogą być toksyczne?
 Katedra Matematyki Finansowej Wydział Matematyki Stosowanej AGH 11 maja 2012 Kurs walutowy Kurs walutowy cena danej waluty wyrażona w innej walucie np. 1 USD = 3,21 PLN; USD/PLN = 3,21 Rodzaje kursów walutowych:
Katedra Matematyki Finansowej Wydział Matematyki Stosowanej AGH 11 maja 2012 Kurs walutowy Kurs walutowy cena danej waluty wyrażona w innej walucie np. 1 USD = 3,21 PLN; USD/PLN = 3,21 Rodzaje kursów walutowych:
Arkusze maturalne poziom podstawowy
 Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
F : R 0;1 rozkład prawdopodobieństwa stopy zwrotu.
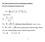 Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
EUR / USD 1,3615 / 1,3620
 EUR / USD 1,3615 / 1,3620 waluta kupno / sprzedaŝ bazowa / notowana BID / OFFER (ASK) Zadanie 1 Bank kwotuje następujący kurs walutowy: USD/SEK = 7,3020/40 Wyznacz: 1. walutę bazową.. 4. kurs sprzedaŝy
EUR / USD 1,3615 / 1,3620 waluta kupno / sprzedaŝ bazowa / notowana BID / OFFER (ASK) Zadanie 1 Bank kwotuje następujący kurs walutowy: USD/SEK = 7,3020/40 Wyznacz: 1. walutę bazową.. 4. kurs sprzedaŝy
Korekta nierównowagi zewnętrznej
 Wykład 4 Korekta nierównowagi zewnętrznej Plan wykładu 1. System kursu walutowego 2. Korekta przy sztywnym kursie 1. System kursu walutowego W systemie płynnych kursów walutowych cena waluty jest wyznaczona
Wykład 4 Korekta nierównowagi zewnętrznej Plan wykładu 1. System kursu walutowego 2. Korekta przy sztywnym kursie 1. System kursu walutowego W systemie płynnych kursów walutowych cena waluty jest wyznaczona
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja
 Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Październik 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Październik 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę
Arytmetyka finansowa Wykład 5 Dr Wioletta Nowak
 Aymeyka finansowa Wykład 5 D Wiolea Nowak Bon skabowy Insumen dłużny, emiowany pzez Skab ańswa za pośednicwem Miniseswa Finansów. Temin wykupu dzień w kóym emien dokonuje wykupu, Skab ańswa zwaca dług
Aymeyka finansowa Wykład 5 D Wiolea Nowak Bon skabowy Insumen dłużny, emiowany pzez Skab ańswa za pośednicwem Miniseswa Finansów. Temin wykupu dzień w kóym emien dokonuje wykupu, Skab ańswa zwaca dług
Instrumenty pochodne Instrumenty wbudowane
 www.pwcacademy.pl Instrumenty pochodne Instrumenty wbudowane Jan Domanik Instrumenty pochodne ogólne zasady ujmowania i wyceny 2 Instrument pochodny definicja. to instrument finansowy: którego wartość
www.pwcacademy.pl Instrumenty pochodne Instrumenty wbudowane Jan Domanik Instrumenty pochodne ogólne zasady ujmowania i wyceny 2 Instrument pochodny definicja. to instrument finansowy: którego wartość
TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE
 TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE 1 SWAP - fixed-to-floating rate IRS - swap procentowy jest umową, w której dwie strony uzgadniają, że będą w ustalonych terminach
TRANSAKCJE SWAP: - PROCENTOWE - WALUTOWE - WALUTOWO-PROCENTOWE - KREDYTOWE 1 SWAP - fixed-to-floating rate IRS - swap procentowy jest umową, w której dwie strony uzgadniają, że będą w ustalonych terminach
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy
05-530 Góra Kalwaria, ul. Pijarska 21 tel.: [22] 717-82-65 fax: [22] 717-82-66 kom.: [0] 692-981-991, [0] 501-633-694 Info: 0 708 288 308
![05-530 Góra Kalwaria, ul. Pijarska 21 tel.: [22] 717-82-65 fax: [22] 717-82-66 kom.: [0] 692-981-991, [0] 501-633-694 Info: 0 708 288 308 05-530 Góra Kalwaria, ul. Pijarska 21 tel.: [22] 717-82-65 fax: [22] 717-82-66 kom.: [0] 692-981-991, [0] 501-633-694 Info: 0 708 288 308](/thumbs/24/2783348.jpg) 05-530 Góra Kalwaria, ul. Pijarska 21 tel.: [22] 717-82-65 fax: [22] 717-82-66 kom.: [0] 692-981-991, [0] 501-633-694 Info: 0 708 288 308 biuro@assman.com.pl http://www.assman.com.pl 21-11-2006 W części
05-530 Góra Kalwaria, ul. Pijarska 21 tel.: [22] 717-82-65 fax: [22] 717-82-66 kom.: [0] 692-981-991, [0] 501-633-694 Info: 0 708 288 308 biuro@assman.com.pl http://www.assman.com.pl 21-11-2006 W części
Subfundusz wydzielony w ramach Allianz Fundusz Inwestycyjny Otwarty
 Subfundusz wydzielony w ramach Allianz Fundusz Inwestycyjny Otwarty Aktywa subfunduszu są inwestowane w instrumenty finansowe o ograniczonym ryzyku np. papiery wartościowe emitowane przez najbardziej wiarygodnych
Subfundusz wydzielony w ramach Allianz Fundusz Inwestycyjny Otwarty Aktywa subfunduszu są inwestowane w instrumenty finansowe o ograniczonym ryzyku np. papiery wartościowe emitowane przez najbardziej wiarygodnych
Przejmowanie ciepła przy konwekcji swobodnej w przestrzeni ograniczonej (szczeliny)
 inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
Opcje III. 1. Opcje na indeksy
 . Opcje na ineksy Opcje III Na wielu giełach notowane są opcje na ineksy giełowe, w których instrumentem bazowym jest ineks. Najbarziej popularnymi opcjami ineksowymi są: opcja na ineks S&P500 (opcja typu
. Opcje na ineksy Opcje III Na wielu giełach notowane są opcje na ineksy giełowe, w których instrumentem bazowym jest ineks. Najbarziej popularnymi opcjami ineksowymi są: opcja na ineks S&P500 (opcja typu
Plan wykładu 8 Równowaga ogólna w małej gospodarce otwartej
 Plan wykładu 8 Równowaga ogólna w małej gospodarce otwartej 1. Model Mundella Fleminga 2. Dylemat polityki gospodarczej małej gospodarki otwartej 3. Skuteczność polityki monetarnej i fiskalnej w warunkach
Plan wykładu 8 Równowaga ogólna w małej gospodarce otwartej 1. Model Mundella Fleminga 2. Dylemat polityki gospodarczej małej gospodarki otwartej 3. Skuteczność polityki monetarnej i fiskalnej w warunkach
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 Zadanie 1. Wycena stałej stopy swap Bank A podpisuje z Bankiem B swap na stopy procentowe. Wyznacz wartość teoretyczną oprocentowania stałego, wiedząc że swap ma być o terminie 1 rok, a
Ćwiczenia ZPI 1 Zadanie 1. Wycena stałej stopy swap Bank A podpisuje z Bankiem B swap na stopy procentowe. Wyznacz wartość teoretyczną oprocentowania stałego, wiedząc że swap ma być o terminie 1 rok, a
Swap. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Swap Ćwiczenia ZPI 1 Obliczanie ceny swapa za pomocą kontraktów FRA Ile wynosi cena swapa odsetkowego, gdzie płacimy stałą stopę procentową, a w zamian chcemy otrzymywać 3M WIBOR. Swap zawierany w celu
Swap Ćwiczenia ZPI 1 Obliczanie ceny swapa za pomocą kontraktów FRA Ile wynosi cena swapa odsetkowego, gdzie płacimy stałą stopę procentową, a w zamian chcemy otrzymywać 3M WIBOR. Swap zawierany w celu
Swap. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Swap Ćwiczenia ZPI 1 Obliczanie ceny swapa za pomocą kontraktów FRA Ile wynosi cena swapa odsetkowego, gdzie płacimy stałą stopę procentową, a w zamian chcemy otrzymywać 3M WIBOR. Swap zawierany w celu
Swap Ćwiczenia ZPI 1 Obliczanie ceny swapa za pomocą kontraktów FRA Ile wynosi cena swapa odsetkowego, gdzie płacimy stałą stopę procentową, a w zamian chcemy otrzymywać 3M WIBOR. Swap zawierany w celu
DOLNOŚLĄSKA WOJEWÓDZKA KOMENDA OCHOTNICZYCH HUFCÓW PRACY
 DOLNOŚLĄSKA WOJEWÓDZKA KOMENDA OCHOTNICZYCH HUFCÓW PRACY 0- Wocław, Wybzeże J. Słowackiego 9 tel. (07) -6-70, -9-08 e-mail: dolnoslaska@ohp.pl fax (07) -9-0 N konta: NBP O/Wocław 9 00 67 009 88 000 0000
DOLNOŚLĄSKA WOJEWÓDZKA KOMENDA OCHOTNICZYCH HUFCÓW PRACY 0- Wocław, Wybzeże J. Słowackiego 9 tel. (07) -6-70, -9-08 e-mail: dolnoslaska@ohp.pl fax (07) -9-0 N konta: NBP O/Wocław 9 00 67 009 88 000 0000
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 Obliczanie ceny swapa za pomocą kontraktów FRA Ile wynosi cena swapa odsetkowego, gdzie płacimy stałą stopę procentową, a w zamian chcemy otrzymywać 3M WIBOR. Swap zawierany w celu zabezpieczenia
Ćwiczenia ZPI 1 Obliczanie ceny swapa za pomocą kontraktów FRA Ile wynosi cena swapa odsetkowego, gdzie płacimy stałą stopę procentową, a w zamian chcemy otrzymywać 3M WIBOR. Swap zawierany w celu zabezpieczenia
Powtórzenie. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja
 Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę terminową
Inżynieria Finansowa: 2. Ceny terminowe i prosta replikacja Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Marzec 2017 r. Warszawa, Szkoła Główna Handlowa Zadanie z ostatniego wykładu: ustal cenę terminową
BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO NA IDENTYFIKACJĘ CHAOSU DETERMINISTYCZNEGO W EKONOMICZNYCH SZEREGACH CZASOWYCH
 Katazyna Zeug-Żebo Uniwesytet Śląski w Katowicach BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO NA IDENTYFIKACJĘ CHAOSU DETERMINISTYCZNEGO W EKONOMICZNYCH SZEREGACH CZASOWYCH Wpowazenie Wieloletnie baania
Katazyna Zeug-Żebo Uniwesytet Śląski w Katowicach BADANIE WPŁYWU REDUKCJI POZIOMU SZUMU LOSOWEGO NA IDENTYFIKACJĘ CHAOSU DETERMINISTYCZNEGO W EKONOMICZNYCH SZEREGACH CZASOWYCH Wpowazenie Wieloletnie baania
Metoda odbić zwierciadlanych
 Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa
Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa
Kursy walutowe wprowadzenie
 Kursy walutowe wprowadzenie Krzysztof Radojewski Koło Naukowe Zarządzania Finansami http://knmanager.ae.wroc.pl e-mail: knmanager@ae.wroc.pl Spis treści podstawowe pojęcia, ewolucja międzynarodowego systemu
Kursy walutowe wprowadzenie Krzysztof Radojewski Koło Naukowe Zarządzania Finansami http://knmanager.ae.wroc.pl e-mail: knmanager@ae.wroc.pl Spis treści podstawowe pojęcia, ewolucja międzynarodowego systemu
METODA CIASNEGO (silnego) WIĄZANIA (TB)
 MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
WSPÓŁCZYNNIK THETA OPCJI BARIEROWYCH
 Ewa Dziawgo Uniwesye Mikołaja openika w ouniu Wyział auk Ekonomicznych i Zazązania aea Ekonomeii i aysyki ziawew@umk.pl WPÓŁCZYI EA OPCJI BARIEROWYC eszczenie: W aykule pzesawiono zaganienia związane z
Ewa Dziawgo Uniwesye Mikołaja openika w ouniu Wyział auk Ekonomicznych i Zazązania aea Ekonomeii i aysyki ziawew@umk.pl WPÓŁCZYI EA OPCJI BARIEROWYC eszczenie: W aykule pzesawiono zaganienia związane z
MATEMATYKA FINANSOWA. Zadanie 1 Od jakiej kwoty otrzymano 15 zł odsetek za okres 2 miesięcy przy stopie procentowej 18% w skali roku.
 MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
MATEMATYA FIASWA Rachuek osetek postych Wykozystyway w okesie kótki o 1 oku Wzó oóly * * t Wzó pzy uwzlęieiu oiesieia czasoweo t * * t * T p. w pzypaku okesu zieeo t * * 360 Zaaie 1 jakiej kwoty otzyao
WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE
 WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE PYTANIA KONTROLNE Różnica pomiędzy: inwestycją, projektem inwestycyjnym, przedsięwzięciem inwestycyjnym Rodzaje inwestycji ze względu na cel Wartość pieniądza w
WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE PYTANIA KONTROLNE Różnica pomiędzy: inwestycją, projektem inwestycyjnym, przedsięwzięciem inwestycyjnym Rodzaje inwestycji ze względu na cel Wartość pieniądza w
Forward kontrakt terminowy o charakterze rzeczywistym (z dostawą instrumentu bazowego).
 Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Oprocentowanie w stosunku rocznym Obowiązuje od 03.07.2014 r.
 Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Oprocentowanie w stosunku rocznym Obowiązuje od 03.07.2014 r. Spis treści I. Rachunki bieżące:... 3 - Rachunek bieżący prowadzony
Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Oprocentowanie w stosunku rocznym Obowiązuje od 03.07.2014 r. Spis treści I. Rachunki bieżące:... 3 - Rachunek bieżący prowadzony
MIĘDZYNARODOWE STOSUNKI GOSPODARCZE Kursy i rynki walutowe - synteza
 MIĘDZYNARODOWE STOSUNKI GOSPODARCZE 2017 Kursy i rynki walutowe - synteza Rodzaje notowań 2 Pośrednie liczba jednostek pieniądza zagranicznego przypadającego na jednostkę pieniądza krajowego 0,257 PLN/EUR
MIĘDZYNARODOWE STOSUNKI GOSPODARCZE 2017 Kursy i rynki walutowe - synteza Rodzaje notowań 2 Pośrednie liczba jednostek pieniądza zagranicznego przypadającego na jednostkę pieniądza krajowego 0,257 PLN/EUR
Wynik finansowy transakcji w momencie jej zawierania jest nieznany z uwagi na zmienność ceny przedmiotu transakcji, czyli instrumentu bazowego
 .Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
.Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
Przekształcenie całkowe Fouriera
 Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
1. SZCZEGÓLNE PRZYPADKI ŁUKÓW.
 Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Różnice kursowe. Prowadzący: dr Gyöngyvér Takáts
 Różnice kursowe Prowadzący: dr Gyöngyvér Takáts Różnice kursowe Różnice kursowe to różnice wynikające ze zmiany (zwiększenia lub zmniejszenia) kursów walut obcych w stosunku do złotego, występujące między
Różnice kursowe Prowadzący: dr Gyöngyvér Takáts Różnice kursowe Różnice kursowe to różnice wynikające ze zmiany (zwiększenia lub zmniejszenia) kursów walut obcych w stosunku do złotego, występujące między
PROPOZYCJA FORMUŁY SPRZEDAŻNEJ WE GLA KOKSOWEGO
 PROPOZYCJA FORMUŁY SPRZEDAŻNEJ WE GLA KOKSOWEGO Uszula Ozga-Blaschke 1) 1) D inż.; Polska Akaemia Nauk, Instytut Gospoaki Suowcami Minealnymi i Enegią, Zakła Ekonomiki i Baań Rynku Paliwowo-Enegetycznego;
PROPOZYCJA FORMUŁY SPRZEDAŻNEJ WE GLA KOKSOWEGO Uszula Ozga-Blaschke 1) 1) D inż.; Polska Akaemia Nauk, Instytut Gospoaki Suowcami Minealnymi i Enegią, Zakła Ekonomiki i Baań Rynku Paliwowo-Enegetycznego;
Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Oprocentowanie w stosunku rocznym Obowiązuje od r.
 Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Oprocentowanie w stosunku rocznym Obowiązuje od 05.03.205 r. Spis treści I. Rachunki bieżące:... 3 - Rachunek bieżący prowadzony
Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Oprocentowanie w stosunku rocznym Obowiązuje od 05.03.205 r. Spis treści I. Rachunki bieżące:... 3 - Rachunek bieżący prowadzony
INSTRUMENTY DŁUŻNE. Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
WYKŁAD nr Ekstrema funkcji jednej zmiennej o ciągłych pochodnych. xˆ ( ) 0
 WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
Spis treści. Część trzecia Kursy walutowe i makroekonomia gospodarki otwartej
 Spis treści Część trzecia Kursy walutowe i makroekonomia gospodarki otwartej Rozdział 12. Rachunkowość dochodu narodowego i bilans płatniczy Rachunki dochodu narodowego Produkt narodowy i dochód narodowy
Spis treści Część trzecia Kursy walutowe i makroekonomia gospodarki otwartej Rozdział 12. Rachunkowość dochodu narodowego i bilans płatniczy Rachunki dochodu narodowego Produkt narodowy i dochód narodowy
ZASADY WYCENY AKTYWÓW FUNDUSZU WPROWADZONE ZE WZGLĘDU NA ZMIANĘ NORM PRAWNYCH. Wycena aktywów Funduszu, ustalenie zobowiązań i wyniku z operacji
 ZASADY WYCENY AKTYWÓW FUNDUSZU WPROWADZONE ZE WZGLĘDU NA ZMIANĘ NORM PRAWNYCH Wycena aktywów Funduszu, ustalenie zobowiązań i wyniku z operacji 1. Wycena Aktywów Funduszu oraz ustalenie Wartości Aktywów
ZASADY WYCENY AKTYWÓW FUNDUSZU WPROWADZONE ZE WZGLĘDU NA ZMIANĘ NORM PRAWNYCH Wycena aktywów Funduszu, ustalenie zobowiązań i wyniku z operacji 1. Wycena Aktywów Funduszu oraz ustalenie Wartości Aktywów
Makroekonomia II Polityka fiskalna
 Makroekonomia II Polityka fiskalna D R A D A M C Z E R N I A K S Z K O Ł A G Ł Ó W N A H A N D L O W A W W A R S Z A W I E K A T E D R A E K O N O M I I I I 2 MIERNIKI RÓWNOWAGI FISKALNEJ wykład I Co składa
Makroekonomia II Polityka fiskalna D R A D A M C Z E R N I A K S Z K O Ł A G Ł Ó W N A H A N D L O W A W W A R S Z A W I E K A T E D R A E K O N O M I I I I 2 MIERNIKI RÓWNOWAGI FISKALNEJ wykład I Co składa
Bankowość Zajęcia nr 5 i 6
 Motto zajęć: "za złoty dukat co w słońcu błyszczy" Bankowość Zajęcia nr 5 i 6 Ryzyko bankowe Ryzyko płynności Rola bilansu i cash flow; Metoda luki: Aktywa określonego rodzaju (AOR), Pasywa określonego
Motto zajęć: "za złoty dukat co w słońcu błyszczy" Bankowość Zajęcia nr 5 i 6 Ryzyko bankowe Ryzyko płynności Rola bilansu i cash flow; Metoda luki: Aktywa określonego rodzaju (AOR), Pasywa określonego
Nadmierne zadłużanie się
 Nadmierne zadłużanie się Kredyt jako kategoria ekonomiczna Kredyt bankowy to stosunek prawno - finansowy pomiędzy bankiem a kredytobiorcą. Stosunek ten wyraża się przekazaniem przez bank określonej kwoty
Nadmierne zadłużanie się Kredyt jako kategoria ekonomiczna Kredyt bankowy to stosunek prawno - finansowy pomiędzy bankiem a kredytobiorcą. Stosunek ten wyraża się przekazaniem przez bank określonej kwoty
Temat 4 - Model ISLM
 mg Batłomiej Rokicki Ćwiczenia z Makoekonomii I 2005/2006 Temat 4 - Model ISLM Podstawowe założenia modelu: pieniądz odgywa ważną olę pzy deteminowaniu poziomu dochodu i zatudnienia inwestycje nie mają
mg Batłomiej Rokicki Ćwiczenia z Makoekonomii I 2005/2006 Temat 4 - Model ISLM Podstawowe założenia modelu: pieniądz odgywa ważną olę pzy deteminowaniu poziomu dochodu i zatudnienia inwestycje nie mają
IV OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy część 2 ZADANIA 29 lutego 2012r.
 V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
V OGÓLNOPOLSK KONKS Z FZYK Fizyka się liczy część ZADANA 9 lutego 0.. Dwie planety obiegają Słooce po, w pzybliżeniu, kołowych obitach o pomieniach 50 0 km (Ziemia) i 080 km (Wenus). Znaleź stosunek ich
TRANSAKCJE KASOWE. Sekcja I (produkty inwestycyjne)
 Kwestionariusz oceny odpowiedniości w odniesieniu do transakcji skarbowych Zgodnie z Dyrektywą MIFID, Alior Bank SA, świadcząc usługi nabywania i zbywania instrumentów finansowych na własny rachunek, jest
Kwestionariusz oceny odpowiedniości w odniesieniu do transakcji skarbowych Zgodnie z Dyrektywą MIFID, Alior Bank SA, świadcząc usługi nabywania i zbywania instrumentów finansowych na własny rachunek, jest
Gospodarka otwarta i bilans płatniczy
 Gospodarka otwarta i bilans płatniczy Zagregowane wydatki w gospodarce otwartej Jeżeli przyjmiemy, że wydatki krajowe na dobra wytworzone w kraju zależą od poziomu dochodu Y oraz realnej stopy procentowej
Gospodarka otwarta i bilans płatniczy Zagregowane wydatki w gospodarce otwartej Jeżeli przyjmiemy, że wydatki krajowe na dobra wytworzone w kraju zależą od poziomu dochodu Y oraz realnej stopy procentowej
Analiza Matematyczna MAEW101 MAP1067
 1 Analiza Matematyczna MAEW101 MAP1067 Wydział Elektroniki Przykłady do Listy Zadań nr 14 Funkcje wielu zmiennych. Płaszczyzna styczna. Ekstrema Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania
1 Analiza Matematyczna MAEW101 MAP1067 Wydział Elektroniki Przykłady do Listy Zadań nr 14 Funkcje wielu zmiennych. Płaszczyzna styczna. Ekstrema Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania
Ryzyko walutowe i zarządzanie nim. dr Grzegorz Kotliński, Katedra Bankowości AE w Poznaniu
 1 Ryzyko walutowe i zarządzanie nim 2 Istota ryzyka walutowego Istota ryzyka walutowego sprowadza się do konieczności przewalutowania należności i zobowiązań (pozycji bilansu banku) wyrażonych w walutach
1 Ryzyko walutowe i zarządzanie nim 2 Istota ryzyka walutowego Istota ryzyka walutowego sprowadza się do konieczności przewalutowania należności i zobowiązań (pozycji bilansu banku) wyrażonych w walutach
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
Determinanty kursu walutowego w ujęciu modelowym
 Determinanty kursu walutowego w ujęciu modelowym Model portfelowy Makroekonomia Gospodarki Otwartej II dr Dagmara Mycielska c by Dagmara Mycielska Wprowadzenie Idea modelu Poziom kursu walutowego jest
Determinanty kursu walutowego w ujęciu modelowym Model portfelowy Makroekonomia Gospodarki Otwartej II dr Dagmara Mycielska c by Dagmara Mycielska Wprowadzenie Idea modelu Poziom kursu walutowego jest
WYTYCZNE EUROPEJSKIEGO BANKU CENTRALNEGO
 L 247/38 Dziennik Urzędowy Unii Europejskiej 18.9.2013 WYTYCZNE WYTYCZNE EUROPEJSKIEGO BANKU CENTRALNEGO z dnia 30 lipca 2013 r. zmieniające wytyczne EBC/2011/23 w sprawie wymogów sprawozdawczości statystycznej
L 247/38 Dziennik Urzędowy Unii Europejskiej 18.9.2013 WYTYCZNE WYTYCZNE EUROPEJSKIEGO BANKU CENTRALNEGO z dnia 30 lipca 2013 r. zmieniające wytyczne EBC/2011/23 w sprawie wymogów sprawozdawczości statystycznej
Tabela oprocentowania kont oraz lokat terminowych dla klientów indywidualnych
 1 Rachunki prowadzone w złotych polskich KONTA OSOBISTE Konto Godne Polecenia 0,00% Konto Aktywni 50+ 0,00% Konto VIP 0,00% Konto 123 przy wpływach na rachunek w poprzednim miesiącu kalendarzowym w wysokości
1 Rachunki prowadzone w złotych polskich KONTA OSOBISTE Konto Godne Polecenia 0,00% Konto Aktywni 50+ 0,00% Konto VIP 0,00% Konto 123 przy wpływach na rachunek w poprzednim miesiącu kalendarzowym w wysokości
BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH OPARTYCH NA ANALIZIE TECHNICZNEJ WPROWADZENIE
 Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
POLITECHNIKA OPOLSKA Wydział Elektrotechniki i Automatyki
 POLITECHNIKA OPOLSKA Wydział Elektotechniki i Automatyki Mg inż. Michał Tomaszewski MODEL PRZEDSIĘBIORSTWA DYSTRYBUCYJNEGO DZIAŁAJĄCEGO NA OTWARTYM RYNKU ENERGII ELEKTRYCZNEJ Autoefeat pacy doktoskiej
POLITECHNIKA OPOLSKA Wydział Elektotechniki i Automatyki Mg inż. Michał Tomaszewski MODEL PRZEDSIĘBIORSTWA DYSTRYBUCYJNEGO DZIAŁAJĄCEGO NA OTWARTYM RYNKU ENERGII ELEKTRYCZNEJ Autoefeat pacy doktoskiej
Dr hab. Renata Karkowska, ćwiczenia Zarządzanie ryzykiem 1
 1 Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu. Ryzyko podstawy
1 Rodzaje i źródła ryzyka stopy procentowej: Ryzyko niedopasowania terminów przeszacowania, np. 6M kredyt o stałym oprocentowaniu finansowany miesięcznymi lokatami o zmiennym oprocentowaniu. Ryzyko podstawy
Tabela oprocentowania kont oraz lokat terminowych dla klientów indywidualnych
 1 Rachunki prowadzone w złotych polskich KONTA OSOBISTE Konto Godne Polecenia 0,00% Konto Aktywni 50+ 0,00% Konto VIP 0,00% Konto 123 przy wpływach na rachunek w poprzednim miesiącu kalendarzowym w wysokości
1 Rachunki prowadzone w złotych polskich KONTA OSOBISTE Konto Godne Polecenia 0,00% Konto Aktywni 50+ 0,00% Konto VIP 0,00% Konto 123 przy wpływach na rachunek w poprzednim miesiącu kalendarzowym w wysokości
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
Podstawowe wskaźniki makroekonomiczne mld BYR mld USD 1. Produkt krajowy brutto*** ,8 I XII 2013
 PODSTAWOWE WSKAŹNIKI MAKROEKONOMICZNE GOSPODARKI BIAŁORUSI ZA 2013 r. (WSTĘPNE DANE - w oparciu o źródła białoruskie) Mińsk, dnia 03.03.2014 r. L.P. P a r a m e t r Dane 1. Produkt krajowy brutto*** 636
PODSTAWOWE WSKAŹNIKI MAKROEKONOMICZNE GOSPODARKI BIAŁORUSI ZA 2013 r. (WSTĘPNE DANE - w oparciu o źródła białoruskie) Mińsk, dnia 03.03.2014 r. L.P. P a r a m e t r Dane 1. Produkt krajowy brutto*** 636
Determinanty kursu walutowego w ujęciu modelowym
 Determinanty kursu walutowego w ujęciu modelowym Model portfelowy Makroekonomia Gospodarki Otwartej II dr Dagmara Mycielska 2014/2015 c by Dagmara Mycielska Wprowadzenie Idea modelu Poziom kursu walutowego
Determinanty kursu walutowego w ujęciu modelowym Model portfelowy Makroekonomia Gospodarki Otwartej II dr Dagmara Mycielska 2014/2015 c by Dagmara Mycielska Wprowadzenie Idea modelu Poziom kursu walutowego
Makroekonomia 1 - ćwiczenia
 Makroekonomia 1 - ćwiczenia mgr Małgorzata Kłobuszewska Zajęcia 6 Model klasyczny Plan Założenia modelu: Produkcja skąd się bierze? Gospodarka zamknięta Gospodarka otwarta Stopa procentowa w gospodarce
Makroekonomia 1 - ćwiczenia mgr Małgorzata Kłobuszewska Zajęcia 6 Model klasyczny Plan Założenia modelu: Produkcja skąd się bierze? Gospodarka zamknięta Gospodarka otwarta Stopa procentowa w gospodarce
Zalecenia do dyplomów z Kanalizacji
 Zalecenia o yplomów z Kanalizacji A Kanalizacja eszczowa - miejskiej jenostki osaniczej Aktualny stan prawny nakłaa na projektantów systemów kanalizacyjnych obowiązek bezpiecznego ich wymiarowania, tj.
Zalecenia o yplomów z Kanalizacji A Kanalizacja eszczowa - miejskiej jenostki osaniczej Aktualny stan prawny nakłaa na projektantów systemów kanalizacyjnych obowiązek bezpiecznego ich wymiarowania, tj.
Ważny przykład oscylator harmoniczny
 6.03.00 6. Ważny przykła oscylator harmoniczny 73 Rozział 6 Ważny przykła oscylator harmoniczny 6. Wprowazenie Klasyczny, jenowymiarowy oscylator harmoniczny opowiaa potencjałowi energii potencjalnej:
6.03.00 6. Ważny przykła oscylator harmoniczny 73 Rozział 6 Ważny przykła oscylator harmoniczny 6. Wprowazenie Klasyczny, jenowymiarowy oscylator harmoniczny opowiaa potencjałowi energii potencjalnej:
dr Bartłomiej Rokicki Katedra Makroekonomii i Teorii Handlu Zagranicznego Wydział Nauk Ekonomicznych UW
 Katedra Makroekonomii i Teorii Handlu Zagranicznego Wydział Nauk Ekonomicznych UW arytet siły nabywczej () arytet siły nabywczej jest wyprowadzany w oparciu o prawo jednej ceny. rawo jednej ceny zakładając,
Katedra Makroekonomii i Teorii Handlu Zagranicznego Wydział Nauk Ekonomicznych UW arytet siły nabywczej () arytet siły nabywczej jest wyprowadzany w oparciu o prawo jednej ceny. rawo jednej ceny zakładając,
pieniężnej. Jak wpłynie to na: krzywą LM... krajową stopę procentową... kurs walutowy... realny kurs walutowy ( przyjmij e ) ... K eksport netto...
 ZADANIA, TY I 1. Rozważmy model gospodarki otwartej (IS-LM i B), z płynnym kursem walutowym, gdy (nachylenie LM > nachylenie B). aństwo decyduje się na prowadzenie ekspansywnej polityki krzywą LM krajową
ZADANIA, TY I 1. Rozważmy model gospodarki otwartej (IS-LM i B), z płynnym kursem walutowym, gdy (nachylenie LM > nachylenie B). aństwo decyduje się na prowadzenie ekspansywnej polityki krzywą LM krajową
INSTYTUT ENERGOELEKTRYKI POLITECHNIKI WROCŁAWSKIEJ Raport serii SPRAWOZDANIA Nr
 Na prawach rękopisu o użytku służbowego INSTYTUT ENEROEEKTRYKI POITECHNIKI WROCŁAWSKIEJ Raport serii SPRAWOZDANIA Nr ABORATORIUM UKŁADÓW IMPUSOWYCH la kierunku AiR Wyziału Mechanicznego INSTRUKCJA ABORATORYJNA
Na prawach rękopisu o użytku służbowego INSTYTUT ENEROEEKTRYKI POITECHNIKI WROCŁAWSKIEJ Raport serii SPRAWOZDANIA Nr ABORATORIUM UKŁADÓW IMPUSOWYCH la kierunku AiR Wyziału Mechanicznego INSTRUKCJA ABORATORYJNA
System finansowy gospodarki. Zajęcia nr 3 Rynek walutowy
 System finansowy gospodarki Zajęcia nr 3 Rynek walutowy Podział rynków walutowych Detaliczne Międzybankowe, hurtowe oraz FOREX Międzynarodowe. Systemy kursów walutowych Kurs stały (dewaluacja, rewaluacja),
System finansowy gospodarki Zajęcia nr 3 Rynek walutowy Podział rynków walutowych Detaliczne Międzybankowe, hurtowe oraz FOREX Międzynarodowe. Systemy kursów walutowych Kurs stały (dewaluacja, rewaluacja),
BILANS PŁATNICZY. Aktywa (Kredyt +) Pasywa (Debet -) 1. Eksport towarów i usług. 1. Import towarów i usług. 2. Dary i przekazy jednostronne
 BILANS PŁATNICZY Aktywa (Kredyt +) Pasywa (Debet -) 1. Eksport towarów i usług. 1. Import towarów i usług. 2. Dary i przekazy jednostronne 2. Dary i przekazy jednostronne dla otrzymane z zagranicy. zagranicy.
BILANS PŁATNICZY Aktywa (Kredyt +) Pasywa (Debet -) 1. Eksport towarów i usług. 1. Import towarów i usług. 2. Dary i przekazy jednostronne 2. Dary i przekazy jednostronne dla otrzymane z zagranicy. zagranicy.
Akademia Młodego Ekonomisty. Walutowa Wieża Babel
 Akademia Młodego Ekonomisty Walutowa Wieża Babel Dr Andrzej Dzun Uniwersytet w Białymstoku 20 listopada 2014 r. Pieniądz- powszechnie akceptowany z mocy prawa lub zwyczaju środek regulowania zobowiązań,
Akademia Młodego Ekonomisty Walutowa Wieża Babel Dr Andrzej Dzun Uniwersytet w Białymstoku 20 listopada 2014 r. Pieniądz- powszechnie akceptowany z mocy prawa lub zwyczaju środek regulowania zobowiązań,
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 16 maja 2005 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A.
 Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Tabele stóp procentowych mbanku w Polsce dla firm Oprocentowanie w stosunku rocznym (obowiązuje od 09.01.2014 r.) 2/6 Spis
Tabele stóp procentowych dla firm w ramach bankowości detalicznej mbanku S.A. Tabele stóp procentowych mbanku w Polsce dla firm Oprocentowanie w stosunku rocznym (obowiązuje od 09.01.2014 r.) 2/6 Spis
Model IS-LM. Dr Michał Gradzewicz Katedra Ekonomii I KAE. Makroekonomia I Wykład 8
 odel IS-L D ichał Gadzewicz Kateda Ekonomii I KAE akoekonomia I Wykład 8 lan wykładu Łączny popyt w gospodace Funkcja konsumpcji lanowane i zeczywiste wydatki i kzyż Keynesowski Efekt mnożnikowy opyt inwestycyjny
odel IS-L D ichał Gadzewicz Kateda Ekonomii I KAE akoekonomia I Wykład 8 lan wykładu Łączny popyt w gospodace Funkcja konsumpcji lanowane i zeczywiste wydatki i kzyż Keynesowski Efekt mnożnikowy opyt inwestycyjny
ZWIĄZEK FUNKCJI OMEGA Z DOMINACJĄ STOCHASTYCZNĄ
 Studia konomiczne. Zeszyty Naukowe Uniwesytetu konomicznego w Katowicach ISSN 283-86 N 237 25 Infomatyka i konometia 2 wa Michalska Uniwesytet konomiczny w Katowicach Wydział Infomatyki i Komunikacji Kateda
Studia konomiczne. Zeszyty Naukowe Uniwesytetu konomicznego w Katowicach ISSN 283-86 N 237 25 Infomatyka i konometia 2 wa Michalska Uniwesytet konomiczny w Katowicach Wydział Infomatyki i Komunikacji Kateda
ROZDZIAŁ 5. Renty życiowe
 ROZDZIAŁ 5 Renty życiowe Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy czy osoba której przyszły czas
ROZDZIAŁ 5 Renty życiowe Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy czy osoba której przyszły czas
3b. ELEKTROSTATYKA. r r. 4πε. 3.4 Podstawowe pojęcia. kqq0 E =
 3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
Regulamin Opcje na stopy procentowe
 Regulamin Opcje na stopy procentowe Warszawa, Listopa 2013 mank.pl Spis treści: Rozział I Postanowienia ogólne...3 Rozział II Warunki transakcji sprzeaży opcji na stopy procentowe...4 Rozział III Zasay
Regulamin Opcje na stopy procentowe Warszawa, Listopa 2013 mank.pl Spis treści: Rozział I Postanowienia ogólne...3 Rozział II Warunki transakcji sprzeaży opcji na stopy procentowe...4 Rozział III Zasay
MSSF 7 - potencjalny wpływ ryzyka rynkowego
 *connectedthinking Aktualności MSSF Wyjaśnienie działań IASB* MSSF 7 - dodatek l MSSF 7 - potencjalny wpływ ryzyka rynkowego Potencjalny wpływ ryzyk rynkowych jest jednym z ważniejszych problemów, na jakie
*connectedthinking Aktualności MSSF Wyjaśnienie działań IASB* MSSF 7 - dodatek l MSSF 7 - potencjalny wpływ ryzyka rynkowego Potencjalny wpływ ryzyk rynkowych jest jednym z ważniejszych problemów, na jakie
Teoria Przekształtników - Kurs elementarny
 W. PRZEKSZTAŁTNIKI SIECIOWE 1 ( AC/DC; AC/AC) Ta wielka grupa przekształtników swą nazwę wywozi z tego, że są one ołączane bezpośrenio o sieci lub systemu energetycznego o napięciu przemiennym 50/60 Hz
W. PRZEKSZTAŁTNIKI SIECIOWE 1 ( AC/DC; AC/AC) Ta wielka grupa przekształtników swą nazwę wywozi z tego, że są one ołączane bezpośrenio o sieci lub systemu energetycznego o napięciu przemiennym 50/60 Hz
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Tabela Oprocentowania Produktów Bankowych. Spółdzielczego Banku Rozwoju
 Załącznik do Uchwały nr 37/4/2017 Zarządu Spółdzielczego Rozwoju z dnia 27.06.2018 r. Tabela Oprocentowania Spółdzielczego Rozwoju Obowiązuje od 007.2018 r. A. KLIENCI INDYWIDUALNI Lp. Nazwa produktu Stopa
Załącznik do Uchwały nr 37/4/2017 Zarządu Spółdzielczego Rozwoju z dnia 27.06.2018 r. Tabela Oprocentowania Spółdzielczego Rozwoju Obowiązuje od 007.2018 r. A. KLIENCI INDYWIDUALNI Lp. Nazwa produktu Stopa
