Dobór zmiennych do modelu ekonometrycznego
|
|
|
- Błażej Nowakowski
- 7 lat temu
- Przeglądów:
Transkrypt
1 Dobó zmiennych do modelu ekonometycznego
2 Metody dobou zmiennych do modelu ekonometycznego opate na teście F
3 Model zedukowany ya 0 +a x+a x+.+a x Model pełny ya 0 +a x+a x+.+a x +a + x + + +a k x k
4 Częściowy test F k 0 j + H : α j k gdzie: 0 H : α j 0 j + F (, n( k ) ) SSER SSE SSEF n k F SSE R SSE F - suma kwadatów eszt modelu zedukowanego, - suma kwadatów eszt pełnego modelu, n liczba obsewacji, k liczba zmiennych objaśniających w pełnym modelu, liczba zmiennych objaśniających w modelu zedukowanym.
5 Metoda eliminacji wstecznej 0) Zaczynamy od modelu ze wszystkimi zmiennymi objaśniającymi. )Dla każdej zmiennej wyznaczamy statystykę częściową F, tak jakby była ona ostatnią zmienną objaśniającą włączaną do modelu. Z modelu usuwamy zmienną, dla któej istotność statystyki częściowej F jest α Poceduę kontynuujemy do momentu, gdy nie ma zmiennej objaśniającej, któa mogłaby być wyłączona z modelu
6 KROK 0. Budujemy egesję dla wszystkich sześciu zmiennych objaśniających. Taktując ją jako model pełny wyznaczamy statystykę SSE R KROK. Budujemy modele egesji zedukowanej z pięcioma zmiennymi usuwając z modelu pełnego po jednej zmiennej objaśniającej. Dla każdego modelu obliczamy statystykę SSE R i wyznaczamy statystykę F testu częściowego oaz jej istotność, tabela 4. Tabela 4. Statystyki modelu pełnego i zedukowanego (kok ). Zmienne w modelu SSE F Istotność F Model pełny: Z(t-7) Tempeatua Punkt Rosy Wilgotność Ciśnienie Pędkość Wiatu Model zedukowany bez zmiennej Z(t-7) ,0907 0,00 Model zedukowany bez zmiennej Tempeatua ,0080 0,99 Max Model zedukowany bez zmiennej Punkt Rosy , ,769 Model zedukowany bez zmiennej Wilgotność , ,43 Model zedukowany bez zmiennej Ciśnienie , ,76 Model zedukowany bez zmiennej Pędkość Wiatu , ,47
7 Maksymalna istotność statystyki F odpowiada zmiennej Tempeatua i jest większa od pzyjętego poziomu istotności 0,. Zmienną Tempeatua usuwamy z modelu. Nie wnosi ona dodatkowej infomacji do modelu, w któym występują pozostałe zmienne - zatem eliminujemy ją z modelu.
8 W kolejnym koku z tego samego powodu eliminujemy z modelu kolejną zmienną objaśniającą: Ciśnienie, Ostatecznie w modelu zostają następujące zmienne objaśniające Z t- Pędkość wiatu, Wilgotność, Punkt osy.
9 Końcowy model Multiple Regession Analysis Dependent vaiable: Z t Standad T Paamete Estimate Eo Statistic P-Value CONSTANT -930,4 460,4-0, ,5356 Z t- 0, , , ,0000 PunkRosy -597, ,43 -,767 0,0983 Wilgotnosc 78, ,83,9666 0,044 Pedkosc wiatu 675,34 4,5,6466 0,
10 Step 0: vaiables in the model. 3 d.f. fo eo. R-squaed 86,35% Adjusted R-squaed 80,05% MSE 4,98E7 Step : Removing vaiable Tempeatua with F-to-emove 0,083 istotność0,99 5 vaiables in the model. 4 d.f. fo eo. R-squaed 86,4% Adjusted R-squaed 8,3% MSE 4,60484E7
11 Step Removing vaiable Ciśnienie with F-to-emove 0,435 istotność 0,78 4 vaiables in the model. 5 d.f. fo eo. R-squaed 85,8% Adjusted R-squaed 8,03% MSE 4,43055E7 Step 3: Max watość statystyki F dla Pędkość wiatu with F-to-emove,69506 istotność0,054 <0, 4 vaiables in the model. 6 d.f. fo eo. Final model selected
12 Metoda dobou w pzód 0) Statujemy z modelem bez zmiennych objaśniających. ) Rozpatujemy wszystkie k modeli z jedną zmienną objaśniającą. Wybieamy model o max watości statystyki F (pzy czym istotność statystyki F musi być < α ) ) Badamy zmienne poza modelem. Wyznaczamy dla nich statystyki częściowe F. Do modelu włączamy jedną zmienną o max watości statystyki częściowej F (pzy czym istotność statystyki F < α musi być ) Poceduę kontynuujemy do momentu, gdy nie ma zmiennej objaśniającej, któa mogłaby być włączona do modelu
13 Step 0: vaiables in the model. 9 d.f. fo eo. R-squaed 0,00% Adjusted R-squaed 0,00% MSE,465E8 Step : Adding vaiable Zt- with F-to-ente 6, vaiables in the model. 8 d.f. fo eo. R-squaed 77,53% Adjusted R-squaed 76,9% MSE 5,84544E7 Final model selected.
14 Końcowy model Zˆ t 36759, + 0,83395Z t
15 Metoda kokowa 0) Statujemy z modelem bez zmiennych objaśniających. ) Rozpatujemy wszystkie k modeli z jedną zmienną objaśniającą. Wybieamy model o max watości statystyki F (pzy czym istotność statystyki F musi być < Pin ) ) Badamy zmienne poza modelem. Wyznaczamy dla nich statystyki częściowe F. Do modelu włączamy jedną zmienną o max watości statystyki częściowej F (pzy czym istotność statystyki F musi być > Pout ) Spawdzamy, czy po włączeniu nowej zmiennej wszystkie zmienne spełniają kyteium pozostania w modelu Poceduę kontynuujemy do momentu, gdy nie ma poza modelem zmiennej objaśniającej, któa mogłaby być włączona do modelu oaz nie ma w modelu zmiennej, któa mogłaby być usunięta.
16 Oblicz watość statystyki F dla każdej zmiennej poza modelem Czy jest pzynajmniej jedna zmienna istotna p<pin NIE STOP TAK Włącz do modelu zmienną o największej istotności ( o najmniejszym p) Oblicz watość statystyki częściowej F dla wszystkich zmiennych właczonych do modelu Czy istnieje zmienna o watości p>pout TAK Usuń tą zmienną NIE
17 Metody dobou zmiennych do modelu ekonometycznego opate o współczynnik koelacji
18 Zmienne objaśniające w liniowym modelu ekonometycznym powinny być: silnie skoelowane ze zmienną objaśnianą, słabo skoelowane między sobą, silnie skoelowane z innymi zmiennymi objaśniającymi, któe nie weszły do modelu (są ich epezentantami).
19 Estymato zgodny współczynnika koelacji ( )( ) ( ) ( ) y y x x y y x x n i i n i i n i i i Zał. Cechy X, Y mają dwuwymiaowy ozkład nomalny
20 Dzień Y Z [KWh] X Z(t-7) [KWh] X Tempeatua [F] X3 Punkt Rosy [F] X4 Wilgotność [%] X5 Ciśnienie [In] X6 Pędkość Wiatu [MPH] , , , , , , , , , , , , , , , , , , , ,06 6
21 Wekto współczynników koelacji R ZMIENNA Z Z(t-7) [KWH] 0,88 Tempeatua [F] -0,5 Punkt Rosy [F] -0,0 Wilgotność [%] 0,0 Ciśnienie [In] -0, Pędkość Wiatu [MPH] 0,0
22 Test istotności współczynnika koelacji Zał.:. Cechy X, Y mają dwuwymiaowy ozkład nomalny H H ( Zt, Zt ) 0 ( Z, Z ) 0 0 : ρ : ρ t t t n 0,88 0,88 0 7,86 t 7,86 > t, ( 8), Odzucamy hipotezę H 0na kozyść H Współczynnik koelacji jest istotnie óżny od zea
23 METODA GRAFOWA
24 Współczynnik koelacji R 0 L m -wekto współczynników koelacji zmiennej objaśnianej y ze zmiennymi objaśniającymi X j ( j,,..., m) R... m... m m m... mm - maciez współczynników koelacji zmiennych objaśniających.
25 Maciez współczynników koelacji R 0 ZMIENNA Z (t-7) [KW h] Z(t-7),00 Tempeatu a [F] Tempeatua [F] -0,0,00 Punkt Rosy [F] Punkt Rosy [F] 0,7 0,4,00 Wilgotno ść [%] Wilgotność [%] -0, -0,04 0,4,00 Ciśnien ie [In] Ciśnienie [In] -0,30-0,4-0,49 0,8,00 Pędkość Wiatu [MPH] Pędkość Wiatu [MPH] -0,0 0,6-0, -0,4-0,,00
26 Kytyczny współczynnik koelacji * t α t α ( n ) ( n ) + n - kytyczny współczynnik koelacji ij ( X, X ) 0 * < ρ i j
27 n0 alfa0, * α t t α + n,734, ,378
28 Ustalenie zmiennych istotnie skoelowanych Jeśli dla pay zmiennych X i, X j zachodzi * ij to pzyjmujemy, że koelacja pomiędzy tymi zmiennymi jest istotna statystycznie. W pzeciwnym pzypadku * ij < koelację uznajemy za nieistotną.
29 Budowa maciezy koelacji istotnej R 0 ( 0 ij) 0 0 ij jeśli koelacja pomiędzy zmiennymi objaśniającymi X i, X j jest nieistotna, 0 ij jeśli koelacja pomiędzy zmiennymi objaśniającymi X i, X j jest istotna,
30 ZMIENNA Z (t-7) [KWh] Tempeatua [F] Punkt Rosy [F] Wilgotność [%] Ciśnienie [In] Pędkość Wiatu [MPH] Z(t-7),00 R 0 Tempeatua [F] -0,0,00 Punkt Rosy [F] 0,7 0,4,00 *0,378 Wilgotność [%] -0, -0,04 0,4,00 Ciśnienie [In] -0,30-0,4-0,49 0,8,00 Pędkość Wiatu [MPH] -0,0 0,6-0, -0,4-0,,00 ZMIENNA Z (t-7) [KWh] Tempeatua [F] Punkt Rosy [F] Wilgotność [%] Ciśnienie [In] Pędkość Wiatu [MPH] Z(t-7) [KWH] R 0 Tempeatua [F] 0 Punkt Rosy [F] 0 Wilgotność [%] Ciśnienie [In] Pędkość Wiatu [MPH]
31 Gaf koelacji G (V,A) Wiezchołkami gafu są zmienne objaśniające X,,X n. Pzyjmuje się, że jeśli element 0 ij maciezy R 0 jest ówny, to łuk pomiędzy wiezchołkami występuje w gafie, w pzeciwnym pzypadku bak takiego łuku.
32 Gaf koelacji G(V, A) P R Z C W T P W
33 Gaf G(V,A) może być gafem niespójnym. Jeśli gaf G składa się z kilku spójnych podgafów, to zmienne występujące w dwóch óżnych podgafach są ze sobą nieskoelowane. Z każdej spójnej składowej gafu do modelu ekonometycznego wybieamy jedną zmienną objaśniającą.
34 Wybó zmiennych jest dwukyteialny Pioytetowym kyteium jest maksymalna liczba powiązań z innymi zmiennymi, to znaczy, że do modelu wchodzi ta zmienna, któa jest skoelowana z największą liczbą innych zmiennych objaśniających. Jeśli zmiennych spełniających to kyteium jest kilka, to wybieamy tą zmienną objaśniajacą, któa jest najbadziej skoelowana ze zmienną objaśnianą Y.
35 Gaf koelacji G(V, A) ZMIENNA Z Z(t-7) [KWH] Z 0,88 Tempeatua [F] T -0,5 Punkt Rosy [F] PR -0,0 Wilgotność [%] W 0,0 Ciśnienie [In] C -0, Pędkość Wiatu [MPH] PW 0,0 T P R C Z P W W Ya 0 +a Z+a PR+a 3 PW
36 Multiple Regession Analysis Dependent vaiable: Z(t) Standad T Paamete Estimate Eo Statistic P-Value CONSTANT -493,6 4769,6 -,0300 0,383 Z(t-7) 790,788 43,889,83 0,0858 Wilgotność 0,8633 0, ,7659 0,0000 Pędkość Wiatu 78,03 377,5, , Analysis of Vaiance Souce Sum of Squaes Df Mean Squae F-Ratio P-Value Model 3,885E9 3,9375E9 5,80 0,0000 Residual 8,046E8 6 5,0404E Total (Co.) 4,68349E9 9 R-squaed 8,8708 pecent R-squaed (adjusted fo d.f.) 79,659 pecent Standad Eo of Est. 7080,99 Mean absolute eo 596,84 Dubin-Watson statistic,6588
37 Metoda Hellwiga
38 Definicja: KOMBINACJA DOWOLNY PODZBIÓR ZMIENNYCH OBJAŚNIAJĄCYCH: h j + j i j ij j tej -pojemność indywidualna zmiennej objaśniającej H l h j X j K l - pojemność integalnal tej kombinacji zmiennych objaśniających WYBIERAMY PODZBIÓR o MAX POJEMNOŚCI INTEGRALNEJ
39 0,7744 0,88 t t Z Z h H pedkoscwiatu otnosc wi t Z K X j h h h h H l j + + lg KOMBINACJA Zt- KOMBINACJA Zt-, Wilgotność, Pedkośćwiatu 0,779 0,0085 0,0003 0,763 0,0085 0,4) ( 0,0) ( 0,0 0,0003 0,4) ( 0,) ( 0,0 0,763 0,0) ( 0,) ( 0,88 lg, P, P P P,P lg, lg lg lg,p lg, H h h h otnosc edkoscwiatu Wi Z edkoscwiatu edkoscwiatu edkoscwiatu edkoscwiatu otnosc Wi Z otnosz Wi otnosc Wi otnosc Wi edkoscwiatu Z otnosz Wi Z Z Z t t t t t t
40 Model Zˆ t 36759, + 0,83395Z t
Dobór zmiennych objaśniających do liniowego modelu ekonometrycznego
Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
1. Eliminuje się ze zbioru potencjalnych zmiennych te zmienne dla których korelacja ze zmienną objaśnianą jest mniejsza od krytycznej:
Metoda analizy macierzy współczynników korelacji Idea metody sprowadza się do wyboru takich zmiennych objaśniających, które są silnie skorelowane ze zmienną objaśnianą i równocześnie słabo skorelowane
Analiza wariancji w analizie regresji - weryfikacja prawdziwości przyjętego układu ograniczeń Problem Przykłady
Analiza wariancji w analizie regresji - weryfikacja prawdziwości przyjętego układu ograniczeń 1. Problem ozwaŝamy zjawisko (model): Y = β 1 X 1 X +...+ β k X k +Z Ηβ = w r Hipoteza alternatywna: Ηβ w r
Matematyka ubezpieczeń majątkowych r.
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Ekonometria, lista zadań nr 6 Zadanie 5 H X 1, X 2, X 3
Ekonometria, lista zadań nr 6 Zadanie 5 Poniższy diagram przedstawia porządek między rozważanymi modelami oparty na relacji zawierania pomiędzy podzbiorami zbioru zmiennych objaśniających: H, X 2, X 3
Analiza zależności cech ilościowych regresja liniowa (Wykład 13)
Analiza zależności cech ilościowych regresja liniowa (Wykład 13) dr Mariusz Grządziel semestr letni 2012 Przykład wprowadzajacy W zbiorze danych homedata (z pakietu R-owskiego UsingR) można znaleźć ceny
Regresja liniowa wprowadzenie
Regresja liniowa wprowadzenie a) Model regresji liniowej ma postać: gdzie jest zmienną objaśnianą (zależną); są zmiennymi objaśniającymi (niezależnymi); natomiast są parametrami modelu. jest składnikiem
JEDNORÓWNANIOWY LINIOWY MODEL EKONOMETRYCZNY
JEDNORÓWNANIOWY LINIOWY MODEL EKONOMETRYCZNY Będziemy zapisywać wektory w postaci (,, ) albo traktując go jak macierz jednokolumnową (dzięki temu nie będzie kontrowersji przy transponowaniu wektora ) Model
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
(LMP-Liniowy model prawdopodobieństwa)
OGÓLNY MODEL REGRESJI BINARNEJ (LMP-Liniowy model prawdopodobieństwa) Dla k3 y α α α α + x + x + x 2 2 3 3 + α x x α x x + α x x + α x x + ε + x 4 2 5 3 6 2 3 7 2 3 Zał.: Wszystkie zmienne interakcyjne
Model regresji wielokrotnej Wykład 14 ( ) Przykład ceny domów w Chicago
Model regresji wielokrotnej Wykład 14 (4.06.2007) Przykład ceny domów w Chicago Poniżej są przedstawione dane dotyczące cen domów w Chicago (źródło: Sen, A., Srivastava, M., Regression Analysis, Springer,
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y. 2. Współczynnik korelacji Pearsona
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
Tradycyjne mierniki ryzyka
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Testy post-hoc. Wrocław, 6 czerwca 2016
Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
Stanisław Cichocki. Natalia Nehrebecka. Wykład 9
Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Regresja wielokrotna. PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
Regresja wielokrotna Model dla zależności liniowej: Y=a+b 1 X 1 +b 2 X 2 +...+b n X n Cząstkowe współczynniki regresji wielokrotnej: b 1,..., b n Zmienne niezależne (przyczynowe): X 1,..., X n Zmienna
Kognitywistyka II r. Teoria rzetelności wyników testu. Teorie inteligencji i sposoby jej pomiaru (4) Rzetelność czyli dokładność pomiaru
Kognitywistyka II Teoie inteligencji i sposoby jej pomiau (4) Teoia zetelności wyników testu Rzetelność czyli dokładność pomiau W języku potocznym temin zetelność oznacza niezawodność (dokładność). W psychometii
Rozdział 8. Regresja. Definiowanie modelu
Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Zmienne zależne i niezależne
Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Ekonometria dla IiE i MSEMat Z7
Ekonometria dla IiE i MSEMat Z7 Rafał Woźniak Faculty of Economic Sciences, University of Warsaw Warszawa, 21-11-2016 Na podstawie zbioru danych cps_small.dat z książki Principles of Econometrics oszacowany
BADANIE ZALEśNOŚCI CECHY Y OD CECHY X - ANALIZA REGRESJI PROSTEJ
WYKŁAD 3 BADANIE ZALEśNOŚCI CECHY Y OD CECHY X - ANALIZA REGRESJI PROSTEJ Było: Przykład. Z dziesięciu poletek doświadczalnych zerano plony ulw ziemniaczanych (cecha X) i oznaczono w nich procentową zawartość
Przyczynowość Kointegracja. Kointegracja. Kointegracja
korelacja a związek o charakterze przyczynowo-skutkowym korelacja a związek o charakterze przyczynowo-skutkowym Przyczynowość w sensie Grangera Zmienna x jest przyczyną w sensie Grangera zmiennej y jeżeli
Testowanie hipotez statystycznych związanych ą z szacowaniem i oceną ą modelu ekonometrycznego
Testowanie hipotez statystycznych związanych ą z szacowaniem i oceną ą modelu ekonometrycznego Ze względu na jakość uzyskiwanych ocen parametrów strukturalnych modelu oraz weryfikację modelu, metoda najmniejszych
Metodologia badań psychologicznych. Wykład 12. Korelacje
Metodologia badań psychologicznych Lucyna Golińska SPOŁECZNA AKADEMIA NAUK Wykład 12. Korelacje Korelacja Korelacja występuje wtedy gdy dwie różne miary dotyczące tych samych osób, zdarzeń lub obiektów
TECHNIKI INFORMATYCZNE W ODLEWNICTWIE
ECHNIKI INFORMAYCZNE W ODLEWNICWIE Janusz LELIO Paweł ŻAK Michał SZUCKI Faculty of Foundy Engineeing Depatment of Foundy Pocesses Engineeing AGH Univesity of Science and echnology Kakow Data ostatniej
parametrów strukturalnych modelu = Y zmienna objaśniana, X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających,
诲 瞴瞶 瞶 ƭ0 ƭ 瞰 parametrów strukturalnych modelu Y zmienna objaśniana, = + + + + + X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających, α 0, α 1, α 2,,α k parametry strukturalne modelu, k+1 parametrów
Regresja liniowa w R Piotr J. Sobczyk
Regresja liniowa w R Piotr J. Sobczyk Uwaga Poniższe notatki mają charakter roboczy. Mogą zawierać błędy. Za przesłanie mi informacji zwrotnej o zauważonych usterkach serdecznie dziękuję. Weźmy dane dotyczące
Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: y t. X 1 t. Tabela 1.
tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
Statystyka matematyczna dla kierunku Rolnictwo w SGGW. BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH. ANALIZA KORELACJI PROSTEJ.
BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH. ANALIZA KORELACJI PROSTEJ. IDEA OPISU WSPÓŁZALEśNOŚCI CECH X, Y cechy obserwowane w doświadczeniu, n liczba jednostek doświadczalnych, Wyniki doświadczenia: wartości
TEST STATYSTYCZNY. Jeżeli hipotezę zerową odrzucimy na danym poziomie istotności, to odrzucimy ją na każdym większym poziomie istotności.
TEST STATYSTYCZNY Testem statystycznym nazywamy regułę postępowania rozstrzygająca, przy jakich wynikach z próby hipotezę sprawdzaną H 0 należy odrzucić, a przy jakich nie ma podstaw do jej odrzucenia.
Wprowadzenie do analizy korelacji i regresji
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
PAKIETY STATYSTYCZNE
. Wykład wstępny PAKIETY STATYSTYCZNE 2. SAS, wprowadzenie - środowisko Windows, Linux 3. SAS, elementy analizy danych edycja danych 4. SAS, elementy analizy danych regresja liniowa, regresja nieliniowa
Egzamin z ekonometrii wersja IiE, MSEMAT
Egzamin z ekonometrii wersja IiE, MSEMAT 04-02-2016 Pytania teoretyczne 1. Za pomocą jakiego testu weryfikowana jest normalność składnika losowego? Jakiemu założeniu KMRL odpowiada w tym teście? Jakie
Siła tarcia. Tarcie jest zawsze przeciwnie skierowane do kierunku ruchu (do prędkości). R. D. Knight, Physics for scientists and engineers
Siła tacia Tacie jest zawsze pzeciwnie skieowane do kieunku uchu (do pędkości). P. G. Hewitt, Fizyka wokół nas, PWN R. D. Knight, Physics fo scientists and enginees Symulacja molekulanego modelu tacia
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI. Test zgodności i analiza wariancji Analiza wariancji
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
Graf skierowany. Graf zależności dla struktur drzewiastych rozgrywających parametrycznie
Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
Ekonometria Ćwiczenia 19/01/05
Oszacowano regresję stopy bezrobocia (unemp) na wzroście realnego PKB (pkb) i stopie inflacji (cpi) oraz na zmiennych zero-jedynkowych związanymi z kwartałami (season). Regresję przeprowadzono na danych
EKONOMETRIA. Prof. dr hab. Eugeniusz Gatnar.
EKONOMETRIA Prof. dr hab. Eugeniusz Gatnar egatnar@mail.wz.uw.edu.pl Sprawy organizacyjne Wykłady - prezentacja zagadnień dotyczących: budowy i weryfikacji modelu ekonometrycznego, doboru zmiennych, estymacji
należą do grupy odbiorników energii elektrycznej idealne elementy rezystancyjne przekształcają energię prądu elektrycznego w ciepło
07 0 Opacował: mg inż. Macin Wieczoek www.mawie.net.pl. Elementy ezystancyjne. należą do gupy odbioników enegii elektycznej idealne elementy ezystancyjne pzekształcają enegię pądu elektycznego w ciepło.
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych.
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Idea. θ = θ 0, Hipoteza statystyczna Obszary krytyczne Błąd pierwszego i drugiego rodzaju p-wartość
Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
II.6. Wahadło proste.
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
X Y 4,0 3,3 8,0 6,8 12,0 11,0 16,0 15,2 20,0 18,9
Zadanie W celu sprawdzenia, czy pipeta jest obarczona błędem systematycznym stałym lub zmiennym wykonano szereg pomiarów przy różnych ustawieniach pipety. Wyznacz równanie regresji liniowej, które pozwoli
1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe
Zjazd 7. SGGW, dn. 28.11.10 r. Matematyka i statystyka matematyczna Tematy 1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe nna Rajfura 1 Zagadnienia Przykład porównania wielu obiektów w
Badanie zgodności dwóch rozkładów - test serii, test mediany, test Wilcoxona, test Kruskala-Wallisa
Badanie zgodności dwóch rozkładów - test serii, test mediany, test Wilcoxona, test Kruskala-Wallisa Test serii (test Walda-Wolfowitza) Założenie. Rozpatrywane rozkłady są ciągłe. Mamy dwa uporządkowane
WYKŁAD 11 OPTYMALIZACJA WIELOKRYTERIALNA
WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
Temat: BADANIE NIEZALEśNOŚCI DWÓCH CECH JAKOŚCIOWYCH TEST CHI KWADRAT. Anna Rajfura 1
Temat: BADANIE NIEZALEśNOŚCI DWÓCH CECH JAKOŚCIOWYCH TEST CHI KWADRAT Anna Rajfura 1 Przykład W celu porównania skuteczności wybranych herbicydów: A, B, C sprawdzano, czy masa chwastów na poletku zaleŝy
Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą w oddzielnej kolumnie.
STATISTICA INSTRUKCJA - 1 I. Wprowadzanie danych Podstawowe / Nowy / Arkusz Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą
2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
Sprawdzanie założeń przyjętych o modelu (etap IIIC przyjętego schematu modelowania regresyjnego) 1. Szum 2. Założenie niezależności zakłóceń modelu - autokorelacja składnika losowego - test Durbina - Watsona
Testowanie hipotez statystycznych. Wnioskowanie statystyczne
Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Matematyka i statystyka matematyczna dla rolników w SGGW WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE
WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE Było: Przykład. W doświadczeniu polowym załoŝonym w układzie całkowicie losowym w czterech powtórzeniach porównano
Ćwiczenia IV
Ćwiczenia IV - 17.10.2007 1. Spośród podanych macierzy X wskaż te, których nie można wykorzystać do estymacji MNK parametrów modelu ekonometrycznego postaci y = β 0 + β 1 x 1 + β 2 x 2 + ε 2. Na podstawie
KURS GEOMETRIA ANALITYCZNA
KURS GEOMETRIA ANALITYCZNA Lekcja 2 Działania na wektoach w układzie współzędnych. ZADANIE DOMOWE www.etapez.pl Stona 1 Część 1: TEST Zaznacz popawną odpowiedź (tylko jedna jest pawdziwa). Pytanie 1 Któe
Model klasyczny gospodarki otwartej
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Zadanie 1. Za pomocą analizy rzetelności skali i wspólczynnika Alfa- Cronbacha ustalić, czy pytania ankiety stanowią jednorodny zbiór.
L a b o r a t o r i u m S P S S S t r o n a 1 W zbiorze Pytania zamieszczono odpowiedzi 25 opiekunów dzieci w wieku 8. lat na następujące pytania 1 : P1. Dziecko nie reaguje na bieżące uwagi opiekuna gdy
Egzamin z ekonometrii wersja IiE, MSEMat Pytania teoretyczne
Egzamin z ekonometrii wersja IiE, MSEMat 31-01-2014 Pytania teoretyczne 1. Podać postać przekształcenia Boxa-Coxa i wyjaśnić, do czego jest stosowane w ekonometrii. 2. Wyjaśnić, jakie korzyści i niebezpieczeństwa
Ekonometria - wykªad 8
Ekonometria - wykªad 8 3.1 Specykacja i werykacja modelu liniowego dobór zmiennych obja±niaj cych - cz ± 1 Barbara Jasiulis-Goªdyn 11.04.2014, 25.04.2014 2013/2014 Wprowadzenie Ideologia Y zmienna obja±niana
Matematyka i statystyka matematyczna dla rolników w SGGW
Było: Testowanie hipotez (ogólnie): stawiamy hipotezę, wybieramy funkcję testową f (test statystyczny), przyjmujemy poziom istotności α; tym samym wyznaczamy obszar krytyczny testu (wartość krytyczną funkcji
Regresja - zadania i przykłady.
Regresja - zadania i przykłady. W5 e0 Zadanie 1. Poniżej zamieszczono fragmenty wydruków dotyczących dopasowania modelu regresji do zmiennej ozone w oparciu o promieniowanie (radiation), oraz w oparciu
Permutacyjna metoda oceny istotności regresji
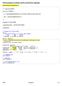Permutacyjna metoda oceny istotności regresji (bez założenia normalności) f
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
5. Rozwiązywanie układów równań liniowych
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
Egzamin z ekonometrii - wersja ogólna
Egzamin z ekonometrii - wersja ogólna 06-02-2019 Regulamin egzaminu 1. Egzamin trwa 90 min. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Budowa modelu i testowanie hipotez
Problemy metodologiczne Gdzie jest problem? Obciążenie Lovella Dysponujemy oszacowaniami parametrów następującego modelu y t = β 0 + β 1 x 1 +... + β k x k + ε t Gdzie jest problem? Obciążenie Lovella
Czasowy wymiar danych
Problem autokorelacji Model regresji dla szeregów czasowych Model regresji dla szeregów czasowych y t = X t β + ε t Zasadnicze różnice 1 Budowa prognoz 2 Problem stabilności parametrów 3 Problem autokorelacji
P: Czy studiujący i niestudiujący preferują inne sklepy internetowe?
2 Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia czy pomiędzy zmiennymi istnieje związek/zależność. Stosujemy go w sytuacji, kiedy zmienna zależna mierzona jest na skali
5. Model sezonowości i autoregresji zmiennej prognozowanej
5. Model sezonowości i autoregresji zmiennej prognozowanej 1. Model Sezonowości kwartalnej i autoregresji zmiennej prognozowanej (rząd istotnej autokorelacji K = 1) Szacowana postać: y = c Q + ρ y, t =
Egzamin z ekonometrii wersja ogolna
Egzamin z ekonometrii wersja ogolna 04-02-2016 Pytania teoretyczne 1. Wymienić założenia Klasycznego Modelu Regresji Liniowej (KMRL). 2. Wyprowadzić estymator MNK dla modelu z wieloma zmiennymi objaśniającymi.
Ocena siły oddziaływania procesów objaśniających dla modeli przestrzennych
Michał Benad Pietzak * Ocena siły oddziaływania pocesów objaśniających dla modeli pzestzennych Wstęp Ekonomiczne analizy pzestzenne są ważnym kieunkiem ozwoju ekonometii pzestzennej Wynika to z faktu,
Stosowana Analiza Regresji
prostej Stosowana Wykład I 5 Października 2011 1 / 29 prostej Przykład Dane trees - wyniki pomiarów objętości (Volume), średnicy (Girth) i wysokości (Height) pni drzew. Interesuje nas zależność (o ile
Statystyka w analizie i planowaniu eksperymentu
23 kwietnia 2014 Korelacja - wspó lczynnik korelacji 1 Gdy badamy różnego rodzaju rodzaju zjawiska (np. przyrodnicze) możemy stwierdzić, że na każde z nich ma wp lyw dzia lanie innych czynników; Korelacja
WYKŁAD 1. W przypadku zbiornika zawierającego gaz, stan układu jako całości jest opisany przez: temperaturę, ciśnienie i objętość.
WYKŁAD 1 Pzedmiot badań temodynamiki. Jeśli chcemy opisać układ złożony z N cząstek, to możemy w amach mechaniki nieelatywistycznej dla każdej cząstki napisać ównanie uchu: 2 d i mi = Fi, z + Fi, j, i,
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
Uwagi: LABORATORIUM WYTRZYMAŁOŚCI MATERIAŁÓW. Ćwiczenie nr 16 MECHANIKA PĘKANIA. ZNORMALIZOWANY POMIAR ODPORNOŚCI MATERIAŁÓW NA PĘKANIE.
POLITECHNIKA KRAKOWSKA WYDZIAŁ MECHANZNY INSTYTUT MECHANIKI STOSOWANEJ Zakład Mechaniki Doświadczalnej i Biomechaniki Imię i nazwisko: N gupy: Zespół: Ocena: Uwagi: Rok ak.: Data ćwicz.: Podpis: LABORATORIUM
KINEMATYCZNE WŁASNOW PRZEKŁADNI
KINEMATYCZNE WŁASNOW ASNOŚCI PRZEKŁADNI Waunki współpacy pacy zazębienia Zasada n 1 - koła zębate mogą ze sobą współpacować, kiedy mają ten sam moduł m. Czy to wymaganie jest wystaczające dla pawidłowej
Stanisław Cichocki. Natalia Nehrebecka. Wykład 14
Stanisław Cichocki Natalia Nehrebecka Wykład 14 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne Obserwacje nietypowe i błędne Współliniowość - Mamy 2 modele: y X u 1 1 (1) y X X 1 1 2 2 (2)
Natalia Nehrebecka Stanisław Cichocki. Wykład 13
Natalia Nehrebecka Stanisław Cichocki Wykład 13 1 1. Zmienne pominięte 2. Zmienne nieistotne 3. Obserwacje nietypowe i błędne 4. Współliniowość 2 1. Zmienne pominięte 2. Zmienne nieistotne 3. Obserwacje
4. Średnia i autoregresja zmiennej prognozowanej
4. Średnia i autoregresja zmiennej prognozowanej 1. Średnia w próbie uczącej Własności: y = y = 1 N y = y t = 1, 2, T s = s = 1 N 1 y y R = 0 v = s 1 +, 2. Przykład. Miesięczna sprzedaż żelazek (szt.)
Weryfikacja hipotez statystycznych
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817
Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817 Zadanie 1: wiek 7 8 9 1 11 11,5 12 13 14 14 15 16 17 18 18,5 19 wzrost 12 122 125 131 135 14 142 145 15 1 154 159 162 164 168 17 Wykres
Stanisław Cichocki. Natalia Nehrebecka. Wykład 12
Stanisław Cichocki Natalia Nehrebecka Wykład 12 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne 2. Autokorelacja o Testowanie autokorelacji 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne
Ekonometria egzamin 06/03/ W trakcie egzaminu wolno używać jedynie długopisu o innym kolorze atramentu niż czerwony oraz kalkulatora.
imię, nazwisko, nr indeksu: Ekonometria egzamin 06/03/2019 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
Próba określenia miary jakości informacji na gruncie teorii grafów dla potrzeb dydaktyki
Póba okeślenia miay jakości infomacji na guncie teoii gafów dla potzeb dydaktyki Zbigniew Osiak E-mail: zbigniew.osiak@gmail.com http://ocid.og/0000-0002-5007-306x http://via.og/autho/zbigniew_osiak Steszczenie
Analiza wariancji. Źródło: Aczel A. D. Statystyka w zarządzaniu. Barbara Gładysz
Analiza wariancji Źródło: Aczel A. D. Statystyka w zarządzaniu Analiza wariancji jednoczynnikowa Populacja Pole trójkąty 1 4 5 3 7 4 8 kwadraty 1 10 11 3 1 4 13 kółka 1 1 3 3 Populacja Pole trójkąty 1
Egzamin z ekonometrii wersja ogólna Pytania teoretyczne
Egzamin z ekonometrii wersja ogólna 31-01-2014 Pytania teoretyczne 1. Podać postać przekształcenia Boxa-Coxa i wyjaśnić, do czego jest stosowane w ekonometrii. 2. Porównaj zastosowania znanych ci kontrastów
Stanisław Cichocki. Natalia Nehrebecka. Wykład 4
Stanisław Cichocki Natalia Nehrebecka Wykład 4 1 1. Własności hiperpłaszczyzny regresji 2. Dobroć dopasowania równania regresji. Współczynnik determinacji R 2 Dekompozycja wariancji zmiennej zależnej Współczynnik
Analiza autokorelacji
Analiza autokorelacji Oblicza się wartości współczynników korelacji między y t oraz y t-i (dla i=1,2,...,k), czyli współczynniki autokorelacji różnych rzędów. Bada się statystyczną istotność tych współczynników.
Ekonometria egzamin 02/02/ W trakcie egzaminu wolno używać jedynie długopisu o innym kolorze atramentu niż czerwony oraz kalkulatora.
imię, nazwisko, nr indeksu: Ekonometria egzamin 0/0/0. Egzamin trwa 90 minut.. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu. Złamanie
Wykład 8 Dane kategoryczne
Wykład 8 Dane kategoryczne Wrocław, 19.04.2017r Zmienne kategoryczne 1 Przykłady zmiennych kategorycznych 2 Zmienne nominalne, zmienne ordynalne (porządkowe) 3 Zmienne dychotomiczne kodowanie zmiennych
ρ siła związku korelacyjnego brak słaba średnia silna bardzo silna
Ćwiczenie 4 ANALIZA KORELACJI, BADANIE NIEZALEŻNOŚCI Analiza korelacji jest działem statystyki zajmującym się badaniem zależności pomiędzy rozkładami dwu lub więcej badanych cech w populacji generalnej.
EKONOMETRYCZNA PROGNOZA ODPŁYWÓW Z BEZROBOCIA
EKONOMETRYCZNA PROGNOZA ODPŁYWÓW Z BEZROBOCIA W OPARCIU O KONCEPCJĘ FUNKCJI DOPASOWAŃ Adam Kowol 2 1. Sformułowanie zadania prognostycznego Celem niniejszej pracy jest próba prognozy kształtowania się
Regresja - zadania i przykłady.
Regresja - zadania i przykłady. W5 e0 Zadanie 1. Poniżej zamieszczono fragmenty wydruków dotyczących dopasowania modelu regresji do zmiennej ozone w oparciu o promieniowanie (radiation), oraz w oparciu
Analiza składowych głównych. Wprowadzenie
Wprowadzenie jest techniką redukcji wymiaru. Składowe główne zostały po raz pierwszy zaproponowane przez Pearsona(1901), a następnie rozwinięte przez Hotellinga (1933). jest zaliczana do systemów uczących
Hipoteza: Dziewczynki częściej niż chłopcy mają sprecyzowane plany dotyczące dalszego kształcenia (dlaczego?)
Problem: Czy płeć różnicuje plany edukacyjne uczniów? Hipoteza: Dziewczynki częściej niż chłopcy mają sprecyzowane plany dotyczące dalszego kształcenia (dlaczego?) Hipoteza zerowa: Płeć nie różnicuje precyzji
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
1. Ciało sztywne, na które nie działa moment siły pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym.
Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
Wydział Matematyki. Testy zgodności. Wykład 03
Wydział Matematyki Testy zgodności Wykład 03 Testy zgodności W testach zgodności badamy postać rozkładu teoretycznego zmiennej losowej skokowej lub ciągłej. Weryfikują one stawiane przez badaczy hipotezy
Wprowadzenie Modele o opóźnieniach rozłożonych Modele autoregresyjne o opóźnieniach rozłożonych. Modele dynamiczne.
opisują kształtowanie się zjawiska w czasie opisują kształtowanie się zjawiska w czasie Najważniejszymi zastosowaniami modeli dynamicznych są opisują kształtowanie się zjawiska w czasie Najważniejszymi
Wykład Centralne twierdzenie graniczne. Statystyka matematyczna: Estymacja parametrów rozkładu
Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)