Zarządzanie ryzykiem. Lista 3
|
|
|
- Bartosz Janicki
- 9 lat temu
- Przeglądów:
Transkrypt
1 Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa waość zagożona pofela zawieającego 100 szuk akcji A i 60 B? San ynku Pawdopodobieńswo Sopa zwou akcji A Sopa zwou akcji B i p i R A_i R B_i 1 0,0-10% 8% 0,04-6% 4% 3 0,61 0% % 4 0,5 17% -1% 5 0,08 31% -3%. Inweso posiada pofel o waości ynkowej PLN złożony z akcji nie płacących dywidendy. Są o akcje 0 spółek, pzy czym udział jednej spółki wynosi 10%, innej 18%, a udziały pozosałych są jednakowe. Waiancje dziennych sóp zwou dla wszyskich ych spółek są ówne i wynoszą 0,0004. Kowaiancje dla każdej pay spółek są ównież jednakowe i maja waość 0,0004. Zaządzający pofelem pzyjął, że waości oczekiwane sóp zwou można pominąć pzy szacowaniu yzyka dla kókich hoyzonów inwesycyjnych. Ile wynosi pięciopocenowa dzienna waość zagożona ej inwesycji pzy założeniu wielowymiaowego ozkładu nomalnego sóp zwou? 3. Załóżmy, że insyucja finansowa uzymuje pozycję księgi handlowej w akcjach o waości 1 mln. dolaów. Pofel ej insyucji ma współczynnik bea 1, względem szeokiego indeksu ynku, np. S&P500. Pofel jes dobze zdywesyfikowany. Na podsawie danych z osaniego oku oszacowano odchylenie sandadowe dziennej sopy zwou indeksu na poziomie 3,3% (w skali dziennej). Sopy zwou z indeksu ynku i analizowanego pofela mają ozkład nomalny. Ile wynosi dzienna i 10-dniowa waość zagożona pofela na poziomie oleancji 5%? a) Oblicz waość zagożoną pzy założeniu, że śednia sopa zwou nie jes isonie óżna od zea. b) Oblicz waość zagożoną uwzględniając śednią dzienną sopę zwou z indeksu ynku na poziomie 0,076%, pzy sopie wolnej od yzyka w wysokości 0,019% w skali dziennej, i założeniu, że ozpaywany pofel jes dobze wyceniony pzez ynek. 4. Insyucja finansowa z siedzibą w Polsce uzymuje pozycję na ynku spo we fanku szwajcaskim w wysokości 1,6 miliona CHF na zakończenie dnia. Kus wymiany PLN/CHF na ynku międzybankowym wynosi obecnie: bid:.708, ask:.836. Dzienna zmienność sopy zwou z kusu PLN/CHF, oszacowana na podsawie danych z 3 osanich miesięcy, wynosiła 80 bp (0,8 punku pocenowego). Zakładając, że sopa zwou z kusu wymiany ma ozkład nomalny o śedniej bliskiej zeu, oblicz dzienną i 10-dniową waość zagożoną o poziomie oleancji 1%. 5. Insyucja posiada 1000 dwulenich obligacji skabowych o sałym opocenowaniu 4,75% w skali oku, kapializacja oczna, o waości nominalnej 100 zł każda. Na zakończenie dnia kwoowania zeokuponowych sóp pocenowych bid na ynku spo wynosiły 4,7% dla ocznego i 4,86% dla dwuleniego okesu zapadalności. Na podsawie podobnych noowań z okesów popzednich oszacowano zmienność sopy zwou z ocznego czynnika dyskonowego (hipoeycznej ocznej jednoskowej obligacji zeokuponowej) na 1,09% w skali ocznej, a z dwuleniego na 3,44% w skali ocznej. Współczynnik koelacji wynosi 0,5. Ile wynosi pięciopocenowa dzienna i 10-dniowa waość zagożona ej pozycji? Śednia sopa zwou z czynnika dyskonowego wynosi 3,16% w skali ocznej dla hoyzonu ocznego i 7,49% w skali ocznej dla dwuleniego. Pzyjęo konwencję 365 dni w oku. 6. Inweso posiada 50 akcji szwajcaskiej spółki noowanej na SIX Swiss Exchange i 100 obligacji, do kóych wykupu pozosało 30 dni. Obligacje e były wyemiowane ok i 11 miesięcy emu jako dwulenie 1
2 Zaządzanie yzykiem zeokuponowe. Ich waość nominalna o 100 PLN. W chwili obecnej waość całego pofela wynosi zł. Na podsawie cen hisoycznych z osanich 501 dni oboczych (500 sóp zwou) pzepowadzono symulację hisoyczną w celu oszacowania dziennej waości zagożonej pzy poziomie oleancji 5% dla nasępnego dnia. Tabela. pzedsawia dane dla 5 dni, od kóych dni były gosze i 473 lepsze pod względem zealizowanej dziennej sopy zwou z pofela ( dni były gosze od najgoszego z ozpaywanych pięciu, a 473 były lepsze od najlepszego z ych pięciu). Dane w abeli są upoządkowane chonologicznie, a nie według zealizowanej sopy zwou. Ile wynosi waość zagożona? Czas do wykupu Obligacji w dniach Renowność z uwzględnieniem upływu czasu do eminu wykupu (w skali ocznej) Kus (PLN za 1 CHF) Cena akcji (CHF) ,86% 7,77%,93,114 77,08 75, ,98% 6,77%,318, ,91 53, ,48% 7,57%,5575, ,87 53, ,74% 7,46%,4837, ,60 50, ,01% 10,50% 3,053, ,49 48,74 Zdania dodakowe (nieobowiązujące na kolokwium, za dwa plusy) 7. Insyucja szacuje waość zagożoną pzy poziomie oleancji 1%. W ciągu osanich 500 dni dzienna saa pzekoczyła waość zagożoną pognozowaną na dany dzień w 7 pzypadkach. Do esowania modelu VaR wykozysano es pzekoczeń Kupca. Pzyjęo 5% poziom isoności esu. Czy należy odzucić model sosowany pzez ę insyucję ze względu na liczbę pzekoczeń? 8. Waość zagożona jes szacowana pzy poziomie oleancji 1%. W ciągu osanich 500 dni dzienna saa pzekoczyła waość zagożoną pognozowaną na dany dzień w 7 pzypadkach. Pzy ym były 3 dni akie, że pzekoczenie nasąpiło po dniu, w kóym nie było pzekoczenia i 4 akie, że pzekoczenie nasąpiło po dniu, w kóym było pzekoczenie. Okesów dwudniowych, w kóych żadnego dnia nie wysąpiło pzekoczenie było 488. Dni, bez pzekoczenia, popzedzonych dniem z pzekoczeniem było 5. Do esowania modelu VaR wykozysano es Chisoffesena niezależności pzekoczeń w czasie. Pzyjęo, że poziom isoności esu wynosi 5%. Czy należy odzucić model sosowany pzez ę insyucję ze względu na zależność pzekoczeń? 9. Model waości zagożonej zakłada ozkład nomalny sopy zwou z odchyleniem sandadowym % oaz niezależność sóp zwou w czasie. Zaządzający yzykiem na podsawie 50 obsewacji pzepowadza es dla waiancji na poziomie isoności 5%. Tes jes dwusonny, czyli hipoeza alenaywna o: H 1 : 0. Saysyka esowa wyaża się wzoem (n1)s / 0 i ma ozkład z n1 sopniami swobody, gdzie n jes liczebnością póby, s waiancją z póby, a 0 waiancją zakładaną w hipoezie zeowej esu. Pzy 49 sopniach swobody ozkład saysyki esowej można pzybliżyć ozkładem nomalnym o śedniej ównej liczbie sopni swobody i waiancji ównej podwojonej liczbie sopni swobody. Jeżeli zeczywiście sopy zwou są niezależne w czasie, ale zmienność jes wyższa i wynosi,5%, o jakie jes pawdopodobieńswo błędu dugiego odzaju pzy weyfikacji ego paameu modelu (pawdopodobieńswo, że nie zosanie odzucony sosowany model, mimo że jes on błędny)? Jak oceniłbyś moc esu? 10. Wyniki zasosowania dwóch modeli waości zagożonej dla ej samej inwesycji w ciągu osanich 1000 dni zosały pzedsawione w poniższych abelach (Tabela 1 i Tabela ) w posaci szeegów ozdzielczych pzedziałowych. Każdy wiesz abeli odpowiada zealizowanym sopom zwou, w podziale na 8 pzedziałów klasowych. Kolumny odpowiadają pognozowanej na dany dzień waości zagożonej, w podziale na 5 pzedziałów klasowych. Waości w polach abeli oznaczają liczbę obsewacji. Np. liczba 50 w 3 wieszu i 4 kolumnie oznacza, że było 50 akich dni, w kóych zealizowana sopa zwou mieściła się w pzedziale [-
3 Zaządzanie yzykiem %, %), a jednodniowa waość zagożona pognozowana na każdy z ych dni była liczbą z pzedziału [3%, %). Analiyk wykozysuje funkcję say zapoponowaną pzez Lopeza. Jes ona nasępującej posaci (ównanie (1)): (1) 1 1 VaR VaR q L VaR q 1,. Lopez VaR Kóy model uzna za lepszy, jeżeli kyeium jes śednia waość funkcji say? Pzy obliczaniu śedniej wykozysaj śodki pzedziałów klasowych dla sopy zwou (nie dla waości funkcji say) i dla VaR. q Tabela 1. Szeeg ozdzielczy zealizowanych sóp zwou i pognoz VaR w modelu 1 Model 1: VaR Liczba [6%, 5%) [5%, 4%) [4%, 3%) [3%, %) [%, 1%] obsewacji [-10%, -6%) [ -6%, -%) [ -%, %) [ %, 6%) [ 6%, 10%) [ 10%, 14%) [ 14%, 18%) [ 18%, %] Tabela. Szeeg ozdzielczy zealizowanych sóp zwou i pognoz VaR w modelu Model : VaR Liczba [6%, 5%) [5%, 4%) [4%, 3%) [3%, %) [%, 1%] obsewacji [-10%, -6%) [ -6%, -%) [ -%, %) [ %, 6%) [ 6%, 10%) [ 10%, 14%) [ 14%, 18%) [ 18%, %] Wykozysując dane z popzedniego zadania (zad. 10) ozważ, czy decyzja inwesoa zmieni się, jeśli zamias funkcji Lopeza będzie sosował funkcję Samy-Thomas-Shaha, kazącą ównież pzeszacowanie yzyka. Funkcja a jes dana nasępującym wzoem (ównanie ()): () 1 VaR 1 VaR q L VaR q STS, 1 1 VaR Pzyjęo współczynnik na poziomie 0,4. Zinepeuj wynik. 1 VaR q. 3
4 Zaządzanie yzykiem Załącznik. Tablice Tabela 3. Rozkład (F (x) = P(X x)) k = 1 k = k = 3 k = 4 k = 5 k = 6 k = 49 k = 50 x F, k (x) x F, k (x) x F, k (x) x F, k (x) x F, k (x) x F, k (x) x F, k (x) x F, k (x) 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,3750 0,4597 0,4500 0,015 0,550 0,0866 0,5750 0,034 0,650 0,013 0,6750 0, ,760 0, ,6484 0,0063 0,7500 0,6135 0,9000 0,364 1,0500 0,108 1,1500 0,1137 1,500 0,0600 1,3500 0,031 01,6837 0,015 0,5833 0,015 1,150 0,711 1,3500 0,4908 1,5750 0,3349 1,750 0,138 1,8750 0,1338,050 0,086 04,813 0, ,781 0,0188 1,5000 0,7793 1,8000 0,5934,1000 0,4481,3000 0,319,5000 0,35,7000 0, ,1856 0,050 08,0978 0,050 1,8750 0,891,500 0,6753,650 0,5469,8750 0,410 3,150 0,3193 3,3750 0,395 09,1098 0, ,063 0,0313,500 0,8664,7000 0,7408 3,1500 0,6309 3,4500 0,5145 3,7500 0,4141 4,0500 0, ,747 0, ,6674 0,0375,650 0,8948 3,1500 0,7930 3,6750 0,701 4,050 0,5974 4,3750 0,503 4,750 0,405 1,180 0, ,1054 0,0438 3,0000 0,9167 3,6000 0,8347 4,000 0,7593 4,6000 0,6691 5,0000 0,5841 5,4000 0, ,4653 0, ,3916 0,0500 3,3750 0,9338 4,0500 0,8680 4,750 0,8069 5,1750 0,730 5,650 0,6556 6,0750 0,585 19,371 0,0875 0,663 0,0875 3,7500 0,947 4,5000 0,8946 5,500 0,8456 5,7500 0,7814 6,500 0,7174 6,7500 0,6554 3,5770 0,150 4,554 0,150 4,150 0,9577 4,9500 0,9158 5,7750 0,8769 6,350 0,838 6,8750 0,7699 7,450 0,7167 7,0447 0,165 8,0006 0,165 4,5000 0,9661 5,4000 0,938 6,3000 0,901 6,9000 0,8587 7,5000 0,8140 8,1000 0, ,0506 0,000 31,018 0,000 4,8750 0,978 5,8500 0,9463 6,850 0,93 7,4750 0,887 8,150 0,8505 8,7750 0,8134 3,7551 0,375 33,731 0,375 5,500 0,9781 6,3000 0,9571 7,3500 0,9385 8,0500 0,910 8,7500 0,8805 9,4500 0,850 35,50 0,750 36,5 0,750 5,650 0,983 6,7500 0,9658 7,8750 0,9513 8,650 0,988 9,3750 0, ,150 0, ,6019 0,315 38,5799 0,315 6,0000 0,9857 7,000 0,977 8,4000 0,9616 9,000 0, ,0000 0,948 10,8000 0,905 39,8470 0, ,897 0,3500 6,3750 0,9884 7,6500 0,978 8,950 0,9697 9,7750 0, ,650 0, ,4750 0,95 4,019 0, ,0064 0,3875 6,7500 0,9906 8,1000 0,986 9,4500 0, ,3500 0, ,500 0,9534 1,1500 0, ,1437 0,450 45,135 0,450 7,150 0,994 8,5500 0,9861 9,9750 0,981 10,950 0,976 11,8750 0,9635 1,850 0, ,41 0,465 47,379 0,465 7,5000 0,9938 9,0000 0, ,5000 0,985 11,5000 0,9785 1,5000 0, ,5000 0, ,3337 0, ,3337 0,5000 7,8750 0,9950 9,4500 0, ,050 0,9884 1,0750 0,983 13,150 0, ,1750 0,973 50,4370 0, ,4413 0,5375 8,500 0,9959 9,9000 0,999 11,5500 0,9909 1,6500 0, ,7500 0,987 14,8500 0,9785 5,5713 0, ,5798 0,5750 8,650 0, ,3500 0,9943 1,0750 0,999 13,50 0, ,3750 0, ,550 0, ,7571 0,615 55,7699 0,615 9,0000 0, ,8000 0,9955 1,6000 0, ,8000 0,990 15,0000 0, ,000 0, ,018 0, ,0355 0,6500 9,3750 0, ,500 0, ,150 0, ,3750 0, ,650 0,990 16,8750 0,990 59,3839 0, ,4058 0,6875 9,7500 0,998 11,7000 0, ,6500 0, ,9500 0,995 16,500 0, ,5500 0,995 61,8916 0,750 6,9184 0,750 10,150 0,9985 1,1500 0, ,1750 0, ,550 0, ,8750 0, ,50 0, ,594 0,765 65,645 0,765 10,5000 0,9988 1,6000 0,998 14,7000 0, ,1000 0, ,5000 0, ,9000 0, ,5609 0, ,5986 0, ,8750 0, ,0500 0, ,50 0, ,6750 0, ,150 0,997 19,5750 0, ,9138 0, ,9579 0, ,500 0,999 13,5000 0, ,7500 0, ,500 0, ,7500 0,9979 0,500 0, ,8541 0, ,9057 0, ,650 0, ,9500 0, ,750 0, ,850 0, ,3750 0,9984 0,950 0, ,791 0,915 80,859 0,915 1,0000 0, ,4000 0, ,8000 0,999 18,4000 0,9990 0,0000 0,9988 1,6000 0, ,8078 0, ,8815 0,9500 1,3750 0, ,8500 0, ,350 0, ,9750 0,999 0,650 0,9990,750 0, ,3766 0, ,4531 0,9563 1,7500 0, ,3000 0, ,8500 0, ,5500 0,9994 1,500 0,9993,9500 0,999 90,1447 0,965 91,45 0,965 13,150 0, ,7500 0, ,3750 0,9996 0,150 0,9995 1,8750 0,9994 3,650 0,9994 9,1815 0, ,649 0, ,5000 0, ,000 0, ,9000 0,9997 0,7000 0,9996,5000 0,9996 4,3000 0, ,6008 0, ,6886 0, ,8750 0, ,6500 0, ,450 0,9998 1,750 0,9997 3,150 0,9997 4,9750 0, ,5990 0,981 98,691 0,981 14,500 0, ,1000 0, ,9500 0,9998 1,8500 0,9998 3,7500 0,9998 5,6500 0, ,6386 0, ,7389 0, ,650 0, ,5500 0,9998 0,4750 0,9999,450 0,9998 4,3750 0,9998 6,350 0, ,1100 0, ,16 0, ,0000 0, ,0000 0,9999 1,0000 0,9999 3,0000 0,9999 5,0000 0,9999 7,0000 0, ,6615 0, ,877 0,9999 Dla k > 30 ozkład sandadowym (k) 0,5 ) można pzybliżać ozkładem nomalnym o śedniej k i waiancji k (odchyleniu 4
5 Zaządzanie yzykiem Tabela 4. Waości kyyczne esu ( P(X x i ) = ) Tablica waości kyycznych esu chi-kwada P(X x i ) = 0,99 0,95 0,9 0,8 0,7 0,6 0,5 0,3 0, 0,1 0,05 0,0 0,01 k 1 0,000 0,004 0,016 0,064 0,148 0,75 0,455 1,074 1,64,706 3,841 5,41 6,635 0,00 0,103 0,11 0,446 0,713 1,0 1,386,408 3,19 4,605 5,991 7,84 9,10 3 0,115 0,35 0,584 1,005 1,44 1,869,366 3,665 4,64 6,51 7,815 9,837 11, ,97 0,711 1,064 1,649,195,753 3,357 4,878 5,989 7,779 9,488 11,668 13,77 5 0,554 1,145 1,610,343 3,000 3,655 4,351 6,064 7,89 9,36 11,070 13,388 15, ,87 1,635,04 3,070 3,88 4,570 5,348 7,31 8,558 10,645 1,59 15,033 16,81 7 1,39,167,833 3,8 4,671 5,493 6,346 8,383 9,803 1,017 14,067 16,6 18, ,646,733 3,490 4,594 5,57 6,43 7,344 9,54 11,030 13,36 15,507 18,168 0,090 9,088 3,35 4,168 5,380 6,393 7,357 8,343 10,656 1,4 14,684 16,919 19,679 1,666 10,558 3,940 4,865 6,179 7,67 8,95 9,34 11,781 13,44 15,987 18,307 1,161 3, ,053 4,575 5,578 6,989 8,148 9,37 10,341 1,899 14,631 17,75 19,675,618 4,75 1 3,571 5,6 6,304 7,807 9,034 10,18 11,340 14,011 15,81 18,549 1,06 4,054 6, ,107 5,89 7,04 8,634 9,96 11,19 1,340 15,119 16,985 19,81,36 5,47 7, ,660 6,571 7,790 9,467 10,81 1,078 13,339 16, 18,151 1,064 3,685 6,873 9, ,9 7,61 8,547 10,307 11,71 13,030 14,339 17,3 19,311,307 4,996 8,59 30, ,81 7,96 9,31 11,15 1,64 13,983 15,338 18,418 0,465 3,54 6,96 9,633 3, ,408 8,67 10,085 1,00 13,531 14,937 16,338 19,511 1,615 4,769 7,587 30,995 33, ,015 9,390 10,865 1,857 14,440 15,893 17,338 0,601,760 5,989 8,869 3,346 34, ,633 10,117 11,651 13,716 15,35 16,850 18,338 1,689 3,900 7,04 30,144 33,687 36, ,60 10,851 1,443 14,578 16,66 17,809 19,337,775 5,038 8,41 31,410 35,00 37,566 Tabela 5. Dysybuana sandadowego ozkładu nomalnego ( () = P(X )) () () () () () () () () -4,00 0, ,00 0, ,00 0,075-1,00 0, ,00 0, ,00 0,84134,00 0,9775 3,00 0, ,95 0, ,95 0, ,95 0,0559-0,95 0, ,05 0, ,05 0,85314,05 0,9798 3,05 0, ,90 0, ,90 0, ,90 0,087-0,90 0, ,10 0, ,10 0,86433,10 0,9814 3,10 0, ,85 0, ,85 0,0019-1,85 0,0316-0,85 0, ,15 0,5596 1,15 0,87493,15 0,984 3,15 0, ,80 0, ,80 0,0056-1,80 0, ,80 0,1186 0,0 0,5796 1,0 0,88493,0 0, ,0 0, ,75 0, ,76 0,0089-1,75 0, ,75 0,663 0,5 0, ,5 0,89435,5 0, ,5 0,9994-3,70 0, ,70 0, ,70 0, ,70 0,4196 0,30 0, ,30 0,9030,30 0,9898 3,30 0,9995-3,65 0, ,65 0,0040-1,65 0, ,65 0,5785 0,35 0, ,35 0,91149,35 0, ,35 0, ,60 0, ,60 0, ,60 0, ,60 0,745 0,40 0,6554 1,40 0,9194,40 0, ,40 0, ,55 0, ,55 0, ,55 0, ,55 0,9116 0,45 0, ,45 0,9647,45 0,9986 3,45 0,9997-3,50 0,0003 -,50 0,0061-1,50 0, ,50 0, ,50 0, ,50 0,93319,50 0, ,50 0, ,45 0,0008 -,45 0, ,45 0, ,45 0,3636 0,55 0, ,55 0,93943,55 0, ,55 0, ,40 0, ,40 0,0080-1,40 0, ,40 0, ,60 0,7575 1,60 0,9450,60 0, ,60 0, ,35 0, ,35 0, ,35 0, ,35 0, ,65 0,7415 1,65 0,95053,65 0, ,65 0, ,30 0, ,30 0,0107-1,30 0, ,30 0,3809 0,70 0, ,70 0,95543,70 0, ,70 0, ,5 0, ,5 0,01-1,5 0, ,5 0,4019 0,75 0, ,75 0,95994,75 0,9970 3,75 0, ,0 0, ,0 0, ,0 0, ,0 0,4074 0,80 0, ,80 0,96407,80 0, ,80 0, ,15 0,0008 -,15 0, ,15 0,1507-0,15 0, ,85 0,8034 1,85 0,96784,85 0, ,85 0, ,10 0, ,10 0, ,10 0, ,10 0, ,90 0, ,90 0,9718,90 0, ,90 0, ,05 0, ,05 0,0018-1,05 0, ,05 0, ,95 0,8894 1,96 0,97500,95 0, ,95 0,
METODA ZDYSKONTOWANYCH SALD WOLNYCH PRZEPŁYWÓW PIENIĘŻNYCH
 METODA ZDYSONTOWANYCH SALD WOLNYCH PRZEPŁYWÓW PIENIĘŻNYCH W meodach dochodowych podsawową wielkością, kóa okeśla waość pzedsiębioswa są dochody jakie mogą być geneowane z powadzenia działalności gospodaczej
METODA ZDYSONTOWANYCH SALD WOLNYCH PRZEPŁYWÓW PIENIĘŻNYCH W meodach dochodowych podsawową wielkością, kóa okeśla waość pzedsiębioswa są dochody jakie mogą być geneowane z powadzenia działalności gospodaczej
Arytmetyka finansowa Wykład 5 Dr Wioletta Nowak
 Aymeyka finansowa Wykład 5 D Wiolea Nowak Bon skabowy Insumen dłużny, emiowany pzez Skab ańswa za pośednicwem Miniseswa Finansów. Temin wykupu dzień w kóym emien dokonuje wykupu, Skab ańswa zwaca dług
Aymeyka finansowa Wykład 5 D Wiolea Nowak Bon skabowy Insumen dłużny, emiowany pzez Skab ańswa za pośednicwem Miniseswa Finansów. Temin wykupu dzień w kóym emien dokonuje wykupu, Skab ańswa zwaca dług
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
PROCEDURA WYBORU PORTFELA AKCJI ZAPEWNIAJĄCA KONTROLĘ RYZYKA NIESYSTEMATYCZNEGO
 B A D A I A O P E R A C Y J E I D E C Y Z J E 3 4 2004 omasz BRZĘCZEK* PROCEDURA WYBORU PORFELA AKCJI ZAPEWIAJĄCA KOROLĘ RYZYKA IESYSEMAYCZEGO Pzedsawiono poceduę wybou pofela akci zapewniaącą konolę yzyka
B A D A I A O P E R A C Y J E I D E C Y Z J E 3 4 2004 omasz BRZĘCZEK* PROCEDURA WYBORU PORFELA AKCJI ZAPEWIAJĄCA KOROLĘ RYZYKA IESYSEMAYCZEGO Pzedsawiono poceduę wybou pofela akci zapewniaącą konolę yzyka
F : R 0;1 rozkład prawdopodobieństwa stopy zwrotu.
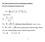 Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
WYKORZYSTANIE TRÓJSEKTOROWEGO MODELU WZROSTU DO ANALIZY WPŁYWU OGRANICZENIA EMISJI GHG NA WYBÓR TECHNOLOGII PRODUKCJI.
 Zeszyy Naukowe Wydziału nfomaycznych Technik Zaządzania Wyższej Szkoły nfomayki Sosowanej i Zaządzania Współczesne Poblemy Zaządzania N /2009 WYKORZYSTANE TRÓJSEKTOROWEGO ODELU WZROSTU DO ANALZY WPŁYWU
Zeszyy Naukowe Wydziału nfomaycznych Technik Zaządzania Wyższej Szkoły nfomayki Sosowanej i Zaządzania Współczesne Poblemy Zaządzania N /2009 WYKORZYSTANE TRÓJSEKTOROWEGO ODELU WZROSTU DO ANALZY WPŁYWU
LABORATORIUM PODSTAWY ELEKTRONIKI Badanie Bramki X-OR
 LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
Marża zakupu bid (pkb) Marża sprzedaży ask (pkb)
 Swap (IRS) i FRA Przykład. Sandardowy swap procenowy Dealer proponuje nasępujące sałe sopy dla sandardowej "plain vanilla" procenowej ransakcji swap. ermin wygaśnięcia Sopa dla obligacji skarbowych Marża
Swap (IRS) i FRA Przykład. Sandardowy swap procenowy Dealer proponuje nasępujące sałe sopy dla sandardowej "plain vanilla" procenowej ransakcji swap. ermin wygaśnięcia Sopa dla obligacji skarbowych Marża
Matematyka finansowa 20.03.2006 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r.
 Komisja Egzaminacyjna dla Akuariuszy XXXVIII Egzamin dla Akuariuszy z 20 marca 2006 r. Część I Maemayka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minu 1 1. Ile
Komisja Egzaminacyjna dla Akuariuszy XXXVIII Egzamin dla Akuariuszy z 20 marca 2006 r. Część I Maemayka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minu 1 1. Ile
Analiza i Zarządzanie Portfelem cz. 6 R = Ocena wyników zarządzania portfelem. Pomiar wyników zarządzania portfelem. Dr Katarzyna Kuziak
 Ocena wyników zarządzania porelem Analiza i Zarządzanie Porelem cz. 6 Dr Kaarzyna Kuziak Eapy oceny wyników zarządzania porelem: - (porolio perormance measuremen) - Przypisanie wyników zarządzania porelem
Ocena wyników zarządzania porelem Analiza i Zarządzanie Porelem cz. 6 Dr Kaarzyna Kuziak Eapy oceny wyników zarządzania porelem: - (porolio perormance measuremen) - Przypisanie wyników zarządzania porelem
Akademia Ekonomiczna im. Oskara Langego we Wrocławiu Katedra Inwestycji Finansowych i Ubezpieczeń
 Krzyszof Pionek Akademia Ekonomiczna im. Oskara Langego we Wrocławiu Kaedra Inwesycji Finansowych i Ubezpieczeń Przegląd i porównanie meod oceny modeli VaR Wsęp - Miara VaR Warość zagrożona (warość narażona
Krzyszof Pionek Akademia Ekonomiczna im. Oskara Langego we Wrocławiu Kaedra Inwesycji Finansowych i Ubezpieczeń Przegląd i porównanie meod oceny modeli VaR Wsęp - Miara VaR Warość zagrożona (warość narażona
Stanisław Cichocki Natalia Nehrebecka. Wykład 3
 Sanisław Cichocki Naalia Nehrebecka Wykład 3 1 1. Zmienne sacjonarne 2. Zmienne zinegrowane 3. Regresja pozorna 4. Funkcje ACF i PACF 5. Badanie sacjonarności Tes Dickey-Fullera (DF) 2 1. Zmienne sacjonarne
Sanisław Cichocki Naalia Nehrebecka Wykład 3 1 1. Zmienne sacjonarne 2. Zmienne zinegrowane 3. Regresja pozorna 4. Funkcje ACF i PACF 5. Badanie sacjonarności Tes Dickey-Fullera (DF) 2 1. Zmienne sacjonarne
System zielonych inwestycji (GIS Green Investment Scheme)
 PROGRAM PRIORYTETOWY Tyuł programu: Sysem zielonych inwesycji (GIS Green Invesmen Scheme) Część 6) SOWA Energooszczędne oświelenie uliczne. 1. Cel programu Ograniczenie lub uniknięcie emisji dwulenku węgla
PROGRAM PRIORYTETOWY Tyuł programu: Sysem zielonych inwesycji (GIS Green Invesmen Scheme) Część 6) SOWA Energooszczędne oświelenie uliczne. 1. Cel programu Ograniczenie lub uniknięcie emisji dwulenku węgla
2014-06-03. Empiryczne modele stóp zwrotu z portfeli inwestycyjnych. Modele, metody inwestowania oraz ocena działalności funduszu
 Empiyczne modele sóp zwou z pofeli inwesycyjnych Wojciech Gabowski Wydział Nauk Ekonomicznych Uniwesye Waszawski Rynki Finansowe 2013/14 Modele, meody inwesowania oaz ocena działalności funduszu -Meody
Empiyczne modele sóp zwou z pofeli inwesycyjnych Wojciech Gabowski Wydział Nauk Ekonomicznych Uniwesye Waszawski Rynki Finansowe 2013/14 Modele, meody inwesowania oaz ocena działalności funduszu -Meody
Studia Ekonomiczne. Zeszyty Naukowe Uniwersytetu Ekonomicznego w Katowicach ISSN 2083-8611 Nr 219 2015
 Sudia Ekonomiczne. Zeszyy Naukowe Uniwersyeu Ekonomicznego w Kaowicach ISSN 2083-86 Nr 29 205 Alicja Ganczarek-Gamro Uniwersye Ekonomiczny w Kaowicach Wydział Informayki i Komunikacji Kaedra Demografii
Sudia Ekonomiczne. Zeszyy Naukowe Uniwersyeu Ekonomicznego w Kaowicach ISSN 2083-86 Nr 29 205 Alicja Ganczarek-Gamro Uniwersye Ekonomiczny w Kaowicach Wydział Informayki i Komunikacji Kaedra Demografii
Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO. z dnia 2 czerwca 2017 r.
 DZIENNIK URZĘDOWY NARODOWEGO BANKU POLSKIEGO Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO z dnia 2 czerwca 2017 r. zmieniająca uchwałę w sprawie wprowadzenia
DZIENNIK URZĘDOWY NARODOWEGO BANKU POLSKIEGO Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO z dnia 2 czerwca 2017 r. zmieniająca uchwałę w sprawie wprowadzenia
Strategie zarz~dzania kapitatem obrotowym a wzrost wartosci MSP
 Ne Woking Capial Managemen Saegies as a Faco o Shaping Small Fim Value (Saegie zaządzania kapiałem Waszawa 005 SSN: 134-887 p 90-10 3 imes cied (see: hp://michalskigcom/indekshdoc) " Gzegoz Michalski Akademia
Ne Woking Capial Managemen Saegies as a Faco o Shaping Small Fim Value (Saegie zaządzania kapiałem Waszawa 005 SSN: 134-887 p 90-10 3 imes cied (see: hp://michalskigcom/indekshdoc) " Gzegoz Michalski Akademia
Politechnika Częstochowska Wydział Inżynierii Mechanicznej i Informatyki. Sprawozdanie #2 z przedmiotu: Prognozowanie w systemach multimedialnych
 Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
WYCENA KONTRAKTÓW FUTURES, FORWARD I SWAP
 Krzyszof Jajuga Kaedra Inwesycji Finansowych i Zarządzania Ryzykiem Uniwersye Ekonomiczny we Wrocławiu WYCENA KONRAKÓW FUURES, FORWARD I SWAP DWA RODZAJE SYMERYCZNYCH INSRUMENÓW POCHODNYCH Symeryczne insrumeny
Krzyszof Jajuga Kaedra Inwesycji Finansowych i Zarządzania Ryzykiem Uniwersye Ekonomiczny we Wrocławiu WYCENA KONRAKÓW FUURES, FORWARD I SWAP DWA RODZAJE SYMERYCZNYCH INSRUMENÓW POCHODNYCH Symeryczne insrumeny
WNIOSKOWANIE STATYSTYCZNE
 Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Stanisław Cichocki Natalia Nehrebecka. Wykład 3
 Sanisław Cichocki Naalia Nehrebecka Wykład 3 1 1. Regresja pozorna 2. Funkcje ACF i PACF 3. Badanie sacjonarności Tes Dickey-Fullera (DF) Rozszerzony es Dickey-Fullera (ADF) 2 1. Regresja pozorna 2. Funkcje
Sanisław Cichocki Naalia Nehrebecka Wykład 3 1 1. Regresja pozorna 2. Funkcje ACF i PACF 3. Badanie sacjonarności Tes Dickey-Fullera (DF) Rozszerzony es Dickey-Fullera (ADF) 2 1. Regresja pozorna 2. Funkcje
INSTRUMENTY DŁUŻNE. Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
PROGNOZOWANIE I SYMULACJE. mgr Żaneta Pruska. Ćwiczenia 2 Zadanie 1
 PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE
 RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE PYTANIA KONTROLNE Czym charakeryzują się wskaźniki saycznej meody oceny projeku inwesycyjnego Dla kórego wskaźnika wyliczamy średnią księgową
RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE PYTANIA KONTROLNE Czym charakeryzują się wskaźniki saycznej meody oceny projeku inwesycyjnego Dla kórego wskaźnika wyliczamy średnią księgową
DYNAMICZNE MODELE EKONOMETRYCZNE
 DYNAMICZNE MODEE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Joanna Małgorzaa andmesser Szkoła Główna
DYNAMICZNE MODEE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Joanna Małgorzaa andmesser Szkoła Główna
DYNAMICZNE MODELE EKONOMETRYCZNE
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Gdański Zasosowanie modelu
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Gdański Zasosowanie modelu
Alicja Ganczarek Akademia Ekonomiczna w Katowicach. Analiza niezależności przekroczeń VaR na wybranym segmencie rynku energii
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Akademia Ekonomiczna w Kaowicach Analiza
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Akademia Ekonomiczna w Kaowicach Analiza
ESTYMACJA KRZYWEJ DOCHODOWOŚCI STÓP PROCENTOWYCH DLA POLSKI
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/3, 202, sr. 253 26 ESTYMACJA KRZYWEJ DOCHODOWOŚCI STÓP PROCENTOWYCH DLA POLSKI Adam Waszkowski Kaedra Ekonomiki Rolnicwa i Międzynarodowych Sosunków
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/3, 202, sr. 253 26 ESTYMACJA KRZYWEJ DOCHODOWOŚCI STÓP PROCENTOWYCH DLA POLSKI Adam Waszkowski Kaedra Ekonomiki Rolnicwa i Międzynarodowych Sosunków
Makroekonomia 1 Wykład 8: Wprowadzenie do modelu ISLM: krzywa LM oraz krzywa IS
 Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Deteminanty popytu na pieniądz Równowaga na ynku
Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Deteminanty popytu na pieniądz Równowaga na ynku
Stanisław Cichocki Natalia Nehrebecka. Wykład 4
 Sanisław Cichocki Naalia Nehrebecka Wykład 4 1 1. Badanie sacjonarności: o o o Tes Dickey-Fullera (DF) Rozszerzony es Dickey-Fullera (ADF) Tes KPSS 2. Modele o rozłożonych opóźnieniach (DL) 3. Modele auoregresyjne
Sanisław Cichocki Naalia Nehrebecka Wykład 4 1 1. Badanie sacjonarności: o o o Tes Dickey-Fullera (DF) Rozszerzony es Dickey-Fullera (ADF) Tes KPSS 2. Modele o rozłożonych opóźnieniach (DL) 3. Modele auoregresyjne
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
i 0,T F T F 0 Zatem: oprocentowanie proste (kapitalizacja na koniec okresu umownego 0;N, tj. w momencie t N : F t F 0 t 0;N, F 0
 Maemayka finansowa i ubezpieczeniowa - 1 Sopy procenowe i dyskonowe 1. Sopa procenowa (sopa zwrou, sopa zysku) (Ineres Rae). Niech: F - kapiał wypoŝyczony (zainwesowany) w momencie, F T - kapiał zwrócony
Maemayka finansowa i ubezpieczeniowa - 1 Sopy procenowe i dyskonowe 1. Sopa procenowa (sopa zwrou, sopa zysku) (Ineres Rae). Niech: F - kapiał wypoŝyczony (zainwesowany) w momencie, F T - kapiał zwrócony
EKONOMETRIA wykład 2. Prof. dr hab. Eugeniusz Gatnar.
 EKONOMERIA wykład Prof. dr hab. Eugeniusz Ganar eganar@mail.wz.uw.edu.pl Przedziały ufności Dla paramerów srukuralnych modelu: P bˆ j S( bˆ z prawdopodobieńswem parameru b bˆ S( bˆ, ( m j j j, ( m j b
EKONOMERIA wykład Prof. dr hab. Eugeniusz Ganar eganar@mail.wz.uw.edu.pl Przedziały ufności Dla paramerów srukuralnych modelu: P bˆ j S( bˆ z prawdopodobieńswem parameru b bˆ S( bˆ, ( m j j j, ( m j b
OPTYMALIZACJA PORTFELA INWESTYCYJNEGO ZE WZGLĘDU NA MINIMALNY POZIOM TOLERANCJI DLA USTALONEGO VaR
 Daniel Iskra Uniwersye Ekonomiczny w Kaowicach OPTYMALIZACJA PORTFELA IWESTYCYJEGO ZE WZGLĘDU A MIIMALY POZIOM TOLERACJI DLA USTALOEGO VaR Wprowadzenie W osanich laach bardzo popularną miarą ryzyka sała
Daniel Iskra Uniwersye Ekonomiczny w Kaowicach OPTYMALIZACJA PORTFELA IWESTYCYJEGO ZE WZGLĘDU A MIIMALY POZIOM TOLERACJI DLA USTALOEGO VaR Wprowadzenie W osanich laach bardzo popularną miarą ryzyka sała
O MIERNIKACH DOKŁADNOŚCI PROGNOZ EX POST W PROGNOZOWANIU ZMIENNYCH O SILNYM NATĘŻENIU SEZONOWOŚCI
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/, 0, s. 3 O MIERNIKACH DOKŁADNOŚCI PROGNOZ EX POST W PROGNOZOWANIU ZMIENNYCH O SILNYM NATĘŻENIU SEZONOWOŚCI Maia Szmuksa Zawadzka Sudium Maemayki Zachodniopomoski
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/, 0, s. 3 O MIERNIKACH DOKŁADNOŚCI PROGNOZ EX POST W PROGNOZOWANIU ZMIENNYCH O SILNYM NATĘŻENIU SEZONOWOŚCI Maia Szmuksa Zawadzka Sudium Maemayki Zachodniopomoski
Arytmetyka finansowa. Dr Wioletta Nowak
 Aymeya finansowa Wiolea Nowa Bon sabowy Insumen dłużny, emiowany pzez Sab ańswa za pośednicwem Miniseswa Finansów. Temin wyupu dzień w óym emien doonuje wyupu, Sab ańswa zwaca dłu posiadaczowi bonu saboweo.
Aymeya finansowa Wiolea Nowa Bon sabowy Insumen dłużny, emiowany pzez Sab ańswa za pośednicwem Miniseswa Finansów. Temin wyupu dzień w óym emien doonuje wyupu, Sab ańswa zwaca dłu posiadaczowi bonu saboweo.
REGULAMIN FUNDUSZU ROZLICZENIOWEGO
 REGULAMIN FUNDUSZU ROZLICZENIOEGO przyjęy uchwałą nr 10/60/98 Rady Nadzorczej Krajowego Depozyu Papierów arościowych S.A. z dnia 28 września 1998 r., zawierdzony decyzją Komisji Papierów arościowych i
REGULAMIN FUNDUSZU ROZLICZENIOEGO przyjęy uchwałą nr 10/60/98 Rady Nadzorczej Krajowego Depozyu Papierów arościowych S.A. z dnia 28 września 1998 r., zawierdzony decyzją Komisji Papierów arościowych i
EFEKT DŹWIGNI NA GPW W WARSZAWIE WPROWADZENIE
 Paweł Kobus, Rober Pierzykowski Kaedra Ekonomerii i Informayki SGGW e-mail: pawel.kobus@saysyka.info EFEKT DŹWIGNI NA GPW W WARSZAWIE Sreszczenie: Do modelowania asymerycznego wpływu dobrych i złych informacji
Paweł Kobus, Rober Pierzykowski Kaedra Ekonomerii i Informayki SGGW e-mail: pawel.kobus@saysyka.info EFEKT DŹWIGNI NA GPW W WARSZAWIE Sreszczenie: Do modelowania asymerycznego wpływu dobrych i złych informacji
Wpływ rentowności skarbowych papierów dłużnych na finanse przedsiębiorstw i poziom bezrobocia
 Wpływ renowności skarbowych papierów dłużnych na inanse przedsiębiorsw i poziom bezrocia Leszek S. Zaremba Sreszczenie W pracy ej wykażemy prawidłowość, kóra mówi, że im wyższa jes renowność bezryzykownych
Wpływ renowności skarbowych papierów dłużnych na inanse przedsiębiorsw i poziom bezrocia Leszek S. Zaremba Sreszczenie W pracy ej wykażemy prawidłowość, kóra mówi, że im wyższa jes renowność bezryzykownych
XLI OLIMPIADA FIZYCZNA ETAP I Zadanie doświadczalne
 XLI OLIPIADA FIZYCZNA EAP I Zadanie doświadczalne ZADANIE D Pod działaniem sil zewnęznych ciała sale ulęgają odkszałceniom. Wyznacz zależność pomienia obszau syczniści szklanej soczewki z płyka szklana
XLI OLIPIADA FIZYCZNA EAP I Zadanie doświadczalne ZADANIE D Pod działaniem sil zewnęznych ciała sale ulęgają odkszałceniom. Wyznacz zależność pomienia obszau syczniści szklanej soczewki z płyka szklana
Laboratorium Półprzewodniki, Dielektryki i Magnetyki Ćwiczenie nr 10 Pomiary czasu życia nośników w półprzewodnikach
 Laboaoium Półpzewodniki, Dielekyki i Magneyki Ćwiczenie n 10 Pomiay czasu życia nośników w półpzewodnikach I. Zagadnienia do pzygoowania: 1. Pojęcia: nośniki mniejszościowe i większościowe, ównowagowe
Laboaoium Półpzewodniki, Dielekyki i Magneyki Ćwiczenie n 10 Pomiay czasu życia nośników w półpzewodnikach I. Zagadnienia do pzygoowania: 1. Pojęcia: nośniki mniejszościowe i większościowe, ównowagowe
EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH. dr inż. Robert Stachniewicz
 EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH dr inż. Rober Sachniewicz METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH Jednymi z licznych celów i zadań przedsiębiorswa są: - wzros warości przedsiębiorswa
EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH dr inż. Rober Sachniewicz METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH Jednymi z licznych celów i zadań przedsiębiorswa są: - wzros warości przedsiębiorswa
WAHADŁO OBERBECKA V 6 38a
 Wahadło Obebecka V 6-38a WAHADŁO OBERBECKA V 6 38a Wahadło ma zasosowanie na lekcjach fizyki w klasie I i III liceum ogólnokszałcącego. Pzyząd sanowi byłę szywną uwozoną pzez uleję (1) i czey wkęcone w
Wahadło Obebecka V 6-38a WAHADŁO OBERBECKA V 6 38a Wahadło ma zasosowanie na lekcjach fizyki w klasie I i III liceum ogólnokszałcącego. Pzyząd sanowi byłę szywną uwozoną pzez uleję (1) i czey wkęcone w
Analiza metod oceny efektywności inwestycji rzeczowych**
 Ekonomia Menedżerska 2009, nr 6, s. 119 128 Marek Łukasz Michalski* Analiza meod oceny efekywności inwesycji rzeczowych** 1. Wsęp Podsawowymi celami przedsiębiorswa w długim okresie jes rozwój i osiąganie
Ekonomia Menedżerska 2009, nr 6, s. 119 128 Marek Łukasz Michalski* Analiza meod oceny efekywności inwesycji rzeczowych** 1. Wsęp Podsawowymi celami przedsiębiorswa w długim okresie jes rozwój i osiąganie
Wykorzystanie wielorównaniowych modeli AR-GARCH w pomiarze ryzyka metodą VaR
 Krzyszof Pionek Daniel Papla Kaedra Inwesycji Finansowych i Ubezpieczeń Akademia Ekonomiczna we Wrocławiu Wykorzysanie wielorównaniowych modeli AR-GARCH w pomiarze ryzyka meodą VaR Wsęp Wśród różnych meod
Krzyszof Pionek Daniel Papla Kaedra Inwesycji Finansowych i Ubezpieczeń Akademia Ekonomiczna we Wrocławiu Wykorzysanie wielorównaniowych modeli AR-GARCH w pomiarze ryzyka meodą VaR Wsęp Wśród różnych meod
Niestacjonarne zmienne czasowe własności i testowanie
 Maeriał dla sudenów Niesacjonarne zmienne czasowe własności i esowanie (sudium przypadku) Nazwa przedmiou: ekonomeria finansowa I (22204), analiza szeregów czasowych i prognozowanie (13201); Kierunek sudiów:
Maeriał dla sudenów Niesacjonarne zmienne czasowe własności i esowanie (sudium przypadku) Nazwa przedmiou: ekonomeria finansowa I (22204), analiza szeregów czasowych i prognozowanie (13201); Kierunek sudiów:
Analiza i prognozowanie szeregów czasowych
 Analiza i pognozowanie szeegów czasowych Pojęcie szeegu czasowego Szeeg czasowy (chonologiczny, dynamiczny, ozwojowy) pezenuje ozwój wybanego zjawiska w czasie; zawiea waości zjawiska y w jednoskach czasu,,
Analiza i pognozowanie szeegów czasowych Pojęcie szeegu czasowego Szeeg czasowy (chonologiczny, dynamiczny, ozwojowy) pezenuje ozwój wybanego zjawiska w czasie; zawiea waości zjawiska y w jednoskach czasu,,
Rozdział VIII KINETYKA NASYCANIA POWIERZCHNI. 1. Wstęp
 83 Rozdział VIII KINETYKA NASYCANIA POWIERZCHNI 1. Wsęp W akcie wykonywania zewnęznyc oconnyc wasw ynku, jak i konsewacji isniejącyc deali budowli zabykowyc zacodzi częso konieczność oceny sopnia peneacji
83 Rozdział VIII KINETYKA NASYCANIA POWIERZCHNI 1. Wsęp W akcie wykonywania zewnęznyc oconnyc wasw ynku, jak i konsewacji isniejącyc deali budowli zabykowyc zacodzi częso konieczność oceny sopnia peneacji
Kombinowanie prognoz. - dlaczego należy kombinować prognozy? - obejmowanie prognoz. - podstawowe metody kombinowania prognoz
 Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
Krzysztof Piontek Weryfikacja modeli Blacka-Scholesa dla opcji na WIG20
 Akademia Ekonomiczna im. Oskara Langego we Wrocławiu Wydział Zarządzania i Informayki Kaedra Inwesycji Finansowych i Zarządzania Ryzykiem Krzyszof Pionek Weryfikacja modeli Blacka-Scholesa oraz AR-GARCH
Akademia Ekonomiczna im. Oskara Langego we Wrocławiu Wydział Zarządzania i Informayki Kaedra Inwesycji Finansowych i Zarządzania Ryzykiem Krzyszof Pionek Weryfikacja modeli Blacka-Scholesa oraz AR-GARCH
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
SIMR 2017/18, Statystyka, Przykładowe zadania do kolokwium - Rozwiązania
 SIMR 7/8, Statystyka, Przykładowe zadania do kolokwium - Rozwiązania. Dana jest gęstość prawdopodobieństwa zmiennej losowej ciągłej X : { a( x) dla x [, ] f(x) = dla pozostałych x Znaleźć: i) Wartość parametru
SIMR 7/8, Statystyka, Przykładowe zadania do kolokwium - Rozwiązania. Dana jest gęstość prawdopodobieństwa zmiennej losowej ciągłej X : { a( x) dla x [, ] f(x) = dla pozostałych x Znaleźć: i) Wartość parametru
WYKORZYSTANIE MODELI SIGN RCA DO PROGNOZY
 Joanna Góka Wyższa Szkoła Infomayki i Ekonomii WP w Olszynie WYKORZYSANIE MODELI SIGN RCA DO PROGNOZY WAROŚCI NARAŻONEJ NA RYZYKO Do kwanyfikowania yzyka ynkowego używana jes częso waość naażona na yzyko
Joanna Góka Wyższa Szkoła Infomayki i Ekonomii WP w Olszynie WYKORZYSANIE MODELI SIGN RCA DO PROGNOZY WAROŚCI NARAŻONEJ NA RYZYKO Do kwanyfikowania yzyka ynkowego używana jes częso waość naażona na yzyko
6.4. Model zdyskontowanych zysków Metoda skorygowanej wartości bieżącej (APV)
 6.4. Model zdyskonowanych zysków Jeśli za mienik waości pzyjęy zosanie zysk neo, obliczenie waości wewnęznej odbywać się będzie ak samo, jak miało o miejsce w pzypadku modeli dywidendowych i cash flow.
6.4. Model zdyskonowanych zysków Jeśli za mienik waości pzyjęy zosanie zysk neo, obliczenie waości wewnęznej odbywać się będzie ak samo, jak miało o miejsce w pzypadku modeli dywidendowych i cash flow.
Analiza rynku projekt
 Analiza rynku projek A. Układ projeku 1. Srona yułowa Tema Auor 2. Spis reści 3. Treść projeku 1 B. Treść projeku 1. Wsęp Po co? Na co? Dlaczego? Dlaczego robię badania? Jakimi meodami? Dla Kogo o jes
Analiza rynku projek A. Układ projeku 1. Srona yułowa Tema Auor 2. Spis reści 3. Treść projeku 1 B. Treść projeku 1. Wsęp Po co? Na co? Dlaczego? Dlaczego robię badania? Jakimi meodami? Dla Kogo o jes
BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH OPARTYCH NA ANALIZIE TECHNICZNEJ WPROWADZENIE
 Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Magdalena Osińska, Marcin Fałdziński Uniwersytet Mikołaja Kopernika w Toruniu. Modele GARCH i SV z zastosowaniem teorii wartości ekstremalnych
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarim Nakowe 4 6 września 2007 w Torni Kaedra Ekonomerii i Saysyki Uniwersye Mikołaja Kopernika w Torni Magdalena Osińska Marcin Fałdziński Uniwersye
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarim Nakowe 4 6 września 2007 w Torni Kaedra Ekonomerii i Saysyki Uniwersye Mikołaja Kopernika w Torni Magdalena Osińska Marcin Fałdziński Uniwersye
1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt)
 II Etap Maj 2013 Zadanie 1 II Etap Maj 2013 1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt) 1.1/podaj definicję składnika
II Etap Maj 2013 Zadanie 1 II Etap Maj 2013 1/ W oparciu o znajomość MSSF, które zostały zatwierdzone przez UE (dalej: MSR/MSSF): (Punktacja dot. pkt 1, razem: od 0 do 20 pkt) 1.1/podaj definicję składnika
Parytet stóp procentowych a premia za ryzyko na przykładzie kursu EURUSD
 Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Marcin Gajewski Uniwersye Łódzki 4.12.2008 Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Niezabazpieczony UIP)
Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Marcin Gajewski Uniwersye Łódzki 4.12.2008 Parye sóp procenowych a premia za ryzyko na przykładzie kursu EURUD Niezabazpieczony UIP)
1. Szereg niesezonowy 1.1. Opis szeregu
 kwaralnych z la 2000-217 z la 2010-2017.. Szereg sezonowy ma charaker danych model z klasy ARIMA/SARIMA i model eksrapolacyjny oraz d prognoz z ych modeli. 1. Szereg niesezonowy 1.1. Opis szeregu Analizowany
kwaralnych z la 2000-217 z la 2010-2017.. Szereg sezonowy ma charaker danych model z klasy ARIMA/SARIMA i model eksrapolacyjny oraz d prognoz z ych modeli. 1. Szereg niesezonowy 1.1. Opis szeregu Analizowany
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
ANNA GÓRSKA MONIKA KRAWIEC Szkoła Główna Gospodarstwa Wiejskiego w Warszawie
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 768 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 63 013 ANNA GÓRSKA MONIKA KRAWIEC Szkoła Główna Gospodarswa Wiejskiego w Warszawie BADANIE EFEKTYWNOŚCI INFORMACYJNEJ
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 768 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 63 013 ANNA GÓRSKA MONIKA KRAWIEC Szkoła Główna Gospodarswa Wiejskiego w Warszawie BADANIE EFEKTYWNOŚCI INFORMACYJNEJ
DYNAMICZNE MODELE EKONOMETRYCZNE
 DYNAMICZNE MODELE EKONOMETRYCZNE IX Ogólnopolskie Seminarium Naukowe, 6 8 września 005 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Pior Fiszeder Uniwersye Mikołaja Kopernika
DYNAMICZNE MODELE EKONOMETRYCZNE IX Ogólnopolskie Seminarium Naukowe, 6 8 września 005 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Pior Fiszeder Uniwersye Mikołaja Kopernika
Powtórzenie. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Ewa Dziawgo Uniwersytet Mikołaja Kopernika w Toruniu. Analiza wrażliwości modelu wyceny opcji złożonych
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 7 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika w Toruniu
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 7 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika w Toruniu
Analiza danych DRZEWA DECYZYJNE. Drzewa decyzyjne. Entropia. http://zajecia.jakubw.pl/ test 1 dopełnienie testu 1
 Analiza danych Drzewa decyzyjne. Enropia. Jakub Wróblewski jakubw@pjwsk.edu.pl hp://zajecia.jakubw.pl/ DRZEWA DECYZYJNE Meoda reprezenacji wiedzy (modelowania ablic decyzyjnych). Pozwala na przejrzysy
Analiza danych Drzewa decyzyjne. Enropia. Jakub Wróblewski jakubw@pjwsk.edu.pl hp://zajecia.jakubw.pl/ DRZEWA DECYZYJNE Meoda reprezenacji wiedzy (modelowania ablic decyzyjnych). Pozwala na przejrzysy
Ocena płynności wybranymi metodami szacowania osadu 1
 Bogdan Ludwiczak Wprowadzenie Ocena płynności wybranymi meodami szacowania osadu W ubiegłym roku zaszły znaczące zmiany doyczące pomiaru i zarządzania ryzykiem bankowym. Są one konsekwencją nowowprowadzonych
Bogdan Ludwiczak Wprowadzenie Ocena płynności wybranymi meodami szacowania osadu W ubiegłym roku zaszły znaczące zmiany doyczące pomiaru i zarządzania ryzykiem bankowym. Są one konsekwencją nowowprowadzonych
E k o n o m e t r i a S t r o n a 1. Nieliniowy model ekonometryczny
 E k o n o m e r i a S r o n a Nieliniowy model ekonomeryczny Jednorównaniowy model ekonomeryczny ma posać = f( X, X,, X k, ε ) gdzie: zmienna objaśniana, X, X,, X k zmienne objaśniające, ε - składnik losowy,
E k o n o m e r i a S r o n a Nieliniowy model ekonomeryczny Jednorównaniowy model ekonomeryczny ma posać = f( X, X,, X k, ε ) gdzie: zmienna objaśniana, X, X,, X k zmienne objaśniające, ε - składnik losowy,
DYNAMICZNE MODELE EKONOMETRYCZNE
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Pior Fiszeder Uniwersye Mikołaja Kopernika
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Pior Fiszeder Uniwersye Mikołaja Kopernika
BEZRYZYKOWNE BONY I LOKATY BANKOWE ALTERNATYWĄ DLA PRZYSZŁYCH EMERYTÓW. W tym krótkim i matematycznie bardzo prostym artykule pragnę osiągnąc 3 cele:
 1 BEZRYZYKOWNE BONY I LOKATY BANKOWE ALTERNATYWĄ DLA PRZYSZŁYCH EMERYTÓW Leszek S. Zaremba (Polish Open Universiy) W ym krókim i maemaycznie bardzo prosym arykule pragnę osiągnąc cele: (a) pokazac że kupowanie
1 BEZRYZYKOWNE BONY I LOKATY BANKOWE ALTERNATYWĄ DLA PRZYSZŁYCH EMERYTÓW Leszek S. Zaremba (Polish Open Universiy) W ym krókim i maemaycznie bardzo prosym arykule pragnę osiągnąc cele: (a) pokazac że kupowanie
PROCEDURA WYBORU PORTFELA AKCJI ZAPEWNIAJĄCA KONTROLĘ RYZYKA NIESYSTEMATYCZNEGO
 B A D A I A O P E R A C Y J E I D E C Y Z J E 3 4 2004 omasz BRZĘCZEK* PROCEDURA WYBORU PORFELA AKCJI ZAPEWIAJĄCA KOROLĘ RYZYKA IESYSEMAYCZEGO Pzedsawiono poceduę wybou pofela akci zapewniaącą konolę yzyka
B A D A I A O P E R A C Y J E I D E C Y Z J E 3 4 2004 omasz BRZĘCZEK* PROCEDURA WYBORU PORFELA AKCJI ZAPEWIAJĄCA KOROLĘ RYZYKA IESYSEMAYCZEGO Pzedsawiono poceduę wybou pofela akci zapewniaącą konolę yzyka
STATYSTYCZNA WERYFIKACJA MODELU CAPM NA PRZYKŁADZIE POLSKIEGO RYNKU KAPITAŁOWEGO WPROWADZENIE METODOLOGIA TESTOWANIA MODELU
 GraŜyna Trzpio, Dominik KręŜołek Kaedra Saysyki Akademii Ekonomicznej w Kaowicach e-mail rzpio@sulu.ae.kaowice.pl, dominik_arkano@wp.pl STATYSTYCZNA WERYFIKACJA MODELU CAPM NA PRZYKŁADZIE POLSKIEGO RYNKU
GraŜyna Trzpio, Dominik KręŜołek Kaedra Saysyki Akademii Ekonomicznej w Kaowicach e-mail rzpio@sulu.ae.kaowice.pl, dominik_arkano@wp.pl STATYSTYCZNA WERYFIKACJA MODELU CAPM NA PRZYKŁADZIE POLSKIEGO RYNKU
Analiza opłacalności inwestycji logistycznej Wyszczególnienie
 inwesycji logisycznej Wyszczególnienie Laa Dane w ys. zł 2 3 4 5 6 7 8 Przedsięwzięcie I Program rozwoju łańcucha (kanału) dysrybucji przewiduje realizację inwesycji cenrum dysrybucyjnego. Do oceny przyjęo
inwesycji logisycznej Wyszczególnienie Laa Dane w ys. zł 2 3 4 5 6 7 8 Przedsięwzięcie I Program rozwoju łańcucha (kanału) dysrybucji przewiduje realizację inwesycji cenrum dysrybucyjnego. Do oceny przyjęo
ANALIZA DANYCH W STATA 8.0
 ANALIZA DANYCH W STATA 8.0 ZAJĘCIA 3 1. Rozpoczęcie 1. Stwozyć w katalogu C:/temp katalog stata_3 2. Ściągnąć z intenetu ze stony http://akson.sgh.waw.pl/~mpoch plik zajecia3.zip (kyje się on pod tekstem
ANALIZA DANYCH W STATA 8.0 ZAJĘCIA 3 1. Rozpoczęcie 1. Stwozyć w katalogu C:/temp katalog stata_3 2. Ściągnąć z intenetu ze stony http://akson.sgh.waw.pl/~mpoch plik zajecia3.zip (kyje się on pod tekstem
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1
 ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
METODY STATYSTYCZNE W FINANSACH
 METODY STATYSTYCZNE W FINANSACH Krzyszof Jajuga Akademia Ekonomiczna we Wrocławiu, Kaedra Inwesycji Finansowych i Ubezpieczeń Wprowadzenie W osanich kilkunasu laach na świecie obserwuje się dynamiczny
METODY STATYSTYCZNE W FINANSACH Krzyszof Jajuga Akademia Ekonomiczna we Wrocławiu, Kaedra Inwesycji Finansowych i Ubezpieczeń Wprowadzenie W osanich kilkunasu laach na świecie obserwuje się dynamiczny
Komisja Egzaminacyjna dla Aktuariuszy. XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rachunki oszczędnościowe
Ryzyko walutowe. Kursy walutowe spot i forward. Teorie kursów walutowych
 Ryzyko walutowe. Kusy walutowe spot i owa. eoie kusów walutowych Postawowe pojęcia Deinicja yzyka walutowego - schemat z piewszego wykłau. Zazązanie yzykiem walutowym obejmuje wybó instumentów (aktywów)
Ryzyko walutowe. Kusy walutowe spot i owa. eoie kusów walutowych Postawowe pojęcia Deinicja yzyka walutowego - schemat z piewszego wykłau. Zazązanie yzykiem walutowym obejmuje wybó instumentów (aktywów)
Klasyfikacja modeli. Metoda najmniejszych kwadratów
 Konspek ekonomeria: Weryfikacja modelu ekonomerycznego Klasyfikacja modeli Modele dzielimy na: - jedno- i wielorównaniowe - liniowe i nieliniowe - sayczne i dynamiczne - sochasyczne i deerminisyczne -
Konspek ekonomeria: Weryfikacja modelu ekonomerycznego Klasyfikacja modeli Modele dzielimy na: - jedno- i wielorównaniowe - liniowe i nieliniowe - sayczne i dynamiczne - sochasyczne i deerminisyczne -
WYBRANE TESTY NIEOBCIĄŻONOŚCI MIAR RYZYKA NA PRZYKŁADZIE VALUE AT RISK
 Przemysław Jeziorski Uniwersye Ekonomiczny w Kaowicach Wydział Informayki i Komunikacji Zakład Demografii i Saysyki Ekonomicznej przemyslaw.jeziorski@ue.kaowice.pl WYBRANE TESTY NIEOBCIĄŻONOŚCI MIAR RYZYKA
Przemysław Jeziorski Uniwersye Ekonomiczny w Kaowicach Wydział Informayki i Komunikacji Zakład Demografii i Saysyki Ekonomicznej przemyslaw.jeziorski@ue.kaowice.pl WYBRANE TESTY NIEOBCIĄŻONOŚCI MIAR RYZYKA
OeconomiA copernicana. Małgorzata Madrak-Grochowska, Mirosława Żurek Uniwersytet Mikołaja Kopernika w Toruniu
 OeconomiA copernicana 2011 Nr 4 Małgorzaa Madrak-Grochowska, Mirosława Żurek Uniwersye Mikołaja Kopernika w Toruniu TESTOWANIE PRZYCZYNOWOŚCI W WARIANCJI MIĘDZY WYBRANYMI INDEKSAMI RYNKÓW AKCJI NA ŚWIECIE
OeconomiA copernicana 2011 Nr 4 Małgorzaa Madrak-Grochowska, Mirosława Żurek Uniwersye Mikołaja Kopernika w Toruniu TESTOWANIE PRZYCZYNOWOŚCI W WARIANCJI MIĘDZY WYBRANYMI INDEKSAMI RYNKÓW AKCJI NA ŚWIECIE
Ocena efektywności procedury Congruent Specyfication dla małych prób
 243 Zeszyy Naukowe Wyższej Szkoły Bankowej we Wrocławiu Nr 20/2011 Wyższa Szkoła Bankowa w Toruniu Ocena efekywności procedury Congruen Specyficaion dla małych prób Sreszczenie. Procedura specyfikacji
243 Zeszyy Naukowe Wyższej Szkoły Bankowej we Wrocławiu Nr 20/2011 Wyższa Szkoła Bankowa w Toruniu Ocena efekywności procedury Congruen Specyficaion dla małych prób Sreszczenie. Procedura specyfikacji
UMK w Toruniu ANALIZA ZALEŻNOŚCI MIĘDZY INDEKSEM WIG A WYBRANYMI INDEKSAMI RYNKÓW AKCJI NA ŚWIECIE
 Pior Fiszeder UMK w Toruniu ANALIZA ZALEŻNOŚCI MIĘDZY INDEKSEM WIG A WYBRANYMI INDEKSAMI RYNKÓW AKCJI NA ŚWIECIE. Wprowadzenie Rynki kapiałowe na świecie są coraz silniej powiązane. Do najważniejszych
Pior Fiszeder UMK w Toruniu ANALIZA ZALEŻNOŚCI MIĘDZY INDEKSEM WIG A WYBRANYMI INDEKSAMI RYNKÓW AKCJI NA ŚWIECIE. Wprowadzenie Rynki kapiałowe na świecie są coraz silniej powiązane. Do najważniejszych
Wykład 6. Badanie dynamiki zjawisk
 Wykład 6 Badanie dynamiki zjawisk Krzywa wieża w Pizie 1 2 3 4 5 6 7 8 9 10 11 12 13 y 4,9642 4,9644 4,9656 4,9667 4,9673 4,9688 4,9696 4,9698 4,9713 4,9717 4,9725 4,9742 4,9757 Szeregiem czasowym nazywamy
Wykład 6 Badanie dynamiki zjawisk Krzywa wieża w Pizie 1 2 3 4 5 6 7 8 9 10 11 12 13 y 4,9642 4,9644 4,9656 4,9667 4,9673 4,9688 4,9696 4,9698 4,9713 4,9717 4,9725 4,9742 4,9757 Szeregiem czasowym nazywamy
Wytrzymałość śruby wysokość nakrętki
 Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
LIST EMISYJNY nr 3 /2014 Ministra Finansów
 LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
EFEKTYWNOŚĆ INWESTYCJI W ZAPASY W OPODATKOWANYCH I NIE OPODATKOWANYCH ORGANIZACJACH 1
 GRZEGORZ MICHALSKI EFEKTYWNOŚĆ INWESTYCJI W ZAPASY W OPODATKOWANYCH I NIE OPODATKOWANYCH ORGANIZACJACH 1 1. Wsęp Organizacje, mogą działać jako opodakowane przedsiębiorswa działające na zasadach komercyjnych
GRZEGORZ MICHALSKI EFEKTYWNOŚĆ INWESTYCJI W ZAPASY W OPODATKOWANYCH I NIE OPODATKOWANYCH ORGANIZACJACH 1 1. Wsęp Organizacje, mogą działać jako opodakowane przedsiębiorswa działające na zasadach komercyjnych
WYKORZYSTANIE MIERNIKÓW KREOWANIA WARTOŚCI W RACHUNKU ODPOWIEDZIALNOŚCI
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 668 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 41 2011 BARTŁOMIEJ NITA Uniwersye Ekonomiczny we Wrocławiu WYKORZYSTANIE MIERNIKÓW KREOWANIA WARTOŚCI W RACHUNKU
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 668 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 41 2011 BARTŁOMIEJ NITA Uniwersye Ekonomiczny we Wrocławiu WYKORZYSTANIE MIERNIKÓW KREOWANIA WARTOŚCI W RACHUNKU
Wyższa Szkoła Marketingu i Zarządzania w Lesznie
 Wyższa Szkoła Markeingu i Zarządzania w Lesznie MATERIAŁY ROBOCZE NA ZAJĘCIA Z PRZEDMIOTU BIZNES PLAN Opracowali: dr Jacek Kowalewski mgr Kazimierz Linowski Leszno 2008 2 S P I S T R E Ś C I WPROWADZENIE.
Wyższa Szkoła Markeingu i Zarządzania w Lesznie MATERIAŁY ROBOCZE NA ZAJĘCIA Z PRZEDMIOTU BIZNES PLAN Opracowali: dr Jacek Kowalewski mgr Kazimierz Linowski Leszno 2008 2 S P I S T R E Ś C I WPROWADZENIE.
Finanse. cov. * i. 1. Premia za ryzyko. 2. Wskaźnik Treynora. 3. Wskaźnik Jensena
 Finanse 1. Premia za ryzyko PR r m r f. Wskaźnik Treynora T r r f 3. Wskaźnik Jensena r [ rf ( rm rf ] 4. Porfel o minimalnej wariancji (ile procen danej spółki powinno znaleźć się w porfelu w a w cov,
Finanse 1. Premia za ryzyko PR r m r f. Wskaźnik Treynora T r r f 3. Wskaźnik Jensena r [ rf ( rm rf ] 4. Porfel o minimalnej wariancji (ile procen danej spółki powinno znaleźć się w porfelu w a w cov,
DYNAMICZNE MODELE EKONOMETRYCZNE
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika Zależność
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika Zależność
KONCEPCJA WARTOŚCI ZAGROŻONEJ VaR (VALUE AT RISK)
 KONCEPCJA WARTOŚCI ZAGROŻONEJ VaR (VALUE AT RISK) Kaarzyna Kuziak Akademia Ekonomiczna we Wrocławiu, Kaedra Inwesycji Finansowych i Ubezpieczeń Wprowadzenie W 1994 roku insyucja finansowa JP Morgan opublikowała
KONCEPCJA WARTOŚCI ZAGROŻONEJ VaR (VALUE AT RISK) Kaarzyna Kuziak Akademia Ekonomiczna we Wrocławiu, Kaedra Inwesycji Finansowych i Ubezpieczeń Wprowadzenie W 1994 roku insyucja finansowa JP Morgan opublikowała
Miara ryzyka estymacji parametrów modelu VaR
 Zeszyy Uniwersye Ekonomiczny w Krakowie Naukowe 4 (976) ISSN 1898-6447 e-issn 2545-3238 Zesz. Nauk. UEK, 2018; 4 (976): 183 200 hps://doi.org/10.15678/znuek.2018.0976.0411 Miara ryzyka esymacji paramerów
Zeszyy Uniwersye Ekonomiczny w Krakowie Naukowe 4 (976) ISSN 1898-6447 e-issn 2545-3238 Zesz. Nauk. UEK, 2018; 4 (976): 183 200 hps://doi.org/10.15678/znuek.2018.0976.0411 Miara ryzyka esymacji paramerów
PROGRAM PRIORTYTETOWY. Program dla przedsięwzięć w zakresie odnawialnych źródeł energii i obiektów wysokosprawnej kogeneracji Część 1)
 Tyuł Programu: PROGRAM PRIORTYTETOWY Program dla przedsięwzięć w zakresie odnawialnych źródeł energii i obieków wysokosprawnej kogeneracji Część 1) 1. Cel Programu Dofinansowanie duŝych inwesycji wpisujących
Tyuł Programu: PROGRAM PRIORTYTETOWY Program dla przedsięwzięć w zakresie odnawialnych źródeł energii i obieków wysokosprawnej kogeneracji Część 1) 1. Cel Programu Dofinansowanie duŝych inwesycji wpisujących
Analiza stabilności parametrów hybrydowych modeli market-timing polskich funduszy inwestycyjnych 1
 Joanna Olbryś * Analiza sabilności paramerów hybrydowych modeli marke-iming polskich funduszy inwesycyjnych Wsęp Hybrydowe czeroczynnikowe modele marke-iming funduszy inwesycyjnych akcji polskich zosały
Joanna Olbryś * Analiza sabilności paramerów hybrydowych modeli marke-iming polskich funduszy inwesycyjnych Wsęp Hybrydowe czeroczynnikowe modele marke-iming funduszy inwesycyjnych akcji polskich zosały
Finanse ubezpieczeń społecznych
 Finanse ubezpieczeń społecznych Wykład 7. Kapiałowe ubezpieczenia eeyalne. Pywane plany eeyalne Aeing (994), Wiśniewski (999) Pywane plany eeyalne:. Zaley: -Nie wyagają działań ze sony pańswa, poza ewenualnie
Finanse ubezpieczeń społecznych Wykład 7. Kapiałowe ubezpieczenia eeyalne. Pywane plany eeyalne Aeing (994), Wiśniewski (999) Pywane plany eeyalne:. Zaley: -Nie wyagają działań ze sony pańswa, poza ewenualnie
Witold Orzeszko Uniwersytet Mikołaja Kopernika w Toruniu
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika w Toruniu
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika w Toruniu
Jerzy Czesław Ossowski Politechnika Gdańska. Dynamika wzrostu gospodarczego a stopy procentowe w Polsce w latach
 DYNAMICZNE MODELE EKONOMETRYCZNE IX Ogólnopolskie Seminarium Naukowe, 6 8 września 2005 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Poliechnika Gdańska Dynamika wzrosu
DYNAMICZNE MODELE EKONOMETRYCZNE IX Ogólnopolskie Seminarium Naukowe, 6 8 września 2005 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Poliechnika Gdańska Dynamika wzrosu
Model segmentowy bezzatrudnieniowego wzrostu gospodarczego
 Maria Jadamus-Hacura * Krysyna Melich-Iwanek ** Model segmenowy bezzarudnieniowego wzrosu gospodarczego Wsęp Wzros gospodarczy jes jednym z podsawowych czynników kszałujących rynek pracy. Rynek en jes
Maria Jadamus-Hacura * Krysyna Melich-Iwanek ** Model segmenowy bezzarudnieniowego wzrosu gospodarczego Wsęp Wzros gospodarczy jes jednym z podsawowych czynników kszałujących rynek pracy. Rynek en jes
