ANALIZA MATEMATYCZNA 1
|
|
|
- Adrian Chmielewski
- 7 lat temu
- Przeglądów:
Transkrypt
1 ANALIZA MATEMATYCZNA 1
2 Maria Gewert Zbigiew Skoczylas ANALIZA MATEMATYCZNA 1 Defiicje, twierdzeia, wzory Wydaie dwudzieste czwarte zmieioe Oficya Wydawicza GiS Wrocław 2015
3 Maria Gewert Wydział Matematyki Politechika Wrocławska pwr.edu.pl Zbigiew Skoczylas Wydział Matematyki Politechika Wrocławska pwr.edu.pl Projekt okładki IMPRESJA Studio Grafiki Reklamowej Copyright c , 2015 by Oficya Wydawicza GiS Utwór w całości ai we fragmetach ie może być powielay ai rozpowszechiay za pomocą urządzeń elektroiczych, mechaiczych, kopiujących, agrywających i iych. Poadto utwór ie może być umieszczay ai rozpowszechiay w postaci cyfrowej zarówo w Iterecie, jak i w sieciach lokalych, bez pisemej zgody posiadacza praw autorskich. Składwykoaowsystemie L A TEX. ISBN Wydaie XXIV zmieioe, Wrocław 2015 Oficya Wydawicza GiS, s.c., Druk i oprawa: Oficya Wydawicza ATUT 4
4 Spis treści Wstęp 7 0 Zbiory i fukcje liczbowe Liczbyrzeczywiste Fukcje podstawoweokreśleia Złożeiafukcjiifukcjeodwrote Fukcjeelemetareiiektóreieelemetare Ciągi liczbowe Podstawoweokreśleia Graiceciągów Twierdzeiaograicachciągów Graice i ciągłość fukcji Defiicjegraicfukcji Twierdzeiaograicachfukcji Asymptotyfukcji Ciągłośćfukcji Działaiaafukcjachciągłych Twierdzeiaofukcjachciągłych Pochode fukcji Podstawowepojęcia Pochodejedostroeipochodeiewłaściwe Twierdzeiaopochodejfukcji Różiczkafukcji Pochodewyższychrzędów Pochodefukcjiwektorowych Zastosowaia pochodych Twierdzeiaowartościśrediej Twierdzeiaograicachieozaczoych RozwiięcieTaylorafukcji Ekstremafukcji
5 4.5 Fukcjewypukłeipuktyprzegięcia Przybliżoerozwiązywaierówań Badaiefukcji Całki ieozaczoe Fukcjepierwoteicałkiiezaczoe Twierdzeiaocałkachieozaczoych Całkowaiefukcjiwymierych Całkowaiefukcjitrygoometryczych Całkowaiefukcjiziewymierościami Całki ozaczoe Podstawowepojęcia Metodyobliczaiacałekozaczoych Własościcałekozaczoych Fukcjagórejgraicycałkowaia* Przybliżoemetodyobliczaiacałek* Zastosowaie całek ozaczoych Zastosowaiawgeometrii Zastosowaiawfizyce Dowody wybraych twierdzeń i faktów 128 Odpowiedzi i wskazówki 147 Literatura 168 6
6 1 Wstęp Niiejsza książka jest pierwszą częścią zestawu podręczików do Aalizy matematyczej 1. Pozostałymi częściami są zbiór pt. Aaliza matematycza 1. Przykłady i zadaia oraz opracowaie Aaliza matematycza 1. Kolokwia i egzamiy. Podręcziki te są przezaczoe główie dla studetów politechik. Mogą z ich korzystać także studeci wydziałów auk ścisłych i przyrodiczych uiwersytetów oraz uczeli ekoomiczych, pedagogiczych i roliczych. Opracowaie zawiera defiicje, twierdzeia i wzory z rachuku różiczkowego oraz całkowego fukcji jedej zmieej wraz z zastosowaiami. Wszystkie zagadieia teoretycze zakończoo ćwiczeiami, przy czym początkowe z ich są z reguły ajprostsze. Podręczik jest bogato ilustrowayzawiera poad 300 rysuków), ułatwia to przyswajaie wiedzy. Na końcu książki umieszczoo dowody większości twierdzeńw tekście twierdzeia te ozaczoe są symbolem ). Fragmety materiału ozaczoe gwiazdką iezaczie wykraczają poza aktualy program przedmiotu. Tak samo ozaczoo trudiejsze ćwiczeia. Dodatkowy materiał, trudiejsze ćwiczeia oraz dowody twierdzeń dołączoo z myślą o studetach, którzy chcą rozszerzyć swoją wiedzę z aalizy matematyczej. Rówolegle do materiału omawiaego a wykładzie studeci powii przerabiać samodzielie i a ćwiczeiach odpowiedio dobrae zadaia. Przykładową listę zadań wraz z metodami ich rozwiązywaia moża zaleźć w drugiej części podręczika. Ćwiczeia z tego podręczika oraz zadaia z listy zadań są podobych typów i mają te sam stopień trudości jak zadaia, które zwykle pojawiają a kolokwiach i egzamiach. Zestawy zadań, które w poprzedich latach studeci Politechiki Wrocławskiej rozwiązywali a sprawdziaach, są umieszczoe w trzeciej części podręczika. W obecym wydaiu podręczika zmieioo układ materiału oraz dodao owy paragraf Przybliżoerozwiązywaierówań.Jedocześieprzeredagowaosformułowaia wszystkich defiicji i twierdzeń. Poadto zwiększoo liczbę łatwych ćwiczeń, dołączoo owe rysuki oraz dowody kolejych twierdzeń. Poprawioo także błędy i usterki zgłoszoe przez studetów i wykładowców. Dzięki temu książka stała się bardziej przyjazda dla czytelika. 7
7 8 Wstęp Serdeczie dziękujemy Pai dr Teresie Jurlewicz za przygotowaie odpowiedzi do ćwiczeń z wcześiejszych wydań. Szczególe podziekowaia składamy Paom dr. Maciejowi Bureckiemu, prof. dr. hab. Jauszowi Mierczyńskiemu oraz prof. dr. hab. Krzysztofowi Stempakowi za licze spostrzeżeia, które pozwalały ulepszać koleje wydaia. Dziękujemy także Koleżakom i Kolegom z Wydziału Matematyki Politechiki Wrocławskiej oraz aszym Studetom za uwagi o poprzedich wydaiach. Dziękujemy rówież Koleżakom i Kolegom z iych uczeli za kometarze dotyczące zakresu i sposobu ujęcia materiału. Uprzejmie prosimy wykładowców i studetów o przesyłaie uwag o podręcziku oraz iformacji o dostrzeżoych błędach i usterkach. Maria Gewert Zbigiew Skoczylas
8 1 Ciągiliczbowe Podstawoweokreśleia Defiicja ciąg liczbowy) Ciągiem liczbowym azywamy fukcję określoą a zbiorze liczb aturalych i przyjmującą wartości ze zbioru liczb rzeczywistych. Wartość tej fukcji dla liczby aturalej azywamy-tymwyrazemciąguiozaczamyp.przeza.ciągotakichwyrazachozaczamyprzeza ).Zbiórwyrazówciągua ),tj.{a : N},ozaczamy krótkoprzez{a }.Ciągibędziemyprzedstawialiapłaszczyźie,jakozbiorypuktówowspółrzędych,a ),gdzie N,albojakoideksowaepuktyaosiliczb rzeczywistych. a) a b) 1,a 1 ) 2,a 2 ) 3,a 3 ) 4,a 4 ) 5,a 5 ) a 1 a 2 a 3... a Rys Ilustracja ciągua) a płaszczyźie,b) a prostej Obrazowo: ciąg moża traktować jako zbiór poumerowaych liczb rzeczywistych, które są ustawioe według rosących umerów a 1,a 2,a 3,...,a,... Przykład Ciągi możemy określać: wzorem: a)a =2, b)b = 1 si, c)c = +1, d)d = , e)e = , f)f = { 3 dlaieparzystych, 3 dlaparzystych; 27
9 28 Ciągi liczbowe rekurecyjietz. kolejy wyraz ciągu wyraża się przez iektóre poprzedie): a)a 1 =7,a +1 =a +3 ciągarytmetyczy, b)b 1 =1,b +1 =2b ciąggeometryczy, c)c 1 =1,c 2 =1,c +2 =c +c +1 ciągfiboacciego, d)d 1 =2,d +1 =2 d1 ; opisowo: a)a -tacyfrapoprzecikuwrozwiięciudziesiętymliczbyπ, b)p -taliczbapierwsza, c)c przedostatiacyfrarozwiięciadziesiętegoliczby+3) 2. Defiicja ciągi ograiczoe) Mówimy,żeciąga )jestograiczoyzdołu,jeżeliistiejeliczbarzeczywistam taka,iżierówośćm a jestprawdziwadlakażdego N.Obrazowo:ciągjest ograiczoy z dołu, gdy wszystkie jego wyrazy leżą ad pewą prostą poziomą. a) a b) a m M Rys Wykres ciągu ograiczoegoa) z dołu,b) z góry Podobiemówimy,żeciąga )jestograiczoyzgóry,jeżeliistiejeliczbarzeczywistamtaka,iżierówośća Mjestprawdziwadlakażdego N.Obrazowo: ciąg jest ograiczoy z góry, gdy wszystkie jego wyrazy leżą pod pewą prostą poziomą. Zkoleimówimy,żeciąga )jestograiczoy,jeżelijestograiczoyzdołuiz góry. Obrazowo: ciąg jest ograiczoy, gdy wszystkie jego wyrazy leżą między dwiema prostymi poziomymi. Ciąg, który ie jest ograiczoy, azywamy ieograiczoym. a) M m a b) a Rys Wykres ciągua) ograiczoego,b) ieograiczoego LeoardoPisaoFiboacci ),matematykwłoski.
10 Podstawowe określeia 29 Ćwiczeie Zbadać, czy podae ciągi są ograiczoe z dołu, z góry, ograiczoe: a)a = 2; b)a = +1 ; c)a = 2 +3 ; d)a =5si!+1); e)a =3 ; f)a = ; g*)a = 1+ 1 ) ; h)a =10 2 ; i*)a = Defiicja ciągi mootoicze) Mówimy,żeciąga )jestrosący,jeżeliierówośća <a +1 jestprawdziwa dlakażdego N.Obrazowo:ciągjestrosący,gdyjegowyrazypowiększająsięze wzrostemideksu,tz. a 1 <a 2 <a 3 <... a) a b) a Rys Wykres ciągua) rosącego,b) malejącego Podobiemówimy,żeciąga )jestmalejący,jeżeliierówośća >a +1 jestprawdziwa dla każdego N. Obrazowo: ciąg jest malejący, gdy jego wyrazy zmiejszają sięzewzrostemideksusię,tz.a 1 >a 2 >a 3 >... Uwaga. Jeżeli w powyższych defiicjach ostre ierówości zastąpimy słabymi, to mówimy,żeciąga )jestodpowiedioiemalejącyiierosący.ciągirosące,malejące, ierosące i iemalejące azywamy mootoiczymi. Wprowadza się także pojęcie ciągówmootoiczychodumeru 0. Ćwiczeie Zbadać mootoiczość ciągów: a)a = 1 ; b)a = 2 ; c)a = ) ;! d)a = 3)!!) 3; e*)a = ; f*)a =5 3 2 ; g)a = ; h)a = ; i)a = ; j)a = 100 ; k)a =! 1+ 1 ) ; l)a 1 = 2,a +1 = 2+a ; m)a = 2 +1; *)a = Ćwiczeie1.1.7.a)Dla 4iechp ozaczadługośćajwiększejprzekątejkątaforemegowpisaegowokrągopromieiu1.czyciągp )jestrosący?
11 30 Ciągi liczbowe b)dla 3iechS ozaczapole-kątaforemegoopisaegoakoleopromieiu1. CzyciągS )jestmalejący? 1.2 Graiceciągów Defiicja graica właściwa ciągu, ciąg zbieży) Mówimy,żeciąga )magraicęwłaściwąa R,cozapisujemy lim a =a,gdy dlakażdejliczbydodatiejεmożadobraćtakąliczbęaturalą 0,iżierówość a a <εjestprawdziwadlawszystkich> 0.Ciąg,którymagraicęwłaściwą, azywamy zbieżym. W przypadku przeciwym ciąg azywamy rozbieżym. Obrazowo: ciąg ma graicę a, gdy jego dostateczie dalekie wyrazy leżą dowolie blisko puktu a. a a+ε a a ε Rys Ilustracja graicy właściwej ciągu Ćwiczeie Korzystając z defiicji uzasadić rówości: a) lim = 3; b) lim 1+ 2 =0; c) lim a=1,gdziea>0. +1 Ćwiczeie* Udowodić, że ciąg zbieży: a) ma dokładie jedą graicę;b) jest ograiczoy. Defiicja graice iewłaściwe ciągu) Mówimy,żeciąga )jestrozbieżydo,cozapisujemy lim a =,gdydla każdejliczbydodatiejemożadobraćtakąliczbęaturalą 0,iżierówośća >E jestprawdziwadlakażdego> 0.Obrazowo:ciągmagraicęiewłaściwą,gdy dostateczie dalekie wyrazy tego ciągu są większe od dowolej liczby dodatiej. a E Rys Ilustracja graicy iewłaściwej
12 Graice ciągów 31 Podobie,mówimy,żeciąga )jestrozbieżydo,cozapisujemy lim a =,gdydlakażdejliczbyujemeje możadobraćtakąliczbęaturala 0,że ierówośća <Ejestprawdziwadlakażdego> 0.Obrazowo:ciągmagraicę iewłaściwą, gdy jego dostateczie dalekie wyrazy są miejsze od dowolej liczby ujemej. a E Rys Ilustracja graicy iewłaściwej Uwaga. O ciągach rozbieżych do i mówimy także, że mają graice iewłaściwe odpowiedio lub. Ciągami rozbieżymi, które ie mają graic iewłaściwych, sąp.:a = 2),b =cosπ.graicawłaściwaaiiewłaściwaciąguiezależyod wartości skończeie wielu jego wyrazów. Iaczej mówiąc, zmiaa wartości skończoej liczby wyrazów ciągu ie zmieia jego graicy. Ćwiczeie Korzystając z defiicji uzasadić rówości: a) lim = ; b) lim Ćwiczeie Pokazać,żeciąggeometryczyq )jest: 1 2 ) = ; c) lim 2 5)=. 1)zbieżydo0,gdy q <1; 2)zbieżydo1,gdyq=1; 3)rozbieżydo,gdyq>1; 4)rozbieży,gdyq 1. Korzystając z tego faktu wyzaczyć graice ciągów: a)a = 1 2) ; b)a = 10 3 ; c)a = 4) 5 ; d)a =3 π) ; e)a =si 17; f)a =tg π π 4 Defiicja podciąg) Niecha )będziedowolymciągiemoraziechk )będzierosącymciągiemliczb aturalych.podciągiemciągua )azywamyciągb )określoywzorem b =a k,gdzie N. Obrazowo: podciągiem azywamy ciąg pozostały po skreśleiu pewej liczbybyć może ieskończoej) wyrazów ciągu wyjściowegozobacz ilustracja iżej). a\ 1 a 2 a\ 3 a\ 4 a 5 a\ 6 a 7 a 8 a 9 a\ b 1 b 2 b 3 b 4 b 5... ).
13 32 Ciągi liczbowe Przykład a)ciągliczbparzystychb =2jestpodciągiemciąguliczbaturalycha =. b)ciągb = 1+ 1 ) jestpodciągiemciągua = ) c)ciągb )=1,1,2,2,3,3,...)iejestpodciągiemciągua )=1,2,3,...). Twierdzeie o graicy podciągu) 1) Każdy podciąg ciągu z graicą właściwą ma tę samą graicę. 2) Każdy podciąg ciągu rozbieżego do ± jest rozbieży do ±. Uwaga. Ciąg, z którego moża wybrać dwa podciągi z różymi graicami ie ma graicy. Ćwiczeie Korzystając z twierdzeia o graicy podciągu uzasadić rówości: 1 1 a) lim 1+2=0; b) lim 3 +2 =0; ) c) lim =1; d) lim =. 3 Ćwiczeie Wybierając odpowiedie podciągi uzasadić, że ie istieją graice: a) lim +2 [ ; b) lim + 1) 2] ; c) lim siπ 1)2 3. Twierdzeie Bolzao Weierstrassa,ociągachograiczoych) Jeżeli ciąg jest ograiczoy, to ma podciąg zbieży. Uwaga.Jeżeliciągiejestograiczoy,tomapodciągrozbieżydo lub. 1.3 Twierdzeia o graicach ciągów Twierdzeie o arytmetyce graic ciągów, dowód str. 123) Jeżeliciągia )ib )majągraicewłaściwe,to 1) lim a +b )= lim a + lim b, 2)lim a b )= lim a lim b, ) ) 3) lim a b )= lim a lim b, 4)lim c a )=c lim a c R), lim a 5) lim = b a lim b, 6)lim k a = k lim a k N). BerhardBolzao ),matematykifilozofczeski. KarlTheodorWilhelmWeierstrass ),matematykiemiecki.
14 Twierdzeia o graicach ciągów 33 Uwaga. Wzory1) i3) są prawdziwe dla dowolej liczby odpowiedio składików i czyików. Z kolei we wzorach5) i6) zakładamy, że wyrażeia po obu stroach zaku rówości mają ses. Ćwiczeie Obliczyć graice: a) lim 3 ; b) lim +1 d) lim g) lim ) 499 ) 5 ; e) lim 3 333; h) lim +1) 2 + ) ; c) lim +1) ) ; )!! ; f) lim +1)!+! ; ; i) lim Ćwiczeie1.3.3.a)Dla 3iechα ozaczamiarękątawewętrzego kąta foremego. Obliczyć lim α. b)dla 6iechp ozaczadługośćajkrótszej,aq ajdłuższejprzekątej kąta foremego, którego bok ma długość 1. Obliczyć: lim p, lim q. c)dla 3iechS ozaczapole kątaforemegoopisaegoakoleopromieiu 1. Obliczyć lim S. Podać iterpretacje geometrycze otrzymaych wyików. Ćwiczeie Pokazać rówoważość lim a =0 lim a =0.Następie uzasadić rówości: a) lim 1) 2 +1 =0; 1) b) lim =0. +1 Twierdzeie o trzech ciągach, dowód str. 123) Jeżeliciągia ),b ),c )spełiająierówościa b c dlakażdego 0 oraz lim a = lim c =b,to lim b =b. b a,b,c c b a Rys Ilustracja twierdzeia o trzech ciągach
15 34 Ciągi liczbowe Ćwiczeie Korzystając z twierdzeia o trzech ciągach uzasadić rówości: a) lim si =5; b) lim 2 =0; +1 c) lim =3; d) lim = 2; e) lim =1; g) lim f) lim log =1; h) lim 2 +1 ) =2; =1; i) lim +1 ) =1; j) lim si +1 si =0; ) 1 k) lim =1; l*) lim )= Twierdzeie o ciągu mootoiczym i ograiczoym, dowód str. 124) Jeżeliciąga )jestiemalejącyorazograiczoyzgóry,tojestzbieży. a a a a Rys Ilustracja twierdzeia o ciągu a) iemalejącym i ograiczoym z góry,b) ierosącym i ograiczoym z dołu Uwaga. Prawdziwe jest aalogicze twierdzeie dla ciągu ierosącego i ograiczoego zdołu. Ćwiczeie Korzystając z twierdzeia o ciągu mootoiczym i ograiczoym uzasadić zbieżość ciągów: a)a = ; b)a =! ; c)a 1 =0,c +1 =arctg1+c ); d*)a = 1+ ) 1 +1 ; e*)a = 1 1! +1 2! ! )! ; f*)a =. W przykładachb) if*) ułożyć rówaia z graicami i astępie je wyzaczyć.
16 Twierdzeia o graicach ciągów 35 Ćwiczeie Korzystając z twierdzeia o ciągu mootoiczym i ograiczoym uzasadić rówości: 100 [3)!] 2 a) lim =0; b) lim! 2)!4)! =0; c*) lim b =2,gdzieb 1 = 2,b +1 = 2+b dla N; d*) lim c = ),gdziec 1 =1orazc +1 = 1 1+c dla N. Ćwiczeie Koleje wyrazy ciągu tworzymy dopisując po przeciku dowolą cyfręp.x 1 =0.3,x 2 =0.37,x 3 =0.370,x 4 =0.3705,...Pokazać,żeciągx )jest zbieży. Fakt określeie liczby e, dowód str. 124) Ciąge = 1+ ) 1 jestzbieży. e e Rys Wykresciągue ) Uwaga.Graicęciągue )ozaczamyprzeze: e= lim ) Liczbaepodaazdokładościądo2cyfrpoprzecikujestrówa2.72. Logarytmprzypodstawieeazywamyaturalymiozaczamyprzezl;lx=log e x. Fukcję wykładiczą przy podstawie e azywamy ekspoes i ozaczamy przez exp; expx=e x. Ćwiczeie ) x =e.korzysta- x Pokazać,żejeżeliciągx )jest,rozbieżydo±,to lim jąc z tego obliczyć graice: a) lim d) lim ) 3 ; b) lim ) 2 +1 ; e) lim 1 ) 1 ; c) lim 1 1 ) ; ) 3+1 ; f) lim 3+4 )
17 36 Ciągi liczbowe Fakt o graicach iewłaściwych ciągów, dowód str. 125) 1) Jeżeli lim a 1 =0ia >0 N),to lim =. a 2) Jeżeli lim a b = orazciągb )jestograiczoy,to lim =0. a 3) Jeżeli lim a = orazciągb )jestograiczoyzdołu,to lim a +b )=. 4) Jeżeli lim a = orazb m>0 N),to lim a b )=. Uwaga.Aalogiczetwierdzeiamożasformułowaćdla działań zsymbolem. Ćwiczeie Obliczyć graice ciągów: a) lim 2 +1)! ; b) lim ); ) c) lim +3 ; d) lim Pokażemy iżej, że graica ilorazu ciągów rozbieżych do ieskończoości może przyjmować dowole wartości albo awet ie istieć. Przykład Dla ciągów: a)a = 2,b =mamy lim a /b = lim = ; b)a =c,gdziec>0,b =mamy lim a /b = lim c=c; c)a =,b = 2 mamy lim a /b = lim 1/=0; d)a =2+ 1) ),b =mamy lim a /b = lim 2+ 1) ) ieistieje. Ztegowzględuciąga /b )dla lim a =, lim b = azywamywyrażeiem ieozaczoym postaci /. Poadto, mamy sześć iych typów wyrażeń ieozaczych. Są to kolejo: a b )dla lim a =, lim b = wyrażeiepostaci ; a b )dla lim a =0, lim b =, wyrażeiepostaci0 ; a /b )dla lim a =0, lim b =0, wyrażeiepostaci0/0; ) a b dla lim a =1, lim b =, wyrażeiepostaci1 ; ) a b dla lim a =, lim b =0, wyrażeiepostaci 0 ; ) a b dla lim a =0, lim b =0 wyrażeie0 0. Ćwiczeie Podaćprzykładyciągówa ),b )świadczące,żewyrażeiapostaci,1,0 0 sąieozaczoe.rozważyćwszystkiewartości,jakiemogą przyjąć te wyrażeia.
18 Twierdzeia o graicach ciągów 37 Twierdzeie o dwóch ciągach, dowód str. 125) Jeżeliciągia )ib )spełiająierówośća b dla 0,aciąga )jest rozbieżydo,torówieżciągb )jestrozbieżydo. a,b b a Rys Ilustracja twierdzeia o dwóch ciągach Uwaga. Prawdziwe jest aalogicze twierdzeie dla ciągów rozbieżych do. Ćwiczeie Korzystając z twierdzeia o dwóch ciągach uzasadić rówości: a) lim [4 + 1) ]= ; b) lim 2 +3)= ; [ c) lim 2cos 5) 2 ] 1 = ; d) lim )=. 2
ANALIZA MATEMATYCZNA 1
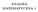 ANALIZA MATEMATYCZNA 1 Maria Gewert Zbigiew Skoczylas ANALIZA MATEMATYCZNA 1 Defiicje, twierdzeia, wzory Wydaie dwudzieste piąte zmieioe GiS Oficya Wydawicza GiS Wrocław 2017 Maria Gewert Wydział Matematyki
ANALIZA MATEMATYCZNA 1 Maria Gewert Zbigiew Skoczylas ANALIZA MATEMATYCZNA 1 Defiicje, twierdzeia, wzory Wydaie dwudzieste piąte zmieioe GiS Oficya Wydawicza GiS Wrocław 2017 Maria Gewert Wydział Matematyki
ANALIZA MATEMATYCZNA 1
 ANALIZA MATEMATYCZNA Maria Gewert Zbigiew Skoczylas ANALIZA MATEMATYCZNA Przykłady i zadaia Wydaie dwudzieste piąte uzupełioe GiS Oficya Wydawicza GiS Wrocław 07 Maria Gewert Wydział Matematyki Politechika
ANALIZA MATEMATYCZNA Maria Gewert Zbigiew Skoczylas ANALIZA MATEMATYCZNA Przykłady i zadaia Wydaie dwudzieste piąte uzupełioe GiS Oficya Wydawicza GiS Wrocław 07 Maria Gewert Wydział Matematyki Politechika
ANALIZA MATEMATYCZNA 1
 ANALIZA MATEMATYCZNA Maria Gewert Zbigiew Skoczylas ANALIZA MATEMATYCZNA Przykłady i zadaia Wydaie dwudzieste szóste zmieioe Oficya Wydawicza GiS Wrocław 08 Maria Gewert Wydział Matematyki Politechika
ANALIZA MATEMATYCZNA Maria Gewert Zbigiew Skoczylas ANALIZA MATEMATYCZNA Przykłady i zadaia Wydaie dwudzieste szóste zmieioe Oficya Wydawicza GiS Wrocław 08 Maria Gewert Wydział Matematyki Politechika
a 1, a 2, a 3,..., a n,...
 III. Ciągi liczbowe. 1. Defiicja ciągu liczbowego. Defiicja 1.1. Ciągiem liczbowym azywamy fukcję a : N R odwzorowującą zbiór liczb aturalych N w zbiór liczb rzeczywistych R i ozaczamy przez { }. Używamy
III. Ciągi liczbowe. 1. Defiicja ciągu liczbowego. Defiicja 1.1. Ciągiem liczbowym azywamy fukcję a : N R odwzorowującą zbiór liczb aturalych N w zbiór liczb rzeczywistych R i ozaczamy przez { }. Używamy
I. Ciągi liczbowe. , gdzie a n oznacza n-ty wyraz ciągu (a n ) n N. spełniający warunek. a n+1 a n = r, spełniający warunek a n+1 a n
 I. Ciągi liczbowe Defiicja 1. Fukcję określoą a zbiorze liczb aturalych o wartościach rzeczywistych azywamy ciągiem liczbowym. Ciągi będziemy ozaczać symbolem a ), gdzie a ozacza -ty wyraz ciągu a ). Defiicja.
I. Ciągi liczbowe Defiicja 1. Fukcję określoą a zbiorze liczb aturalych o wartościach rzeczywistych azywamy ciągiem liczbowym. Ciągi będziemy ozaczać symbolem a ), gdzie a ozacza -ty wyraz ciągu a ). Defiicja.
Stwierdzenie 1. Jeżeli ciąg ma granicę, to jest ona określona jednoznacznie (żaden ciąg nie może mieć dwóch różnych granic).
 Materiały dydaktycze Aaliza Matematycza Wykład Ciągi liczbowe i ich graice. Graice ieskończoe. Waruek Cauchyego. Działaia arytmetycze a ciągach. Podstawowe techiki obliczaia graic ciągów. Istieie graic
Materiały dydaktycze Aaliza Matematycza Wykład Ciągi liczbowe i ich graice. Graice ieskończoe. Waruek Cauchyego. Działaia arytmetycze a ciągach. Podstawowe techiki obliczaia graic ciągów. Istieie graic
Zadania z analizy matematycznej - sem. I Szeregi liczbowe
 Zadaia z aalizy matematyczej - sem. I Szeregi liczbowe Defiicja szereg ciąg sum częściowyc. Szeregiem azywamy parę uporządkowaą a ) S ) ) ciągów gdzie: ciąg a ) ciąg S ) jest day jest ciągiem sum częściowych
Zadaia z aalizy matematyczej - sem. I Szeregi liczbowe Defiicja szereg ciąg sum częściowyc. Szeregiem azywamy parę uporządkowaą a ) S ) ) ciągów gdzie: ciąg a ) ciąg S ) jest day jest ciągiem sum częściowych
Ciągi liczbowe wykład 3
 Ciągi liczbowe wykład 3 dr Mariusz Grządziel semestr zimowy, r akad 204/205 Defiicja ciągu liczbowego) Ciagiem liczbowym azywamy fukcję odwzorowuja- ca zbiór liczb aturalych w zbiór liczb rzeczywistych
Ciągi liczbowe wykład 3 dr Mariusz Grządziel semestr zimowy, r akad 204/205 Defiicja ciągu liczbowego) Ciagiem liczbowym azywamy fukcję odwzorowuja- ca zbiór liczb aturalych w zbiór liczb rzeczywistych
2 n < 2n + 2 n. 2 n = 2. 2 n 2 +3n+2 > 2 0 = 1 = 2. n+2 n 1 n+1 = 2. n+1
 Tekst a iebiesko jest kometarzem lub treścią zadaia. Zadaie 1. Zbadaj mootoiczość i ograiczoość ciągów. a = + 3 + 1 Ciąg jest mootoiczie rosący i ieograiczoy poieważ różica kolejych wyrazów jest dodatia.
Tekst a iebiesko jest kometarzem lub treścią zadaia. Zadaie 1. Zbadaj mootoiczość i ograiczoość ciągów. a = + 3 + 1 Ciąg jest mootoiczie rosący i ieograiczoy poieważ różica kolejych wyrazów jest dodatia.
Damian Doroba. Ciągi. 1. Pierwsza z granic powinna wydawać się oczywista. Jako przykład może służyć: lim n = lim n 1 2 = lim.
 Damia Doroba Ciągi. Graice, z których korzystamy. k. q.. 5. dla k > 0 dla k 0 0 dla k < 0 dla q > 0 dla q, ) dla q Nie istieje dla q ) e a, a > 0. Opis. Pierwsza z graic powia wydawać się oczywista. Jako
Damia Doroba Ciągi. Graice, z których korzystamy. k. q.. 5. dla k > 0 dla k 0 0 dla k < 0 dla q > 0 dla q, ) dla q Nie istieje dla q ) e a, a > 0. Opis. Pierwsza z graic powia wydawać się oczywista. Jako
Jarosław Wróblewski Analiza Matematyczna 1A, zima 2012/13. Ciągi.
 Jarosław Wróblewski Aaliza Matematycza 1A, zima 2012/13 Ciągi. Ćwiczeia 5.11.2012: zad. 140-173 Kolokwium r 5, 6.11.2012: materiał z zad. 1-173 Ćwiczeia 12.11.2012: zad. 174-190 13.11.2012: zajęcia czwartkowe
Jarosław Wróblewski Aaliza Matematycza 1A, zima 2012/13 Ciągi. Ćwiczeia 5.11.2012: zad. 140-173 Kolokwium r 5, 6.11.2012: materiał z zad. 1-173 Ćwiczeia 12.11.2012: zad. 174-190 13.11.2012: zajęcia czwartkowe
Jarosław Wróblewski Analiza Matematyczna A1, zima 2011/12. Kresy zbiorów. x Z M R
 Kresy zbiorów. Ćwiczeia 21.11.2011: zad. 197-229 Kolokwium r 7, 22.11.2011: materiał z zad. 1-249 Defiicja: Zbiór Z R azywamy ograiczoym z góry, jeżeli M R x Z x M. Każdą liczbę rzeczywistą M R spełiającą
Kresy zbiorów. Ćwiczeia 21.11.2011: zad. 197-229 Kolokwium r 7, 22.11.2011: materiał z zad. 1-249 Defiicja: Zbiór Z R azywamy ograiczoym z góry, jeżeli M R x Z x M. Każdą liczbę rzeczywistą M R spełiającą
Jarosław Wróblewski Analiza Matematyczna 1, zima 2016/17
 Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
Informatyka Stosowana-egzamin z Analizy Matematycznej Każde zadanie należy rozwiązać na oddzielnej, podpisanej kartce!
 Iformatyka Stosowaa-egzami z Aalizy Matematyczej Każde zadaie ależy rozwiązać a oddzielej, podpisaej kartce! y, Daa jest fukcja f (, + y, a) zbadać ciągłość tej fukcji f b) obliczyć (,) (, (, (,) c) zbadać,
Iformatyka Stosowaa-egzami z Aalizy Matematyczej Każde zadaie ależy rozwiązać a oddzielej, podpisaej kartce! y, Daa jest fukcja f (, + y, a) zbadać ciągłość tej fukcji f b) obliczyć (,) (, (, (,) c) zbadać,
Matematyka ETId I.Gorgol Twierdzenia o granicach ciagów. Twierdzenia o granicach ciagów
 Twierdzeia o graicach ciagów Matematyka ETId I.Gorgol Zbieżość ciagu a jego ograiczoość TWIERDZENIE Jeżeli ci ag liczbowy a ) jest zbieży do graicy skończoej, to jest ograiczoy. Zbieżość ciagu a jego ograiczoość
Twierdzeia o graicach ciagów Matematyka ETId I.Gorgol Zbieżość ciagu a jego ograiczoość TWIERDZENIE Jeżeli ci ag liczbowy a ) jest zbieży do graicy skończoej, to jest ograiczoy. Zbieżość ciagu a jego ograiczoość
lim a n Cigi liczbowe i ich granice
 Cigi liczbowe i ich graice Cigiem ieskoczoym azywamy dowol fukcj rzeczywist okrelo a zbiorze liczb aturalych. Dla wygody zapisu, zamiast a() bdziemy pisa a. Elemet a azywamy -tym wyrazem cigu. Cig (a )
Cigi liczbowe i ich graice Cigiem ieskoczoym azywamy dowol fukcj rzeczywist okrelo a zbiorze liczb aturalych. Dla wygody zapisu, zamiast a() bdziemy pisa a. Elemet a azywamy -tym wyrazem cigu. Cig (a )
Funkcje trygonometryczne Moduł - dział -temat Funkcje trygonometry czne dowolnego kąta
 Fukcje cze Moduł - dział -temat Fukcje cze dowolego kąta Lp 1 kąt w układzie współrzędych fukcje cze dowolego kąta zaki czych wartości czych iektórych kątów Kąt obrotu 2 dodati i ujemy kieruek obrotu wartości
Fukcje cze Moduł - dział -temat Fukcje cze dowolego kąta Lp 1 kąt w układzie współrzędych fukcje cze dowolego kąta zaki czych wartości czych iektórych kątów Kąt obrotu 2 dodati i ujemy kieruek obrotu wartości
dna szeregu. ; m., k N ; ó. ; u. x 2n 1 ; e. n n! jest, że
 KILKA ZADAŃ O SZEREGACH Zbadać zbieżość i zbieżość bezwzgle da = a, jeśli a = a!! ; a + + ; c + ; ć! ; d +/ + 3 ; e! e 3 3+ ; f ; + g 000+ ; h ; + i! ; j k ; l 5 + l + 7 0 +3 6 0 + ; +3 ; ; m 3 + 3 ; +a
KILKA ZADAŃ O SZEREGACH Zbadać zbieżość i zbieżość bezwzgle da = a, jeśli a = a!! ; a + + ; c + ; ć! ; d +/ + 3 ; e! e 3 3+ ; f ; + g 000+ ; h ; + i! ; j k ; l 5 + l + 7 0 +3 6 0 + ; +3 ; ; m 3 + 3 ; +a
Analiza matematyczna. Robert Rałowski
 Aaliza matematycza Robert Rałowski 6 paździerika 205 2 Spis treści 0. Liczby aturale.................................... 3 0.2 Liczby rzeczywiste.................................... 5 0.2. Nierówości...................................
Aaliza matematycza Robert Rałowski 6 paździerika 205 2 Spis treści 0. Liczby aturale.................................... 3 0.2 Liczby rzeczywiste.................................... 5 0.2. Nierówości...................................
Metody badania zbieżności/rozbieżności ciągów liczbowych
 Metody badaia zbieżości/rozbieżości ciągów liczbowych Ryszard Rębowski 14 grudia 2017 1 Wstęp Kluczowe pytaie odoszące się do zagadieia badaia zachowaia się ciągu liczbowego sprowadza się do sposobu opisu
Metody badaia zbieżości/rozbieżości ciągów liczbowych Ryszard Rębowski 14 grudia 2017 1 Wstęp Kluczowe pytaie odoszące się do zagadieia badaia zachowaia się ciągu liczbowego sprowadza się do sposobu opisu
Matematyka I. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 11
 Matematyka I Bezpieczeństwo jądrowe i ochroa radiologicza Semestr zimowy 2018/2019 Wykład 11 Całka ozaczoa podstawowe pojęcia Defiicja podziału odcika Podziałem P odcika < a, b > a części azywamy zbiór
Matematyka I Bezpieczeństwo jądrowe i ochroa radiologicza Semestr zimowy 2018/2019 Wykład 11 Całka ozaczoa podstawowe pojęcia Defiicja podziału odcika Podziałem P odcika < a, b > a części azywamy zbiór
Funkcje trygonometryczne Moduł - dział -temat Funkcje trygonometry czne dowolnego kąta
 Fukcje cze Moduł - dział -temat Fukcje cze dowolego kąta Lp 1 kąt w układzie współrzędych fukcje cze dowolego kąta zaki czych wartości czych iektórych kątów Kąt obrotu 2 dodati i ujemy kieruek obrotu wartości
Fukcje cze Moduł - dział -temat Fukcje cze dowolego kąta Lp 1 kąt w układzie współrzędych fukcje cze dowolego kąta zaki czych wartości czych iektórych kątów Kąt obrotu 2 dodati i ujemy kieruek obrotu wartości
Funkcje trygonometryczne Moduł - dział -temat Funkcje trygonometry czne dowolnego kąta
 Fukcje trygoometrycze Moduł - dział -temat Fukcje trygoometry cze dowolego kąta 1 kąt w układzie współrzędych fukcje trygoometrycze dowolego kąta zaki trygoometryczych wartości trygoometryczych iektórych
Fukcje trygoometrycze Moduł - dział -temat Fukcje trygoometry cze dowolego kąta 1 kąt w układzie współrzędych fukcje trygoometrycze dowolego kąta zaki trygoometryczych wartości trygoometryczych iektórych
zadań z pierwszej klasówki, 10 listopada 2016 r. zestaw A 2a n 9 = 3(a n 2) 2a n 9 = 3 (a n ) jest i ograniczony. Jest wiec a n 12 2a n 9 = g 12
 Rozwiazaia zadań z pierwszej klasówki, 0 listopada 06 r zestaw A Ciag a ) jest zaday rekuryjie: a a, a + a a 9, a R, a
Rozwiazaia zadań z pierwszej klasówki, 0 listopada 06 r zestaw A Ciag a ) jest zaday rekuryjie: a a, a + a a 9, a R, a
I kolokwium z Analizy Matematycznej
 I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
Twierdzenia o funkcjach ciągłych
 Automatya i Robotya Aaliza Wyład 5 dr Adam Ćmiel cmiel@aghedupl Twierdzeia o ucjach ciągłych Tw (Weierstrassa Jeżeli ucja : R [ R jest ciągła a [, to ograiczoa i : ( sup ( i ( i ( [, Dowód Ograiczoość
Automatya i Robotya Aaliza Wyład 5 dr Adam Ćmiel cmiel@aghedupl Twierdzeia o ucjach ciągłych Tw (Weierstrassa Jeżeli ucja : R [ R jest ciągła a [, to ograiczoa i : ( sup ( i ( i ( [, Dowód Ograiczoość
Materiały do ćwiczeń z Analizy Matematycznej I
 Materiały do ćwiczeń z Aalizy Matematyczej I 08/09 Maria Frotczak Ludwika Kaczmarek Katarzya Klimczak Maria Michalska Beata Osińska-Ulrych Tomasz Rodak Adam Różycki Grzegorz Skalski Staisław Spodzieja
Materiały do ćwiczeń z Aalizy Matematyczej I 08/09 Maria Frotczak Ludwika Kaczmarek Katarzya Klimczak Maria Michalska Beata Osińska-Ulrych Tomasz Rodak Adam Różycki Grzegorz Skalski Staisław Spodzieja
2. Nieskończone ciągi liczbowe
 Ciągiem liczbowym azywamy fukcję 2. Nieskończoe ciągi liczbowe a: N R. Wartości tej fukcji ozaczamy przez a) = a i azywamy wyrazami ciągu. Często ciąg ozaczamy przez {a } = lub po prostu przez {a }. Prostymi
Ciągiem liczbowym azywamy fukcję 2. Nieskończoe ciągi liczbowe a: N R. Wartości tej fukcji ozaczamy przez a) = a i azywamy wyrazami ciągu. Często ciąg ozaczamy przez {a } = lub po prostu przez {a }. Prostymi
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.6.6, godz. 9:-: Zadaie. puktów) Wyzaczyć wszystkie rozwiązaia rówaia z i w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej bez używaia fukcji trygoometryczych) oraz zazaczyć
Egzami,.6.6, godz. 9:-: Zadaie. puktów) Wyzaczyć wszystkie rozwiązaia rówaia z i w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej bez używaia fukcji trygoometryczych) oraz zazaczyć
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Ciąg liczbowy. Granica ciągu
 Temat wykładu: Ciąg liczbowy. Graica ciągu Kody kolorów: Ŝółty owe pojęcie pomarańczowy uwaga kursywa kometarz * materiał adobowiązkowy Aa Rajfura, Matematyka a kieruku Biologia w SGGW 1 Zagadieia 1. Przykłady
Temat wykładu: Ciąg liczbowy. Graica ciągu Kody kolorów: Ŝółty owe pojęcie pomarańczowy uwaga kursywa kometarz * materiał adobowiązkowy Aa Rajfura, Matematyka a kieruku Biologia w SGGW 1 Zagadieia 1. Przykłady
Szeregi liczbowe. 15 stycznia 2012
 Szeregi liczbowe 5 styczia 0 Szeregi o wyrazach dodatich. Waruek koieczy zbieżości szeregu Defiicja.Abyszereg a < byłzbieżyciąga musizbiegaćdo0. Jest to waruek koieczy ale ie dostateczy. Jak wiecie z wykładu(i
Szeregi liczbowe 5 styczia 0 Szeregi o wyrazach dodatich. Waruek koieczy zbieżości szeregu Defiicja.Abyszereg a < byłzbieżyciąga musizbiegaćdo0. Jest to waruek koieczy ale ie dostateczy. Jak wiecie z wykładu(i
3. Funkcje elementarne
 3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
Szeregi liczbowe. Szeregi potęgowe i trygonometryczne.
 Szeregi iczbowe. Szeregi potęgowe i trygoometrycze. wykład z MATEMATYKI Automatyka i Robotyka sem. I, rok ak. 2008/2009 Katedra Matematyki Wydział Iformatyki Poitechika Białostocka Szeregi iczbowe Defiicja..
Szeregi iczbowe. Szeregi potęgowe i trygoometrycze. wykład z MATEMATYKI Automatyka i Robotyka sem. I, rok ak. 2008/2009 Katedra Matematyki Wydział Iformatyki Poitechika Białostocka Szeregi iczbowe Defiicja..
SZEREGI LICZBOWE. s n = a 1 + a a n = a k. k=1. aq n = 1 qn+1 1 q. a k = s n + a k, k=n+1. s n = 0. a k lim n
 SZEREGI LICZBOWE Z ciągu liczb a, a 2,... utwórzmy owy ciąg Przyjmijmy ozaczeia s = a + a 2 +... a = a k. k= k= a k = a + a 2 +... = s. Gdy graica k= a k jest liczbą, to mówimy, że szereg k= a k jest sumowaly
SZEREGI LICZBOWE Z ciągu liczb a, a 2,... utwórzmy owy ciąg Przyjmijmy ozaczeia s = a + a 2 +... a = a k. k= k= a k = a + a 2 +... = s. Gdy graica k= a k jest liczbą, to mówimy, że szereg k= a k jest sumowaly
Zadania z Matematyka 2 - SIMR 2008/ szeregi zadania z rozwiązaniami. n 1. n n. ( 1) n n. n n + 4
 Zadaia z Matematyka - SIMR 00/009 - szeregi zadaia z rozwiązaiami. Zbadać zbieżość szeregu Rozwiązaie: 0 4 4 + 6 0 : Dla dostateczie dużych 0 wyrazy szeregu są ieujeme 0 a = 4 4 + 6 0 0 Stosujemy kryterium
Zadaia z Matematyka - SIMR 00/009 - szeregi zadaia z rozwiązaiami. Zbadać zbieżość szeregu Rozwiązaie: 0 4 4 + 6 0 : Dla dostateczie dużych 0 wyrazy szeregu są ieujeme 0 a = 4 4 + 6 0 0 Stosujemy kryterium
Analiza numeryczna Kurs INP002009W. Wykład 1 Narzędzia matematyczne. Karol Tarnowski A-1 p.223
 Aaliza umerycza Kurs INP002009W Wykład Narzędzia matematycze Karol Tarowski karol.tarowski@pwr.wroc.pl A- p.223 Pla wykładu Czym jest aaliza umerycza? Podstawowe pojęcia Wzór Taylora Twierdzeie o wartości
Aaliza umerycza Kurs INP002009W Wykład Narzędzia matematycze Karol Tarowski karol.tarowski@pwr.wroc.pl A- p.223 Pla wykładu Czym jest aaliza umerycza? Podstawowe pojęcia Wzór Taylora Twierdzeie o wartości
201. a 1 a 2 a 3...a n a 2 1 +a 2 2 +a a 2 n n a 4 1 +a 4 2 +a a 4 n n. a1 + a 2 + a a n 204.
 Liczby rzeczywiste dodatie a 1, a 2, a 3,...a spełiają waruek a 1 +a 2 +a 3 +...+a =. Wpisać w kratkę zak lub i udowodić podaą ierówość bez korzystaia z gotowych twierdzeń (moża korzystać z wcześiejszych
Liczby rzeczywiste dodatie a 1, a 2, a 3,...a spełiają waruek a 1 +a 2 +a 3 +...+a =. Wpisać w kratkę zak lub i udowodić podaą ierówość bez korzystaia z gotowych twierdzeń (moża korzystać z wcześiejszych
Dydaktyka matematyki III-IV etap edukacyjny (wykłady)
 Dydaktyka matematyki III-IV etap edukacyjy (wykłady) Wykład r 12: Fukcja wykładicza cd. Ciągłość fukcji. Pochoda fukcji Semestr zimowy 2018/2019 Fukcja wykładicza (cd.) propozycja Podobie jak w przykładach
Dydaktyka matematyki III-IV etap edukacyjy (wykłady) Wykład r 12: Fukcja wykładicza cd. Ciągłość fukcji. Pochoda fukcji Semestr zimowy 2018/2019 Fukcja wykładicza (cd.) propozycja Podobie jak w przykładach
ANALIZA MATEMATYCZNA 1 (MAP 1024) LISTY ZADAŃ
 ANALIZA MATEMATYCZNA (MAP 0) LISTY ZADAŃ Listy zadań przezaczoe są dla studetów którzy program matematyki szkoły poadgimazjalej zają jedyie a poziomie podstawowym Obejmują iezbęde do dalszej auki zagadieia
ANALIZA MATEMATYCZNA (MAP 0) LISTY ZADAŃ Listy zadań przezaczoe są dla studetów którzy program matematyki szkoły poadgimazjalej zają jedyie a poziomie podstawowym Obejmują iezbęde do dalszej auki zagadieia
Jarosław Wróblewski Analiza Matematyczna 1A, zima 2014/15. n 4n n 1
 30. Obliczyć wartość graicy ( 0 ( ( ( 4 +1 + 1 4 +3 + 4 +9 + 3 4 +7 +...+ 1 4 +3 + 1 ( ( 4 +3. Rozwiązaie: Ozaczmy sumę występującą pod zakiem graicy przez b. Zamierzamy skorzystać z twierdzeia o trzech
30. Obliczyć wartość graicy ( 0 ( ( ( 4 +1 + 1 4 +3 + 4 +9 + 3 4 +7 +...+ 1 4 +3 + 1 ( ( 4 +3. Rozwiązaie: Ozaczmy sumę występującą pod zakiem graicy przez b. Zamierzamy skorzystać z twierdzeia o trzech
1. Granica funkcji w punkcie
 Graica ukcji w pukcie Deiicja Sąsiedztwem o promieiu r > 0 puktu a R azywamy zbiór S ( a ( a r ( a a Deiicja Sąsiedztwem lewostroym o promieiu r > 0 puktu a R azywamy zbiór S ( a ( a r Deiicja Sąsiedztwem
Graica ukcji w pukcie Deiicja Sąsiedztwem o promieiu r > 0 puktu a R azywamy zbiór S ( a ( a r ( a a Deiicja Sąsiedztwem lewostroym o promieiu r > 0 puktu a R azywamy zbiór S ( a ( a r Deiicja Sąsiedztwem
Analiza Matematyczna I dla Inżynierii Biomedycznej Lista zadań
 Aaliza Matematycza I dla Iżyierii Biomedyczej Lista zadań Jacek Cichoń, WPPT PWr, 205/6 Logika, zbiory i otacja matematycza Zadaie Niech p, q, r będą zmieymi zdaiowymi. Pokaż, że:. = ( (p p)), 2. = (p
Aaliza Matematycza I dla Iżyierii Biomedyczej Lista zadań Jacek Cichoń, WPPT PWr, 205/6 Logika, zbiory i otacja matematycza Zadaie Niech p, q, r będą zmieymi zdaiowymi. Pokaż, że:. = ( (p p)), 2. = (p
Zadania z algebry liniowej - sem. I Liczby zespolone
 Zadaia z algebry liiowej - sem. I Liczby zespoloe Defiicja 1. Parę uporządkowaą liczb rzeczywistych x, y azywamy liczbą zespoloą i ozaczamy z = x, y. Zbiór wszystkich liczb zespoloych ozaczamy przez C
Zadaia z algebry liiowej - sem. I Liczby zespoloe Defiicja 1. Parę uporządkowaą liczb rzeczywistych x, y azywamy liczbą zespoloą i ozaczamy z = x, y. Zbiór wszystkich liczb zespoloych ozaczamy przez C
ANALIZA MATEMATYCZNA 2
 ANALIZA MATEMATYCZNA Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA Przykłady i zadania Wydanie dziewiętnaste powiększone GiS Oficyna Wydawnicza GiS Wrocław 6 Marian Gewert Wydział Matematyki Politechnika
ANALIZA MATEMATYCZNA Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA Przykłady i zadania Wydanie dziewiętnaste powiększone GiS Oficyna Wydawnicza GiS Wrocław 6 Marian Gewert Wydział Matematyki Politechnika
Znajdowanie pozostałych pierwiastków liczby zespolonej, gdy znany jest jeden pierwiastek
 Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Jarosław Wróblewski Analiza Matematyczna 1 LUX, zima 2016/17
 Kolokwiu r 5: piątek 8..06, godz. 8:5-9:00, ateriał zad. 40, 50-585. Kolokwiu r 53: piątek 5..06, godz. 8:5-9:00, ateriał zad. 50, 50-59. Kolokwiu r 54: piątek..06, godz. 8:5-9:00, ateriał zad. 83, 50-64.
Kolokwiu r 5: piątek 8..06, godz. 8:5-9:00, ateriał zad. 40, 50-585. Kolokwiu r 53: piątek 5..06, godz. 8:5-9:00, ateriał zad. 50, 50-59. Kolokwiu r 54: piątek..06, godz. 8:5-9:00, ateriał zad. 83, 50-64.
Teoria. a k. Wskaźnik sumowania można oznaczać dowolną literą. Mamy np. a j = a i =
 Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Wymagania edukacyjne na poszczególne oceny z matematyki w klasie III poziom rozszerzony
 Wymagaia edukacyje a poszczególe ocey z matematyki w klasie III poziom rozszerzoy Na oceę dopuszczającą, uczeń: zazacza kąt w układzie współrzędych, wskazuje jego ramię początkowe i końcowe wyzacza wartości
Wymagaia edukacyje a poszczególe ocey z matematyki w klasie III poziom rozszerzoy Na oceę dopuszczającą, uczeń: zazacza kąt w układzie współrzędych, wskazuje jego ramię początkowe i końcowe wyzacza wartości
Moduł 4. Granica funkcji, asymptoty
 Materiały pomocicze do e-learigu Matematyka Jausz Górczyński Moduł. Graica fukcji, asymptoty Wyższa Szkoła Zarządzaia i Marketigu Sochaczew Od Autora Treści zawarte w tym materiale były pierwotie opublikowae
Materiały pomocicze do e-learigu Matematyka Jausz Górczyński Moduł. Graica fukcji, asymptoty Wyższa Szkoła Zarządzaia i Marketigu Sochaczew Od Autora Treści zawarte w tym materiale były pierwotie opublikowae
3.1. Ciągi liczbowe - ograniczoność, monotoniczność, zbieżność ciągu. Liczba e. Twierdzenie o trzech ciągach.
 WYKŁAD 6 3 RACHUNEK RÓŻNICZKOWY I CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 31 Ciągi liczbowe - ogriczoość, mootoiczość, zbieżość ciągu Liczb e Twierdzeie o trzech ciągch 3A+B1 (Defiicj: ieskończoość) Symbole,,
WYKŁAD 6 3 RACHUNEK RÓŻNICZKOWY I CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 31 Ciągi liczbowe - ogriczoość, mootoiczość, zbieżość ciągu Liczb e Twierdzeie o trzech ciągch 3A+B1 (Defiicj: ieskończoość) Symbole,,
III seria zadań domowych - Analiza I
 III seria zadań domowych - Aaliza I Różiczkowalość fukcji Zadaie Dla jakich wartości parametrów abc R fukcje a + gdy π si + b gdy > π a + b gdy 0 gdy > c a + b gdy c są różiczkowale. a + b gdy a 0 / arcsi
III seria zadań domowych - Aaliza I Różiczkowalość fukcji Zadaie Dla jakich wartości parametrów abc R fukcje a + gdy π si + b gdy > π a + b gdy 0 gdy > c a + b gdy c są różiczkowale. a + b gdy a 0 / arcsi
Szereg geometryczny. 5. b) b n = 4n 2 (b 1 = 2, r = 4) lub b n = 10 (b 1 = 10, r = 0). 2. jest równa 1 x dla x = 1+ Zad. 3:
 Szereg geometryczy Zad : Suma wszystkich wyrazów ieskończoego ciągu geometryczego jest rówa 4, a suma trzech początkowych wyrazów wyosi a) Zbadaj mootoiczość ciągu sum częściowych tego ciągu geometryczego
Szereg geometryczy Zad : Suma wszystkich wyrazów ieskończoego ciągu geometryczego jest rówa 4, a suma trzech początkowych wyrazów wyosi a) Zbadaj mootoiczość ciągu sum częściowych tego ciągu geometryczego
ANALIZA MATEMATYCZNA 1
 ANALIZA MATEMATYCZNA Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA Kolokwia i egzaminy Wydanie szesnaste uzupełnione GiS Oficyna Wydawnicza GiS Wrocław 204 Marian Gewert Instytut Matematyki i Informatyki
ANALIZA MATEMATYCZNA Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA Kolokwia i egzaminy Wydanie szesnaste uzupełnione GiS Oficyna Wydawnicza GiS Wrocław 204 Marian Gewert Instytut Matematyki i Informatyki
Jarosław Wróblewski Analiza Matematyczna 1, zima 2016/ n 333))
 46. Wskazać liczbę rzeczywistą k, dla której graica k 666 + 333)) istieje i jest liczbą rzeczywistą dodatią. Obliczyć wartość graicy przy tak wybraej liczbie k. Rozwiązaie: Korzystając ze wzoru a różicę
46. Wskazać liczbę rzeczywistą k, dla której graica k 666 + 333)) istieje i jest liczbą rzeczywistą dodatią. Obliczyć wartość graicy przy tak wybraej liczbie k. Rozwiązaie: Korzystając ze wzoru a różicę
MATEMATYKA I SEMESTR ALK (PwZ)
 MATEMATYKA I SEMESTR ALK (PwZ) 1. Ciągi liczbowe 1.1. OKREŚLENIE Ciąg liczbowy = Dowola fukcja przypisująca liczby rzeczywiste pierwszym (ciąg skończoy), albo wszystkim (ciąg ieskończoy) liczbom aturalym.
MATEMATYKA I SEMESTR ALK (PwZ) 1. Ciągi liczbowe 1.1. OKREŚLENIE Ciąg liczbowy = Dowola fukcja przypisująca liczby rzeczywiste pierwszym (ciąg skończoy), albo wszystkim (ciąg ieskończoy) liczbom aturalym.
Jarosław Wróblewski Analiza Matematyczna 2, lato 2018/19
 47. W każdym z zadań 47.-47.5 podaj wzór a fukcję różiczkowalą f :D f R o podaym wzorze a pochodą oraz o podaej wartości w podaym pukcie. 47.. f x 4x 5 54 f D f R 4x 555 fx + 47.. f x x+ f D f, + fx 9
47. W każdym z zadań 47.-47.5 podaj wzór a fukcję różiczkowalą f :D f R o podaym wzorze a pochodą oraz o podaej wartości w podaym pukcie. 47.. f x 4x 5 54 f D f R 4x 555 fx + 47.. f x x+ f D f, + fx 9
Jarosław Wróblewski Analiza Matematyczna 1A, zima 2014/15. n = Rozwiązanie: Stosując wzór na wartość współczynnika dwumianowego otrzymujemy
 12. Dowieść, że istieje ieskończeie wiele par liczb aturalych k < spełiających rówaie ( ) ( ) k. k k +1 Stosując wzór a wartość współczyika dwumiaowego otrzymujemy ( ) ( )!! oraz k k! ( k)! k +1 (k +1)!
12. Dowieść, że istieje ieskończeie wiele par liczb aturalych k < spełiających rówaie ( ) ( ) k. k k +1 Stosując wzór a wartość współczyika dwumiaowego otrzymujemy ( ) ( )!! oraz k k! ( k)! k +1 (k +1)!
Egzaminy. na wyższe uczelnie 2003. zadania
 zadaia Egzamiy wstępe a wyższe uczelie 003 I. Akademia Ekoomicza we Wrocławiu. Rozwiąż układ rówań Æ_ -9 y - 5 _ y = 5 _ -9 _. Dla jakiej wartości parametru a suma kwadratów rozwiązań rzeczywistych rówaia
zadaia Egzamiy wstępe a wyższe uczelie 003 I. Akademia Ekoomicza we Wrocławiu. Rozwiąż układ rówań Æ_ -9 y - 5 _ y = 5 _ -9 _. Dla jakiej wartości parametru a suma kwadratów rozwiązań rzeczywistych rówaia
ANALIZA MATEMATYCZNA 1
 ANALIZA MATEMATYCZNA 1 Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA 1 Kolokwia i egzaminy Wydanie siedemnaste zmienione GiS Oficyna Wydawnicza GiS Wrocław 2018 Marian Gewert Wydział Matematyki
ANALIZA MATEMATYCZNA 1 Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA 1 Kolokwia i egzaminy Wydanie siedemnaste zmienione GiS Oficyna Wydawnicza GiS Wrocław 2018 Marian Gewert Wydział Matematyki
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Techikum Nr 2 im. ge. Mieczysława Smorawińskiego w Zespole Szkół Ekoomiczych w Kaliszu Wymagaia edukacyje iezbęde do uzyskaia poszczególych śródroczych i roczych oce klasyfikacyjych z obowiązkowych zajęć
Techikum Nr 2 im. ge. Mieczysława Smorawińskiego w Zespole Szkół Ekoomiczych w Kaliszu Wymagaia edukacyje iezbęde do uzyskaia poszczególych śródroczych i roczych oce klasyfikacyjych z obowiązkowych zajęć
Wykªad 2. Szeregi liczbowe.
 Wykªad jest prowadzoy w oparciu o podr czik Aaliza matematycza 2. Deicje, twierdzeia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 2. Szeregi liczbowe. Deicje i podstawowe twierdzeia Deicja Szeregiem liczbowym
Wykªad jest prowadzoy w oparciu o podr czik Aaliza matematycza 2. Deicje, twierdzeia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 2. Szeregi liczbowe. Deicje i podstawowe twierdzeia Deicja Szeregiem liczbowym
Analiza matematyczna I. Pula jawnych zadań na kolokwia.
 Aaliza matematycza I. Pula jawych zadań a kolokwia. Wydział MIiM UW, 23/4 ostatie poprawki: 6 listopada 23 Szaowi Państwo, zgodie z zapowiedzią, a każdym kolokwium w pierwszym semestrze co ajmiej 2 zadaia
Aaliza matematycza I. Pula jawych zadań a kolokwia. Wydział MIiM UW, 23/4 ostatie poprawki: 6 listopada 23 Szaowi Państwo, zgodie z zapowiedzią, a każdym kolokwium w pierwszym semestrze co ajmiej 2 zadaia
RÓWNANIA RÓŻNICZKOWE WYKŁAD 11
 RÓWNANIA RÓŻNICZKOWE WYKŁAD Szeregi potęgowe Defiicja Fukcja y = f () jest klasy C jeżeli jest -krotie różiczkowala i jej -ta pochoda jest fukcją ciągłą. Defiicja Fukcja y = f () jest klasy C, jeżeli jest
RÓWNANIA RÓŻNICZKOWE WYKŁAD Szeregi potęgowe Defiicja Fukcja y = f () jest klasy C jeżeli jest -krotie różiczkowala i jej -ta pochoda jest fukcją ciągłą. Defiicja Fukcja y = f () jest klasy C, jeżeli jest
Analiza matematyczna I. Pula jawnych zadań na kolokwia.
 Aaliza matematycza I. Pula jawych zadań a kolokwia. Wydział MIiM UW, 25/6 ostatie poprawki: 8 styczia 26 Szaowi Państwo, zgodie z zapowiedzią, a każdym kolokwium w pierwszym semestrze co ajmiej jeda trzecia
Aaliza matematycza I. Pula jawych zadań a kolokwia. Wydział MIiM UW, 25/6 ostatie poprawki: 8 styczia 26 Szaowi Państwo, zgodie z zapowiedzią, a każdym kolokwium w pierwszym semestrze co ajmiej jeda trzecia
Materiały do wykładu Matematyka Stosowana 1. Dariusz Chrobak
 Materiały do wykładu Matematyka Stosowaa Dariusz Chrobak 7 styczia 207 Spis treści Zbiory liczbowe i fukcje 2. Zbiór liczb wymierych Q...................... 2.2 Liczby iewymiere.........................
Materiały do wykładu Matematyka Stosowaa Dariusz Chrobak 7 styczia 207 Spis treści Zbiory liczbowe i fukcje 2. Zbiór liczb wymierych Q...................... 2.2 Liczby iewymiere.........................
ALGEBRA I GEOMETRIA ANALITYCZNA
 ALGEBRA I GEOMETRIA ANALITYCZNA Opracowanie Marian Gewert Zbigniew Skoczylas ALGEBRA I GEOMETRIA ANALITYCZNA Kolokwia i egzaminy Wydanie piętnaste zmienione GiS Oficyna Wydawnicza GiS Wrocław 2014 Marian
ALGEBRA I GEOMETRIA ANALITYCZNA Opracowanie Marian Gewert Zbigniew Skoczylas ALGEBRA I GEOMETRIA ANALITYCZNA Kolokwia i egzaminy Wydanie piętnaste zmienione GiS Oficyna Wydawnicza GiS Wrocław 2014 Marian
Funkcja wykładnicza i logarytm
 Rozdział 3 Fukcja wykładicza i logarytm Potrafimy już defiiować potęgi liczb dodatich o wykładiku wymierym: jeśli a > 0 i x = p/q Q dla p, q N, to aturalie jest przyjąć a x = a 1/q) p = a 1/q } {{... a
Rozdział 3 Fukcja wykładicza i logarytm Potrafimy już defiiować potęgi liczb dodatich o wykładiku wymierym: jeśli a > 0 i x = p/q Q dla p, q N, to aturalie jest przyjąć a x = a 1/q) p = a 1/q } {{... a
Rekursja 2. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Rekursja Materiały pomocicze do wykładu wykładowca: dr Magdalea Kacprzak Rozwiązywaie rówań rekurecyjych Jedorode liiowe rówaia rekurecyje Twierdzeie Niech k będzie ustaloą liczbą aturalą dodatią i iech
Rekursja Materiały pomocicze do wykładu wykładowca: dr Magdalea Kacprzak Rozwiązywaie rówań rekurecyjych Jedorode liiowe rówaia rekurecyje Twierdzeie Niech k będzie ustaloą liczbą aturalą dodatią i iech
+ ln = + ln n + 1 ln(n)
 "Łatwo z domu rzeczywistości zajśd do lasu matematyki, ale ieliczi tylko umieją wrócid." Hugo Dyoizy Steihaus Niech (a ) będzie ieskooczoym ciągiem rzeczywistym. Def. Szeregiem = a azywamy parę ciągów
"Łatwo z domu rzeczywistości zajśd do lasu matematyki, ale ieliczi tylko umieją wrócid." Hugo Dyoizy Steihaus Niech (a ) będzie ieskooczoym ciągiem rzeczywistym. Def. Szeregiem = a azywamy parę ciągów
ĆWICZENIA NR 1 Z MATEMATYKI (Finanse i Rachunkowość, studia zaoczne, I rok) Zad. 1. Wyznaczyć dziedziny funkcji: 1 = 1, b) ( x) , c) h ( x) x x
 ĆWICZENIA NR Z MATEMATYKI (Fiase i Rachukowość studia zaocze I rok) Zad Wyzaczyć dziedziy fukcji: a) f ( ) b) ( ) + + 6 f c) f ( ) + + d) f ( ) + e) ( ) f l f) f ( ) l( + ) + l( ) g) f ( ) l( si ) h) f
ĆWICZENIA NR Z MATEMATYKI (Fiase i Rachukowość studia zaocze I rok) Zad Wyzaczyć dziedziy fukcji: a) f ( ) b) ( ) + + 6 f c) f ( ) + + d) f ( ) + e) ( ) f l f) f ( ) l( + ) + l( ) g) f ( ) l( si ) h) f
Poziom rozszerzony. 5. Ciągi. Uczeń:
 PIOTR LUDWIKOWSKI Materiał z wykładu z aalizy dla uczestików koerecji Podstawa programowa z kometarzami Tom 6 Edukacja matematycza i techicza w szkole podstawowej, gimazjum i liceum matematyka, zajęcia
PIOTR LUDWIKOWSKI Materiał z wykładu z aalizy dla uczestików koerecji Podstawa programowa z kometarzami Tom 6 Edukacja matematycza i techicza w szkole podstawowej, gimazjum i liceum matematyka, zajęcia
3 Arytmetyka. 3.1 Zbiory liczbowe.
 3 Arytmetyka. 3.1 Zbiory liczbowe. Bóg stworzył liczby aturale, wszystko ie jest dziełem człowieka. Leopold Kroecker Ozaczeia: zbiór liczb aturalych: N = {1, 2,...} zbiór liczb całkowitych ieujemych: N
3 Arytmetyka. 3.1 Zbiory liczbowe. Bóg stworzył liczby aturale, wszystko ie jest dziełem człowieka. Leopold Kroecker Ozaczeia: zbiór liczb aturalych: N = {1, 2,...} zbiór liczb całkowitych ieujemych: N
ZAGADNIENIA Z MATEMATYKI DLA STUDENTÓW I ROKU WIMiR Semestr zimowy 2017/18
 dr Aa Barbaszewska-Wiśiowska ZAGADNIENIA Z MATEMATYKI DLA STUDENTÓW I ROKU WIMiR Semestr zimowy 17/18 1 Elemety logiki matematyczej Zdaia i formy zdaiowe fuktory zdaiotwórcze Tautologie Wartości logicze
dr Aa Barbaszewska-Wiśiowska ZAGADNIENIA Z MATEMATYKI DLA STUDENTÓW I ROKU WIMiR Semestr zimowy 17/18 1 Elemety logiki matematyczej Zdaia i formy zdaiowe fuktory zdaiotwórcze Tautologie Wartości logicze
Jarosław Wróblewski Analiza Matematyczna 2 (LUX), lato 2017/18. a n n = 10.
 Czy istieje ciąg (a ) taki, że (podać przykład lub dowieść, że ie istieje) : 576. a > 1 dla ieskończeie wielu, a > 0, szereg a jest zbieży. N 577. a = 1 2 dla ieskończeie wielu, a = 10. 578. a 2 = 1 N,
Czy istieje ciąg (a ) taki, że (podać przykład lub dowieść, że ie istieje) : 576. a > 1 dla ieskończeie wielu, a > 0, szereg a jest zbieży. N 577. a = 1 2 dla ieskończeie wielu, a = 10. 578. a 2 = 1 N,
f '. Funkcja h jest ciągła. Załóżmy, że ciąg (z n ) n 0, z n+1 = h(z n ) jest dobrze określony, tzn. n 0 f ' ( z n
 Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
Metoda Newtoa i rówaie z = 1 Załóżmy, że fucja f :C C ma ciągłą pochodą. Dla (prawie) ażdej liczby zespoloej z 0 tworzymy ciąg (1) (z ) 0, z 1 = z f ( z ), ciąg te f ' (z ) będziemy azywać orbitą liczby
Matematyka. Zakres podstawowy. Nawi zanie do gimnazjum. n/m Rozwi zywanie zada Zadanie domowe Dodatkowe Komunikaty Bie ce materiały
 Lekcja 1. Lekcja orgaizacyja kotrakt Podręczik: W. Babiański, L. Chańko, D. Poczek Mateatyka. Zakres podstawowy. Wyd. Nowa Era. Zakres ateriału: Liczby rzeczywiste Wyrażeia algebraicze Rówaia i ierówości
Lekcja 1. Lekcja orgaizacyja kotrakt Podręczik: W. Babiański, L. Chańko, D. Poczek Mateatyka. Zakres podstawowy. Wyd. Nowa Era. Zakres ateriału: Liczby rzeczywiste Wyrażeia algebraicze Rówaia i ierówości
Zauważone błędy bardzo proszę zgłaszać mailem lub na ćwiczeniach. Z góry dziękuję :-)
 Odpowiedzi do zadań z szeregów, cz I. Zauważoe błędy bardzo proszę zgłaszać mailem lub a ćwiczeiach. Z góry dziękuję :-. a +, wsk. skorzystać z rówości a b a b, astępie a+b wyciągąć ajwyższe potęgi z liczika
Odpowiedzi do zadań z szeregów, cz I. Zauważoe błędy bardzo proszę zgłaszać mailem lub a ćwiczeiach. Z góry dziękuję :-. a +, wsk. skorzystać z rówości a b a b, astępie a+b wyciągąć ajwyższe potęgi z liczika
Jarosław Wróblewski Analiza Matematyczna 1 LUX, zima 2016/17
 585. Wskaż liczbę rzeczywistą k, dla której podaa graica istieje i jest dodatią liczbą rzeczywistą. Podaj wartość graicy dla tej wartości parametru k. Jeżeli odpowiedź jest liczbą wymierą, podaj ją w postaci
585. Wskaż liczbę rzeczywistą k, dla której podaa graica istieje i jest dodatią liczbą rzeczywistą. Podaj wartość graicy dla tej wartości parametru k. Jeżeli odpowiedź jest liczbą wymierą, podaj ją w postaci
Zasada indukcji matematycznej. Dowody indukcyjne.
 Zasada idukcji matematyczej Dowody idukcyje Z zasadą idukcji matematyczej i dowodami idukcyjymi sytuacja jest ajczęściej taka, że podaje się w szkole treść zasady idukcji matematyczej, a astępie omawia,
Zasada idukcji matematyczej Dowody idukcyje Z zasadą idukcji matematyczej i dowodami idukcyjymi sytuacja jest ajczęściej taka, że podaje się w szkole treść zasady idukcji matematyczej, a astępie omawia,
Wektory Funkcje rzeczywiste wielu. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
Wzór Taylora. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Wzór Taylora Szeregi potęgowe Matematyka Studium doktorackie KAE SGH Semestr leti 8/9 R. Łochowski Graica fukcji w pukcie Niech f: R D R, R oraz istieje ciąg puktów D, Fukcja f ma w pukcie graicę dowolego
Wzór Taylora Szeregi potęgowe Matematyka Studium doktorackie KAE SGH Semestr leti 8/9 R. Łochowski Graica fukcji w pukcie Niech f: R D R, R oraz istieje ciąg puktów D, Fukcja f ma w pukcie graicę dowolego
I. Podzielność liczb całkowitych
 I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
Przykładowe zadania dla poziomu rozszerzonego
 Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
Wyk lad 8 Zasadnicze twierdzenie algebry. Poj. ecie pierścienia
 Wy lad 8 Zasadicze twierdzeie algebry. Poj ecie pierścieia 1 Zasadicze twierdzeie algebry i jego dowód Defiicja 8.1. f: C C postaci Wielomiaem o wspó lczyiach zespoloych azywamy fucj e f(x) = a x + a 1
Wy lad 8 Zasadicze twierdzeie algebry. Poj ecie pierścieia 1 Zasadicze twierdzeie algebry i jego dowód Defiicja 8.1. f: C C postaci Wielomiaem o wspó lczyiach zespoloych azywamy fucj e f(x) = a x + a 1
Analiza numeryczna. Stanisław Lewanowicz. Aproksymacja funkcji
 http://www.ii.ui.wroc.pl/ sle/teachig/a-apr.pdf Aaliza umerycza Staisław Lewaowicz Grudzień 007 r. Aproksymacja fukcji Pojęcia wstępe Defiicja. Przestrzeń liiową X (ad ciałem liczb rzeczywistych R) azywamy
http://www.ii.ui.wroc.pl/ sle/teachig/a-apr.pdf Aaliza umerycza Staisław Lewaowicz Grudzień 007 r. Aproksymacja fukcji Pojęcia wstępe Defiicja. Przestrzeń liiową X (ad ciałem liczb rzeczywistych R) azywamy
Analiza matematyczna dla informatyków
 Aaliza matematycza dla iformatyków Sprawdziay do Wykładów dla pierwszego roku iformatyki a Wydziale Matematyki, Iformatyki i Mechaiki Uiwersytetu Warszawskiego w latach 2007/8, 2008/9, 2009/0, 20/2, 202/3,
Aaliza matematycza dla iformatyków Sprawdziay do Wykładów dla pierwszego roku iformatyki a Wydziale Matematyki, Iformatyki i Mechaiki Uiwersytetu Warszawskiego w latach 2007/8, 2008/9, 2009/0, 20/2, 202/3,
Analiza I.1, zima globalna lista zadań
 Aaliza I., zima 207 - globala lista zadań Marci Kotowsi 8 styczia 208 Podstawy Zadaie. Udowodij, że dla ażdego aturalego liczby 7 2 + oraz 7 2 dzielą się przez 6. Zadaie 2. Rozstrzygij, czy poiższe liczby
Aaliza I., zima 207 - globala lista zadań Marci Kotowsi 8 styczia 208 Podstawy Zadaie. Udowodij, że dla ażdego aturalego liczby 7 2 + oraz 7 2 dzielą się przez 6. Zadaie 2. Rozstrzygij, czy poiższe liczby
Analiza matematyczna dla informatyków
 Aaliza matematycza dla iformatyków Sprawdziay do Wykładów dla pierwszego roku iformatyki a Wydziale Matematyki, Iformatyki i Mechaiki Uiwersytetu Warszawskiego w latach 2007/8, 2008/9, 2009/0, 20/2, 202/3,
Aaliza matematycza dla iformatyków Sprawdziay do Wykładów dla pierwszego roku iformatyki a Wydziale Matematyki, Iformatyki i Mechaiki Uiwersytetu Warszawskiego w latach 2007/8, 2008/9, 2009/0, 20/2, 202/3,
Zdarzenia losowe, definicja prawdopodobieństwa, zmienne losowe
 Metody probabilistycze i statystyka Wykład 1 Zdarzeia losowe, defiicja prawdopodobieństwa, zmiee losowe Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki
Metody probabilistycze i statystyka Wykład 1 Zdarzeia losowe, defiicja prawdopodobieństwa, zmiee losowe Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki
a n 7 a jest ciągiem arytmetycznym.
 ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
Geometrycznie o liczbach
 Geometryczie o liczbach Geometryczie o liczbach Łukasz Bożyk Dodatią liczbę całkowitą moża iterpretować jako pole pewej figury składającej się z kwadratów jedostkowych Te prosty pomysł pozwala w aturaly
Geometryczie o liczbach Geometryczie o liczbach Łukasz Bożyk Dodatią liczbę całkowitą moża iterpretować jako pole pewej figury składającej się z kwadratów jedostkowych Te prosty pomysł pozwala w aturaly
O liczbach naturalnych, których suma równa się iloczynowi
 O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
Prace domowe z matematyki Semestr zimowy 2010/2011. Zoa Zieli«ska-Kolasi«ska
 Prace domowe z matematyki Semestr zimowy 2010/2011 Zoa Zieli«ska-Kolasi«ska 5 pa¹dzierika 2010 Rozdziaª 0 Uwagi Prace domowe ie s obowi zkowe aczkolwiek zach cam gor co do ich robieia i oddawaia mi a kartkach.
Prace domowe z matematyki Semestr zimowy 2010/2011 Zoa Zieli«ska-Kolasi«ska 5 pa¹dzierika 2010 Rozdziaª 0 Uwagi Prace domowe ie s obowi zkowe aczkolwiek zach cam gor co do ich robieia i oddawaia mi a kartkach.
5. Szeregi liczbowe. A n = A = lim. a k = lim a k, a k = a 1 + a 2 + a
 5. Szeregi liczbowe Niech będzie day iesończoy ciąg liczbowy {a }. Ciąg A = azywamy ciągiem sum częściowych ciągu {a }. Jeżeli ciąg {A } jest zbieży, mówimy, że ciąg {a } jest sumowaly, a graicę a A =
5. Szeregi liczbowe Niech będzie day iesończoy ciąg liczbowy {a }. Ciąg A = azywamy ciągiem sum częściowych ciągu {a }. Jeżeli ciąg {A } jest zbieży, mówimy, że ciąg {a } jest sumowaly, a graicę a A =
CIĄGI LICZBOWE. Poziom podstawowy
 CIĄGI LICZBOWE Poziom podstawowy Zadaie ( pkt) + 0 Day jest ciąg o wyrazie ogólym a =, N+ + jest rówy? Wyzacz a a + Czy istieje wyraz tego ciągu, który Zadaie (6 pkt) Marek chce przekopać swój przydomowy
CIĄGI LICZBOWE Poziom podstawowy Zadaie ( pkt) + 0 Day jest ciąg o wyrazie ogólym a =, N+ + jest rówy? Wyzacz a a + Czy istieje wyraz tego ciągu, który Zadaie (6 pkt) Marek chce przekopać swój przydomowy
UKŁADY RÓWNAŃ LINOWYCH
 Ekoeergetyka Matematyka. Wykład 4. UKŁADY RÓWNAŃ LINOWYCH Defiicja (Układ rówań liiowych, rozwiązaie układu rówań) Układem m rówań liiowych z iewiadomymi,,,, gdzie m, azywamy układ rówań postaci: a a a
Ekoeergetyka Matematyka. Wykład 4. UKŁADY RÓWNAŃ LINOWYCH Defiicja (Układ rówań liiowych, rozwiązaie układu rówań) Układem m rówań liiowych z iewiadomymi,,,, gdzie m, azywamy układ rówań postaci: a a a
MATURA 2014 z WSiP. Zasady oceniania zadań
 MATURA 0 z WSiP Matematyka Poziom rozszerzoy Zasady oceiaia zadań Copyright by Wydawictwa Szkole i Pedagogicze sp z oo, Warszawa 0 Matematyka Poziom rozszerzoy Kartoteka testu Numer zadaia Sprawdzaa umiejętość
MATURA 0 z WSiP Matematyka Poziom rozszerzoy Zasady oceiaia zadań Copyright by Wydawictwa Szkole i Pedagogicze sp z oo, Warszawa 0 Matematyka Poziom rozszerzoy Kartoteka testu Numer zadaia Sprawdzaa umiejętość
Wykład 7. Przestrzenie metryczne zwarte. x jest ciągiem Cauchy ego i posiada podciąg zbieżny. Na mocy
 Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
Krzysztof Rykaczewski. Analiza matematyczna I Zbiór zadań
 Krzysztof Rykaczewski Aaliza matematycza I Zbiór zadań Motto: Powiedz mi a zapomę Pokaż mi a zapamiętam Pozwól mi zrobić a zrozumiem. Cofucius : Zbiór zadań z aalizy matematyczej Uiwersytet Mikołaja Koperika
Krzysztof Rykaczewski Aaliza matematycza I Zbiór zadań Motto: Powiedz mi a zapomę Pokaż mi a zapamiętam Pozwól mi zrobić a zrozumiem. Cofucius : Zbiór zadań z aalizy matematyczej Uiwersytet Mikołaja Koperika
