Wyk lady z funkcji zespolonych
|
|
|
- Daria Stanisława Dobrowolska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Wyk lady z funkcji zespolonych III semestr 2009/0 oprac. Janina Kotus
2 Spis treści. Poj ecia podstawowe str. 5. Rzut stereograficzny str. 5.2 Metryki w C i C str Funkcje zespolone str Granica i ciag lość str Pochodna str Pochodne formalne str Pochodna kierunkowa funkcji str Funkcje holomorficzne str Funkcje elementarne str Funkcja wyk ladnicza str Funkcje trygonometryczne str Funkcje hiperboliczne str Funkcja logarytmiczna str Funkcja pot egowa str Powierzchnie Riemanna funkcji wielowartościowych str Szeregi funkcyjne str Szeregi liczbowe str Rodzaje zbieżności szeregów funkcyjnych str Szeregi pot egowe str Funkcje analityczne str Odwzorowania konforemne str Interpretacja geometryczna pochodnej zespolonej str Interpretacja geometryczna równań Cauchy ego-riemanna str Odwzorowania konforemne str. 35 2
3 6. Ca lka z funkcji zespolonej str Ca lka z funkcji zespolonej zmiennej rzeczywistej str Ca lka z funkcji zespolonej zmiennej zespolonej str Twierdzenia i wzory ca lkowe Cauchy ego str Funkcje holomorficzne w C str Zera funkcji holomorficznej str Szeregi Laurenta str. 6. Punkty osobliwe str. 65. Punkty osobliwe izolowane str Zachowanie si e funkcji holomorficznej w punkcie str Klasyfikacja funkcji holomorficznych ze wzgl edu na ich punkty osobliwe str Obliczanie ca lek za pomoca residuów str Geometryczna teoria funkcji str Przed lużenia analityczne str Rodziny normalne funkcji str Funkcje harmoniczne str. 97 3
4 . 4
5 Poj ecia podstawowe Zbiór liczb zespolonych C = {z = x + iy : x, y R} można utożsamiać z p laszczyzna dwuwymiarowa, która bedziemy oznaczać symbolem C i nazywać p laszczyzna zespolona otwarta. Aby zdefiniować jej domkni ecie podamy najpierw definicj e przekszta lcenia zwanego rzutem stereograficznym.. Rzut stereograficzny W przestrzeni R 3 definiujemy sfere x 2 + y 2 + ( z 2) 2 = o środku w punkcie (x 4 0, y 0, z 0 ) = (0, 0, ) i promieniu r =, styczn a 2 2 do p laszczyzny uk ladu OXY w poczatku uk ladu wspó lrzednych. Punkt N = (0, 0, ) S 2 nazywać bedziemy biegunem pó lnocnym sfery. Konstrukcja rzutu stereograficznego Każdemu punktowi z = x + iy C przyporzadkujemy punkt Z(ξ, η, ζ) S 2 {N} bed acy punktem przeciecia odcinka l acz acego punkt z C z punktem N. Definicja. Odwzorowanie gdzie ξ = P : C nazywamy rzutem stereograficznym. z = Z S 2 {N}, z = x + iy = Z = (ξ, η, ζ), x + z 2, η = y z 2, ζ = + z 2 + z 2, Uwaga. Rzut stereograficzny posiada przekszta lcenie odwrotne P : S 2 {N} = C, Z = (ξ, η, ζ) = z = x + iy, zdefiniowane wzorem x = ξ η, y =. ζ ζ Zatem rzut stereograficzny jest bijekcja miedzy p laszczyzna otwarta C i sfera bez bieguna pó lnocnego, któremu nie odpowiada żaden punkt na p laszczyźnie. 5
6 Uwaga.2 Umówimy si e, że punktowi N odpowiada punkt w nieskończoności (ozn. ). Definicja.2 P laszczyzna domnkiet a, która oznaczamy symbolem C nazywamy sume C { } i utożsamiamy ja z dwywymiarowa sfera zwana sfera Riemanna..2 Metryki w C i C W p laszczyźnie otwartej C wprowadzamy metryke euklidesowa d(z, z 2 ) := (Rez Rez 2 ) 2 + (Imz Imz 2 ) 2 = z z 2. W p laszczyźnie domknietej C wprowadzamy metryke sferyczna, w której odleg lość miedzy punktami z, z 2 rozumiemy odleg lość euklidesowa miedzy ich obrazami przy rzucie stereograficznym na sferze tzn. ρ(z, z 2 ) := d(p (z ), P (z 2 )) = ρ(z, ) := z z 2 + z 2 + z 2 2 z = z 2 C,, z =. + z 2 Uwaga.3 Aby otrzymać drugi wzór z pierwszego należy za z mianownik przez z 2. podstawić z i podzielić licznik oraz ρ(z, z 2 ) = z z 2 + z 2 + z 2 2 = Uwaga.4 z, z 2 C, 0 ρ(z, z 2 ). z z 2 + z 2 + z 2 2 z z 2 jesli z 2. Uwaga.5 P laszczyzna domknieta C z metryka sferyczna jest przestrzenia metryczna zwarta. Uwaga.6 Na zbiorach ograniczonych, zawartych w C obie metryki euklidesowa i sferyczna sa równoważne tzn. jeśli A {z : z R}, (R < ), to z z 2 + R 2 ρ(z, z 2 ) z z 2 z, z 2 A. 6
7 Definicja.3 Zbiór U(z 0, ε) = {z C : d(z, z 0 ) = z z 0 < ε} nazywamy ε-otoczeniem punktu z 0 C w p laszczyźnie C (otwartej). Definicja.4 Zbiór U(z 0, ε) = {z C : ρ(z, z 0 ) < ε} nazywamy ε-otoczeniem punktu z 0 C w p laszczyźnie C (domkni etej). Zatem: U(, ε) = {z C : ρ(z, ) < ε} = {z C : {z C : z > ε 2 }, + z 2 < ε} = ε ma le. Otoczeniem punktu w w p laszczyźnie C jest dope lnienie domkni etego ko la o środku w zerze. Definicja.5 - Otoczeniem nak lutym punktu z 0 C w p laszczyźnie C nazywamy zbiór U(z 0, ε) {z 0 } = {z C : 0 < z z 0 < ε}. - Otoczeniem nak lutym punktu z 0 C w p laszczyźnie C nazywamy zbiór U(z 0, ε) {z 0 } = {z C : 0 < ρ(z, z 0 ) < ε}. Definicja.6 Obszarem D nazywamy zbiór punktów p laszczyzny C spe lniajacy warunki: - (otwartość) a D U(a, ε)-otoczenie takie, że U(a, ε) D, - ( lukowa spójność) a, b D istnieje droga o końcach a,b zawarta w D. Droga o końcach a, b nazywamy funkcje ciag l a γ : [t 0, t ] C taka, że γ(t 0 ) = a, γ(t ) = b. Stwierdzenie. Dla zbiorów otwartych zawartych w C (odpow. w C) lukowa spójność pokrywa sie ze spojnościa zbiorów. Definicja.7* Obszar D C (odpow. D C) nazywamy jednospójnym, jeśli jego brzeg jest zbiorem spójnym. W przeciwnym przypadku obszar nazywamy wielospójnym. (*) Później podamy inna definicje jednospójności. 7
8 2 Funkcje zespolone Definicja 2. Odwzorowanie f : D C, z w = f(z) nazywamy funkcje zespolona zmiennej zespolonej. D C Argument z funkcji f i jej wartość w = f(z) rozk ladamy na cześć rzeczywista i urojona tzn. z = x + iy, w = u + iv. Otrzymujemy w ten sposób rozk lad funkcji w = f(x + iy) = u(x, y) + iv(x, y) na cześć rzeczywista Ref(z) := u(x, y) i cześć urojona Imf(z) := v(x, y). Cześć rzeczywista i urojona funkcji zespolonej f jest funkcja rzeczywista dwóch zmiennych x, y. Przyk lad 2. Znaleźć cześć rzeczywista i urojona funkcji f(z) = iz 2. Zatem f(z) = iz 2 = i(x + iy) 2 = i(x 2 + 2ixy y 2 ) = ix 2 2xy iy 2 = 2xy + i(x 2 y 2 ). Ref(z) = u(x, y) = 2xy, Imf(z) = v(x, y) = x 2 y 2. Przyk lad 2.2 Dane sa cześć rzeczywista u(x, y) = x y i urojona v(x, y) = 4xy funkcji zespolonej f. Przedstawić funkcje f jako funkcje zmiennej zespolonej z. z = x + iy, z = x iy x = z + z 2 z z, y =. 2i Podstawiamy ( ) ( ) ( ) ( ) z + z z z z + z z z f(z) = u(x, y) + iv(x, y) = (x y) + i4xy = + i4 2 2i 2 2i ( = z 2 ) ( + z 2i 2 + ) ( ) ( ) (z 2 z 2 ) = z 2i 2 + i + z 2 2 i + z 2 z
9 2. Granica i ciag lość Definicja 2.2 lim f(z) = g ε > 0 δ > 0 z D 0 < d(z, z 0 ) < δ d(f(z), g) < ε. z z 0 Stwierdzenie 2. lim f(z) = g lim u(x, y) = Reg i lim v(x, y) = Img. z z 0 (x,y) (x 0,y 0 ) (x,y) (x 0,y 0 ) Definicja 2.3 Funkcja f jest ciag la w z 0 lim z z0 f(z) = f(z 0 ). Twierdzenie 2. Funkcja f(z) = u(x, y) + iv(x, y) jest ciag la w z 0 funkcje u i v sa ciag le w (x 0, y 0 ). Definicja 2.4 Funkcja f jest ciag la w, jeśli funkcja f( ) jest ci ag la z w zerze. 2.2 Pochodna Definicja 2.5 Granice w laściwa ilorazu różnicowego f(z + Δz) f(z) lim Δz 0 Δz nazywamy pochodna funkcji f w punkcie z i oznaczamy f (z). f (z) := lim Δz 0 f(z + Δz) f(z), Δz f (z 0 ) := lim z z0 f(z) f(z 0 ) z z 0. Jeżeli funkcje f i g maja pochodna w punkcie z, to. (f ± g) (z) = f (z) ± g (z). 2. (fg) (z) = f (z)g(z) + f(z)g (z). ( ) f 3. g (z) = f (z)g(z) f(z)g (z) dla z / g (0). [g(z)] 2 9
10 Jeżeli funkcja f ma pochodna w punkcie g(z) i g ma pochodna w punkcie z, to (f g) (z) = f (g(z))g (z). Twierdzenie 2.2 (warunek konieczny istnienia pochodnej) Jeżeli funkcja f(z) = u(x, y)+iv(x, y) ma w punkcie z 0 = x 0 +iy 0 pochodna f (z 0 ), to istnieja w punkcie (x 0, y 0 ) pochodne czastkowe u, u, v, v i spe lniaj a x y x y w punkcie (x 0, y 0 ) warunki: u x (x 0, y 0 ) = v y (x 0, y 0 ), u y (x 0, y 0 ) = v x (x 0, y 0 ), zwane warunkami Cauchy ego-riemanna. Dowód. Zak ladamy, że istnieje Niech Δz = Δx + iδy f (z 0 ) = lim Δz 0 f(z 0 + Δz) f(z 0 ). Δz () Δy = 0 Δz = Δx f u(x 0 + Δx, y 0 ) + iv(x 0 + Δx, y 0 ) u(x 0, y 0 ) iv(x 0, y 0 ) (z 0 ) = lim Δx 0 [ Δx u(x0 + Δx, y 0 ) u(x 0, y 0 ) = lim + i v(x ] 0 + Δx, y 0 ) v(x 0, y 0 ) Δx 0 Δx Δx = u x (x 0, y 0 ) + i v x (x 0, y 0 ). (2) Δx = 0 Δz = iδy f u(x 0, y 0 + Δy) + iv(x 0, y 0 + Δy) u(x 0, y 0 ) iv(x 0, y 0 ) (z 0 ) = lim Δy 0 iδy [ u(x0, y 0 + Δy) u(x 0, y 0 ) = lim + v(x ] 0, y 0 + Δy) v(x 0, y 0 ) Δy 0 iδy Δy = i u y (x 0, y 0 ) + v y (x 0, y 0 ). Zatem u x (x 0, y 0 ) + i v x (x 0, y 0 ) = i u y (x 0, y 0 ) + v y (x 0, y 0 ). 0
11 Stad u x (x 0, y 0 ) = v y (x 0, y 0 ) oraz u y (x 0, y 0 ) = v x (x 0, y 0 ). Wniosek 2. Jeżeli istnieje pochodna funkcji f w punkcie z 0, to: f (z 0 ) = u x (x 0, y 0 ) + i v x (x 0, y 0 ) = v y (x 0, y 0 ) i u y (x 0, y 0 ) = u x (x 0, y 0 ) i u y (x 0, y 0 ) = v y (x 0, y 0 ) + i v x (x 0, y 0 ). Wniosek 2.2 Pochodne czastkowe funkcji f wyrażaja sie wzorami f x f y (x, y) = u x (x, y) = u y (x, y) + i v (x, y) x (x, y) + i v (x, y). y Stad i z wniosku 2. otrzymamy nastepuj ace wzory na pochodna funkcji f w punkcie z 0. f (z 0 ) = f x (x 0, y 0 ) = i f y (x 0, y 0 ). Twierdzenie 2.3 (warunek dostateczny istnienia pochodnej) Jeżeli funkcje u(x, y) i v(x, y) sa rózniczkowalne w punkcie (x 0, y 0 ) i spe lniaja w tym punkcie warunki Cauchy ego Riemanna, to funkcja f(z) = u(x, y) + iv(x, y) ma pochodna f (z 0 ). Dowód. Funkcje u i v sa różniczkowalne w punkcie (x 0, y 0 ), wiec () Δu(x 0, y 0 ) = u(x, y) u(x 0, y 0 ) = u x (x 0, y 0 )Δx + u y (x 0, y 0 )Δy + o ( Δz ), gdzie Δz = (Δx) 2 + (Δy) 2, o jest wielkościa ma lego rzedu tzn. Analogicznie lim Δz 0 o ( Δz ) Δz = 0. (2) Δv(x 0, y 0 ) = v(x, y) v(x 0, y 0 ) = v x (x 0, y 0 )Δx + v y (x 0, y 0 )Δy + o 2 ( Δz ), o o 2 jest wielkościa ma lego rzedu tzn. lim 2 ( Δz ) Δz 0 = 0. Δz Δf(z 0 ) = f(z) f(z 0 ).
12 (3) Δf(z 0 ) = f(z) f(z 0 ) = Δu(x 0, y 0 ) + iδv(x 0, y 0 ). Podstawiajac () i (2) do (3) otrzymamy: Δf Δz (z 0) = Δu Δz (x 0, y 0 ) + i Δv Δz (x 0, y 0 ) = ( u x (x 0, y 0 ) Δx Δz + u y (x 0, y 0 ) Δy ) + o ( Δz ) Δz Δz ( u x (x 0, y 0 ) + i v ) Δx x (x 0, y 0 ) Δz + ( v + i ( u y (x 0, y 0 ) + i v y (x 0, y 0 ) x (x 0, y 0 ) Δx Δz + v y (x 0, y 0 ) Δy ) Δz ) Δy Δz + o ( Δz ) Δz + i o 2( Δz ) Δz + i o 2( Δz ). Δz = Korzystajac z za lożenia, że funkcje u(x, y) i v(x, y) spe lniaja warunki Cauchy ego-riemanna otrzymamy, że Zatem Δf Δz (z 0) = u x (x 0, y 0 ) = v y (x 0, y 0 ) i u y (x 0, y 0 ) = v x (x 0, y 0 ) ( u x (x 0, y 0 ) + i v ) ( ) Δx + iδy x (x 0, y 0 ) Δz + o ( Δz ) Δz ( Δf u lim Δz 0 Δz (z 0) = lim Δz 0 x (x 0, y 0 ) + i v ) x (x 0, y 0 ) + o ( Δz ) Δz + i o 2( Δz ). Δz + i o 2( Δz ). Δz Stad wynika, że istnieje granica w laściwa ilorazu różnicowego w punkcie z 0, czyli istnieje pochodna f (z 0 ). Przyk lad 2.3 Dla jakich punktów z C funkcja f(z) = z z = z 2 = x 2 + y 2 ma pochodna? Ref(z) = u(x, y) = x 2 + y 2, Imf(z) = v(x, y) 0. Funkcje u i v sa różniczkowalne dla (x, y) R 2. Sprawdzamy warunki C-R. Stad u x = 2x, u y = 2y, v x = v y = 0. u x = v y x = 0, u y = v x y = 0. Zatem warunki Cauche go Riemanna sa spe lnione tylko w punkcie z 0 = 0. Z Twierdzenia 2.2 wynika, że tylko w tym punkcie spe lniony jest warunek konieczny istnienia pochodnej. Z twierdzenia 2.3 zaś wynika, że w punkcie z 0 = 0 spe lnione sa również warunki dostateczne istnienia pochodnej funkcji f. Pochodna funkcji policzymy z definicji. f (0) = lim z 0 f(z) f(0) z 0 2 z z = lim z 0 z = lim z = 0. z 0
13 2.3 Pochodne formalne Niech f(z) = u(x, y) + iv(x, y). Za lóżmy, że funkcje u(x, y) i v(x, y) sa różniczkowalne w punkcie z 0 = (x 0, y 0 ). Wyprowadzimy wzory na pochodne formalne f(z). Ponieważ dz = dx + idy i d z = dx idy, to df = du + idv =(u xdx + u ydy) + i(v xdx + v ydy) =(u xdx + iv xdx) + (u ydy + iv ydy) = f f dx + x y dy. (2.) Wstawiajac (2.2) do (2.) otrzymamy dx = 2 (dz + d z), dy = (dz d z). (2.2) 2i df = f f (dz + d z) + x 2 y 2i = ( ) f 2 x i f dz + y 2 = f f dz + z z d z. (dz d z) ( f x + i f y ) d z Definicja 2.6. Pochodne formalne funkcji f(z) definiujemy nastepuj aco: f z := ( ) f 2 x i f f, y z := ( ) f 2 x + i f. y (2.3) Twierdzenie 2.4 (warunek różniczkowalności funkcji w postaci zespolonej) Niech f(z) = u(x, y) + iv(x, y). Zak ladamy, że funkcje u(x, y) i v(x, y) sa różniczkowalne w punkcie z 0 = (x 0, y 0 ). Wtedy funkcja f(z) ma pochodna w punkcie z 0 = x 0 + iy 0 wtedy i tylko wtedy gdy f (z z 0) = 0. Dowód Korzystajac z definicji pochodnej formalnej mamy, że f z = ( ) f 2 x + i f = ( u y 2 x + iv x + i(u y + iv y) ) = ( u 2 x v y + i(u x + iv y) ). Zauważmy, że warunek f (z z 0) = 0 zachodzi wtedy i tylko wtedy gdy u x(x 0, y 0 ) = v y(x 0, y 0 ) i u y(x 0, y 0 ) = v x(x 0, y 0 ), czyli gdy spe lnione sa warunki Cauchy ego-riemanna w punkcie z 0. 3
14 Uwaga 2. f (z 0 ) = f z (z 0) Dowód ( ) Z wniosku 2. wynika, że f (z 0 ) = u(x x 0, y 0 ) + i v (x x 0, y 0 ). Natomiast f = f f i = z 2 x y ( 2 u x + iv x i(u y + iv y) ) ( = 2 (u x + v y) + i(v x u y) ). Korzystajac z faktu, że jeśli istnieje f (z 0 ) to f spe lnia w punkcie z 0 warunki Cauchy ego-riemanna otrzymamy, że f z (z 0) = [ u 2 x (x 0, y 0 ) + v y(x 0, y 0 ) + i(v x(x 0, y 0 ) u y(x 0, y 0 )) ] = 2 [2u x(x 0, y 0 ) + i2v x(x 0, y 0 )] = f (z 0 ) 2.4 Pochodna kierunkowa funkcji Niech D C, f : D C, z 0 D. Wtedy Δf = f(z) f(z 0 ), Δz = z z 0, Δ z = z z 0. Zatem Δf = f z f Δz + Δ z + o(δz), z o(δz) gdzie o(δz) oznacza ma l a wyższego rzedu wzgledem Δ tzn. lim Δz 0 Δz Δz = Δz e iθ, wtedy Δ z = Δz e iθ. = 0. Zapiszemy gdzie η(δz) = o(δz) Δz dla Δz 0. Δf Δz = f z + f z e 2iθ + η(δz), Do istnienia granicy ilorazu Δf dla Δz 0 potrzeba i wystarcza, aby przy d ażeniu Δz Δz 0 kat θ = arg(δz) daży l do pewnej granicy φ. Granica ilorazu Δf gdy arg(δz) d aży Δz do kata φ nazywamy pochodna funkcji f w kierunku kata φ w punkcie z 0 i oznaczamy symbolem f f = f z φ z + f z e 2iφ. Uwaga 2.2 Jeżeli f (z z 0) = 0, to pochodne kierunkowe w tym punkcie zależa od od kierunku. z φ. 4
15 Uwaga 2.3 Funkcja ma pochodna w punkcie z 0 f (z z 0) = 0 gdy pochodna funkcji f nie zależy od od kierunku φ w punkcie z Funkcje holomorficzne Definicja 2.7 Funkcje f(z) nazywamy holomorficzna (różniczkowalna w sensie zespolonym) w obszarze D jeśli w każdym punkcie z D istnieje pochodna f (z). Ozn. f H(D). Definicja 2.8 Funkcje f(z) nazywamy holomorficzna (różniczkowalna w sensie zespolonym) w punkcie z 0 D jeśli jest holomorficzna w pewnym otoczeniu tego punktu. Przyk lad 2.4 Zbadać holomorficzność funkcji f(z) = z 2 = z z. Wiadomomo, że f (z 0 ) istnieje wtedy i tylko wtedy gdy f (z z 0) = 0. Policzymy f (z) = z. z Stad f (z) = 0 z = 0. Zatem f ma pochodn a z tylko w z 0 = 0. Policzymy ja z definicji f (z 0 ) = lim z 0 f(z) f(z 0 ) z z 0 z z 0 = lim z 0 z 0 = lim z = 0. z 0 - f ma pochodna tylko w zerze, zatem nie jest holomorficzna ani w punkcie z 0 = 0, ani w ca lej p laszczyźnie C. Przyk lad 2.5 Zbadać holomorficzność funkcji f(z) = z 2 z. Policzymy f (z) = z z2. St Policzymy ja z definicji ad f (z) = 0 z = 0. Zatem f ma pochodn a z tylko w z 0 = 0. f (z 0 ) = lim z 0 f(z) f(z 0 ) z z 0 = lim z 0 z 2 z 0 z 0 = lim z 0 z z = 0 - f ma pochodna tylko w zerze, zatem nie jest holomorficzna ani w punkcie z 0 = 0, ani w ca lej p laszczyźnie C. Jest to kolejny przyk lad funkcji, która ma pochodna w punkcie ale nie jest w nim holomorficzna. 5
16 W lasności funkcji holomorficznych:. Jeśli f, g H(D), to (f ± g) H(D) oraz fg H(D). 2. Jeśli f, g H(D), to f g H(D (g (0)). 3. Jeśli g H(D), f H(f(D)), to (f g) H(D). 3 Funkcje elementarne 3. Funkcja wyk ladnicza Funkcje wyk ladnicza w dziedzinie zespolonej zdefiniujemy tak samo jak w analizie rzeczywistej tzn. exp(z) := lim ( + z ) n. n n Wykażemy istnienie tej granicy dla każdego z C.. Najpierw pokażemy zbieżność modu lów tzn. ( lim + n) z n = e x. (3.) n Skorzystamy z w lasności, że z n = z n. Zatem ( + z ) n [ ( = + x ] 2 y + n n) 2 n/2 = [ + 2xn ] n + x2 + y 2 n/2. 2 n 2 Przechodzac do granicy otrzymamy, że ( lim + n) z n = e x, czyli zachodzi (3.). n 2. Niech Argz oznacza argument g lówny liczby z. Pokażemy, że lim ( Arg + z ) n = y. (3.2) n n Zauważmy najpierw, że Ponieważ Arg(z n ) = narg(z), to ( Arg + z ) n y n = arctg + x. n ( Arg + n) z ( n y = narctg n + x n 6 ).
17 Przechodzac do granicy otrzymamy, że czyli zachodzi (3.2). lim n ( narctg ( y n + x n )) = y, Z jednoznaczności zapisu liczby ( zespolonej w postaci trygonometrycznej otrzymamy, że modu l liczby e z czyli e z = lim n + z n n) = e x, zaś Arg(e z ) = lim n Arg ( + n) z n = y. St ad exp(z) = e z = e x+iy = e x (cosy + isiny). (3.3) Podstawiajac za z = 0 + iy otrzymamy wzór Eulera tzn. y IR e iy = cosy + isiny (3.4) Wracajac do definicji funkcji wyk ladniczej e z (znowu korzystajac z jednoznaczności zapisu liczby zespolonej w postaci trygonometrycznej) otrzymamy, że W lasności e z = e x+iy = e x e iy = e x (cosy + isiny). a) Cześć rzeczywista i urojona funkcji f(z) = e z wynosza odpowiednio u(x, y) = e x cosy, v(x, y) = e x siny. b) e z = e x. c) funkcja e z jest holomorficzna w C oraz (e z ) = e z. Jest oczywiste, że cześć rzeczywista i urojona funkcji sa klasy C (R 2 ). Pokażemy, że spe lniaja równania Cauchy ego-riemanna: u x(x, y) = e x cosy, u y(x, y) = e x siny, v x(x, y) = e x siny, v y(x, y) = e x cosy, u x(x, y) = v y(x, y), u y(x, y) = v x(x, y). f (z) = f z = u x + iv x = e x cosy + ie x siny = e x (cosy + isiny) = e z. d) z, z 2 C, e z +z 2 = e z e z 2. e z e z 2 = e x (cosy + isiny )e x 2 (cosy 2 + isiny 2 ) = e x +x 2 (cos(y + y 2 ) + isin(y + y 2 )). = e (x +x 2 )+i(y +y 2 ) = e z +z 2. 7
18 e) z C, e z = 0. Przypuśćmy, że e z = 0 e x (cosy + isiny) = 0 e x cosy = 0 e x siny = 0. Ponieważ e x = 0 to cosy = 0 i siny = 0. Pierwsza równość zachodzi dla y = π + kπ, 2 druga zaś dla y = kπ, gdzie k Z. Ponieważ obie równości nie moga zachodzić jednocześnie, otrzymana sprzeczność dowodzi, że e z = 0 dla każdego z C. f) funkcja e z jest okresowa o okresie podstawowym T = 2πi. Dla k Z korzystajac z okresowości funkcji trygonometrycznych sinx i cosx mamy e z+2kπi = e z e 2kπi = e z (cos(2kπ) + isin(2kπ)) = e z ( + i0) = e z. g) funkcja e z jest rozszerzeniem do dziedziny zespolonej funkcji wyk ladniczej e x. Niech z = x + i0 R. Wtedy e z = e x (cos0 + isin0) = e x ( + i0) = e x. Uwaga 3. Zostanie później udowodnione, że funkcja wyk ladnicza e z rozwinie sie w szereg Maclaurina tzn. e z z k = dla każdego z C. k! k= 3.2 Funkcje trygonometryczne Funkcje cosz i sinz w dziedzinie zespolonej definiujemy nastepuj aco: W lasności tgz = sinz cosz = cosz := eiz + e iz, sinz := eiz e iz, 2 2i eiz e iz i(e iz + e iz ), cosz ctgz = sinz = i(eiz + e iz ) (e iz e iz ). a) Sa to funkcje holomorficzne w swojej dziedzinie tzn. sinz i cosz dla z C, tgz dla z {z C : z = kπ + π, k Z}, ctgz dla z {z C : z = kπ, k Z}. 2 8
19 Korzystamy z faktu, że funkcja wyk ladnicza e z jest funkcja holomorficzna oraz z w lasności dzia lań na tych funkcjach. Stad można wyprowadzić wzory na pochodna: (cosz) = 2 (ieiz ie iz ) = i 2 (eiz e iz ) = 2i (eiz e iz ) = sinz. (sinz) = 2i (ieiz + ie iz ) = i 2i (eiz + e iz ) = 2 (eiz + e iz ) = cosz. b) cos 2 z + sin 2 z =. (tgz) = cos 2 z (ctgz) = sin 2 z. ( ) e cos 2 z + sin 2 iz + e iz 2 ( ) e iz e iz 2 z = + 2 2i = ( e 2iz + 2e iz e iz + e 2iz) ( e 2iz 2e iz e iz + e 2iz) 4 4 = 4eiz e 2iz 4 =. c) Cześci rzeczywiste i urojone funkcji trygonometrycznych wynosza odpowiednio: Dowód podamy dla funkcji sinz sinz = sinxchy + icosxshy cosz = cosxchy isinxshy sin2x tgz = cos2x + ch2y + i sh2y cos2x + ch2y sinz = eiz e iz 2i = ei(x+iy) e i(x+iy) 2i = e y (cosx + isinx) e y (cosx isinx) ( ) 2i ( ) e y e y e y + e y = cosx + isinx 2i 2i = sinxchy + icosxshy. = e y+ix e y ix 2i d) Funkcje trygonometryczne sinz, cosz, tgz sa rozszerzeniem do dziedziny zespolonej funkcji sinx, cosx, tgx. 9
20 Niech z = x + i0 IR. Wtedy sinz = sinxch0 + icos0sh0 = sinx + i0 = sinx. cosz = cosxch0 icosxsh0 = cosx i0 = cosx. sin2x tgz = cos2x + ch0 + i sh0 cos2x + ch0 = 2sinxcosx + (2cos 2 x ) = tgx. e) Funkcje trygonometryczne sa okresowe tzn. sinz i cosz o okresie podstawowym T = 2π. tgz i ctgz o okresie podstawowym T = π. sin(z + 2π) =sin(x + iy + 2π) = sin(x + 2π)chy + icos(x + 2π)shy Dowód dla cosz jest analogiczny. =sin(x)chy + icos(x)shy = sinz. sin2(x + π) tg(z + π) = cos2(x + π) + ch2y + i sh2y cos2(x + π) + ch2y sin2x = cos2x + ch2y + i sh2y cos2x + ch2y = tgz. f) sinz = sin 2 x + sh 2 y oraz cosz = cos 2 x + sh 2 y. Ponieważ funkcja hiperboliczna shy jest nieograniczona, wynika sta, że w przeciwieństwie do funkcji rzeczywistych funkcje sinz i cosz sa nieograniczone. g) sinz, tgz, ctz to funkcje nieparzyste, natomiast cosz jest funkcja parzysta tzn. sin( z) = sinz, coz( z) = cosz. h) sin( z) = sinz, cos( z) = cosz tg( z) = tgz ctg( z) = ctgz. i) sin(z ± z 2 ) = sinz cosz 2 ± cosz sinz 2. cos(z + z 2 ) = cosz cosz 2 sinz sinz 2. cos(z z 2 ) = cosz cosz 2 + sinz sinz 2. j) Funkcje sinz oraz cosz przyjmuja wszystkie wartości z p laszczyzny otwartej C. Funkcje tgz i ctgz omijaja dwie wartości i, i, natomiast przyjmuja wartość, tgz w punktach z k = π + kπ, ctgz w punktach z 2 k = kπ, k Z. 20
21 3.3 Funkcje hiperboliczne Funkcje chz i shz w dziedzinie zespolonej definiujemy tak samo jak w dziedzinie rzeczywistej tzn. chz := ez + e z, shz := ez e z, 2 2 W lasności thz := shz chz = ez e z e z + e z, chz cthz := shz = ez + e z e z e. z a) Sa to funkcje holomorficzne w swojej dziedzinie tzn. shz i chz dla z C, thz dla z {z C : z = i(kπ + π ), k Z}, cthz dla z {z C : z = ikπ, k Z}. 2 (chz) = shz, (shz) = chz, (thz) = ch 2 z, (cthz) = sh 2 z. b) ch 2 z sh 2 z = dla z C. c) Cześci rzeczywiste i urojone funkcji hiperbolicznych wynosza odpowiednio: shz = shxcosy + ichxsiny, chz = chxcosy + ishxsiny, sh2x thz = ch2x + cos2y + i sin2y ch2x + cos2y. d) Funkcje hiperboliczne shz, chz, thz, cthz sa rozszerzeniem do dziedziny zespolonej funkcji shx, chx, thx, cthx. e) Funkcje hiperboliczne sa okresowe tzn. shz i chz o okresie podstawowym T = 2πi. thz i cthz o okresie podstawowym T = πi. f) shz = sh 2 x + sin 2 y oraz chz = sh 2 x + cos 2 y. g) cosiz = chz, siniz = ish(z). 2
22 3.4 Funkcja logarytmiczna Niech z C {0}. Każda liczbe zespolona w spe lniajac a równanie e w = z nazywamy logarytmem liczby z i oznaczamy lnz. Niech z = x + iy = e w = e u+iv = e u (cosv + isinv). (3.5) Zatem z = e u czyli u = ln z = ln x 2 + y 2. Z (3.5) wynika, że v = Argz +2kπ dla pewnego k Z, gdzie Argz oznacza argument g lówny liczby z. Każda liczba zespolona z C {0} ma nieskończenie wiele logarytmów wyrażonych wzorem Funkcja zdefiniowa wzorem w = u + iv = ln z + i(argz + 2kπ), k Z. lnz = ln z + iargz (3.6) dla z = 0 nazywamy funkcja logarytmiczna. Funkcja lnz jest nieskończenie wielowartościowa. Funkcje Lnz = ln z + iargz, π < Argz π (3.7) nazywamy ga lezia g lówna logarytmu. Z (3.6) i (3.7) wynika, że lnz = Lnz + i2kπ, k Z. W każdym obszarze jednospójnym nie zawierajacym 0 i istnieje jednoznaczna ga l aź logarytmu. Takim obszarem jest np. p laszczyzna rozcieta wzd luż osi ujemnej tzn. 3.5 Funkcja pot egowa E = C {x R : x 0}. Niech μ bedzie dowolna liczba zespolona, E obszarem spójnym w którym istnieje jednoznaczna ga l aź logarytmu zmiennej z. Funkcje potegowa o wyk ladniku μ nazywamy funkcje zdefiniowana wzorem z μ = e μlnz. (3.8) Jest to także fukcja wielowartościowa. Ga l ezi a g lówna tej funkcji nazywamy ga l aź zdefiniowana za pomoca ga l ezi g lównej logarytmu tzn. e μlnz. Szczególnym przyk ladem funkcji potegowej jest funkcja n z = e (/n)lnz zwana pierwiastkiem n-stopnia z liczby z C {0}. W każdym obszarze jednospójnym nie zawierajacym zera i istnieje dok ladnie n ga l ezi różniacych sie czynnikiem e 2kπi/n, k = 0,,... n. 22
23 3.6 Powierzchnie Riemanna funkcji wielowartościowych Funkcja lnz zdefiniowana dla z C {0} jest nieskończenie wielowartościowa. Na p laszczyźnie rozcietej wzd luż pó losi rzeczywistej ujemnej istnieje nieskończenie wiele ga l ezi jednoznacznych logarytmu Lnz + 2kπi, k Z. Utwórzmy nieskończony ciag tak rozcietych p laszczyzn i ponumerujmy je liczbami k Z. Z każdej p laszczyzny usuwamy punkt 0. L aczymy górny brzeg rozciecia każdej z nich z dolnym brzegiem rozciecia nastepnej tak aby punkty brzegowe o tych samych wspó lrzednych tworzy ly jeden punkt. Otrzymamy nieskończenie wielolistna powierzchnie z lożona z plaszczyzn zwanych liściami. Taka powierzchnia przedstawia powierzchnie Riemanna pe lnej funkcji lnz. Punktom p laszczyzny oznaczonej liczba 0 przyporzadkujemy wartości ga l ezi g lownej Lnz. Ogólnie, punktowi z n-p laszczyzny przyporzadkowujemy wartości Lnz + i2nπ. W ten sposób każdej wartości funkcji lnz zostaje przyporzadkowany dok ladnie jeden punkt powierzchni i na odwrót. Na tej powierzchni lnz jest funkcja jednoznaczna. Startujac z pewnego punktu z i okrażaj ac punkt 0 dojdziemy po jednym okrażeniu do punktu z ± 2πi zależnie od tego czy okrażamy punkt 0 w dodatniej czy ujemnej orientacji. Funkcja n z ma n ga l ezi jednoznacznych na ca lej p lasczyźnie rozcietej wzd luż pó losi rzeczywistej ujemnej. Gdy okrażamy raz punkt 0 wzd luż pewnej krzywej zamknietej w kierunku dodatnim na p laszczyźnie nierozcietej, wówczas każda ga l aź przechodzi w nastepn a. Wartość funkcji zostaje pomnożona przez e 2πi/n. Po n-krotnym okrażeniu punktu 0 wartość funkcji wraca do swej poczatkowej wartości bo zmieni sie o czynnik e 2πi/n =. n Aby skonstruować powierzchnie Riemanna funkcji z umieszczamy n rozcietych p laszczyzn wzdluż osi rzeczywistej ujemnej i l aczymy górny brzeg rozciecia każdej p laszczyzny z dolnym brzegiem rozciecia nastepnej. Tak samo po l aczymy górny brzeg ostatniej p laszczyzny z dolnym brzegiem pierwszej. Zawsze l aczymy punkty o tych samych wspó lrzednych. Otrzymana n w ten sposób n-listna powierzchnia przedstawia powierzchnie Riemanna pe lnej funkcji z. Na jednym liściu tej powierzchni rozmieśćmy wartości jednoznacznej ga l ezi naszej funkcji, a na każdym nastepnym liściu wartości tej ga l ezi pomnożonej przez e 2πi/n. W ten sposób n każdej wartości funkcji z zostaje przyporzadkowany dok ladnie jeden punkt powierzchni i n na odwrót. Na tej powierzchni z jest funkcja jednoznaczna. 4 Szeregi funkcyjne 4. Szeregi liczbowe Definicja 4. Szereg a 0 + a + a = a n o dowolnych wyrazach zespolonych nazywamy zbieżnym do sumy s, gdy ciag sum czastkowych s n = n k=0 a n, n N, jest zbieżny do granicy s. 23
24 Definicja 4.2 Szereg a n nazywamy: i) bezwzgl ednie zbieżnym jeśli a n jest zbieżny, ii) warunkowo zbieżnym jeśli jest zbieżny ale nie jest bezwgl ednie zbieżny. Twierdzenie 4. i) Jeżeli szereg a n jest zbieżny, to lim n a n = 0. ii) Szereg bezwzglednie zbieżny jest zbieżny przy dowolnym uporzadkowaniu wyrazów i jego suma nie zależy od porzadku wyrazów. iii) Szereg a n, gdzie a n = α n +iβ n, jest zbieżny do sumy s = α+β wtedy i tylko wtedy, gdy szeregi α n i β n sa zbieżne tzn. α n = α i β n = β. Twierdzenie 4.2 (Kryterium porównawcze) Jeżeli dla prawie wszystkich wyrazów szeregu a n zachodzi nierówność a n A n i szereg A n jest zbieżny, to szereg a n jest zbieżny bezwzglednie. Twierdzenie 4.3 (Kryterium d Alamberta) Szereg a a n jest bezwzglednie zbieżny, gdy lim n+ n a n < oraz rozbieżny, gdy lim n a n+ a n >. Twierdzenie 4.4 (Kryterium Cauchy ego) Szereg a n jest bezwzglednie zbieżny, gdy lim sup n n a n < oraz rozbieżny, gdy lim sup n n a n >. Twierdzenie 4.5 (Kryterium Dirichleta) Szereg a nb n jest zbieżny, jeśli wyrazy a n sa rzeczywiste, dodatnie i ze wzrostem n maleja do zera, a ciag sum czastkowych szeregu b n jest ograniczony. Przyk lad 4. Szereg z n n= jest zbieżny dla z =, z =, bo przyjmuj ac n a n =, b n n = z n, z = i z > η otrzymamy s n = z + z z n = z( z n ) z < 2 η, a wiec za lożenia kryterium Dirichleta sa spe lnione. Zauważmy, że ten szereg nie jest zbieżny bezwglednie dla z takich, że z =, ponieważ z n n= n = n= =. n 24
25 4.2 Rodzaje zbieżności szeregów funkcyjnych Definicja 4.3 Niech D C zbiór (czesto otwarty lub obszar), f n : D C ciag funkcji. Powiemy, że szereg funkcyjny n= f n(z) jest zbieżny w D jeżeli ciag {s n (z) = n k= f k(z)} jest zbieżny w D tzn. jeśli granica lim n s n (z) = s(z) jest funkcja dobrze określona w zbiorze D. Taki rodzaj zbieżności nazywamy zbieżnościa punktowa. Zbieżność w D nazywamy jednostajna, jeśli ε N(ε) n > N(ε) z D s n (z) s(z) < ε. Warunek jednostajnej zbieżności szeregu n= f n(z) można także sformu lować nastepuj aco: ε N(ε) n > N(ε) z D n=n+ f n (z) < ε. Funkcje graniczna s(z) = lim n s n (z) nazywamy suma danego szeregu. Uwaga 4. Niech D C zbiór otwarty (lub obszar), f n : D C ciag funkcji ciag lych. Jeżeli ciag funkcyjny (szereg funkcyjny n= f n(z)) jest zbieżny jednostajnie w D, to granica ciagu (suma szeregu) jest funkcja ciag l a w D. Twierdzenie 4.6 (Weierstrassa) Szereg n= f n(z) jest zbieżny jednostajnie w zbiorze D C, jeśli istnieje ciag liczbowy {a n } n= taki, że n N, f n (z) a n i szereg n= a n jest zbieżny. Definicja 4.4 Niech D C, f n : D C ciag funkcji. Szereg funkcyjny n= f n(z) nazywamy zbieżnym niemal jednostajnie w zbiorze D, jeśli jest on zbieżny jednostajnie na każdym zwartym podzbiorze zbioru D. Uwaga 4.2 Zbieżność jednostajna można czesto zastapić zbieżnościa niemal jednostajna. Granica zbieżnego niemal jednostajnie ciagu (szeregu) funkcji ciag lych jest funkcja ciag l a. 25
26 4.3 Szeregi pot egowe Definicja 4.5 Szeregiem pot egowym o środku w punkcie z 0 nazywamy szereg postaci gdzie a n C. a n (z z 0 ) n, (4.) Definicja 4.6 Promieniem zbieżności szeregu potegowego (4.) nazywamy kres górny zbioru tych liczb r, że dany szereg jest zbieżny w kole {z : z z 0 < r}. Wzór Cauchy ego-hadamarda Niech dany b edzie szereg pot egowy (4.) i lim sup n n an = R, (4.2) gdzie 0 R (przyjmujemy, że =, = 0). Wówczas szereg (4.) jest zbieżny w 0 każdym punkcie z, dla którego z z 0 < R, i jest rozbieżny w każdym punkcie z, dla którego z z 0 > R. Dowód Niech 0 < R <. Wtedy dla każdego ε > 0 istnieje N N takie, że dla n N mamy n an < /R + ε. Stad [( ) n a n (z z 0 ) n < R + ε z z 0 ]. (4.3) Jeśli z z 0 < R, to ε można dobrać tak ma le, że spe lniona bedzie nierówność ( ) R + ε z z 0 = q <. Wówczas z (4.3) widać, że wyrazy szeregu (4.) dla n N sa majoryzowane przez wyrazy szeregu geometrycznego qn i w konsekwencji szereg (4.) jest zbieżny, gdy z z 0 < R. Z definicji granicy górnej wynika, że dla dowolnej liczby ε > 0 istnieje taki podciag n k, że n k a nk > /R ε. 26
27 Zatem a nk (z z 0 ) n k > [( ) nk R ε z z 0 ]. (4.4) Jeśli z z 0 > R, to liczbe ε można dobrać tak ma l a aby (/R ε) z z 0 >. Wówczas z (4.4) wynika, że a nk (z z 0 ) n k >, a w konsekwencji nie zachodzi warunek konieczny zbieżności szeregu (4.), wiec szereg ten jest rozbieżny dla z z 0 > R. Wniosek 4. Obszarem zbieżności szeregu potegowego (4.) jest ko lo {z : z z 0 < R}, gdzie R jest liczba wyznaczona ze wzoru Cauchy ego-hadamarda. Przyk lad 4.2. Szereg zn jest zbieżny w kole K(0, ) = {z : z < }, ponieważ lim sup n n an = R =. Jeśli z =, to szereg n= zn nie jest zbieżny, bo nie zachodzi warunek konieczny zbieżności - wyraz z n = e inφ ma modu l równy, czyli nie daży do zera. 2. Szereg z n n= n 2 oraz n N z n n 2 n 2. ( jest zbieżny w kole K(0, ) = {z : z }, ponieważ lim sup n n 2 n = R = n 2 <.) Zatem szereg jest zbieżny w kole i na brzegu. 3. Dla szeregu nn z n promień zbieżności R = 0, ponieważ lim sup n Szereg jest zbieżny tylko dla z = 0. n nn = lim sup n n = = R. Twierdzenie 4.7 (Abela) Jeżeli szereg potegowy a nz n jest zbieżny w punkcie z = 0, to jest on bezwglednie zbieżny w kole K(0, z ) = {z : z < z } oraz jest zbieżny jednostajnie w każdym kole K(0, ρ), gdzie ρ < z. 27
28 Dowód. Ponieważ szereg a nz n jest zbieżny, to zachodzi warunek konieczny zbieżności, czyli lim n a n z n 0. Zatem Stad wynika, że M > 0 N > 0 n N a n z n < M. M > 0 N > 0 n N z z < z a n z n < M. ( ) Pokażemy, że szereg a nz n jest zbieżny w K(0, z ) = {z : z < z }. Mamy a n z n = a nz n z n = a nz n z n M z n = Mqn, z n gdzie q := z z <. Ponieważ q <, szereg geometyczny n= Mqn jest zbieżny. Korzystajac z kryterium porównawczego otrzymamy, że szereg n= a nz n jest zbieżny bezwzglednie w kole K(0, z ) = {z : z < z }. Niech ρ < z. Weźmy z takie, że z ρ. Wtedy istnieje ρ takie, że ρ < ρ < z. a n z n = a nρ n z n ρ n = a nρ n z n ρ n Mpn, gdzie p := z ρ <, gdzie an ρ n < M z (*). Zatem z kryterium Weierstrassa szereg n= a nz n jest zbieżny bezwgl ednie jednostajnie w kole K(0, ρ) = {z : z ρ}. Zatem w kole K(0, z ) = {z : z < z } szereg pot egowy jest zbieżny niemal jednostajnie. Twierdzenie 4.8 (o holomorficzności sumy szeregu potegowego) Jeżeli promień R zbieżności szeregu potegowego a nz n jest dodatni, to f-suma tego szeregu jest funkcja holomorficzna w kole K(0, R) = {z : z < R} i dla każdego z K(0, R) f (z) = na n z n. (Szereg potegowy wewnatrz ko la zbieżności można różniczkować wyraz po wyrazie). Dowód Napiszemy szereg pochodnych formalnych n= z n na n z n. n= 28 z n
29 Promień zbieżności tego szeregu jest taki sam jak szeregu n= a nz n, ponieważ n n lim sup n an = lim sup an. n n Z Twierdzenia Abela wynika, że szereg n= a nz n jest zbieżny jednostajnie, w każdym kole K(0, ρ), gdzie ρ < R. Weźmy z 0 K(0, R), gdzie z 0 < ρ < R. Rozpatrzmy iloraz różnicowy f(z) f(z 0 ) z z 0 = a n z n z n 0 z z 0 = ( ) a n z n + z n 2 z zz0 n 2 + z0 n, gdzie z K(0, R). Wykażemy, że otrzymany szereg jest bezwglednie jednostajnie zbieżny (skorzystamy z tw. Weierstrassa). ( ) an z n + z n 2 z zz0 n 2 + z0 n an n ρ n jeśli z ρ. Weźmy ρ takie, że ρ < ρ < R. Wtedy szereg a n ρ n jest zbieżny, zatem lim n a n ρ n = 0. Stad istnieje M > 0 takie, że dla każdego n N, a n ρ n M. Niech q := ρ ρ < oraz ( ) n ρ a n nρ n a n nρ n ρ M ρ nqn. Szereg M q <. Szereg szereg ρ ρ nqn n M jest zbieżny bo z kryterium Cauchy ego wynika, że lim sup n ρ nqn = M ρ nqn potraktujemy jako majorante w twierdzeniu Weierstrassa. Stad ( ) a n z n + z n 2 z zz0 n 2 + z0 n jest bezwgl ednie jednostajnie zbieżny w otoczeniu z 0, a dok ladniej dla z ρ. Wtedy istnieje granica tego szeregu dla z z 0. Zatem f (z 0 ) = lim z z0 f(z) f(z 0 ) z z 0 = lim z z0 Czyli f jest holomorficzna K(0, R). ( a n z n + z n 2 z zz0 n 2 + z0 n ) = na n z n 0. 29
30 Wniosek 4.2 Szereg potegowy ma pochodna dowolnego rzedu: k N f (k) (z) = n(n )... (n k + )a n z n k. n=k Otrzymane wnioski można uogólnić na przypadek szeregów postaci a n(z z 0 ) n. Twierdzenie 4.9 Jeżeli funkcje f można przedstawić w kole K(z 0, r) = {z : z z 0 < r} w postaci sumy szeregu potegowego f(z) = (z z 0 ) n, to wspó lczynniki tego szeregu sa wyznaczone jednoznaczne i określaja je wzory a n = f (n) (z 0 ), n = 0,, 2,... n! Dowód Wstawiajac do wzoru na szereg za z punkt z 0 otrzymamy f(z 0 ) = a 0. Różniczkujac wyraz po wyrazie dostaniemy f (z) = a + 2a 2 (z z 0 ) + 3a 3 (z z 0 ) Podstawiajac za z = z 0 otrzymamy, że f (z 0 ) = a. Po n-krotnym zróżniczkowaniu dostaniemy, że f (n) (z) = n!a n + a (z z 0 ) + a 2 (z z 0 ) Dla z = z 0 dostaniemy, że f (n) (z 0 ) = n!a n. Stad a n = f (n) (z 0 ). n! Uwaga 4.3 (Inne brzmienie powyższego twierdzenia) Każdy zbieżny szereg pot egowy jest szeregiem Taylora swojej sumy. 4.4 Funkcje analityczne Definicja 4.7 Niech D C obszar, funkcje f : D C nazywamy analityczna w D gdy dla każdego z 0 D istnieje szereg potegowy postaci a n(z z 0 ) n zbieżny w kole K(z 0, r) D taki, że f(z) = (z z 0) n dla z K(z 0, r). 30
31 Ozn. A(D) oznacza zbiór wszystkich funkcji analitycznych w D. Z twierdzenia 4.8 wynikaja nastepuj ace wnioski. Wniosek 4.3 Zachodzi inkluzja A(D) H(D). Wniosek 4.4 Jeżeli f A(D), to f posiada pochodne dowolnego rz edu. (Porównać z wnioskiem 4.2). Wniosek 4.5 Suma szeregu potegowego jest funkcja analityczna w kole zbieżnosci tego szeregu. (Porównać z twierdzeniem 4.9). Definicja 4.8 Iloczynem szeregów potegowych a n(z z 0 ) n i b n(z z 0 ) n nazywamy szereg potegowy postaci (a 0 b n + a b n a n b 0 )(z z 0 ) n. Twierdzenie 4.0 (Cauchy ego) Jeżeli szeregi a n(z z 0 ) n i b n(z z 0 ) n sa zbieżne odpowiednio w ko lach K(z 0, r ) i K(z 0, r 2 ), to ich iloczyn (a 0 b n + a b n a n b 0 )(z z 0 ) n jest zbieżny w kole K(z 0, r), gdzie r = min{r, r 2 }. Bez dowodu. Twierdzenie 4. Jeżeli f, g A(D), to f ± g A(D), fg A(D). Bez dowodu. Przyk lad 4.3 Rozwinać f(z) = z w szereg wokó l 3
32 (a) punktu z 0 = 2, z = (z ) = zbieżny w kole {z : z 2 < 2 }. 2(z 2 ) = 2 ( 2 n z ) n 2 (b) z 0 = 2 zbieżny w kole K( 2, 3 2 ). z = 2 3 2(z + ) = n (z + 2 )n Uwaga 4.4 Promień zbieżności szeregu jest wyznaczony przez odleg lość punktu z 0 - środka szeregu od najbliższego punktu nieholomorficzności. 3 n 5 Odwzorowania konforemne 5. Interpretacja geometryczna pochodnej zespolonej Niech I :=< α, β > R. Funkcj e < α, β > t z(t) = x(t) + iy(t) C nazywamy funkcja zespolona zmiennej rzeczywistej. Definicja 5. Funkcja z(t) jest ciag la w t 0 jeśli lim t t0 z(t) = z(t 0 ). Definicja 5.2 Pochodna funkcji z(t) w punkcie t 0 I definiujemy jako granice ilorazu różnicowego tzn. ( z z(t) z(t 0 ) x(t) x(t0 ) (t 0 ) = lim = lim + i y(t) y(t ) 0). t t0 t t 0 t t0 t t 0 t t 0 Zatem z (t 0 ) = x (t 0 ) + iy (t 0 ). Definicja 5.3 Równanie postaci z = z 0 + at, t R, a, z C, a = 0, określa prosta przechodzac a przez punkt z 0. Kat nachylenia prostej do osi OX jest określony przez argument g lówny liczby a. 32
33 Definicja 5.4 Wykres funkcji ciag lej z(t) nazywamy krzywa i oznaczmy symbolem γ. Równanie siecznej do wykresu γ przechodzacej przez punkty z(t 0 ) i z(t ) ma postać z = z(t 0 ) + z(t ) z(t 0 ) t t 0 t, t I. Gdy t t 0, to sieczna daży do stycznej w punkcie z 0 = z(t 0 ). Stad równanie stycznej w tym punkcie ma postać z = z 0 + z (t 0 )t, a argument g lówny φ = Argz (t 0 ) jest katem nachylenia stycznej do osi Ox. Niech D C obszar, f : D C funkcja holomorficzna, z 0 D oraz f (z 0 ) = 0. Niech γ bedzie lukiem g ladkim o równaniu z(t), t I (tzn. funkcja z(t) jest funkcja klasy C ) wychodzacym z punktu z 0 = z(t 0 ). Wtedy funkcja f przekszta lca luk γ na luk Γ = f(γ) o równaniu w = f(z(t)) = w(t) wychodzacy z punktu w 0 = f(z 0 ). Z tożsamości w(t) w(t 0 ) = f(z(t) f(z(t 0) t t 0 z(t) z(t 0 ) z(t) z(t 0 ) t t 0 dla t t 0 otrzymujemy w (t 0 ) = f (z(z 0 ))z (t 0 ), wiec styczna do Γ w punkcie w 0 tworzy z osia rzeczywista kat Φ := Argw (t 0 ) = Arg (f (z 0 )z (t 0 )) = Argf (z 0 ) + φ. (5.) Uwaga 5. Przy odwzorowaniu holomorficznym w otoczeniu punktu z 0 takiego, że f (z 0 ) = 0, nachylenie φ do osi Ox każdego g ladkiego luku γ wychodzacego z punktu z 0 wzrasta o kat równy argumentowi pochodnej f (z 0 ). Gdy z z 0, wówczas stosunek odleg lości w w 0 = f(z) f(z 0 ) do odleg lości z z 0 daży do f (z 0 ). Granice tego stosunku czyli f (z 0 ) nazywamy dylatacja odwzorowania f w punkcie z 0. Uwaga 5.2 Przy odwzorowaniu holomorficznym w otoczeniu punktu z 0 takiego, że f (z 0 ) = 0, każdy luk wychodzacy z punktu z 0 wyd luża sie lub wzglednie skraca sie w pobliżu punktu z 0 w tym samym stosunku równym dylatacji f (z 0 ). 33
34 Uwaga 5.4 Niech D C obszar, f : D C funkcja holomorficzna, z 0 D oraz f (z 0 ) = 0. Niech styczne do krzywych g ladkich γ, γ 2 wychodzacych z punktu z 0 maja katy nachylenia równe odpowiednio φ, φ 2. Definujemy Γ = f(γ ), Γ 2 = f(γ 2 ). Ponieważ f jest funkcja holomorficzna w D, to Γ i Γ 2 sa krzywymi g ladkimi. Kat nachylenia stycznej do krzywych Γ, Γ 2 w w 0 = f(z 0 ) oznaczmy przez Φ, Φ 2. Wtedy Φ 2 Φ = (Argf (z 0 ) + φ 2 ) (Argf (z 0 ) + φ ) = φ 2 φ. (5.2) Definicja 5.4 Katem miedzy krzywymi g ladkimi γ i γ 2 wychodzacymi z punktu z 0 nazywamy kat skierowany miedzy miedzy stycznymi do krzywych γ i γ 2 w punkcie z 0. Wniosek 5. Z Uwagi 5.4 wynika, że jeśli f (z 0 ) = 0, to odzworowanie holomorficzne f zachowuje kat miedzy krzywymi g ladkimi w ma lym otoczeniu tego punktu tzn. kat skierowany miedzy obrazami krzywych jest taki sam jak kat skierowany miedzy krzywymi. 5.2 Interpretacja geometryczna równań Cauchy ego-riemanna Niech f(z) = u(x, y) + iv(x, y) bedzie funkcja holomorficzna w obszarze D C. Rozpatrzmy rodziny krzywych u(x, y) = c, v(x, y) = c, gdzie c, c oznaczaja sta le rzeczywiste. Weźmy punkt z 0 w którym pochodna f (z 0 ) = 0. Styczne do wykresu tych krzywych opisuja sie równaniami u x(x 0, y 0 )(x x 0 ) + u y(x 0, y 0 )(y y 0 ) = 0 v x(x 0, y 0 )(x x 0 ) + v y(x 0, y 0 )(y y 0 ) = 0. (5.3) Na mocy równań Cauchy ego-riemanna mamy, że u x(x 0, y 0 )v x(x 0, y 0 ) + u y(x 0, y 0 )v y(x 0, y 0 ) = 0. (5.4) To oznacza, że styczne sa prostopad le. Aby to zobaczyć spróbujemy rozwik lać równanie u(x, y) = c w otoczeniu (x 0, y 0 ). Ponieważ f (z 0 ) = 0, to u y(x 0, y 0 ) = 0 lub v y(x 0, y 0 ) = 0. Jeśli u y(x 0, y 0 ) = 0, to z twiedzenia o funkcjach uwik lanych równanie u(x, y) = c opisuje fukcje uwik lana y A (x) oraz u x(x 0, y 0 ) + u y(x 0, y 0 )y A (x 0) = 0. Stad y A(x 0 ) = u x(x 0, y 0 ) u y(x 0, y 0 ). (5.5) 34
35 Analogicznie jeśli v y(x 0, y 0 ) = 0, to z twiedzenia o funkcjach uwik lanych równanie v(x, y) = c opisuje fukcje uwik lana y B (x) oraz v x(x 0, y 0 ) + v y(x 0, y 0 )y B (x 0) = 0. Stad Z równań (5.5) i (5.6) wynika, że ( ) ( ) u y A(x 0 )y B(x 0 ) = x (x 0, y 0 ) v x (x 0, y 0 ) = u y(x 0, y 0 ) v y(x 0, y 0 ) y B(x 0 ) = v x(x 0, y 0 ) v y(x 0, y 0 ). (5.6) ( v y (x 0, y 0 ) v x(x 0, y 0 ) ) ( ) v x (x 0, y 0 ) =. v y(x 0, y 0 ) 5.3 Odworowania konforemne Niech D C zbiór otwarty, f H(D). Funkcj e f(z) = u(x, y)+iv(x, y) możemy potraktować jako odzworowanie rzeczywiste (x, y) (u(x, y), v(x, y)). W punkcie z 0 D rozpatrzmy odwzorowanie styczne [Δx, Δy] [Δu, Δv], gdzie Δx = x x 0, Δy = y y 0, u u 0 = Δu = u(x x 0, y 0 )Δx + u(x y 0, y 0 )Δy, Δv = v v 0 = v (x x 0, y 0 )Δx + v (x y 0, y 0 )Δy. Odwzorowanie styczne do f w punkcie z 0 możemy też zapisać w postaci zespolonej w w 0 = f z (z 0)(z z 0 ) + f z (z 0)( z z 0 ), gdzie w 0 = f(z 0 ) = u 0 + iv 0. Jakobian tego przekszta lcenia wyraża sie wzorem (u, v) J = (x, y) = u v x y u 2 2 v y x = f z f z. Definicja 5.5 Odwzorowanie holomorficzne f nazywamy konforemnym w punkcie z 0, jeśli zachowuje kat skierowany miedzy dowolnymi krzywymi wychodzacymi z punktu z 0. Definicja 5.6 Odwzorowanie holomorficzne, które jest różnowartościowe i konforemne w każdym punkcie obszaru D nazywamy konforemnym w D. 35
36 Twierdzenie 5. Odwzorowanie holomorficzne f jest konforemne w punkcie z 0 wtedy i tylko wtedy, gdy f (z 0 ) = 0. Dowód Implikacja zosta la już udowodniona (patrz wniosek 4.).. Przypuśćmy, że f (z 0 ) = 0. Rozpatrzmy dwa wektory Δz = z z 0 = oraz Δz 2 = z z 0 = i. Wektory te sa prostopad le (Δz 2 = iδz ). Odworowanie styczne Δz Δw w punkcie z 0 przyjmuje wartość Δw = f (z z 0) + f (z z 0) = 0 jeśli Δz = oraz Δw 2 = f (z z 0)i + f (z z 0)i = 0. dla Δz = i. Ponieważ wektory Δz = i Δz 2 = i sa prostopad le, a f zachowuje katy w z = z 0, zatem wektor Δw = jet prostopad ly do wektora Δw 2. Tymczasem wektory Δw 2 i Δw sa zerowe, zatem nie można zdefiniować kata miedzy nimi, co przeczy za lożeniu, że f jest konforemne. Uwaga 5.5 Za lożenie, że f (z 0 ) = 0 jest istotne. Dowód Rozpatrzmy funkcje f(z) = z 2 oraz krzywa γ = {z : x = t, y = 0, t R + } {0} i γ 2 = {z = re i π 4, r R + } {0}. Kat w z 0 miedzy γ i γ 2 wynosi π. Obrazem γ 4 jest γ, zaś f(γ 2 ) = {z = re 2i π 4 = re i π 2, r R + }. Zatem kat miedzy obrazami krzywych γ i γ 2 w punkcie w 0 = f(z 0 ) = 0 wynosi π, czyli f nie zachowuje k atów 2 w z 0 = 0. Wniosek 5.2 Jeżeli funkcja f jest różnowartościowa i holomorficzna w obszarze D oraz dla każdego z D, f (z 0 ) = 0, to f jest konforemne w D. Definicja 5.7 Odwzorowanie postaci f(z) = az+b, ad bc = 0, a, b, c, d C nazywamy homografi a. cz+d f( d ) =. Odzworowanie odwrotne do f(z) jest także homo- c Przyjmujemy, że f( ) = a c grafia tzn. f (w) = dw b a cw. Twierdzenie 5.2 (o konforemności homografii) Homografia jest konforemnym przekszta lceniem C na C. Dowód 36
37 Latwo sprawdzić, że homografia jest różnowartościowa. Policzymy pochodna homografii. f (z) = a(cz + d) c(az + b) (cz + d) 2 = ad cb (cz + d) 2 = 0 dla z C { d c }. Zatem homografia jest konforemnna w C { d }. Zanim skończymy dowód podamy jeszcze c kilka definicji. Definicja 5.8 Kat w punkcie miedzy krzywymi γ i γ 2 definiujemy jako kat miedzy obrazami krzywych Γ i Γ 2 przy przekszta lceniu z Z = w punkcie Z = 0. z Pokażemy, że homografia jest konforemna w z = d. Wiemy, że f( d) =. Niech γ c c i γ 2 bed a krzywymi przechodzacymi przez d. Wtedy ich obrazy Γ c = f(γ ) i Γ 2 = f(γ 2 ) bed a krzywymi przechodzacymi przez. Kat miedzy Γ i Γ 2 jest równy katowi miedzy krzywymi Γ, Γ 2, które sa obrazami Γ i Γ 2 przy odwzowowaniu W =, gdy W = 0. Zatem w W (z) = = cz+d. St ad f(z) az+b dw dz = c(az + b) a(cz + d) (az + b) 2 = cb ad (az + b) 2. Zatem dla z = d, W ( d ) = 0, czyli homografia jest w tym punkcie konforemna. c c Pozostaje sprawdzić, że homografia jest konforemna w. Wtedy rozpatrujemy ( ) a + bz H(z) = f = z c + dz w punkcie z = 0. Stad dh dz = b(c + dz) d(a + bz) (c + dz) 2 = cb ad (c + dz) 2. Zatem dla H (0) = 0 o ile c = 0. Dla c = 0 mamy przekszta lcenie liniowe f(z) = az +b, a = 0. W tym przypadku rozpatrujemy F (z) = dh. Wtedy = a = 0 dla z = 0. f(/z) dz (a+bz) 2 Twierdzenie 5.3 Zbiór przekszta lceń homograficznych tworzy grupe nieabelowa z dzia laniem sk ladania przekszta lceń. Definicja 5.9 Okregiem na p laszczyźnie domknietej C nazywamy okrag na p laszczyźnie otwartej lub prosta. 37
38 Twierdzenie 5.4 Homografia przekszta lca okr egi na C na okr egi na C. Dowód Przedstawimy homografi e jako superpozycj e trzech przekszta lceń. w = L : z z D - translacja, az + b cz + d = a ad bc c c(cz + d) = A + B z D = L 3 L 2 L L 2 : z z - inwersja (szczególny przypadek homografii), L 3 : z A + Bz - z lożenie translacji i obrotu (ewentualnie jednok ladności gdy B R.) Translacja L przekszta lca okregi na okregi i proste na proste. Z lożenie translacji i obrotu ma też taka w lasność. Zosta lo do pokazania, że inwersja przekszta lca okregi na C na okregi na C. Napiszemy ogólne równanie okregu: γ : α(x 2 + y 2 ) + β x + β 2 y + δ = 0. Wstawimy z + z z z x =, y = 2 2i do równania okregu. Wtedy otrzymamy: γ : α(z z) + θz + θ z + δ = 0, gdzie θ = (β 2 iβ 2 ), θ = (β 2 + iβ 2 ). Przekszta lceniem odwrotnym do inwersji w = jest z też inwersja z =. W miejsce z wstawimy do równania okregu w z =. St ad w ( ) α + θ + θ + δ = 0. w w w w Mnożac stronami przez w w dostaniemy Jest to równanie okr egu. α + θ w + θw + δw w = 0. Definicja 5.0 Dwa punkty p i q sa symetryczne wzgledem okregu {z : z z 0 = r}, jeśli. p = z 0, q = z 0, p, q leża na jednej pó lprostej wychodzacej z z 0 tj. Arg(p z 0 ) = Arg(q z 0 ), 38
39 2. p z 0 q z 0 = r 2. Z tej definicji wynika, że punktem symetrycznym do z 0 jest. Twiedzenie 5.5 Homografia przekszta lca punkty symetryczne wzgl edem okr egów na C na punkty symetryczne wzgl edem ich obrazów. Problem Mamy dane przekszta lcenie f i obszar D. Znaleźć obraz f(d). Problem 2 Dane sa dwa obszary D i D 2. Znaleźć przkszta lcenie konforemne z D na D 2. Przyk lad 5. Wyznaczyć wszystkie homografie, które przekszta lcaja D = {z : Imz > 0} na kolo D(0, ). Wybierzmy punkt a taki, że Ima > 0. Punktem symetrycznym do niego wzgledem brzegu, czyli osi OX jest punkt a. Szukana homografia musi przekszta lcić punkt a na punkt należacy do D(0, ). Możemy przyjać, że f(a) = 0. Wtedy homografia f punkt a musi przekszta lcić na punkt symetryczny wzgledem 0 czyli na. Zatem f(a) = 0, f( a) =. Stad możemy napisać f(z) = k z a Pokażemy, że k = z a eiφ. Ponieważ f przekszta lca oś OX na okrag jednostkowy, to f() =. Korzystajac z tego dostaniemy = f() = k a a. Należy zauważyć, że z a = z a, wiec a = a. Stad a a = i w konsekwencji k =, czyli k = e iφ. Szukane homografie maja nastepuj ac a postać iφ z a f(z) = e, Ima > 0, φ [0, 2π). z a Twierdzenie 5.6 (Riemanna dla odwzorowań konforemnych) Jeżeli:. D i D obszary jednospójne takie, że brzeg każdego z nich zawiera co najmniej 2 punkty, 2. z 0 D, w 0 D dowolne punkty; φ [0, 2π). Wówczas istnieje dok ladnie jedno przekszta lcenie konforemne, które odwzorowuje obszar D na D i takie, że f(z 0 ) = w 0, Argf (z 0 ) = φ. 39
40 6 Ca lka z funkcji zespolonej 6. Ca lka z funkcji zespolonej zmiennej rzeczywistej Definicja 6. Niech < α, β > R. Dana jest funkcja zespolona ograniczona zmiennej rzeczywistej < α, β > t f(t) = u(t) + iv(t) C. Weźmy podzia l normalny odcinka < α, β > tzn. α = t 0 < t < t 2... t n = β, obierzmy w każdym przedziale punkt θ j < t j, t j > i utwórzmy sume ca lkowa S n = n f(θ j )(t j t j ), n =, 2,... j= Jeżeli dla każdego normalnego ciagu podzia lów przedzia lu < α, β > ciag sum cześciowych (S n ) jest zbieżny do tej samej granicy, niezależnej od wyboru punktów θ k, to granice te nazywamy ca lka funkcji zespolonej f po odcinku < α, β > R i oznaczamy Sume ca lkowa S n funkcji f tzn. jako S n = β α f(t)dt. można zapisać jako sumy ca lkowe cz eści rzeczywistej i cz eści urojonej n n u(θ j )(t j t j ) + i v(θ j )(t j t j ), n =, 2,.... j= j= Ponieważ lim n S n istnieje wtedy i tylko wtedy, gdy istnieja granice ciagu sum cześciowych odpowiadajacych cześci rzeczywistej u(t) i cześci urojonej v(t), zatem Uwaga 6. Funkcja f(t) = u(t) + iv(t) jest ca lkowalna na przedziale < α, β > wtedy i tylko wtedy, gdy funkcje u(t) i v(t) sa ca lkowalne na przedziale < α, β > oraz W lasności β α f(t)dt = β α β u(t)dt + i v(t)dt. α. Jeżeli funkcja f(t) jest ciag la w przedziale domknietym (lub ogólniej: ograniczona i majaca skończona ilość punktów nieciag lości) to jest ca lkowalna na przedziale < α, β >, ponieważ wtedy funkcje u(t) i v(t) sa ca lkowalne na przedziale < α, β >. 40
41 2. Jeżeli γ (α, β) to β α f(t)dt = γ α f(t)dt + β γ f(t)dt. 3. Jeżeli funkcja f(t) jest ca lkowalna, to jej modu l jest funkcja ca lkowalna oraz β β f(t)dt f(t) dt. α 4. Jeżeli funkcja f(t) jest ciag la w przedziale < α, β >, to funkcja F (t) zdefiniowana wzorem F (t) = t α α f(s)ds, t < α, β > jest funkcja pierwotna funkcji f(t) tzn. F (t) ma pochodna F (t) = f(t) określona w ca lym przedziale < α, β >. 5. Jeżeli funkcja F (t) jest funkcja pierwotna funkcji f(t) w przedziale < α, β >, to β α f(t)dt = F (β) F (α). Przyk lad 6. Funkcja f(t) = (a + it) n ma funkcje pierwotna równa (a+it)n + C, st ad i(n+) 0 [ (a + it) (a + it) n n+ dt = i(n + ) ] 0 = (a + i)n+ i(n + ) an+ i(n + ). Przyk lad 6.2 Funkcja f(t) = e t+it ma funkcje pierwotna równa et+it + C, stad +i 0 [ e e t+it t+it dt = + i ] 0 = e+i + i + i. Przyk lad 6.3 Funkcja f(t) = sin(at + b), a = 0 ma funkcje pierwotna równa cos(at + b) + C. a 4
ANALIZA ZESPOLONA. IV semestr 2013/14. oprac. Janina Kotus
 ANALIZA ZESPOLONA IV semestr 203/4 oprac. Janina Kotus Spis treści. Poj ecia podstawowe str. 5. Rzut stereograficzny str. 5.2 Metryki w C i C str. 6 2. Funkcje zespolone str. 8 2. Granica i ciag lość str.
ANALIZA ZESPOLONA IV semestr 203/4 oprac. Janina Kotus Spis treści. Poj ecia podstawowe str. 5. Rzut stereograficzny str. 5.2 Metryki w C i C str. 6 2. Funkcje zespolone str. 8 2. Granica i ciag lość str.
Indeks odwzorowania zmiennej zespolonej wzgl. krzywej zamknietej
 Indeks odwzorowania zmiennej zespolonej wzgl edem krzywej zamkni etej 1. Liczby zespolone - konstrukcja Hamiltona 2. Homotopia odwzorowań na okr egu 3. Indeks odwzorowania ciag lego wzgledem krzywej zamknietej
Indeks odwzorowania zmiennej zespolonej wzgl edem krzywej zamkni etej 1. Liczby zespolone - konstrukcja Hamiltona 2. Homotopia odwzorowań na okr egu 3. Indeks odwzorowania ciag lego wzgledem krzywej zamknietej
1. Liczby zespolone Zadanie 1.1. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone (1) 1 i (2) (5)
 . Liczby zespolone Zadanie.. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone () i +i, () 3i, (3) ( + i 3) 6, (4) (5) ( +i ( i) 5, +i 3 i ) 4. Zadanie.. Znaleźć moduł i argument główny
. Liczby zespolone Zadanie.. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone () i +i, () 3i, (3) ( + i 3) 6, (4) (5) ( +i ( i) 5, +i 3 i ) 4. Zadanie.. Znaleźć moduł i argument główny
Matematyka - semestr III
 Matematyka - semestr III Spis treści Analiza zespolona 4 Postacie liczby zespolonej i dzia lania na nich 4 2 Metryka w C, otoczenia i obszary 5 3 Pojecie funkcji, cześci rzeczywiste i urojone 6 4 Granica
Matematyka - semestr III Spis treści Analiza zespolona 4 Postacie liczby zespolonej i dzia lania na nich 4 2 Metryka w C, otoczenia i obszary 5 3 Pojecie funkcji, cześci rzeczywiste i urojone 6 4 Granica
c n (z z 0 ) n (2) Powiemy, że szereg Laurenta (2) jest zbieżny, jeśli każdy z szeregów zdefiniowanych w (1) jest f(z). Sume
 Szeregi Laurenta, punkty osobliwe izolowane, klasyfikacja funkcji ze wzgl edu na osobliwości Dane s dwa szeregi postaci c n (z z 0 ) n i c n (z z 0 ) n. (1) n=1 1 Pierwszy z tych szeregów jest zbieżny
Szeregi Laurenta, punkty osobliwe izolowane, klasyfikacja funkcji ze wzgl edu na osobliwości Dane s dwa szeregi postaci c n (z z 0 ) n i c n (z z 0 ) n. (1) n=1 1 Pierwszy z tych szeregów jest zbieżny
FUNKCJE ZESPOLONE Lista zadań 2005/2006
 FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
FUNKCJE ZMIENNEJ ZESPOLONEJ
 FUNKCJE ZMIENNEJ ZESPOLONEJ MiNI - zbiór zadań (wybór i opracowanie zadań Agnieszka Badeńska) Spis treści I. Liczby zespolone dzia lania i w lasności 3 II. Pochodna funkcji zespolonej, holomorficzność
FUNKCJE ZMIENNEJ ZESPOLONEJ MiNI - zbiór zadań (wybór i opracowanie zadań Agnieszka Badeńska) Spis treści I. Liczby zespolone dzia lania i w lasności 3 II. Pochodna funkcji zespolonej, holomorficzność
Kurs wyrównawczy - teoria funkcji holomorficznych
 Kurs wyrównawczy - teoria funkcji holomorficznych wykład 1 Gniewomir Sarbicki 15 lutego 2011 Struktura ciała Zbiór par liczb rzeczywistych wyposażamy w działania: { + : (a, b) + (c, d) = (a + c, b + d)
Kurs wyrównawczy - teoria funkcji holomorficznych wykład 1 Gniewomir Sarbicki 15 lutego 2011 Struktura ciała Zbiór par liczb rzeczywistych wyposażamy w działania: { + : (a, b) + (c, d) = (a + c, b + d)
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3
 WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania
 Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1 + iϕ n. = cos ϕ + i sin ϕ. e n z n n n. c M n z n, c n z Mn.
 WRAiT 2 #1 1. Dla jakich a C ciągi o wyrazach na n, a n 1 + a n, an /n, są zbieżne? 2. Wykaż zbieżność i znajdź granice ciągów n a k, a n 1 + a 2n ( a < 1), a n 1 + a 2n ( a > 1), 1 n 3. Dla danego ϕ R
WRAiT 2 #1 1. Dla jakich a C ciągi o wyrazach na n, a n 1 + a n, an /n, są zbieżne? 2. Wykaż zbieżność i znajdź granice ciągów n a k, a n 1 + a 2n ( a < 1), a n 1 + a 2n ( a > 1), 1 n 3. Dla danego ϕ R
Wyk lad 7 Baza i wymiar przestrzeni liniowej
 Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
w teorii funkcji. Dwa s lynne problemy. Micha l Jasiczak
 Równania różniczkowe czastkowe w teorii funkcji. Dwa s lynne problemy. Micha l Jasiczak Horyzonty 2014 Podstawowy obiekt wyk ladu: funkcje holomorficzne wielu zmiennych Temat: dwa problemy, których znane
Równania różniczkowe czastkowe w teorii funkcji. Dwa s lynne problemy. Micha l Jasiczak Horyzonty 2014 Podstawowy obiekt wyk ladu: funkcje holomorficzne wielu zmiennych Temat: dwa problemy, których znane
Niezb. ednik matematyczny. Niezb. ednik matematyczny
 Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
Funkcje analityczne. Wykład 4. Odwzorowania wiernokątne. Paweł Mleczko. Funkcje analityczne (rok akademicki 2016/2017) dla każdego s = (s.
 Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2016/2017) 1 Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2016/2017) 1 Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
WYKŁAD Z ANALIZY MATEMATYCZNEJ I. dr. Elżbieta Kotlicka. Centrum Nauczania Matematyki i Fizyki
 WYKŁAD Z ANALIZY MATEMATYCZNEJ I dr. Elżbieta Kotlicka Centrum Nauczania Matematyki i Fizyki http://im0.p.lodz.pl/~ekot Łódź 2006 Spis treści 1. CIĄGI LICZBOWE 2 1.1. Własności ciągów liczbowych o wyrazach
WYKŁAD Z ANALIZY MATEMATYCZNEJ I dr. Elżbieta Kotlicka Centrum Nauczania Matematyki i Fizyki http://im0.p.lodz.pl/~ekot Łódź 2006 Spis treści 1. CIĄGI LICZBOWE 2 1.1. Własności ciągów liczbowych o wyrazach
Wykład 5. Zagadnienia omawiane na wykładzie w dniu r
 Wykład 5. Zagadnienia omawiane na wykładzie w dniu 14.11.2018r Definicja (iloraz różnicowy) Niech x 0 R oraz niech funkcja f będzie określona przynajmnniej na otoczeniu O(x 0 ). Ilorazem różnicowym funkcji
Wykład 5. Zagadnienia omawiane na wykładzie w dniu 14.11.2018r Definicja (iloraz różnicowy) Niech x 0 R oraz niech funkcja f będzie określona przynajmnniej na otoczeniu O(x 0 ). Ilorazem różnicowym funkcji
dkowanych par liczb rzeczywistych postaci z = (a, b). W zbiorze tym wprowadzamy dzia lania +, w naste dziemy z liczba
 1. Liczby zespolone Cia lo liczb rzeczywistych be dziemy oznaczać symbolem R, pierścień liczb ca lkowitych symbolem Z, a zbiór liczb naturalnych symbolem N. Przyjmujemy, że 0 / N. Rozważmy zbiór C = R
1. Liczby zespolone Cia lo liczb rzeczywistych be dziemy oznaczać symbolem R, pierścień liczb ca lkowitych symbolem Z, a zbiór liczb naturalnych symbolem N. Przyjmujemy, że 0 / N. Rozważmy zbiór C = R
z n n=1 S n nazywamy sum a szeregu. Szereg, który nie jest zbieżny, nazywamy rozbieżnym. n=1
 3 Szeregi zespolone 3. Szeregi liczbowe Mówimy, że szereg o wyrazach zespolonych jest zbieżny, jeżeli ci ag jego sum czȩściowych {S n }, gdzie S n = z + z +... + jest zbieżny do granicy w laściwej. Granicȩ
3 Szeregi zespolone 3. Szeregi liczbowe Mówimy, że szereg o wyrazach zespolonych jest zbieżny, jeżeli ci ag jego sum czȩściowych {S n }, gdzie S n = z + z +... + jest zbieżny do granicy w laściwej. Granicȩ
Funkcje analityczne. Wykład 3. Funkcje holomorficzne. Paweł Mleczko. Funkcje analityczne (rok akademicki 2016/2017) z = x + iy A
 Funkcje analityczne Wykład 3. Funkcje holomorficzne Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Funkcje zespolone zmiennej zespolonej Funkcje zespolone zmiennej zespolonej Niech A C. Funkcja
Funkcje analityczne Wykład 3. Funkcje holomorficzne Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Funkcje zespolone zmiennej zespolonej Funkcje zespolone zmiennej zespolonej Niech A C. Funkcja
Funkcje analityczne. Wykład 4. Odwzorowania wiernokątne. Paweł Mleczko. Funkcje analityczne (rok akademicki 2017/2018)
 Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) 1. Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
Funkcje analityczne Wykład 4. Odwzorowania wiernokątne Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) 1. Przekształcenia płaszczyzny Płaszczyzna jako przestrzeń liniowa, odwzorowania liniowe
jest ciągiem elementów z przestrzeni B(R, R)
 Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
Funkcje analityczne. Wykład 12
 Funkcje analityczne. Wykład 2 Szeregi Laurenta. Osobliwości funkcji zespolonych. Twierdzenie o residuach Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Plan wykładu W czasie wykładu omawiać
Funkcje analityczne. Wykład 2 Szeregi Laurenta. Osobliwości funkcji zespolonych. Twierdzenie o residuach Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Plan wykładu W czasie wykładu omawiać
Grupy i cia la, liczby zespolone
 Rozdzia l 1 Grupy i cia la, liczby zespolone Dla ustalenia uwagi, b edziemy używać nast epuj acych oznaczeń: N = { 1, 2, 3,... } - liczby naturalne, Z = { 0, ±1, ±2,... } - liczby ca lkowite, W = { m n
Rozdzia l 1 Grupy i cia la, liczby zespolone Dla ustalenia uwagi, b edziemy używać nast epuj acych oznaczeń: N = { 1, 2, 3,... } - liczby naturalne, Z = { 0, ±1, ±2,... } - liczby ca lkowite, W = { m n
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Rozdzia l 11. Przestrzenie Euklidesowe Definicja, iloczyn skalarny i norma. iloczynem skalarnym.
 Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
4. Równania Cauchy ego Riemanna. lim. = c.. dz z=a Zauważmy, że warunkiem równoważnym istnieniu pochodnej jest istnienie liczby c C, takiej że
 4. Równania Caucy ego Riemanna Niec Ω C będzie zbiorem otwartym i niec f : Ω C. Mówimy, że f ma w punkcie a Ω pocodną w sensie zespolonym (jest olomorficzna w a równą c C, jeśli f(z f(a lim = c. z a Piszemy
4. Równania Caucy ego Riemanna Niec Ω C będzie zbiorem otwartym i niec f : Ω C. Mówimy, że f ma w punkcie a Ω pocodną w sensie zespolonym (jest olomorficzna w a równą c C, jeśli f(z f(a lim = c. z a Piszemy
Wyk lad 3 Wielomiany i u lamki proste
 Wyk lad 3 Wielomiany i u lamki proste 1 Konstrukcja pierścienia wielomianów Niech P bedzie dowolnym pierścieniem, w którym 0 1. Oznaczmy przez P [x] zbiór wszystkich nieskończonych ciagów o wszystkich
Wyk lad 3 Wielomiany i u lamki proste 1 Konstrukcja pierścienia wielomianów Niech P bedzie dowolnym pierścieniem, w którym 0 1. Oznaczmy przez P [x] zbiór wszystkich nieskończonych ciagów o wszystkich
Wyk lad 12. (ii) najstarszy wspó lczynnik wielomianu f jest elementem odwracalnym w P. Dowód. Niech st(f) = n i niech a bedzie
 1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
FUNKCJE LICZBOWE. x 1
 FUNKCJE LICZBOWE Zbiory postaci {x R: x a}, {x R: x a}, {x R: x < a}, {x R: x > a} oznaczane sa symbolami (,a], [a, ), (,a) i (a, ). Nazywamy pó lprostymi domknie tymi lub otwartymi o końcu a. Symbol odczytujemy
FUNKCJE LICZBOWE Zbiory postaci {x R: x a}, {x R: x a}, {x R: x < a}, {x R: x > a} oznaczane sa symbolami (,a], [a, ), (,a) i (a, ). Nazywamy pó lprostymi domknie tymi lub otwartymi o końcu a. Symbol odczytujemy
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne.
 Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
Ekonomia matematyczna i dynamiczna optymalizacja
 Ekonomia matematyczna i dynamiczna optymalizacja Ramy wyk ladu i podstawowe narz edzia matematyczne SGH Semestr letni 2012-13 Uk lady dynamiczne Rozwiazanie modelu dynamicznego bardzo czesto można zapisać
Ekonomia matematyczna i dynamiczna optymalizacja Ramy wyk ladu i podstawowe narz edzia matematyczne SGH Semestr letni 2012-13 Uk lady dynamiczne Rozwiazanie modelu dynamicznego bardzo czesto można zapisać
Wykład 15. Matematyka 3, semestr zimowy 2011/ listopada 2011
 Wykład 5 Matematyka 3, semestr zimowy / 9 listopada W trakcie tego i następnych kilku wykładów zajmować się będziemy analizą zespoloną, czyli różniczkowaniem i całkowaniem funkcji argumentu zespolonego
Wykład 5 Matematyka 3, semestr zimowy / 9 listopada W trakcie tego i następnych kilku wykładów zajmować się będziemy analizą zespoloną, czyli różniczkowaniem i całkowaniem funkcji argumentu zespolonego
Wyk lad 5 Grupa ilorazowa, iloczyn prosty, homomorfizm
 Wyk lad 5 Grupa ilorazowa, iloczyn prosty, homomorfizm 1 Grupa ilorazowa Niech H b edzie dzielnikiem normalnym grupy G. Oznaczmy przez G/H zbiór wszystkich warstw lewostronnych grupy G wzgl edem podgrupy
Wyk lad 5 Grupa ilorazowa, iloczyn prosty, homomorfizm 1 Grupa ilorazowa Niech H b edzie dzielnikiem normalnym grupy G. Oznaczmy przez G/H zbiór wszystkich warstw lewostronnych grupy G wzgl edem podgrupy
Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera
 Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera Określenie podpierścienia Definicja 9.. Podpierścieniem pierścienia (P, +,, 0, ) nazywamy taki podzbiór A P, który jest pierścieniem ze wzgledu
Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera Określenie podpierścienia Definicja 9.. Podpierścieniem pierścienia (P, +,, 0, ) nazywamy taki podzbiór A P, który jest pierścieniem ze wzgledu
AM1.2 zadania 14. Zadania z numerami opatrzonymi gwiazdka
 AM.2 zadania 4 Tekst poprawiony 24 kwietnia 206 r. Zadania 26, 28, 29, 3, 33, 34, 35, 36, 40, 42, 62 i inne z wykrzyknikiem obok numeru sa obowiazkowe! Zadania z numerami opatrzonymi gwiazdka można napisać
AM.2 zadania 4 Tekst poprawiony 24 kwietnia 206 r. Zadania 26, 28, 29, 3, 33, 34, 35, 36, 40, 42, 62 i inne z wykrzyknikiem obok numeru sa obowiazkowe! Zadania z numerami opatrzonymi gwiazdka można napisać
P (x, y) + Q(x, y)y = 0. g lym w obszrze G R n+1. Funkcje. zania uk ladu (1) o wykresie przebiegaja
 19. O ca lkach pierwszych W paragrafie 6 przy badaniu rozwia zań równania P (x, y) + Q(x, y)y = 0 wprowadzono poje cie ca lki równania, podano pewne kryteria na wyznaczanie ca lek równania. Znajomość ca
19. O ca lkach pierwszych W paragrafie 6 przy badaniu rozwia zań równania P (x, y) + Q(x, y)y = 0 wprowadzono poje cie ca lki równania, podano pewne kryteria na wyznaczanie ca lek równania. Znajomość ca
6. Punkty osobliwe, residua i obliczanie całek
 6. Punkty osobliwe, residua i obliczanie całek Mówimy, że funkcja holomorficzna f ma w punkcie a zero krotności k, jeśli f(a) = f (a) = = f (k ) (a) = 0, f (k) (a) 0. Rozwijając f w szereg Taylora w otoczeniu
6. Punkty osobliwe, residua i obliczanie całek Mówimy, że funkcja holomorficzna f ma w punkcie a zero krotności k, jeśli f(a) = f (a) = = f (k ) (a) = 0, f (k) (a) 0. Rozwijając f w szereg Taylora w otoczeniu
Rozdział 5. Szeregi liczbowe. 5.1 Szeregi liczbowe. Definicja sumy częściowej ciągu. Niech dany będzie ciąg liczbowy (a n ) n=1.
 Rozdział 5 Szeregi liczbowe 5. Szeregi liczbowe Definicja sumy częściowej ciągu. Niech dany będzie ciąg liczbowy ( ). Ciąg (s n ) określony wzorem s n = n a j, n N, nazywamy ciągiem sum częściowych ciągu
Rozdział 5 Szeregi liczbowe 5. Szeregi liczbowe Definicja sumy częściowej ciągu. Niech dany będzie ciąg liczbowy ( ). Ciąg (s n ) określony wzorem s n = n a j, n N, nazywamy ciągiem sum częściowych ciągu
Wyk lad 1 Podstawowe struktury algebraiczne
 Wyk lad 1 Podstawowe struktury algebraiczne 1 Dzia lanie w zbiorze Majac dane dowolne dwa przedmioty a b możemy z nich utworzyć pare uporzadkowan a (a b) o poprzedniku a i nastepniku b. Warunek na równość
Wyk lad 1 Podstawowe struktury algebraiczne 1 Dzia lanie w zbiorze Majac dane dowolne dwa przedmioty a b możemy z nich utworzyć pare uporzadkowan a (a b) o poprzedniku a i nastepniku b. Warunek na równość
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji.
 I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ
 ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
POCHODNA KIERUNKOWA. DEFINICJA Jeśli istnieje granica lim. to granica ta nazywa siȩ pochodn a kierunkow a funkcji f(m) w kierunku osi l i oznaczamy
 POCHODNA KIERUNKOWA Pochodne cz astkowe funkcji f(m) = f(x, y, z) wzglȩdem x, wzglȩdem y i wzglȩdem z wyrażaj a prȩdkość zmiany funkcji w kierunku osi wspó lrzȩdnych; np. f x jest prȩdkości a zmiany funkcji
POCHODNA KIERUNKOWA Pochodne cz astkowe funkcji f(m) = f(x, y, z) wzglȩdem x, wzglȩdem y i wzglȩdem z wyrażaj a prȩdkość zmiany funkcji w kierunku osi wspó lrzȩdnych; np. f x jest prȩdkości a zmiany funkcji
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Analiza dla informatyków 2 DANI LI2 Pawe l Domański szkicowe notatki do wyk ladu
 Analiza dla informatyków 2 DANI LI2 Pawe l Domański szkicowe notatki do wyk ladu Wyk lad 5 1. Iloczyn ortogonalny funkcji Wróćmy na chwilȩ do dowodu wzorów Eulera-Fouriera. Kluczow a rolȩ odgrywa l wzór:
Analiza dla informatyków 2 DANI LI2 Pawe l Domański szkicowe notatki do wyk ladu Wyk lad 5 1. Iloczyn ortogonalny funkcji Wróćmy na chwilȩ do dowodu wzorów Eulera-Fouriera. Kluczow a rolȩ odgrywa l wzór:
Pochodna funkcji. Pochodna funkcji w punkcie. Różniczka funkcji i obliczenia przybliżone. Zastosowania pochodnych. Badanie funkcji.
 Pochodna funkcji Pochodna funkcji w punkcie. Różniczka funkcji i obliczenia przybliżone. Zastosowania pochodnych. Badanie funkcji. Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika
Pochodna funkcji Pochodna funkcji w punkcie. Różniczka funkcji i obliczenia przybliżone. Zastosowania pochodnych. Badanie funkcji. Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika
Funkcje Analityczne, ćwiczenia i prace domowe
 Funkcje Analityczne, ćwiczenia i prace domowe P. Wojtaszczyk 29 maja 22 Ten plik będzie progresywnie modyfikowany. Będzie on zawierał. Zadanie omówione na ćwiczeniach 2. Zadania ćwiczebne do samodzielnego
Funkcje Analityczne, ćwiczenia i prace domowe P. Wojtaszczyk 29 maja 22 Ten plik będzie progresywnie modyfikowany. Będzie on zawierał. Zadanie omówione na ćwiczeniach 2. Zadania ćwiczebne do samodzielnego
Wyk lad 9 Baza i wymiar przestrzeni liniowej
 Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Liczby zespolone. x + 2 = 0.
 Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Wyk lad 11 1 Wektory i wartości w lasne
 Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Zajęcia nr 1 (1h) Dwumian Newtona. Indukcja. Zajęcia nr 2 i 3 (4h) Trygonometria
 Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
stosunek przyrostu funkcji y do odpowiadajacego dy dx = lim y wielkości fizycznej x, y = f(x), to pochodna dy v = ds edkości wzgl edem czasu, a = dv
 Matematyka Pochodna Pochodna funkcji y = f(x) w punkcie x nazywamy granice, do której daży stosunek przyrostu funkcji y do odpowiadajacego mu przyrostu zmiennej niezaleźnej x, g przyrost zmiennej daży
Matematyka Pochodna Pochodna funkcji y = f(x) w punkcie x nazywamy granice, do której daży stosunek przyrostu funkcji y do odpowiadajacego mu przyrostu zmiennej niezaleźnej x, g przyrost zmiennej daży
III. Funkcje rzeczywiste
 . Pojęcia podstawowe Załóżmy, że dane są dwa niepuste zbiory X i Y. Definicja. Jeżeli każdemu elementowi x X przyporządkujemy dokładnie jeden element y Y, to mówimy, że na zbiorze X została określona funkcja
. Pojęcia podstawowe Załóżmy, że dane są dwa niepuste zbiory X i Y. Definicja. Jeżeli każdemu elementowi x X przyporządkujemy dokładnie jeden element y Y, to mówimy, że na zbiorze X została określona funkcja
Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala
 Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala November 12, 2009 Przyk ladowe zadania z rozwi azaniami Zadanie 1. Oblicz pochodne nastȩpuj
Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala November 12, 2009 Przyk ladowe zadania z rozwi azaniami Zadanie 1. Oblicz pochodne nastȩpuj
Wyk lad 6 Podprzestrzenie przestrzeni liniowych
 Wyk lad 6 Podprzestrzenie przestrzeni liniowych 1 Określenie podprzestrzeni Definicja 6.1. Niepusty podzbiór V 1 V nazywamy podprzestrzeni przestrzeni liniowej V, jeśli ma on nastepuj ace w lasności: (I)
Wyk lad 6 Podprzestrzenie przestrzeni liniowych 1 Określenie podprzestrzeni Definicja 6.1. Niepusty podzbiór V 1 V nazywamy podprzestrzeni przestrzeni liniowej V, jeśli ma on nastepuj ace w lasności: (I)
Szeregi funkcyjne. Szeregi potęgowe i trygonometryczne. Katedra Matematyki Wydział Informatyki Politechnika Białostocka
 Szeregi funkcyjne Szeregi potęgowe i trygonometryczne Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika Białostocka Szeregi funkcyjne str. 1/36 Szereg potęgowy Szeregiem potęgowym o
Szeregi funkcyjne Szeregi potęgowe i trygonometryczne Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika Białostocka Szeregi funkcyjne str. 1/36 Szereg potęgowy Szeregiem potęgowym o
Sterowalność liniowych uk ladów sterowania
 Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Informacja o przestrzeniach Hilberta
 Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Funkcje analityczne. Wykład 2. Płaszczyzna zespolona. Paweł Mleczko. Funkcje analityczne (rok akademicki 2017/2018)
 Funkcje analityczne Wykład 2. Płaszczyzna zespolona Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) Plan wykładu W czasie wykładu omawiać będziemy różne reprezentacje płaszczyzny zespolonej
Funkcje analityczne Wykład 2. Płaszczyzna zespolona Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) Plan wykładu W czasie wykładu omawiać będziemy różne reprezentacje płaszczyzny zespolonej
1 Funkcje dwóch zmiennych podstawowe pojęcia
 1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Je zeli ka zdemu punktowi P o wspó rzednych x; y) z pewnego obszaru D na p aszczyźnie R 2 przyporzadkujemy w sposób jednoznaczny liczb e rzeczywista z, to przyporzadkowanie to nazywamy
Funkcje dwóch zmiennych Je zeli ka zdemu punktowi P o wspó rzednych x; y) z pewnego obszaru D na p aszczyźnie R 2 przyporzadkujemy w sposób jednoznaczny liczb e rzeczywista z, to przyporzadkowanie to nazywamy
Blok V: Ciągi. Różniczkowanie i całkowanie. c) c n = 1 ( 1)n n. d) a n = 1 3, a n+1 = 3 n a n. e) a 1 = 1, a n+1 = a n + ( 1) n
 V. Napisz 4 początkowe wyrazy ciągu: Blok V: Ciągi. Różniczkowanie i całkowanie a) a n = n b) a n = n + 3 n! c) a n = n! n(n + ) V. Oblicz (lub zapisz) c, c 3, c k, c n k dla: a) c n = 3 n b) c n = 3n
V. Napisz 4 początkowe wyrazy ciągu: Blok V: Ciągi. Różniczkowanie i całkowanie a) a n = n b) a n = n + 3 n! c) a n = n! n(n + ) V. Oblicz (lub zapisz) c, c 3, c k, c n k dla: a) c n = 3 n b) c n = 3n
Analiza Matematyczna MAEW101
 Analiza Matematyczna MAEW Wydział Elektroniki Listy zadań nr 8-4 (część II) na podstawie skryptów: M.Gewert, Z Skoczylas, Analiza Matematyczna. Przykłady i zadania, GiS, Wrocław 5 M.Gewert, Z Skoczylas,
Analiza Matematyczna MAEW Wydział Elektroniki Listy zadań nr 8-4 (część II) na podstawie skryptów: M.Gewert, Z Skoczylas, Analiza Matematyczna. Przykłady i zadania, GiS, Wrocław 5 M.Gewert, Z Skoczylas,
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera
 Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
Wyk lad 4 Warstwy, dzielniki normalne
 Wyk lad 4 Warstwy, dzielniki normalne 1 Warstwy grupy wzgl edem podgrupy Niech H bedzie podgrupa grupy (G,, e). W zbiorze G wprowadzamy relacje l oraz r przyjmujac, że dla dowolnych a, b G: a l b a 1 b
Wyk lad 4 Warstwy, dzielniki normalne 1 Warstwy grupy wzgl edem podgrupy Niech H bedzie podgrupa grupy (G,, e). W zbiorze G wprowadzamy relacje l oraz r przyjmujac, że dla dowolnych a, b G: a l b a 1 b
Wyk lad 5. Analiza dla informatyków 1 DANI LI1 Pawe l Domański szkicowe notatki do wyk ladu. 1. Granice niew laściwe
 Analiza dla informatyków 1 DANI LI1 Pawe l Domański szkicowe notatki do wyk ladu Wyk lad 5 1. Granice niew laściwe Definicja 1 Ci ag (x n ) d aży do (jest rozbieżny do) + jeśli c R N n > N x n > c a do
Analiza dla informatyków 1 DANI LI1 Pawe l Domański szkicowe notatki do wyk ladu Wyk lad 5 1. Granice niew laściwe Definicja 1 Ci ag (x n ) d aży do (jest rozbieżny do) + jeśli c R N n > N x n > c a do
Funkcje wielu zmiennych
 Funkcje wielu zmiennych Wykresy i warstwice funkcji wielu zmiennych. Granice i ciagłość funkcji wielu zmiennych. Pochodne czastkowe funkcji wielu zmiennych. Gradient. Pochodna kierunkowa. Różniczka zupełna.
Funkcje wielu zmiennych Wykresy i warstwice funkcji wielu zmiennych. Granice i ciagłość funkcji wielu zmiennych. Pochodne czastkowe funkcji wielu zmiennych. Gradient. Pochodna kierunkowa. Różniczka zupełna.
Matematyka i Statystyka w Finansach. Rachunek Różniczkowy
 Rachunek Różniczkowy Ciąg liczbowy Link Ciągiem liczbowym nieskończonym nazywamy każdą funkcję a która odwzorowuje zbiór liczb naturalnych N w zbiór liczb rzeczywistych R a : N R. Tradycyjnie wartość a(n)
Rachunek Różniczkowy Ciąg liczbowy Link Ciągiem liczbowym nieskończonym nazywamy każdą funkcję a która odwzorowuje zbiór liczb naturalnych N w zbiór liczb rzeczywistych R a : N R. Tradycyjnie wartość a(n)
Wyk lad 14 Cia la i ich w lasności
 Wyk lad 4 Cia la i ich w lasności Charakterystyka cia la Określenie cia la i w lasności dzia lań w ciele y ly omówione na algerze liniowej. Stosujac terminologie z teorii pierścieni możemy powiedzieć,
Wyk lad 4 Cia la i ich w lasności Charakterystyka cia la Określenie cia la i w lasności dzia lań w ciele y ly omówione na algerze liniowej. Stosujac terminologie z teorii pierścieni możemy powiedzieć,
Definicja punktu wewnętrznego zbioru Punkt p jest punktem wewnętrznym zbioru, gdy należy do niego wraz z pewnym swoim otoczeniem
 Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
II. FUNKCJE WIELU ZMIENNYCH
 II. FUNKCJE WIELU ZMIENNYCH 1. Zbiory w przestrzeni R n Ustalmy dowolne n N. Definicja 1.1. Zbiór wszystkich uporzadkowanych układów (x 1,..., x n ) n liczb rzeczywistych, nazywamy przestrzenią n-wymiarową
II. FUNKCJE WIELU ZMIENNYCH 1. Zbiory w przestrzeni R n Ustalmy dowolne n N. Definicja 1.1. Zbiór wszystkich uporzadkowanych układów (x 1,..., x n ) n liczb rzeczywistych, nazywamy przestrzenią n-wymiarową
Zadania z analizy matematycznej - sem. I Pochodne funkcji, przebieg zmienności funkcji
 Zadania z analizy matematycznej - sem. I Pochodne funkcji przebieg zmienności funkcji Definicja 1. Niech f : (a b) R gdzie a < b oraz 0 (a b). Dla dowolnego (a b) wyrażenie f() f( 0 ) = f( 0 + ) f( 0 )
Zadania z analizy matematycznej - sem. I Pochodne funkcji przebieg zmienności funkcji Definicja 1. Niech f : (a b) R gdzie a < b oraz 0 (a b). Dla dowolnego (a b) wyrażenie f() f( 0 ) = f( 0 + ) f( 0 )
Zadania z funkcji zespolonych. III semestr
 Zadania z funkcji zespolonych III semestr 1 Spis treści 1. Liczby zespolone - dzia lania i w lasności Zad. 1 1. Pochodna funkcji zmiennej zespolonej, holomorficzność Zad. 11-19 3. Funkcje elementarne Zad.
Zadania z funkcji zespolonych III semestr 1 Spis treści 1. Liczby zespolone - dzia lania i w lasności Zad. 1 1. Pochodna funkcji zmiennej zespolonej, holomorficzność Zad. 11-19 3. Funkcje elementarne Zad.
Matematyka A, klasówka, 24 maja zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le. rozwia
 Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
3. Funkcje wielu zmiennych
 3 Funkcje wielu zmiennych 31 Ciagłość Zanim podamy definicję ciagłości dla funkcji wielu zmiennych wprowadzimy bardzo ogólne i abstrakcyjne pojęcie przestrzeni metrycznej Przestrzeń metryczna Metryka w
3 Funkcje wielu zmiennych 31 Ciagłość Zanim podamy definicję ciagłości dla funkcji wielu zmiennych wprowadzimy bardzo ogólne i abstrakcyjne pojęcie przestrzeni metrycznej Przestrzeń metryczna Metryka w
ELEKTROTECHNIKA Semestr 1 Rok akad / ZADANIA Z MATEMATYKI Zestaw Przedstaw w postaci algebraicznej liczby zespolone: (3 + 2j)(5 2j),
 ELEKTROTECHNIKA Semestr Rok akad. / 5 ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na płaszczyźnie: +j
ELEKTROTECHNIKA Semestr Rok akad. / 5 ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na płaszczyźnie: +j
2. Definicja pochodnej w R n
 2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
Pochodną funkcji w punkcie (ozn. ) nazywamy granicę ilorazu różnicowego:
 Podstawowe definicje Iloraz różnicowy funkcji Def. Niech funkcja będzie określona w pewnym przedziale otwartym zawierającym punkt. Ilorazem różnicowym funkcji w punkcie dla przyrostu nazywamy funkcję Pochodna
Podstawowe definicje Iloraz różnicowy funkcji Def. Niech funkcja będzie określona w pewnym przedziale otwartym zawierającym punkt. Ilorazem różnicowym funkcji w punkcie dla przyrostu nazywamy funkcję Pochodna
Rachunek różniczkowy i całkowy 2016/17
 Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Rozdział 6. Ciągłość. 6.1 Granica funkcji
 Rozdział 6 Ciągłość 6.1 Granica funkcji Podamy najpierw dwie definicje granicy funkcji w punkcie i pokażemy ich równoważność. Definicja Cauchy ego granicy funkcji w punkcie. Niech f : X R, gdzie X R oraz
Rozdział 6 Ciągłość 6.1 Granica funkcji Podamy najpierw dwie definicje granicy funkcji w punkcie i pokażemy ich równoważność. Definicja Cauchy ego granicy funkcji w punkcie. Niech f : X R, gdzie X R oraz
WYK LAD 2: PODSTAWOWE STRUKTURY ALGEBRAICZNE, PIERWIASTKI WIELOMIANÓW, ROZK LAD FUNKCJI WYMIERNEJ NA U LAMKI PROSTE
 WYK LAD 2: PODSTAWOWE STRUKTURY ALGEBRAICZNE, PIERWIASTKI WIELOMIANÓW, ROZK LAD FUNKCJI WYMIERNEJ NA U LAMKI PROSTE Definicja 1 Algebra abstrakcyjna nazywamy teorie, której przedmiotem sa dzia lania na
WYK LAD 2: PODSTAWOWE STRUKTURY ALGEBRAICZNE, PIERWIASTKI WIELOMIANÓW, ROZK LAD FUNKCJI WYMIERNEJ NA U LAMKI PROSTE Definicja 1 Algebra abstrakcyjna nazywamy teorie, której przedmiotem sa dzia lania na
Liczby zespolone, liniowa zależność i bazy Javier de Lucas. a d b c. ad bc
 Liczby zespolone, liniowa zależność i bazy Javier de Lucas Ćwiczenie. Dowieść, że jeśli µ := c d d c, to homografia h(x) = (ax+b)/(cx+d), a, b, c, d C, ad bc, odwzorowuje oś rzeczywist a R C na okr ag
Liczby zespolone, liniowa zależność i bazy Javier de Lucas Ćwiczenie. Dowieść, że jeśli µ := c d d c, to homografia h(x) = (ax+b)/(cx+d), a, b, c, d C, ad bc, odwzorowuje oś rzeczywist a R C na okr ag
czastkowych Państwo przyk ladowe zadania z rozwiazaniami: karpinw adres strony www, na której znajda
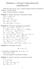 Zadania z równań różniczkowych czastkowych Za l aczam adres strony www, na której znajda Państwo przyk ladowe zadania z rozwiazaniami: http://math.uni.lodz.pl/ karpinw Zadanie 1. Znaleźć wszystkie rozwiazania
Zadania z równań różniczkowych czastkowych Za l aczam adres strony www, na której znajda Państwo przyk ladowe zadania z rozwiazaniami: http://math.uni.lodz.pl/ karpinw Zadanie 1. Znaleźć wszystkie rozwiazania
Niech X bȩdzie dowolnym zbiorem. Dobry porz adek to relacja P X X (bȩdziemy pisać x y zamiast x, y P ) o w lasnościach:
 Teoria miary WPPT IIr semestr zimowy 2009 Wyk lad 4 Liczby kardynalne, indukcja pozaskończona DOBRY PORZA DEK 14/10/09 Niech X bȩdzie dowolnym zbiorem Dobry porz adek to relacja P X X (bȩdziemy pisać x
Teoria miary WPPT IIr semestr zimowy 2009 Wyk lad 4 Liczby kardynalne, indukcja pozaskończona DOBRY PORZA DEK 14/10/09 Niech X bȩdzie dowolnym zbiorem Dobry porz adek to relacja P X X (bȩdziemy pisać x
Agata Boratyńska ZADANIA Z MATEMATYKI, I ROK SGH GRANICA CIĄGU
 Agata Boratyńska Zadania z matematyki Agata Boratyńska ZADANIA Z MATEMATYKI, I ROK SGH GRANICA CIĄGU. Korzystając z definicji granicy ciągu udowodnić: a) n + n+ = 0 b) n + n n+ = c) n + n a =, gdzie a
Agata Boratyńska Zadania z matematyki Agata Boratyńska ZADANIA Z MATEMATYKI, I ROK SGH GRANICA CIĄGU. Korzystając z definicji granicy ciągu udowodnić: a) n + n+ = 0 b) n + n n+ = c) n + n a =, gdzie a
Rozdział 2. Liczby zespolone
 Rozdział Liczby zespolone Zbiór C = R z działaniami + oraz określonymi poniżej: x 1, y 1 ) + x, y ) := x 1 + x, y 1 + y ), 1) x 1, y 1 ) x, y ) := x 1 x y 1 y, x 1 y + x y 1 ) ) jest ciałem zob rozdział
Rozdział Liczby zespolone Zbiór C = R z działaniami + oraz określonymi poniżej: x 1, y 1 ) + x, y ) := x 1 + x, y 1 + y ), 1) x 1, y 1 ) x, y ) := x 1 x y 1 y, x 1 y + x y 1 ) ) jest ciałem zob rozdział
ci agi i szeregi funkcji Javier de Lucas Ćwiczenie 1. Zbadać zbieżność (punktow a i jednostajn a) ci agu funkcji nx 2 + x
 ci agi i szeregi funkcji Javier de Lucas Ćwiczenie 1 Zbadać zbieżność (punktow a i jednostajn a) ci agu funkcji f n : [, [ x nx + x nx + 1, Rozwi azanie: Mówi siȩ, że ci ag funkcji f n zd aży punktowo
ci agi i szeregi funkcji Javier de Lucas Ćwiczenie 1 Zbadać zbieżność (punktow a i jednostajn a) ci agu funkcji f n : [, [ x nx + x nx + 1, Rozwi azanie: Mówi siȩ, że ci ag funkcji f n zd aży punktowo
Notatki z Analizy Matematycznej 3. Jacek M. Jędrzejewski
 Notatki z Analizy Matematycznej 3 Jacek M. Jędrzejewski ROZDZIAŁ 6 Różniczkowanie funkcji rzeczywistej 1. Pocodna funkcji W tym rozdziale rozważać będziemy funkcje rzeczywiste określone w pewnym przedziale
Notatki z Analizy Matematycznej 3 Jacek M. Jędrzejewski ROZDZIAŁ 6 Różniczkowanie funkcji rzeczywistej 1. Pocodna funkcji W tym rozdziale rozważać będziemy funkcje rzeczywiste określone w pewnym przedziale
Analiza dla informatyków 1 DANI LI1 Pawe l Domański szkicowe notatki do wyk ladu
 Analiza dla informatyków 1 DANI LI1 Pawe l Domański szkicowe notatki do wyk ladu Wyk lad 4 1. Zbiory otwarte i domkniȩte Pojȩcia które teraz wprowadzimy można rozpatrywać w każdej przestrzeni metrycznej
Analiza dla informatyków 1 DANI LI1 Pawe l Domański szkicowe notatki do wyk ladu Wyk lad 4 1. Zbiory otwarte i domkniȩte Pojȩcia które teraz wprowadzimy można rozpatrywać w każdej przestrzeni metrycznej
ZADANIA Z FUNKCJI ANALITYCZNYCH LICZBY ZESPOLONE
 . Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
. Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
Roksana Gałecka Okreslenie pochodnej funkcji, podstawowe własnosci funkcji różniczkowalnych
 Temat. Okreslenie pochodnej funkcji, podstawowe własnosci funkcji różniczkowalnych.twierdzenia o wartosci sredniej w rachunku różniczkowalnym i ich zastosowania. Roksana Gałecka 20..204 Spis treści Okreslenie
Temat. Okreslenie pochodnej funkcji, podstawowe własnosci funkcji różniczkowalnych.twierdzenia o wartosci sredniej w rachunku różniczkowalnym i ich zastosowania. Roksana Gałecka 20..204 Spis treści Okreslenie
1 Szeregi potęgowe. 1.1 Promień zbieżności szeregu potęgowego. Wydział Informatyki, KONWERSATORIUM Z MATEMATYKI, 2008/2009.
 Szeregi potęgowe Definicja.. Szeregiem potęgowym o środku w punkcie R nazywamy szereg postaci: gdzie x R oraz c n R dla n = 0,, 2,... c n (x ) n, Przyjmujemy, że 0 0 def =. Liczby c n nazywamy współczynnikami
Szeregi potęgowe Definicja.. Szeregiem potęgowym o środku w punkcie R nazywamy szereg postaci: gdzie x R oraz c n R dla n = 0,, 2,... c n (x ) n, Przyjmujemy, że 0 0 def =. Liczby c n nazywamy współczynnikami
1 Pochodne wyższych rzędów
 Pochodne wyższych rzędów Pochodną rzędu drugiego lub drugą pochodną funkcji y = f(x) nazywamy pochodną pierwszej pochodnej tej funkcji. Analogicznie definiujemy pochodne wyższych rzędów, jako pochodne
Pochodne wyższych rzędów Pochodną rzędu drugiego lub drugą pochodną funkcji y = f(x) nazywamy pochodną pierwszej pochodnej tej funkcji. Analogicznie definiujemy pochodne wyższych rzędów, jako pochodne
Funkcje wielu zmiennych
 Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Notatki z Analizy Matematycznej 2. Jacek M. Jędrzejewski
 Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
1 Przestrzenie unitarne i przestrzenie Hilberta.
 Przestrzenie unitarne i przestrzenie Hilberta.. Wykazać, że iloczyn skalarny w przestrzeni wektorowej X nad cia lem K ma nastepuj ace w lasności: (i) x, y + z = x, y + x, z, (ii) x, λy = λ x, y, (iii)
Przestrzenie unitarne i przestrzenie Hilberta.. Wykazać, że iloczyn skalarny w przestrzeni wektorowej X nad cia lem K ma nastepuj ace w lasności: (i) x, y + z = x, y + x, z, (ii) x, λy = λ x, y, (iii)
