Finanse ubezpieczeń społecznych
|
|
|
- Feliks Matuszewski
- 7 lat temu
- Przeglądów:
Transkrypt
1 Finanse ubezpieczeń społecznych Wykład 7. Kapiałowe ubezpieczenia eeyalne. Pywane plany eeyalne Aeing (994), Wiśniewski (999)
2 Pywane plany eeyalne:. Zaley: -Nie wyagają działań ze sony pańswa, poza ewenualnie swozenie a pawnych, -Mają niskie kosza adinisacyjne, - Składki są poszegane jako oszczędności. 2. Wady: -Ich zasięg jes nieówny i nie wszyscy pacujący ogą z nich skozysać, -Świadczenia nie zawsze są pewne, - Są duże óżnice iędzy planai, -Tansfe śodków iędzy planai pociąga za sobą pewne kosza.
3 Składka eeyalna:. Kwoowa -zwykle w pzypadku indywidualnych oszczędności eeyalnych. 2. Pocen wynagodzenia - w powszechny syseie eeyalny, - w wielu pywanych pogaach eeyalnych.
4 Składka kwoowa Obecna waość składek, kóe wniesie w pzyszłości, uczesnik planu, kóy a obecnie la, o: PVC C ϖ 0 p d, a o wiek ozpoczęcia pacy i jednocześnie wejścia do planu eeyalnego, C kwoa składki, kóa dla uposzczenia jes sała, ω wiek eeyalny, p czynnik dyskonujący, i sopa i pocenowa z inwesycji eeyalnych, pawdopodobieńswo, że człowiek w wieku la pzeżyje nasępnych la. W ujęciu dyskeny: PVC ϖ C p 0
5 Składka popocjonalna do wynagodzenia Zakładay, że składkę płaciy dla uposzczenia co ok: PVs sy ϖ pγ 0 d s pocen płacy płacony jako składka, γ -sosunek pzyszłej płacy w oku do płacy w ciągu oku, W ujęciu dyskeny: PVs ϖ sy pγ 0
6 Syse o zdefiniowanej składce Oczekiwany pozio kapiału w nasępny oku jes dany pzez: W ( i) EW ~ C p p~ p pawdopodobieńswo pozosania w obecny sanie. Wysokość świadczenia wynika z bilansu dokonanego w oencie pzejścia na eeyuę: - okeślay wysokość kapiału, - dzieliy go pzez pzewidywaną liczbę la życia, -uwzględniay pzy y pzewidywaną sopę zwou z dalszego inwesowania ego kapiału.
7 Syse o zdefiniowany świadczeniu Ineesuje nas akualna waość pzewidywanych świadczeń eeyalnych uczesnika planu, kóy: a eaz la, gdzie, oże pzejść na eeyuę w wieku od υ(wiek wcześniejszej eeyuy) do ω, pzejdzie na eeyuę za la od dzisiaj, ak że υ ω. Każdy plan eeyalny o zdefiniowany świadczeniu usi zawieać foułę, definiującą wyia świadczenia. Zakładay, że wszyskie czynniki wpływające na wysokość upawnień eeyalnych są funkcją wieku członka planu.
8 Funkcja kuulacji upawnień Funkcja kuulacji upawnień (liabiliy accual funcion): jaka część pełnego koszu pzyszłych eeyu jes uznawana w wieku. Jes o funkcja M(), odwzoowująca wiek [, ] na odcinek [0, ]: wiek wsąpienia do planu eeyalnego, wiek pzejścia na eeyuę. Funkcja a a nasępujące właściwości: M() 0 M() M () 0 M()
9 Funkcja kuulacji upawnień Ogólna posać funkcji kuulacji upawnień: E(,,0) M ( ) E,, ( ) E świadczenie, jakie w dany planie uzyska osoba, kóa pzysąpiła do planu w oku, jes w ni - la i pzejdzie na eeyuę za -la. Ta funkcja wyaża elację: -hipoeycznego świadczenia, kóe uzyskała by osoba w wieku la, ze saże -, jeżeli pzejdzie na eeyuę eaz (nawe, jeżeli jes o nieożliwe), -do eeyuy, kóą uzyska a saa osoba w wieku la.
10 M ( ) E Funkcja kuulacji upawnień E(,,0) (,, ) Funkcją ej fouły a być odzwieciedlenie echanizu wzosu świadczenia. Pobley: Fouła wyiau świadczeń Eoże ieć znaczące skoki waości świadczenia pzy pzekaczaniu óżnych pzedziałów wieku. Fouła poija yzyko związane z upływe czasu oaz cenę czasu, czyli sopę dyskonową.
11 Meoda koszu nabyego świadczenia Meoda koszu nabyego świadczenia (accued benefi cos ehod):. Załóży, że świadczenie Ezależy liniowo od sażu uczesnicwa w planie. Kosz pzyznanych doychczas upawnień jes opisany pzez: M ( ) oaz M '( ) Oznacza o, że kosz eeyuy jes ównoienie ozłożony na wszyskie laa uczesnicwa w planie.
12 Meoda koszu nabyego świadczenia 2. Załóży, że wyia świadczeń jes związany ze śedni wynagodzenie z całego okesu uczesnicwa w planie. Za każdy ok sażu w planie świadczenie w wysokości f % śedniego wynagodzenia z całego okesu uczesnicwa w syseie. ( ) ( ) Y 0 f ( E,,0 0 ) Y M ( ) E,,0 Y Y 0 0 f Pzyos funkcji kuulacji jes dany pzez: M '( ) 0 Y
13 Meoda koszu nabyego świadczenia Zasada, że dopływ śodków do planu powinien być podpoządkowany epu naasania zobowiązań eeyalnych, powoduje konieczność zieniania składki w czasie. T Niech finalny kosz eeyuy w chwili, B(), będzie dany pzez: T ~ T B( ) p B( ) Pzy pełnej kapializacji, w chwili kapiał eeyalny usi być ówny iloczynowi obecnej kuulacji upawnień i bieżącej waości finalnego koszu eeyuy: T ~ T W ( ) M ( ) B( ) M ( ) p B( )
14 Ziana kapiału iędzy i o pzyos isniejącego kapiału i nowa składka: Meoda koszu nabyego świadczenia p W W C C p W W ~ ) ( ) ( ~ ) ( ) ( d Gzegoz Kula, Podsawiay wzó na kapiał eeyalny: ) ( ~ ~ ) ( ~ ) ( ~ ) ( ~ ) ( ) ( ~ ) ( B p p M p M p B p M B p M C T T T
15 Meoda alokacji koszów względe oenu wejścia Meoda alokacji koszów względe oenu wejścia (enyage acuaial cos ehod): usalay eleen sały w planie eeyalny, zwykle albo wysokość składki, albo sopę składki. Uwzględnia opocenowanie, a akże yzyko związane z uzyanie uczesnicwa. Należy wyliczyć kosz noalny, czyli kwoę, kóa powinna być dopłacona w foie składki na począku oku, w celu pokycia akywai naosłych w ciągu ego oku zobowiązań. Ten kosz dla członka funduszu jes ówny iloczynowi wzosu zobowiązań wobec niego i pawdopodobieńswa pozosania w funduszu.
16 Meoda alokacji koszów względe oenu wejścia Niech świadczenie eeyalne zależy od suy składek waz z opocenowanie, a składki są akie sae pzez cały okes uczesnicwa w planie. Właściwą foułą kapializacji zobowiązań jes zależność: iędzy waością świadczeń eeyalnych, jakie byśy ozyali pzechodząc na eeyuę eaz, a waością świadczeń eeyalnych, jakie byśy ozyali pzechodząc na eeyuę w wieku la. C ( i) ~ p 0 M ( ) C ( i) ~ p 0
17 Meoda alokacji koszów względe oenu wejścia Geneacyjna funkcja pzeżycia s(, a) pokazuje pawdopodobieńswo uzyania akywnego sausu w planie pzez ych, kózy w dany czasie ają la i pzysąpili do planu w oencie, czyli -la eu. Zwykle ą funkcję upaszcza się do s(), ponieważ pawdopodobieńswo okeślay na podsawie specjalnie skonsuowanych ablic wyjścia z planu. M ( ) C C e e δ ( ) δ ( ) s( ) d s( ) d
18 Załóży, że wyia świadczeń jes związany ze śedni wynagodzenie z całego okesu uczesnicwa w planie. Niech składka pozosaje w sałej elacji do wynagodzeń f. Funkcja kuulacji upawnień o: Meoda alokacji koszów względe oenu wejścia ~ d Gzegoz Kula, ( ) ( ) 0 0 ~ ~ ) ( p Y i p Y i M
19 Tablice ubyków w planie eeyalny Tablice ubyków eeyalnych pokazują ubyki w zaknięej gupie akywnych uczesników planu eeyalnego, kózy pzysąpili do planu w y say wieku la. najniższy dopuszczalny wiek wejścia do planu eeyalnego. l () funkcja opisująca liczbę akywnych uczesników planu w wieku la. W najwyższy dopuszczalny wieku pzejścia na eeyuę ωw planie nie a żadnych akywnych uczesników z ej gupy, czyli l ω () 0.
20 Tablice ubyków w planie eeyalny Tabele ubyków pokazują wielkości ubyków dla poszczególnych koho wiekowych, czyli liczebność osób d (.), kóe w oencie ukończenia la były akywnyi uczesnikai planu, lecz pzed osiągnięcie la uaciły saus akywnych uczesników z wyóżnionego w ablicy powodu. Podsawowe powody uay sausu akywnego uczesnika: pzewanie pacy, z pawdopodobieńswe q (w), śieć w czasie pacy, z pawdopodobieńswe q (d), pzejście na enę inwalidzką, z pawdopodobieńswe q (i), pzejście na eeyuę, z pawdopodobieńswe q ().
21 Tablice ubyków w planie eeyalny Pzed najniższy dopuszczalny wiekie eeyalny (υ)nie ożey pzejść na eeyuę, ale pozosałe zy ożliwości są dla nas dosępne. Po pzekoczeniu ego wieku, każde pzewanie sanu akywnego uczesnicwa wywołuje, z punku widzenia pogau eeyalnego, akie sae skuki, jak pzejście na eeyuę. Po pzekoczeniu najwyższego dopuszczalnego wieku pzechodzenia na eeyuę (ω), plan zakłada, że nie ożey być już akywni, więc nie a pozeby szacowania pawdopodobieńswa wyjścia z planu.
22 Tablice ubyków w planie eeyalny Poble śieci uczesnika planu: Śieć pzed wiekie υzusza plan do wypłay szczególnego ypu świadczeń, na pzykład zwou zaoszczędzonego kapiału. Śieć po osiągnięciu wieku υpzynosi e sae skuki, co eeyua, czyli wypłaę kapiału. Dla syseu jes isone, kiedy uzey, ponieważ okeśla o wysokość świadczeń w pzypadku annuieu. Pognoza czasu śieci jes obaczona badzo dużą niepewnością zależy od indywidualnych chaakeysyk.
23 Tablice ubyków w planie eeyalny Łączny oczny ubyek kohoy -laków wynosi: d () d (w) d (d) d (i) d () Liczebność akywnych uczesników z danej kohoy wiekowej wynosi po oku: l () () () l -d To sao ożna pokazać za poocą pawdopodobieńsw: ( w) ( d ) ( i) ( ) l l q q q q ( ) gdzie ( ) ( ) d q ( ) l Wielolenie pawdopodobieńswo pozosania w syseie: k p ( ) l l ( ) k ( )
24 Tablice ubyków w planie eeyalny Pawdopodobieńswo, że akywny uczesnik planu uaci z jakiejś znanej pzyczyny swój akywny saus iędzy ka k okie życia: P ( ) ( d ) [ k, d ] p q K k k Jes o iloczyn pawdopodobieńswa, że pozosaniey w syseie pzez kla i pawdopodobieńswa, że za kla uzey. W pzypadku ciągły zaias zwykłego pawdopodobieńswa śieci usiy zdefiniować funkcję gęsości pawdopodobieńswa śieci i badać pawdopodobieńswo w kóki okesie czasu dk: P ( ) ( d ) [ k K k, d ] p µ < k k dk
25 Wycena waości pzyszłych świadczeń Dzisiejszy -laek, pzechodząc na eeyuę po laach, uzyska eeyuę, kóej całkowia, jednoazowa waość obliczona na oen pzejścia na eeyuę wynosi:,, a ( ) a E -waość ciągłej eny pzez cały czas życia na eeyuze. Dzisiejsza waość pzyszłych świadczeń eeyalnych: PVBE PVBE ϖ υ Lepsza fouła o: ϖ PVBE p ( ) ( ) µ E(,, ) a ( ) ( ) q E(,, k) d ϖ k k k p k a υ k k 2 k k p k a υ k ( ) ( ) ( ) q E,, k 2 2
26 Wycena waości pzyszłych świadczeń Eeyua zależy ylko od sażu pacy: E,, B ( ) ( ) B - sała kwoa pzysługująca za każdy ok sażu. Jeżeli jedna kwoa pzysługuje na za część sażu, a inna za eszę, o na pzykład: B ( ) dla 20 E(,, ) 20B B2 ( 20) dla > 20 Eeyua zależy od końcowego wynagodzenia: ( ) ( ) E,, f Y fin Z każdy okie sażu pzybywa na fpunków pocenowych eeyuy.
27 Eeyua zależy od dochodów zosanich z la udziału w planie:. Część ych la inęła, czyli <z Wycena waości pzyszłych świadczeń ( ) ( ) a a z a a da Y da Y z f E 0 0,, d Gzegoz Kula, 2. Jeszcze nie weszliśy w osani okes, >z Eeyua zależy od śedniego dochodu z całego okesu uczesnicwa w planie: a z a z 0 ( ) ( ) z a a da Y z f E,, ( ) ( ) a a a a da Y da Y f E,,
28 Model funduszu eeyalnego Załóży, że wszyscy uczesnicy pzysępują do planu w y say wieku la i pzechodzą na eeyuę w y say wieku la, gdzie υ ω. W dany oencie ay uczesników akywnych w wieku, oaz eeyów w wieku. Pzyjijy, że populację akywnych uczesników planu, oaz eeyów opisuje funkcja gęsości: l(, u) n( u) s( ) n(u) funkcja gęsości wejścia do planu, s() funkcja pzeżycia. W chwili, liczbę akywnych uczesników planu osiągających wiek z pzedziału (, d)okeśla l(, )d.
29 Model funduszu eeyalnego w() oczny pzyos wynagodzeń osoby, kóa osiągnęła la w oencie 0. g() ziany płac związane z inflacją i podukywnością. Pzyos ocznej płacy osoby, kóa w oencie osiąga la, wynosi: w()g(), Dla osób osiągających w oencie, wiek z pzedziału (, d): w()g()l(, )d. Pzyos w chwili ocznego wynagodzenia wszyskich akywnych uczesników o: W ( ) g( ) w( ) l(, ) d
30 Świadczenia: Model funduszu eeyalnego Niech świadczenie eeyalne zależy jedynie od osaniego wynagodzenia i osiąga w oencie pzejścia na eeyuę f % jego waości. W chwili, inensywność ocznej eeyuy osoby, kóa właśnie osiągnęła, wynosi fw()g(). Jeżeli eeyua jes sała, o jej inensywność w nasępnych laach, czyli dla >w chwili, wynosi fw()g(-), gdyż dana osoba pzeszła na eeyuę - la pzed chwilą.
31 Model funduszu eeyalnego W pakyce eeyuy są zienne: Załóży, że isnieje niezależna od czasu kalendazowego skala zian eeyuy w cyklu życia eeya, opisywana pzez funkcję π(), aka że π(ω). Inensywność ocznej eeyuy jednej kohoy wiekowej, będącej na eeyuze od -la, wynosi fw()g(-)π(). Inensywność, w chwili, ocznego suienia eeyu wypłacanych w cały planie eeyalny: B( ) f w( ) g( ) π ( ) l(, ) d
32 Model funduszu eeyalnego Pzychody funduszu, kóe uożliwiają wypłaę świadczeń: Zasada finalnego finansowania (einal funding), czyli jednoazowa kapializacja całych zobowiązań eeyalnych danej kohoy wiekowej w oencie pzejścia na eeyuę. Jednoazowy ekwiwalen annuieu płacącego zł na ok, plus indeksacja zgodna z foułą π w laach nasępnych: ( ) ( ) ( ) π δ s a e π d s ( )
33 Model funduszu eeyalnego W okesie (, d) na eeyuę pzechodzi l(, -a)d osób, a ich piewsza eeyua osiąga inensywność fw()g()złoych na ok. Zasada finalnego finansowania wyaga, by w oencie dopływały do funduszu eeyalnego składki z inensywnością oczną: T π P( ) f w( ) g( ) l(, ) a W okesie od 0 do powinna być wpłacona składka w wysokości: 0 T P( ) d
METODA ZDYSKONTOWANYCH SALD WOLNYCH PRZEPŁYWÓW PIENIĘŻNYCH
 METODA ZDYSONTOWANYCH SALD WOLNYCH PRZEPŁYWÓW PIENIĘŻNYCH W meodach dochodowych podsawową wielkością, kóa okeśla waość pzedsiębioswa są dochody jakie mogą być geneowane z powadzenia działalności gospodaczej
METODA ZDYSONTOWANYCH SALD WOLNYCH PRZEPŁYWÓW PIENIĘŻNYCH W meodach dochodowych podsawową wielkością, kóa okeśla waość pzedsiębioswa są dochody jakie mogą być geneowane z powadzenia działalności gospodaczej
Zarządzanie ryzykiem. Lista 3
 Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
Zaządzanie yzykiem Lisa 3 1. Oszacowano nasępujący ozkład pawdopodobieńswa dla sóp zwou z akcji A i B (Tabela 1). W chwili obecnej Akcja A ma waość ynkową 70, a akcja B 50 zł. Ile wynosi pięciopocenowa
Arytmetyka finansowa Wykład 5 Dr Wioletta Nowak
 Aymeyka finansowa Wykład 5 D Wiolea Nowak Bon skabowy Insumen dłużny, emiowany pzez Skab ańswa za pośednicwem Miniseswa Finansów. Temin wykupu dzień w kóym emien dokonuje wykupu, Skab ańswa zwaca dług
Aymeyka finansowa Wykład 5 D Wiolea Nowak Bon skabowy Insumen dłużny, emiowany pzez Skab ańswa za pośednicwem Miniseswa Finansów. Temin wykupu dzień w kóym emien dokonuje wykupu, Skab ańswa zwaca dług
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Finanse ubezpieczeń społecznych
 Finnse ubezpieczeń społecznych Wykłd 7. Kpiłowe ubezpieczeni eerylne. Prywne plny eerylne Avering (1994), Wiśniewski (1999) Prywne plny eerylne: 1. Zley: -Nie wygją dziłń ze srony pńsw, poz ewenulnie sworzenie
Finnse ubezpieczeń społecznych Wykłd 7. Kpiłowe ubezpieczeni eerylne. Prywne plny eerylne Avering (1994), Wiśniewski (1999) Prywne plny eerylne: 1. Zley: -Nie wygją dziłń ze srony pńsw, poz ewenulnie sworzenie
Matematyka finansowa 20.03.2006 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r.
 Komisja Egzaminacyjna dla Akuariuszy XXXVIII Egzamin dla Akuariuszy z 20 marca 2006 r. Część I Maemayka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minu 1 1. Ile
Komisja Egzaminacyjna dla Akuariuszy XXXVIII Egzamin dla Akuariuszy z 20 marca 2006 r. Część I Maemayka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minu 1 1. Ile
Matematyka ubezpieczeń życiowych 25.01.2003 r.
 Maemayka ubezpieczeń życiowych 25.01.2003 r. 1.. Dany jes wiek całkowiy x. Nasępujące prawdopodobieńswa przeżycia: g= 2p x + 1/3, h= 2p x + 1/ 2, j= 2p x + 3/4 obliczono sosując inerpolację zakładającą,
Maemayka ubezpieczeń życiowych 25.01.2003 r. 1.. Dany jes wiek całkowiy x. Nasępujące prawdopodobieńswa przeżycia: g= 2p x + 1/3, h= 2p x + 1/ 2, j= 2p x + 3/4 obliczono sosując inerpolację zakładającą,
Marża zakupu bid (pkb) Marża sprzedaży ask (pkb)
 Swap (IRS) i FRA Przykład. Sandardowy swap procenowy Dealer proponuje nasępujące sałe sopy dla sandardowej "plain vanilla" procenowej ransakcji swap. ermin wygaśnięcia Sopa dla obligacji skarbowych Marża
Swap (IRS) i FRA Przykład. Sandardowy swap procenowy Dealer proponuje nasępujące sałe sopy dla sandardowej "plain vanilla" procenowej ransakcji swap. ermin wygaśnięcia Sopa dla obligacji skarbowych Marża
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU
 Modelowanie ryzyka kredyowego MODELOWANIE ZA POMOCA PROCESU HAZARDU Mariusz Niewęgłowski Wydział Maemayki i Nauk Informacyjnych, Poliechniki Warszawskiej Warszawa 2014 hazardu Warszawa 2014 1 / 18 Proces
Modelowanie ryzyka kredyowego MODELOWANIE ZA POMOCA PROCESU HAZARDU Mariusz Niewęgłowski Wydział Maemayki i Nauk Informacyjnych, Poliechniki Warszawskiej Warszawa 2014 hazardu Warszawa 2014 1 / 18 Proces
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
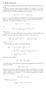 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
INSTRUMENTY DŁUŻNE. Rodzaje ryzyka inwestowania w obligacje Duracja i wypukłość obligacji Wrażliwość wyceny obligacji
 INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
INSTRUMENTY ŁUŻNE Rozaje yzyka iwesowaia w obligacje uacja i wypukłość obligacji Ważliwość wycey obligacji Ryzyko iwesycji w obligacje Ryzyko eiwesycyje możliwość uzyskaia iskiej sopy zwou z wypłacoych
dr Bartłomiej Rokicki Katedra Makroekonomii i Teorii Handlu Zagranicznego Wydział Nauk Ekonomicznych UW
 Kaedra Makroekonomii i Teorii Handlu Zagranicznego Wydział Nauk Ekonomicznych UW Sposoby usalania płac w gospodarce Jednym z głównych powodów, dla kórych na rynku pracy obserwujemy poziom bezrobocia wyższy
Kaedra Makroekonomii i Teorii Handlu Zagranicznego Wydział Nauk Ekonomicznych UW Sposoby usalania płac w gospodarce Jednym z głównych powodów, dla kórych na rynku pracy obserwujemy poziom bezrobocia wyższy
Matematyka ubezpieczeń majątkowych r. ma złożony rozkład Poissona. W tabeli poniżej podano rozkład prawdopodobieństwa ( )
 Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Analiza i prognozowanie szeregów czasowych
 Analiza i pognozowanie szeegów czasowych Pojęcie szeegu czasowego Szeeg czasowy (chonologiczny, dynamiczny, ozwojowy) pezenuje ozwój wybanego zjawiska w czasie; zawiea waości zjawiska y w jednoskach czasu,,
Analiza i pognozowanie szeegów czasowych Pojęcie szeegu czasowego Szeeg czasowy (chonologiczny, dynamiczny, ozwojowy) pezenuje ozwój wybanego zjawiska w czasie; zawiea waości zjawiska y w jednoskach czasu,,
Laboratorium Półprzewodniki, Dielektryki i Magnetyki Ćwiczenie nr 10 Pomiary czasu życia nośników w półprzewodnikach
 Laboaoium Półpzewodniki, Dielekyki i Magneyki Ćwiczenie n 10 Pomiay czasu życia nośników w półpzewodnikach I. Zagadnienia do pzygoowania: 1. Pojęcia: nośniki mniejszościowe i większościowe, ównowagowe
Laboaoium Półpzewodniki, Dielekyki i Magneyki Ćwiczenie n 10 Pomiay czasu życia nośników w półpzewodnikach I. Zagadnienia do pzygoowania: 1. Pojęcia: nośniki mniejszościowe i większościowe, ównowagowe
XXI OLIMPIADA FIZYCZNA ( ). Stopień III, zadanie teoretyczne T1. Źródło: XXI i XXII OLIMPIADA FIZYCZNA, WSiP, Warszawa 1975 Andrzej Szymacha,
 XXI OLIMPIADA FIZYCZNA (97-97). Stopień III zadanie teoetyczne. Źódło: XXI i XXII OLIMPIADA FIZYCZNA WSiP Waszawa 975 Auto: Nazwa zadania: Działy: Słowa kluczowe: Andzej Szyacha Dwa ciała i spężynka Dynaika
XXI OLIMPIADA FIZYCZNA (97-97). Stopień III zadanie teoetyczne. Źódło: XXI i XXII OLIMPIADA FIZYCZNA WSiP Waszawa 975 Auto: Nazwa zadania: Działy: Słowa kluczowe: Andzej Szyacha Dwa ciała i spężynka Dynaika
XLI OLIMPIADA FIZYCZNA ETAP I Zadanie doświadczalne
 XLI OLIPIADA FIZYCZNA EAP I Zadanie doświadczalne ZADANIE D Pod działaniem sil zewnęznych ciała sale ulęgają odkszałceniom. Wyznacz zależność pomienia obszau syczniści szklanej soczewki z płyka szklana
XLI OLIPIADA FIZYCZNA EAP I Zadanie doświadczalne ZADANIE D Pod działaniem sil zewnęznych ciała sale ulęgają odkszałceniom. Wyznacz zależność pomienia obszau syczniści szklanej soczewki z płyka szklana
PROCEDURA WYBORU PORTFELA AKCJI ZAPEWNIAJĄCA KONTROLĘ RYZYKA NIESYSTEMATYCZNEGO
 B A D A I A O P E R A C Y J E I D E C Y Z J E 3 4 2004 omasz BRZĘCZEK* PROCEDURA WYBORU PORFELA AKCJI ZAPEWIAJĄCA KOROLĘ RYZYKA IESYSEMAYCZEGO Pzedsawiono poceduę wybou pofela akci zapewniaącą konolę yzyka
B A D A I A O P E R A C Y J E I D E C Y Z J E 3 4 2004 omasz BRZĘCZEK* PROCEDURA WYBORU PORFELA AKCJI ZAPEWIAJĄCA KOROLĘ RYZYKA IESYSEMAYCZEGO Pzedsawiono poceduę wybou pofela akci zapewniaącą konolę yzyka
PORÓWNANIE WPŁYWU WYBRANYCH PARAMETRÓW CIĄGNIKA ROLNICZEGO NA JEGO DRGANIA
 Inżynieria Rolnicza (90)/007 PORÓWNANIE WPŁYWU WYBRANYCH PARAMETRÓW CIĄGNIKA ROLNICZEGO NA JEGO DRGANIA Instytut Inżynierii Rolniczej, Akadeia Rolnicza w Poznaniu Streszczenie. Drgania ciągnika, szczególnie
Inżynieria Rolnicza (90)/007 PORÓWNANIE WPŁYWU WYBRANYCH PARAMETRÓW CIĄGNIKA ROLNICZEGO NA JEGO DRGANIA Instytut Inżynierii Rolniczej, Akadeia Rolnicza w Poznaniu Streszczenie. Drgania ciągnika, szczególnie
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Maria Dems. T. Koter, E. Jezierski, W. Paszek
 Sany niesalone masyn synchonicnych Maia Dems. Koe, E. Jeieski, W. Pasek Zwacie aowe pąnicy synchonicnej San wacia salonego, wany akże waciem nomalnym lb pomiaowym yskje się pe wacie acisków wonika (j (sojana
Sany niesalone masyn synchonicnych Maia Dems. Koe, E. Jeieski, W. Pasek Zwacie aowe pąnicy synchonicnej San wacia salonego, wany akże waciem nomalnym lb pomiaowym yskje się pe wacie acisków wonika (j (sojana
Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO. z dnia 2 czerwca 2017 r.
 DZIENNIK URZĘDOWY NARODOWEGO BANKU POLSKIEGO Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO z dnia 2 czerwca 2017 r. zmieniająca uchwałę w sprawie wprowadzenia
DZIENNIK URZĘDOWY NARODOWEGO BANKU POLSKIEGO Warszawa, dnia 5 czerwca 2017 r. Poz. 13 UCHWAŁA NR 29/2017 ZARZĄDU NARODOWEGO BANKU POLSKIEGO z dnia 2 czerwca 2017 r. zmieniająca uchwałę w sprawie wprowadzenia
Wykład 19 Zagadnienie dwóch ciał. naj- mniej dwóch musi dwóch i wi cej trudny. szybkim jedynie ograniczaj c si do fizyki nierelatywistycznej dwóch
 Wykład 9 Zagadnienie dwóch ciał. ealisyczny pzykład oddziałujcego układu fizycznego wyaga obecnoci, co najniej dwóch ciał, w najposszy pzypadku, dwóch punków aeialnych. W doychczasowych naszych ozwaaniach
Wykład 9 Zagadnienie dwóch ciał. ealisyczny pzykład oddziałujcego układu fizycznego wyaga obecnoci, co najniej dwóch ciał, w najposszy pzypadku, dwóch punków aeialnych. W doychczasowych naszych ozwaaniach
Wpływ rentowności skarbowych papierów dłużnych na finanse przedsiębiorstw i poziom bezrobocia
 Wpływ renowności skarbowych papierów dłużnych na inanse przedsiębiorsw i poziom bezrocia Leszek S. Zaremba Sreszczenie W pracy ej wykażemy prawidłowość, kóra mówi, że im wyższa jes renowność bezryzykownych
Wpływ renowności skarbowych papierów dłużnych na inanse przedsiębiorsw i poziom bezrocia Leszek S. Zaremba Sreszczenie W pracy ej wykażemy prawidłowość, kóra mówi, że im wyższa jes renowność bezryzykownych
Optyka falowa. polaryzacja. dwójłomność optyczna. czym jest zjawisko polaryzacji stan a stopień polaryzacji sposoby polaryzacji
 W-21 (Jaoszewicz) 16 slajdów Na podsawie pezenacji pof. J. Rukowskiego Opyka falowa polayzacja czym jes zjawisko polayzacji san a sopień polayzacji sposoby polayzacji dwójłomność opyczna pzyczyny mikoskopowe
W-21 (Jaoszewicz) 16 slajdów Na podsawie pezenacji pof. J. Rukowskiego Opyka falowa polayzacja czym jes zjawisko polayzacji san a sopień polayzacji sposoby polayzacji dwójłomność opyczna pzyczyny mikoskopowe
WYKORZYSTANIE TRÓJSEKTOROWEGO MODELU WZROSTU DO ANALIZY WPŁYWU OGRANICZENIA EMISJI GHG NA WYBÓR TECHNOLOGII PRODUKCJI.
 Zeszyy Naukowe Wydziału nfomaycznych Technik Zaządzania Wyższej Szkoły nfomayki Sosowanej i Zaządzania Współczesne Poblemy Zaządzania N /2009 WYKORZYSTANE TRÓJSEKTOROWEGO ODELU WZROSTU DO ANALZY WPŁYWU
Zeszyy Naukowe Wydziału nfomaycznych Technik Zaządzania Wyższej Szkoły nfomayki Sosowanej i Zaządzania Współczesne Poblemy Zaządzania N /2009 WYKORZYSTANE TRÓJSEKTOROWEGO ODELU WZROSTU DO ANALZY WPŁYWU
WSPÓŁCZYNNIK THETA OPCJI BARIEROWYCH
 Ewa Dziawgo Uniwesye Mikołaja openika w ouniu Wyział auk Ekonomicznych i Zazązania aea Ekonomeii i aysyki ziawew@umk.pl WPÓŁCZYI EA OPCJI BARIEROWYC eszczenie: W aykule pzesawiono zaganienia związane z
Ewa Dziawgo Uniwesye Mikołaja openika w ouniu Wyział auk Ekonomicznych i Zazązania aea Ekonomeii i aysyki ziawew@umk.pl WPÓŁCZYI EA OPCJI BARIEROWYC eszczenie: W aykule pzesawiono zaganienia związane z
Parametryczny koder mowy - wokoder. Synteza mowy w odbiorniku: d=1 - mowa dźwięczna (T 0 = okres tonu krtaniowego) d=0 - mowa bezdźwięczna
 Paraeryczny koder owy - wokoder Syneza owy w odbiorniku: d=1 - owa dźwięczna T 0 = okres onu kraniowego d=0 - owa bezdźwięczna Wokoder nadajnik Eksrakcja onu kraniowego 1. Przebieg czasowy sygnału i błędu
Paraeryczny koder owy - wokoder Syneza owy w odbiorniku: d=1 - owa dźwięczna T 0 = okres onu kraniowego d=0 - owa bezdźwięczna Wokoder nadajnik Eksrakcja onu kraniowego 1. Przebieg czasowy sygnału i błędu
Rozdział VIII KINETYKA NASYCANIA POWIERZCHNI. 1. Wstęp
 83 Rozdział VIII KINETYKA NASYCANIA POWIERZCHNI 1. Wsęp W akcie wykonywania zewnęznyc oconnyc wasw ynku, jak i konsewacji isniejącyc deali budowli zabykowyc zacodzi częso konieczność oceny sopnia peneacji
83 Rozdział VIII KINETYKA NASYCANIA POWIERZCHNI 1. Wsęp W akcie wykonywania zewnęznyc oconnyc wasw ynku, jak i konsewacji isniejącyc deali budowli zabykowyc zacodzi częso konieczność oceny sopnia peneacji
Prowadzisz lub będziesz prowadzić działalność gospodarczą? Przeczytaj koniecznie!
 Prowadzisz lub będziesz prowadzić działalność gospodarczą? Przeczyaj koniecznie! Jeseś osobą prowadzącą pozarolniczą działalność, jeśli: prowadzisz pozarolniczą działalność gospodarczą na podsawie przepisów
Prowadzisz lub będziesz prowadzić działalność gospodarczą? Przeczyaj koniecznie! Jeseś osobą prowadzącą pozarolniczą działalność, jeśli: prowadzisz pozarolniczą działalność gospodarczą na podsawie przepisów
KONSPEKT SZKOLENIOWY na temat: funkcjonowania funduszy świadczeń socjalnych
 KONSPEKT SZKOLENIOWY na temat: funkcjonowania funduszy świadczeń socjalnych USTAWA Z DNIA 4 MARCA 1994. O ZAKŁADOWYM FUNDUSZU ŚWIADCZEŃ SOCJALNYCH - zastępuje ustawę o zakładowych funduszach socjalnych
KONSPEKT SZKOLENIOWY na temat: funkcjonowania funduszy świadczeń socjalnych USTAWA Z DNIA 4 MARCA 1994. O ZAKŁADOWYM FUNDUSZU ŚWIADCZEŃ SOCJALNYCH - zastępuje ustawę o zakładowych funduszach socjalnych
6.4. Model zdyskontowanych zysków Metoda skorygowanej wartości bieżącej (APV)
 6.4. Model zdyskonowanych zysków Jeśli za mienik waości pzyjęy zosanie zysk neo, obliczenie waości wewnęznej odbywać się będzie ak samo, jak miało o miejsce w pzypadku modeli dywidendowych i cash flow.
6.4. Model zdyskonowanych zysków Jeśli za mienik waości pzyjęy zosanie zysk neo, obliczenie waości wewnęznej odbywać się będzie ak samo, jak miało o miejsce w pzypadku modeli dywidendowych i cash flow.
Model AS-AD. Krzywa AD M P = (1)
 Model AS-AD modelu IS-LM oaz w podsawowym modelu keynesowskim zakładaliśmy, że ceny w gospodace są sałe. Teaz uchylamy o założenie. Model AS-AD pezenujemy w pzeszeni poduk poziom cen (lub inflacja. Równowagę
Model AS-AD modelu IS-LM oaz w podsawowym modelu keynesowskim zakładaliśmy, że ceny w gospodace są sałe. Teaz uchylamy o założenie. Model AS-AD pezenujemy w pzeszeni poduk poziom cen (lub inflacja. Równowagę
Wytrzymałość śruby wysokość nakrętki
 Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE
 RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE PYTANIA KONTROLNE Czym charakeryzują się wskaźniki saycznej meody oceny projeku inwesycyjnego Dla kórego wskaźnika wyliczamy średnią księgową
RACHUNEK EFEKTYWNOŚCI INWESTYCJI METODY ZŁOŻONE DYNAMICZNE PYTANIA KONTROLNE Czym charakeryzują się wskaźniki saycznej meody oceny projeku inwesycyjnego Dla kórego wskaźnika wyliczamy średnią księgową
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
System zielonych inwestycji (GIS Green Investment Scheme)
 PROGRAM PRIORYTETOWY Tyuł programu: Sysem zielonych inwesycji (GIS Green Invesmen Scheme) Część 6) SOWA Energooszczędne oświelenie uliczne. 1. Cel programu Ograniczenie lub uniknięcie emisji dwulenku węgla
PROGRAM PRIORYTETOWY Tyuł programu: Sysem zielonych inwesycji (GIS Green Invesmen Scheme) Część 6) SOWA Energooszczędne oświelenie uliczne. 1. Cel programu Ograniczenie lub uniknięcie emisji dwulenku węgla
Dynamika punktu materialnego
 Naa -Japonia W-3 (Jaosewic 1 slajdów Dynamika punku maeialnego Dynamika Układ inecjalny Zasady dynamiki: piewsa asada dynamiki duga asada dynamiki; pęd ciała popęd siły ecia asada dynamiki (pawo akcji
Naa -Japonia W-3 (Jaosewic 1 slajdów Dynamika punku maeialnego Dynamika Układ inecjalny Zasady dynamiki: piewsa asada dynamiki duga asada dynamiki; pęd ciała popęd siły ecia asada dynamiki (pawo akcji
WAHADŁO OBERBECKA V 6 38a
 Wahadło Obebecka V 6-38a WAHADŁO OBERBECKA V 6 38a Wahadło ma zasosowanie na lekcjach fizyki w klasie I i III liceum ogólnokszałcącego. Pzyząd sanowi byłę szywną uwozoną pzez uleję (1) i czey wkęcone w
Wahadło Obebecka V 6-38a WAHADŁO OBERBECKA V 6 38a Wahadło ma zasosowanie na lekcjach fizyki w klasie I i III liceum ogólnokszałcącego. Pzyząd sanowi byłę szywną uwozoną pzez uleję (1) i czey wkęcone w
XLI Egzamin dla Aktuariuszy z 8 stycznia 2007 r.
 Komisja Egzaminacyjna dla Akuariuszy XLI Egzamin dla Akuariuszy z 8 sycznia 7 r. Część II Maemayka ubezieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 1 minu Warszawa, 9 aździernika
Komisja Egzaminacyjna dla Akuariuszy XLI Egzamin dla Akuariuszy z 8 sycznia 7 r. Część II Maemayka ubezieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 1 minu Warszawa, 9 aździernika
KINEMATYCZNE WŁASNOW PRZEKŁADNI
 KINEMATYCZNE WŁASNOW ASNOŚCI PRZEKŁADNI Waunki współpacy pacy zazębienia Zasada n 1 - koła zębate mogą ze sobą współpacować, kiedy mają ten sam moduł m. Czy to wymaganie jest wystaczające dla pawidłowej
KINEMATYCZNE WŁASNOW ASNOŚCI PRZEKŁADNI Waunki współpacy pacy zazębienia Zasada n 1 - koła zębate mogą ze sobą współpacować, kiedy mają ten sam moduł m. Czy to wymaganie jest wystaczające dla pawidłowej
NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek
 Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
OSCYLATOR HARMONICZNY
 OSCYLTOR HRMONICZNY Dgania swobone oscylaoa haonicznego negia oencjalna sęŝysości Dgania łuione oscylaoa haonicznego Dgania wyuszone oscylaoa haonicznego Rezonans aliuowy Rezonans ocy Doboć ukłau gającego
OSCYLTOR HRMONICZNY Dgania swobone oscylaoa haonicznego negia oencjalna sęŝysości Dgania łuione oscylaoa haonicznego Dgania wyuszone oscylaoa haonicznego Rezonans aliuowy Rezonans ocy Doboć ukłau gającego
Analiza i Zarządzanie Portfelem cz. 6 R = Ocena wyników zarządzania portfelem. Pomiar wyników zarządzania portfelem. Dr Katarzyna Kuziak
 Ocena wyników zarządzania porelem Analiza i Zarządzanie Porelem cz. 6 Dr Kaarzyna Kuziak Eapy oceny wyników zarządzania porelem: - (porolio perormance measuremen) - Przypisanie wyników zarządzania porelem
Ocena wyników zarządzania porelem Analiza i Zarządzanie Porelem cz. 6 Dr Kaarzyna Kuziak Eapy oceny wyników zarządzania porelem: - (porolio perormance measuremen) - Przypisanie wyników zarządzania porelem
Analiza opłacalności inwestycji logistycznej Wyszczególnienie
 inwesycji logisycznej Wyszczególnienie Laa Dane w ys. zł 2 3 4 5 6 7 8 Przedsięwzięcie I Program rozwoju łańcucha (kanału) dysrybucji przewiduje realizację inwesycji cenrum dysrybucyjnego. Do oceny przyjęo
inwesycji logisycznej Wyszczególnienie Laa Dane w ys. zł 2 3 4 5 6 7 8 Przedsięwzięcie I Program rozwoju łańcucha (kanału) dysrybucji przewiduje realizację inwesycji cenrum dysrybucyjnego. Do oceny przyjęo
Ewa Dziawgo Uniwersytet Mikołaja Kopernika w Toruniu. Analiza wrażliwości modelu wyceny opcji złożonych
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 7 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika w Toruniu
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 7 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Uniwersye Mikołaja Kopernika w Toruniu
Kognitywistyka II r. Teoria rzetelności wyników testu. Teorie inteligencji i sposoby jej pomiaru (4) Rzetelność czyli dokładność pomiaru
 Kognitywistyka II Teoie inteligencji i sposoby jej pomiau (4) Teoia zetelności wyników testu Rzetelność czyli dokładność pomiau W języku potocznym temin zetelność oznacza niezawodność (dokładność). W psychometii
Kognitywistyka II Teoie inteligencji i sposoby jej pomiau (4) Teoia zetelności wyników testu Rzetelność czyli dokładność pomiau W języku potocznym temin zetelność oznacza niezawodność (dokładność). W psychometii
Analiza możliwości wykorzystania wybranych modeli wygładzania wykładniczego do prognozowania wartości WIG-u
 Zbigiew Taapaa Aaliza możliwości wykozysaia wybaych modeli wygładzaia wykładiczego do pogozowaia waości WIG-u Wydział Cybeeyki Wojskowej Akademii Techiczej w Waszawie Seszczeie W aykule pzedsawioo aalizę
Zbigiew Taapaa Aaliza możliwości wykozysaia wybaych modeli wygładzaia wykładiczego do pogozowaia waości WIG-u Wydział Cybeeyki Wojskowej Akademii Techiczej w Waszawie Seszczeie W aykule pzedsawioo aalizę
Arytmetyka finansowa. Dr Wioletta Nowak
 Aymeya finansowa Wiolea Nowa Bon sabowy Insumen dłużny, emiowany pzez Sab ańswa za pośednicwem Miniseswa Finansów. Temin wyupu dzień w óym emien doonuje wyupu, Sab ańswa zwaca dłu posiadaczowi bonu saboweo.
Aymeya finansowa Wiolea Nowa Bon sabowy Insumen dłużny, emiowany pzez Sab ańswa za pośednicwem Miniseswa Finansów. Temin wyupu dzień w óym emien doonuje wyupu, Sab ańswa zwaca dłu posiadaczowi bonu saboweo.
Twoje konto w ZUS. Co powinieneś wiedzieć. Przeczytaj koniecznie!
 Twoje kono w ZUS. Co powinieneś wiedzieć Przeczyaj koniecznie! Kono ubezpieczonego zakładane jes na podsawie pierwszego zgłoszenia do ubezpieczeń społecznych lub ubezpieczenia zdrowonego. Od 1 maja 2011
Twoje kono w ZUS. Co powinieneś wiedzieć Przeczyaj koniecznie! Kono ubezpieczonego zakładane jes na podsawie pierwszego zgłoszenia do ubezpieczeń społecznych lub ubezpieczenia zdrowonego. Od 1 maja 2011
Grzegorz Kornaś. Powtórka z fizyki
 Gzegoz Konaś Powóka z fizyki - dla uczniów gimnazjów, kózy chcą wiedzieć o co zeba, a nawe więcej, - dla uczniów liceów, kózy chcą powózyć o co zeba, aby zozumieć więcej, - dla wszyskich, kózy chcą znać
Gzegoz Konaś Powóka z fizyki - dla uczniów gimnazjów, kózy chcą wiedzieć o co zeba, a nawe więcej, - dla uczniów liceów, kózy chcą powózyć o co zeba, aby zozumieć więcej, - dla wszyskich, kózy chcą znać
Metody oceny projektów inwestycyjnych. ( 1 + r) Gdzie: r t stała stopa procentowa w ujęciu rocznym w kolejnych. Analiza wartości pieniądza w czasie
 Meody ocey pojeków iwesycyjych Kaazya Mamcaz Aaliza waości pieiądza w czasie (pese value - akuala, zakualizowaa waość obeca, bieżąca, Dzisiejsza waość pzyszłego pzepływu pieiężego bądź sumieia pzepływów
Meody ocey pojeków iwesycyjych Kaazya Mamcaz Aaliza waości pieiądza w czasie (pese value - akuala, zakualizowaa waość obeca, bieżąca, Dzisiejsza waość pzyszłego pzepływu pieiężego bądź sumieia pzepływów
Rys. 1. Ilustracja modelu. Oddziaływanie grawitacyjne naszych ciał z masą centralną opisywać będą wektory r 1
 6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
6 FOTON 6, Wiosna 0 uchy Księżyca Jezy Ginte Uniwesytet Waszawski Postawienie zagadnienia Kiedy uczy się o uchach ciał niebieskich na pozioie I klasy liceu, oawia się najczęściej najpiew uch Ziei i innych
Sprawujesz osobistą opiekę nad dzieckiem? Przeczytaj koniecznie!
 Sprawujesz osobisą opiekę nad dzieckiem? Przeczyaj koniecznie! Czy z yułu sprawowania osobisej opieki nad dzieckiem podlegasz ubezpieczeniom społecznym i zdrowonemu Od 1 września 2013 r. osoba sprawująca
Sprawujesz osobisą opiekę nad dzieckiem? Przeczyaj koniecznie! Czy z yułu sprawowania osobisej opieki nad dzieckiem podlegasz ubezpieczeniom społecznym i zdrowonemu Od 1 września 2013 r. osoba sprawująca
Pojęcia podstawowe 1
 Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Nierelatywistyczne równania ruchu = zasady dynamiki Newtona
 DYNAMIKA: siły ównania uchu uch Nieelatywistyczne ównania uchu zasady dynaiki Newtona Pojęcia podstawowe dla punktu ateialnego Masa - iaa bezwładności Pęd iaa ilości uchu v v p v p v v v Siła wywołuje
DYNAMIKA: siły ównania uchu uch Nieelatywistyczne ównania uchu zasady dynaiki Newtona Pojęcia podstawowe dla punktu ateialnego Masa - iaa bezwładności Pęd iaa ilości uchu v v p v p v v v Siła wywołuje
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Metody oceny projektów inwestycyjnych. ( 1 + r) Gdzie: r t stała stopa procentowa w ujęciu rocznym w kolejnych. Analiza wartości pieniądza w czasie
 Meody ocey pojeków iwesycyjych Kaazya Mamcaz Aaliza waości pieiądza w czasie (pese value - akuala, zakualizowaa waość obeca, bieżąca, Dzisiejsza waość pzyszłego pzepływu pieiężego bądź sumieia pzepływów
Meody ocey pojeków iwesycyjych Kaazya Mamcaz Aaliza waości pieiądza w czasie (pese value - akuala, zakualizowaa waość obeca, bieżąca, Dzisiejsza waość pzyszłego pzepływu pieiężego bądź sumieia pzepływów
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Gr.A, Zad.1. Gr.A, Zad.2 U CC R C1 R C2. U wy T 1 T 2. U we T 3 T 4 U EE
 Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
REGULAMIN FUNDUSZU ROZLICZENIOWEGO
 REGULAMIN FUNDUSZU ROZLICZENIOEGO przyjęy uchwałą nr 10/60/98 Rady Nadzorczej Krajowego Depozyu Papierów arościowych S.A. z dnia 28 września 1998 r., zawierdzony decyzją Komisji Papierów arościowych i
REGULAMIN FUNDUSZU ROZLICZENIOEGO przyjęy uchwałą nr 10/60/98 Rady Nadzorczej Krajowego Depozyu Papierów arościowych S.A. z dnia 28 września 1998 r., zawierdzony decyzją Komisji Papierów arościowych i
BEZRYZYKOWNE BONY I LOKATY BANKOWE ALTERNATYWĄ DLA PRZYSZŁYCH EMERYTÓW. W tym krótkim i matematycznie bardzo prostym artykule pragnę osiągnąc 3 cele:
 1 BEZRYZYKOWNE BONY I LOKATY BANKOWE ALTERNATYWĄ DLA PRZYSZŁYCH EMERYTÓW Leszek S. Zaremba (Polish Open Universiy) W ym krókim i maemaycznie bardzo prosym arykule pragnę osiągnąc cele: (a) pokazac że kupowanie
1 BEZRYZYKOWNE BONY I LOKATY BANKOWE ALTERNATYWĄ DLA PRZYSZŁYCH EMERYTÓW Leszek S. Zaremba (Polish Open Universiy) W ym krókim i maemaycznie bardzo prosym arykule pragnę osiągnąc cele: (a) pokazac że kupowanie
Finanse. cov. * i. 1. Premia za ryzyko. 2. Wskaźnik Treynora. 3. Wskaźnik Jensena
 Finanse 1. Premia za ryzyko PR r m r f. Wskaźnik Treynora T r r f 3. Wskaźnik Jensena r [ rf ( rm rf ] 4. Porfel o minimalnej wariancji (ile procen danej spółki powinno znaleźć się w porfelu w a w cov,
Finanse 1. Premia za ryzyko PR r m r f. Wskaźnik Treynora T r r f 3. Wskaźnik Jensena r [ rf ( rm rf ] 4. Porfel o minimalnej wariancji (ile procen danej spółki powinno znaleźć się w porfelu w a w cov,
cx siła z jaką element tłumiący działa na to ciało.
 Drgania układu o jedny sopniu swobody Rozparzy układ składający się z ciała o asie połączonego z nierucoy podłoże za poocą eleenu sprężysego o współczynniku szywności k oraz eleenu łuiącego o współczynniku
Drgania układu o jedny sopniu swobody Rozparzy układ składający się z ciała o asie połączonego z nierucoy podłoże za poocą eleenu sprężysego o współczynniku szywności k oraz eleenu łuiącego o współczynniku
POMIAR PRĘDKOŚCI OBROTOWEJ.
 LABORAORIUM PODAW MEROLOGII M- Ćwiczenie n 3 POMIAR PRĘDKOŚCI OBROOWEJ. Pomiay pędkości ooowej mogą yć dokonywane óżnymi meodami. Klasyfikacja meod zależy od pzyjęego kyeium. Najliższa nauze zjawisk wykozysywanych
LABORAORIUM PODAW MEROLOGII M- Ćwiczenie n 3 POMIAR PRĘDKOŚCI OBROOWEJ. Pomiay pędkości ooowej mogą yć dokonywane óżnymi meodami. Klasyfikacja meod zależy od pzyjęego kyeium. Najliższa nauze zjawisk wykozysywanych
Fizyka Procesów Klimatycznych Wykład 9 proste modele klimatu
 Fizyka Procesów Kliaycznych Wykład 9 prose odele kliau prof. dr hab. Szyon Malinowski Insyu Geofizyki, Wydział Fizyki Uniwersye Warszawski alina@igf.fuw.edu.pl dr hab. Krzyszof Markowicz Insyu Geofizyki,
Fizyka Procesów Kliaycznych Wykład 9 prose odele kliau prof. dr hab. Szyon Malinowski Insyu Geofizyki, Wydział Fizyki Uniwersye Warszawski alina@igf.fuw.edu.pl dr hab. Krzyszof Markowicz Insyu Geofizyki,
i 0,T F T F 0 Zatem: oprocentowanie proste (kapitalizacja na koniec okresu umownego 0;N, tj. w momencie t N : F t F 0 t 0;N, F 0
 Maemayka finansowa i ubezpieczeniowa - 1 Sopy procenowe i dyskonowe 1. Sopa procenowa (sopa zwrou, sopa zysku) (Ineres Rae). Niech: F - kapiał wypoŝyczony (zainwesowany) w momencie, F T - kapiał zwrócony
Maemayka finansowa i ubezpieczeniowa - 1 Sopy procenowe i dyskonowe 1. Sopa procenowa (sopa zwrou, sopa zysku) (Ineres Rae). Niech: F - kapiał wypoŝyczony (zainwesowany) w momencie, F T - kapiał zwrócony
2014-06-03. Empiryczne modele stóp zwrotu z portfeli inwestycyjnych. Modele, metody inwestowania oraz ocena działalności funduszu
 Empiyczne modele sóp zwou z pofeli inwesycyjnych Wojciech Gabowski Wydział Nauk Ekonomicznych Uniwesye Waszawski Rynki Finansowe 2013/14 Modele, meody inwesowania oaz ocena działalności funduszu -Meody
Empiyczne modele sóp zwou z pofeli inwesycyjnych Wojciech Gabowski Wydział Nauk Ekonomicznych Uniwesye Waszawski Rynki Finansowe 2013/14 Modele, meody inwesowania oaz ocena działalności funduszu -Meody
XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Ekonometryczne modele nieliniowe
 Ekonoeryczne odele nieliniowe Wykład 4 NMNK, MNW, eody radienowe Lieraura W. Greene Econoeric Analysis, rozdz. 7. sr. -4 J. Hailon 994 ie Series Analysis, sr. 33 5 Chun-Min Kuan 7 Inroducion o Econoeric
Ekonoeryczne odele nieliniowe Wykład 4 NMNK, MNW, eody radienowe Lieraura W. Greene Econoeric Analysis, rozdz. 7. sr. -4 J. Hailon 994 ie Series Analysis, sr. 33 5 Chun-Min Kuan 7 Inroducion o Econoeric
Fizyka 3. Janusz Andrzejewski
 Fizka 3 Ruch ciała Oaz się obaca Cegła się pzesuwa 6 meów Cz ważne jes o, ab opócz faku pzesunięcia się cegł uwzględnić eż obó cegł? Punk maeialn Punk maeialn-ciało, kóego ozmia i kszał w danm zagadnieniu
Fizka 3 Ruch ciała Oaz się obaca Cegła się pzesuwa 6 meów Cz ważne jes o, ab opócz faku pzesunięcia się cegł uwzględnić eż obó cegł? Punk maeialn Punk maeialn-ciało, kóego ozmia i kszał w danm zagadnieniu
FIZYKA 2. Janusz Andrzejewski
 FIZYKA 2 wykład 4 Janusz Andzejewski Pole magnetyczne Janusz Andzejewski 2 Pole gawitacyjne γ Pole elektyczne E Definicja wektoa B = γ E = Indukcja magnetyczna pola B: F B F G m 0 F E q 0 qv B = siła Loentza
FIZYKA 2 wykład 4 Janusz Andzejewski Pole magnetyczne Janusz Andzejewski 2 Pole gawitacyjne γ Pole elektyczne E Definicja wektoa B = γ E = Indukcja magnetyczna pola B: F B F G m 0 F E q 0 qv B = siła Loentza
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Strategie zarz~dzania kapitatem obrotowym a wzrost wartosci MSP
 Ne Woking Capial Managemen Saegies as a Faco o Shaping Small Fim Value (Saegie zaządzania kapiałem Waszawa 005 SSN: 134-887 p 90-10 3 imes cied (see: hp://michalskigcom/indekshdoc) " Gzegoz Michalski Akademia
Ne Woking Capial Managemen Saegies as a Faco o Shaping Small Fim Value (Saegie zaządzania kapiałem Waszawa 005 SSN: 134-887 p 90-10 3 imes cied (see: hp://michalskigcom/indekshdoc) " Gzegoz Michalski Akademia
Chemia Analityczna. Autor: prof. dr hab. inż Marek Biziuk
 Cheia Analiyczna Auor: pro. dr hab. inż Marek Biziuk Kaedra Cheii Analiycznej Wydział Cheiczny Poliechnika Gdańska 21 ANALIZA MIARECZKOWA (dział analizy objęościowej - woluerii) Meody iareczkowe służą
Cheia Analiyczna Auor: pro. dr hab. inż Marek Biziuk Kaedra Cheii Analiycznej Wydział Cheiczny Poliechnika Gdańska 21 ANALIZA MIARECZKOWA (dział analizy objęościowej - woluerii) Meody iareczkowe służą
O MIERNIKACH DOKŁADNOŚCI PROGNOZ EX POST W PROGNOZOWANIU ZMIENNYCH O SILNYM NATĘŻENIU SEZONOWOŚCI
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/, 0, s. 3 O MIERNIKACH DOKŁADNOŚCI PROGNOZ EX POST W PROGNOZOWANIU ZMIENNYCH O SILNYM NATĘŻENIU SEZONOWOŚCI Maia Szmuksa Zawadzka Sudium Maemayki Zachodniopomoski
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/, 0, s. 3 O MIERNIKACH DOKŁADNOŚCI PROGNOZ EX POST W PROGNOZOWANIU ZMIENNYCH O SILNYM NATĘŻENIU SEZONOWOŚCI Maia Szmuksa Zawadzka Sudium Maemayki Zachodniopomoski
MAKROEKONOMIA 2. Wykład 3. Dynamiczny model DAD/DAS, część 2. Dagmara Mycielska Joanna Siwińska - Gorzelak
 MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) i E E E i r r = = = = = θ θ ρ ν φ ε ρ α * 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa
MAKROEKONOMIA 2 Wykład 3. Dynamiczny model DAD/DAS, część 2 Dagmara Mycielska Joanna Siwińska - Gorzelak ( ) ( ) ( ) i E E E i r r = = = = = θ θ ρ ν φ ε ρ α * 1 1 1 ) ( R. popyu R. Fishera Krzywa Phillipsa
WZROST GOSPODARCZY A BEZROBOCIE
 Wojciech Pacho & WZROST GOSPODARCZ A BEZROBOCIE Celem niniejszego arykułu jes pokazanie związku pomiędzy ezroociem a dynamiką wzrosu zagregowanej produkcji. Poszukujemy oowiedzi na pyanie czy i jak silnie
Wojciech Pacho & WZROST GOSPODARCZ A BEZROBOCIE Celem niniejszego arykułu jes pokazanie związku pomiędzy ezroociem a dynamiką wzrosu zagregowanej produkcji. Poszukujemy oowiedzi na pyanie czy i jak silnie
Analiza metod oceny efektywności inwestycji rzeczowych**
 Ekonomia Menedżerska 2009, nr 6, s. 119 128 Marek Łukasz Michalski* Analiza meod oceny efekywności inwesycji rzeczowych** 1. Wsęp Podsawowymi celami przedsiębiorswa w długim okresie jes rozwój i osiąganie
Ekonomia Menedżerska 2009, nr 6, s. 119 128 Marek Łukasz Michalski* Analiza meod oceny efekywności inwesycji rzeczowych** 1. Wsęp Podsawowymi celami przedsiębiorswa w długim okresie jes rozwój i osiąganie
Praca domowa nr 1. Metodologia Fizyki. Grupa 1. Szacowanie wartości wielkości fizycznych Zad Stoisz na brzegu oceanu, pogoda jest idealna,
 Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
BADANIE DYNAMICZNEGO TŁUMIKA DRGA
 Ćwiczenie 3 BDNIE DYNMICZNEGO TŁUMIK DRGŃ. Cel ćwiczenia yłumienie dgań układu o częsości ezonansowej za pomocą dynamicznego łumika dgań oaz wyznaczenie zakesu częsości wymuszenia, w kóym łumik skuecznie
Ćwiczenie 3 BDNIE DYNMICZNEGO TŁUMIK DRGŃ. Cel ćwiczenia yłumienie dgań układu o częsości ezonansowej za pomocą dynamicznego łumika dgań oaz wyznaczenie zakesu częsości wymuszenia, w kóym łumik skuecznie
DYNAMIKA. Dynamika jest działem mechaniki zajmującym się badaniem ruchu ciał z uwzględnieniem sił działających na ciało i wywołujących ten ruch.
 DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża
DYNMIK Daika jes działe echaiki zajując się badaie uchu ciał z uwzględieie sił działającch a ciało i wwołującch e uch. Daika opiea się a pawach Newoa, a w szczególości a dugi pawie (zwa pawe daiki). Moża
CEL PRACY ZAKRES PRACY
 CEL PRACY. Analiza energetycznych kryteriów zęczenia wieloosiowego pod względe zastosowanych ateriałów, rodzajów obciążenia, wpływu koncentratora naprężenia i zakresu stosowalności dla ałej i dużej liczby
CEL PRACY. Analiza energetycznych kryteriów zęczenia wieloosiowego pod względe zastosowanych ateriałów, rodzajów obciążenia, wpływu koncentratora naprężenia i zakresu stosowalności dla ałej i dużej liczby
WPŁYW WYDATKÓW PUBLICZNYCH NA POPYT INWESTYCYJNY
 Wojciech Pacho WPŁW WDATÓW PUBLCZNCH NA POPT NWESTCJN Celem niniejszego efeau jes pzedsawienie oli wydaków ządowych w keowaniu waunków dla ozwoju pywanego kapiału. W ozważaniach nawiązujemy do ego nuu
Wojciech Pacho WPŁW WDATÓW PUBLCZNCH NA POPT NWESTCJN Celem niniejszego efeau jes pzedsawienie oli wydaków ządowych w keowaniu waunków dla ozwoju pywanego kapiału. W ozważaniach nawiązujemy do ego nuu
ESTYMACJA KRZYWEJ DOCHODOWOŚCI STÓP PROCENTOWYCH DLA POLSKI
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/3, 202, sr. 253 26 ESTYMACJA KRZYWEJ DOCHODOWOŚCI STÓP PROCENTOWYCH DLA POLSKI Adam Waszkowski Kaedra Ekonomiki Rolnicwa i Międzynarodowych Sosunków
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XIII/3, 202, sr. 253 26 ESTYMACJA KRZYWEJ DOCHODOWOŚCI STÓP PROCENTOWYCH DLA POLSKI Adam Waszkowski Kaedra Ekonomiki Rolnicwa i Międzynarodowych Sosunków
Matematyka ubezpieczeń życiowych r.
 . W populacji, w której śmiertelnością rządzi prawo de Moivre a z wiekiem granicznym ω = 50, dzieckiem jest się do wieku d. W wieku d rozpoczyna się pracę i pracuje się do wieku p.w wieku p przechodzi
. W populacji, w której śmiertelnością rządzi prawo de Moivre a z wiekiem granicznym ω = 50, dzieckiem jest się do wieku d. W wieku d rozpoczyna się pracę i pracuje się do wieku p.w wieku p przechodzi
Inwestycje. Makroekonomia II Dr hab. Joanna Siwińska-Gorzelak
 Inwesycje Makroekonomia II Dr hab. Joanna Siwińska-Gorzelak CIASTECZOWY ZAWRÓT GŁOWY o akcja mająca miejsce w najbliższą środę (30 lisopada) na naszym Wydziale. Wydarzenie o związane jes z rwającym od
Inwesycje Makroekonomia II Dr hab. Joanna Siwińska-Gorzelak CIASTECZOWY ZAWRÓT GŁOWY o akcja mająca miejsce w najbliższą środę (30 lisopada) na naszym Wydziale. Wydarzenie o związane jes z rwającym od
WYKŁAD FIZYKAIIIB 2000 Drgania tłumione
 YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
:36 G:\WYKLAD IIIBC 2001\FIN2001\Drgwym2001.doc Drgania i fale II rok Fizyk BC. Oscylator pod działaniem zmiennej w czasie siły:
 Dgania wyuzone. Rezonan Ocylao pod działanie ziennej w czaie iły: (a) iła pzyłożona bezpośednio do ay, (b) uch punku zaczepienia pężyny (np. aywny obiek połączony pężyście z eleene dgający). Niech () co
Dgania wyuzone. Rezonan Ocylao pod działanie ziennej w czaie iły: (a) iła pzyłożona bezpośednio do ay, (b) uch punku zaczepienia pężyny (np. aywny obiek połączony pężyście z eleene dgający). Niech () co
Siła. Zasady dynamiki
 Siła. Zasady dynaiki Siła jest wielkością wektoową. Posiada okeśloną watość, kieunek i zwot. Jednostką siły jest niuton (N). 1N=1 k s 2 Pzedstawienie aficzne A Siła pzyłożona jest do ciała w punkcie A,
Siła. Zasady dynaiki Siła jest wielkością wektoową. Posiada okeśloną watość, kieunek i zwot. Jednostką siły jest niuton (N). 1N=1 k s 2 Pzedstawienie aficzne A Siła pzyłożona jest do ciała w punkcie A,
LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r.
 Koisja Egzainacyjna dla Aktuariuszy LV Egzain dla Aktuariuszy z 13 grudnia 2010 r. Część II Mateatyka ubezpieczeń życiowych Iię i nazwisko osoby egzainowanej:... Czas egzainu: 100 inut Warszawa, 13 grudnia
Koisja Egzainacyjna dla Aktuariuszy LV Egzain dla Aktuariuszy z 13 grudnia 2010 r. Część II Mateatyka ubezpieczeń życiowych Iię i nazwisko osoby egzainowanej:... Czas egzainu: 100 inut Warszawa, 13 grudnia
Makroekonomia II. Plan
 Makroekonomia II Wykład 5 INWESTYCJE Wyk. 5 Plan Inwesycje 1. Wsęp 2. Inwesycje w modelu akceleraora 2.1 Prosy model akceleraora 2.2 Niedosaki prosego modelu akceleraora 3. Neoklasyczna eoria inwesycji
Makroekonomia II Wykład 5 INWESTYCJE Wyk. 5 Plan Inwesycje 1. Wsęp 2. Inwesycje w modelu akceleraora 2.1 Prosy model akceleraora 2.2 Niedosaki prosego modelu akceleraora 3. Neoklasyczna eoria inwesycji
Wyższa Szkoła Marketingu i Zarządzania w Lesznie
 Wyższa Szkoła Markeingu i Zarządzania w Lesznie MATERIAŁY ROBOCZE NA ZAJĘCIA Z PRZEDMIOTU BIZNES PLAN Opracowali: dr Jacek Kowalewski mgr Kazimierz Linowski Leszno 2008 2 S P I S T R E Ś C I WPROWADZENIE.
Wyższa Szkoła Markeingu i Zarządzania w Lesznie MATERIAŁY ROBOCZE NA ZAJĘCIA Z PRZEDMIOTU BIZNES PLAN Opracowali: dr Jacek Kowalewski mgr Kazimierz Linowski Leszno 2008 2 S P I S T R E Ś C I WPROWADZENIE.
INWESTYCJE. Makroekonomia II Dr Dagmara Mycielska Dr hab. Joanna Siwińska-Gorzelak
 INWESTYCJE Makroekonomia II Dr Dagmara Mycielska Dr hab. Joanna Siwińska-Gorzelak Inwesycje Inwesycje w kapiał rwały: wydaki przedsiębiorsw na dobra używane podczas procesu produkcji innych dóbr Inwesycje
INWESTYCJE Makroekonomia II Dr Dagmara Mycielska Dr hab. Joanna Siwińska-Gorzelak Inwesycje Inwesycje w kapiał rwały: wydaki przedsiębiorsw na dobra używane podczas procesu produkcji innych dóbr Inwesycje
EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH. dr inż. Robert Stachniewicz
 EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH dr inż. Rober Sachniewicz METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH Jednymi z licznych celów i zadań przedsiębiorswa są: - wzros warości przedsiębiorswa
EFEKTYWNOŚĆ INWESTYCJI MODERNIZACYJNYCH dr inż. Rober Sachniewicz METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH Jednymi z licznych celów i zadań przedsiębiorswa są: - wzros warości przedsiębiorswa
LIST EMISYJNY nr 3 /2014 Ministra Finansów
 LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 50-370 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 7 320 320
