VII. Drgania układów nieliniowych
|
|
|
- Laura Cieślik
- 6 lat temu
- Przeglądów:
Transkrypt
1 VII. Drgania układów nieliniowych 1. Drgania anharmoniczne spowodowane symetryczna siła zwrotna 1.1 Różniczkowe równanie ruchu Rozważamy teraz drgania swobodne masy m przytwierdzonej do sprężyny o współczynniku sprężystości k, gdy siła zwrotna F s zależy nieliniowo od przemieszczenia x, a zależność ta dana jest równaniem: Powyższe równanie możemy zapisać w postaci: F s = kx cx 3. (1) F s = (1 + α x 2 )kx, (2) gdzie parametr α powiązany jest z współczynnikami k i c z równania (1) zależnością α = c/k. Nowo wprowadzona stała α może być dodatnia (α > 0) lub ujemna (α < 0) (patrz rysunek). Będziemy rozpatrywać przypadek, gdy nieliniowość układu drgającego jest bardzo mała, czyli, gdy spełniona jest relacja αx 2 1. (3) Różniczkowe równanie ruchu masy m (II zasada dynamiki Newtona) ma postać a po podstawieniu siły (2) otrzymujemy równanie które możemy zapisać w postaci gdzie wprowadziliśmy ω 2 0 = k/m. 1.2 Własności drgań swobodnych Drgania swobodne opisane równaniem (6) mają następujące własności: mẍ = F s, (4) mẍ = (1 + α x 2 )kx, (5) ẍ + (1 + αx 2 )ω 2 0x = 0, (6) (a). Ponieważ nie występuje tłumienie, ruch jest ruchem periodycznym (ale nie harmonicznym) z okresem T s, czyli zachodzi x(t) = x(t + T s ), (7) (b). Ponieważ moduł siły F s jest symetryczny względem x = 0, to ruch po lewej stronie x = 0 ( a więc dla x < 0) jest lustrzanym odbiciem ruchu po prawej stronie x = 0 (a więc dla x > 0), czyli zachodzi relacja x(t + T s ) = x(t). (8) 2 1
2 1.3 Równanie ruchu x(t) i jego własności Jak wiadomo każde drganie periodyczne o okresie T s może być przedstawione jako superpozycja drgań harmonicznych o częstościach nω s (ω s = 2π/T s ), czyli w postaci szeregu Fouriera: x(t) = A 0 + A 1 cos(ω s t + δ 1 ) + A 2 cos(2ω s t + δ 2 ) + A 3 cos(3ω s t + δ 3 ) +. (9) Przyjmijemy następujący warunek początkowy omawianego ruchu: ẋ(0) = 0 (10) oznaczający, że prędkość w chwili początkowej t = 0 jest równa zero. Zobaczmy,jak ten warunek wpływa na postać ogólnego rozwiązania (9). Obliczając ẋ(t) z równania (9), mamy: ẋ(t) = ω s A 1 sin(ω s t + δ 1 ) 2ω s A 2 sin(2ω s t + δ 2 ) 3ω s A 3 sin(3ω s t + δ 3 ). (11) Stosując do powyższego równania warunek (10), otrzymujemy wyrażenie ẋ(0) = ω s A 1 sin δ 1 2ω s A 2 sin δ 2 3ω s A 3 sin δ 3 = 0, (12) które jest spełnione tylko wówczas, gdy Szereg Fouriera (9) dany jest więc teraz równaniem δ 1 = δ 2 = δ 3 = = 0. (13) x(t) = A 0 + A 1 cos ω s t + A 2 cos 2ω s t + A 3 cos 3ω s t +, (14) które musi spełniać również warunek (8). Warunek ten spełniają tylko harmoniki nieparzyste równania (14), nie spełniają natomiast harmoniki parzyste oraz niezależny od czasu człon A 0 (tzw. harmonika zerowa). Pokażemy to na przykładzie pierwszej i drugiej harmoniki. Dla pierwszej harmoniki mamy: natomiast dla drugiej harmoniki cos ω s (t + T s 2 ) = cos(ω st ω st s ) = cos(ω s t + π) = cos ω s t, (15) cos 2ω s (t + T s 2 ) = cos(2ω st + ω s T s ) = cos(2ω s t + 2π) = cos 2ω s t, (16) gdzie skorzystaliśmy z zależności ω s = 2π/T s. Równanie (15) świadczy o tym, że człon A 1 cosω s t w równaniu (14) spełnia relację (8); podobie spełniają ją wszystkie pozostałe człony z harmonikami nieparzystymi (można dla nich otrzymać związki analogiczne do (15)). Natomiast równanie (16) wskazuje, że relacja (8) nie jest spełniona przez człon z drugą harmoniką w równaniu (14); relację (8) również nie spełniają pozostałe człony z harmonikami parzystymi w równaniu (14) oraz człon z A 0 (harmonika zerowa), dla których łatwo można otrzymać relacje analogiczne do (16). 2
3 Tak więc rozwiązanie równania różniczkowego (6) jest dane tylko przez sumę nieparzystych harmonik. Przy bardzo małej nieliniowości określonej równaniem (3) możemy ograniczyć się tylko do dwóch pierwszych członów, zaniedbując pozostałe czyli x(t) = A 1 cosω s t + A 3 cos 3ω s t +. (17) Powyższe równanie możemy zapisać w następującej wygodnej postaci: x = A(cosω s t + ε cos 3ω s t + ), (18) gdzie A A 1 jest amplitudą drgań swobodnych o częstości podstawowej ω s, 3ω s jest częstością trzeciej harmonicznej, a parametr anharmoniczności ε = A 3 /A 1 (wskazuje on na udział trzeciej harmonicznej w drganiach omawianego ukadu nieliniowego). Równanie (18) musi spełniać różniczkowe równanie ruchu (6), które teraz zapiszemy w postaci. ẍ + ω0x 2 + αω0x 2 3 = 0. (19) Korzystając z faktu, że (18) jest rozwiązaniem równania (19), znajdziemy teraz postać, jaką powinny mieć częstość kołowa ω s i parametr ε, aby tak było. W tym celu obliczmy ẍ i x 3, a potem wspólnie z x podstawmy do równaia (19): ẋ = ω s A sin ω s t 3ω s εa sin 3ω s t, (20) ẍ = ω 2 sa cos ω s t 9ω 2 saε cos 3ω s t = ω 2 sa(cosω s t + 9ε cos 3ω s t), (21) x 3 = A 3 (cos 3 ω s t + 3ε cos 2 ω s t cos 3ω s t + 3ε 2 cos ω s t cos 2 3ω s t + ε 3 cos 3 3ω s t), (22) przy czym dwa ostatnie człony w równaniu (22) możemy teraz pominąć, ze względu na to, że bardzo mały parametr ε występuje w nich w drugiej i trzeciej potędze. W dalszej części obliczeń pomijane będą wyrazy bardzo małe, zawierające: ε 2, α 2, εα oraz ich wyższe potęgi. Podstawiając ẍ, x 3 oraz x do równania (19) mamy: ωsa 2 (cos ω s t + 9ε cos 3ω s t) + ω0a 2 (cos ω s t + ε cos 3ω s t +...) + + αω0a 2 3 ( 1 4 cos 3ω st cos ω st +...) = 0, (23) przy czym w ostatnim nawiasie powyższego równania wykorzystaliśmy następującą relację cos 3 ω s t = 1 4 cos 3ω st cos ω st. (24) Grupując człony z tymi samymi harmonikami, możemy równanie (23) zapisać w postaci: ( ωsa 2 + ω0a αω2 0A 3 ) cos ω s t + ( 9εωsA 2 + εω0a αω2 0A 3 ) cos 3ω s t = 0. (25) 3
4 Powyższe równanie jest spełnione dla dowolnego t tylko wówczas, gdy współczynniki przy poszczególnych harmonikach są równe zero (jest to równanie typu a cos ω s t + b cos 3ω s t = 0, które jest spełnione dla dowolnej chwili t tylko wówczas, gdy a = b = 0). Przyrównując więc współczynnik stojący w równaniu (25) przy cos ω s t, mamy: ωsa 2 + ω0a αω2 0A 3 = 0, (26) a stąd ω 2 s = ω 2 0( αa2 ), (27) czyli ω s = ω αa2. (28) Ponieważ rozwinięcie funkcji 1 + x w szereg ma dla małych warości x ( x 1) postać 1 + x x +..., więc dla bardzo małej nieliniowości ( αa2 1) mamy ω s ω 0 ( αa2 ). (29) Tak więc pojawienie się członu nieliniowego w sile zwrotnej (2) może zwiększać lub zmniejszać częstość podstawowa drgań ω s : ω s > ω 0 dla α > 0, ω s < ω 0 dla α < 0, a różnica częstości ω s ω 0 zależy od amplitudy A drgań z częstością podstawową ω s i jest proporcjonalna do jej kwadraty: ω s ω ω 0αA 2. (30) Przyrównując teraz do zera czynnik przy cos 3ω s t w równaniu (25), mamy 9εω 2 sa + εω 2 0A αω2 0A 3 = 0. (31) Podstawiając teraz w miejsce ω 2 s wyrażenie (27), otrzymujemy a po dokonaniu uproszczeń i prostych przekształceń mamy: 8εω 2 0A 27 4 εαa3 ω αω2 0A 3 = 0, (32) ε( αa2 ) = 1 32 αa2. (33) 4
5 W powyższym równaniu możemy zaniedbać bardzo mały drugi człon w nawiasie (patrz warunek bardzo małej nieliniowości (3)) i wyznaczyć ε: ε 1 32 αa2. (34) Z powyższego równania wynika, że dla bardzo małej nieliniowości αa 2 1 również parametr anharmoniczności ε jest bardzo mały ( ε 1. Z równań (18) i (34) wynika, że anharmoniczność ruchu zwiększa się wraz z amplitudą drgań, a parametr ε, charakteryzujący anharmoniczność drgań, jest proporcjonalny do kwadratu amplitudy. Otrzymane powyżej wzory (28) i (34) na ω s i ε są tylko wyrażeniami przybliżonymi. Jeżeli chcielibyśmy uzyskać bardziej dokładne wyrażenia, musielibyśmy uwzględnić człony zaniedbane podczas dotychczasowych obliczeń (proporcjanalne do αε, α 2, itd). Przyjrzyjmy się jeszcze średniemu położeniu ciała drgającego anharmonicznie przy działaniu symetrycznej siły zwrotnej. W czasie ruchu jego położenie opisane równaniem (18) przyjmuje zarówno dodatnie jak i ujemne wartości współrzędnej x wyznaczanej względem położenia równowagi trwałej. Oznaczając symbolem < x(t) > średnie w czasie położenie drgającego ciała, mamy: < x(t) >= A(< cos ω s t > +ε < cos 3ω s t >) = 0, (35) ponieważ średnia wartość funkcji cosinus liczona dla okresu lub jego wielokrotności jest równa zero: < cos ω s t >=< cos 3ω s t >= 0 (36) 1.4. Przykład: Wahadło matematyczne jako układ nieliniowy Równanie ruchu obrotowego wahadła matematycznego (wyprowadzone już wcześniej): możemy zapisać w postaci θ + g sin θ = 0, (37) L θ + ω 2 0 sin θ = 0, (38) gdzie ω 2 0 = g L. (39) Rozwijając funkcję sin θ w szereg: sin θ = θ 1 3! θ3 + (40) 5
6 i podstawiając (40) do (38) oraz korzystając z wyrażenia 3! = 6 otrzymujemy θ + (1 1 6 θ2 ) ω 2 0 θ = 0, (41) co możemy zapisać w postaci θ + (1 + α θ 2 ) ω 2 0 θ = 0, (42) gdzie α = 1 6. Równanie (42) jest równaniem drgań anharmonicznych, analogicznym do poznanego już równania drgań anharmonicznych podczas działania symetrycznej siły zwrotnej: ẍ + (1 + α x 2 ) ω 2 0 x = 0. (43) A więc wahadło matematyczne jest nieliniowym układem fizycznym, którego drgania, opisane różniczkowym równaniem (42), mają własności drgań zachodzących przy działaniu symetrycznej siły zwrotnej. Korzystając więc z wcześniej uzyskanych wyników mamy: (a) równanie ruchu θ(t) θ(t) = A(cos ω s t + ε cos 3ω s t) (44) gdzie A θ m jest amplitudą wychylenia; (b) częstość kołowa drgań ω s ω s ω 0 ( αa2 ) = ω 0 ( A2 ) (45) (c) parametr nieliniowości ε Dla amplitudy drgań A = 10 o 0, 1744 rad mamy αa 2 0, 005 oraz ε 1 32 αa2 = A2 (46) ω ω 0 = ω s ω 0 ω 0 = 3 8 αa2 = 1 16 A2 0, 002, (47) ε = A (48) 6
7 2. Drgania anharmoniczne spowodowane asymetryczna siła zwrotna 2.1 Różniczkowe równanie ruchu Przykładem asymetrycznej siły zwrotnej jest siła, która zależy od przemieszczenia x zarówno w pierwszej jak i w drugiej potędze: F s = kx bx 2. (49) Możemy zapisać ją w postaci F s = (1 + β x)kx, (50) gdzie β = b/k jest stałą dla danego układu drgającego. Wartość siły zwrotnej F s jest inna dla tej samej warości x przy rozciąganiu i ściskaniu sprężyny (patrz rysunek dla β > 0). Omawiać będziemy drgania układu o bardzo małej nieliniowości, a więc drgania dla których β x 1. (51) Różniczkowe równanie ruchu mẍ = F s (52) ma po podstawieniu siły (50) postać ẍ + (1 + β x)ω 2 0 x = 0, (53) gdzie ω0 2 = k/m. 2.2 Równanie ruchu x(t) i jego własności Podobnie jak w przypadku działania symetrycznej siły zwrotnej, ruch będzie ruchem periodycznym (ale nie ruchem harmonicznym) o okresie T s i może być przedstawiony w postaci szeregu Fouriera. Ponieważ w przypadku asymetrycznej siły zwrotnej nie zachodzi warunek (8), to rozwiązanie równania (53) będzie zawierać w ogólności wszystkie harmoniki (łącznie z zerową) i będzie miało postać (9). Ograniczając się do bardzo małej nieliniowości (51) oraz przyjmując warunek początkowy dla prędkości ẋ(0) = 0 (stałe δ n w szeregu Fouriera są wówczas równe zero, co pokazaliśmy w części VII.1.3 ), szereg Fouriera będący rozwiązaniem równania (53) ma postać x = A 0 + A 1 cos ω s t + A 2 cos 2ω s t +, (54) co możemy zapisać w postaci x = A 0 + A(cosω s t + η cos 2ω s t + ), (55) 7
8 gdzie ω s = 2π/T s jest częstością podstawową drgań, 2ω s częstością drugiej harmonicznej, A A 1, natomiast parametr η = A 2 /A 1 określa wielkość anharmoniczności drgań. Dla bardzo małej nieliniowości, a więc, gdy spełniony jest warunek (51) możemy postępować podobnie jak w części 1.3, gdzie zajmowaliśmy się symetryczną siłą zwrotną. Korzystając, podobnie jak poprzednio z tego, że równanie (55) jest rozwiązaniem równania różniczkowego (53), które zapiszemy teraz w postaci ẍ + ω0x 2 + βω0 2 x 2 = 0, (56) będziemy mogli wyznaczyć wielkości ω s, η i A 0 występujące w równaniu (55). W tym celu obliczymy najpierw ẍ, x 2 : ẋ = ω s A sin ω s t 2ω s Aη sin 2ω s t +..., (57) ẍ = ω 2 sa cos ω s t 4ω 2 saη cos 2ω s t +... = ω 2 sa(cos ω s t + 4η cos 2ω s t +...) (58) x 2 = A A 0 A(cosω s t + η cos 2ω s t) + A 2 (cos 2 ω s t + 2η cosω s t cos 2ω s t +...). (59) Podstawiając teraz wyrażenia (55), (58) i (59) do (56) otrzymujemy: ω 2 sa(cos ω s t + 4η cos 2ω s t) + ω 2 0[A 0 + A(cos ω s t + η cos 2ω s t)] + + βω 2 0[A A 0 A cos ω s t A2 (1 + cos 2ω s t)] = 0, (60) gdzie pominięte zostały człony bardzo małe zawierające iloczyny lub potęgi parametrów η i β, a w ostatnim nawiasie wykorzystana została relacja cos 2 ω s t = 1(1 + cos 2ω 2 st). Można dokonać pogrupowania wyrazów zawierających odpowiednio drugą, pierwszą i zerową harmonikę: ( 4ηωsA 2 + ηω0a βω2 0A 2 ) cos 2ω s t + ( ωsa 2 + ω0a 2 + 2A 0 Aβω0) 2 cos ω s t + + (ω0a βω0a A2 βω0) 2 = 0. (61) Powyższe równanie jest spełnione dla dowolnego t tylko wówczas, gdy czynniki przy wszystkich harmonikach, łącznie z zerową, są równe zero. Z warunku zerowania się tych czynników, ograniczonych nawiasami w równaniu (61) możemy wyznaczyć interesujące nas wielkości η, ω s oraz A 0. Przyrównując do zera czynnik przy harmonice zerowej ω0a βω0a A2 βω0 2 = 0 (62) mamy A 0 (1 + βa 0 ) = 1 2 β A2. (63) 8
9 A ponieważ przy bardzo małej nieliniowości (51) zachodzi β A 0 1, (64) więc A β A2. (65) Przyrównując do zera czynnik pierwszej harmonice (cos ω s t) ω 2 sa + ω 2 0A + 2A 0 Aβω 2 0 = 0 (66) mamy ω 2 s = ω 2 0(1 + 2βA 0 ). (67) Uwzględniając (64) otrzymujemy ω 2 s ω 2 0, (68) czyli ω s ω 0. (69) Porównując natomiast do zera czynnik prz drugiej harmonice (cos 2ω s t) 4ηω 2 sa + ηω 2 0A βω2 0A 2 = 0 (70) i biorąc po uwagę (69) otrzymujemy η 1 β A, (71) 6 Uwagi: (a). Średnie przemieszczenie < x > nie jest równe zero i wynosi < x >= A β A2. (72) (b).równanie (71) pokazuje, że anharmoniczność drgań rośnie wraz z amplitudą drgań. Parametr η określający amplitudę drugiej harmonicznej zależy liniowo od amplitudy A (amplituda drugiej harmonicznej w równaniu (55) wynosi ηa), podczas gdy dla symetrycznej siły zwrotnej parametr anharmoniczności ε zależy kwadratowo od amplitudy A (patrz równania (18) i (34) ) (amplituda trzeciej harmonicznej w równaniu (18) wynosi εa). 9
10 3. Drgania wymuszone układów nieliniowych 3.1. Siła wymuszajaca zmieniajaca się harmonicznie Zajmować się będziemy drganiami układu o słabym tłumieniu (γ < 2ω 0 ), gdy częstość siły wymuszającej ω ω 0. Z wcześniejszej analizy drgań wymuszonych wiemy, że dla takich częstości drgania ustalone zależą głównie od własności sprężystych układu (amplituda drgań A F 0 /k), a nie zależą od drgającej masy; ponadto przesunięcie fazowe Φ = 0. Stwierdziliśmy wówczas, że dla siły wymuszającej przemieszczenie x wynosi co możemy zapisać w postaci F = F 0 cos ωt (73) x A cos ωt, (74) x a F, (75) gdzie a 1/k. Powyższy wynik uzyskaliśmy dla układu drgającego, w którym nie uwzględniliśmy jego własności nieliniowych. Natomiast dla słabo nieliniowego układu drgającego (np. układu z sprężyną wykazującą słabe własności nieliniowe) przemieszczenie x spowodowane działaniem siły wymuszającej F możemy wyrazić w postaci szeregu gdzie a, b i c są stałymi. x a F + bf 2 + c F , (76) Pokażemy, że jeżeli siła wymuszająca zmienia się harmonicznie, czyli dana jest równaniem (73) to nieliniowość układu prowadzi do drgań anharmonicznych, które mogą być przedstawione jako superpozycja drgania o częstości podstawowej ω i drgań o częstościach będących wyższymi harmonicznymi tej częstości. Podstawiając (73) do równania (76) otrzymujemy Wprowadzając do równania (76) znane relacje x af 0 cos ωt + bf 2 0 cos 2 ωt + cf 3 0 cos 3 ωt. (77) cos 2 ωt = 1 (1 + cos 2ωt), (78) 2 cos 3 ωt = 1 4 cos 3ωt cosωt, (79) po wykonaniu prostych przekształceń mamy: x bf 0 2 ( 2 + af ) 4 cf 0 3 cos ωt + b2 F0 2 2 cos 2ωt + cf cos 3ωt. (80) Równanie (80) pokazuje, że podczas drgań wymuszanych częstością ω nieliniowość drgań dana równaniem (76) prowadzi do pojawienia się drgań harmonicznych z częstościami nω (n = 0, 1, 2, 3,...). 10
11 3.2. Rezonanse dla częstości subharmonicznych Dla układu liniowego rezonans występował tylko dla jednej częstości ω = ω 0, a krzywa rezonansowa A(ω) miała tylko jedno maksimum. Inna sytuacja będzie w przypadku układu nieliniowego. Jeżeli dla układu nieliniowego zmniejszalibyśmy częstość ω siły wymuszającej poczynając od częstości rezonansowej ω = ω 0, to częstość ω przechodziłaby przez wartości ω = ω 0 /2, ω = ω 0 /3..., dla których odpowiednie harmoniczne częstości ω są równe częstości rezonansowej (2ω = ω 0, 3ω = ω 0, itd). To jest przyczyną pojawienia się dodatkowych maksimów na krzywej rezonansowej A(ω) właśnie dla takich częstości ω, których harmoniczne są równe częstości rezonansowej ω Częstości kombinacyjne Przyjrzyjmy się teraz sytuacji, gdy na nieliniowy układ drgający działają dwie harmonicznie zmieniające się siły wymuszające F 1 cos ω 1 t i F 2 cos ω 2 t o różnych częstościach ω 1 i ω 2. Wypadkowa siła działająca na układ jest wówczas sumą tych sił: F = F 1 cos ω 1 t + F 2 cos ω 2 t. (81) Zakładając tylko liniową i kwadratową zależność w równaniu (76), mamy x af + bf 2 = a(f 1 cos ω 1 t + F 2 cos ω 2 t) + b(f 1 cos ω 1 t + F 2 cosω 2 t) 2, (82) a po wykonaniu potęgowania x af 1 cos ω 1 t + af 2 cos ω 2 t + bf1 2 cos 2 ω 1 t + bf2 2 cos 2 ω 2 t + 2bF 1 F 2 cosω 1 t cosω 2 t. (83) Pierwszy człon po prawej stronie powyższego równania przedstawia drgania harmoniczne z częstością ω 1, drugi drgania z częstością ω 2. Człon trzeci bf1 2 cos 2 ω 1 t = 1 2 bf 1 2 (1 + cos 2ω 1 t) (84) i czwarty bf2 2 cos 2 ω 2 t = 1 2 bf 2 2 (1 + cos 2ω 2 t) (85) dają zarówno wyrazy stałe w czasie, jak i drgania harmoniczne z częstościami odpowiednio 2ω 1 oraz 2ω 2. Przyjrzyjmy się członowi ostatniemu w równaniu (83). Ponieważ 2 cos ω 1 t cosω 2 t = cos(ω 1 + ω 2 )t + cos(ω 2 ω 1 )t, (86) to człon ten możemy zapisać w postaci 2F 1 F 2 cos ω 1 t cos ω 2 t = F 1 F 2 cos(ω 1 + ω 2 )t + F 1 F 2 cos(ω 2 ω 1 )t, (87) a to oznacza, że w wypadkowym drganiu (83) mamy również drgania z częstością będącą sumą (ω 1 + ω 2 ) i różnicą (ω 2 ω 1 ) częstości sił wymuszających ω 1 i ω 2. Częstości te, ω 1 + ω 2 i ω 2 ω 1, nazywamy częstościami kombinacyjnymi. 11
α - stałe 1 α, s F ± Ψ taka sama Drgania nieliniowe (anharmoniczne) Harmoniczne: Inna zależność siły od Ψ : - układ nieliniowy,
 Drgania nieliniowe (anharmoniczne) Harmoniczne: F s s Inna zależność siły od : - układ nieliniowy, Symetryczna siła zwrotna Niech: F s ( ) s Symetryczna wartość - drgania anharmoniczne α, s F s dla α -
Drgania nieliniowe (anharmoniczne) Harmoniczne: F s s Inna zależność siły od : - układ nieliniowy, Symetryczna siła zwrotna Niech: F s ( ) s Symetryczna wartość - drgania anharmoniczne α, s F s dla α -
Podstawy fizyki sezon 1 VII. Ruch drgający
 Podstawy fizyki sezon 1 VII. Ruch drgający Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Ruch skutkiem działania
Podstawy fizyki sezon 1 VII. Ruch drgający Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Ruch skutkiem działania
MECHANIKA II. Drgania wymuszone
 MECHANIKA II. Drgania wymuszone Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny Daniel Lewandowski (I-19) MECHANIKA II. Drgania wymuszone 1 / 30 Układ drgajacy o jednym stopniu swobody
MECHANIKA II. Drgania wymuszone Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny Daniel Lewandowski (I-19) MECHANIKA II. Drgania wymuszone 1 / 30 Układ drgajacy o jednym stopniu swobody
Drgania i fale II rok Fizyk BC
 00--07 5:34 00\FIN00\Drgzlo00.doc Drgania złożone Zasada superpozycji: wychylenie jest sumą wychyleń wywołanych przez poszczególne czynniki osobno. Zasada wynika z liniowości związku między wychyleniem
00--07 5:34 00\FIN00\Drgzlo00.doc Drgania złożone Zasada superpozycji: wychylenie jest sumą wychyleń wywołanych przez poszczególne czynniki osobno. Zasada wynika z liniowości związku między wychyleniem
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
MECHANIKA 2. Drgania punktu materialnego. Wykład Nr 8. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 8 Drgania punktu materialnego Prowadzący: dr Krzysztof Polko Wstęp Drgania Okresowe i nieokresowe Swobodne i wymuszone Tłumione i nietłumione Wstęp Drgania okresowe ruch powtarzający
MECHANIKA 2 Wykład Nr 8 Drgania punktu materialnego Prowadzący: dr Krzysztof Polko Wstęp Drgania Okresowe i nieokresowe Swobodne i wymuszone Tłumione i nietłumione Wstęp Drgania okresowe ruch powtarzający
Wykład 6 Drgania. Siła harmoniczna
 Wykład 6 Drgania Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym (periodycznym). Przemieszczenie cząstki w ruchu periodycznym można wyrazić za pomocą funkcji sinus albo
Wykład 6 Drgania Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym (periodycznym). Przemieszczenie cząstki w ruchu periodycznym można wyrazić za pomocą funkcji sinus albo
Drgania układu o wielu stopniach swobody
 Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ruch drgajacy. Drgania harmoniczne. Drgania harmoniczne... Drgania harmoniczne... Notatki. Notatki. Notatki. Notatki. dr inż.
 Ruch drgajacy dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 1 dr inż. Ireneusz Owczarek Ruch drgajacy Drgania harmoniczne Drgania oscylacje to cykliczna
Ruch drgajacy dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 1 dr inż. Ireneusz Owczarek Ruch drgajacy Drgania harmoniczne Drgania oscylacje to cykliczna
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Wykład FIZYKA I. Dr hab. inż. Władysław Artur Woźniak. Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska
 Wykład FIZYKA I 1. Ruch drgający tłumiony i wymuszony Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html DRGANIA HARMONICZNE
Wykład FIZYKA I 1. Ruch drgający tłumiony i wymuszony Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html DRGANIA HARMONICZNE
Ruch drgający. Ruch harmoniczny prosty, tłumiony i wymuszony
 Ruch drgający Ruch harmoniczny prosty, tłumiony i wymuszony Ruchem drgającym nazywamy ruch ciała zachodzący wokół stałego położenia równowagi. Ruchy drgające dzielimy na ruchy: okresowe, nieokresowe. Ruch
Ruch drgający Ruch harmoniczny prosty, tłumiony i wymuszony Ruchem drgającym nazywamy ruch ciała zachodzący wokół stałego położenia równowagi. Ruchy drgające dzielimy na ruchy: okresowe, nieokresowe. Ruch
MECHANIKA II. Drgania wymuszone
 MECHANIKA II. Drgania wymuszone Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/ daniel.lewandowski@pwr.edu.pl
MECHANIKA II. Drgania wymuszone Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/ daniel.lewandowski@pwr.edu.pl
Drgania wymuszone - wahadło Pohla
 Zagadnienia powiązane Częstość kołowa, częstotliwość charakterystyczna, częstotliwość rezonansowa, wahadło skrętne, drgania skrętne, moment siły, moment powrotny, drgania tłumione/nietłumione, drgania
Zagadnienia powiązane Częstość kołowa, częstotliwość charakterystyczna, częstotliwość rezonansowa, wahadło skrętne, drgania skrętne, moment siły, moment powrotny, drgania tłumione/nietłumione, drgania
RUCH HARMONICZNY. sin. (r.j.o) sin
 RUCH DRGAJĄCY Ruch harmoniczny Rodzaje drgań Oscylator harmoniczny Energia oscylatora harmonicznego Wahadło matematyczne i fizyczne Drgania tłumione Drgania wymuszone i zjawisko rezonansu Politechnika
RUCH DRGAJĄCY Ruch harmoniczny Rodzaje drgań Oscylator harmoniczny Energia oscylatora harmonicznego Wahadło matematyczne i fizyczne Drgania tłumione Drgania wymuszone i zjawisko rezonansu Politechnika
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Wykład FIZYKA I. 10. Ruch drgający tłumiony i wymuszony. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 1. Ruch drgający tłumiony i wymuszony Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html Siły oporu (tarcia)
Wykład FIZYKA I 1. Ruch drgający tłumiony i wymuszony Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html Siły oporu (tarcia)
Ćwiczenie M-2 Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego Cel ćwiczenia: II. Przyrządy: III. Literatura: IV. Wstęp. l Rys.
 Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
INSTRUKCJA DO ĆWICZENIA NR 5
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 5 PRZEDMIOT TEMAT OPRACOWAŁ MODELOWANIE UKŁADÓW MECHANICZNYCH Badania analityczne układu mechanicznego
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 5 PRZEDMIOT TEMAT OPRACOWAŁ MODELOWANIE UKŁADÓW MECHANICZNYCH Badania analityczne układu mechanicznego
dr inż. Paweł Szeptyński materiały pomocnicze do przedmiotu MECHANIKA TEORETYCZNA DYNAMIKA - ZADANIA
 NAZEWNICTWO LINIOWE RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE O STAŁYCH WSPÓŁCZYNNIKACH d n u a n d x + a d n 1 u n n 1 d x +... + a d 2 u n 1 2 d x + a d u 2 1 d x + a u = b( x) Powyższe równanie o niewiadomej funkcji
NAZEWNICTWO LINIOWE RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE O STAŁYCH WSPÓŁCZYNNIKACH d n u a n d x + a d n 1 u n n 1 d x +... + a d 2 u n 1 2 d x + a d u 2 1 d x + a u = b( x) Powyższe równanie o niewiadomej funkcji
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
DRGANIA OSCYLATOR HARMONICZNY
 DRGANIA OSCYLATOR HARMONICZNY wyklad8 2012/2013, zima 1 Własności sprężyste ciał stałych naprężenie rozciągające naprężenie ścinające naprężenie objętościowe Względne odkształcenie ciała zależy od naprężenia
DRGANIA OSCYLATOR HARMONICZNY wyklad8 2012/2013, zima 1 Własności sprężyste ciał stałych naprężenie rozciągające naprężenie ścinające naprężenie objętościowe Względne odkształcenie ciała zależy od naprężenia
Drgania. W Y K Ł A D X Ruch harmoniczny prosty. k m
 Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Laboratorium Mechaniki Technicznej
 Laboratorium Mechaniki Technicznej Ćwiczenie nr 5 Badanie drgań liniowych układu o jednym stopniu swobody Katedra Automatyki, Biomechaniki i Mechatroniki 90-924 Łódź, ul. Stefanowskiego 1/15, budynek A22
Laboratorium Mechaniki Technicznej Ćwiczenie nr 5 Badanie drgań liniowych układu o jednym stopniu swobody Katedra Automatyki, Biomechaniki i Mechatroniki 90-924 Łódź, ul. Stefanowskiego 1/15, budynek A22
Wykład z modelowania matematycznego. Przykłady modelowania w mechanice i elektrotechnice.
 Wykład z modelowania matematycznego. Przykłady modelowania w mechanice i elektrotechnice. 1 Wahadło matematyczne. Wahadłem matematycznym nazywamy punkt materialny o masie m zawieszony na długiej, cienkiej
Wykład z modelowania matematycznego. Przykłady modelowania w mechanice i elektrotechnice. 1 Wahadło matematyczne. Wahadłem matematycznym nazywamy punkt materialny o masie m zawieszony na długiej, cienkiej
m Jeżeli do końca naciągniętej (ściśniętej) sprężyny przymocujemy ciało o masie m., to będzie na nie działała siła (III zasada dynamiki):
 Ruch drgający -. Ruch drgający Ciało jest sprężyste, jeżei odzyskuje pierwotny kształt po ustaniu działania siły, która ten kształt zmieniła. Właściwość sprężystości jest ograniczona, to znaczy, że przy
Ruch drgający -. Ruch drgający Ciało jest sprężyste, jeżei odzyskuje pierwotny kształt po ustaniu działania siły, która ten kształt zmieniła. Właściwość sprężystości jest ograniczona, to znaczy, że przy
Plan wykładu. Ruch drgajacy. Drgania harmoniczne... Drgania harmoniczne. Oscylator harmoniczny Przykłady zastosowań. dr inż.
 Plan wykładu Ruch drgajacy 1 Przykłady zastosowań dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 01/13 Drgania wymuszone 3 Drgania zachodzace w tym samym kierunku
Plan wykładu Ruch drgajacy 1 Przykłady zastosowań dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 01/13 Drgania wymuszone 3 Drgania zachodzace w tym samym kierunku
3 Podstawy teorii drgań układów o skupionych masach
 3 Podstawy teorii drgań układów o skupionych masach 3.1 Drgania układu o jednym stopniu swobody Rozpatrzmy elementarny układ drgający, nazywany też oscylatorem harmonicznym, składający się ze sprężyny
3 Podstawy teorii drgań układów o skupionych masach 3.1 Drgania układu o jednym stopniu swobody Rozpatrzmy elementarny układ drgający, nazywany też oscylatorem harmonicznym, składający się ze sprężyny
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej
 MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
Wykład 1: Fale wstęp. Drgania Katarzyna Weron. WPPT, Matematyka Stosowana
 Wykład 1: Fale wstęp. Drgania Katarzyna Weron WPPT, Matematyka Stosowana Sposoby komunikacji Chcesz się skontaktować z przyjacielem Wysyłasz list? Wykorzystujesz cząstki Telefonujesz? Wykorzystujesz fale
Wykład 1: Fale wstęp. Drgania Katarzyna Weron WPPT, Matematyka Stosowana Sposoby komunikacji Chcesz się skontaktować z przyjacielem Wysyłasz list? Wykorzystujesz cząstki Telefonujesz? Wykorzystujesz fale
Siła sprężystości - przypomnienie
 Siła sprężystości - przypomnienie Pomiary siły sprężystości wykonane kilka wykładów wcześniej (z uwzględnieniem kierunku siły). F = kx = 0.13x 0 F x cm mg Prawo Hooke a Ciało m na idealnie gładkiej powierzchni
Siła sprężystości - przypomnienie Pomiary siły sprężystości wykonane kilka wykładów wcześniej (z uwzględnieniem kierunku siły). F = kx = 0.13x 0 F x cm mg Prawo Hooke a Ciało m na idealnie gładkiej powierzchni
Natomiast dowolny ruch chaotyczny, np. ruchy Browna, czy wszelkie postacie ruchu postępowego są przykładami ruchu nie będącego ruchem drgającym.
 Wstęp Z wszelkiego radzaju drganiami mamy doczyniania w życiu codziennym. Na przykład codziennie korzystamy z prądu. Gdy pobieramy go z sieci miejskiej natężenie prądu zmienia się periodycznie z czasem.
Wstęp Z wszelkiego radzaju drganiami mamy doczyniania w życiu codziennym. Na przykład codziennie korzystamy z prądu. Gdy pobieramy go z sieci miejskiej natężenie prądu zmienia się periodycznie z czasem.
DRGANIA MECHANICZNE. Poniższe materiały tylko dla studentów uczęszczających na zajęcia. Zakaz rozpowszechniania i powielania bez zgody autora.
 DRGANIA MECHANICZNE materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak część 3 drgania wymuszone siłą harmoniczną drgania
DRGANIA MECHANICZNE materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak część 3 drgania wymuszone siłą harmoniczną drgania
n=0 (n + r)a n x n+r 1 (n + r)(n + r 1)a n x n+r 2. Wykorzystując te obliczenia otrzymujemy, że lewa strona równania (1) jest równa
 Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO
 ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
Podstawy fizyki wykład 7
 Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Wykład 9. Fizyka 1 (Informatyka - EEIiA 2006/07)
 Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
Prosty oscylator harmoniczny
 Ruch drgający i falowy Siła harmoniczna, drgania swobodne Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym. Przemieszczenie cząstki w ruchu periodycznym można zawsze wyrazić
Ruch drgający i falowy Siła harmoniczna, drgania swobodne Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym. Przemieszczenie cząstki w ruchu periodycznym można zawsze wyrazić
Siła elektromotoryczna
 Wykład 5 Siła elektromotoryczna Urządzenie, które wykonuje pracę nad nośnikami ładunku ale różnica potencjałów między jego końcami pozostaje stała, nazywa się źródłem siły elektromotorycznej. Energia zamieniana
Wykład 5 Siła elektromotoryczna Urządzenie, które wykonuje pracę nad nośnikami ładunku ale różnica potencjałów między jego końcami pozostaje stała, nazywa się źródłem siły elektromotorycznej. Energia zamieniana
drgania h armoniczne harmoniczne
 ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
Drgania. O. Harmoniczny
 Dobrej fazy! Drgania O. Harmoniczny Położenie równowagi, 5 lipca 218 r. 1 Zadanie Zegar Małgorzata Berajter, update: 217-9-6, id: pl-ciepło-5, diff: 2 Pewien zegar, posiadający wahadło ze srebra, odmierza
Dobrej fazy! Drgania O. Harmoniczny Położenie równowagi, 5 lipca 218 r. 1 Zadanie Zegar Małgorzata Berajter, update: 217-9-6, id: pl-ciepło-5, diff: 2 Pewien zegar, posiadający wahadło ze srebra, odmierza
TEORIA DRGAŃ Program wykładu 2016
 TEORIA DRGAŃ Program wykładu 2016 I. KINEMATYKA RUCHU POSTE POWEGO 1. Ruch jednowymiarowy 1.1. Prędkość (a) Prędkość średnia (b) Prędkość chwilowa (prędkość) 1.2. Przyspieszenie (a) Przyspieszenie średnie
TEORIA DRGAŃ Program wykładu 2016 I. KINEMATYKA RUCHU POSTE POWEGO 1. Ruch jednowymiarowy 1.1. Prędkość (a) Prędkość średnia (b) Prędkość chwilowa (prędkość) 1.2. Przyspieszenie (a) Przyspieszenie średnie
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
DRGANIA OSCYLATOR HARMONICZNY
 DRGANIA OSCYLATOR HARMONICZNY wyklad 8 017/018, zima 1 Własności sprężyste ciał stałych Przedmiot: Fizyka naprężenie rozciągające naprężenie ścinające naprężenie objętościowe Względne odkształcenie ciała
DRGANIA OSCYLATOR HARMONICZNY wyklad 8 017/018, zima 1 Własności sprężyste ciał stałych Przedmiot: Fizyka naprężenie rozciągające naprężenie ścinające naprężenie objętościowe Względne odkształcenie ciała
DRGANIA OSCYLATOR HARMONICZNY
 DRGANIA OSCYLATOR HARMONICZNY wyklad 10 015/016, zima 1 Własności sprężyste ciał stałych Przedmiot: Fizyka naprężenie rozciągające naprężenie ścinające naprężenie objętościowe Względne odkształcenie ciała
DRGANIA OSCYLATOR HARMONICZNY wyklad 10 015/016, zima 1 Własności sprężyste ciał stałych Przedmiot: Fizyka naprężenie rozciągające naprężenie ścinające naprężenie objętościowe Względne odkształcenie ciała
Funkcja liniowa - podsumowanie
 Funkcja liniowa - podsumowanie 1. Funkcja - wprowadzenie Założenie wyjściowe: Rozpatrywana będzie funkcja opisana w dwuwymiarowym układzie współrzędnych X. Oś X nazywana jest osią odciętych (oś zmiennych
Funkcja liniowa - podsumowanie 1. Funkcja - wprowadzenie Założenie wyjściowe: Rozpatrywana będzie funkcja opisana w dwuwymiarowym układzie współrzędnych X. Oś X nazywana jest osią odciętych (oś zmiennych
Fale mechaniczne i akustyka
 Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
Fale mechaniczne i akustyka Wstęp: siła jako element decydujący o rodzaju ruchu Na pierwszym wykładzie, dynamiki Newtona omawiając II zasadę dr d r F r,, t = m dt dt powiedzieliśmy, że o tym, jakim ruchem
WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII.
 ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
1 + x 1 x 1 + x + 1 x. dla x 0.. Korzystając z otrzymanego wykresu wyznaczyć funkcję g(m) wyrażającą liczbę pierwiastków równania.
 10 1 Wykazać, że liczba 008 008 10 + + jest większa od Nie używając kalkulatora, porównać liczby a = log 5 log 0 + log oraz b = 6 5 Rozwiązać równanie x + 4y + x y + 1 = 4xy 4 W prostokątnym układzie współrzędnych
10 1 Wykazać, że liczba 008 008 10 + + jest większa od Nie używając kalkulatora, porównać liczby a = log 5 log 0 + log oraz b = 6 5 Rozwiązać równanie x + 4y + x y + 1 = 4xy 4 W prostokątnym układzie współrzędnych
FUNKCJA LINIOWA - WYKRES. y = ax + b. a i b to współczynniki funkcji, które mają wartości liczbowe
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
2.6.3 Interferencja fal.
 RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
RUCH FALOWY 1.6.3 Interferencja fal. Pojęcie interferencja odnosi się do fizycznych efektów nie zakłóconego nakładania się dwóch lub więcej ciągów falowych. Doświadczenie uczy, że fale mogą przebiegać
WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ DYNAMICZNĄ
 ĆWICZENIE 12 WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ DYNAMICZNĄ Cel ćwiczenia: Wyznaczanie modułu sztywności drutu metodą sprężystych drgań obrotowych. Zagadnienia: sprężystość, naprężenie ścinające, prawo
ĆWICZENIE 12 WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ DYNAMICZNĄ Cel ćwiczenia: Wyznaczanie modułu sztywności drutu metodą sprężystych drgań obrotowych. Zagadnienia: sprężystość, naprężenie ścinające, prawo
RUCH DRGAJĄCY RZESZOTA PRZESIEWACZA DWUCZĘSTOŚCIOWEGO**
 Górnictwo i Geoinżynieria Rok 34 Zeszyt 4/1 2010 Remigiusz Modrzewski*, Piotr Wodziński* RUCH DRGAJĄCY RZESZOTA PRZESIEWACZA DWUCZĘSTOŚCIOWEGO** 1. Wstęp Przesiewacz dwuczęstościowy zbudowany jest z dwóch
Górnictwo i Geoinżynieria Rok 34 Zeszyt 4/1 2010 Remigiusz Modrzewski*, Piotr Wodziński* RUCH DRGAJĄCY RZESZOTA PRZESIEWACZA DWUCZĘSTOŚCIOWEGO** 1. Wstęp Przesiewacz dwuczęstościowy zbudowany jest z dwóch
FUNKCJA LINIOWA - WYKRES
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
Ć W I C Z E N I E N R M-2
 INSYU FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I ECHNOLOGII MAERIAŁÓW POLIECHNIKA CZĘSOCHOWSKA PRACOWNIA MECHANIKI Ć W I C Z E N I E N R M- ZALEŻNOŚĆ OKRESU DRGAŃ WAHADŁA OD AMPLIUDY Ćwiczenie M-: Zależność
INSYU FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I ECHNOLOGII MAERIAŁÓW POLIECHNIKA CZĘSOCHOWSKA PRACOWNIA MECHANIKI Ć W I C Z E N I E N R M- ZALEŻNOŚĆ OKRESU DRGAŃ WAHADŁA OD AMPLIUDY Ćwiczenie M-: Zależność
FUNKCJE ELEMENTARNE I ICH WŁASNOŚCI
 FUNKCJE ELEMENTARNE I ICH WŁASNOŚCI DEFINICJA (funkcji elementarnych) Podstawowymi funkcjami elementarnymi nazywamy funkcje: stałe potęgowe wykładnicze logarytmiczne trygonometryczne Funkcje, które można
FUNKCJE ELEMENTARNE I ICH WŁASNOŚCI DEFINICJA (funkcji elementarnych) Podstawowymi funkcjami elementarnymi nazywamy funkcje: stałe potęgowe wykładnicze logarytmiczne trygonometryczne Funkcje, które można
XIXOLIMPIADA FIZYCZNA (1969/1970). Stopień W, zadanie doświadczalne D.. Znaleźć doświadczalną zależność T od P. Rys. 1
 KOOF Szczecin: www.of.szc.pl XIXOLIMPIADA FIZYCZNA (1969/197). Stopień W, zadanie doświadczalne D. Źródło: Olimpiady fizyczne XIX i XX Autor: Waldemar Gorzkowski Nazwa zadania: Drgania gumy. Działy: Drgania
KOOF Szczecin: www.of.szc.pl XIXOLIMPIADA FIZYCZNA (1969/197). Stopień W, zadanie doświadczalne D. Źródło: Olimpiady fizyczne XIX i XX Autor: Waldemar Gorzkowski Nazwa zadania: Drgania gumy. Działy: Drgania
Drgania w obwodzie LC. Autorzy: Zbigniew Kąkol Kamil Kutorasiński
 Drgania w obwodzie L Autorzy: Zbigniew Kąkol Kamil Kutorasiński 016 Drgania w obwodzie L Autorzy: Zbigniew Kąkol, Kamil Kutorasiński Rozpatrzmy obwód złożony z szeregowo połączonych indukcyjności L (cewki)
Drgania w obwodzie L Autorzy: Zbigniew Kąkol Kamil Kutorasiński 016 Drgania w obwodzie L Autorzy: Zbigniew Kąkol, Kamil Kutorasiński Rozpatrzmy obwód złożony z szeregowo połączonych indukcyjności L (cewki)
Wykład Drgania elektromagnetyczne Wstęp Przypomnienie: masa M na sprężynie, bez oporów. Równanie ruchu
 Wykład 7 7. Drgania elektromagnetyczne Wstęp Przypomnienie: masa M na sprężynie, bez oporów. Równanie ruchu M d x kx Rozwiązania x = Acost v = dx/ =-Asint a = d x/ = A cost przy warunku = (k/m) 1/. Obwód
Wykład 7 7. Drgania elektromagnetyczne Wstęp Przypomnienie: masa M na sprężynie, bez oporów. Równanie ruchu M d x kx Rozwiązania x = Acost v = dx/ =-Asint a = d x/ = A cost przy warunku = (k/m) 1/. Obwód
Wyznaczanie prędkości lotu pocisku na podstawie badania ruchu wahadła balistycznego
 Ćwiczenie nr Wyznaczanie prędkości lotu pocisku na podstawie badania ruchu wahadła balistycznego. Wymagania do ćwiczenia 1. ynamika ruchu obrotowego.. rgania harmoniczne Literatura:. Halliday, R. Resnick,
Ćwiczenie nr Wyznaczanie prędkości lotu pocisku na podstawie badania ruchu wahadła balistycznego. Wymagania do ćwiczenia 1. ynamika ruchu obrotowego.. rgania harmoniczne Literatura:. Halliday, R. Resnick,
Nazwisko i imię: Zespół: Data: Ćwiczenie nr 1: Wahadło fizyczne. opis ruchu drgającego a w szczególności drgań wahadła fizycznego
 Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
LABORATORIUM ELEKTROAKUSTYKI. ĆWICZENIE NR 1 Drgania układów mechanicznych
 LABORATORIUM ELEKTROAKUSTYKI ĆWICZENIE NR Drgania układów mechanicznych Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z właściwościami układów drgających oraz metodami pomiaru i analizy drgań. W ramach
LABORATORIUM ELEKTROAKUSTYKI ĆWICZENIE NR Drgania układów mechanicznych Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z właściwościami układów drgających oraz metodami pomiaru i analizy drgań. W ramach
1.5 Badanie drgań modelu cząsteczki czteroatomowej(m20)
 Badanie drgań modelu cząsteczki czteroatomowej(m20) 37 1.5 Badanie drgań modelu cząsteczki czteroatomowej(m20) Celem ćwiczenia jest wyznaczenie widma drgań układu czterech wahadeł sprzężonych oraz wyznaczenie
Badanie drgań modelu cząsteczki czteroatomowej(m20) 37 1.5 Badanie drgań modelu cząsteczki czteroatomowej(m20) Celem ćwiczenia jest wyznaczenie widma drgań układu czterech wahadeł sprzężonych oraz wyznaczenie
Funkcja kwadratowa. f(x) = ax 2 + bx + c = a
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
4.2 Analiza fourierowska(f1)
 Analiza fourierowska(f1) 179 4. Analiza fourierowska(f1) Celem doświadczenia jest wyznaczenie współczynników szeregu Fouriera dla sygnałów okresowych. Zagadnienia do przygotowania: szereg Fouriera; sygnał
Analiza fourierowska(f1) 179 4. Analiza fourierowska(f1) Celem doświadczenia jest wyznaczenie współczynników szeregu Fouriera dla sygnałów okresowych. Zagadnienia do przygotowania: szereg Fouriera; sygnał
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 9 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 9 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Funkcja kwadratowa. f(x) = ax 2 + bx + c,
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Zadanie domowe z drgań harmonicznych - rozwiązanie trzech wybranych zadań
 - rozwiązanie trzech wybranych zadań Ireneusz Mańkowski I LO im. Stefana Żeromskiego w Lęborku ul. Dygasińskiego 14 28 kwietnia 2016 Wybrane zadania domowe 1 Zadanie 5.4.4 Rozwiązanie zadania 5.4.4 2 Zadanie
- rozwiązanie trzech wybranych zadań Ireneusz Mańkowski I LO im. Stefana Żeromskiego w Lęborku ul. Dygasińskiego 14 28 kwietnia 2016 Wybrane zadania domowe 1 Zadanie 5.4.4 Rozwiązanie zadania 5.4.4 2 Zadanie
a, F Włodzimierz Wolczyński sin wychylenie cos cos prędkość sin sin przyspieszenie sin sin siła współczynnik sprężystości energia potencjalna
 Włodzimierz Wolczyński 3 RUCH DRGAJĄCY. CZĘŚĆ 1 wychylenie sin prędkość cos cos przyspieszenie sin sin siła współczynnik sprężystości sin sin 4 3 1 - x. v ; a ; F v -1,5T,5 T,75 T T 8t x -3-4 a, F energia
Włodzimierz Wolczyński 3 RUCH DRGAJĄCY. CZĘŚĆ 1 wychylenie sin prędkość cos cos przyspieszenie sin sin siła współczynnik sprężystości sin sin 4 3 1 - x. v ; a ; F v -1,5T,5 T,75 T T 8t x -3-4 a, F energia
I. DYNAMIKA PUNKTU MATERIALNEGO
 I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku.
 Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
Ruch falowy. Fala zaburzenie wywoane w jednym punkcie ośrodka, które rozchodzi się w każdym dopuszczalnym kierunku. Definicje: promień fali kierunek rozchodzenia się fali powierzchnia falowa powierzchnia,
Indukcja matematyczna
 Indukcja matematyczna Zadanie. Zapisać, używając symboli i, następujące wyrażenia (a) n!; (b) sin() + sin() sin() +... + sin() sin()... sin(n); (c) ( + )( + /)( + / + /)... ( + / + / +... + /R). Zadanie.
Indukcja matematyczna Zadanie. Zapisać, używając symboli i, następujące wyrażenia (a) n!; (b) sin() + sin() sin() +... + sin() sin()... sin(n); (c) ( + )( + /)( + / + /)... ( + / + / +... + /R). Zadanie.
Funkcje wymierne. Jerzy Rutkowski. Działania dodawania i mnożenia funkcji wymiernych określa się wzorami: g h + k l g h k.
 Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
WYZNACZENIE GĘSTOŚCI MATERIAŁU STRUNY
 ĆWICZENIE 103 WYZNACZENIE GĘSTOŚCI MATERIAŁU STRUNY Cel ćwiczenia: Wyznaczenie gęstości materiału, z którego jest wykonana badana struna. Zagadnienia: definicja fali, parametry opisujące falę (położenie
ĆWICZENIE 103 WYZNACZENIE GĘSTOŚCI MATERIAŁU STRUNY Cel ćwiczenia: Wyznaczenie gęstości materiału, z którego jest wykonana badana struna. Zagadnienia: definicja fali, parametry opisujące falę (położenie
ver b drgania harmoniczne
 ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
1 Pochodne wyższych rzędów
 Pochodne wyższych rzędów Pochodną rzędu drugiego lub drugą pochodną funkcji y = f(x) nazywamy pochodną pierwszej pochodnej tej funkcji. Analogicznie definiujemy pochodne wyższych rzędów, jako pochodne
Pochodne wyższych rzędów Pochodną rzędu drugiego lub drugą pochodną funkcji y = f(x) nazywamy pochodną pierwszej pochodnej tej funkcji. Analogicznie definiujemy pochodne wyższych rzędów, jako pochodne
WIBROIZOLACJA określanie właściwości wibroizolacyjnych materiałów
 LABORATORIUM DRGANIA I WIBROAUSTYA MASZYN Wydział Budowy Maszyn i Zarządzania Zakład Wibroakustyki i Bio-Dynamiki Systemów Ćwiczenie nr WIBROIZOLACJA określanie właściwości wibroizolacyjnych materiałów
LABORATORIUM DRGANIA I WIBROAUSTYA MASZYN Wydział Budowy Maszyn i Zarządzania Zakład Wibroakustyki i Bio-Dynamiki Systemów Ćwiczenie nr WIBROIZOLACJA określanie właściwości wibroizolacyjnych materiałów
Ruch drgający i falowy
 Ruch drgający i falowy 1. Ruch harmoniczny 1.1. Pojęcie ruchu harmonicznego Jednym z najbardziej rozpowszechnionych ruchów w mechanice jest ruch ciała drgającego. Przykładem takiego ruchu może być ruch
Ruch drgający i falowy 1. Ruch harmoniczny 1.1. Pojęcie ruchu harmonicznego Jednym z najbardziej rozpowszechnionych ruchów w mechanice jest ruch ciała drgającego. Przykładem takiego ruchu może być ruch
Rozdział 8. Analiza fourierowska. 8.1 Rozwinięcie w szereg Fouriera
 Rozdział 8 Analiza fourierowska 8.1 Rozwinięcie w szereg Fouriera Rozważmy funkcję rzeczywistą f określoną na okręgu o promieniu jednostkowym. Parametryzując okrąg przy pomocy kąta φ [, π] otrzymujemy
Rozdział 8 Analiza fourierowska 8.1 Rozwinięcie w szereg Fouriera Rozważmy funkcję rzeczywistą f określoną na okręgu o promieniu jednostkowym. Parametryzując okrąg przy pomocy kąta φ [, π] otrzymujemy
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego (Katera)
 Politechnika Łódzka FTMS Kierunek: nformatyka rok akademicki: 2008/2009 sem. 2. Termin: 6 V 2009 Nr. ćwiczenia: 112 Temat ćwiczenia: Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Politechnika Łódzka FTMS Kierunek: nformatyka rok akademicki: 2008/2009 sem. 2. Termin: 6 V 2009 Nr. ćwiczenia: 112 Temat ćwiczenia: Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
1.1 Wahadło anharmoniczne(m5)
 10 Mechanika 1.1 Wahadło anharmoniczne(m5) Celem ćwiczenia jest zbadanie drgań anharmonicznych wahadła fizycznego(zależność okresu drgań wahadła od amplitudy jego drgań, bilans energetyczny wahadła). Zagadnienia
10 Mechanika 1.1 Wahadło anharmoniczne(m5) Celem ćwiczenia jest zbadanie drgań anharmonicznych wahadła fizycznego(zależność okresu drgań wahadła od amplitudy jego drgań, bilans energetyczny wahadła). Zagadnienia
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Fizyka I (Mechanika) Wykład II: Pojęcia podstawowe punkt materialny, układ odniesienia, układ współrzędnych tor, prędkość, przyspieszenie Ruch jednostajny, ruch jednostajnie przyspieszony
Kinematyka: opis ruchu Fizyka I (Mechanika) Wykład II: Pojęcia podstawowe punkt materialny, układ odniesienia, układ współrzędnych tor, prędkość, przyspieszenie Ruch jednostajny, ruch jednostajnie przyspieszony
Równanie Schrödingera
 Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
DRGANIA ELEMENTÓW KONSTRUKCJI
 DRGANIA ELEMENTÓW KONSTRUKCJI (Wprowadzenie) Drgania elementów konstrukcji (prętów, wałów, belek) jak i całych konstrukcji należą do ważnych zagadnień dynamiki konstrukcji Przyczyna: nawet niewielkie drgania
DRGANIA ELEMENTÓW KONSTRUKCJI (Wprowadzenie) Drgania elementów konstrukcji (prętów, wałów, belek) jak i całych konstrukcji należą do ważnych zagadnień dynamiki konstrukcji Przyczyna: nawet niewielkie drgania
Wykład FIZYKA I. 5. Energia, praca, moc. http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 5. Energia, praca, moc Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html ENERGIA, PRACA, MOC Siła to wielkość
Wykład FIZYKA I 5. Energia, praca, moc Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html ENERGIA, PRACA, MOC Siła to wielkość
Mechanika analityczna. Małe drgania układów zachowawczych
 Mechanika analityczna. Małe drgania układów zachowawczych. Drgania swobodne układów o jednym stopniu swobody.. Wprowadzenie teoretyczne Załóżmy, że układ materialny o jednym stopniu swobody i więzach idealnych,
Mechanika analityczna. Małe drgania układów zachowawczych. Drgania swobodne układów o jednym stopniu swobody.. Wprowadzenie teoretyczne Załóżmy, że układ materialny o jednym stopniu swobody i więzach idealnych,
O 2 O 1. Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
 msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
Równania różniczkowe liniowe rzędu pierwszego
 Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
1.1 Oscylator harmoniczny prosty
 1 Wstęp 1.1 Oscylator harmoniczny prosty Oscylator harmoniczny prosty jest to każdy układ, którego ruch opisuje funkcja będąca rozwiązaniem równania różniczkowego postaci: d x(t) dt + ω 0x(t) = 0 (1) Rysunek
1 Wstęp 1.1 Oscylator harmoniczny prosty Oscylator harmoniczny prosty jest to każdy układ, którego ruch opisuje funkcja będąca rozwiązaniem równania różniczkowego postaci: d x(t) dt + ω 0x(t) = 0 (1) Rysunek
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Zasady oceniania karta pracy
 Zadanie 1.1. 5) stosuje zasadę zachowania energii oraz zasadę zachowania pędu do opisu zderzeń sprężystych i niesprężystych. Zderzenie, podczas którego wózki łączą się ze sobą, jest zderzeniem niesprężystym.
Zadanie 1.1. 5) stosuje zasadę zachowania energii oraz zasadę zachowania pędu do opisu zderzeń sprężystych i niesprężystych. Zderzenie, podczas którego wózki łączą się ze sobą, jest zderzeniem niesprężystym.
PRZYKŁADY RUCHU HARMONICZNEGO. = kx
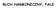 RUCH HARMONICZNY; FALE PRZYKŁADY RUCHU HARMONICZNEGO F d k F s k Gdowski F k Każdy ruch w którym siła starająca się przywrócić położenie równowagi jest proporcjonalna do wychylenia od stanu równowagi jest
RUCH HARMONICZNY; FALE PRZYKŁADY RUCHU HARMONICZNEGO F d k F s k Gdowski F k Każdy ruch w którym siła starająca się przywrócić położenie równowagi jest proporcjonalna do wychylenia od stanu równowagi jest
Projekt Inżynier mechanik zawód z przyszłością współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia wyrównawcze z izyki -Zestaw 13 -eoria Drgania i ale. Ruch drgający harmoniczny, równanie ali płaskiej, eekt Dopplera, ale stojące. Siła harmoniczna, ruch drgający harmoniczny Siłą harmoniczną (sprężystości)
Zajęcia wyrównawcze z izyki -Zestaw 13 -eoria Drgania i ale. Ruch drgający harmoniczny, równanie ali płaskiej, eekt Dopplera, ale stojące. Siła harmoniczna, ruch drgający harmoniczny Siłą harmoniczną (sprężystości)
