ANALIZA STRATEGII MONETARNYCH I FISKALNYCH Z WYKORZYSTANIEM TEORII GIER
|
|
|
- Nadzieja Nowacka
- 7 lat temu
- Przeglądów:
Transkrypt
1 Zeszt Naukowe Wdziału Infomatcznch Technik Zaządzania Wższej Szkoł Infomatki Stosowanej i Zaządzania Współczesne Polem Zaządzania N 1/016 ANALIZA STRATEGII MONETARNYCH I FISKALNYCH Z WYKORZYSTANIEM TEORII GIER Iena Wooniecka-Leciejewicz Wższa Szkoła Infomatki Stosowanej i Zaządzania, Waszawa, ul. Newelska 6 Insttut Badań Sstemowch PAN, Waszawa, ul. Newelska 6 Steszczenie: Atkuł pzedstawia analizę stategii monetanch i fiskalnch z wkozstaniem teoii gie. Rozważana jest ga monetano-fiskalna pz óżnch założeniach i uwaunkowaniach ekonomicznch. Pzedmiotem adań jest analiza optmalnch stategii monetanch i fiskalnch (stategii optmalnch odpowiedzi) oaz stanów ównowagi g. Wkonano smulacje, mające na celu zadanie wpłwu piote-tów władz monetanch i fiskalnch na ównowagę g i wó polic mix. Paca zawiea podsumowanie uzskanch w tm zakesie wników. Pzedstawiono analizę g i stanów ównowagi Nasha dla óżnch talic wpłat, oliczanch z zastosowaniem zmodfikowanej funkcji logistcznej. Na podstawie uzskanch wników pzedstawiono analizę izokwant wzostu PKB i inflacji, pokazującch, jakie altenatwne policies-mix o okeślonm stopniu estkcjności umożliwiają osiągnięcie pzjętej dnamiki PKB i założonego poziomu inflacji. Słowa kluczowe: politka monetana, politka fiskalna, Polic mix, teoia gie, ównowaga Nasha, Paeto optmalność, wzost PKB, inflacja. 1. Wpowadzenie Paca pzedstawia polem wou polic mix w kontekście teoii gie i wzajemnch inteakcji deczjnch międz władzami fiskalnmi (ządem) a monetanmi (ankiem centalnm). Polic mix stanowi w tm ujęciu kominację politki monetanej i fiskalnej o okeślonm stopniu estkcjności/ekspanswności każdej z nich. Pzedmiotem pezentowanej w niniejszm atkule analiz jest ga międz ankiem centalnm a ządem, zwana gą monetano-fiskalną, ze skończoną liczą stategii w zakesie politki pieniężnej i udżetowej. Zakłada się, że władze monetane i fiskalne podejmują deczje niezależnie, a stan ównowagi Nasha (Nash, 1953) w takiej gze utożsamian jest z woem okeślonej kominacji politki pieniężnej i udżetowej.
2 I. Wooniecka-Leciejewicz Celem adań jest analiza efektwności deczji w oszaze polic mix z wkozstaniem teoii gie na podstawie analiz stanów ównowagi Nasha, Paeto optmalności ozwiązań oaz wpłwu piotetów władz monetanch i fiskalnch na wó politki makoekonomicznej. Uzskane wniki mogą stanowić asumpt do odpowiedzi na ptanie: cz i w jakich waunkach wó polic mix popzez niezależne od sieie władze monetane i fiskalne powadzi do efektwnch ekonomicznie deczji, a kied niezędna jest koodnacja. W dskusjach, toczącch się wokół polemu wou polic mix, pztaczane są zaówno agument za jak i pzeciw niezależności anku centalnego. Na zecz niezależności anku pzemawiają, międz innmi, większa skuteczność walki z inflacją, mniejsza zmienność inflacji oaz poztwne oddziałwanie na poziom i zmienność podukcji (Eijffinge, DeHaan, 1996; Wojtna, 1996, 1998; Maszałek, 005, 009). Jednak z dugiej ston, niezależność anku centalnego może stwazać tudności koodnacji politki monetanej i fiskalnej. Ich źódło tkwi pzede wszstkim w odmiennch celach władz monetanch i fiskalnch oaz óżnch ocenach możliwch skutków politki makoekonomicznej. Badania, dotczące współzależności międz politką pieniężną a fiskalną zapoczątkowali, m. in., Sagent i Wallace (1981), fomułując koncepcję tzw. niepzjemnej atmetki monetastcznej (unpleasant monetaist aithmetic). W dskusji nad koodnacją politki makoekonomicznej podkeśla się ównież znaczenie wiagodności i pzejzstości powadzonej politki (Binde, 000; Blackun, Chistensen, 1989; Wojtna, 1998; Walsh, 001; Gjedem, 001). W ozstzgnięciu kwestii niezależności anku centalnego oaz polemu wou międz politką makoekonomiczną, stanowioną pzez niezależne od sieie władze monetane i fiskalne a koodnacją tej politki pomocna jest analiza z zastosowaniem teoii gie. Jedną z piewszch pac poświęconch polematce wou polic mix w ujęciu teoii gie ł atkuł Blindea (Blinde, 1983), w któm pzedmiotem analiz ła ga monetano-fiskalna w uposzczonej wesji, uwzględniającej dwie stategie monetane i dwie fiskalne: estkcjną i ekspanswną. Badziej szczegółowo zagadnienie to jest omówione w Rozdziale tego atkułu. Inteesujące adania polic mix z wkozstaniem g monetano-fiskalnej w kontekście wou międz niezależnością władz fiskalnch i monetanch a koodnacją polic mix powadził D. Nodhaus (Nodhaus, 1994). Do analiz zastosował gę monetano-fiskalną, azującą na stosunkowo postm modelu makoekonomicznm. W modelu tm uwzględnione został zaówno instument politki jak i stan gospodaki, chaaktezowan pzez tz zmienne: inflację, ezoocie i stopę wzostu potencjalnego poduktu. Bezoocie w modelu zostało uzależnione od instumentów politki fiskalnej i monetanej oaz od zmiennch egzogenicznch, takich jak zasó kapitału, technologii, podukcji zaganicznej (Nodhaus pzjął, że zmienne te nie ulegają zmianie w kótkim okesie, a taki ozpatwał w modelu). Równanie inflacji w modelu Nodhausa odzwieciedla połączenie koncepcji wmienności międz inflacją a ezoociem (kzwa Phillipsa) oaz oczekiwań inflacjnch. W związku z tm, że 8
3 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie inflacja zależ od ezoocia, to jest ównież pośednio uzależniona od instumentów ou politk. Z kolei stopa wzostu potencjalnego poduktu jest w modelu deteminowana pzez nadwżkę udżetową. Funkcje użteczności ządu i anku centalnego zależą od wmienionch tzech zmiennch, opisującch stan gospodaki, a pośednio od instumentów politki fiskalnej i monetanej. W tm pzpadku, podonie jak w niektóch innch pulikacjach (np. Wooniecka-Leciejewicz, 01, 015) model dał spowadzić się do pzjęcia okeślonch funkcji opisującch wpłw instumentów politki na wane kategoie chaaktezujące stan gospodaki. W gze jednoetapowej, na podstawie funkcji użteczności decdentów, chaaktezującch ich pefeencje, Nodhaus wznaczł kzwe oojętności, a także izokwant poptu gloalnego na poziomie watości pożądanch (pefeowanch) pzez władze monetane i fiskalne oaz funkcje eakcji (optmalnch odpowiedzi) ou decdentów. Zakłada on pz tm, że funkcja eakcji anku centalnego pokwa się z jego izokwantą poptu gloalnego, pzjmując tm samm, że politka anku centalnego eaguje jednie na stuację gospodaczą, nie zmienia się zaś w odpowiedzi ezpośednio na politkę fiskalną (w podejściu pezentowanm pzez autokę niniejszej pulikacji jest inaczej). Analiza i poównanie ozwiązań niekoopeacjnch i koopeacjnch powadzi do wniosku, że koodnacja politk popawia stuację ou decdentów w poównaniu z ównowagą Nasha. Pzcznę konfliktu międz władzami Nodhaus upatuje w odmiennch pefeencjach władz monetanch i fiskalnch. Model g Nodhausa stanowił punkt wjścia do dalszch adań inteakcji międz politką monetaną a fiskalną. W swojej monogafii Maszałek (Maszałek 009, ss ) pzedstawił zestawienie wanch modeli gie stailizacjnch międz ankiem centalnm a ządem, waz z ich chaaktestką. Wato zwócić uwagę m. in. na gę zapoponowaną pzez Dixita i Lametiniego (001), któz, ozważając niekoopeacjną gę monetano-fiskalną stwiedzili, że istotne znaczenie dla wniku g ma to, cz zoowiązania ston są wiagodne. W pzeciwnm azie pzjmuje się, że ston podejmują deczje jednocześnie, co powadzi do ównowagi Nasha, czli ozwiązania suoptmalnego. Lepszm ozwiązaniem od ównowagi Nasha jest, zdaniem autoów, ównowaga Stackelega, gd jeden z decdentów jest lideem i to ez względu na to, cz jest to władza fiskalna cz monetana. Ważnm wnikiem pzepowadzonch adań, opócz konstatacji, znanej już z wcześniejszch pulikacji innch autoów, że, ze względu na odmienne pefeencje, politka monetana ez koodnacji nie zapewnia stailności cen, jest dodatkow wniosek, a mianowicie że ak dscplin fiskalnej oganicza skuteczność eguł anku centalnego. Z tmi adaniami koespondują wniki pzedstawione w pzez Lametiniego i Rovelliego (003). Analizowali oni dwie stuacje: w piewszej ząd jest zainteesowan jednie stailizacją podukcji (teasu view), w dugiej także stailizacją inflacji (govenment view). Rozpatując gę Nasha i Stackelega, stwiedzili oni, że oie ston osiągają lepsz wnik w tm dugim pzpadku. Inaczej jednak niż we wcześniej wspomnianej pac (Dixit, Lametini, 001), uznali, że ma jednak znaczenie 9
4 I. Wooniecka-Leciejewicz to, kto jest lideem w gze Stackelega kozstniejsze jest, gd jest nim władza fiskalna. Wielu autoów wkazuje, że w powższch niekoopeacjnch modelach gie monetano-fiskalnch ozwiązania nie są optmalne i powadzą do wou nieoptmalnej polic mix. Można wskazać tu na następujące pzesłanki tego zjawiska (Danault, Kutos, 005; Wojtna, 1996; Maszałek 009). Po piewsze, gacze, czli władze monetane i fiskalne, mają odmienne cele lu pzpisują im inne pefeencje (większość opacowań), po dugie mogą oni óżnić się w pzewidwaniu efektów zastosowanej politki fiskalnej i monetanej, jeżeli dsponują innmi modelami (np. Fankel, 1998). Niestet, na tle liteatu światowej, polskie pulikacje poświęcone powższej tematce są nieliczne. Można wskazać wpawdzie na pace, któe dotczą polematki polic mix i koodnacji politki monetanej i fiskalnej, np. Danault, Kutos (005), Stawska (014), któe zawieają inteesujące wnioski z analiz danch statstcznch dla Polski w ozważanm aspekcie, niemniej jednak adania te nie są opate na ujęciu sticte modelowm, autoz nie pzedstawili g monetano-fiskalnej ani modelu makoekonomicznego z nią powiązanego. Wato ównież odnieść się do pac Danaulta i Kutosa (005), któz, nawiązując do adań i ozważań dotczącch gie monetano-fiskalnch, powadzonch pzez Blindea (1980), Bennetta i Loazę (001) oaz Dixita i Lametiniego (001), pzedstawiają analizę polic mix w Polsce w latach , opatą na danch statstcznch. Fomułują oni inteesujące wnioski, uważają mianowicie, że teoetcznm ujęciem najadziej adekwatnm do opisu ieżącej polic mix w Polsce i jej insttucjonalnch uwaunkowań jest model niekoopeacjnej g Stackelega z władzami fiskalnmi jako lideem (leade) i władzami monetanmi jako wczekującm (followe). Rekomendacją dla popaw efektwności polic mix w takim pzpadku jest, zdaniem autoów, zwiększenie wiagodności i pzewidwalności działań władz fiskalnch, szczególnie w zwiększaniu dscplin fiskalnej. Póę pzedstawienia modelu inteakcji monetano-fiskalnch w ujęciu teoii gie podjęto w pulikacjach Wooniecka-Leciejewicz (01, 015a, 015) oaz Kuś, Wooniecka-Leciejewicz (015). W ostatniej pac gę monetano-fiskalna opato na modelu makoekonomicznm (Wooniecka-Leciejewicz, 015), któ z jednej ston opisuje mechanizm cklu koniunktualnego i pozwala śledzić pzeieg koniunktu gospodaczej w czasie, z dugiej odzwieciedla wpłw instumentów politki monetanej i fiskalnej na gospodakę. Na podstawie pzepowadzonch smulacji wskazano stategie optmalnch odpowiedzi oaz ównowagi Nasha. Wkozstując metod optmalizacji wielokteialnej zadano Paeto optmalność stanów ównowagi i w uzasadnionch pzpadkach wznaczono ozwiązania koopeacjne. 10
5 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie Według adań pzedstawionch pzez Liicha, Nguena i Stehlika (014) dla óżnch kajów świata, Polska plasuje się w centalnej części pzestzeni pzwództwa monetanego/fiskalnego (moneta vs fiscal leadeship space), co wskazuje, że nie wstępuje tu ani silna pzewaga władz fiskalnch ani monetanch. Może to stanowić agument na zecz pzedstawionej w niniejszm atkule g monetano-fiskalnej, w któej zakłada się, że ston podejmują niezależnie deczje ównocześnie, uwzględniając stuację stategiczną i możliwe posunięcia dugiego gacza. Pzedstawiona w pac analiza stanowi podsumowanie i kontnuację adań autoki (Wooniecka-Leciejewicz, pace z lat ), dotczącch polematki wou polic mix z wkozstaniem g monetano-fiskalnej. Pzedmiotem pezentowanej w niniejszm atkule analiz jest ga, któej istota zawata jest w Taeli 1, zawieającej talicę wpłat. Taela 1. Ga monetano-fiskalna talica wpłat Talica wpłat Bank centaln - politka monetana estkcjna ekspanswna Stategia monetana M1 (stopa poc. 1 ) Stategia monetana M (stopa poc. ) Stategia monetana Mn (stopa poc. n) Rząd politka fiskalna ekspanswna estkcjna Stategia fiskalna F1 (defict udżetow 1 ) Stategia fiskalna F (defict udżetow ) Stategia fiskalna Fm (defict udżetow m ) p11 p1 p1n n p1 p pn 1 n pm1 pm pmn m1 m mn Źódło: Wooniecka-Leciejewicz (010a), s. 191 Ga analizowana jest pz pzjęciu pewnch założeń, dotczącch wpłwu instumentów politki fiskalnej i monetanej na stan gospodaki, odzwieciedlan pzez wzost PKB i inflację. Zakłada się, że wzost ealnej stop pocentowej, ceteis paius, wwołuje spadek tempa wzostu PKB oaz oganiczenie inflacji, a wzost defictu udżetowego, ceteis paius, pzcznia się do wzostu inflacji. Polem może stanowić pzjęcie założenia dotczącego wpłwu defictu udżetowego na ealn wzost podukcji w gospodace, można owiem ozważać tu dwa waiant: A - zakładając, że wzost defictu udżetu państwa, ceteis paius, powoduje zwięk- 11
6 I. Wooniecka-Leciejewicz szenie tempa wzostu PKB, oaz altenatwne założenie B - że wzost defictu udżetowego oganicza tempo wzostu gospodaczego. W niniejszm opacowaniu analiza g koncentuje się na waiancie A, któ wdaje się adziej ealistcznie odzwieciedlać wpłw politki fiskalnej na możliwości wzostu gospodaczego w kótkim okesie. i i i1 0 j j j1 Dodatkowo, zakłada się, że:, 0. Założenie to stanowi odzwieciedlenie schematu konstukcji talic wpłat, jak w Taeli 1, dotczącego pzjętej kolejności stategii fiskalnch i monetanch zacznając od estkcjnch, pzechodząc do ekspanswnch, pz czm wzost stopnia ekspanswności politki fiskalnej następuje waz z osnącm defictem udżetowm, a wzost stopnia ekspanswności politki monetanej waz z malejącą stopą pocentową. Poponuje się pzedstawienie stuacji deczjnej w zakesie wou polic mix jako dwuosoowej g międz ankiem centalnm a ządem. Jest to jednoetapowa ga o sumie niezeowej z pełną infomacją. Każd z gacz podejmuje deczje niezależnie, ioąc pod uwagę pawdopodoną eakcję dugiego gacza. Stategie władz fiskalnch oznaczają stategie politki udżetowej od skajnie estkcjnej w piewszm wieszu do skajnie ekspanswnej w ostatnim. Jako mienik stopnia estkcjności/ekspanswności politki fiskalnej pzjęto poziom defictu udżetowego w elacji do PKB. Analogicznie, stategie władz monetanch oznaczają stategie politki pieniężnej od skajnie estkcjnej w piewszej kolumnie do skajnie ekspanswnej w ostatniej, pz czm jako wznacznik estkcjności/ekspanswności politki monetanej pzjęto wsokość ealnej stop pocentowej. Wpłat został oznaczone w następując sposó: ij - wpłata władz fiskalnch (tempo wzostu PKB) w pzpadku, gd ząd stosuje stategię fiskalną F i, a ank centaln stategię monetaną M j, p ij - wpłata władz monetanch (inflacja) w tej samej stuacji stategicznej. Smolem i oznaczono defict udżetow w elacji do PKB, chaaktezując i-tą stategię fiskalną, natomiast j - ealną stopę pocentową pzpisaną j-tej stategii pieniężnej. Początkowo pzjęto, że władze monetane dążą do minimalizacji inflacji, a fiskalne do maksmalizacji ealnego wzostu gospodaczego. Takie podejście zastosowano pzede wszstkim do analiz g z dwoma jakościowo óżnmi stategiami (estkcjną i ekspanswną) dla każdej z politk: udżetowej jak i pieniężnej. W dalszej części adań ozszezono analizę na pzpadek g z większą liczą stategii, pzjmując, że celem władz monetanch jest osiągnięcie pożądanego poziomu inflacji, tzw. celu inflacjnego, podczas, gd władze fiskalne dążą do osiągnięcia pożądanego (zaplanowanego) wzostu gospodaczego. Tm samm wpłat zdefiniowano jako odchlenia mieników kondcji gospodaki naodowej: tempa wzostu PKB i 1
7 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie inflacji od watości pożądanch odpowiednio z punktu widzenia ządu i anku centalnego (kteium minimalizacji kwadatów odchleń). Pzepowadzono szeeg adań smulacjnch z wkozstaniem powższej g ze skończoną liczą stategii fiskalnch i monetanch. Do odzwieciedlenia zależności międz instumentami politki monetanej (ealną stopą pocentową) i fiskalnej (defictem udżetowm w elacji do PKB) a uzskanmi w wniku ich zastosowania efektami ekonomicznmi wkozstano zmodfikowaną funkcję logistczną. Pzjęta metoda adawcza umożliwiła uwzględnienie specfiki wpłwu tch instumentów na koniunktuę, polegającej na oganiczonch możliwościach stosowania skajnie estkcjnch ądź skajnie ekspanswnch politk i skuteczności ich oddziałwania na gospodakę. Badania smulacjne pozwolił na pzeanalizowanie óżnch pzpadków g: istnienia jednego stanu ównowagi Nasha utożsamianego z woem okeślonej kominacji politki pieniężnej i udżetowej, kilku ównowag lu jej aku w ozważanm zakesie instumentów w zależności od pzjętch watości paametów oaz celów władz monetanch i fiskalnch. Jednm z istotnch celów tej pac ło ównież pokazanie wpłwu celów władz monetanch i fiskalnch na uzskane wniki, na stan ównowagi Nasha i tm samm na wó polic mix.. Ga monetano-fiskalna z dwiema stategiami Na wstępie pzeanalizowano pzkład g uwzględniającej dwie jakościowo óżne stategie: estkcjną i ekspanswną zaówno po stonie politki fiskalnej jak i monetanej (Taela ). Taela. Ga monetano-fiskalna z dwiema stategiami Bank centaln Talica Stategia M1 Stategia M wpłat estkcjna (1) ekspanswna () Rząd Stategia F1 estkcjna Stategia F1 estkcjna p11 p1 1 p1 p Źódło: opacowanie własne, tu i dalej, jeśli nie zaznaczono inaczej Pzjmuje się, że ank centaln, dążąc do oniżania inflacji (p), wiea międz politką estkcjną, chaaktezującą się wższą ealną stopą pocentową 1 a ekspanswną, chaaktezującą się niższą stopą pocentową. Rząd, podejmując de- 13
8 I. Wooniecka-Leciejewicz czje dotczące politki udżetowej, skłania się ądź do wou politki estkcjnej, któej towazsz niższ poziom defictu udżetu państwa 1, ądź ekspanswnej (wższ defict ), dążąc do osiągnięcia jak najwższego tempa wzostu PKB (). Lewa kolumna odzwieciedla estkcjną politkę pieniężną, pawa - ekspanswną, analogicznie gón wiesz oznacza estkcjną, a doln ekspanswną politkę fiskalną. Ga analizowana jest pz pzjęciu założeń dotczącch wpłwu instumentów politki fiskalnej i monetanej na stan gospodaki pzedstawionch w Rozdziale 1 niniejszej pac. Koncepcja powższej g monetano-fiskalnej pzedstawiona została we wcześniejszch pacach autoki (Wooniecka, 008, 010a). Analogiczna ga ła ozpatwana, m. in., w pacach Blindea (1983) oaz Bennetta i Loaz (001). Wkazują oni, że niezależnie działające władze monetane i fiskalne ędą dążć, zgodnie z ównowagą Nasha, do estkcjnej politki pieniężnej i ekspanswnej udżetowej, a to oznacza ozwiązanie nieoptmalne w sensie Paeto, podonie jak w dlemacie więźnia. Zdaniem autoów, lepsz wó jest w stanie zapewnić jednie koodnacja ou politk. Ilustuje to taela 3 zawieająca pefeencje władz monetanch i fiskalnch według Blindea dla óżnch kominacji polic mix. Taela 3. Pefeencje w gze monetano-fiskalnej według Blindea Politka monetana Politka fisklana Kontakcja Ekspansja Kontakcja Ekspansja Źódło: Blinde (1983), s. 3 Blinde pzjął, że połączenie estkcjnej politki pieniężnej i udżetowej jest waiantem najadziej pożądanm z punktu widzenia władz monetanch, natomiast najmniej w ocenie ządu. Dokładnie odwotne pefeencje pzpiswane są ekspanswnemu chaakteowi ou politk. Wdaje się jednak, że dość aitalnie pzjęto tu pefeencje dla pozostałch dwóch waiantów, zakładając, że adziej pefeowan pzez oa podmiot deczjne jest stan gospodaki, w któm powadzona jest politka, ędąca kominacją estkcjnej politki monetanej i ekspanswnej fiskalnej niż odwotnie. 14
9 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie Nieco inaczej podchodzą do tego zagadnienia Bennett i Loaza (001) (Taela 4). Nie ozstzgają oni, któe z dwóch ozwiązań jest kozstniejsze z punktu widzenia władz monetanch oaz fiskalnch: twada politka pieniężna i luźna fiskalna cz odwotnie, pzjmując, że skutkują one podonm poziomem inflacji i zatudnienia. Dlatego pzpisują im jednakowe pefeencje. Wdaje się inteesujące zadanie, cz zeczwiście watości inflacji i ezoocia, okeślone jako śednie dla kominacji politk: twadej monetanej i luźnej fiskalnej oaz odwotnie: luźnej monetanej i twadej fiskalnej, są jednakowe, o jeśli nie, to fakt, że mogą ć niższe lu wższe ędzie miał istotn wpłw na Paeto optmalność ozwiązań i wstępowanie (lu nie) dlematu więźnia. W tm celu, pzedstawiona wcześniej ga monetano-fiskalna została pzeanalizowana pod kątem Paeto optmalności ozwiązań, z zastzeżeniem, że w odóżnieniu od wspomnianego opacowania Bennetta i Loaz, jako wznacznik koniunktu gospodaczej pzjęto tempo wzostu PKB, a nie poziom zatudnienia. Taela 4. Wpłat w gze monetano-fiskalnej według Bennetta i Loaz Władza fiskalna Twada politka fiskalna Luźna politka fiskalna Twada politka monetana Wniki: niska inflacja niskie zatudnienie Wpłat: Bank centaln: 6+1=7 Władza fiskalna: 3+1=4 Wniki: śednia inflacja śednie zatudnienie Wpłat: Bank centaln: 4+=6 Władza fiskalna: +4=6 Bank centaln Luźna politka monetana Wniki: śednia inflacja śednie zatudnienie Wpłat: Bank centaln: 4+=6 Władza fiskalna: +4=6 Wniki: wsoka inflacja wsokie zatudnienie Wpłat: Bank centaln: 1+3=4 Władza fiskalna: 1+6=7 Bank centaln Władza fiskalna Wpłat poziom niski poziom śedni poziom wsoki Inflacja 4 Zatudnienie 4 Źódło: Bennett, Loaza (001), s
10 I. Wooniecka-Leciejewicz 16 Analizę g pzepowadzono dla nieliniowch zależności międz mienikami stanu gospodaki (tj. wzostu gospodaczego oaz inflacji) a instumentami polic mix (czli defictem udżetowm w elacji do PKB oaz ealną stopą pocentową), z wkozstaniem ozwinięcia w szeeg Taloa z dokładnością do dugiej pochodnej. Pozwoliło to na wpowadzenie fomuł, okeślającch zależności tempa wzostu PKB oaz inflacji od zmian defictu udżetowego i stop pocentowej w talic wpłat fomuł te pokazane został w Taeli 5. Najniższa inflacja i jednocześnie najniższ wzost gospodacz wstępują w pzpadku wou kominacji estkcjnch politk: monetanej oaz fiskalnej (lew gón óg talic wpłat). Waz z oniżaniem stop pocentowej (pzejście do pawej kolumn) zwiększa się inflacja i ośnie tempo wzostu PKB. Również, na skutek osnącego defictu udżetowego, następuje wzost inflacji i podukcji (pzejście do dolnego wiesza). Najwższą inflacją, ale i najszszm wzostem podukcji chaaktezuje się gospodaka, wówczas, gd zaówno politka pieniężna jak i fiskalna mają chaakte ekspanswn (paw doln óg talic). Taela 5. Równowaga w gze monetano-fiskalnej z dwoma stategiami. Pzpadek maksmalizacji tempa wzostu PKB i minimalizacji inflacji Wpłat Bank centaln politka monetana wższa stopa pocentowa 1 niższa stopa pocentowa Rząd politka fiskalna niższ defict 1 p 1 p p p 1 wższ defict i 1 p p p 1 1 p p p p p p 1 1 1
11 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie Bank centaln dla każdej możliwej stategii fiskalnej (dla każdego wiesza) wiea optmalną stategię monetaną (stategię optmalnej odpowiedzi), któa minimalizuje poziom inflacji. Uwzględniając fomuł, opisujące dnamikę inflacji, oznacza to, że odpowie estkcjną stategią pieniężną (lewa kolumna) zaówno na estkcjną, jak i na ekspanswną stategię udżetową. Stąd wniosek, że estkcjna politka monetana stanowi dla anku centalnego stategię dominującą, któa jest optmalna (stanowi optmalną odpowiedź), niezależnie od tego, jaką politkę fiskalną wieze ząd estkcjną cz ekspanswną. Z kolei ząd, dążąc do maksmalizacji ealnego wzostu PKB, w odpowiedzi na dowolną stategię monetaną estkcjną ądź ekspanswną (epezentowaną pzez każdą z kolumn) wiea zawsze stategię ekspanswną (doln wiesz). Tak więc, ząd, podonie jak ank centaln, ma stategię dominującą, któą jest ekspanswna politka fiskalna. Jest ona z punktu widzenia ządu stategią optmalną (stanowi optmalną odpowiedź) niezależnie od tego, jakie deczje odnośnie wsokości stóp pocentowch podejmie ank centaln. Pz ozważanch dotchczas założeniach, oznaczającch m. in. dążenie władz fiskalnch do maksmalizacji wzostu gospodaczego, a władz monetanch do minimalizacji inflacji, stan ównowagi znajduje się w lewm dolnm ogu talic wpłat. Jest to nie tlko ównowaga Nasha, jest to ównowaga deteminowana pzez stategie dominujące. Powadzi do wou estkcjnej politki monetanej i ekspanswnej politki fiskalnej. Rzeczwiście, w Polsce pzez szeeg lat osewowano, że w odpowiedzi na zt ekspanswną politkę fiskalną i wsoki poziom defictu udżetowego, ank centaln powadził politkę estkcjną, utzmując stop pocentowe na stosunkowo wsokim poziomie. Inteesujące jest ptanie, cz ównowaga ta jest Paeto optmalna. W tm sensie szczególnie ważne jest poównanie dwóch waiantów ozwiązań stategicznch: stanu ównowagi odzwieciedlającego stategie dominujące, tzn. ekspanswną politkę fiskalną i estkcjną pieniężną (lew doln óg talic) oaz altenatwnego ozwiązania kominacji estkcjnej politki udżetowej i ekspanswnej monetanej (paw gón óg talic). Ponieważ, jak się wdaje, nie ma odpowiedzi uniwesalnej, ozważone mogą ć czte pzpadki. Pzpadek A1: 17 p p p p. Waunek, okeślając Pzpadek A1, oznacza, że po piewsze, zwiększenie tempa wzostu PKB wwołane, ceteis paius, wzostem defictu udżetowego, stanowi efekt silniejsz niż zwiększenie wzostu PKB wwołane oniżeniem stop pocentowej, ceteis paius. Po dugie efekt inflacjn osnącego defictu finansów pulicznch jest silniejsz w poównaniu ze skutkiem inflacjnm oniżki stop pocentowej. W pozostałch pzpadkach intepetacja założeń jest analogiczna. (1)
12 I. Wooniecka-Leciejewicz Pzpadek A: p p p p. () Pzpadek A3: p p p p. (3) Pzpadek A4: p p p p. (4) Taele 6-7 pzedstawiają pefeencje w gze monetano-fiskalnej dla powższch altenatwnch założeń. W pzpadku A1, stan ównowagi, epezentując kominację ekspanswnej politki fiskalnej i estkcjnej monetanej, stanowi ozwiązanie Paeto optmalne, tempo wzostu PKB jest wższe, a inflacja niższa w poównaniu z ozwiązaniem altenatwnm (paw gón óg talic), oznaczającm połączenie estkcjnej politki udżetowej i ekspanswnej pieniężnej. Pzjęcie stategii dominującch jest kozstniejszm ozwiązaniem dla ou gacz: ządu i anku centalnego. Również w pzpadkach A i A3 ównowaga jest Paeto optmalna, pz czm każd z tch pzpadków stanowi zwieciadlane odicie dugiego. Pz założeniach A stan ównowagi jest kozstniejszm ozwiązaniem z punktu widzenia władz fiskalnch, pozwala osiągnąć wższą dnamikę PKB, jednak goszm w ocenie anku centalnego, ponieważ poztwn efekt pzspieszenia wzostu gospodaczego oaczon jest kosztem inflacjnm. W pzpadku A3 stan ównowagi jest pefeowan pzez władze monetane (niższa inflacja), jednak pzez władze fiskalne pefeowane jest ozwiązanie altenatwne, tj. kominacja estkcjnej politki udżetowej i ekspanswnej pieniężnej (wższ wzost PKB). Rząd A1 1 Taela 6. Pefeencje w gze monetano-fiskalnej. Pzpadki A1-A3 Bank centaln A Bank centaln A3 Bank centaln Rząd 1 1 Rząd
13 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie W pzpadku A4 (zilustowanm w Taeli 7) stan ównowagi chaaktezuje się goszmi, w poównaniu z altenatwną paą stategii z pawego gónego ogu talic, wskaźnikami gospodaczmi (niższ wzost PKB i wższa inflacja). W tm pzpadku wó stategii dominującch pzez oa podmiot kształtujące politkę makoekonomiczną nie oznacza ozwiązania Paeto optmalnego. Pzpadek ten odzwieciedla stuację znaną w liteatuze jako dlemat więźnia, w któm wstępuje chaaktestczn konflikt międz acjonalnością indwidualną, epezentowaną pzez kteium stategii dominującej, a acjonalnością gupową, epezentowaną pzez kteium Paeto optmalności. Podmiot dające o swoje indwidualne intees dopowadzają do wniku niekozstnego dla ogółu i dla uczestniczącch podmiotów z osona. Taela 7. Pzpadek A4 dlemat więźnia Rząd A4 1 Bank centaln Na podstawie powższej analiz można wskazać cznniki, od któch zależ, cz ównowaga Nasha (w analizowanm polemie wznaczana pzez stategie dominujące) stanowi jednocześnie ozwiązanie Paeto optmalne. Uzskane wniki pokazują, że Paeto optmalność ozwiązań zależ od skuteczności instumentów politki monetanej i fiskalnej w oddziałwaniu na gospodakę, w szczególności na wzost gospodacz i na inflację, a także od tego, któ instument podlega silniejszm zmianom: stopa pocentowa (instument politki pieniężnej) cz defict udżetow (instument politki fiskalnej). Po pzepowadzeniu analiz Paeto optmalności ozwiązań dla g uwzględniającej dwie jakościowo óżne stategie politki fiskalnej i pieniężnej, wskazano na możliwość zaistnienia czteech óżnch pzpadków, z któch tz dotczą stuacji, gd ównowaga Nasha stanowi jednocześnie ozwiązanie Paeto optmalne. W tch pzpadkach samodzielne kształtowanie politki monetanej i fiskalnej pzez ank centaln i ząd powadzi do efektwnch ozwiązań. Jednie jeden z analizowanch waiantów wskazuje na wstępowanie znanego w liteatuze pzpadku dlematu więźnia, do któego odwołują się ównież autoz pac z zakesu koodnacji politki monetanej i fiskalnej. Wstępuje tu konflikt międz acjonalnością indwidualną, gd ozstzgającm kteium wou jest posiadanie pzez gacz stategii dominującch, a acjonalnością gupową, gd o woze decduje Paeto optmalność ozwiązań. Taka stuacja ma miejsce, gd politka mone- 19
14 I. Wooniecka-Leciejewicz tana oddziałuje skuteczniej na wzost gospodacz niż na inflację i pzeciwnie, politka fiskalna wpłwa efektwniej na inflację niż na wzost PKB. Pzpadek ten wskazuje na konieczność koodnacji politki anku centalnego i ządu. Należ jednak zaznaczć, że wnioski te uzskano analizując uposzczoną wesję g monetanej, uwzględniającą tlko dwie stategie dla każdego gacza oaz zakładającą ich dążenie do maksmalizacji (minimalizacji) celów gospodaczch. Badziej ealistczne podejście zostanie pzedstawione w kolejnch ozdziałach, zakłada się w nim dążenie władz fiskalnch i monetanch do osiągnięcia z gó wznaczonch celów, co oznacza pzjęcie kteium minimalizacji odchleń od watości pożądanch dnamiki PKB i inflacji w woze stategii optmalnch. 3. Ga monetano-fiskalna z zastosowaniem zmodfikowanej funkcji logistcznej. Równowaga w gze Celem uzupełnienia teoetcznch ozważań zawatch w popzednim ozdziale o analizę smulacjną, pozwalającą na ozpatzenie óżnch waiantów w gze monetano-fiskalnej z szeokim wachlazem możliwch stategii, zapoponowano zastosowanie zmodfikowanej funkcji logistcznej. Funkcja logistczna pozwala uwzględnić specfikę oddziałwania instumentów politki fiskalnej i monetanej na stan gospodaki (w tm na dnamikę PKB i inflację). Specfika ta polega na oganiczonch możliwościach stosowania skajnie estkcjnch ądź skajnie ekspanswnch politk i ich wpłwu na gospodakę. Instument monetane i fiskalne są skuteczne jednie w pewnm pzedziale wahań, poza nim ich skuteczność maleje. Oznacza to m.in., że możliwości oniżania inflacji popzez stosowanie coaz adziej estkcjnej politki monetanej są oganiczone, podonie jak możliwości poudzania wzostu gospodaczego pzez coaz adziej ekspanswną politkę fiskalną. Zastosowanie funkcji logistcznej do odzwieciedlenia oddziałwania instumentów polic mix na stan gospodaki w gze monetano-fiskalnej z uwzględnieniem istotnch w tm kontekście własności funkcji i intepetacji paametów pzedstawiono w popzednich pulikacjach autoki (Wooniecka-Leciejewicz 01, 015a). Funkcja logistczna o analitcznej postaci: f 1 e ( x) (pz założeniu, x że paamet >0) odzwieciedla monotoniczne pzejście zmiennej ojaśnianej od początkowej watości f(x 0)=0 do osiągnięcia końcowej watości f(x k)= (dla >0) lu od watości f(x 0)= do osiągnięcia końcowej zeowej watości (dla <0). W zależności od paametów i, funkcja logistczna pzedstawia wzost zmiennej ojaśnianej (dla ou paametów dodatnich lu ou ujemnch) ądź spadek w pzeciwnm pzpadku (gd paamet i mają óżne znaki). Uzupełnienie funkcji logistcznej o 0
15 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie stałą : f ( x) x 1 e umożliwia odzwieciedlenie pzejścia zmiennej ojaśnianej od dowolnej watości początkowej do osiągnięcia dowolnej watości końcowej, pzjmując odpowiednie watości paametów i. Oliczenia smulacjne wkonano dla paametu > 0. Wpłw instumentu fiskalnego, tj. defictu udżetowego w elacji do PKB (), na tempo wzostu gospodaczego () chaaktezuje osnąca funkcja logistczna: 1 f ( ) 1, pz czm >0, >0, >0. Oznacza to, że wzost defictu udżetowego, ceteis paius, pzcznia się do ożwienia wzostu gospoda e czego ( 0 ), ale skuteczność oddziałwania politki udżetowej na koniunktuę gospodaczą jest oganiczona tlko do pewnego pzedziału wahań instumentu. Zakłada się, że oganiczone są zaówno możliwości poudzania wzostu popzez stosowanie coaz adziej ekspanswnej politki fiskalnej (podwższanie defictu), jak i możliwości negatwnego wpłwu na dnamikę podukcji pzez coaz adziej estkcjną politkę polegającą na edukcji defictu. Pz skajnie estkcjnej politce fiskalnej wzost PKB jest najniższ i ówn 1 ( min = 1), a dalsz wzost estkcjności politki nie ma już wpłwu na dnamikę podukcji. Analogicznie, pz skajnie ekspanswnej politce najwższ ealn wzost PKB jest ówn ( max = 1 + 1), a dalsze zwiększanie jej ekspanswności pzestaje ć skuteczne. Analogicznie okeślono oddziałwanie instumentu monetanego na inflację oaz ou instumentów na wzostu gospodaczego i inflację. Powższą postać funkcji logistcznej wkozstano do oliczenia wpłat w gze monetano-fiskalnej. Zaówno wpłata władz fiskalnch tempo wzostu PKB (), jak i władz monetanch inflacja (p), zależą od instumentów polic mix: defictu udżetowego w elacji do PKB ( i) i ealnej stop pocentowej ( j): 1 ij f ( i, j ) 1, (5) 1 1 i j 1e 1 e 3 p 4 ij f ( i, j ). (6) 1 3 i 4j 3e 1 4e Pzkładowe wniki oliczeń dla wanch paametów w postaci talic wpłat zawato w Taeli 8. Dla każdej kominacji politki fiskalnej i monetanej oliczono tempo wzostu PKB (lew doln óg każdej komóki) oaz poziom inflacji (paw gón óg). 1
16 I. Wooniecka-Leciejewicz Najniższa inflacja, ale jednocześnie najniższ wzost gospodacz wstępuje w pzpadku wou kominacji skajnie estkcjnch politk: monetanej i fiskalnej (lew gón óg talic wpłat). Waz ze wzostem stopnia ekspanswności politki monetanej ceteis paius i oniżaniem stop pocentowej (pzejście w pawo) zwiększa się inflacja i ośnie tempo wzostu PKB. Również na skutek wzostu ekspansji politki fiskalnej ceteis paius i osnącego defictu udżetowego (pzejście w dół) następuje wzost inflacji i dnamiki podukcji. Najwższą inflacją, ale i najszszm wzostem PKB chaaktezuje się gospodaka, wted, gd zaówno politka pieniężna jak i udżetowa mają chaakte skajnie ekspanswn (paw doln óg talic). Taela 8. Talica wpłat dla g monetano-fiskalnej ze zmodfikowaną funkcją logistczną -1,0 0,0 1,0 1,4 1,6 1,8,0,4 3,0 6,0 3,0,4,0 1,8 1,0 0,0 #### -1,13 #### -0,74 #### -0,34 #### -0,09 #### 1,30 #### 3,84-0,15 #### 0,03 #### 0,1 #### 0,3 #### 0,96 ####,11 #### #### 0,0 #### 0,41 #### 0,81 #### 1,06 ####,46 #### 5,00 1,4 #### 1,4 #### 1,60 #### 1,71 ####,34 #### 3,50 #### #### 1,18 #### 1,57 #### 1,97 ####, #### 3,61 #### 6,16,6 ####,80 ####,98 #### 3,10 #### 3,73 #### 4,89 #### #### 1,53 #### 1,93 ####,3 ####,57 #### 3,97 #### 6,51 3,05 #### 3,3 #### 3,41 #### 3,5 #### 4,16 #### 5,31 #### #### 1,68 ####,07 ####,47 ####,7 #### 4,1 #### 6,66 3,3 #### 3,41 #### 3,59 #### 3,70 #### 4,34 #### 5,49 #### #### 1,81 ####,1 ####,60 ####,85 #### 4,5 #### 6,79 3,39 #### 3,56 #### 3,74 #### 3,86 #### 4,49 #### 5,65 #### #### 1,93 ####,3 ####,7 ####,96 #### 4,36 #### 6,90 3,5 #### 3,70 #### 3,88 #### 3,99 #### 4,63 #### 5,78 #### ####,11 ####,50 ####,90 #### 3,14 #### 4,54 #### 7,08 3,74 #### 3,9 #### 4,10 #### 4,1 #### 4,85 #### 6,00 #### ####,8 ####,68 #### 3,07 #### 3,3 #### 4,7 #### 7,6 3,95 #### 4,13 #### 4,31 #### 4,4 #### 5,06 #### 6, #### ####,51 ####,90 #### 3,30 #### 3,55 #### 4,95 #### 7,49 4, #### 4,40 #### 4,58 #### 4,69 #### 5,33 #### 6,49 #### Paamet: =6; =1; =1; =-5; =1; =1;=3; =5; =1; =1; =-11; =1; =1;=8. Władze monetane i fiskalne, wieając stategie optmalnch odpowiedzi, kieują się własnmi celami. W pezentowanch tutaj adaniach ozważono dwa pzpadki: piewsz, w któm zakłada się, że władze monetane dążą do minimalizacji inflacji, a fiskalne do maksmalizacji tempa wzostu PKB, oaz dugi, w któm pzjmuje się, że władze monetane i fiskalne wznaczają własne konketne cele, któe chcą osiągnąć, okeślając pożądan cel inflacjn i planowaną dnamikę PKB.
17 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie W piewszm pzpadku, władze monetane, dla każdej stategii fiskalnej i wieają stategię optmalnej odpowiedzi (stategię optmalną) j*(i), któa chaaktezuje się minimalnm poziomem inflacji: min jp ij. Analogicznie, władze fiskalne dla każdej stategii monetanej j wieają stategię optmalnej odpowiedzi i*(j) maksmalizując tempo wzostu PKB: max i ij. W takiej stuacji, władze fiskalne dsponują stategią dominującą, tzn. taką, któa jest stategią optmalną z punktu widzenia ządu, niezależnie od tego, jakie deczje odnośnie wsokości stóp pocentowch podejmie ank centaln. Stategią dominującą władz fiskalnch jest skajnie ekspanswna politka udżetowa. Analogicznie, skajnie estkcjna politka pieniężna stanowi dla władz monetanch stategię dominującą, któa jest optmalna niezależnie od tego, jaką stategię fiskalną wieze ząd. Równowaga w gze w jest wówczas deteminowana pzez stategie dominujące, skłaniające do wou kominacji skajnie estkcjnej politki monetanej i skajnie ekspanswnej fiskalnej (pzedstawia to Rs. 1). instument politki monetanej - ealna stopa pocentowa politka estkcjna politka ekspanswna instument politki fiskalnej - defict / PKB ekspanswna estkcjna inflacja min W dugim pzpadku zakłada się, że władze monetane i fiskalne dążą do minimalizacji odchleń, odpowiednio, wzostu PKB i inflacji od watości pożądanch (celów politki monetanej i fiskalnej). Pzjmuje się, że władze monetane dla każdej stategii fiskalnej i wieają optmalną stategię monetaną j*(i), któa chaaktezuje się minimalnm kwadatem odchlenia inflacji od watości pożądanej (celu inflacjnego), a więc wieają min j(p ij p*). Analogicznie, władze fiskalne, dla każstan ównowagi wzost PKB max Rs. 1. Dominujące stategie fiskalne i monetane pzpadek maksmalizacji ealnego wzostu PKB i minimalizacji inflacji 3
18 I. Wooniecka-Leciejewicz dej stategii monetanej j wieają optmalną stategię fiskalną i*(j), tak, minimalizować kwadat odchlenia wzostu PKB od pożądanej watości, czli wieają min i( ij *). Optmalne stategie pieniężne chaaktezują więc eakcję władz monetanch na óżne stategie fiskalne, i vice vesa, optmalne stategie udżetowe opisują eakcję władz fiskalnch na możliwe posunięcia anku centalnego. Dla pzpadku, gd władze monetane i fiskalne dążą do minimalizacji odchleń, odpowiednio, ealnego wzostu gospodaczego i inflacji od watości pożądanch, wkonano oliczenia dla altenatwnch założeń. Ustuowanie stanu ównowagi nie jest już najmniej oczwiste i zależ m. in. od skuteczności oddziałwania instumentów politki fiskalnej i monetanej, odzwieciedlanej pzez paamet funkcji logistcznej, oaz od celów ządu i anku centalnego w powadzeniu politki. Rsunek pezentuje stategie optmalnch odpowiedzi: władz monetanch dla celu inflacjnego na poziomie,5% oaz władz fiskalnch dla 3,5-pocentowego wzostu PKB jako watości pożądanej. Stategie optmalnch odpowiedzi pzedstawiono z pzjęciem niewielkich skokowch zmian instumentów politki fiskalnej i monetanej ( i i j ówne 0,1 punktu pocentowego). Rs. odzwieciedla pzpadek g, pzedstawion wcześniej w Taeli 8 (ta sama talica wpłat, oliczona dla tch samch watości paametów funkcji logistcznej). Na sunku celowo pokazano szesz zakes wahań instumentów w poównaniu z taelą dzięki temu waźnie widoczna jest specfika oddziałwania instumentów na stan gospodaki, w tm na tempo wzostu PKB i inflację. W pewnm pzedziale wahań instumentów politki fiskalnej i monetanej, któ można nazwać efektwnm, ich oddziałwanie na koniunktuę gospodaczą jest skuteczne, natomiast poza nim, pz ekstemalnie niskich/wsokich watościach instumentów, odpowiadającch skajnie estkcjnemu ądź ekspanswnemu nastawieniu politki ich skuteczność zdecdowanie maleje. Można zaosewować, że w efektwnm pzedziale wahań instumentów fiskalnch, wó optmalnej politki monetanej (stopień jej estkcjności/ekspanswności) zależ od tego, jaką politkę fiskalną wieze ząd. Im adziej ekspanswna jest politka fiskalna, tm adziej estkcjną politkę pieniężną w odpowiedzi stosuje ank centaln, a uniknąć nadmienej inflacji, pzekaczającej cel inflacjn. Dla wższch watości defictu udżetowego pożądana watość inflacji jest osiągana pz odpowiednio wższch stopach pocentowch. Analogicznie, gd ząd powadzi adziej estkcjną politkę udżetową, ank centaln, dążąc do osiągnięcia celu inflacjnego, może pzstać na mniej estkcjną (adziej ekspanswną) politkę pieniężną z odpowiednio niższmi stopami pocentowmi. Poza tm (efektwnm) pzedziałem instumentów fiskalnch, pod wpłwem dalszego zaostzania politki udżetowej lu zwiększania stopnia jej ekspanswności, optmalna stategia monetana zmieza w kieunku stategii dominującej. 4
19 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie Rs.. Optmalne stategie monetane i fiskalne i ównowaga Nasha dla celów gospodaczch: wzost PKB = 3,5%, inflacja=,5%. Wniki smulacji dla paametów z Taeli 8 Można zaosewować, że w efektwnm pzedziale wahań instumentów fiskalnch, wó optmalnej politki monetanej (stopień jej estkcjności/ekspanswności) zależ od tego, jaką politkę fiskalną wieze ząd. Im adziej ekspanswna jest politka fiskalna, tm adziej estkcjną politkę pieniężną w odpowiedzi stosuje ank centaln, a uniknąć nadmienej inflacji, pzekaczającej cel inflacjn. Dla wższch watości defictu udżetowego pożądana watość inflacji jest osiągana pz odpowiednio wższch stopach pocentowch. Analogicznie, gd ząd powadzi adziej estkcjną politkę udżetową, ank centaln, dążąc do osiągnięcia celu inflacjnego, może pzstać na mniej estkcjną (adziej ekspanswną) politkę pieniężną z odpowiednio niższmi stopami pocentowmi. Poza tm (efektwnm) pzedziałem instumentów fiskalnch, pod wpłwem dalszego zaostzania politki udżetowej lu zwiększania stopnia jej ekspanswności, optmalna stategia monetana zmieza w kieunku stategii dominującej. Analogicznie, stopień estkcjności/ekspanswności politki fiskalnej zależ od stosowanej pzez ank centaln politki monetanej. Im adziej estkcjna jest politka pieniężna, tm w odpowiedzi adziej ekspanswna jest politka udżetowa, ponieważ osiągniecie pożądanego tempa wzostu gospodaczego pz wższm poziomie stóp pocentowch wmaga adziej zdecdowanej, powzostowej, ekspanswnej politki fiskalnej, chaaktezującej się wższm defictem udżetu. I odwotnie, w odpowiedzi na adziej ekspanswną politkę pieniężną, ząd oganicza 5
20 I. Wooniecka-Leciejewicz stopień ekspansji udżetowej powadząc odpowiednio adziej estkcjną politkę fiskalną. Ale poza tm pzedziałem (jest to waźniej widoczne na Rs. 3 i 4), kieując się do skajnie estkcjnej politki pieniężnej optmalna stategia fiskalna nie zmienia się pod wpłwem dalszego zaostzania pzez ank centaln politki monetanej. Podonie, pzechodząc w kieunku skajnie ekspanswnej politki monetanej optmalna stategia fiskalna pzestaje eagować na dalsze łagodzenie politki pieniężnej. Podsumowując, w oszaze skajnie estkcjnch lu skajnie ekspanswnch stategii stóp pocentowch optmalna stategia fiskalna pzechodzi w stategię dominującą. Dla pzjętch paametów oaz celów władz monetanch i fiskalnch w pzedziale dopuszczalnch zmian instumentów wstępuje jeden stan ównowagi Nasha (Rs. ), któ odpowiada kominacji stosunkowo neutalnch politk: zaówno monetanej jak i fiskalnej, chaaktezowanch pzez ealną stopę pocentową na poziomie ok. 1,9% oaz defict udżetu państwa w elacji do PKB na poziomie ok. 1,4%. Rsunek 3 pzedstawia izokwant wzostu PKB i izokwant inflacji, pokazujące jakie altenatwne policies-mix (stanowiące kominacje politki fiskalnej i monetanej o okeślonm stopniu estkcjności/ekspanswności) umożliwiają osiągnięcie pzjętej dnamiki PKB i założonego poziomu inflacji (ze zmieniającm się dopuszczalnm pzedziałem wahań wokół watości pożądanej). Można zauważć, że ozwiązania mieszczące się w wąskim pzedziale dopuszczalnch odchleń od watości pożądanch jednocześnie dla wzostu gospodaczego i inflacji znajdują się w małm otoczeniu ównowagi Nasha. Jeżeli dopuścim większ zakes odchleń od wznaczonch celów makoekonomicznch, zwiększa się osza ozwiązań wstaczająco doch (liskich pożądanm watościom z pzjętm dopuszczalnm odchleniem zaówno dla dnamiki PKB jak i inflacji). Widoczna jest waźna asmetia w ich ustuowaniu osza ozwiązań liskich optmalnm z dopuszczalnm odchleniem zwiększa się szczególnie w kieunku kominacji politk adziej estkcjnch monetanch i adziej ekspanswnch fiskalnch w poównaniu ze stanem ównowagi Nasha. W dalszej kolejności pzedstawiono wniki smulacji, wskazujące na możliwość wstąpienia óżnch stuacji, opisującch ównowagę w zdefiniowanej powżej gze monetano-fiskalnej, w tm ównież pzpadków, gd istnieje kilka stanów ównowagi (Rs. 4 i 5) ądź, gd w ozpatwanm zakesie wahań instumentów ównowagi nie ma (Rs. 8). I tak, pzkładowo, na Rs. 4 widoczne są tz stan ównowagi Nasha: jeden odnosi się do neutalnej polic-mix: ealna stopa pocentowa na poziomie ok. 0,65% oaz defict udżetu państwa w elacji do PKB na poziomie ok. 0,85%, kolejn punkt ównowagi odzwieciedla estkcjną politkę monetaną i ekspanswną fiskalną, a tzeci stan ównowagi, odwotnie ekspanswną politkę pieniężną i estkcjną udżetową. 6
21 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie instument politki monetanej - ealna stopa pocentowa (w %) politka estkcjna politka ekspanswna instument politki fiskalnej - defict do PKB (w %) politka ekspanswna politka estkcjna izokwanta inflacji wastw ównowaga Nasha izokwanta wzostu PKB wastw Rs. 3. Izokwant wkes wastwow z dopuszczalnmi wahaniami wokół założonch watości: wzost PKB = 3,5%, inflacja =,5%. Wniki smulacji dla paametów z Taeli 8 Rs. 4. Optmalne stategie fiskalne i monetane dla celów gospodaczch: wzost PKB = 3,5%, inflacja=,5%. Tz stan ównowagi. Wniki smulacji (paamet: =6; =1; =1; =-5; =5; =4;=3; =5; =10; =; =-11; =1; =1;=8) 7
22 I. Wooniecka-Leciejewicz Rs. 5. Optmalne stategie fiskalne i monetane dla celów gospodaczch: wzost PKB = 3,5%, inflacja=,5%. Tz stan ównowagi. Wniki smulacji (paamet: =6; =; =1; =-5; =4,5; =5;=3; =5; =1; =5; =-11; =1; =;=8) 4. Wpłw celów władz monetanch i fiskalnch na wó polic mix Wkonano ównież smulacje mające na celu zadanie wpłwu celów władz monetanch i fiskalnch na wó polic mix. Pzkładowe wniki pezentowane są na kolejnch wkesach (Rs. 6-8). Wkes te pzedstawiają zmian w zakesie stategii optmalnch odpowiedzi władz monetanch i fiskalnch pod wpłwem celów, jakie soie stawiają ealizując własną politkę, a w ezultacie jak zmienia się ustuowanie stanów ównowagi Nasha. Punktem wjścia ł pzpadek pzedstawion na Rs., gd władze monetane dążą do ealizacji celu inflacjnego na poziomie,5%, a władze fiskalne do wzostu gospodaczego na poziomie 3,5% PKB. Dla danch paametów funkcji logistcznej istnieje wówczas jeden stan ównowagi Nasha, znajdując się w punkcie pzecięcia stategii najlepszch odpowiedzi w oszaze dopuszczalnch zmian instumentów. Stanowi on jednocześnie ozwiązanie Paeto optmalne. Można zauważć, że zaostzanie celów politki pieniężnej (np. oniżenie celu inflacjnego do %) powoduje pzesunięcie optmalnch stategii monetanch w lewo, w kieunku adziej estkcjnch stategii pzedstawia to Rs. 6. Rezultatem jest zmiana stanu ównowagi i polic mix na kominację adziej estkcjnej politki monetanej i zaazem adziej ekspanswnej politki fiskalnej. Analogicznie, 8
23 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie Rs. 7. Optmalne stategie monetane i fiskalne i ównowaga Nasha dla celów gospodaczch: wzost PKB = 4,0%, inflacja=,5%. Wniki smulacji (paamet: =6; =1; =1; =-5; =1; =1;=3; =5; =1; =1; =-11; =1; =1;=8) Rs. 8. Optmalne stategie monetane i fiskalne dla celów gospodaczch: wzost PKB = 4,0%, inflacja=,0%. Wniki smulacji (paamet: =6; =1; =1; =-5; =1; =1;=3; =5; =1; =1; =-11; =1; =1;=8) 9
24 I. Wooniecka-Leciejewicz pzjęcie łagodniejszch celów pzez władze monetane powadzi do zmian stategii pieniężnch na adziej ekspanswne (pzesunięcie w pawo), w wniku czego punkt ównowagi pzesuwa się w kieunku łagodniejszej politki pieniężnej i adziej estkcjnej udżetowej. Rsunek 7 pzedstawia wpłw pzjęcia pzez władze fiskalne adziej amitnch celów, podwższenia pożądanego wzostu PKB z 3,5% do 4%. Skutkiem jest pzesunięcie optmalnch stategii fiskalnch w dół, w kieunku adziej ekspanswnm. Równowagę Nasha zapewnia wówczas kominacja adziej ekspanswnej politki udżetowej i jednocześnie adziej estkcjnej pieniężnej. Odwotnie, gd władze fiskalne godzą się na ealizację niższego wzostu gospodaczego, następuje pzesunięcie optmalnch stategii udżetowch w góę, w kieunku adziej estkcjnm, a stan ównowagi odpowiada polic mix łączącej adziej estkcjną politkę fiskalną i adziej ekspanswną monetaną. Jeśli, jak na Rsunkach, 6 i 7, punkt pzecięcia optmalnch stategii monetanch i fiskalnch znajdują się w dopuszczalnm pzedziale wahań instumentów, to tm samm stanowią stan ównowagi Nasha, któe są ozwiązaniami Paeto optmalnmi. Wkes na Rs. 8 jest ilustacją dla innego pzpadku, gd nadmienie wsokie oczekiwania i nieealistczne cele władz monetanch i fiskalnch uniemożliwiają osiągnięcie Paeto optmalnego stanu ównowagi w pzjętm dopuszczalnm pzedziale instumentów i tm samm utudniają acjonaln wó w zakesie polic-mix. Wgóowane cele władz monetanch i fiskalnch skłaniają do wou skajnie estkcjnej politki pieniężnej i/lu skajnie ekspanswnej udżetowej, a więc do wou polic mix, któa nie jest Paeto efektwna. Pezentowan pzkład oliczeniow pokazuje, że wznaczanie pzez władze monetane silnie estkcjnego celu inflacjnego (np. inflacji na niskim poziomie %), a jednocześnie dążenie władz fiskalnch do zdecdowanie wsokiej dnamiki PKB (np. 4%) powadzi do takiej właśnie stuacji. Możliwość wstąpienia tego tpu pzpadków wskazuje na celowość koodnacji politki pieniężnej i fiskalnej. 5. Podsumowanie W pac pzedstawiono omówienie liteatu pzedmiotu w zakesie polematki wou polic mix z wkozstaniem g monetano-fiskalnej, a także podsumowanie dotchczasowch adań autoki w tm oszaze oaz ich kontnuację. Pzedmiotem analiz ła dwuosoowa, jednoetapowa ga, w któej władze monetane i fiskalne podejmują deczje niezależnie. Dokonując podsumowania dotchczasowch adań autoki wskazano na post pzpadek g, uwzględniającej dwie jakościowo óżne stategie, zaówno monetane jak i fiskalne (estkcjną i ekspanswną), a następnie ozważono gę z większą liczą stategii. Za mienik stopnia estkcjności/ekspanswności stategii pzjęto instument politki: ealną stopę 30
25 Analiza stategii monetanch i fiskalnch z wkozstaniem teoii gie pocentową dla politki pieniężnej oaz defict udżetow w elacji do PKB dla politki fiskalnej. Początkowe założenie, że władze monetane dążą do minimalizacji inflacji, a fiskalne do maksmalizacji wzostu gospodaczego, w dalszej części adań zmodfikowano, pzjmując, że celem anku centalnego jest osiągnięcie pożądanego poziomu inflacji, tzw. celu inflacjnego, podczas, gd ząd dąż do osiągnięcia pożądanego (zaplanowanego) poziomu wzostu gospodaczego. Pzepowadzono szeeg adań smulacjnch z zastosowaniem powższej g. Do odzwieciedlenia zależności międz zastosowanmi instumentami polic mix a uzskanmi efektami ekonomicznmi wkozstano zmodfikowaną funkcję logistczną, co umożliwiło uwzględnienie specfiki wpłwu instumentów na koniunktuę, w tm oganiczonej skuteczności oddziałwania skajnie estkcjnch/skajnie ekspanswnch politk na gospodakę. Rozważając gę z dwoma stategiami dokonano analiz stanów ównowagi i Paeto-optmalności ozwiązań. Pokazano, że stan ównowagi Nasha w analizowanej gze jest wznaczon pzez stategie dominujące i powadzi do wou kominacji estkcjnej politki monetanej i ekspanswnej fiskalnej, co odpowiada zeczwistej stuacji, jaka miała miejsce w Polsce, gd w odpowiedzi na zt ekspanswną politkę fiskalną i wsoki poziom defictu udżetowego, ank centaln powadził politkę estkcjną, utzmując ealne stop pocentowe na wsokim poziomie. Pzepowadzono ównież analizę Paeto-optmalności ozwiązań g, wskazując na możliwość zaistnienia czteech óżnch pzpadków. Tz z tch czteech pzpadków dotczą stuacji, gd ównowaga Nasha stanowi jednocześnie ozwiązanie Paeto optmalne, a jednie jeden wskazuje na znan w liteatuze pzpadek dlematu więźnia, gd wstępuje konflikt międz acjonalnością indwidualną, odzwieciedlaną pzez kteium dominacji, a acjonalnością gupową w postaci kteium Paeto. W pac pzedstawiono także waunki, od jakich zależ, z któm z wmienionch pzpadków możem mieć do cznienia. Odniesiono się do wników uzskanch w tej dziedzinie pzez Blindea oaz Bennetta i Loazę. Wkazują oni, że niezależnie działające władze monetane i fiskalne ędą dążć, podonie jak w dlemacie więźnia, do stanu ównowagi Nasha, wznaczanego pzez stategie dominujące: estkcjną politkę pieniężną i ekspanswną fiskalną, a to oznacza pzjęcie ozwiązania nieoptmalnego w sensie Paeto. Stanowi to, w ich opinii, pzesłankę do stwiedzenia, że niezędna jest koodnacja ou politk, ponieważ powadzi do lepszch ozwiązań niż niezależne działania anku centalnego i władz fiskalnch. Uzskane w pac wniki, wskazują, że dlemat więźnia jest zaledwie jednm z kilku możliwch pzpadków, jakie mogą mieć miejsce. W większości pzpadków ównowaga w gze jest Paeto optmalna, co oznacza, że niezależność anku centalnego w kształtowaniu politki monetanej powadzi do efektwnch ozwiązań. Odpowiedź, z któm pzpadkiem ędziem mieć do cznienia w paktce, i tm samm, cz pożądana jest koodnacja politk, zależ od uwaunkowań koniunktu gospodaczej i wkozstania instumentów, w szczególności zaś od tego, któa politka: monetana cz fiskalna skuteczniej wpłwa na wzost gospodacz oaz któa z nich efektwniej 31
ANALIZA POLICY-MIX Z UWZGLĘDNIENIEM INTERAKCJI DECYZYJNYCH MIĘDZY BANKIEM CENTRALNYM A RZĄDEM I ICH PRIORYTETÓW
 Zeszt Naukowe Wdziału Infomatcznch Technik Zaządzania Wższej Szkoł Infomatki Stosowanej i Zaządzania Wsółczesne Polem Zaządzania N /0 ANALIZA POLICY-MIX Z UWZGLĘDNIENIEM INTERAKCJI DECYZYJNYCH MIĘDZY BANKIEM
Zeszt Naukowe Wdziału Infomatcznch Technik Zaządzania Wższej Szkoł Infomatki Stosowanej i Zaządzania Wsółczesne Polem Zaządzania N /0 ANALIZA POLICY-MIX Z UWZGLĘDNIENIEM INTERAKCJI DECYZYJNYCH MIĘDZY BANKIEM
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Uniwersytet Warszawski Teoria gier dr Olga Kiuila LEKCJA 2
 LEKCJA 2 Pzykład: Dylemat Cykoa (albo Poke Dogowy) Dwie osoby wsiadają w samochody, ozpędzają się i z dużą pędkością jadą na siebie - ten kto piewszy zahamuje lub zjedzie z tasy jest "cykoem" i pzegywa.
LEKCJA 2 Pzykład: Dylemat Cykoa (albo Poke Dogowy) Dwie osoby wsiadają w samochody, ozpędzają się i z dużą pędkością jadą na siebie - ten kto piewszy zahamuje lub zjedzie z tasy jest "cykoem" i pzegywa.
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Wykład 9. Model ISLM: część I
 Makoekonomia 1 Wykład 9 Model ISLM: część I Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Model ISLM Równowaga gaficzna Równowaga algebaiczna Skutki zmian paametów egzogenicznych
Makoekonomia 1 Wykład 9 Model ISLM: część I Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Model ISLM Równowaga gaficzna Równowaga algebaiczna Skutki zmian paametów egzogenicznych
Temat 4 - Model ISLM
 mg Batłomiej Rokicki Ćwiczenia z Makoekonomii I 2005/2006 Temat 4 - Model ISLM Podstawowe założenia modelu: pieniądz odgywa ważną olę pzy deteminowaniu poziomu dochodu i zatudnienia inwestycje nie mają
mg Batłomiej Rokicki Ćwiczenia z Makoekonomii I 2005/2006 Temat 4 - Model ISLM Podstawowe założenia modelu: pieniądz odgywa ważną olę pzy deteminowaniu poziomu dochodu i zatudnienia inwestycje nie mają
WYKŁAD 11 OPTYMALIZACJA WIELOKRYTERIALNA
 WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
Teoria i metody optymalizacji
 eoia dualności dla zadania pogamowania liniowego PL EORIA I MEODY OPYMALIZACJI Zadanie liniowego pogamowania całkowitoliczbowego PCL Wdział Elektoniki Kie. Automatka i Robotka Studia II t. NZ d inż. Ewa
eoia dualności dla zadania pogamowania liniowego PL EORIA I MEODY OPYMALIZACJI Zadanie liniowego pogamowania całkowitoliczbowego PCL Wdział Elektoniki Kie. Automatka i Robotka Studia II t. NZ d inż. Ewa
Programowanie nieliniowe optymalizacja funkcji wielu zmiennych
 Ekonomia matematczna II Ekonomia matematczna II Prowadząc ćwiczenia Programowanie nieliniowe optmalizacja unkcji wielu zmiennch Modele programowania liniowego często okazują się niewstarczające w modelowaniu
Ekonomia matematczna II Ekonomia matematczna II Prowadząc ćwiczenia Programowanie nieliniowe optmalizacja unkcji wielu zmiennch Modele programowania liniowego często okazują się niewstarczające w modelowaniu
METEMATYCZNY MODEL OCENY
 I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
Podejmowanie decyzji w warunkach niepełnej informacji. Tadeusz Trzaskalik
 Podejmowanie deczji w warunkach niepełnej informacji Tadeusz Trzaskalik 5.. Wprowadzenie Słowa kluczowe Niepełna informacja Stan natur Macierz wpłat Podejmowanie deczji w warunkach rzka Podejmowanie deczji
Podejmowanie deczji w warunkach niepełnej informacji Tadeusz Trzaskalik 5.. Wprowadzenie Słowa kluczowe Niepełna informacja Stan natur Macierz wpłat Podejmowanie deczji w warunkach rzka Podejmowanie deczji
Makroekonomia 1 Wykład 8: Wprowadzenie do modelu ISLM: krzywa LM oraz krzywa IS
 Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Deteminanty popytu na pieniądz Równowaga na ynku
Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Plan wykładu Deteminanty popytu na pieniądz Równowaga na ynku
Wykład 5: Handel międzynarodowy a zasoby czynników produkcji część II
 Handel międzynaodowy Wykład 5: Handel międzynaodowy a zasoby czynników podukcji część II Gabiela Gotkowska Plan wykładu 5 odel HO w wesji z technologią Cobba- Douglasa Wybó techniki podukcji pzez poducenta
Handel międzynaodowy Wykład 5: Handel międzynaodowy a zasoby czynników podukcji część II Gabiela Gotkowska Plan wykładu 5 odel HO w wesji z technologią Cobba- Douglasa Wybó techniki podukcji pzez poducenta
Ruch dwu i trójwymiarowy
 Wkład z fizki. Piot Posmkiewicz 1 W Y K Ł A D Ruch dwu i tójwmiaow 3-1 Wekto pzemieszczenia. JeŜeli uch odbwa się w dwu lub tzech wmiaach, to pzemieszczenie ma okeśloną zaówno watość, jak i kieunek w pzestzeni.
Wkład z fizki. Piot Posmkiewicz 1 W Y K Ł A D Ruch dwu i tójwmiaow 3-1 Wekto pzemieszczenia. JeŜeli uch odbwa się w dwu lub tzech wmiaach, to pzemieszczenie ma okeśloną zaówno watość, jak i kieunek w pzestzeni.
Model IS-LM. Dr Michał Gradzewicz Katedra Ekonomii I KAE. Makroekonomia I Wykład 8
 odel IS-L D ichał Gadzewicz Kateda Ekonomii I KAE akoekonomia I Wykład 8 lan wykładu Łączny popyt w gospodace Funkcja konsumpcji lanowane i zeczywiste wydatki i kzyż Keynesowski Efekt mnożnikowy opyt inwestycyjny
odel IS-L D ichał Gadzewicz Kateda Ekonomii I KAE akoekonomia I Wykład 8 lan wykładu Łączny popyt w gospodace Funkcja konsumpcji lanowane i zeczywiste wydatki i kzyż Keynesowski Efekt mnożnikowy opyt inwestycyjny
Między teorią a praktyką oceniania zadań optymalizacyjnych.
 Anna Boniaczk, III Liceum Ogólnokształcące w Łodzi Jacek Człapiński (ed, doadca metodczn w ŁCDNiK w Łodzi, XXV Liceum Ogólnokształcące w Łodzi Izabela Głowacka Wzesień, Zespół Szkół zemsłu Mod w Łodzi
Anna Boniaczk, III Liceum Ogólnokształcące w Łodzi Jacek Człapiński (ed, doadca metodczn w ŁCDNiK w Łodzi, XXV Liceum Ogólnokształcące w Łodzi Izabela Głowacka Wzesień, Zespół Szkół zemsłu Mod w Łodzi
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
Ocena siły oddziaływania procesów objaśniających dla modeli przestrzennych
 Michał Benad Pietzak * Ocena siły oddziaływania pocesów objaśniających dla modeli pzestzennych Wstęp Ekonomiczne analizy pzestzenne są ważnym kieunkiem ozwoju ekonometii pzestzennej Wynika to z faktu,
Michał Benad Pietzak * Ocena siły oddziaływania pocesów objaśniających dla modeli pzestzennych Wstęp Ekonomiczne analizy pzestzenne są ważnym kieunkiem ozwoju ekonometii pzestzennej Wynika to z faktu,
() ( ) Równowaga w warunkach autarkii:
 Opracował J.J. Michałek C:\DYDAKTYK\teoriahan\Brander-Krugman.doc Model Brandera-Krugmana (wersja uproszczona) (98): A Reciprocal Dumping Model of International Trade (Rethinking International...) - jakie
Opracował J.J. Michałek C:\DYDAKTYK\teoriahan\Brander-Krugman.doc Model Brandera-Krugmana (wersja uproszczona) (98): A Reciprocal Dumping Model of International Trade (Rethinking International...) - jakie
Nr 2. Politechnika Poznańska Instytut Technologii Mechanicznej. Laboratorium Maszyn i urządzeń technologicznych. Właściwości i kształtowanie ewolwenty
 1 Politechnika Poznańska Insttut Technologii Mechanicznej Laoatoium Maszn i uządzeń technologicznch N Właściwości i kształtowanie ewolwent Opacował: D inż. Piot Fąckowiak Poznań 009 1. CEL ĆWICZENI Celem
1 Politechnika Poznańska Insttut Technologii Mechanicznej Laoatoium Maszn i uządzeń technologicznch N Właściwości i kształtowanie ewolwent Opacował: D inż. Piot Fąckowiak Poznań 009 1. CEL ĆWICZENI Celem
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
Makroekonomia 1 Wykład 8: Wprowadzenie do modelu ISLM: krzywa LM oraz krzywa IS
 Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS D hab. Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Nasz mapa dogowa Kzyż keynesowski Teoia pefeencji płynności
Makoekonomia 1 Wykład 8: Wpowadzenie do modelu ISLM: kzywa LM oaz kzywa IS D hab. Gabiela Gotkowska Kateda Makoekonomii i Teoii Handlu Zaganicznego Nasz mapa dogowa Kzyż keynesowski Teoia pefeencji płynności
Materiały pomocnicze dla studentów I roku do wykładu Wstęp do fizyki I Wykład 1
 Mateiał pomocnicze dla studentów I oku do wkładu Wstęp do fizki I Wkład 1 I. Skala i Wekto. Skala: Jest to wielkość, któą można jednoznacznie okeślić za pomocą liczb i jednostek; a więc mająca jednie watość,
Mateiał pomocnicze dla studentów I oku do wkładu Wstęp do fizki I Wkład 1 I. Skala i Wekto. Skala: Jest to wielkość, któą można jednoznacznie okeślić za pomocą liczb i jednostek; a więc mająca jednie watość,
Dobór zmiennych objaśniających do liniowego modelu ekonometrycznego
 Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Graf skierowany. Graf zależności dla struktur drzewiastych rozgrywających parametrycznie
 Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
Gaf skieowany Gaf skieowany definiuje się jako upoządkowaną paę zbioów. Piewszy z nich zawiea wiezchołki gafu, a dugi składa się z kawędzi gafu, czyli upoządkowanych pa wiezchołków. Ruch po gafie możliwy
ZWIĄZEK FUNKCJI OMEGA Z DOMINACJĄ STOCHASTYCZNĄ
 Studia konomiczne. Zeszyty Naukowe Uniwesytetu konomicznego w Katowicach ISSN 283-86 N 237 25 Infomatyka i konometia 2 wa Michalska Uniwesytet konomiczny w Katowicach Wydział Infomatyki i Komunikacji Kateda
Studia konomiczne. Zeszyty Naukowe Uniwesytetu konomicznego w Katowicach ISSN 283-86 N 237 25 Infomatyka i konometia 2 wa Michalska Uniwesytet konomiczny w Katowicach Wydział Infomatyki i Komunikacji Kateda
Minimalizacja kosztów
 Minimalizacja kosztów 1. (na wkładzie) Firma genealogiczna Korzenie produkuje dobro korzstając z jednego nakładu x użwając funkcji produkcji f(x) = x. (a) Ile jednostek x jest potrzebnch do wprodukowania
Minimalizacja kosztów 1. (na wkładzie) Firma genealogiczna Korzenie produkuje dobro korzstając z jednego nakładu x użwając funkcji produkcji f(x) = x. (a) Ile jednostek x jest potrzebnch do wprodukowania
Efekty restrykcyjnej polityki fiskalnej w zmodyfikowanym modelu Mankiwa-Summersa
 24 Makoekonomia Bank i Kedyt czewiec 2007 fekty estykcyjnej polityki fiskalnej w zmodyfikowanym modelu Mankiwa-Summesa ffects of Tight Fiscal Policy in Modified Mankiw and Summes Model Andzej Rzońca* piewsza
24 Makoekonomia Bank i Kedyt czewiec 2007 fekty estykcyjnej polityki fiskalnej w zmodyfikowanym modelu Mankiwa-Summesa ffects of Tight Fiscal Policy in Modified Mankiw and Summes Model Andzej Rzońca* piewsza
LIST EMISYJNY nr 3 /2014 Ministra Finansów
 LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
LIST EMISYJNY n /0 Minista Finansów z dnia stycznia 0. w spawie emisji kótkookesowych oszczędnościowych obligacji skabowych o opocentowaniu stałym ofeowanych w sieci spzedaży detalicznej Na podstawie at.
Modelowanie zmienności i dokładność oszacowania jakości węgla brunatnego w złożu Bełchatów (pole Bełchatów)
 Akademia Góniczo-Hutnicza, Kopalnia Węgla Bunatnego, Wydział Geologii, Geofizyki i Ochony śodowiska Bełchatów Wasztaty Gónicze 24 Jacek Mucha, Tadeusz Słomka, Wojciech Mastej, Tomasz Batuś Akademia Góniczo-Hutnicza,
Akademia Góniczo-Hutnicza, Kopalnia Węgla Bunatnego, Wydział Geologii, Geofizyki i Ochony śodowiska Bełchatów Wasztaty Gónicze 24 Jacek Mucha, Tadeusz Słomka, Wojciech Mastej, Tomasz Batuś Akademia Góniczo-Hutnicza,
WYKŁAD 1. W przypadku zbiornika zawierającego gaz, stan układu jako całości jest opisany przez: temperaturę, ciśnienie i objętość.
 WYKŁAD 1 Pzedmiot badań temodynamiki. Jeśli chcemy opisać układ złożony z N cząstek, to możemy w amach mechaniki nieelatywistycznej dla każdej cząstki napisać ównanie uchu: 2 d i mi = Fi, z + Fi, j, i,
WYKŁAD 1 Pzedmiot badań temodynamiki. Jeśli chcemy opisać układ złożony z N cząstek, to możemy w amach mechaniki nieelatywistycznej dla każdej cząstki napisać ównanie uchu: 2 d i mi = Fi, z + Fi, j, i,
TERMODYNAMIKA PROCESOWA. Wykład V
 ERMODYNAMIKA PROCESOWA Wykład V Równania stanu substancji czystych Równanie stanu gazu doskonałego eoia stanów odpowiadających sobie Równania wiialne Pof. Antoni Kozioł, Wydział Chemiczny Politechniki
ERMODYNAMIKA PROCESOWA Wykład V Równania stanu substancji czystych Równanie stanu gazu doskonałego eoia stanów odpowiadających sobie Równania wiialne Pof. Antoni Kozioł, Wydział Chemiczny Politechniki
ĆWICZENIE 3 REZONANS W OBWODACH ELEKTRYCZNYCH
 ĆWZENE 3 EZONANS W OBWODAH EEKTYZNYH el ćwiczenia: spawdzenie podstawowych właściwości szeegowego i ównoległego obwodu ezonansowego pzy wymuszeniu napięciem sinusoidalnym, zbadanie wpływu paametów obwodu
ĆWZENE 3 EZONANS W OBWODAH EEKTYZNYH el ćwiczenia: spawdzenie podstawowych właściwości szeegowego i ównoległego obwodu ezonansowego pzy wymuszeniu napięciem sinusoidalnym, zbadanie wpływu paametów obwodu
Modelowanie przepływu cieczy przez ośrodki porowate Wykład III
 Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
Modelowanie pzepływu cieczy pzez ośodki poowate Wykład III 6 Ogólne zasady ozwiązywania ównań hydodynamicznego modelu pzepływu. Metody ozwiązania ównania Laplace a. Wpowadzenie wielkości potencjału pędkości
ROLA ZWIĄZKÓW ZAWODOWYCH NA RYNKU PRACY W POLSCE
 KATEDRA NAUK EKONOMICZNYCH Kacpe Stachowski Autoefeat ozpawy doktoskiej ROLA ZWIĄZKÓW ZAWODOWYCH NA RYNKU PRACY W POLSCE Pomoto D hab. Nelly Daszkiewicz, pof. nadzw. PG Wydział Zaządzania i Ekonomii Kateda
KATEDRA NAUK EKONOMICZNYCH Kacpe Stachowski Autoefeat ozpawy doktoskiej ROLA ZWIĄZKÓW ZAWODOWYCH NA RYNKU PRACY W POLSCE Pomoto D hab. Nelly Daszkiewicz, pof. nadzw. PG Wydział Zaządzania i Ekonomii Kateda
Makroekonomia 1 dla MSEMen. Gabriela Grotkowska
 Makoekonomia 1 dla MSEMen Gabiela Gotkowska Rozszezamy analizę pzyczyn wahao koniunktualnych W czasie dwóch ostatnich zajęd zajmowaliśmy się analizą deteminantów wielkości PKB w kótkim okesie Analiza ta
Makoekonomia 1 dla MSEMen Gabiela Gotkowska Rozszezamy analizę pzyczyn wahao koniunktualnych W czasie dwóch ostatnich zajęd zajmowaliśmy się analizą deteminantów wielkości PKB w kótkim okesie Analiza ta
Wartości wybranych przedsiębiorstw górniczych przy zastosowaniu EVA *
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO n 786 Finanse, Rynki Finansowe, Ubezpieczenia n 64/1 (2013) s. 269 278 Watości wybanych pzedsiębiostw góniczych pzy zastosowaniu EVA * Adam Sojda ** Steszczenie:
BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH OPARTYCH NA ANALIZIE TECHNICZNEJ WPROWADZENIE
 Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Arytmetyka finansowa Wykład 6 Dr Wioletta Nowak
 Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
MIERNICTWO WIELKOŚCI ELEKTRYCZNYCH I NIEELEKTRYCZNYCH
 Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
Politechnika Białostocka Wydział Elektyczny Kateda Elektotechniki Teoetycznej i Metologii nstukcja do zajęć laboatoyjnych z pzedmiotu MENCTWO WEKOŚC EEKTYCZNYCH NEEEKTYCZNYCH Kod pzedmiotu: ENSC554 Ćwiczenie
MODEL AS-AD. Dotąd zakładaliśmy (w modelu IS-LM oraz w krzyżu keynesowskim), że ceny w gospodarce są stałe. Model AS-AD uchyla to założenie.
 MODEL AS-AD Dotąd zakładaliśmy (w modelu IS-LM oraz w krzyżu keynesowskim), że ceny w gospodarce są stałe. Model AS-AD uchyla to założenie. KRZYWA AD Krzywą AD wyprowadza się z modelu IS-LM Każdy punkt
MODEL AS-AD Dotąd zakładaliśmy (w modelu IS-LM oraz w krzyżu keynesowskim), że ceny w gospodarce są stałe. Model AS-AD uchyla to założenie. KRZYWA AD Krzywą AD wyprowadza się z modelu IS-LM Każdy punkt
Próba określenia miary jakości informacji na gruncie teorii grafów dla potrzeb dydaktyki
 Póba okeślenia miay jakości infomacji na guncie teoii gafów dla potzeb dydaktyki Zbigniew Osiak E-mail: zbigniew.osiak@gmail.com http://ocid.og/0000-0002-5007-306x http://via.og/autho/zbigniew_osiak Steszczenie
Póba okeślenia miay jakości infomacji na guncie teoii gafów dla potzeb dydaktyki Zbigniew Osiak E-mail: zbigniew.osiak@gmail.com http://ocid.og/0000-0002-5007-306x http://via.og/autho/zbigniew_osiak Steszczenie
dr inż. Małgorzata Langer Architektura komputerów
 Instukcja współfinansowana pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego w pojekcie Innowacyjna dydaktyka bez oganiczeń zintegowany ozwój Politechniki Łódzkiej zaządzanie Uczelnią, nowoczesna
Instukcja współfinansowana pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego w pojekcie Innowacyjna dydaktyka bez oganiczeń zintegowany ozwój Politechniki Łódzkiej zaządzanie Uczelnią, nowoczesna
Wyznaczanie współczynnika wzorcowania przepływomierzy próbkujących z czujnikiem prostokątnym umieszczonym na cięciwie rurociągu
 Wyznaczanie współczynnika wzocowania pzepływomiezy póbkujących z czujnikiem postokątnym umieszczonym na cięciwie uociągu Witold Kiese W pacy pzedstawiono budowę wybanych czujników stosowanych w pzepływomiezach
Wyznaczanie współczynnika wzocowania pzepływomiezy póbkujących z czujnikiem postokątnym umieszczonym na cięciwie uociągu Witold Kiese W pacy pzedstawiono budowę wybanych czujników stosowanych w pzepływomiezach
ROZKŁAD NORMALNY. 2. Opis układu pomiarowego
 ROZKŁAD ORMALY 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DYDAKTYKA FIZYKA ĆWICZEIA LABORATORYJE (Wstęp do teoii pomiaów). 2. Opis układu pomiaowego Ćwiczenie
ROZKŁAD ORMALY 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DYDAKTYKA FIZYKA ĆWICZEIA LABORATORYJE (Wstęp do teoii pomiaów). 2. Opis układu pomiaowego Ćwiczenie
Pola siłowe i ich charakterystyka
 W-6 (Jaosewic) 10 slajdów Pola siłowe i ich chaaktestka Pola siłowe: pojęcie i odaje pól siłowch, wielkości chaakteujące pola siłowe Pola achowawce Pole gawitacjne: uch w polu gawitacjnm 3/10 L.R. Jaosewic
W-6 (Jaosewic) 10 slajdów Pola siłowe i ich chaaktestka Pola siłowe: pojęcie i odaje pól siłowch, wielkości chaakteujące pola siłowe Pola achowawce Pole gawitacjne: uch w polu gawitacjnm 3/10 L.R. Jaosewic
PRZEMIANA ENERGII ELEKTRYCZNEJ W CIELE STAŁYM
 PRZEMIANA ENERGII ELEKTRYCZNE W CIELE STAŁYM Anaizowane są skutki pzepływu pądu pzemiennego o natężeniu I pzez pzewodnik okągły o pomieniu. Pzyęto wstępne założenia upaszcząace: - kształt pądu est sinusoidany,
PRZEMIANA ENERGII ELEKTRYCZNE W CIELE STAŁYM Anaizowane są skutki pzepływu pądu pzemiennego o natężeniu I pzez pzewodnik okągły o pomieniu. Pzyęto wstępne założenia upaszcząace: - kształt pądu est sinusoidany,
POLITECHNIKA OPOLSKA Wydział Elektrotechniki i Automatyki
 POLITECHNIKA OPOLSKA Wydział Elektotechniki i Automatyki Mg inż. Michał Tomaszewski MODEL PRZEDSIĘBIORSTWA DYSTRYBUCYJNEGO DZIAŁAJĄCEGO NA OTWARTYM RYNKU ENERGII ELEKTRYCZNEJ Autoefeat pacy doktoskiej
POLITECHNIKA OPOLSKA Wydział Elektotechniki i Automatyki Mg inż. Michał Tomaszewski MODEL PRZEDSIĘBIORSTWA DYSTRYBUCYJNEGO DZIAŁAJĄCEGO NA OTWARTYM RYNKU ENERGII ELEKTRYCZNEJ Autoefeat pacy doktoskiej
f x f y f, jest 4, mianowicie f = f xx f xy f yx
 Zestaw 14 Pochodne wŝszch rzędów Niech będzie dana funkcja x f określona w pewnm obszarze D Przpuśćm Ŝe f x istnieją pochodne cząstkowe tej funkcji x x Pochodne cząstkowe tch pochodnch jeŝeli istnieją
Zestaw 14 Pochodne wŝszch rzędów Niech będzie dana funkcja x f określona w pewnm obszarze D Przpuśćm Ŝe f x istnieją pochodne cząstkowe tej funkcji x x Pochodne cząstkowe tch pochodnch jeŝeli istnieją
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
Zadanie. W kolejnych okesach czasu t =,,3,... ubezpieczony, chaakteyzujący się paametem yzyka Λ, geneuje szkód. Dla danego Λ = λ zmienne N t N, N, N 3,... są waunkowo niezależne i mają (bzegowe) ozkłady
POMIAR PĘTLI HISTEREZY MAGNETYCZNEJ
 POMAR PĘTL STEREZ MAGNETZNEJ 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DDAKTKA FZKA ĆZENA LABORATORJNE.. Opis układu pomiaowego Mateiały feomagnetyczne (feyt,
POMAR PĘTL STEREZ MAGNETZNEJ 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DDAKTKA FZKA ĆZENA LABORATORJNE.. Opis układu pomiaowego Mateiały feomagnetyczne (feyt,
L(x, 0, y, 0) = x 2 + y 2 (3)
 0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
Zawiadomienie o wyborze najkorzystniejszej oferty
 Kaków, dnia 28 wześnia 2015. Nasz znak: KZ.II.272.10.2015 Dotyczy: postępowania o udzielenie publicznego w tybie pzetagu nieoganiczonego pn.: Pzygotowanie i pzepowadzenie kampanii infomacyjno edukacyjnej,
Kaków, dnia 28 wześnia 2015. Nasz znak: KZ.II.272.10.2015 Dotyczy: postępowania o udzielenie publicznego w tybie pzetagu nieoganiczonego pn.: Pzygotowanie i pzepowadzenie kampanii infomacyjno edukacyjnej,
KINEMATYKA. Kinematyka jest częścią mechaniki opisującą ruch obiektów bez wchodzenia w
 KINEMATYKA Kinematka jet częścią mechaniki opiującą uch iektów bez wchodzenia w pzczn wtępowania uchu Ruch jet względn i zawze jet opiwan w okeślonm układzie wpółzędnch nazwanm układem odnieienia Układ
KINEMATYKA Kinematka jet częścią mechaniki opiującą uch iektów bez wchodzenia w pzczn wtępowania uchu Ruch jet względn i zawze jet opiwan w okeślonm układzie wpółzędnch nazwanm układem odnieienia Układ
PRACA MOC ENERGIA. Z uwagi na to, że praca jest iloczynem skalarnym jej wartość zależy również od kąta pomiędzy siłą F a przemieszczeniem r
 PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
PRACA MOC ENERGIA Paca Pojęcie pacy używane jest zaówno w fizyce (w sposób ścisły) jak i w życiu codziennym (w sposób potoczny), jednak obie te definicje nie pokywają się Paca w sensie potocznym to każda
PRÓBA OCENY KIERUNKÓW I TEMPA ZMIAN INFRASTRUKTURY TRANSPORTOWEJ W KRAJACH NOWO PRZYJĘTYCH I ASPIRUJĄCYCH DO UNII EUROPEJSKIEJ
 B A D A N I A O P E A C Y J N E I D E C Y Z J E N 006 Kaol KUKUŁA*, Jacek STOJNY* PÓBA OCENY KIEUNKÓW I TEMPA ZMIAN INFASTUKTUY TANSPOTOWEJ W KAJACH NOWO PZYJĘTYCH I ASPIUJĄCYCH DO UNII EUOPEJSKIEJ Pzedstawiono
B A D A N I A O P E A C Y J N E I D E C Y Z J E N 006 Kaol KUKUŁA*, Jacek STOJNY* PÓBA OCENY KIEUNKÓW I TEMPA ZMIAN INFASTUKTUY TANSPOTOWEJ W KAJACH NOWO PZYJĘTYCH I ASPIUJĄCYCH DO UNII EUOPEJSKIEJ Pzedstawiono
Wykład 11. Pompa ciepła - uzupełnienie II Zasada Termodynamiki Entropia w ujęciu termodynamicznym c.d. Entropia w ujęciu statystycznym
 Wykład 11 Pompa ciepła - uzupełnienie II Zasada emodynamiki Entopia w ujęciu temodynamicznym c.d. Entopia w ujęciu statystycznym W. Dominik Wydział Fizyki UW emodynamika 2018/2019 1/30 G Pompa cieplna
Wykład 11 Pompa ciepła - uzupełnienie II Zasada emodynamiki Entopia w ujęciu temodynamicznym c.d. Entopia w ujęciu statystycznym W. Dominik Wydział Fizyki UW emodynamika 2018/2019 1/30 G Pompa cieplna
WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POLITECHNIKI KRAKOWSKIEJ Instytut Fizyki LABORATORIUM PODSTAW ELEKTROTECHNIKI, ELEKTRONIKI I MIERNICTWA
 WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POITEHNIKI KRAKOWSKIEJ Instytut Fizyki ABORATORIUM PODSTAW EEKTROTEHNIKI, EEKTRONIKI I MIERNITWA ĆWIZENIE 7 Pojemność złącza p-n POJĘIA I MODEE potzebne do zozumienia
WYDZIAŁ FIZYKI, MATEMATYKI I INFORMATYKI POITEHNIKI KRAKOWSKIEJ Instytut Fizyki ABORATORIUM PODSTAW EEKTROTEHNIKI, EEKTRONIKI I MIERNITWA ĆWIZENIE 7 Pojemność złącza p-n POJĘIA I MODEE potzebne do zozumienia
Analiza obecnej sytuacji Miasta Lublin według kluczowych elementów
 Analiza obecnej sytuacji Miasta Lublin według kluczowych elementów Pzedmiot zamówienia ealizowany w amach Regionalnego Pogamu Opeacyjnego Województwa Lubelskiego na lata 2007-2013 Spis teści Diagnoza sytuacji
Analiza obecnej sytuacji Miasta Lublin według kluczowych elementów Pzedmiot zamówienia ealizowany w amach Regionalnego Pogamu Opeacyjnego Województwa Lubelskiego na lata 2007-2013 Spis teści Diagnoza sytuacji
PODSTAWOWE POJĘCIA OPTYMALIZACJI [M. Ostwald: Podstawy optymalizacji konstrukcji, Wyd. Politechniki Poznańskiej, 2005]
![PODSTAWOWE POJĘCIA OPTYMALIZACJI [M. Ostwald: Podstawy optymalizacji konstrukcji, Wyd. Politechniki Poznańskiej, 2005] PODSTAWOWE POJĘCIA OPTYMALIZACJI [M. Ostwald: Podstawy optymalizacji konstrukcji, Wyd. Politechniki Poznańskiej, 2005]](/thumbs/63/49371066.jpg) PODSTAWOWE POJĘCIA OPTYMALIZACJI [M. Ostwald: Podstaw optmalizacji konstrukcji, Wd. Politechniki Poznańskiej, 2005] POW Problem optmalnego wboru PWOW Problem wielokrterialnego wboru OW Optmalizacja wielokrterialna
PODSTAWOWE POJĘCIA OPTYMALIZACJI [M. Ostwald: Podstaw optmalizacji konstrukcji, Wd. Politechniki Poznańskiej, 2005] POW Problem optmalnego wboru PWOW Problem wielokrterialnego wboru OW Optmalizacja wielokrterialna
Całkowanie przez podstawianie i dwa zadania
 Całkowanie przez podstawianie i dwa zadania Antoni Kościelski Funkcje dwóch zmiennch i podstawianie Dla funkcji dwóch zmiennch zachodzi następując wzór na całkowanie przez podstawianie: f(x(a, b), (a,
Całkowanie przez podstawianie i dwa zadania Antoni Kościelski Funkcje dwóch zmiennch i podstawianie Dla funkcji dwóch zmiennch zachodzi następując wzór na całkowanie przez podstawianie: f(x(a, b), (a,
Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony
 Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
Wykład: praca siły, pojęcie energii potencjalnej. Zasada zachowania energii.
 Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
Wykład: paca siły, pojęcie enegii potencjalnej. Zasada zachowania enegii. Uwaga: Obazki w tym steszczeniu znajdują się stonie www: http://www.whfeeman.com/tiple/content /instucto/inde.htm Pytanie: Co to
DOLNOŚLĄSKA WOJEWÓDZKA KOMENDA OCHOTNICZYCH HUFCÓW PRACY
 DOLNOŚLĄSKA WOJEWÓDZKA KOMENDA OCHOTNICZYCH HUFCÓW PRACY - Wocław, Wybzeże J. Słowackiego 9 tel. (7) --7, -9-8 e-mail: dolnoslaska@ohp.pl fax (7) -9- N konta: NBP O/Wocław 9 7 9 88 N egon: 78 NIP: 89---9
DOLNOŚLĄSKA WOJEWÓDZKA KOMENDA OCHOTNICZYCH HUFCÓW PRACY - Wocław, Wybzeże J. Słowackiego 9 tel. (7) --7, -9-8 e-mail: dolnoslaska@ohp.pl fax (7) -9- N konta: NBP O/Wocław 9 7 9 88 N egon: 78 NIP: 89---9
Założenia prognostyczne WPF
 Załącznik nr 3 do Uchwał o Wieloletniej Prognozie Finansowej Założenia prognostczne WPF Wieloletnia Prognoza Finansowa opiera się na długoterminowej prognozie nadwżki operacjnej, która obrazują zdolność
Załącznik nr 3 do Uchwał o Wieloletniej Prognozie Finansowej Założenia prognostczne WPF Wieloletnia Prognoza Finansowa opiera się na długoterminowej prognozie nadwżki operacjnej, która obrazują zdolność
Mikroekonomia II Semestr Letni 2014/2015 Ćwiczenia 4, 5 & 6. Technologia
 Mikroekonomia II 050-792 Semestr Letni 204/205 Ćwiczenia 4, 5 & 6 Technologia. Izokwanta produkcji to krzywa obrazująca różne kombinacje nakładu czynników produkcji, które przynoszą taki sam zysk. P/F
Mikroekonomia II 050-792 Semestr Letni 204/205 Ćwiczenia 4, 5 & 6 Technologia. Izokwanta produkcji to krzywa obrazująca różne kombinacje nakładu czynników produkcji, które przynoszą taki sam zysk. P/F
F : R 0;1 rozkład prawdopodobieństwa stopy zwrotu.
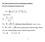 Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek
 Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Fizyka 3. Janusz Andrzejewski
 Fizka 3 Ruch ciała Oaz się obaca Cegła się pzesuwa 6 meów Cz ważne jes o, ab opócz faku pzesunięcia się cegł uwzględnić eż obó cegł? Punk maeialn Punk maeialn-ciało, kóego ozmia i kszał w danm zagadnieniu
Fizka 3 Ruch ciała Oaz się obaca Cegła się pzesuwa 6 meów Cz ważne jes o, ab opócz faku pzesunięcia się cegł uwzględnić eż obó cegł? Punk maeialn Punk maeialn-ciało, kóego ozmia i kszał w danm zagadnieniu
PROJEKT Umowa sprzedaży węgla energetycznego dla ciepłowni w Sokółce. 1 Przedmiot Umowy
 PROJEKT Umowa spzedaży węgla enegetycznego dla ciepłowni w Sokółce zawata w dniu. w Skażysku-Kamiennej pomiędzy: 1. Pomec Spółka z o.o. z siedzibą w Skażysku-Kamiennej, pod adesem: ul. 11 Listopada 7,
PROJEKT Umowa spzedaży węgla enegetycznego dla ciepłowni w Sokółce zawata w dniu. w Skażysku-Kamiennej pomiędzy: 1. Pomec Spółka z o.o. z siedzibą w Skażysku-Kamiennej, pod adesem: ul. 11 Listopada 7,
Cykl III ćwiczenie 3. Temat: Badanie układów logicznych
 Ckl III ćwiczenie Temat: Badanie układów logicznch Ćwiczenie składa się z dwóch podtematów: Poziom TTL układów logicznch oraz Snteza układów kombinacjnch Podtemat: Poziom TTL układów logicznch. Wprowadzenie
Ckl III ćwiczenie Temat: Badanie układów logicznch Ćwiczenie składa się z dwóch podtematów: Poziom TTL układów logicznch oraz Snteza układów kombinacjnch Podtemat: Poziom TTL układów logicznch. Wprowadzenie
INSTRUKCJA DO ĆWICZENIA
 NSTRKJA DO ĆWZENA Temat: Rezonans w obwodach elektycznych el ćwiczenia elem ćwiczenia jest doświadczalne spawdzenie podstawowych właściwości szeegowych i ównoległych ezonansowych obwodów elektycznych.
NSTRKJA DO ĆWZENA Temat: Rezonans w obwodach elektycznych el ćwiczenia elem ćwiczenia jest doświadczalne spawdzenie podstawowych właściwości szeegowych i ównoległych ezonansowych obwodów elektycznych.
KOLOKACJA SYSTEMÓW BEZPRZEWODOWYCH NA OBIEKTACH MOBILNYCH
 KOLOKACJA SYSTEMÓW BEZPRZEWODOWYCH NA OBIEKTACH MOBILNYCH Janusz ROMANIK, Kzysztof KOSMOWSKI, Edwad GOLAN, Adam KRAŚNIEWSKI Zakład Radiokomunikacji i Walki Elektonicznej Wojskowy Instytut Łączności 05-30
KOLOKACJA SYSTEMÓW BEZPRZEWODOWYCH NA OBIEKTACH MOBILNYCH Janusz ROMANIK, Kzysztof KOSMOWSKI, Edwad GOLAN, Adam KRAŚNIEWSKI Zakład Radiokomunikacji i Walki Elektonicznej Wojskowy Instytut Łączności 05-30
Stanisław Cichocki. Natalia Nehrebecka. Zajęcia 1-2
 Stanisław Cichocki Natalia Nehreecka Zajęcia - . Model liniow Postać modelu liniowego Zapis macierzow modelu liniowego. Estmacja modelu Przkład Wartość teoretczna (dopasowana) Reszt 3. MNK - przpadek wielu
Stanisław Cichocki Natalia Nehreecka Zajęcia - . Model liniow Postać modelu liniowego Zapis macierzow modelu liniowego. Estmacja modelu Przkład Wartość teoretczna (dopasowana) Reszt 3. MNK - przpadek wielu
Elektroenergetyczne sieci rozdzielcze SIECI 2004 V Konferencja Naukowo-Techniczna
 Elektoenegetyczne sieci ozdzielcze SIECI 2004 V Konfeencja Naukowo-Techniczna Politechnika Wocławska Instytut Enegoelektyki Andzej SOWA Jaosław WIATER Politechnika Białostocka, 15-353 Białystok, ul. Wiejska
Elektoenegetyczne sieci ozdzielcze SIECI 2004 V Konfeencja Naukowo-Techniczna Politechnika Wocławska Instytut Enegoelektyki Andzej SOWA Jaosław WIATER Politechnika Białostocka, 15-353 Białystok, ul. Wiejska
STANDARDY EMISJI ZANIECZYSZCZEŃ DO POWIETRZA Z PROCESÓW ENERGETYCZNEGO SPALANIA PALIW ANALIZA ZMIAN
 STANISŁAW KIRSEK, JOANNA STUDENCKA STANDARDY EMISJI ZANIECZYSZCZEŃ DO POWIETRZA Z PROCESÓW ENERGETYCZNEGO SPALANIA PALIW ANALIZA ZMIAN THE STANDARDS OF AIR POLLUTION EMISSION FROM THE FUELS COMBUSTION
STANISŁAW KIRSEK, JOANNA STUDENCKA STANDARDY EMISJI ZANIECZYSZCZEŃ DO POWIETRZA Z PROCESÓW ENERGETYCZNEGO SPALANIA PALIW ANALIZA ZMIAN THE STANDARDS OF AIR POLLUTION EMISSION FROM THE FUELS COMBUSTION
2 Przykład C2a C /BRANCH C. <-I--><Flux><Name><Rmag> TRANSFORMER RTop_A RRRRRRLLLLLLUUUUUU 1 P1_B P2_B 2 S1_B SD_B 3 SD_B S2_B
 PRZYKŁAD A Utwozyć model sieci z dwuuzwojeniowym, tójfazowym tansfomatoem 110/0kV. Model powinien zapewnić symulację zwać wewnętznych oaz zadawanie watości początkowych indukcji w poszczególnych fazach.
PRZYKŁAD A Utwozyć model sieci z dwuuzwojeniowym, tójfazowym tansfomatoem 110/0kV. Model powinien zapewnić symulację zwać wewnętznych oaz zadawanie watości początkowych indukcji w poszczególnych fazach.
Ćwiczenie 9 ZASTOSOWANIE ŻYROSKOPÓW W NAWIGACJI
 9.1. Cel ćwiczenia Ćwiczenie 9 ZASTSWANIE ŻYRSKPÓW W NAWIGACJI Celem ćwiczenia jest pezentacja paktycznego wykozystania efektu żyoskopowego w lotniczych pzyządach nawigacyjnych. 9.2. Wpowadzenie Żyoskopy
9.1. Cel ćwiczenia Ćwiczenie 9 ZASTSWANIE ŻYRSKPÓW W NAWIGACJI Celem ćwiczenia jest pezentacja paktycznego wykozystania efektu żyoskopowego w lotniczych pzyządach nawigacyjnych. 9.2. Wpowadzenie Żyoskopy
Przedziały ufności i testy parametrów. Przedziały ufności dla średniej odpowiedzi. Interwały prognoz (dla przyszłych obserwacji)
 Wkład 1: Prosta regresja liniowa Statstczn model regresji liniowej Dane dla prostej regresji liniowej Przedział ufności i test parametrów Przedział ufności dla średniej odpowiedzi Interwał prognoz (dla
Wkład 1: Prosta regresja liniowa Statstczn model regresji liniowej Dane dla prostej regresji liniowej Przedział ufności i test parametrów Przedział ufności dla średniej odpowiedzi Interwał prognoz (dla
Rozwiązywanie belek prostych i przegubowych wyznaczanie reakcji i wykresów sił przekrojowych 6
 ozwiązwanie beek prostch i przegubowch wznaczanie reakcji i wkresów sił przekrojowch 6 Obciążenie beki mogą stanowić sił skupione, moment skupione oraz obciążenia ciągłe q rs. 6.. s. 6. rzed przstąpieniem
ozwiązwanie beek prostch i przegubowch wznaczanie reakcji i wkresów sił przekrojowch 6 Obciążenie beki mogą stanowić sił skupione, moment skupione oraz obciążenia ciągłe q rs. 6.. s. 6. rzed przstąpieniem
25. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU. y +y tgx=sinx
 5. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU 5.1. Pojęcia wstępne. Klasfikacja równań i rozwiązań Rozróżniam dwa zasadnicze tp równań różniczkowch: równania różniczkowe zwczajne i równania różniczkowe cząstkowe.
5. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU 5.1. Pojęcia wstępne. Klasfikacja równań i rozwiązań Rozróżniam dwa zasadnicze tp równań różniczkowch: równania różniczkowe zwczajne i równania różniczkowe cząstkowe.
Raport dotyczący wskazania branż podstawowych i wspierających rozwój miasta Lublin
 Rapot dotyczący wskazania banż podstawowych i wspieających ozwój miasta Lublin Pzedmiot zamówienia ealizowany w amach Regionalnego Pogamu Opeacyjnego Województwa Lubelskiego na lata 2007-2013 Spis teści
Rapot dotyczący wskazania banż podstawowych i wspieających ozwój miasta Lublin Pzedmiot zamówienia ealizowany w amach Regionalnego Pogamu Opeacyjnego Województwa Lubelskiego na lata 2007-2013 Spis teści
Wykład 17. 13 Półprzewodniki
 Wykład 17 13 Półpzewodniki 13.1 Rodzaje półpzewodników 13.2 Złącze typu n-p 14 Pole magnetyczne 14.1 Podstawowe infomacje doświadczalne 14.2 Pąd elektyczny jako źódło pola magnetycznego Reinhad Kulessa
Wykład 17 13 Półpzewodniki 13.1 Rodzaje półpzewodników 13.2 Złącze typu n-p 14 Pole magnetyczne 14.1 Podstawowe infomacje doświadczalne 14.2 Pąd elektyczny jako źódło pola magnetycznego Reinhad Kulessa
WYKORZYSTANIE TRÓJSEKTOROWEGO MODELU WZROSTU DO ANALIZY WPŁYWU OGRANICZENIA EMISJI GHG NA WYBÓR TECHNOLOGII PRODUKCJI.
 Zeszyy Naukowe Wydziału nfomaycznych Technik Zaządzania Wyższej Szkoły nfomayki Sosowanej i Zaządzania Współczesne Poblemy Zaządzania N /2009 WYKORZYSTANE TRÓJSEKTOROWEGO ODELU WZROSTU DO ANALZY WPŁYWU
Zeszyy Naukowe Wydziału nfomaycznych Technik Zaządzania Wyższej Szkoły nfomayki Sosowanej i Zaządzania Współczesne Poblemy Zaządzania N /2009 WYKORZYSTANE TRÓJSEKTOROWEGO ODELU WZROSTU DO ANALZY WPŁYWU
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI
 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
Zależność natężenia oświetlenia od odległości
 Zależność natężenia oświetlenia CELE Badanie zależności natężenia oświetlenia powiezchni wytwazanego pzez żaówkę od niej. Uzyskane dane są analizowane w kategoiach paw fotometii (tzw. pawa odwotnych kwadatów
Zależność natężenia oświetlenia CELE Badanie zależności natężenia oświetlenia powiezchni wytwazanego pzez żaówkę od niej. Uzyskane dane są analizowane w kategoiach paw fotometii (tzw. pawa odwotnych kwadatów
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ.
 ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
ĆWICZENIE 4. PODSTAWY OPTYKI FALOWEJ. GENERACJA I ANALIZA ELEMENTARNYCH FRONTÓW FALOWYCH
 ĆWICZENIE 4. PODSTAWY OPTYKI FALOWEJ. GENERACJA I ANALIZA ELEMENTARNYCH FRONTÓW FALOWYCH Wstęp teoetczn Font falow Światło jest falą elektomagnetczną, zatem związana jest z nią funkcja Ψ (,t, opisująca
ĆWICZENIE 4. PODSTAWY OPTYKI FALOWEJ. GENERACJA I ANALIZA ELEMENTARNYCH FRONTÓW FALOWYCH Wstęp teoetczn Font falow Światło jest falą elektomagnetczną, zatem związana jest z nią funkcja Ψ (,t, opisująca
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
LINIOWA MECHANIKA PĘKANIA
 odstawowe infomacje nt. LNOWA MECHANA ĘANA Wytzymałość mateiałów J. Geman OLE NARĘŻEŃ W LNOWO SRĘŻYSTYM OŚRODU ZE SZCZELNĄ oe napężeń w dwuwymiaowym ośodku iniowo-spężystym ze szczeiną zostało wyznaczone
odstawowe infomacje nt. LNOWA MECHANA ĘANA Wytzymałość mateiałów J. Geman OLE NARĘŻEŃ W LNOWO SRĘŻYSTYM OŚRODU ZE SZCZELNĄ oe napężeń w dwuwymiaowym ośodku iniowo-spężystym ze szczeiną zostało wyznaczone
1. Ciało sztywne, na które nie działa moment siły pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym.
 Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
Wykład 3. Zasada zachowania momentu pędu. Dynamika punktu mateialnego i były sztywnej. Ruch obotowy i postępowy Większość ciał w pzyodzie to nie punkty mateialne ale ozciągłe ciała sztywne tj. obiekty,
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
Rodzajowy rachunek kosztów Wycena zuŝycia materiałów
 Rodzajowy achunek kosztów (wycena zuŝycia mateiałów) Wycena zuŝycia mateiałów ZuŜycie mateiałów moŝe być miezone, wyceniane, dokumentowane i ewidencjonowane w óŝny sposób. Stosowane metody wywieają jednak
Rodzajowy achunek kosztów (wycena zuŝycia mateiałów) Wycena zuŝycia mateiałów ZuŜycie mateiałów moŝe być miezone, wyceniane, dokumentowane i ewidencjonowane w óŝny sposób. Stosowane metody wywieają jednak
Metodyka obliczeń wartości parametrów technicznoekonomicznych
 Metodyka obliczeń watości paametów technicznoekonomicznych Wesja: 1.1 Konstancin-Jeziona, siepień 2018. Histoia aktualizacji Data Fima Wesja Opis zmiany 24.08.2018 PSE S.A. 1.0 Publikacja dokumentu 28.08.2018
Metodyka obliczeń watości paametów technicznoekonomicznych Wesja: 1.1 Konstancin-Jeziona, siepień 2018. Histoia aktualizacji Data Fima Wesja Opis zmiany 24.08.2018 PSE S.A. 1.0 Publikacja dokumentu 28.08.2018
= ± Ne N - liczba całkowita.
 POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
Coba, Mexico, August 2015
 Coba, Meico, August 015 W-6 (Jaosewic) 10 sladów Pola siłowe i ich chaaktestka Pola siłowe: poęcie i odae pól siłowch, wielkości chaakteuące pola siłowe Pola achowawce Pole gawitacne: uch w polu gawitacnm
Coba, Meico, August 015 W-6 (Jaosewic) 10 sladów Pola siłowe i ich chaaktestka Pola siłowe: poęcie i odae pól siłowch, wielkości chaakteuące pola siłowe Pola achowawce Pole gawitacne: uch w polu gawitacnm
Spis treści. Rozdział 1 Charakterystyka i klasyfikacja instrumentów finansowych. Ryzyko w działalności przedsiębiorstwa
 Spis teści Wstęp.......................................... 7 Rozdział 1 Chaakteystyka i klasyfikacja instumentów finansowych. Ryzyko w działalności pzedsiębiostwa 1.1. Istota instumentów finansowych........................
Spis teści Wstęp.......................................... 7 Rozdział 1 Chaakteystyka i klasyfikacja instumentów finansowych. Ryzyko w działalności pzedsiębiostwa 1.1. Istota instumentów finansowych........................
00502 Podstawy kinematyki D Część 2 Iloczyn wektorowy i skalarny. Wektorowy opis ruchu. Względność ruchu. Prędkość w ruchu prostoliniowym.
 1 00502 Kinematyka D Dane osobowe właściciela akusza 00502 Podstawy kinematyki D Część 2 Iloczyn wektoowy i skalany. Wektoowy opis uchu. Względność uchu. Pędkość w uchu postoliniowym. Instukcja dla zdającego
1 00502 Kinematyka D Dane osobowe właściciela akusza 00502 Podstawy kinematyki D Część 2 Iloczyn wektoowy i skalany. Wektoowy opis uchu. Względność uchu. Pędkość w uchu postoliniowym. Instukcja dla zdającego
