Równanie falowe. elektro magnetyczne) równanie falowe (dla struny) u(x,t) x=p. x=l. T 2 (II zasada Newtona F=ma) x+dx. x T 1

Transkrypt

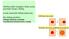
1 Równanie falowe Równanie dyfuzji oraz dyfuzji adwekcji typowe paraboliczne Dziś zajmiemy się typowym równaniem hiperbolicznym równanie falowe (dla struny) (opisuje dążenie do równowagi). (oscylacje: mechaniczne, elektryczne, elektro magnetyczne) x=l u(x,t) x=p x+dx β T 2 (II zasada Newtona F=ma) α x T siła naciągu struny T (kierunek poziomy):

2 Równanie dyfuzji oraz dyfuzji adwekcji typowe paraboliczne Dziś zajmiemy się typowym równaniem hiperbolicznym równanie falowe (dla struny) (dążenie do równowagi). (oscylacje) x=l u(x,t) x=p x+dx β uwaga: α x T 2 T dx 0 (prędkość rozchodzenia się drgań) 2

3 c stałe: Ogólne rozwiązanie dla nieskończonego ośrodka (d Alamberta) dowolna funkcja drgania rozchodzące się bez zmiany kształtu [brak dyspersji w równaniu falowym] Liniowość równania: zasada superpozycji 3

4 Liniowość równania i zasada superpozycji: Sygnały rozchodzą się niezależnie od siebie F=exp( (x 0.5+ct) ( 2 ) +exp( (x+0.5 ct) 2 ) t x Sygnały mijają się bez zmiany kształtu [(jedna fala przenika drugą.] ponieważ równanie liniowe: jeśli wskażemy bazę zupełną funkcji ze znaną ewolucją czasową = problem rozwiązany baza: mody normalne (fale stojące) (drgania własne) 4

5 baza: mody normalne (fale stojące) (drgania własne) Dwupunktowe warunki brzegowe u(0,t)=u(l,t)=0 x=l x=0 x0 Poszukajmy rozwiązań, w których tylko amplituda (a nie kształt fali) nie zależy od czasu: u(x,t)=x(x)t(t) t0 t=0 t=t2 t=t3 t=t T(t)=cos(ω t+φ)= C cos(ω t)+d sin(ω t) [gdy gęstość struny zmienna c może być funkcją położenia] 5

6 Równanie na część przestrzenną fal stojących (drania własne, drgania normalne) Dla c niezależnego od x: X n () (x)=sin(ki (k n x) k liczba cbafalowa, a, wektor falowy k = 2π/ λ tutaj λ długość fali k=ω / c WB: spełnione, gdy X(0)=X(L)=0 k n =nπ /L Fale stojące: Między warunkami brzegowymi całkowita liczba połówek długości fal.. 0 L 6

7 warunki brzegowe: kwantyzacja k kwantyzacja w X n (x)=sin(k n x), T n =sin(w n t), cos(w n t) T k n =nπ /L k=ω / c ω n =ck n T oznacza naciąg struny przestrzenne drgania własne nie zależą od c, ale częstości tak. Wiemy, że niższe tony dają struny o większej grubości [ ρ ]. Wiemy również, ż że im silniej struna naciągnięta tym wyższy dźwięk. 7

8 Drgania własne dla zmiennej gęstości struny W przypadku ogólnym [c=c(x)] przyda się rachunek numeryczny. Wyliczyć X n oraz ω n ρ(x) Dyskretyzujemy drugą pochodną, liczymy X n (x+dx) 8

9 Równanie własne z warunkami brzegowymi: Metoda strzałów. w parametr równania ω dokładna wartość własna w=ω w<ω w>ω w X 0 wstawić warunek brzegowy ale co wstawić za X?? (dla równania Poissona opisywanego dla metody Numerowa to był poważny problem) dla drgań własnych wstawiamy cokolwiek (równanie własne jest jednorodne rozwiązania określone co do stałej multiplikatywnej ) 9

10 Test metody dla ρ(x)= (L=, T 0 =) Analityczne: k n =nπ /L X k=k k k=.5π/l k =0.5π/L k= 0.66 =k =π/l 6 π/l X (L L) 80 Miejsca zerowe wartości własne przy których funkcje własne 40 spełniają prawy warunek brzegowy 0 L k=k 2 =2π/L x x ω / π 0

11 Przykład: ρ(x)=+4α(x /2) 2 (struna cięższa przy mocowaniach) X X 4 π ω / X α=500 X 3-0 x α α=0 częstości ę własne równoodległe Częstości własne maleją z α (cięższa struna) duże α częstości grupują się w pary W każdej parze: funkcja parzysta i nieparzysta. Środek struny prawie nieważki, na częstości wpływ ma kształt funkcji przy brzegach a tam zbliżony dla każdej funkcji z pary

12 Drgania własne a ogólne rozwiązania równania falowego Równanie ogólne: Warunki początkowe: u(x,t=0) oraz v(x,t=0)=du/dt Zadać wychylenie i prędkości rozłożyć ł ż ć warunki początkowe na drgania własneł problem zależności czasowych jest rozwiązany 2

13 Drgania normalne a ogólne rozwiązania równania falowego Równanie ogólne: Warunki początkowe: u(x,t=0) oraz v(x,t=0)=du/dt Zadać wychylenie i prędkości ę rozłożyć warunki początkowe na drgania własne problem zależności czasowych jest rozwiązany w chwili t=0, za kształt struny odpowiadają współczynniki c n a za prędkość współczynniki s n 3

14 Superpozycja drgań własnych: Warunki początkowe Uwaga: dla równań dyfuzji i adwekcji warunek początkowy był tylko jeden czasowy rząd równania był =. Dla równania drugiego rzędu w czasie, wartość u(x,t=0) nie wystarczy dla jednoznacznego określenia rozwiązania. dla drgań własnych jednorodnej struny: Dyskretna sinusowa transformata Fouriera 4

15 rozkład na mody normalne na przedziale (0,L) Rozwinięcie w szereg Fouriera: g(x) = okresowa, odcinkowo ciągła z okresem T: Rozkład na drgania normalne a szereg Fouriera: drgania podległe warunkom brzegowym g(0)=g(l)=0. dla naszego problemu L to długość struny i nie ma interpretacji okresu (na strunie mieści się połowa długości fali). 5

16 6 Warunki Dirichleta zbieżności szeregu Fouriera Rozwinięcie Fouriera zbieżne w sensie jednorodnym N o ile g(x) ) całkowalna w kwadracie 2) odcinkowo ciągła rozwinięcie Fouriera dąży do g(x) prawie wszędzie tzn. poza punktami dyskretnymi punktami (rozwinięcie Fouriera jest wszędzie ciągłe!) Twierdzenie Dirichleta: W punktach nieciągłości szereg Fouriera zbieżny do g(x)=[ g(x 0)+g(x+0) ] / 2 tw. Dirichleta nie rozwiązuje wszystkich problemów

17 7 dla struny: pewien praktyczny problem z kanciastymi (nieróżniczkowalnymi) warunkami początkowymi. π 0 π Fala prostokątna ą W punkcie nieciągłości = [g(0 )+g(0+) ]/2 = ( + ) / 2 =0

18 Nd Nad nieciągłością i ł ś i wartość schodka przestrzelona o około 8% N=5 N=5 N=55 +2w ππ 0 π N=5 N=55 N=00 Zjawisko Gibbsa w= (stała Wibrahama Gibbsa) Na PC pracujemy ze skończonymi bazami: Równania różniczkowego przez rozkład warunku początkowego na drgania własne nie rozwiążemy dokładnie, jeśli ten jest nieciągły x 8

19 Na PC pracujemy ze skończonymi bazami... Zbieżność szeregu Fouriera w sensie bezwzględnym ę Szereg jest bezwzględnie zbieżny jeśli można go obciąć na pewnym wyrazie rozwinięcia: Rozwinięcie fali prostokątnej nie jest bezwzględnie zbieżne: 2 g(x) - schodkowa, bn Bo ogólny szereg harmoniczny jest rozbieżny 0 h(x)=exp(-x 2 ), a n Wniosek: w skończonej bazie funkcji własnych możemy rozwiązywać tylko problemy z warunkiem początkowym, 0 kó którego rozwinięcie w szereg Fouriera jest bezwzględnie zbieżne n 9

20 równanie falowe ciąg dalszy metoda różnic skończonych, zamiast rozkładu na drgania własne (który może być wolnozbieżny) Rozwiązanie numeryczne: dzielimy strunę na N fragmentów, dla każdego z nich rozwiązujemy równania Newtona (zabieg odwrotny do wyprowadzenia równania różniczkowego) v(x,t) - prędkość u(x,t) - wychylenie z równania falowego: 20

21 2 Schemat Verleta (popularny dla symulacji dynamiki molekularnej) m F V Schemat Verleta Phys. Rev. 59, 98 (967) Pomysł: rozwinąć położenie r w chwili t+δt i t-δt w szereg Taylora tylko o jeden rząd mniej dokładny niż RK4

22 Schemat Verleta Jeśli chodzi nam tylko o tor ruchu: świetny schemat. Nie używa prędkości, ale ta często potrzebna potrzebna: np do wyliczenia energii, ale również : sił (np. oporu, Lorentza) jeśli siły niezależne od prędkości, a informacja o nich potrzebna jest do innych celów można - wykonać krok do t+δt, a potem rządbłędu wyższy, wciąż dokładnie dla ruchu jednostajnie przyspieszonego a stałe między ę t a Δt jeśli siły zależą od prędkości: nie wykonamy kroku do t+δt, możemy co najwyżej: kiepsko: wynik dokładny tylko dla a=0 22

23 23 prędkościowa wersja schematu Verleta (dający ypę prędkości jednocześnie z położeniami) Położenia poświęcamy jeden rząd dokładności: Potrzebny przepis na prędkość w chwili t + Δtzbłędem z O(Δt 2 ): Rozwinąć r w Taylora względem punktu t+ Δt: Dodać stronami: (wzór potencjalnie niejawny) Wzory podkreślone na czerwono Verlet prędkościowy.

24 24 Verlet prędkościowy Inny (popularny) zapis wzorów w czerwonej ramce uwaga: jeśli siły (przyspieszenia) zależą od prędkości ostatnie równanie jest niejawne

25 Rozwiązania numeryczne. (laboratorium) L= u(x,t=0)=exp[-00(x-0.5)2] v(x,t=0)=0 u(x,t) (,) x 0.0 t=0 0.5 t=0.4 t=0. 2 t 3 Odbicie ze zmianą fazy (idzie górą, wraca dołem) t= v(x t) v(x,t) x x u(x,t) t

26 26 Rozwiązanie numeryczne 2. Swobodne warunki brzegowe: na brzegach na strunę nie działa żadna siła pionowa: Może się swobodnie przesuwać po mocowaniu Warunek brzegowy Neumana (na pochodną) zamiast Dirichleta (na wartość funkcji).00 Odbicie bez zmiany fazy: idzie górą, górą wraca 0.80 u u v x

27 energia drgania: kinetyczna Potencjalna: odkształcenie struny Dla ρ(x)=ρ( ) Dla pojedynczego modu własnego ω=kc T 0 =ρc 2 Kinetyczna na potencjalną się zmienia, całkowita zachowana 27

28 Analiza chwilowa drgania Rozwiązując równanie falowe schematem Verleta można z zależności czasowych wydobyć częstości własne bez konieczności rozwiązywania równania własnego Gdy drgania tłumione - częstość przestrzenna modów własnych nie ulega zmianie (zobaczymy), ale czasowa tak. Analiza chwilowa drgania na podstawie wychylenia zależności położeniowych = wychylenia g(x) i prędkości h(x) w danej chwili. 28

29 Równanie fali tłumionej a >0 = stała ł tłumienia i c niezależna od położenia Opory związane z prędkością struny [np. powietrza] Warunki brzegowe u(x=0,t)=u(x=l,t)=0 Warunki początkowe u(x,t) oraz v(x,t). Mody normalne dla fali tłumionej: Poszukajmy rozwiązania metodą separacji zmiennych u(x,t)=x(x)t(t) część przestrzenna bez zmian! X n (x)=sin(k n x) k n =nπ /L k=ω /c 29

30 30 Część przestrzenna: wstawiamy T=exp(rt), równanie charakterystyczne: exp(rt) [ r 2 +2ar+w n2 ] = 0, szukamy rozwiązań ą na r możliwe przypadki: 2 pierwiastki rzeczywiste, jeden podwójny, obydwa zespolone Warunki początkowe: Struna spoczywa w chwili początkowej Rozwiązanie określone co do stałej multiplikatywnej (równanie jednorodne)

31 ω n = ncπ /L L=, c=, ω n = nπ Drganie Słabe tłumienie a<ω a=8, ω i ω2 = przetłumione pozostałe tłumione a=0.5 a=0.2.0 z ω 0.8 n= 0.5 T (t) Poza zanikiem drgania widzimy zmniejszenie częstości T (t) Najpierw zgasną wyższe tłumienia 3

32 32 Rozwiązanie równania fali tłumionej rozwiązanie ogólne: Położeniowa ł ż analiza Fourierowska -rozkład na mody normalne w danej chwili : c n (t) = część przestrzenna nie zmienia się pod wpływem tłumienia. aby wydobyć c n : drugie równanie w ogólności ś wydzielimy przez ω n, podniesiemy zależne od czasu w kwadracie i dodamy

33 udział względny: x t Przykład: L= E=K+P K+P(kinetyczna+potencjalna) t W chwili początkowej pakiet f(x,t=0)=exp(-00(x-0.5) 2 ) a=0.5 a=2 a=4 a= ene ergia P 8 4 E K a= t Spadek E najszybszy gdy K największe

34 a= n= c n t Parzyste n nie wnoszą przyczynku (symetria) a=0.5 2 c n r n n= ω n =nπ n= t t Wszystkie mody tłumione równie silnie oscylujący y udział modów normalnych im wyższe ω n tym bardziej stały względny udział 34

35 a= n= a= n= 2 r n r n t a=4, większe tylko od ω r n n= t a=2 większe od ω i ω 3 2 r n t n= t 35

36 Laboratorium: R. hiperboliczne z niejednorodnością: Drgania tłumione z siłą wymuszającą F Siła przyłożona punktowo niejednorodność wymuszenie periodycznie zmienne 36

37 Dla t=0 struna spoczywa (v(x,t)=0)w położeniu równowagi (u(x,t)=0) Prędkość dźwięku = Siła przyłożona w środku struny x0=/2 u(x,t) ( ) a= w=0.5π pojawia się stan ustalony = drgania periodyczne. aa= w=2π x a=3 w=2π czas W stanie t i ustalonym t l ruchh jest j t periodyczny i d z okresem k siły wymuszającej (mode locking). 37

38 Stan ustalony a energia struny Średnia energia w stanie ustalonym: Siła przyłożona w środku struny x 0 =/2 Rezonans a= Brakuje w 2n?? Dlaczego? <E> w / pi 38

39 Stan ustalony a energia struny Średnia energia w stanie ustalonym: Siła przyłożona w środku struny x 0 =/2 Rezonans n= a= n=2 <E> Brakuje w 2n?? W środku studni = węzeł dla parzystych n w / pi 39

40 mody z parzystym n wzbudzone gdy punkt przyłożenia przesunąć ą ze środka a= x = <E> Krzywa rezonansowa w przybliżeniu opisana przez sumę funkcji Lorentza x = w / pi Siła sprzężenia = kwadrat wartości modu normalnego w miejscu przyłożenia siły: 40

41 Średnie energie stanu ustalonego a wzory lorentowskie a= a= a= <E> <E> <E> x = w / pi x = w / pi x 0 = w / pi <E E> a= a=.5 a=2 a=3 a=4 Rezonans a stała tłumienia w / pi 4

42 Laboratorium 2: odbicie pakietu od granicy ośrodków ρ 0 = V= położenie 0.5 V= czas

43 V= ρ 0 =2 ρ 0 = położenie ρ 0 = ρ 0 = czas 43

44 Część energii, która pozostaje po lżejszej stronie struny ρ= po odbiciu ρ 0 =2 44

45 Domena zależności (Domain of Dependence) i kryterium stabilności CFL (Courant-Friedrichs-Lewy) t x domena zależności: tylko zdarzenia z trójkąta ograniczonego charakterystykami mogą mieć wpływ na rozwiązanie w punkcie P 45

46 Numeryczna domena zależności [NUMERYCZNA PRZESZŁOŚĆ] kryterium stabilności CFL (Courant-Friedrichs-Lewy) schemat Verleta dla przyspieszenia danego przez prawą stronę równania: czas położenie 46

47 47 kryterium stabilności CFL (Courant-Friedrichs-Lewy) numeryczna dokładna warunek: jak dla adwekcji aby przekroczyć ć kryterium CFL (prędkość dźwięku): schematy niejawne ne dla równań mechaniki standardowy schemat niejawny = schemat Newmarka (dlaczego Crank-Nicolson się nie stosuje?)

48 algorytm Newmarka (uogólnienie prędkościowego Verleta, standardowy chemat niejawny dla równań opisujących układy dynamiczne) w Verlecie prędkościowym używamy przepisów: z γ=/2 u(t+dt)=u(t)+v(t)dt+dt 2 /2 a(t) v(t+dt)=v(t)+dt [(-γ)a(t)+γa(t+dt)] Czyli: w Verlecie: jawna formuła na położenie, potencjalnie niejawna na prędkość ta nie wystarczy dla bezwzględnej stabilności przy kroku czasowym cdt>dx (zobaczymy analizą v.neumanna) dla Newmarka: wprowadzamy niejawność (ważenie przyspieszeń z teraźniejszości i przyszłości) również do wzoru na położenia: u(t+dt)=u(t)+v(t)dt+dt 2 /2 [(-2β)a(t)+2βa(t+dt)] algorytm prędkościowy Newmarka źródło: WJT DANIEL, computational mechanics 20 (997) 272 zróbmy z tego formułę położeniową: bez prędkości, za to dwupoziomową (t+dt) względem t, t-dt wyeliminować prędkości : 48

49 u(t+dt)=u(t)+v(t)dt+dt 2 /2 [(-2β)a(t)+2βa(t+dt)] (*) v(t+dt)=v(t)+dt [(-γ)a(t)+γa(t+dt)] dla kroku poprzedniego= u(t)=u(t-dt)+v(t-dt)dt+dt 2 /2 [(-2β)a(t-dt)+2βa(t)] dla kroku poprzedniego = v(t)=v(t-dt)+dt [(-γ)a(t-dt)+γa(t)] u(t)=u(t-dt)+v(t)dt+dt 2 /2 [(-2β)a(t-dt)+2βa(t)]-dt 2 [(-γ)a(t-dt)+γa(t)] u(t)=u(t-dt)+v(t)dt+dt 2 /2 [(2γ-2β )a(t-dt)+(2β 2γ)a(t)] u(t-dt)=u(t)-v(t)dt-dt 2 /2 [(2γ-2β )a(t-dt)+(2β 2γ)a(t)] (*) dodamy stronami gwiazdki aby usunąć prędkość ze schematu 49

50 u(t+dt)=u(t)+v(t)dt+dt 2 /2 [(-2β)a(t)+2βa(t+dt)] + stronami u(t-dt)=u(t)-v(t)dt+dt 2 /2 [(-2γ+2β+)a(t-dt)+(2γ 2β)a(t)] skasujemy prędkość u(t-dt)+u(t+dt)=2u(t) +dt 2 /2[2βa(t+dt)+(-4β+2γ)a(t)+(-2γ+2β+)a(t-dt)] u(t+dt)=2u(t) -u(t-dt)+dt 2 [βa(t+dt)+(/2-2β+γ)a(t)+(-γ+β+/2)a(t-dt)] dla porównania Verlet położeniowy algorytm Newmark = wersja położeniowa, dwa parametry γβ γ,β wagi przy przyspieszeniu: β+/2 2β+γ γ+β+/2= (wszystkie wybory dają schemat, który w granicy małego dt redukuje się do Verleta) Newmark sprowadza się do Verleta gdy γ=/2, β=0 (maks dokładność lkl lokalny błąd czwartego rzędu) d) rola γ, β zobaczymy jak się sprawdzają w praktyce 50

51 u(t+dt)=2u(t) -u(t-dt)+dt 2 [βa(t+dt)+(/2-2β+γ)a(t)+(-γ+β+/2)a(t-dt)] u(t+dt)=2u(t) -u(t-dt)+dt 2 [βa(t+dt)+αa(t)+δa(t-dt)] jak wykonać krok czasowy? sposób rozwiązywania zależy od wyrażanie na a dla struny: Po przegrupowaniu wyrazów: układ równań liniowych z macierzą trójprzekątniową stencil: 5

52 dokładny schemat Newmark MRS, struna dt=dx 0 węzłów Verlet (β=0, γ=/2) (β=/2, γ=/2) (β=/2, γ=) β=.9 γ=/2 czas położenie dla dt=dx najlepszy wybór β=0, γ=/2 (jawny, Verlet) 52

53 dla dt=dx najlepszy wybór β=0, γ=/2 (jawny, Verlet) Verlet dla dt=dx* widzimy eksplozję rozwiązania z maksymalną malną zmiennością przestrzenną: Newmark jest po to aby przekroczyć kryterium CFL 53

54 rola γ (dt=.5dx, β=0.5) γ= węzłów MRS: schemat Newmark rola parametrów metody β>0 wynosi stabilność poza kryterium CFL, kosztem generacji wyższych częstości przestrzennych γ>/2 ogranicza wzmacnianie wyższych częstości kosztem dyssypacji (zaniku całego pakietu) γ</2 schemat jest niestabilny zostawmy γ=/2 (jak dla Verleta) i manipulujmy β 54

55 0 węzłów MRS poza CFL: dt > cdx dt=.5dx, γ=0.5, schemat staje się stabilny dla β>0.5 b 5 b=.5 b 2 b=.2 b 25 b= b= rosnące beta generuje wyższe częstości wniosek: najlepszy minimalne β przy którym schemat jeszcze stabilny czy można je wyznaczyć analitycznie?

56 Projektowanie schematu Newmarka dla zadanego kroku czasowego. dobrać minimalne β aby metoda była stabilna dla danego dt? Będziemy wiedzieli, że po wyższe β nie warto sięgać. analiza von Neumanna dla γ=/2 u(t+dt)=2u(t) (t) -u(t-dt)+dt 2 [βa(t+dt)+(/2-2β+γ)a(t)+(-γ+β+/2)a(t-dt)] 2β+ )(t)+( +β+/2) (tdt)] u(t+dt)-dt 2 βa(t+dt) =2u(t) -u(t-dt)+dt 2 [(-2β)a(t)+βa(t-dt)] Ansatz von Neumanna: 56

57 Sytuacja będzie taka: dopóki Δ<0 : 2 pierwiastki, o module nie większym od gdy Δ>0 metoda stanie się niestabilna 57

58 -2<c<0 zawsze żeby b pod pierwiastkiem i liczba ujemna potrzeba aby: λ 2 <? daje ten sam wynik β>/4 metoda stabilna dla dowolnego t [ ponieważ c < 0] uwaga: możemy sobie teraz sprawdzić stabilność Verleta dla dt=dx oraz beta=0, ¼+/(2c) <0 [ok.] 58

59 dobór beta zapewniającego stabilność schematu Newmark w MRS dla zadanego kroku czasowego dt=.5dx β c 59

60 dobór beta zapewniającego stabilność schematu Newmark w MRS dla zadanego kroku czasowego / / dt=dx dt=5dx c

61 2.00 struna, b. wiele chwil czasowych dt=5dx.00 β=.25 MRS, Newmark, γ=/ dt=5dx β=.24 bo beta była zbyt mała: Ze schematem Newmarka spotkamy się ponownie przy omawianiu MES, Pokażemy, że umożliwia on skuteczne prowadzenie Rachunków dla lokalnie zagęszczonej siatki