Automatyka i robotyka
|
|
|
- Robert Wieczorek
- 6 lat temu
- Przeglądów:
Transkrypt
1 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43
2 Plan wykładu Wprowadzenie Stabilność modeli stanowych Uchyb w stanie ustalonym Dobór struktury i parametrów regulatora 2 z 43
3 Plan wykładu Wprowadzenie Stabilność modeli stanowych Uchyb w stanie ustalonym Dobór struktury i parametrów regulatora 2 z 43
4 Plan wykładu Wprowadzenie Stabilność modeli stanowych Uchyb w stanie ustalonym Dobór struktury i parametrów regulatora 2 z 43
5 Plan wykładu Wprowadzenie Stabilność modeli stanowych Uchyb w stanie ustalonym Dobór struktury i parametrów regulatora 2 z 43
6 Stabilność a niestabilność Fakty Najważniejszy problem do rozwiązania dla układów regulacji automatycznej. W układach z zamkniętą pętlą sprzężenia zwrotnego musimy szczególnie dbać o stabilność Nie możemy określić wymagań jakościowych regulacji dla układów niestabilnych Nie wiemy do jak określić wartość wyjścia układu niestabilnego w stanie ustalonym 3 z 43
7 Stabilność układów Odpowiedź układu na wymuszenie y(t) = y wymuszona (t) + y naturalna (t) Dla układów liniowych Odpowiedź naturalna zawsze dąży do zera dla t gdy układ jest stabilny. Odpowiedź naturalna zawsze rośnie (bez ograniczenia) dla t gdy układ jest niestabilny. Odpowiedź naturalna nie rośnie ani nie maleje lub oscyluje dla t gdy układ jest na granicy stabilności. 4 z 43
8 Stabilność układów dynamicznych Warunek konieczny stabilności Równanie charakterystyczne dla G(s) = L(s) M(s) M(s)= n i=1 Można pokazać, że a i s i =a n s n +a n 1 s n a 1 s 1 + a 0 = 0 układ jest stabilny a i > 0 i lub a i < 0 i (czyli współczynniki maja te same znaki) układ jest na granicy stabilności gdy a 0 = 0 5 z 43
9 Stabilność układów dynamicznych Warunek konieczny stabilności a) M(s) = s 5 + 5s 4 + 3s 3 2s 2 + s + 8 = 0 warunek konieczny nie jest spełniony (a 2 < 0) b) M(s) = s 5 + 5s 4 + 3s 3 + 2s = 0 warunek konieczny nie jest spełniony (a 1 = 0) c) M(s) = s 5 + 5s 4 + 3s 3 + 2s 2 + s = 0 warunek konieczny nie jest spełniony (a 0 = 0 - na granicy stabilności) d) M(s) = s 5 5s 4 3s 3 2s 2 s 8 = 0 warunek konieczny jest spełniony (a i < 0 i) 6 z 43
10 Stabilność układów dynamicznych Kryterium Routh a W celu sprawdzenia stabilności korzystamy z algebraicznego warunku Routh a efektywna (tj. szybka) metoda sprawdzenia stabilności bazujemy tylko na współczynnikach wielomianu charakterystycznego. wyznaczamy liczbę biegunów w lewej (prawej) półpłaszczyźnie ale nie ich dokładne położenie ma szerokie zastosowanie jeśli mamy wyznaczyć regiony stabilności (kiedy współczynniki są parametrami o nieznanych wartościach) 7 z 43
11 Stabilność układów dynamicznych Kryterium Routh a (1877) Wielomian charakterystyczny M(s) = 1 i=n a n s n = 0 0 s n a n a n 2 a n 4 a n 6 1 s n 1 a n 1 a n 3 a n 5 a n 7 2 s n 2 b 1 b 2 b 3 b 4 3 s n 3 c 1 c 2 c 3 c 4 8 z n-1 s 1 y 1 y 2 n s 0 z 1 b 1 = (a na n 3 a n 1 a n 2 ) a 1 b 2 = (a na n 5 a n 1 a n 4 ) a 1,... c 1 = (a n 1b 2 b 1 a n 3 ) b 1 c 2 = (a n 1b 3 b 1 a n 5 ) b 1,...
12 Stabilność układów dynamicznych Kryterium Routh a - przykład 1 Sprawdzić stabilność układu, którego wielomian charakterystyczny to Tablica Routh a M(s) = s 4 + s 3 + s 2 + 2s + 3 = 0 0 s s s s s 0 3 Wniosek: Dwukrotna zmiana znaku w pierwszej kolumnie = dwa bieguny w prawej półpłaszczyźnie (istotnie, bieguny to ± j0.706 i ± j1.219) 9 z 43
13 Stabilność układów dynamicznych Kryterium Routh a - przykład 2 Sprawdzić stabilność układu regulacji, gdzie regulatorem jest regulator proporcjonalny, a transmitancja obiektu regulacji to G(s) = L(s) M(s) = s + 1 Transmitancja układu zamkniętego to G cl (s) = a wielomian charakterystyczny to 1513 (s s ) KG(s) 1 + KG(s) 1 + KG(s)= s s s K =0 Czyli badamy stabilność w odniesieniu do wartości parametru K 10 z 43
14 Stabilność układów dynamicznych Kryterium Routh a - przykład 2 Tworzymy odpowiednią tablice Routh a 0 s s K 2 s K 0 3 s K 0 Układ będzie stabilny dla K > 0 i K < 89.85/10.86 K < z 43
15 Stabilność układów dynamicznych Kryterium Routh a Przypadek szczególny Pojawienie sie wartości 0 w pierwszej kolumnie oznacza niestabilność lub w najlepszym przypadku układ na granicy stabilności. Dalsze tworzenie tabeli jest niemożliwe ponieważ wymagane będzie dzielenie przez 0 - musimy poszukać alternatywnego rozwiązania W przypadku wystąpienia wartości 0 w pierwszej kolumnie dokonuje my wprowadzenia symbolu δ 0 aby kontynuować sprawdzanie zmian znaków 12 z 43
16 Stabilność układów dynamicznych Kryterium Routh a - przykład 3 Sprawdź stabilność układu, którego wielomian charakterystyczny to M(s) = s 5 + 2s 4 + 2s 3 + 4s 2 + s + 1 = 0 Zaczynamy oczywiście od tworzenia tablicy Routh a 0 s s s Mamy w pierwszej kolumnie wartość 0 - zastępujemy ją nową zmienną δ z 43
17 Stabilność układów dynamicznych Kryterium Routh a - przykład 3 Podstawiamy δ i tworzymy dalej tablice Routh a 0 s s s 3 δ s 2-1/δ 1 4 s s 0 1 Ostatecznie mamy dwie zmiany znaku czyli układ jest niestabilny (istotnie, bieguny układu to: 0.09 ± j0.533, ± j1.274 i 1.957). 14 z 43
18 Stabilność układów dynamicznych Kryterium Routh a Przypadek szczególny Pojawienie się wartości 0 w całym wierszu oznacza istnienie dzielnika wielomianu, którego pierwiastki są symetryczne w odniesieniu do początku układu współrzędnych. Pierwiastki wielomianu to s = ±σ lub s = ±jβ lub σ ± jβ i σ ± jβ Dzielnikiem wielomianu będzie F (s) wzięty z pierwszego niezerowego wiersza powyżej wiersza zerowego. Współczynniki które wpiszemy w wiersz zerowy uzupełniamy z wyrażenia df (s) ds 15 z 43
19 Stabilność układów dynamicznych Kryterium Routh a - przykład 4 Dany jest układ regulacji, gdzie regulatorem jest regulator proporcjonalny, czyli transmitancja układu otwartego to G ol (s) = KG(s) = K 1 s(s + 1)(s 2 + s + 1) Znajdź wartość K dla której układ po zamknięciu pętli sprzężenia zwrotnego będzie na granicy stabilności i wyznacz pulsacje oscylacji. Wielomian charakterystyczny układu zamkniętego to M(s) = s 4 + 2s 3 + 2s 2 + s + K = 0 16 z 43
20 Stabilność układów dynamicznych Kryterium Routh a - przykład 4 Tworzymy odpowiednią tablice Routh a 0 s K 1 s s K 3 s 1 1-4K/3 Dla K = 0.75 w wierszu 3 mamy 0. Oznacza to, że dzielnikiem wielomianu charakterystycznego będzie (pobrany z wiersza nr 2) F (s) = 3 2 s = 0 F (s) = 2s2 + 1 = 0 17 z 43
21 Stabilność układów dynamicznych Kryterium Routh a - przykład 4 Równanie charakterystyczne to M(s) = (2s 2 + 1)(0.5s 2 + s ) i uzupełniamy tablicę Routh a gdzie 3 wiersz wypełniamy współczynnikami df (s)/ds i otrzymujemy (dla K = 0.75) 0 s s s s s z 43
22 Stabilność układów dynamicznych Kryterium Routh a - przykład 4 Poza wierszem 3 nie ma zmian znaków ani elementów o wartości 0 - nie ma pierwiastków w prawej półpłaszczyźnie. Pierwiastki muszą leżeć na osi urojonej (dla K = 0.75). Wartość pulsacji odnajdziemy gdy s = jω czyli ω = 1 2 [rad/sec] F (jω) = 2ω = 0 19 z 43
23 Stabilność modeli stanowych Modele w przestrzeni stanów Wartości własne macierzy A to bieguny układu, które wyznaczamy tak det(si A) = 0 Lokalizacje biegunów możemy wyznaczyć numerycznie (polecenie eig(a) w Matlab ie) Możemy wykorzystać tabele Routh a sprawdzając położenie pierwiastków wielomianu det(si A) 20 z 43
24 Przykład Rozważmy następujący układ ẋ(t) = x(t) u(t) gdzie (si A) = y(t) = [ ] x(t) s s s = s s s + 2 i dlatego det(si A) = s 3 6s 2 7s z 43
25 Przykład Tworzymy tabelę Routh a s s s s Układ niestabilny (jedna zmiana w pierwszej kolumnie - jeden biegun w prawej półpłaszczyźnie) 22 z 43
26 Śledzenie sygnału referencyjnego R(s) E(s) U(s) Y(s) - C(s) G(s) Problem: Jak układ zamknięty śledzi zadany sygnał referencyjny? Podstawowe sygnały referencyjne R(s) = 1 s r(t) = 1(t) (pozycja) R(s) = 1 r(t) = t (prędkość) s 2 R(s) = 1 s 3 r(t) = t2 2 (przyspieszenie) 23 z 43
27 Uchyb w stanie ustalonym R(s) E(s) U(s) Y(s) - C(s) G(s) E(s) = Uchyb w stanie ustalonym 1 R(s) gdzie L(s) = G(s)C(s) 1 + L(s) s s e ss = lim se(s) = lim R(s) = lim s 0 s L(s) s L(s) 1 s k 24 z 43
28 Uchyb w stanie ustalonym Definicja Uchyb w stanie ustalonym to błąd po zaniku odpowiedzi przejściowej Układ otwarty Układ zamknięty E(s) = R(s) Y (s) = (1 G o (s))r(s) E(s) = R(s) Y (s) = G o (s) - transmitancja układu otwartego G o (s) R(s) 25 z 43
29 Uchyb w stanie ustalonym Twierdzenie o wartości końcowej Uchyb w stanie ustalonym wyzanczamy z pomocą twierdzenia o wartości końcowej Przykład dla R(s) = A s Układ otwarty e ss = lim s 0 s(1 G o (s)) Układ zamknięty 26 z 43 e ss = lim s 0 s e ss = lim t e(t) = lim s 0 se(s) (skok jednostkowy) ( ( ) A = lim A(1 G o (s))=a(1 G o (0)) s s 0 )( ) 1 A = 1+G o (s) s A 1+G o (0)
30 Uchyb w stanie ustalonym Przypadek ogólny (dla skoku jednostkowego) Własności: G o (s) = K M i=1 (s + z i) s N Q k=1 (s + p k) Bład ustalony zależy od liczby układów całkujacych N, Dla N > 0 G o (0) i e ss 0, N oznacza typ układu, dla N = 0 1 e ss = 1 + G o (0) = 1 ( ) 1 + K M i=1 (s + z i)/ Q k=1 (s + p k) 27 z 43
31 Uchyb w stanie ustalonym Zdefiniujmy stałą uchybu pozycyjnego i wtedy Łatwo też sprawdzić, że dla N 1 K p = lim s 0 (G o (s)) e ss = K p e ss = lim ( ) 1 + K M i=1 (s + z i)/s N Q k=1 (s + p k) s 0 1 = lim s 0 s N ( ) = 0 s N + K M i=1 (s + z i)/ Q k=1 (s + p k) 28 z 43
32 Uchyb w stanie ustalonym Dla sygnału referencyjnego r(t) = A t 1(t) (funkcja liniowo narastająca - prędkość) s(a/s 2 ) e ss = lim s G(s) = lim A s 0 s + sg(s) A = lim s 0 sg(s) 29 z 43
33 Uchyb w stanie ustalonym Stała uchybu prędkościowego Zdefiniujmy stałą uchybu prędkościowego i wtedy dla N = 1 Oznacza to, że dla N 2 to e ss = 0 dla N = 1 to e ss 0 dla N = 0 to e ss = 30 z 43 K v = lim s 0 s(g(s)) A e ss = ( = K M i=1 (s + z i)/ Q k=1 k)) A (s + p K v
34 Uchyb w stanie ustalonym Dla sygnału referencyjnego r(t) = A t 2 /2 1(t) (funkcja paraboliczna - przyspieszenie) s(a/s 3 ) e ss = lim s G(s) = lim A s 0 s 2 G(s) 31 z 43
35 Uchyb w stanie ustalonym Stała uchybu przyspieszeniowego Zdefiniujmy stałą uchybu przyspieszeniowego i wtedy dla N = 2 Oznacza to, że dla N 3 to e ss = 0 dla N = 2 to e ss 0 dla N = 1 to e ss = dla N = 0 to e ss = 32 z 43 K a = lim s 0 s 2 (G 0 (s)) A e ss = ( = K M i=1 (s + z i)/ Q k=1 k)) A (s + p K a
36 Uchyb w stanie ustalonym Przykład 1 Zadanie Wyznacz uchyb w stanie ustalonym w układzie zamkniętym po podaniu sygnału zadanego o postaci funkcji r(t) = 5t1(t). Transmitancja układu otwartego to 10(s + 1) G o (s) = s(s + 2)(s + 5) Wyznaczamy Transformatę Laplace a sygnału r(t) Transmitancję układu zamkniętego 33 z 43 G z (s) = R(s) = 5 s 2 G o 10s + 1 = 1 + G o s 3 + 7s s + 10
37 Uchyb w stanie ustalonym Przykład 1 Obliczenia: Stała uchybu prędkościowego K v = lim s 0 (sg o (s)) = lim Uchyb w stanie ustalonym s 0 s 10(s + 1) s(s + 2)(s + 5) = 1 e ss = A K v = 5 1 = 5 34 z 43
38 Sterowanie proporcjonalne (P) d(t) r(t) e(t) - P u(t) Obiekt y(t) Regulator: statyczny współczynnik wzmocnienia K p u(t) = K p e(t) = K p (r(t) y(t)) 35 z 43
39 Sterowanie proporcjonalne (P) Obiekt (przykład): G(s) = K s(s+a) Regulator proporcjonalny: C(s) = K p Bieguny układu zamkniętego: rozwiązanie równania czyli 1 + KK p s(s + a) = 0 s 2 + as + KK p = 0 Wniosek: K p ma niewielki(!!!) wpływ na położenie biegunów 36 z 43
40 Sterowanie proporcjonalno-różniczkujące (PD) d(t) r(t) e(t) - PD u(t) Obiekt y(t) Regulator: dynamika regulatora: u(t) = K p e(t) + K d de(t) dt Problem: Dobór współczynników wzmocnienia K p i K d 37 z 43
41 Sterowanie proporcjonalno-różniczkujące (PD) Obiekt (przykład): G(s) = K s(s+a) Regulator proporcjonalny: C(s) = K p + K d s Bieguny układu zamkniętego: rozwiązanie równania czyli 1 + K(K p + K d s) s(s + a) = 0 s 2 + (a + KK d )s + KK p = 0 Wniosek: K p i K d dokładnie określają wszystkie położenia biegunów układu 2-ego rzędu (i tylko takiego!) 38 z 43
42 Sterowanie proporcjonalno-całkująco-różniczkujące (PID) d(t) r(t) e(t) - PID u(t) Obiekt y(t) Regulator: dynamika regulatora u(t) = K p e(t) + K i t 0 e(τ)dτ + K d de(t) dt Problem: Dobór współczynników wzmocnienia K p, K i i K d 39 z 43
43 Kiedy używamy akcji całkującej? eliminacja uchybu regulacji podwyższenie rzędu układu otwartego Przykład Układ otwarty: L(s) = G(s)K p = KK p τs+1 Sygnał referencyjny: R(s) = 1 s Wymaganie: brak uchybu czyli e ss = 0 Wniosek: Uchyb w stanie ustalonym 0 - trzeba użyć regulatora PI 40 z 43
44 Wpływ akcji całkującej Obiekt (przykład): y(t) + bẏ = u(t) (Y (s) + bsy (s) = U(s)) Regulator typu P: u(t) = K p (r(t) y(t)) Równanie układu zamkniętego: y(t) + bẏ = K p r(t) K p y(t) Y (s) + bsy (s) = K p R(s) K p Y (s) Stan ustalony (ẏ = 0) y(t) = K p 1 + K p y(t) r(t) (dlak p 1) Wniosek: Uchyb w stanie ustalonym 0 41 z 43
45 Regulator PI Obiekt (przykład): y(t) + bẏ = u(t) (Y (s) + bsy (s) = U(s)) Regulator typu PI: u(t) = K p (r(t) y(t)) + K t i 0 (r(τ) y(τ))dτ Równanie układu zamkniętego: Stan ustalony (ẏ = 0, ÿ = 0) ẏ + bÿ = K i r(t) K p ẏ K i y(t) 0 = K i r(t) K i y(t) y(t) = r(t) Wniosek:Brak uchybu w stanie ustalonym! 42 z 43
46 Wpływ parametrów regulatora PID K p przyspieszenie odpowiedzi ale i większe oscylacje K d zmniejszenie oscylacji ale większa wrażliwość na szumy K i usuwa błąd w stanie ustalonym ale zwiększa przeregulowanie Dobór parametrów regulatora PID Eksperymentalny dobór parametrów K p, K d, K i (często wspomagany komputerowo). Analiza i synteza z użyciem modelu obiektu (procesu). 43 z 43
Inżynieria Systemów Dynamicznych (5)
 Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Automatyka i robotyka
 Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Projektowanie układów regulacji w dziedzinie częstotliwości. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Techniki regulacji automatycznej
 Techniki regulacji automatycznej Metoda linii pierwiastkowych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 25 Plan wykładu Podstawy metody linii pierwiastkowych
Techniki regulacji automatycznej Metoda linii pierwiastkowych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 25 Plan wykładu Podstawy metody linii pierwiastkowych
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Automatyka i robotyka
 Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
PAiTM. materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż.
 PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Stabilność. Krzysztof Patan
 Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Badanie stabilności liniowych układów sterowania
 Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Automatyka i robotyka ETP2005L. Laboratorium semestr zimowy
 Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
układu otwartego na płaszczyźnie zmiennej zespolonej. Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:
 Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Kompensator PID. 1 sω z 1 ω. G cm. aby nie zmienić częstotliwości odcięcia f L. =G c0. s =G cm. G c. f c. /10=500 Hz aby nie zmniejszyć zapasu fazy
 Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ. T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
 REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Podstawy Automatyki. Wykład 2 - modelowanie matematyczne układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Podstawy Automatyki. Wykład 6 - Miejsce i rola regulatora w układzie regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Obiekt. Obiekt sterowania obiekt, który realizuje proces (zaplanowany).
 SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
Plan wykładu. Własności statyczne i dynamiczne elementów automatyki:
 Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Kompensacja wyprzedzająca i opóźniająca fazę. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Automatyka i sterowanie w gazownictwie. Regulatory w układach regulacji
 Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 1 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 30 Plan wykładu Podstawowe informacje Modele układów elektrycznych
Technika regulacji automatycznej Wykład 1 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 30 Plan wykładu Podstawowe informacje Modele układów elektrycznych
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa.
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Inżynieria Systemów Dynamicznych (4)
 Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Wprowadzenie do technik regulacji automatycznej. prof nzw. dr hab. inż. Krzysztof Patan
 Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Podstawy Automatyki. Wykład 2 - modelowanie matematyczne układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Analiza ustalonego punktu pracy dla układu zamkniętego
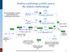 Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
Podstawy Automatyki. Wykład 2 - matematyczne modelowanie układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - matematyczne modelowanie układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - matematyczne modelowanie układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie. Sterowanie ciągłe. Teoria sterowania układów jednowymiarowych
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Podstawy środowiska Matlab
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
Regulator P (proporcjonalny)
 Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Badanie wpływu parametrów korektora na własności dynamiczne układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Automatyzacji
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Badanie wpływu parametrów korektora na własności dynamiczne układu regulacji Ćwiczenia Laboratoryjne Podstawy Automatyki i Automatyzacji mgr inż.
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Badanie wpływu parametrów korektora na własności dynamiczne układu regulacji Ćwiczenia Laboratoryjne Podstawy Automatyki i Automatyzacji mgr inż.
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
SIMATIC S Regulator PID w sterowaniu procesami. dr inż. Damian Cetnarowicz. Plan wykładu. I n t e l i g e n t n e s y s t e m y z e
 Plan wykładu I n t e l i g e n t n e s y s t e m y z e s p r zężeniem wizyjnym wykład 6 Sterownik PID o Wprowadzenie o Wiadomości podstawowe o Implementacja w S7-1200 SIMATIC S7-1200 Regulator PID w sterowaniu
Plan wykładu I n t e l i g e n t n e s y s t e m y z e s p r zężeniem wizyjnym wykład 6 Sterownik PID o Wprowadzenie o Wiadomości podstawowe o Implementacja w S7-1200 SIMATIC S7-1200 Regulator PID w sterowaniu
Dobór parametrów regulatora - symulacja komputerowa. Najprostszy układ automatycznej regulacji można przedstawić za pomocą
 Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Systemy. Krzysztof Patan
 Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji
 Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
Automatyzacja. Ćwiczenie 9. Transformata Laplace a sygnałów w układach automatycznej regulacji
 Automatyzacja Ćwiczenie 9 Transformata Laplace a sygnałów w układach automatycznej regulacji Rodzaje elementów w układach automatyki Blok: prostokąt ze strzałkami reprezentującymi jego sygnał wejściowy
Automatyzacja Ćwiczenie 9 Transformata Laplace a sygnałów w układach automatycznej regulacji Rodzaje elementów w układach automatyki Blok: prostokąt ze strzałkami reprezentującymi jego sygnał wejściowy
3. WRAŻLIWOŚĆ I BŁĄD USTALONY. Podstawowe wzory. Wrażliwość Wrażliwość transmitancji względem parametru. parametry nominalne
 3. WRAŻLIWOŚĆ I BŁĄD USTALONY Podstawowe wzory Wrażliwość Wrażliwość transmitancji względem parametru (3.1a) parametry nominalne (3.1b) Wrażliwość układu zamkniętego (3.2a) (3.2b) Uwaga. Dla Zmiana odpowiedzi
3. WRAŻLIWOŚĆ I BŁĄD USTALONY Podstawowe wzory Wrażliwość Wrażliwość transmitancji względem parametru (3.1a) parametry nominalne (3.1b) Wrażliwość układu zamkniętego (3.2a) (3.2b) Uwaga. Dla Zmiana odpowiedzi
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
Wydział Fizyki i Informatyki Stosowanej
 Wydział Fizyki i Informatyki Stosowanej Podstawy inżynierii sterowania Ćwiczenia laboratoryjne Laboratorium 3: Regulacja ciągła dr inż. Dominika Gołuńska dr inż. Szymon Łukasik 1. Regulatory ciągłe liniowe.
Wydział Fizyki i Informatyki Stosowanej Podstawy inżynierii sterowania Ćwiczenia laboratoryjne Laboratorium 3: Regulacja ciągła dr inż. Dominika Gołuńska dr inż. Szymon Łukasik 1. Regulatory ciągłe liniowe.
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ
 REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ 1 1. Zadania regulatorów w układach regulacji automatycznej Do podstawowych zadań regulatorów w układach regulacji automatycznej należą: porównywanie wartości
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ 1 1. Zadania regulatorów w układach regulacji automatycznej Do podstawowych zadań regulatorów w układach regulacji automatycznej należą: porównywanie wartości
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
LINIOWE UKŁADY DYSKRETNE
 LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
Języki Modelowania i Symulacji
 Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Sterowanie w programie ADAMS regulator PID. Przemysław Sperzyński
 Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie. Sterowanie ciągłe. Teoria sterowania układów jednowymiarowych
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
KRYTERIA ALGEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH
 KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
I. KARTA PRZEDMIOTU CEL PRZEDMIOTU
 I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: SYSTEMY DYNAMICZNE 2. Kod przedmiotu: Esd 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Techniki Komputerowe
I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: SYSTEMY DYNAMICZNE 2. Kod przedmiotu: Esd 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Techniki Komputerowe
Realizacja regulatorów analogowych za pomocą wzmacniaczy operacyjnych. Instytut Automatyki PŁ
 ealizacja regulatorów analogowych za pomocą wzmacniaczy operacyjnych W6-7/ Podstawowe układy pracy wzmacniacza operacyjnego Prezentowane schematy podstawowych układów ze wzmacniaczem operacyjnym zostały
ealizacja regulatorów analogowych za pomocą wzmacniaczy operacyjnych W6-7/ Podstawowe układy pracy wzmacniacza operacyjnego Prezentowane schematy podstawowych układów ze wzmacniaczem operacyjnym zostały
Korekcja układów regulacji
 Korekcja układów regulacji Powszechnym sposobem wpływania na jakość procesów regulacji jest wprowadzenie urządzeń (członów) korekcyjnych. W przeważającej większości przypadków niezbędne jest umieszczenie
Korekcja układów regulacji Powszechnym sposobem wpływania na jakość procesów regulacji jest wprowadzenie urządzeń (członów) korekcyjnych. W przeważającej większości przypadków niezbędne jest umieszczenie
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
( 1+ s 1)( 1+ s 2)( 1+ s 3)
 Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
Stabilność II Metody Lapunowa badania stabilności
 Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Podstawy Automatyki. Wykład 4 - algebra schematów blokowych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
Opis systemów dynamicznych w przestrzeni stanu. Wojciech Kurek , Gdańsk
 Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT. Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA
 AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA II rok Kierunek Transport Temat: Transmitancja operatorowa. Badanie odpowiedzi układów automatyki. Opracował
AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA II rok Kierunek Transport Temat: Transmitancja operatorowa. Badanie odpowiedzi układów automatyki. Opracował
