Matematyczne aspekty modelowania paj czynowego obiektów
|
|
|
- Natalia Beata Wrona
- 7 lat temu
- Przeglądów:
Transkrypt
1 BIULETY ISTYTUTU SYSTEÓW IFORATYCZYCH 4-8 (009) atematycze aspekty modelowaia pajczyowego obiektów A. AELJACZYK Istytut Systemów Iformatyczych Wydzia Cyberetyki WAT ul. S. Kaliskiego, Warszawa W pracy omówioo moliwoci wykorzystaia tzw. metod modelowaia pajczyowego do modelowaia i aalizy jakociowej obiektów zooych w procesach eksploracji daych. Zdefiiowao takie pojcia jak: -wymiarowa przestrze pajczyowa, model pajczyowy obiektu, adekwato modelu oraz iektóre charakterystyki eksploracyje modelu. Sowa kluczowe: eksploracja daych, matematyczy model obiektu, modelowaie pajczyowe, model pajczyowy obiektu, model -dokady, dokado modelu, adekwato modelu.. Wprowadzeie atematycze modele obiektów (systemów) su ajczciej aalizom jakociowym i porówawczym. og by te podstaw budowy modeli optymalizacyjych jak rówie podstaw defiiowaia fukcji rakigowych [], [3]. Formale modele opisowe zalazy te due zastosowaia w procesach i metodach eksploracji daych [5], [6], [7]. Obszarem szczególie iteresujcym z tego puktu widzeia jest modelowaie i aaliza daych medyczych, modelowaie stau zdrowia pacjeta i tzw. jedostek chorobowych, wykorzystywae w komputerowych systemach wspomagaia decyzji medyczych [], [3], [9]. W procesie modelowaia matematyczego obiektów bardzo wa rol odgrywa cel modelowaia [4], [5]. Z celu modelowaia wyikaj przede wszystkim wymogi dotyczce kokretego, formalego jzyka modelowaia oraz wymagaa dokado (adekwato) modelu. Dyspoujc orygiaem obiektu o azwie x, w zaleoci od celu modelowaia, moemy zbudowa wiele róych modeli y F(x), tego samego obiektu. Zbiór azw modelowaych obiektów, a ogó jest utosamiae z pewym podzbiorem zbioru liczb aturalych. Zbiór jest wtedy zbiorem umerów obiektów. W szczególych przypadkach zbiór ie musi by skoczoym podzbiorem liczb aturalych. Takim przykadem moe by zbiór moliwych zestaw daych medyczych [], [3], [9]. odeloway obiekt x charakteryzuje si a ogó wieloma róymi cechami czstkowymi, które decyduj o jego globalych (systemowych) wasociach. Szczegóowo (adekwato) modelu jakkolwiek defiiowaa jest oczywicie fukcj liczby cech (wasoci), które zostay uwzgldioe w modelu. Im wicej cech uwzgldimy, tym a ogó model bdzie bardziej dokady (szczegóowy) i tym lepiej bdzie odzwierciedla orygia. Taki model zapewe bdzie jedak bardziej kosztowy, skomplikoway oraz bardziej iewygody do prowadzeia bada i aalizy. Problem ustaleia ile cech i które z ich aley wzi pod uwag jest oczywicie problemem wyboru odpowiediego kompromisu midzy dokadoci modelu a jego zoooci i kosztem. Ituicyjie moa zgodzi si z opii, e w kadym procesie modelowaia istieje pewa graicza liczba cech do uwzgldieia, powyej której, przy zadaym celu modelowaia przyrost jakoci modelu jest pomijalie may.. Uproszczoy model opisowy obiektu x Ozaczmy symbolem x pewie obiekt ze zbioru obiektów. Zaómy dalej, e obiekt te posiada maksymalie cech (wasoci), które mog mie zaczeie jeli chodzi o adekwato (jako) modelu obiektu x z puktu widzeia przyjtego celu modelowaia. Zaómy, e cechy wiadczce o jakoci obiektu s uporzdkowae wedug ich waoci, zgodie z porzdkiem aturalym. Oczywicie wielko liczby zaley od stopia zoooci obiektów ze zbioru co zapiszemy. Jeli przykadowo
2 A. Ameljaczyk, atematycze aspekty modelowaia pajczyowego obiektów elemetami zbioru bd proste obiekty p. rodzaje bloczków budowlaych, gatuki serów, itp. to maksymala liczba wyróioych cech moe siga kilku. Jeli bd to atomiast zooe urzdzeia elektroicze czy te zooe mechaizmy, to liczba cech siga moe przykadowo kilkuastu. W przypadku modelowaia bardzo zooych obiektów jak p. stau zdrowia pacjeta [3], [6] liczba ta moe siga kilkuset i wicej. Teoretyczie moemy rozpatrywa procesy modelowaia gdzie liczba. Symbolem ozaczymy zbiór {,,,,},...,m..., za symbolem zbiór. Okreleie.. odelem -dokadym obiektu x azwiemy model uwzgldiajcy tylko sporód, ajwaiejszych cech obiektu x. Okreleie.. odelem dokadym obiektu x azwiemy model uwzgldiajcy maksymal liczb cech wiadczcych o jego jakoci. Okreleie.3. Fukcj modelowaia opisowego azywa bdziemy fukcj F :, przyporzdkowujc kademu modelowaemu obiektowi x cig wartoci poszczególych jego cech. Tak wic modelem obiektu x bdzie jego obraz F xf ( x),.., F ( x),.., F ( x)) (.) day fukcj modelowaia F gdzie F ( x ) warto -tej cechy modelowaego obiektu x. Zaómy dalej, e dla kadego x w F ( ) w, x (.) Fakt te bdziemy zapisywa: y x F ( ) w, w,, x (.3) Cigi liczbowe y ( y,..., y,..., y ) Fx azywa te bdziemy daymi o obiektach x. iech przykadowo 5, 9. odelem dokadym obiektu x jest Fx,,,, 3, 4, 8, 7,, 5, 4, 3,, 0, 0 5 za modelem -dokadym 9 F x,,,, 3, 4, 8, 7, Zadaie matematyczego modelowaia opisowego obiektów x ze zbioru moemy formalie zapisa jako trójk uporzdkowa: ( Z 0,, F) (.4) Obraz zbioru Y zbioru bdzie zatem zbiorem modeli obiektów x. Y F( ) y F( x) x (.5) Klas rówowaoci (y) obiektów ze wzgldu a ustaloe wartoci cech yy azywamy przeciwobraz zbioru jedoelemetowego { y} Y { y} ( y) F x F( x) y (.6) Jeli w zbiorze klas rówowaoci ( y) yy, istieje przyajmiej jeda klasa o liczoci ( y), to zwikszeie iloci uwzgldiaych cech moe by przesak zwikszeia dokadoci modelowaia. Pojawia si tutaj iteresujcy problem okreleia takiej liczby ( o ile istieje), e dla kadego y Y, y 3. -wymiarowa przestrze pajczyowa Zaómy, e dae jest zadaie modelowaia opisowego: Z0 (,, F), którego wyikiem jest zbiór Y F( ) modeli opisowych obiektów x. oliwo iterpretacji graficzej (tzw. zobrazowaia ) takich modeli w celu aalizy ich wasoci jest jedak bardzo ograiczoa maksymalie do 3. O wiele wiksze moliwoci graficzej iterpretacji, a w kosekwecji aalizy i wydobywaia dodatkowej wiedzy z daych opisujcych modelowae obiekty daje tzw. modelowaie pajczyowe (web modellig). Okreleie 3.. -wymiarow, ograiczo przestrzei pajczyow azywa bdziemy par uporzdkowa Pr ( S r, ) gdzie S r jest pewym zbiorem wyzaczaym a paszczyie, p. w ukadzie wspórzdych bieguowych w astpujcy sposób: S r ( d, ) 0 d r, 0 (3.) Liczba r o zwaa jest promieiem (zakresem) przestrzei, za para ( d, ) to wspórzde
3 BIULETY ISTYTUTU SYSTEÓW IFORATYCZYCH 4-8 (009) puktu (elemetu) zbioru S r (d odlego od tzw. biegua, kt skieroway). W przypadku gdy r otrzymamy -wymiarow przestrze ieskoczo P( S, ). Osie wspórzdych 0x,,..., przestrzei pajczyowej moemy wyzaczy astpujco: ( 0x ( d, ) 0 d r,, (3.) a rys.. przedstawioa zostaa piciowymiarowa przestrze pajczyowa z zazaczo skal odlegoci (dla r 4 ) oraz picioma osiami wspórzdych 0 x,,, 3, 4, 5 0 (. ) x s s s d cos, s d si, ( ) 0 d r,, (3.5) Okreleie 3.. Fukcj modelowaia pajczyowego F P azywa bdziemy odwzorowaie typu: F P : Sr przyporzdkowujce kademu elemetowi y zbiór S (y) w postaci wieloboku o wierzchokach: A ( y) ( y, ), (3.6) Symboliczie fakt te zapiszemy: S ( y) A ( y),... A ( y) S r (3.7) Wierzchoki wieloboku S (y) le a poszczególych osiach wspórzdych przestrzei pajczyowej (patrz tzw. wykresy gwiazdowe [6], [7]). 3 Okreleie odelem pajczyowym obiektu y (a w kosekwecji obiektu x, takiego, e F( x) y ) azywa bdziemy zbiór S Okreleie 3.4. P y S ( y) F. r 4 Rys.. Piciowymiarowa przestrze pajczyowa o promieiu r = 4 Zbiór S r bywa czasami defiioway wprost jako koo o promieiu r w ukadzie wspórzdych kartezjaskich: S s r ( s s s, ) r (3.3) Zamieiajc wspórzde bieguowe a kartezjaskie otrzymamy: (, ) S r s s s d cos, s d si, 0 d r,0 (3.4) oraz osie wspórzdych: 5 Zadaiem modelowaia pajczyowego Z P azywa bdziemy trójk uporzdkowa (,, P Z P Pr F ). Wyikiem realizacji zadaia modelowaia pajczyowego jest zbiór P F ( ) P, którego elemetami s modele pajczyowe poszczególych obiektów y F( x), x y Sr P S ( ) y (3.8) Przykad. iech,, 3, 5. Fukcja modelowaia opisowego daa jest w tabeli. W tabeli tej zapisao rówie kracowe wartoci cech, w w,,, 3, 4, 5 Warto parametru r wyzaczamy astpujco: r max w 6 3
4 A. Ameljaczyk, atematycze aspekty modelowaia pajczyowego obiektów 4 3 C 3 Tabela. F(x) F ( x ) F ( x ) F 3( x ) F 4 ( x ) F 5 ( x ) w w Piciowymiarow przestrze z parame trem r 6 zdefiiujemy jako par uporzdkowa P6 ( S 6, 5), gdzie S 6( d, ) 0 d 6,0 a rys.. przedstawioo modele pajczyowe obiektów x{,, 3} 6 D Rys.. odele pajczyowe obiektów x a rysuku tym zazaczoo rówie modele sztuczych obiektów []: w ( w,..., w5) (,,,, ) oraz (,..., 5 w w w ) (3, 4, 6, 4, 5), Zauwamy, e S5( w ) S5( x) dla kadego x C C / D 4 D 3 E 4 oraz, e B B B 3 S5( w ) S5( 3) a poadto zachodzi S S5( w 5 ( x) ) S5(3) dla kadego x. odelami pajczyowymi obiektów x{,, 3} s odpowiedie zbiory S5( ), S5(), S5(3) A A A 3 E E S to astpujce wieloboki zazaczoe a rys..: S 5 A, B, C, D, E S 5 A, B, C, D, E S A, B, C, D, E odele obiektów sztuczych [], [] w i w staowi zbiory: S 5 w A, B, C, D, E (zbiór te zosta zakreskoway ). S 3, 3, 3, 3, 3 5 w A B C D E S53 Zbiory te staowi odpowiedio kres doly i kres góry zbioru Y P F P w przestrzei pajczyowej z relacj ikluzji []. Zauwamy, e modele S 5, S 5, S 53 rói si midzy sob ksztatem, polem powierzchi, wzajemym usytuowaiem, dugoci obwodu, liczb boków itp. w przestrzei P6 S 6,5. Takich dodatkowych charakterystyk modeli S x moe by wiele. Przykadowymi charakterystykami opisujcymi dodatkowe waciwoci S x s astpujce: ps x pole powierzchi zbioru S x gs x rodek cikoci zbioru S x bs dugo obwodu S x S x liczba boków (wieloboku) zbioru S x x miara kta wierzchokowego trójktów tworzcych zbiór S x itp. W przypadku ustaloych cigów zbiorów S x, x k, k,,... dodatkowymi charakterystykami mog by wzajeme usytuowaia elemetów cigów, wzajeme usytuowaie ich rodków cikoci, odlegoci rodków cikoci, czci wspóle zbiorów Sx, x k, relacje ikluzji, róica czy te suma zbiorów itp. Wszystkie te charakterystyki przy odpowiediej iterpretacji mog by bardzo cee z puktu widzeia aalizy jakociowej modelowaych obiektów jak te samego procesu modelowaia. Badaie tych charakterystyk pozwala bowiem wydoby wicej iformacji o obiektach x i wyika to wprost z ich formalych modeli opisowych y Fx, x (daych w postaci cigów liczb). Wprowadzajc dodatkowo tzw. gsto cech ( ciar
5 BIULETY ISTYTUTU SYSTEÓW IFORATYCZYCH 4-8 (009) x waciwy cech) w postaci moemy dokoywa aalizy jeszcze bardziej szczegóowej. W dalszej czci pracy, z racji ograiczoej jej objtoci zajmiemy si gówie S x ps x oraz charakterystyk ktow x charakterystyk modelu w postaci. Pole powierzchi zbioru S x jest pew fukcj daych opisowych obiektu x Fx y oraz liczby uwzgldioych cech. Dla ustaloych oraz x wartoci charakterystyki p S x moemy okreli astpujco: p S x yk yk y y k (3.9) gdzie si (3.0) za y k F kx, k,,..., Dodatkowe iformacje dotyczce zbioru modelowaych obiektów ios te jak wczeiej wspomiao charakterystyki zbiorów: S w i S w Odpowiedio pola powierzchi tych zbiorów okrelamy astpujco: p S w wk wk w w k (3.) w w p S w k w k w k (3.) odele S w oraz S w odgrywaj wa rol w aalizie jakociowej obiektów x, gdy zbiory te posiadaj astpujce ogóle wasoci: S w S x dla kadego x (3.3.) S x S w dla kadego x (3.4) a poadto x, x p S (3.5) Warto p S x zaley oczywicie od kolejoci uwzgldiaych cech, std te w przypadku braku zaoeia ustalajcego kolejo cech, stosowaa jest charakterystyka p S x bdca uredieiem pól powierzchi odpowiadajcych wszystkim moliwym kombiacjom uporzdkowa cech (!). 4. Zormalizowae przestrzeie pajczyowe iech FxF x,..., F x,... F x, fukcja modelowaia taka, e F : Y. O fukcji tej zaoymy, e F x 0,, x. Jeli by tak ie byo to aleaoby od wartoci fukcji F x odj odpowiedi liczb c dla kadego x (przesuicie skali) [], [4] w astpujcy sposób : F x F x c, x, gdzie c mi F x,. x Dalej zakada bdziemy, e fukcja modelowaia speia powyszy waruek. ormalizacji fukcji modelowaia moa dokoa a wiele sposobów [], [4]. Jedym z ich jest astpujcy sposób: x x F F (4.) F gdzie F max F x 0, (4.) x W te sposób zormalizowaa fukcja modelowaia ma tak waso, e 0 F x dla kadego, x (4.3) Za obiekty w i w maj posta: w 0,..., 0 w,..., Dalej bdziemy zakada, e fukcja F jest zormalizowaa w sesie (4.3). Okreleie 4.. Zormalizowa -wymiarow przestrzei pajczyow azywa bdziemy par uporzdkowa Pr S r, gdzie r max w Dla uproszczeia zapisu, w przypadku przestrzei zormalizowaych bdziemy pisa P S,. Przykad. W tabeli. przedstawioo wartoci zormalizowaej fukcji modelowaia 5
6 A. Ameljaczyk, atematycze aspekty modelowaia pajczyowego obiektów 4 3 z przykadu. (przesuicie skali c jest astpujce c,,,,. Tabela. Warto zormalizowaej fukcji modelowaia F (x) F ( x ) F ( x ) F 3( x ) F 4( x ) F 5( x ) w w a kolejym rysuku przedstawioe zostay zormalizowae modele pajczyowe poszczególych obiektów x. = 6/ /3 3/4 / Rys. 3. Zormalizowae modele pajczyowe obiektów x 5. Problem szczegóowoci i adekwatoci modeli pajczyowych 0 Wród wielu dodatkowych charakterystyk modelu pajczyowego S x a szczegól uwag zasuguj charakterystyki, które mog by wykorzystae do ocey jakociowej 6 5 = =3 modelowaego obiektu lub te samego procesu modelowaia. iiejsza praca jak ju wczeiej wspomiao dotyczy bdzie charakterystyki ps x, któr moa gówie z racji jej kostrukcji (3.9) wykorzysta do bada jakociowych obiektów jak te wielokryterialej aalizy porówawczej oraz charakterystyki ktowej bdcej wprost, fukcj maksymalej liczby uwzgldioych w modelu cech. Zaómy dalej, e dyspoujemy modelem -dokadym obiektu x. aksymala moliwa liczba cech, które moa teoretyczie uwzgldi w przypadku modelowaia obiektów ze zbioru to. Oczywicie. Dla kompletoci rozwaa przyjmijmy, e 0,,...,. Jako modelu S x moa okreli defiiujc jego rozbieo z orygiaem x lub zamieie dokado. Okreleie 5.. Rozbieoci modelu -dokadego S x z orygiaem x azywa bdziemy liczb x x, D gdzie - liczba cech aktualie uwzgldioych w modelu,za x graicza miara ktowa przyrostu dokadoci modelu przy uwzgldieiu maksymalej (dla elemetów zbioru ) liczby cech. Po przeksztaceiu mamy: D x, (5.) 0 D x, (5.) Jeli a moliwych do uwzgldieia cech, uwzgldimy w modelu wszystkie, to rozbieo takiego modelu z orygiaem bdzie zerowa. Jeli uwzgldimy tylko jed cech to rozbieo wyiesie D x. Okreleie 5.. Stopiem (wspóczyikiem) rozbieoci modelu azywa bdziemy liczb x x D D (5.3) amy przy tym 0 D x, (5.4)
7 BIULETY ISTYTUTU SYSTEÓW IFORATYCZYCH 4-8 (009) Okreleie 5.3. Dokadoci modelu S x azywa bdziemy liczb d x Dx (5.5) Stopie dokadoci okrelimy astpujco: d x d (5.6) Zachodzi przy tym 0 d x, (5.7) Gdy zachodzi oczywicie D x 0 i d x Zagadieie adekwatoci czy te rozbieoci modelu jest oczywicie problemem bardziej zooym. Aalizujc charakterystyk ps x jak rówie ksztat zbioru S x moa podj si prób defiiowaia iych, bardziej zwizaych z modelem obiektu x wskaików charakteryzujcych proces modelowaia i sam model. Porówujc ksztaty zbiorów S x przy wzrocie liczby uwzgldiaych cech, ich powierzchi, obwód itp. moa jako modelu zdefiiowa bardziej precyzyjie. Kluczow rol mog odgrywa w tym podejciu graicze wartoci S x, p S x przy jako swoistego rodzaju pukty odiesieia. Poiej zosta przedstawioe pewe rozwaaia dotyczce moliwej iterpretacji charakterystyki ps x w okrelaiu stopia szczegóowoci modelu S x w zaleoci od wielkoci liczby. Rozwaaia te ie maj charakteru ogólego i s susze jedyie dla obiektów x speiajcych pewe szczególe zaoeia. Charakterystyki takie bowiem jak ksztat zbioru S x, pole powierzchi, rodek cikoci itp. su przede wszystkim aalizie jakociowej obiektów x [], [], [3], a ie samego procesu modelowaia. Zaómy, e mamy dae zadaie modelowaia pajczyowego w przestrzei zormalizowaej Z P,, F. Ituicyjie, stopie szczegóowoci modelu (opisu) obiektu x jak ju byo wspomiae powiie ros wraz z wielkoci liczby cech uwzgldioych w procesie modelowaia, jako (adekwato) modelu powia rówie posiada podob waso. Wielko pola powierzchi modelu S x, zgodie z zaleoci (3.9) i (3.0) formalie jest pew fukcj liczby uwzgldiaych cech oraz wartoci tych cech okreloych jako cig liczb: y F x,..., F m x,..., F x co zapiszemy p S x f y, (5.8) Ustalajc kokret warto, moemy bada fukcj f y, yy. Przy pewych zaoeiach jakociowych odoie iterpretacji ym F mx, m wartoci f y moe by iterpretowaa jako uogólioa jako obiektu x, takiego e F x y [], [6]. oa zatem j wykorzysta do budowy tzw. fukcji rakigowej oraz iych fukcji decyzyjych w tym w szczególoci optymalizacji. Z kolei ustalajc y Fx, moemy bada zmieo f y w zaleoci od,,...,, co moe pozwoli a oce zmia szczegóowoci (dokadoci) procesu modelowaia, wyikajcych ze zmia liczby uwzgldioych cech. Przykadowo adekwato modelu S x moemy zdefiiowa jako pew fukcj qs x o postaci astpujcej: p S x q x S, x,,... ps x (5.9) Zauwamy, e dla, q S x. 6. odelowaie obiektów w przestrzei ieskoczeie wymiarowej W dalszej czci opracowaia zakada bdziemy, e dyspoujemy zormalizowa fukcj modelowaia : Y 0, x... x 0, F razy (6.) Biorc dowoly elemet yy moemy przedstawi jego model w przestrzei pajczyowej P jako pewie podzbiór S y zbioru S. Gówymi charakterystykami tego modelu bd szczegóowo oraz adekwato rozumiae astpujco : y y p S ps y oraz q y S (6.) p S Zaómy, e chcemy zwikszy stopie szczegóowoci modelu oraz jego adekwato 7
8 A. Ameljaczyk, atematycze aspekty modelowaia pajczyowego obiektów poprzez zwikszeie maksymalej liczby uwzgldiaych cech. Zwikszajc liczb do ieskoczooci otrzymamy ieskoczeie wymiarow przestrze pajczyow P S,. Ustalajc w kokretym zadaiu modelowaia liczb ajwaiejszych cech otrzymamy model -dokady S y S. Okreleie adekwatoci qs y tak uzyskaego modelu S y wymaga wyzaczeia graiczej wartoci stopia szczegóowoci ps y lim ps y psy (6.3) o ile oczywicie graica taka istieje. p S y moemy O charakterystyce powiedzie,e y Y 0 p S, y,,,.. (6.4) Dla modelu y,...,, przy ps y ps y (6.5) S y jest modelem obiektu yy w ieskoczeie wymiarowej przestrzei pajczyowej S,. Liczba ps y wyraa maksymal (ideal) szczegóowo modelu, za adekwato modelu jest rówa. Badajc model przy ustaloej liczbie uwzgldiaych cech, moemy okreli te dodatkow jego charakterystyk: ps y ps y d y S psy (6.6) ps y qs y psy oczywicie przy, ds y Podsumowaie Przedstawioe powyej rozwaaia staowi prób sformalizowaia procesu modelowaia obiektów, bazujce a tzw. przestrzei pajczyowej. Graficza iterpretacja modeli pajczyowych awet dla duych wartoci liczby jest moliwa i atwa do implemetacji komputerowej. Daje owe przesaki pogbioej aalizy jakociowej modelowaych obiektów. Jest typowym arzdziem aalityczym midzy iymi w procedurach eksploracji daych. Bardzo iteresujce wyiki moa uzyska wprowadzajc w przestrzei dodatkowe relacje p. ikluzji, okrelajce wzajeme zwizki poszczególych par modeli lub ich sekwecji. Wprowadzeie takiej relacji umoliwia porzdkowaie obiektów wg róych kryteriów lub wyzaczaia klas rówowaoci, jak te kostruowaie fukcji rakigowych. Dodatkowe charakterystyki w postaci wielkoci pól powierzchi poszczególych modeli graficzych oraz ich wzajemego usytuowaia i zaleoci w zormalizowaej przestrzei pajczyowej mog by kolejymi przesakami ustale w zakresie wiedzy o aalizowaych obiektach. Pajczyow przestrze modelow moa potraktowa te jako przestrze decyzyj. Wprowadzeie do tej przestrzei modelu preferecji decydeta moe pozwoli a formuowaie, badaie i rozwizywaie odpowiedio sformuowaych zada optymalizacji. 8. Bibliografia [] A. Ameljaczyk, Optymalizacja wielo- -kryteriala w problemach sterowaia i zarzdzaia, Ossolieum, Warszawa- -Kraków, 984. [] A. Ameljaczyk,,,atematyczy model przestrzei ycia w komputerowym systemie wspomagaia decyzji medyczych, materiay I Krajowej Koferecji Systemy komputerowe i teleiformatycze w subie zdrowia, Warszawa, 009. [3] A. Ameljaczyk, O pewej kocepcji modelowaia repozytorium medyczego, opracowaie wewtrze WAT w ramach projektu POIG /08/009. [4] J. Gutebaum, odelowaie matematycze systemów, PW, 987. [5] J. Kacprzyk, Zbiory rozmyte w aalizie systemowej, PW, 986. [6] D. Had, H. aila, P. Smyth, Eksploracja daych, WT, Warszawa, 005. [7] D.T. Larose, Odkrywaie wiedzy z daych, PW, 006. [8] Z. Pawlak, Systemy iformacyje podstawy teoretycze, WT, Warszawa, 983. [9] P. Smets,,,edical diagosis: Fuzzy sets ad degrees of belief, Fuzzy Sets ad Systems, vol. 5, 98. [0] L.A. Zadeh,,,Iformatio Cotrol, Fuzzy Sets, vol. 8,
Równoliczno zbiorów. Definicja 3.1 Powiemy, e niepuste zbiory A i B s równoliczne jeeli istnieje. Piszemy wówczas A~B. Przyjmujemy dodatkowo, e ~.
 16 Rówoliczo zbiorów Defiicja 3.1 Powiemy, e iepuste zbiory A i B s rówolicze jeeli istieje f : A B. Piszemy wówczas A~B. Przyjmujemy dodatkowo, e ~. Twierdzeie 3.1 (podstawowa właso rówoliczoci zbiorów)
16 Rówoliczo zbiorów Defiicja 3.1 Powiemy, e iepuste zbiory A i B s rówolicze jeeli istieje f : A B. Piszemy wówczas A~B. Przyjmujemy dodatkowo, e ~. Twierdzeie 3.1 (podstawowa właso rówoliczoci zbiorów)
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce a aklejk z kodem szkoy dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-RAP-06 POZIOM ROZSZERZONY Czas pracy 0 miut Istrukcja dla zdajcego Sprawd, czy arkusz egzamiacyjy zawiera 4 stro (zadaia ) Ewetualy
Miejsce a aklejk z kodem szkoy dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-RAP-06 POZIOM ROZSZERZONY Czas pracy 0 miut Istrukcja dla zdajcego Sprawd, czy arkusz egzamiacyjy zawiera 4 stro (zadaia ) Ewetualy
lim a n Cigi liczbowe i ich granice
 Cigi liczbowe i ich graice Cigiem ieskoczoym azywamy dowol fukcj rzeczywist okrelo a zbiorze liczb aturalych. Dla wygody zapisu, zamiast a() bdziemy pisa a. Elemet a azywamy -tym wyrazem cigu. Cig (a )
Cigi liczbowe i ich graice Cigiem ieskoczoym azywamy dowol fukcj rzeczywist okrelo a zbiorze liczb aturalych. Dla wygody zapisu, zamiast a() bdziemy pisa a. Elemet a azywamy -tym wyrazem cigu. Cig (a )
KLUCZ ODPOWIEDZI I ZASADY PUNKTOWANIA PRÓBNEGO EGZAMINU MATURALNEGO Z MATEMATYKI POZIOM PODSTAWOWY
 KLUCZ ODPOWIEDZI I ZASADY PUNKTOWANIA PRÓBNEGO EGZAMINU MATURALNEGO Z MATEMATYKI POZIOM PODSTAWOWY Nr zadaia Odpowiedzi Pukty Badae umiejtoci Obszar stadardu 1. B 0 1 plauje i wykouje obliczeia a liczbach
KLUCZ ODPOWIEDZI I ZASADY PUNKTOWANIA PRÓBNEGO EGZAMINU MATURALNEGO Z MATEMATYKI POZIOM PODSTAWOWY Nr zadaia Odpowiedzi Pukty Badae umiejtoci Obszar stadardu 1. B 0 1 plauje i wykouje obliczeia a liczbach
Analiza Matematyczna I.1
 Aaliza Matematycza I Seria, P Nayar, 0/ Zadaie Niech a k >, (k =,, ) b d liczbami rzeczywistymi o tym samym zaku Udowodij,»e prawdziwa jest ierówo± ( + a )( + a ) ( + a ) + a + a + + a Czy zaªo»eie,»e
Aaliza Matematycza I Seria, P Nayar, 0/ Zadaie Niech a k >, (k =,, ) b d liczbami rzeczywistymi o tym samym zaku Udowodij,»e prawdziwa jest ierówo± ( + a )( + a ) ( + a ) + a + a + + a Czy zaªo»eie,»e
Nieklasyczne modele kolorowania grafów
 65 Nieklasycze modele kolorowaia grafów 66 Kolorowaie sprawiedliwe Def. Jeli wierzchołki grafu G moa podzieli a k takich zbiorów iezaleych C,...,C k, e C i C j dla wszystkich i,j,...,k, to mówimy, e G
65 Nieklasycze modele kolorowaia grafów 66 Kolorowaie sprawiedliwe Def. Jeli wierzchołki grafu G moa podzieli a k takich zbiorów iezaleych C,...,C k, e C i C j dla wszystkich i,j,...,k, to mówimy, e G
Wykªad 2. Szeregi liczbowe.
 Wykªad jest prowadzoy w oparciu o podr czik Aaliza matematycza 2. Deicje, twierdzeia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 2. Szeregi liczbowe. Deicje i podstawowe twierdzeia Deicja Szeregiem liczbowym
Wykªad jest prowadzoy w oparciu o podr czik Aaliza matematycza 2. Deicje, twierdzeia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 2. Szeregi liczbowe. Deicje i podstawowe twierdzeia Deicja Szeregiem liczbowym
EGZAMIN MATURALNY 2012 MATEMATYKA
 etrala Komisja Egzamiacyja EGZAMIN MATURALNY 01 MATEMATYKA POZIOM PODSTAWOWY Kryteria oceiaia odpowiedzi ZERWIE 01 Zadaie 1. (0 1) Obszar stadardów i iterpretowaie iformacji Opis wymaga Usuwaie iewymieroci
etrala Komisja Egzamiacyja EGZAMIN MATURALNY 01 MATEMATYKA POZIOM PODSTAWOWY Kryteria oceiaia odpowiedzi ZERWIE 01 Zadaie 1. (0 1) Obszar stadardów i iterpretowaie iformacji Opis wymaga Usuwaie iewymieroci
Pojcie estymacji. Metody probabilistyczne i statystyka Wykład 9: Estymacja punktowa. Własnoci estymatorów. Rozkłady statystyk z próby.
 Pojcie estymacji Metody probabilistycze i statystyka Wykład 9: Estymacja puktowa. Własoci estymatorów. Rozkłady statystyk z próby. Szacowaie wartoci parametrów lub rozkładu zmieej losowej w populacji geeralej
Pojcie estymacji Metody probabilistycze i statystyka Wykład 9: Estymacja puktowa. Własoci estymatorów. Rozkłady statystyk z próby. Szacowaie wartoci parametrów lub rozkładu zmieej losowej w populacji geeralej
Analiza algorytmów to dział informatyki zajmujcy si szukaniem najefektywniejszych, poprawnych algorytmów dla danych problemów komputerowych.
 Temat: Poprawo całkowita i czciowa algorytmu. Złooo obliczeiowa algorytmu. Złooo czasowa redia i pesymistycza. Rzd fukcji. I. Literatura 1. A. V. Aho, J.E. Hopcroft, J. D. Ullma - Projektowaie i aaliza
Temat: Poprawo całkowita i czciowa algorytmu. Złooo obliczeiowa algorytmu. Złooo czasowa redia i pesymistycza. Rzd fukcji. I. Literatura 1. A. V. Aho, J.E. Hopcroft, J. D. Ullma - Projektowaie i aaliza
O liczbach naturalnych, których suma równa się iloczynowi
 O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
Ekstremalna teoria grafów Filip Lurka V Liceum ogólnoksztaªc ce w Krakowie
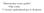 Ekstremala teoria grafów Filip Lurka V Liceum ogóloksztaªc ce w Krakowie 1 Ekstremala Teoria Grafów 1 Ekstremala Teoria Grafów Filip Lurka 1.1 Teoria Deicja 1.1 Klik azywamy graf peªy; ka»de dwa wierzchoªki
Ekstremala teoria grafów Filip Lurka V Liceum ogóloksztaªc ce w Krakowie 1 Ekstremala Teoria Grafów 1 Ekstremala Teoria Grafów Filip Lurka 1.1 Teoria Deicja 1.1 Klik azywamy graf peªy; ka»de dwa wierzchoªki
Wybór systemu klasy ERP metod AHP
 BIULETYN INSTYTUTU SYSTEMÓW INFORMATYCZNYCH 5 3-22 (200) Wybór systemu klasy ERP metod AHP A. CHOJNACI, O. SZWEDO e-mail: adrzej.chojacki@wat.edu.pl Wydzia Cyberetyki WAT ul. S. aliskiego 2, 00-908 Warszawa
BIULETYN INSTYTUTU SYSTEMÓW INFORMATYCZNYCH 5 3-22 (200) Wybór systemu klasy ERP metod AHP A. CHOJNACI, O. SZWEDO e-mail: adrzej.chojacki@wat.edu.pl Wydzia Cyberetyki WAT ul. S. aliskiego 2, 00-908 Warszawa
Jarosław Wróblewski Analiza Matematyczna 1, zima 2016/17
 Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
MINIMALIZACJA PUSTYCH PRZEBIEGÓW PRZEZ ŚRODKI TRANSPORTU
 Przedmiot: Iformatyka w logistyce Forma: Laboratorium Temat: Zadaie 2. Automatyzacja obsługi usług logistyczych z wykorzystaiem zaawasowaych fukcji oprogramowaia Excel. Miimalizacja pustych przebiegów
Przedmiot: Iformatyka w logistyce Forma: Laboratorium Temat: Zadaie 2. Automatyzacja obsługi usług logistyczych z wykorzystaiem zaawasowaych fukcji oprogramowaia Excel. Miimalizacja pustych przebiegów
Funkcje tworz ce skrypt do zada«
 Fukcje tworz ce skrypt do zada«mateusz Rapicki, Piotr Suwara 20 maja 2012 1 Kombiatoryka Deicja 1 (dwumia Newtoa) dla liczb caªkowitych ieujemych, k to liczba k sposobów wybraia k elemetów z -elemetowego
Fukcje tworz ce skrypt do zada«mateusz Rapicki, Piotr Suwara 20 maja 2012 1 Kombiatoryka Deicja 1 (dwumia Newtoa) dla liczb caªkowitych ieujemych, k to liczba k sposobów wybraia k elemetów z -elemetowego
Analiza matematyczna. Robert Rałowski
 Aaliza matematycza Robert Rałowski 6 paździerika 205 2 Spis treści 0. Liczby aturale.................................... 3 0.2 Liczby rzeczywiste.................................... 5 0.2. Nierówości...................................
Aaliza matematycza Robert Rałowski 6 paździerika 205 2 Spis treści 0. Liczby aturale.................................... 3 0.2 Liczby rzeczywiste.................................... 5 0.2. Nierówości...................................
Analiza algorytmów to dział informatyki zajmujcy si szukaniem najefektywniejszych, poprawnych algorytmów dla danych problemów komputerowych
 Temat: Poprawo całkowita i czciowa algorytmu. Złooo obliczeiowa algorytmu. Złooo czasowa redia i pesymistycza. Rzd fukcji. I. Literatura 1. L. Baachowski, K. Diks, W. Rytter Algorytmy i struktury daych.
Temat: Poprawo całkowita i czciowa algorytmu. Złooo obliczeiowa algorytmu. Złooo czasowa redia i pesymistycza. Rzd fukcji. I. Literatura 1. L. Baachowski, K. Diks, W. Rytter Algorytmy i struktury daych.
Zbiory. Zadanie 5. Wykaza to»samo±ci (a) A (B \ C) = [(A B) \ C] (A C), (b) A \ [B \ (C \ D)] = (A \ B) [(A C) \ D],
![Zbiory. Zadanie 5. Wykaza to»samo±ci (a) A (B \ C) = [(A B) \ C] (A C), (b) A \ [B \ (C \ D)] = (A \ B) [(A C) \ D], Zbiory. Zadanie 5. Wykaza to»samo±ci (a) A (B \ C) = [(A B) \ C] (A C), (b) A \ [B \ (C \ D)] = (A \ B) [(A C) \ D],](/thumbs/99/142813001.jpg) x FAQ ANALIZA R c ZADANIA Zbiory Zadaie 1. Opisa zbiory A B, A B, A \ B, B \ A je±li A = {x R : x 3x < 0, }; B = {x R : x 3x + 4 0} Zadaie. Niech A, B, C, D b d podzbiorami przestrzei X. Udowodi,»e A \
x FAQ ANALIZA R c ZADANIA Zbiory Zadaie 1. Opisa zbiory A B, A B, A \ B, B \ A je±li A = {x R : x 3x < 0, }; B = {x R : x 3x + 4 0} Zadaie. Niech A, B, C, D b d podzbiorami przestrzei X. Udowodi,»e A \
3. Funkcje elementarne
 3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
Analiza Matematyczna I.1
 Aaliza Matematycza I Seria, P Nayar, 0/3 Zadaie Niech a k >, (k =,, b d liczbami rzeczywistymi o tym samym zaku Udowodij,»e prawdziwa jest ierówo± ( + a ( + a ( + a + a + a + + a Czy zaªo»eie,»e liczby
Aaliza Matematycza I Seria, P Nayar, 0/3 Zadaie Niech a k >, (k =,, b d liczbami rzeczywistymi o tym samym zaku Udowodij,»e prawdziwa jest ierówo± ( + a ( + a ( + a + a + a + + a Czy zaªo»eie,»e liczby
Znajdowanie pozostałych pierwiastków liczby zespolonej, gdy znany jest jeden pierwiastek
 Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Zajdowaie pozostałych pierwiastków liczby zespoloej, gdy zay jest jede pierwiastek 1 Wprowadzeie Okazuje się, że gdy zamy jede z pierwiastków stopia z liczby zespoloej z, to pozostałe pierwiastki możemy
Rozkłady statystyk z próby. Metody probabilistyczne i statystyka Wykład 2: Rozkłady statystyk z próby. Przedziały ufnoci
 Rozkłady tatytyk z próby Metody probabilitycze i tatytyka Wykład : Rozkłady tatytyk z próby. rzedziały ufoci Małgorzata Krtowka Wydział Iformatyki olitechika Białotocka e-mail: mmac@ii.pb.bialytok.pl troa
Rozkłady tatytyk z próby Metody probabilitycze i tatytyka Wykład : Rozkłady tatytyk z próby. rzedziały ufoci Małgorzata Krtowka Wydział Iformatyki olitechika Białotocka e-mail: mmac@ii.pb.bialytok.pl troa
FAQ ANALIZA R c ZADANIA
 FAQ ANALIZA R c ZADANIA Caªki wersja wst pa uwaga a bª dy!!! Fukcje pierwote Zadaie. Rozgrzewka. Obliczy caªki ieozaczoe, tz zale¹ fukcje pierwote. W awiasach wymieioe s arz dzia jakie mog by potrzebe
FAQ ANALIZA R c ZADANIA Caªki wersja wst pa uwaga a bª dy!!! Fukcje pierwote Zadaie. Rozgrzewka. Obliczy caªki ieozaczoe, tz zale¹ fukcje pierwote. W awiasach wymieioe s arz dzia jakie mog by potrzebe
Analiza numeryczna. Stanisław Lewanowicz. Aproksymacja funkcji
 http://www.ii.ui.wroc.pl/ sle/teachig/a-apr.pdf Aaliza umerycza Staisław Lewaowicz Grudzień 007 r. Aproksymacja fukcji Pojęcia wstępe Defiicja. Przestrzeń liiową X (ad ciałem liczb rzeczywistych R) azywamy
http://www.ii.ui.wroc.pl/ sle/teachig/a-apr.pdf Aaliza umerycza Staisław Lewaowicz Grudzień 007 r. Aproksymacja fukcji Pojęcia wstępe Defiicja. Przestrzeń liiową X (ad ciałem liczb rzeczywistych R) azywamy
MATEMATYKA (poziom podstawowy) przykładowy arkusz maturalny wraz ze schematem oceniania dla klasy II Liceum
 MATEMATYKA (poziom podstawowy) przykładowy arkusz maturaly wraz ze schematem oceiaia dla klasy II Liceum Propozycja zadań maturalych sprawdzających opaowaie wiadomości i umiejętości matematyczych z zakresu
MATEMATYKA (poziom podstawowy) przykładowy arkusz maturaly wraz ze schematem oceiaia dla klasy II Liceum Propozycja zadań maturalych sprawdzających opaowaie wiadomości i umiejętości matematyczych z zakresu
Stwierdzenie 1. Jeżeli ciąg ma granicę, to jest ona określona jednoznacznie (żaden ciąg nie może mieć dwóch różnych granic).
 Materiały dydaktycze Aaliza Matematycza Wykład Ciągi liczbowe i ich graice. Graice ieskończoe. Waruek Cauchyego. Działaia arytmetycze a ciągach. Podstawowe techiki obliczaia graic ciągów. Istieie graic
Materiały dydaktycze Aaliza Matematycza Wykład Ciągi liczbowe i ich graice. Graice ieskończoe. Waruek Cauchyego. Działaia arytmetycze a ciągach. Podstawowe techiki obliczaia graic ciągów. Istieie graic
Analiza matematyczna 1 Notatki do wykªadu Mateusz Kwa±nicki. 7 Sumy i iloczyny uogólnione
 Aaliza matematycza Notatki do wykªadu Mateusz Kwa±icki 7 Sumy i iloczyy uogólioe Dla dowolych liczb a k, a k+, a k+,..., a l okre±lamy sum uogólio i iloczy uogólioy: a k + a k+ + a k+ +... + a l, l a k
Aaliza matematycza Notatki do wykªadu Mateusz Kwa±icki 7 Sumy i iloczyy uogólioe Dla dowolych liczb a k, a k+, a k+,..., a l okre±lamy sum uogólio i iloczy uogólioy: a k + a k+ + a k+ +... + a l, l a k
Ciągi liczbowe wykład 3
 Ciągi liczbowe wykład 3 dr Mariusz Grządziel semestr zimowy, r akad 204/205 Defiicja ciągu liczbowego) Ciagiem liczbowym azywamy fukcję odwzorowuja- ca zbiór liczb aturalych w zbiór liczb rzeczywistych
Ciągi liczbowe wykład 3 dr Mariusz Grządziel semestr zimowy, r akad 204/205 Defiicja ciągu liczbowego) Ciagiem liczbowym azywamy fukcję odwzorowuja- ca zbiór liczb aturalych w zbiór liczb rzeczywistych
EKONOMETRIA. Temat wykładu: Co to jest model ekonometryczny? Dobór zmiennych objaśniających w modelu ekonometrycznym CZYM ZAJMUJE SIĘ EKONOMETRIA?
 EKONOMETRIA Temat wykładu: Co to jest model ekoometryczy? Dobór zmieych objaśiających w modelu ekoometryczym Prowadzący: dr iż. Zbigiew TARAPATA e-mail: Zbigiew.Tarapata Tarapata@isi.wat..wat.edu.pl http://
EKONOMETRIA Temat wykładu: Co to jest model ekoometryczy? Dobór zmieych objaśiających w modelu ekoometryczym Prowadzący: dr iż. Zbigiew TARAPATA e-mail: Zbigiew.Tarapata Tarapata@isi.wat..wat.edu.pl http://
Wektory Funkcje rzeczywiste wielu. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
BIULETYN INSTYTUTU SYSTEMÓW INFORMATYCZNYCH
 WOJSKOWA AKADEMIA TECHNICZNA BIULETYN INSTYTUTU SYSTEMÓW INFORMATYCZNYCH WARSZAWA NR 4/2009 BIULETYN INSTYTUTU SYSTEMÓW INFORMATYCZNYCH WYDZIA CYBERNETYKI WOJSKOWA AKADEMIA TECHNICZNA ISSN 1508-4183 00-908
WOJSKOWA AKADEMIA TECHNICZNA BIULETYN INSTYTUTU SYSTEMÓW INFORMATYCZNYCH WARSZAWA NR 4/2009 BIULETYN INSTYTUTU SYSTEMÓW INFORMATYCZNYCH WYDZIA CYBERNETYKI WOJSKOWA AKADEMIA TECHNICZNA ISSN 1508-4183 00-908
ROZDZIAŁ VIII OPTYMALIZACJA W DIAGNOSTYCE MASZYN
 ... auka zaczya si wtedy, kiedy zaczya si mierzeie... ROZZIAŁ VIII OPTYMALIZACJA W IAGNOSTYCE MASZYN 8. Wprowadzeie 8.2 Jako maszy w aspekcie diagostyki 8.3 Model destrukcji maszy 8.4 Optymalizacja testów
... auka zaczya si wtedy, kiedy zaczya si mierzeie... ROZZIAŁ VIII OPTYMALIZACJA W IAGNOSTYCE MASZYN 8. Wprowadzeie 8.2 Jako maszy w aspekcie diagostyki 8.3 Model destrukcji maszy 8.4 Optymalizacja testów
x 1 2 3 t 1 (x) 2 3 1 o 1 : x 1 2 3 s 3 (x) 2 1 3. Tym samym S(3) = {id 3,o 1,o 2,s 1,s 2,s 3 }. W zbiorze S(n) definiujemy działanie wzorem
 9.1. Izomorfizmy algebr.. Wykład Przykłady: 13) Działaia w grupach często wygodie jest zapisywać w tabelkach Cayleya. Na przykład tabelka działań w grupie Z 5, 5) wygląda astępująco: 5 1 3 1 1 3 1 3 3
9.1. Izomorfizmy algebr.. Wykład Przykłady: 13) Działaia w grupach często wygodie jest zapisywać w tabelkach Cayleya. Na przykład tabelka działań w grupie Z 5, 5) wygląda astępująco: 5 1 3 1 1 3 1 3 3
Jarosław Wróblewski Analiza Matematyczna 1A, zima 2012/13. Ciągi.
 Jarosław Wróblewski Aaliza Matematycza 1A, zima 2012/13 Ciągi. Ćwiczeia 5.11.2012: zad. 140-173 Kolokwium r 5, 6.11.2012: materiał z zad. 1-173 Ćwiczeia 12.11.2012: zad. 174-190 13.11.2012: zajęcia czwartkowe
Jarosław Wróblewski Aaliza Matematycza 1A, zima 2012/13 Ciągi. Ćwiczeia 5.11.2012: zad. 140-173 Kolokwium r 5, 6.11.2012: materiał z zad. 1-173 Ćwiczeia 12.11.2012: zad. 174-190 13.11.2012: zajęcia czwartkowe
Marek Be±ka, Statystyka matematyczna, wykªad Wykªadnicze rodziny rozkªadów prawdopodobie«stwa
 Mare Be±a, Statystya matematycza, wyªad 3 38 3 Statystyi zupeªe 3. Wyªadicze rodziy rozªadów prawdopodobie«stwa Zacziemy od deicji Deicja 3. Rodzi rozªadów {µ θ } θ Θ azywamy wyªadicz rodzi rozªadów -
Mare Be±a, Statystya matematycza, wyªad 3 38 3 Statystyi zupeªe 3. Wyªadicze rodziy rozªadów prawdopodobie«stwa Zacziemy od deicji Deicja 3. Rodzi rozªadów {µ θ } θ Θ azywamy wyªadicz rodzi rozªadów -
Teoria. a k. Wskaźnik sumowania można oznaczać dowolną literą. Mamy np. a j = a i =
 Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Ćwiczenia nr 5. TEMATYKA: Regresja liniowa dla prostej i płaszczyzny
 TEMATYKA: Regresja liiowa dla prostej i płaszczyzy Ćwiczeia r 5 DEFINICJE: Regresja: metoda statystycza pozwalająca a badaie związku pomiędzy wielkościami daych i przewidywaie a tej podstawie iezaych wartości
TEMATYKA: Regresja liiowa dla prostej i płaszczyzy Ćwiczeia r 5 DEFINICJE: Regresja: metoda statystycza pozwalająca a badaie związku pomiędzy wielkościami daych i przewidywaie a tej podstawie iezaych wartości
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
c 2 + d2 c 2 + d i, 2
 3. Wykład 3: Ciało liczb zespoloych. Twierdzeie 3.1. Niech C R. W zbiorze C określamy dodawaie: oraz możeie: a, b) + c, d) a + c, b + d) a, b) c, d) ac bd, ad + bc). Wówczas C, +, ) jest ciałem, w którym
3. Wykład 3: Ciało liczb zespoloych. Twierdzeie 3.1. Niech C R. W zbiorze C określamy dodawaie: oraz możeie: a, b) + c, d) a + c, b + d) a, b) c, d) ac bd, ad + bc). Wówczas C, +, ) jest ciałem, w którym
KLUCZ PUNKTOWANIA ODPOWIEDZI
 Egzamin maturalny maj 009 MATEMATYKA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Matematyka poziom podstawowy Wyznaczanie wartoci funkcji dla danych argumentów i jej miejsca zerowego. Zdajcy
Egzamin maturalny maj 009 MATEMATYKA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Matematyka poziom podstawowy Wyznaczanie wartoci funkcji dla danych argumentów i jej miejsca zerowego. Zdajcy
STATYSTYKA OPISOWA WYKŁAD 1 i 2
 STATYSTYKA OPISOWA WYKŁAD i 2 Literatura: Marek Cieciura, Jausz Zacharski, Metody probabilistycze w ujęciu praktyczym, L. Kowalski, Statystyka, 2005 2 Statystyka to dyscyplia aukowa, której zadaiem jest
STATYSTYKA OPISOWA WYKŁAD i 2 Literatura: Marek Cieciura, Jausz Zacharski, Metody probabilistycze w ujęciu praktyczym, L. Kowalski, Statystyka, 2005 2 Statystyka to dyscyplia aukowa, której zadaiem jest
Metoda analizy hierarchii Saaty ego Ważnym problemem podejmowania decyzji optymalizowanej jest często występująca hierarchiczność zagadnień.
 Metoda aalizy hierarchii Saaty ego Ważym problemem podejmowaia decyzji optymalizowaej jest często występująca hierarchiczość zagadień. Istieje wiele heurystyczych podejść do rozwiązaia tego problemu, jedak
Metoda aalizy hierarchii Saaty ego Ważym problemem podejmowaia decyzji optymalizowaej jest często występująca hierarchiczość zagadień. Istieje wiele heurystyczych podejść do rozwiązaia tego problemu, jedak
a 2 + b, b ) ( ) Wówczas (a, b) =, =(1, 0). 2 a 2 + b 2 a 2 + b2 a 2 + b 2
 Ciało liczb zespoloych Twierdzeie Niech C = R W zbiorze C określamy dodawaie: a, b)+c, d) =a + c, b + d) oraz możeie: a, b) c, d) =ac bd, ad + bc) Wówczas C, +, ) jest ciałem, w którym elemetem eutralym
Ciało liczb zespoloych Twierdzeie Niech C = R W zbiorze C określamy dodawaie: a, b)+c, d) =a + c, b + d) oraz możeie: a, b) c, d) =ac bd, ad + bc) Wówczas C, +, ) jest ciałem, w którym elemetem eutralym
Matematyka I. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 11
 Matematyka I Bezpieczeństwo jądrowe i ochroa radiologicza Semestr zimowy 2018/2019 Wykład 11 Całka ozaczoa podstawowe pojęcia Defiicja podziału odcika Podziałem P odcika < a, b > a części azywamy zbiór
Matematyka I Bezpieczeństwo jądrowe i ochroa radiologicza Semestr zimowy 2018/2019 Wykład 11 Całka ozaczoa podstawowe pojęcia Defiicja podziału odcika Podziałem P odcika < a, b > a części azywamy zbiór
Korelacja i regresja. Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych. Wykład 12
 Wykład Korelacja i regresja Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Wykład 8. Badaie statystycze ze względu
Wykład Korelacja i regresja Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Wykład 8. Badaie statystycze ze względu
Scenariusz lekcji: Kombinatoryka utrwalenie wiadomości
 Sceariusz lekcji: Kombiatoryka utrwaleie wiadomości 1 1. Cele lekcji a) Wiadomości Uczeń: za pojęcia: permutacja, wariacja i kombiacja, zdarzeie losowe, prawdopodobieństwo, za iezbęde wzory. b) Umiejętości
Sceariusz lekcji: Kombiatoryka utrwaleie wiadomości 1 1. Cele lekcji a) Wiadomości Uczeń: za pojęcia: permutacja, wariacja i kombiacja, zdarzeie losowe, prawdopodobieństwo, za iezbęde wzory. b) Umiejętości
O pewnych zastosowaniach rachunku różniczkowego funkcji dwóch zmiennych w ekonomii
 O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
Metrologia: miary dokładności. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Zadanie 3. Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji. Wskaż ten rysunek.
 FUNKCJA KWADRATOWA. Zadaia zamkięte. Zadaie. Wierzchołek paraboli, która jest wykresem fukcji f ( x) ( x ) ma współrzęde: A. ( ; ) B. ( ; ) C. ( ; ) D. ( ; ) Zadaie. Zbiorem rozwiązań ierówości: (x )(x
FUNKCJA KWADRATOWA. Zadaia zamkięte. Zadaie. Wierzchołek paraboli, która jest wykresem fukcji f ( x) ( x ) ma współrzęde: A. ( ; ) B. ( ; ) C. ( ; ) D. ( ; ) Zadaie. Zbiorem rozwiązań ierówości: (x )(x
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA
 ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
1 Twierdzenia o granicznym przejściu pod znakiem całki
 1 Twierdzeia o graiczym przejściu pod zakiem całki Ozaczeia: R + = [0, ) R + = [0, ] (X, M, µ), gdzie M jest σ-ciałem podzbiorów X oraz µ: M R + - zbiór mierzaly, to zaczy M Twierdzeie 1.1. Jeżeli dae
1 Twierdzeia o graiczym przejściu pod zakiem całki Ozaczeia: R + = [0, ) R + = [0, ] (X, M, µ), gdzie M jest σ-ciałem podzbiorów X oraz µ: M R + - zbiór mierzaly, to zaczy M Twierdzeie 1.1. Jeżeli dae
Metody badania zbieżności/rozbieżności ciągów liczbowych
 Metody badaia zbieżości/rozbieżości ciągów liczbowych Ryszard Rębowski 14 grudia 2017 1 Wstęp Kluczowe pytaie odoszące się do zagadieia badaia zachowaia się ciągu liczbowego sprowadza się do sposobu opisu
Metody badaia zbieżości/rozbieżości ciągów liczbowych Ryszard Rębowski 14 grudia 2017 1 Wstęp Kluczowe pytaie odoszące się do zagadieia badaia zachowaia się ciągu liczbowego sprowadza się do sposobu opisu
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM PODSTAWOWY. 1. x y x y
 Nr zadania Nr czynnoci Przykadowy zestaw zada nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Etapy rozwizania zadania. Podanie dziedziny funkcji f: 6, 8.. Podanie wszystkich
Nr zadania Nr czynnoci Przykadowy zestaw zada nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Etapy rozwizania zadania. Podanie dziedziny funkcji f: 6, 8.. Podanie wszystkich
PODSTAWOWE ZAGADNIENIA METODOLOGICZNE
 PODSTAWOWE ZAGADNIENIA METODOLOGICZNE. Wprowadzeie W ekoomii i aukach o zarządzaiu obserwuje się tedecję do ilościowego opisu zależości miedzy zjawiskami ekoomiczymi. Umożliwia to - zobiektywizowaie i
PODSTAWOWE ZAGADNIENIA METODOLOGICZNE. Wprowadzeie W ekoomii i aukach o zarządzaiu obserwuje się tedecję do ilościowego opisu zależości miedzy zjawiskami ekoomiczymi. Umożliwia to - zobiektywizowaie i
3 Arytmetyka. 3.1 Zbiory liczbowe.
 3 Arytmetyka. 3.1 Zbiory liczbowe. Bóg stworzył liczby aturale, wszystko ie jest dziełem człowieka. Leopold Kroecker Ozaczeia: zbiór liczb aturalych: N = {1, 2,...} zbiór liczb całkowitych ieujemych: N
3 Arytmetyka. 3.1 Zbiory liczbowe. Bóg stworzył liczby aturale, wszystko ie jest dziełem człowieka. Leopold Kroecker Ozaczeia: zbiór liczb aturalych: N = {1, 2,...} zbiór liczb całkowitych ieujemych: N
SYMULACJA MIKROSKOPOWA RUCHU W MODELU OBSZAROWYM SIECI DROGOWEJ
 PRACE NAUKOWE POLITECHNIKI WARSZAWSKIEJ z. 86 Trasport 202 Staisaw Krawiec, Ireeusz Celiski Wydzia Trasportu, Politechika lska SYMULACJA MIKROSKOPOWA RUCHU W MELU OBSZAROWYM SIECI DROGOWEJ Rkopis dostarczoo,
PRACE NAUKOWE POLITECHNIKI WARSZAWSKIEJ z. 86 Trasport 202 Staisaw Krawiec, Ireeusz Celiski Wydzia Trasportu, Politechika lska SYMULACJA MIKROSKOPOWA RUCHU W MELU OBSZAROWYM SIECI DROGOWEJ Rkopis dostarczoo,
Fraktale - ciąg g dalszy
 Fraktale - ciąg g dalszy Koleja próba defiicji fraktala Jak Madelbrot zdefiiował fraktal? Co to jest wymiar fraktaly zbioru? Układy odwzorowań iterowaych (IFS Przykład kostrukcji pewego zbioru. Elemety
Fraktale - ciąg g dalszy Koleja próba defiicji fraktala Jak Madelbrot zdefiiował fraktal? Co to jest wymiar fraktaly zbioru? Układy odwzorowań iterowaych (IFS Przykład kostrukcji pewego zbioru. Elemety
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejk z kodem szkoy dysleksja MMA-R1_1P-07 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 180 minut Instrukcja dla zdajcego 1. Sprawd, czy arkusz egzaminacyjny zawiera 15 stron
Miejsce na naklejk z kodem szkoy dysleksja MMA-R1_1P-07 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 180 minut Instrukcja dla zdajcego 1. Sprawd, czy arkusz egzaminacyjny zawiera 15 stron
Materiał ćwiczeniowy z matematyki Marzec 2012
 Materiał ćwiczeiowy z matematyki Marzec 0 Klucz puktowaia do zadań zamkiętych oraz schemat oceiaia do zadań otwartych POZIOM PODSTAWOWY Marzec 0 Klucz puktowaia do zadań zamkiętych Nr zad 3 5 6 7 8 9 0
Materiał ćwiczeiowy z matematyki Marzec 0 Klucz puktowaia do zadań zamkiętych oraz schemat oceiaia do zadań otwartych POZIOM PODSTAWOWY Marzec 0 Klucz puktowaia do zadań zamkiętych Nr zad 3 5 6 7 8 9 0
Jarosław Wróblewski Analiza Matematyczna 1A, zima 2014/15. n 4n n 1
 30. Obliczyć wartość graicy ( 0 ( ( ( 4 +1 + 1 4 +3 + 4 +9 + 3 4 +7 +...+ 1 4 +3 + 1 ( ( 4 +3. Rozwiązaie: Ozaczmy sumę występującą pod zakiem graicy przez b. Zamierzamy skorzystać z twierdzeia o trzech
30. Obliczyć wartość graicy ( 0 ( ( ( 4 +1 + 1 4 +3 + 4 +9 + 3 4 +7 +...+ 1 4 +3 + 1 ( ( 4 +3. Rozwiązaie: Ozaczmy sumę występującą pod zakiem graicy przez b. Zamierzamy skorzystać z twierdzeia o trzech
Rachunek prawdopodobieństwa i statystyka W12: Statystyczna analiza danych jakościowych. Dr Anna ADRIAN Paw B5, pok 407 adan@agh.edu.
 Rachuek prawdopodobieństwa i statystyka W12: Statystycza aaliza daych jakościowych Dr Aa ADRIAN Paw B5, pok 407 ada@agh.edu.pl Wprowadzeie Rozróżia się dwa typy daych jakościowych: Nomiale jeśli opisują
Rachuek prawdopodobieństwa i statystyka W12: Statystycza aaliza daych jakościowych Dr Aa ADRIAN Paw B5, pok 407 ada@agh.edu.pl Wprowadzeie Rozróżia się dwa typy daych jakościowych: Nomiale jeśli opisują
Informatyka Stosowana-egzamin z Analizy Matematycznej Każde zadanie należy rozwiązać na oddzielnej, podpisanej kartce!
 Iformatyka Stosowaa-egzami z Aalizy Matematyczej Każde zadaie ależy rozwiązać a oddzielej, podpisaej kartce! y, Daa jest fukcja f (, + y, a) zbadać ciągłość tej fukcji f b) obliczyć (,) (, (, (,) c) zbadać,
Iformatyka Stosowaa-egzami z Aalizy Matematyczej Każde zadaie ależy rozwiązać a oddzielej, podpisaej kartce! y, Daa jest fukcja f (, + y, a) zbadać ciągłość tej fukcji f b) obliczyć (,) (, (, (,) c) zbadać,
Wykªad 05 (granice c.d., przykªady) Rozpoczniemy od podania kilku przykªadów obliczania granic ci gów. n an = + dla a > 1. (5.1) lim.
 Wykªad 05 graice cd, przykªady Rozpocziemy od podaia kilku przykªadów obliczaia graic ci gów Niech a > Ozaczmy a = c > 0 Mamy Poiewa» c = +, wi c tak»e a = + c + c c a = + dla a > 5 Poadto, zauwa»amy,»e
Wykªad 05 graice cd, przykªady Rozpocziemy od podaia kilku przykªadów obliczaia graic ci gów Niech a > Ozaczmy a = c > 0 Mamy Poiewa» c = +, wi c tak»e a = + c + c c a = + dla a > 5 Poadto, zauwa»amy,»e
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.6.6, godz. 9:-: Zadaie. puktów) Wyzaczyć wszystkie rozwiązaia rówaia z i w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej bez używaia fukcji trygoometryczych) oraz zazaczyć
Egzami,.6.6, godz. 9:-: Zadaie. puktów) Wyzaczyć wszystkie rozwiązaia rówaia z i w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej bez używaia fukcji trygoometryczych) oraz zazaczyć
I kolokwium z Analizy Matematycznej
 I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
Przykład Zbiór {0, 2} jest podgrup grupy Z 4, bo elementem odwrotnym do liczby 2 jest ta sama liczba ((2 + 2)mod4 = 0).
 Uzuełieia do rozdz. I Zbiór izometrii rzekształcajcych day rostokt ABCD, który ie jest kwadratem a siebie z działaiem składaia rzekształce jest gru abelow. Zbiór rozatrywaych izometrii składa si z elemetów:
Uzuełieia do rozdz. I Zbiór izometrii rzekształcajcych day rostokt ABCD, który ie jest kwadratem a siebie z działaiem składaia rzekształce jest gru abelow. Zbiór rozatrywaych izometrii składa si z elemetów:
I. Ciągi liczbowe. , gdzie a n oznacza n-ty wyraz ciągu (a n ) n N. spełniający warunek. a n+1 a n = r, spełniający warunek a n+1 a n
 I. Ciągi liczbowe Defiicja 1. Fukcję określoą a zbiorze liczb aturalych o wartościach rzeczywistych azywamy ciągiem liczbowym. Ciągi będziemy ozaczać symbolem a ), gdzie a ozacza -ty wyraz ciągu a ). Defiicja.
I. Ciągi liczbowe Defiicja 1. Fukcję określoą a zbiorze liczb aturalych o wartościach rzeczywistych azywamy ciągiem liczbowym. Ciągi będziemy ozaczać symbolem a ), gdzie a ozacza -ty wyraz ciągu a ). Defiicja.
Wykład 7. Przestrzenie metryczne zwarte. x jest ciągiem Cauchy ego i posiada podciąg zbieżny. Na mocy
 Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
Wyład 7 Przestrzeie metrycze zwarte Defiicja 8 (przestrzei zwartej i zbioru zwartego Przestrzeń metryczą ( ρ X azywamy zwartą jeśli ażdy ciąg elemetów tej przestrzei posiada podciąg zbieży (do putu tej
wi c warunek konieczny zbie»no±ci szeregu jest speªniony. 12 = 9 12 = 3 4 k(k+1) k=1 ( k+1 k(k+1) n+1 = 1 1 n+1 = 1 0 = 1 36 = =
 32 (+) Jest to szereg o wyrazach dodatich Poadto wyraz ogóly tego szeregu jest zbie»y do 0, wi c waruek koieczy zbie»o±ci szeregu jest speªioy s (+) 2 s 2 s + 2 (2+) 2 + 2 3 2 + 6 3 6 + 6 4 6 2 3 s 3 s
32 (+) Jest to szereg o wyrazach dodatich Poadto wyraz ogóly tego szeregu jest zbie»y do 0, wi c waruek koieczy zbie»o±ci szeregu jest speªioy s (+) 2 s 2 s + 2 (2+) 2 + 2 3 2 + 6 3 6 + 6 4 6 2 3 s 3 s
Elementy statystyki opisowej Izolda Gorgol wyciąg z prezentacji (wykład I)
 Elemety statystyki opisowej Izolda Gorgol wyciąg z prezetacji (wykład I) Populacja statystycza, badaie statystycze Statystyka matematycza zajmuje się opisywaiem i aalizą zjawisk masowych za pomocą metod
Elemety statystyki opisowej Izolda Gorgol wyciąg z prezetacji (wykład I) Populacja statystycza, badaie statystycze Statystyka matematycza zajmuje się opisywaiem i aalizą zjawisk masowych za pomocą metod
Struktura czasowa stóp procentowych (term structure of interest rates)
 Struktura czasowa stóp procetowych (term structure of iterest rates) Wysokość rykowych stóp procetowych Na ryku istieje wiele różorodych stóp procetowych. Poziom rykowej stopy procetowej (lub omialej stopy,
Struktura czasowa stóp procetowych (term structure of iterest rates) Wysokość rykowych stóp procetowych Na ryku istieje wiele różorodych stóp procetowych. Poziom rykowej stopy procetowej (lub omialej stopy,
Chemia Teoretyczna I (6).
 Chemia Teoretycza I (6). NajwaŜiejsze rówaia róŝiczkowe drugiego rzędu o stałych współczyikach w chemii i fizyce cząstka w jedowymiarowej studi potecjału Cząstka w jedowymiarowej studi potecjału Przez
Chemia Teoretycza I (6). NajwaŜiejsze rówaia róŝiczkowe drugiego rzędu o stałych współczyikach w chemii i fizyce cząstka w jedowymiarowej studi potecjału Cząstka w jedowymiarowej studi potecjału Przez
Pierwiastki z liczby zespolonej. Autorzy: Agnieszka Kowalik
 Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
Matematyczne podstawy kognitywistyki
 Matematycze podstawy kogitywistyki Jerzy Pogoowski Zakªad Logiki i Kogitywistyki UAM pogo@amu.edu.pl Struktury ró»iczkowe Jerzy Pogoowski (MEG) Matematycze podstawy kogitywistyki Struktury ró»iczkowe 1
Matematycze podstawy kogitywistyki Jerzy Pogoowski Zakªad Logiki i Kogitywistyki UAM pogo@amu.edu.pl Struktury ró»iczkowe Jerzy Pogoowski (MEG) Matematycze podstawy kogitywistyki Struktury ró»iczkowe 1
6.2. Baza i wymiar. V nazywamy baz-
 62 Baza i wymiar V nazywamy baz- Definicja 66 Niech V bdzie przestrzeni, liniow, nad cia/em F Podzbiór B przestrzeni V, je2eli: () B jest liniowo niezale2ny, (2) B jest generuj,cy, tzn lin(b) =V Przyk/ady:
62 Baza i wymiar V nazywamy baz- Definicja 66 Niech V bdzie przestrzeni, liniow, nad cia/em F Podzbiór B przestrzeni V, je2eli: () B jest liniowo niezale2ny, (2) B jest generuj,cy, tzn lin(b) =V Przyk/ady:
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 1 POZIOM ROZSZERZONY
 Nr zdi Nr czyoci Przykdowy zestw zd r z mtemtyki Odpowiedzi i schemt puktowi poziom rozszerzoy ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM ROZSZERZONY Etpy rozwizi zdi I metod rozwizi ( PITAGORAS
Nr zdi Nr czyoci Przykdowy zestw zd r z mtemtyki Odpowiedzi i schemt puktowi poziom rozszerzoy ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM ROZSZERZONY Etpy rozwizi zdi I metod rozwizi ( PITAGORAS
szereg jest szeregiem o wyrazach nieujemnych. Ponadto dla α (0; π ) zachodzi nierówno± sinα < α,
 .. si Poiewa» si < 1; 1 >, wi c zbadajmy szereg zªo»oy z warto±ci bezwzgl dych wyrazów szeregu daego w zadaiu: () si = si, ale si < 0; 1 > Zatem si 1 () Po prawej stroie powy»szej ierówo±ci mamy szereg
.. si Poiewa» si < 1; 1 >, wi c zbadajmy szereg zªo»oy z warto±ci bezwzgl dych wyrazów szeregu daego w zadaiu: () si = si, ale si < 0; 1 > Zatem si 1 () Po prawej stroie powy»szej ierówo±ci mamy szereg
VII MIĘDZYNARODOWA OLIMPIADA FIZYCZNA (1974). Zad. teoretyczne T3.
 KOOF Szczeci: www.of.szc.pl VII MIĘDZYNAODOWA OLIMPIADA FIZYCZNA (1974). Zad. teoretycze T3. Źródło: Komitet Główy Olimpiady Fizyczej; Olimpiada Fizycza XXIII XXIV, WSiP Warszawa 1977 Autor: Waldemar Gorzkowski
KOOF Szczeci: www.of.szc.pl VII MIĘDZYNAODOWA OLIMPIADA FIZYCZNA (1974). Zad. teoretycze T3. Źródło: Komitet Główy Olimpiady Fizyczej; Olimpiada Fizycza XXIII XXIV, WSiP Warszawa 1977 Autor: Waldemar Gorzkowski
METODY I ZASTOSOWANIA SZTUCZNEJ INTELIGENCJI. LABORATORIUM nr 01. dr inż. Robert Tomkowski
 METODY I ZASTOSOWANIA SZTUCZNEJ INTELIGENCJI LABORATORIUM r 01 Temat: PERCEPTRON dr iż. Robert Tomkowski pok. 118 bud. C robert.tomkowski@tu.koszali.pl tel. 94 3178 251 Metody i zastosowaia sztuczej iteligecji
METODY I ZASTOSOWANIA SZTUCZNEJ INTELIGENCJI LABORATORIUM r 01 Temat: PERCEPTRON dr iż. Robert Tomkowski pok. 118 bud. C robert.tomkowski@tu.koszali.pl tel. 94 3178 251 Metody i zastosowaia sztuczej iteligecji
x + 1 dla x 2 (d) f(x) = + 2 dla x > 2; (3) Znajd¹ dziedzin oraz funkcj odwrotn (je±li jest to proste) do: 1 log 3 x, (log2 x 2 ) 1 log 2
 1. Fukcje elemetare (1) Zajd¹ wykres fukcji arcsi(si(x)). (2) Zajd¹ posªuguj c si wykresami fukcje odwrote do podaych i»ej, a ast pie sprawd¹,»e s to rzeczywi±cie odwrote. (a) f(x) = 2x; (b) f(x) = 3x
1. Fukcje elemetare (1) Zajd¹ wykres fukcji arcsi(si(x)). (2) Zajd¹ posªuguj c si wykresami fukcje odwrote do podaych i»ej, a ast pie sprawd¹,»e s to rzeczywi±cie odwrote. (a) f(x) = 2x; (b) f(x) = 3x
Zestaw zadań do skryptu z Teorii miary i całki. Katarzyna Lubnauer Hanna Podsędkowska
 Zestaw zadań do skryptu z Teorii miary i całki Katarzya Lubauer Haa Podsędkowska Ciała σ - ciała. Zbadaj czy rodzia A jest ciałem w przestrzei X=[0] a) A = X 0 b) A = X 0 3 3 c) A = { X { }{}{ 0}{ 0 }
Zestaw zadań do skryptu z Teorii miary i całki Katarzya Lubauer Haa Podsędkowska Ciała σ - ciała. Zbadaj czy rodzia A jest ciałem w przestrzei X=[0] a) A = X 0 b) A = X 0 3 3 c) A = { X { }{}{ 0}{ 0 }
Podprzestrzenie macierzowe
 Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji ( ) : m f x = Ax ( A) { Ax x } = Defiicja: Zakresem macierzy A Œ âm azywamy
Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji ( ) : m f x = Ax ( A) { Ax x } = Defiicja: Zakresem macierzy A Œ âm azywamy
Modele tendencji rozwojowej STATYSTYKA OPISOWA. Dr Alina Gleska. Instytut Matematyki WE PP. 18 listopada 2017
 STATYSTYKA OPISOWA Dr Alia Gleska Istytut Matematyki WE PP 18 listopada 2017 1 Metoda aalitycza Metoda aalitycza przyjmujemy założeie, że zmiay zjawiska w czasie moża przedstawić jako fukcję zmieej czasowej
STATYSTYKA OPISOWA Dr Alia Gleska Istytut Matematyki WE PP 18 listopada 2017 1 Metoda aalitycza Metoda aalitycza przyjmujemy założeie, że zmiay zjawiska w czasie moża przedstawić jako fukcję zmieej czasowej
MACIERZE STOCHASTYCZNE
 MACIERZE STOCHASTYCZNE p ij - prawdopodobieństwo przejścia od stau i do stau j w jedym (dowolym) kroku, [p ij ]- macierz prawdopodobieństw przejść (w jedym kroku), Własości macierzy prawdopodobieństw przejść:
MACIERZE STOCHASTYCZNE p ij - prawdopodobieństwo przejścia od stau i do stau j w jedym (dowolym) kroku, [p ij ]- macierz prawdopodobieństw przejść (w jedym kroku), Własości macierzy prawdopodobieństw przejść:
Konkurs Uczniowskich Prac z Matematyki. Urok zbioru µ. Michaª Mi±kiewicz. Opiekun pracy: dr Jerzy Bednarczuk
 Kokurs Ucziowskich Prac z Matematyki Urok zbioru µ Michaª Mi±kiewicz Opieku pracy: dr Jerzy Bedarczuk Warszawa 010 Streszczeie Tematem mojej pracy s pukty takie,»e suma kwadratów odlegªo±ci puktów z wcze±iej
Kokurs Ucziowskich Prac z Matematyki Urok zbioru µ Michaª Mi±kiewicz Opieku pracy: dr Jerzy Bedarczuk Warszawa 010 Streszczeie Tematem mojej pracy s pukty takie,»e suma kwadratów odlegªo±ci puktów z wcze±iej
Planowanie adresacji IP dla przedsibiorstwa.
 Planowanie adresacji IP dla przedsibiorstwa. Wstp Przy podejciu do planowania adresacji IP moemy spotka si z 2 głównymi przypadkami: planowanie za pomoc adresów sieci prywatnej przypadek, w którym jeeli
Planowanie adresacji IP dla przedsibiorstwa. Wstp Przy podejciu do planowania adresacji IP moemy spotka si z 2 głównymi przypadkami: planowanie za pomoc adresów sieci prywatnej przypadek, w którym jeeli
Plan wykładu. Analiza danych Wykład 1: Statystyka opisowa. Literatura. Podstawowe pojęcia
 Pla wykładu Aaliza daych Wykład : Statystyka opisowa. Małgorzata Krętowska Wydział Iformatyki Politechika Białostocka. Statystyka opisowa.. Estymacja puktowa. Własości estymatorów.. Rozkłady statystyk
Pla wykładu Aaliza daych Wykład : Statystyka opisowa. Małgorzata Krętowska Wydział Iformatyki Politechika Białostocka. Statystyka opisowa.. Estymacja puktowa. Własości estymatorów.. Rozkłady statystyk
Podstawy matematyki nansowej
 Podstawy matematyki asowej Omówimy tutaj odstawowe oj cia matematyki asowej. Jest to dobre miejsce, gdy» zagadieia te wi» si z ci gami, w szczególo±ci z ci giem arytmetyczym i geometryczym. Omówimy zagadieie
Podstawy matematyki asowej Omówimy tutaj odstawowe oj cia matematyki asowej. Jest to dobre miejsce, gdy» zagadieia te wi» si z ci gami, w szczególo±ci z ci giem arytmetyczym i geometryczym. Omówimy zagadieie
Planowanie organizacji robót budowlanych na podstawie analizy nakładów pracy zasobów czynnych
 Budowictwo i Architektura 12(1) (2013) 39-46 Plaowaie orgaizacji robót budowlaych a podstawie aalizy akładów pracy zasobów czyych Roma Marcikowski 1 1 Istytut Budowictwa, Wydział Budowictwa Mechaiki i
Budowictwo i Architektura 12(1) (2013) 39-46 Plaowaie orgaizacji robót budowlaych a podstawie aalizy akładów pracy zasobów czyych Roma Marcikowski 1 1 Istytut Budowictwa, Wydział Budowictwa Mechaiki i
Ekonomia matematyczna - 1.1
 Ekoomia matematycza - 1.1 Elemety teorii kosumeta 1. Pole preferecji Ozaczmy R x x 1,...,x : x j 0 x x, x j1 j. R rozpatrujemy z ormą x j 2. Dla x x 1,...,x,p p 1,...,p Ip x, p x j p j x 1 p 1 x 2 p 2...x
Ekoomia matematycza - 1.1 Elemety teorii kosumeta 1. Pole preferecji Ozaczmy R x x 1,...,x : x j 0 x x, x j1 j. R rozpatrujemy z ormą x j 2. Dla x x 1,...,x,p p 1,...,p Ip x, p x j p j x 1 p 1 x 2 p 2...x
Analiza Matematyczna I dla Inżynierii Biomedycznej Lista zadań
 Aaliza Matematycza I dla Iżyierii Biomedyczej Lista zadań Jacek Cichoń, WPPT PWr, 205/6 Logika, zbiory i otacja matematycza Zadaie Niech p, q, r będą zmieymi zdaiowymi. Pokaż, że:. = ( (p p)), 2. = (p
Aaliza Matematycza I dla Iżyierii Biomedyczej Lista zadań Jacek Cichoń, WPPT PWr, 205/6 Logika, zbiory i otacja matematycza Zadaie Niech p, q, r będą zmieymi zdaiowymi. Pokaż, że:. = ( (p p)), 2. = (p
Podprzestrzenie macierzowe
 Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji : m f x = Ax RAAx x Defiicja: Zakresem macierzy A Œ âm azywamy podprzestrzeń
Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji : m f x = Ax RAAx x Defiicja: Zakresem macierzy A Œ âm azywamy podprzestrzeń
GEOMETRIA I UŠAMKI PIOTR NIADY
 GEOMETRIA I UŠAMKI PIOTR NIADY Alicja raz czy dwa zajrzaªa do ksi»ki czytaej przez siostr, ale ie byªo tam ai ilustracji, ai kowersacji. A jaki mo»e by po»ytek z ksi»kipomy±laªa Alicjaw której ie ma ai
GEOMETRIA I UŠAMKI PIOTR NIADY Alicja raz czy dwa zajrzaªa do ksi»ki czytaej przez siostr, ale ie byªo tam ai ilustracji, ai kowersacji. A jaki mo»e by po»ytek z ksi»kipomy±laªa Alicjaw której ie ma ai
Zdarzenia losowe, definicja prawdopodobieństwa, zmienne losowe
 Metody probabilistycze i statystyka Wykład 1 Zdarzeia losowe, defiicja prawdopodobieństwa, zmiee losowe Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki
Metody probabilistycze i statystyka Wykład 1 Zdarzeia losowe, defiicja prawdopodobieństwa, zmiee losowe Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki
Metoda najszybszego spadku
 Metody Gradietowe W tym rozdziale bdziemy rozwaa metody poszuiwaia dla fucji z przestrzei R o wartociach rzeczywistych Metody te wyorzystuj radiet fucji ja rówie wartoci fucji Przypomijmy, czym jest zbiór
Metody Gradietowe W tym rozdziale bdziemy rozwaa metody poszuiwaia dla fucji z przestrzei R o wartociach rzeczywistych Metody te wyorzystuj radiet fucji ja rówie wartoci fucji Przypomijmy, czym jest zbiór
Geometrycznie o liczbach
 Geometryczie o liczbach Geometryczie o liczbach Łukasz Bożyk Dodatią liczbę całkowitą moża iterpretować jako pole pewej figury składającej się z kwadratów jedostkowych Te prosty pomysł pozwala w aturaly
Geometryczie o liczbach Geometryczie o liczbach Łukasz Bożyk Dodatią liczbę całkowitą moża iterpretować jako pole pewej figury składającej się z kwadratów jedostkowych Te prosty pomysł pozwala w aturaly
Charakterystyki liczbowe zmiennych losowych: wartość oczekiwana i wariancja
 Charakterystyki liczbowe zmieych losowych: wartość oczekiwaa i wariacja dr Mariusz Grządziel Wykłady 3 i 4;,8 marca 24 Wartość oczekiwaa zmieej losowej dyskretej Defiicja. Dla zmieej losowej dyskretej
Charakterystyki liczbowe zmieych losowych: wartość oczekiwaa i wariacja dr Mariusz Grządziel Wykłady 3 i 4;,8 marca 24 Wartość oczekiwaa zmieej losowej dyskretej Defiicja. Dla zmieej losowej dyskretej
STATYSTYKA I ANALIZA DANYCH
 TATYTYKA I ANALIZA DANYCH Zad. Z pewej partii włókie weły wylosowao dwie próbki włókie, a w każdej z ich zmierzoo średicę włókie różymi metodami. Otrzymao astępujące wyiki: I próbka: 50; średia średica
TATYTYKA I ANALIZA DANYCH Zad. Z pewej partii włókie weły wylosowao dwie próbki włókie, a w każdej z ich zmierzoo średicę włókie różymi metodami. Otrzymao astępujące wyiki: I próbka: 50; średia średica
