Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci standardowej.
|
|
|
- Artur Piekarski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Zadania Zadanie Wyznaczyć dopuszczalne rozwiązanie bazowe układu x 1 x 2 + 2x 3 = 2 x 2-3x 3 = 6 x 1 + x 3 + x 4 =2 x 1, x 2,x 3 0 Zadanie Wyznaczyć dopuszczalne rozwiązanie bazowe układu x 1 x 2 + x 3 - x 4 + x 5 = 6 2x 2 - x 3-3x 4 = 4 3x 1 +2x 3 + x 4 =2 x 1, x 2,x 3, x 4, x 5 0 Zadanie Wyznaczyć dopuszczalne rozwiązanie bazowe układu x x 4 + x 5 = 2 x 3 - x 4 + 2x 5 = -3 2x 2 + x 4-2x 5 = -10 x 1, x 2,x 3, x 4, x 5 0 Zadanie Układ warunków, jakie mają spełniać niewiadome x i sprowadzić do równoważnego układu równań 2x 1 x 2-3x 4 + x 5 = 2 x 3 - x 4 + 2x 5-3 2x 2 + x 4-2x 5-10 Zadanie Układ warunków, jakie mają spełniać niewiadome x i sprowadzić do równoważnego układu równań x 1 x 2 + x 3 - x 4 + x 5 6 2x 2 - x 3-3x 4 = 4 3x 1 +2x 3 + x 4 2 x 1, x 2,x 3, x 4, x 5 0 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci standardowej. 3x 1 2x 2 + x 3-3x 4 max 2x 1 x 2 + 2x 3-2 6x 2-3x 3 6 x 1 + x 3 + x 4 =2 x 1, x 2,x 3, x 4 0
2 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci standardowej. 3x 1 +4x 2 + x 3-3x 4 max 2x 1 4x 2-3x 4 + x 5 = 2 x 3 + 2x 4 + 2x 5-3 2x 2 + x 4-2x 5 10 x 1, x 2,x 3, x 4 0, x 5 dowolnego znaku Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci standardowej. 3x 1 2x 2 + x 3-3x 4 min 2x 1 x 2-5x 3 2 6x 2 + 3x 3 6 x 1 + 2x 3 + x 4 = -6 x 1, x 2,x 3, x 4 0 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci kanonicznej. 3x 1 2x 2 + x 3-3x 4 max x 1 x 2 + 2x 3-2 6x 2-3x 3 6 2x 1 + x 3 + x 4 = 7 x 1, x 2,x 3, x 4 0 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci kanonicznej. 3x 1 +4x 2 + x 3-3x 4 max 2x 1 4x 2-3x 4 - x 5 = 2 x 3 + 2x 4 + 2x 5 3 2x 2 - x 4 - x 5 10 x 1, x 2,x 3, x 4 0, x 5 dowolnego znaku Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci kanonicznej. x 1 2x 2 + x 3-3x 4 min 2x 1 x 2-5x 3 2 6x 2 + 3x 3 9 x 1 + 2x 3 + x 4 = -6 x 1, x 2,x 3, x 4 0 Zadanie Metodą graficzną wyznaczyć rozwiązania optymalne zagadnienia programowania liniowego. x 1 2x 2 min x 1 x 2 1 x 1 + x 2 2 x 1-2x 2 0 x 1, x 2 0
3 Zadanie Metodą graficzną wyznaczyć rozwiązania optymalne zagadnienia programowania liniowego. 5x 1 + 2x 2 min 3x 1 + 5x x 1 + 2x 2 10 x 1, x 2 0 Zadanie Metodą graficzną wyznaczyć rozwiązania optymalne zagadnienia programowania liniowego. x 1 + 2x 2 max x 1 x 2 1 2x 1 + x 2 2 x 1 - x 2 0 x 1, x 2 0 Zadanie Metodą graficzną wyznaczyć rozwiązania optymalne zagadnienia programowania liniowego. x 1 + 3x 2 max -x 1 x 2-3 6x 1 + x x 1-3 x 2 6 x 1 + x 2 4 x 1, x 2 0 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci dualnej. x 1 +4x 2 + x 3-3x 4 max 2x 1 4x 2 + x 3-3x 4 + x 5 = 2 x 3 + 2x 4 + 2x 5-3 2x 2 + x 4-2x 5 10 x 1, x 2,x 3, x 4, x 5 0 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci dualnej. Rozwiązać metodą graficzną zagadnienie dualne, a następnie posługując się twierdzeniem o komplementarności wyznaczyć rozwiązanie zagadnienia pierwotnego. 3x 1 2x 2 + x 3-3x 4 min 2x 1 x 2-5x 3 2 6x 2 + 3x 3 6 x 1, x 2,x 3, x 4 0 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci dualnej. Rozwiązać metodą graficzną zagadnienie dualne, a następnie posługując się twierdzeniem o komplementarności wyznaczyć rozwiązanie zagadnienia pierwotnego.. 3x 1 2x 2 + x 3-3x 4 max x 1 x 2 + 2x 3 2
4 2x 2-3x 3-6 x 1, x 2,x 3, x 4 0 Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci dualnej. Rozwiązać metodą graficzną zagadnienie dualne, a następnie posługując się twierdzeniem o komplementarności wyznaczyć rozwiązanie zagadnienia pierwotnego. 3x 1 +4x 2 + x 3-3x 4 max x 3 + 2x 4 + 2x 5 3 2x 2 - x 4 - x 5 10 x 1, x 2,x 3, x 4 0, x 5 dowolnego znaku Zadanie Następujące zadanie programowania liniowego sprowadzić do postaci dualnej. Rozwiązać metodą graficzną zagadnienie dualne, a następnie posługując się twierdzeniem o komplementarności wyznaczyć rozwiązanie zagadnienia pierwotnego. x 1 2x 2 + x 3-3x 4 min 2x 1 x 2-5x 3 2 6x 2 + 3x 3 9 x 1, x 2,x 3, x 4 0 Zadanie Zdolność produkcyjna zakładu umożliwia wytwarzanie 300 silniczków typu A lub 600 silniczków typu B w ciągu jednej zmiany. Ustalić ile silniczków każdego typu powinien produkować zakład aby wytworzyć maksymalną liczbę silniczków? Zagadnienie rozwiązać metodą graficzną. Zadanie Zdolność produkcyjna zakładu umożliwia wytwarzanie 200 silniczków typu A lub 250 silniczków typu B w ciągu jednej zmiany. Ustalić ile silniczków każdego typu powinien produkować zakład aby osiągnąć maksymalny zysk, jeśli zysk ze sprzedaży jednego silniczka typu A jest dwa razy większy od zysku ze sprzedaży silniczka typu B? Zagadnienie rozwiązać metodą graficzną. Zadanie Zdolność produkcyjna wydziału obróbki cieplnej zakładu umożliwia wytwarzanie w ciągu miesiąca 600 detali typu X lub 1200 detali typu Y. Po obróbce cieplnej detale trafiają do wydziału obróbki mechanicznej. Zdolności produkcyjne tego wydziału pozwalają dokonać obróbki 1200 detali X lub 800 detali Y w ciągu miesiąca. Ustalić ile detali powinien produkować miesięcznie zakład aby osiągnąć maksymalny przychód jeśli ceny obu detali są jednakowe? Zagadnienie rozwiązać metodą graficzną. Zadanie Fabryka zabawek może wytwarzać dwa typy samochodzików A i B sterowanych radiem.zdolności produkcyjne poszczególnych wydziałów przedstawiono w tablicy Wydział Liczba samochodzików wytworzonych w ciągu miesiąca A B
5 Przygotowania produkcji Tłoczenia karoserii Montowania silniczków Montowania radia Kontroli i pakowania Określić miesięczny plan produkcji samochodzików przynoszący maksymalny zysk jeśli zysk ze sprzedaży jednego samochodziku A wynosi 20 jp., samochodziku B- 30 jp. Zadanie Pan Karol posiada pewną kwotę, którą chciałby zainwestować w akcje i lokaty. Wiadomo, że akcje mogą przynieść zysk w wysokości 19% zainwestowanej w nie kwoty, natomiast obligacje - 16%. W jaki sposób powinna zostać optymalnie zainwestowana posiadana przez pana Karola kwota jeśli zakłada, że zyski powinny być nie mniejsze niż 17% zainwestowanej kwoty, a kwota zainwestowana w akcje nie powinna przekraczać 60% całej kwoty przeznaczonej na inwestycje. Zadanie Rolnik posiada dwa pola o powierzchniach odpowiednio 15 ha i 30 ha. W związku ze specjalizacją produkcji zamierza wprowadzić jedynie trzy uprawy: szparagi, kapustę pekińską oraz orzeszki ziemne. W zależności od rodzaju uprawy zmienia się koszt uprawy jednego hektara. Dla szparagów wynosi on 1500 zł, dla kapusty 1000 zł, dla orzeszków 1200 zł. Na wydajność z hektara ma wpływ pogoda. W przypadku pogody umiarkowanej wydajność kształtuje się na poziomie 2 q/ha, 3 q/ha i 2.5 q/ha odpowiednio dla szparagów, kapusty, orzeszków stanowiąc jednocześnie poziom odniesienia dla pozostałych wydajności. W przypadku wystąpienia upałów wydajność zmniejsza się o 15%, w przypadku deszczy wydajność spada do 65% założonych wydajności w przypadku umiarkowanej pogody. Cena, za jaką rolnik sprzedaje swoje uprawy jest stała, niezależna od pogody i wynosi odpowiednio dla szparagów, kapusty, orzeszków :100 zł/q, 80 zł/q i 70 zł/q. Rolnik uznaje, że opłaca mu się uprawiać ziemię, kiedy jego oczekiwany zysk jest nie mniejszy niż zł. Długoterminowa prognoza zakłada, że deszcze wystąpią z prawdopodobieństwem 0,15, upały 0,35,a pogoda umiarkowana 0,5. Zapisać program linowy pomocny w podjęciu decyzji o uprawach. Zadanie Krawcowa może zakupić nie więcej niż 32 małych odpadków materiału po 5 zł za sztukę lub nie więcej niż 45 dużych po 15 zł za sztukę. Z jednego małego kawałka wykrawa 40 kwadraty,30 trójkątów i 50 rombów albo 10 kwadratów 50 trójkątów i 100 rombów. Duży kawałek może być rozcinany na dwa sposoby pierwszy z nich pozwala uzyskać 50 kwadratów, 20 trójkątów i 150 rombów. Drugim sposobem otrzyma 120 trójkątów i 200 rombów. Kawałki zszywane są ze sobą, w ten sposób powstaje zabawna pacynka (5 kwadraty, 4 trójkąty i 10 rombów) sprzedawana po 7 zł. Zapisz program liniowy, który pozwoli na maksymalizowanie zysku krawcowej. Zadanie Mroźna zima i lawinowo rosnące zamówienia zmusiły frmę PTASI-BAR wzmożenia produkcji karmników. Firma w magazynie posiada 20 płyt dużych i 15 małych. Płyty te rozcinane są na kawałki w trzech typach A, B, C. Z dużej płyty można wyciąć 120 kawałków A, 130- B i D. Jeżeli zastosuje się inny sposób cięcia otrzymać można 50 kawałków A, 30 - B i D. Małe płyty można również rozkrawać na dwa sposoby: 30 kawałków A, 40 - B, 20 - C albo 50 -B i 40 - C. Zapisać program liniowy maksymalizujący wartość sprzedaży karmników wiedząc, że na jeden karmnik przypadają 2 elementy A, 3- B i 4 -C oraz karmniki sprzedawane są po 15 zł. Zadanie Rozdzielić produkcję 4 elementów na 3 maszyny. Jedna maszyna może produkować, co najwyżej jeden element, żaden element nie może być produkowany więcej niż na
6 jednej maszynie. Tabela podaje koszty produkcji partii elementów w tysiącach złotych oraz jej wielkość w tysiącach sztuk w rozbiciu na poszczególne maszyny. Podana jest cena, za jaką zakład może sprzedać jedną sztukę wyprodukowanego elementu w zł. W jaki sposób przydzielić poszczególne maszyny do produkcji elementów aby osiągnąć maksymalny zysk? Element Wielkość produkowanej partii na Koszt produkcji partii elementów Cena maszynie w tys. szt. w tys. zł. elementu M 1 M 2 M 3 M 1 M 2 M 3 A 1 2 0, B 2 1,5 1,5 3,5 4,5 5,5 5 C ,5 4,5 7 7 D ,5 6 9 Zadanie Rafineria wytwarza trzy rodzaje olejów A, B, C z trzech surowców I, II, III, których może zamówić odpowiednio 200 tys. ton, 300 tys. ton i 250 tys. ton. Do produkcji oleju A należy użyć surowców I, II, III odpowiednio w proporcjach 2:4:3, do oleju B surowca II i III w proporcji 3:4, do oleju C surowców I, II, III odpowiednio w proporcjach 4:3:2. Koszt jednej tony surowca I, II, III wynosi odpowiednio 23, 55, 40 jp. Oleje A, B, C rafineria sprzedaje odpowiednio po 70, 50, 65 jp. Ustalić plan zamówień surowców oraz produkcji mający na uwadze maksymalizacje zysku i wyprodukowanie minimum po 50 tysięcy ton każdego oleju. Zadanie Przetwórnia ropy naftowej wytwarza trzy rodzaje benzyn A, B, C z trzech surowców I, II, III,. Do zakładu dostarczono 200 tys. ton surowca I, 300 tys. ton surowca II i 250 tys. ton surowca III. Do produkcji benzyny A należy użyć surowców I, II, III odpowiednio w proporcjach 2:4:3, do benzyny B surowca I i III w proporcji 2:3, do benzyny C- surowców I, II, III odpowiednio w proporcjach 2:5:4. Ustalić plan produkcji benzyn mający na uwadze maksymalne wykorzystanie surowca. Zadanie Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące kosztów przewozu jednostki z magazynu do sklepu oraz wielkości zapasów i zapotrzebowania zamieszczono w tabeli. Określić plan przewozu minimalizujący koszty. Magazyn M 1 M 2 M 3 M 4 Zapotrzebowanie Sklep w sklepie S S S S S Zapas w magazynie Zadanie Odlewnia pomników ma zamówienie na wykonanie pomnika ze specjalnego stopu, który ma zawierać nie mniej niż 14% C, nie więcej niż 6% Mn, nie więcej niż 5% S i nie mniej niż 23% Sn. Odlewnia może zamówić trzy stopy sprzedawane w odlewach. Zminimalizować koszt materiału potrzebnego na odlanie pomnika, który ma ważyć 1 tonę, jeżeli proces technologiczny
7 produkcji stopu polegać ma na stopieniu dostarczonych odlewów. W tabeli podano procentowe zawartości pierwiastków w poszczególnych stopach, ceny odlewów i ich masę Pierwiastek Stop C Mn S Sn Cena odlewu I II III Masa odlewu kg Zadanie Zakład RURA ma wyprodukować 100 rur o długości 5,5 m i 150 o długości 7,5 m. Zakład ma do dyspozycji rury o długości 17 m. Jak należy pociąć rury, aby odpad był najmniejszy? Pozostałe rury długości 5,5 i 7,5 stanowią odpad. Zapisz odpowiedni program liniowy. Zadanie Zakład dysponuje czterema typami koparek oraz ma wykonać usługi polegające na wykopaniu odpowiednich rowów. Tabela podaje liczby odpowiednich typów koparek w zakładzie, ich wydajności przy poszczególnych pracach, koszty eksploatacji oraz minimalne ilości m 3. Wydajność m3 / dzień Liczba koparek Koszty Koparka Rów 1 Rów 2 Rów 3 w zakładzie eksploatacji A B C D Minimalna dzienna wydajność m Zapisać program liniowy wyznaczający przydział koparek do prac minimalizujący koszty prac. Zadanie Fabryka produkująca fortepiany i pianina ma w ciągu 90 dni wykonać 13 fortepianów, 20 pianin Pianola, 25 pianin Elita. W fabryce znajduję się 4 brygady potrafiące wykonywać te instrumenty. Brygady różnią się pod względem wydajności i kosztów wytwarzania. Rozdzielić prace pomiędzy brygady w taki sposób, aby zrealizować zadanie w terminie i po jak najmniejszych kosztach. Brygada Czas produkcji jednej sztuki w dniach Koszty produkcji jednej sztuki Fortepian Pianola Elita Fortepian Pianola Elita Zadanie Przedsiębiorstwo przewozowe Świeża rybka zajmuje się dostarczaniem śledzi solonych do sklepów. Dane dotyczące kosztów przewozu kubełka śledzi z magazynu do sklepu oraz
8 wielkości zapasów i zapotrzebowania ( w kubełkach) zamieszczono w tabeli. Określić plan przewozu minimalizujący koszty. Magazyn M 1 M 2 M 3 M 4 Zapotrzebowanie Sklep w sklepie S S S S S Zapas w magazynie Zadanie Zakład otworzył nowy oddział, na którym zainstalowano dwie nowoczesne obrabiarki. Na każdej z nich można wykonywać kilka różnych prac. Zakład produkuje wirniki do silników różnych typów. Postanowiono, że na nowym oddziale będą produkowane tylko trzy typy wirników. Zakład pracuje 8 godzin i obrabiarki mogą pracować przez całą zmianę bez potrzeby zatrzymywania się. Czasy jednostkowe produkcji, jednostkowe koszty produkcji, cenę zbytu oraz wielkości zamówień podaje tabela. Jak rozdzielić pracę pomiędzy obrabiarki aby maksymalizować zysk zakładu jeśli zakłada się, że zamówienia mają zostać zrealizowane w ciągu jednej zmiany? Obrabiarka Zużycie czasu pracy w min. na jedną sztukę Jednostkowy koszt produkcji jednego wirnika T 1 T 2 T 3 T 1 T 2 T Zamówienie Cena 1 szt Zadanie Krawcowa z dostarczanych odpadków materiału szyje ubranka dla lalek. Są dwa rodzaje odpadków i w zależności od ich typu można z nich uszyć różne ubranka. Krawcowa dostała zlecenie na uszycie większej liczby ubranek, które ma dostarczyć w kompletach. Jak należy ustalić produkcję, aby ogólna liczba wykorzystanych odpadów materiału była najmniejsza? Odpad Typ ubranka Zapas odpadu ADA ALA OLA u krawcowej Komplet Zamówienie szt. Mini Mini MAX
9 Zadanie Tartak produkuje altanki mając do dyspozycji dwa rodzaje bali, z których może wycinać deski na altanki. W tabeli podano wszystkie możliwe sposoby cięcia bali i ich zapasy. Należy tak ustawić produkcję, aby wytworzyć jak największą liczbę altanek. Bal i sposoby Rodzaj deski jego cięcia A B C 1/ / / / / Liczba desek potrzebna na altankę Zapas bali w tartaku Zadanie Zakład posiada 4 oddziały na których obecnie można produkować trzy typy elementów A, B, C. Dyrektor zakładu postanowił, że na oddziałach będzie wprowadzona specjalizacja to znaczy każdy oddział będzie produkował tylko jeden typ elementów, a każdy typ elementu może być produkowany na jednym oddziale. Dane dotyczące obecnych zdolności produkcyjnych przedstawia tabela. Zakład posiada kontrakt, który musi wypełnić i należy wyprodukować odpowiednie ilości elementów A, B, C. Należy przedstawić najlepszy plan specjalizacji oddziałów, mający na celu realizację zamówienia oraz maksymalizację ogólnej ilości wytworzonych sztuk. Element Oddział A B C Zamówienie Uwaga. Przez zdolności produkcyjne rozumie się maksymalną liczbę sztuk wyrobów produkowanych w jednostce czasu w przypadku gdy oddział produkuje tylko ten wyrób. Zadanie Zakład krawiecki posiada 3 oddziały, na których może szyć trzy rodzaje garniturów: klasyczny, sportowy i elegancki. Wyposażenie oddziałów sprawia, że koszt produkcji i jej czas są zróżnicowane dla poszczególnych oddziałów. Jak należy rozdzielić produkcję na poszczególne oddziały, aby koszty jej były jak najmniejsze oraz zostały zrealizowane tygodniowe zamówienia. Oddział Zdolności produkcyjne oddziału w sztukach na tydzień Jednostkowe koszty produkcji Klasyczny Sportowy Elegancki Klasyczny Sportowy Elegancki Mały Średni Duży Zamówienia
10 Uwaga. Przez zdolności produkcyjne rozumie się maksymalną liczbę garniturów, które oddział może wyprodukować w ciągu tygodnia w przypadku gdy będzie produkował tylko tego typu garnitury. Staż pracowników Lata Doświadczenie Punkty Liczba pracowników Zadanie Przedsiębiorstwo KOLOPEX zamierza przejąć 60 nowych pracowników z przedsiębiorstwa MAPS-PEX. Dotychczas KOLOPEX zatrudniał 140 pracowników, struktura zatrudnienia przedstawiała się w sposób następujący: średni staż 15 lat, średnie doświadczenie 12 punktów. Dane dotyczące struktury zatrudnienia MAPS- PEX u przedstawiono w tabeli. Zapisać program liniowy rozwiązujący zagadnienie optymalnego zatrudnienia, jeżeli należy maksymalizować średnie doświadczenie pracowników gdy staż pracy nowej załogi nie może się zmienić o więcej niż 10%. Zadanie Dla zwiększenia produkcji firma DACH-TEX zamierza zatrudnić nowych pracowników. Szacuje się, że potrzeba od 30 do 75 nowych pracowników. Zatrudnienie doświadczonego pracownika związane jest z dodatkowymi kosztami, które musi ponieść firma na podkupienie pracownika z konkurencyjnej firmy. Nowy pracownik jest o wiele tańszy. Obecnie zatrudnionych jest 150 pracowników, średni wiek pracowników wynosi 38 lat a średnie doświadczenie 20 pkt. Na ogłoszenie zgłosiło się 200 chętnych do pracy. Dane o nich zestawiono w tabeli. Zapisać program liniowy mający za zadanie minimalizację kosztów ponoszonych przy zatrudnianiu nowych pracowników i uwzględniający następujące warunki: średni wiek ma pozostać na poziomie lat, średnie doświadczenie nie może się zmienić o więcej niż 15%. Wiek pracownika Ilość pracowników Doświadczenie Koszty zatrudnienia
11 Zadanie Przedsiębiorstwo przewozowe Lśniący bucik zajmuje się dostarczaniem butów do sklepów. Dane dotyczące kosztów przewozu jednej pary butów z magazynu do sklepu oraz wielkości zapasów i zapotrzebowania zamieszczono w tabeli. określić plan przewozu minimalizujący koszty. Magazyn M 1 M 2 M 3 M 4 Zapotrzebowanie Sklep w sklepie S S S S S Zapas w magazynie Zadanie Należy podjąć decyzję o zamknięciu jednego z 4 oddziałów mając na uwadze największy zysk przedsiębiorstwa. Dane dotyczące oddziałów przedstawia tabela. Oddział Dane A B C D Ilość pracowników Koszt utrzymania 1 pracownika Średni poziom kwalifikacji Średni wiek pracownika Wartość produkcji 1 pracownika Ponadto założono, że po zamknięciu w przedsiębiorstwie poniższe wielkości mają kształtować się następująco: 1. Średnie koszty utrzymania pracownika nie mogą być większe niż 12,5. 2. Średnia wartość produkcji jednego pracownika nie może być mniejsza niż Średnie kwalifikacje nie mniejsze niż 8 4. Średni wiek nie większy niż 35. Napisać program liniowy, który pozwoli rozwiązać problem zamknięcia oddziału. Zadanie Sześć przedsiębiorstw postanowiło zawiązać konsorcjum. Na zebraniu prezesów rad nadzorczych ustalono kryteria zawiązania i przystępowania przedsiębiorstw do konsorcjum. Po burzliwych debatach ustalono następujące kryteria: Średnie kwalifikacje pracowników konsorcjum powinny być na poziomie nie mniejszym niż 25. Średni wiek pracowników powinien zawierać się pomiędzy 25 a 38 lat. Średnia wartość produkcji jednego pracownika nie powinna być mniejsza niż 152. Średnie koszty utrzymania jednego pracownika nie powinny być większe niż 93. Dane przedstawiają wyniki przedsiębiorstw w badanym okresie. Przedsiębiorstwo Ilość zatrudnianych pracowników Średnie kwalifikacje Średni wiek pracownikó w Średnia wartość produkcji Średnie koszty utrzymania A
12 B C D E F Napisać program liniowy, którego rozwiązaniem jest maksymalna liczba przedsiębiorstw, które mogą zawiązać konsorcjum. Zadanie Fabryka mebli wytwarza dwa rodzaje szaf, dwa rodzaje regałów i jeden typ barku. Następnie składa je w trzy komplety mebli: Agata, Beata, Cecylia. Szafa 1 Szafa 2 Regał 1 Regał 2 Barek 1 Agata Beata Cecylia Fabryka posiada dwa zakłady produkujące poszczególne elementy i dwa sklepy firmowe. W sklepach ogółem złożono zamówienia na 30 zestawów Agata, 35 zestawów Beata i 25 zestawów Cecylia ( w sklepie pierwszym odpowiednio 20, 15, 15 ). Tabele przedstawiają zdolności produkcyjne poszczególnych zakładów koszty wytworzenie jednego elementu oraz ceny transportu poszczególnych elementów do poszczególnych sklepów. Zakład 1 produkcja Koszt Zdolności produkcyjne Koszt transportu do sklepu 1 Koszt transportu do sklepu 2 Szafa Szafa Regał Barek Zakład 2 produkcja Koszt Zdolności produkcyjne Koszt transportu do sklepu 1 Koszt transportu do sklepu 2 Szafa Regał Regał Barek Ustalić plan produkcji minimalizujący koszty produkcji oraz transportu. Zadanie Podjąć decyzję o zwolnieniu pracowników w fabryce. Strukturę zatrudnienia przedstawia tabela. wiek ilość pracowników średni wiek pracownika średnie doświadczenie średnie koszty utrzymania 1 średni przychód od
13 pracownika w danej grupie w danej grupie wiekowej pracownika w danej grupie ( od 0 do 10 ) pracownika danej grupy jednego pracownika danej grupy starsi średni młodzi Założono dodatkowo, że: nie można zwolnić więcej niż 15 % wszystkich pracowników. średni wiek pracowników nie powinien się zmienić o więcej niż 10%. średnie doświadczenie pracowników nie powinno być mniejsze niż 6.5. Jako jedyne kryterium postanowiono zastosować kryterium zysku przedsiębiorstwa. Zadanie Fabryka rowerów ma cztery zakłady, w których wytwarzane są trzy rodzaje rowerów. Nowe kierownictwo podjęło decyzję o specjalizacji zakładów. Dokonać podziału mając na uwadze maksymalny zysk zakładu ze sprzedaży wytworzonych rowerów przyjmując, że praca na zmianie trwa 450 minut. Czas produkcji jednego roweru na zmianie [ min ]. Zakład Składak Górski Turystyczny Cena zbytu Zadanie Fabryka mebli dostała zamówienie na wykonanie 20 tapczanów, 10 sof, 14 kanap i 30 leżanek. Do realizacji tego zadanie wyznaczono 4 brygady. Mając podane nakłady czasu na wykonanie jednego mebla przez brygadę należy tak rozdzielić pracę tak, aby czas jej wykonania był jak najkrótszy. Brygada Tapczan Sofa Kanapa Leżanka
14 Zadanie Rolnik ze wsi Bystra Wola ma do dyspozycji 5 ha ziemi i 600 godzin wolnego czasu. Chcąc poprawić swój budżet udał się do punktu konsultacyjnego. Prześliczna pani w okienku podała rolnikowi zestawienie proponowanych upraw oraz poinformowała rolnika z uśmiechem, że jest to jej pierwszy dzień pracy i więcej informacji mu nie może udzielić. Rolnik z otrzymaną kartką przyjechał do domu i stwierdził, że z proponowanych 6 upraw wybrać może tylko, co najwyżej 4, a jego wymagająca żona stwierdziła, że dla bezpieczeństwa powinien uprawiać, co najmniej dwie. Uprawa Powierzchnia potrzebna do uprawy [ ha ] Ilość godzin potrzebnych do uprawy Wydajność z 1 ha w q Cena jednego q w skupie Wskaźnik Z nakłady pracy do zysku na 1 ha zasiewu A 1, % B 1, % C 2, % D 1, % E % F 0, % G 0, % Napisać program liniowy mający na celu otrzymanie jak największej ilości gotówki po sprzedaniu upraw oraz zapewniający średni poziom wskaźnika Z z wybranych upraw na poziomie, co najwyżej 50%. Zadanie Korporacja ZBO składa się z trzech przedsiębiorstw, dwa z nich to zakłady produkcyjne, trzecim jest wyspecjalizowana montownia. Zakład pierwszy specjalizuje się w produkcji kapsuł, pojemników i kontenerów. Tabela 1 podaje zdolności produkcyjne na każdy z produktów, koszty wytworzenia, oraz cenę sprzedaży elementów oraz minimalną produkcję przeznaczoną do sprzedaży poza kompletami. Zakład drugi wytwarza specjalistyczne podstawki i opakowania. Tabela 2. podaje parametry produkcji, które należy uwzględnić w modelu matematycznym. W montowni składa się w komplety produkowane elementy. Warunki produkcji i sprzedaży podaje Tabela 3. Tabela 1. Cena sprzedaży Minimalna Koszty Zdolności produkcja wytworzenia produkcyjne Kapsuła Pojemnik Kontener Tabela 2 Cena Minimalna Koszty Zdolności sprzedaży produkcja wytworzenia produkcyjne Podstawka
15 Podstawka Opakowanie Tabela 3 Elementy składowe kompletu Cena Komplet Kapsuła Kontener Podstawka 1 Opakowanie Ola Ola Jak należy ustalić produkcję w trzech zakładach dla osiągnięcia największego zysku? Zadanie Rozdzielić produkcję trzech detali 1, 2, 3 pomiędzy dwa typy tokarek tak, aby maksymalizować liczbę kompletów wytwarzanych w ciągu dnia. Na jeden komplet składają się detale w proporcjach 2:3:1. Dzienna wydajność każdej z maszyn w zależności od poszczególnych detali podana jest w tabeli. Detale 1, 2, 3 produkowane są w całości na jednej z obrabiarek, wykończenie ich przebiega na automacie. Zapisać program liniowy dla powyższego zagadnienia. Obrabiarki Wydajność maszyn w detalach na dzień Tokarka I Tokarka II Automat Zadanie Dla wytworzenia trzech dużych maskotek A, B, C fabryka zużywa pewne ilości pluszu i kolorowych materiałów. Zasoby materiałów, siły roboczej, zużycie materiałów na maskotkę w metrach oraz liczbę wyprodukowanych maskotek w ciągu godziny podaje tabela. Rozmiar zasobów Maskotka A B C Plusz 125 m Materiał kolorowy 252 m Siła robocza 1540 h Zysk Wyznaczyć plan produkcji maksymalizujący zysk, sformułować program liniowy. Zadanie Firma SOHO zajmuje się składaniem komputerów i dostarczaniem ich do sklepów. Firma posiada dwie montownie, w których można zmontować 150 i 400 komputerów w ciągu miesiąca. Dzięki dobrej pozycji na rynku firma nawiązała współpracę z trzema sklepami A, B, C, do których dostarcza komputery. W przeciągu najbliższego miesiąca sklepy zamówią odpowiednio 180, 200, 150 komputerów. Ponieważ komputery dowożone są po telefonie ze sklepu przyjmuje się, że koszty jednostkowe transportu komputera wynoszą z montowni mniejszej odpowiednio 50 zł, 35 zł i 25 zł. Jednostkowe koszty transportu z większej montowni wynoszą: 75 zł, 55 zł i 60 zł. Firma kupuje części w dwóch różnych hurtowniach. Znaczące różnice cen dotyczą dysków twardych, procesorów i płyt głównych, nie bez znaczenia jest również producent sprzętu (ze względu na wadliwość elementów). Dewizą firmy jest w przypadku stwierdzenia wadliwości elementu natychmiastowa wymiana go na nowy, co niewątpliwie ma znaczący wpływ na koszty.
16 Obecnie w hurtowniach znajdują się następujące oferty dotyczące sprzętu. Firma dokonuje zakupu raz w miesiącu, wtedy udzielany jest jej znaczny rabat. Hurtownia MAXMIN: LP Nazwa towaru Producent Cena zł Ilość szt. 1 Procesor Chiny Płyta główna Chiny Dysk twardy Tajwan Hurtownia MINMAX: LP Nazwa towaru Producent Cena zł Ilość szt. 1 Procesor Tajwan Płyta główna Chiny Dysk twardy Tajwan Dotychczasowe doświadczenia dotyczące wadliwości oferowanych części pozwalają na stwierdzenie, że 5% produkcji z Chin jest wadliwa, natomiast elementy pochodzące z Tajwanu charakteryzują się 10% wadliwością. Firma stara się o kontrakt rządowy, który będzie korzystny dla firmy, jeżeli koszty ponoszone przez nią wyniosą 75% wartości sprzedaży. Wyliczono, że firma sprzedaje komputery do sklepów, po odliczeniu wartości pozostałych elementów za cenę 2000 zł. Zapisać program liniowy pomocny w podjęciu decyzji dotyczącej dalszych starań o kontrakt, na podstawie doświadczeń z zaopatrywaniem sklepów. Zadanie Przydzielić 3 maszyny do proponowanej przez firmę Ma-XXXIII produkcji czterech elementów A, B, C, D. Tabela podaje czas produkcji każdego elementu (w rozbiciu na maszyny) na zmianę ( 8 godzin), koszty produkcji elementów przez poszczególne maszyny, ceny sprzedaży. Zapisać program liniowy realizujący zagadnienie przedziału zapewniający jak największy zysk, przy założeniu, że żaden element nie jest produkowany na dwóch maszynach, element nieukończony na zmianie ulega zniszczeniu. Maszyny mogą pracować bez przerwy całą zmianę Zadanie Przedsiębiorstwo wielobranżowe sprzedaje komplety uszczelek. Jeden komplet to 5 dużych uszczelek, 15 średnich i 20 małych, jego cena to 5 zł. W tabeli podano wielkości partii, ceny Maszyna Czas produkcji elementu w minutach Koszt produkcji elementu w zł A B C D A B C D M M M Cena sprzedaży elementu w zł uzyskiwane u producentów uszczelek oraz liczbę partii uszczelek, które można zakupić u producentów. Zapisz program liniowy maksymalizujący zysk przedsiębiorstwa.
17 Producent GUMPOL POLGUM Ilość uszczelek w partii Cena partii w Liczba partii Duże Średnie Małe zł. w zapasie Zadanie Zakład produkuje 4 rodzaje opon. Do ich wytworzenia potrzeba użyć czterech maszyn, każda z nich wykonuje inną czynność. Tabela podaje maksymalny czas pracy maszyny na 3 zmianach. Oraz minimalne ilości opon do wyprodukowania podczas zmiany. Jak ustalić produkcję, aby wytworzyć maksymalną liczbę opon? Zużycie czasu pracy w [szt/h] Opona Czas pracy Zima Sporting HighLife Super CX maszyny Maszyna [ min] M M M M Minimalne zamówienie Zadanie Zakład produkuje 4 rodzaje opon. Do ich wytworzenia można używać zamiennie czterech maszyn. Jedna opona produkowana jest tylko na jednej maszynie. Tabela podaje maksymalny czas pracy maszyn na 3 zmianach oraz minimalne ilości opon, które mają być wyprodukowane podczas zmiany. Jak ustalić produkcję, aby wytworzyć maksymalną liczbę opon? Zużycie czasu pracy w [szt/h] Opona Czas pracy Zima Sporting HighLife Super CX maszyny Maszyna [ min] M M M M Minimalne zamówienie Zadanie Tartak produkuje wiaty na przystanki autobusowe. Do produkcji jednego przystanku zużywa się 3 deski typu A, 7 desek typu B i 12 desek typu C. Deski te dostaje się tnąc
18 dwa rodzaje bali dużych i małych odpowiednimi sposobami ( tabelka ). W magazynie jest 200 bali dużych i 500 małych. Jaką największą liczbę przystanków jest w stanie wyprodukować tartak? Ilość desek otrzymanych z bali ciętych odpowiednimi sposobami. A B C duże I duże II małe I małe II małe III Zadanie Zakład otworzył nowy oddział, na którym zainstalowano dwie nowoczesne obrabiarki. Na każdej z nich można wykonywać kilka różnych prac. Zakład produkuje elementy do rakiet różnych typów. Postanowiono, że na nowym oddziale będą produkowane tylko trzy typy. Zakład pracuje 8 godzin i obrabiarki mogą pracować przez całą zmianę bez potrzeby zatrzymywania się. Zdolności produkcyjne, koszty wytworzenia, cenę zbytu oraz minimalne wielkości zamówień podaje tabela. Obrabiarka Ilość sztuk produkowanych w czasie 30 minut Jednostkowy koszt produkcji jednego elementu E 1 E 2 E 3 E 1 E 2 E Minimalne zamówienie Cena 1 szt Zadanie Rafineria sprowadza ropę naftową R1, R2 z dwóch źródeł różniących się między sobą jakością i ceną. Produkcję rafinerii stanowią dwa rodzaje benzyn E98 i E94 oraz olej opałowy. Ile trzeba kupić ropy R1 a ile R2, aby móc otrzymać co najmniej l E94, co najmniej l E98 oraz l oleju opałowego starając się minimalizować koszty zakupu? Ropa Ilość litrów uzyskiwanych produktów z jednej tony ropy Cena jednej tony E98 E94 OP ropy R R Zadanie Huta dostała zamówienie na wyprodukowanie 100 ton ściśle określonej stali. Stal ta zawierać ma % C, % Mn, % Si. Huta ma w swoich magazynach zalegające trzy rodzaje stali o procentowych zawartościach pierwiastków podanych w tabeli. Czy można z posiadanych zasobów wykonać zamówienie, jeżeli tak, to jakie ilości odpowiednich stali należy ze sobą stopić, aby łączna masa zużytych stali była najmniejsza?
19 Stal Pierwiastek C Mn Si Zasoby stali w magazynie. Stal A Stal B Stal C Zadanie Dokonać rozdziału produkcji 4 elementów na 4 maszyny tak, aby każda maszyna wykonywała dokładnie jeden typ elementów, a każdy typ elementu wykonywany był tylko przez jedną maszynę. W tabeli podano czas wykonywania jednego elementu przez odpowiednią maszynę ( min / szt. ) oraz maksymalny czas pracy maszyny na zmianie. Dokonać podziału czynności tak, aby wykonać jak najwięcej elementów w ciągu jednej zmiany. Element Maszyna Czas pracy maszyny Zadanie Zakład produkuje łyżki i widelce. Podczas ich produkcji można użyć zamiennie maszyn M 1, M 2, M 3, których czas pracy jest limitowany. Dane liczbowe zawiera tabela. Z maszyny schodzi gotowy produkt. Maszyna Ilość sztuk w ciągu [ h ] Limit czasowy łyżka 1 [ szt./h ] łyżka 2 [ szt./h ] łyżka 3 [ szt./h ] widelec 1 [ szt.\h ] widelec 2 [ szt.\h ] maszyny [ h ] M M M Cena Ustalić rozmiary produkcji przy założeniu, że wartość sprzedaży ma być maksymalna przy założeniu, że trzeba wyprodukować co najmniej po 100 sztuk każdego z wyrobów. Zadanie Rolnik ma trzy pola, które różnią się wielkością oraz klasą gleby; 100 ha klasy I, 150 ha klasy II i 300 ha klasy IV. Trzon jego produkcji rolnej tworzą ziemniaki, pszenica i kukurydza. Średnie zbiory z 1 ha wynoszą: 45q pszenicy, 200q ziemniaków, 45q kukurydzy z hektara. Zbiory mogą być większe lub mniejsze w zależności od klasy gruntu użytego pod uprawę. Przewiduje się, że ceny na poszczególne produkty będą następujące 100, 20, 75 j.p.. Rolnik zobowiązał się dostarczyć co najmniej 140q pszenicy, 150q ziemniaków, 160q kukurydzy. Tabela zawiera wzrost lub obniżkę plonów w q z ha w zależności od klasy gleby użytej pod uprawę.
20 Zmiana wydajności % Pszenica Ziemniaki kukurydza Klasa ziemi I II IV Ustalić plan zasiewów mający na uwadze maksymalizacją zysków rolnika i dotrzymanie zobowiązań. Zadanie Z hurtowni należy dostarczyć towar do sklepów. Ilości towarów w hurtowniach i zapotrzebowanie w sklepach oraz koszty transportu jednostki towaru podaje tabela. W jaki sposób należy dostarczyć towary do sklepów, aby koszty transportu były jak najniższe. Hurtownia Sklep A B C D Zapotrzebowanie W sklepie Zapas Zadanie Zakład produkuje gumowe uszczelki wykrawając je z większych kawałków. Uszczelki produkuje się w trzech typach i sprzedaje w kompletach 2 duże, 3 średnie i 5 małych. Tabela podaje ilości typów wykrojonych uszczelek przy odpowiednim sposobie cięcia oraz odpad. Sformułować program liniowy zapewniający minimalny odpad jeśli zakład ma zamówienie na 300 kompletów uszczelek. sposób cięcia typ uszczelki Duża Średnia Mała odpad cm Zadanie Dieta młodego goryla powinna zawierać składniki A, B, C, D. Składniki dostarczane są w podstawowych produktach: bananach i pomarańczy, jabłkach, sałacie, kukurydzy. Dane dotyczące zawartości 100 mg składnika w kilogramie produktu oraz minimalną i maksymalną dawkę zawarte są w tabeli. Składniki Banany kg/100mg Jabłka kg/100mg Kukurydz. kg/100mg Sałata kg/100mg Pom. kg/100mg min. dawka [ mg ] mak. dawka [ mg ] A B C D
21 Cena [zł/kg] 2,50 3,75 4,00 4,95 3, Ustalić dietę goryla, której koszty będą najmniejsze. Zadanie Prawidłowe nawożenie pola powinno zawierać składniki mineralne A, B, C, D. Składniki dostarczane są w produkowanych nawozach dostępnych w paczkach po 50 kg. Dane dotyczące ilości paczek 50 kilogramowych nawozu potrzebnych do dostarczenie 100g składnika mineralnego oraz minimalną i maksymalną dawkę odpowiednich składników potrzebnych do prawidłowego nawożenia pola zawarto w tabeli. Składniki Nawóz 1 50 kg/100g Nawóz 2 50 kg/100g Nawóz 3 50 kg/100g Nawóz 4 50kg/100g Mini. Dawka [ 100g ] mak. dawka [ 100g ] A B C D Cena [zł/50kg] 2,50 4,50 3,50 3, Ustalić nawożenie, dla którego koszty będą najmniejsze. Zadanie Załadować pociąg o wolnej przestrzeni ładunkowej o objętości m 3 i obciążeniu 5600 tonami towaru. W magazynach znajdują się towary, które można załadować na pociąg. W tabeli przedstawiono dane dotyczące objętości, wagi, ilości, czasu załadunku w minutach oraz zysku z przewiezienia jednostki danego towaru. Pociąg ma wyjechać za 30 godzin, załadunek może odbywać się bez przerwy. Towar Ciężar j. w [ t ] Objętość j. [ m 3 ] Ilość j. w magaz. Zysk z j. [ $ ] Czas zał. j. A B C D E F G Wyznaczyć plan załadunku pociągu, który zapewni maksymalny zysk. Zadanie Przedsiębiorstwo produkuje wyroby A, B, C, D, E używając do ich produkcji zamiennie czterech maszyn. Maszyny nie mogą pracować dłużej niż określone normy. Wiadomo, że na wytworzenie jednej sztuki wyrobu maszyna potrzebuje określony czas, tabela podaje normy czasowe wykonania poszczególnych wyrobów na kolejnych maszynach w min/szt., ceny zbytu wyrobów oraz maksymalny czas pracy maszyn. Zaplanować produkcję maksymalizując zyski. Koszt wyprodukowania jednej sztuki wyrobu stanowi 75% jego ceny. Wyrób Maszyna A B C D E Maks. czas pracy maszyny [min]
22 M M M M Cena zbytu Zadanie Przedsiębiorstwo produkuje wyroby A, B, C, D, E używając do ich produkcji czterech maszyn (wyrób przechodzi przez wszystkie maszyny). Maszyny nie mogą pracować dłużej niż określone normy. Wiadomo, że na wytworzenie jednej sztuki wyrobu maszyna potrzebuje określony czas, tabela podaje wydajności maszyn w szt/min., ceny zbytu wyrobów oraz maksymalny czas pracy maszyn. Zaplanować produkcję maksymalizując zyski. Koszt Zaplanować produkcję maksymalizując zyski. Wyrób Maszyna A B C D E maks. czas pracy maszyny [min] M M M M Cena zbytu Zadanie Zakład zagospodarowujący odpady produkuje 3 rodzaje jednorazowych opakowań. W zależności od jakości użytego surowca do produkcji danego opakowania zakład ponosi pewne koszty. Przez najbliższy miesiąc nie będzie więcej dostaw surowca. Dane dotyczące wielkości zasobów surowca w 1000 kg, nakłady na produkcję poszczególnego typu opakowania w miligramach oraz zapotrzebowanie na opakowania podaje tabela. Określić plan produkcji zapewniający zaspokojenie potrzeb rynku oraz minimalizujący nakłady na produkcję. Opakowanie I typ II typ III typ Zasoby surowca Surowiec I klasa II klasa III klasa Zapotrzebowania Zadanie Trzech przewoźników stara o obsługę czterech linii transportowych. W składanej przez nich ofercie podano koszty jakie musi ponieść miasto chcąc zapewnić komunikację na danej linii. Dokonać wyboru przewoźnika mając na uwadze minimalizację kosztów ponoszonych przez miasto jeśli każdy przewoźnik może obsługiwać tylko jedną trasę, a każda trasa może być obsługiwana tyko przez jednego przewoźnika. Dane z ofert przedstawia tabela. Trasa A B C D
23 Przewoźnik POLTRANS TIRPOL BUS-MAX Zadanie Zakład krawiecki ma dostarczyć 700 kompletów obrusów. Jeden komplet składa się z dwóch dużych obrusów o wymiarach 2m x 3,5 m i siedmiu o wymiarach 1,5 m x 2 m. Obrusy produkuje się z kawałków materiałów o wymiarach 2 m x 4 m za które płaci 10 jp. Określić sposób pocięcia zapewniający realizację zamówienia oraz minimalizację kosztów. Zadanie Spółdzielnia rzemieślnicza produkuje drewniane skrzynie. Sprzedaje je w kompletach 1 duża o wymiarach 1 m x 1 m x 0,5 m i 2 mniejsze 1 m x 0,5 m x 0,5 m. W magazynie znajduje się 150 płyt o wymiarach 2 m x 2 m i 200 o wymiarach 1 m x 1,5 m. Zorganizować produkcję mając na uwadze wyprodukowanie maksymalnej liczby kompletów. Zadanie Rolnik posiada 3 pola o powierzchni 100 ha, 150 ha i 250 ha. Rolnik może zasadzić cztery zboża: pszenicę, jęczmień, żyto, owies. Średnią wielkość zbiorów w [ q/ha ] z danego pola, cenę 1 q zboża oraz minimalną wielkość produkcji podano w tabeli. Określić optymalną strukturę zasiewów zapewniający maksymalny zysk rolnika. POLE Cena minimalny 100 ha 150 ha 250 ha ZBOŻE 1 q w j.p. zbiór w [ q ] Pszenica Żyto Jęczmień Owies Zadanie Rolnik posiada gospodarstwo rolne składające się z 45 ha o różnych klasach 15 ha w I klasie, 10 ha w II klasie i 20 ha w III klasie. Ponadto posiada 100 krów i 200 sztuk trzody chlewnej, które utrzymuje z własnej produkcji rolnej. Zapotrzebowania na składniki odżywcze potrzebne do prawidłowego żywienia stad przez rok podaje Tabela 1. W Tabeli 2 podano zawartości poszczególnych składników w płodach rolnych. Tabela 3 podaje wydajności z hektara poszczególnych płodów w zależności od klasy ziemi na jakiej zostały posiane oraz cenę ich zbytu. Tabela 1 Wielkości składników potrzebne na utrzymanie wszystkich zwierząt [js]. Składnik 1 Składnik 2 Składnik 3 Krowy Trzoda Tabela 2
24 Zawartość [js] składnika w 1 q płodu Rodzaj płodu Składnik 1 Składnik 2 Składnik 3 A B Tabela 3 Wydajność w q z ha Cena Klasa I Klasa II Klasa III A 1, B 2, Określić strukturę zasiewów dającą rolnikowi maksymalny zysk, przy zapewnieniu utrzymania stada, bez dodatkowych zakupów. Zadanie W zakładzie produkowane są elementy do trzech typów samochodów Opel, Fiat, Ford. Parametry produkcji potrzebne do sformułowania modelu matematycznego znajdują się w tabelach 1,2. Zakładamy, że wadliwość nie zależy od rodzaju produkowanego elementu, ale od ilości elementów wyprodukowanych na maszynie. Koszt jednostkowy, podobnie jak wadliwość nie zależy od rodzaju produkowanego elementu. Tabela 1. Cena Zużycie surowca potrzebne do Minimalna wyprodukowania jednego elementu produkcja Surowiec 1 Surowiec 2 Surowiec 3 Opel Fiat Ford Zapas surowca Tabela 2. Zdolności produkcyjne maszyn, stosowanych zamiennie do produkcji elementów. Maszyna 1 Maszyna 2 Opel Fiat Ford Koszt jednostkowy 10 9 Wadliwość produkcji 0,1 0,5 Jak należy ustalić produkcję, aby wyprodukować jak najwięcej elementów? Zadanie Jak zmieni się produkcja jeżeli chcemy osiągnąć największy zysk w zadaniu ?
25 Zadanie Przedsiębiorstwo rozpisało przetarg na produkcję 3 podzespołów. Należy dokonać wyboru pomiędzy pięcioma ofertami złożonymi przez różne przedsiębiorstwa. Dane dotyczące ofert przedstawia tabela 1. Warunki przetargu są następujące: Jedno przedsiębiorstwo może produkować co najwyżej 2 podzespoły. Średni poziom ryzyka całej inwestycji nie powinien być większy niż 125 pkt. Średnia wartość współczynnika zaufania do firmy nie powinna być mniejsza niż 22 pkt. Tabela 1 L&L L&X X&L X&X Ilość podzespołów w pakiecie Cena pakietu Ryzyko Pkt. Zaufanie Pkt. Podzespół Podzespół Podzespół Podzespół Podzespół Podzespół Podzespół Podzespół Podzespół Podzespół Podzespół Podzespół Tabela 2. Podzespół 1 Podzespół 2 Podzespół 3 Wielkość przetargu Jak należy wybrać oferty, jeżeli kryterium mają być najmniejsze koszy łączne ponoszone przez przedsiębiorstwo w związku z zleceniami?
26
Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ).
 PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
Statystyka. Zadanie 1.
 Statystyka Zadanie 1. W przedsiębiorstwie Statexport pracuje 100 pracowników fizycznych i 25 umysłowych. Typowy wiek pracownika fizycznego kształtuje się w przedziale od 30 do 40 lat. Średnia wieku pracowników
Statystyka Zadanie 1. W przedsiębiorstwie Statexport pracuje 100 pracowników fizycznych i 25 umysłowych. Typowy wiek pracownika fizycznego kształtuje się w przedziale od 30 do 40 lat. Średnia wieku pracowników
Zagadnienie transportowe i zagadnienie przydziału
 Temat: Zagadnienie transportowe i zagadnienie przydziału Zadanie 1 Trzy piekarnie zlokalizowane na terenie miasta są zaopatrywane w mąkę z trzech magazynów znajdujących się na peryferiach. Zasoby mąki
Temat: Zagadnienie transportowe i zagadnienie przydziału Zadanie 1 Trzy piekarnie zlokalizowane na terenie miasta są zaopatrywane w mąkę z trzech magazynów znajdujących się na peryferiach. Zasoby mąki
Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych"
 Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych" 1. Zbudować model optymalizacyjny problemu opisanego w zadaniu z tabeli poniżej. 2. Rozwiązać zadanie jak w tabeli poniżej z wykorzystaniem
Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych" 1. Zbudować model optymalizacyjny problemu opisanego w zadaniu z tabeli poniżej. 2. Rozwiązać zadanie jak w tabeli poniżej z wykorzystaniem
Badania operacyjne. Lista zadań projektowych nr 2
 Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
Lista 1 PL metoda geometryczna
 Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Ekonometria Programowanie Liniowe. Robert Pietrzykowski
 Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
ZADANIE TRANSPORTOWE I PROBLEM KOMIWOJAŻERA
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 3 ZADANIE TRANSPORTOWE I PROBLEM KOMIWOJAŻERA 3.3. ZADANIA Wykorzystując
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 3 ZADANIE TRANSPORTOWE I PROBLEM KOMIWOJAŻERA 3.3. ZADANIA Wykorzystując
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700
 Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
Halabarda A Halabarda B Zapas [t] Stal Drewno
![Halabarda A Halabarda B Zapas [t] Stal Drewno Halabarda A Halabarda B Zapas [t] Stal Drewno](/thumbs/53/31217238.jpg) Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
Halabarda A Halabarda B Zapas [t] Stal 1 2 20 Drewno 2 1 18
![Halabarda A Halabarda B Zapas [t] Stal 1 2 20 Drewno 2 1 18 Halabarda A Halabarda B Zapas [t] Stal 1 2 20 Drewno 2 1 18](/thumbs/27/9894738.jpg) Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
1-2. Formułowanie zadań decyzyjnych. Metoda geometryczna
 -. Formułowanie zadań decyzyjnych. Metoda geometryczna Zagadnienie wyznaczania optymalnego asortymentu produkcji Firma zamierza uruchomić produkcję dwóch wyrobów A i B. Cenę zbytu oszacowano na zł/kg dla
-. Formułowanie zadań decyzyjnych. Metoda geometryczna Zagadnienie wyznaczania optymalnego asortymentu produkcji Firma zamierza uruchomić produkcję dwóch wyrobów A i B. Cenę zbytu oszacowano na zł/kg dla
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Optymalizacja
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Optymalizacja Dla podanych niżej problemów decyzyjnych (zad.1 zad.5) należy sformułować zadania optymalizacji, tj.: określić postać zmiennych
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Optymalizacja Dla podanych niżej problemów decyzyjnych (zad.1 zad.5) należy sformułować zadania optymalizacji, tj.: określić postać zmiennych
Metody Ilościowe w Socjologii
 Metody Ilościowe w Socjologii wykład 4 BADANIA OPERACYJNE dr inż. Maciej Wolny AGENDA I. Badania operacyjne podstawowe definicje II. Metodologia badań operacyjnych III. Wybrane zagadnienia badań operacyjnych
Metody Ilościowe w Socjologii wykład 4 BADANIA OPERACYJNE dr inż. Maciej Wolny AGENDA I. Badania operacyjne podstawowe definicje II. Metodologia badań operacyjnych III. Wybrane zagadnienia badań operacyjnych
Standardowe zadanie programowania liniowego. Gliwice 1
 Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
Przed Tobą zestaw zadań konkursowych. Na ich rozwiązanie masz 90 minut. wybieraj tak, aby osiągnąć jak najlepszy wynik. POWODZENIA
 GIMNAZJUM Przed Tobą zestaw zadań konkursowych. Na ich rozwiązanie masz 90 minut. wybieraj tak, aby osiągnąć jak najlepszy wynik. POWODZENIA Zadanie 1. Trzy lata temu posadzono przed domem krzew. Co roku
GIMNAZJUM Przed Tobą zestaw zadań konkursowych. Na ich rozwiązanie masz 90 minut. wybieraj tak, aby osiągnąć jak najlepszy wynik. POWODZENIA Zadanie 1. Trzy lata temu posadzono przed domem krzew. Co roku
Rozwiązanie Ad 1. Model zadania jest następujący:
 Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
METODY OBLICZENIOWE OPTYMALIZACJI zadania
 METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
Badania operacyjne. Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie:
 Badania operacyjne Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia
Badania operacyjne Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia
1. Który z warunków nie jest właściwy dla powyższego zadania programowania liniowego? 2. Na podstawie poniższej tablicy można odczytać, że
 Stwierdzeń będzie. Przy każdym będzie należało ocenić, czy jest to stwierdzenie prawdziwe, czy fałszywe i zaznaczyć x w tabelce odpowiednio przy prawdzie, jeśli jest ono prawdziwe lub przy fałszu, jeśli
Stwierdzeń będzie. Przy każdym będzie należało ocenić, czy jest to stwierdzenie prawdziwe, czy fałszywe i zaznaczyć x w tabelce odpowiednio przy prawdzie, jeśli jest ono prawdziwe lub przy fałszu, jeśli
Zad.1. Microsoft Excel - Raport wyników Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto
 Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
Programowanie liniowe. Tadeusz Trzaskalik
 Programowanie liniowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Model matematyczny Cel, środki, ograniczenia Funkcja celu funkcja kryterium Zmienne decyzyjne Model optymalizacyjny Układ warunków
Programowanie liniowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Model matematyczny Cel, środki, ograniczenia Funkcja celu funkcja kryterium Zmienne decyzyjne Model optymalizacyjny Układ warunków
ZAGADNIENIA PROGRAMOWANIA LINIOWEGO
 ZAGADNIENIA PROGRAMOWANIA LINIOWEGO Maciej Patan Uniwersytet Zielonogórski WSTĘP często spotykane w życiu codziennym wybór asortymentu produkcji jakie wyroby i w jakich ilościach powinno produkować przedsiębiorstwo
ZAGADNIENIA PROGRAMOWANIA LINIOWEGO Maciej Patan Uniwersytet Zielonogórski WSTĘP często spotykane w życiu codziennym wybór asortymentu produkcji jakie wyroby i w jakich ilościach powinno produkować przedsiębiorstwo
Wydział Matematyki Programowanie liniowe Ćwiczenia. Zestaw 1. Modelowanie zadań programowania liniowego.
 Wydział Matematyki Programowanie liniowe Ćwiczenia Zestaw. Modelowanie zadań programowania liniowego. Zadania dotyczące zagadnienia planowania produkcji Zadanie.. Zapisać następujące zadanie w postaci
Wydział Matematyki Programowanie liniowe Ćwiczenia Zestaw. Modelowanie zadań programowania liniowego. Zadania dotyczące zagadnienia planowania produkcji Zadanie.. Zapisać następujące zadanie w postaci
Przykład: frytki i puree Analiza wrażliwości współczynników funkcji celu
 Analiza wrażliwości: współczynników funkcji celu analiza wrażliwości pozwala odpowiedzieć na pytanie, w jakich granicach mogą się zmieniać te parametry, aby dotychczasowe rozwiązanie było optymalne, wyrazów
Analiza wrażliwości: współczynników funkcji celu analiza wrażliwości pozwala odpowiedzieć na pytanie, w jakich granicach mogą się zmieniać te parametry, aby dotychczasowe rozwiązanie było optymalne, wyrazów
OPTYMALIZACJA W LOGISTYCE
 OPTYMALIZACJA W LOGISTYCE Zagadnienie przydziału dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie przydziału 1 Można wyodrębnić kilka grup problemów, których zadaniem jest alokacja szeroko
OPTYMALIZACJA W LOGISTYCE Zagadnienie przydziału dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie przydziału 1 Można wyodrębnić kilka grup problemów, których zadaniem jest alokacja szeroko
Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli?
 Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli? : Proces zmieniania wartości w komórkach w celu sprawdzenia, jak
Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli? : Proces zmieniania wartości w komórkach w celu sprawdzenia, jak
Rozdział 2 PROGRAMOWANIE LINIOWE CAŁKOWITOLICZBOWE
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 2 PROGRAMOWANIE LINIOWE CAŁKOWITOLICZBOWE 2.3. ZADANIA W zadaniach 2.1 2.20
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 2 PROGRAMOWANIE LINIOWE CAŁKOWITOLICZBOWE 2.3. ZADANIA W zadaniach 2.1 2.20
Analiza korelacji i regresji dwóch zmiennych losowych
 Analiza korelacji i regresji dwóch zmiennych losowych 1. Badano zależność między ilością godzin przebywania samolotu w powietrzu ( nalot lotniczy) a ilością wypadków. Na podstawie zebranych danych z pewnego
Analiza korelacji i regresji dwóch zmiennych losowych 1. Badano zależność między ilością godzin przebywania samolotu w powietrzu ( nalot lotniczy) a ilością wypadków. Na podstawie zebranych danych z pewnego
Badania operacyjne. te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze.
 BADANIA OPERACYJNE Badania operacyjne Badania operacyjne są sztuką dawania złych odpowiedzi na te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze. T. Sayty 2 Standardowe zadanie
BADANIA OPERACYJNE Badania operacyjne Badania operacyjne są sztuką dawania złych odpowiedzi na te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze. T. Sayty 2 Standardowe zadanie
Pyt.1. Podać warunki jakie musi spełniać model matematyczny dla możliwości rozwiązywania metodami programowania liniowego.
 Firma produkująca płatki śniadaniowe rozważa wypuszczenie na rynek nowego produktu. Ma to być mieszanka pszenicy, ryżu i kukurydzy. Normy zawartości przedstawia tabela: Dane Pszenica Ryż Kukurydza Zawartość
Firma produkująca płatki śniadaniowe rozważa wypuszczenie na rynek nowego produktu. Ma to być mieszanka pszenicy, ryżu i kukurydzy. Normy zawartości przedstawia tabela: Dane Pszenica Ryż Kukurydza Zawartość
Modelowanie całkowitoliczbowe
 1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne. Temat ćwiczenia:
 Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne Temat ćwiczenia: Programowanie liniowe, metoda geometryczna, dobór struktury asortymentowej produkcji Zachodniopomorski Uniwersytet
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne Temat ćwiczenia: Programowanie liniowe, metoda geometryczna, dobór struktury asortymentowej produkcji Zachodniopomorski Uniwersytet
Programowanie liniowe
 Badania operacyjne Ćwiczenia 4 Programowanie liniowe Dualizm w programowaniu liniowym Plan zajęć Dualizm w programowaniu liniowym Projektowanie programu dualnego Postać programu dualnego Przykład 1 Rozwiązania
Badania operacyjne Ćwiczenia 4 Programowanie liniowe Dualizm w programowaniu liniowym Plan zajęć Dualizm w programowaniu liniowym Projektowanie programu dualnego Postać programu dualnego Przykład 1 Rozwiązania
Zadanie A. Pestycydy. Wejście. Wyjście. Przykłady. Techniki optymalizacyjne Sosnowiec, semestr zimowy 2016/2017
 Zadanie A. Pestycydy Aby uprawiać pewną roślinę musimy ją nawozić mieszanką zawierającą wszystkie potrzebne składniki odżywcze w ilości (podawanej w gramach) nie mniejszej niż przewiduje norma. Taką mieszankę
Zadanie A. Pestycydy Aby uprawiać pewną roślinę musimy ją nawozić mieszanką zawierającą wszystkie potrzebne składniki odżywcze w ilości (podawanej w gramach) nie mniejszej niż przewiduje norma. Taką mieszankę
Badania Operacyjne Ćwiczenia nr 5 (Materiały)
 ZADANIE 1 Zakład produkuje trzy rodzaje papieru: standardowy do kserokopiarek i drukarek laserowych (S), fotograficzny (F) oraz nabłyszczany do drukarek atramentowych (N). Każdy z rodzajów papieru wymaga
ZADANIE 1 Zakład produkuje trzy rodzaje papieru: standardowy do kserokopiarek i drukarek laserowych (S), fotograficzny (F) oraz nabłyszczany do drukarek atramentowych (N). Każdy z rodzajów papieru wymaga
4. PROGRAMOWANIE LINIOWE
 4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
( 1) ( ) 16 Warunki brzegowe [WB] Funkcja celu [FC] Ograniczenia [O] b i ( 2) ( ) ( ) 14. FC max. Kompletna postać bazowa
![( 1) ( ) 16 Warunki brzegowe [WB] Funkcja celu [FC] Ograniczenia [O] b i ( 2) ( ) ( ) 14. FC max. Kompletna postać bazowa ( 1) ( ) 16 Warunki brzegowe [WB] Funkcja celu [FC] Ograniczenia [O] b i ( 2) ( ) ( ) 14. FC max. Kompletna postać bazowa](/thumbs/45/23284662.jpg) Standardowe zadanie PL () Należy zaplanować produkcję zakładu w pewnym tygodniu w taki sposób, aby osiągnięty zysk był maksymalny. akład może wytwarzać dwa wyroby: P i P. Ich produkcja jest limitowana
Standardowe zadanie PL () Należy zaplanować produkcję zakładu w pewnym tygodniu w taki sposób, aby osiągnięty zysk był maksymalny. akład może wytwarzać dwa wyroby: P i P. Ich produkcja jest limitowana
Środki produkcji Jedn. nakłady środka W1 Jedn. nakłady środka W2 I 6 6 II 10 5
 PROGRAMOWANIE LINIOWE ZADANIA TEKSTOWE 5. Zakład produkuje dwa typy wózków: S i H. Zysk ze sprzedaży jednego wózka typu S wynosi 2850 zł a wózka typu H 6270 zł. Koszt produkcji jednego wózka typu S wynosi
PROGRAMOWANIE LINIOWE ZADANIA TEKSTOWE 5. Zakład produkuje dwa typy wózków: S i H. Zysk ze sprzedaży jednego wózka typu S wynosi 2850 zł a wózka typu H 6270 zł. Koszt produkcji jednego wózka typu S wynosi
Elementy Modelowania Matematycznego
 Elementy Modelowania Matematycznego Wykład 6 Metoda simpleks Spis treści Wstęp Zadanie programowania liniowego Wstęp Omówimy algorytm simpleksowy, inaczej metodę simpleks(ów). Jest to stosowana w matematyce
Elementy Modelowania Matematycznego Wykład 6 Metoda simpleks Spis treści Wstęp Zadanie programowania liniowego Wstęp Omówimy algorytm simpleksowy, inaczej metodę simpleks(ów). Jest to stosowana w matematyce
Elementy programowania liniowego
 Instytut Sterowania i Systemów Informatycznych Politechnika Zielonogórska Metody i techniki optymalizacji Elementy programowania liniowego Poniższe zadania należy rozwiązać z zastosowaniem programów Excel
Instytut Sterowania i Systemów Informatycznych Politechnika Zielonogórska Metody i techniki optymalizacji Elementy programowania liniowego Poniższe zadania należy rozwiązać z zastosowaniem programów Excel
1. Udział dochodów z działalności rolniczej w dochodach gospodarstw domowych z użytkownikiem gospodarstwa rolnego w 2002 r.
 1 UWAGI ANALITYCZNE 1. Udział dochodów z działalności rolniczej w dochodach gospodarstw domowych z użytkownikiem gospodarstwa rolnego w 2002 r. W maju 2002 r. w województwie łódzkim było 209,4 tys. gospodarstw
1 UWAGI ANALITYCZNE 1. Udział dochodów z działalności rolniczej w dochodach gospodarstw domowych z użytkownikiem gospodarstwa rolnego w 2002 r. W maju 2002 r. w województwie łódzkim było 209,4 tys. gospodarstw
Metody kalkulacji kosztu jednostkowego
 Metody kalkulacji kosztu jednostkowego Dane dotyczące produkcji w firmie X w styczniu przedstawiają się następująco: saldo początkowe produkcji w toku 0 liczba wyrobów przekazanych do magazynu 20 000 liczba
Metody kalkulacji kosztu jednostkowego Dane dotyczące produkcji w firmie X w styczniu przedstawiają się następująco: saldo początkowe produkcji w toku 0 liczba wyrobów przekazanych do magazynu 20 000 liczba
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE
 PROBLEMY DECYZYJNE KRÓTKOOKRESOWE OPTYMALNA STRUKTURA PRODUKCJI Na podstawie: J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 2013 1 DECYZJE KRÓTKOOKRESOWE Decyzje krótkookresowe to takie, które dotyczą
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE OPTYMALNA STRUKTURA PRODUKCJI Na podstawie: J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 2013 1 DECYZJE KRÓTKOOKRESOWE Decyzje krótkookresowe to takie, które dotyczą
Wprowadzenie do badań operacyjnych
 Wprowadzenie do badań operacyjnych Hanna Furmańczyk 10 października 2008 Badania operacyjne (ang. operations research) - dyscyplina naukowa związana z teorią decyzji pozwalająca wyznaczyć metodę i rozwiązanie
Wprowadzenie do badań operacyjnych Hanna Furmańczyk 10 października 2008 Badania operacyjne (ang. operations research) - dyscyplina naukowa związana z teorią decyzji pozwalająca wyznaczyć metodę i rozwiązanie
Barbadoska 16 mb 24 mb Afrykańska 16 mb 10 mb
 I. Ćwiczenia 2 Firma McCain jest światowym potentatem w branży frytek. W swojej fabryce, która znajduje się w Buriey (stan Idaho), produkuje frytki Golden Longs oraz frytki My Fries Classic. Fabryka zaopatruje
I. Ćwiczenia 2 Firma McCain jest światowym potentatem w branży frytek. W swojej fabryce, która znajduje się w Buriey (stan Idaho), produkuje frytki Golden Longs oraz frytki My Fries Classic. Fabryka zaopatruje
PROGRAMOWANIE WIELOKRYTERIALNE (CELOWE)
 PROGRAMOWANIE WIELOKRYTERIALNE (CELOWE) Przykład 14. Zakład zamierza rozpocząć produkcję wyrobów W 1 i W 2. Wśród środków produkcyjnych, które zostaną użyte w produkcji dwa są limitowane. Limity te wynoszą:
PROGRAMOWANIE WIELOKRYTERIALNE (CELOWE) Przykład 14. Zakład zamierza rozpocząć produkcję wyrobów W 1 i W 2. Wśród środków produkcyjnych, które zostaną użyte w produkcji dwa są limitowane. Limity te wynoszą:
NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI ZADANIE 1 ZADANIE 2
 ZADANIE 1 Wyznacz najmniejsza i największa wartość funkcji f (x) = (x 2)(x + 1) w przedziale 0; 4. ZADANIE 2 Wyznacz najmniejsza i największa wartość funkcji f (x) = x 2 4x 2 w przedziale 2; 2. 1 ZADANIE
ZADANIE 1 Wyznacz najmniejsza i największa wartość funkcji f (x) = (x 2)(x + 1) w przedziale 0; 4. ZADANIE 2 Wyznacz najmniejsza i największa wartość funkcji f (x) = x 2 4x 2 w przedziale 2; 2. 1 ZADANIE
RACHUNEK KOSZTÓW _ ZADANIA
 RACHUNEK KOSZTÓW _ ZADANIA Zadania_Kalkulacja podziałowa prosta, współczynnikowa i odjemna Przykład_1 wyprodukowano 80 sztuk wyrobów gotowych i 50 sztuk wyrobów zaawansowanych w 40% z punktu widzenia poniesionych
RACHUNEK KOSZTÓW _ ZADANIA Zadania_Kalkulacja podziałowa prosta, współczynnikowa i odjemna Przykład_1 wyprodukowano 80 sztuk wyrobów gotowych i 50 sztuk wyrobów zaawansowanych w 40% z punktu widzenia poniesionych
Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02
 Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Teoria Estymacji. Do Powyżej
 Teoria Estymacji Zad.1. W pewnym przedsiębiorstwie wylosowano niezależnie próbę 25 pracowników. Staż pracy (w latach) tych pracowników w 1996 roku był następujący: 37; 34; 0*; 5; 17; 17; 0*; 2; 24; 33;
Teoria Estymacji Zad.1. W pewnym przedsiębiorstwie wylosowano niezależnie próbę 25 pracowników. Staż pracy (w latach) tych pracowników w 1996 roku był następujący: 37; 34; 0*; 5; 17; 17; 0*; 2; 24; 33;
ZADANIA MATURALNE LICZBY RZECZYWISTE - POZIOM PODSTAWOWY. Opracowała mgr Danuta Brzezińska
 ZADANIA MATURALNE LICZBY RZECZYWISTE - POZIOM PODSTAWOWY Zad1 ( 5 pkt) 1 0 8 1 2 11 5 4 Dane są liczby x 5, y 5 2 2 1 5 a) Wyznacz liczbę, której 60% jest równe x Wynik podaj z dokładnością do 0,01 b)
ZADANIA MATURALNE LICZBY RZECZYWISTE - POZIOM PODSTAWOWY Zad1 ( 5 pkt) 1 0 8 1 2 11 5 4 Dane są liczby x 5, y 5 2 2 1 5 a) Wyznacz liczbę, której 60% jest równe x Wynik podaj z dokładnością do 0,01 b)
Polityka rachunkowości Łukasz Szydełko. Lista 1
 Polityka rachunkowości Łukasz Szydełko Lista 1 Zad.1 W polityce rachunkowości piekarni Ela Sp. z o.o. przyjęto, że wartość materiałów bezpośrednio po zakupie odpisywana jest w koszty. W celu ustalenia
Polityka rachunkowości Łukasz Szydełko Lista 1 Zad.1 W polityce rachunkowości piekarni Ela Sp. z o.o. przyjęto, że wartość materiałów bezpośrednio po zakupie odpisywana jest w koszty. W celu ustalenia
Rynek zbóż i żywca: ceny w dół!
 https://www. Rynek zbóż i żywca: ceny w dół! Autor: Elżbieta Sulima Data: 13 kwietnia 2016 Ceny zdecydowanie lecą w dół. Sytuacja ta dotyczy nie tylko zbóż, ale również wieprzowiny, brojlerów, cen skupu
https://www. Rynek zbóż i żywca: ceny w dół! Autor: Elżbieta Sulima Data: 13 kwietnia 2016 Ceny zdecydowanie lecą w dół. Sytuacja ta dotyczy nie tylko zbóż, ale również wieprzowiny, brojlerów, cen skupu
Praca Dyplomowa Magisterska. Zastosowanie algorytmów genetycznych w zagadnieniach optymalizacji produkcji
 Praca Dyplomowa Magisterska Zastosowanie algorytmów genetycznych w zagadnieniach optymalizacji produkcji Cel pracy zapoznanie się z zasadami działania ania algorytmów genetycznych przedstawienie możliwo
Praca Dyplomowa Magisterska Zastosowanie algorytmów genetycznych w zagadnieniach optymalizacji produkcji Cel pracy zapoznanie się z zasadami działania ania algorytmów genetycznych przedstawienie możliwo
Ćwiczenia laboratoryjne - 7. Zagadnienie transportowoprodukcyjne. programowanie liniowe
 Ćwiczenia laboratoryjne - 7 Zagadnienie transportowoprodukcyjne ZT-P programowanie liniowe Ćw. L. 8 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym
Ćwiczenia laboratoryjne - 7 Zagadnienie transportowoprodukcyjne ZT-P programowanie liniowe Ćw. L. 8 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym
Wykład 7. Informatyka Stosowana. Magdalena Alama-Bućko. 16 kwietnia Magdalena Alama-Bućko Wykład 7 16 kwietnia / 23
 Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE. WYTWORZYĆ CZY KUPIĆ? outsourcing
 PROBLEMY DECYZYJNE KRÓTKOOKRESOWE WYTWORZYĆ CZY KUPIĆ? outsourcing 1. Produkować samemu czy zlecić wytwarzanie na zewnątrz ( outsourcing)? Rozstrzygnięcie tego problemu decyzyjnego wymaga porównania ceny
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE WYTWORZYĆ CZY KUPIĆ? outsourcing 1. Produkować samemu czy zlecić wytwarzanie na zewnątrz ( outsourcing)? Rozstrzygnięcie tego problemu decyzyjnego wymaga porównania ceny
OPTYMALNA POLITYKA ZAPASÓW
 Dorota Miszczyńska Postawowe modele zapasów OPTYMALNA POLITYKA ZAPASÓW Problemy zapasów, kształtowania ich wielkości dotyczą dwóch rodzajów działalności: produkcyjnej oraz handlowej. Celem jest zapewnienie
Dorota Miszczyńska Postawowe modele zapasów OPTYMALNA POLITYKA ZAPASÓW Problemy zapasów, kształtowania ich wielkości dotyczą dwóch rodzajów działalności: produkcyjnej oraz handlowej. Celem jest zapewnienie
SCENARIUSZ LEKCJI. Streszczenie. Czas realizacji. Podstawa programowa Etap edukacyjny: IV, przedmiot: informatyka (poziom podstawowy )
 SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
Sprawdzian 1. Zadanie 3. (0 1). Dokończ poniższe zdanie wybierz odpowiedź spośród podanych.
 Sprawdzian Zadanie. (0 ). Podaj poprawne wartości poniższych wyrażeń arytmetycznych. Wybierz liczbę spośród oznaczonych literami A i B oraz liczbę spośród oznaczonych literami C i D. 27 7 2 A / B A. 3
Sprawdzian Zadanie. (0 ). Podaj poprawne wartości poniższych wyrażeń arytmetycznych. Wybierz liczbę spośród oznaczonych literami A i B oraz liczbę spośród oznaczonych literami C i D. 27 7 2 A / B A. 3
EGZAMIN POTWIERDZAJĄCY KWALIFIKACJE W ZAWODZIE Rok 2019 CZĘŚĆ PRAKTYCZNA
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 2018 Nazwa kwalifikacji: Organizacja i prowadzenie prac związanych z przeładunkiem oraz magazynowaniem towarów
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 2018 Nazwa kwalifikacji: Organizacja i prowadzenie prac związanych z przeładunkiem oraz magazynowaniem towarów
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Struktury i Algorytmy Wspomagania Decyzji Zadanie projektowe 2 Czas realizacji: 6 godzin Maksymalna liczba
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Struktury i Algorytmy Wspomagania Decyzji Zadanie projektowe 2 Czas realizacji: 6 godzin Maksymalna liczba
RACHUNKOWOŚĆ ZARZĄDCZA
 RACHUNKOWOŚĆ ZARZĄDCZA wykład VII dr Marek Masztalerz Uniwersytet Ekonomiczny w Poznaniu 2011 PRÓG RENTOWNOŚCI PRODUKCJA JEDNOASORTYMENTOWA przychody Sx PRw margines bezpieczeństwa margines bezpieczeństwa
RACHUNKOWOŚĆ ZARZĄDCZA wykład VII dr Marek Masztalerz Uniwersytet Ekonomiczny w Poznaniu 2011 PRÓG RENTOWNOŚCI PRODUKCJA JEDNOASORTYMENTOWA przychody Sx PRw margines bezpieczeństwa margines bezpieczeństwa
Logistyka produkcji i zaopatrzenia - projekt. Mgr. inż. MONIKA KOSACKA Pokój 110A
 Logistyka produkcji i zaopatrzenia - projekt Mgr. inż. MONIKA KOSACKA Pokój 110A E-mail: monika.kosacka@put.poznan.pl 1. Warunki zaliczenia 2. WPROWADZENIE DO PROJEKTU 3. STRUKTURA WYROBU 4. Make or buy
Logistyka produkcji i zaopatrzenia - projekt Mgr. inż. MONIKA KOSACKA Pokój 110A E-mail: monika.kosacka@put.poznan.pl 1. Warunki zaliczenia 2. WPROWADZENIE DO PROJEKTU 3. STRUKTURA WYROBU 4. Make or buy
Definicja problemu programowania matematycznego
 Definicja problemu programowania matematycznego minimalizacja lub maksymalizacja funkcji min (max) f(x) gdzie: x 1 x R n x 2, czyli: x = [ ] x n przy ograniczeniach (w skrócie: p.o.) p.o. g i (x) = b i
Definicja problemu programowania matematycznego minimalizacja lub maksymalizacja funkcji min (max) f(x) gdzie: x 1 x R n x 2, czyli: x = [ ] x n przy ograniczeniach (w skrócie: p.o.) p.o. g i (x) = b i
Wskaźniki pomiaru i oceny podsystemu - zaopatrzenia
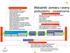 1 S T W Zaopatrzenie zakupy Mierniki strukturalne i ramowe liczba zakupionych części wolumen zakupionych materiałów pozycje zamówień na miesiąc liczba dostawców kwota umów ramowych struktura zamówień liczba
1 S T W Zaopatrzenie zakupy Mierniki strukturalne i ramowe liczba zakupionych części wolumen zakupionych materiałów pozycje zamówień na miesiąc liczba dostawców kwota umów ramowych struktura zamówień liczba
Zadanie transportowe i problem komiwojażera. Tadeusz Trzaskalik
 Zadanie transportowe i problem komiwojażera Tadeusz Trzaskalik 3.. Wprowadzenie Słowa kluczowe Zbilansowane zadanie transportowe Rozwiązanie początkowe Metoda minimalnego elementu macierzy kosztów Metoda
Zadanie transportowe i problem komiwojażera Tadeusz Trzaskalik 3.. Wprowadzenie Słowa kluczowe Zbilansowane zadanie transportowe Rozwiązanie początkowe Metoda minimalnego elementu macierzy kosztów Metoda
Liczby i działania str. 1/6
 Liczby i działania str. 1/6 1. Rysunek, na którym zacieniowano 4 figury, to rysunek: 2. Odwrotnością liczby 1 1 jest: 6 B. 6 C. 1 1 D. 1 1 3. Odwrotnością liczby 2 7 jest: 2 7 B. 3 1 2 C. 7 2 D. 2 7 4.
Liczby i działania str. 1/6 1. Rysunek, na którym zacieniowano 4 figury, to rysunek: 2. Odwrotnością liczby 1 1 jest: 6 B. 6 C. 1 1 D. 1 1 3. Odwrotnością liczby 2 7 jest: 2 7 B. 3 1 2 C. 7 2 D. 2 7 4.
UWAGI ANALITYCZNE. Gospodarstwa z użytkownikiem gospodarstwa indywidualnego. Wyszczególnienie. do 1 ha użytków rolnych. powyżej 1 ha.
 UWAGI ANALITYCZNE UDZIAŁ DOCHODÓW Z DZIAŁALNOŚCI ROLNICZEJ W DOCHODACH OGÓŁEM GOSPODARSTW DOMOWYCH W Powszechnym Spisie Rolnym w woj. dolnośląskim spisano 140,7 tys. gospodarstw domowych z użytkownikiem
UWAGI ANALITYCZNE UDZIAŁ DOCHODÓW Z DZIAŁALNOŚCI ROLNICZEJ W DOCHODACH OGÓŁEM GOSPODARSTW DOMOWYCH W Powszechnym Spisie Rolnym w woj. dolnośląskim spisano 140,7 tys. gospodarstw domowych z użytkownikiem
KOSZTY, PRZYCHODY I ZYSKI W RÓŻNYCH STRUKTURACH RYNKOWYCH. I. Koszty całkowite, przeciętne i krańcowe. Pojęcie kosztów produkcji
 KOSZTY, PRZYCHODY I ZYSKI W RÓŻNYCH STRUKTURACH RYNKOWYCH Opracowanie: mgr inż. Dorota Bargieł-Kurowska I. Koszty całkowite, przeciętne i krańcowe. Pojęcie kosztów produkcji Producent, podejmując decyzję:
KOSZTY, PRZYCHODY I ZYSKI W RÓŻNYCH STRUKTURACH RYNKOWYCH Opracowanie: mgr inż. Dorota Bargieł-Kurowska I. Koszty całkowite, przeciętne i krańcowe. Pojęcie kosztów produkcji Producent, podejmując decyzję:
Zawartość składników pokarmowych w roślinach
 Zawartość składników pokarmowych w roślinach Poszczególne rośliny różnią się zawartością składników pokarmowych zarówno w organach wegetatywnych, jak i generatywnych. Wynika to z różnych funkcji, jakie
Zawartość składników pokarmowych w roślinach Poszczególne rośliny różnią się zawartością składników pokarmowych zarówno w organach wegetatywnych, jak i generatywnych. Wynika to z różnych funkcji, jakie
Programowanie liniowe całkowitoliczbowe
 Programowanie liniowe całkowitoliczbowe Jeżeli w zadaniu programowania liniowego pewne (lub wszystkie) zmienne musza przyjmować wartości całkowite, to takie zadanie nazywamy zadaniem programowania liniowego
Programowanie liniowe całkowitoliczbowe Jeżeli w zadaniu programowania liniowego pewne (lub wszystkie) zmienne musza przyjmować wartości całkowite, to takie zadanie nazywamy zadaniem programowania liniowego
ETAP SZKOLNY V Wojewódzki Konkurs Matematyczny dla uczniów szkół podstawowych województwa wielkopolskiego
 Informacje do zadań 1 3 Mieszkający w Poznaniu państwo Pyrkowscy bardzo lubią spędzać weekendy poza miastem. Pierwszego stycznia podjęli noworoczne postanowienie, że zakupią działkę rekreacyjną, żeby więcej
Informacje do zadań 1 3 Mieszkający w Poznaniu państwo Pyrkowscy bardzo lubią spędzać weekendy poza miastem. Pierwszego stycznia podjęli noworoczne postanowienie, że zakupią działkę rekreacyjną, żeby więcej
METODY WIELOKRYTERIALNE
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 4 METODY WIELOKRYTERIALNE 4.3. ZADANIA Zadanie 4.1 Wykorzystując tryb konwersacyjny
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 4 METODY WIELOKRYTERIALNE 4.3. ZADANIA Zadanie 4.1 Wykorzystując tryb konwersacyjny
OPTYMALIZACJA W LOGISTYCE
 OPTYMALIZACJA W LOGISTYCE Zagadnienie transportowe 1 dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Klasyczne zagadnienie transportowe 1 Klasyczne zadanie transportowe problem najtańszego przewozu
OPTYMALIZACJA W LOGISTYCE Zagadnienie transportowe 1 dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Klasyczne zagadnienie transportowe 1 Klasyczne zadanie transportowe problem najtańszego przewozu
szt. produkcja rzeczywista
 128 000 zł 100 000 zł linia budżetu przeliczonego 10 000 szt. produkcja rzeczywista 14 000 szt. produkcja planowana Wydział przedsiębiorstwa produkcyjnego ponosi stałe koszty w wysokości 30 000 zł w miesiącu
128 000 zł 100 000 zł linia budżetu przeliczonego 10 000 szt. produkcja rzeczywista 14 000 szt. produkcja planowana Wydział przedsiębiorstwa produkcyjnego ponosi stałe koszty w wysokości 30 000 zł w miesiącu
Wykład z modelowania matematycznego. Zagadnienie transportowe.
 Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane wyniki.
 ZAD.1. Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha dla 7 niezależnych upraw przedstawia tabela: y X 17 11 19 15 19 20 20 25 20 24 22 39 23 41
ZAD.1. Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha dla 7 niezależnych upraw przedstawia tabela: y X 17 11 19 15 19 20 20 25 20 24 22 39 23 41
Ćwiczenia laboratoryjne - 7. Problem (diety) mieszanek w hutnictwie programowanie liniowe. Logistyka w Hutnictwie Ćw. L. 7
 Ćwiczenia laboratoryjne - 7 Problem (diety) mieszanek w hutnictwie programowanie liniowe Ćw. L. 7 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym zapisem
Ćwiczenia laboratoryjne - 7 Problem (diety) mieszanek w hutnictwie programowanie liniowe Ćw. L. 7 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym zapisem
EGZAMIN POTWIERDZAJĄCY KWALIFIKACJE W ZAWODZIE Rok 2019 CZĘŚĆ PRAKTYCZNA
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 2019 Nazwa kwalifikacji: Zarządzanie środkami technicznymi podczas realizacji procesów transportowych Oznaczenie
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 2019 Nazwa kwalifikacji: Zarządzanie środkami technicznymi podczas realizacji procesów transportowych Oznaczenie
Iwona Konarzewska Programowanie celowe - wprowadzenie. Katedra Badań Operacyjnych UŁ
 1 Iwona Konarzewska Programowanie celowe - wprowadzenie Katedra Badań Operacyjnych UŁ 2 Programowanie celowe W praktycznych sytuacjach podejmowania decyzji często występuje kilka celów. Problem pojawia
1 Iwona Konarzewska Programowanie celowe - wprowadzenie Katedra Badań Operacyjnych UŁ 2 Programowanie celowe W praktycznych sytuacjach podejmowania decyzji często występuje kilka celów. Problem pojawia
Przykładowe zadania rozwiązywane na ćwiczeniach
 Przykładowe zadania rozwiązywane na ćwiczeniach Zad.. Określić ilość kursów poszczególnych środków transportu, przy których koszty przewozu gotowych wyrobów z przedsiębiorstwa do hurtowni będą najniższe.
Przykładowe zadania rozwiązywane na ćwiczeniach Zad.. Określić ilość kursów poszczególnych środków transportu, przy których koszty przewozu gotowych wyrobów z przedsiębiorstwa do hurtowni będą najniższe.
Strategie wspó³zawodnictwa
 Strategie wspó³zawodnictwa W MESE można opracować trzy podstawowe strategie: 1) niskich cen (dużej ilości), 2) wysokich cen, 3) średnich cen. STRATEGIA NISKICH CEN (DUŻEJ ILOŚCI) Strategia ta wykorzystuje
Strategie wspó³zawodnictwa W MESE można opracować trzy podstawowe strategie: 1) niskich cen (dużej ilości), 2) wysokich cen, 3) średnich cen. STRATEGIA NISKICH CEN (DUŻEJ ILOŚCI) Strategia ta wykorzystuje
Lista powtórkowa. 1. Lista płac Jank K - 5500 zł ; dokonaj odpowiednich naliczeń i zaksięguj, także po stronie pracodawcy
 Lista powtórkowa Zadanie 1 Zadanie 2 Zadanie 3 Zadanie 4 Zadanie 5 Zadanie 6 Zadanie 7 1. Saldo początkowe Środków Trwałych 50 000 zł 2. Na stanie środków trwałych znajduje się komputer, którego wartość
Lista powtórkowa Zadanie 1 Zadanie 2 Zadanie 3 Zadanie 4 Zadanie 5 Zadanie 6 Zadanie 7 1. Saldo początkowe Środków Trwałych 50 000 zł 2. Na stanie środków trwałych znajduje się komputer, którego wartość
Badania operacyjne. Dr Michał Kulej. Pokój 509, budynek B4 Forma zaliczenia wykładu: egzamin pisemny.
 Badania operacyjne Dr Michał Kulej. Pokój 509, budynek B4 michal.kulej@pwr.wroc.pl Materiały do zajęć będa dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia wykładu: egzamin
Badania operacyjne Dr Michał Kulej. Pokój 509, budynek B4 michal.kulej@pwr.wroc.pl Materiały do zajęć będa dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia wykładu: egzamin
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
ZAGADNIENIE TRANSPORTOWE
 ZAGADNENE TRANSPORTOWE Definicja: Program liniowy to model, w którym warunki ograniczające oraz funkcja celu są funkcjami liniowymi. W skład każdego programu liniowego wchodzą: zmienne decyzyjne, ograniczenia
ZAGADNENE TRANSPORTOWE Definicja: Program liniowy to model, w którym warunki ograniczające oraz funkcja celu są funkcjami liniowymi. W skład każdego programu liniowego wchodzą: zmienne decyzyjne, ograniczenia
Firma JCo wytwarza dwa wyroby na dwóch maszynach. Jednostka wyrobu 1 wymaga 2 godzin pracy na maszynie 1 i 1 godziny pracy na maszynie 2.
 Przykład Elementy analizy wrażliwości Firma JCo wytwarza dwa wyroby na dwóch maszynach. Jednostka wyrobu 1 wymaga 2 godzin pracy na maszynie 1 i 1 godziny pracy na maszynie 2. Dla wyrobu 2 czasy te wynosza
Przykład Elementy analizy wrażliwości Firma JCo wytwarza dwa wyroby na dwóch maszynach. Jednostka wyrobu 1 wymaga 2 godzin pracy na maszynie 1 i 1 godziny pracy na maszynie 2. Dla wyrobu 2 czasy te wynosza
LOGISTYKA PRODUKCJI. dr inż. Andrzej KIJ
 LOGISTYKA PRODUKCJI dr inż. Andrzej KIJ TEMAT ĆWICZENIA: PLANOWANIE POTRZEB MATERIAŁOWYCH METODA MRP Opracowane na podstawie: Praca zbiorowa pod redakcją, A. Kosieradzkiej, Podstawy zarządzania produkcją
LOGISTYKA PRODUKCJI dr inż. Andrzej KIJ TEMAT ĆWICZENIA: PLANOWANIE POTRZEB MATERIAŁOWYCH METODA MRP Opracowane na podstawie: Praca zbiorowa pod redakcją, A. Kosieradzkiej, Podstawy zarządzania produkcją
Porównanie wyników produkcyjnych gospodarstw w zależności od klas wielkości ekonomicznej
 Porównanie wyników produkcyjnych gospodarstw w zależności od klas wielkości ekonomicznej Krystyna Maciejak Dz. Ekonomiki i zarządzania gospodarstwem rolnym 18.10.2017 r. FADN to europejski system zbierania
Porównanie wyników produkcyjnych gospodarstw w zależności od klas wielkości ekonomicznej Krystyna Maciejak Dz. Ekonomiki i zarządzania gospodarstwem rolnym 18.10.2017 r. FADN to europejski system zbierania
Ścieżki technologiczne, a szerokość opon
 .pl https://www..pl Ścieżki technologiczne, a szerokość opon Autor: dr hab. inż. Krzysztof Pieczarka Data: 27 marca 2018 O zasadności zakładania ścieżek w uprawach polowych zwłaszcza zbóż nie trzeba dziś
.pl https://www..pl Ścieżki technologiczne, a szerokość opon Autor: dr hab. inż. Krzysztof Pieczarka Data: 27 marca 2018 O zasadności zakładania ścieżek w uprawach polowych zwłaszcza zbóż nie trzeba dziś
WYŻSZA SZKOŁA LOGISTYKI
 WYŻSZA SZKOŁA LOGISTYKI POZNAŃ ZARZĄDZANIE MAGAZYNEM MSU NAZWISKO IMIĘ NUMER ZESTAWU MSU/03/ 2010 POZNAŃ, 2010 ROK TABLICA W-1. Postać fizyczna asortymentów Lp. Asortyment Wymiary opz [mm] Masa q opz X
WYŻSZA SZKOŁA LOGISTYKI POZNAŃ ZARZĄDZANIE MAGAZYNEM MSU NAZWISKO IMIĘ NUMER ZESTAWU MSU/03/ 2010 POZNAŃ, 2010 ROK TABLICA W-1. Postać fizyczna asortymentów Lp. Asortyment Wymiary opz [mm] Masa q opz X
b) PLN/szt. Jednostkowa marża na pokrycie kosztów stałych wynosi 6PLN na każdą sprzedają sztukę.
 Poniżej znajdują się przykłady rozwiązań tylko niektórych, spośród prezentowanych na zajęciach, zadań. Wszystkie pochodzą z podręcznika autorstwa Kotowskiej, Sitko i Uziębło. Kolokwium swoim zakresem obejmuje
Poniżej znajdują się przykłady rozwiązań tylko niektórych, spośród prezentowanych na zajęciach, zadań. Wszystkie pochodzą z podręcznika autorstwa Kotowskiej, Sitko i Uziębło. Kolokwium swoim zakresem obejmuje
Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa
 Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa dr Jarosław Kotowicz 02 października 2015r. Zadanie 1 ([1, Przykład
Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa dr Jarosław Kotowicz 02 października 2015r. Zadanie 1 ([1, Przykład
OPTYMALIZACJA DYSKRETNA
 Temat nr a: odelowanie problemów decyzyjnych, c.d. OPTYALIZACJA DYSKRETA Zagadnienia decyzyjne, w których chociaż jedna zmienna decyzyjna przyjmuje wartości dyskretne (całkowitoliczbowe), nazywamy dyskretnymi
Temat nr a: odelowanie problemów decyzyjnych, c.d. OPTYALIZACJA DYSKRETA Zagadnienia decyzyjne, w których chociaż jedna zmienna decyzyjna przyjmuje wartości dyskretne (całkowitoliczbowe), nazywamy dyskretnymi
