Zadanie A. Pestycydy. Wejście. Wyjście. Przykłady. Techniki optymalizacyjne Sosnowiec, semestr zimowy 2016/2017
|
|
|
- Zdzisław Wolski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Zadanie A. Pestycydy Aby uprawiać pewną roślinę musimy ją nawozić mieszanką zawierającą wszystkie potrzebne składniki odżywcze w ilości (podawanej w gramach) nie mniejszej niż przewiduje norma. Taką mieszankę można sporządzić z dostępnej grupy pestycydów. Wiemy, ile kosztuje kilogram określonego pestycydu i ile zawiera on gram danego składnika. Zakładamy ponadto, że pestycydy mogą być mieszane w dowolnych proporcjach. Jaki jest minimalny koszt sporządzenia mieszanki nawozowej? Plik z danymi (w modelu danych języka GNU MathProg) zawiera wszystkie potrzebne informacje, czyli: zbiór dostępnych pestycydów, zbiór składników, zawartości składników w pestycydach, cenę pestycydów i wymagany udział poszczególnych składników w mieszance nawozowej. Liczba rzeczywista określająca koszt mieszanki do sporządzenia. Rozwiązanie podaj z dokładnością do dwóch miejsc po kropce dziesiętnej. Strona 1 z 5
2 Zadanie B. Inwestowanie Mamy do dyspozycji kwotę X zł, którą należy gdzieś zainwestować. Możliwości są trzy: fundusz A dający 9% zysku, fundusz B dający 11% zysku i lokata bankowa dająca 10% zysku (podane punkty procentowe dotyczą tego samego okresu rozliczeniowego). Załóżmy, że w funduszach można zainwestować co najwyżej połowę z całej zainwestowanej kwoty; inwestycja w funduszu B nie może przekroczyć kwoty Y zł; natomiast lokata nie może być mniejsza niż Z zł. Jaki jest możliwy maksymalny zysk? Plik z danymi (w modelu danych języka GNU MathProg) zawiera wszystkie potrzebne informacje, czyli kwoty: X, Y i Z. Liczba rzeczywista określająca zysk w złotówkach. Rozwiązanie podaj z dokładnością do dwóch miejsc po kropce dziesiętnej. Strona 2 z 5
3 Zadanie C. Fabryka W pewnej fabryce mamy P[m 2 ] powierzchni użytkowej, na której można ustawić, jedna obok drugiej, szereg maszyn różnego rodzaju. Każda maszyna rodzaju R zajmuje Z R [m 2 ] powierzchni i w ciągu minuty produkuje W R [m] blachy. Załóżmy, że fabryka ta musi w ciągu minuty wytworzyć w sumie co najmniej N[m] blachy. Ile kupić maszyn danego rodzaju, aby zminimalizować koszt ich zakupu, jeśli wiemy, że jedna maszyna rodzaju R kosztuje C R zł. Plik z danymi (w modelu danych języka GNU MathProg) zawiera wszystkie potrzebne informacje, czyli: powierzchnię użytkową fabryki, wielkość zapotrzebowania na blachę, rodzaje maszyn oraz wydajność, cenę i zajmowaną powierzchnię dla poszczególnych rodzajów maszyn. Dla każdego rodzaju maszyny w oddzielnym wierszu należy podać nazwę typu i liczbę zakupionych maszyn. Strona 3 z 5
4 Zadanie D. Sklepy Znana sieć handlowa ma zamiar otworzyć sklepy w k wybranych miastach pewnego województwa. W celu równomiernego pokrycia całej powierzchni województwa, miasta te powinny być tak wybrane spośród dostępnych n (3 n 100) kandydatów aby zmaksymalizować minimalną odległość pomiędzy dowolną parą wybranych miast. Plik z danymi (w modelu danych języka GNU MathProg) zawiera odległości pomiędzy każdą parą dostępnych miast. Zakładamy, że miasta ponumerowano kolejnymi liczbami naturalnymi, a odległości leżą w przedziale [0; 10.0]. Posortowane numery wybranych miast, każdy w oddzielnym wierszu. Strona 4 z 5
5 Zadanie E. Drukarnia Kierownik drukarni ma następujący problem. Aby wykonać zlecenie klienta należy zrealizować n (1 n 100) zadań, z których każde wymaga takiego samego czasu pracy. Nie jest jednak identyczny czas c ij potrzebny na przejście od zadania i do zadania j. Należy określić kolejność wykonywania zadań, tak aby zminimalizować całkowity czas realizacji zlecenia. Zakładamy, że realizacja zlecenia rozpoczyna się od stanu spoczynku (oznaczonego liczbą 0) oraz że po wykonaniu ostatniego zadania wracamy do stanu spoczynku. Plik z danymi (w modelu danych języka GNU MathProg) zawiera liczbę zadań i czasy przejścia pomiędzy nimi. Zadania ponumerowano kolejnymi liczbami naturalnymi, 1, 2,, n. Zero, 0, oznacza stan spoczynku Optymalny czas realizacji zlecenia sumując wyłącznie czasy przejść. Rozwiązanie podaj z dokładnością do dwóch miejsc po kropce dziesiętnej. Strona 5 z 5
Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02
 Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Ogłoszenie o zmianie statutu KBC ALFA Specjalistycznego Funduszu Inwestycyjnego Otwartego Warszawa, 2 stycznia 2012 r.
 Ogłoszenie o zmianie statutu KBC ALFA Specjalistycznego Funduszu Inwestycyjnego Otwartego Warszawa, 2 stycznia 2012 r. KBC Towarzystwo Funduszy Inwestycyjnych S.A. działające jako organ KBC ALFA Specjalistycznego
Ogłoszenie o zmianie statutu KBC ALFA Specjalistycznego Funduszu Inwestycyjnego Otwartego Warszawa, 2 stycznia 2012 r. KBC Towarzystwo Funduszy Inwestycyjnych S.A. działające jako organ KBC ALFA Specjalistycznego
Klasyczne zagadnienie przydziału
 Klasyczne zagadnienie przydziału Można wyodrębnić kilka grup problemów, w których zadaniem jest odpowiednie rozmieszczenie posiadanych zasobów. Najprostszy problem tej grupy nazywamy klasycznym zagadnieniem
Klasyczne zagadnienie przydziału Można wyodrębnić kilka grup problemów, w których zadaniem jest odpowiednie rozmieszczenie posiadanych zasobów. Najprostszy problem tej grupy nazywamy klasycznym zagadnieniem
Przykład: frytki i puree Analiza wrażliwości współczynników funkcji celu
 Analiza wrażliwości: współczynników funkcji celu analiza wrażliwości pozwala odpowiedzieć na pytanie, w jakich granicach mogą się zmieniać te parametry, aby dotychczasowe rozwiązanie było optymalne, wyrazów
Analiza wrażliwości: współczynników funkcji celu analiza wrażliwości pozwala odpowiedzieć na pytanie, w jakich granicach mogą się zmieniać te parametry, aby dotychczasowe rozwiązanie było optymalne, wyrazów
Lista 1 PL metoda geometryczna
 Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 28 maja 2015 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 28 maja 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 28 maja 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
Wydział Matematyki I Informatyki ul. Słoneczna Olsztyn
 Klucz Napisać program sprawdzający czy dany klucz pasuje do danego zamka. Dziurka w zamku reprezentowana jest w postaci tablicy zero-jedynkowej i jest spójna. Klucz zakodowany jest jako ciąg par liczb
Klucz Napisać program sprawdzający czy dany klucz pasuje do danego zamka. Dziurka w zamku reprezentowana jest w postaci tablicy zero-jedynkowej i jest spójna. Klucz zakodowany jest jako ciąg par liczb
Zagadnienie transportowe i zagadnienie przydziału
 Temat: Zagadnienie transportowe i zagadnienie przydziału Zadanie 1 Trzy piekarnie zlokalizowane na terenie miasta są zaopatrywane w mąkę z trzech magazynów znajdujących się na peryferiach. Zasoby mąki
Temat: Zagadnienie transportowe i zagadnienie przydziału Zadanie 1 Trzy piekarnie zlokalizowane na terenie miasta są zaopatrywane w mąkę z trzech magazynów znajdujących się na peryferiach. Zasoby mąki
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 22 czerwca 2015 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 22 czerwca 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 22 czerwca 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
Wykład 7. Informatyka Stosowana. Magdalena Alama-Bućko. 16 kwietnia Magdalena Alama-Bućko Wykład 7 16 kwietnia / 23
 Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700
 Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
Ekonometria Programowanie Liniowe. Robert Pietrzykowski
 Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
lokata ze strukturą Czarne Złoto
 lokata ze strukturą Czarne Złoto Lokata ze strukturą Czarne Złoto jest produktem łączonym. Składa się z lokaty promocyjnej i produktu strukturyzowanego Czarne Złoto inwestycji w formie ubezpieczenia na
lokata ze strukturą Czarne Złoto Lokata ze strukturą Czarne Złoto jest produktem łączonym. Składa się z lokaty promocyjnej i produktu strukturyzowanego Czarne Złoto inwestycji w formie ubezpieczenia na
Modelowanie całkowitoliczbowe
 1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
Deterministyczne Modele Badań Operacyjnych Semestr letni 2015 Praca domowa IV
 Deterministyczne Modele Badań Operacyjnych Semestr letni 2015 Praca domowa IV 29/05/2015 Polecenie a) Ten zestaw zadań jest zestawem dodatkowym, nie jest on obowiązkowy dla wszystkich studentów. Tą pracę
Deterministyczne Modele Badań Operacyjnych Semestr letni 2015 Praca domowa IV 29/05/2015 Polecenie a) Ten zestaw zadań jest zestawem dodatkowym, nie jest on obowiązkowy dla wszystkich studentów. Tą pracę
Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ).
 PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
EGZAMIN MATURALNY Z INFORMATYKI
 WPISUJE ZDAJĄCY NUMER UCZNIA EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY CZĘŚĆ II ARKUSZ EGZAMINACYJNY PROJEKTU INFORMATURA DATA: 13 LUTEGO 2015 R. CZAS PRACY: 150 MINUT LICZBA PUNKTÓW DO UZYSKANIA:
WPISUJE ZDAJĄCY NUMER UCZNIA EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY CZĘŚĆ II ARKUSZ EGZAMINACYJNY PROJEKTU INFORMATURA DATA: 13 LUTEGO 2015 R. CZAS PRACY: 150 MINUT LICZBA PUNKTÓW DO UZYSKANIA:
SIEĆ NEURONOWA DO OCENY KOŃCOWEJ PRZEDSIĘWZIĘCIA (PROJEKTU)
 SIEĆ NEURONOWA DO OCENY KOŃCOWEJ PRZEDSIĘWZIĘCIA (PROJEKTU) 1. Opis problemu - ocena końcowa projektu Projekt jako nowe, nietypowe przedsięwzięcie wymaga właściwego zarządzania. Podjęcie się realizacji
SIEĆ NEURONOWA DO OCENY KOŃCOWEJ PRZEDSIĘWZIĘCIA (PROJEKTU) 1. Opis problemu - ocena końcowa projektu Projekt jako nowe, nietypowe przedsięwzięcie wymaga właściwego zarządzania. Podjęcie się realizacji
Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony.
 GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
Liczby i działania str. 1/6
 Liczby i działania str. 1/6 1. Rysunek, na którym zacieniowano 4 figury, to rysunek: 2. Odwrotnością liczby 1 1 jest: 6 B. 6 C. 1 1 D. 1 1 3. Odwrotnością liczby 2 7 jest: 2 7 B. 3 1 2 C. 7 2 D. 2 7 4.
Liczby i działania str. 1/6 1. Rysunek, na którym zacieniowano 4 figury, to rysunek: 2. Odwrotnością liczby 1 1 jest: 6 B. 6 C. 1 1 D. 1 1 3. Odwrotnością liczby 2 7 jest: 2 7 B. 3 1 2 C. 7 2 D. 2 7 4.
ING BANK ŚLĄSKI S.A.
 ING BANK ŚLĄSKI S.A. Informacja o kosztach i opłatach dla usług przyjmowania i przekazywania zleceń nabycia lub odkupienia tytułów uczestnictwa w instytucjach wspólnego inwestowania ( Informacja o kosztach
ING BANK ŚLĄSKI S.A. Informacja o kosztach i opłatach dla usług przyjmowania i przekazywania zleceń nabycia lub odkupienia tytułów uczestnictwa w instytucjach wspólnego inwestowania ( Informacja o kosztach
Optymalizacja programu produkcji
 ZARZĄDZANIE PRODUKCJĄ I USŁUGAMI Ćwiczenie 3 Optymalizacja programu produkcji Co i ile produkować i sprzedawać, aby zmaksymalizować zysk? Programowanie produkcji ZADANIE odpowiedź na pytania Co produkować?
ZARZĄDZANIE PRODUKCJĄ I USŁUGAMI Ćwiczenie 3 Optymalizacja programu produkcji Co i ile produkować i sprzedawać, aby zmaksymalizować zysk? Programowanie produkcji ZADANIE odpowiedź na pytania Co produkować?
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 21 grudnia 2015 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 21 grudnia 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 21 grudnia 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
Zadanie 1. (7pkt./18min.)
 Zadanie 1. (7pkt./18min.) 29 maja 2014r. masz zamiar wybrać się do Kina Helios w Opolu, na seans filmowy Powstanie Warszawskie. Korzystając ze strony http://www.helios.pl/17,opole odpowiedz na pytania:
Zadanie 1. (7pkt./18min.) 29 maja 2014r. masz zamiar wybrać się do Kina Helios w Opolu, na seans filmowy Powstanie Warszawskie. Korzystając ze strony http://www.helios.pl/17,opole odpowiedz na pytania:
3. Macierze i Układy Równań Liniowych
 3. Macierze i Układy Równań Liniowych Rozważamy równanie macierzowe z końcówki ostatniego wykładu ( ) 3 1 X = 4 1 ( ) 2 5 Podstawiając X = ( ) x y i wymnażając, otrzymujemy układ 2 równań liniowych 3x
3. Macierze i Układy Równań Liniowych Rozważamy równanie macierzowe z końcówki ostatniego wykładu ( ) 3 1 X = 4 1 ( ) 2 5 Podstawiając X = ( ) x y i wymnażając, otrzymujemy układ 2 równań liniowych 3x
MSR 23 Koszty finansowania zewnętrznego
 MSR 23 Koszty finansowania zewnętrznego Ujęcie kosztów finansowania zewnętrznego przed 2009r ROZWIĄZANIE WZORCOWE Koszty finansowania zewnętrznego ujmowane są jako koszt w rachunku zysków i strat w okresie,
MSR 23 Koszty finansowania zewnętrznego Ujęcie kosztów finansowania zewnętrznego przed 2009r ROZWIĄZANIE WZORCOWE Koszty finansowania zewnętrznego ujmowane są jako koszt w rachunku zysków i strat w okresie,
1. Co to jest lokata? 2. Rodzaje lokat bankowych 3. Lokata denominowana 4. Lokata inwestycyjna 5. Lokata negocjowana 6. Lokata nocna (overnight) 7.
 Lokaty 1. Co to jest lokata? Spis treści 2. Rodzaje lokat bankowych 3. Lokata denominowana 4. Lokata inwestycyjna 5. Lokata negocjowana 6. Lokata nocna (overnight) 7. Lokata progresywna 8. Lokata rentierska
Lokaty 1. Co to jest lokata? Spis treści 2. Rodzaje lokat bankowych 3. Lokata denominowana 4. Lokata inwestycyjna 5. Lokata negocjowana 6. Lokata nocna (overnight) 7. Lokata progresywna 8. Lokata rentierska
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
METODY OBLICZENIOWE OPTYMALIZACJI zadania
 METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
Rozwiązanie Ad 1. Model zadania jest następujący:
 Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
Inwestor musi wybrać następujące parametry: instrument bazowy, rodzaj opcji (kupna lub sprzedaży, kurs wykonania i termin wygaśnięcia.
 Opcje na GPW (II) Wbrew ogólnej opinii, inwestowanie w opcje nie musi być trudne. Na rynku tym można tworzyć strategie dla doświadczonych inwestorów, ale również dla początkujących. Najprostszym sposobem
Opcje na GPW (II) Wbrew ogólnej opinii, inwestowanie w opcje nie musi być trudne. Na rynku tym można tworzyć strategie dla doświadczonych inwestorów, ale również dla początkujących. Najprostszym sposobem
Metody numeryczne. materiały do wykładu dla studentów. 7. Całkowanie numeryczne
 Metody numeryczne materiały do wykładu dla studentów 7. Całkowanie numeryczne 7.1. Całkowanie numeryczne 7.2. Metoda trapezów 7.3. Metoda Simpsona 7.4. Metoda 3/8 Newtona 7.5. Ogólna postać wzorów kwadratur
Metody numeryczne materiały do wykładu dla studentów 7. Całkowanie numeryczne 7.1. Całkowanie numeryczne 7.2. Metoda trapezów 7.3. Metoda Simpsona 7.4. Metoda 3/8 Newtona 7.5. Ogólna postać wzorów kwadratur
Firma JCo wytwarza dwa wyroby na dwóch maszynach. Jednostka wyrobu 1 wymaga 2 godzin pracy na maszynie 1 i 1 godziny pracy na maszynie 2.
 Przykład Elementy analizy wrażliwości Firma JCo wytwarza dwa wyroby na dwóch maszynach. Jednostka wyrobu 1 wymaga 2 godzin pracy na maszynie 1 i 1 godziny pracy na maszynie 2. Dla wyrobu 2 czasy te wynosza
Przykład Elementy analizy wrażliwości Firma JCo wytwarza dwa wyroby na dwóch maszynach. Jednostka wyrobu 1 wymaga 2 godzin pracy na maszynie 1 i 1 godziny pracy na maszynie 2. Dla wyrobu 2 czasy te wynosza
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 30 września 2015 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 30 września 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 30 września 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
Programowanie liniowe
 Badania operacyjne Problem Model matematyczny Metoda rozwiązania Znaleźć optymalny program produkcji. Zmaksymalizować 1 +3 2 2 3 (1) Przy ograniczeniach 3 1 2 +2 3 7 (2) 2 1 +4 2 12 (3) 4 1 +3 2 +8 3 10
Badania operacyjne Problem Model matematyczny Metoda rozwiązania Znaleźć optymalny program produkcji. Zmaksymalizować 1 +3 2 2 3 (1) Przy ograniczeniach 3 1 2 +2 3 7 (2) 2 1 +4 2 12 (3) 4 1 +3 2 +8 3 10
Forma prawna Agent Ubezpieczyciel. Euro Bank S.A. Okres Odpowiedzialności Wiek Zwrot kapitału. 18-77 lat (włącznie)
 produkt strukturyzowany Kurs na Amerykę Forma prawna Agent Ubezpieczyciel indywidualne ubezpieczenie na życie i dożycie Euro Bank S.A. Towarzystwo Ubezpieczeń na Życie Europa S.A. Okres Odpowiedzialności
produkt strukturyzowany Kurs na Amerykę Forma prawna Agent Ubezpieczyciel indywidualne ubezpieczenie na życie i dożycie Euro Bank S.A. Towarzystwo Ubezpieczeń na Życie Europa S.A. Okres Odpowiedzialności
4. Ubezpieczenie Życiowe
 4. Ubezpieczenie Życiowe Składka ubezpieczeniowa musi brać pod uwagę następujące czynniki: 1. Kwotę wypłaconą przy śmierci ubezpieczonego oraz jej wartość aktualną. 2. Rozkład czasu do śmierci ubezpieczonego
4. Ubezpieczenie Życiowe Składka ubezpieczeniowa musi brać pod uwagę następujące czynniki: 1. Kwotę wypłaconą przy śmierci ubezpieczonego oraz jej wartość aktualną. 2. Rozkład czasu do śmierci ubezpieczonego
Rady Nadzorczej Jeleniogórskiej Spółdzielni Mieszkaniowej w Jeleniej Górze z dnia 11 marca 2008 roku
 UCHWAŁA nr 4 /2008 Rady Nadzorczej Jeleniogórskiej Spółdzielni Mieszkaniowej w Jeleniej Górze z dnia 11 marca 2008 roku w sprawie uchwalenia Zasad ustalania i rozliczania kosztów termomodernizacji budynków
UCHWAŁA nr 4 /2008 Rady Nadzorczej Jeleniogórskiej Spółdzielni Mieszkaniowej w Jeleniej Górze z dnia 11 marca 2008 roku w sprawie uchwalenia Zasad ustalania i rozliczania kosztów termomodernizacji budynków
Straty funduszy akcyjnych z ostatnich czterech miesięcy średnio przekraczają już 20%.
 Straty funduszy akcyjnych z ostatnich czterech miesięcy średnio przekraczają już 20%. Straty funduszy akcyjnych z ostatnich czterech miesięcy średnio przekraczają już 20%. Choć jak to zazwyczaj bywa opinie
Straty funduszy akcyjnych z ostatnich czterech miesięcy średnio przekraczają już 20%. Straty funduszy akcyjnych z ostatnich czterech miesięcy średnio przekraczają już 20%. Choć jak to zazwyczaj bywa opinie
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania)
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 7 maja 2018 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 7 maja 2018 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima
WYŁĄCZENIE ODPOWIEDZIALNOŚCI ZWIĄZANEJ Z RYZYKIEM
 WYŁĄCZENIE ODPOWIEDZIALNOŚCI ZWIĄZANEJ Z RYZYKIEM Prawnie obowiązującą wersją tego dokumentu jest wersja angielska. Niniejsze tłumaczenie ma jedynie charakter informacyjny. Kliknij tutaj, aby otworzyć
WYŁĄCZENIE ODPOWIEDZIALNOŚCI ZWIĄZANEJ Z RYZYKIEM Prawnie obowiązującą wersją tego dokumentu jest wersja angielska. Niniejsze tłumaczenie ma jedynie charakter informacyjny. Kliknij tutaj, aby otworzyć
Listopad 2011. Nowa Perspektywa II subskrypcja produktu
 Listopad 2011 Nowa Perspektywa II subskrypcja produktu Nowa Perspektywa - charakterystyka produktu Ubezpieczenie z elementami inwestycji Nowa Perspektywa to ubezpieczenia na życie i dożycie z Ubezpieczeniowym
Listopad 2011 Nowa Perspektywa II subskrypcja produktu Nowa Perspektywa - charakterystyka produktu Ubezpieczenie z elementami inwestycji Nowa Perspektywa to ubezpieczenia na życie i dożycie z Ubezpieczeniowym
1. Wzrost zbyt szybki prowadzi do utraty samodzielności firmy (take-over). 2. Jednym z założeń modelu wzrostu zrównoważonego jest płynna struktura
 1. Wzrost zbyt szybki prowadzi do utraty samodzielności firmy (take-over). 2. Jednym z założeń modelu wzrostu zrównoważonego jest płynna struktura kapitałowa. 3. Wskaźnik zysku zatrzymanego to iloraz przyrostu
1. Wzrost zbyt szybki prowadzi do utraty samodzielności firmy (take-over). 2. Jednym z założeń modelu wzrostu zrównoważonego jest płynna struktura kapitałowa. 3. Wskaźnik zysku zatrzymanego to iloraz przyrostu
Zestaw zadań konkursowych XVII Regionalnego Konkursu Informatycznego
 Zestaw zadań konkursowych XVII Regionalnego Konkursu Informatycznego Instytut Informatyki UwB 1.04.2017 r. Uwaga: Wersje źródłowe i skompilowane programy mają być umieszczone na Pulpicie w katalogu o nazwie
Zestaw zadań konkursowych XVII Regionalnego Konkursu Informatycznego Instytut Informatyki UwB 1.04.2017 r. Uwaga: Wersje źródłowe i skompilowane programy mają być umieszczone na Pulpicie w katalogu o nazwie
2.1 Wartość Aktualna Renty Stałej
 2.1 Wartość Aktualna Renty Stałej Zakładamy że dana osoba ma dostać kwotę o stałej wartości nominalnej x przez N okresów (zwykle miesięcznie lub rocznie), np. stała renta/emerytura. Zakładamy że pierwsza
2.1 Wartość Aktualna Renty Stałej Zakładamy że dana osoba ma dostać kwotę o stałej wartości nominalnej x przez N okresów (zwykle miesięcznie lub rocznie), np. stała renta/emerytura. Zakładamy że pierwsza
4. PROGRAMOWANIE LINIOWE
 4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
Wozy paszowe. produkujące inny rodzaj mieszanki - potwierdzone przez rolników uzyskanie wyższej produkcji z mniejszej ilości paszy
 Wozy paszowe produkujące inny rodzaj mieszanki - potwierdzone przez rolników uzyskanie wyższej produkcji z mniejszej ilości paszy Różnica tkwi w mieszance Karmienie zwierząt (przeżuwaczy) opiera się głównie
Wozy paszowe produkujące inny rodzaj mieszanki - potwierdzone przez rolników uzyskanie wyższej produkcji z mniejszej ilości paszy Różnica tkwi w mieszance Karmienie zwierząt (przeżuwaczy) opiera się głównie
OPTYMALIZACJA W LOGISTYCE
 OPTYMALIZACJA W LOGISTYCE Zagadnienie przydziału dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie przydziału 1 Można wyodrębnić kilka grup problemów, których zadaniem jest alokacja szeroko
OPTYMALIZACJA W LOGISTYCE Zagadnienie przydziału dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie przydziału 1 Można wyodrębnić kilka grup problemów, których zadaniem jest alokacja szeroko
EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY CZĘŚĆ II MAJ 2014 WYBRANE: Czas pracy: 150 minut. Liczba punktów do uzyskania: 30 WPISUJE ZDAJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 2013 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 2013 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY
Specyfikacja pliku komunikacyjnego Tabela przedstawia format dokumentu XML opisującego Fakturę dla branŝy Farmaceutycznej. Wersja 1.00.
 Specyfikacja pliku komunikacyjnego Tabela przedstawia format dokumentu XML opisującego Fakturę dla branŝy Farmaceutycznej. Wersja 1.00. M M M M InvoiceNumber_1
Specyfikacja pliku komunikacyjnego Tabela przedstawia format dokumentu XML opisującego Fakturę dla branŝy Farmaceutycznej. Wersja 1.00. M M M M InvoiceNumber_1
TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA KLIENTÓW INDYWIDUALNYCH obowiązuje od 16 lutego 2016 r.
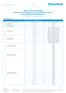 Duma Przedsiębiorcy 1/16 1. Oprocentowanie TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA KLIENTÓW INDYWIDUALNYCH obowiązuje od 16 lutego 2016 r. TERMINOWE LOKATY OSZCZĘDNOŚCIOWE
Duma Przedsiębiorcy 1/16 1. Oprocentowanie TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA KLIENTÓW INDYWIDUALNYCH obowiązuje od 16 lutego 2016 r. TERMINOWE LOKATY OSZCZĘDNOŚCIOWE
Deterministyczne Modele Badań Operacyjnych Semestr letni 2015 Praca domowa III
 Deterministyczne Modele Badań Operacyjnych Semestr letni 2015 Praca domowa III 15/05/2015 Polecenie Zestaw składa się z trzech zadań, za każde z nich można zdobyć 10p. Rozwiązania do zadań należy wysłać
Deterministyczne Modele Badań Operacyjnych Semestr letni 2015 Praca domowa III 15/05/2015 Polecenie Zestaw składa się z trzech zadań, za każde z nich można zdobyć 10p. Rozwiązania do zadań należy wysłać
Umowa na usługę doradczą w zakresie optymalizacji kosztów zakupu energii elektrycznej
 Umowa na usługę doradczą w zakresie optymalizacji kosztów zakupu energii elektrycznej 1 POSTANOWIENIA OGÓLNE i DEFINICJE 1) Niniejszy dokument określa zasady świadczenia usługi optymalizacji zakupu energii
Umowa na usługę doradczą w zakresie optymalizacji kosztów zakupu energii elektrycznej 1 POSTANOWIENIA OGÓLNE i DEFINICJE 1) Niniejszy dokument określa zasady świadczenia usługi optymalizacji zakupu energii
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 3 października 2017 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 3 października 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 3 października 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
TABELA OPROCENTOWANIA PRODUKTÓW DEPOZYTOWYCH DLA KLIENTÓW INDYWIDUALNYCH BANKU SPÓŁDZIELCZEGO W LUBAWIE obowiązująca od dnia r.
 ZRZESZENIE BANKU POLSKIEJ SPÓŁDZIELCZOŚCI BANK SPÓŁDZIELCZY W LUBAWIE Rok założenia 1870 Załącznik do Uchwały nr 88/2017 Zarządu Banku Spółdzielczego w Lubawie z dnia 7 sierpnia 2017r. TABELA OPROCENTOWANIA
ZRZESZENIE BANKU POLSKIEJ SPÓŁDZIELCZOŚCI BANK SPÓŁDZIELCZY W LUBAWIE Rok założenia 1870 Załącznik do Uchwały nr 88/2017 Zarządu Banku Spółdzielczego w Lubawie z dnia 7 sierpnia 2017r. TABELA OPROCENTOWANIA
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 1 września 2017 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 1 września 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 1 września 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima
Ekonomiczny Uniwersytet Dziecięcy. Czarodziejski młynek do pomnażania pieniędzy
 Ekonomiczny Uniwersytet Dziecięcy Czarodziejski młynek do pomnażania pieniędzy dr inż. Krzysztof Świetlik Politechnika Gdańska 7 marca 2019 r. Czym jest akcja? Mianem tym określa się papier wartościowy
Ekonomiczny Uniwersytet Dziecięcy Czarodziejski młynek do pomnażania pieniędzy dr inż. Krzysztof Świetlik Politechnika Gdańska 7 marca 2019 r. Czym jest akcja? Mianem tym określa się papier wartościowy
OPTYMALIZACJA W LOGISTYCE
 OPTYALIZACJA W LOGISTYCE Zagadnienie transportowe 2 dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie transportowe z kryterium czasu I rodzaju () Jeżeli w modelu klasycznego zagadnienia transportowego
OPTYALIZACJA W LOGISTYCE Zagadnienie transportowe 2 dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie transportowe z kryterium czasu I rodzaju () Jeżeli w modelu klasycznego zagadnienia transportowego
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 26 września 2017 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 26 września 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 26 września 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
Regulamin Promocji Lokaty z Funduszem Do Pary. I. Organizator Promocji
 Regulamin Promocji Lokaty z Funduszem Do Pary I. Organizator Promocji 1. Promocja Lokaty z Funduszem Do Pary, zwana dalej Promocją organizowana jest przez BRE Bank SA (MultiBank) z siedzibą w Warszawie
Regulamin Promocji Lokaty z Funduszem Do Pary I. Organizator Promocji 1. Promocja Lokaty z Funduszem Do Pary, zwana dalej Promocją organizowana jest przez BRE Bank SA (MultiBank) z siedzibą w Warszawie
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 27 listopada 2015 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 27 listopada 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 27 listopada 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
REGULAMIN PROGRAMU INWESTYCYJNEGO
 REGULAMIN PROGRAMU INWESTYCYJNEGO 1 1. Słownik wyrażeń użytych w poniższym regulaminie: Bank Bank BGŻ BNP Paribas Spółka Akcyjna z siedzibą w Warszawie przy ul. Kasprzaka 10/16, 01-211 Warszawa. Program
REGULAMIN PROGRAMU INWESTYCYJNEGO 1 1. Słownik wyrażeń użytych w poniższym regulaminie: Bank Bank BGŻ BNP Paribas Spółka Akcyjna z siedzibą w Warszawie przy ul. Kasprzaka 10/16, 01-211 Warszawa. Program
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 9 lutego 2016 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 9 lutego 2016 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 9 lutego 2016 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
Zestaw 1 Organizacja plików: Oddajemy tylko źródła programów (pliki o rozszerzeniach.adb)!!! trójki sąsiednich elementów tablicy
 Zestaw 1 1. Napisać program pobierający od użytkownika liczbę całkowitą dodatnią R i liczbę rzeczywistą dodatnią S, a następnie informujący ile kolejnych liczb z ciągu 1, 1+R, 1+2R, 1+3R, należy dodać,
Zestaw 1 1. Napisać program pobierający od użytkownika liczbę całkowitą dodatnią R i liczbę rzeczywistą dodatnią S, a następnie informujący ile kolejnych liczb z ciągu 1, 1+R, 1+2R, 1+3R, należy dodać,
UCHWAŁA NR 35/2016 SENATU POLITECHNIKI RZESZOWSKIEJ. z dnia 19 maja 2016r w sprawie: zasad podziału dotacji budżetowej oraz rozliczeń finansowych
 UCHWAŁA NR 35/2016 SENATU POLITECHNIKI RZESZOWSKIEJ z dnia 19 maja 2016r w sprawie: zasad podziału dotacji budżetowej oraz rozliczeń finansowych dotyczących budżetu Uczelni na 2016r Senat Politechniki
UCHWAŁA NR 35/2016 SENATU POLITECHNIKI RZESZOWSKIEJ z dnia 19 maja 2016r w sprawie: zasad podziału dotacji budżetowej oraz rozliczeń finansowych dotyczących budżetu Uczelni na 2016r Senat Politechniki
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 15 listopada 2017 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 15 listopada 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 15 listopada 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
L.p. Nazwa Lokaty Okres Umowny Oprocentowanie w skali roku. 2. Lokata HAPPY PLUS 3 miesiące 3,25%
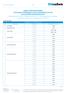 Duma Przedsiębiorcy 1/16 1. Oprocentowanie TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA KLIENTÓW INDYWIDUALNYCH (zaktualizowana w dniu 30 października 2015 r. i obowiązująca do
Duma Przedsiębiorcy 1/16 1. Oprocentowanie TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA KLIENTÓW INDYWIDUALNYCH (zaktualizowana w dniu 30 października 2015 r. i obowiązująca do
Zadania do wykonania. Rozwiązując poniższe zadania użyj pętlę for.
 Zadania do wykonania Rozwiązując poniższe zadania użyj pętlę for. 1. apisz program, który przesuwa w prawo o dwie pozycje zawartość tablicy 10-cio elementowej liczb całkowitych tzn. element t[i] dla i=2,..,9
Zadania do wykonania Rozwiązując poniższe zadania użyj pętlę for. 1. apisz program, który przesuwa w prawo o dwie pozycje zawartość tablicy 10-cio elementowej liczb całkowitych tzn. element t[i] dla i=2,..,9
Regulamin uczestnictwa w programie oszczędnościowoinwestycyjnym
 Regulamin uczestnictwa w programie oszczędnościowoinwestycyjnym Lokata Plus z dnia 05.07.2012 r. Art. 1 [Definicje] 1. W niniejszy Regulaminie użyto następujących wyrażeń i definicji: 1) Bank bank, będący
Regulamin uczestnictwa w programie oszczędnościowoinwestycyjnym Lokata Plus z dnia 05.07.2012 r. Art. 1 [Definicje] 1. W niniejszy Regulaminie użyto następujących wyrażeń i definicji: 1) Bank bank, będący
Badania operacyjne. Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie:
 Badania operacyjne Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia
Badania operacyjne Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 8 kwietnia 2016 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 8 kwietnia 2016 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 8 kwietnia 2016 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
Regulamin Promocji Lokaty z funduszem (ed.2) Obowiązuje od r. do r.
 Regulamin Promocji Lokaty z funduszem (ed.2) Obowiązuje od 20.06.2017 r. do 30.11.2017r. 1 Organizator Promocji 1. Promocja Lokata z funduszem, zwana dalej Promocją, organizowana jest przez mbank S.A.
Regulamin Promocji Lokaty z funduszem (ed.2) Obowiązuje od 20.06.2017 r. do 30.11.2017r. 1 Organizator Promocji 1. Promocja Lokata z funduszem, zwana dalej Promocją, organizowana jest przez mbank S.A.
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 20 listopada 2017 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 20 listopada 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 20 listopada 2017 r. Część 1. A. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont
Zad.1. Microsoft Excel - Raport wyników Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto
 Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
Standardowe zadanie programowania liniowego. Gliwice 1
 Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
ZARZĄDZENIE NR 2/2001
 ZARZĄDZENIE NR 2/2001 Dyrektora IOŚ w sprawie wprowadzenia nowego systemu ekonomicznego IOŚ z dnia 02 stycznia 2001r Na podstawie 19 p.1 regulaminu organizacyjnego IOŚ, zarządzam, co następuje: 1 1. Z
ZARZĄDZENIE NR 2/2001 Dyrektora IOŚ w sprawie wprowadzenia nowego systemu ekonomicznego IOŚ z dnia 02 stycznia 2001r Na podstawie 19 p.1 regulaminu organizacyjnego IOŚ, zarządzam, co następuje: 1 1. Z
TABELA OPROCENTOWANIA PRODUKTÓW DEPOZYTOWYCH DLA KLIENTÓW INDYWIDUALNYCH BANKU SPÓŁDZIELCZEGO W LUBAWIE
 ZRZESZENIE BANKU POLSKIEJ SPÓŁDZIELCZOŚCI BANK SPÓŁDZIELCZY W LUBAWIE Rok założenia 1870 TABELA OPROCENTOWANIA PRODUKTÓW DEPOZYTOWYCH DLA KLIENTÓW INDYWIDUALNYCH BANKU SPÓŁDZIELCZEGO W LUBAWIE (obowiązuje
ZRZESZENIE BANKU POLSKIEJ SPÓŁDZIELCZOŚCI BANK SPÓŁDZIELCZY W LUBAWIE Rok założenia 1870 TABELA OPROCENTOWANIA PRODUKTÓW DEPOZYTOWYCH DLA KLIENTÓW INDYWIDUALNYCH BANKU SPÓŁDZIELCZEGO W LUBAWIE (obowiązuje
3.1 Analiza zysków i strat
 3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty poniesione
3.1 Analiza zysków i strat Zakładamy że firma decyduje czy ma wdrożyć nowy produkt lub projekt. Firma musi rozważyć czy przyszłe zyski (dyskontowane w czasie) z tego projektu są większe niż koszty poniesione
Badania operacyjne. Lista zadań projektowych nr 2
 Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 12 lipca 2017 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 12 lipca 2017 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 12 lipca 2017 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
24-miesięczna lokata strukturyzowana Wielka 20-tka
 24-miesięczna lokata strukturyzowana Wielka 20-tka Okres subskrypcji: 25.05.2010-08.06.2010 Okres trwania lokaty: 9.06.2010-08.06.2012 Aktywo bazowe: kontrakt terminowy na WIG20 Minimalna kwota wpłaty:
24-miesięczna lokata strukturyzowana Wielka 20-tka Okres subskrypcji: 25.05.2010-08.06.2010 Okres trwania lokaty: 9.06.2010-08.06.2012 Aktywo bazowe: kontrakt terminowy na WIG20 Minimalna kwota wpłaty:
Wykład z modelowania matematycznego. Zagadnienie transportowe.
 Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Scenariusz zajęć z przedmiotu podstawy przedsiębiorczości
 Scenariusz zajęć z przedmiotu podstawy przedsiębiorczości Temat: Dochody z kapitału Opracowała Grażyna Drożdżowska Uwagi realizacyjne Lekcja jest przewidziana jako jednostka 2- godzinna stanowiąca utrwalenie
Scenariusz zajęć z przedmiotu podstawy przedsiębiorczości Temat: Dochody z kapitału Opracowała Grażyna Drożdżowska Uwagi realizacyjne Lekcja jest przewidziana jako jednostka 2- godzinna stanowiąca utrwalenie
PRÓBNY EGZAMIN MATURALNY Z INFORMATYKI STYCZEŃ Arkusz II. Czas pracy: 150 minut Liczba punktów do uzyskania: 35
 Organizatorzy: Uniwersytet Mikołaja Kopernika w Toruniu Wydział Matematyki i Informatyki Oddział Kujawsko-Pomorski Polskiego Towarzystwa Informatycznego Centrum Kształcenia Ustawicznego TODMiDN w Toruniu
Organizatorzy: Uniwersytet Mikołaja Kopernika w Toruniu Wydział Matematyki i Informatyki Oddział Kujawsko-Pomorski Polskiego Towarzystwa Informatycznego Centrum Kształcenia Ustawicznego TODMiDN w Toruniu
Optymalizacja programu produkcji (programowanie produkcji)
 ZARZĄDZANIE PRODUKCJĄ i USŁUGAMI Ćwiczenia audytoryjne 1 Optymalizacja programu produkcji (programowanie produkcji) Co i ile produkować i sprzedawać aby zmaksymalizować zysk? Programowanie produkcji ZADANIE
ZARZĄDZANIE PRODUKCJĄ i USŁUGAMI Ćwiczenia audytoryjne 1 Optymalizacja programu produkcji (programowanie produkcji) Co i ile produkować i sprzedawać aby zmaksymalizować zysk? Programowanie produkcji ZADANIE
Cena Bid, Ask i spread
 Jesteś tu: Bossa.pl» Oferta» Forex» Podstawowe informacje Cena Bid, Ask i spread Po uruchuchomieniu platformy możemy zaobserwować, że instrumenty finansowe są kwotowane w dwóch cenach, po cenie Bid i cenie
Jesteś tu: Bossa.pl» Oferta» Forex» Podstawowe informacje Cena Bid, Ask i spread Po uruchuchomieniu platformy możemy zaobserwować, że instrumenty finansowe są kwotowane w dwóch cenach, po cenie Bid i cenie
dla lokat otwartych w Pocztowych Kontach i w sklepie internetowym
 (obowiązujący od 01 1 lipca lutego 2015 2016 r.) r.) Rodzaj lokaty Termin lokaty Rodzaj oprocentowania Wysokość oprocentowania w kolejnych miesiącach trwania lokaty, podane w skali roku dla lokat otwartych
(obowiązujący od 01 1 lipca lutego 2015 2016 r.) r.) Rodzaj lokaty Termin lokaty Rodzaj oprocentowania Wysokość oprocentowania w kolejnych miesiącach trwania lokaty, podane w skali roku dla lokat otwartych
Programowanie liniowe całkowitoliczbowe. Tadeusz Trzaskalik
 Programowanie liniowe całkowitoliczbowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Rozwiązanie całkowitoliczbowe Założenie podzielności Warunki całkowitoliczbowości Czyste zadanie programowania
Programowanie liniowe całkowitoliczbowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Rozwiązanie całkowitoliczbowe Założenie podzielności Warunki całkowitoliczbowości Czyste zadanie programowania
Finanse dla sprytnych
 Ekonomiczny Uniwersytet Dziecięcy Uniwersytet w Białymstoku 28 kwietnia 2011 r. Finanse dla sprytnych Dlaczego inteligencja finansowa popłaca? dr Adam Wyszkowski EKONOMICZNY UNIWERSYTET DZIECIĘCY WWW.UNIWERSYTET-DZIECIECY.PL
Ekonomiczny Uniwersytet Dziecięcy Uniwersytet w Białymstoku 28 kwietnia 2011 r. Finanse dla sprytnych Dlaczego inteligencja finansowa popłaca? dr Adam Wyszkowski EKONOMICZNY UNIWERSYTET DZIECIĘCY WWW.UNIWERSYTET-DZIECIECY.PL
Skrypt 4. Liczby rzeczywiste: Opracowanie L5
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 4 Liczby rzeczywiste: 26.
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 4 Liczby rzeczywiste: 26.
DA.III.272.1.10.2015 Zielona Góra, 2015-10 - 14 ZMIANA TREŚCI SPECYFIKACJI ISTOTNYCH WARUNKÓW ZAMÓWIENIA (1)
 65-057 Zielona Góra ul. Podgórna 7 tel. +48 /68/456 52 00, 320 20 37 fax +48 /68/456 52 96 www.lubuskie.pl DA.III.272.1.10.2015 Zielona Góra, 2015-10 - 14 Wg rozdzielnika ZMIANA TREŚCI SPECYFIKACJI ISTOTNYCH
65-057 Zielona Góra ul. Podgórna 7 tel. +48 /68/456 52 00, 320 20 37 fax +48 /68/456 52 96 www.lubuskie.pl DA.III.272.1.10.2015 Zielona Góra, 2015-10 - 14 Wg rozdzielnika ZMIANA TREŚCI SPECYFIKACJI ISTOTNYCH
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 27 lipca 2017 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 27 lipca 2017 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 27 lipca 2017 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
Egzamin z Podstaw informatyki i programowania 2007/2008
 Egzamin z Podstaw informatyki i programowania 2007/2008 Imię i nazwisko:... 1 2 3 4 5 6 7 8 9 10 11 12 13 14 suma 1. Napisz funkcję logiczną, która dla zadanej parametrem wartości rzeczywistej x, oblicza
Egzamin z Podstaw informatyki i programowania 2007/2008 Imię i nazwisko:... 1 2 3 4 5 6 7 8 9 10 11 12 13 14 suma 1. Napisz funkcję logiczną, która dla zadanej parametrem wartości rzeczywistej x, oblicza
Instrukcja obsługi programu PIT. wersja 10.xx
 Instrukcja obsługi programu PIT dla użytkowników KSP wersja 10.xx Katowice 2005 1. Instalacja Użytkownik programu KSP nie powinien mieć problemów z jego manualna obsługą. Należy czytać informacje umieszczone
Instrukcja obsługi programu PIT dla użytkowników KSP wersja 10.xx Katowice 2005 1. Instalacja Użytkownik programu KSP nie powinien mieć problemów z jego manualna obsługą. Należy czytać informacje umieszczone
Każde państwo posiada walutę, w której rozlicza się wszelkie płatności na jego terenie. W Polsce jest nią złoty, dzielący się na 100 groszy.
 Każde państwo posiada walutę, w której rozlicza się wszelkie płatności na jego terenie. W Polsce jest nią złoty, dzielący się na 100 groszy. Państwo: Sprawuje kontrolę nad stabilnością swojej waluty.(np.,
Każde państwo posiada walutę, w której rozlicza się wszelkie płatności na jego terenie. W Polsce jest nią złoty, dzielący się na 100 groszy. Państwo: Sprawuje kontrolę nad stabilnością swojej waluty.(np.,
