1-2. Formułowanie zadań decyzyjnych. Metoda geometryczna
|
|
|
- Henryk Stefański
- 9 lat temu
- Przeglądów:
Transkrypt
1 -. Formułowanie zadań decyzyjnych. Metoda geometryczna Zagadnienie wyznaczania optymalnego asortymentu produkcji Firma zamierza uruchomić produkcję dwóch wyrobów A i B. Cenę zbytu oszacowano na zł/kg dla każdego z wyrobów. Możliwości przerobu dwóch surowców które limitują możliwości produkcyjne wynoszą odpowiednio 8 i 4 t w okresie planistycznym. Pozostałe środki produkcji nie ograniczają wielkości produkcji. Nakłady surowców (kg) niezbędne do wytworzenia jednostki wyrobów podaje tabela. 6 4 A = 3 4 a) Wyznaczyć plan produkcji maksymalizujący przychód, b) Powiedzmy, że wielkość produkcji wyrobu A nie może przekroczyć 000 sztuk. W jaki sposób wpłynie to na rozwiązanie z pkt. a) i wielkość przychodu? c) Wielkość produkcji wyrobu A nie może przekroczyć wielkości produkcji wyrobu B. W jaki sposób wpłynie to na rozwiązanie z pkt. a) i wielkość przychodu? d) W jakim przedziale musi zawierać się cena wyrobu A, aby zmiana ceny nie wpłynęła na rozwiązanie z pkt. a)? Czy zmiany ceny wpłyną na wartość przychodu? e) Jakie założenia ekonomiczne trzeba było przyjąć aby problem wyznaczania optymalnego asortymentu produkcji można było sprowadzić do zadania PL? f) O popełnieniu jakich błędów modelowania świadczy brak skończonego optimum oraz pustość zbioru rozwiązań dopuszczalnych? Zagadnienie rozkroju Tartak otrzymał zamówienie na 00 desek o długości m, 50 desek o długości,5m i 00 desek o długości 3,5m. Deski otrzymuje się dokonując cięcia kłód o długości 0m. a) Wyznaczyć kombinację sposobów rozkroju kłód minimalizującą wielkość odpadu. W jaki sposób można zagwarantować niesprzeczność zadania? b) W jaki sposób liczba rozkrojów wpływa na rozwiązanie? Czy jest celowe generowanie dużej liczby rozkrojów? c) Podać uzasadnienie ekonomiczne wykorzystywania funkcji postulującej minimalizację odpadu. Zagadnienie diety Racjonalna hodowla trzody chlewnej wymaga dostarczenia co najmniej 4 kg składnika odżywczego S i 49 kg S oraz nie więcej niż 70 kg S3 dziennie. Składniki te dostarcza się skarmiając trzodę dwoma paszami : P i P. Zawartość składników odżywczych w paszach (kg/kg) oraz ceny ich zakupu (zł/kg) podaje tabela. Składnik Pasza odżywczy P P S 0,04 0, S 0,4 0,07 S3 0, 0, Cena zbytu 3,5 Ilość dziennie dostarczanych pasz wynosi 500 kg. a) Ustalić dzienne zapotrzebowanie na pasze P i P minimalizujące koszty zakupu, zapewniające dostarczenie składników odżywczych w wymaganych ilościach. b) Przy jakiej cenie paszy P nastąpi zmiana rozwiązania z pkt. a)? c) Powiedzmy, że dziennie możemy dostarczać 400 kg pasz. W jaki sposób wpłynie to na rozwiązanie z pkt. a)?
2 Problem wyboru optymalnego składu mieszanki Dwa gatunki węgla A i B zawierają zanieczyszczenia w postaci fosforu i popiołu. W pewnym procesie przemysłowym potrzeba co najmniej 90 t paliwa zawierającego nie więcej niż 0,03% fosforu i nie więcej niż 4% popiołu. Stopień zanieczyszczenia obu gatunków węgla oraz ceny zakupu podaje tabela. Gatunek Zanieczyszczenia (%) Cena zbytu węgla Fosfor Popiół (zł/t) A 0, B a) W jakiej proporcji należy zmieszać gatunki węgla, aby uzyskać paliwo o minimalnym koszcie spełniające normy ekologiczne? b) Powiedzmy że cena węgla gatunku B wzrosła do 500 zł/t. W jaki sposób wpłynie to na rozwiązanie optymalne z pkt. a) i koszt zakupu? c) Dokonano złagodzenia norm ekologicznych dopuszczając maksymalną zawartość fosforu w paliwie w wysokości 0,04%. W jaki sposób wpłynie to na rozwiązanie z pkt. a)? Metoda geometryczna : przykłady zadań Rozwiązać następujące zadania programowania liniowego. Przeprowadzić analizę wrażliwości dla wag przy zmiennych decyzyjnych i prawych stron. Przeprowadzić analizę wrażliwości dla wag i prawych stron. x 6x 3x + x + 4x x, x + 4x 0 max 4 8 x 4x 3x x + 3x + 3x + 6x x x, x 0 min 8 4x x x + x x + x x x, x max
3 3. Programowanie wielokryterialne Zagadnienie wyznaczania optymalnej strategii marketingowej W tabeli podano zyski (mln zł) i udział w rynku (%), jaki firma spodziewa się osiągnąć stosując wybrane strategie marketingowe. Kryteria Strategie marketingowe A B C D E Zysk (mln zł) ( f ) Udział w rynku (%) ( f ) a) Wyznaczyć strategie Pareto optymalne w przestrzeni kryterialnej. b) Wyznaczyć strategie Pareto optymalne konstruując diagram Hassego. c) Powiedzmy, że wyniku powtórnej ewaluacji strategii przyjęto, że zysk w przypadku strategii D będzie wynosić 3 mln zł. Czy zbiór strategii Pareto - optymalnych ulegnie zmianie? d) Zakładając, że osiągniecie dużego udziału w rynku jest dwa razy ważniejsze od realizacji zysku, wyznaczyć strategię optymalną wykorzystując właściwe metakryterium. Zagadnienie oceny efektywności funkcjonowania kopalni W tabeli podano trzy podstawowe parametry: zysk (w zł/ton), wydajność (w tonach na osobę), wypadkowość (liczba zabitych/ mln ton) dla 5 kopalń należących do holdingu węglowego. Kryteria A B C D E Zysk Wydajność Wypadkowość a) Utworzyć macierz stopni realizacji celów cząstkowych. b) Uporządkować kopalnie kierując się maksymalizacją minimalnych stopni realizacji celów cząstkowych. c) Na podstawie macierzy stopni realizacji, stosując właściwe metakryterium z wagami /, /4, /4, uporządkować kopalnie od najlepszej do najgorszej. d) Które kopalnie należy zamknąć, jeżeli wiadomo, że wydajność w każdej z kopalń musi być nie mniejsza niż 40% wydajności w kopalni najlepszej? Czy po zmodyfikowaniu zbioru kopalń, w powtórnie sporządzonym rankingu, relacje między kopalniami będą takie same jak w rankingu wyjściowym? 3
4 4. Podejmowanie decyzji w warunkach niepewności Zagadnienie wyboru struktury zasiewów Rolnik na polu o powierzchni 0 ha może uprawiać pszenicę, żyto, lub na połowie areału pszenicę a na połowie żyto. Przychody jakie przynosi uprawa zbóż zależą od warunków pogodowych wywierających wpływ na wielkość plonów oraz koniunktury na płody rolne decydującej o cenie zbytu. W tab. podano wielkość spodziewanych zbiorów (q/ha) dla uprawianych zbóż w zależności od stanu pogody, a w tab. ceny zbytu zbóż w zależności od koniunktury gospodarczej (zł/t). Wielkość plonów Stan pogody P P Żyto 0 5 Pszenica 40 0 Tabela Ceny zbytu Koniunktura K K Żyto Pszenica Tabela Wyznaczyć optymalną decyzje dot. struktury zasiewów stosując regułę Walda, Hurvicza (dla współczynnika optymizmu równego 0,5), Savage'a i Bayesa. Wyznaczając stany natury przyjąć, że koniunktura na płody rolne praktycznie nie zależy od stanu pogody. 4
5 5. Teoria gier Problem opanowania rynku na jednorodny produkt Macierz wypłat opisuje szacowane zyski dwóch firm pragnących opanować rynek na pewien produkt. Zakłada się, że potencjalny popyt jest mniejszy od sumy zdolności produkcyjnych obu firm. Każda z firm dysponuje dwiema strategiami : W - wejść na rynek, N - zrezygnować. I W N II W (, ) (0, 5) N (7, 0) (0, 0). a) Uzasadnić strukturę wypłat. b) Wyznaczyć równowagę w sensie Nasha. Jeżeli istnieje więcej równowag, która z nich zostanie wybrana z większym prawdopodobieństwem? c) Czy można oczekiwać współpracy firm? d) Powiedzmy, że wypłatę (-,-) zastępuje wypłata (,). Czy odpowiedź na pytanie z pkt. c) ulegnie zmianie? 5
6 6. Drzewa decyzyjne Zagadnienie wyboru strategii prowadzenia prac badawczo - rozwojowych W tabeli podano wielkość nakładów, zysków oraz prawdopodobieństwa ich osiągnięcia związanych z wyborem jednej z konkurencyjnych metod prowadzenia prac badawczo-rozwojowych. Metoda Nakłady (mln dol.) Wynik Prawdopodobieństwo wyniku Zysk (mln dol.) bez wydatków na B+R Biochemiczna 0 Sukces 0,7 90 Porażka 0,3 50 Biogenetyczna 0 Sukces 0, 00 Porażka 0,8 0 Skonstruować drzewa decyzyjne pozwalające na wyznaczenie oczekiwanego zysku w przypadku, gdy prace nad metodą biochemiczną i biogenetyczną mogą być prowadzone równolegle. 6
Ćwiczenia laboratoryjne - 7. Problem (diety) mieszanek w hutnictwie programowanie liniowe. Logistyka w Hutnictwie Ćw. L. 7
 Ćwiczenia laboratoryjne - 7 Problem (diety) mieszanek w hutnictwie programowanie liniowe Ćw. L. 7 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym zapisem
Ćwiczenia laboratoryjne - 7 Problem (diety) mieszanek w hutnictwie programowanie liniowe Ćw. L. 7 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym zapisem
Metody Ilościowe w Socjologii
 Metody Ilościowe w Socjologii wykład 4 BADANIA OPERACYJNE dr inż. Maciej Wolny AGENDA I. Badania operacyjne podstawowe definicje II. Metodologia badań operacyjnych III. Wybrane zagadnienia badań operacyjnych
Metody Ilościowe w Socjologii wykład 4 BADANIA OPERACYJNE dr inż. Maciej Wolny AGENDA I. Badania operacyjne podstawowe definicje II. Metodologia badań operacyjnych III. Wybrane zagadnienia badań operacyjnych
Badania operacyjne. Lista zadań projektowych nr 2
 Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
Zad.1. Microsoft Excel - Raport wyników Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto
 Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
ZAGADNIENIA PROGRAMOWANIA LINIOWEGO
 ZAGADNIENIA PROGRAMOWANIA LINIOWEGO Maciej Patan Uniwersytet Zielonogórski WSTĘP często spotykane w życiu codziennym wybór asortymentu produkcji jakie wyroby i w jakich ilościach powinno produkować przedsiębiorstwo
ZAGADNIENIA PROGRAMOWANIA LINIOWEGO Maciej Patan Uniwersytet Zielonogórski WSTĘP często spotykane w życiu codziennym wybór asortymentu produkcji jakie wyroby i w jakich ilościach powinno produkować przedsiębiorstwo
PROGRAMOWANIE WIELOKRYTERIALNE (CELOWE)
 PROGRAMOWANIE WIELOKRYTERIALNE (CELOWE) Przykład 14. Zakład zamierza rozpocząć produkcję wyrobów W 1 i W 2. Wśród środków produkcyjnych, które zostaną użyte w produkcji dwa są limitowane. Limity te wynoszą:
PROGRAMOWANIE WIELOKRYTERIALNE (CELOWE) Przykład 14. Zakład zamierza rozpocząć produkcję wyrobów W 1 i W 2. Wśród środków produkcyjnych, które zostaną użyte w produkcji dwa są limitowane. Limity te wynoszą:
METODY OBLICZENIOWE OPTYMALIZACJI zadania
 METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
Gry z naturą 1. Przykład
 Gry z naturą 1 Gry z naturą to gry dwuosobowe, w których przeciwnikiem jest natura. Przeciwnik ten nie jest zainteresowany wynikiem gry, a więc grę rozwiązuje się z punktu widzenia jednego z graczy. Optymalną
Gry z naturą 1 Gry z naturą to gry dwuosobowe, w których przeciwnikiem jest natura. Przeciwnik ten nie jest zainteresowany wynikiem gry, a więc grę rozwiązuje się z punktu widzenia jednego z graczy. Optymalną
ZASTOSOWANIE PROGRAMOWANIA LINIOWEGO W ZAGADNIENIACH WSPOMAGANIA PROCESU PODEJMOWANIA DECYZJI
 Wstęp ZASTOSOWANIE PROGRAMOWANIA LINIOWEGO W ZAGADNIENIACH WSPOMAGANIA PROCESU PODEJMOWANIA DECYZJI Problem podejmowania decyzji jest jednym z zagadnień sterowania nadrzędnego. Proces podejmowania decyzji
Wstęp ZASTOSOWANIE PROGRAMOWANIA LINIOWEGO W ZAGADNIENIACH WSPOMAGANIA PROCESU PODEJMOWANIA DECYZJI Problem podejmowania decyzji jest jednym z zagadnień sterowania nadrzędnego. Proces podejmowania decyzji
Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych"
 Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych" 1. Zbudować model optymalizacyjny problemu opisanego w zadaniu z tabeli poniżej. 2. Rozwiązać zadanie jak w tabeli poniżej z wykorzystaniem
Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych" 1. Zbudować model optymalizacyjny problemu opisanego w zadaniu z tabeli poniżej. 2. Rozwiązać zadanie jak w tabeli poniżej z wykorzystaniem
Elementy Modelowania Matematycznego
 Elementy Modelowania Matematycznego Wykład 6 Metoda simpleks Spis treści Wstęp Zadanie programowania liniowego Wstęp Omówimy algorytm simpleksowy, inaczej metodę simpleks(ów). Jest to stosowana w matematyce
Elementy Modelowania Matematycznego Wykład 6 Metoda simpleks Spis treści Wstęp Zadanie programowania liniowego Wstęp Omówimy algorytm simpleksowy, inaczej metodę simpleks(ów). Jest to stosowana w matematyce
Ekonometria Programowanie Liniowe. Robert Pietrzykowski
 Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
4. PROGRAMOWANIE LINIOWE
 4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
Wprowadzenie do badań operacyjnych
 Wprowadzenie do badań operacyjnych Hanna Furmańczyk 10 października 2008 Badania operacyjne (ang. operations research) - dyscyplina naukowa związana z teorią decyzji pozwalająca wyznaczyć metodę i rozwiązanie
Wprowadzenie do badań operacyjnych Hanna Furmańczyk 10 października 2008 Badania operacyjne (ang. operations research) - dyscyplina naukowa związana z teorią decyzji pozwalająca wyznaczyć metodę i rozwiązanie
BADANIA OPERACYJNE PROGRAMOWANIE WIELOKRYTERIALNE
 DR ADAM SOJDA Czasem istnieje wiele kryteriów oceny. Kupno samochodu: cena prędkość maksymalna spalanie kolor typ nadwozia bagażnik najniższa najwyższa najniższe {czarny*, czerwony, } {sedan, coupe, SUV,
DR ADAM SOJDA Czasem istnieje wiele kryteriów oceny. Kupno samochodu: cena prędkość maksymalna spalanie kolor typ nadwozia bagażnik najniższa najwyższa najniższe {czarny*, czerwony, } {sedan, coupe, SUV,
WPROWADZENIE DO EKONOMII MENEDŻERSKIEJ.
 Wykład 1 Wprowadzenie do ekonomii menedżerskiej 1 WPROWADZENIE DO EKONOMII MENEDŻERSKIEJ. PODEJMOWANIE OPTYMALNYCH DECYZJI NA PODSTAWIE ANALIZY MARGINALNEJ. 1. EKONOMIA MENEDŻERSKA ekonomia menedżerska
Wykład 1 Wprowadzenie do ekonomii menedżerskiej 1 WPROWADZENIE DO EKONOMII MENEDŻERSKIEJ. PODEJMOWANIE OPTYMALNYCH DECYZJI NA PODSTAWIE ANALIZY MARGINALNEJ. 1. EKONOMIA MENEDŻERSKA ekonomia menedżerska
Programowanie liniowe. Tadeusz Trzaskalik
 Programowanie liniowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Model matematyczny Cel, środki, ograniczenia Funkcja celu funkcja kryterium Zmienne decyzyjne Model optymalizacyjny Układ warunków
Programowanie liniowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Model matematyczny Cel, środki, ograniczenia Funkcja celu funkcja kryterium Zmienne decyzyjne Model optymalizacyjny Układ warunków
Lista 1 PL metoda geometryczna
 Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Programowanie liniowe
 Programowanie liniowe Schemat postępowania w badaniach operacyjnych decydent sytuacja decyzyjna decyzje decyzje dopuszczalne niedopuszczalne kryterium wyboru zadanie decyzyjne zmienne decyzyjne warunki
Programowanie liniowe Schemat postępowania w badaniach operacyjnych decydent sytuacja decyzyjna decyzje decyzje dopuszczalne niedopuszczalne kryterium wyboru zadanie decyzyjne zmienne decyzyjne warunki
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
Wielokryteriowa optymalizacja liniowa
 Wielokryteriowa optymalizacja liniowa 1. Przy decyzjach złożonych kierujemy się zwykle więcej niż jednym kryterium. Postępowanie w takich sytuacjach nie jest jednoznaczne. Pojawiło się wiele sposobów dochodzenia
Wielokryteriowa optymalizacja liniowa 1. Przy decyzjach złożonych kierujemy się zwykle więcej niż jednym kryterium. Postępowanie w takich sytuacjach nie jest jednoznaczne. Pojawiło się wiele sposobów dochodzenia
Definicja problemu programowania matematycznego
 Definicja problemu programowania matematycznego minimalizacja lub maksymalizacja funkcji min (max) f(x) gdzie: x 1 x R n x 2, czyli: x = [ ] x n przy ograniczeniach (w skrócie: p.o.) p.o. g i (x) = b i
Definicja problemu programowania matematycznego minimalizacja lub maksymalizacja funkcji min (max) f(x) gdzie: x 1 x R n x 2, czyli: x = [ ] x n przy ograniczeniach (w skrócie: p.o.) p.o. g i (x) = b i
Standardowe zadanie programowania liniowego. Gliwice 1
 Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
Optymalizacja procesów technologicznych przy zastosowaniu programowania liniowego
 Optymalizacja procesów technologicznych przy zastosowaniu programowania liniowego Wstęp Spośród różnych analitycznych metod stosowanych do rozwiązywania problemów optymalizacji procesów technologicznych
Optymalizacja procesów technologicznych przy zastosowaniu programowania liniowego Wstęp Spośród różnych analitycznych metod stosowanych do rozwiązywania problemów optymalizacji procesów technologicznych
Programowanie liniowe
 Badania operacyjne Ćwiczenia 4 Programowanie liniowe Dualizm w programowaniu liniowym Plan zajęć Dualizm w programowaniu liniowym Projektowanie programu dualnego Postać programu dualnego Przykład 1 Rozwiązania
Badania operacyjne Ćwiczenia 4 Programowanie liniowe Dualizm w programowaniu liniowym Plan zajęć Dualizm w programowaniu liniowym Projektowanie programu dualnego Postać programu dualnego Przykład 1 Rozwiązania
Pyt.1. Podać warunki jakie musi spełniać model matematyczny dla możliwości rozwiązywania metodami programowania liniowego.
 Firma produkująca płatki śniadaniowe rozważa wypuszczenie na rynek nowego produktu. Ma to być mieszanka pszenicy, ryżu i kukurydzy. Normy zawartości przedstawia tabela: Dane Pszenica Ryż Kukurydza Zawartość
Firma produkująca płatki śniadaniowe rozważa wypuszczenie na rynek nowego produktu. Ma to być mieszanka pszenicy, ryżu i kukurydzy. Normy zawartości przedstawia tabela: Dane Pszenica Ryż Kukurydza Zawartość
Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa
 Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa dr Jarosław Kotowicz 02 października 2015r. Zadanie 1 ([1, Przykład
Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa dr Jarosław Kotowicz 02 października 2015r. Zadanie 1 ([1, Przykład
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700
 Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
Programowanie liniowe
 Badania operacyjne Ćwiczenia 2 Programowanie liniowe Metoda geometryczna Plan zajęć Programowanie liniowe metoda geometryczna Przykład 1 Zbiór rozwiązań dopuszczalnych Zamknięty zbiór rozwiązań dopuszczalnych
Badania operacyjne Ćwiczenia 2 Programowanie liniowe Metoda geometryczna Plan zajęć Programowanie liniowe metoda geometryczna Przykład 1 Zbiór rozwiązań dopuszczalnych Zamknięty zbiór rozwiązań dopuszczalnych
Teoria gier matematyki). optymalności decyzji 2 lub więcej Decyzja wpływa na wynik innych graczy strategiami
 Teoria gier Teoria gier jest częścią teorii decyzji (czyli gałęzią matematyki). Teoria decyzji - decyzje mogą być podejmowane w warunkach niepewności, ale nie zależą od strategicznych działań innych Teoria
Teoria gier Teoria gier jest częścią teorii decyzji (czyli gałęzią matematyki). Teoria decyzji - decyzje mogą być podejmowane w warunkach niepewności, ale nie zależą od strategicznych działań innych Teoria
PODEJMOWANIE DECYZJI W WARUNKACH NIEPEŁNEJ INFORMACJI
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 5 PODEJMOWANIE DECYZJI W WARUNKACH NIEPEŁNEJ INFORMACJI 5.2. Ćwiczenia komputerowe
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 5 PODEJMOWANIE DECYZJI W WARUNKACH NIEPEŁNEJ INFORMACJI 5.2. Ćwiczenia komputerowe
doc. dr Beata Pułska-Turyna Zarządzanie B506 mail: mgr Piotr J. Gadecki Zakład Badań Operacyjnych Zarządzania B 505.
 doc. dr Beata Pułska-Turyna Zakład Badań Operacyjnych Zarządzanie B506 mail: turynab@wz.uw.edu.pl mgr Piotr J. Gadecki Zakład Badań Operacyjnych Zarządzania B 505. Tel.: (22)55 34 144 Mail: student@pgadecki.pl
doc. dr Beata Pułska-Turyna Zakład Badań Operacyjnych Zarządzanie B506 mail: turynab@wz.uw.edu.pl mgr Piotr J. Gadecki Zakład Badań Operacyjnych Zarządzania B 505. Tel.: (22)55 34 144 Mail: student@pgadecki.pl
Optymalizacja wielokryterialna
 Optymalizacja wielokryterialna Optymalizacja wielokryterialna Dział badań operacyjnych zajmujący się wyznaczaniem optymalnej decyzji w przypadku, gdy występuje więcej niż jedno kryterium Problem wielokryterialny
Optymalizacja wielokryterialna Optymalizacja wielokryterialna Dział badań operacyjnych zajmujący się wyznaczaniem optymalnej decyzji w przypadku, gdy występuje więcej niż jedno kryterium Problem wielokryterialny
Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony.
 GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych. Badania operacyjne. Dr inż.
 Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych Badania operacyjne Dr inż. Artur KIERZKOWSKI Wprowadzenie Badania operacyjne związana jest ściśle z teorią podejmowania
Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych Badania operacyjne Dr inż. Artur KIERZKOWSKI Wprowadzenie Badania operacyjne związana jest ściśle z teorią podejmowania
1 Przykładowe klasy zagadnień liniowych
 & " 1 PRZYKŁADOWE KLASY ZAGADNIEŃ LINIOWYCH 1 1 Przykładowe klasy zagadnień liniowych Liniowy model produkcji Zakład może prowadzić rodzajów działalności np. produkować różnych wyrobów). Do prowadzenia
& " 1 PRZYKŁADOWE KLASY ZAGADNIEŃ LINIOWYCH 1 1 Przykładowe klasy zagadnień liniowych Liniowy model produkcji Zakład może prowadzić rodzajów działalności np. produkować różnych wyrobów). Do prowadzenia
Materiał dydaktyczny dla nauczycieli przedmiotów ekonomicznych. Mikroekonomia. w zadaniach. Gry strategiczne. mgr Piotr Urbaniak
 Materiał dydaktyczny dla nauczycieli przedmiotów ekonomicznych Mikroekonomia w zadaniach Gry strategiczne mgr Piotr Urbaniak Teoria gier Dział matematyki zajmujący się badaniem optymalnego zachowania w
Materiał dydaktyczny dla nauczycieli przedmiotów ekonomicznych Mikroekonomia w zadaniach Gry strategiczne mgr Piotr Urbaniak Teoria gier Dział matematyki zajmujący się badaniem optymalnego zachowania w
Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli?
 Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli? : Proces zmieniania wartości w komórkach w celu sprawdzenia, jak
Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli? : Proces zmieniania wartości w komórkach w celu sprawdzenia, jak
Badania operacyjne. te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze.
 BADANIA OPERACYJNE Badania operacyjne Badania operacyjne są sztuką dawania złych odpowiedzi na te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze. T. Sayty 2 Standardowe zadanie
BADANIA OPERACYJNE Badania operacyjne Badania operacyjne są sztuką dawania złych odpowiedzi na te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze. T. Sayty 2 Standardowe zadanie
Mikroekonomia II: Kolokwium, grupa II
 Mikroekonomia II: Kolokwium, grupa II Prowadząca: Martyna Kobus 2012-06-11 Piszemy 90 minut. Sprawdzian jest za 70 punktów. Jest 10 pytań testowych, każde za 2 punkty (łącznie 20 punktów za test) i 3 zadania,
Mikroekonomia II: Kolokwium, grupa II Prowadząca: Martyna Kobus 2012-06-11 Piszemy 90 minut. Sprawdzian jest za 70 punktów. Jest 10 pytań testowych, każde za 2 punkty (łącznie 20 punktów za test) i 3 zadania,
Badania Operacyjne Ćwiczenia nr 1 (Materiały)
 Wprowadzenie Badania operacyjne (BO) to stosunkowo młoda dyscyplina naukowa, która powstała w czasie II Wojny Światowej, w związku z utworzeniem przy niektórych sztabach sił zbrojnych specjalnych grup
Wprowadzenie Badania operacyjne (BO) to stosunkowo młoda dyscyplina naukowa, która powstała w czasie II Wojny Światowej, w związku z utworzeniem przy niektórych sztabach sił zbrojnych specjalnych grup
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne. Temat ćwiczenia:
 Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne Temat ćwiczenia: Programowanie liniowe, metoda geometryczna, dobór struktury asortymentowej produkcji Zachodniopomorski Uniwersytet
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne Temat ćwiczenia: Programowanie liniowe, metoda geometryczna, dobór struktury asortymentowej produkcji Zachodniopomorski Uniwersytet
Podstawowe warunki konkurencyjności koksowni na wolnym rynku
 Podstawowe warunki konkurencyjności koksowni na wolnym rynku Edward Szlęk Prezes Zarządu JSW KOKS S.A. Konferencja naukowo-techniczna KOKSOWNICTWO 2014 Wyzwania dla konkurencyjnej koksowni Spełnienie wymagań
Podstawowe warunki konkurencyjności koksowni na wolnym rynku Edward Szlęk Prezes Zarządu JSW KOKS S.A. Konferencja naukowo-techniczna KOKSOWNICTWO 2014 Wyzwania dla konkurencyjnej koksowni Spełnienie wymagań
Materiał dydaktyczny dla nauczycieli przedmiotów ekonomicznych MENEDŻER. Wprowadzenie do problematyki decyzji menedżerskich. Mgr Piotr Urbaniak
 Materiał dydaktyczny dla nauczycieli przedmiotów ekonomicznych MENEDŻER Wprowadzenie do problematyki decyzji menedżerskich Mgr Piotr Urbaniak Wprowadzenie 1 2 3 4 Czym jest ekonomia menedżerska? Etapy
Materiał dydaktyczny dla nauczycieli przedmiotów ekonomicznych MENEDŻER Wprowadzenie do problematyki decyzji menedżerskich Mgr Piotr Urbaniak Wprowadzenie 1 2 3 4 Czym jest ekonomia menedżerska? Etapy
Ekonometria - ćwiczenia 11
 Ekonometria - ćwiczenia 11 Mateusz Myśliwski Zakład Ekonometrii Stosowanej Instytut Ekonometrii Kolegium Analiz Ekonomicznych Szkoła Główna Handlowa 21 grudnia 2012 Na poprzednich zajęciach zajmowaliśmy
Ekonometria - ćwiczenia 11 Mateusz Myśliwski Zakład Ekonometrii Stosowanej Instytut Ekonometrii Kolegium Analiz Ekonomicznych Szkoła Główna Handlowa 21 grudnia 2012 Na poprzednich zajęciach zajmowaliśmy
D. Miszczyńska, M.Miszczyński KBO UŁ, Badania operacyjne [1]
![D. Miszczyńska, M.Miszczyński KBO UŁ, Badania operacyjne [1] D. Miszczyńska, M.Miszczyński KBO UŁ, Badania operacyjne [1]](/thumbs/51/27962896.jpg) D. Miszczyńska, M.Miszczyński KBO UŁ, Badania operacyjne [1] Co to są badania operacyjne? Termin "badanie operacji" (Operations' Research) powstał podczas II wojny światowej i przetrwał do dzisiaj. W terminologii
D. Miszczyńska, M.Miszczyński KBO UŁ, Badania operacyjne [1] Co to są badania operacyjne? Termin "badanie operacji" (Operations' Research) powstał podczas II wojny światowej i przetrwał do dzisiaj. W terminologii
Badania Operacyjne Ćwiczenia nr 4 (Materiały)
 Analiza wrażliwości Rozwiązanie programu liniowego jest dopiero początkiem analizy. Z punktu widzenia decydenta (menadżera) jest istotne, żeby wiedzieć jak na rozwiązanie optymalne wpływają zmiany parametrów
Analiza wrażliwości Rozwiązanie programu liniowego jest dopiero początkiem analizy. Z punktu widzenia decydenta (menadżera) jest istotne, żeby wiedzieć jak na rozwiązanie optymalne wpływają zmiany parametrów
Wykład 7. Informatyka Stosowana. Magdalena Alama-Bućko. 16 kwietnia Magdalena Alama-Bućko Wykład 7 16 kwietnia / 23
 Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
EKONOMIA MENEDŻERSKA. Wykład 5 Oligopol. Strategie konkurencji a teoria gier. 1 OLIGOPOL. STRATEGIE KONKURENCJI A TEORIA GIER.
 Wykład 5 Oligopol. Strategie konkurencji a teoria gier. 1 OLIGOPOL. STRATEGIE KONKURENCJI A TEORIA GIER. 1. OLIGOPOL Oligopol - rynek, na którym działa niewiele przedsiębiorstw (od do 10) Cecha charakterystyczna
Wykład 5 Oligopol. Strategie konkurencji a teoria gier. 1 OLIGOPOL. STRATEGIE KONKURENCJI A TEORIA GIER. 1. OLIGOPOL Oligopol - rynek, na którym działa niewiele przedsiębiorstw (od do 10) Cecha charakterystyczna
Rozwiązaniem Pareto-optymalnym jest łamana ABC. x 2 A 2 6 B 10 7,5. x 1
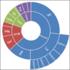 Zadanie ). (PROGRMOWNIE WIELOKRYTERILNE IĄGŁE): a) pełen model dla zadania dwukryterialnego: obszar uprawy pszenicy [ha] obszar uprawy ziemniaków [ha] fc1: +15 max (dochody) istnieje izokwanta przecinająca
Zadanie ). (PROGRMOWNIE WIELOKRYTERILNE IĄGŁE): a) pełen model dla zadania dwukryterialnego: obszar uprawy pszenicy [ha] obszar uprawy ziemniaków [ha] fc1: +15 max (dochody) istnieje izokwanta przecinająca
Elementy Modelowania Matematycznego Wykład 7 Programowanie nieliniowe i całkowitoliczbowe
 Spis treści Elementy Modelowania Matematycznego Wykład 7 i całkowitoliczbowe Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 Spis treści Spis treści 1 Wstęp
Spis treści Elementy Modelowania Matematycznego Wykład 7 i całkowitoliczbowe Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 Spis treści Spis treści 1 Wstęp
Programowanie wielocelowe lub wielokryterialne
 Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe.
Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe.
Rozwiązanie Ad 1. Model zadania jest następujący:
 Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Optymalizacja
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Optymalizacja Dla podanych niżej problemów decyzyjnych (zad.1 zad.5) należy sformułować zadania optymalizacji, tj.: określić postać zmiennych
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Optymalizacja Dla podanych niżej problemów decyzyjnych (zad.1 zad.5) należy sformułować zadania optymalizacji, tj.: określić postać zmiennych
Plan wykładu. Przykład. Przykład 3/19/2011. Przykład zagadnienia transportowego. Optymalizacja w procesach biznesowych Wykład 2 DECYZJA?
 /9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
/9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
Rachunki Decyzyjne. Katedra Rachunkowości US
 Rachunki Decyzyjne Katedra Rachunkowości US Rachunki Decyzyjne Wykorzystywane do optymalizacji efektów przy istniejącym profilu działalności w krótkich okresach czasu. Podstawą analizy są relacje pomiędzy
Rachunki Decyzyjne Katedra Rachunkowości US Rachunki Decyzyjne Wykorzystywane do optymalizacji efektów przy istniejącym profilu działalności w krótkich okresach czasu. Podstawą analizy są relacje pomiędzy
Algebra liniowa. Macierze i układy równań liniowych
 Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Jaka będzie cena śruty sojowej?
 .pl https://www..pl Jaka będzie cena śruty sojowej? Autor: Ewa Ploplis Data: 19 kwietnia 2017 Prawdopodobnie ceny śruty sojowej nie ulegną dużym zmianom. W pierwszej połowie 2017 r. powinny być relatywnie
.pl https://www..pl Jaka będzie cena śruty sojowej? Autor: Ewa Ploplis Data: 19 kwietnia 2017 Prawdopodobnie ceny śruty sojowej nie ulegną dużym zmianom. W pierwszej połowie 2017 r. powinny być relatywnie
Wielokryteriowa optymalizacja liniowa cz.2
 Wielokryteriowa optymalizacja liniowa cz.2 Metody poszukiwania końcowych rozwiązań sprawnych: 1. Metoda satysfakcjonujących poziomów kryteriów dokonuje się wyboru jednego z kryteriów zadania wielokryterialnego
Wielokryteriowa optymalizacja liniowa cz.2 Metody poszukiwania końcowych rozwiązań sprawnych: 1. Metoda satysfakcjonujących poziomów kryteriów dokonuje się wyboru jednego z kryteriów zadania wielokryterialnego
=B8*E8 ( F9:F11 F12 =SUMA(F8:F11)
 Microsoft EXCEL - SOLVER 2. Elementy optymalizacji z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
Microsoft EXCEL - SOLVER 2. Elementy optymalizacji z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
Zagadnienia programowania liniowego dotyczą modelowania i optymalizacji wielu problemów decyzyjnych, na przykład:
 Programowanie liniowe. 1. Aktywacja polecenia Solver. Do narzędzia Solver można uzyskać dostęp za pomocą polecenia Dane/Analiza/Solver, bądź Narzędzia/Solver (dla Ex 2003). Jeżeli nie można go znaleźć,
Programowanie liniowe. 1. Aktywacja polecenia Solver. Do narzędzia Solver można uzyskać dostęp za pomocą polecenia Dane/Analiza/Solver, bądź Narzędzia/Solver (dla Ex 2003). Jeżeli nie można go znaleźć,
Programowanie wielocelowe lub wielokryterialne
 Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe
Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe
Iwona Konarzewska Programowanie celowe - wprowadzenie. Katedra Badań Operacyjnych UŁ
 1 Iwona Konarzewska Programowanie celowe - wprowadzenie Katedra Badań Operacyjnych UŁ 2 Programowanie celowe W praktycznych sytuacjach podejmowania decyzji często występuje kilka celów. Problem pojawia
1 Iwona Konarzewska Programowanie celowe - wprowadzenie Katedra Badań Operacyjnych UŁ 2 Programowanie celowe W praktycznych sytuacjach podejmowania decyzji często występuje kilka celów. Problem pojawia
Wyznacz łączne zmiany wartości, ilości i cen sprzedaży w październiku i listopadzie oraz zinterpretuj otrzymane wyniki.
 ZAD.1. Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha dla 7 niezależnych upraw przedstawia tabela: y X 17 11 19 15 19 20 20 25 20 24 22 39 23 41
ZAD.1. Dane dotyczące zależności pomiędzy wielkością plonów w q/ha (y), a zużyciem określonego nawozu w kg/ha dla 7 niezależnych upraw przedstawia tabela: y X 17 11 19 15 19 20 20 25 20 24 22 39 23 41
Mikroekonomia II Semestr Letni 2014/2015 Ćwiczenia 4, 5 & 6. Technologia
 Mikroekonomia II 050-792 Semestr Letni 204/205 Ćwiczenia 4, 5 & 6 Technologia. Izokwanta produkcji to krzywa obrazująca różne kombinacje nakładu czynników produkcji, które przynoszą taki sam zysk. P/F
Mikroekonomia II 050-792 Semestr Letni 204/205 Ćwiczenia 4, 5 & 6 Technologia. Izokwanta produkcji to krzywa obrazująca różne kombinacje nakładu czynników produkcji, które przynoszą taki sam zysk. P/F
Skowrońska-Szmer. Instytut Organizacji i Zarządzania Politechniki Wrocławskiej Zakład Zarządzania Jakością. 04.01.2012r.
 mgr inż. Anna Skowrońska-Szmer Instytut Organizacji i Zarządzania Politechniki Wrocławskiej Zakład Zarządzania Jakością 04.01.2012r. 1. Cel prezentacji 2. Biznesplan podstawowe pojęcia 3. Teoria gier w
mgr inż. Anna Skowrońska-Szmer Instytut Organizacji i Zarządzania Politechniki Wrocławskiej Zakład Zarządzania Jakością 04.01.2012r. 1. Cel prezentacji 2. Biznesplan podstawowe pojęcia 3. Teoria gier w
Elementy Modelowania Matematycznego
 Elementy Modelowania Matematycznego Wykład 8 Programowanie nieliniowe Spis treści Programowanie nieliniowe Zadanie programowania nieliniowego Zadanie programowania nieliniowego jest identyczne jak dla
Elementy Modelowania Matematycznego Wykład 8 Programowanie nieliniowe Spis treści Programowanie nieliniowe Zadanie programowania nieliniowego Zadanie programowania nieliniowego jest identyczne jak dla
Optymalizacją wielokryterialną nazwiemy próbę znalezienia wektora zmiennych decyzyjnych: x = [x 1
 1 Optymalizacją wielokryterialną nazwiemy próbę znalezienia wektora zmiennych decyzyjnych: x = [x 1,x 2,,x k ], który spełnia warunki ograniczające: g i (x) 0 (i = 1 m), h i (x) = 0 (i = 1 p) oraz optymalizuje
1 Optymalizacją wielokryterialną nazwiemy próbę znalezienia wektora zmiennych decyzyjnych: x = [x 1,x 2,,x k ], który spełnia warunki ograniczające: g i (x) 0 (i = 1 m), h i (x) = 0 (i = 1 p) oraz optymalizuje
Statystyka. Zadanie 1.
 Statystyka Zadanie 1. W przedsiębiorstwie Statexport pracuje 100 pracowników fizycznych i 25 umysłowych. Typowy wiek pracownika fizycznego kształtuje się w przedziale od 30 do 40 lat. Średnia wieku pracowników
Statystyka Zadanie 1. W przedsiębiorstwie Statexport pracuje 100 pracowników fizycznych i 25 umysłowych. Typowy wiek pracownika fizycznego kształtuje się w przedziale od 30 do 40 lat. Średnia wieku pracowników
WOJEWÓDZTWO LUBELSKIE
 Okręgowa Komisja Egzaminacyjna w Krakowie, Wydział Egzaminów Zawodowych os. Szkolne 37, 31 978 Kraków, tel. (1) 68 3 181-183 fax: (1) 68 3 18 e-mail: oke@oke.krakow.pl, egzzaw@oke.krakow.pl; www.oke.krakow.pl
Okręgowa Komisja Egzaminacyjna w Krakowie, Wydział Egzaminów Zawodowych os. Szkolne 37, 31 978 Kraków, tel. (1) 68 3 181-183 fax: (1) 68 3 18 e-mail: oke@oke.krakow.pl, egzzaw@oke.krakow.pl; www.oke.krakow.pl
Podejmowanie decyzji gospodarczych
 Podejmowanie decyzji gospodarczych Zakres podejmowanych decyzji jest bardzo szeroki zarówno na poziomie przedsiębiorstwa jak i na szczeblu państwa. W każdym przypadku sensowna analiza wariantów decyzji
Podejmowanie decyzji gospodarczych Zakres podejmowanych decyzji jest bardzo szeroki zarówno na poziomie przedsiębiorstwa jak i na szczeblu państwa. W każdym przypadku sensowna analiza wariantów decyzji
EKONOMIA MENEDŻERSKA
 oraz na kierunku zarządzanie i marketing (jednolite studia magisterskie) 1 EKONOMIA MENEDŻERSKA PROGRAM WYKŁADÓW Wykład 1. Wprowadzenie do ekonomii menedŝerskiej. Podejmowanie optymalnych decyzji na podstawie
oraz na kierunku zarządzanie i marketing (jednolite studia magisterskie) 1 EKONOMIA MENEDŻERSKA PROGRAM WYKŁADÓW Wykład 1. Wprowadzenie do ekonomii menedŝerskiej. Podejmowanie optymalnych decyzji na podstawie
PODSTAWY WSPOMAGANIA PODEJMOWANIA DECYZJI W ZARZĄDZANIU BEZPIECZEŃSTWEM. cz. 6. dr BOŻENA STARUCH
 PODSTAWY WSPOMAGANIA PODEJMOWANIA DECYZJI W ZARZĄDZANIU BEZPIECZEŃSTWEM cz. 6 dr BOŻENA STARUCH bostar@matman.uwm.edu.pl Optymalizacja wielokryterialna Optymalizacją wielokryterialną nazwiemy próbę znalezienia
PODSTAWY WSPOMAGANIA PODEJMOWANIA DECYZJI W ZARZĄDZANIU BEZPIECZEŃSTWEM cz. 6 dr BOŻENA STARUCH bostar@matman.uwm.edu.pl Optymalizacja wielokryterialna Optymalizacją wielokryterialną nazwiemy próbę znalezienia
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE
 PROBLEMY DECYZYJNE KRÓTKOOKRESOWE OPTYMALNA STRUKTURA PRODUKCJI Na podstawie: J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 2013 1 DECYZJE KRÓTKOOKRESOWE Decyzje krótkookresowe to takie, które dotyczą
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE OPTYMALNA STRUKTURA PRODUKCJI Na podstawie: J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 2013 1 DECYZJE KRÓTKOOKRESOWE Decyzje krótkookresowe to takie, które dotyczą
Analiza korelacji i regresji dwóch zmiennych losowych
 Analiza korelacji i regresji dwóch zmiennych losowych 1. Badano zależność między ilością godzin przebywania samolotu w powietrzu ( nalot lotniczy) a ilością wypadków. Na podstawie zebranych danych z pewnego
Analiza korelacji i regresji dwóch zmiennych losowych 1. Badano zależność między ilością godzin przebywania samolotu w powietrzu ( nalot lotniczy) a ilością wypadków. Na podstawie zebranych danych z pewnego
Zawartość składników pokarmowych w roślinach
 Zawartość składników pokarmowych w roślinach Poszczególne rośliny różnią się zawartością składników pokarmowych zarówno w organach wegetatywnych, jak i generatywnych. Wynika to z różnych funkcji, jakie
Zawartość składników pokarmowych w roślinach Poszczególne rośliny różnią się zawartością składników pokarmowych zarówno w organach wegetatywnych, jak i generatywnych. Wynika to z różnych funkcji, jakie
Sytuacja ekonomiczno-finansowa sektora cukrowniczego
 Sytuacja ekonomiczno-finansowa sektora cukrowniczego Dr inż. Piotr SZAJNER IERiGZ-PIB ul. Świętokrzyska 20 PL 00-002 Warszawa E-mail: szajner@ierigz.waw.pl Plan prezentacji Wyniki finansowe przemysłu cukrowniczego;
Sytuacja ekonomiczno-finansowa sektora cukrowniczego Dr inż. Piotr SZAJNER IERiGZ-PIB ul. Świętokrzyska 20 PL 00-002 Warszawa E-mail: szajner@ierigz.waw.pl Plan prezentacji Wyniki finansowe przemysłu cukrowniczego;
Ocena potencjału biomasy stałej z rolnictwa
 Ocena potencjału biomasy stałej z rolnictwa dr Zuzanna Jarosz Inżynieria rolnicza w ochronie i kształtowaniu środowiska Lublin, 23-24 września 2015 Głównym postulatem Unii Europejskiej, a także Polski,
Ocena potencjału biomasy stałej z rolnictwa dr Zuzanna Jarosz Inżynieria rolnicza w ochronie i kształtowaniu środowiska Lublin, 23-24 września 2015 Głównym postulatem Unii Europejskiej, a także Polski,
TOZ -Techniki optymalizacji w zarządzaniu
 TOZ -Techniki optymalizacji w zarządzaniu Wykład dla studentów II roku studiów II stopnia na kierunku Zarządzanie Semestr zimowy 2009/2010 Wykładowca: prof. dr hab. inż. Michał Inkielman Wykład 2 Optymalizacja
TOZ -Techniki optymalizacji w zarządzaniu Wykład dla studentów II roku studiów II stopnia na kierunku Zarządzanie Semestr zimowy 2009/2010 Wykładowca: prof. dr hab. inż. Michał Inkielman Wykład 2 Optymalizacja
Gry o sumie niezerowej
 Gry o sumie niezerowej Równowagi Nasha 2011-12-06 Zdzisław Dzedzej 1 Pytanie Czy profile równowagi Nasha są dobrym rozwiązaniem gry o dowolnej sumie? Zaleta: zawsze istnieją (w grach dwumacierzowych, a
Gry o sumie niezerowej Równowagi Nasha 2011-12-06 Zdzisław Dzedzej 1 Pytanie Czy profile równowagi Nasha są dobrym rozwiązaniem gry o dowolnej sumie? Zaleta: zawsze istnieją (w grach dwumacierzowych, a
Badania Operacyjne Ćwiczenia nr 2 (Materiały)
 Zbiór rozwiązań dopuszczalnych programu liniowego Zbiór rozwiązań dopuszczalnych programu linowego to taki zbiór, który spełnia warunki ograniczające (funkcyjne oraz brzegowe) programu liniowego. Przy
Zbiór rozwiązań dopuszczalnych programu liniowego Zbiór rozwiązań dopuszczalnych programu linowego to taki zbiór, który spełnia warunki ograniczające (funkcyjne oraz brzegowe) programu liniowego. Przy
METODA DEA W ANALIZIE EFEKTYWNOŚCI NAKŁADÓW NA GOSPODARKĘ ODPADAMI
 Katedra Statystyki METODA DEA W ANALIZIE EFEKTYWNOŚCI NAKŁADÓW NA GOSPODARKĘ ODPADAMI XX MIĘDZYNARODOWA KONFERENCJA NAUKOWA GOSPODARKA LOKALNA I REGIONALNA W TEORII I PRAKTYCE Mysłakowice k. Karpacza 17-18
Katedra Statystyki METODA DEA W ANALIZIE EFEKTYWNOŚCI NAKŁADÓW NA GOSPODARKĘ ODPADAMI XX MIĘDZYNARODOWA KONFERENCJA NAUKOWA GOSPODARKA LOKALNA I REGIONALNA W TEORII I PRAKTYCE Mysłakowice k. Karpacza 17-18
METODY WIELOKRYTERIALNE
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 4 METODY WIELOKRYTERIALNE 4.3. ZADANIA Zadanie 4.1 Wykorzystując tryb konwersacyjny
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 4 METODY WIELOKRYTERIALNE 4.3. ZADANIA Zadanie 4.1 Wykorzystując tryb konwersacyjny
Wydział Matematyki Programowanie liniowe Ćwiczenia. Zestaw 1. Modelowanie zadań programowania liniowego.
 Wydział Matematyki Programowanie liniowe Ćwiczenia Zestaw. Modelowanie zadań programowania liniowego. Zadania dotyczące zagadnienia planowania produkcji Zadanie.. Zapisać następujące zadanie w postaci
Wydział Matematyki Programowanie liniowe Ćwiczenia Zestaw. Modelowanie zadań programowania liniowego. Zadania dotyczące zagadnienia planowania produkcji Zadanie.. Zapisać następujące zadanie w postaci
Badania Operacyjne Ćwiczenia nr 6 (Materiały)
 Otwarte zagadnienie transportowe Jeżeli łączna podaż dostawców jest większa niż łączne zapotrzebowanie odbiorców to mamy do czynienia z otwartym zagadnieniem transportowym. Warunki dla dostawców (i-ty
Otwarte zagadnienie transportowe Jeżeli łączna podaż dostawców jest większa niż łączne zapotrzebowanie odbiorców to mamy do czynienia z otwartym zagadnieniem transportowym. Warunki dla dostawców (i-ty
2010 W. W. Norton & Company, Inc. Oligopol
 2010 W. W. Norton & Company, Inc. Oligopol Oligopol Monopol jedna firma na rynku. Duopol dwie firmy na rynku. Oligopol kilka firm na rynku. W szczególności decyzje każdej firmy co do ceny lub ilości produktu
2010 W. W. Norton & Company, Inc. Oligopol Oligopol Monopol jedna firma na rynku. Duopol dwie firmy na rynku. Oligopol kilka firm na rynku. W szczególności decyzje każdej firmy co do ceny lub ilości produktu
KONKURENCYJNOŚĆ PRODUKCJI SEKTORA ROLNEGO UKRAINY. Profesor dr hab. Tatjana Mostenska Państwowy Uniwersytet Przetwórstwa Żywności Ukrainy
 KONKURENCYJNOŚĆ PRODUKCJI SEKTORA ROLNEGO UKRAINY Profesor dr hab. Tatjana Mostenska Państwowy Uniwersytet Przetwórstwa Żywności Ukrainy Konkurencyjność produkcji wyznaczają wskaźniki: jakości, właściwości
KONKURENCYJNOŚĆ PRODUKCJI SEKTORA ROLNEGO UKRAINY Profesor dr hab. Tatjana Mostenska Państwowy Uniwersytet Przetwórstwa Żywności Ukrainy Konkurencyjność produkcji wyznaczają wskaźniki: jakości, właściwości
Ekonomiczne uwarunkowania rozwoju produkcji, oraz systemu obrotu roślin strączkowych na cele paszowe, jako czynnik bezpieczeństwa żywnościowego kraju
 Uniwersytet Przyrodniczy w Poznaniu Zakład Rynków Finansowych i Towarowych w Gospodarce Żywnościowej Ekonomiczne uwarunkowania rozwoju produkcji, oraz systemu obrotu roślin strączkowych na cele paszowe,
Uniwersytet Przyrodniczy w Poznaniu Zakład Rynków Finansowych i Towarowych w Gospodarce Żywnościowej Ekonomiczne uwarunkowania rozwoju produkcji, oraz systemu obrotu roślin strączkowych na cele paszowe,
Środki produkcji Jedn. nakłady środka W1 Jedn. nakłady środka W2 I 6 6 II 10 5
 PROGRAMOWANIE LINIOWE ZADANIA TEKSTOWE 5. Zakład produkuje dwa typy wózków: S i H. Zysk ze sprzedaży jednego wózka typu S wynosi 2850 zł a wózka typu H 6270 zł. Koszt produkcji jednego wózka typu S wynosi
PROGRAMOWANIE LINIOWE ZADANIA TEKSTOWE 5. Zakład produkuje dwa typy wózków: S i H. Zysk ze sprzedaży jednego wózka typu S wynosi 2850 zł a wózka typu H 6270 zł. Koszt produkcji jednego wózka typu S wynosi
8. Podejmowanie Decyzji przy Niepewności
 8. Podejmowanie Decyzji przy Niepewności Wcześniej, losowość (niepewność) nie była brana pod uwagę (poza przypadkiem ubezpieczenia życiowego). Na przykład, aby brać pod uwagę ryzyko że pożyczka nie zostanie
8. Podejmowanie Decyzji przy Niepewności Wcześniej, losowość (niepewność) nie była brana pod uwagę (poza przypadkiem ubezpieczenia życiowego). Na przykład, aby brać pod uwagę ryzyko że pożyczka nie zostanie
Zadania 1. Czas pracy przypadający na jednostkę wyrobu (w godz.) M 1. Wyroby
 Zadania 1 Przedsiębiorstwo wytwarza cztery rodzaje wyrobów: A, B, C, D, które są obrabiane na dwóch maszynach M 1 i M 2. Czas pracy maszyn przypadający na obróbkę jednostki poszczególnych wyrobów podany
Zadania 1 Przedsiębiorstwo wytwarza cztery rodzaje wyrobów: A, B, C, D, które są obrabiane na dwóch maszynach M 1 i M 2. Czas pracy maszyn przypadający na obróbkę jednostki poszczególnych wyrobów podany
Analiza wielokryterialna
 Analiza wielokryterialna dr hab. inż. Krzysztof Patan, prof. PWSZ Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa w Głogowie k.patan@issi.uz.zgora.pl Wprowadzenie Wielokryterialny wybór wariantu
Analiza wielokryterialna dr hab. inż. Krzysztof Patan, prof. PWSZ Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa w Głogowie k.patan@issi.uz.zgora.pl Wprowadzenie Wielokryterialny wybór wariantu
MATEMATYCZNE METODY WSPOMAGANIA PROCESÓW DECYZYJNYCH
 MATEMATYCZNE METODY WSPOMAGANIA PROCESÓW DECYZYJNYCH 1. Przedmiot nie wymaga przedmiotów poprzedzających 2. Treść przedmiotu Proces i cykl decyzyjny. Rola modelowania matematycznego w procesach decyzyjnych.
MATEMATYCZNE METODY WSPOMAGANIA PROCESÓW DECYZYJNYCH 1. Przedmiot nie wymaga przedmiotów poprzedzających 2. Treść przedmiotu Proces i cykl decyzyjny. Rola modelowania matematycznego w procesach decyzyjnych.
Metody ilościowe w badaniach ekonomicznych
 prof. dr hab. Tadeusz Trzaskalik dr hab. Maciej Nowak, prof. UE Wybór portfela projektów z wykorzystaniem wielokryterialnego programowania dynamicznego Metody ilościowe w badaniach ekonomicznych 19-06-2017
prof. dr hab. Tadeusz Trzaskalik dr hab. Maciej Nowak, prof. UE Wybór portfela projektów z wykorzystaniem wielokryterialnego programowania dynamicznego Metody ilościowe w badaniach ekonomicznych 19-06-2017
Wykład z modelowania matematycznego. Algorytm sympleks.
 Wykład z modelowania matematycznego. Algorytm sympleks. 1 Programowanie matematyczne jest to zbiór metod poszukiwania punktu optymalizującego (minimalizującego lub maksymalizującego) wartość funkcji rzeczywistej
Wykład z modelowania matematycznego. Algorytm sympleks. 1 Programowanie matematyczne jest to zbiór metod poszukiwania punktu optymalizującego (minimalizującego lub maksymalizującego) wartość funkcji rzeczywistej
METODA SYMPLEKS. Maciej Patan. Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski
 METODA SYMPLEKS Maciej Patan Uniwersytet Zielonogórski WSTĘP Algorytm Sympleks najpotężniejsza metoda rozwiązywania programów liniowych Metoda generuje ciąg dopuszczalnych rozwiązań x k w taki sposób,
METODA SYMPLEKS Maciej Patan Uniwersytet Zielonogórski WSTĘP Algorytm Sympleks najpotężniejsza metoda rozwiązywania programów liniowych Metoda generuje ciąg dopuszczalnych rozwiązań x k w taki sposób,
KOSZTY W UJĘCIU ZARZĄDCZYM. Karolina Szyderska Anna Szymaniak
 KOSZTY W UJĘCIU ZARZĄDCZYM Karolina Szyderska Anna Szymaniak KOSZTY W PROCESIE DECYZYJNYM Koszt stanowi wyrażone w pieniądzu celowe zużycie majątku trwałego i obrotowego, usług obcych, nakładów pracy oraz
KOSZTY W UJĘCIU ZARZĄDCZYM Karolina Szyderska Anna Szymaniak KOSZTY W PROCESIE DECYZYJNYM Koszt stanowi wyrażone w pieniądzu celowe zużycie majątku trwałego i obrotowego, usług obcych, nakładów pracy oraz
Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ).
 PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI
 DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI mgr Marcin Pawlak Katedra Inwestycji i Wyceny Przedsiębiorstw Plan wystąpienia
DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI mgr Marcin Pawlak Katedra Inwestycji i Wyceny Przedsiębiorstw Plan wystąpienia
