Spinori na zakrivljenom nekomutativnom prostoru
|
|
|
- Seweryna Lis
- 6 lat temu
- Przeglądów:
Transkrypt
1 Spinori na zakrivljenom nekomutativnom prostoru Luka Nenadović Visoka tehnološka škola, Šabac Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
2 Pregled 1 Spinorska reprezentacija u N dimenzija 2 Diferencijalne forme 3 Tetradni formalizam 4 Odsečena Hajzenbergova algebra 5 Spinori na odsečenoj Hajzenbergovoj algebri Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
3 point by point-splitting coupling bythe Fermi. interaction Although according successful to theat Feynman energies graphs well depicted. below 100 GeV, The Feynman diagrams of (tree-level) quantum gravity suggest The apresent similar approach theory of weak interactions, due to Glashow, Salam, and Weinberg, solves this problem uniquely by point-splitting the interaction according to the Feynman graphs depicted. The Feynman diagrams of (tree-level) quantum gravity suggest a similar approach Problemi the Fermi gravitacije theory sufferedkao fromkvantne UV divergences. teorije polja G F 4-point Fermi G F Spontaneously broken YM to alleviate the UV desaster. Further smearing of the three-point couplings naturally (uniquely?) Fermijeva 4-point leads Fermi teorija one to considerelektroslaba Spontaneously extended objects, broken teorija i.e. strings YM in the first place. From the string diagram it becomes obvious that the notion of a to alleviate the UV desaster. Further smearing of the three-point couplings naturally (uniquely?) leads one to consider extended objects, i.e. strings in the first place. From the string diagram it becomes obvious that the notion of a Quantum Razmena Gravitygravitona String Struna theory Quantum Gravity 2 String theory Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
4 Nekomutativna geometrija [x µ, x ν ] = i kj µν. (1) [x µ, x ν ] = iθ µν, θ µν = const. (2) Nepostojanje tačke na Plankovij skali Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
5 Spinorska reprezentacija u N dimenzija N matrica γ µ koje zadovoljavaju: {γ µ, γ ν } = 2δ µν 1, µ, ν = 1,..., N. (3) Matrica 1 je iste dimenzije. Uslov ermitnosti: γ µ = γ µ. (4) SO(N) generatori: Σ µν = 1 4 [γ µ, γ ν ] = Σ νµ. (5) [Σ µν, Σ ρσ ] = δ µσ Σ νρ + δ νρ Σ νσ δ µρ Σ νσ δ νσ Σ µρ. (6) SO(N) spinori su objekti koji se pri SO(N) tranformišu kao: Spinori su kolone iste dimenzije kao γ-matrice. Zadatak: Naći reprezentaciju γ-matrica δψ = 1 2 θµν Σ µν ψ (7) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
6 Reprezentacija γ-matrica u parnom broju dimenzija Za N = 2n, uvedemo matrice: b i = 1 2 (γ i + iγ i+n ), b i = 1 2 (γ i iγ i+n ). i = 1,..., n (8) Algebra fermionskog oscilatora: {b i, b j} = δ ij, {b i, b j } = {b i, b j } = 0 (9) Dvodimenzionalni Hilbertov prostor za svako i-operatori krecije i anihilacije: b 0 = 0, b 0 = 1, b 1 = 0, b 1 = 0, (10) 0 je vakuum, a 1 prvo pobudjeno stanje. Ukupan Hilbertov prostor razapet vektorima: 0, b i 0, b i 1 b i 2 0,..., b 1 b n 0. Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
7 Jedno vakumsko stanje 0 annihilirano svim b i, n stanja b i 0 dobijenih dejstvom i operatora kreacije na vakuum. Zbog antikomutiranja b i b operatora, postoji 1 2n(n 1) stanja koja se dobijaju dejstvom ovih operatora Zbog Grasmanovske prirode ovih operatora (Paulijev Princip), (b ) 2 = 0, postoji konačan broj stanja. Najviše stanje je: b 1 b n 0. Ukupan broj stanja: 1 + n + 1 n ( n 2 p) n(n 1) = = 2 n (11) Invertovanjem definicije za b operatore: p=1 γ i = 1 2 (b i + b i ), γ i+n = i 2 (b i b i ) (12) konstruisali smo jednu reprezentaciju 2 n 2 n -dimenzionalnih γ-matrica (do na γ µ = S 1 γ µ S) koje deluju na spinore ψ = ψ 1. ψ 2n. Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
8 Matrica kiralnosti Postoji još jedna linearno nezavisna matrica: γ = αγ 1... γ N, γ = γ, γ 2 = 1. (13) γ 2 = α 2 γ 1... γ N γ 1... γ N = α 2 ( 1) (N 1)N 2 = 1 α = ( 1) N 1 2, N = 2n Ova matrica komutira sa svim ostalim γ-matricama: {γ µ, γ} = γ µ γ + αγ 1 γ N γ µ = γ µ γ + ( 1) N 1 γ µ αγ 1 γ N = γ komutira sa SO(N) generatorima: {γ, γ µ } = 0. (14) [γ, Σ µν ] = 0, Σ µν = 1 4 [γ µ, γ ν ]. (15) γ 2 = 1 = svojstvene vrednosti γ su ±1. Postoje dva svojstvena vektora: γψ + = ψ +, γψ = ψ (16) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
9 Invarijantni potprostori Pri SO(N) transformacijama δψ = 1 2 θµν Σ µν ψ: δψ ± = δγψ = 1 2 θµν γσ µν ψ = 1 2 θµν Σ µν γψ = 1 2 θµν Σ µν ψ ± (17) = nema mešanja svojstvenih vektora Ovo važi i za SO(1, N 1) Lorncove transformacije u prostoru Minkovskog ψ + ψ +, ψ ψ. = Reprezentacija je reducibilna Cikličnost traga: trγ = tr(αγ 1 γ N ) = tr(αγ N γ 1 γ N 1 ) = trγ: trγ = 0. (18) = Jednak broj pozitivnih i negativnih svojstvenih vrednosti Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
10 Dirakov i Vajlovi spinori = 2 n -dimenzionalni prostor IR se razlaže na dva potprostora dimenzije 2 n 1 : ( ) ψ+ ψ =. (19) ψ je Dirakov spinor, a ψ ψ +, ψ Vajlovi ili kiralni levi i desni spinor Reprezentacija Klifordove algebre dobijena na ovaj način naziva se Spinorska reprezentacija Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
11 Spinorska reprezentacija u neparnom broju dimenzija N = 2n + 1 Potrebno je 2n + 1 matrica: γ 1,..., γ 2n, γ 2n+1 {γ µ, γ ν } = 2δ µν 1, µ, ν = 1,... 2n + 1. (20) Već imamo γ 1,..., γ 2n i γ = αγ 1 γ 2n Proglasimo γ 2n+1 = γ: γ 2n+1 = γ 2n+1, γ 2 2n+1 = 1, {γ 2n+1, γ i } = 0 (21) za neko i = 1,..., 2n i opet imamo celu Klifordovu algebru Ali nemamo više matricu kiralnosti = nema više Vajlovih spinora γ 1 γ 2n γ 2n+1 = αγ 1 γ 2n γ 1 γ 2n = ±η1, η C U neparnom broju dimenzija postoje dve neekvivalentne IR Izbor γ 2n+1 ili γ 2n+1 Različiti znaci ±η odgovaraju različitim reprezentacijama Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
12 Glatka mnogostrukost Realna mnogostrukost M dimenzije n (dim R M = n) je Hausdorfov topološki prostor koji lokalno liči na R n To je skup otvornih podskupova U i zajedno sa homeomorfizmima U i φ i R n koji se nazivaju karte. Skup karata koji pokriva celu mnogostrukost naziva se atlas Mnogostrukost M je diferencijabilna ili glatka ako na preseku karti: U i U j φ 1 i φ j R n φ 1 φ i j R n postoji glatka funkcija prelaza g ij = φ 1 i φ j (difeomorfizam) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
13 Diferencijalne forme Razmotrimo antisimetrične tenzore ranga p, 0 p n Uvodimo diferencijal dx µ, µ = 1,..., n na datoj lokalnoj karti Definišemo kosi proizvod kao antisimetrični tenzorski proizvod: dx µ dx ν = 1 2 (dx µ dx ν dx ν dx µ ) = dx ν dx µ (22) Definišemo diferencijalnu p-formu: α p = 1 p! α µ 1 µ p dx µ 1 dx µp. (23) Primeri: 0-forma je obična skalarna funkcija: α 0 = φ(x), 1-forma je kovarijantni vektor: α 1 = A = A µ dx µ, 2-forma je antisimetrični tenzor ranga 2: α 2 = B = 1 2 B µνdx µ dx ν Skup svih p-formi: Ω p (M) Kosi proizvod p-forme α p and q-forme β q je preslikavanje: Ω p (M) Ω q (M) Ω p+q (M) : λ p+q = α p β q = ( 1) pq β q α p (24) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
14 Spoljašnji izvod Spoljašnji izvod je preslikavanje : d : Ω p (M) Ω p+1 (M) U koordinatnoj reprezentaciji d = dx µ µ Primer (skalarno polje): dφ = µ φdx µ = gradφ Primer (gradijentni potencijal): da = µ dx µ A ν dx ν = µ A ν dx µ dx ν = 1 2 ( µa ν ν A µ )dx µ dx ν = 1 2 F µνdx µ dx ν F µν = µ A ν ν A µ Spoljašnji izvod je rotor kada deluje na 1-formu u 3 dimenzije. Zadovoljava Lajbnicovo pravilo: Uslov nilpotentnosti: d(α p β q ) = (dα p ) β q + ( 1) p α p dβ q. (25) d 2 = 0. (26) Lako se pokazuje: d 2 α p = d(dx µ µ α p ) = dx ν dx µ µ ν α p = 0. Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
15 Stoksova teorema i Hodžov dual Stoksova teorema: Za dim R M = n važi dα n 1 = gde je M granica mnogostrukosti M. M M α n, (27) Za datu Rimanovu mnogostrukost (M, g) uvodimo Hodžov -dual kao preslikavanje : Ω p (M) Ω n p (M) definisano: dx µ 1 dx µp = g (n p)! ɛµ 1...µ pµp+1...µ n dx µ p+1 dx µn. (28) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
16 Najviša forma element zapremine Definišemo meru integracije: g Vol = 1 = n! ɛ µ 1...µ n dx µ 1 dx µn (29) = gdx 1 dx n gd n x. (30) Vol = 1, gdx µ 1 dx µn = ɛ µ 1...µ n Vol. (31) Uvodjenje Hodžovog -duala omogućava izražavanje divergencije vektora U ravnom prostoru sa euklidskom signaturom: g = 1, ako je A 1-forma: ( ) 1 d A = d (n 1)! A νɛ ν µ 2...µ n dx µ 2... dx µn 1 = (n 1)! A ν,ρɛ ν µ 2...µ n dx ρ dx µ 2... dx µn 1 = (n 1)! A ν,ρ(n 1)!g νρ Vol = VolA µ,µ = Vol diva. (32) Još jedan Hodžov dual daje: d A = diva. (33) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
17 Metrički unutrašnji proizvod Metrički unutrašnji proizvod na Ω p (M,R): (α, β) = α β, α, β Ω p (M,R) (34) M U komponentama: g α β = α p!(n p)! β µ 1...µ p ɛ µ 1...µ pµp+1...µ n dx µ p+1 dx µn g = p! 2 (n p)! α µ 1 µ p β ν1...ν p ɛ ν 1...ν p µp+1...µ n dx µ 1 dx µp dx µ p+1 dx µn g = p! 2 (n p)! α µ 1 µ p β ν1...ν p ɛ ν 1...ν p µp+1...µ n ɛ µ 1...µ n dx 1 dx n Vol = p! 2 (n p)! α µ 1 µ p β ν1...ν p p!(n p)!g µ 1ν1 g µpνp = Vol p! αµ 1 µ p β µ1...µ p. (35) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
18 Kinetički članovi Integracijom unutrašnjeg metričkog proizvoda: α β = Vol 1 p! αµ 1 µ p β µ1...µ p. (36) M M Kinetički član za realno skalarno polje: S φ = 1 gd n x µ φ µ φ = dφ dφ. (37) Kinetički član za Abelovo gradijentno polje jačine F = 1 2 F µνdx µ dx ν koje je 2-forma: 1 gd n xf µνf µν = F F. (38) 2 Za kompleksno skalarno polje: gd S φ = n x µ φ µ φ = dφ dφ. (39) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
19 Lokalne teorije, kovarijantni izvod Spinori su prirodno definisani u Lorencovom (euklidskom) prostoru Svaka mnogostrukost je lokalno ravna Spinorsko polje ψ(x) se lokalno transformiše pri dejstvu Spin grupe: Invarijantnost lagranžijana kovarijantni izvod i koneksija ω(x) koja se transformiše kao: Zahtevamo da se Dψ transformiše kao spinor: ψ g(x)ψ (40) D = d + ω (41) ω g 1 (ω + d)g. (42) Dψ (d + gωg 1 + gdg 1 )gψ = (dg)ψ + gdψ + gωg 1 ψ + g(dg 1 )gψ = dgψ + gdψ + gωψ gg 1 dgψ = g(d + ω)ψ = gdψ. (43) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
20 Ortonormalni bazis u tangentnom prostoru U koordinatnom bazisu { µ } na tangentnom prostoru T p (M) mnogostrukosti M u tački p Korišćenjem inverzne tetrade e µ α konstruišemo ortonormalni bazis {e α }: Ortonormalnost: e α (x) = e µ α(x) µ, α = 1,..., dim R M. (44) e µ α(x)e ν β(x)g µν = η αβ. (45) Svakom vektoru v T p (M) odgovara dualni vektor (kovektor) koji je functional: ω : T p (M) R, ω(v) = ω v R. (46) Kovektori obrazuju kotangentni prostor T p (M) U koordinatnoj reprezentaciji{dx µ } je bazis kotangentnog prostora: dx µ ν = ν (dx µ ) = δ µ ν. (47) Bazisni vektori kotangentnog prostora su 1-forme Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
21 Tetrada i metrika Korišćenjem tetrade definišemo ortonormalni bazis 1-formi: Ortogonalnost: dx µ = e µ αθ α = metrički tenzor: Provera konzistentnosti: θ α (x) = θ α µ(x)dx µ. (48) θ α µ(x)θ β ν (x)g µν (x) = η αβ. (49) g = g µν dx µ dx ν = η αβ θ α θ β. (50) θ α e β = θ α µdx µ e ν β ν = θ α µe ν β dx µ ν = θ α µe µ β = δα β (51) Tetrade θ α µ i e µ α su inverzi: θ α µe ν α = δ ν µ, θ α µe µ β = δα β (52) Lokalnom Lorencovom metrikom η αβ i inverzom η αβ podižemo i spuštamo indekse Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
22 Spinska koneksija Izbor ortonormalnog bazisa je jedinstven do na lokalne Lorencove transformacije: θ α (x) θ α (x) = Λ 1α β (x)θβ (x). (53) Lokalna simetrija gradijentno polje, 1-forma sa transformacijom: 1-forma koneksije se naziva spinska koneksija Dekorisano indeksima: ω ω = Λ 1 (ω + d)λ. (54) ω α β ω α β = Λ 1α γ ωγ δ Λδ β + Λ 1α γ dλγ β. (55) Kao 1-forma može da se razvije u ortonormalnom bazisu: Kovarijantni izvod za Lorencovu grupu: Σ αβ = 1 4 [γα, γ β ] su Lorencovi generatori ω α β = ω α µβdx µ = ω α γβθ γ. (56) D = d ω αβσ αβ, (57) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
23 Strukturne jednačine Elementi koordinatnog bazisa medjusobno komutiraju [ µ, ν ] = 0 Elementi ortonormalnog bazisa, ne nužno: C γ αβ [e α, e β ] = C γ αβ e γ. (58) su strukturne konstante ili objekti anholonomije [e α, e β ] = e α e µ β µ e β e µ α µ = (e α e µ β e βe µ α)θ γ µe γ. (59) Diferencijal tetrade: C γ αβ = θγ µ(e α e µ β e βe µ α). (60) dθ γ = dθ γ µ dx µ = (e α θ γ µ)θ α e µ β θβ = 1 2 θγ µ(e α e µ β e βe µ α)θ α θ β = 1 2 Cγ αβ θα θ β. (61) Strukturne jednačine: dθ α = 1 2 Cα βγθ β θ γ. (62) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
24 1. Kartanova jednačina strukture torzija Spoljašnji izvod tetradne 1-forme je 2-forma: dθ α = µ dx µ θν α dx ν = 1 2 ( µθν α ν θµ)dx α µ dx ν. (63) Transformiše se kao 2-forma, ali ne i kao Lorencov vektor dθ = d(λ 1 θ) = Λ 1 dθ + (dλ 1 )θ (64) Uvedemo član ω θ sadrži spinsku koneksiju: ω = Λ 1 dλ + Λ 1 ωλ (65) Transformacija novog izraza: dθ + ω θ = Λ 1 dθ + dλ 1 θ + (Λ 1 dλ + Λ 1 ωλ) Λ 1 θ = Λ 1 dθ + dλ 1 θ Λ 1 Λ dλ 1 θ + Λ 1 ω θ = Λ 1 (dθ + ω θ). (66) Definišemo 1-formu torzije: T α = dθ α + ω α β θ β. (67) Prva Kartanova jednačina strukture Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
25 2. Kartanova jednačina strukture krivina Komutator dva kovarijantna izvoda: D D = D α θ α D β θ β = D µ dx µ D ν dx ν = 1 2 (D αd β D β D α )θ α θ β = 1 2 (D µd ν D ν D µ )dx µ dx ν = 1 2 R αβθ α θ β = 1 2 R µνdx µ dx ν (68) Prepoznajemo Rimanov tenzor u ortogonalnom i koordinatnom bazisu Ova 2-forma je krivina spinske koneksije 2-forma krivine: U komponentama: Ω = D D = (d + ω) (d + ω) = dω + ω ω (69) Ovo je druga Kartanova jednačina strukture U ortogonalnom i koordinatnom bazisu: Ω α β = dω α β + ω α γ ω γ β. (70) Ω α β = 1 2 Rα βγδθ γ θ δ = 1 2 Rα βµνdx µ dx ν, (71) R α βγδ = e µ γ e ν δ R α βµν, R α βµν = θ γ µθ δ νr α βγδ. (72) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
26 Kartanove strukturne jednačine Kartanove strukturne jednačine u matričnoj formi: T = dθ + ω θ, Ω = dω + ω ω. (73) Delovanjem spoljšnjim izvodom: dt = dω θ ω dθ = dω θ ω (T ω θ) = dω θ ω T + ω ω θ = Ω θ ω T, (74) dω = dω ω ω dω = (Ω ω ω) ω ω (Ω ω ω) = Ω ω ω Ω, (75) Bjankijevi identiteti: dt + ω T = Ω θ, dω + ω Ω Ω ω = 0. (76) Kartanove strukturne jednačine i tetradni formalizam omogućavaju kuplovanje fermiona sa gravitacijom, što u slučaju Rimanove geometrije nije moguće Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
27 Odsečena Hajzenbergova algebra Odsečena Hajzenbergova algebra je matrična aproksimacija Hajzenbergove algebre Dobija se odsecanjem beskonačnih matrica koje reprezentuju koordinatu i impuls linearnog harmonijskog oscilatora Zadata je komutacionim relacijama: [µx, µy] = iɛ(1 z), (77) [µx, µz] = iɛµ(yz + zy), [µy, µz] = iɛµ(xz + zx). U nekomutativnoj geometriji, moguće je identifikovati fazni prostor sa pozicionim prostorom U slučaju unutrašnjih izvoda e α, za date impulse p α A: e α f = [p α, f ] (78) e µ α = [p α, x µ ] (79) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
28 Impulsi Identifikujemo impulse: ɛp 1 = iµ 2 y, ɛp 2 = iµ 2 x, ɛp 3 = iµ(µz 1 2 ) (80) Algebra impulsa [Madore]: [p 1, p 2 ] = µ2 2i + µp 3, (81) [p 2, p 3 ] = µp 1 iɛ(p 1 p 3 + p 3 p 1 ), [p 3, p 1 ] = µp 2 iɛ(p 2 p 3 + p 3 p 2 ). Uopštene komutacione relacije za p uz uslov d 2 = 0: 2P γδ αβp γ p δ F γ αβp γ 1 iɛ K αβ = 0 (82) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
29 Koneksija Izborom koneksije (µ = ɛ = 1)[Buric, Madore, Grosse, Wohlgenannt]: ω 12 = ω 21 = ( ip 3)θ 3 = ( 1 2 2z)θ3, (83) ω 13 = ω 31 = 1 2 θ2 + 2ip 2 θ 3 = 1 2 θ2 + 2xθ 3, ω 23 = ω 32 = 1 2 θ1 2ip 1 θ 3 = 1 2 θ1 + 2yθ 3. U komponentama ω 132 = ω 231 = 1 2z, (84) 2 ω 123 = ω 321 = 1 2, ω 133 = ω 331 = 2x, ω 213 = ω 312 = 1 2, ω 233 = ω 332 = 2y. Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
30 Ortonormalni bazis i 3-forma zapremine Komutacione relacije za ortogonalni bazis: (θ 1 ) 2 = 0, (θ 2 ) 2 = 0, (θ 3 ) 2 = 0, {θ 1, θ 2 } = 0 (85) {θ 1, θ 3 } = iɛ(θ 2 θ 3 θ 3 θ 2 ), {θ 2, θ 3 } = iɛ(θ 3 θ 1 θ 1 θ 3 ) (86) Ekstenzijom na algebru 3-formi: θ 1 θ 3 θ 1 = θ 2 θ 3 θ 2, θ 3 θ 1 θ 3 = θ 3 θ 1 θ 3 = 0 (87) θ 1 θ 2 θ 3 = θ 2 θ 1 θ 3 = θ 3 θ 1 θ 2 = θ 3 θ 2 θ 1 = i ɛ2 1 θ 2 θ 3 θ 2 2ɛ (88) θ 1 θ 3 θ 2 = θ 2 θ 3 θ 1 = i ɛ2 + 1 θ 2 θ 3 θ 2 2ɛ (89) Postoji samo jedna linearno nezavisna forma zapremine: Θ = i 2ɛ θ2 θ 3 θ 2 (90) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
31 Dirakove matrice u dve i tri dimenzije U dve i tri dimenzije spinorska reprezentacija je dvodimenzionalna Prirodni izbor Dirakovih matrica su Paulijeve matrice: ( ) 0 1 γ 1 = σ 1 =, γ = σ 2 = Ermitske matrice koje zadovoljavaju: Matrica kiralnosti u dve dimenzije: ( 0 i i 0 ). (91) {γ α, γ β } = 2δ αβ, α, β = 1, 2. (92) γ 3 = iγ 1 γ 2 = ( ) 1 0 = σ (93) Ove tri matrice formiraju Klifordovu algebru u 3 dimenzije Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
32 Dirakov spinor u 3 dimenzije Za Klifordovu algebru u 3 dimenzije {γ α, γ β } = 2δ αβ, α, β = 1, 2, 3. (94) Postoje dve neekvivalentne ireducibilne reprezentacije. Biramo: γ 4 = iγ 1 γ 2 γ 3 = 1 (95) Pri Spin(3) transformacijama, Dirakov spinor se transformiše: δψ = 1 4 ωαβ γ αβ ψ, (96) gse je γ αβ = γ α γ β za α β, a nula inače Zahtevamo da Dirakov konjugovani spinor ψ poništi ovu transformaciju formirajući skalar ψψ ( ) ( ) 1 δψ = ψ 4 ωαβ γ 14 αβ = ψ ωαβ γ βα = ψ ( 14 ) ωαβ γ αβ (97) = ψ = ψ Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
33 Dejstvo Fermionsko dejstvo u tri dimenzije u izraženo preko formi: S Dirac = Tr[(Dψ) ψ ψd ψ] V V γ 4. (98) Postoji torzija koju neminimalno kuplujemo sa fermionima: S tor = Trψ ψt α γ α V. (99) ( ) 1 T 1 = µ 2 µz (θ 2 θ 3 + θ 3 θ 2 ) ( ) 1 T 2 = µ 2 µz (θ 1 θ 3 + θ 3 θ 1 ) T 3 = µ 2 x(θ 1 θ 3 + θ 3 θ 1 ) µ 2 y(θ 2 θ 3 + θ 3 θ 2 ). (100) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
34 Dirakovo dejstvo Raspisano preko komponenata: S Dirac = Tr[(Dψ) ψ ψd ψ] V V γ 4 = Tr[(D α ψ) ψ ψd α ψ]θ α θ β γ β θ γ γ γ = TrX α γ β γ γ θ α θ β θ γ, (101) gde je: X α = (D α ψ) ψ ψd α ψ. (102) Sumiranjem komponenti: S Dirac = TrX α γ β γ γ θ α θ β θ γ = Tr(X 1 γ 3 γ 1 θ 1 θ 3 θ 1 + X 1 γ 2 γ 3 θ 1 θ 2 θ 3 + X 1 γ 3 γ 2 θ 1 θ 3 θ 2 + X 2 γ 3 γ 2 θ 2 θ 3 θ 2 + X 2 γ 1 γ 3 θ 2 θ 1 θ 3 + X 2 γ 3 γ 1 θ 2 θ 3 θ 1 + X 3 γ 1 γ 2 θ 3 θ 1 θ 2 + X 3 γ 2 γ 1 θ 3 θ 2 θ 1 ). (103) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
35 Dirakovo dejstvo 2 Izražavanjem preko jedinstvene forme zapremine θ 2 θ 3 θ 2 : S Dirac = i ( Tr X 1 γ 2 + X 1 γ 1 i ɛ2 1 X 1 γ 1 i ɛ ɛ 2ɛ X 2 γ 1 + X 2 γ 2 i ɛ2 1 2ɛ + X 3 γ 3 i ɛ2 1 2ɛ + X 3 γ 3 i ɛ2 1 2ɛ X 2 γ 2 i ɛ ɛ ) θ 2 θ 3 θ 2. (104) Θ = i 2ɛ θ2 θ 3 θ 2 : ( S Dirac =2ɛ Tr [X 1 γ 2 i ) ( ɛ γ 1 X 2 γ 1 + i ) ( ɛ γ 2 + X 3 γ 3 ɛ 1 )] Θ. (105) ɛ Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
36 Kovarijantni izvodi S Dirac = 1 Tr[X 1 ( ɛγ 2 + iγ 1 ) + X 2 (ɛγ 1 + iγ 2 ) + ix 3 γ 3 (1 ɛ 2 )]Θ 2 = S D1 + S D2 + S D3. (106) ( D 1 ψ = e 1 i 4 µγ1) ψ, D 1 ψ = e 1 ψ + i 4 µ ψγ 1 ( D 2 ψ = e 2 i 4 µγ2) ψ, D 2 ψ = e 2 ψ + i 4 µ ψγ 2 [ D 3 ψ = e 3 + i ] 4 µγ3 iµ 2 (xγ 2 yγ 1 + zγ 3 ) ψ, D 3 ψ = e 3 ψ ψ[ i ] 4 µγ3 + iµ 2 (xγ 2 yγ 1 + zγ 3 ) (107) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
37 Primer računa S D1 = 1 Tr[X 1 ( ɛγ 2 + iγ 1 )]Θ 2 = 1 2 = 1 2 = 1 2 { Tr [(D 1 ψ) ψ } ψd 1 ψ]( ɛγ2 + iγ 1 ) Θ {[( Tr e 1 i ) ] 4 µγ i 1 ψ ψ ψe1 ψ [ Tr ɛ(e 1 ψ) ψγ 2 + ɛψe 1 ψγ2 + i(e 1 ψ) ψγ 1 iψe 1 ψγ1 4 µψ ψγ } 1 ( ɛγ 2 + iγ 1 )Θ + i 4 ɛµγ 1ψ ψγ 2 + i 4 ɛµψ ψγ 1 γ µγ 1ψ ψγ µψ ψγ 1 γ 1 ]Θ = 1 [ Tr i ψγ 1 e 1 ψ i(e 1 ψ)γ 1 ψ + 1 ] 2 2 µψ ψ ɛ ψγ 2 e 1 ψ + ɛ(e 1 ψ)γ 2 ψ Θ. (108) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
38 Dirakov i torzioni član S Dirac = 1 { Tr i 2 ψγ α e α ψ i(e α ψ)γ α ψ µ ψψ + 2µ 2 z ψψ [ + ɛ i ψγ ] α γ 3 e α ψ i(e α ψ)γ α γ 3 ψ ɛ 2[ i ψγ 3 e 3 ψ i(e 3 ψ)γ 3 ψ 1 2 µ ψψ + 2µ 2 z ψψ ]} Θ (109) za α = 1, 2. S tor = 1 2 Tr{ψ ψ[ɛµ(γ 3 µxγ 2 + µyγ 1 2µzγ 3 ) ɛ 2 µ(1 2µz)]}Θ. (110) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
39 Rezultat Ukupno dejstvo: S = 1 { Tr i 2 ψγ α e α ψ i(e α ψ)γ α ψ µ ψψ + 2µ 2 z ψψ [ + ɛ i ψγ α γ 3 e α ψ i(e α ψ)γ α γ 3 ψ + µ ψ(γ ] 3 µxγ 2 + µyγ 1 2µzγ 3 )ψ ɛ 2[ i ψγ 3 e 3 ψ i(e 3 ψ)γ 3 ψ µ ψψ ]} Θ (111) Posle dimenzione redukcije z = 0, e 3 = 0 dobijamo dejstvo S = 1 { Tr i 2 ψγ α e α ψ i(e α ψ)γ α ψ µ ψψ [ + ɛ i ψγ α γ 3 e α ψ i(e α ψ)γ α γ 3 ψ + µ ψ(γ ] 3 µxγ 2 + µyγ 1 )ψ ɛ2 2 µ ψψ } Θ (112) Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
40 Zaključak Kvadrat kernela ovog dejstva u slučaju velike nekomutativnosti odgovara Melerovom kernelu koji je u primeru kalibracionih teorija omogućio dobro UV ponašanje Očekujemo da će i teorija sa fermionima imati dobro UV ponašanje Luka Nenadović Spinori na zakrivljenom nekomutativnom prostoru Novi Sad, / 40
PARCIJALNE DIFERENCIJALNE JEDNAČINE. , odnosno
 PARCIJALNE DIFERENCIJALNE JEDNAČINE. Odrediti Košijevo rešenje parijalne diferenijalne jednačine : p + q + 0 koje adovoljava uslov : 0 i p + q + 0 Najpre moramo da prebaimo na drugu stranu! p + q Sada
PARCIJALNE DIFERENCIJALNE JEDNAČINE. Odrediti Košijevo rešenje parijalne diferenijalne jednačine : p + q + 0 koje adovoljava uslov : 0 i p + q + 0 Najpre moramo da prebaimo na drugu stranu! p + q Sada
R Z N C. p11. a!b! = b (a b)!b! d n dx n [xn sin x] = x n(n k) (sin x) (n) = n(n 1) (n k + 1) sin(x + kπ. n(n 1) (n k + 1) sin(x + lπ 2 )
![R Z N C. p11. a!b! = b (a b)!b! d n dx n [xn sin x] = x n(n k) (sin x) (n) = n(n 1) (n k + 1) sin(x + kπ. n(n 1) (n k + 1) sin(x + lπ 2 ) R Z N C. p11. a!b! = b (a b)!b! d n dx n [xn sin x] = x n(n k) (sin x) (n) = n(n 1) (n k + 1) sin(x + kπ. n(n 1) (n k + 1) sin(x + lπ 2 )](/thumbs/102/156200514.jpg) 5 Z N p ) a a + b)! b ) a!b! a a! b a b)!b! p n n k nn k) n ) n k) d n d n [n sin ] n nn k) sin ) n) k n nn ) n k + ) sin + lπ ) k d n d n [n sin ] n k ) n n ) n k) sin ) k) k n k ) n nn ) n k + ) sin
5 Z N p ) a a + b)! b ) a!b! a a! b a b)!b! p n n k nn k) n ) n k) d n d n [n sin ] n nn k) sin ) n) k n nn ) n k + ) sin + lπ ) k d n d n [n sin ] n k ) n n ) n k) sin ) k) k n k ) n nn ) n k + ) sin
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Podstawy robotyki. Wykład II. Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska
 Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Neprekidnost i limes. Definicija. Neka je I R otvoreni interval i c I. Funkcija. f : I {c} R
 4 Neprekidnost i es Definicija. Neka je I R otvoreni interval i c I. Funkcija f : I {c} R ima es u točki c jednak L R ako za svaki niz ( n ) u I {c} vrijedi n = c = n + f( n) = L. n + Može se pokazati
4 Neprekidnost i es Definicija. Neka je I R otvoreni interval i c I. Funkcija f : I {c} R ima es u točki c jednak L R ako za svaki niz ( n ) u I {c} vrijedi n = c = n + f( n) = L. n + Može se pokazati
Fizyka bez stałych fizycznych
 Fizyka bez stałych fizycznych Edward Kapuścik WFiIS AGH 24 marzec 2014 Fizycy stale zajęci są różnorakimi pomiarami. Pomiary wymagają opracowania określonych metod pomiarowych oraz przyjęcia pewnych jednostek,
Fizyka bez stałych fizycznych Edward Kapuścik WFiIS AGH 24 marzec 2014 Fizycy stale zajęci są różnorakimi pomiarami. Pomiary wymagają opracowania określonych metod pomiarowych oraz przyjęcia pewnych jednostek,
v = v i e i v 1 ] T v =
![v = v i e i v 1 ] T v = v = v i e i v 1 ] T v =](/thumbs/97/130738346.jpg) v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
Atom dwupoziomowy w niezerowej temperaturze
 Seminarium CFT p. 1/24 Atom dwupoziomowy w niezerowej temperaturze Tomasz Sowiński 1 paździenika 2008 Seminarium CFT p. 2/24 Atom dwupoziomowy Hamiltonian Ĥ = Ĥ0 + ĤI Ĥ 0 = mσ z + 0 dk k a (k)a(k), Ĥ I
Seminarium CFT p. 1/24 Atom dwupoziomowy w niezerowej temperaturze Tomasz Sowiński 1 paździenika 2008 Seminarium CFT p. 2/24 Atom dwupoziomowy Hamiltonian Ĥ = Ĥ0 + ĤI Ĥ 0 = mσ z + 0 dk k a (k)a(k), Ĥ I
dt dt 2 2t = 3 (1 + t). y (x) = x. ] b) x = sin 2 t, y = cos 2 t [ 1 ] c) x = e 2t cos 2 t, y = e 2t sin 2 t [ tg t tg (t + π/4) ]
![dt dt 2 2t = 3 (1 + t). y (x) = x. ] b) x = sin 2 t, y = cos 2 t [ 1 ] c) x = e 2t cos 2 t, y = e 2t sin 2 t [ tg t tg (t + π/4) ] dt dt 2 2t = 3 (1 + t). y (x) = x. ] b) x = sin 2 t, y = cos 2 t [ 1 ] c) x = e 2t cos 2 t, y = e 2t sin 2 t [ tg t tg (t + π/4) ]](/thumbs/93/118020274.jpg) 168 Glava 3. Diferencijalni račun 487. Funkcija y = f(x) je zadata parametarskim jednačinama: Naći y (x). x = 2t t 2, y = 3t t 3 (t > 1). y (x) = dy dx = dy dt dt dx = ẏ ẋ = 3 3t2 2 2t = 3 (1 + t). 2 Iz
168 Glava 3. Diferencijalni račun 487. Funkcija y = f(x) je zadata parametarskim jednačinama: Naći y (x). x = 2t t 2, y = 3t t 3 (t > 1). y (x) = dy dx = dy dt dt dx = ẏ ẋ = 3 3t2 2 2t = 3 (1 + t). 2 Iz
Strings on Celestial Sphere. Stephan Stieberger, MPP München
 Strings on Celestial Sphere Stephan Stieberger, MPP München String Theory from a Worldsheet Perspective Galileo Galilei Institute, Firenze April 15-19, 2019 based on: St.St., T.R. Taylor: Strings on Celestial
Strings on Celestial Sphere Stephan Stieberger, MPP München String Theory from a Worldsheet Perspective Galileo Galilei Institute, Firenze April 15-19, 2019 based on: St.St., T.R. Taylor: Strings on Celestial
Numeryczne aproksymacje prawdopodobieństwa ruiny
 Numeryczne aproksymacje prawdopodobieństwa ruiny Krzysztof Burnecki Aleksander Weron Centrum Metod Stochastycznych im. Hugona Steinhausa Instytut Matematyki i Informatyki Politechnika Wrocławska www.im.pwr.wroc.pl/
Numeryczne aproksymacje prawdopodobieństwa ruiny Krzysztof Burnecki Aleksander Weron Centrum Metod Stochastycznych im. Hugona Steinhausa Instytut Matematyki i Informatyki Politechnika Wrocławska www.im.pwr.wroc.pl/
Zasada najmniejszego działania
 Zasada najmniejszego działania S = T dtl(x, ẋ) gdzie L(x, ẋ) jest lagrangianem. Dokonajmy przesuniecia x = x + y, ẋ = ẋ + ẏ, gdzie y(0) = y(t ) = 0. Wtedy T T S = dt L(x, ẋ ) = dt L(x + y, ẋ = ẋ + ẏ) 0
Zasada najmniejszego działania S = T dtl(x, ẋ) gdzie L(x, ẋ) jest lagrangianem. Dokonajmy przesuniecia x = x + y, ẋ = ẋ + ẏ, gdzie y(0) = y(t ) = 0. Wtedy T T S = dt L(x, ẋ ) = dt L(x + y, ẋ = ẋ + ẏ) 0
Metoda funkcji Greena
 Metoda funkcji Greena - dla układów jednoczastkowych Równania liniowe w fizyce Równanie liniowe niejednorodne ma postać ogólna: (z I L) ψ = f, z C Przykłady: 1. Równanie Poissona: L - operator liniowy,
Metoda funkcji Greena - dla układów jednoczastkowych Równania liniowe w fizyce Równanie liniowe niejednorodne ma postać ogólna: (z I L) ψ = f, z C Przykłady: 1. Równanie Poissona: L - operator liniowy,
Elektrodynamika. Część 8. Fale elektromagnetyczne. Ryszard Tanaś. Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Wykłady z Mechaniki Kwantowej
 Wykłady z Mechaniki Kwantowej Mechanika Kwantowa, Relatywistyczna Mechanika Kwantowa Wykład dla doktorantów (2017) Wykład 7 Jesteśmy uczniami w szkole natury i kształtujemy nasze pojęcia z lekcji na lekcję.
Wykłady z Mechaniki Kwantowej Mechanika Kwantowa, Relatywistyczna Mechanika Kwantowa Wykład dla doktorantów (2017) Wykład 7 Jesteśmy uczniami w szkole natury i kształtujemy nasze pojęcia z lekcji na lekcję.
v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q =
![v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q = v = v i e i v 1 ] T v = = v 1 v n v n ] a r +q = a a r 3q =](/thumbs/93/112711008.jpg) v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v v v v n 3q q q q r q = r 3q = E = E q E 3q E q = k q rq 3 k 3q r 3q 3 r q = k q rq 3 = kq 4 3 ) 4 q d b d c d d X d ± = d r = x y T d ± r ±
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v v v v n 3q q q q r q = r 3q = E = E q E 3q E q = k q rq 3 k 3q r 3q 3 r q = k q rq 3 = kq 4 3 ) 4 q d b d c d d X d ± = d r = x y T d ± r ±
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU. Janusz Adamowski
 II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU Janusz Adamowski 1 1 Przestrzeń Hilberta Do opisu stanów kwantowych używamy przestrzeni Hilberta. Przestrzenią Hilberta H nazywamy przestrzeń wektorową
II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU Janusz Adamowski 1 1 Przestrzeń Hilberta Do opisu stanów kwantowych używamy przestrzeni Hilberta. Przestrzenią Hilberta H nazywamy przestrzeń wektorową
O RELACJACH KOMUTACJI I NIEOZNACZONOŚCI W TEORII KWANTOWEJ
 O RELACJACH KOMUTACJI I NIEOZNACZONOŚCI W TEORII KWANTOWEJ Andrzej Herdegen Instytut Fizyki UJ 3 grudnia 2015 Przypomnę matematyczne i fizyczne tło tytułowych zagadnień. Pokażę dlaczego spacer przez algebrę
O RELACJACH KOMUTACJI I NIEOZNACZONOŚCI W TEORII KWANTOWEJ Andrzej Herdegen Instytut Fizyki UJ 3 grudnia 2015 Przypomnę matematyczne i fizyczne tło tytułowych zagadnień. Pokażę dlaczego spacer przez algebrę
Matematička analiza 4
 Matematička analiza 4 zadaci za vežbu Dragan S. Dor dević 1.3.13. Glava 1 Integrali Izračunati sledeće dvostruke integrale: 1.1. I(a) = G ( + y) a, gde je skup G odre den nejednačinama: >, y >, < a +
Matematička analiza 4 zadaci za vežbu Dragan S. Dor dević 1.3.13. Glava 1 Integrali Izračunati sledeće dvostruke integrale: 1.1. I(a) = G ( + y) a, gde je skup G odre den nejednačinama: >, y >, < a +
VI. Równania różniczkowe liniowe wyższych rzędów
 VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
Baze podataka (vježbe) SQL - uvod i osnove naredbe SELECT. Sveučilište u Zagrebu PMF Matematički odsjek
 Baze podataka (vježbe) SQL - uvod i osnove naredbe SELECT Sveučilište u Zagrebu PMF Matematički odsjek Kako započeti? Ulogirajte se na student (bilo kojim ssh klijentom). Kako započeti? Ulogirajte se na
Baze podataka (vježbe) SQL - uvod i osnove naredbe SELECT Sveučilište u Zagrebu PMF Matematički odsjek Kako započeti? Ulogirajte se na student (bilo kojim ssh klijentom). Kako započeti? Ulogirajte se na
Model Standardowy. Elementy fizyki czastek elementarnych. Wykład VI
 Model Standardowy Wykład VI elementy teorii kwantowej symetrie a prawa zachowania spontaniczne łamanie symetrii model Weinberga-Salama testy Modelu Standardowego poszukiwanie bozonu Higgsa Elementy fizyki
Model Standardowy Wykład VI elementy teorii kwantowej symetrie a prawa zachowania spontaniczne łamanie symetrii model Weinberga-Salama testy Modelu Standardowego poszukiwanie bozonu Higgsa Elementy fizyki
Prawdopodobieństwo i statystyka
 Wykład XI: Testowanie hipotez statystycznych 12 stycznia 2015 Przykład Motywacja X 1, X 2,..., X N N (µ, σ 2 ), Y 1, Y 2,..., Y M N (ν, δ 2 ). Chcemy sprawdzić, czy µ = ν i σ 2 = δ 2, czyli że w obu populacjach
Wykład XI: Testowanie hipotez statystycznych 12 stycznia 2015 Przykład Motywacja X 1, X 2,..., X N N (µ, σ 2 ), Y 1, Y 2,..., Y M N (ν, δ 2 ). Chcemy sprawdzić, czy µ = ν i σ 2 = δ 2, czyli że w obu populacjach
Fizyka dla Informatyków Wykład 7 Mechanika Ośrodków Ciągłych
 Fizyka dla Informatyków Wykład 7 Mechanika Ośrodków Ciągłych Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało sprężyste Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało
Fizyka dla Informatyków Wykład 7 Mechanika Ośrodków Ciągłych Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało sprężyste Spis treści Spis treści 1 Wstęp 2 3 4 5 Ciało
Gazy kwantowe. Jacek Jurkowski, Fizyka Statystyczna. Instytut Fizyki
 Instytut Fizyki 2015 Cele Cele Wyznaczenie średniego obsadzenia średniej energii równania stanu dla nieodziałujących gazów kwantowych fermionowego (gaz elektronowy w ciele stałym) bozonowego (kondensaty)
Instytut Fizyki 2015 Cele Cele Wyznaczenie średniego obsadzenia średniej energii równania stanu dla nieodziałujących gazów kwantowych fermionowego (gaz elektronowy w ciele stałym) bozonowego (kondensaty)
Mechanika kwantowa ćwiczenia, 2007/2008, Zestaw II
 1 Dane są następujące operatory: ˆD = x, ˆQ = π 0 x, ŝin = sin( ), ĉos = cos( ), ˆπ = π, ˆ0 = 0, przy czym operatory ˆπ oraz ˆ0 są operatorami mnożenia przez opowienie liczby (a) Wyznacz kwarat oraz owrotność
1 Dane są następujące operatory: ˆD = x, ˆQ = π 0 x, ŝin = sin( ), ĉos = cos( ), ˆπ = π, ˆ0 = 0, przy czym operatory ˆπ oraz ˆ0 są operatorami mnożenia przez opowienie liczby (a) Wyznacz kwarat oraz owrotność
Wstęp do Modelu Standardowego
 Wstęp do Modelu Standardowego Plan (Uzupełnienie matematyczne II) Abstrakcyjna przestrzeń stanów Podstawowe własności Iloczyn skalarny amplitudy prawdopodobieństwa Operatory i ich hermitowskość Wektory
Wstęp do Modelu Standardowego Plan (Uzupełnienie matematyczne II) Abstrakcyjna przestrzeń stanów Podstawowe własności Iloczyn skalarny amplitudy prawdopodobieństwa Operatory i ich hermitowskość Wektory
1 Formy hermitowskie. GAL (Informatyka) Wykład - formy hermitowskie. Paweł Bechler
 GAL (Informatyka) Wykład - formy hermitowskie Wersja z dnia 23 stycznia 2014 Paweł Bechler 1 Formy hermitowskie Niech X oznacza przestrzeń liniową nad ciałem K. Definicja 1. Funkcję φ : X X K nazywamy
GAL (Informatyka) Wykład - formy hermitowskie Wersja z dnia 23 stycznia 2014 Paweł Bechler 1 Formy hermitowskie Niech X oznacza przestrzeń liniową nad ciałem K. Definicja 1. Funkcję φ : X X K nazywamy
Rynek, opcje i równania SDE
 Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Wstęp do Teorii Oddziaływań Fundamentalnych
 Wstęp do Teorii Oddziaływań Fundamentalnych Igor Nowicki 12 czerwca 214 Spis treści 1 Wstęp do Teorii Oddziaływań Fundamentalnych 3 1.1 Zasada najmniejszego działania i równania ruchu w klasycznej teorii
Wstęp do Teorii Oddziaływań Fundamentalnych Igor Nowicki 12 czerwca 214 Spis treści 1 Wstęp do Teorii Oddziaływań Fundamentalnych 3 1.1 Zasada najmniejszego działania i równania ruchu w klasycznej teorii
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 6, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
7 Twierdzenie Fubiniego
 M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
q (s, z) = ( ) (λ T) ρc = q
 M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X W Y Z N A C Z A N I E O D K S Z T A C E T O W A R Z Y S Z Ą C Y C H H A R T O W A N I U P O W I E R Z C H N I O W Y M W I E
M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X W Y Z N A C Z A N I E O D K S Z T A C E T O W A R Z Y S Z Ą C Y C H H A R T O W A N I U P O W I E R Z C H N I O W Y M W I E
M W M Z correlation. πα 1 M G F 2 = 2M 2 W 2 W
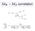 M W M Z correlation µ W ν µ e ν e G F 2 = 2M 2 W πα ( 1 M 2 W /MZ) 2 with loop contributions G F 2 = 2M 2 W (1+ r) πα ( 1 M 2 W /MZ) 2 1-loop examples ØÓÔ ÕÙ Ö r : quantum correction r = r(m t,m H ) Ï
M W M Z correlation µ W ν µ e ν e G F 2 = 2M 2 W πα ( 1 M 2 W /MZ) 2 with loop contributions G F 2 = 2M 2 W (1+ r) πα ( 1 M 2 W /MZ) 2 1-loop examples ØÓÔ ÕÙ Ö r : quantum correction r = r(m t,m H ) Ï
Wstęp do astrofizyli i kosmologia
 Wstęp do astrofizyli i kosmologia Ryszard Mańka-Marcisz 25 kwietnia 2004 1 Elementy Ogólnej Teorii Względności Obiekty astronomiczne są wynikiem istnienia równowagi miedzy zapadaniem grawitacyjnym a ciśniemiem
Wstęp do astrofizyli i kosmologia Ryszard Mańka-Marcisz 25 kwietnia 2004 1 Elementy Ogólnej Teorii Względności Obiekty astronomiczne są wynikiem istnienia równowagi miedzy zapadaniem grawitacyjnym a ciśniemiem
Analiza i aproksymacja nieliniowego modelu elastycznego ograniczaj cego odksztaªcenie
 Analiza i aproksymacja nieliniowego modelu elastycznego ograniczaj cego odksztaªcenie Wojciech O»a«ski 9 Kwi 2015 Przykªad ukªadu mechanicznych o ograniczaj cym odksztaªceniu: nierozciagliwa struna σ spreżyna
Analiza i aproksymacja nieliniowego modelu elastycznego ograniczaj cego odksztaªcenie Wojciech O»a«ski 9 Kwi 2015 Przykªad ukªadu mechanicznych o ograniczaj cym odksztaªceniu: nierozciagliwa struna σ spreżyna
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..)
 Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
5.6 Klasyczne wersje Twierdzenia Stokes a
 Ostatecznie f = 1 r 2 f ) r 2 r r + ctg ϑ f r 2 ϑ + 1 2 f r 2 ϑ + 1 2 2 f r 2 sin 2 ϑ ϕ 2 56 Klasyczne wersje Twierdzenia Stokes a Odpowiedniość między polami wektorowymi i jednoformami lub n 1)-formami
Ostatecznie f = 1 r 2 f ) r 2 r r + ctg ϑ f r 2 ϑ + 1 2 f r 2 ϑ + 1 2 2 f r 2 sin 2 ϑ ϕ 2 56 Klasyczne wersje Twierdzenia Stokes a Odpowiedniość między polami wektorowymi i jednoformami lub n 1)-formami
Aksjony w teorii cząstek elementarnych i kosmologii
 Uniwersytet Warszawski Wydział Fizyki Andrzej Hryczuk Nr albumu: 211 075 Aksjony w teorii cząstek elementarnych i kosmologii Praca magisterska na kierunku FIZYKA w zakresie FIZYKA TEORETYCZNA Praca wykonana
Uniwersytet Warszawski Wydział Fizyki Andrzej Hryczuk Nr albumu: 211 075 Aksjony w teorii cząstek elementarnych i kosmologii Praca magisterska na kierunku FIZYKA w zakresie FIZYKA TEORETYCZNA Praca wykonana
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
Formy kwadratowe. Mirosław Sobolewski. Wydział Matematyki, Informatyki i Mechaniki UW. wykład z algebry liniowej Warszawa, styczeń 2009
 Formy kwadratowe Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW wykład z algebry liniowej Warszawa, styczeń 2009 Mirosław Sobolewski (UW) Warszawa, 2009 1 / 15 Definicja Niech V, W,
Formy kwadratowe Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW wykład z algebry liniowej Warszawa, styczeń 2009 Mirosław Sobolewski (UW) Warszawa, 2009 1 / 15 Definicja Niech V, W,
Zadania z Analizy Funkcjonalnej I Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?
 Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi? a) X = R, d(x, y) = arctg x y ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i
Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi? a) X = R, d(x, y) = arctg x y ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i
Mechanika Kwantowa. Maciej J. Mrowiński. 24 grudnia Funkcja falowa opisująca stan pewnej cząstki ma następującą postać: 2 x 2 )
 Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Zadania z mechaniki kwantowej
 Zadania z mechaniki kwantowej Gabriel Wlazłowski 13 maja 2016 Rachunek zaburzeń bez czasu 1. Metodą rachunku zaburzeń obliczyć pierwszą i drugą poprawkę dla poziomów energetycznych oscylatora harmonicznego
Zadania z mechaniki kwantowej Gabriel Wlazłowski 13 maja 2016 Rachunek zaburzeń bez czasu 1. Metodą rachunku zaburzeń obliczyć pierwszą i drugą poprawkę dla poziomów energetycznych oscylatora harmonicznego
OD MODELU STANDARDOWEGO DO M-TEORII. modele teoriopolowe. elementarnych.
 J. Lukierski Gdańsk 09. 2003 OD MODELU STANDARDOWEGO DO M-TEORII 1859 1925 1. Podstawowe relatywistyczne modele teoriopolowe. 1968 1971 2. Model standardowy teorii cząstek elementarnych. 1921 1925 3. Pierwsze
J. Lukierski Gdańsk 09. 2003 OD MODELU STANDARDOWEGO DO M-TEORII 1859 1925 1. Podstawowe relatywistyczne modele teoriopolowe. 1968 1971 2. Model standardowy teorii cząstek elementarnych. 1921 1925 3. Pierwsze
4. P : P SO P Spin, π : P M: 6. F = P Spin Spin(n) S, F ± = P Spin Spin(n) S ± 7. ω: Levi-Civita, R:, K:
 /, Dirac,, Bismut[B]., [B], [B],, [K], [T], [W].,,,,, /.,.,,,..,.. M, g): n = l,. P SO : T M, M SOn) 3. P Spin : M Spinn), P SO 4. P : P SO P Spin, π : P M: 5. S = S + S : Spinn) l S +, S l ) 6. F = P
/, Dirac,, Bismut[B]., [B], [B],, [K], [T], [W].,,,,, /.,.,,,..,.. M, g): n = l,. P SO : T M, M SOn) 3. P Spin : M Spinn), P SO 4. P : P SO P Spin, π : P M: 5. S = S + S : Spinn) l S +, S l ) 6. F = P
O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego
 O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego Jan Ligęza Instytut Matematyki Wisła Letnia Szkoła Instytutu Matematyki wrzesień 2010 r. [1] S. Łojasiewicz, J. Wloka, Z. Zieleżny; Über eine
O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego Jan Ligęza Instytut Matematyki Wisła Letnia Szkoła Instytutu Matematyki wrzesień 2010 r. [1] S. Łojasiewicz, J. Wloka, Z. Zieleżny; Über eine
3. Iloczyn zewnętrzny w ogólności nie jest przemienny, ale zachodzi wzór:
 2 Iloczyn zewnętrzny jest łączny, tzn: (α β) γ α (β γ) 3 Iloczyn zewnętrzny w ogólności nie jest przemienny, ale zachodzi wzór: α β ( 1) kl β α Dowód: Punkt (1) wynika łatwo z definicji Dowód punktu (2)
2 Iloczyn zewnętrzny jest łączny, tzn: (α β) γ α (β γ) 3 Iloczyn zewnętrzny w ogólności nie jest przemienny, ale zachodzi wzór: α β ( 1) kl β α Dowód: Punkt (1) wynika łatwo z definicji Dowód punktu (2)
Obroty, czyli MINIMUM niezbędne każdemu fizykowi!
 Obroty, czyli MINIMUM niezbędne każdemu fizykowi! Paweł Rzońca 4 września 2015 Spis treści 1 Wstęp z algebry 2 1.1 Przestrzeń liniowa (V )...................................... 2 2 Forma metryczna w przestrzeni
Obroty, czyli MINIMUM niezbędne każdemu fizykowi! Paweł Rzońca 4 września 2015 Spis treści 1 Wstęp z algebry 2 1.1 Przestrzeń liniowa (V )...................................... 2 2 Forma metryczna w przestrzeni
Fizyka gwiazd. 1 Budowa gwiazd. 19 maja Stosunek r g R = 2GM
 Fizyka gwiazd 19 maja 2004 1 Budowa gwiazd Stosunek r g R = 2GM c 2 R (gdzie M, R jest masa i promieniem gwiazdy) daje nam informację konieczności uwzględnienia poprawek relatywistycznych. 0-0 Rysunek
Fizyka gwiazd 19 maja 2004 1 Budowa gwiazd Stosunek r g R = 2GM c 2 R (gdzie M, R jest masa i promieniem gwiazdy) daje nam informację konieczności uwzględnienia poprawek relatywistycznych. 0-0 Rysunek
Wprowadzenie do fal grawitacyjnych
 Wprowadzenie do fal grawitacyjnych Jacek Jurkowski Instytut Fizyki 2016 Jacek Jurkowski, Instytut Fizyki UMK Fale grawitacyjne 1(126) Plan wykładu Jacek Jurkowski, Instytut Fizyki UMK Fale grawitacyjne
Wprowadzenie do fal grawitacyjnych Jacek Jurkowski Instytut Fizyki 2016 Jacek Jurkowski, Instytut Fizyki UMK Fale grawitacyjne 1(126) Plan wykładu Jacek Jurkowski, Instytut Fizyki UMK Fale grawitacyjne
CZY STAŁA STRUKTURY SUBTELNEJ JEST WŁASNOŚCIĄ PRZESTRZENI?
 CZY STAŁA STRUKTURY SUBTELNEJ JEST WŁASNOŚCIĄ PRZESTRZENI? O KWANTOWEJ TEORII LICZBY 137.035999... Łukasz Bratek Zakład Fizyki Matematycznej i Astrofizyki Teoretycznej Instytut Fizyki Jądrowej PAN Seminarium
CZY STAŁA STRUKTURY SUBTELNEJ JEST WŁASNOŚCIĄ PRZESTRZENI? O KWANTOWEJ TEORII LICZBY 137.035999... Łukasz Bratek Zakład Fizyki Matematycznej i Astrofizyki Teoretycznej Instytut Fizyki Jądrowej PAN Seminarium
Matematička analiza 4
 Matematička analiza 4 zadaci za vežbu Dragan S. Dor dević 21.3.213. 2 Sadržaj 1 Integrali 5 1.1 Dvostruki integrali........................ 5 1.2 Trostruki integrali......................... 9 1.3 Nesvojstveni
Matematička analiza 4 zadaci za vežbu Dragan S. Dor dević 21.3.213. 2 Sadržaj 1 Integrali 5 1.1 Dvostruki integrali........................ 5 1.2 Trostruki integrali......................... 9 1.3 Nesvojstveni
Równania różniczkowe liniowe rzędu pierwszego
 Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Funkcje odpowiedzi dla CCQE i wiązek MiniBooNE (cz. I)
 Funkcje odpowiedzi dla CCQE i wiązek MiniBooNE (cz. I) Marcin Gonera Instytut Fizyki Teoretycznej Uniwersytet Wrocławski 23.05.2011 Oddziaływanie EM Rozpraszanie elastyczne elektron-nukleon Foton opisany
Funkcje odpowiedzi dla CCQE i wiązek MiniBooNE (cz. I) Marcin Gonera Instytut Fizyki Teoretycznej Uniwersytet Wrocławski 23.05.2011 Oddziaływanie EM Rozpraszanie elastyczne elektron-nukleon Foton opisany
Tryb Matematyczny w L A TEX-u
 Tryb Matematyczny w L A TEX-u Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-12-13 1 2 Tekst w trybie matematycznym Ściąga z symboli 3 Jak nie pisać pracy magisterskiej
Tryb Matematyczny w L A TEX-u Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-12-13 1 2 Tekst w trybie matematycznym Ściąga z symboli 3 Jak nie pisać pracy magisterskiej
5 Wielokowektory i wieloformy na powierzchni
 5 Wielokowektory i wieloformy na powierzchni Poniższe notatki powstały z użyciem notatek do wykładów Matematyka II i Matematyka III, więc mogą Państwo mieć czasami wrażenie, że autor niepotrzebnie rozdziela
5 Wielokowektory i wieloformy na powierzchni Poniższe notatki powstały z użyciem notatek do wykładów Matematyka II i Matematyka III, więc mogą Państwo mieć czasami wrażenie, że autor niepotrzebnie rozdziela
Zad Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji.
 Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Sekantooptyki owali i ich własności
 Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Spis wszystkich symboli
 1 Spis wszystkich symboli Symbole podstawowe - pojedyncze znaki, alfabet grecki α β γ Γ δ ξ η ε ϕ ν ρ τ θ Θ ψ Ψ φ Φ Ω Υ Σ -alfa -beta - gamma - gamma (duże) - delta (małe) - delta (duże) -ksi -eta - epsilon
1 Spis wszystkich symboli Symbole podstawowe - pojedyncze znaki, alfabet grecki α β γ Γ δ ξ η ε ϕ ν ρ τ θ Θ ψ Ψ φ Φ Ω Υ Σ -alfa -beta - gamma - gamma (duże) - delta (małe) - delta (duże) -ksi -eta - epsilon
Wiadomości wstępne. Krótka historia Przekrój czynny Układ jednostek naturalnych Eksperymenty formacji i produkcji
 Wiadomości wstępne Krótka historia Przekrój czynny Układ jednostek naturalnych Eksperymenty formacji i produkcji Historia fizyki cząstek w pigułce 1930 1940 1950 1960 1970 1980 1990 000 Bevatron PS AGS
Wiadomości wstępne Krótka historia Przekrój czynny Układ jednostek naturalnych Eksperymenty formacji i produkcji Historia fizyki cząstek w pigułce 1930 1940 1950 1960 1970 1980 1990 000 Bevatron PS AGS
WYBUCHY ROZWIA ZAŃ NIELINIOWYCH RÓWNAŃ PARABOLICZNYCH: nieliniowe równanie ciep la, model Keller Segela chemotaksji
 WYBUCHY ROZWIA ZAŃ NIELINIOWYCH RÓWNAŃ PARABOLICZNYCH: nieliniowe równanie ciep la, model Keller Segela chemotaksji Piotr BILER Instytut Matematyczny, Uniwersytet Wroc lawski, pl. Grunwaldzki 2/4, 50 384
WYBUCHY ROZWIA ZAŃ NIELINIOWYCH RÓWNAŃ PARABOLICZNYCH: nieliniowe równanie ciep la, model Keller Segela chemotaksji Piotr BILER Instytut Matematyczny, Uniwersytet Wroc lawski, pl. Grunwaldzki 2/4, 50 384
Zadania z Analizy Funkcjonalnej I Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?
 Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?. a) X = R, x = arctg x ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i y i ;
Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?. a) X = R, x = arctg x ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i y i ;
WYKŁAD 2: CAŁKI POTRÓJNE
 WYKŁAD : CAŁKI OTRÓJNE 1 CAŁKI OTRÓJNE O ROSTOADŁOŚCIANIE Oznaczenia w definicji całi po prostopadłościanie: = {(: a x, c y d, p z q} prostopadłościan w przestrzeni; = { 1,,, n } podział prostopadłościanu
WYKŁAD : CAŁKI OTRÓJNE 1 CAŁKI OTRÓJNE O ROSTOADŁOŚCIANIE Oznaczenia w definicji całi po prostopadłościanie: = {(: a x, c y d, p z q} prostopadłościan w przestrzeni; = { 1,,, n } podział prostopadłościanu
INTEGRALI I TEORIJA POLJA. - zadaci za vežbu -
 INTEGRALI I TEORIJA POLJA - zadaci za vežbu -. Izračunati direktno krivolinijski integral: ydx x dy zdz duž presečne krive površi: C z x a y b i x a y b x a y b, orjentisane u pozitivnom smeru ako se posmatra
INTEGRALI I TEORIJA POLJA - zadaci za vežbu -. Izračunati direktno krivolinijski integral: ydx x dy zdz duž presečne krive površi: C z x a y b i x a y b x a y b, orjentisane u pozitivnom smeru ako se posmatra
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
Wprowadzenie do modelu standardowego cz astek elementarnych
 Wprowadzenie do modelu standardowego cz astek elementarnych Krzysztof Golec Biernat Instytut Fizyki Ja drowej PAN w Krakowie 15 września 2011 Wersja robocza nie do dystrybucji Kraków 2003/04 Spis treści
Wprowadzenie do modelu standardowego cz astek elementarnych Krzysztof Golec Biernat Instytut Fizyki Ja drowej PAN w Krakowie 15 września 2011 Wersja robocza nie do dystrybucji Kraków 2003/04 Spis treści
Analiza II.2*, lato komentarze do ćwiczeń
 Analiza.2*, lato 2018 - komentarze do ćwiczeń Marcin Kotowski 5 czerwca 2019 1 11 2019, zadanie 2 z serii domowej 1 Pokażemy, że jeśli f nie jest stała, to całka: f(x f(y B B x y dx dy jest nieskończona.
Analiza.2*, lato 2018 - komentarze do ćwiczeń Marcin Kotowski 5 czerwca 2019 1 11 2019, zadanie 2 z serii domowej 1 Pokażemy, że jeśli f nie jest stała, to całka: f(x f(y B B x y dx dy jest nieskończona.
Elektrodynamika. Część 9. Potencjały i pola źródeł zmiennych w czasie. Ryszard Tanaś
 Elektrodynamika Część 9 Potencjały i pola źródeł zmiennych w czasie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 10 Potencjały i pola źródeł zmiennych w
Elektrodynamika Część 9 Potencjały i pola źródeł zmiennych w czasie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 10 Potencjały i pola źródeł zmiennych w
Fizyka ośrodków ciągłych
 Notatki do wykładu Fizyka ośrodków ciągłych Fizyka techniczna sem. VI Spis treści Wprowadzenie.............................................. 5 Rozdział 1. Przypomnienie z algebry...............................
Notatki do wykładu Fizyka ośrodków ciągłych Fizyka techniczna sem. VI Spis treści Wprowadzenie.............................................. 5 Rozdział 1. Przypomnienie z algebry...............................
Ergodyczność procesów filtracji - o wieloletnim błędzie i próbach jego poprawienia
 Ergodyczność procesów filtracji - o wieloletnim błędzie i próbach jego poprawienia Łukasz Stettner Instytut Matematyczny PAN VI Wykład im. Profesora Andrzeja Lasoty, UŚ, 11 stycznia 2013 Prof. Andrzej
Ergodyczność procesów filtracji - o wieloletnim błędzie i próbach jego poprawienia Łukasz Stettner Instytut Matematyczny PAN VI Wykład im. Profesora Andrzeja Lasoty, UŚ, 11 stycznia 2013 Prof. Andrzej
Notatki do wykładu Geometria Różniczkowa I
 Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 22 października 2013 1 Przestrzeń styczna i kostyczna c.d. Pora na podsumowanie: Zdefiniowaliśmy przestrzeń styczną do przestrzeni afinicznej
Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 22 października 2013 1 Przestrzeń styczna i kostyczna c.d. Pora na podsumowanie: Zdefiniowaliśmy przestrzeń styczną do przestrzeni afinicznej
Rozdział 1 Wiadomości wstępne. Krótka historia Przekrój czynny, świetlność Układ jednostek naturalnych Eksperymenty formacji i produkcji
 Rozdział 1 Wiadomości wstępne Krótka historia Przekrój czynny, świetlność Układ jednostek naturalnych Eksperymenty formacji i produkcji Historia fizyki cząstek w pigułce 1930 1940 1950 1960 1970 1980 1990
Rozdział 1 Wiadomości wstępne Krótka historia Przekrój czynny, świetlność Układ jednostek naturalnych Eksperymenty formacji i produkcji Historia fizyki cząstek w pigułce 1930 1940 1950 1960 1970 1980 1990
Fizyka zderzeń relatywistycznych jonów
 Fizyka zderzeń relatywistycznych jonów kilka pytań i możliwe odpowiedzi Stanisław Mrówczyński Uniwersytet Jana Kochanowskiego, Kielce & Instytut Problemów Jądrowych, Warszawa 1 Programy eksperymentalne
Fizyka zderzeń relatywistycznych jonów kilka pytań i możliwe odpowiedzi Stanisław Mrówczyński Uniwersytet Jana Kochanowskiego, Kielce & Instytut Problemów Jądrowych, Warszawa 1 Programy eksperymentalne
 Ś Ś Ś Ś Ś Ś Ę Ą Ę ŚĘ Ę Ś ń Ę Ę Ą Ł Ż Ń Ł ć Ą ć Ł Ę Ó ć Ź ć ź ń Ń ń Ś Ą Ę Ł Ę Ą Ę ń ć ń Ź ć ń ć ń Ś ń ŚĆ ć ź Ł Ę Ę Ś Ę Ę Ę ń ŚĘ Ń Ę Ę ń ŚĘ Ę Ę Ś Ś ć ń Ę ń Ś Ę ć ć Ę Ę ć ź ć ń Ę Ń ń ć Ł Ę Ę Ę Ę ć Ę ć ć ź
Ś Ś Ś Ś Ś Ś Ę Ą Ę ŚĘ Ę Ś ń Ę Ę Ą Ł Ż Ń Ł ć Ą ć Ł Ę Ó ć Ź ć ź ń Ń ń Ś Ą Ę Ł Ę Ą Ę ń ć ń Ź ć ń ć ń Ś ń ŚĆ ć ź Ł Ę Ę Ś Ę Ę Ę ń ŚĘ Ń Ę Ę ń ŚĘ Ę Ę Ś Ś ć ń Ę ń Ś Ę ć ć Ę Ę ć ź ć ń Ę Ń ń ć Ł Ę Ę Ę Ę ć Ę ć ć ź
Fizykaatmosfergwiazdowych
 Krzysztof Gęsicki Fizykaatmosfergwiazdowych Wykład kursowy dla studentów astronomii 2 stopnia wykład 6 atom trójpoziomowy itp. pamiętamy z poprzedniego wykładu: Bliżej powierzchni gwiazdy fotony mogą przez
Krzysztof Gęsicki Fizykaatmosfergwiazdowych Wykład kursowy dla studentów astronomii 2 stopnia wykład 6 atom trójpoziomowy itp. pamiętamy z poprzedniego wykładu: Bliżej powierzchni gwiazdy fotony mogą przez
Algorytmy MCMC i ich zastosowania statystyczne
 Algorytmy MCMC i ich zastosowania statystyczne Wojciech Niemiro Uniwersytet Mikołaja Kopernika, Toruń i Uniwersytet Warszawski Statystyka Matematyczna Wisła, grudzień 2010 Wykład 3 1 Łańcuchy Markowa Oznaczenia
Algorytmy MCMC i ich zastosowania statystyczne Wojciech Niemiro Uniwersytet Mikołaja Kopernika, Toruń i Uniwersytet Warszawski Statystyka Matematyczna Wisła, grudzień 2010 Wykład 3 1 Łańcuchy Markowa Oznaczenia
Rozdział 3. Tensory. 3.1 Krzywoliniowe układy współrzędnych
 Rozdział 3 Tensory 3.1 Krzywoliniowe układy współrzędnych W kartezjańskim układzie współrzędnych punkty P są scharakteryzowane przez współrzędne kartezjańskie wektora wodzącego r = x 1 i 1 + x 2 i 2 +
Rozdział 3 Tensory 3.1 Krzywoliniowe układy współrzędnych W kartezjańskim układzie współrzędnych punkty P są scharakteryzowane przez współrzędne kartezjańskie wektora wodzącego r = x 1 i 1 + x 2 i 2 +
Elektrodynamika Część 10 Promieniowanie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 10 Promieniowanie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 11 Promieniowanie 3 11.1 Promieniowanie dipolowe............... 3 11
Elektrodynamika Część 10 Promieniowanie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 11 Promieniowanie 3 11.1 Promieniowanie dipolowe............... 3 11
Rozprawa doktorska. Oscylacje akceleratorowych neutrin z uwzględnieniem ich niestandardowych oddziaływań. Sebastian Zając
 Uniwersytet Śląski w Katowicach Wydział Matematyki Fizyki i Chemii Instytut Fizyki Rozprawa doktorska Oscylacje akceleratorowych neutrin z uwzględnieniem ich niestandardowych oddziaływań Sebastian Zając
Uniwersytet Śląski w Katowicach Wydział Matematyki Fizyki i Chemii Instytut Fizyki Rozprawa doktorska Oscylacje akceleratorowych neutrin z uwzględnieniem ich niestandardowych oddziaływań Sebastian Zając
Reprezentacja martyngałowa względem addytywnych procesów Markowa-Itô
 Reprezentacja martyngałowa względem addytywnych procesów Markowa-Itô Instytut Matematyk Unwersytetu Jagellońskego Instytut Nauk Ekonomcznych PAN Wynk wspólne z prof. Ł. Stettnerem (IM PAN) prof. Z. Palmowskm
Reprezentacja martyngałowa względem addytywnych procesów Markowa-Itô Instytut Matematyk Unwersytetu Jagellońskego Instytut Nauk Ekonomcznych PAN Wynk wspólne z prof. Ł. Stettnerem (IM PAN) prof. Z. Palmowskm
Funkcje Analityczne, ćwiczenia i prace domowe
 Funkcje Analityczne, ćwiczenia i prace domowe P. Wojtaszczyk 29 maja 22 Ten plik będzie progresywnie modyfikowany. Będzie on zawierał. Zadanie omówione na ćwiczeniach 2. Zadania ćwiczebne do samodzielnego
Funkcje Analityczne, ćwiczenia i prace domowe P. Wojtaszczyk 29 maja 22 Ten plik będzie progresywnie modyfikowany. Będzie on zawierał. Zadanie omówione na ćwiczeniach 2. Zadania ćwiczebne do samodzielnego
Światło widzialne a widmo elektromagnetyczne
 Światło widzialne a widmo elektromagnetyczne 10 3 λ [nm] λ 10 6 10 12 fale radiowe 1 mm 10 9 10 12 10 9 10 6 mikrofale 100 µm 10 µm 10 15 10 18 10 21 10 3 1 10 3 widmo optyczne prom. X promienie gamma
Światło widzialne a widmo elektromagnetyczne 10 3 λ [nm] λ 10 6 10 12 fale radiowe 1 mm 10 9 10 12 10 9 10 6 mikrofale 100 µm 10 µm 10 15 10 18 10 21 10 3 1 10 3 widmo optyczne prom. X promienie gamma
Rozkłady wielu zmiennych
 Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Wyk lad 13 Funkcjona ly dwuliniowe
 1 Izomorfizmy kanoniczne Wyk lad 13 Funkcjona ly dwuliniowe Definicja 13.1. Niech V i W bed przestrzeniami liniowymi. Funkcje ξ : V W R nazywamy funkcjona lem dwuliniowym, jeżeli i a,b R α,β V γ W ξa α
1 Izomorfizmy kanoniczne Wyk lad 13 Funkcjona ly dwuliniowe Definicja 13.1. Niech V i W bed przestrzeniami liniowymi. Funkcje ξ : V W R nazywamy funkcjona lem dwuliniowym, jeżeli i a,b R α,β V γ W ξa α
V. Jednorodne układy równań różniczkowych liniowych o stałych współczynnikach
 V. Jednorodne układy równań różniczkowych liniowych o stałych współczynnikach 1. Niezależność wielomianów, funkcji wykładniczych i trygonometrycznych W paragrafie tym podamy pewien lemat 1 potrzebny w
V. Jednorodne układy równań różniczkowych liniowych o stałych współczynnikach 1. Niezależność wielomianów, funkcji wykładniczych i trygonometrycznych W paragrafie tym podamy pewien lemat 1 potrzebny w
Interesujące fazy ewolucji masywnej gwiazdy:
 1/26 Asymetria ν ν w widmie pre-supernowej A. Odrzywołek Asymetria ν ν w (termicznym) widmie pre-supernowej IDEA: Przewidzieć wybuch supernowej opierając się na detekcji neutrin z pre-supernowej Interesujące
1/26 Asymetria ν ν w widmie pre-supernowej A. Odrzywołek Asymetria ν ν w (termicznym) widmie pre-supernowej IDEA: Przewidzieć wybuch supernowej opierając się na detekcji neutrin z pre-supernowej Interesujące
Implementacja efektywnych metod opisu korelacji elektronowej w dużych układach molekularnych
 Implementacja efektywnych metod opisu korelacji elektronowej w dużych układach molekularnych Krzysztof Kowalczyk Wydział Chemii UJ Zakład Metod Obliczeniowych Chemii promotor: dr Marcin Makowski 27 maja
Implementacja efektywnych metod opisu korelacji elektronowej w dużych układach molekularnych Krzysztof Kowalczyk Wydział Chemii UJ Zakład Metod Obliczeniowych Chemii promotor: dr Marcin Makowski 27 maja
Pojam matrice je, neovisno o primjenama, uveden potkraj 19. st., a povezuje se s imenima J.J. Sylvester-a i A. Cayley-a;
 2. MATRICE I DETERMINANTE Matrice (pravokutne sheme brojeva) susrećemo kod raznih problema u matematici, ali i u kemiji, zici, ekonomiji..., jer se s njima relativno jednostavno racuna; Pojam matrice je,
2. MATRICE I DETERMINANTE Matrice (pravokutne sheme brojeva) susrećemo kod raznih problema u matematici, ali i u kemiji, zici, ekonomiji..., jer se s njima relativno jednostavno racuna; Pojam matrice je,
Zadania z Analizy Funkcjonalnej I* - 1
 Zadania z Analizy Funkcjonalnej I* - 1 1. Która z następujących przestrzeni jest przestrzenią Banacha w normie supremum: C(R); C ogr (R) przestrzeń funkcji ciągłych ograniczonych; C zw (R) przestrzeń funkcji
Zadania z Analizy Funkcjonalnej I* - 1 1. Która z następujących przestrzeni jest przestrzenią Banacha w normie supremum: C(R); C ogr (R) przestrzeń funkcji ciągłych ograniczonych; C zw (R) przestrzeń funkcji
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty
 WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 4 / 9 Przekształcenia zmiennej losowej X
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 4 / 9 Przekształcenia zmiennej losowej X
Estymatory nieobciążone o minimalnej wariancji
 Estymatory ieobciążoe o miimalej wariacji Model statystyczy (X, {P θ, θ Θ}); g : Θ R 1 Zadaie: oszacować iezaą wartość g(θ) Wybrać takie δ(x 1, X 2,, X ) by ( θ Θ) ieobciążoość E θ δ(x 1, X 2,, X ) = g(θ)
Estymatory ieobciążoe o miimalej wariacji Model statystyczy (X, {P θ, θ Θ}); g : Θ R 1 Zadaie: oszacować iezaą wartość g(θ) Wybrać takie δ(x 1, X 2,, X ) by ( θ Θ) ieobciążoość E θ δ(x 1, X 2,, X ) = g(θ)
JAK UCZYĆ KWANTOWEJ TEORII POLA
 JAK UCZYĆ KWANTOWEJ TEORII POLA Piotr Chankowski KMMF 17.05.2012 Pomys l nie doszed l do skutku ponieważ autorzy postawili sobie zbyt ambitne zadanie napisania podr ecznika bezb l ednego w warstwie matematycznej
JAK UCZYĆ KWANTOWEJ TEORII POLA Piotr Chankowski KMMF 17.05.2012 Pomys l nie doszed l do skutku ponieważ autorzy postawili sobie zbyt ambitne zadanie napisania podr ecznika bezb l ednego w warstwie matematycznej
1. Obciążenie statyczne
 . Obciążenie statyczne.. Obliczenie stopnia kinematycznej niewyznaczalności n = Σ ϕ + Σ = + = p ( ) Σ = w p + d u = 5 + 5 + 0 0 =. Schemat podstawowy metody przemieszczeń . Schemat odkształceń łańcucha
. Obciążenie statyczne.. Obliczenie stopnia kinematycznej niewyznaczalności n = Σ ϕ + Σ = + = p ( ) Σ = w p + d u = 5 + 5 + 0 0 =. Schemat podstawowy metody przemieszczeń . Schemat odkształceń łańcucha
Notatki do wykładu Geometria Różniczkowa I
 Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 17 listopada 2013 1 Wielokowektory i wieloformy na powierzchni Poprzedni wykład zakończyliśmy na sformułowaniu następującego faktu:
Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 17 listopada 2013 1 Wielokowektory i wieloformy na powierzchni Poprzedni wykład zakończyliśmy na sformułowaniu następującego faktu:
Prawdopodobieństwo i statystyka
 Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Masywne neutrina w teorii i praktyce
 Instytut Fizyki Teoretycznej Uniwersytet Wrocławski Wrocław, 20 czerwca 2008 1 Wstęp 2 3 4 Gdzie znikają neutrina słoneczne (elektronowe)? 4p 4 2He + 2e + + 2ν e 100 miliardów neutrin przez paznokieć kciuka
Instytut Fizyki Teoretycznej Uniwersytet Wrocławski Wrocław, 20 czerwca 2008 1 Wstęp 2 3 4 Gdzie znikają neutrina słoneczne (elektronowe)? 4p 4 2He + 2e + + 2ν e 100 miliardów neutrin przez paznokieć kciuka
