Model Standardowy. Elementy fizyki czastek elementarnych. Wykład VI
|
|
|
- Włodzimierz Stefaniak
- 5 lat temu
- Przeglądów:
Transkrypt
1 Model Standardowy Wykład VI elementy teorii kwantowej symetrie a prawa zachowania spontaniczne łamanie symetrii model Weinberga-Salama testy Modelu Standardowego poszukiwanie bozonu Higgsa Elementy fizyki czastek elementarnych
2 Oddziaływania słabe... Bozony W ± i Z Dziś jest dla nas oczywiste, że oddziaływania słabe s a przenoszone przez ciężkie nośniki. Jednak ich istnienie zostało doświadczalnie potwierdzone dopiero 15 lat po ich wprowadzeniu do teorii przez Weinberg a i Salam a. Dlaczego byli przekonani o ich istnieniu? Odkrycie bozonów Z i W ± przez eksperymenty UA1 i UA2 (1983):! " $ " " " ( "! " )!!! * + ( "(,, (- " + * + ". ( ( / ( ( !! " " * * ( + " 2! * " " " " " ( ( " " " ( * * * * * 2 * * * * * 5 * + * " " " " " 3 (! 2 2 " 6 ( (!! ( + + ( +! ( ( 2 /! 2!! 2 "! " * ( ( ( " * ( * " ( +2 + " A.F.Żarnecki Wykład VI 1
3 Elementy teorii Mechanika klasyczna Jedna z postaci w jakich możemy przedstawić równania ruchu układu czastek jest równanie Lagrange a d dt ( L q i ) L q i = 0 Lagrangian układu jest różnica energii kinetycznej i potencjalnej L(q i, q i, t) = T V i zależy od współrzędnych uogólnionych q i oraz ich pochodnych po czasie q i. Przykład Jednowymiarowy ruch w stałym polu grawitacyjnym: T = mv2 2 V = mgx = mẋ2 2 L(x, ẋ, t) = mẋ2 2 mgx z równania Lagrange a: mẍ = mg A.F.Żarnecki Wykład VI 2
4 Elementy teorii Teoria kwantowa Zamiast od klasycznych współrzędnych uogólnionych q i gęstość lagrangianu zależy od pola cz astki φ(x µ ): q i φ(x µ ) q i φ µ φ x µ gęstość lagrangianu: L(q i, q i, t) L ( φ, φ x µ, x µ ) Równanie Lagrangea: ( µ=0,1,2,3) x µ L ( ) φ x µ L φ = 0 Definiujac lagrangian jednoznacznie definuijemy teorię: opisywane czastek i ich oddziaływania. W oparciu o lagrangian definiuje się wszystkie reguły rachunkowe (w tym diagramy Faynmana). Symetria teorii symetria lagrangianu A.F.Żarnecki Wykład VI 3
5 Symetrie Twierdzenie Noether (1918) Niezmienniczości teorii względem każdej grupy symetrii odpowiada zasada zachowania. symetria przesunięcie w czasie energia przesunięcie w przestrzeni pęd zachowana wielkość obrót moment pędu odbicie inwersja przestrzenna parzystość P sprzężenie czastka-antycz astka parzystość ładunkowa C A.F.Żarnecki Wykład VI 4
6 Symetrie Transformacja cechowania Lagrangian dla swobodnego elektronu L = i ψγ µ µ ψ m ψψ gdzie ψ jest spinorem Diraca o czterech składowych zespolonych (tyle potrzeba, żeby opisać elektron i pozyton lewo- i prawo skrętny). równanie Diraca: (iγ µ µ m) ψ = 0 por. równanie Schrödingera: (h 1) (i t m 2 x ) ψ = 0 Pola sa zespolone, ale lagrangian nie zależy od fazy dodatkowa symetria cechowania : ψ(x) e iα ψ(x) Transformacje obrotu fazy o kat α: U(α) = e iα tworza grupę abelowa znana jako U(1). Niezmienniczość względem transformacji cechowania z twierdzenia Noether: zasada zachowania ładunku A.F.Żarnecki Wykład VI 5
7 Symetrie Transformacja cechowania Czy nasza teoria jest też niezmiennicza względem lokalnej symetrii cechowania: ψ(x) e iα(x) ψ(x) gdzie kat obrotu fazy α(x) zależy od położenia i czasu? Dla swobodnego elektronu: NIE, lagrangian zawiera pochodne pola. Ale jeśli dodamy do teorii pole wektorowe A µ, które transformuje się zgodnie z: A µ A µ + 1 ( e µα µ α α ) x µ i jednocześnie zastapimy zwykła pochodna przez pochodna kowariantna D µ µ iea µ lagrangian niezmienniczy względem transformacji lokalnej A µ - pole (bozon) cechowania A.F.Żarnecki Wykład VI 6
8 QED Symetrie Uwzględniajac dodatkowo energię kinetyczna dla pola A µ otrzymujemy lagrangian: L = ψ (iγ µ µ m) ψ + e ψγ µ A µ ψ 1 4 F µνf µν gdzie F µν µ A ν ν A µ Z warunku niezmienniczości teorii czastki swobodnej względem lokalnej zmiany fazy otrzymaliśmy... Elektrodynamikę kwantowa pełna teorię oddziałujacych ładnuków elektrycznych pole A µ - foton Okazuje się, że foton MUSI być bezmasowy! Dodanie do L członu masowego dla fotonu prowadziłoby do nieusuwalnych rozbieżności A.F.Żarnecki Wykład VI 7
9 Model klasyczny Najprostrzy model: drgajaca struna z Spontaniczne łamanie symetrii Energia potencjalna jest funkcja wychylenia φ = symetria teorii względem obrotu wokół osi Z. x 2 + y 2 x y Stan podstawowy układu: φ = x + iy = 0 stan podstawowy zachowuje symetrię teorii (obrotu wokół osi Z) Ale wcale tak nie musi być... A.F.Żarnecki Wykład VI 8
10 Spontaniczne łamanie symetrii Model klasyczny Inny model: drgania ściskanego pręta Energia potencjalna, a więc i cała teorii wciaż ma symetrię względem obrotu wokół osi Z. Ale stan podstawowy (o najniższej energii) odpowiada φ 0 Zbiór stanów o φ = v wciaż jest osiowo symetryczny (pręt mógłby się wybrzuszyć w dowolna stronę) Ale Przyroda musi wybrać jeden stan podstawowy spontanicznie łamie symetrię teorii pręt wybrzusza się tracac symetrię osiowa... A.F.Żarnecki Wykład VI 9
11 Peter W. Higgs Na możliwość nadania mas nośnikom oddziaływań poprzez spontaniczne łamanie symetrii wskazał czterdzieści lat temu (1964) Peter W. Higgs. Mechanizm spontanicznego łamania symetrii, zwany także mechanizmem Higgsa, jest podstawa współczesnej teorii oddziaływań elektrosłabych. A.F.Żarnecki Wykład VI 10
12 Model Weinberga-Salama Grupa SU(2) Doświadczenia wskazywały, że do opisu oddziaływań słabych potrzebne sa przynajmniej trzy nośniki. Najprostrza grupa cechowania, która daje nam trzy pola cechowania jest SU(2) (macierze unitarne 2 2 z wyznacznikiem 1) otrzymujemy trzy bozony cechowania: W +, W i W. Mechanizm Higgsa Możemy nadać masy bozonom W wprowadzajac dodatkowe pole skalarne φ o potencjale: V (φ) = µ 2 φ φ + λ ( φ φ ) 2 Jeśli λ < 0 potencjał ma minimum dla φ 0 spontaniczne łamanie symetrii Możemy przedefiniować nasze pola rozwijajac potencjał w szereg wokół minimum φ, φ 2 v2 2 poprzez oddziaływanie z polem φ bozony cechowania uzyskuja masę M W = 1 2 gv (g - stała sprzężenia) Nadajemy masy nie łamiac symetrii teorii (L) A.F.Żarnecki Wykład VI 11
13 Mechanizm Higgsa Wyobraźmy sobie salę bankietowa równomiernie wypełniona ludźmi: (pole Higgsa) A.F.Żarnecki Wykład VI 12
14 Mechanizm Higgsa Pojawia się sławny naukowiec (bozon cechowania) przyciagaj ac uwagę zebranych... A.F.Żarnecki Wykład VI 13
15 Mechanizm Higgsa Ludzie cisnacy się wokół naukowca utrudniaja mu poruszanie się (nadaja mu masę) A.F.Żarnecki Wykład VI 14
16 Model Weinberga-Salama Grupa SU(2) U(1) Masa bozonu Z jest wyższa niż masy bozonów W ± Aby to wytłumaczyć musimy wprowadzić mieszanie neutralnych pól cechowania: pola W µ grupy SU(2) i pola B µ grupy U(1) Pola fizyczne fotonu i bozonu Z definiujemy jako: A µ = cos θ W B µ + sin θ W W µ Z µ = sin θ W B µ + cos θ W W µ gdzie θ W jest katem mieszania (katem Weinberga) Otrzymujemy zwiazek na masy bozonów M W M Z = cos θ W m γ 0 Sprzężenie z polem φ pozwala też nadać masy pozostałym czastkom teorii (fermionom) Cena : (nagroda?) dodatkowa czastka fizyczna - bozon Higgsa A.F.Żarnecki Wykład VI 15
17 Mechanizm Higgsa Ludzie na bankiecie moga też spontanicznie tworzyć zgęszczenia (bozon Higgsa) A.F.Żarnecki Wykład VI 16
18 Model Weinberga-Salama Nagrody Nobla Sheldon L.Glashow, Abdus Salam i Steven Weinberg Za stworzenie model oddziaływań elektro-słabych oraz przewidzenie istnienia bozonów W ± i Z Carlo Rubia i Simon Van der Meer Za odkrycie bozonów W ± i Z Gerardus T Hooft i Martinus J.G.Veltman Za wykazanie spójności modelu Model oddziaływań elektrosłabych +chromodynamika kwantowa (QCD): Model Standardowy SU(2) U(1) SU(3) A.F.Żarnecki Wykład VI 17
19 e + e Z Testy Modelu Standardowego Model Standardowy został bardzo dokładnie przetestowany w zderzeniach e + e w akceleratorach LEP i SLC. W przekroju czynnym na produkcję hadronów widać wyraźne maksimum odpowiadajace produkcji rzeczywistego Z A.F.Żarnecki Wykład VI 18
20 Testy Modelu Standardowego Liczba neutrin Z rozpada się na kwarki, naładowane leptony i neutrina. Stosunki rozpadów proporcjonalne sa do liczby stanów. Im więcej neutrin tym mniej rozpadów na inne czastki. mierzac całkowity przekrój czynny w rezonansie Z możemy wyznaczyć liczbę bezmasowych neutrin σ (nb) νs 3 νs 4 νs ALEPH DELPHI L3 OPAL s = E cm (GeV) N ν = ± EPS 2001 A.F.Żarnecki Wykład VI 19
21 Testy Modelu Standardowego e + e Z Z 11/07/2003 Dla s > 2M Z możliwa jest produkcja pary bozonów Z σ ZZ (pb) 1 LEP PRELIMINARY ZZTO and YFSZZ 9;: 9=< > > 9: 9 < > > 0.5 Bardzo dobra zgodność z przewidywaniami Modelu Standardowego s (GeV) A.F.Żarnecki Wykład VI 20
22 Testy Modelu Standardowego e + e W + W Wkład od trzech różnych procesów: e+ W + e + γ W + ν e + e W e Z ο W + W σ WW (pb) LEP PRELIMINARY 17/02/2005 e W Sprzężenia wynikaja z przyjętych symetrii cechowania ścisłe przewidywania modelu Doświadczalnie potwierdzone kasowanie wkładów od różnych procesów 10 0 YFSWW/RacoonWW no ZWW vertex (Gentle) only ν e exchange (Gentle) s (GeV) A.F.Żarnecki Wykład VI 21
23 Testy Modelu Standardowego Porównanie Model Standardowy ma jedynie trzy wolne parametry opisujace oddziaływania (+ masy fermionów i Higgsa). Można wybrać np. α em, G F i M Z. Model tłumaczy wyniki wszystkich dotychczasowych pomiarów oddziaływań elektrosłabych! Miara zgodności: pull X meas X SM σ X Measurement Fit O meas O fit /σ meas α (5) had (m Z ) ± m Z [GeV] ± Γ Z [GeV] ± σ 0 had [nb] ± R l ± A 0,l fb ± A l (P τ ) ± R b ± R c ± A 0,b fb ± A 0,c fb ± A b ± A c ± A l (SLD) ± sin 2 θ lept eff (Q fb ) ± m W [GeV] ± Γ W [GeV] ± m t [GeV] ± A.F.Żarnecki Wykład VI 22
24 Testy Modelu Standardowego Poprawki Wielkości fizyczne zmierzone w LEP czułe sa na poprawki wyższych rzędów. Poprawki pochodza w szczególności od procesów z wirualna wymiana bozonu W ±, kwarku t, bozonu Higgsa lub innych ciężkich czastek... σ had [nb] ALEPH DELPHI L3 OPAL Γ Z σ 0 Precyzyjne pomiary w LEP i innych eksperymentach pozwalaja wnioskować o masie bozonu Higgsa, m h. 10 measurements, error bars increased by factor 10 σ from fit QED unfolded M Z E cm [GeV] A.F.Żarnecki Wykład VI 23
25 Testy Modelu Standardowego Poprawki Nie po raz pierwszy staramy się wyznaczyć masy ciężkich czastek na podstawie analizy precyzyjnych pomiarów przy niższych energiach. Dla bozonu W ± i kwarku t wyniki bardzo dobrze zgodziły się z bezpośrednimi pomiarami m W [GeV] LEP1, SLD data LEP2 (prel.), pp data 68 CL α 80.3 m H [GeV] m t [GeV] A.F.Żarnecki Wykład VI 24
26 Testy Modelu Standardowego Masa higgsa Pojedyńcze pomiary dopuszczaja szeroki zakres wartości m t i m H. Jednak z ich łacznej analizy możemy uzyskać istotne ograniczenia CL 200 High Q 2 except m t 68 CL Γ l m t [GeV] m W prel. sin 2 θ lept eff α R b m t [GeV] 180 m t (Tevatron) m H [GeV] 160 Excluded m H [GeV] Zależność od m H logarytmiczna!... A.F.Żarnecki Wykład VI 25
27 Testy Modelu Standardowego Masa higgsa Analiza wszystkich dostępnych danych wskazuje, że masa Higgsa powinna wynosić około GeV m h = GeV lub: m h <280 GeV (95 CL) Dlaczego wciaż go nie widzimy?... χ Theory uncertainty α had = α (5) ± ± incl. low Q 2 data Z bezpośrednich poszukiwań: m h >114.4 GeV (95 CL) wszystkie dane LEP: ALEPH + DELPHI + L3 + OPAL 1 0 Excluded m H [GeV] A.F.Żarnecki Wykład VI 26
28 Poszukiwanie Higgsa Kanały rozpadu Czastka Higgsa zajmuje bardzo szczególne miejsce w teorii. Ma też szczególne własności... Sprzężenie Higgsa do czastek sa proporcjonalne do masy rozpada się najchętniej na najcięższe dostępne stany... SM Higgs Branching Ratio bb + τ τ - gg cc + W W - Dla m h <135 GeV dominuje rozpad w pary b b... W LEP szukano przypadków produkcji Higgsa: 10-3 γγ (GeV) M H e + e h Z b b X A.F.Żarnecki Wykład VI 27
29 Kandydat na Higgsa... A.F.Żarnecki Wykład VI 28
30 candidate for e + e Hνν 2 jets + missing energy Jet Jet 1 L3 Jet 1 Jet 2 Jet 2 A.F.Żarnecki Wykład VI 29
31 Poszukiwanie Higgsa Rozkład masy Events / 3 GeV/c łagodna selekcja s = GeV LEP loose background Events / 3 GeV/c ostra selekcja s = GeV LEP tight background 15 hz Signal 4 hz Signal 10 5 (m h =115 GeV) all > 109 GeV cnd= bgd= sgl= (m h =115 GeV) all > 109 GeV cnd= 22 4 bgd= sgl= Reconstructed Mass m H [GeV/c 2 ] Reconstructed Mass m H [GeV/c 2 ] W obszarze m h 115 GeV widać niewielki nadmiar przypadków, który może pochodzić od produkcji Higgsa Niestety, jest to efekt na poziomie 2σ LEP wyłaczono zanim zdołał wyjaśnić ten efekt... A.F.Żarnecki Wykład VI 30
32 Poszukiwanie Higgsa Poszukiwania bozonu Higgsa a następnie pomiar jego parametrów będzie jednym z głównych tematów badań w przyszłych akceleratorach. LHC W zderzeniach pp tło hadronowe jest bardzo duże. Najbardziej obiecuj acy jest kanał: pp H Z Z l + l l + l gdyż naładowane leptony (e ± i µ ± ) można łatwo zidentyfikować Jeśli Higgs ma rzeczywiście około 115 GeV zobaczymy go już wkrótce w Tewatronie! CMS Warszawa A.F.Żarnecki Wykład VI 31
33 Eksperyment CMS przy LHC Symulacja działania detektora CMS dla przypadku H ZZ µ + µ µ + µ A.F.Żarnecki Wykład VI 32
34 Poszukiwanie Higgsa TESLA e + e Proces: e + e Z h Number of Events / 1.5 GeV Recoil Mass [GeV] Data Z H µµ X m H = 120 GeV Wybór przypadków Z µ + µ rekonstrukcja niezależna od rozpadu h Number of events per 2.5 GeV bin TESLA Photon Collider Proces: γγ h, σ/σ = 2.1 h b b Higgs signal M h = 120 GeV Background: bb (g) cc (g) uu,dd,ss τ + τ resolved Total L γγ = 410 fb W corr [GeV] Pomiar sprzężenia hγγ bardzo czułego na nowa fizykę TESLA Warszawa A.F.Żarnecki Wykład VI 33
35 Poszukiwanie Higgsa W rozszerzeniach Modelu Standardowego bozon Higgsa może być cięższy... TESLA e + e TESLA Photon Collider Proces: e + e Z h, h ZZ, W W Proces: γγ h, h ZZ Events 60 Simulated data Signal Combinatoric Background TESLA 500 GeV L = 500 fb -1 m H = 200 GeV events 300 simulation m h =300 GeV Parameterization: m h =300 GeV NZK. 200 no Higgs Di-boson mass (GeV) M llqq [GeV] TESLA Warszawa A.F.Żarnecki Wykład VI 34
Model Standardowy. Elementy fizyki czastek elementarnych. Wykład VI
 Model Standardowy Wykład VI elementy teorii kwantowej symetrie a prawa zachowania spontaniczne łamanie symetrii model Weinberga-Salama testy Modelu Standardowego poszukiwanie bozonu Higgsa Elementy fizyki
Model Standardowy Wykład VI elementy teorii kwantowej symetrie a prawa zachowania spontaniczne łamanie symetrii model Weinberga-Salama testy Modelu Standardowego poszukiwanie bozonu Higgsa Elementy fizyki
Na tropach czastki Higgsa
 Na tropach czastki Higgsa Wykład inauguracyjny 2004/2005 A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Na tropach czastki Higgsa Wykład inauguracyjny 2004/2005
Na tropach czastki Higgsa Wykład inauguracyjny 2004/2005 A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Na tropach czastki Higgsa Wykład inauguracyjny 2004/2005
Skad się bierze masa Festiwal Nauki, Wydział Fizyki U.W. 25 września 2005 A.F.Żarnecki p.1/39
 Skad się bierze masa Festiwal Nauki Wydział Fizyki U.W. 25 września 2005 dr hab. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Skad się bierze masa Festiwal Nauki,
Skad się bierze masa Festiwal Nauki Wydział Fizyki U.W. 25 września 2005 dr hab. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Skad się bierze masa Festiwal Nauki,
Poszukiwany: bozon Higgsa
 Poszukiwany: bozon Higgsa Higgs widoczny w świetle kolajdera liniowego Fizyka Czastek i Oddziaływań Fundamentalnych: TESLA & ZEUS Poszukiwane: czastki sypersymetryczne (SUSY) Fizyka Czastek i Oddziaływań
Poszukiwany: bozon Higgsa Higgs widoczny w świetle kolajdera liniowego Fizyka Czastek i Oddziaływań Fundamentalnych: TESLA & ZEUS Poszukiwane: czastki sypersymetryczne (SUSY) Fizyka Czastek i Oddziaływań
Bozon Higgsa oraz SUSY
 Bozon Higgsa oraz SUSY Bozon Higgsa Poszukiwania bozonu Higgsa w LEP i Tevatronie - otrzymane ograniczenia na masę H Plany poszukiwań w LHC Supersymetria (SUSY) Zagadkowe wyniki CDF Masy cząstek cząstki
Bozon Higgsa oraz SUSY Bozon Higgsa Poszukiwania bozonu Higgsa w LEP i Tevatronie - otrzymane ograniczenia na masę H Plany poszukiwań w LHC Supersymetria (SUSY) Zagadkowe wyniki CDF Masy cząstek cząstki
Oddziaływania elektrosłabe
 Oddziaływania elektrosłabe X ODDZIAŁYWANIA ELEKTROSŁABE Fizyka elektrosłaba na LEPie Liczba pokoleń. Bardzo precyzyjne pomiary. Obserwacja przypadków. Uniwersalność leptonów. Mieszanie kwarków. Macierz
Oddziaływania elektrosłabe X ODDZIAŁYWANIA ELEKTROSŁABE Fizyka elektrosłaba na LEPie Liczba pokoleń. Bardzo precyzyjne pomiary. Obserwacja przypadków. Uniwersalność leptonów. Mieszanie kwarków. Macierz
Zasada najmniejszego działania
 Zasada najmniejszego działania S = T dtl(x, ẋ) gdzie L(x, ẋ) jest lagrangianem. Dokonajmy przesuniecia x = x + y, ẋ = ẋ + ẏ, gdzie y(0) = y(t ) = 0. Wtedy T T S = dt L(x, ẋ ) = dt L(x + y, ẋ = ẋ + ẏ) 0
Zasada najmniejszego działania S = T dtl(x, ẋ) gdzie L(x, ẋ) jest lagrangianem. Dokonajmy przesuniecia x = x + y, ẋ = ẋ + ẏ, gdzie y(0) = y(t ) = 0. Wtedy T T S = dt L(x, ẋ ) = dt L(x + y, ẋ = ẋ + ẏ) 0
Unifikacja elektro-słaba
 Unifikacja elektro-słaba ee + Anihilacja Oddziaływania NC (z wymianą bozonu ) - zachowanie zapachów Potrzeba unifikacji Warunki unifikacji elektro-słabej Rezonans Liczenie zapachów neutrin (oraz generacji)
Unifikacja elektro-słaba ee + Anihilacja Oddziaływania NC (z wymianą bozonu ) - zachowanie zapachów Potrzeba unifikacji Warunki unifikacji elektro-słabej Rezonans Liczenie zapachów neutrin (oraz generacji)
Elementy Modelu Standardowego
 Elementy Modelu Standardowego Funkcja Lagrange a Model Standardowy, który opisuje wszystkie oddziaływania (poza grawitacyjnym) pomiędzy cząstkami elementarnymi, opiera się na kwantowej teorii pola. Podstawowym
Elementy Modelu Standardowego Funkcja Lagrange a Model Standardowy, który opisuje wszystkie oddziaływania (poza grawitacyjnym) pomiędzy cząstkami elementarnymi, opiera się na kwantowej teorii pola. Podstawowym
LHC i po co nam On. Piotr Traczyk CERN
 LHC i po co nam On Piotr Traczyk CERN LHC: po co nam On Piotr Traczyk CERN Detektory przy LHC Planowane są 4(+2) eksperymenty na LHC ATLAS ALICE CMS LHCb 5 Program fizyczny LHC 6 Program fizyczny LHC
LHC i po co nam On Piotr Traczyk CERN LHC: po co nam On Piotr Traczyk CERN Detektory przy LHC Planowane są 4(+2) eksperymenty na LHC ATLAS ALICE CMS LHCb 5 Program fizyczny LHC 6 Program fizyczny LHC
Wielka Unifikacja. Elementy fizyki czastek elementarnych. Wykład XI. Co to jest ładunek?... Biegnaca stała sprzężenia i renormalizacja w QED Pomiar
 Wielka Unifikacja Wykład XI Co to jest ładunek?... Elementy fizyki czastek elementarnych Biegnaca stała sprzężenia i renormalizacja w QED Pomiar Biegnaca stała sprzężenia QCD Unifikacja SU(5) Leptokwarki
Wielka Unifikacja Wykład XI Co to jest ładunek?... Elementy fizyki czastek elementarnych Biegnaca stała sprzężenia i renormalizacja w QED Pomiar Biegnaca stała sprzężenia QCD Unifikacja SU(5) Leptokwarki
Zderzenia relatywistyczne
 Zderzenia relatywistyczne Fizyka I (B+C) Wykład XIX: Zderzenia nieelastyczne Energia progowa Rozpady czastek Neutrina Zderzenia relatywistyczne Zderzenia elastyczne 2 2 Czastki rozproszone takie same jak
Zderzenia relatywistyczne Fizyka I (B+C) Wykład XIX: Zderzenia nieelastyczne Energia progowa Rozpady czastek Neutrina Zderzenia relatywistyczne Zderzenia elastyczne 2 2 Czastki rozproszone takie same jak
Bozon Higgsa prawda czy kolejny fakt prasowy?
 Bozon Higgsa prawda czy kolejny fakt prasowy? Sławomir Stachniewicz, IF PK 1. Standardowy model cząstek elementarnych Model Standardowy to obecnie obowiązująca teoria cząstek elementarnych, które są składnikami
Bozon Higgsa prawda czy kolejny fakt prasowy? Sławomir Stachniewicz, IF PK 1. Standardowy model cząstek elementarnych Model Standardowy to obecnie obowiązująca teoria cząstek elementarnych, które są składnikami
Zderzenia relatywistyczne
 Zderzenia relatywistyczne Fizyka I (B+C) Wykład XVIII: Zderzenia nieelastyczne Energia progowa Rozpady czastek Neutrina Zderzenia relatywistyczne Zderzenia nieelastyczne Zderzenia elastyczne - czastki
Zderzenia relatywistyczne Fizyka I (B+C) Wykład XVIII: Zderzenia nieelastyczne Energia progowa Rozpady czastek Neutrina Zderzenia relatywistyczne Zderzenia nieelastyczne Zderzenia elastyczne - czastki
LHC: program fizyczny
 LHC: program fizyczny Piotr Traczyk CERN Detektory przy LHC Planowane są 4(+2) eksperymenty na LHC ATLAS ALICE CMS LHCb 2 Program fizyczny LHC Model Standardowy i Cząstka Higgsa Poza Model Standardowy:
LHC: program fizyczny Piotr Traczyk CERN Detektory przy LHC Planowane są 4(+2) eksperymenty na LHC ATLAS ALICE CMS LHCb 2 Program fizyczny LHC Model Standardowy i Cząstka Higgsa Poza Model Standardowy:
WYKŁAD 8. Maria Krawczyk, Wydział Fizyki UW. Oddziaływania słabe
 Wszechświat cząstek elementarnych WYKŁAD 8 Maria Krawczyk, Wydział Fizyki UW Oddziaływania słabe Cztery podstawowe siłyprzypomnienie Oddziaływanie grawitacyjne Działa między wszystkimi cząstkami, jest
Wszechświat cząstek elementarnych WYKŁAD 8 Maria Krawczyk, Wydział Fizyki UW Oddziaływania słabe Cztery podstawowe siłyprzypomnienie Oddziaływanie grawitacyjne Działa między wszystkimi cząstkami, jest
Jak to działa: poszukiwanie bozonu Higgsa w eksperymencie CMS. Tomasz Früboes
 Plan wystąpienia: 1.Wprowadzenie 2.Jak szukamy Higgsa na przykładzie kanału H ZZ 4l? 3.Poszukiwanie bozonu Higgsa w kanale ττ μτjet 4.Właściwości nowej cząstki Częste skróty: LHC Large Hadron Collider
Plan wystąpienia: 1.Wprowadzenie 2.Jak szukamy Higgsa na przykładzie kanału H ZZ 4l? 3.Poszukiwanie bozonu Higgsa w kanale ττ μτjet 4.Właściwości nowej cząstki Częste skróty: LHC Large Hadron Collider
Fizyka cząstek elementarnych i oddziaływań podstawowych
 Fizyka cząstek elementarnych i oddziaływań podstawowych Wykład 1 Wstęp Jerzy Kraśkiewicz Krótka historia Odkrycie promieniotwórczości 1895 Roentgen odkrycie promieni X 1896 Becquerel promieniotwórczość
Fizyka cząstek elementarnych i oddziaływań podstawowych Wykład 1 Wstęp Jerzy Kraśkiewicz Krótka historia Odkrycie promieniotwórczości 1895 Roentgen odkrycie promieni X 1896 Becquerel promieniotwórczość
Wszechświat czastek elementarnych
 Wszechświat czastek elementarnych Wykład 9: Współczesne eksperymenty prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład
Wszechświat czastek elementarnych Wykład 9: Współczesne eksperymenty prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład
Cząstki i siły. Piotr Traczyk. IPJ Warszawa
 Cząstki i siły tworzące nasz wszechświat Piotr Traczyk IPJ Warszawa Plan Wstęp Klasyfikacja cząstek elementarnych Model Standardowy 2 Wstęp 3 Jednostki, konwencje Prędkość światła c ~ 3 x 10 8 m/s Stała
Cząstki i siły tworzące nasz wszechświat Piotr Traczyk IPJ Warszawa Plan Wstęp Klasyfikacja cząstek elementarnych Model Standardowy 2 Wstęp 3 Jednostki, konwencje Prędkość światła c ~ 3 x 10 8 m/s Stała
Maria Krawczyk, Wydział Fizyki UW. Oddziaływania słabe 4.IV.2012
 Wszechświat cząstek elementarnych WYKŁAD 8sem.letni.2011-12 Maria Krawczyk, Wydział Fizyki UW Oddziaływania słabe Cztery podstawowe siły Oddziaływanie grawitacyjne Działa między wszystkimi cząstkami, jest
Wszechświat cząstek elementarnych WYKŁAD 8sem.letni.2011-12 Maria Krawczyk, Wydział Fizyki UW Oddziaływania słabe Cztery podstawowe siły Oddziaływanie grawitacyjne Działa między wszystkimi cząstkami, jest
Wszechświat Cząstek Elementarnych dla Humanistów Diagramy Faynmana
 Wszechświat Cząstek Elementarnych dla Humanistów Diagramy Faynmana Aleksander Filip Żarnecki Wykład ogólnouniwersytecki Wydział Fizyki Uniwersytetu Warszawskiego 21 listopada 2017 A.F.Żarnecki WCE Wykład
Wszechświat Cząstek Elementarnych dla Humanistów Diagramy Faynmana Aleksander Filip Żarnecki Wykład ogólnouniwersytecki Wydział Fizyki Uniwersytetu Warszawskiego 21 listopada 2017 A.F.Żarnecki WCE Wykład
Wstęp do Modelu Standardowego
 Wstęp do Modelu Standardowego Plan Wstęp do QFT (tym razem trochę równań ) Funkcje falowe a pola Lagranżjan revisited Kilka przykładów Podsumowanie Tomasz Szumlak AGH-UST Wydział Fizyki i Informatyki Stosowanej
Wstęp do Modelu Standardowego Plan Wstęp do QFT (tym razem trochę równań ) Funkcje falowe a pola Lagranżjan revisited Kilka przykładów Podsumowanie Tomasz Szumlak AGH-UST Wydział Fizyki i Informatyki Stosowanej
Fizyka cząstek elementarnych. Tadeusz Lesiak
 Fizyka cząstek elementarnych Tadeusz Lesiak 1 WYKŁAD IX Oddziaływania słabe T.Lesiak Fizyka cząstek elementarnych 2 Rola oddziaływań słabych w przyrodzie Oddziaływania słabe są odpowiedzialne (m.in.) za:
Fizyka cząstek elementarnych Tadeusz Lesiak 1 WYKŁAD IX Oddziaływania słabe T.Lesiak Fizyka cząstek elementarnych 2 Rola oddziaływań słabych w przyrodzie Oddziaływania słabe są odpowiedzialne (m.in.) za:
czastki elementarne Czastki elementarne
 czastki elementarne "zwykła" materia, w warunkach które znamy na Ziemi, które panuja w ekstremalnych warunkach na Słońcu: protony, neutrony, elektrony. mówiliśmy również o neutrinach - czastki, które nie
czastki elementarne "zwykła" materia, w warunkach które znamy na Ziemi, które panuja w ekstremalnych warunkach na Słońcu: protony, neutrony, elektrony. mówiliśmy również o neutrinach - czastki, które nie
Wszechświat Cząstek Elementarnych dla Humanistów Diagramy Faynmana
 Wszechświat Cząstek Elementarnych dla Humanistów Aleksander Filip Żarnecki Wykład ogólnouniwersytecki 27 listopada 2018 A.F.Żarnecki WCE Wykład 8 27 listopada 2018 1 / 28 1 Budowa materii (przypomnienie)
Wszechświat Cząstek Elementarnych dla Humanistów Aleksander Filip Żarnecki Wykład ogólnouniwersytecki 27 listopada 2018 A.F.Żarnecki WCE Wykład 8 27 listopada 2018 1 / 28 1 Budowa materii (przypomnienie)
Fizyka na LHC - Higgs
 Fizyka na LHC - Higgs XI Program fizyczny LHC. Brakujący element. Pole Higgsa. Poszukiwanie Higgsa na LEP. Produkcja Higgsa na LHC. ATLAS. Wyniki doświadczalne Teraz na LHC 1 FIZYKA NA LHC Unifikacja oddziaływań
Fizyka na LHC - Higgs XI Program fizyczny LHC. Brakujący element. Pole Higgsa. Poszukiwanie Higgsa na LEP. Produkcja Higgsa na LHC. ATLAS. Wyniki doświadczalne Teraz na LHC 1 FIZYKA NA LHC Unifikacja oddziaływań
Wstęp do chromodynamiki kwantowej
 Wstęp do chromodynamiki kwantowej Wykład 1 przez 2 tygodnie wykład następnie wykład/ćwiczenia/konsultacje/lab proszę pamiętać o konieczności posiadania kąta gdy będziemy korzystać z labolatorium (Mathematica
Wstęp do chromodynamiki kwantowej Wykład 1 przez 2 tygodnie wykład następnie wykład/ćwiczenia/konsultacje/lab proszę pamiętać o konieczności posiadania kąta gdy będziemy korzystać z labolatorium (Mathematica
Supersymetria. Elementy fizyki czastek elementarnych. Wykład XII
 Supersymetria Wykład XII Elementy fizyki czastek elementarnych Problemy Modelu Standardowego Supersymetria Widmo czastek Przewidywania Obecne wyniki Przyszłe poszukiwania Model Standardowy Przypomnienie
Supersymetria Wykład XII Elementy fizyki czastek elementarnych Problemy Modelu Standardowego Supersymetria Widmo czastek Przewidywania Obecne wyniki Przyszłe poszukiwania Model Standardowy Przypomnienie
WYKŁAD 8. Wszechświat cząstek elementarnych dla przyrodników
 Wszechświat cząstek elementarnych dla przyrodników WYKŁAD 8 1 Maria Krawczyk, Wydział Fizyki UW 2.12. 2009 Współczesne eksperymenty-wprowadzenie Detektory Akceleratory Zderzacze LHC Mapa drogowa Tevatron-
Wszechświat cząstek elementarnych dla przyrodników WYKŁAD 8 1 Maria Krawczyk, Wydział Fizyki UW 2.12. 2009 Współczesne eksperymenty-wprowadzenie Detektory Akceleratory Zderzacze LHC Mapa drogowa Tevatron-
Salam,Weinberg (W/Z) t Hooft, Veltman 1999 (renomalizowalność( renomalizowalność)
 Teoria cząstek elementarnych 23.IV.08 1948 nowa faza mechaniki kwantowej precyzyjne pomiary wymagały precyzyjnych obliczeń metoda Feynmana Diagramy Feynmana i reguły Feynmana dziś uniwersalne narzędzie
Teoria cząstek elementarnych 23.IV.08 1948 nowa faza mechaniki kwantowej precyzyjne pomiary wymagały precyzyjnych obliczeń metoda Feynmana Diagramy Feynmana i reguły Feynmana dziś uniwersalne narzędzie
Fizyka cząstek 5: Co dalej? Brakujące wątki Perspektywy Astrocząstki
 Fizyka cząstek 5: Co dalej? Brakujące wątki Perspektywy Astrocząstki Brakujące ogniwo Przypomnienie: brakujący bozon Higgsa! Oczekiwania: nietrwały, sprzężenie najsilniejsze do najcięższych cząstek. Ważny
Fizyka cząstek 5: Co dalej? Brakujące wątki Perspektywy Astrocząstki Brakujące ogniwo Przypomnienie: brakujący bozon Higgsa! Oczekiwania: nietrwały, sprzężenie najsilniejsze do najcięższych cząstek. Ważny
Czego brakuje w Modelu Standardowym
 Czego brakuje w Modelu Standardowym What is missing in the Standard Model concepts and ideas Instytut Problemów Jądrowych im. A. Sołtana w Świerku 1 Plan Równania Maxwella droga do QED Symetria cechowania
Czego brakuje w Modelu Standardowym What is missing in the Standard Model concepts and ideas Instytut Problemów Jądrowych im. A. Sołtana w Świerku 1 Plan Równania Maxwella droga do QED Symetria cechowania
Boska cząstka odkryta?
 FOTON 118, Jesień 2012 27 Boska cząstka odkryta? Krzysztof Fiałkowski Instytut Fizyki UJ 4 lipca 2012 roku w wielkiej sali seminaryjnej CERNu w Genewie odbyło się nadzwyczajne seminarium. Organizatorzy
FOTON 118, Jesień 2012 27 Boska cząstka odkryta? Krzysztof Fiałkowski Instytut Fizyki UJ 4 lipca 2012 roku w wielkiej sali seminaryjnej CERNu w Genewie odbyło się nadzwyczajne seminarium. Organizatorzy
Obserwacja Nowej Cząstki o Masie 125 GeV
 Obserwacja Nowej Cząstki o Masie 125 GeV Eksperyment CMS, CERN 4 lipca 2012 Streszczenie Na wspólnym seminarium w CERN i na konferencji ICHEP 2012 [1] odbywającej się w Melbourne, naukowcy pracujący przy
Obserwacja Nowej Cząstki o Masie 125 GeV Eksperyment CMS, CERN 4 lipca 2012 Streszczenie Na wspólnym seminarium w CERN i na konferencji ICHEP 2012 [1] odbywającej się w Melbourne, naukowcy pracujący przy
Symetrie. D. Kiełczewska, wykład 5 1
 Symetrie Symetrie a prawa zachowania Spin Parzystość Spin izotopowy Multiplety hadronowe Niezachowanie parzystości w oddz. słabych Sprzężenie ładunkowe C Symetria CP Zależność spinowa oddziaływań słabych
Symetrie Symetrie a prawa zachowania Spin Parzystość Spin izotopowy Multiplety hadronowe Niezachowanie parzystości w oddz. słabych Sprzężenie ładunkowe C Symetria CP Zależność spinowa oddziaływań słabych
WYKŁAD 6. Oddziaływania kolorowe cd. Oddziaływania słabe. Wszechświat cząstek elementarnych dla przyrodników
 Wszechświat cząstek elementarnych dla przyrodników WYKŁAD 6 Maria Krawczyk, Wydział Fizyki UW 11.XI.2009 Oddziaływania kolorowe cd. Oddziaływania słabe Cztery podstawowe oddziaływania Oddziaływanie grawitacyjne
Wszechświat cząstek elementarnych dla przyrodników WYKŁAD 6 Maria Krawczyk, Wydział Fizyki UW 11.XI.2009 Oddziaływania kolorowe cd. Oddziaływania słabe Cztery podstawowe oddziaływania Oddziaływanie grawitacyjne
Symetrie. D. Kiełczewska, wykład 5 1
 Symetrie Symetrie a prawa zachowania Spin Parzystość Spin izotopowy Multiplety hadronowe Niezachowanie parzystości w oddz. słabych Sprzężenie ładunkowe C Symetria CP Zależność spinowa oddziaływań słabych
Symetrie Symetrie a prawa zachowania Spin Parzystość Spin izotopowy Multiplety hadronowe Niezachowanie parzystości w oddz. słabych Sprzężenie ładunkowe C Symetria CP Zależność spinowa oddziaływań słabych
Supersymetria. Elementy fizyki czastek elementarnych. Wykład XII. Założenia. Widmo czastek Przewidywania Obecne wyniki Przyszłe poszukiwania
 Supersymetria Wykład XII Założenia Elementy fizyki czastek elementarnych Widmo czastek Przewidywania Obecne wyniki Przyszłe poszukiwania Mały Higgs Problem hierarchi Czy Model Standardowy może pozostać
Supersymetria Wykład XII Założenia Elementy fizyki czastek elementarnych Widmo czastek Przewidywania Obecne wyniki Przyszłe poszukiwania Mały Higgs Problem hierarchi Czy Model Standardowy może pozostać
Oddziaływania fundamentalne
 Oddziaływania fundamentalne Silne: krótkozasięgowe (10-15 m). Siła rośnie ze wzrostem odległości. Znaczna siła oddziaływania. Elektromagnetyczne: nieskończony zasięg, siła maleje z kwadratem odległości.
Oddziaływania fundamentalne Silne: krótkozasięgowe (10-15 m). Siła rośnie ze wzrostem odległości. Znaczna siła oddziaływania. Elektromagnetyczne: nieskończony zasięg, siła maleje z kwadratem odległości.
Struktura protonu. Elementy fizyki czastek elementarnych. Wykład IV
 Struktura protonu Wykład IV akcelerator HERA Elementy fizyki czastek elementarnych rekonstrukcja przypadków NC DIS wyznaczanie funkcji struktury równania ewolucji QCD struktura fotonu % & lub NC DIS Deep
Struktura protonu Wykład IV akcelerator HERA Elementy fizyki czastek elementarnych rekonstrukcja przypadków NC DIS wyznaczanie funkcji struktury równania ewolucji QCD struktura fotonu % & lub NC DIS Deep
WYKŁAD Wszechświat cząstek elementarnych. 24.III.2010 Maria Krawczyk, Wydział Fizyki UW. Masa W
 Wszechświat cząstek elementarnych WYKŁAD 6 24 24.III.2010 Maria Krawczyk, Wydział Fizyki UW Oddziaływania kolorowe i biegnąca stała sprzężenia α s Oddziaływania słabe Masa W Stałe sprzężenia Siła elementarnego
Wszechświat cząstek elementarnych WYKŁAD 6 24 24.III.2010 Maria Krawczyk, Wydział Fizyki UW Oddziaływania kolorowe i biegnąca stała sprzężenia α s Oddziaływania słabe Masa W Stałe sprzężenia Siła elementarnego
Compact Muon Solenoid
 Compact Muon Solenoid (po co i jak) Piotr Traczyk CERN Compact ATLAS CMS 2 Muon Detektor CMS był projektowany pod kątem optymalnej detekcji mionów Miony stanowią stosunkowo czysty sygnał Pojawiają się
Compact Muon Solenoid (po co i jak) Piotr Traczyk CERN Compact ATLAS CMS 2 Muon Detektor CMS był projektowany pod kątem optymalnej detekcji mionów Miony stanowią stosunkowo czysty sygnał Pojawiają się
Oddziaływania grawitacyjne. Efekt Dopplera. Photon Collider. Efekt Comptona. Odkrycie fotonu. Wykład XIX: Fizyka I (B+C) Foton
 Wykład XIX: Odkrycie fotonu Efekt Comptona Photon Collider Efekt Dopplera Oddziaływania grawitacyjne Foton Fizyka I (B+C) A.F.Żarnecki Wykład XIX Doświadczenia wskazały, że energia uwalnianych elektronów
Wykład XIX: Odkrycie fotonu Efekt Comptona Photon Collider Efekt Dopplera Oddziaływania grawitacyjne Foton Fizyka I (B+C) A.F.Żarnecki Wykład XIX Doświadczenia wskazały, że energia uwalnianych elektronów
M W M Z correlation. πα 1 M G F 2 = 2M 2 W 2 W
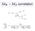 M W M Z correlation µ W ν µ e ν e G F 2 = 2M 2 W πα ( 1 M 2 W /MZ) 2 with loop contributions G F 2 = 2M 2 W (1+ r) πα ( 1 M 2 W /MZ) 2 1-loop examples ØÓÔ ÕÙ Ö r : quantum correction r = r(m t,m H ) Ï
M W M Z correlation µ W ν µ e ν e G F 2 = 2M 2 W πα ( 1 M 2 W /MZ) 2 with loop contributions G F 2 = 2M 2 W (1+ r) πα ( 1 M 2 W /MZ) 2 1-loop examples ØÓÔ ÕÙ Ö r : quantum correction r = r(m t,m H ) Ï
Perspektywy fizyki czastek elementarnych
 Perspektywy fizyki czastek elementarnych Wykład XIII Nowe projekty akceleratorowe: CLIC ( VLHC ( Photon Collider zderzenia ) Elementy fizyki czastek elementarnych ) fabryki neutrin Astro-cz astki?!...
Perspektywy fizyki czastek elementarnych Wykład XIII Nowe projekty akceleratorowe: CLIC ( VLHC ( Photon Collider zderzenia ) Elementy fizyki czastek elementarnych ) fabryki neutrin Astro-cz astki?!...
Wszechświat czastek elementarnych
 Wszechświat czastek elementarnych Wykład 8: Współczesne eksperymenty prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład
Wszechświat czastek elementarnych Wykład 8: Współczesne eksperymenty prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład
Struktura protonu. Elementy fizyki czastek elementarnych. Wykład V. spin protonu struktura fotonu
 Struktura protonu Wykład V równania ewolucji QCD spin protonu struktura fotonu Elementy fizyki czastek elementarnych Funkcja struktury Różniczkowy przekrój czynny na NC DIS elektron proton: d 2 σ dx dq
Struktura protonu Wykład V równania ewolucji QCD spin protonu struktura fotonu Elementy fizyki czastek elementarnych Funkcja struktury Różniczkowy przekrój czynny na NC DIS elektron proton: d 2 σ dx dq
Cząstki elementarne wprowadzenie. Krzysztof Turzyński Wydział Fizyki Uniwersytet Warszawski
 Cząstki elementarne wprowadzenie Krzysztof Turzyński Wydział Fizyki Uniwersytet Warszawski Historia badania struktury materii XVII w.: ruch gwiazd i planet, zasady dynamiki, teoria grawitacji, masa jako
Cząstki elementarne wprowadzenie Krzysztof Turzyński Wydział Fizyki Uniwersytet Warszawski Historia badania struktury materii XVII w.: ruch gwiazd i planet, zasady dynamiki, teoria grawitacji, masa jako
Wstęp do Modelu Standardowego
 Wstęp do Modelu Standardowego Dynamika oddziaływań cząstek Elektrodynamika kwantowa (QED) Chromodynamika kwantowa (QCD) Oddziaływania słabe Tomasz Szumlak AGH-UST Wydział Fizyki i Informatyki Stosowanej
Wstęp do Modelu Standardowego Dynamika oddziaływań cząstek Elektrodynamika kwantowa (QED) Chromodynamika kwantowa (QCD) Oddziaływania słabe Tomasz Szumlak AGH-UST Wydział Fizyki i Informatyki Stosowanej
Oddziaływania silne. Również na tym wykładzie Wielkie unifikacje. Mówiliśmy na poprzednich wykładach o: rezonansach hadronowych multipletach
 Oddziaływania silne Mówiliśmy na poprzednich wykładach o: rezonansach hadronowych multipletach Tu powiemy więcej o: Kolorze QCD czyli chromodynamice kwantowej Symetrii SU(3) kolor Uwięzieniu kwarków i
Oddziaływania silne Mówiliśmy na poprzednich wykładach o: rezonansach hadronowych multipletach Tu powiemy więcej o: Kolorze QCD czyli chromodynamice kwantowej Symetrii SU(3) kolor Uwięzieniu kwarków i
Bozon Higgsa & SUSY & DM
 Bozon Higgsa & SUSY & DM Niezmienniczość cechowania Bozon Higgsa Poszukiwanie bozonu Higgsa w LEP i LHC Supersymetria Ciemna materia Unifikacja elektrosłaba (slajd z wykładu 6) e + g w W + ν ν e µ µ +
Bozon Higgsa & SUSY & DM Niezmienniczość cechowania Bozon Higgsa Poszukiwanie bozonu Higgsa w LEP i LHC Supersymetria Ciemna materia Unifikacja elektrosłaba (slajd z wykładu 6) e + g w W + ν ν e µ µ +
Struktura porotonu cd.
 Struktura porotonu cd. Funkcje struktury Łamanie skalowania QCD Spinowa struktura protonu Ewa Rondio, 2 kwietnia 2007 wykład 7 informacja Termin egzaminu 21 czerwca, godz.9.00 Wiemy już jak wygląda nukleon???
Struktura porotonu cd. Funkcje struktury Łamanie skalowania QCD Spinowa struktura protonu Ewa Rondio, 2 kwietnia 2007 wykład 7 informacja Termin egzaminu 21 czerwca, godz.9.00 Wiemy już jak wygląda nukleon???
Oddziaływania słabe i elektrosłabe
 Oddziaływania słabe i elektrosłabe IX ODDZIAŁYWANIA SŁABE Kiedy są widoczne. Jak bardzo są słabe. Teoria Fermiego Ciężkie bozony pośredniczące. Łamanie parzystości P. ODDZIAŁYWANIA ELEKTROSŁABE Słabe a
Oddziaływania słabe i elektrosłabe IX ODDZIAŁYWANIA SŁABE Kiedy są widoczne. Jak bardzo są słabe. Teoria Fermiego Ciężkie bozony pośredniczące. Łamanie parzystości P. ODDZIAŁYWANIA ELEKTROSŁABE Słabe a
r. akad. 2008/2009 V. Precyzyjne testy Modelu Standardowego w LEP, TeVatronie i LHC
 V. Precyzyjne testy Modelu Standardowego w LEP, TeVatronie i LHC 1 V.1 WYNIKI LEP 2 e + e - Z 0 Calkowity przekroj czynny 3 4 r. akad. 2008/2009 s Q N 3 4 s M s N Q I M 12 s ) M (s s s 2 f C 2 Z C f f
V. Precyzyjne testy Modelu Standardowego w LEP, TeVatronie i LHC 1 V.1 WYNIKI LEP 2 e + e - Z 0 Calkowity przekroj czynny 3 4 r. akad. 2008/2009 s Q N 3 4 s M s N Q I M 12 s ) M (s s s 2 f C 2 Z C f f
Wielka Unifikacja. Elementy fizyki czastek elementarnych. Wykład XI. Co to jest ładunek?...
 Wielka Unifikacja Wykład XI Co to jest ładunek?... Elementy fizyki czastek elementarnych Biegnaca stała sprzężenia i renormalizacja w QED Asymptotyczna swoboda QCD Unifikacja SU(5) Problemy Modelu Standardowego
Wielka Unifikacja Wykład XI Co to jest ładunek?... Elementy fizyki czastek elementarnych Biegnaca stała sprzężenia i renormalizacja w QED Asymptotyczna swoboda QCD Unifikacja SU(5) Problemy Modelu Standardowego
Wszechświat czastek elementarnych
 Wszechświat czastek elementarnych Wykład 7: Współczesne eksperymenty prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład
Wszechświat czastek elementarnych Wykład 7: Współczesne eksperymenty prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład
1. Wcześniejsze eksperymenty 2. Podstawowe pojęcia 3. Przypomnienie budowy detektora ATLAS 4. Rozpady bozonów W i Z 5. Tło 6. Detekcja sygnału 7.
 Weronika Biela 1. Wcześniejsze eksperymenty 2. Podstawowe pojęcia 3. Przypomnienie budowy detektora ATLAS 4. Rozpady bozonów W i Z 5. Tło 6. Detekcja sygnału 7. Obliczenie przekroju czynnego 8. Porównanie
Weronika Biela 1. Wcześniejsze eksperymenty 2. Podstawowe pojęcia 3. Przypomnienie budowy detektora ATLAS 4. Rozpady bozonów W i Z 5. Tło 6. Detekcja sygnału 7. Obliczenie przekroju czynnego 8. Porównanie
Dziwny jest ten świat: czastki elementarne
 Dziwny jest ten świat: czastki elementarne Wykłady z fizyki doświadczalnej Wydział Fizyki U.W. 17 grudnia 2005 prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej
Dziwny jest ten świat: czastki elementarne Wykłady z fizyki doświadczalnej Wydział Fizyki U.W. 17 grudnia 2005 prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej
Wielka Unifikacja. Elementy fizyki czastek elementarnych. Wykład IX. Co to jest ładunek?...
 Wielka Unifikacja Wykład IX Co to jest ładunek?... Elementy fizyki czastek elementarnych Biegnaca stała sprzężenia i renormalizacja w QED Asymptotyczna swoboda QCD Unifikacja SU(5) QED Ładunek elektryczny
Wielka Unifikacja Wykład IX Co to jest ładunek?... Elementy fizyki czastek elementarnych Biegnaca stała sprzężenia i renormalizacja w QED Asymptotyczna swoboda QCD Unifikacja SU(5) QED Ładunek elektryczny
Ostatnie uzupełnienia
 Ostatnie uzupełnienia 00 DONUT: oddziaływanie neutrina taonowego (nikt nie wątpił, ale ) Osiągnięta skala odległości: 100GeV 1am; ew. struktura kwarków i leptonów musi być mniejsza! Listy elementarnych
Ostatnie uzupełnienia 00 DONUT: oddziaływanie neutrina taonowego (nikt nie wątpił, ale ) Osiągnięta skala odległości: 100GeV 1am; ew. struktura kwarków i leptonów musi być mniejsza! Listy elementarnych
Atomowa budowa materii
 Atomowa budowa materii Wszystkie obiekty materialne zbudowane są z tych samych elementów cząstek elementarnych Cząstki elementarne oddziałują tylko kilkoma sposobami oddziaływania wymieniając kwanty pól
Atomowa budowa materii Wszystkie obiekty materialne zbudowane są z tych samych elementów cząstek elementarnych Cząstki elementarne oddziałują tylko kilkoma sposobami oddziaływania wymieniając kwanty pól
Cząstki elementarne i ich oddziaływania III
 Cząstki elementarne i ich oddziaływania III 1. Przekrój czynny. 2. Strumień cząstek. 3. Prawdopodobieństwo procesu. 4. Szybkość reakcji. 5. Złota Reguła Fermiego 1 Oddziaływania w eksperymencie Oddziaływania
Cząstki elementarne i ich oddziaływania III 1. Przekrój czynny. 2. Strumień cząstek. 3. Prawdopodobieństwo procesu. 4. Szybkość reakcji. 5. Złota Reguła Fermiego 1 Oddziaływania w eksperymencie Oddziaływania
Fizyka cząstek elementarnych warsztaty popularnonaukowe
 Fizyka cząstek elementarnych warsztaty popularnonaukowe Spotkanie 3 Porównanie modeli rozpraszania do pomiarów na Wielkim Zderzaczu Hadronów LHC i przyszłość fizyki cząstek Rafał Staszewski Maciej Trzebiński
Fizyka cząstek elementarnych warsztaty popularnonaukowe Spotkanie 3 Porównanie modeli rozpraszania do pomiarów na Wielkim Zderzaczu Hadronów LHC i przyszłość fizyki cząstek Rafał Staszewski Maciej Trzebiński
REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA
 REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA Opis układu cząsteczek w mechanice kwantowej: 1. Funkcja falowa, 2. Wektora stanu ψ. TRANSFORMACJE UKŁADU CZĄSTEK: 1.
REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA Opis układu cząsteczek w mechanice kwantowej: 1. Funkcja falowa, 2. Wektora stanu ψ. TRANSFORMACJE UKŁADU CZĄSTEK: 1.
LEPTON TAU : jako taki, oraz zastosowania. w niskich i wysokich energiach. Zbigniew Wąs
 LEPTON TAU : jako taki, oraz zastosowania w niskich i wysokich energiach Zbigniew Wąs Podziękowania: A. Kaczmarska, E. Richter-Wąs (Atlas); A. Bożek (Belle); T. Przedziński, P. Golonka (IT); R. Decker,
LEPTON TAU : jako taki, oraz zastosowania w niskich i wysokich energiach Zbigniew Wąs Podziękowania: A. Kaczmarska, E. Richter-Wąs (Atlas); A. Bożek (Belle); T. Przedziński, P. Golonka (IT); R. Decker,
A/H ττ µ + hadrony + X detektorze CMS
 Poszukiwanie bozonów Higgsa w kanale A/H ττ µ + hadrony + X detektorze CMS Artur Kalinowski Instytut Fizyki Doświadczalnej, Uniwersytet Warszawski 31 Marca 006 Poszukiwanie bozonów H i A w detektorze CMS
Poszukiwanie bozonów Higgsa w kanale A/H ττ µ + hadrony + X detektorze CMS Artur Kalinowski Instytut Fizyki Doświadczalnej, Uniwersytet Warszawski 31 Marca 006 Poszukiwanie bozonów H i A w detektorze CMS
Oddziaływania. Zachowanie liczby leptonowej i barionowej Diagramy Feynmana. Elementy kwantowej elektrodynamiki (QED)
 Oddziaływania Zachowanie liczby leptonowej i barionowej Diagramy Feynmana Elementy kwantowej elektrodynamiki (QED) Teoria Yukawy Zasięg oddziaływań i propagator bozonowy Równanie Diraca Antycząstki; momenty
Oddziaływania Zachowanie liczby leptonowej i barionowej Diagramy Feynmana Elementy kwantowej elektrodynamiki (QED) Teoria Yukawy Zasięg oddziaływań i propagator bozonowy Równanie Diraca Antycząstki; momenty
Oddziaływania podstawowe
 Oddziaływania podstawowe grawitacyjne silne elektromagnetyczne słabe 1 Uwięzienie kwarków (quark confinement). Przykład działania mechanizmu uwięzienia: Próba oderwania kwarka d od neutronu (trzy kwarki
Oddziaływania podstawowe grawitacyjne silne elektromagnetyczne słabe 1 Uwięzienie kwarków (quark confinement). Przykład działania mechanizmu uwięzienia: Próba oderwania kwarka d od neutronu (trzy kwarki
Unifikacja elektro-s!aba
 Unifikacja elektro-s!aba! Potrzeba unifikacji! Warunki unifikacji elektro-s!abej! Model Weinberga-Salama! Rezonans Z 0! Liczenie zapachów neutrin (oraz generacji) D. Kie!czewska, wyk!ad 7 1 Rozwa"my proces:
Unifikacja elektro-s!aba! Potrzeba unifikacji! Warunki unifikacji elektro-s!abej! Model Weinberga-Salama! Rezonans Z 0! Liczenie zapachów neutrin (oraz generacji) D. Kie!czewska, wyk!ad 7 1 Rozwa"my proces:
Struktura protonu. Elementy fizyki czastek elementarnych. Wykład IV. rekonstrukcja przypadków NC DIS wyznaczanie funkcji struktury.
 Struktura protonu Wykład IV akcelerator HERA Elementy fizyki czastek elementarnych rekonstrukcja przypadków NC DIS wyznaczanie funkcji struktury równania ewolucji QCD struktura fotonu NC DIS Deep Inelastic
Struktura protonu Wykład IV akcelerator HERA Elementy fizyki czastek elementarnych rekonstrukcja przypadków NC DIS wyznaczanie funkcji struktury równania ewolucji QCD struktura fotonu NC DIS Deep Inelastic
Supersymetria. Elementy fizyki czastek elementarnych. Wykład XII
 Supersymetria Wykład XII Problemy Modelu Standardowego Supersymetria Widmo czastek Przewidywania Obecne wyniki Przyszłe poszukiwania Mały Higgs Elementy fizyki czastek elementarnych Model Standardowy Przypomnienie
Supersymetria Wykład XII Problemy Modelu Standardowego Supersymetria Widmo czastek Przewidywania Obecne wyniki Przyszłe poszukiwania Mały Higgs Elementy fizyki czastek elementarnych Model Standardowy Przypomnienie
Wszechświat cząstek elementarnych WYKŁAD 5
 Wszechświat cząstek elementarnych WYKŁAD 5 Maria Krawczyk, Wydział Fizyki UW 17.III.2010 Oddziaływania: elektromagnetyczne i grawitacyjne elektromagnetyczne i silne (kolorowe) Biegnące stałe sprzężenia:
Wszechświat cząstek elementarnych WYKŁAD 5 Maria Krawczyk, Wydział Fizyki UW 17.III.2010 Oddziaływania: elektromagnetyczne i grawitacyjne elektromagnetyczne i silne (kolorowe) Biegnące stałe sprzężenia:
Spis treści. Fizyka wczoraj, dziś, jutro. Z naszych lekcji. Olimpiady, konkursy, zadania. Astronomia dla każdego
 Spis treści Fizyka wczoraj, dziś, jutro Archeologia XXI wieku 4 Sławomir Jędraszek Tajemnica Gwiazdy 19 Betlejemskiej okiem astronoma Piotr Gronkowski, Marcin Wesołowski Z naszych lekcji Dlaczego warto
Spis treści Fizyka wczoraj, dziś, jutro Archeologia XXI wieku 4 Sławomir Jędraszek Tajemnica Gwiazdy 19 Betlejemskiej okiem astronoma Piotr Gronkowski, Marcin Wesołowski Z naszych lekcji Dlaczego warto
Dynamika relatywistyczna
 Dynamika relatywistyczna Fizyka I (Mechanika) Wykład XII: masa niezmiennicza i układ środka masy zderzenia elastyczne czastki elementarne rozpady czastek rozpraszanie nieelastyczne Dynamika relatywistyczna
Dynamika relatywistyczna Fizyka I (Mechanika) Wykład XII: masa niezmiennicza i układ środka masy zderzenia elastyczne czastki elementarne rozpady czastek rozpraszanie nieelastyczne Dynamika relatywistyczna
Podstawy fizyki subatomowej
 Podstawy fizyki subatomowej Zenon Janas Zakład Fizyki Jądrowej IFD UW ul. Pasteura 5 p..81 tel. 55 3 681 e-mail: janas@fuw.edu.pl http://www.fuw.edu.pl/~janas/fsuba/fizsub.htm Zasady zaliczenia Obecność
Podstawy fizyki subatomowej Zenon Janas Zakład Fizyki Jądrowej IFD UW ul. Pasteura 5 p..81 tel. 55 3 681 e-mail: janas@fuw.edu.pl http://www.fuw.edu.pl/~janas/fsuba/fizsub.htm Zasady zaliczenia Obecność
Dodatkowe wymiary. Elementy fizyki czastek elementarnych. Wykład XI
 Dodatkowe wymiary Wykład XI Dodatkowe wymiary Jak dobrze znamy grawitacje Grawitacja w świecie czastek Perspektywy Elementy fizyki czastek elementarnych Dodatkowe wymiary Skala Plancka Problem hierarchii
Dodatkowe wymiary Wykład XI Dodatkowe wymiary Jak dobrze znamy grawitacje Grawitacja w świecie czastek Perspektywy Elementy fizyki czastek elementarnych Dodatkowe wymiary Skala Plancka Problem hierarchii
Wszechświat czastek elementarnych
 Wszechświat czastek elementarnych Wykład 6: prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład 6: 27 marca 2013 p.1/43
Wszechświat czastek elementarnych Wykład 6: prof. A.F.Żarnecki Zakład Czastek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wszechświat czastek elementarnych Wykład 6: 27 marca 2013 p.1/43
WYKŁAD Prawdopodobieństwo procesów dla bardzo dużych energii, konieczność istnienia cząstki Higgsa
 Wszechświat cząstek elementarnych WYKŁAD 10 29.04 29.04.2009.2009 1 Prawdopodobieństwo procesów dla bardzo dużych energii, konieczność istnienia cząstki Higgsa Cząstki fundamentalne w Modelu Standardowym
Wszechświat cząstek elementarnych WYKŁAD 10 29.04 29.04.2009.2009 1 Prawdopodobieństwo procesów dla bardzo dużych energii, konieczność istnienia cząstki Higgsa Cząstki fundamentalne w Modelu Standardowym
Poszukiwania bozonu Higgsa w rozpadzie na dwa leptony τ w eksperymencie CMS
 Poszukiwania bozonu Higgsa w rozpadzie na dwa leptony τ w eksperymencie CMS Artur Kalinowski Wydział Fizyki Uniwersytet Warszawski Warszawa, 7 grudnia 2012 DETEKTOR CMS DETEKTOR CMS Masa całkowita : 14
Poszukiwania bozonu Higgsa w rozpadzie na dwa leptony τ w eksperymencie CMS Artur Kalinowski Wydział Fizyki Uniwersytet Warszawski Warszawa, 7 grudnia 2012 DETEKTOR CMS DETEKTOR CMS Masa całkowita : 14
WYKŁAD IV.2013
 Wszechświat cząstek elementarnych WYKŁAD 10 24.IV.2013 Maria Krawczyk, Wydział Fizyki UW Teoria cząstek elementarnych- opis zdarzeń Rachunek zaburzeń i nieskończoności Renormalizacja Prawdopodobieństwo
Wszechświat cząstek elementarnych WYKŁAD 10 24.IV.2013 Maria Krawczyk, Wydział Fizyki UW Teoria cząstek elementarnych- opis zdarzeń Rachunek zaburzeń i nieskończoności Renormalizacja Prawdopodobieństwo
Struktura protonu. Elementy fizyki czastek elementarnych. Wykład IV
 Struktura protonu Wykład IV akcelerator HERA Elementy fizyki czastek elementarnych rekonstrukcja przypadków NC DIS wyznaczanie funkcji struktury równania ewolucji QCD struktura fotonu NC DIS Deep Inelastic
Struktura protonu Wykład IV akcelerator HERA Elementy fizyki czastek elementarnych rekonstrukcja przypadków NC DIS wyznaczanie funkcji struktury równania ewolucji QCD struktura fotonu NC DIS Deep Inelastic
IV.4.4 Ruch w polach elektrycznym i magnetycznym. Siła Lorentza. Spektrometry magnetyczne
 r. akad. 005/ 006 IV.4.4 Ruch w polach elektrycznym i magnetycznym. Siła Lorentza. Spektrometry magnetyczne Jan Królikowski Fizyka IBC 1 r. akad. 005/ 006 Pole elektryczne i magnetyczne Pole elektryczne
r. akad. 005/ 006 IV.4.4 Ruch w polach elektrycznym i magnetycznym. Siła Lorentza. Spektrometry magnetyczne Jan Królikowski Fizyka IBC 1 r. akad. 005/ 006 Pole elektryczne i magnetyczne Pole elektryczne
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 6 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 6 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
VI. 6 Rozpraszanie głębokonieelastyczne i kwarki
 r. akad. 005/ 006 VI. 6 Rozpraszanie głębokonieelastyczne i kwarki 1. Fale materii. Rozpraszanie cząstek wysokich energii mikroskopią na bardzo małych odległościach.. Akceleratory elektronów i protonów.
r. akad. 005/ 006 VI. 6 Rozpraszanie głębokonieelastyczne i kwarki 1. Fale materii. Rozpraszanie cząstek wysokich energii mikroskopią na bardzo małych odległościach.. Akceleratory elektronów i protonów.
Zderzenia. Fizyka I (B+C) Wykład XVI: Układ środka masy Oddziaływanie dwóch ciał Zderzenia Doświadczenie Rutherforda
 Zderzenia Fizyka I (B+C) Wykład XVI: Układ środka masy Oddziaływanie dwóch ciał Zderzenia Doświadczenie Rutherforda Układ środka masy Układ izolowany Izolowany układ wielu ciał: m p m 4 CM m VCM p 4 3
Zderzenia Fizyka I (B+C) Wykład XVI: Układ środka masy Oddziaływanie dwóch ciał Zderzenia Doświadczenie Rutherforda Układ środka masy Układ izolowany Izolowany układ wielu ciał: m p m 4 CM m VCM p 4 3
Struktura protonu. Elementy fizyki czastek elementarnych. Wykład III
 Struktura protonu Elementy fizyki czastek elementarnych Wykład III kinematyka rozpraszania doświadczenie Rutherforda rozpraszanie nieelastyczne partony i kwarki struktura protonu Kinematyka Rozpraszanie
Struktura protonu Elementy fizyki czastek elementarnych Wykład III kinematyka rozpraszania doświadczenie Rutherforda rozpraszanie nieelastyczne partony i kwarki struktura protonu Kinematyka Rozpraszanie
WYKŁAD 9. Wszechświat cząstek elementarnych dla przyrodników
 Wszechświat cząstek elementarnych dla przyrodników WYKŁAD 9 Maria Krawczyk, Wydział Fizyki UW 1.XII.2010 Teoria cząstek elementarnych- opis zdarzeń Rachunek zaburzeń i nieskończoności Renormalizacja Prawdopodobieństwo
Wszechświat cząstek elementarnych dla przyrodników WYKŁAD 9 Maria Krawczyk, Wydział Fizyki UW 1.XII.2010 Teoria cząstek elementarnych- opis zdarzeń Rachunek zaburzeń i nieskończoności Renormalizacja Prawdopodobieństwo
Michał Praszałowicz, pok. 438. michal@if.uj.edu.pl strona www: th-www.if.uj.edu.pl/~michal wykład 3 godz. za wyjątkiem listopada Egzamin: esej max.
 Michał Praszałowicz, pok. 438. michal@if.uj.edu.pl strona www: th-www.if.uj.edu.pl/~michal wykład 3 godz. za wyjątkiem listopada Egzamin: esej max. 10 stron na jeden z listy tematów + rozmowa USOS! 1 Model
Michał Praszałowicz, pok. 438. michal@if.uj.edu.pl strona www: th-www.if.uj.edu.pl/~michal wykład 3 godz. za wyjątkiem listopada Egzamin: esej max. 10 stron na jeden z listy tematów + rozmowa USOS! 1 Model
Cząstki elementarne. Składnikami materii są leptony, mezony i bariony. Leptony są niepodzielne. Mezony i bariony składają się z kwarków.
 Cząstki elementarne Składnikami materii są leptony, mezony i bariony. Leptony są niepodzielne. Mezony i bariony składają się z kwarków. Cząstki elementarne Leptony i kwarki są fermionami mają spin połówkowy
Cząstki elementarne Składnikami materii są leptony, mezony i bariony. Leptony są niepodzielne. Mezony i bariony składają się z kwarków. Cząstki elementarne Leptony i kwarki są fermionami mają spin połówkowy
Teorie wielkich unifikacji
 Teorie wielkich unifikacji Sukcesy i porażki Modelu Standardowego Przesłanki dla wielkich unifikacji Biegnące stałe sprzężenia Teoria SU(5) i przewidywania rozpadu protonu Poszukiwanie rozpadu protonu
Teorie wielkich unifikacji Sukcesy i porażki Modelu Standardowego Przesłanki dla wielkich unifikacji Biegnące stałe sprzężenia Teoria SU(5) i przewidywania rozpadu protonu Poszukiwanie rozpadu protonu
Rozszerzenia Modelu Standardowego
 Rozszerzenia Modelu Standardowego Wykład XIII Mały Higgs Elementy fizyki czastek elementarnych Dodatkowe wymiary Jak dobrze znamy grawitacje Grawitacja w świecie czastek Nowe oddziaływania W W Rozszerzenia
Rozszerzenia Modelu Standardowego Wykład XIII Mały Higgs Elementy fizyki czastek elementarnych Dodatkowe wymiary Jak dobrze znamy grawitacje Grawitacja w świecie czastek Nowe oddziaływania W W Rozszerzenia
Symetrie i prawa zachowania Wykład 6
 Symetrie i prawa zachowania Wykład 6 Karol Kołodziej Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna 1/29 Rola symetrii Największym
Symetrie i prawa zachowania Wykład 6 Karol Kołodziej Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna 1/29 Rola symetrii Największym
Pierwsze dwa lata LHC
 Pierwsze dwa lata LHC Barbara Wosiek Instytut Fizyki Jądrowej im. Henryka Niewodniczańskiego, Polskiej Akademii Nauk Radzikowskiego 152, 31-342 Kraków barbara.wosiek@ifj.edu.pl 2011-10-21 B. Wosiek, Sem.
Pierwsze dwa lata LHC Barbara Wosiek Instytut Fizyki Jądrowej im. Henryka Niewodniczańskiego, Polskiej Akademii Nauk Radzikowskiego 152, 31-342 Kraków barbara.wosiek@ifj.edu.pl 2011-10-21 B. Wosiek, Sem.
Sylwa czyli silva rerum na temat fizyki cz astek elementarnych
 Sylwa czyli silva rerum na temat fizyki cz astek elementarnych Barbara Badełek Uniwersytet Warszawski i Uniwersytet Uppsalski Nauczyciele fizyki w CERN 20 26 maja 2007 B. Badełek (Warsaw and Uppsala) Silva
Sylwa czyli silva rerum na temat fizyki cz astek elementarnych Barbara Badełek Uniwersytet Warszawski i Uniwersytet Uppsalski Nauczyciele fizyki w CERN 20 26 maja 2007 B. Badełek (Warsaw and Uppsala) Silva
Model Standardowy i model Higgsa. Sławomir Stachniewicz, IF PK
 Model Standardowy i model Higgsa Sławomir Stachniewicz, IF PK 1. Wstęp. Model Standardowy to obecnie obowiązująca teoria cząstek elementarnych, które są składnikami materii. Model Higgsa to dodatek do
Model Standardowy i model Higgsa Sławomir Stachniewicz, IF PK 1. Wstęp. Model Standardowy to obecnie obowiązująca teoria cząstek elementarnych, które są składnikami materii. Model Higgsa to dodatek do
Fizyka cząstek elementarnych. Tadeusz Lesiak
 Fizyka cząstek elementarnych Tadeusz Lesiak 1 WYKŁAD III Rola symetrii w fizyce cząstek elementarnych T.Lesiak Fizyka cząstek elementarnych 2 Rola symetrii w fizyce Symetria mnie uspokaja. Brak symetrii
Fizyka cząstek elementarnych Tadeusz Lesiak 1 WYKŁAD III Rola symetrii w fizyce cząstek elementarnych T.Lesiak Fizyka cząstek elementarnych 2 Rola symetrii w fizyce Symetria mnie uspokaja. Brak symetrii
Wszechświat Cząstek Elementarnych dla Humanistów Oddziaływania silne
 Wszechświat Cząstek Elementarnych dla Humanistów Oddziaływania silne Aleksander Filip Żarnecki Wykład ogólnouniwersytecki 6 listopada 2018 A.F.Żarnecki WCE Wykład 5 6 listopada 2018 1 / 37 Oddziaływania
Wszechświat Cząstek Elementarnych dla Humanistów Oddziaływania silne Aleksander Filip Żarnecki Wykład ogólnouniwersytecki 6 listopada 2018 A.F.Żarnecki WCE Wykład 5 6 listopada 2018 1 / 37 Oddziaływania
Wybrane Dzialy Fizyki
 Wybrane Dzialy Fizyki (2) Elementy fizyki środowiskowej Energia - podstawowy element rozwoju społeczeństwa Podstawowe poj ecia Formy energii Współczesne źródła energii Środowisko zanieczyszczenia i jego
Wybrane Dzialy Fizyki (2) Elementy fizyki środowiskowej Energia - podstawowy element rozwoju społeczeństwa Podstawowe poj ecia Formy energii Współczesne źródła energii Środowisko zanieczyszczenia i jego
Wstęp do Modelu Standardowego
 Paweł Malecki Instytut Fizyki Jądrowej Polskiej Akademii Nauk Kraków PL Wstęp do Modelu Standardowego 1 Plan Rys historyczny Pierwsze cząstki Cząstki co jest elementarne? Oddziaływania Symetrie Mechanizm
Paweł Malecki Instytut Fizyki Jądrowej Polskiej Akademii Nauk Kraków PL Wstęp do Modelu Standardowego 1 Plan Rys historyczny Pierwsze cząstki Cząstki co jest elementarne? Oddziaływania Symetrie Mechanizm
