WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład VII Przekształcenie Fouriera.
|
|
|
- Bożena Świderska
- 6 lat temu
- Przeglądów:
Transkrypt
1 7. Całka Fouriera w posaci rzeczywisej. Wykład VII Przekszałcenie Fouriera. Doychczas rozparywaliśmy szeregi Fouriera funkcji w ograniczonym przedziale [ l, l] lub [ ] Teraz pokażemy analogicznie przedsawienie funkcji w przedziale (, ) lub ( ) załóżmy, że funkcja f ( x ) określona w przedziale (, ) jes w ym przedziale bezwzględnie całkowalna: ( ),l.,. W ym celu f x dx < (7.) Dalej, że w każdym skończonym przedziale spełnia pierwszy i drugi warunek Dirichlea. Oznaczmy I przedsawimy funkcję f ( x ) w przedziale [ l, l] l = (7.) za pomocą jej szeregu Fouriera: a nx nx f ( x) = + an sin + bn cos ( x ( l, l) ) n= λ λ (7.3) O współczynnikach danych wzorami Eulera-Fouriera, kóre przybiorą posać: a b n n ( ) cos n = f * ( n,,... ) = (7.4) sin λ Wsawmy prawe srony związków (7.4) do równości (7.3). Orzymamy: nx n nx n f ( x) = f ( ) f ( ) cos cos sin sin + n= + = λ λ λ λ ( ) n x = f ( ) f ( ) cos + π n= λ λ (7.5) i przejdźmy do granicy, gdy l lub, co jes równoważne, gdy λ. Z założenia bezwzględnej całkowalności wynika, że pierwsza z całek po prawej sronie w powyższej równości jes zbieżna, a ponieważ mianownik rośnie nieograniczenie, więc: Oznaczmy Wobec czego lim f ( ) = λ (7.6) n ωn = ( n =,,3,... ) (7.7) λ
2 Wprowadzając nową funkcję: n n ωn = ωn ωn = = λ λ λ φ ( ω, x, λ ) = f ( ) cos( ω ( x )) (7.8) Możemy szereg w równości (7.5) napisać w posaci I uznać za sumę przybliżona całki Co nie jes ścisłe, bo (, x, ) n= (, x, ) φ ω λ ω n (, x, ) n φ ω λ d ω (7.9) φ ω λ n zależy od ω n =, poza ym nie jes o suma lecz szereg. λ Przejście graniczne przy λ daje całkę: Łącząc zależności (7.9) I (7.) orzymujemy wierdzenie: Twierdzenie Funkcję f ( x ) bezwzględnie całkowalną w przedziale (, ) φ ( ω, x) = f ( ) cos( ω ( x )) (7.) spełniajaca w nim pierwszy i drugi warunek Dirichlea można przedsawić za pomocą zw. wzoru całkowego Fouriera: f ( x) = dω f ( ) cos ( ω ( x ) ) π (7.) Isnieje ścisły dowód równości (7.), ale znacznie bardziej skomplikowany i dłuższy od powyżej podanego... Prawa srona wzoru (7.) nazywa się całką Fouriera funkcji f ( x ). Przekszałcając ja dosajemy: Co zapiszemy w posaci f ( x) = dω f ( ) cosω cosωx + f ( ) sinω sinωx π (7.) f ( x) = a cosωx + b sinωx dω (7.3)
3 Przy czym oznaczamy a b = f ω π (7.4) sin ( ) cos Wzór (7.3) będący analogiem szeregu Fouriera dla funkcji w przedziale ograniczonym, mówi, że, rozłożyć na drgania harmoniczne o f ( x ) można w nieograniczony przedziale ( ) częsoliwości zmieniającej się w sposób ciągły od zera do nieskończoności. Funkcje a( ω ) i b( ω ) nazywają się współczynnikami widma ciągłego funkcji f ( ) nasępujące własności, x. Funkcje e mają a = a b = b (7.5) Funkcję, kórej warość w każdym punkcie jes równa warości jej całki Fouriera, nazywamy rozwijalną na całkę Fouriera. Dla akiej funkcji zachodzi wedy analagon równości Parsevala f ( ) = a + b dω 7. Całka Fouriera funkcji parzysej lub nieparzysej. (7.6) Niech funkcja f ( x ) rozwijalna na całkę Fouriera, będzie funkcją parzysą. Wedy b funkcja podcałkowa we wzorach (7.4) będzie nieparzysa. Naomias Wzór całkowy dla funkcji parzysej przybiera posać, bo a = f ( ) cos( ω) π (7.7) f x = a ω ωx dω (7.8) ( ) ( ) cos( ) Analogicznie w przypadku funkcji nieparzysej orzymujemy 7.3 Całka Fouriera funkcji w przedziale (, ). b( ω ) = f ( ) sin ( ω) π ( ) = ( ) sin ( ) f x b ω ωx dω (7.9) Rozparzmy funkcję f ( x) zadana w przedziale [, ) i w nim bezwzględnie całkowalną oraz spełniająca pierwszy i drugi warunek Dirichlea. Uwórzmy funkcję pomocniczą określoną w sposób nasępujący
4 φ ( x) f ( x) gdy x (, ) ( ) (,) = f x gdy x (7.) Funkcja φ ( x) jes oczywiście rozwijalna na całkę Fouriera, mianowicie ( x) = a ( ) cos ( x) d x (, ) φ ω ω ω a = f ( ) cos( ω ) π Wobec czego w przedziale (, ) zachodzi równość f ( x ) cos ( ωx ) dω f ( ) cos ( ω ) π = (7.) Analogicznie worząc nieparzysą funkcję pomocniczą orzymujemy f x sin x d f sin x, π ( ) = ( ω ) ω ( ) ( ω ) ( ) (7.) Każdą z równości (7.) i (7.) nazywamy wzorem Fouriera w przedziale (, ), a prawe srony ych wzorów nazywamy całkami Fouriera w przedziale (, ). Funkcję, kóra w przedziale (, ) da się przedsawić równością (7.) lub (7.) nazywamy funkcją rozwijalną na całkę Fouriera w przedziale (, ). 7.4 Sinusowe i cosinusowe przekszałcenie Fouriera. Załóżmy, że funkcja f ( x ) jes rozwijalna na całkę Fouriera w przedziale (, ). Wedy (7.) i (7.): Przyjmijmy oznaczenia: Wobec czego f ( x) = f ( ) sinω sinωxdω π = f xd x π ( ) cosω cosω ω (, ) F = f (7.3) s c ( ω ) ( ) sin ( ω ) F = f (7.4) ( ) cos( ω )
5 Fs sin ( ω ) = f ( ) π (7.5) Oraz Fc cos( ω) = f ( ) π (7.6) Wzór (7.3) nazywamy prosym sinusowym przekszałceniem Fouriera, zaś (7.5) przekszałceniem sinusowym Fouriera odwronym (względem niego). Analogicznie wzory (7.4) i (7.6) nazywają się prosym i odwronym cosinusowym przekszałceniem Fouriera. Związek między funkcją f ( ) a jej sinusową lub cosinusową ransformaą F s lub F c będziemy oznaczać nasępująco: ( ), ( ) ( ), ( ) Fs = s f f = s Fs Fc = c f f = c Fs (7.7) W dalszym ciągu zajmiemy się obliczaniem sinusowego i cosinusowego przekszałcenia pochodnych i całki funkcji f ( ). Oznaczmy przez k i k prawosronne granice w począku układu: ( ), '( ) k = f + k = f + (7.8) Obliczmy ransformay pierwszych pochodnych funkcji f ( ) przy założeniu ( ), f gdy s f ' = sin = f sin f cos = F ( ) ( ω ) ( ) ( ω ) ω ( ) ( ω ) ω c f ' = cos = f cos + f sin = k + Fs ( ) ( ω ) ( ) ( ω ) ω ( ) ( ω ) ω c (7.9) Przy obliczaniu drugich pochodnych załóżmy ponao, że [ k F ] k F ( ) ( ) f ', gdy d f s f ''( ) = sin ( ω) = sin ( ω) ω cos( ω) = = ω + ω = ω ω ω s s d f c f '' = cos = cos + sin = k Fc ( ) ( ω ) ( ω ) ω ( ω ) ω ( ω ) Przy obliczaniu ransforma całki (7.3)
6 f ( τ ) dτ Załóżmy, że ( ) f τ dτ, gdy f ( τ ) dτ = f ( τ ) dτ sinω = s = f d f Fc ω + = ω ω ( τ ) τ cos( ω ) ( ) cos( ω ) f ( τ ) dτ = f ( τ ) dτ cosω = c = f d f Fs ω = ω ω ( τ ) τ sin ( ω ) ( ) sin ( ω ) ( ω ) (7.3) (7.3) Treść zadania Przykład obliczeniowy x Znaleźć ransformaę sinusową funkcji f ( x) = e gdy x [, ) Rozwiązanie Fs 7.5 Całka Fouriera w posaci zespolonej. π ( ω ) = sin ( ω ) ω ω + Niech funkcja f ( x ) będzie rozwijalną na całkę Fouriera. Wedy x dx f ( x) = dω f ( ) cos ( ω ( x ) ) π (7.33) Wewnęrzna całka jes parzysą funkcją zmiennej ω, wobec czego można zewnęrzną całkę rozciągnąć na przedział (, ) dzieląc jednocześnie całą prawą sronę równości (7.33) przez. Wobec ego będzie f ( x) = dω f ( ) cos ω ( x ) π ( ) (7.34) Gdybyśmy eraz w prawej sronie równości (7.33) zasąpili cosinus sinusem, o całka wewnęrzna byłaby nieparzysą zmiennej ω, wobec czego całka zewnęrzna sałaby się równa zeru. Byłoby wedy
7 = sin π dω f ( ) ( ω ( x ) ) (7.35) Dodajmy sronami równość (7.34) do równości (7.35) pomnożonej przez j, pamięając jednocześnie, że wzór Eulera pozwala zapisać: Orzymamy ( ) sinω ( ) j cosω x + j x = e ω ( x ) jω ( x ) f ( x) dω f ( ) e π = (7.36) Wzór (7.36) nazywa się wzorem całkowym Fouriera w posaci zespolonej, zaś jego prawa srona zespoloną całką Fouriera. 7.6 Zespolone przekszałcenie Fouriera. Zapiszmy równość (7.36) korzysając z własności dodawania argumenów funkcji wykładniczej: Oznaczmy całkę wewnęrzną Wedy równość (7.37) przybierze posać: jω jωx f ( x) = f ( ) e e dω π z (7.37) z (7.38) j ( ) ( ) F = f e = f jωx f ( x) = Fz e dω = z Fz π (7.39) Wzór (7.38) nazywamy prosym zespolonym przekszałceniem Fouriera (niekiedy dodajemy dwusronnym), zaś (7.39) nazywamy zespolonym przekszałceniem odwronym. Funkcja f ( ) nazywa się oryginałem albo funkcją oryginalną przekszałcenia, zaś ( ) ansformaą lub przekszałceniem odwronym. F ω - obrazem, Transformaę Fz ( ω ) nazywamy akże zespolonym widmem ciągłym funkcji f ( ). Aby znaleźć związek miedzy zespolonym widmem ciągłym i widmami rzeczywisymi, danymi wzorami (7.4) zauważymy, że: F ω f ω j f ω z ( ) = ( ) cos ( ) ( ) sin ( ) Oznaczając, zgodnie z wzorami (7.4) z
8 A = π a = f ( ) cos( ω) B = πb = f ( ) sin ( ω) (7.4) Możemy widmo zespolone przedsawić w posaci: ( ) ( ) ( ) Fz ω = A ω jb ω = Fz ω e Widmo ampliudy Fz ( ω ) i widmo fazy z ( ) rzeczywisych. Mianowicie: Wobec czego: Oczywiście re( Fz ) jargf z Arg F ω da się obliczyć w zaleznosci od widm A = F Arg F, B = F Arg F z z z z F = A + B z = A jes funkcją parzysą, a im( F ) 7.7 Przekszałcenie Fouriera operacji różniczkowych i całkowych. Załóżmy, że pochodne pierwsza i druga oraz całka f ( τ ) dτ funkcji ( ) z = B jes funkcją nieparzysą argumenu ω. f, mającej ransformaę Fouriera, akże są ransformowalne oraz że spełnione są nasępujące warunki graniczne: Obliczmy: Pierwsza pochodna Druga pochodna Całka ( ) ( ) ( τ ) f, f ', f dτ, gdy (7.4) z f = e = f e + j f e = j F jω jω jω '( ) ( ) ω ( ) ω z [ ω] (7.4) Można orzymane wyniki wysłowić jak nasępuje: ( ) z f '' = j Fz (7.43) z f ( τ ) dτ = Fz (7.44) jω
9 Różniczkowanie oryginału jes równoważne mnożeniu obrazu przez jω, całkowanie (w granicach (, ) ) oryginału jes równoważne dzieleniu obrazu przez jω. 7.8 Funkcja Heaviside a. Pseudofunkcją Heaviside a nazywamy fumkcję określoną w sposób nasępujący:, gdy x > η ( ) =, gdy x =, gdy x < (7.45) Na rys. 7. przedsawiono funkcje Heaviside a η ( ), zaś na rys. 7. ę samą funkcję z opóźnionym argumenem η ( ). Rys. 7. Funkcja Heaviside a η ( ): a) =, b) Operację polegajaca na przemnożeniu funkcji f ( ) przez funkcję Feaviside a η ( ) nazywamy gaszeniem funkcji. Przykłady funkcji zgaszonych zosały przedsawione na rys. 7. ( ) sin η sin i rys. 7.3 [ e η e ] ( ) ( ) ( ) ( ) ( )
10 Rys. 7. Zgaszona funkcja sin ( ) Rys. 7.3 Zgaszona funkcja ( ) e Zauważmy, że funkcja Heaviside a spełnia warunki Dirichlea w każdym przedziale skończonym, naomias nie jes rozwijalna na całkę Fouriera, gdyż nie jes bezwzględnie całkowalna na całej osi rzeczywisej. 7.9 Prawosronne zespolone przekszałcenie Laplace a. Zakładając, że funkcję η ( ) f ( ) można poddać przekszałceniu Fouriera, zdefiniujmy nasępujące przekszałcenia:
11 jω ( ) ( ) F = f e = f (7.46) jω η ( ) f ( ) = F e dω = F π (7.47) Wzór (7.46) nosi nazwę prosego prawosronnego przekszałcenia Fouriera, zaś (7.47) odwronego prawosronnego zespolonego przekszałcenia Fouriera. W prawosronnym zespolonym przekszałceniu Fouriera będziemy zapisywać funkcję f, uważając ja od razu za zgaszoną. Wedy w ransformowaną zamias ( ) f ( ) η króko ( ) formule (7.47) można pominąć η ( ). Załozmy eraz, że funkcja f ( ) i jej pochodna f '( ) oryginałami przekszałcenia Fouriera i przyjmijmy założenia: ( ) ( ) ( τ ) są f, f ', f dτ, gdy (7.48) Oraz ( ), '( ) f + = k f + = k (7.49) Wedy (7.5) jω jω jω ( ) ( ) ω ( ) ω f ' = e = f e + j f e = k + j F ( ) ω f '' = k j k + j F Przy odpowiednich założeniach doyczących całek f ( ). 7. Splo. (7.5) f ( τ ) dτ = F (7.5) ω Zauważmy, że wszyskie doychczas przez nas poznane przekszałcenia są liniowe. Zapiszmy en fak, np. dla dwusronnego zespolonego przekszałcenia Fouriera, oznaczając: = ( ), [ ω] = ( ) Fz z f Gz z g I zakładając isnienie wprowadzonych wyżej funkcji i odwronych ransforma Fouriera. Zachodzą mianowicie nasępujące równości: ( ) ( ) [ ] ( ) z α f + β g = α Fz ω + βgz ω (7.53) ( ) + ( ) = ( ) + [ ] α f β g z α Fz ω βgz ω (7.54) Dowód ych własności opiera się na liniowości całki oznaczonej.
12 Równość (7.53) można wysłowić: Obrazem kombinacji liniowej oryginałów jes aka sama kombinacja liniowa obrazów. Równość (7.54) : Oryginałem kombinacji liniowej oryginałów jes aka sama kombinacja liniowa oryginałów. Zakładając eraz, że obie funkcje f ( ) i g ( ) są całkowalne z kwadraem, poszukujemy związku między oryginałami, odpowiadającego iloczynowi obrazów ych funkcji. W ym celu wyraźmy iloczyn obrazów za pomocą całki podwójnej jωτ jωτ Fz Gz = f ( τ ) e dτ g ( τ ) e dτ = = jω( τ+ τ ) ( ) ( ) f τ g τ e dτ dτ (7.55) A nasępnie zasosujmy zamianę zmiennych τ i τ na zmienne, τ. τ + τ =, τ = τ, czyli τ = τ (7.56) Jakobian ej zmiany jes równy : ( τ, τ ) ( τ, ) = = Jes przekszałcenie płaszczyzny τ, τ w płaszczyznę,τ.
13 Rys. 7.3 Przekszałcenie płaszczyzny τ, τ w płaszczyznę, τ Zauważymy, że przy ym przekszałceniu pierwsza ćwiarka opisująca się nierównościami (rys. 7.3) : τ >, τ > Zosaje odwzorowana na obszar opisujący się nierównościami < τ <, > Wyraźmy całkę, wysępującą w iloczynie obrazów (7.55), za pomocą całki ierowanej w nowym układzie współrzędnych. Będzie wedy jω Fz Gz = f ( τ ) g ( τ ) dτ e Całkę wewnęrzną w prawej sronie zależności (7.57) oznaczymy: (7.57) ( ) ( ) I nazywamy sploem lub konwolucją funkcji f ( ) i f ( ). f * f = f τ f τ dτ (7.58) Symbol nazywamy symbolem splaania lub mnożenia sploowego. Wobec definicji (7.58) możemy zależność (7.57) zapisać
14 Co jes reścią wierdzenia Borela: Twierdzenie Borela jω Fz Gz ( ω ) z ( f * g ) ( f * g ) e = = (7.59) W zespolonym przekszałceniu Fouriera mnożeniu obrazów odpowiada splaanie oryginałów. Posługując się odwronym przekszałceniem Fouriera możemy zależność (7.59) zapisać w posaci zwanej wzorem całkowym Fouriera dla splou funkcji: z z z z z π Podsawowymi własnościami splaania są: przemienność Łączność [ ] ( ) ( ) jω F G = F ω G ω e dω = f * g (7.6) f * f = f * f (7.6) ( f * f )* f f *( f * f ) = (7.6) 3 3 Można wykazać, że jeżeli f ( ) i f ( ) są bezwzględnie całkowalne w przedziale (, ) a) co najmniej jedna z nich jes w przedziale (, + ) ograniczona lub + oraz b) obie funkcje są całkowalne z kwadraem w przedziale (, + ), o splo ych funkcji jes w przedziale (, + ) funkcją ciągłą. W prawosronnym zespolonym przekszałceniu Fouriera wysępuje funkcja zgaszona. Dla akiej funkcji definicja splou podana wzorem (7.58) ma posać: ( ) ( ) f * f f τ f τ dτ (7.63) Gdzie ( τ ) η ( τ ) ( τ ), ( τ ) = η ( τ ) ( τ ) f f f f Oczywiście zachowują się poprzednio wykazane własności splou, a mianowicie przemienność i łączność. Splo zapisany równością (7.63) nazywamy niekiedy prawosronnym sploem funkcji f i f. Robiąc analogiczne założenia co do funkcji oraz ę samą zamianę zmiennych (7.56) i obliczając iloczyn prawosronnych zespolonych ransforma orzymujemy:
15 jωτ jωτ F G = f ( τ) e dτ g ( τ ) e dτ = jω( τ + τ ) = f τ g τ e dτ dτ = ( ) ( ) = f g d e = f g jω ( τ ) ( τ ) τ ( * ) Z czego wynika, że wierdzenie Borela jes prawdziwe akże w przypadku prawosronnego zespolonego przekszałcenia Fouriera.
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Całka nieoznaczona Andrzej Musielak Str 1. Całka nieoznaczona
 Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
TRANSFORMATA FOURIERA
 TRANSFORMATA FOURIERA. Wzór całkowy Fouriera Wzór ten wykorzystujemy do analizy funkcji nieokresowych; funkcje te mogą opisywać np.przebiegi eleektryczne. Najpierw sformułujmy tzw. warunki Dirichleta.
TRANSFORMATA FOURIERA. Wzór całkowy Fouriera Wzór ten wykorzystujemy do analizy funkcji nieokresowych; funkcje te mogą opisywać np.przebiegi eleektryczne. Najpierw sformułujmy tzw. warunki Dirichleta.
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Całki podwójne. Definicja całki podwójnej. Jacek Kłopotowski. 25 maja Katedra Matematyki i Ekonomii Matematycznej
 Definicja całki podwójnej Katedra Matematyki i Ekonomii Matematycznej 25 maja 2016 Definicja całki podwójnej Załóżmy, że f : K R, gdzie K = a, b c, d R 2, jest funkcją ograniczoną. Niech x 0, x 1,...,
Definicja całki podwójnej Katedra Matematyki i Ekonomii Matematycznej 25 maja 2016 Definicja całki podwójnej Załóżmy, że f : K R, gdzie K = a, b c, d R 2, jest funkcją ograniczoną. Niech x 0, x 1,...,
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Szeregi Fouriera. Powyższe współczynniki można wyznaczyć analitycznie z następujących zależności:
 Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Całka podwójna po prostokącie
 Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Liczby zespolone. x + 2 = 0.
 Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Wykład 2: Szeregi Fouriera
 Rachunek prawdopodobieństwa MAP64 Wydział Elektroniki, rok akad. 8/9, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład : Szeregi Fouriera Definicja. Niech f(t) będzie funkcją określoną na R, okresową
Rachunek prawdopodobieństwa MAP64 Wydział Elektroniki, rok akad. 8/9, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład : Szeregi Fouriera Definicja. Niech f(t) będzie funkcją określoną na R, okresową
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Rachunek całkowy funkcji wielu zmiennych
 Rachunek całkowy funkcji wielu zmiennych Całki potrójne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki olitechnika Białostocka 1
Rachunek całkowy funkcji wielu zmiennych Całki potrójne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki olitechnika Białostocka 1
Teoria sygna³ów. Wstêp. Wydanie II poprawione i uzupe³nione
 IDZ DO PRZYK ADOWY ROZDZIA KATALOG KSI EK ZAMÓW DRUKOWANY KATALOG Wydawnicwo Helion ul Chopina 6 44- Gliwice el (32)23-98-63 e-mail: helion@helionpl TWÓJ KOSZYK CENNIK I INFORMACJE ZAMÓW INFORMACJE ONOWOŒCIACH
IDZ DO PRZYK ADOWY ROZDZIA KATALOG KSI EK ZAMÓW DRUKOWANY KATALOG Wydawnicwo Helion ul Chopina 6 44- Gliwice el (32)23-98-63 e-mail: helion@helionpl TWÓJ KOSZYK CENNIK I INFORMACJE ZAMÓW INFORMACJE ONOWOŒCIACH
Informacja o przestrzeniach Hilberta
 Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
FUNKCJE ZESPOLONE Lista zadań 2005/2006
 FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
Matematyczne Metody Fizyki II
 Matematyczne Metody Fizyki II Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 7 M. Przybycień (WFiIS AGH) Matematyczne Metody Fizyki II Wykład 7 1 / 11 Reprezentacja
Matematyczne Metody Fizyki II Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 7 M. Przybycień (WFiIS AGH) Matematyczne Metody Fizyki II Wykład 7 1 / 11 Reprezentacja
Dystrybucje. Marcin Orchel. 1 Wstęp Dystrybucje Pochodna dystrybucyjna Przestrzenie... 5
 Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Wykład 5 Elementy teorii układów liniowych stacjonarnych odpowiedź na dowolne wymuszenie
 Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
Przekształcenie całkowe Fouriera
 Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
Wojciech Grąziewicz. Skrypt dla studentów politechnik. Centrum Nauczania Matematyki i Kształcenia na Odległość
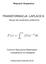 Wojciech Grąziewicz Skryp dla sudenów poliechnik Cenrum Nauczania Maemayki i Kszałcenia na Odległość Poliechnika Gdańska 26 SPIS TREŚCI Skryp przeznaczony jes głównie dla sudenów kierunków elekrycznych,
Wojciech Grąziewicz Skryp dla sudenów poliechnik Cenrum Nauczania Maemayki i Kszałcenia na Odległość Poliechnika Gdańska 26 SPIS TREŚCI Skryp przeznaczony jes głównie dla sudenów kierunków elekrycznych,
Funkcje analityczne. Wykład 3. Funkcje holomorficzne. Paweł Mleczko. Funkcje analityczne (rok akademicki 2016/2017) z = x + iy A
 Funkcje analityczne Wykład 3. Funkcje holomorficzne Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Funkcje zespolone zmiennej zespolonej Funkcje zespolone zmiennej zespolonej Niech A C. Funkcja
Funkcje analityczne Wykład 3. Funkcje holomorficzne Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Funkcje zespolone zmiennej zespolonej Funkcje zespolone zmiennej zespolonej Niech A C. Funkcja
Kurs wyrównawczy - teoria funkcji holomorficznych
 Kurs wyrównawczy - teoria funkcji holomorficznych wykład 1 Gniewomir Sarbicki 15 lutego 2011 Struktura ciała Zbiór par liczb rzeczywistych wyposażamy w działania: { + : (a, b) + (c, d) = (a + c, b + d)
Kurs wyrównawczy - teoria funkcji holomorficznych wykład 1 Gniewomir Sarbicki 15 lutego 2011 Struktura ciała Zbiór par liczb rzeczywistych wyposażamy w działania: { + : (a, b) + (c, d) = (a + c, b + d)
Przekształcenie Laplace a. Definicja i własności, transformaty podstawowych sygnałów
 Przekzałcenie Laplace a Deinicja i właności, ranormay podawowych ygnałów Tranormaą Laplace a unkcji je unkcja S zmiennej zepolonej, kórą oznacza ię naępująco: L[ ] unkcja S nazywana bywa również unkcją
Przekzałcenie Laplace a Deinicja i właności, ranormay podawowych ygnałów Tranormaą Laplace a unkcji je unkcja S zmiennej zepolonej, kórą oznacza ię naępująco: L[ ] unkcja S nazywana bywa również unkcją
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Podstawowe wyidealizowane elementy obwodu elektrycznego Rezystor ( ) = ( ) ( ) ( ) ( ) ( ) ( ) ( τ ) i t i t u ( ) u t u t i ( ) i t. dowolny.
 Tema. Opracował: esław Dereń Kaedra Teorii Sygnałów Insyu Telekomunikacji Teleinformayki i Akusyki Poliechnika Wrocławska Prawa auorskie zasrzeżone Podsawowe wyidealizowane elemeny obwodu elekrycznego
Tema. Opracował: esław Dereń Kaedra Teorii Sygnałów Insyu Telekomunikacji Teleinformayki i Akusyki Poliechnika Wrocławska Prawa auorskie zasrzeżone Podsawowe wyidealizowane elemeny obwodu elekrycznego
SZEREGI LICZBOWE I FUNKCYJNE
 Mając dowolny ciąg można z niego utworzyć nowy ciąg sum częściowych: Ten nowy rodzaj ciągu nazywamy szeregiem liczbowym, a jeśli to mamy do czynienia z nieskończonym szeregiem liczbowym, który oznaczany
Mając dowolny ciąg można z niego utworzyć nowy ciąg sum częściowych: Ten nowy rodzaj ciągu nazywamy szeregiem liczbowym, a jeśli to mamy do czynienia z nieskończonym szeregiem liczbowym, który oznaczany
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Rachunek całkowy - całka oznaczona
 SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
VII. ZAGADNIENIA DYNAMIKI
 Konderla P. Meoda Elemenów Skończonych, eoria i zasosowania 47 VII. ZAGADNIENIA DYNAMIKI. Równanie ruchu dla zagadnienia dynamicznego Q, (7.) gdzie M NxN macierz mas, C NxN macierz łumienia, K NxN macierz
Konderla P. Meoda Elemenów Skończonych, eoria i zasosowania 47 VII. ZAGADNIENIA DYNAMIKI. Równanie ruchu dla zagadnienia dynamicznego Q, (7.) gdzie M NxN macierz mas, C NxN macierz łumienia, K NxN macierz
Wykłady z Matematyki stosowanej w inżynierii środowiska, II sem. 2. CAŁKA PODWÓJNA Całka podwójna po prostokącie
 Wykłady z Matematyki stosowanej w inżynierii środowiska, II sem..1. Całka podwójna po prostokącie.. CAŁKA POWÓJNA.. Całka podwójna po obszarach normalnych..3. Całka podwójna po obszarach regularnych..4.
Wykłady z Matematyki stosowanej w inżynierii środowiska, II sem..1. Całka podwójna po prostokącie.. CAŁKA POWÓJNA.. Całka podwójna po obszarach normalnych..3. Całka podwójna po obszarach regularnych..4.
Równania różniczkowe liniowe wyższych rzędów o stałych współcz
 Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
Rachunek różniczkowy i całkowy w przestrzeniach R n
 Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ
 METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 6 Transformata Laplace a Funkcje specjalne Przekształcenia całkowe W wielu zastosowaniach dużą rolę odgrywają tzw. przekształcenia całkowe
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 6 Transformata Laplace a Funkcje specjalne Przekształcenia całkowe W wielu zastosowaniach dużą rolę odgrywają tzw. przekształcenia całkowe
SZEREG TRYGONOMETRYCZNY FOURIERA
 SZEREG TRYGONOMETRYCZNY FOURIERA Rozważmy ciag funkcji: 1, cos πx πx 2πx, sin, cos, sin 2πx,..., cos nπx, sin nπx,...}, gdzie jest pewną iczbą dodatnią. Zauważmy, że na przedziae , da dowonych dwóch
SZEREG TRYGONOMETRYCZNY FOURIERA Rozważmy ciag funkcji: 1, cos πx πx 2πx, sin, cos, sin 2πx,..., cos nπx, sin nπx,...}, gdzie jest pewną iczbą dodatnią. Zauważmy, że na przedziae , da dowonych dwóch
Analiza funkcjonalna 1.
 Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Wykład 7: Szeregi liczbowe i potęgowe. S 1 = a 1 S 2 = a 1 + a 2 S 3 = a 1 + a 2 + a 3. a k
 Wykład 7: Szeregi liczbowe i potęgowe. Definicja 1. Niech (a n ) - ustalony ciąg liczbowy. Określamy nowy ciąg: S 1 = a 1 S 2 = a 1 + a 2 S 3 = a 1 + a 2 + a 3. S n =. Ciąg sum częściowych (S n ) nazywamy
Wykład 7: Szeregi liczbowe i potęgowe. Definicja 1. Niech (a n ) - ustalony ciąg liczbowy. Określamy nowy ciąg: S 1 = a 1 S 2 = a 1 + a 2 S 3 = a 1 + a 2 + a 3. S n =. Ciąg sum częściowych (S n ) nazywamy
Praca domowa nr 1. Metodologia Fizyki. Grupa 1. Szacowanie wartości wielkości fizycznych Zad Stoisz na brzegu oceanu, pogoda jest idealna,
 Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Równanie przewodnictwa cieplnego (II)
 Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
Szeregi funkcyjne. Szeregi potęgowe i trygonometryczne. Katedra Matematyki Wydział Informatyki Politechnika Białostocka
 Szeregi funkcyjne Szeregi potęgowe i trygonometryczne Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika Białostocka Szeregi funkcyjne str. 1/36 Szereg potęgowy Szeregiem potęgowym o
Szeregi funkcyjne Szeregi potęgowe i trygonometryczne Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika Białostocka Szeregi funkcyjne str. 1/36 Szereg potęgowy Szeregiem potęgowym o
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ
 RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ Wykorzysano: M A T E M A T Y K A Wykład dla sudenów Część Krzyszo KOŁOWROCKI, ZBIÓR ZADAŃ Z RACHUNKU CAŁKOWEGO Krzyszo PISKÓRZ Deinicja CAŁKA NIEOZNACZONA Funkcję
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ Wykorzysano: M A T E M A T Y K A Wykład dla sudenów Część Krzyszo KOŁOWROCKI, ZBIÓR ZADAŃ Z RACHUNKU CAŁKOWEGO Krzyszo PISKÓRZ Deinicja CAŁKA NIEOZNACZONA Funkcję
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej. Całki nieoznaczone
 Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Całki nieoznaczone 1. Definicja całki nieoznaczonej Definicja 1. Funkcja F jest funkcją pierwotną funkcji f na przedziale I, jeżeli F (x) =
Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Całki nieoznaczone 1. Definicja całki nieoznaczonej Definicja 1. Funkcja F jest funkcją pierwotną funkcji f na przedziale I, jeżeli F (x) =
5 Równania różniczkowe zwyczajne rzędu drugiego
 5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
Całki niewłaściwe. Całki w granicach nieskończonych
 Całki niewłaściwe Całki w granicach nieskończonych Wiemy, co to jest w przypadku skończonego przedziału i funkcji ograniczonej. Okazuje się potrzebne uogólnienie tego pojęcia w różnych kierunkach (przedział
Całki niewłaściwe Całki w granicach nieskończonych Wiemy, co to jest w przypadku skończonego przedziału i funkcji ograniczonej. Okazuje się potrzebne uogólnienie tego pojęcia w różnych kierunkach (przedział
ĆWICZENIE 7 WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA. Wprowadzenie
 ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
Definicja punktu wewnętrznego zbioru Punkt p jest punktem wewnętrznym zbioru, gdy należy do niego wraz z pewnym swoim otoczeniem
 Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Funkcje analityczne. Wykład 2. Płaszczyzna zespolona. Paweł Mleczko. Funkcje analityczne (rok akademicki 2017/2018)
 Funkcje analityczne Wykład 2. Płaszczyzna zespolona Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) Plan wykładu W czasie wykładu omawiać będziemy różne reprezentacje płaszczyzny zespolonej
Funkcje analityczne Wykład 2. Płaszczyzna zespolona Paweł Mleczko Funkcje analityczne (rok akademicki 2017/2018) Plan wykładu W czasie wykładu omawiać będziemy różne reprezentacje płaszczyzny zespolonej
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
oznacza przyrost argumentu (zmiennej niezależnej) x 3A82 (Definicja). Granicę (właściwą) ilorazu różnicowego funkcji f w punkcie x x x e x lim x lim
 WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
Lista nr Znaleźć rozwiązania ogólne następujących równań różniczkowych: a) y = y t,
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład II
 Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład VIII Przekształcenie Laplace a
 8. Geneza przekzałcenia Laplace a. Wykład VIII Przekzałcenie Laplace a Warunek bezwzględnej całkowalności w przedziale niekończonym, nakładany na oryginały przekzałceń Fouriera, bardzo ogranicza ich klaę.
8. Geneza przekzałcenia Laplace a. Wykład VIII Przekzałcenie Laplace a Warunek bezwzględnej całkowalności w przedziale niekończonym, nakładany na oryginały przekzałceń Fouriera, bardzo ogranicza ich klaę.
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
Całka nieoznaczona, podstawowe wiadomości
 Całka nieoznaczona, podstawowe wiadomości Funkcją pierwotną funkcji w przedziale nazywamy funkcję taką, że dla każdego punktu z tego przedziału zachodzi Różnica dwóch funkcji pierwotnych w przedziale danej
Całka nieoznaczona, podstawowe wiadomości Funkcją pierwotną funkcji w przedziale nazywamy funkcję taką, że dla każdego punktu z tego przedziału zachodzi Różnica dwóch funkcji pierwotnych w przedziale danej
Wykład 14 i 15. Równania różniczkowe. Równanie o zmiennych rozdzielonych. Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie
 Wykład 14 i 15 Równania różniczkowe Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (x, y, y, y,..., y (n) ) = 0 (1) gdzie: y = y(x) niewiadoma funkcja zmiennej rzeczywistej
Wykład 14 i 15 Równania różniczkowe Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (x, y, y, y,..., y (n) ) = 0 (1) gdzie: y = y(x) niewiadoma funkcja zmiennej rzeczywistej
Wykład X. ε, ε, ε = ε oznaczają współrzędne tensora odkształcenia, u i w są współrzędnymi wektora WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ
 Wykład X ROZWIĄZANIE RÓWNAŃ RÓŻNICZKOWYC Z WYKORZYSTANIEM TRANSFORMACJI LAPLACE A i FOURIERA CIĄG DALSZY. Konsolidacja półprzesrzeni konsolidujące pod działaniem ruchomego obciążenia skupionego. Rozważmy
Wykład X ROZWIĄZANIE RÓWNAŃ RÓŻNICZKOWYC Z WYKORZYSTANIEM TRANSFORMACJI LAPLACE A i FOURIERA CIĄG DALSZY. Konsolidacja półprzesrzeni konsolidujące pod działaniem ruchomego obciążenia skupionego. Rozważmy
Wykłady... b i a i. i=1. m(d k ) inf
 Wykłady... CŁKOWNIE FUNKCJI WIELU ZMIENNYCH Zaczniemy od konstrukcji całki na przedziale domkniętym. Konstrukcja ta jest, w gruncie rzeczy, powtórzeniem definicji całki na odcinku domkniętym w R 1. Przedziałem
Wykłady... CŁKOWNIE FUNKCJI WIELU ZMIENNYCH Zaczniemy od konstrukcji całki na przedziale domkniętym. Konstrukcja ta jest, w gruncie rzeczy, powtórzeniem definicji całki na odcinku domkniętym w R 1. Przedziałem
Wykład 21 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej
 Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
1. Liczby zespolone Zadanie 1.1. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone (1) 1 i (2) (5)
 . Liczby zespolone Zadanie.. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone () i +i, () 3i, (3) ( + i 3) 6, (4) (5) ( +i ( i) 5, +i 3 i ) 4. Zadanie.. Znaleźć moduł i argument główny
. Liczby zespolone Zadanie.. Przedstawić w postaci a + ib, a, b R, następujące liczby zespolone () i +i, () 3i, (3) ( + i 3) 6, (4) (5) ( +i ( i) 5, +i 3 i ) 4. Zadanie.. Znaleźć moduł i argument główny
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ
 ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
Temat 6. ( ) ( ) ( ) k. Szeregi Fouriera. Własności szeregów Fouriera. θ możemy traktować jako funkcje ω, których dziedziną jest dyskretny zbiór
 ema 6 Opracował: Lesław Dereń Kaedra eorii Sygnałów Insyu eleomuniacji, eleinformayi i Ausyi Poliechnia Wrocławsa Prawa auorsie zasrzeżone Szeregi ouriera Jeżeli f ( ) jes funcją oresową o oresie, czyli
ema 6 Opracował: Lesław Dereń Kaedra eorii Sygnałów Insyu eleomuniacji, eleinformayi i Ausyi Poliechnia Wrocławsa Prawa auorsie zasrzeżone Szeregi ouriera Jeżeli f ( ) jes funcją oresową o oresie, czyli
Matematyka liczby zespolone. Wykład 1
 Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
CAŁKI NIEOZNACZONE C R}.
 CAŁKI NIEOZNACZONE Definicja 1 Funkcja F jest funkcją pierwotną funkcji f na przedziale I, jeżeli F (x) = f(x) dla każdego x I. Np. funkcjami pierwotnymi funkcji f(x) = sin x na R są cos x, cos x+1, cos
CAŁKI NIEOZNACZONE Definicja 1 Funkcja F jest funkcją pierwotną funkcji f na przedziale I, jeżeli F (x) = f(x) dla każdego x I. Np. funkcjami pierwotnymi funkcji f(x) = sin x na R są cos x, cos x+1, cos
Przekształcenia całkowe. Wykład 1
 Przekształcenia całkowe Wykład 1 Przekształcenia całkowe Tematyka wykładów: 1. Liczby zespolone -wprowadzenie, - funkcja zespolona zmiennej rzeczywistej, - funkcja zespolona zmiennej zespolonej. 2. Przekształcenie
Przekształcenia całkowe Wykład 1 Przekształcenia całkowe Tematyka wykładów: 1. Liczby zespolone -wprowadzenie, - funkcja zespolona zmiennej rzeczywistej, - funkcja zespolona zmiennej zespolonej. 2. Przekształcenie
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
Analityczne reprezentacje sygnałów ciągłych
 Analiyczne reprezenacje sygnałów ciągłych Przedsawienie sygnału w posaci analiycznej: umożliwia uproszczenie i unifiację meod analizy, pozwala na prosszą inerpreację nieórych jego cech fizycznych. W eorii
Analiyczne reprezenacje sygnałów ciągłych Przedsawienie sygnału w posaci analiycznej: umożliwia uproszczenie i unifiację meod analizy, pozwala na prosszą inerpreację nieórych jego cech fizycznych. W eorii
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
( ) ( ) ( τ) ( t) = 0
 Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Wykłady ostatnie. Rodzinę P podzbiorów przestrzeni X nazywamy σ - algebrą, jeżeli dla A, B P (2) A B P, (3) A \ B P,
 Wykłady ostatnie CAŁKA LBSGU A Zasadnicza różnica koncepcyjna między całką Riemanna i całką Lebesgue a polega na zamianie ról przestrzeni wartości i przestrzeni argumentów przy konstrukcji sum górnych
Wykłady ostatnie CAŁKA LBSGU A Zasadnicza różnica koncepcyjna między całką Riemanna i całką Lebesgue a polega na zamianie ról przestrzeni wartości i przestrzeni argumentów przy konstrukcji sum górnych
7 Twierdzenie Fubiniego
 M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
Wykład 15. Matematyka 3, semestr zimowy 2011/ listopada 2011
 Wykład 5 Matematyka 3, semestr zimowy / 9 listopada W trakcie tego i następnych kilku wykładów zajmować się będziemy analizą zespoloną, czyli różniczkowaniem i całkowaniem funkcji argumentu zespolonego
Wykład 5 Matematyka 3, semestr zimowy / 9 listopada W trakcie tego i następnych kilku wykładów zajmować się będziemy analizą zespoloną, czyli różniczkowaniem i całkowaniem funkcji argumentu zespolonego
1 Równania różniczkowe zwyczajne o rozdzielonych zmiennych
 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Funkcje analityczne. Wykład 12
 Funkcje analityczne. Wykład 2 Szeregi Laurenta. Osobliwości funkcji zespolonych. Twierdzenie o residuach Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Plan wykładu W czasie wykładu omawiać
Funkcje analityczne. Wykład 2 Szeregi Laurenta. Osobliwości funkcji zespolonych. Twierdzenie o residuach Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Plan wykładu W czasie wykładu omawiać
Funkcje analityczne. Wykład 1. Co to są i do czego służą funkcje analityczne? Funkcje analityczne (rok akademicki 2016/2017)
 Funkcje analityczne Wykład 1. Co to są i do czego służą funkcje analityczne? Funkcje analityczne (rok akademicki 2016/2017) Paweł Mleczko Uniwersytet im. Adama Mickiewicza w Poznaniu 1. Sprawy organizacyjne
Funkcje analityczne Wykład 1. Co to są i do czego służą funkcje analityczne? Funkcje analityczne (rok akademicki 2016/2017) Paweł Mleczko Uniwersytet im. Adama Mickiewicza w Poznaniu 1. Sprawy organizacyjne
Funkcja pierwotna. Całka nieoznaczona. Podstawowe wzory. Autorzy: Konrad Nosek
 Funkcja pierwotna. Całka nieoznaczona. Podstawowe wzory Autorzy: Konrad Nosek 09 Funkcja pierwotna. Całka nieoznaczona. Podstawowe wzory Autor: Konrad Nosek DEFINICJA Definicja : Funkcja pierwotna Rozważmy
Funkcja pierwotna. Całka nieoznaczona. Podstawowe wzory Autorzy: Konrad Nosek 09 Funkcja pierwotna. Całka nieoznaczona. Podstawowe wzory Autor: Konrad Nosek DEFINICJA Definicja : Funkcja pierwotna Rozważmy
13 Równanie struny drgającej. Równanie przewodnictwa ciepła.
 Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
"Potęga matematyki polega na pomijaniu wszystkich myśli zbędnych i cudownej oszczędności operacji myślowych. Ernst Mach. IV. Funkcja wykładnicza
 "Poęga maemayki polega na pomijaniu wszyskich myśli zbędnych i cudownej oszczędności operacji myślowych. Erns Mach IV. Funkcja wykładnicza Def. Funkcją wykładniczą nazywamy funkcję posaci f = a, gdzie
"Poęga maemayki polega na pomijaniu wszyskich myśli zbędnych i cudownej oszczędności operacji myślowych. Erns Mach IV. Funkcja wykładnicza Def. Funkcją wykładniczą nazywamy funkcję posaci f = a, gdzie
Rachunek różniczkowy i całkowy 2016/17
 Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
macierze jednostkowe (identyczności) macierze diagonalne, które na przekątnej mają same
 1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
Rozdział XV CAŁKI KRZYWOLINIOWE. CAŁKA STIELTJESA
 Księgarnia PWN: Grigorij M. Fichtenholz Rachunek różniczkowy i całkowy. T. 3 Rozdział XV CAŁKI KRZYWOLINIOWE. CAŁKA STIELTJESA 1. Całki krzywoliniowe pierwszego rodzaju 543. Definicja całki krzywoliniowej
Księgarnia PWN: Grigorij M. Fichtenholz Rachunek różniczkowy i całkowy. T. 3 Rozdział XV CAŁKI KRZYWOLINIOWE. CAŁKA STIELTJESA 1. Całki krzywoliniowe pierwszego rodzaju 543. Definicja całki krzywoliniowej
5. Całka nieoznaczona
 5. Całka nieoznaczona Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5. Całka nieoznaczona zima 2017/2018 1 / 31 Całka nieoznaczona
5. Całka nieoznaczona Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5. Całka nieoznaczona zima 2017/2018 1 / 31 Całka nieoznaczona
2. P (E) = 1. β B. TSIM W3: Sygnały stochastyczne 1/27
 SYGNAŁY STOCHASTYCZNE Przestrzeń probabilistyczna i zmienna losowa Definicja Przestrzenią probabilistyczną (doświadczeniem) nazywamy trójkę uporządkowaną (E, B, P ), gdzie: E przestrzeń zdarzeń elementarnych;
SYGNAŁY STOCHASTYCZNE Przestrzeń probabilistyczna i zmienna losowa Definicja Przestrzenią probabilistyczną (doświadczeniem) nazywamy trójkę uporządkowaną (E, B, P ), gdzie: E przestrzeń zdarzeń elementarnych;
Całki krzywoliniowe wiadomości wstępne
 Całki krzywoliniowe wiadomości wstępne Łuk na płaszczyźnie to zbiór punktów (x, y o współrzędnych x = x(t, y = y(t, gdzie (x(t, y(t są funkcjami ciągłymi określonymi na przedziale bez punktów wielokrotnych.
Całki krzywoliniowe wiadomości wstępne Łuk na płaszczyźnie to zbiór punktów (x, y o współrzędnych x = x(t, y = y(t, gdzie (x(t, y(t są funkcjami ciągłymi określonymi na przedziale bez punktów wielokrotnych.
Wykład 2. Transformata Fouriera
 Wykład 2. Transformata Fouriera Transformata Fouriera jest podstawowym narzędziem analizy harmonicznej i teorii analizy i przetwarzania sygnału. Z punktu widzenia teorii matematycznej transformata Fouriera
Wykład 2. Transformata Fouriera Transformata Fouriera jest podstawowym narzędziem analizy harmonicznej i teorii analizy i przetwarzania sygnału. Z punktu widzenia teorii matematycznej transformata Fouriera
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
6. Całka nieoznaczona
 6. Całka nieoznaczona Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 6. Całka nieoznaczona 1 / 35 Całka nieoznaczona - motywacja Wiemy
6. Całka nieoznaczona Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 6. Całka nieoznaczona 1 / 35 Całka nieoznaczona - motywacja Wiemy
Lista 6. Kamil Matuszewski 13 kwietnia D n =
 Lista 6 Kamil Matuszewski 3 kwietnia 6 3 4 5 6 7 8 9 Zadanie Mamy Pokaż, że det(d n ) = n.... D n =.... Dowód. Okej. Dla n =, n = trywialne. Załóżmy, że dla n jest ok, sprawdzę dla n. Aby to zrobić skorzystam
Lista 6 Kamil Matuszewski 3 kwietnia 6 3 4 5 6 7 8 9 Zadanie Mamy Pokaż, że det(d n ) = n.... D n =.... Dowód. Okej. Dla n =, n = trywialne. Załóżmy, że dla n jest ok, sprawdzę dla n. Aby to zrobić skorzystam
1. Liczby zespolone. Jacek Jędrzejewski 2011/2012
 1. Liczby zespolone Jacek Jędrzejewski 2011/2012 Spis treści 1 Liczby zespolone 2 1.1 Definicja liczby zespolonej.................... 2 1.2 Postać kanoniczna liczby zespolonej............... 1. Postać
1. Liczby zespolone Jacek Jędrzejewski 2011/2012 Spis treści 1 Liczby zespolone 2 1.1 Definicja liczby zespolonej.................... 2 1.2 Postać kanoniczna liczby zespolonej............... 1. Postać
Wykład 4: Transformata Laplace a
 Rachunek prawdopodobieńwa MAP164 Wydział Elekroniki, rok akad. 28/9, em. leni Wykładowca: dr hab. A. Jurlewicz Wykład 4: Tranformaa Laplace a Definicja. Niech f() będzie funkcją określoną na R, przy czym
Rachunek prawdopodobieńwa MAP164 Wydział Elekroniki, rok akad. 28/9, em. leni Wykładowca: dr hab. A. Jurlewicz Wykład 4: Tranformaa Laplace a Definicja. Niech f() będzie funkcją określoną na R, przy czym
