Wste p 3. 1 Przegla d w laściwości sieci Sieć Bravais Dyfrakcyjne metody badania sieci krystalicznych...6
|
|
|
- Bogna Szewczyk
- 6 lat temu
- Przeglądów:
Transkrypt
1 Spis treści Wste p 3 1 Przegla d w laściwości sieci Sieć Bravais Dyfrakcyjne metody badania sieci krystalicznych Sieć odwrotna i jej zwia zek z dyfrakcja Rola drgań sieci krystalicznej a) Model Einsteina b) Model Debye a W laściwości gazu elektronów swobodnych Model gazu Fermiego Rola wzbudzeń termicznych Zjawiska magnetyczne w cia lach sta lych Podstawy magnetyzmu a) Podejście klasyczne b) Podejście mechaniki kwantowej Paramagnetyzm Pauliego Oddzia lywanie wymienne Uporza dkowanie typu ferromagnetycznego Uporza dkowanie typu antyferromagnetycznego Struktura pasmowa cia l sta lych Blochowski charakter elektronów w kryszta lach Przypadek elektronów s labo sprze żonych z siecia Przypadek elektronów ciasno sprze żonych z jonami Klasyfikacja cia l sta lych pod wzgle dem struktury pasmowej
2 4.5 Koncentracja nośników w pó lprzewodnikach...59 a) Pó lprzewodniki samoistne...61 b) Pó lprzewodniki domieszkowane Struktura pasmowa grafenu Zjawiska transportowe Klasyczne podejście Drudego Kwantowomechaniczny opis zjawisk transportu Z la cza tunelowe - kwant przewodnictwa Nadprzewodnictwo i jego zastosowania Podstawowe cechy stanu nadprzewodza cego Teoria Londonów Podejście Ginzburga - Landaua Elementy mikroskopowej teorii nadprzewodnictwa Przegla d odkryć nadprzewodników Wspó lczesne wykorzystanie nadprzewodnictwa Literatura 113 2
3 Wste p Obecny kurs Fizyki materii skondensowanej zosta l opracowany z przeznaczoniem dla studentów 3 roku licencjackich studiów Fizyki Technicznej na Uniwersytecie M. Curie Sk lodowskiej w Lublinie. Jest to kontynuacja zagadnień realizowanych wcześniej na 2 roku studiów dla wspomnianego kierunku w ramach przedmiotu pt. Fizyka cia la sta lego. Z tego powodu w obecnym opracowaniu kursu fizyki materii skondensowanej niektóre zagadnienia celowo pominie to lub potraktowano skrótowo, mie dzy innymi: problematyke wia zań w cia lach sta lych, elementy krystalografii, opis dyfrakcji fal na kryszta lach itp. Zasadnicza cze ść niniejszego opracowania stanowia zagadnienia kwantowego opisu uk ladu elektronów swobodnych (rozdzia l 2), magnetyzmu (rozdzia l 3), struktury pasmowej elektronów sprze żonych z siecia [w tym również niedawno odkrytego grafenu] (rozdzia l 4), klasyczny i kwantowy opis transportu elektronowego w cia lach sta lych oraz strukturach hybrydowych z wbudowanymi nanostrukturami (rozdzia l 5). Ostatni rozdzia l 6 omawia ważniejsze aspekty zagadnienia nadprzewodnictwa. W szczególności przedstwiono tam: przegla d charakterystycznych cech nadprzewodników, pó lklasyczna interpretacje zjawiska idealnego oporu (czyli podejście Fritza i Heinza Londonów), fenomenologiczny opis Ginzburga Landaua oparty na koncepcji przejścia fazowego, mikroskopowa teorie J. Bardeena, L. Coppera i R. Schrieffera a także przegla d aktualnych zastosowań nadprzewodników w przemyśle, nauce i medycynie. Wybór powyższych zagadnień by l oczywiście subiektywny. Wydaje sie jednak, że wybrane zaganienia należa do zasadniczych z obszernego zakresu problematyki fizyki materii skondensowanej. Studentom korzystaja cym z obecnego opracowania życze mi lej lektury, zache cam do pog le biania wiedzy w oparciu o podana literature a także prosze o wszelkie uwagi krytyczne. Lublin, sierpień 2013 r. Tadeusz Domański 3
4 1. Przegla d w laściwości sieci Stabilność oraz periodyczne uporza dkowanie materii skondensowanej jest rezultatem najbardziej korzystnej konfiguracji (pod wzgle dem energetycznym) w ca lkowitym bilansie energii wia zań i energii kinetycznej atomów. Zależnie od rodzaju materia lu dominuja ce znaczenie odgrywać moga wia zania: van der Waalsa (w kryszta lach skondensowanych atomów gazów szlachetnych), jonowe (w kryszta lach zjonizowanych atomów i pozosta lej chmury elektronów we drownych), kowalencyjne (np. w kryszta lach germanu, krzemu lub w alotropowych formach we gla), metaliczne (w przewodnikach) lub wodorowe (w materii organicznej). Na poziomie mikroskopowym sieć krystaliczna możemy sobie wyobrazić jako periodycznie powtarzaja ce sie sekwencje atomów lub grup atomów (moleku l). W najprostszym przypadku powielanym elementem może być pojedynczy lub pdwójny atom (np. w metalach). Taki powtarzaja cy sie w przestrzeni segment atomów nazywamy baza. Przestrzenne rozmieszczenie powilanych elementów bazy opisuje formalnie tzw. sieć Bravais. Jest to geometryczna konstrukcja z lożona z punktów (tzw. we z lów), których rozmieszczenie odzwierciedla rodzaje symetrii realizowanych w konkretnych kryszta lach. W poniższym podrozdziale przedstawimy krótki przegla d typowych sieci Bravais. 1.1 Sieć Bravais Geometryczna konstrukcja sieci Bravais polega na powieleniu wyjściowego we z la (który możemy utożsamić z po lożeniem wybranego punktu bazy) poprzez transformacje translacji T = n 1 a + n 2 b + n 3 c, (1) gdzie a, b oraz c sa tzw. wektorami prostymi zaś n i oznaczaja liczby ca lkowite. W ten sposób uzyskujemy zbiór punktów (we z lów sieci Bravais). Dla konkretnych kryszta lów konstrukcje sieci Bravais można przeprowadzić dobieraja c różne zestawy wektorów prostych. Dowolność wyboru ograniczona jest jedynie wymogiem, aby transformacja (1) odtwarza la wszystkie po lożenia we z lów w sieci krystalicznej (nie można pomina ć żadnego we z la). 4
5 Z wyborem konkretnego zestawu wektorów a, b, c jest ściśle zwia zany kszta lt tzw. komórek prostych zbudowanych na tych wektorach. Niekiedy wygodniejsze sa do analizy komórki elementarne, które sa wielokrotnościa komorek prostych. Jako przyk lad na poniższym rysunku przedstawione sa charakterystyczne komórki proste lub elementarne dla kryszt lów dwuwymiarowych, czyli dla struktur p laskich. Rys. 1.1 Pie ć dopuszczalnych typów dwuwymiarowej sieci Bravais. Wyodre bnienie poszczególnych sieci jest uzasadnione niezmienniczościa sieci na transformacje : obrotu, inwersji, odbicia zwierciadlanego itp. W przypadku dwywymiarowej sieci symetrie można jednoznacznie scharakteryzować za pomoca d lugości wektorów prostych oraz ka ta φ mie dzy nimi. W rezultacie wyróżnia sie naste puja ce rodzaje: sieć kwadratowa a = b, φ = 90 o, sieć prostoka tna a b, φ = 90 o, sieć prostoka tna centrowana wewne trznie a b, φ = 90 o, sieć heksagonalna a = b, φ = 120 o oraz sieć skośna a b, φ 90 o i φ 120 o. W przypadku trójwymiarowym istnieje 14 różnych typów sieci Bravais. Niektóre z nich maja kilka specificznych wariantów, np. sieć regularna (ang. simple cubic) z dodatkowym we z lem w środku (ang. body centered cubic) lub z we z lami na każdej p laszczyźnie komórki prostej (ang. face centered cubic). Szczegó ly dotycza ce trójwymiarowych sieci sa wyczerpuja co opisane niemal w każdym podre czniku fizyki cia la sta lego. Poszczególne rodzaje sieci Bravais można charakyteryzować za pomoca wspó lczynnika upakowania oraz liczby koordynacyjnej. 5
6 1.2 Dyfrakcyjne metody badania sieci krystalicznych Odleg lości mie dzy atomami w sieciach krystalicznych wynosza zazwyczaj od kilku do kilkunastu Å. Najwcześniejsze doświdczalne metody badania struktury krystalograficznej wykorzystywa ly zjawisko dyfrakcji fal (elektromagnetycznych lub fal materii). Efekty interferencyjne moga być obserwowalne, jeżeli d lugość fal λ nie przekracza odleg lości mie dzyp laszczyznowych d. Idee uzyskiwania wzmocnienia/wygaszenia interferencyjnego przedstawia poniṡzy rysunek. Rys. 1.2 Schemat odbicia fal o d lugości λ d od pierwszej i drugiej warstwy p laszczyzny krystalicznej. Dla interferencji kluczowe znaczenie ma różnica dróg optycznych 2d sin (θ). Fala padaja ca pod ka tem θ na p lytke krystaliczna cze ściowo ulega odbiciu od powierzchni a cze ściowo wnika do g le bszych warstw. Fale odbite od pierwszej warstwy atomów interferuja z falami odbitymi od kolejnych warstw. G lówny wk lad do interferencji wnosza fale odbite od p laszczyzn po lożonych najbliżej powierzchni kryszta lu, gdyż wraz z g le bokościa fale ulegaja znacznemu t lumieniu. Aby określić warunki interferencji konstruktywnej lub destruktywnej należy uwzgle dnić różnice dróg optycznych 2d sin (θ). Wzmocnienie dyfrakcyjne zachodzi, jeśli ta różnica dróg optycznych jest równa wielokrotności d lugości fali 2d sin (θ) = nλ, gdzie n = 1, 2, 3,... (2) Interferencja fal o przeciwnych fazach prowadzi natomiast do wygaszenia dyfrakcyjnego. Ma ono miejsce, gdy 2d sin (θ) = ( n + 1 ) λ. (3) 2 Przedstawione powyżej rozumowanie jest treścia braggowskiego prawa dyfrakcji, formalnie 6
7 wyrażonego wzorami (2,3). Jeszcze raz należy podkreślicć, że ze wzgle du na sin (θ) 1 wzmocnienie dyfrakcyjne jest obserwowalne wy la cznie przy użyciu fal o d lugości λ 2d. Do tego można wie c wykorzystać fale rentgenowskie lub falowy charakter cza stek materialnych (elektronów lub neutronów/protonów) o odpowiedniej energii kinetycznej. Rys. 1.3 Metoda Lauego, która jest użyteczna g lównie do określenia symetrii kryszta lu. Rys. 1.4 Metoda proszkowa (Debye a Scherrera) dostarcza informacji o odleg lościach d. Do badania kryszta lów wykorzystywano dwa różne sposoby doświadczalne: a) metode Lauego oraz b) metode Debye a Scherrera. W pierwszym przypadku wia zke fal polichromatycznej kierowano na monokryszta l i zależnie od ka ta odchylenia 2θ obserwowano obraz dyfrakcyjny pochodza cy od różnych fal. W drugiej metodzie używano próbek proszkowych (polikrystalicznych) na które kierowano wia zke fali monochromatycznej. Metody te zilustrrowane sa na powyższych rysunkach, które zaczerpnie to z podre cznika. Z. Bojarski, La giewka, Rentgenowska analiza strukturalna, PWN Warszawa (1988). 7
8 1.3 Sieć odwrotna i jej zwia zek z dyfrakcja Wygodnym sposobem analizy obrazów dyfrakcyjnych jest wykorzystanie koncepcji tzw. sieci odwrotnej. Aby zrozumieć istote konstrukcji sieci odwrotnej warto przeprowadzić analize fourierowska periodycznego potencja lu krystalicznego U(r) = U(r + T), (4) gdzie T jest wektorem translacji (1). Transformaty Fouriera U(r) 1 u k e ikr) (5) V takiego periodycznego potencja lu (4) spe lniaja relacje k 1 V u k e ikr = 1 k V u k e ik(r+t), (6) k zatem wektory k musza charakteryzować sie naste puja ca w lasnościa matematyczna 1 = e ikt. (7) Wektory k określone powyższym warunkiem (7) nazywamy wektorami sieci odwrotnej i be dziemy oznaczać je symbolem G. Takie wektory sieci odwrotnej można przedstawić w naste puja cej postaci G = ha + kb + lc, (h,k,l sa liczbami ca lkowitymi) (8) gdzie a, b oraz c sa zdefionwane przez a = 2π b c a (b c), b = 2π c a a (b c), c = 2π a b.) (9) a (b c) Powyższy wybór implikuje ortogonalność a a, b b i podobnie c c. Latwo wykazać ponadto, że a a = 2π, b b = 2π, c c = 2π. Zatem T G = (n 1 a + n 2 b + n 3 c) (ha + kb + lc ) = (n 1 h + n 2 k + n 3 l) }{{} liczba ca lkowita 2π, (10) co faktycznie spe lnia wymóg (7), determinuja cy wektory sieci odwrotnej. Każdej konkretnej sieci Bravais można na tej zasadzie przypisać określona sieć odwrotna, zdefiniowana poprzez zbiór wektorów G określonych wyrażeniem (8) i (9). 8
9 Opis dyfrakcji wed lug Lauego Rozpatrzmy wia zke monochromatycznych fal padaja cych na próbke krystaliczna (lub w ogólności polikrystaliczna ). Wia zka fal jest opisana wektorem falowym k, którego zwrot oznacza kierunek padania zaś modu l określa d lugość fal k = 2π/λ. Po rozproszeniu na próbce fale ulegaja ugie ciu. Za lożymy, że rozpraszanie jest elastyczne (czyli d lugość fal nie ulega zmianie). Ca lkowita amplitude F fali rozproszonej do wektora k można wyznaczyć dokonuja c ca lkowania czynnika fazowego w ca lej obje tości próbki F = dre i(k k ) r n(r). Wprowadzaja c wektor ugie cia fali k = k k i wykorzystuja c fakt, że koncentracja n(r) charakteryzuje sie periodycznościa n(r) = 1 V G e ig r n G otrzymujemy F = dre i k r 1 e ig r n(g) = 1 n(g) V V G G dre i(g k) r. (11) Maksymalna wartość amplitudy fali rozproszonej otrzymamy zatem, jeżeli k = G, (12) co implikuje warunek dyfrakcji Lauego a k = 2π n 1, b k = 2π n 2, c k = 2π n 3, (13) gdzie n i sa dowolnymi liczbami ca lkowitymi. Poszczególne równania Lauego oznaczaja, że wzmocnienie dyfrakcyjne realizuje sie na n 1 -tym stożku wokó l wektora a, oraz odpowiednio podobnie z pozosta lymi wektorami. W trójwymiarowej przestrzeni spe lnienie takich relacji Lauego jest dość trudne. Określenie kierunków wzmocnień dyfrakcyjnych można latwo uzyskać stosuja c konstrukcje geometryczna Ewalda (patrz rysunek 1.5). W sieci odwrotnej (której we z ly oznaczono na rysunku symbolem x) zaznaczamy wektor fali padaja cej k, tak aby jego zakończenie znajdowa lo sie na jednym z we z lów sieci odwrotnej. Kreślimy naste pnie okra g (a przypadku w trójwymiarowym sfere ) o promieniu k = k i sprawdzamy ewentualne punkty przecie cia okre gu z we z lami sieci odwrotnej. Każdy punkt przecie cia wyznacza wartość k = k k. Punkty przecinania sie we z lów sieci odwrotnej z promieniem o d lugości k = k wskazuja kierunek wzmocnienia dyfrakcyjnego, dla którego różnica wektora fal rozproszonej i odbitej k spe lnia warunek (12). 9
10 Rys. 1.5 Geometryczny schemat Ewalda, s luża cy do określenia kierunków wzmocnień dyfrakcyjnych na podstawie kryterium k 1 k = G. Rysunek zaczerpnie to z podre cznika. Powyższy rysunek pochodzi z podre cznika. Warunek dyfrakcyjny (12) można przekszta lcić do równoważnej postaci (k ) 2 = (k + G) 2 k 2 = k 2 + 2k G + G 2, (14) który w przypadku rozpraszania spre zystego k = k implikuje D lugość wektora sieci odwrotnej niesie informacje 0 = 2k G + G 2. (15) o odleg lości d hkl = 2π G hkl mie dzy p laszczyznami o wskaźnikach Millera (hkl) zaś d lugość fali wynosi k = 2π/λ, zatem warunek (15) faktycznie odtwarza prawo Bragga 2 k G sin (θ hkl ) = G 2 znane w postaci sin (θ hkl ) = λ. (16) 2d hkl Powyższy schemat zosta l wykorzystany przez L. Brillouina do zdefiniowania specjalnych obszarów przestrzeni odwrotnej, dla których zachodzi warunek wzmocnienia dyfrakcyjnego. Sa one obecnie nazywane w literaturze strefami Brillouina. Graficzna konstrukcje pierwszej strefy Brillouina ilustruje rysunek 1.6 zaczerpnie ty z monografii. H. Ibach, H. Lüth, Fizyka cia la sta lego, Wydawnictwo Naukowe PWN, Warszawa (1996). L. Sander, Advanced Condensed Matter Physics, Cambridge Univ. Press, Cambridge (2009). 10
11 Rys. 1.6 Ilustracja I-ej strefy Brillouina dla dwywymiarowej (dim=2) sieci heksagonalnej. O niekwestionawalnej przydatności stref Brillouina przekonamy sie w dalszej cze ści obecnego kursu (rozdzia l 4) przy analizowaniu uk ladu elektronów poruszaja cych sie w periodycznej sieci. Tymczasem, w konteście zjawiska dyfrakcji fal, wprawadźmy pomocniczo wektor sieci odwrotnej G = G, kiedy warunek (14) można zapisać jako k G = G 2. Każdy wektor 2 2 falowy k, którego rzut na G jest równy d lugości wektora 2 G gwarantuje spe lnienie warunku 2 dyfrakcyjnego. Zmiana wektorów falowych k jest wówczas równa G, zgodnie z wymogiem 2 (12). W przypadku, gdy d lugość wektora G jest 2 najmniejsza z możliwych, wówczas obszar wydzielony w przestrzeni odwrotnej oznacza tzw. pierwsza strefa Brillouina (patrz ilustracja graficzna na poprzedniej stronie). Z formalnego punktu widzenia, konstrukcja pierwszej strefy Brillouina jest równoważna konstrukcji komórki Wignera-Seitza w przestrzeni odwrotnej. 1.4 Rola drgań sieci krystalicznej Różne czynniki zaburzaja ce (np. lokalne pola eletryczne i magnetyczne, napre żenia, gradienty temperatur itp.) powoduja wyprowadzenie atomów z po lożeń równowagi r 0. Dla niewielkich wychyleń efektywny bilans si l prowadzi do si ly harmonicznej F κ (r r 0 ), gdyż w bliskim otoczeniu po lożenia równowagi r 0 energia ca lkowita E calk (r) E calk (r 0 ) + d2 E calk (r 0 ) dr 2 r r
12 W wyniku dzia lania takiej si ly poszczególne atomy sieci sa wprawione w ruch drgaja cy. Do opisu tego zjawiska używany fenomenologiczny parametr κ (w laściwie macierz), który można interpretować jako sta la spre żystości. Wartość liczbowa takiego parametru jest pośrednio wyznaczalna z pomiarów energii drgań sieci krystalicznej (poprzez pomiar ciep la w laściwego). Z analizy drgań sieci w podejściu klasycznym wynika, że w sieci moga rozchodzić sie fale o wektorze falowym k i odpowiednio przyporza dkowanej cze stości. W przypadku lańcucha atomów o masie m relacja dyspersyjna ma naste puja ca postać ω k = 4κ M ( ) ka sin 2. (17) W zakresie drgań niskoenergetycznych powyższa relacja (17) redukuje sie do zależności liniowej ω k 4κ M ( ) ka κ 2 = a }{{ M} k, (18) =v s gdzie v s ma sens pre dkości dźwie ku. W przypadku lańcuchów atomowych z lożonych z dwóch rodzajów atomów (o masach M 1 i M 2 ) w relacji dyspersyjej dopuszczone sa dwie ga le zie drgań (akustyczne i optyczne). Ga la ź akustyczna w granicy d lugofalowej charekterystyczna posiada liniowa zależność cze stości od d lugości wektora falowego k. Ga la ź optyczna jest praktycznie bardzo s labo zależna od d lugości fali, można ja wre cz określić jako bezdyspersyjna. Jakościowo ilustruje to poniższy rysunek. ω k ω k g. optyczna -π/a 0 π/a k g. akustyczna -π/2a 0 π/2a k Rys. 1.7 Charakterystyczna zależność mie dzy cze stościa drgań ω i wektorem falowym k dla lańcucha mono- (rysunek a zlewej strony) i dwu-atomowego (rysunek po prawej stronie). W przypadku realnych trójwymiarowych kryszta lów, których komórki elementarne zawieraja s atomów w ogólności możliwe jest wygenerowanie 3s różnych ga le zi drgań. Wśród nich 2s typów dotyczy polaryzacji poprzecznej a pozosta le 1s opisuje drgania pod lużne (gdy atomy drgaja wzd luż kierunku rozchodzenia sie fali). 12
13 Opis kwantowomechaniczny uk ladu drgaja cych atomów jest zagadnieniem bardzo trudnym. G lównym problemem jest olbrzymia liczba obiektów sprze żonych ze soba. Do szacunkowego opisu wykorzystuje sie podejście statystyczne. Energie uk ladu N drgaja cych atomów przedstawia sie jako sume energii oscylatorów kwantowych. a) Model Einsteina W przypadku drgań typu optycznego adekwatnym jest scenariusz Einsteina, zak ladaja cy identyczna cze stość drgań ω wszystkich oscylatorów. Uwzgle dniaja c charakter energii w lasnych oscylatorów oraz prawdopodobieństwo obsadzenia poszczególnych poziomów energetycznych w stanie równowagi termicznej ca lkowita energia uk ladu wynosi E(T) = 3N hω +3N }{{ 2} E 0 exp { hω k B T hω }, (19) 1 gdzie E 0 jest tzw. energia drgań zerowych (nieznikaja ca nawet w garnicy temperatury T 0) a drugi sk ladnik oznacza energie wzbudzeń termicznych (cze ść zależna od T). W granicy wysokich temperatur k B T hω energia uk ladu drgaja cych atomów hω E(T) = E 0 + 3N ( 1 + hω + k B T...) 1 E 0 + 3Nk B T (20) poprawnie odtwarza klasyczna zasade ekwipartycji energii i empiryczne prawo Dulonga-Petit a c mol = 3R (gdzie R = N A k B jest uniwersalna sta la gazowa ). Ogólniej jednak ciep lo w laściwe zależy od temperatury poprzez relacje c mol = 3N A k B }{{} =R ( hω k B T ) 2 exp { hω ( exp { hω k B T k B T } } 1 ) 2 (21) Zanik ciep la w laściwego w granicy niskich temperatur jest zgodny z trzecia zasada termodynamiki (która mówi o nieosia galności temperatury zera bezwgle dnego). Należy jednak pamie tać, że drgania optyczne odgrywaja w niskich temperaturach marginalna role dlatego do opisu ciep la w laściwego realnych cia l sta lych należy drgania typu akustycznego. 13
14 3R c mol (T) 0 Temperatura Rys. 1.7 Temperaturowa zależność ciep la w laściwego optycznych drgań sieci (model Einsteina). b) Model Debye a Do oszacowania ca lkowitej energii drgań akustycznych powszechny jest tzw. model Debye a, zak ladaja cy liniowa zależność dyspersyjna ω k = v k. (22) Ponadto zak lada sie istnienie jedynie drgań poniżej charakterytsycznej wartości maksymalnej ω D (zwanej cze stościa Debye a). Jej wartość liczbowa jest zdeterminowana doste pnymi stopniami swobody, czyli 3N = k δ (ω D ω k ). (23) Aby wyznaczyć ω D przypomnijmy, że na jeden stan kwantowy w przestrzeni kwazipe du k przypada obje tość (2π)3 L 3 ca lkowanie k ( 2π L (z powodu warunków brzegowych). Stosuja c wie c zamiane sumowania na ) 3 dk oraz wprowadzaja c wspó lrzedne uk ladu sferycznego znajdujemy 3N = V (2π) 4π k 2 dk θ (ω 3 D v k) = V (ω D /v) 3. (24) 0 2π 2 3 Tak wie c ω D = 3 v (2π 2 n) 1 3, gdzie n jest koncentracja atomów zaś v uśredniona pre dkościa. Podobnie jak w podejściu Einsteina ca lkowita energie drgań akustycznych możemy wyznaczyć korzystaja c z regu l fizyki statystycznej E(T) = E 0 + k exp { hω k k B T sumowanie wzgle dem k poprzez ca lke energia ca lkowita przyjmuje postać 1 } 1 hω k. Zaste puja c 14
15 E(T) = E 0 + V 2π 2 kd 0 k 2 dk h vk exp { }. (25) h vk k B T 1 Proste podstawienie pomicniczej zmiennej x granicy niskich temperatur k v k B T pozwala wyznaczyć energie ca lkowita w E(T) E 0 + V 2π 2 (k B T D ) 4 ( h v) 3 π (26) Molowe ciep lo w laściwe jest wówczas kubiczna funkcja temperatury c mol = N A 3π 4 5 4k 4 BT 3 D h 3 ω 3 D = 12π4 5 N A k B }{{} =R ( T TD ) 3. (27) W zakresie wysokich temperatur ca lkowita energia drgaja cych jonów (26) jest oczywiście nadal zgodna z oszacowaniem wg zasady ekwipartycji E(T) = E 0 + k k BT hω k hω k = E 0 + k B T k 1 = E 0 + 3Nk B T, implikuja c klasyczne prawo Dulonga-Petit a. Specyficzna zależność niskotemperaturowa (27) jest rozpoznawalnym znakiem wk ladu energetycznego drgań akustycznych. Jako uwage na marginesie, warto tutaj wspomnieć iż taka zależnośc swterdzona empirycznie w nadciek lym helu 4 He zainspirowa la Landaua do (trafnego) odgadnie cia efektywnych kwazicza stek (kolektywnych drgań typu fali dźwie kowej). 15
16 2. W laściwości gazu elektronów swobodnych Na strukture cia la sta lego sk lada sie uk lad jonów (nukleonów wraz z ciasno zwia zanymi elektronami rdzenia) oraz uk lad elektronów, które sa mniej lub bardziej mobilne w sieci jonowej. Na przyk lad w kryszta lach metalicznych (lit, sód, potas, rubid, cez) periodyczna sieć jonów (tzn. ja dro atomowe wraz z elektronami wewne trzych pow lok) ma w niskich temperaturach niemal zaniedbywalny wp lyw na zachowanie elektronów z peryfereyjnych pow lok atomowych. Rys. 2.1 Schemat rozk ladu materii ja drowej (czarne punkty), elektronów rdzenia (czerwony kolor) oraz elektronów walencyjnych (zielony kolor) dla pojedynczych atomów [rysunek z lewej strony] i w materii skondensowanej [rysunek po prawej stronie]. Uk lad elektronów odgrywa pierwszoplanowa role dla wie kszości obserwowalnych w laściwościach fizycznych cia l sta lych. Pod wp lywem zewne trznego pola elektromagnetycznego uk lad elektronowy jest odpowiedzialny za przep lyw ladunku oraz zjawiska uporza dkowania magnetycznego. Przep lyw elektronów w uk ladach obje tościowych i innych strukturach hybrydowych stanowi podstawe wspó lczesnej elektroniki. W strukturach o zredukowanej wymiarowości możliwy jest również kontrolowalny przep lyw pra du spinowego, co jest bardzo poważna perspektywa dla nowej generacji elektroniki określanej cze sto jako spintronika. W niniejszym kursie przedstawione zostana wste pne informacje na temat w laściwości uk ladów elektronowych. Jako punkt startowy rozpatrzymy przypadek gazu elektronowego (kwantowego gazu cza stek swobodnych) zaniedbuja c jakiekolwiek oddzia lywania elektronów z jonami i elektronów mie dzy soba. Wp lyw oddzia lywań zostanie omówiony w rozdziale 4, przy okazji omawiania struktury pasmowej cia l sta lych. 16
17 2.1 Model gazu Fermiego Ze wzgle du na niewielka mase i zwia zana z tym duża d lugość fali de Broglie a (czyli korpuskularno-falowa nature elektronów) do opisu ich w laściwości musimy koniecznie pos lużyć sie podejściem mechaniki kwantowej. Szczególnie istotna role odgrywa w tym wypadku zasada Pauliego. Model elektronów traktowanych jako kwantowy gaz swobodnych cza stek podlegaja cych zasadzie Pauliego jest w literaturze nazywany modelem gazu Fermiego. Wp lyw oddzia lywań jest oczywiście bardzo ważny, ale w pierwszym kroku dla uproszczenia analizy pominiemy wszelkie efekty korelacyjne. Za lóżmy, że próbka o makroskopowych rozmiarach L L L zawiera N elektronów (ang. confined electrons). Równanie Schrödingera dla uk ladu nieoddzia luja cych cza stek Ĥ kin Ψ k (r) = ε k Ψ k (r) (28) (gdzie Ĥkin = h2 2 2m p laskich jest operatorem energii kinetycznej) dopuszcza rozwia zania w postaci fal Ψ k (r) = 1 L 3 eikr. (29) Energie elektronów ε k = h2 k 2 2m (30) zależa od wektora falowego k, którego sens fizyczny ma ścis ly zwia zek z kwazipe dem cza stek p = hk. Dopuszczalne wartości liczbowe energii ε k oraz kwazipe du sa zdeterminowane przez warunki brzegowe. Dla prostoty za lóżmy naste puja ce warunki periodyczne (Borna-Karmanna) Ψ k (r) Ψ k (x,y,z) = Ψ k (x + L,y,z) (31) i podobnie dla pozosta lych wspó lrze dnych y oraz z. Wektor falowy k = (k x,k y,k z ) może wie c przyjmować wartości dyskretne k i = 2π L n i (gdzie n i = 0, ±1, ±2,...) (32) 17
18 gdzie i jest dowolna wspó lrze dna x, y oraz z. W przestrzeni wektora falowego na jeden stan kwantowy przyda obje tość k = 1 ( ) 2π 3 (33) 2 L gdzie czynnik 1 2 uwzgle dnia degeneracje spinowa (czyli dwa możliwe rzuty spinu). Dyskretyzacja (32) sk ladowych wektora falowego ma wp lyw na energie ca lkowita uk ladu N elektronów. W stanie podstawowym (czyli dla temperatury zera bezwzgle dnego) elektrony obsadzaja poziomy energetyczne, pocza wszy od najniżej wartości zerowej aż do wartości maksymalnej ε kf, która nosi nazwe energii Fermiego. W zakresie 0,ε kf ) nie pomijane sa żadne dopuszczalne energie. Graficzna ilustracje obsadzonych stanów elektronowych przedstawia poniższy rysunek. Rys. 2.2 W temperaturze zera bezwgle dnego obsadzone stany trójwymiarowego gazu elektronów swobodnych tworza w przestrzeni pe dowej k = (k x, k y, k z ) tzw. kule Fermiego. Wartość energii Fermiego ε kf można w latwy sposób wyznaczyć w oparciu o znajomość koncentracji elektronowej n = N, gdzie V = V L3 oznacza obje tość próbki. W tym celu pos lużymy sie dwoma sposobami. Sposób I. W przestrzeni wektora falowego k na jeden stan elektronowy przypada obje tość k wyrażona wzorem (33). Do obliczenia promienia kuli Fermiego k F dla uk ladu N elektronów 18
19 możemy wykorzystać naste puja ca regu le matematyczna 1 elektron 1 (2π) 2 2 V N elektronów 4 3 πk3 F Z tej relacji proporcjonalności wynika, że N 4 3 πk3 F = 1 (2π)2 2V zatem promień kuli Fermiego k F = ( 3π 2N ) 1 3 V (34) oraz odpowiednia energia Fermiego ( ε F = h2 3π 2N ) 2 3. (35) 2m V Typowe odleg lości mie dzy elektronami przewodnictwa w metalach sa rze du kilku Å, dlatego na podstawie (34) promień kuli Fermiego wynosi szacunkowo oko lo m 1 (czyli 1 Å 1 ). Liczbowe wartości koncentrancji elektronów przewodnictwa n = N V 1023 cm 3 implikuja energie Fermiego (35) rze du kilku elektronowoltów. Niekiedy poprzez klasyczna relacje mie dzy energia kinetyczna i pre dkościa definiowana jest również pre dkość Fermiego ε F = mvf. 2 Typowe wartości v F sa rze du 10 6 m/sek, czyli niemal pre dkości relatywistyczne. Z tego powodu zamiast podejścia Schrödingera należo loby stosować formalizm Kleina-Gordona lub Diraca, uwzgle dniaja cy relatywistyczny charakter gazu elektronowego. Oprócz charakterystycznych paramatrów k F, v F dość powszechne jest ponadto pos lugiwanie sie temperatura Fermiego T F = ε F /k B. Liczbowe wartości T F sa na poziomie 10 4 K. Sposób II. Inna metoda s luża ca do wyznaczenia energii Fermiego bazuje na użytecznym poje ciu tzw. ge stości stanów zdefiowanej poprzez ρ(ε) 2 k δ (ε ε k ), (36) gdzie czynnik 2 po po znaku równości uwzgle dnia degeneracje spinowa. Pogla dowo można wyjaśnić, że funkcja (36) określa ilość doste pnych stanów elektronowych przypadaja cych na jednoskowy przedzia l energii ρ(ε) = dn dε. 19
20 Rys. 2.3 Graficzny schemat idei ge stości stanów ρ(ε) = dn dε stanów w przestrzeni wektora falowego k w zakresie energii ε; ε + dε. zilustrowanej na rysunku jako suma Jako przyk lad przedstawimy poniżej schemat wyznaczenia ge stości stanów ρ(ε) dla trówymiarowego gazu elektronów swobodnych. W tym celu przejdziemy od dyskretnego sumowania k do ca lki dk uwzgle dniajaa c fakt, iż na jeden stan elektronowy w przestrzeni wektora k przypada obje tość (2π) 3 /V = k 1 (2π) 3 /V dk. (37) Dalsza procedura obliczeniowa jest dość latwa, jeżeli przejdziemy od wspó lrze dnych kartezjańskich k x,k y,k z do wspó lrze dnych sferycznych. W przypadku ca lkowania otrzymujemy ρ(ε) 2 k ( δ ε h2 k 2 ) 2m ( π dφ sin θdθ δ ε h2 k 2 ) 0 0 }{{} 2m dkx dk y dk z δ (ε ε k ) = 2 (2π) 3 /V = 2 V (2π) 3 0 2π k 2 dk = V ( k 2 dk δ ε h2 k 2 π 2 0 2m = V m 2mx π 2 0 h 2dx h 2 4π ) { = x h2 k 2 } h2, dx = 2m m kdk ( ) 2m 3/2 ε. (38) h 2 δ(ε x) = V 2π 2 W przypadku trójwymiarowego gazu elektronów swobodnych ge stość stanów zależy wie c od energii elektronów ε poprzez ρ(ε) = V 2π 2 ( ) 2m 3/2 ε. (39) h 2 Znaja c ge stość stanów ρ(ε) energie Fermiego możemy wyznaczyć z warunku 20
21 εf N = dερ(ε) = V 0 2π 2 ( ) 2m 3/2 εf h 2 dε ε = V 0 2π 2 ( ) 2m 3/2 2 h 2 3 ε3/2 F = V ( ) 3/2 2mεF 3π 2 h 2 (40) Na podstawie (40) dostajemy te sama wartość ε F, która zosta la podana we wzorze (35). Analogiczny rachunek przeprowadzony dla uk ladu dwuwymiarowego implikuje st la wartość ge stości stanów ρ dim=2 (ε) = const, zaś dla uk ladu jednowymiarowego ρ dim=1 (ε) 1 ε. Na konkretna funkcje ρ(ε) zasadnicze znaczenie ma ponadto relacja mie dzy pe dem i energia (tzw. zależność dyspersyjna) dlatego w praktyce istotny wp lyw ma pośrednio również symetria sieci krystalicznej. Konkretne przyk lady zostana omówione w rozdziale 4, przy okazji analizy opartej na metodzie ciasnego wia zania. 2.2 Rola wzbudzeń termicznych Dla uk ladów wielu cza stek typu fermionowego prawdopodobieństwo obsadzenia poziomu ε k jest w równowadze termodynamicznej określone funkcja rozk ladu Fermiego - Dirac a f FD (ε k,t) = exp ( ε k µ k B T ), (41) Rys. 2.4 Zależność funkcji Fermiego-Diraca od energii dla T = 0 (linia przerywana) oraz T = 0, 03ε F /k B (linia cia g la) [rysunek po lewej stronie]. Środkowy rysunek pokazuje pochodna funkcji Fermiego Diraca d dt f FD(ω, T) natomiast rysunek z prawej strony rozk lad obsadzonych stanów f FD (ε, T) ρ(ε). gdzie µ oznacza tzw. potencja l chemiczny. Wielkość ta zależy od temperatury i jej wartość jest zdeterminowana warunkiem k f FD (ε k,t) = N. W przypadku stanu podstawowego potencja l chemiczny jest równoważny energii Fermiego, ponieważ wszystkie stany poniżej energii µ(t = 0) 21
22 sa obsadzone z prawdopodobieństwen 1 a pozosta le sa kompletnie pouste. Dla T 0 rozk lad Fermiego-Diraca staje sie rozmyty wokó l ε F, jak pokazuje rysunek 2.4. Do oszacowania energii wzbudzeń termicznych niezbe dna jest znajomość potencja lu chemicznego od temperatury. Poniżej przedstawimy sposób oparty na rozwinie ciu Sommerfelda. Dla temperatur pokojowych (a także w zakresie znacznie wyższych temperatur) spe lniona jest naste puja ca relacja k B T ε F. W takich warunkach stosowalne jest rozwinie cie Sommerfelda 0 dεg(ε)f FD (ε,t) µ 0 dεg(ε) + π2 6 (k BT) 2 g (µ), (42) gdzie g(ε) jest dowolna funkcja wolnozmienna w pobliżu potencja lu chemicznego. Rozwinie cie Sommerfelda (42) możemy udowodnić wprowadzaja c pomocnicza funkcje G(ε) = ε 0 dx g(x), która posiada naste puja ca w laściwość matematyczna G (ε) = g(ε). Przy takim wygodnym oznaczeniu możemy wykonać ca lkowanie iloczynu funkcji g(ε)f FD (ε,t) przez cze ści wed lug naste puja cego schematu 0 dεg(ε)f FD (ε,t) 0 dεg (ε)f FD (ε,t) = G(ε)f FD (ε,t) [ dεg(ε) df ] FD(ε,T). (43) dε Pierwszy wyraz po znaku równości znika, ponieważ G(0) = 0 oraz f FD (,T) = 0. Aby wyznaczyć drugi wyraz po prawej stronie wyrażenia (43) uwzgle dnimy, że pochodna d dε f FD(ε,T) = e ε µ k B T 1 ) (e ε µ 2 k BT k + 1 B T przyjmuje istotne (nieznikaj,ace) wartości jedynie w pobliżu µ i jest funkcja symetryczna (44) wzgle dem µ. Rozwijaja c funkcje G(ε) w szereg pote gowy wzgle dem ε = µ dostajemy 0 [ dεg(ε) df ] FD(ε,T) dε [ G (µ) (ε µ)dε df ] FD(ε,T) +G (µ) 0 dε }{{} 0 [ G(µ) dε df ] FD(ε,T) + 0 dε }{{} =1 0 (ε µ) 2 2 [ dε df ] FD(ε,T). (45) dε Trzeci wyraz po prawej stronie możemy precyzyjnie określić w oparciu o jawna postać pochodnej (44) 0 (ε µ) 2 2 [ dε df ] FD(ε,T) = dε 0 = (k BT) (ε µ) 2 dε 2 e ε µ k B T (e ε µ k BT + 1 x2 e x 1 ) 2 k B T dx µ/k BT (e x + 1) 2. (46) }{{} = π2 3
23 W ostatnim wyrażeniu przyje liśmy dolna granice ca lkowania w przybliżeniu równa µ k BT, co jest dobrze uzasadnione ponieważ funkcja podca lkowa szybko zanika w dużej odleg lości od zera. Po uwzgle dnieniu rozwinie cia w szereg do trzeciego wyrazu (45) oraz wykonaniu ca lkowania (46) przyjmuje wartość 0 dεg(ε)f FD (ε,t) 0 dεg (ε)f FD (ε,t) G(µ) + π2 6 G (µ)(k B T) 2. (47) Biora c pod uwage, iż G(µ) = µ 0 dεg(ε) oraz G (µ) = g (µ) wzór (47) odtwarza relacje Sommerfelda (42). W pierwszej kolejności zastosujemy rozwinie cie Sommerfelda (42) do oszacowania temperaturowej zależności potencja lu chemicznego. Równanie N = 0 dε ρ(ε) f FD (ε,t) rozwia żemy analitycznie, stosuja c zwyk le podstawienie g(ε) ρ(ε), czyli N µ 0 dερ(ε) + π2 6 (k BT) 2 ρ (µ). (48) Ca lke po prawej stronie powyższej równości wyrazimy w postaci sumy µ 0 = ε F 0 + µ ε F N εf dερ(ε) + 0 } {{ } =N µ ε F dερ(ε) }{{} (µ ε F )ρ(ε F ) + π2 6 (k BT) 2 ρ (µ). (49) }{{} ρ (ε F ) Z otrzymanego oszacowania µ ε F + π2 6 (k BT) 2 ρ (ε F ) = 0 wyznaczamy potencja l chemiczny µ ε F + π2 6 (k BT) 2 ρ (ε F ). (50) W szczególności dla trójwymiarowego gazu elektronów swobodnych ρ (ε) = 1 2ε ρ(ε) (51) równanie (50) określa naste puja ca zależność µ ε F 1 + π2 12 ( ) 2 kb T. (52) ε F Wyjściowe po lożenie poziomu chemicznego nie ulega wie c poważniejszemu przesunie ciu ze wzrostem temperatury. W zakresie temperatur pokojowych wzgle dna zmiana potencja lu chemicznego jest na poziomie Identyczny schemat rachunkowy może być przeprowadzony do oszacowania ca lkowitej energii uk ladu elektronowego 23
24 E el (T) = k ε k f FD (ε k,t) = 0 dε ρ(ε) ε f FD (ε,t). (53) Stosuja c rozwinie cie Sommerfelda (42) z postawieniem g(ε) = ε ρ(ε) uzyskujemy E el (T) = µ dε ρ(ε) ε 0 }{{} E el (T=0) + π2 6 (k BT) 2 ρ(µ). (54) }{{} ρ(ε F ) Na podstawie powyższego oszacowania (54) otrzymujemy bardzo ważna informacje, dotycza ca temperaturowej zależności elektronowego ciep la w laściwego c el (T) = d dt E el(t) = π2 3 k2 BT ρ(ε F ). (55) Biora c pod uwage ge stość stanów trójwymiarowego uk ladu (51) ciep lo w laściwe wynosi Molowe ciep lo w laściwe c mol el (T) = π2 k B T 2 ε F c el (T) = π2 2 k2 BT N ε F. (56) k B N A można wie c zapisać w postaci iloczynu wartości 3R/2 przewidywanej na gruncie fizyki klasycznej oraz czynnika uwzgle dniaja cego wp lyw efektów kwantowych c mol el (T) = 3 2 R }{{} klas. T π2 3 T F }{{} kwant. gdzie R jest uniwersalna sta la gazowa. Liniowa zależność c el (T) T wskazuje na zanik ciep la w laściwego dla temperatur da ża cych do zera bezwgle dnego (zgodnie z trzecia zasada termodynamiki). Z fizycznego punktu widzenia efekt ten jest spowodowany zasada Pauliego. Na ca lkowita energie (i ciep lo w laściwe) maja wp lyw zarówno wzbudzenia uk ladu elektronowego jak też drgania sieci krystalicznej. Jeśli chodzi o drgania sieci, to w niskich temperaturach zasadniczy wk lad wnosza drgania typu akustycznego dobrze opisane wed lug scenariusza Debye a. Efektywne ciep lo molowe spe lnia wie c naste puja ca (empirycznie potwierdzona ) zależność temperaturowa (57) c mol total(t) = α T + β T 3. (58) Na gruncie przedstawionej w tym rozdziale analizy wzbudzeń elektronowych (57) wspó lczynnik przy wyrazie liniowym może być zidentyfikowany jako α = π R T F.
25 Rys. 2.5 Empiryczna zależność ciep la w laściwego od temperatury w metalach. Na osi pionowej podano c mol /T zaś na osi poziomej T 2. Teoretyczna wartość elektronowego wspó lczynnika wynosi α teor 6, J mol 1 K 2. Wartość ta dobrze zgadza sie z oszacowaniem α dosw 6, J mol 1 K 2 uzyskanym empirycznie dla srebra i z lota (wed lug sposobu zilustrowanego na powyższym rysunku). Również dla miedzi i innych metali alkalicznych (z wyja tkiem litu) zgodność jest satysfakcjonuja ca. Znane sa jednak istotne odste pstwa, jak w przypadku manganu, gdzie model elektronów swobodnych nie uwgle dnia wp lywu innych ważnych czynników (np. korelacji). 25
26 3. Zjawiska magnetyczne w cia lach sta lych Pod wzgle dem w laściwości magnetycznych można wyróżnić naste puja ce podstawowe rodzaje materia lów: diamagnetyki, paramagnetyki, ferromagnetyki oraz antyferromagnetyki. Przynależność konkretnego materia lu do jednego z wymienionych typów uporza dkowania zależy od namagnesowania M w obecności zewne trznego pola magnetycznego B. Magnetyzm w materii skondensowanej jest (g lównie) konsekwencja polaryzowania momentów magnetycznych elektronów z zewne trznych pow lok atomowych (w cia lach sta lych mamy na myśli elektrony z peryferyjnych pasm). Aby u latwić zrozumienie tego zgadnienia dokonamy najpierw krótkiego przypomnienia elementarnych informacji na temat magnetyzmu na gruncie fizyki klasycznej a w naste pnej kolejności omówione zostana zagadnienia magnetyzmu w uje ciu wspó lczesnej mechaniki kwantowej. 3.1 Podstawy magnetyzmu a) Podejście klasyczne Pola magnetyczne wytwarzane sa przez poruszaja ce sie ladunki elektryczne. Jako przyk lad rozpatrzmy przypadek prostoliniowego przewodnika, w którym p lynie pra d o nate żeniu I. Wokó l przewodnika wytwarzane jest pole megnetyczne, którego indukcje B można określić na podstawie prawa Ampere a B ds = µ 0 I, (59) gdzie µ 0 oznacza przenikalność magnetyczna próżni. Wybieraja c kontur zamknie ty w postaci okre gu o promieniu r możemy wyznaczyć ca lke okre żna B ds = B 2πr. Zatem w odleg lości r od prostoliniowego przewodnika pole magnetyczne wynosi B(r) = µ 0 2π I r. (60) Wektor indukcji pola magnetycznego B wytworzonego przez przewodnik o dowolnym kszta lcie, w którym p lynie pra d o nate żeniu I możemy wyznaczyć korzystaja c na podstawie tzw. prawa Biota-Savarta 26
27 db = µ 0I 4π dl r r3, (61) gdzie dl oznacza infinitezymalny fragment przewodnika. Ca lkowity wektor indukcji pola magnetycznego B = db wyznaczamy poprzez wyca lkowanie po ca lej d lugości przewodnika. Jednostka indukcji magnetycznej jest tesla, której umownym symbolem jest litera T. Duże elektromagnesy wytwarzaja zwykle pola rze du kilku tesli, pola zwyk lych magnesów sztabkowych wynosza oko lo 10 2 T natomiast pole magnetyczne przy powierzchni Ziemi jest zaledwie rze du 10 4 T. Bardzo istotne znaczenie w klasycznej elektrodynamice ma również czasowa zależność pra dów oraz zwia zana z tym dynamika pola elektrycznego E oraz magnetycznego B. Wzajemna wspó lzależność tych wielkości fizycznych określa uk lad klasycznych równań Maxwella. Równania te (w postaci ca lkowej) można wyrazić naste puja co E ds = q, ε 0 prawo Gaussa dla elektryczności (62) B ds = 0, prawo Gaussa dla magnetyzmu (63) E dl = dφ B, dt prawo indukcji Faradaya (64) B dl = µ 0 ε 0 dφ B dt + µ 0 I. prawo Ampere a (65) Pierwsze z równań (62) determinuje wartość pola elektrostatycznego wytworzonego wokó l ladunku q. Naste pne równanie (63) jest odpowiednikiem prawa Gaussa dla pola magnetycznego i implikuje brak wyste powania monopoli magnetycznych. Równanie (64) opisuje indukcje pola elektrycznego przez zmienne pole magnetyczne (lub ściślej mówia c przez zmienny strumień pola magnetycznego φ B ). Ostatnie z równań (65) stanowi uogólnienie prawa Ampere a o tzw. pra d przesunie cia. Wraz z warunkiem cia g lości (czyli warunkiem zachowania ladunku) równania Maxwella (62-65) jednoznacznie determinuja wspó lzależność pól elektrycznego i magnetycznego oraz pra du poruszaja cych sie ladunków. b) Podejście mechaniki kwantowej Jako wprowadzenie rozpatrzmy najpierw magnetyczne w laściwości pojedyńczego atomu. 27
28 W uje ciu mechaniki kwantowej obserwablom (czyli mierzalnym wielkościom fizycznym) przyporza dkowuje sie odpowiednie operatory. Moment magnetyczny elektronów jest w takim podejściu określony porzez klasyczny zwia zek z orbitalnym momentem pe du µ l = e hl (66) 2m natomiast operator momentu pe du l jest zdefiowany relacjami komutacyjnymi [l x,l y ] = hl z. Rozwia zanie równania w lasnego na kwadrat momentu pe du l 2 oraz sk ladowa momentu pe du wzd luż wybranej osi (np. l z ) pokazuje, że dopuszxzalne sa tylko dyskretne wartości tych wielkości fizycznych. Zarówno wie c moment pe du jak też moment magnetyczny sa wielkościami skwantowanymi. Wartość momentu pe du wynosi h l(l + 1), gdzie l może być liczba ca lkowita lub po lówkowa. Wartość sk ladowej momentu pe du w kierunku umownej osi kwantowania przyjmować może 2l+1 wartości dyskretnych wynosza cych ( l) h, ( l +1) h,..., l h. Podobnie jest z ca lkowitym momementem magnetycznym oraz jego sk ladowymi. Wygodna jednostka momentu magnetycznego elektronu jest tzw. magneton Bohra wynosza cy µ B = e h 2m (gdzie m oznacza mase elektronu). Wartość magnetonu Bohra wynosi 5, ev/t. Ca lkowity orbitalny moment magnetyczny wynis wie c µ l = µ B l(l + 1), zaś sk ladowe w kierunku wybranej osi odpowiednio lµ B, ( l + 1)µ B,..., lµ B. Oprócz orbitalnego momentu pe du elektrony charakteryzuja sie również momentem wewne trzym, tzw. spinem hs. Rzut spinu na wybrana oś kwantowania z dopuszcza dwie wartości s z = ± 1. Z 2 obecnościa spinu jest stowarzyszony wewne trzny moment magnetyczny gdzie g s oznacza wspó lczynik giromagnetyczny g s = 2, g s µ B s. (67) Wartość oczekiwana momentu magnetycznego pojedynczego atomu może być wyznaczona w oparciu o znajomość funkcji falowej, znakowanej zestawem naste puja cych liczb kwantowych: liczby orbitalnej n, momentu orbirtalnego l, rzutu momentu l z oraz rzutu spinu s z. Konkretne obliczenia sa przedmiotem badań fizyki atomowej. W realnych makroskopowych uk ladach (z lożonych z N atomów) obliczenia z pierwszych zasad by lyby kompletnie niewykonywalne dlatego do tego celu wykorzystuje sie 28
29 podejście statystyczne. Jako cza stki elemtarne elektrony podlegaja statystyce Fermiego-Diraca (czyli sa fermionami). Cecha charakterystyczna fermionów jest respektowanie regu ly Pauliego. Każdy rozróżnialny stan kwantowy może być obsadzony przez co najwyżej jeden elektron. Pewne elementy analizy kwantowego gazu elektronów swobodnych przedstawiliśmy w poprzednim rozdziale w ramach tzw. modelu gazu Fermiego. Poniżej przedstawimy prosta argumentacje uzasadniaja cy pochodzenie uporza dkowania typu paramagnetycznego, ferromagnetycznego i antyferromagnetycznego elektronów w cia lach sta lych. Moment magnetyczny nukleonów jest trzy rze dy wielkości mniejszy od magnetonu Bohra, dlatego uporza dkowanie magnetyczne cia l sta lych jest niemal ca lkowicie konsekwencja uporza dkowania momentów magnetycznych uk ladu elektronowego. 3.2 Paramagnetyzm Pauliego Rozpatrzmy gaz elektronów swobodnych (gaz Fermiego) w obecności zewne trznego pola magnetycznego B = (0, 0,B z ). Wyjściowe poziomy energetyczne we drownych elektronów ε k,σ = h 2 k 2 2m o rzucie spinu σ = oraz ulegaja przesunie ciu o tzw. energie Zeemana ε = ε ε = gµ B B. (68) Zazwyczaj liczbowa wartość przesunie cia Zeemana ε jest znacznie mniejsze od typowych energii Fermiego ε kf,σ 1 5 ev. Na tej podstawie możemy z dobrym przybliżeniem oszacować różnice liczebności elektronów N o spinie skierowanym wzd luż B i elektronów N o rzucie spinu przeciwnym wzgle dem wektora pola magnetycznego. Dla prostoty dokonajmy najpierw oszacowania różnicy N N w przypadku stanu podstawowego (tzn. dla temperatury T = 0). W tym celu wykorzystamy poje cie ge stości stanów wprowadzonej w ramach modelu Fermiego w poprzednim rozdziale. Dla elektronów o rzucie spinu σ ge stość stanów w uk ladzie trójwymiarowym wynosi ρ σ (ε) = V 4π 2 ( 2m h 2 ) 3/2 ε. 29
30 3.1 Ge stość stanów elektronów o rzucie spinu i dla przypadów: a ) bez pola magnetycznego (rysunek z lewej strony), b) w obecności pola (panel z prawej strony). Po przy lożeniu pola zewne trznego stany oznaczone kolorem szarym (elektronów o spinie ) zostaja opróżnione, natomiast stany oznaczone kolorem czarnym (elektronów o spinie ) ulegaja obasadzeniu. Ca lkowita liczba elektronów jest zachowana N + N = const. Powyższa ilustracja ge stości stanów ρ σ (ε) Wskazuje, że różnice liczebności elektronów o różnych rzutach spinu możemy wyznaczyć w naste puja cy sposób N N = εf gµ B B/2 dερ (ε) εf gµ B B/2 dερ (ε) (69) Dla realnych nate żeń pól magnetycznych B = B przesunie cie Zeemana ε jest znacznie mniejsze od energii Fermiego ε F. Z tego powodu w bliskim sa siedztwie energii Fermiego ge stość stanów poszczególnych spinów jest w przybliżeniu sta la (tzn. jest wolnozmienna funkcja energii) i można przyja c ρ (ε) 1 2 ρ(ε F) = ρ (ε), gdzie ρ(ε) V 2π 2 ( 2m h 2 ) 3/2 ε. Na tej podstawie N N εf +gµ B B/2 ε F gµ B B/2 dε ρ(ε F) 2 = ρ(ε F ) gµ B B. (70) Ponieważ wk lad pojedynczego elektronu do namagnesowania wynosi ±gµ B 1 2 (gdzie znak plus odnosi sie do spinów natomiast znak minus do ). Efektywne namagnesowanie materia lu w kierunku zwrotu pola magnetycznego wyniesie zatem M z = N gµ B /2 + N ( gµ B /2) = (N N ) gµ B /2 ρ(ε F) 2 g 2 µ 2 B B 2. (71) 30
31 sta d podaność przewodników metalicznych wynosi ( ) gµb 2 χ = ρ(εf ). (72) 2 Zeemanowskie przesunie cie poziomów energetycznych implikuje wie c s labe namagnesowanie gazu elektronowego w kierunku przy lożonego pola. Wed lug klasyfikacji przedstawionej na wste pie obecnego rozdzia lu mamy tutaj do czynienia ze zjawiskiem paramagnetyzmu. Podatność uporza dkowania paramagnetycznego (72) jest pośrednio miara ge stości stanów w okolicach energii Fermiego. Im zatem wie ksza koncentracja elektronów w pasmie przewodnictwa tym wie ksza podatność magnetyczna uk ladu. Powyżej przedstawiony schemat rachunkowy dotyczy temperatury zera bezwgle dnego. W przypadku wyższych temperatur należa loby uwzgle dnić rozmycie termiczne prawdopodobieństwa obszadzeń poziomów elektronowych w pobliżu energii Fermiego. Rozmycie termiczne (opisane funkcja rozk ladu Fermiego-Diraca) jest jednak identyczne dla obu komponentów spinowych. W tej sytuacji jedyny poważny wp lyw temperatury przejawi sie poprzez [ ( ) przesunie cie poziomu chemicznego µ(t) = ε F 1 π2 kb T 2 12 ε F ]. Uwzgle dnienie wp lywu temperatury prowadzi do naste puja cej efektywnej podatności ( ) ( ) gµb 2 2 χ(t) = ρ(εf ) 1 π2 kb T (73) 2 12 ε F W zakresie temperatur pokojowych T 300 K wartość liczbowa u lamka k BT ε F dla zwyk lych metali jest rze du Wyrażenie (73) wskazuje wie c, że wp lyw temperatury daje wk lad do poprawki rze du 0, 01%. Tak znikomo niewielki wp lyw można wie c pomina ć. 3.3 Oddzia lywanie wymienne O wiele bardziej istotna role odgrywaja zjawiska uporza dkowania magnetycznego w uk ladach elektronów silnie skorelowanych. Zagadnienie korelacji znacznie wykracza poza zakres niniejszego kursu, dlatego w celach pogla dowych pos lużymy sie uproszczonym schematem, który w literaturze specjalistycznej jest nazywany teoria Weissa. Elementem zasadniczym takiego podejścia jest fakt, iż poziomy energetyczne oddzia luja cych elektronów różnia sie w zależności 31
32 od wzgle dnego ustawienia spinów. Różnica energetyczna konfiguracji spinów spolaryzowanych równolegle i antyrównolegle jest nazywana energia wymiany. Aby uzasadnić pochodzenie energii wemiennej można pos lużyć sie naste puja cym schematem rozumowania. Rozpatrzmy model uk ladu dwuatomowego opisanego hamiltonianem Ĥ = ĤA + ĤB + ˆV A B. (74) Pierwsze dwa wyrazy po prawej stronie równania oznaczaja energie kinetyczne cza stki A i cza stki B. Kolejny wyraz odnosi sie natomiast do energii oddzia lywania tych obiektów. Stan podstawowy (tzn. stan o najniższej energii) można wyznaczyć z procedury minimalizacji energii E = drψ (r)ĥψ(r) drψ (r)ψ(r). Zasadniczym problemem jest jednak określenie struktury funkcji falowej. Jedna z możliwości wyboru jest przedstawienie takiej funkcji w postaci liniowej superpozycji iloczynu indywidualnych funkcji Ψ A, Ψ B. Pomijaja c szczegó ly rachunkowe można pokazać, w stanie podstawowym dopuszczalne sa naste puja ce dwa warianty Ψ(r,r ) = 1 2 ( ΨA (r)ψ B (r ) ± Ψ B (r)ψ A (r ) ). (75) Stan wia ża cy opisany jest znakiem plus i dotyczy obiektów (np. elektronów) o przeciwnych spinach, gdyż w przeciwnym wypadku zasada Pauliego zabrania laby znajdowaniu sie identycznych obiektów w po lowie odleg lości. Stan taki oznacza wie c wzrost prawdopopodobieństwa elektronów pomie dzy atomami. Mówimy wtedy o uwspólnieniu elektronów, które prowadzi znaczego do obniżenia energii uk ladu. Z elementarnych przekszta lceń wartość energii wynosi gdzie elementy macierzowe [ E I = drψ A(r) C = e2 4πǫ 0 A = e2 4πǫ 0 S = h2 2 r 2m E = 2E I + C ± A 1 ± S, (76) ] e2 Ψ A (r) (77) 4πǫ 0 r drdr ( 1 R AB + 1 r 12 1 r A2 1 r B1 drdr ( 1 R AB + 1 r 12 1 r A2 1 r B1 ) Ψ A (r) 2 Ψ B (r ) 2 (78) ) Ψ A (r)ψ A (r )Ψ B (r )Ψ B (r) (79) drdr Ψ A (r)ψ A (r )Ψ B (r )Ψ B (r). (80) Parametry te maja sens energii jonizacji E I, energii kulombowskiej C, ca lki wymiany A oraz ca lki przekrycia funkcji falowych S. Ewentualny proces przejścia z jednej w druga konfirguracje (tzn. 32
33 ze stanu wia ża cego w antywia ża cy) wymaga nak ladu energetycznego. Różnice nazywany nazywamy energia wymiany. Mikroskopowo takim przejściom towarzyszy odwracanie spinów cza stek i stanowia istote mechanizmu zjawisk uporza dkowania ferromagnetycznego lub antyferromagnetycznego. Do opisu oddzia lywania wymiennego na poziomie mikroskopowym W. Heisenberg zaproponowa lnaste puja cy model Ĥ exch = 2J Ŝ1 Ŝ2. (81) Fenomenologiczny parametr J nazywa sie energia (lub sta la ) wymiany. Wartość J może być zarówno dodatnia (poniżej przekonamy sie, że prowadzi to do zjawiska ferromagnetyzmu) lub ujemna (odpowiedzialna wówczas za uporza dkowanie antyferromagnetyczne). W uk ladzie z lożonym z makroskopowej liczby N elektronów ca lkowity wp lyw wzajemnych oddzia lywań można wyrazić naste puja co J i,j Ŝ i Ŝj = i,j i,j J i,j Ŝ i Ŝj. (82) Czynnik 1 2 wprowadzono dla uniknie cia podwójnego zliczania oddzia lywania cza stki i-tej z j-ta oraz j-tej z i-ta. Ogólnie rzecz biora c, sta la wymiany może zależeć od po lożeń elektronów. Zależy ona w praktyce od wzgle dnej odleg lości elektronów, co ma wp lyw na stopień przekrywania sie funkcji falowej. W stanie równowagi termodynamicznej uk lad elektronów preferuje taka konfiguracje spinowa, która zapewnia minimalna energie. W naturalny sposób możemy oczekiwać wie c uporza dkowania ferromagnetycznego, jeżeli energia wymiany J jest dodatnia oraz antyferromagnetycznego jeżeli J < 0. Poniżej przedstawimy zarys analizy uzasadnija cej powyższe stwierdzenie. 3.4 Uporza dkowanie typu ferromagnetycznego W uk ladzie N elektronów zlokalizowanych w we z lach sieci krystalicznej r i ca lkowite namagnesowanie jest suma momentów magnetycznych poszczególnych elektronów M = g µ B s i. (83) i 33
34 3.2 Ferromagnetyczne uporza dkowanie spinów elektronów na dwuwymiarowej sieci regularnej w stanie podstawowym (lewa strona rysunku) oraz w stanie wzbudzeń magnonowych dla T 0 (rysunek po prawej). Wprowadzaja c wartość średnia (w sensie statystycznym) spinu elektronowego ŝ i wyrażenie (83) może być przedstawione jako M = N g µ B s i. (84) Podobnie jak w rodziale 3.2 za lóżmy, że przy lożone jest zewne trzne pole magnetyczne B 0 = (0, 0,B 0 ). Pole to oddzia luje z wyindukowanym namagnesowaniem poprzez M B 0. Operator energii ca lkowitej uk ladu przyjmuje naste puja ca postać Ĥ = J ij Ŝ i Ŝj i,j }{{} oddz. wymiany gµ B B 0 i Ŝ i } {{ } oddz. Zeemana. (85) Do wyznaczenia namagnesowania uk ladu pos lużymy sie przybliżeniem średniego pola. W wyrażeniu na energie oddzia lywań wymiennych wprowadzimy uśredniona wartość Ĥ ĤMF = i,j Ĥ MF = i J ij Ŝ i Ŝ j gµb B 0 Ŝ i i Ŝ i J ij Ŝj + gµb B 0. (86) j Wyraz w nawiasie pe lni role efektywnego pola J ij Ŝj + gµb B 0 gµ B B eff. (87) j 34
35 Ze wzgle du na translacyjna niezmienniczość uk ladu wartość uśredniona Ŝ j nie powinna zależeć od po lożenia r i dlatego be dziemy oznaczać ja symbolem Ŝ i w konsekwencji namagnesowanie (84) ma odpowiednio postać M = N g µ B s. (88) Aby określić temperaturowa zależność namagnesowania za lożymy dodatkowo, że oddzia lywania wymienne realizuja sie tylko pomie dzy elektronami z najbliższych we z lów sieci krystalicznej J gdy i,j J ij = sa najbliższymi sa siednimi we z lami, (89) 0 w pozosta lych przypadkach. Przy takich za lożeniach równanie (87) upraszcza sie do B eff = B J ij Ŝj = B0 + zj Ŝ, (90) gµ B gµ B j gdzie z jest liczba koordynacyjna (która określa liczbe najbliższych we z lów sieci krystalicznej). Drugi sk ladnik po prawej stronie wyrażenia (90) nazywany jest polem molekularnym B MF = zj gµ B Ŝ. (91) Na podstawie równania (88) pole molekularne w bezpośredni sposób jest zwia zane z namagnesowaniem próbki B MF = zj 2 M. (92) N (gµ B ) Skoro pole magnetyczne zosta lo przy lożone w kierunku z oczekujemy, że również wektor namagnesowania skierowany be dzie w tym samym kierunku M = (0, 0,M). Sk ladowa z tego wektora może być określona jednoznacznie w oparciu o równanie (83) M = gµ B h 2 (N N ) (93) gdyż z-towa sk ladowa spinu elektronów przyjmuje wartości ± h 2 zaś ilość elekronów o dodatnim rzucie oznaczyliśmy jako N natomiast ilość elektronów o spinie ujemnym przez N. Liczebność elektronów o poszczególnych rzutach z-towej sk ladowej możemy wyznaczyć na podstawie warunków równowagi termodynamicznej. Zauważmy przy tym, że z powodu oddzia- lywania elektronów z polem magnetycznym dochodzi do rozszczepienia wyjściowego poziomu energetycznego o wartość wynosza ca 35
36 ε = gµ B h 2 B eff ε = +gµ B h 2 B eff. (94) W stanie równowagi termodynamicznej prawdopodobieństwo obsadzenia tych poziomów zależy od energii. Wed lug zasady Boltzmanna prawdopodobieństwo jest wprost proporcjonalne do czynnika e βε gdzie β 1/k B T. Na tej podstawie iloraz liczby elektronów w poszczególnych konfiguracjach wyniesie N N = const e βε const e βε = e β(ε ε ) = exp {βgµb hb eff }. (95) Ca lkowita liczba wszystkich elektronów N jest ustalona (nie zależy ona ani od temperatury T ani od wartości pola zewne trznego B 0 ) dlatego różnice N N pojawiaja ca sie we wzorze (93) można wyrazić korzystaja c z ilorazu (95) za pomoca naste puja cej tożsamości matematycznej N N = (N N ) N N N + N = N N N 1 N N + 1 N N = N exp {βgµ ( B hb eff } 1 βgµb hb exp {βgµ B hb eff } + 1 = N tgh eff 2 W ten sposób uzyskaliśmy warunek na z-towa sk ladowa namagnesowania próbki M = Ngµ B h 2 ). (96) ( ) βgµb hb eff tgh. (97) 2 Efektywne (tzn. ca lkowite) pole magnetyczne w próbce B eff sk lada sie z pola zewne trznego B 0 oraz pola molekularnego (92) B eff = B 0 + zj N (gµ B ) 2 M (98) dlatego ostatecznie równanie (97) na z-towa sk ladowa namagnesowania przyjmuje postać naste puja ca równania nieliniowego M = Ngµ B h 2 [ ( )] βgµb h zj tgh B N (gµ B ) 2 M. (99) Powyższe rówanie jest rezultatem przybliżenia średniego pola (86) zaś analiza prowadza ca do (99) jest w specjalistycznej literaturze nazywana teoria Weissa. Pogla dowo można wie c powiedzieć, że namagnesowanie M jest funkcja c lkowitego pola magnetycznego z lożonego z 36
37 przy lożonego pola oraz pola wyindukowanego B MF M gdzie wartość tego namagnesowania należy wyznaczyć rozwia zuja c w samozgodny sposób równanie (99). Technicznie jest to dość trudne zadanie. Do wyznaczenia zależności namagnesowania od przy lożonego pola zewne trznego a także od temperatury T rozpatrzymy pewne przypadki skrajne. 1 o. Przypadek bez pola magnetycznego Równanie pola średniego (99) nie wyklucza pojawienia sie spontanicznego namagnesowania nawet pod nieobecność pola magnetycznego. W przypadku B 0 = 0 równanie to upraszcza sie do naste puja cej postaci M = Ngµ B h 2 tgh [ βgµb h 2 ] zj N (gµ B ) 2 M. (100) a) Stan podstawowy (T = 0) W granicy temperatury da ża cej do zera bezwgle dnego T 0 argument funcji tangensa hiperbolitycznego da ży do + gdyż wszystkie wielkości wyste puja ce w nawiasie kwadratowym maja wartość dodatnia, natomiast β = 1/(k B T). W takim granicznym przypadku funkcja tgh (x) = ex e x 1 e 2x = lim e x + e x 1 + e 2x x tgh (x) = 1. (101) Implikuje to, iż namagnesowanie stanu podstawowego wynosi M(T 0) = Ngµ B h 2. (102) Powyższa wartość namagnesowania jest maksymalna z możliwych i odpowiada sytuacji gdy wszystkie elektrony w uk ladzie ma zwrot swoich momentów magnetycznych w kierunku osi z, czyli N = N oraz N = 0. b) Temperatura krytyczna (T = T c ) Postarajmy sie teraz określić wartość cherakterystycznej temperatury T c, przy zbliżaniu sie do której spontaniczne namagnesowanie zanika M(T = T c ) 0 +. (103) 37
38 Dla infinitezymalnie ma lego namagnesowania argument funkcji tangesa hiperbolicznego jest liczba bliska zera, dlatego na podstawie rozwinie cia w szereg tgh (x) = x x3 + O(x 5 ) (104) możemy ograniczyć sie do pierwszego nieznikaja cego wyrazu [ ] zjβ h lim tgh M zjβ h M (105) T Tc 2Ngµ B 2Ngµ B Równanie (100) ma wie c rozwia zanie M Ngµ B h 2 zjβ 2Ngµ B M, z którego wynika naste puja ca wartość temperatury krytycznej 1 = zjβ 4, (106) T c = zj 4k B. (107) Temperatura krytyczna spontanicznego namagnesowania odzwierciedla wie c wartość energii wymiany dzie ki czemu możliwa jest empiryczna metoda oszacowania tej wartości. Wprowadzaja c oznaczenie M 0 M(T =0) i zaste puja c energie wymiany poprzez temperature krytyczna J = 4k B T c /z możemy przepisać równanie na namagnesowanie (100) w postaci [ ] M(T) Tc M(T) = tgh. (108) M 0 T M 0 Temperaturowa zależność namagnesowania M(T) w pobliżu temperatury krytycznej jest możliwa do wyznaczenia analitycznie jeśli skorzystamy z dwów wyrazów po prawej stronie rozwinie cia (104). Warunek (108) ma wówczas naste puja ca przybliżona postać [ ] M(T) Tc M(T) = tgh T cm(t) + 1 ( ) 3 Tc M(T), (109) M 0 T M 0 TM 0 12 TM 0 która implikuje, że 1 T c T T T c ( Tc T ) 3 [ M(T) M 0 ] 2 [ ] 2 Tc M(T). (110) 38 T M 0
39 Proste przekszta lcenie algebraiczne daje ostatecznie naste puja ca zależność temperaturowa M(T) 12 T 1 T M 0. (111) T c T c W ogólności rozwia zanie nieliniowego równania (100) jest niemożliwe. Rozwia zanie można wyznaczyć numerycznie. Temperaturowa zależnośc magnetyzacji ilustruje poniższy rysunek. M(T) T / T c 3.3 Zależność namagnesowania M(T) od temperatury. 2 o. Wp lyw zewne trznego pola magnetycznego Aby określić w jaki sposób spiny elektronowe zachowuja sie pod wp lywem zewne trznego pola magnetycznego ograniczymu uwage do temperatur znacznie przewyższaja cych T c. W takich warunkach możemy oczekiwać, iż namagnesowanie M be dzie dużo mniejsze od wartości przy lożonego pola B 0. W takich warunkach spe lnione jest przybliżenie liniowości dla funkcji tangensa hiberbolicznego [ ( )] βgµb zj tgh B N (gµ B ) 2 M βgµ B 2 ( B 0 + ) zj N (gµ B ) 2 M. (112) Równanie (99) s luża ce do wyznaczenia namagnesowania próbki redukuje sie wie do naste puja cej relacji linowej M(T) M 0 M(T) M 0 βgµ B 2 ( B 0 + gµ B 2k B T B 0 + T c T 39 ) zj N (gµ B ) 2 M M(T) M 0. (113)
40 Na podstawie przybliżonego równania (113) możemy dość latwo określić zależność namagnesowania od temperatury i pola magnetycznego. Proste przekszta lcenia daja M(T) M 0 (1 T Tc ) Z powyższej relacji wynika bardzo znane prawo Curie-Weissa = gµ B 2k B T B 0. (114) M(T) = M 0 gµ B 2k B B 0 T T c, (115) które przewiduje naste puja ca postać podatności magnetycznej χ(t) = N (gµ B) 2 4k B 1 T T c. (116) Prawo Curie - Weissa 1 / χ(t) 0 0,5 1 1,5 2 2,5 3 T / T c 3.4 Zależność od temperatury odwrotności podatności magnetycznej. Wed lug prawa Curie- Weissa zależność ta powinna być liniowa (jak pokazaje linia przerywana). W rzeczywistych uk ladach fizycznych w pobliżu T c pojawia sie modyfikacja z powodu spontanicznego namagnesowania (ilustruje to linia cia g la). Prawo Curie-Weissa (116) pokazane na powyższym rysunku jest spe lnione w zakresie powyżej temperatury krytycznej T c. Wraz z obniżaniem temperatury pojawia sie dodatkowy przyczynek do namagnesowania pochodza cy od spontanicznego ferromagnetyzmu. Dodatkowe modyfikacje pojawiaja sie oczywiście również dla silnych pól magnetycznych takich, że B 0 M 0. Argument funkcji tangesa hiperbolicznego jest wówczas duża liczba dlatego, stosuja c (101), znajdujemy M(T) M 0. Silne pola magnetyczne polaryzuja wie c momonety magnetyczne wszystkich elektronów w kierunku pola bez wzgle du na temperature. 40
41 3.5 Uporza dkowanie typu antyferromagnetycznego Niektóre zwia zki, na przyk lad tlenki żelaza, kobaltu lub niklu, wykazuja ujemna energie oddzia lywania wymiany J < 0. Można oczekiwać, iż w granicy T 0 spiny elektronów be da da ży ly do konfiguracji, w której na sa siednich we z lach sieci sa przeciwnie skierowane. 3.5 Ilustracja antyferromagnetycznego uporza dkowania spinów elektronowych dla dwuwymiarowej sieci regularnej. Taka konfiguracja jest stanem podstawowym w przypadku ujemnej energii wymiany J < 0. Do ilościowego opisu uporza dkowania antyferromagnetycznego wygodnie jest zdefiniować dwie naprzemienne podsieci. Oznaczmy je odpowiednio symbolem A oraz B. Analize przybliżenia pola średniego można wtedy przeprowadzić dla każdej z tych podsieci. Namagnesowanie poszczególnych podsieci wynosi odpowiednio M A = 1 2 gµb ( N A N A ), gdzie M A = gµ B S A (117) M B = 1 2 gµb ( N B N B ), M B = gµ B S B. (118) W przypadku bez zewne trznego pola magnetycznego wzgle dna liczebność elektronów o spinach i jest określona regu la Boltzmanna N A N A = exp { βgµ B B eff }. (119) Każdy elektron podsieci A jest otoczony przez z atomów podsieci B (gdzie z oznacza liczbe koordynacyjna ) i podobnie jest w przypadku drugiej podsieci. Efektywne pole magnetyczne 41
42 ,,odczuwane przez elektrony podsieci A wynosi Beff A = zj S B, gµ B (120) Beff A = zj (gµ B ) 2 MB. (121) Na tej podstawie N A N A = exp { βgµ B B A eff { } } βzj = exp M B. (122) gµ B zatem, analogicznie do (100), namagnesowanie podsieci A wynosi M A = 1 2 gµb ( N A + N A ) N A N A N A + NA = gµ BN A 2 tgh [ ] βzjm B 2gµ B N B (123) oraz podobnie w przypadku drugiej podsieci M B = gµ BN B [ ] βzjm A tgh. (124) 2 2gµ B N A Zwróćmy uwage, że równania (123) i (124) dotycza z-towej sk ladowej namagnesowania w poszczególnych posieciach. Ze wzgle du na fakt, iż J < 0 równania te implikuja porza dek typu antyferromagnetycznego, tzn. M B = M A, (125) o czym latwo przekonać sie wstawiaja c (125) do powyższych równań (123,124). Liczebność elektronów w poszczególnych posieciach jest równoliczna N A = N B = N 2 zatem ostatecznie wartość namagnesowania określona jest naste puja cym warunkiem M A = gµ BN 4 [ ] βzjm A tgh. (126) 2gµ B N 2 Oczywiście ca lkowite namagnesowanie wzd luż osi z znika M A + M B = 0 ale w poszczególnych podsieciach może być niezerowe i jest określone równaniem M A [ zj M 0 /2 = tgh 4k B T M A ]. (127) M 0 Odwo luja c sie do analizy skrajnych przypadków omawianych w poprzednim podrozdziale wnioskujemy, że w granicy temperatury zera bezwzgle dnego namagnesowanie da ży do wartości 42
43 lim T 0 MA (T) = M 0 2. (128) natomiast spantaniczne namagnesowanie podsieci zanika w temperaturze krytycznej lim M A (T) = 0 T N = zj. (129) T T N 4k B Krytyczna wartość temperatury T N (która jest oczywiście dodatnia, ponieważ J < 0) poniżej której pojawia sie spontaniczne antyferromagnetyczne namagnesowanie jest w literaturze nazywana temperatura Neela. W obecności zewne trznego pola magnetycznego równiania na namagnesowanie podsieci A i B należy uzupe lnić o cz lon oddzia lywania z polem. Procedura poste powania jest identyczna jak wyprowadzenie wzoru (99). Dla s labych pól magnetycznych B 0 M 0 otrzymujemy wówczas liniowa relacje pomie dzy polem ganetycznym i namagnesowaniem, na podstawie którego podatność magnetyczna przyjmuje postać χ(t) = (gµ B) 2 4k B 1 T + T N. (130) 1 / χ(t) Prawo Neela T N temperatura 3.6 Temperaturowa zależność odwrotności podatności magnetycznej w antyferromagnetykach (linia cia g la) oraz zależność z równania (130). Punkt przecie cia z osia pozioma określa T N. Tego rodzaju zależność temperaturowa jest charakterystyczna dla materia lów antyferromagnetycznych. Szkic takiej zależności jest przedstawiony na powyższym rysunku. 43
44 4. Struktura pasmowa cia l sta lych Dotychczas opisywaliśmy uk lad elektronów przewodnictwa traktuja c je jako cza stki swobodne. W cia lach sta lych takie za lożenie jest nierealne, gdyż elektrony musza poruszać sie w obecności krystalicznej sieci jonów a ponadto odczuwaja silny wp lyw wzajemnych oddzia lywań kulombowskich. Oba czynniki odgrywaja kluczowa role dla w laściwości uk ladu elektronowego. W pierwszej kolejności uwzgle dnimy wp lyw sieci jonów, natomiast drgania sieci krystalicznej oraz wzajemne oddzia lywanie mie dzy elektronami potraktujemy w później. 4.1 Blochowski charakter elektronów w kryszta lach Obecność krystalicznej sieci jonów sprawia, że do kompletnego opisu gazu elektronowego musimy uwzgle dnić cze ść hamiltonianu opisuja ca operator energii kinetycznej Ĥ kin oraz potencja l oddzia lywania elektronów z jonami U jon el. Dopuszczalne energie gazu elektronowego spe lniaja naste puja ce równanie Schrödingera Ĥψ(r) = (Ĥkin + U jon el )ψ(r) = Eψ(r). (131) Powyższy problem wielocia lowy postaramy sie znacza co uprościć, zak ladaja c periodyczność potencja lu oddzia lywania U jon el (r) = U jon el (r + T), (132) gdzie T oznacza wektor translacji T = n 1 a + n 2 b + n 3 c (133) zaś a, b oraz c sa wektorami prostymi sieci krystalicznej. Z fizycznego punktu widzenia za lożenie periodyczności (132) oznacza zaniedbanie wp lywu drgań sieci krystalicznej na ruch elektronów. Za lożenie takie stanowi istote przybliżenia nazywanego w literaturze specjalistycznej jako przybliżenie adiabatyczne. Potencja l (132), który charakteryzuje sie periodycznościa wzgle dem wspó lrze dnych po lożeniowych wygodnie jest przedstawić poprzez odpowiednie transformaty Fouriera 44
45 U jon el (r) = 1 u k e ikr). (134) V Warunek periodyczności potencja lu U jon el (r) = U jon el (r + R) we wspó lrze dnych Fouriera k 1 V u k e ikr = 1 k V u k e ik(r+t) (135) k prowadzi do naste puja cego wniosku 1 = e ikt. (136) Warunek (136) oznacza, że dla potencja lu U jon el (r) dopuszczalne sa tylko takie sk ladowe fourierowskie u k odpowiadaja ce wektorom k równoważnym z wektorami sieci odwrotnej k = G. Wektory G można wyrazić poprzez naste puja ca ogólna postać G = ha + kb + lc. (137) W wyrażeniu (186) wykorzystane sa wektory bazowe a, b oraz c tzw. sieci odwrotnej, które zazwyczaj definiuje sie jako a = 2π b c a (b c), b = 2π c a a (b c), c = 2π a b a (b c). (138) Bezpośrednim rachunkiem latwo możemy sprawdzić, że dowolny wektor k = G zdefiniowany wzorem (186) spe lnia wymóg periodyczności (136) W dalszej kolejności uzasadnimy teraz bardzo ważne twierdzenie, iż równanie Schrödingera ) ( h2 2m 2 r + U jon el (r) Ψ(r) = εψ(r). (139) implikuje postać funkcji falowej Ψ(r), która możemy znakować wektorem falowym k. Aby udowodnić powyższe twierdzenie Blocha spróbujmy najpierw wybrać funkcje falowa jako fale p laska Ψ(r) = c k 1 V e ikr (140) z dowolnym wspó lczynnikiem c k do ustalenia w dalszej kolejności. Po podstawieniu takiego wyboru (140) do wyjściowego równania Schrödingera (139) stwierdzamy konieczność spe lnienia naste puja ce warunku 45
46 ( h 2 k 2 ) 2m ε 1 c k e ikr + 1 u G c k e i(k+g)r = 0, V V G ( h 2 k 2 ) 2m ε 1 c k e ikr + 1 u G c k G e ikr = 0. (141) V V Krytyczna ocena równania (141) zmusza nas do poprawienia wyjściowej propozycji wyboru funkcji falowej (140) do naste puja cej poprawnej postaci G Ψ(r) Ψ k (r) = 1 V G c k G e i(k G)r = 1 V e ikr G c k G e igr } {{ } a k (r) (142) Podstawienie funkcji (142) do równania Schrödingera (139) prowadzi do naste puja cego warunku dla wspó lczynników c k G zdefiniowanych w wyrażeniu (142) ( h 2 k 2 2m ε k ) c k G + G 1 u G1 Gc k G1 = 0. (143) Funcja falowa (142) elektronów w obecności periodycznego potencja lu sieci krystalicznej jest wie c faktycznie znakowana wektorem falowym k. Z formalnego punktu widzenia tzw. funkcje Blocha (142) można zapisać w postaci Ψ k (r) = 1 V e ikr }{{} fala p laska a k (r) (144) która jest iloczynem fali p laskiej (charakterystycznej dla cza stek swobodnych) oraz zależnego od po lożenia r czynnika atomowego a k (r). Czynnik ten jest przejawem wp lywu periodycznej sieci jonowej na zachowanie elektronów. Wspó lczynnik a k (r) charakteryzuje sie taka sama periodycznościa jak potencja l sieci a k (r + T) = G c k G e ig(r+t) = G c k G e igr e igt }{{} =1 a k (r + T) = a k (r). (145) Pogla dowo można zinterpretować funkcje Blocha (144) jako z lożenie cech typowych dla cza stek swobodnych oraz periodycznej modyfikacji wynikaja cej z przestrzennej powtarzalności sieci 46
47 krystalicznej. W pewnym sensie Ψ k (r) reprezentuje periodycznie zdeformowana fale p laska. Poniższy rysunek przedstawia ilustracje Re{ψ k (r)} dla dwóch przyk ladowych czynników u k (r). Rys. 4.1 Pogla dowy wykres cze ści rzeczywistej funkcji falowej typu Blocha (144) dla elektronów pasma przewodnictwa (górny rysunek) oraz walencyjnego (dolny rysunek). Ilustracja ta zosta la zaczerpnie ta z podre cznika N.W. Ashcroft & N.D. Mermin, Fizyka cia la sta lego, PWN Warszawa (1986). Periodyczność potencja lu oddzia lywania elektronów z siecia krystaliczna ma ponadto wp lyw na istotna ceche relacji dyspersyjnej (tzn. zależności energii od wektora falowego ε k ). Dla dowolnego kwazipe du k spe lniona jest naste puja ca tożsamość Ψ k+g (r) = 1 c k+g G1 e i(k+g G 1)r == 1 V G 1 V G c k G e i(k G )r = Ψ k (r). (146) Powyższy wzór implikuje, iż energie elektronów ε k sa niezmiennicze na przesunie cie o dowolny wektor sieci odwrotnej G ε k+g = ε k. (147) W szczególności wystarczy zatem określić relacje dyspersyjna tylko dla zakresu pierwszej strefy Brillouina i naste pnie poprzez (147) powielić ja na zakres kolejnych stref. Ta specyficzna w lasność jest jedna z konsekwencji wp lywu periodycznej sieci jonów na w laściwości elektronowe. Bardzo istotnym skutkiem blochowskiej relacji (147) jest prawo zachowania kwazipe du k spe lnione tylko z dok ladnościa do wektora sieci G. Procesy rozpraszania elektronów spowodowane przez zewne trzne zaburzenia be dziemy opisywać w dalszej cze ści niniejszego kursu przy okazji dyskusji zjawisk transportu ladunkowego w obecności pola elektromagnetycznego. 47
48 4.2 Przypadek elektronów s labo sprze żonych z siecia Ważna fizyczna konsekwencja blochowskiej natury elektronów w sieciach krystalicznych jest powstawanie struktury pasmowej. Widmo energetyczne uk ladu elektronowego sk lada sie z szeregu przedzia lów dopuszczalnej energii (tzw. pasm energetycznych) oddzielonych obszarami energii wzbronionej (tzw. przerw energetycznych). Jako pouczaja cy przyk lad, ilustruja cy koncepcje powstawania pasm energetycznych w cia lach sta lych, rozpatrzmy najpierw przypadek potencja lu oddzia lywania U jon el (r) (oraz transformat Fouriera u G ) znacznie mniejszych od tak charakterystycznych wielkości jak energia Fermiego. Taki model jest w literaturze nazywany scenariuszem prawie swobodnych elektronów. W celu oszacowania wspó lczynników c k G w równaniu (142) pos lużymy sie iteracyjna preocedura, która stanowi przyk lad schematu rachunku zaburzeniowego. 1 o. Dla dowolnego kwazipe du k oszacowujemy wspó lczynniki c k G dla cza stki swobodnej 1 dla G = 0 c 0 k G = (148) 0 dla G 0 Oszacowanie energii elektronów w pierwszym kroku iteracyjnym daje ( ε 0 k ε 1 k) c 0 k + G 1 u G1 Gc 0 k G 1 = 0. ε 1 k = ε 0 k + u 0, (149) gdzie ε 0 k = h2 k 2 2m. Wyrażenie (149) zawiera korekte wyjściowej energii ε0 k z dok ladnościa do pierwszego rzedu rachunku zaburzeniowego wzgle dem potencja lu U jon el (r). 2 o. W naste pnym kroku iteracyjnym uaktualniamy wspó lczynniki c k w opraciu o równanie (143), uzyskuja c ( ε 0 k G ε 0 k) c 1 k G + ( ε 0 k G ε 0 k ) c 1 k G + u G = 0 G 1 u G1 Gc 0 k G 1 = 0 48
49 u G c 1 k G = ε 0 k. (150) ε0 k G 3 o. Dokonanie uaktualnienia wspó lczynników c 0 k G c 1 k G wykorzystane w równaniu (143) prowadzi do naste puja cego oszacowania energii elektronów w kolejnym kroku iteracyjnym ( ε 0 k εk) 2 ck + u G1 c k G1 = 0. G 1 ( ε 0 k εk) 2 c 0 k + u u G1 Gc 1 k G 1 = 0. G 1 ε 2 k = ε 0 k + u 0 + u G u G G 0 ε 0 k = ε 0 ε0 k + u 0 + u G 2 k G G 0 ε 0 k ε0 k G (151) Z formalnego punktu widzenia wyrażenie drugiego rze du rachunku zaburzeń (151) jest niestety k lopotliwe, gdyż obecność jakichkolwiek stanów zdegenerowanych może prowadzić do dzielenia przez zero (rozbieżności wspomnianego wyrażenia). Takie przypadki rzeczywiście moga mieć miejsce, np. dla kwazipe dów z granicy pierwszej strefy Brilouina k G 0 /2 oraz k G 0 G 0 /2. Wynik (151) przestaje być wówczas wiarygodnym narze dziem do analizy wzajemnego wp lywu wymienionych stanów energetycznych. Aby precyzyjniej uwzgle dnić wzajemny wp lyw wspomnianych wyżej stanów dokonamy analizy warunku (143) poza schematem standardowego rachunku zaburzeniowego. Równanie (143) na wspó lczynniki c k G możemy przybliżyć, ograniczaja c sie jedynie do wzajemnego wp lywu tylko wymienionych dwóch stanów ±G 0 /2 (zaniedbuja c kwazipe dy różne od ±G 0 /2). W rezultacie dla k 1G 2 0 uzyskujemy ( ε 0 k ε k ) ck + u G0 c k G0 0 (152) ( ε 0 k G0 ε k G0 ) ck G0 + u G0 c k 0. (153) Twierdzenie Blocha (144) implikuje, że zależność dyspersyjna ε k jest niezmiennicza wzgle dem przesunie cia kwazipe du k o dowolny wektor sieci odwrotnej (czyli w szczególności ε k = ε k G0 ). Zatem równania (152,153) posiadaja rozwia zanie, spe lniaja ce warunek zerowania sie wyznacznika 49
50 (ε 0 k ε k ) u G0 ( ) = 0. (154) u G0 ε 0 k G0 ε k G0 W ten sposób uzyskujemy dwa pierwiastki powyższego równania kwadratowego (154) ε ± k 1 2 ( ) ε 0 k + ε 0 1 (ε k G 0 ± 0 k 2 ) 2 ε0 k G ug0 2. (155) W bardzo bliskim sa siedztwie granicy pierwszej strefy Brillouina k G 0 /2 dopuszczalne sa dwie wartości energii elektronów ε ± k ε0 k ± u G0, (156) pomie dzy którymi wyste puje obszar stanów wzbronionych (czyli przerwa energetyczna). Liczbowo szerokość przerwy energetycznej wynosi 2 u G0. Na poniższym rysunku ilustrujemy idee powstawania przerw energetycznych wskutek braggowskiego rozpraszania elektronów na sieci krystalicznej. Rys. 4.2 Zależność dyspersyjna ε k uk ladu elektronów s labo oddzia luja cych z siecia krystaliczna. Powyższy rysunek zosta l wykorzystany z podre cznika A. Sukiennicki, A. Zagórski, Fizyka cia la sta lego, Wydawnictwo Naukowo Techniczne, Warszawa (1984). Dla stanów k G 0 2 q, k G 0 ( G q) możemy określić relacje dyspersyjna (155) dokonuja c rozwinie cia wzgle dem q G 0 ε ± k = ε0 G 2 /2 ± 1 h 4 2 4m 2 G2 0q u G0 2 (157) 50
51 ( ε ± k ε0 G 2 /2 ± u G0 1 + h4 G 2 0q 2 ). (158) 16m 2 u G0 2 Masa efektywna poszczególnych ga le zi (pasm) elektronów wynosi w pobliżu brzegu pierwszej strefy Brillouina m ± eff = ±16 u G 0 h 2 G 2 0 m. (159) Kwazicza stki o ujemnej masie efektywnej sa nośnikami ladunku typu dziurowego. Na zakończenie tego podrozdzia lu chcielibyśmy również zaznaczyć, że stany zdegenerowane pojawiaja sie także dla wyższych wielokrotności wektora G 0. Wyjściowa dyspersja ε 0 k = h2 k 2 ulega wie c modyfikacjom w pobliżu brzegów kolejnych stref Brillouina, co w konsekwencji indukuje kolejne przerwy energetyczne (patrz rysunek z poprzedniej strony). Wp lyw periodycznego potencja lu sieci krystalicznej powoduje wie c powstawanie pasm oraz przerw energetycznych. W przypadku elektronów s labo sprze żonych z siecia krystaliczna obszary stanów wzbronionych pojawiaja sie w pobliżu krawe dzi stref Brillouina, dlatego można uznać jako rezultat braggowskiego rozpraszania elektronów. 2m 4.3 Przypadek elektronów ciasno zwia zanych z jonami Skrajnie przeciwny przypadek do sytuacji omówionej w poprzednim podrozdziale ma miejsce, gdy elektrony z peryferyjnych pow lok atomowych sa ciasno zwia zane z macierzystymi atomami. Do analizy w laściwości uk ladu elektronowego wygodniej jest wówczas korzystać z reprezentacji atomowych funkcji falowych (w literaturze określanych cze sto terminem orbitali atomowych). Dla uk ladu wieloelektronowego można wybrać funkcje falowa w postaci liniowej superpozycji orbitali atomowych (j.ang. local combination of atomic orbitals, w skrócie LCAO). Za lóżmy, że znamy wszystkie szczagó ly rozwia zania rówania Schrödingera ) ( h2 2m 2 r + V at (r) Φ α (r) = ε α Φ α (r) (160) wybranego pojedynczego atomu. W dalszej analizie skoncentrujemy sie na stanie kwantowym znakowanym liczba α, który odpowiada najwyżej obsadzonej energii elektronowej ε α (formalnie procedura jest jednak identyczna dla dowolnego stanu kwantowego α. W uk ladzie 51
52 makroskopowym (tzn. w sieci krystalicznej z lożonej z periodycznie rozmieszczonych atomów) musimy rozwia zać równanie Schrödingera ) ( h2 2m 2 r + V (r) Ψ k (r) = ε k Ψ k (r) (161) dla mobilnych elektronów, uwzgle dniaja c efektywny potencja l sieci V (r) = R n V at (r R n ), (162) gdzie R n = n 1 a + n 2 b + n 3 c oznacza po lożenia poszczególnych atomów w krysztale. Aby rozwia zać równanie w lasne operatora energii ca lkowitej (161) dokonamy przedstawienia poszukiwanej funkcji falowej Ψ k (r) w postaci liniowej kombinacji funkcji atomowych Ψ k (r) = 1 Φ α (r R n )e ikrn (163) N Tak wybrana funkcja (163) spe lnia wymóg (144) twierdzenia Blocha, ponieważ Ψ k+g (r) = 1 Φ α (r R n )e i(k+g)rn = 1 Φ α (r R n )e ikrn N N n n n e} igrn {{} = Ψ k (r). (164) =1 W dalszej cze ści mówimy procedure wyznaczania energii elektronów w sieci. W tym celu pos lużymy sie naste puja cym wygodnym wyrażeniem ε k = Ψ k(r) Ĥ Ψ k(r), (165) Ψ k (r) Ψ k (r) gdzie symbole bra oraz ket maja naste puja ce znaczenie matematyczne Ψ k (r) Ĥ Ψ k(r) dr Ψ k (r)ĥψ k(r). Mianownik wyrażenia (165) uwzgle dnia konieczność unormowania funkcji falowej i formalnie może być zapisany jako Ψ k (r) Ψ k (r) = 1 N e ik(rm Rn) Φ α (r R m ) Φ α (r R n ). (166) n,m Dokonamy teraz przedefiniowania niemego argumentu r (wzgle dem którego dokonywane jest ca lkowanie), otrzymuja c równoważne wyrażenie Φ α (r R m ) Φ α (r R n ) = Φ α (r R m n )) Φ α (r) c m n, (167) gdzie R m n R m R n. Parametr zespolony c m n jest tzw. ca lka przekrycia orbitalu atomowego centrowanego na atomie n oraz m. Dla funkcji atomowych silnie zlokalizowanych (np. w 52
53 przypadku orbitali z podpow loki f) na wartość ca lki przekrycia maja wp lyw g l ownie przekrycia orbitali atomowych z sa siednich we z lów sieci krystalicznej. Ogólniej jednak przedefiniowanie (167) i wprowadzenie pomocniczego argumentu m = m n daje Ψ k (r) Ψ k (r) = 1 e ikr m Φ α (r R m ) Φ α (r) N n,m = 1 e ikr m Φ α (r R m ) Φ α (r) = N n }{{} m m =1 e ikrm c m. (168) Podobnie można oszaczować elementy macierzowe hamiltonianu, pojawiaja ce sie w liczniku wyrażenia (165) Ψ k (r) Ĥ Ψ k(r) = 1 N = 1 N e ik(rm Rn) Φ α (r R m ) Ĥ Φ α(r R n ) n,m e ikr m n Φ α (r R m n ) Ĥ Φ α(r) n,m = m e ikr m Φ α (r R m ) Ĥ Φ α(r) (169) Dla wygody wyodre bnimy w hamiltonianie cze ść odpowiadaja ca atomowi w po lożeniu zerowym oraz potencja l pozosta lych atomów sieci Ĥ(r) = h2 2m 2 r + V at (r 0) + V at (r n). (170) }{{} n 0 =Ĥat(r) }{{} V (r) W tym przypadku V (r) opisuje oddzia lywanie elektronu atomu centrowanego w po lożeniu zerowym ze wszystkimi pozosta lymi elektronami a także z jonami. Niezmienniczość hamiltonianu na transformacje translacji o dowolny wektor sieci prowadzi do naste puja cego wyrażenia na element macierzowy Ψ k (r) Ĥ Ψ k(r) = m e ikrm Φ α (r R m ) Ĥ Φ α(r) Ψ k (r) Ĥ Ψ k(r) = m e ikrm (ε α c m + S m ). (171) W powyższym wyrażeniu wprowadzili smy pomocniczy parametr S m zdefiniowany przez S m Φ α (r R m ) V (r) Φ α (r). (172) 53
54 Jako pouczaja cy przyk lad rozpatrzmy elektrony w sieci krystalicznej, uwzgle dnimy ca lke przekrycia jedynie pomie dzy atomami z najbliższych we z lów sieci, tzn. 1 gdy m = n, c m n = 0 w pozosta lych przypadkach. (173) Oszacowanie energii elektronów blochowskich w stanie o kwazipe dzie k daje ε k ε α + m 0 S m e ikrm, (174) gdzie elementy macierzowe S m Φ α (r R m ) V (r) Φ α (r) przyjmuja niezerowe wartości tylko dla atomów z najbliższych we z lów sieci. Do wyznaczenia zależności dyspersyjnej ε k rozpatrzmy tutaj trójwymiarowa sieć o strukturze regularnej (simple cubic), wykorzystuja c (174) do wyznaczenia elementów macierzowych od najbliższych sa siadów. Wektor R m la cza cy atomy sa siednich we z lów sieci przyjmuje sześć możliwych form R m = (±a, 0, 0), (0, ±a, 0), (0, 0, ±a), (175) gdzie a jest odleg lościa mie dzyatomowa. Zależność dyspersyjna (174) przyjmuje wie c postać ε k ε α + S 1 ( e ik xa + e ikxa + e ikya + e ikya + e ikza + e ikza) = ε α + 2S 1 (cos k x a + cos k y a + cosk z a) (176) Gdy ca lka przekrycia S 1 jest ujemna, to ε k ma kszta lt odwróconej cosinusoidy (Rys. 4.3). ε k k x Rys. 4.3 Zależność energii elektronów ε k od x-owej sk ladowej kwazipe du k dla elektronów ciasno zwia zanych z jonami dla regularnej sieci kubicznej (tzw. sc). Zgodnie z twierdzeniem Blocha energia elektronów jest monotonicznie powielana z kolejnych strefach Brillouina. 54
55 Stany elektronowe po lożone w pobliżu dolnej oraz górnej granicy pasma można scharakteryzować poprzez tensor masy efektywnej. W pobliżu dolnej krawe dzi pasma możemy rozwina ć cosinusy kierunkowe wzgle dem ma lych argumentów wed lug matematycznej tożsamości cos x 1 + x2. W konsekwencji otrzymujemy 2 ε k ε α + 6S 1 + 2S ( ) 2 k 2 x + ky 2 + kz 2 a 2. (177) 2 Masa efektywna zdefiowana tutaj jako ε k = h2 k 2 2m eff + ε k=0 wynosi wie c m eff = h2 2S 2 a2. (178) W przypadku stanów elektronowych w górnej cze ści pasma można dokonać rozwinie cia cosinusów kierónkowych wzgle dem k i = ±π/a. Po prostych przeliczeniach znajdujemy, że masa efektywna jest wówczas ujemna. Wynik ten sugeruje, iż bardziej adekwatnym rodzajem efektywnych kwazicza stek sa w takich warunkach dziury, czyli niedomiar stanów elektronowych w rozważanym pasmie. Dla arbitranych wektorów k = (k x,k y,k z ) masa efektywna jest wielkościa tensorowa o nieznikaja cych wartościach poza wyrazami diagonalnymi. Jako test na zrozumienie omówionego powyżej schematu zache cam Czytelnika do wyznaczania zależności dyspersyjnej dla sieci regularnej typu fcc oraz bcc. W dalszej cze ści powrócimy jeszcze do metody ciasnego wia zania przy okazji wyznaczania zależności dyspersyjnej pojedynczej p laszczyzny grafenowej (czyli tzw. grafenu). W ostatnich latach problematyka grafenu (a ostatnio również silikenu) cieszy sie duża popularnościa z powodu niezwykle zaskakuja cych w laściwości fizycznych oraz ciekawych perspektyw aplikacyjnych. 4.4 Klasyfikacja cia l sta lych pod wzgle dem struktury pasmowej Jak widzieliśmy na przyk ladzie schematu rachunku zaburzeniowego oraz przybliżenia elektronów ciasno zwia zanych z jonami energie stanów elektronowych ε k,α sa zależne od wektora falowego w różnorodny sposób oraz liczby kwantowej α, znakuja ca wyjściowy stan elektronu w atomie (w praktyce podawana jest informacja nt. pow loki i podpow loki elektronowej). Istnieje wiele metod obliczeniowych struktury pasmowej cia l sta lych. Najbardziej precyzyjnym 55
56 jest algorytm tzw. funkcjona lu ge stości oparty na obliczeniach z pierwszych zasad (ab initio), bazuja cych na schemacie zaproponowanym przez fizyków austriackich z lat 60. XX wieku. W ostatnich latach w zaawansowanych wersjach procedury funkcjona lu ge stości uwzgle dniany jest również wp lyw oddzia lywań kulombowskich mie dzy elektronami (tzw. korelacje elektronowe) np. w uje ciu dynamicznego pola średniego. Takie metody obliczeniowe sa obecnie rozwijane w wielu ośrodkach naukowych (w Zak ladzie Nanotechnologii i Fizyki Powierzchniowej UMCS obliczeniami z pierwszych zasad zajmuje sie dr hab. M. Krawiec). Rys. 4.4 Ilustracja stanów obsadzonych (kolor niebieski) oraz nieobsadzonych (kolor żo lty) w: a) metalach, b) pó lmetalach, c) pó lprzewodnikach samoistnych oraz d) izolatorach. Uniwersalna cecha zależności dyspersyjnej (wyznaczanej różnymi metodami) cia l sta lych jest ich struktura pasmowa. Dla w laściwości transportowych zasadnicze znaczenie odgrywa wówczas po lożenie energii Fermiego. W sposób pogla dowy ilustruje ten fakt powyższy rysunek. P. Hohenberg, W. Kohn, Phys. Rev. 136, B864 (1964); W. Kohn, L.J. Sham, Phys. Rev. 140,A1133 (1964). 56
57 W przypadku cia l metalicznych poziom Fermiego znajduje sie zwyk le dość g le boko w obszarze pasma (tzw. przewodnictwa). Pod wp lywem zewne trzych zaburzeń (pola elektrycznego, magnetycznego, gradientu temperatur itp.) elektrony moga bez wie kszych trudności ulegać wzbudzeniu do stanów pustych powyżej energii Femiego. W konsekwencji reakcja uk ladu na zewne trzne czynniki zaburzaja ce przejawia sie dość dużym pra dem, namagnesowaniem lub dryfem ciep la. Materia ly takie sa wie c dobrymi przewodnikami. Schematycznie sytuacje taka ilustruja dwa panele po lewej stronie rysynku 4.4. W realnych materia lach moga realizować sie również warianty z pozoru dość egzotyczne. Jako przyk lad warto wspomnieć tzw. pó lmetale (drugi panel od lewej na rysunku z poprzedniej strony). Dwa pasma posiadaja zakres przekrywaja cej sie energii jak pokazano na rysunku 4.5. Jeżeli poziom Fermiego znajduje sie dok ladnie w zakresie takiego przekrycia, to pod wp lywem niewielkich zaburzeń możliwe sa wzbudzenia elektronowe zarówno wewna trz poszczególnych pasmow jak też przejścia pomie dzy pasmami. Te drugie wymagaja znacznej zmiany kwazipe du i sa w fizyce nazywane przejściami skośnymi. Wyste puja ca koncentracja elektronów pasma przewodnictwa oraz dziur pasma walencyjnego sprawia, że pó lmetale sa wzgle dnie dobrymi przewodnikami. energia ε k (2) ε F ε k (1) 0 k x π/a Rys. 4.5 Dwa pasma o zależnościach dyspersyjnych ε (1) k oraz ε (2), które sa cze ściowo obsadzone (stany energetyczne poniżej poziomu Fermiego ε F ). Taki scenariusz realizuje sie w pó lmetalach. k W przypadku, gdy poziom Fermiego (którego po lożenie określone jest zdeterminowane koncentracja elektronów, co jest bardziej szczegó lowo omówione w naste pnym podrozdziale) znajduje sie pomie dzy pasmami walencyjnym i przewodnictwa, wówczas wzbudzenia elektronowe wymagaja znaczej energii do pokonania przerwe energetyczna. Zazwyczaj odleg lości 57
58 pomie dzy pasmami moga wynosić od dziesie tnych cze ści do kilku elektronowoltów. Zatem dla niewielkich przerw energetycznych realne sa wzbudzenia zaindukowane różnymi czynnikami (np. wzbudzenia termiczne). Oczywiście wzrost temperatury korzystnie wp lywa na wzrost wzbudzeń termicznych, polepszaja c tym samym charakterystyki transportowe uk ladu elektronowego. Materia ly tego rodzaju nazywane sa pó lprzewodnikami samoistnymi. Dodatkowe domieszki obcych atomów typu donorowego lub akceptorowego moga być źród lem dodatkowych nośników, a czym be dzie mowa w naste pnym podrozdziale. W przypadku, gdy wartość przerwy energetycznej przekracza pu lap 1 ev to jest ona wtedy zbyt duża aby elektrony by le w stanie przedostać sie do pasma przewodnictwa przy wspó ludziale zewne trznych czynników zaburzaja cych. Tak duże bariery energetyczne powoduja, że materia ly staja sie wówczas izolatorami. Relacje dyspersyjne ε k w ogólności cze sto odbiegaja od tradycyjnej zależności parabolicznej, uniemożliwiaja c pos lugiwanie sie koncepcja masy efektywnej. Szczególnym przyk ladem moga być tzw. osobliwości van Hove a. Sa to takie poziomy energetyczne elektronów, dla których gradient zależności dyspersyjnej k ε k da ży do zera. Widmo energetyczne uk ladu elektronowego posiada w takich miejscach ge stość stanów, charakteryzuja ca sie niecia g la pierwsza pochodna. Na przyk lad, w dwywymiarowym uk ladzie elektronów ciasno zwia zanych z siecia jonów o strukturze regularnej osobliwość van Hove a typu logarytmicznego realizuje sie w centrum pasma przewodnictwa. Osobliwości tego typu maja niekiedy duże znaczenie. 4.5 Koncentracja nośników w pó lprzewodnikach Pasmowy charakter widma energetycznego elektronów w kryszta lach odgrywa kluczowa role w zjawiskach transportowych. Z powodu regu ly Pauliego stany elektronowe w pe lni zape lnionych pasm praktycznie nie uczestnicza w transporcie ladunku. Z oczywistych wzgle dów również stany o wysokich energiach (nieobsadzone) nie daja wk ladu do przewodnictwa oraz innych form reakcji na zewne trzne zaburzenia. Najistotniejsze sa takie stany elektronowe, które znajduja sie w pobliżu poziomu Fermiego (lub ściślej mówia c poziomu chemicznego). 58
59 Energia E g E c ε F E v Rys. 4.6 Ilustracja pasmowego charakteru widma elektronów w pó lprzewodnikach samoistnych. Oś pionowa oznacza energie natomiast oś pozioma s luży jedynie do celów graficznych (nie ma g le bszego sensu fizycznego). W temperaturze zera bezwzgle dnego stany energetyczne poniżej przerwy energetycznej (kolor czerwony) sa obsadzone, a powyżej przerwy (kolor szary) sa puste. Linia przerywana pokazuje po lożenie energii Fermiego. Gdy w temperaturze zera bezwzgle dnego pasmo walencyjne jest w pe lni zape lnione natomiast pasmo przewodnictwa jest kompletnie puste to mamy do czynienia z przypadkiem izolatora (dla przerw energetycznych równych lub wie kszych od ev) albo pó lprzewodnika samoistnego. W tym kontekście można zadać pytanie o po lożenie potencja lu chemicznego i jego zależność od temperatury. W dalszej cze ści niniejszego rozdzia lu postaramy sie odpowiedzieć na powyższe pytanie na podstawie wniosków wcześniejszej analizy modelu gazu Fermiego. Za lóżmy, że stany elektronowe w pobliżu dna pasma przewodnictwa można charakteryzować paraboliczna zależnościa dyspersyjna w postaci ε k = E c + h2 k 2, (179) 2m e gdzie E c jest energia dna pasma przewodnictwa. Z elementarnych rozważań dotycza cych ge stości stanów swobodnego gazu cza stek typu fermionowego otrzymujemy w przypadku uk ladu trójwymiarowego ρ(ε) = 1 2π 2 Koncentracja elektronów w pasmie przewodnictwa wyniesie ( )3 2me 2 (ε h 2 Ec ) 1/2 (180) 59
60 1 n = dε ρ(ε) E c 1 + exp ( ), (181) ε µ k B T }{{} funkcja Fermiego gdzie potencja l chemiczny µ jest wielkościa do wyznaczenia. Skorzystamy naste pnie z przybliżenia semiklasycznego exp ( ε µ k B T ) 1 exp ( ε µ k B T ) (182) które jest w pe lni uzasadnione gdy E c µ k B T. Wyrażenie (181) może być wówczas przedstawione w naste puja cej postaci jawnej n 1 2π 2 ( )3 ( ) 2me 2 µ ( ) ε exp h 2 dε (ε E c ) 1/2 exp. (183) k B T E c k B T Za pomoca zmiennej pomocniczej ε = ε E c dostajemy wyrażenie z ca lka typu gaussowskiego n 1 2π 2 ( )3 2me h 2 2 exp ( µ Ec k B T ) 0 ( ) ε d ε ε 1/2 exp, (184) k B T która wynosi n 2 ( me k B T 2π h 2 )3 2 exp ( µ Ec k B T ). (185) Elektrony wzbudzone termicznie do pasma przewodnictwa pozostawiaja po sobie dziury w pasmie walencyjnym. Dla stanów po lożonych blisko górnej krawe dzi E v pasma walencyjnego stosowalne jest przybliżenie masy efektywnej ε k E v h2 k 2 2m h. Odwiednia ge stość stanów dziur wyrażona jest analogicznie do (180) poprzez ρ h (ε) = 1 2π 2 ( )3 2mh 2 h 2 (Ev ε) 1/2 (186) Prawdopodobieństwo wyste powania dziur f h (ε) = 1 1/[1 + exp( ε µ k B )] można w przybliżeniu T semiklasycznym uprościć do postaci f h (ε) = ( ) 1 ε µ 1 + exp( ε+µ ) exp. (187) k B k T B T Po prostych przekszta lceniach koncentracja dziur w pasmie walencyjnym p = E v ρ h(ε)f h (ε) możemy wyrazić przez postać analogiczna do (185), mianowicie 60
61 p 2 ( mh k B T 2π h 2 )3 2 exp ( Ev µ k B T ). (188) Zmnożenie stronami wyrażenia na koncentracje elektronów (185) oraz dziur (188) implikuja tzw. prawo dzia lania mas n p 4 ( ) 3 ( ) kb T 2π h 2 (m e m h ) 3/2 Eg exp, (189) k B T gdzie odleg lość skraju krae wdzi pasma przewodnictwa od pasma walecyjnego oznaczyliśmy symbolicznie jako E g = E c E v. Pó lprzewodniki samoistne W szczególnym przypadku pó lprzewodników samoistnych koncentracja elektronów n jest identyczna z koncentracja dziur p. Przyrównuja c wie c wyrażenia (185) i (188) otrzymujemy warunek ( ) 2µ exp = k B T ( mh który pozwala wyznaczyć wartość potencja lu chemicznego m e µ(t) = 1 2 E g k BT ln ) 3/2 ( ) Eg exp, (190) k B T ( mh m e ). (191) W temperaturze zera bezwzgle dnego potencja l chemiczny (energia Fermiego) znajduje sie wie c dok ladnie w po lowie odleg lości mie dzy pasmem walencyjnym i przewodnictwa. lim µ(t) = E g T 0 2. (192) W temperaturach powyżej zera bezwzgle dnego potencja l chemiczny ulega przesunie ciu w strone pasma przewodnictwa (jeżeli m h > m e ) lub w strone pasma walencyjnego (jeżeli m h < m e ). Koncentracja nośników w pó lprzewodnikach silnie od temperatury. Na podstawie relacji (184,188) dla pó lprzewodników samoistnych otrzymujemy n(t) = p(t) = 2 ( ) 3/2 ( ) kb T 2π h 2 (m e m h ) 3/4 Eg exp. (193) 2k B T W praktyce dla temperatur bliskich pokojowej dominuja cy wp lyw ma ostatni czynnik eksponencjalny. Eksponencjalny wp lyw temperatury na koncentracje nośników ladunku przejawia sie 61
62 pośrednio w pomiarach charakterystyk przewodnictwa. Sta lopra dowe przewodnictwo w laściwe sk lada sie z wk ladu elektronowego i dziurowego poprzez σ(t) = n(t)eµ e + p(t)eµ h, (194) gdzie µ e,h oznacza ruchliwość poszczególnych nośników, zaś e jest wartościa bezwzgle dna ladunku elementarnego. Powyższe wyrażenie (194) wskazuje, iż termiczna aktywacja przewodnictwa jest w pó lprzewodnikach tym bardziej skuteczna im niższa jest przerwa pomie dzy pasmem walencyjnym i pasmem przewodnictwa. Pó lprzewodniki domieszkowane Wprowadzanie nawet niewielkiej ilości domieszek (typu donorowego lub akceptorowego) do wyjściowych pó lprzewodnikach samoistnych stwarza możliwość znacza cego podwyższenia koncentracji nośników ladunku. Aby zilustrować ten proces pod wzgle dem ilościowym rozpatrzmy przypadek pó lprzewodnika typu n. Do pó lprzedwodnika wprowadzane sa wówczas domieszki atomów typu donorowego, których najwyżej obsadzony poziom atomowy E D znajduje sie w przerwie energetycznej w niewielkiej odleg lości od dolnej krawe dzi pasma przewodnictwa E c. Energia E c E v E D Rys. 4.7 Schemat widma energatycznego domieszkowanych pó lprzewodników typu n. W pobliżu dolnej krawe dzi pasma przewodnictwa znajduje sie poziom donorowy E D. Po pokonaniu różnicy energii E c E D dostarczane sa z niego (w temperaturze powyżej 0 K) elektrony do pasma przewodnictwa. Efektywny poziom Fermiego oznaczony jest linia przerywana. 62
63 Przyjmijmy, że koncentracja domieszek donorowych (ich funkcje pe lnia zazwyczaj pie ciowartościowe atomy pierwiastków P, Sn albo As) wynosi N D. W granicy niskich temperatur można oczekiwać, iż niemal wszystkie elektrony pasma przewodnictwa pochodza wskutek termicznego wzbudzeń elektronowych poziomu donorowego E D. Prawdopodobieństwo wzbudzenia elektronów z poziomu donorowego wynosi exp ( ) = E D µ k B T }{{} funkcja Fermiego exp ( E D +µ k B T ( ED µ ) exp k B T ), (195) zatem ca lkowita koncentracja elektronów w pasmie przewodnictwa ( ) ED µ n N D exp. (196) k B T Na podstawie wcześniej wyprowadzonego wzoru (185) możemy wyrazić koncentracje elektronów pasma przewodnictwa jako ( ) µ Ec n = N c exp. (197) k B T Dla skrócenia zapisu wprowadziliśmy w wyrażeniu (197) pomocnicza 2 ( )3 m ek B T 2. Porównuja c równanie (196) z (197) stwierdzamy wie c 2π h 2 ( ) 2µ exp N D exp k B T N c wielkość N c = ( ) ED + E c. (198) k B T Potencja l chemiczny jest zatem po lożony pomie dzy poziomem donorowym i dolna krawe dzia pasma przewodnictwa µ(t) E D + E c 2 + k BT 2 ln ( ND N c ), (199) co ilustruje linia przerywana na rysunku z poprzedniej strony. W fizyce pó lprzewodników zwyczajowo przyje to traktować potencja l chemiczny µ(t) po prostu jako energie Fermiego ε F (T) zależna od temperatury. Zauważmy jednak, że rozumienie energii Fermiego jako najwyżej obsadzonego poziomu energetycznego traci sens w kontekście fizyki pó lprzeowdników (a także w kontekscie materia lów typu izalotorowego). 63
64 Energia E c E v E A Rys. 4.8 Schemat widma energatycznego domieszkowanych pó lprzewodników typu p. W pobliżu górnnej krawe dzi pasma walencyjnego znajduje sie poziom akceptorowy E A. Po pokonaniu różnicy energii E A E v elektrony z pasma walencyjnego sa termicznie wzbudzane na poziom domieszek. Efektywny poziom Fermiego oznaczony jest linia przerywana. Przedstawione powyżej rozumowanie można z latwościa uogólnić również na przypadek domieszkowanych pó lprzewodników typu p. Poziomu donorowe (zazwyczaj trójwartościowych atomów pierwiastków B, Al, Ga lub In) dostarczaja dodatkowego poziomu energetycznego E A tuż powyżej górnej krawe dzi pasma walencyjnego E v. Pod wp lywem wzbudzeń termicznych elektrony pasma walencyjnego obsadzaja ten poziom, dzie ki czemu w pasmie walencyjnym pojawiaja sie mobilne dziury (kwazicza stki o dodatnim ladunku). Prawdopodobieństwo obsadzenia poziomu akceptorowego wynosi ( ) exp ( EA + µ ) exp E A µ k B T k B T }{{} funkcja Fermiego (200) dlatego koncentracje dziur w pasmie pzrewodnictwa możmy oszacować przez ( ) EA + µ p N A exp, (201) k B T gdzie N A jest koncentracja atomów donorowych. Koncentracje dziur w pasmie walencyjnym możemy również oszacować na podstawie warunku (188) poprzez 64
65 ( ) Ev µ p N v exp, (202) k B T gdzie N v = 2 ( )3 m h k B T 2. Z porównania wyrażeń (201) i (202) wynika, że 2π h 2 ( ) 2µ exp N v exp k B T N A ( ) Ev + E A. (203) k B T Potencja l chemiczny w domieszkowanych pó lprzewodnikacj typu p wynosi wie c µ(t) E v + E A 2 + k BT 2 ( ) Nv ln. (204) N A Zarówno w przypadku domieszkowanych pó lprzewodników typu n jak też typu p nośniki ladunku maja ścis ly zwia zek z domieszkami. Wp lyw takich domieszek jest kluczowy w niskich temperaturach. Dominace poszczegolnego rodzaju nośników można wyznaczyć z pomiarów wspó lczynnika Halla. 4.6 Struktura pasmowa grafenu Jednym z materia lów, który w cia gu ostatnich lat cieszy sie olbrzymim zainteresowaniem fizyków cia la sta lego jest grafen. Taka alotropowa postać atomów we gla uda lo sie w warunkach laboratoryjnych po raz pierwszy uzyskać dopiero w dwudziestym pierwszym wieku. Na baze sieci krystalicznej grafenu sk ladaja sie dwa atomy we gla, jak pokazuje poniższy rysunek. A B k y b 1 δ 3 a 1 a 2 δ 1 δ 2 Γ K M K k x Rys. 4.9 Szkic krystalicznej sieci grafenu (typu heksagonalnego), charakteryzuja cej sie dwoma atomami bazy oznaczonych na rysunku (po lewej stronie) odpowiednio kolorem niebieskim i żó ltym. Rysunek z prawej strony przedstawia wektory sieci odwrotnej b 1 oraz b 2. b 2 W dwuwymiarowej p laszczyźnie grafenowej atomy we gla sa sprze żone silnymi wia zaniami kowalencyjnymi. Do wyznaczenia efektywnej zależności dyspersyjnej elektronów grafenu 65
66 może wie c z powodzeniem s lużyć przybliżenie ciasnego wia zania opisane w podrozdziale 4.3. Strukture heksagonala grafenu można opisać naste puja cymi wektorami sieci Bravais a 1 = ( 3, 3 ) a 2, a 2 = ( 3, 3 ) a 2, (205) gdzie odleg lość mie dzy atomami we gla wynosi a 1.42 Å. Odpowiednio przyporza dkowane wektory proste sieci odwrotnej maja postać a 1 = 2π 3a ( 1, 3 ), a 2 = 2π 3a ( 1, 3 ). (206) Wed lug aktualnych obliczeń ab initio ca lka przekrycia funkcji falowej elektronów pomie dzy sa siednimi we z lami wynosi t 2, 8 ev. Dla kolejnych najbliższych sa siadów jej wartość jest szacowana na t 0.1t. Stosuja c formalizm przybliżenia ciasnego wia zania (rozdzia l 4.3) możemy z latwościa wyznaczyć w pierwszej kolejności wk lad do zależności dyspersyjnej pochodza cy od ca lki przeskoku t atomów podsieci A z atomami podsieci B t f k t (1 + e ikxa + e i( kx+ky)a). (207) W naste pnym kroku musimy dokonać transformacji obrotu do bazy prawdziwych stanów w lasnych oraz uwzgle dnić ca lke przeskoku t do kolejnych sa siadów. Ten czysto techniczny aspekt matematyczny zosta l szczegó lowo przeanalizowany ponad pól wieku temu. W rezultacie zależność dyspersyjna elektronów w grafenie przyjmuje naste puja ca postać ε k = ±t 3 + f k t f k. (208) Czynnik geometryczny f k zdefiniowany we wzorze (207) możemy wyrazić w jawnej postaci jako f k = 2 cos ( 3ky a ) + 4 cos ( ) ( ) k ya cos 2 k xa. (209) W wyrażeniu na zależność dyspersyjna (208) wyste puja dwie ga le zie doste pnych stanów elektronowych. Znak + dotyczy tzw. pasma π natomiast znak odpowiednio tzw. pasma π. S. Reich, J. Maultzsch, C. Thomsen, P. Ordejon, Phys. Rev. B 66, (2002). P.R. Wallace, Phys. Rev. 71, 622 (1947). 66
67 W przypadku t = 0 wymienione ga le zie sa symetryczne wzgle dem poziomu Fermiego (który jest w omawianym tutaj przypadku s luży jak punkt odniesienia dla energii, czyli ε F 0). Dla niezerowych wartości t symetria cza stkowo-dziurowa zostaje naruszona. Na poniższym rysunku przedstawiony jest wykres energii ε k wzgle dem sk ladowych wektora kwazipe du k = (k x,k y ). Rys Zależność dyspersyjna dwóch ga le zi stanów elektronowych dla grafenu w przypadku t = 2, 7 ev, t = 0.2t. Poziomy o energii ujemnej sa (w T = 0) stanami obsadzonymi. Z prawej strony pokazano stożek Diraca w pobliżu punktu K (wykres pochodzi z pracy ). Istotna cecha powyżej pokazanej zależności dyspersyjnej (zaczerpnie tej z artyku lu ) jest wyste powanie punktów zetknie cia pasma walencyjnego z pasmem przewodnictwa. Takie dwa wektory kwazipe du z obszaru pierwszej strefy Brillouina maja naste puja ca postać ( ) ( 1 2π K = 1, K = 1, 1 ) 2π 3 3a 3 3a, Z formalnego punktu widzenia grafen posiada wie c widmo energetyczne o zerowej przerwie energetycznej. Dodatkowa niezwykle cenna w laściwościa zależności dyspersyjnej (208) w pobliżu punktów zetknie cia pasma walencyjnego z pasmem przewodnictwa jest liniowa relacja ( 9t ε k 3t a 2 ) ± v F k K ± 3ta2 4 8 sin (3θ k K) k K 2. (210) Pre dkość Fermiego wynosi w tym wypadku v F = 3 ta natomiast pomocniczy ka t θ jest zdefi- 2 niowany jako θ q = arctan ( q x q y ), gdzie q = k K lub q = k K. Obecność t we wzorach A.H. Castro Neto, F. Guinea, N.M.R. Peres, K.S. Novoselov, A.K. Geim, Rev. Mod. Phys. 81, 109 (2009). 67
68 (208,210) powoduje przesunie cie punktów Diraca poza warość zerowa, tym samym naruszaja c symetrie cza stka-dziura. Warto również zwrócić uwage, że zależność dyspersyjna wykazuje niezmienniczość na obrót wektora kwazipe du o 120 o. Fakt ten odzwierciedla symetrie heksagonalnej sieci grafenu. Najciekawsza jednak w laściwościa jest charakter zależności dyspersyjnej w pobliżu punktów K oraz K, gdzie energia liniowo zależy od kwazipe du ε k 3t ±v F k K. Rys Szkic liniowej zależności dyspersyjnej w obszarze stożków Diraca (ang. Dirac cones). Cecha ta przypomina zwia zek pomie dzy energia i pe dem gazu fotonowego, lub w ogólności charakterystyke relatywistycznych fermionów typu Diraca. Z tego powodu punkty zetknie cia sa nazywane punktami Diraca. Co wie cej, pre dkość Fermiego przyjmuje imponuja co duża wartość porównywalna do pre dkości świat la v F c. Elektrony 300 poruszaja sie wie c w p laszczyźnie grafenowej z pre dkościa subświetlna! W pobliżu punktów Diraca poje cie masy efektywnej elektronów traci sens. Inaczej mówia c, elektrony zachowuja sie wówczas jak obiekty bezmasowe. Bezmasowy charakter elektronów w pobliżu punktów Diraca znajduje również odzwierciedlenie w kszta lcie ge stości stanów. Dla prostoty przytoczymy jej jawna postać dla przypadku t = 0, kiedy poziom Fermiego wypada dok ladnie na styku pasma walencyjnego i przewodnictwa ρ(ε) = 4 ( ε π π 2 t 2 Z 1/2 0 F 2, ) Z1 Z 0, (211) gdzie F jest funkcja eliptyczna zupe lna pierwszego rodzaju. Dla ε t parametr Z 1 = 4 ε /t, Z 0 = (1 + ε /t) 2 [(ε/t) 2 1] 2 /4, zaś poza tym zakresem energetycznym Z 0 Z 1. J.P. Hobson, W.A. Nierenberg, Phys. Rev. 89, 662 (1953) 68
69 ρ(ε) t =0.2t ρ(ε) t = ε /t ε /t Rys Efektywna ge stość stanów elektronowych w sieci grafenu dla przypadku t = 0 (rysunki w górnym wierszu) oraz dla t = 0.2t (rysunki w dolnym wierszu). Podsumowuja c wste pne informacje o nietypowej strukturze widma elektronowego w grafenie warto zaznaczyć, że stykanie sie pasma walencyjnego z pasmem przewodnictwa przypomina widmo pó lmetali lub pó lprzewodników o zerowej przerwie energetycznej. Jednakże domieszkowanie grafenu prowadzi do rozdzielenia obu pasm i jednocześnie charakter dirakowski zależności dyspersyjnej ulega zanikowi, co schematycznie ilustruje poniższy rysunek. Rys Zależność dyspersyjna metalu, pó lprzewodnika oraz dwóch różnych form grafenowych. A.H Castro Neto,,,The carbon age, Materials Today 13, 1 (2010). 69
70 5. Zjawiska transportowe W rozdzia lach 2-4 przedstawione zosta ly charakterystyczne cechy uk ladu elektronowego pod ka tem w laściwości termodynamicznych oraz magnetycznych. Nie mniej ważne (a może nawet ważniejsze z praktycznego punktu widzenia) sa charakterystyki transportu ladunkowego. Przep lyw ladunku w cia lach sta lych polega na ruchu elektronów walencyjnych zmuszonych do dryfu pod wp lywem zewne trznego pola elektrycznego. Pogla dowo ilustruje to poniższy rysunek. Rys. 5.1 Dryf elektronów walencyjnych w kierunku przeciwnym do zwrotu pola elektrycznego. Ruch elektronów jest utrudniony koniecznościa przemieszczania sie przez sieć jonów. Nawet idealnie uporza dkowana sieć (tzn. bez wychyleń jonów z po lożeń równowagi) wp lywa na uk lad elektronowy, prowadza c do anizotropii tensora przewodnictwa. Sieć jest odpowiedzialna za braggowskie rozpraszaniem elektronów o wektorach kwazipe du k bliskich krawe dzi strefy Brillouina. Wszelkie realne drgania sieci krystalicznej sa jednym z g lównych czynników rozproszeniowych (ten rodzaj rozpraszania jest w literaturze nazywany mechanizmem fononowym). Kolejnym czynnikiem dyssypacyjnym sa wszelkie niejednorodności w uk ladzie, np. wyste powanie obcych atomów w sieci krystalicznej. Ich wp lyw jest wyraźny zarówno w przypadku domieszek paramagnetycznych i jeszcze silniejszy w przypadku domieszek typu magnetycznego. Poza wymienionymi źród lami rozpraszania również wzajemne oddzia lywania elektronów mie dzy soba (tzw. korelacje elektronowe) diametralnie wp lywaja na charakterystyki transportowe. Spek- 70
71 takularnym przejawem tego wp lywu jest przejscie metal-izolator (tzw. przejście Motta) zaindukowane odpychaniem kulombowskim mie dzy elektronami w sieci. Rys. 5.2 Pogla dowa ilustracja po lożenia jonów (oznaczonych jako na ciemno wype lnione kulki) i rozk ladu ge stości elektronów walencyjnych (kolor żó lty). Wp lyw konkretnej struktury geometrycznej sieci jonów jest odpowiedzialny za anizotropie tensora przewodnictwa. Makroskopowym przejawem efektywnego wp lywu mechanizmów rozpraszania jest zjawisko oporu elektrycznego. Istote zjawiska oporu oddaje naste puja ce empiryczne prawo Ohma I = U/R, (212) gdzie I jest nate żeniem pra du, U różnica potencja lów (napie ciem) a R jest oporem. Ca lkowity opór próbki zależy od jej kszta ltu. Dla kabla o przekroju A i d lugości l (rysunek obok) opór ca lkowity można wyrazić jako R = ρ l A, (213) gdzie ρ oznacza opór w laściwy. Wielkość ta jest charakterystyka nieekstensywna, chociaż jej wartość może zależeć od rodzaju materia lu, temperatury itp. 71
72 Liczbowe wartości oporu w laściwego ρ cia l sta lych moga różnić sie o ponad 30 rze dów wielkości! Jako przyk lad poniżej przedstawione sa wartości oporu w laściwego dla wybranych materia lów w temperaturze pokojowej 20 o C. miedź aluminium żelazo grafit german krzem diament guma teflon 1, Ω m 2, Ω m 1, Ω m 2, Ω m 4, Ω m 6, Ω m Ω m Ω m Ω m Tak duża rozpie tość zmienności oporu w laściwego sprawia, że z praktycznych wzgle dów przyja l sie podzia l materia lów na przewodniki (metale), pó lprzewodniki (np. german lub krzem) oraz izolatory (np. guma, szk lo i różne tworzywa sztuczne). Podzia l ten jest nieostry, gdyż trudno mówić o granicznych wartościach oporu pomiedzy poszczególnymi typami. Co wie cej opór w laściwy jakościowo i ilościowo zależy od temperatury. W pó lprzewodnikach i izolatorach opór eksponencjalnie maleje ze wzrostem temperatury, podczas gdy w metalach opór w laściwy liniowo wzrasta z temperatura. O niuansach zależności temperaturowej oporu w pó lprzewodnikach by la cze ściowo mowa przy okazji omawiania struktury pasmowej. W obecnym rozdziale skoncentrujemy sie na temperaturowej zależności oporu dobrych przewodników. 5.1 Klasyczne podejście Drudego Z historycznych i pogla dowych wzgle dów zajmiemy sie uzasadnieniem prawa Ohma korzystaja c najpierw z fenomenologicznego opisu zaproponowanego przez Petera Drude. Empiryczne prawo Ohma (212) wygodnie jest wyrazić w naste puja cy równoważny sposób 72
73 j = σ E. (214) W wyrażeniu tym σ = 1/ρ jest przewodnictwem w laściwym zaś j oznacza wektor ge stości pra du. Zwrot wektora j jest skierowany w kierunku przep lywu umownego ladunku dodatniego, czyli w kierunku przeciwnym do wektora pre dkości dryfu elektronów. Wartość bezwgle dna natomiast j = I/A określa iloraz nate żenia pra du przypadaja cego na jednostke powierzchni przewodnika. O równoważności powszechnie znanej postaci prawa Ohma (212) z przedstawionym powyżej wyrażeniem (214) można przekonać sie, analizuja c sytuacje przedstawiona na dolnym rysunku z poprzedniej strony. Pra d p lyna cy przez przewodnik o przekroju A jest konsekwencja pola elektrycznego E. Nate żenie pola elektrycznego jest ściśle zwia zane ze spadkiem napie cia U na d lugości l poprzez E = U/l. Bewzgle dna wartość ge stości pra du daje efektywnie nate żenie I = A j zatem wykorzystuja c (214) dostajemy równanie I A = U ρ l R = ρ l A, (215) które jest identyczne z empirycznym prawem (212). Relacja (214) wskazuje, że prawo Ohma stanowi przejaw liniowej reakcji uk ladu na zewne trzne zaburzenie, w tym wypadku pole elektryczne. W ogólniejszej postaci tego rodzaju aspekt stanowi istote tzw. formalizmu Kubo. W ramach schematu liniowej reakcji uk ladu na zaburzenia przewidywana jest relacja typu j µ = ν σ µ,ν E ν (dla µ,ν = x,y,z). (216) gdzie σ µ,ν jest tensorem przewodnictwa. Ponadto w sytuacjach, kiedy w reakcji uk ladu na zaburzenia istotna role odgrywaja efekty retardowania (zwia zane np. z czasem potrzebnym na wymiane fononów) oraz wp lywem niejednorodności wówczas relacja (216) powinna być uogólniona do naste puja cej postaci ca lkowej j µ (r,t) = ν t dr dt σ µ,ν (r,r,t t ) E ν (r,t ). (217) 0 Na poziomie mikroskopowym prawo Ohma (214) zosta lo uzasadnione przez P. Drude jako rezultat wp lywu si ly oporu ośrodka na ruch elektronów. Si la oporu jest wprost proporcjonalna do pre dkości elektronów ale skierowana przeciwnie do kierunku ich ruchu F op = βv. 73
74 Fenomenologiczny parametr β wygodniej jest przedstawić poprzez β = m, gdzie τ oznacza τ tzw. czas relaksacji. Si la oporu F op może cze ściowo lub wre cz ca lkowicie kompensować si le kulombowska qe, gdzie ladunek q = e. Wed lug zasad mechaniki klasycznej równania ruchu ma postać m dv dτ = qe mv τ. (218) Rozwia zanie powyższego równania różniczkowego z warunkiem pocza tkowym v(t = 0) = 0 implikuje v(t) = qτ ( [1 m E exp t )]. (219) τ Zatem w skali d lugoczasowej (t τ) wartość si ly kulombowskiej jest ca lkowicie skompensowana przez si le oporu. W takim stanie stacjonarnym elektrony dryfuja ze sta la pre dkościa v d lim t τ v(t) = qτ m E. (220) Z elementarnych rozważań możemy przedstawić wektor ge stości pra du poprzez j(t) = nqv(t), gdzie n oznacza koncentracje elektronów przewodnictwa. Efektywnie w stanie stacjonarnym j = qnv d = q2 nτ m }{{} σ co odtwarza prawa Ohma zapisane w postaci (214). Opór w laściwy ρ = σ 1 = m e 2 nτ E, (221) w uje ciu Drudego jest wyrażony za pomoca fenomenologicznego parametru τ, który pogla dowo można interpretować jako średni czas pomie dzy zderzeniami elektronów. Na podstawie konkretnych wartości oporu w laściwego (przedstawionych na wste pie niniejszego rozdzia lu) można by loby oszacować czas relaksacji τ. Problem jednak w tym, że we wzorze (221) masa m nie oznacza masy elektronów w próżni m 0. Jest to efektywna masa nośników ladunku i w niektórych przypadkach może być kilkaset lub nawet 1000-krotnie wie ksza od masy m 0 (dla pierwiastków ziem rzadkich nazywanych jako tzw. cie żkie fermiony). Nie mniej jednak czas relaksacji τ można liczbowo oszacować, ponieważ iloraz n m jest dookreślony dodatkowo przez naste puja ca regu le f-sum 0 Re {σ µ,ν (ω)} = π 2 e 2 n m δ µ,ν (222) 74
75 stosowalna do przewodnictwa zmiennopra dowego. Regu la sum (222) wynika z formalizmu Kubo. Dla przewodników metalicznych czas relaksacji w warunkach temperatury pokojowej 300 K jest rze du sekundy. G lówny przyczynek do czasu relaksacji (a tym samym również do przewodnictwa/oporu w laściwego) wnosi rozpraszanie elektronów na fononach (czyli wp lyw drgań sieci krystalicznej). W niskich temperaturach prowadzi to do zależności τ 1 (T) T 5, zaś w wyższych temperaturach do zależności liniowej co ilustruje poniższy 5.3. Rys. 5.3 Typowa zależność oporu w laściwego od temperatury w metalach. Powyższa ilustracja pokazuje wp lyw mechanizmu fononowego poprzez niskotemperaturowa zależność T 5 i wysokotemperaturowa relacje T. Zauważamy też ponadto charakterystyczny opór resztkowy ρ 0 ρ(t 0). Jest on spowodowany rozpraszaniem na domieszkach obcych atomów w sieci. Wp lyw tego rodzaju mechanizmu rozpraszania można z dobrym przybliżeniem traktować jako sk ladnik addytywny do efektywnego oporu w laściwego (Rys. 5.4) Rys. 5.4 Addytywny wp lyw oporu resztkowego na przyk ladzie miedzi i jej stopów. 75
76 5.2 Kwantowomechaniczny opis zjawisk transportu Przedstawiony w poprzednim rozdziale scenariusz Drudego nie uwzgle dnia l istotnych efektów wynikaja cych z kwantowej natury elektronów. W rzeczywistych uk ladach elektronowych kluczowe znaczenie odgrywa zasada Pauliego, która nie dopuszcza aby jakikolwiek stan by l obsadzony przez wie cej niż jedna cza stke. Z tego powodu pod nieobecność zewne trznych pól elektrony w zerowej temperaturze obsadzaja stany wewna trz kuli Fermiego (rozdzia l 2). Temperatura powoduje cze ściowa termiczna aktywacje, wed lug prawdopodobieństwa określonego funkcja rozk ladu Fermiego-Diraca. Rys. 5.5 Obsadzone stany elektronowe w przypadku bez zewne trzego pola elektrycznego (rysunek po lewej stronie) oraz w obecności pola E = (E, 0, 0), gdzie E < 0. Kula Fermiego ulega przesunie ciu. W celach pogla dowych pokazano przesadne przesunie cie kuli Fermiego, które w realnych sytuacjach jest zazwyczaj znacznie mniejsze od promienia k F. Intuicyjnie możemy oczekiwać sie, że w obecności zewne trznego pola elektrycznego E dystrybucja obsadzeń stanów elektronowych ulega poważnym zmianom. W wyniku dzia lania si ly kulombowskiej qe oraz si ly oporu elektrony uzyskuja dodatkowy pe d (dryfu) hδk = qτ E, (223) co prowadzi do przesunie cia kuli Fermiego. Każdy elektron zmienia wie c swój wyjściowy stan k init na k fin = k init + δk. Ilustracje obsadzeń stanów elektronowych o określonym wektorze 76
77 falowym k przedstawia powyższy rysunek. Powyższy intuicyjny wynik można uzasadnić w bardziej formalny sposób, stosuja c podejście Boltzmanna. Wektor ge stości pra du j można przedstawić jako j = q 1 V hk f(ε k,t) = q k }{{} m v k 1 (2π) 3 dk v k f(ε k,t), (224) gdzie f(ε k,t) oznacza prawdopodobieństwo obsadzenia stanu energetycznego k w temperaturze T. W warunkach nierównowagowych funkcje f(ε k,t) można przedstawić w postaci rozwinie cia perturbacyjnego f(ε k,t) = f 0 (ε k,t) + qτ(k) h f 0 k E, (225) gdzie f 0 (ε k,t) jest funkcja Fermiego-Diraca wyjściowego stanu bez zaburzenia polem. Wykorzystuja c definicje pre dkości v k = hk/m możemy zasta pić pochodna f 0 k x = hv x f 0 ε k (226) i ostatecznie x-owa sk ladowa wektora ge stości (224) przyjmie postać j x = q2 8π 3 dk v 2 x(k) τ(k) W granicy temperatur bliskich zera bezwgle dnego dlatego lim T 0 [ f 0(ε k,t) ε k ] [ f 0(ε k,t) ε k ] E x. (227) δ(ε k ε kf ) (228) j x = q2 8π 3 v 2 x (k) τ(k) k=k F E x. (229) Biora c pod uwage zapis prawa Ohma w postaci (214) rozpoznajemy diagonalna cze ść tensora przewodnictwa σ x,x = q2 8π 3 v 2 x (k) τ(k) k=k F (230) i podobnie postać dowolnych elementów tego tensora σ µ,ν = q2 8π 3 v µ (k)v ν (k) τ(k) k=kf. Dla przypadku izotropowego uk ladu elektronów przewodnictwa o masie efektywnej m wyrażenie (230) implikuje znana relacje σ = e2 n m τ(ε F ), gdzie n jest koncentracja elektronów. 77
78 5.3 Z la cza tunelowe - kwant przewodnictwa Bardzo ważnym aspektem zjawisk transportowych sa procesy tunelowania ladunku (pra d ladunkowy), energii (pra d cieplny) oraz spinu (pra d spinowo-rozdzielczy) dla różnych heterostruktur z lożonych z zewne trznych elektrod, które można traktować jako rezerwuary elektronów o zadanym potencjale chemicznym µ i. Tunelowanie zachodzić może przez bariery izolatorowe albo przez obiekty nanoskopowe, takie jak: kropki kwantowe, druty kwantowe, fragmenty p laszczyzn grafenu itp. Rys. 5.6 Dwa odleg le od siebie rezerwuary elektronów (elektroda lewa i elektroda prawa) oraz nanoskopowy obszar z la cza tunelowego mie dzy nimi. Do obliczenia nateżenia pra du p lyna cego mie dzy elektrodami lewa i prawa poprzez dowolna strukture nanoskopowa bardzo powszechna jest procedura Landauera. Jej istota polega na uwzgle dnieniu bariery tunelowania jako sekwencji (infinitezymalnych) pszeszkód o określonym prawdopodobieństwie transmisji. Ca lkowite nate żenie elektronów p lyna cych z elektrody lewej do elektrody prawej I L R można efektywnie wyrazić za pomoca funkcji rozk ladu Fermiego Diraca n L (ε k ) = [1 + exp (ε k µ L /k B T)] 1 i wspó lczynnika transmisji T(ε) poprzez I L R = 2 }{{} spin e h dε n L (ε) T(ε) (231) oraz analogicznie można wyrazić pra d I R L. W warunkach stacjonarnych ustala sie efektywne nate żenie pra du (ang. steady current) o wartości I = I L R I R L = 2e h dε T (ε) [n L (ε) n R (ε)]. (232) Powyższy wzór jest znanym wyrażeniem formalizmu Landauera, które implikuje kilka ważnych M. Di Ventra, Electrical transport in nanoscale systems, Cambridge Univ. Press, Cambridge (2008). 78
79 wniosków fizycznych. Zanim je omówimy zaznaczmy, że napie cie V pojawia sie w wyrażeniu (232) poprzez różnice potencja lów chemicznych µ L µ R = ev. Do zilustrowania użyteczności powyższego wyrażenia Landauera (232) określimy relacje pomie dzy nate żeniem I oraz napie ciem w granicy niedużej wartości V. W tym celu za lożymy infinitezymalnie ma la różnice potencja lów µ L = µ + 1eV, µ 2 R = µ 1 ev i wykorzystamy 2 rozwinie cie w szereg wyrażenia na pra d (232) do pierwszego wyrazu wzgle dem V n L (ε) n R (ε) [ f FD(ε,T) ε ] ( ev ) (233) gdzie f FD (ε,t) = 1/ [1 + exp((ε µ)/k B T)]. Korzystaja c z rozwinie cia (233) otrzymujemy I = 2e2 h }{{} G 0 [ dε T (ε) f ] FD(ε,T) ε }{{} liczba bezwymiarowa V (234) Struktura powyższego wyrażenia spe lnia empiryczne prawo Ohma I = 1 V, gdzie opór R jest R odwrotnościa kwantu przewodnictwa G 0 = 2e2 h (235) i bezwymiarowego czynnika dε T (ε) [ ] f FD (ε,t) ε. Wartość liczby bezwymiarowej wyste puja cej we wzorze (234) zależy zarówno od wspó lczynnika transmisji jakt też od temperatury. W skrajnym przypadku temperatury zera bezwgle dnego lim T 0 [ ] f FD (ε,t) ε = δ(ε µ) dlatego I = G 0 T (µ) V. (236) Maksymalna wartościa wspó lczynnika transmisji T jest wartość idealna równa jeden, zatem jeden kana l transportu elektronowego jest w stanie dostarczyć przewodnictwa o maksymalnej wartości G 0. Odpowiedni kwant oporności wynosi R 0 = 1 G 0 = 2, Ω. (237) W ogólności transport przez uk lady nano- lub mezoskopowe angażuje wie cej ewentualnych kana lów (np. liczniejsza ilość atomów lub poziomów elektronowych) dlatego przewodnictwo 79
80 różniczkowe może być wielokrotnościa kwantu przewodnictwa. W temperaturach wyższych od zera bezwzgle dnego wzbudzenia termiczne sprawiaja, że w transporcie uczestnicza elektrony z pewnego zakresu wokó l potencja lu chemicznego µ + k B T,µ k B T. Do wyznaczenia przewodnictwa z la cza konieczne jest wówczas dokonanie uśrednienia (wyca lkowania) po takim zakresie energetycznym. Liczbowa wartość przewodnictwa może wtedy zależeć od postaci funkcji T (ε). Rys. 5.7 Dyskretne wartości oporu (rysunek po lewej stronie) i konduktacji (rysunek po prawej stronie) w funkcji napie cia V dla z la cza tunelowego heterostruktury GaAs-Al-GaAs. Pierwsza doświadczalna realizacje skwantowanego przewodnictwa różniczkowego uzyskano dla heteroz la cza GaAs-GaAlAs (patrz rysunek powyżej), w którym elektrony zaosta ly spu lapkowane w pobliżu brzegów dwuwymiarowego gazu elektronowego. Za pomoca napie cia bramki modyfikowano ilość aktywnych kana lów transportu, co znalaz lo odzwierciedlenie w wielokrotności kwantu przewodnictwa G = n 2e2. Obecnie tego typu efekty otrzymuje h sie dla wielu różnych z la cz tunelowych z wykorzystaniem kropek kwantowych, drutów kwantowych i innych struktur o zredukowanej wymiarowości. B.J. van Wees et al, Phys. Rev. Lett. 60, 848 (1988). 80
81 6. Nadprzewodnictwo i jego zastosowania Na zakończenie niniejszego kursu omówimy zagadnienie nadprzewodnictwa, które jest jednym z najbardziej intryguja cych zjawisk wspó lczesnej fizyki. Świadczy o tym chociażby liczba nagród noblowskich przyznanych dotychczas już 5-krotnie dla w sumie dziesie ciu badaczy. W pierwszej kolejności przedstawiony zostanie krótki przegla d elementarnych w laściwości nadprzewodników. Naste pnie dokonamy interpretacji uniwersalnych cech stanu nadprzewodza cego w ramach mikroskopowej teorii Bardeena, Coopera i Scrieffera (BCS) oraz w uje ciu fenomenologicznym Ginzburga Landaua. Na koniec przedstawiony zostanie przegla d wybranych zastosowań nadprzewodników. 6.1 Podstawowe cechy stanu nadprzewodza cego Określenie nadprzewodniki wskazuje, iż zasadnicza w laściowścia tak nazywanych materia lów jest zdolność bardzo dobrego przewodzenia pra du elektrycznego. Opór w laściwy zwyk lych przewodników spada przy obniżaniu temperatury do zera bezwgle dnego. W odróżnieniu od takiego zachowania opór (sta lopra dowy) nadprzewodników skokowo zanika do zera w pewnej temperaturze krytycznej, jak pokazuje poniższy rysunek. Rys. 6.1 Zanik oporu sta lopra dowego w temperaturze krytycznej T c nadprzewodników konwencjonalnych (rysunek po lewej stronie) oraz w nadprzewodniku HgBa 2 Ca 2 Cu 3 O 8+δ (rysunek po prawej stronie) o rekordowo wysokiej temperaturze krytycznej T c 135 K. 81
82 Po raz pierwszy przejscie ze stanu normalnego do nadprzewodza cego zosta lo zaobserwowane w 1911 r. w laboratorium niskich temperatur Kammerlingha Onnesa (Lejda, Holandia). Odrycia dokonano przypadkowo podczas pomiarów oporu rte ci w rekordowo niskich (na ówczesne czasy) temperaturach oko lo 4 K. W kolejnych latach podobne przejście do stanu nadprzewodza cego stwierdzone zosta lo również w kilku innych pierwiastkach, np. w o lowiu (Pb) i glinie (Al) oraz w niektórych stopach. Wraz z poszukiwaniem kolejnych materia lów nadprzewodza cych zaobserwowano ponadto, że zjawisko bezdyssypatywnego transport ladunku idzie w parze z doskona lym diamagnetyzmem. W nadprzewodniku sch lodzonym poniżej temperatury przejścia indukuja sie pra dy przypowierzchniowe, które ca lkowicie ekranuja strumień zewne trznego pola magnetycznego. Efekt idealnego diamagnetyzmu jest w literaturze nazywane zjawiskiem Meissnera (lub Meissnera- Ochsenfelda). Jego odkrywcami byli w 1933 roku W. Meissner i R. Ochsenfeld. Rys. 6.2 Zjawisko Meissnera polega w nadprzewodnikach na ca lkowitym wypychaniu linii pola magnetycznego w zakresie temperatur T < T c (próbka w kolorze ciemnym). W stanie normalnym (próbka w kolorze szarym) efekt Meissnera nie wyste puje. Wypychanie linii pola magnetycznego realizuje sie w praktyce poprzez wygenerowanie pra dów na powierzchni naprzewodnika. Zewne trzne pole magnetyczne wynika wie c do pewnych przy- 82
83 powierzchnowych obszarów. W pó lfenomenologiczny sposób aspekt ten dobrze uwzgle dnia równanie braci Londonów j(r) = nse2 A(r), gdzie j oznacza ge stość pra du natomiast A jest m potencja lem wektorowym pola elektromagnetycznego. Zazwyczaj wprowadza sie naste puja ce wygodne oznaczenie nse2 m 1 µ 0 λ 2, definiuja ce tzw. g le bokość wnikania λ. W konwencjonalnych nadprzewodnikach λ wynosi oko lo 2000 Å, zaś w nadprzewodnikach wysokotemperaturowych jest o rza d wielkości mniejsza. B(x) = B 0 e x/λ x Rys. 6.3 Eksponencjalny zanik ca lkowitego nate żenia pola magnetycznego B = µ 0 H zewn + M w nadprzewodnikach spowodowany ekranowaniem przypowierzchniowymi pra dami sta lymi. Z diamagnetyczna reakcja M na zewne trzne pole magnetyczne H jest zwia zana kolejna ważna w laściwość fizyczna. Jest nia krytyczna wartość pola magnetycznego H c, powyżej którego stan nadprzewodza cy ulega zniszczeniu. Pod tym wgzle dem rozróżnić można nadprzewodniki pierwszego i drugiego rodzaju. Poniższy rysunek ilustruje jakościowa różnice w reakcji nadprzewodników I-ego i II-ego rodzaju na pole magnetyczne. Rys. 6.4 Diamagnetyczna reakcja (magnetyzacja M) próbki pod wp lywem zewne trznego pola magnetycznego H w nadprzewodnikach I-ego i II-ego rodzaju. W przypadku nadprzewodników II-ego rodzaju dla pól o nate żeniu H c1 < H < H c2 realizuje sie stan mieszany. 83
84 Pole krytyczne H c nadprzewodników I-ego rodzaju jak również dolne H c1 i górne H c2 pole krytyczne nadprzewodników II-ego rodzaju zależa od temperatury (patrz rysunek poniżej). Rys. 6.5 Temperaturowa zależność pól krytycznych w nadprzewodnikach I-ego i II-ego rodzaju. W temperaturach bliskich krytycznej nawet niewielkie pola zewne trzne maja destrukcyjny wp lyw na stan nadprzewodza cy. Podobna ceche posiadaja także krytyczne nate żenia pra dów, co niestety stanowi poważny problem możliwości praktycznego wykorzystania wielu materia lów nadprzewodza cych. Generalnie rzecz biora c, uporza dkowanie magnetyczne jest czynnikiem rywalizuja cym z obecnościa i koherentnym ruchem par elektronowych w stanie nadprzewodza cym (o czym be dzie wie cej mowy w kolejnych podrozdzia lach). Rys. 6.6 Ilustracja skwantowanych strumieni pola magnetycznego (fluksonów), które penetruja próbke nadprzewodnika II-ego rodzaju w stanie mieszanym H c1 < H < H c2. W stanie mieszanym linie pola magnetycznego przenikaja obszar nadprzewodnika drugiego 84
85 rodzaju, ale odbywa sie to na bardzo specyficznych warunkach. Strumienie pola magnetycznego moga być wy la cznie ca lkowita wielokrotnościa kwantu Φ = hc 2e 2, T m 2, zwanego fluksonem. Po drugie, strumienie pola magnetycznego tworza uporza dkowana sieć typu heksagonalnego. Taka najkorzystniejsza energetycznie forme uporza dkowania wirów kwantowych przewidzia l teoretycznie w latach 60. dwudziestego wieku A.A. Abrikosov, co zosta lo później potwierdzone doświadczalnie (A.A. Abrikosov otrzyma l Nagrode Nobla w 2003 roku). Rys. 6.7 Schemat ge stości stanów dla izotropowego nadprzewodnika, który w stanie normalnym charakteryzuje sie zależnościa ρ(ω) = const ε. W stanie nadprzewodza cym pojawia sie przerwa energetyczna wokó l energii Fermiego ε F. W charakterystykach widma elektronowego (mierzalnego doświadczalnie np. poprzez przewodnictwo pra du tunelowania elektronów dla heteroz la cz typu nadprzewodnik-izolator-metal albo bepośrednio za pomoca fotoemisyjnej spektroskopii zależnej od ka ta ARPES) stwierdzono jeszcze jedna bardzo istotna ceche stanu nadprzewodza cego. W pewnym zakresie (rze du mev) wokó l energii Fermiego stwierdzono wyraźny niedomiar stanów elektronowych. Zjawisko to przejawia sie jako przerwa energetyczna (patrz rysunek powyżej). W anizotropowych materia lach przerwa energetyczna może w ogólności zależeć od kierunków w przestrzeni = kf, tak jest na przyk lad w nadprzewodnikach wysokotemperaturowych. 85
86 Rys. 6.8 Zależność przerwy energetycznej od temperatury w nadprzewodnikach konwencjonalnych. W granicy zera bezwgle dnego wartość przerwy energetycznej jest wspó lmierna z temperatura krytyczna wed lug relacji (T 0) 1, 76k B T c. W wie kszości nadprzewodników przerwa energetyczna zanika przy zbliżaniu sie temperatury do krytycznej (T T c ) = 0. Tego rodzaju konwencjonalne zachowanie ilustruje powyższy rysunek, niskotemperaturowa wartość przerwy energetycznej jest wprost proporcjonalna do temperatury krytycznej (T 0) k B T c 1, 76. Sa jednak wyja tki od takiego zachowania. Na przyk lad w nadprzewodnikach wysokotemperaturowych oraz nadciek lych gazach ultrazimnych atomów (typu fermionowego) przerwa energetyczna zanika dopiero znacznie powyżej T c. Co wie cej, wartość przerwy energetycznej (T 0) nie skaluje sie wówczas z temperatura krytyczna. Nadprzewodniki takie sa określane mianem niekonwencjonalnych. c V (T) ~ e /T 0 0 T c temperatura Rys. 6.9 Temperaturowa zależność ciep la w laściwego w pobliżu T c świadczy, że przejście ze stanu normalnego do nadprzewodza cego ma charakter przejścia fazowego drugiego rodzaju, któremu towarzyszy pojawienie parametru porza dku. 86
87 W nadprzewodnikach konwencjonalnych przerwa energetyczna jest zwykle utożsamiana z parametrem porza dku. Fakt ten jest uzasadniony charakterystyka ciep la w laściwego (zilustrowana na rysunku z poprzedniej strony), która w pobliżu T c wykazuje niecia g lość pierwszej pochodnej typowa dla przejść drugiego rodzaju (wg klasyfikacji Landaua). Skojarzenie przerwy energetycznej z parametrem porza dku ca lkowicie zawodzi jednak w nadprzewodnikach niekonwencjonalnych. O fizycznych przyczynach takiej sytuacji be dzie mowa w dalszej cze ści. Na koniec niniejszego omawiania charakterystycznych w laściwości nadprzewodników powróćmy ponownie do kwestii zaniku oporu elektrycznego. Należy podkreślić, że zanik oporu jest cecha wy la cznie pra dów niezależnych od czasu. W przypadku przewodnictwa zmiennopra dowego sytuacja jest zupe lnie odmienna. Zacznijmy najpierw od przypomnienia, iż w zwyk lych metalach przewodnictwo zmiennopra dowe σ N (ω) jest wielkościa zespolona, która (wed lug uogólnionej teorii Drudego) zależy od ω poprzez σ N (ω) = ne2 τ m 1 1 iωτ, (238) gdzie n jest koncentracja elektronów przewodnictwa, m masa efektywna zaś τ oznacza czas relaksacji. Ten ostatni parametr ma ścis ly zwia zek z wartościa przewodnictwa sta lopra dowego σ N (0). Bez wzgle du na temperaturowa zależność parametrów n, m oraz τ rzeczywista cze ść przewodnictwa spe lniać musi naste puja ca tzw. regu le f-sum Re σ N (ω) = π ne2 m. (239) σ N Re σ(ω) ωτ Rys Zależność rzeczywistej cze ści przewodnictwa zmiennopra dowego od ω w stanie normalnym (rysunek po lewej stronie) oraz w stanie nadprzewodza cym (rysunek z prawej strony). 87
88 W stanie nadprzewodza cym powyższa regu la f-sum (239) jest nadal spe lniona (patrz rysunek powyżej). Jednakże zakres niskich cze stości, poniżej progu absorpcyjnego hω (T), jest niemal kompletnie wyt lumiony. Z fizycznego punktu widzenia oznacza to, że nadprzewodniki nie absorbuja kwantów zewne trznego pola elektromagnetycznego o cze stościach poniżej wartości krytycznej / h. Regu la sum (239) wymusza aby brakuja ca waga spektralna (z obszaru poniżej progu absorpcyjnego) zosta la skumulowana przy tzw. piku Drude go. Fenomenologicznie (co zosta lo zaproponowane przez braci Londonów) można wie c wyróżnić dwie sk ladowe (normalna i nadciek la ) w koncentracji elektronów n = n n (T)+n sc (T). Przejawiaja sie one w przewodnictwie zmiennopra dowym poprzez σ sc (ω) n s δ(ω) + n Ne 2 τm 1 1 iωτ θ ( ω ), (240) gdzie θ(x) = 0 dla x 0 oraz θ(x) = 1 dla x > 0. Sk ladowa normalna n n daje wk lad do zespolonego przewodnictwa powyżej progu absorpcyjnego, natomiast sk ladowa nadciek la n sc jest odpowiedzialna za wage piku Drude go. Odwrotność przewodnictwa w granicy ω 0 daje wie c zerowy opór w laściwy. Ten jakościowo poprawny wniosek jest tutaj uzasadniony jednak w dużym uproszczeniu pe lnej procedury wyznaczania przewodnictwa sta lopra dowego. Rys Wspó lzależność 1 λ 2 (T) = 4πe2 m c 2 n s (T 0) dla różnych rodzin nadprzewodników. Rysunek po lewej stronie dotyczy wartości liczbowych w kierunku p laszczyzny ab natomiast rysunek z prawej strony opisuje w laściwości kierunku prostopad lego, wzd luż osi c. 88
89 Drugi ważny aspekt dotycza cy sk ladowej nadciek lej n sc (T) ma ściś ly zwia zek z efektem Meissnera. Na podstawie wyrażenia Londonów nse2 m 1 µ 0 λ 2 sk ladowa n sc (T) determinuje odwrotność g le bokości wnikania. Relacje taka (która jest określana w literaturze jako skalowanie Uemury) faktycznie potwierdzono empirycznie dla wszystkich znanych klas nadprzewodników, zarówno konwencjonalnych jak i niekonwencjonalnych. W podsumowaniu możemy wie c podkreślić, że pojawienie sie nadciek lej sk ladowej koncentrancji elektronów ma kluczowe znaczenie dla: a) zaniku oporu sta lopra dowego (czyli idealnego przewodnictwa) oraz b) efektu Meissnera (idealnego diamagnetyzmu). Sa to jakby dwie strony medalu tego samego zjawiska. 6.2 Teoria Londonów Pierwsza fenomenologiczna analize konsekwencji spowodowanych zanikiem oporu (czyli ruchu elektronów bez jakichkolwiek strat energetycznych) opracowali w 1935 roku bracia Fritz i Heinz Londonowie. Podejście Londonów oryginalnie by lo zainspirowane koncepcja modelu dwucieczowego zaproponowanego przez L. Tisze w kontekście zagadnienia nadciek lości helu 4 He. Londonowie zastosowali podobne podejście do opisu stanu nadprzewodza cego uk ladu elektronów, zak ladaja c że cze ść elektronów (o koncentracji n s ) jest bezdyssypacyjna pozosta la natomiast frakcja n n = n n s zachowuje sie jak nośniki ladunku w zwyk lych przewodnikach. Z dzisiejszego punktu widzenia powyższe za lożenia nie sa g le biej uzasadnione, warto jednak prześledzić tok rozumowania Londonów gdyż prowadzi on do pewnych poprawnych wniosków. Szczególnie cennym (i nadal aktualnym) elementem analizy braci Londonów jest wniosek, iż uk lad nadprzewodza cych elektronów jest przejawem kondensacji Bosego-Einsteina par elektronowych manifestuja cym sie na skale makroskopowa. Do prześledzenia toku rozumowania braci Londonów rozpatrzmy ruch elektronów o ladunku q = e w zewne trznym polu elektromagnetycznym E = Re {E 0 e iωt }. Pod nieobecność dyssypacji si la kulombowska qe powoduje zmiane pre dkości elektronu wed lug prawa Newtona C.C. Homes, Phys. Rev. B 80, (R) (2009). F. London, H. London, Proc. Roy. Soc. A 149, 71 (1935). 89
90 m d v = qe. (241) dt Bezdyssypacyjny ruch ladunków daje wie c wk lad do nate żenia pra du o ge stości j j = qn s v. (242) Zerowy opór prowadzi poprzez relacje (242) do naste puja cego pierwszego równania Londonów d dt j = n sq 2 m E = n se 2 E. (243) m Zbadamy zaste pnie konsekwencje równania Londonów (243) na reakcje uk ladu wzgle dem zewne trznego pola magnetycznego B. W tym celu skorzystajmy z prawa Faraday a rote = B. (244) t Dzia laja c rotacja na pierwsze równanie Londonów (243) uzyskujemy ( rotj + n se 2 ) t mc B = 0. (245) Zatem ge stość pra du j zależy od pola magnetycznego B poprzez rotj + n se 2 B = const. (246) mc Londonowie zaproponowali, aby w formalnym rozwia zaniu (246) wybrać wartość sta lej równa zero. W ten sposób uzyskuje sie tzw. drugie równanie Londonów rotj = n se 2 B. (247) mc Warto zwrócić uwage, że wybór zerowej sta lej po prawej stronie równania (246) jest niemożliwy do uzasadnienia na gruncie zasad fizyki klasycznej. Ten fragment analizy Londonów jest należy wie c uznać jako niekonsystentny. Dopiero w oparciu o zasady mechaniki kwantowej można uzyskać argumentacje uzasadniaja ca postać równania (247). W literaturze specjalistycznej ten szczególny aspekt jest zwia zany z tzw. mechanizmem Andersona-Higgsa. Wskutek pojawienia sie parametru porza dku (patrz podrozdzia l omawiaja cy teorie BCS) dochodzi do spontanicznego z lamania symetrii cechowania potencja lu wektorowego A, implikuja c wygenerowanie wyrazu masowego w równaniach elektrodynamiki, co jest równoważne zjawisku Meissnera. 90
91 Na obecnym (pogla dowym) etapie analizy zjawiska nadprzewonictwa pokażemy, że drugie równanie Londonów (247) rzeczywiście opisuje zjawisko Meissnera-Ochsenfelda. W tym celu przekszta lcimy nieco postać równania (247), dzia laja c na obie jego strony rotacja. Wykorzystuja c ponadto prawo Ampere a rotb = 4π c j, (248) dostajemy zatem rot (rotb) = 4π c rotb = 4π c ( n se 2 ) B. (249) mc W oparciu o matematyczna tożsamość rot rot = drugie równanie Londonów (247) implikuje wie c B = 1 B, (250) λ 2 L gdzie zdefinowaliśmy naste puja ca tzw. londonowska g le bokość wnikania mc 2 λ L 4πn s e2. (251) Znaczenie tej wielkości fizycznej można latwo zrozumieć gdy rozpatrzymy zależność pola magnetycznego od po lożenia np. w kierunku x. Za lóżmy, że nadprzewodnik zajmuje pó lprzestrzeń x 0 oraz z zewna trz jest przy lożone jest pole magnetyczne B 0. Uwzgle dnienie takich warunków brzegowych w równaniu (250) prowadzi do rozwia zania w postaci B 0 dla x < 0, B(x) = B 0 e x/λ L dla x 0. (252) Aby zrozumieć przyczyne eksponencjalnego zaniku pole magnetycznego (252) w warstwach przypowierzchniowych nadprzewodnika wykorzystajmy ponownie równanie Ampere a (248). Ge stość nate żenia pra dów (ekranuja cych zewne trzne pole magnetyczne) dla tutaj omawianych warunków dane jest w naste puja cej postaci 0 dla x < 0, j(x) = j 0 e x/λ L dla x 0. (253) 91
92 Zanik pola magnetycznego w stanie Meissnera jest wie c spowodowany ekranuja cymi pra dami sta lymi (które sa niekiedy nazywane superpra dami), które p lyna w warstwach przypowierzchniowych nadprzewodnika. Rys Nate żenie pra dów przypowierzchniowych, które ekranuja c zewne trzne pole magnetyczne powoduja idealny diamagnetyzm nadprzewodników (efekt Meissnera). W nadprzewodnikach konwencjonalnych g le bokość wnikania λ L przyjmuje wartości z zakresu od kilkuset do kilkunastu tysie cy Å. G le bokość wnikania λ L jest ponadto zależna od temperatury, co wynika z temperaturowej zależności koncentracji skondensowanych par elektronowych n s = n s (T). W granicy T T c da ży ona do zera. Dla izotropowych nadprzewodników stwierdzono ponadto naste puja ca zależność empiryczna λ L (T) λ(0) (254) 1 (T/T c ) 4. W przypadku nadprzewodników anizotropowych wzrost λ L (T) [czyli zanik n s (T)] ze wzrostem temperatury jest znacznie silniejszy. Np. dla nadprzewodników o symetrii parametru porza dku typu fali-d w pobliżu temperatury krytycznej n s (T) zależy liniowo od T c T. Korzystaja c z definicji potencja lu wektorowego B rota możemy raz jeszcze przepisać równanie (250) w równoważnej postaci j = 1 A. (255) µ 0 λ 2 L Zauważmy, że powyższy wzór może być s luszny jedynie przy odpowiednim wyborze cechowania potencja lu wektorowego A A+ χ(r), gdzie χ(r) jest funkcja skalarna. Zachownie ladunku 92
93 elektrycznego wymaga aby ge stość ladunku ρ(r,t) = e n(r,t) oraz wektor nate żenia pra du j(r,t) spe lnia ly naste puja ce równanie cia g lości ρ t + j = 0. (256) W przypadku statycznym powyższy warunek jest spe lniony, jeśli j = 0. Porównuja c ten warunek z równaniem (255) widzimy, że potencja l wektorowy musi spe lniać A = 0. Taki wybór potencja lu wektorowego jest w literaturze określany jako cechowanie londonowskie. Uogólnienia lokalnej relacji (255) mie dzy ge stościa pra du oraz potencja lem wektorowym na przypadek nielokalny dokona l Pippard. Efektywna wartość ge stości nate żenia pra du j w po lożeniu r jest rezultatem wp lywu pola elektromagnetycznego z sa siednich obszarów r. Relacja Pipparda przewiduje naste puja ca nielokalna zależność j(r) = n se 2 m 3 4πξ 0 dr R(R A(r )) R 4 gdzie R = r r oraz odleg lość r 0 jest zdefiniowana poprzez e R r 0, (257) 1 r 0 = 1 ξ l. (258) W powyższym wyrażeniu l = v F τ jest średnia droga swobodna elektronów (v F oznacza pre dkość Fermiego, zaś τ jest czasem relaksacji) natomiast parametr ξ 0 oznacza tzw. d lugość koherencji. Fizycznie oznacza on przestrzenny rozmiar par elektronowych (par Coopera). W ramach teorii BCS parametr x 0 jest formalnie zdeterminowany wartościa przerwy energetycznej poprzez ξ 0 = hv F π. (259) Relacja Pipparda (257) wskazuje, że elektrodynamiczne w laściwości nadprzewodników jakościowo zależa od wzajemnej relacji pomie dzy parametrami l, ξ 0 oraz λ. Relacja mie dzy g le bokościa wnikania λ i d lugościa koherencji ξ 0 determinuje przynależność nadprzewodnika do typu I (gdy λ ξ) lub typu II (jeżeli λ ξ). Średnia droga swobodna l decyduje natomiast o lokalnym/nielokalnym charakterze elektrodynamiki nadprzewodników, które poprzez (257) przynależa do tzw. clean limit (jeśli l ξ 0 ) albo dirty limit (gdy l < ξ 0 ). A.B. Pippard, Proc. Roy. Soc. A216, 547 (1953). 93
94 Tab. 6.1 Wartości parametrów λ, ξ 0 oraz ilorazu κ = λ/ξ 0 dla różnych nadprzewodników. 6.3 Podejście Ginzburga - Landaua Jeszcze przed opracowaniem mikroskopowej teorii konwencjonalnego nadprzewodnictwa Ginzburg i Landau sformu lowali intuicyjna interpretacje niektórych aspektów tego zjawiska. W fenomenologicznym podejściu zwrócili uwage, iż przejście do stanu nadprzewodza cego jest przejściem fazowym drugiego rodzaju (wskazuje na to temperaturowa zależność ciep la w laściwego). Poniżej temperatury krytycznej pojawić sie zatem musi parametr porza dku. Do jego opisu Ginzburg i Landau zaproponowali zespolona funkcje Ψ(r,t), której modu l utożsamili z koncentracja nadciek lych elektronów n s (r,t) = Ψ(r,t) 2 wykorzystywana w teorii Londonów. Z dzisiejszej perspektywy parametr porza dku Ψ(r,t) moglibyśmy interpretować jako funkcje falowa skondensowanych (w sensie Bosego-Einsteina) par elektronowych. O kolektywnych cechach takiego kondensatu świadczy w skali makroskopowej wiele w laściwości, np. interferencja kwantowa obserwowalna w zjawiskach Josephsona. Z formalnego punktu widzenia zespolony parametr porza dku Ψ(r,t) jest zdefiniowany jedynie poniżej temperatury krytycznej Ψ(r,t) = 0, gdy T > T c Ψ(r,t) 0 dla T T c. (260) V.L. Ginzburg, L.D. Landau, Zh. Eksp. Teor. Fiz. 20, 1064 (1950). 94
95 Oryginalnie Ginzburg i Landau nie znali mikroskopowego pochodzenia parametru porza dku. W oparciu jednak o niezwyk la intuicje wydedukowli, iż bliskim otoczeniu temperatury krytycznej T c wartość bezwgle dna Ψ( r) jest infinitezymalnie ma la. W zwia zku z tym energia swobodna nadprzewodnika F s możne być przedstawiona w postaci pote gowego rozwinie cia wzgle dem wartości F n stanu normalnego z dok ladnościa do wyraów o najniższych wyk ladnikach F s = F n + a Ψ(r,t) b Ψ(r,t) (261) W powyższym wyrażeniu (261) parametry a oraz b sa liczbami rzeczywistymi. Rys Idea rozwinie cia energii swobodnej wzgle dem parametru porza dku Ψ. W nieobecności zewne trznych pól parametr porza dku nie powinien być zależny od zmiennych przestrzennych, dlatego Ginzburg i Landau dodali do powyższego rozwinie cia (261) również wyraz proporcjonalny do Ψ( r), który jest odpowiedzialny za t lumienie przestrzennej zmiany parametru porza dku. W analogii do równania Schrödingera wyraz ten można zapisać w postaci 1 2m i h Ψ(r,t) 2, (262) gdzie m oznacza mase efektywna. W obecności zewne trznych pól wyraz masowy (262) powinien mieć postać niezmiennicza na transformacje cechowania. Taki wymóg narzuca naste puja ca strukture dla wyrazu masowego 95
96 1 2m ) (i h q c A(r,t) Ψ(r, t) (263) gdzie q jest efektywnym ladunkiem kwazicza stek. Biora c pod uwage zwia zek parametru porza dku z koncentracja nadciek lych elektronów Ψ(r,t) 2 = n s (r,t) z faktów empirycznych wynika, że q 2e oraz m = 2m e. Powyższa obserwacje stwierdzi l Ginzburg, co pocza tkowo wbudzi lo zastrzeżenia Landaua. Zbieraja c elementy powyżej przedstawionej argumentacji możemy ostatecznie wyrazić energie swobodna w naste puja cej postaci F s = F n + a Ψ(r,t) b Ψ(r,t) m ) (i h q c A(r,t) Ψ(r, t) + 1 8π B2. (264) Ostatni wyraz opisuje ge stość energii pola magnetycznego B = rota. Energia swobodna Gibbsa jest funkcjona lem parametru porza dku i potencja lu wektorowego G[Ψ,A] = ( dr F s 1 ) 4π B H. (265) W warunkach równowagi wielkość G[Ψ,A] wymaga minimalizacji wzgle dem obu argumentów δg[ψ, A] δψ = 0, δg[ψ, A] δa = 0. (266) Elementarny rachunek wariacyjny daje w rezultacie uk lad równań Ginzburga Landaua aψ( r) + b Ψ(r,t) 2 Ψ(r,t) + 1 (i h q )2 2m c A(r,t) Ψ(r,t) = 0, (267) hq 2im (Ψ (r,t) Ψ(r,t) Ψ(r,t) Ψ (r,t)) (q ) 2 m c Ψ(r,t) 2 A(r,t) = c 4π rotb(r,t). (268) Równania Ginzburga - Landaua (267,268) prowadza do interesuja cych wniosków zarówno w przypadku nadprzewodników jednorodnych jak też w warunkach zależności przestrzennej lub czasowej. Poniżej przedstawimy kilka prostych przyk ladów. a) Jednorodny nadprzewodnik bez zewne trznego pola Dla przypadku jednorodnego nadprzewodnika parametr porza dku jest również wielkościa jednorodna (niezależna od r, t). W nieobecności zewne trznego pola A = 0 równania Ginzburga Landaua (267,268) przyjmuja proste rozwia zanie 0 dla T > T Ψ 2 c, = a/b gdy T T c. (269) 96
97 Energia swobodna zależy wie c od parametru porza dku w ten sposób, że minimum osia ga dla sta lej wartości modu lu Ψ. Przejście ze stanu normalnego (gdy minimum znajduje sie w zerze) do stanu nadprzewodza cego wia że sie z wyborem fazy. W ten sposób uk lad realizuje spontaniczne z lamanie symetrii uk ladu, co ma też ważne implikacje fizyczne. G le bsza analiza Ginzburga i Landaua wskaza la ponadto, że zależność parametru a od temperatury powinna mieć (w pobliżu T c ) charakter liniowy a(t) = a 0 (T c T). Z tego powodu także pole krytyczne stanu Meissnera zależy liniowo od temperatury H c (T) = 4π b a 0 (T c T). (270) b) Uk lad jednowymiarowy bez pola magnetycznego Gdy mamy do czynienia z kwazijednowymiarowym pre tem nadprzewodza cym w warunkach statycznych parametr porza dku zależeć może od wspó lrze dnej z. Pierwsze równanie Ginzburga Landaua (267) możemy wówczas wyrazić jako aψ(z) + b Ψ(z) 2 Ψ(z) h2 d 2 2m dz2ψ(z) = 0. (271) Dla prostoty przyjmijmy, że Ψ(z) jest funkcja rzeczywista (ściślej mówia c, zajmiemy sie modu lem parametru porza dku). Ze wzgle du na asymptotyczna wartość tej funkcji Ψ( ) = a b (272) wygodnie jest wprowadzić pomocnicza wielkość bezwymiarowa f(z) = Ψ(z) Ψ( ) (273) dla której równanie Ginzburga Lanadaua (271) redukuje sie do d 2 f(z) f 3 (z) + h2 2m a dz2f(z) = 0. (274) Równanie (274) określa zależność parametru porza dku Ψ(z) = Ψ( ) f(z) od po lożenia z. W uje ciu Ginzburga Landaua wprowadza sie d lugość koherencji ξ(t) = h 2 2m a(t). (275) 97
98 Wartości asymptotyczne f( ) = 1 oraz f(0) = 0 implikuja co prowadzi ostatecznie do rozwia znia w postaci ξ 2 d2 dz 2 f(z) = f(z) ( 1 f 2 (z) ), (276) Ψ(z) = Ψ( ) tgh ( ) z. (277) 2ξ Zależność parametru porza dku od z realizuje sie zatem w skali porównywalnej do d lugości koherencji ξ. Podobnie jest z wnikaniem pola magnetycznego do obszaru nadprzewodnika na gle bokość λ. Z tego powodu można wyróżnić dwa typy nadprzewodników, kiedy iloraz λ/ξ przyjmuje wartość dużo wie ksza lub dużo mniejsza od jedności. c) Kwantowanie strumienia pola magnetycznego Za lóżmy, że parametr porza dku jest funkcja statyczna (niezależna od czasu) i niemal jednorodna (wolnozmienna wzgle dem r). Drugie równanie Ginzburga Landaua (268) określa pra d pochodza cy od nadprzewodza cych nośników j(r) = (q ) 2 m c n (r) A(r). (278) Ze wzgle du na fakt, że m = 2m e oraz n (r) = 1 2 n s(r) otrzymujemy warunek j(r) = co jest równoważne równaniu Londonów j(r) = e2 m e c n s(r) A(r), (279) c A(r). (280) 4πλ2 G le bokość penetracji jest zwia zana z koncentracja nadciek lych nośników poprzez relacje m λ(t) = c 4π(q ) 2 n (T). (281) Zespolony parametr porza dku może być przedstawiony za pomoca amplitudy i fazy Ψ(r) = Ψ(r) e iφ(r). (282) 98
99 Jeżeli amplituda jest jednorodna (co ma miejsce w sytuacji, gdy koncentracja nadciek lych nośników jest sta la w przestrzeni) wówczas ge stość pra du j(r) zależy wy la cznie od argumentu fazowego poprzez j(r) = q h 2im [ Ψ e iφ Ψ e iφ i φ Ψ e iφ Ψ e iφ ( i φ) ] (q ) 2 m c Ψ 2 A = q h m Ψ 2 φ (q ) 2 m c Ψ 2 A (283) Powyższe równanie (283) możemy wyrazić w naste puja cej równoważnej formie A(r) + m c hc (q ) 2 Ψ 2j(r) = φ(r). (284) q Dokonuja c ca lkowania po konturze zamknie tym (ca lkowicie w obszarze nadprzewodnika) dl A + m c (q ) 2 dl j Ψ = hc 2 q dl φ(r). (285) W oparciu o twierdzenie Stokes a dl A = ds rota = ds Boraz tożsamość matematyczna dl φ(r) = dl dφ(r) dl = 2π n, (gdzie n jest liczbe ca lkowita ) z równania (283) uzyskujemy ds B + m c (q ) 2 dl j Ψ = n hc. (286) 2 q }{{} Φ 0 Po prawej stronie powyższego równania (286) ca lkowita pojawi la sie wielokrotność kwantów strumienia pola magnetycznego (tzw. fluksonów) zdefinowanych jako Φ 0 hc q = hc 2e. (287) Pole magnetyczne może zatem wnikać w obszar nadprzewodników wy la cznie w postaci wielokrotności jednostkowej porcji strumienia Φ 0 2, Wb. Pomimo, iż fenomenologiczna analiza Ginzburga Landaua dotyczy zakresu temperatur bliskich krytycznej to powyższy wniosek (dotycza cy kwantowania strumienia pola magnetycznego) pozostaje s luszny w pe lnym zakresie temperatur T T c. Zauważmy ponadto, że wnikanie pola jest wywo lane lokalnymi pra dami (283), które z formalnego punktu widzenia sa konsekwencja niejednorodności fazy parametru porza dku. Wiadomo również, że strumienie pola magnetycznego organizuja sie w heksagonalna strukture (ponieważ taka konfiguracja jest najkorzystniejsza energetycznie). Tego rodzju sieć Abrikosova jest zwykle określana w literaturze jako sić wirów kwantowych. 99
100 6.4 Elementy mikroskopowej teorii nadprzewodnictwa Do zrozumienia i wyjaśnienia mechanizmu nadprzewodnictwa (konwencjonalnego) kluczowe znaczenie dla mia ly naste puja ce fakty: a) doświadczalne odkrycie efektu izotopowego (1950 r.) T c 1 M (288) gdzie M oznacza masa jonów. Z obserwacji empirycznych stwierdzono, że wartość wyk ladnika wynosi α 0, 5. Taki fakt empiryczny wskazywa l, iż zanik oporu elektronów pasma przewodnictwa jest w pewien sposób zależny od sieci krystalicznej. Wp lyw sieci krystalicznej na uk lad elektronowy realizuje sie poprzez oddzia lywania drgań sieci z gazem elektronowym. b) teoretyczne obliczenia H. Fröhlicha (1950 r.) wskaza ly, że sprze żenie elektronów z drganiami sieci krystalicznej może wygenerować efektywnne oddzia lywanie przycia gaja ce. Zwyk le (odpychaja ce) oddzia lywania kulombowskie opisane sa potencja lem V Coul (q) = e 2 4πε 0 (q 2 + κ 2 ) gdzie κ uwzgle dnia efekty ekranowania. Pod wp lywem sprze żenia U el ph q (289) elektronów z drgaja ca siecia krystaliczna wyindukowana jest naste puja ca korekta dwucia lowych oddzia lywań mie dzy elektronami g k,k,q = Uq el ph 2 ω q (ξ k+q ξ k ) 2 ωq 2 + Uq el ph 2 ω q (ξ k +q ξ k ) 2 ωq 2 (290) We powyższym wzorze (290) wyjściowa energia elektronów jest oznaczona symbolem ε k = h 2 k 2 /2m natomiast ω q oznacza energie kwantu drgań sieci (tzw. fononu). Potencja l odzia lywań g k,k,q przyjmuje charakter przycia gaja cy, gdy zakres energii elektronów znajduje sie w przedziale o szerokości ω D (tzn. energii Debye a) wzgle dem poziomu Fermiego. Efektywnie ca lkowity potencja l V Coul (q) + g kf,k F,q < 0 opisuje wie c wówczas efektywne oddzia lywanie przycia gaja ce. 100
101 c) wniosek analizy L. Coppera Dla elektronów z bliskiego otoczenia energii Fermiego najkorzystniejszym (pod wzgle dem energetycznym) wariantem jest la czenie sie w pary. Pary takie elektronowe sa obcenie nazywane parami Coopera. Zazwyczaj pary tworza sie z elektronów o przeciwnych pe dach (k,-k) oraz przeciwnych spinach (, ). Nie jest to jednak warunek konieczny i znane sa przypadki par elektronowych o ca lkowitym niezerowym pe dzie (stan Fulde-Ferrella- Larkina-Ovchinnikova) lub ca lkowitym niezerowym spinie (np. pary trypletowe). Rys Ilustracja powstawania par elektronowych w nadprzewodnikach konwencjonalnych. Badania Fröhlicha oraz Coopera sta ly sie ważnym krokiem w kierunku opracowania ca lościowej teorii nadprzewodnictwa. Mikroskopowa teorie opracowali wspólnie John Bardeen, Leon Cooper oraz Robert Schrieffer, tzw. teoria BCS. W swoim charakterze jest bazuje na przybliżeniu średniego pola z uwzgle dnieniem anomalnych średnich (lokalnie naruszaja cych zachowanie ladunku), które prowadza do spontaniczne z lamania symetrii cechowania cechowania w uk ladzie. Do zrozumienie teorii BCS konieczna jest znajomość mechaniki kwantowej na poziomie średniozaawansowanym (m.in. znajomość drugiej kwantyzacji) oraz elementów kwantowej teorii pola. Dla osób dociekliwych przedstawiony jest poniżej pobieżny zarys tej teorii. J. Bardeen, L. Cooper, R. Schrieffer, Phys. Rev. 108, 1175 (1957). 101
102 Za lóżmy, że elektrony oddzia luja na siebie potencja lem U (oddzia lywania przecia gaja ce). Przy pomocy operatorów kreacji i anihilacji cza stek w stanach o kwazipe dzie k oraz spinie σ =, operator energii ca lkowitej może być zapisany w postaci Ĥ = k,σ (ε k µ) ĉ k,σĉk,σ U k,k ĉ k, ĉ k, ĉ k, ĉ k,. (291) Do uproszczenia wyrazu oddzia lywań, zastosujmy przybliżenie Hartree-Focka-Bogoliubova U k,k ĉ k, ĉ k, ĉ k, ĉ k, k ĉ k, ĉ k, U k ĉ k, ĉ k, U k ĉ k, ĉ k, ĉ k, ĉ k, + U k ĉ k, ĉ k, ĉ k, ĉ k, (292) Definiuja c pomocniczy parametr (o wymiarze energii) U k ĉ k, ĉ k,, (293) redukujemy hamiltonian (291) do ściśle rozwia zywalnej postaci biliniowej Ĥ ( (ε k µ) ĉ k,σĉk,σ ) ĉ k, ĉ k, + h.c. k,σ k (294) Do dalszej analizy można wykorzystać transformacje kanoniczna Bogoliubowa-Valatina (lub inne metody) z odpowiednio dobranymi wspó lczynnikami liczbowymi u 2 k = 1 2 Powyższa transformacja diagonalizuje hamiltonian BCS do postaci ˆγ k, = u k ĉ k, + v k ĉ k, (295) ˆγ k, = v kĉ k, + u k ĉ k, (296) ( ) 1 + ξ k E k = 1 vk 2, gdzie E k = ξk Ĥ = k,σ E kˆγ k,σˆγ k,σ + const. (297) Ze szczegó lowych przekszta lceń można wówczas latwo wyznaczać dowolne wartości średnie (w sensie statystycznym). Mie dzy innymi równanie na przerwe energetyczna ma naste pujc a postać U k ĉ k, ĉ k, = U k u k v k [1 2f FD (E k )] (298) czyli = U k 2E k [1 2f FD (E k )] = U k ( ) Ek tgh. (299) 2E k 2k B T 102
103 W szczególności, z powyżej uzyskanego rówania (299) można wycia gna ć naste puja ce wnioski charakterystyczne dla nadprzewodników konwencjonalnych: a) granica zera bezwgle dnego T 0 2ω D e 1 Uρ(ε F ). (300) b) granica temperatury krytycznej T T c k B T c 1, 13ω D e 1 Uρ(ε F ). (301) Na podstawie (300) i (301) spe lniona jest wie c relacja (T = 0) k B T c 4 1, 13 = 3, 52. (302) Za opracowanie mikroskopowej teorii nadprzewodnictwa w 1972 roku przyznano Nagrode Nobla dla wszystkich trzech jej autorów. W podsumowaniu obecnego podrozdzia lu warto podsumowáć, iż zjawisko konwencjonalnego nadprzewodnictwa polega na: la czeniu elektronów (z otoczenia powierzchni Fermiego) w pary Coopera kolektywnym reagowaniu par na wszelkie zewne trzne zaburzenia (np. na pole elektromagnetyczne, gradient temperatury itp.) Makroskopowo dostrzegalne zjawiska kolektywne sa konsekwencja kondensacji par Coopera. Kondensat Bosego-Einsteina par Coopera możemy sobie wyobrazić jako coś w rodzaju gigantycznego super-atomu z lożonego z identycznych obiektów (w tym wypadku par)!). Kelektywne zachowanie par przejawia sie w takich zjawiska jak: doskona le przewodnictwo... ruch bez rozpraszania idealny diamagnetyzm...czyli efekt Meissnera inne zjawiska kolektywne...efekt Josephsona itp. 103
104 6.5 Przegla d odkryć nadprzewodników Konwencjonalne nadprzewodnictwo zosta lo odkryte w pierwszej po lowie dwudziestego wieku w szeregu różnych pierwiastków oraz stopów. Poniższy rysunek przedstawia wybrane przyk lady. 80 ciekly N 2 60 T c (K) 40 Nb ciekly H 3 Ge 2 Nb 3 Sn 20 Nb Pb NbN V Si Nb Al Ge 3 Hg rok Rys Historia odkryć nadprzewodników klasycznych. Kolejna fala odkryć mia la miejsce pocza wszy od 1986 roku, kiedy Alex Müller i Georg Bednorz z IBM w Rüschlikon (Szwajcaria) odkryli, że materia l ceramiczny La 2 x Sr x CuO 4 (który dla x=0 jest izolatorem typu Motta) staje sie nadprzewodnikiem w zakresie domieszkowania 0,05 < x < 0,25. Maksymalna temperatura krytyczna tego materia lu wynosi T c =36 K. Odkrycie to zapocza tkowa lo burzliwy okres odkrywania nadprzewodników wysokotemperaturowych * HgBa 2 Ca 2 Cu 3 O 8+δ 140 HgBa 2 Ca 2 Cu 3 O 8+δ 120 Tl 2 Ba 2 Ca 2 Cu 3 O 10 T c (K) ciekly N 2 Bi 2 Ba 2 Ca 2 Cu 3 O 10 YBa 2 Cu 3 O 7 δ 60 La 2 δ Sr δ CuO ciekly H Nb 2 Nb 3 Sn 3 Ge Hg Pb Nb NbN V Si Nb Al Ge rok Rys Historia odkryć nadprzewodników wysokotemperaturowych. 104
105 Kolejny istony etap odkryć mia l miejsce na pocza tku 21 wieku. Nadprzewodnictwo stwierdzono w zwia zkach żelaza (tzw. pniktydach). Temperatury krytyczne tych nadprzewodników nie sa rekordowo wysokie, ale maja one inne szczególne zalety (np. wysokie wartości pra dów krytycznych). Z zastosowaniem nadprzewodników żelazowych wia zane sa olbrzymie nadzieje. Rys Burzliwa epoka odkryć nadprzewodników w zwia zkach żelaza. Poza wymienionymi tutaj g lównymi falami odkryć mia ly również miejsce odkrycia wielu różnych nadprzewodników, niekiedy określanych jako egzotyczne. 105
106 6.6 Wspó lczesne wykorzystanie nadprzewodnictwa 1. Linie przesy lowe pra du sta lego/zmiennego Najbardziej naturalnym aspektem aplikacyjnym wydaja sie być linie do przesy lania pra du elektrucznego. Poważnym k lopotem jest jednak problem pól krytycznych (czyli jednocześnie ograniczenie nate żeń pra d ow do wartości nieprzekraczaja cej nate żeń krytycznych). Innym problemem jest konieczność umieszczenia kabli w odpowieniej os lonie termicznej aby spe lniony by l warunek T < T c. Pomimo tych trudności uda lo sie już zrealizować kilka funkcjonuja cych trakcji energetycznych. Jeden z przyk ladów jest pokazany na poniższej fotografii. Rys Od kwietnia 2008 r. trójfazowa linia wysokiego napie cia firmy Long Island Power Authority (AmSC, USA) zaopatruje w pra d energetyczny oko lo udbiorców indywidualnych. Kable wykonano z nadprzewodnika Y-Ba-Cu-O, które w miedzianej os lonie sa zanurzone w ciek lym azocie (izoluja c od otoczenia). Moc przesy lowa jest identyczna z moca linii przedstwionej po lewej strony fotografii. 106
107 2. Ograniczniki pra du sta lego/zmiennego Kolejne bardzo użyteczne zastosowanie polega na wykorzystaniu fragmentów kabla lub taśmy wykonanej z nadprzewodnika wpie tych w obwód elektryczny (np. w konwencjonalna linie przesy lowa pra du). Wszelkie przepie cia sieci powoduja nate żenia przekraczaja ce wartość krytyczna. Rezystancja fragmentu nadprzewodnikowego wzrasta wówczas w bardzo znacza cy sposób, co poprzez odpowiedni uk lad elektroniczny wykorzystuje sie do zablokowania pra du. Inaczej mówia c, nadprzewodniki s luża jako bezpieczniki lub ograniczniki pra du. Niezwykle cenna zaleta jest fakt, iż takie zawory automatycznie odblokowuja sieć z chwila zaniku przepie cia (w praktyce odblokowanie naste puje po up lywie oko lo 1/60 sekundy). Rys Ogranicznik pra du firmy Nexan SuperConductors (Niemcy). 3. Silniki elektryczne do nape du samochodów Zastosowanie zwojów nadprzewodza cych jest także wykorzystywane w konstrukcji silników elektrycznych. Zasadniczym problemem jest w tym przypadku konieczność zanurzenia silnika w ciek lym azocie w temperaturze poniżej o C (jeżeli zwoje sa wykonane z nadprzewodnika wysokotemperaturowego) lub ciek lym helu (w przupadku konwencjonalnych nadprzewodników). Drugi warianjt by lby ekonomicznie ca lkowicie nieop lacalny. Zazwyczaj w silnikach elektrycznych wykorzystuje sie nadprzewodniki wysokotemperaturowe. Prowadzone sa próby wykorzystania dwuborku magnezu oraz innych niedawno odkrytych nadprzewodników żelazowych. 107
108 Rys Prototyp samochodu Toyota wyposażonego w silnik elektryczny firmy Sumitomo Electric (Japonia). 4. Silniki elektryczne do nape du statków Podobne silniki elektryczne zbudowane z nadprzewodnikowych cewek sa konstruowane z przeznaczeniem do nape du statków. Silniki takie sa 3-krotnie mniejsze od konwecjonalnych oraz lżejsze i cichsze. Niski poziom szumów silników jest niezwykle ważna zaleta, dlatego rza d amerykański zdecydowa l o wyposażeniue wszystkich statków wojskowych wy la cznie w silniki elektryczne wykonane z nadprzewodników wysokotemperaturowych. Rys Silnik o mocy 36,5 MW firmy American Superconductors Corporation (USA). 108
109 5. Magnesy pól sta lych Przep lyw pra du w kablach nadprzewodza cych wytwarza pole magnetyczne, które można odpowiednio profilować poprzez w laściwy dobór geometrii. Olbrzymia zaleta tak wykonanych magnesów sta lych jest brak jakichkowiek strat energetycznych przy przep lywie pra du. Jednym z zastosowań takiego rozwia zania na duża skale jest akcelerator LHC, w którym wykorzystano magnesy wytworzone z nadprzewodza cego stopu NbTi. Rys Schemat i fotografia rzeczywistego tunelu akceleratora w CERN (Szwajcaria/Francja). 6. Obrazowanie rezonansem magnetycznym (MRI) w medycynie Magnesy pól wytworzonych przez pra dy p lyna ce w zwojach nadprzewodnikowych sa ważna cze ścia urza dzeń wykorzystywanych w medycynie. Wykorzystuja c zjawisko ja drowego rezonansu magnetycznego (MRI) wykonuje sie tomografie chorych komórek w organizmie cz lowieka. Zastosowanie nadprzewodników umożliwia latwe sterowanie nate żeniem pola magnetycznego. Rys Aktualnie na świecie jest użytkowanych ponad 20 tys. urza dzeń opartych na MRI. 109
110 7. Zastosowanie intereferometrów SQUID w magnetoencefalografii Najnowsze urza dzenia technologii biomagnetycznej skonstruowane sa w oparciu o zastosowanie nadprzewodza cych interferometrów typu SQUID (Superconducting QUantum Interferometer Device). Zasada ich dzia lania polega na interferencji dwów pra dów Josephsona indukowanych pomie dzy nadprzewodza cymi elektrodami. Urza dzenia sa tak dok ladne, że wyczuwaja pola magnetyczne miliard razy s labsze od pola poruszaja cego ig le w kompasie. Rys Zastosowanie interferometrów SQUID w nieinwazyjnej magnetoencefalografii (fotografia z lewej strony) oraz w gradiometrii (fotografia po prawej stronie). 8. Zastosowanie intereferometrów SQUID w gradiometrii Interferometry SQUID sa też pośrednio wykorzystywane w gradiometrach grawitacyjnych. Bardzo precyzyjne żyroskopy z wbudowanymi interferometrami SQUID stosowano w próbach pomiarów efektów zwia zanych z zakrzywieniem czasoprzestrzeni Ziemi. W badaniach kosmologicznych dotycza cych tzw. ciemnej materii oraz ciemnej energii (95 % Wszechświata) również używane sa ultraprecyzyjne detektory pod la czone do cewek z wbudowanymi SQUID-ami. 110
111 9. Lewituja ce pocia gi MAGLEV Idea wytwarzania pola magnetycznego przez pra dy sta le p lyna ce w nadprzewodnikach wykorzystuje sie do konstrukcji pocia gów lewituja cych nad magnetycznymi torami. Skrótowo pocia gi takie sa nazywane jako MAGLEV = MAGnetically LEvitated Vehicle. Rys Idea magesów wykorzystywanych do unoszenia (lewitacji) pocia gów. W 1996 roku uruchomiono pierwsza linie lewituja cych pocia gów firmy Yamanashi. Testowy pocia g Maglev osiagna l w 2003 roku rekordowa pre dkość 581 km/h. Od 2027 r. linia be dzie obs lugiwa la regularne po la czenia na trasie Tokyo Osaka. Rys Fotografia pocia gu testowej linii MAGLEV oraz schemat regularnego po la czenia pasażerskiego na trasie z Tokyo do Osaki (Japonia). 111
112 Rys Linia MAGLEV wykorzystywana komercyjnie w Sznghaju (Chiny). Regularna linia pocia gów MAGLEV o d lugości 30 km jest już obecnie wykorzystywana komercyjnie do obs lugi pasażerów podróżuja cych z lotniska Pudong do centrum Szanghaju w Chinach. Przedsiewzie cie by lo wspólna inwestycja niemiecko-chińska. Aktualnie Chiny rozbudowuja samodzielnie kolejne odcinki sieci MAGLEV. 112
Kondensacja Bosego-Einsteina
 Kondensacja Bosego-Einsteina W opisie kwantowo-mechanicznym stan konkretnego uk ladu fizycznego jest określony poprzez funkcje falowa ψ r, r 2,...), gdzie r i oznaczaja po lożenia poszczególnych cza stek.
Kondensacja Bosego-Einsteina W opisie kwantowo-mechanicznym stan konkretnego uk ladu fizycznego jest określony poprzez funkcje falowa ψ r, r 2,...), gdzie r i oznaczaja po lożenia poszczególnych cza stek.
3. Drgania sieci krystalicznej
 3. Drgania sieci krystalicznej Pod wp lywem różnych czynników zewne trznych (np. pola eletromagnetycznego, napre żeń, gradientów temperatury itp.) stan równowagi atomów w sieci krystalicznej może zostać
3. Drgania sieci krystalicznej Pod wp lywem różnych czynników zewne trznych (np. pola eletromagnetycznego, napre żeń, gradientów temperatury itp.) stan równowagi atomów w sieci krystalicznej może zostać
cza steczek. W najprostszym przypadku powtarzaja cym sie elementem może być pojedynczy
 2. Sieci krystaliczne Kryszta ly sa periodycznie powtarzaja cymi sie w przestrzeni sekwencjami atomów lub cza steczek. W najprostszym przypadku powtarzaja cym sie elementem może być pojedynczy atom. Z
2. Sieci krystaliczne Kryszta ly sa periodycznie powtarzaja cymi sie w przestrzeni sekwencjami atomów lub cza steczek. W najprostszym przypadku powtarzaja cym sie elementem może być pojedynczy atom. Z
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Oddzia lywania miedzycz. jony molekularne lub atomy. edzy A i B:
 Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
FUNKCJE LICZBOWE. x 1
 FUNKCJE LICZBOWE Zbiory postaci {x R: x a}, {x R: x a}, {x R: x < a}, {x R: x > a} oznaczane sa symbolami (,a], [a, ), (,a) i (a, ). Nazywamy pó lprostymi domknie tymi lub otwartymi o końcu a. Symbol odczytujemy
FUNKCJE LICZBOWE Zbiory postaci {x R: x a}, {x R: x a}, {x R: x < a}, {x R: x > a} oznaczane sa symbolami (,a], [a, ), (,a) i (a, ). Nazywamy pó lprostymi domknie tymi lub otwartymi o końcu a. Symbol odczytujemy
Wzory Viete a i ich zastosowanie do uk ladów równań wielomianów symetrycznych dwóch i trzech zmiennych
 Wzory Viete a i ich zastosowanie do uk ladów równań wielomianów symetrycznych dwóch i trzech zmiennych Pawe l Józiak 007-- Poje cia wste pne Wielomianem zmiennej rzeczywistej t nazywamy funkcje postaci:
Wzory Viete a i ich zastosowanie do uk ladów równań wielomianów symetrycznych dwóch i trzech zmiennych Pawe l Józiak 007-- Poje cia wste pne Wielomianem zmiennej rzeczywistej t nazywamy funkcje postaci:
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków).
 Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
Stara i nowa teoria kwantowa
 Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym
 II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
PODSTAWOWE W LASNOŚCI W ZBIORZE LICZB RZECZYWISTYCH
 PODSTAWOWE W LASNOŚCI DZIA LAŃ I NIERÓWNOŚCI W ZBIORZE LICZB RZECZYWISTYCH W dalszym cia gu be dziemy zajmować sie g lównie w lasnościami liczb rzeczywistych, funkcjami określonymi na zbiorach z lożonych
PODSTAWOWE W LASNOŚCI DZIA LAŃ I NIERÓWNOŚCI W ZBIORZE LICZB RZECZYWISTYCH W dalszym cia gu be dziemy zajmować sie g lównie w lasnościami liczb rzeczywistych, funkcjami określonymi na zbiorach z lożonych
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Kondensat Bosego-Einsteina okiem teoretyka
 Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
JEDNOSTKI ATOMOWE =1, m e =1, e=1, ; 1 E 2 h = 4, J. Energia atomu wodoru lub jonu wodoropodobnego w jednostkach atomowych:
 do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
c a = a x + gdzie = b 2 4ac. Ta postać wielomianu drugiego stopnia zwana jest kanoniczna, a wyrażenie = b 2 4ac wyróżnikiem tego wielomianu.
 y = ax 2 + bx + c WIELOMIANY KWADRATOWE Zajmiemy sie teraz wielomianami stopnia drugiego, zwanymi kwadratowymi. Symbol w be dzie w tym rozdziale oznaczać wielomian kwadratowy, tj. w(x) = ax 2 + bx + c
y = ax 2 + bx + c WIELOMIANY KWADRATOWE Zajmiemy sie teraz wielomianami stopnia drugiego, zwanymi kwadratowymi. Symbol w be dzie w tym rozdziale oznaczać wielomian kwadratowy, tj. w(x) = ax 2 + bx + c
DZYSZKOLNE ZAWODY MATEMATYCZNE. Eliminacje rejonowe. Czas trwania zawodów: 150 minut
 XLIII MIE DZYSZKOLNE ZAWODY MATEMATYCZNE Eliminacje rejonowe Czas trwania zawodów: 150 minut Każdy uczeń rozwia zuje dwadzieścia cztery zadania testowe, w których podano za lożenia oraz trzy (niekoniecznie
XLIII MIE DZYSZKOLNE ZAWODY MATEMATYCZNE Eliminacje rejonowe Czas trwania zawodów: 150 minut Każdy uczeń rozwia zuje dwadzieścia cztery zadania testowe, w których podano za lożenia oraz trzy (niekoniecznie
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
P (x, y) + Q(x, y)y = 0. g lym w obszrze G R n+1. Funkcje. zania uk ladu (1) o wykresie przebiegaja
 19. O ca lkach pierwszych W paragrafie 6 przy badaniu rozwia zań równania P (x, y) + Q(x, y)y = 0 wprowadzono poje cie ca lki równania, podano pewne kryteria na wyznaczanie ca lek równania. Znajomość ca
19. O ca lkach pierwszych W paragrafie 6 przy badaniu rozwia zań równania P (x, y) + Q(x, y)y = 0 wprowadzono poje cie ca lki równania, podano pewne kryteria na wyznaczanie ca lek równania. Znajomość ca
Postulaty mechaniki kwantowej
 Wyk lad 2 Postulaty mechaniki kwantowej 1 wymiar Postulat Stan czastki określa funkcja falowa Ψ = Ψ(x, t) zależna od po lożenia czastki x oraz czasu t. Interpretacje fizyczna ma jedynie kwadrat modu lu
Wyk lad 2 Postulaty mechaniki kwantowej 1 wymiar Postulat Stan czastki określa funkcja falowa Ψ = Ψ(x, t) zależna od po lożenia czastki x oraz czasu t. Interpretacje fizyczna ma jedynie kwadrat modu lu
Zastosowanie metod matematycznych w fizyce i technice - zagadnienia
 Zastosowanie metod matematycznych w fizyce i technice - zagadnienia 1 Metoda ι Grama Schmidta zortogonalizować uk lad funkcji {x n } n= a) na odcinku 1; 1 z waga ι ρx) = 1, b) na prostej ; ) z waga ι ρx)
Zastosowanie metod matematycznych w fizyce i technice - zagadnienia 1 Metoda ι Grama Schmidta zortogonalizować uk lad funkcji {x n } n= a) na odcinku 1; 1 z waga ι ρx) = 1, b) na prostej ; ) z waga ι ρx)
Fizyka materii skondensowanej zajmuje sie badaniem uk ladów z lożonych z dużych liczb
 1.1 Wprowadzenie Fizyka materii skondensowanej zajmuje sie badaniem uk ladów z lożonych z dużych liczb atomów lub moleku l, rze du liczby Avogadro 10 23. Przyk ladami moga być cia la sta le lub ciecze.
1.1 Wprowadzenie Fizyka materii skondensowanej zajmuje sie badaniem uk ladów z lożonych z dużych liczb atomów lub moleku l, rze du liczby Avogadro 10 23. Przyk ladami moga być cia la sta le lub ciecze.
Stany atomu wieloelektronowego o określonej energii. być przypisywane elektrony w tym stanie atomu.
 Notatki do wyk ladu VI Stany atomu wieloelektronowego o określonej energii. Konfiguracja elektronowa atomu - zbiór spinorbitali, wykorzystywanych do konstrukcji funkcji falowej dla danego stanu atomu;
Notatki do wyk ladu VI Stany atomu wieloelektronowego o określonej energii. Konfiguracja elektronowa atomu - zbiór spinorbitali, wykorzystywanych do konstrukcji funkcji falowej dla danego stanu atomu;
po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x)
 Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
FALE MATERII. De Broglie, na podstawie analogii optycznych, w roku 1924 wysunął hipotezę, że
 FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
Rozdział 22 METODA FUNKCJONAŁÓW GĘSTOŚCI Wstęp. Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 22 METODA FUNKCJONAŁÓW GĘSTOŚCI 22.1 Wstęp Definiujemy dla gazu elektronowego operatory anihilacji ψ σ (r) i kreacji ψ σ(r) pola fermionowego ψ σ
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 22 METODA FUNKCJONAŁÓW GĘSTOŚCI 22.1 Wstęp Definiujemy dla gazu elektronowego operatory anihilacji ψ σ (r) i kreacji ψ σ(r) pola fermionowego ψ σ
5. Obliczanie pochodnych funkcji jednej zmiennej
 Kiedy może być potrzebne numeryczne wyznaczenie pierwszej lub wyższej pochodnej funkcji jednej zmiennej? mamy f(x), nie potrafimy znaleźć analitycznie jej pochodnej, nie znamy postaci f(x), mamy stablicowane
Kiedy może być potrzebne numeryczne wyznaczenie pierwszej lub wyższej pochodnej funkcji jednej zmiennej? mamy f(x), nie potrafimy znaleźć analitycznie jej pochodnej, nie znamy postaci f(x), mamy stablicowane
Wykład Budowa atomu 3
 Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Atom wodoru w mechanice kwantowej. Równanie Schrödingera
 Fizyka atomowa Atom wodoru w mechanice kwantowej Moment pędu Funkcje falowe atomu wodoru Spin Liczby kwantowe Poprawki do równania Schrödingera: struktura subtelna i nadsubtelna; przesunięcie Lamba Zakaz
Fizyka atomowa Atom wodoru w mechanice kwantowej Moment pędu Funkcje falowe atomu wodoru Spin Liczby kwantowe Poprawki do równania Schrödingera: struktura subtelna i nadsubtelna; przesunięcie Lamba Zakaz
Elektrodynamika Część 5 Pola magnetyczne w materii Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 5 Pola magnetyczne w materii Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 6 Pola magnetyczne w materii 3 6.1 Magnetyzacja.....................
Elektrodynamika Część 5 Pola magnetyczne w materii Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 6 Pola magnetyczne w materii 3 6.1 Magnetyzacja.....................
Promieniowanie cia la doskonale czarnego
 Rozdzia l 2 Promieniowanie cia la doskonale czarnego 2.1 Wste ι p 1. Stosunek zdolności emisyjnej dowolnego cia la do jego zdolności absorpcyjnej jest sta ly i równy zdolności emisyjnej cia la doskonale
Rozdzia l 2 Promieniowanie cia la doskonale czarnego 2.1 Wste ι p 1. Stosunek zdolności emisyjnej dowolnego cia la do jego zdolności absorpcyjnej jest sta ly i równy zdolności emisyjnej cia la doskonale
Rotacje i drgania czasteczek
 Rotacje i drgania czasteczek wieloatomowych Gdy znamy powierzchnie energii potencjalnej V( R 1, R 2,..., R N ) to możemy obliczyć poziomy energetyczne czasteczki. Poziomy te sa w ogólności efektem: rotacji
Rotacje i drgania czasteczek wieloatomowych Gdy znamy powierzchnie energii potencjalnej V( R 1, R 2,..., R N ) to możemy obliczyć poziomy energetyczne czasteczki. Poziomy te sa w ogólności efektem: rotacji
2a )2 a b2. = 2 4a ====== x + b. nawias
 Wielomiany kwadratowe Wielomian a + + c nazywamy kwadratowym lu wielomianem drugiego stopnia, jeśli a jest licza różna od 0. W dalszym cia gu zak ladamy, że a i a 0. Możemy napisać a + + c = a ( + a )
Wielomiany kwadratowe Wielomian a + + c nazywamy kwadratowym lu wielomianem drugiego stopnia, jeśli a jest licza różna od 0. W dalszym cia gu zak ladamy, że a i a 0. Możemy napisać a + + c = a ( + a )
Struktura elektronowa czasteczek. przybliżenie Borna-Oppenheimera. równania Schrödingera dla elektronów przy ustalonym po lożeniu jader
 Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
i elektronów w czasteczkach (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra 2M b a i b; m -masa elektronu e 2 r ij
 Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
S. Baran - Podstawy fizyki materii skondensowanej Pasma energetyczne. Pasma energetyczne
 Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Fizyka statystyczna Zwyrodniały gaz Fermiego. P. F. Góra
 Fizyka statystyczna Zwyrodniały gaz Fermiego P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Fermiony w niskich temperaturach Wychodzimy ze znanego już wtrażenia na wielka sumę statystyczna: Ξ = i=0
Fizyka statystyczna Zwyrodniały gaz Fermiego P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Fermiony w niskich temperaturach Wychodzimy ze znanego już wtrażenia na wielka sumę statystyczna: Ξ = i=0
S. Baran - Podstawy fizyki materii skondensowanej Fonony. Fonony
 Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
{E n ( k 0 ) + h2 2m (k2 k 2 0 )}δ nn + h m ( k k 0 ) p nn. c nn = E n ( k)c nn (1) gdzie ( r)d 3 r
 to w pobliżu dna (lub szczytu) pasma (k k 0 ) zależność E(k) jest paraboliczna ale z mas a m m 0 Jeśli pasma nie s a energetycznie dobrze separowalne lub energetycznie zdegenerowane (kwazizdegenerowane)
to w pobliżu dna (lub szczytu) pasma (k k 0 ) zależność E(k) jest paraboliczna ale z mas a m m 0 Jeśli pasma nie s a energetycznie dobrze separowalne lub energetycznie zdegenerowane (kwazizdegenerowane)
Fizyka 2. Janusz Andrzejewski
 Fizyka 2 wykład 14 Janusz Andrzejewski Atom wodoru Wczesne modele atomu -W czasach Newtona atom uważany była za małą twardą kulkę co dość dobrze sprawdzało się w rozważaniach dotyczących kinetycznej teorii
Fizyka 2 wykład 14 Janusz Andrzejewski Atom wodoru Wczesne modele atomu -W czasach Newtona atom uważany była za małą twardą kulkę co dość dobrze sprawdzało się w rozważaniach dotyczących kinetycznej teorii
Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych
 LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach
LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Model elektronów swobodnych w metalu
 Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Fizyka 3.3 WYKŁAD II
 Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Atom wodoru i jony wodoropodobne
 Atom wodoru i jony wodoropodobne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści Spis treści 1. Model Bohra atomu wodoru 2 1.1. Porządek
Atom wodoru i jony wodoropodobne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści Spis treści 1. Model Bohra atomu wodoru 2 1.1. Porządek
+ + Struktura cia³a sta³ego. Kryszta³y jonowe. Kryszta³y atomowe. struktura krystaliczna. struktura amorficzna
 Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały
 WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Ciała stałe. Ciała krystaliczne. Ciała amorficzne. Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami.
 Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Uk lady modelowe II - oscylator
 Wyk lad 4 Uk lady modelowe II - oscylator Model Prawo Hooke a F = m d 2 x = kx = dv dt2 dx Potencja l Równanie ruchu V = 1 2 kx2 d 2 x dt 2 + k m x = 0 Obraz klasyczny Rozwiazania k x = A sin t = A sin
Wyk lad 4 Uk lady modelowe II - oscylator Model Prawo Hooke a F = m d 2 x = kx = dv dt2 dx Potencja l Równanie ruchu V = 1 2 kx2 d 2 x dt 2 + k m x = 0 Obraz klasyczny Rozwiazania k x = A sin t = A sin
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
Przejścia kwantowe w półprzewodnikach (kryształach)
 Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Symbol termu: edu (sumy ca lkowitego orbitalnego momentu edu i ca lkowitego spinu) Przyk lad: 2 P 3. kwantowa
 Notatki do wyk ladu VI (z 18.11.2013) Symbol termu: 2S+1 L (1) L -liczba kwantowa ca lkowitego orbitalnego momentu pedu Duże litery S, P, D, F, itd. dla L=0, 1, 2, 3, itd. 2S+1 - multipletowość; S - liczba
Notatki do wyk ladu VI (z 18.11.2013) Symbol termu: 2S+1 L (1) L -liczba kwantowa ca lkowitego orbitalnego momentu pedu Duże litery S, P, D, F, itd. dla L=0, 1, 2, 3, itd. 2S+1 - multipletowość; S - liczba
Czastka swobodna Bariera potencja lu Pud lo jednowymiarowe FEMO Pud la wielowymiarowe. Wyk lad 3. Uk lady modelowe I
 Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Metody obliczeniowe chemii kwantowej oparte na funkcji falowej. Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać:
 Metody obliczeniowe chemii kwantowej oparte na funkcji falowej Równanie Schrödingera: ĤΨ = EΨ Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać: Ĥ = h 2 K α=1 1 2M α 2 α h2 2m
Metody obliczeniowe chemii kwantowej oparte na funkcji falowej Równanie Schrödingera: ĤΨ = EΨ Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać: Ĥ = h 2 K α=1 1 2M α 2 α h2 2m
u nk = n c nn u n 0 wyznacza siȩ empirycznie (elementy przejść) lub próbuje oszacować w obliczeniach typu ab initio Rachunek zaburzeń Löwdina
 Jeśli pasma nie s a energetycznie dobrze separowalne lub energetycznie zdegenerowane (kwazizdegenerowane) to ich wzajemny wp lyw musi być uwzglȩdniony wariacyjnie - w I rzȩdzie RZ dla stanow zdegenerowanych
Jeśli pasma nie s a energetycznie dobrze separowalne lub energetycznie zdegenerowane (kwazizdegenerowane) to ich wzajemny wp lyw musi być uwzglȩdniony wariacyjnie - w I rzȩdzie RZ dla stanow zdegenerowanych
Równania Maxwella. prawo Faraday a. I i uogólnione prawo Ampera. prawo Gaussa. D ds = q. prawo Gaussa dla magnetyzmu. si la Lorentza E + F = q( Fizyka
 Równania Maxwella L L S S Φ m E dl = t Φ e H dl = + t D ds = q B ds = 0 prawo Faraday a n I i uogólnione prawo Ampera i=1 prawo Gaussa prawo Gaussa dla magnetyzmu F = q( E + v B) si la Lorentza 1 Równania
Równania Maxwella L L S S Φ m E dl = t Φ e H dl = + t D ds = q B ds = 0 prawo Faraday a n I i uogólnione prawo Ampera i=1 prawo Gaussa prawo Gaussa dla magnetyzmu F = q( E + v B) si la Lorentza 1 Równania
Elektrodynamika. Część 5. Pola magnetyczne w materii. Ryszard Tanaś. Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.
 Elektrodynamika Część 5 Pola magnetyczne w materii yszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 6 Pola magnetyczne w materii 3 6.1 Magnetyzacja.......................
Elektrodynamika Część 5 Pola magnetyczne w materii yszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 6 Pola magnetyczne w materii 3 6.1 Magnetyzacja.......................
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Budowa atomów. Atomy wieloelektronowe Układ okresowy pierwiastków
 Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Mechanika kwantowa. Erwin Schrödinger ( ) Werner Heisenberg
 Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
c ze wzoru dwumianowego Newtona obliczyć sumy: a) 3 2 obliczyć wartości wyrazów będa cych liczbami ca lkowitymi,
 3 Korzystaja c ze wzoru dwumianowego Newtona obliczyć sumy: a) n ( n n k) ; b) 4 W rozwinie ciu dwumianowym: ( 4 a) ) 1, 3 2 obliczyć wartości wyrazów będa cych liczbami ca lkowitymi, ( ) b) 3 13, 5 +
3 Korzystaja c ze wzoru dwumianowego Newtona obliczyć sumy: a) n ( n n k) ; b) 4 W rozwinie ciu dwumianowym: ( 4 a) ) 1, 3 2 obliczyć wartości wyrazów będa cych liczbami ca lkowitymi, ( ) b) 3 13, 5 +
Matematyka A, egzamin, 17 czerwca 2005 rozwia zania
 Matematyka A, egzamin, 7 czerwca 00 rozwia zania Mam nadzieje, że nie ma tu b le dów poza jakimiś literówkami, od których uwolnić sie trudno. Zache cam do obejrzenia rozwia zań zadań z egzaminu dla matematyki
Matematyka A, egzamin, 7 czerwca 00 rozwia zania Mam nadzieje, że nie ma tu b le dów poza jakimiś literówkami, od których uwolnić sie trudno. Zache cam do obejrzenia rozwia zań zadań z egzaminu dla matematyki
Przerwa energetyczna w germanie
 Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Oddziaływania w magnetykach
 9 Oddziaływania w magnetykach Zjawiska dia- i paramagnetyzmu są odpowiedzią indywidualnych (nieskorelowanych) jonów dia- i paramagnetycznych na działanie pola magnetycznego. Z drugiej strony spontaniczne
9 Oddziaływania w magnetykach Zjawiska dia- i paramagnetyzmu są odpowiedzią indywidualnych (nieskorelowanych) jonów dia- i paramagnetycznych na działanie pola magnetycznego. Z drugiej strony spontaniczne
Pole elektrostatyczne
 Termodynamika 1. Układ termodynamiczny 5 2. Proces termodynamiczny 5 3. Bilans cieplny 5 4. Pierwsza zasada termodynamiki 7 4.1 Pierwsza zasada termodynamiki w postaci różniczkowej 7 5. Praca w procesie
Termodynamika 1. Układ termodynamiczny 5 2. Proces termodynamiczny 5 3. Bilans cieplny 5 4. Pierwsza zasada termodynamiki 7 4.1 Pierwsza zasada termodynamiki w postaci różniczkowej 7 5. Praca w procesie
Rysunek 1: Schemat doświadczenia Sterna-Gerlacha. Rysunek 2: Schemat doświadczenia Sterna-Gerlacha w różnych rzutach przestrzennych.
 VII. SPIN 1 Rysunek 1: Schemat doświadczenia Sterna-Gerlacha. Rysunek 2: Schemat doświadczenia Sterna-Gerlacha w różnych rzutach przestrzennych. 1 Wstęp Spin jest wielkością fizyczną charakteryzującą cząstki
VII. SPIN 1 Rysunek 1: Schemat doświadczenia Sterna-Gerlacha. Rysunek 2: Schemat doświadczenia Sterna-Gerlacha w różnych rzutach przestrzennych. 1 Wstęp Spin jest wielkością fizyczną charakteryzującą cząstki
Rzadkie gazy bozonów
 Rzadkie gazy bozonów Tomasz Sowiński Proseminarium Fizyki Teoretycznej 15 listopada 2004 Rzadkie gazy bozonów p.1/25 Bardzo medialne zdjęcie Rok 1995. Pierwsza kondensacja. Zaobserwowana w przestrzeni
Rzadkie gazy bozonów Tomasz Sowiński Proseminarium Fizyki Teoretycznej 15 listopada 2004 Rzadkie gazy bozonów p.1/25 Bardzo medialne zdjęcie Rok 1995. Pierwsza kondensacja. Zaobserwowana w przestrzeni
Dziedziny Euklidesowe
 Dziedziny Euklidesowe 1.1. Definicja. Dziedzina Euklidesowa nazywamy pare (R, v), gdzie R jest dziedzina ca lkowitości a v : R \ {0} N {0} funkcja zwana waluacja, która spe lnia naste ce warunki: 1. dla
Dziedziny Euklidesowe 1.1. Definicja. Dziedzina Euklidesowa nazywamy pare (R, v), gdzie R jest dziedzina ca lkowitości a v : R \ {0} N {0} funkcja zwana waluacja, która spe lnia naste ce warunki: 1. dla
Funkcja może mieć lokalne ekstrema jedynie w punktach, w których jej gradient, czyli wektor f = grad f = [ f
 Matematyka A, egzamin, 7 czerwca 005 rozwia zania Mam nadzieje, że nie ma tu b le dów poza jakimiś literówkami, od których uwolnić sie jest bardzo trudno. Zache cam do obejrzenia rozwia zań zadań z egzaminu
Matematyka A, egzamin, 7 czerwca 005 rozwia zania Mam nadzieje, że nie ma tu b le dów poza jakimiś literówkami, od których uwolnić sie jest bardzo trudno. Zache cam do obejrzenia rozwia zań zadań z egzaminu
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Hierarchia baz gaussowskich (5)
 Hierarchia baz gaussowskich (5) Bazy split-valence czyli VDZ, VTZ, etc. (np. bazy Pople a 6-31G, 6-311G, etc) Bazy split-valence spolaryzowane VDZP, VTZP, etc. Bazy bazy Dunninga (konsystentne korelacyjnie)
Hierarchia baz gaussowskich (5) Bazy split-valence czyli VDZ, VTZ, etc. (np. bazy Pople a 6-31G, 6-311G, etc) Bazy split-valence spolaryzowane VDZP, VTZP, etc. Bazy bazy Dunninga (konsystentne korelacyjnie)
ROZDZIA l 13. Zbiór Cantora
 ROZDZIA l 3 Zbiór Cantora Jednym z najciekawszych i najcze ściej spotykanych w matematyce zbiorów jest zbiór Cantora W tym rozdziale opiszemy jego podstawowe w lasności topologiczne Najprościej można go
ROZDZIA l 3 Zbiór Cantora Jednym z najciekawszych i najcze ściej spotykanych w matematyce zbiorów jest zbiór Cantora W tym rozdziale opiszemy jego podstawowe w lasności topologiczne Najprościej można go
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3
 WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
WYK LAD 5: GEOMETRIA ANALITYCZNA W R 3, PROSTA I P LASZCZYZNA W PRZESTRZENI R 3 Definicja 1 Przestrzenia R 3 nazywamy zbiór uporzadkowanych trójek (x, y, z), czyli R 3 = {(x, y, z) : x, y, z R} Przestrzeń
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elementy teorii powierzchni metali
 Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Fizyka statystyczna Termodynamika bliskiej nierównowagi. P. F. Góra
 Fizyka statystyczna Termodynamika bliskiej nierównowagi P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Nasze wszystkie dotychczasowe rozważania dotyczyły układów w równowadze termodynamicznej lub
Fizyka statystyczna Termodynamika bliskiej nierównowagi P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Nasze wszystkie dotychczasowe rozważania dotyczyły układów w równowadze termodynamicznej lub
RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU
 X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
Atomowa budowa materii
 Atomowa budowa materii Wszystkie obiekty materialne zbudowane są z tych samych elementów cząstek elementarnych Cząstki elementarne oddziałują tylko kilkoma sposobami oddziaływania wymieniając kwanty pól
Atomowa budowa materii Wszystkie obiekty materialne zbudowane są z tych samych elementów cząstek elementarnych Cząstki elementarne oddziałują tylko kilkoma sposobami oddziaływania wymieniając kwanty pól
II.6 Atomy w zewnętrznym polu magnetycznym
 II.6 Atomy w zewnętrznym polu magnetycznym 1. Kwantowanie przestrzenne w zewnętrznym polu magnetycznym. Model wektorowy raz jeszcze 2. Zjawisko Zeemana Normalne zjawisko Zeemana i jego wyjaśnienie w modelu
II.6 Atomy w zewnętrznym polu magnetycznym 1. Kwantowanie przestrzenne w zewnętrznym polu magnetycznym. Model wektorowy raz jeszcze 2. Zjawisko Zeemana Normalne zjawisko Zeemana i jego wyjaśnienie w modelu
Aby opisać strukturę krystaliczną, konieczne jest określenie jej części składowych: sieci przestrzennej oraz bazy atomowej.
 2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
Fizyka statystyczna Teoria Ginzburga-Landaua w średnim polu. P. F. Góra
 Fizyka statystyczna Teoria Ginzburga-Landaua w średnim polu P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Parametr porzadku W niskich temperaturach układy występuja w fazach, które łamia symetrię
Fizyka statystyczna Teoria Ginzburga-Landaua w średnim polu P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Parametr porzadku W niskich temperaturach układy występuja w fazach, które łamia symetrię
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc
 PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
Zadania z mechaniki kwantowej
 Zadania z mechaniki kwantowej Gabriel Wlazłowski 13 maja 2016 Rachunek zaburzeń bez czasu 1. Metodą rachunku zaburzeń obliczyć pierwszą i drugą poprawkę dla poziomów energetycznych oscylatora harmonicznego
Zadania z mechaniki kwantowej Gabriel Wlazłowski 13 maja 2016 Rachunek zaburzeń bez czasu 1. Metodą rachunku zaburzeń obliczyć pierwszą i drugą poprawkę dla poziomów energetycznych oscylatora harmonicznego
Monika Musia l. METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe)
 Monika Musia l METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe) ĤΨ i = E i Ψ i W metodzie mieszania konfiguracji wariacyjna funkcja falowa, jest liniow a kombinacj a
Monika Musia l METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe) ĤΨ i = E i Ψ i W metodzie mieszania konfiguracji wariacyjna funkcja falowa, jest liniow a kombinacj a
Proste struktury krystaliczne
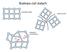 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
WYKŁAD 15. Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego
 WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
2. PRZELICZANIE OBIEKTÓW KOMBINATORYCZNYCH
 2. PRZELICZANIE OBIEKTÓW KOMBINATORYCZNYCH Typeset by AMS-TEX 2. PRZELICZANIE OBIEKTÓW KOMBINATORYCZNYCH 7 Zasada bijekcji. Jeżeli istnieje bijekcja f : A B, tj. f jest funkcja różnowartościowa i,,na (tzn.
2. PRZELICZANIE OBIEKTÓW KOMBINATORYCZNYCH Typeset by AMS-TEX 2. PRZELICZANIE OBIEKTÓW KOMBINATORYCZNYCH 7 Zasada bijekcji. Jeżeli istnieje bijekcja f : A B, tj. f jest funkcja różnowartościowa i,,na (tzn.
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Pisemny egzamin dyplomowy. na Uniwersytecie Wroc lawskim. na kierunku matematyka. zadania testowe. 22czerwca2009r. 60 HS-8-8
 EGZAMIN DYPLOMOWY, cze ść I (testowa) 22.06.2009 INSTRUKCJE DOTYCZA CE WYPE LNIANIA TESTU 1. Nie wolno korzystać z kalkulatorów. 2. Sprawdzić, czy wersja testu podana na treści zadań jest zgodna z wersja
EGZAMIN DYPLOMOWY, cze ść I (testowa) 22.06.2009 INSTRUKCJE DOTYCZA CE WYPE LNIANIA TESTU 1. Nie wolno korzystać z kalkulatorów. 2. Sprawdzić, czy wersja testu podana na treści zadań jest zgodna z wersja
Wykład FIZYKA II. 5. Magnetyzm
 Wykład FIZYKA II 5. Magnetyzm Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska http://www.if.pwr.wroc.pl/~wozniak/fizyka2.html ELEKTRYCZNOŚĆ I MAGNETYZM q q magnetyczny???
Wykład FIZYKA II 5. Magnetyzm Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska http://www.if.pwr.wroc.pl/~wozniak/fizyka2.html ELEKTRYCZNOŚĆ I MAGNETYZM q q magnetyczny???
KOMBINATORYKA 1 WYK LAD 9 Zasada szufladkowa i jej uogólnienia
 KOMBINATORYKA 1 WYK LAD 9 Zasada szufladkowa i jej uogólnienia 18 grudnia 2006 Zasada szufladkowa, zwana też zasada Dirichleta, a w jez. ang.,,pigeonhole Principle może być sformu lowana naste puja co.
KOMBINATORYKA 1 WYK LAD 9 Zasada szufladkowa i jej uogólnienia 18 grudnia 2006 Zasada szufladkowa, zwana też zasada Dirichleta, a w jez. ang.,,pigeonhole Principle może być sformu lowana naste puja co.
Zasady obsadzania poziomów
 Zasady obsadzania poziomów Model atomu Bohra Model kwantowy atomu Fala stojąca Liczby kwantowe -główna liczba kwantowa (n = 1,2,3...) kwantuje energię elektronu (numer orbity) -poboczna liczba kwantowa
Zasady obsadzania poziomów Model atomu Bohra Model kwantowy atomu Fala stojąca Liczby kwantowe -główna liczba kwantowa (n = 1,2,3...) kwantuje energię elektronu (numer orbity) -poboczna liczba kwantowa
Pojȩcie przestrzeni metrycznej
 ROZDZIA l 1 Pojȩcie przestrzeni metrycznej Definicja 1.1. Dowolny niepusty zbiór X z funkcja ρ : X X [0, ), spe lniaja ca naste puja ce trzy warunki M1: ρ(x, y) = 0 x = y, M2: ρ(x, y) = ρ(y, x), M3: ρ(x,
ROZDZIA l 1 Pojȩcie przestrzeni metrycznej Definicja 1.1. Dowolny niepusty zbiór X z funkcja ρ : X X [0, ), spe lniaja ca naste puja ce trzy warunki M1: ρ(x, y) = 0 x = y, M2: ρ(x, y) = ρ(y, x), M3: ρ(x,
