1 Renty życiowe. 1.1 Podstawowe renty życiowe
|
|
|
- Bronisław Rutkowski
- 9 lat temu
- Przeglądów:
Transkrypt
1 Renty życiowe Renta życiowa jest serią płatności okonywanych w czasie życia ubezpieczonego Jej wartość teraźniejsza jest zienną losową (bo zależy o przyszłego czasu życia T, oznaczaną Y Postawowe renty życiowe Renta ożywotnia płatna z góry (ang whole life annuity ue zapewnia coroczną wypłatę kwoty opóki żyje ubezpieczony Płatności są okonywane w oentach 0,,, K Jej wartość teraźniejsza to: May Y = + υ + υ υ K = ä K+ Pr(Y = ä k+ = Pr(K = k = k p x q x+k, la k = 0,, 2, Skłakę netto oznaczay ä x Zate Zienną Y ożna zapisać w postaci gzie ( = jest funkcją inykatorową, a więc ä x = ä k+ kp x q x+k ( Y = υ k (K k, {, jeśli zanie jest prawziwe 0, jeśli zanie jest fałszywe ä x = E(Y = υ k kp x W takiej interpretacji renta jest traktowana jako sua ubezpieczeń na ożycie
2 Uwaga Wzór ( ożna przekształcić bezpośrenio: ä x = = ( k ä k+ kp x q x+k = υ kp i x q x+k = i=0 υ i kp x q x+k = υ i Pr(K = k = υ i ip x i=0 k=i i=0 k=i i=0 Skłakę netto la renty ożna wyrazić w zależności o skłaki la ubezpieczenia na życie May bowie: Y = υk+ υ = υk+ = Z, ä K+ = υk+, (2 ską, obliczając wartości oczekiwane, otrzyujey: lub ä x = A x, = ä x + A x Równość tą ożna interpretować następująco: ług jest spłacany osetkai (z góry i końcową płatnością na koniec roku śierci Wzór (2 ożna również uzyskać traktując rentę ożywotnią jako różnicę wóch rent jenej rozpoczynającej się w chwili 0 (o wartości obecnej, rugiej w chwili K + (o wartości obecnej υ K+ Z zależności Y = Z ożna wyznaczyć oenty ziennej losowej Y, np Var(Y = Var(Z 2 W praktyce renty wypłacane są częściej niż raz w roku, np iesięcznie Ogólnie, załóży, że renta jest płatna -krotnie w ciągu roku Przy rencie płatnej z góry wypłaty w wysokości / następują w chwilach 0,, 2,, tak ługo jak rentobiorca żyje Wartość obecna jest zienną losową Y = ( + υ / + υ 2/ + υ (K+S( / 2
3 Suując otrzyay Inna postać: Y = K+S ( υ k/ = Z υ / Y = υ k/ (T k Jenorazową skłakę netto ( wartość oczekiwaną ziennej Y oznaczay ä ( x Zate ä ( x = E(Y = υ k/ k p x Skłakę netto la renty ożna też wyrazić w zależności o skłaki la ubezpieczenia na życie May bowie: Y = Z υ, / ską, obliczając wartości oczekiwane i uwzglęniając, że ( υ / = ( otrzyujey: ä ( x = A( x ( Rozważyy teraz renty czasowe (terinowe, tj płatne póki ubezpieczony żyje, ale nie łużej niż ustalony okres Dla renty czasowej n-letniej ay: Y = Poobnie jak poprzenio ay: { äk+ la K = 0,,, n ä n la K = n, n +, ä x:n = n ä k+ kp x q x+k + ä n n p x, lub ä x:n = n υ k kp x 3
4 May także Y = Z, gzie { υ Z = K la K = 0,,, n 0 la K = n, n +, Zate ä x:n = A x:n, = ä x:n + A x:n Rozpatrzy teraz renty płatne z ołu Wtey: Y = υ + υ υ K = a K Ta zienna losowa różni się o opowieniej ziennej losowej la rent płatnych z góry jeynie skłanikie stały Zate skłaka netto: Ponieważ la rent stałych: a x = ä x a n = υn, r = ra n + υ n, więc postawiając n = K otrzyujey = ra K + υ K = ra K + ( + rυ K+ Obliczając wartości oczekiwane otrzyujey = ra x + ( + ra x 2 Renty ze zienną wartością Rozważy rentę zapewniającą wypłaty r 0, r, r 2 w oentach 0,,, K Wartość teraźniejsza wynosi: Y = υ k r k (K k 4
5 Stą skłaka netto: E(Y = υ k r k kp x Ogólniej, rozważy rentę złożoną z płatności z 0, z, z 2, w oentach 0,, 2,, K + S( (przyponijy, że S( = [S + ] Najpierw zastąpiy rocznych płatności ich suą: r k = j=0 υ j zk+ j Ponieważ w roku śierci nie bęzie wszystkich płatności, konieczny jest skłanik korygujący ujene ubezpieczenie na życie, przy czy sua ubezpieczenia w chwili k + u, 0 < u <, jest wartością teraźniejszą nieoszłych płatności: c(k + u = υ j u z k+ j, j J gzie J = J(u jest zbiore tych j {, 2,, } la których j > u Wiey już, że przy Założeniu a (tzn u q x = uq x la 0 < u < ; wtey K i S są niezależne: c k+ = Postawiając wartość c(k + u ostajey: c k+ = = 0 ( 0 j J 0 = j J j= c(k + u( + r u u υ j u z k+ j ( + r j zk+ j ( + r u u = u = j( + r j zk+ j A zate jenorazowa skłaka netto la ubezpieczenia z wypłatai razy w roku wynosi: υ k r kk p x c k+ υ k+ kp x q x+k, gzie współczynniki r k i c k określone są wzorai wyżej 5
6 3 Renty stanarowe Rozważy rentę złożoną z płatności r 0, r, r 2,, gzie r k = k + Wtey wartość teraźniejsza wypłaty wynosi: Y = (k + υ k (K k Skłakę netto oznaczay (Iä x Ponieważ: ä n = (Iä n + nυ n, (ożna to interpretować tak: renta w wysokości jest spłacana osetkai z góry w wysokości, 2,, n oraz kwotą n na koniec n-tego roku więc zastępując n przez K + ay: ä K+ = (Iä K+ + (K + υ K+ Obliczając wartości oczekiwane uzyskujey 2 Skłaki netto ä x = (Iä x + (IA x Polisa ubezpieczeniowa określa z jenej strony wypłaty la ubezpieczonego (jenorazowe lub w forie renty, a z rugiej strony skłaki płacone przez niego Można wyróżnić trzy fory płacenia skłaki: skłaka jenorazowa; 2 skłaki okresowe stałe; 3 skłaki okresowe zienne Z zasay skłaki są opłacane z góry Dla anej polisy ubezpieczeniowej określay całkowitą stratę ubezpieczyciela L, jako różnicę ięzy teraźniejszą wartością wypłat a teraźniejszą wartością skłaek Strata jest rozuiana algebraicznie w szczególności oże być ujena Skłakę nazyway skłaką netto, jeśli spełnia zasaę równoważności: E(L = 0 6
7 Jenorazowa skłaka netto, o której była już owa, spełnia ten warunek Przykła Rozważy 0-letnie ubezpieczenie na życie la 40-latka z suą ubezpieczenia C płatną na koniec roku śierci Skłaki w wysokości Π są płacone co roku z góry opóki ubezpieczony żyje, ale nie łużej niż 0 lat Wtey L = { Cυ K+ Πä K+ la K = 0,,, 9 Πä 0 la K 0 Zienna L a rozkła yskretny -punktowy, przy czy: Pr(L = Cυ k+ Πä k+ = k p 40 q 40+k, k = 0,,, 9; Pr(L = Πä 0 = 0 p 40 Wyznaczyy skłakę Π Z zasay równoważności ay 9 9 (Cυ k+ Πä k+ k p 40 q 40+k + ( Πä 0 0 p 40 = 0, ( 9 Cυ k+ kp 40 q 40+k Π ä k+ kp 40 q 40+k + ä 0 0p 40 = 0, więc otrzyujey warunek CA 40:0 Πä 40:0 = 0, Π = C A 40:0 ä 40:0 Dla ilustracji liczbowej weźy r = 4% i załóży, że śiertelność polega prawu e Moivre a, z wiekie końcowy ω = 00 Wtey k p 40 q 40+k =, 60 więc 0 A 40:0 = υ k 60 = 60 a 0 = 0, 352, oraz k= A 40:0 = 5 6 υ0 = 0, 5630, 7
8 zate Ostatecznie: A 40:0 = 0, 6982, ä 40:0 = A 40:0 Π = 0, 072C = 7, 8476 Oczywiście nie ożna oczekiwać, że ubezpieczyciel bęzie wypłacał świaczenia tylko za skłaki netto Pobiera on jeszcze skłakę za ryzyko Metoa wyznaczania tej skłaki opiera się na pojęciu funkcji użyteczności Jest to funkcja, której wartościai są wartości użyteczności (satysfakcji, kofortu psychicznego Można ówić o użyteczności różnych zjawisk Użyteczność pieniąza (bogactwa jest np funkcją, która wartości pieniężnej przyporząkowuje użyteczność la otrzyującego tę wartość Funkcja użyteczności jest pojęcie psychologiczny, co oznacza, że każy a swoją funkcję użyteczności Jenak pewne ogólne własności są wspólne Mianowicie, ponieważ każy woli posiaać więcej niż niej, więc funkcja użyteczności jest rosnąca Ponato krańcowa użyteczność jest alejąca, tzn każy oatkowy procent wzrostu bogactwa powouje coraz niejszy przyrost użyteczności Dla naszych potrzeb bęziey więc zakłaać, że funkcja użyteczności u(x jest funkcją spełniającą warunki: u (x > 0, u (x < 0, i określającą użyteczność posiaania przez ubezpieczyciela wartości (pieniężnej x Przykłaowo, załóży, że u(x = a ( e ax, gzie paraetr a ierzy awersję ubezpieczyciela o ryzyka Po uwzglęnieniu funkcji użyteczności warunek E(L = 0 zostaje zastąpiony warunkie: E(u( L = u(0 Oznacza to, że skłaka jest teraz wyznaczana tak, aby oczekiwana strata użyteczności była równa 0 Dla powyższej funkcji użyteczności ay: E( a ( eal = 0, ( E( E(e al = 0, a 8
9 Dla anych z przykłau: 60 E(e al = 9 exp(acυ k+ aπä k exp( aπä 0 = Wybierzy a = 0 6 aby zobaczyć, jak zieniają się skłaki: Sua ub C Skł netto Skł Π Procskł netto % % % % % Oczywiście teraz skłaka nie jest proporcjonalna o suy ubezpieczenia C Ozwierciela to fakt, że np sua stanowi ałe ryzyko la ubezpieczyciela, stą preia za ryzyko wynosi tylko 4% W przypaku suy ryzyko jest istotne, stą preia za nie wynosi aż 48% Uwaga W praktyce skłaki są jenak proporcjonalne o suy ubezpieczenia Ubezpieczyciel oże np oliczać 53% la każej wartości C Wtey suy ubezpieczenia przekraczające wyagają reasekuracji Natoiast przy kwotach niejszych ubezpieczony przepłaca (to w pewny sensie rekopensuje stosunkowo wyższe kwoty stałe takich polis 3 Postawowe typy ubezpieczeń Rozważy ubezpieczenie na życie w wysokości, płatne na koniec roku śierci, które a być opłacone rocznyi skłakai netto w wysokości P x Strata ubezpieczyciela jest zienną losową: Z warunku E(L = 0 otrzyujey: L = υ K+ P x ä K+ P x = A x ä x Aby obliczyć wariancję wykorzystay wzór (2: ä K+ = υk+ 9
10 A więc: L = υ K+ υ K+ P x = ( + P x υk+ P x Stą ( Var(L = + P x 2Var(υ ( K+ = + P x 2Var(Z Pokazuje to, że ryzyko (ierzone wariancją jest większe w przypaku ubezpieczenia opłacanego rocznyi skłakai niż w przypaku ubezpieczenia opłacanego jenorazową skłaką Dla n-letniego ubezpieczenia na życie (sua ubezpieczenia, płatna na koniec roku śierci skłakę netto oznaczay Px:n Ponieważ strata ubezpieczyciela jest zienną losową: { υ K+ P L = x:n äk+ la K = 0,,, n Px:n än la K n, więc z warunku E(L = 0 ay A x:n P x:n ( n ä K+ kp x q x+k + ä n k p x = 0, P x:n = A x:n ä x:n 3 Ubezpieczenie na ożycie Załóży, że n-letnie ubezpieczenie na ożycie w wysokości opłacane jest rocznyi skłakai Px:n Wtey strata ubezpieczyciela wynosi: { P L = x:n äk+ la K = 0,,, n υ n Px:n än la K n, Zate: 0 = E(L = P x:n ( n ä K+ kp x q x+k ( n Px:n ä K+ kp x q x+k 0 + A x:n P x:n ä n n p x, + ä n n p x = A x:n
11 więc x:n = A x:n ä x:n P 32 Ubezpieczenie na życie i ożycie Skłakę netto oznaczay P x:n May: P x:n = A x:n ä x:n, oraz P x:n = P x:n + P x:n
ROZDZIAŁ 5. Renty życiowe
 ROZDZIAŁ 5 Renty życiowe Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy czy osoba której przyszły czas
ROZDZIAŁ 5 Renty życiowe Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy czy osoba której przyszły czas
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 6: SKŁADKI OKRESOWE Składki okresowe netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 6: SKŁADKI OKRESOWE Składki okresowe netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową
1 Funkcja użyteczności
 1 Funkcja użyteczności Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk. Użyteczność pieniądza
1 Funkcja użyteczności Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk. Użyteczność pieniądza
1. Ubezpieczenia życiowe
 1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
1. Ubezpieczenia życiowe Przy ubezpieczeniach życiowych mamy do czynienia z jednorazową wypłatą sumy ubezpieczenia. Moment jej wypłaty i wielkość wypłaty może być funkcją zmiennej losowej T a więc czas
Składki i rezerwy netto
 ROZDZIAŁ 6 Składki i rezerwy netto 1 Składki netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową Polisa taka zawiera szczegółowe warunki
ROZDZIAŁ 6 Składki i rezerwy netto 1 Składki netto Umowę pomiędzy ubezpieczycielem a ubezpieczonym dotyczącą ubezpieczenia na życie nazywa się polisą ubezpieczeniową Polisa taka zawiera szczegółowe warunki
UBEZPIECZENIE NA ŻYCIE Z LOSOWĄ STOPĄ PROCENTOWĄ
 UBEZPIECZENIE NA ŻYCIE Z LOSOWĄ STOPĄ PROCENTOWĄ Krzysztof Janas Michał Krzeszowiec Koło Nauk Aktuarialnych Politechniki Łódzkiej Warszawa, 09-11.06.2008 r. Plan Założenia wstępne: Teoria oprocentowania
UBEZPIECZENIE NA ŻYCIE Z LOSOWĄ STOPĄ PROCENTOWĄ Krzysztof Janas Michał Krzeszowiec Koło Nauk Aktuarialnych Politechniki Łódzkiej Warszawa, 09-11.06.2008 r. Plan Założenia wstępne: Teoria oprocentowania
UBEZPIECZENIA NA ŻYCIE
 UBEZPIECZENIA NA ŻYCIE M BIENIEK Ubezpieczenie na życie jest to kontrakt pomiędzy ubezpieczycielem a ubezpieczonym gwarantujący, że ubezpieczyciel w zamian za opłacanie składek, wypłaci z góry ustaloną
UBEZPIECZENIA NA ŻYCIE M BIENIEK Ubezpieczenie na życie jest to kontrakt pomiędzy ubezpieczycielem a ubezpieczonym gwarantujący, że ubezpieczyciel w zamian za opłacanie składek, wypłaci z góry ustaloną
REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH
 REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH M. BIENIEK Przypomnijmy, że dla dowolnego wektora przepływów c rezerwę w chwili k względem funkcji dyskonta v zdefiniowaliśmy jako k(c; v) = Val k ( k c; v), k = 0,
REZERWY UBEZPIECZEŃ I RENT ŻYCIOWYCH M. BIENIEK Przypomnijmy, że dla dowolnego wektora przepływów c rezerwę w chwili k względem funkcji dyskonta v zdefiniowaliśmy jako k(c; v) = Val k ( k c; v), k = 0,
= µ. Niech ponadto. M( s) oznacza funkcję tworzącą momenty. zmiennej T( x), dla pewnego wieku x, w populacji A. Wówczas e x wyraża się wzorem: 1
 1. W populacji B natężenie wymierania µ ( B ) x jest większe od natężenia wymierania ( A) µ x w populacji A, jednostajnie o µ > 0, dla każdego wieku x tzn. ( B) ( A) µ µ x = µ. Niech ponadto x M( s) oznacza
1. W populacji B natężenie wymierania µ ( B ) x jest większe od natężenia wymierania ( A) µ x w populacji A, jednostajnie o µ > 0, dla każdego wieku x tzn. ( B) ( A) µ µ x = µ. Niech ponadto x M( s) oznacza
Ubezpieczenia na życie
 ROZDZIAŁ 4 Ubezpieczenia na życie Ubezpieczenie na życie jest to kontrakt (zwany polisą), w którym ubezpieczony zobowiązuje się do opłacenia składki (jednorazowo lub w ratach), a w zamian za to ubezpieczyciel
ROZDZIAŁ 4 Ubezpieczenia na życie Ubezpieczenie na życie jest to kontrakt (zwany polisą), w którym ubezpieczony zobowiązuje się do opłacenia składki (jednorazowo lub w ratach), a w zamian za to ubezpieczyciel
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 4: UBEZPIECZENIA NA ŻYCIE Ubezpieczenie na życie jest to kontrakt (zwany polisą), w którym ubezpieczony zobowiązuje się do opłacenia składki (jednorazowo lub
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 4: UBEZPIECZENIA NA ŻYCIE Ubezpieczenie na życie jest to kontrakt (zwany polisą), w którym ubezpieczony zobowiązuje się do opłacenia składki (jednorazowo lub
LIX Egzamin dla Aktuariuszy z 12 marca 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LIX Egzamin dla Aktuariuszy z 12 marca 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LIX Egzamin dla Aktuariuszy z 12 marca 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Ubezpieczenia życiowe
 Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Ubezpieczenia życiowe 1. Z historii ubezpieczeń W uproszczeniu mówiąc mamy dwa tradycyjne modele ubezpieczeń. Pierwszy ma źródło w towarzystwach
Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Ubezpieczenia życiowe 1. Z historii ubezpieczeń W uproszczeniu mówiąc mamy dwa tradycyjne modele ubezpieczeń. Pierwszy ma źródło w towarzystwach
Przekształcenie całkowe Fouriera
 Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
3 Ubezpieczenia na życie
 3 Ubezpieczenia na życie O ile nie jest powiedziane inaczej, w poniższych zadaniach zakładamy HJP. 3.1. Zadania 7.1-7.26 z Miśkiewicz-Nawrocka, Zeug-Żebro, Zbiór zadań z matematyki finansowej. 3.2. Mając
3 Ubezpieczenia na życie O ile nie jest powiedziane inaczej, w poniższych zadaniach zakładamy HJP. 3.1. Zadania 7.1-7.26 z Miśkiewicz-Nawrocka, Zeug-Żebro, Zbiór zadań z matematyki finansowej. 3.2. Mając
OGÓLNE RENTY ŻYCIOWE
 OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
Matematyka finansowa i ubezpieczeniowa - 11 Ubezpieczenia Ŝyciowe 2
 Matematyka finansowa i ubezpieczeniowa - Ubezpieczenia Ŝyciowe 2 Składki netto w ubezpieczeniach Ŝyciowych Zakład ubezpieczeniowy pobiera za ubezpieczenia składkę brutto, składającą się ze składki netto
Matematyka finansowa i ubezpieczeniowa - Ubezpieczenia Ŝyciowe 2 Składki netto w ubezpieczeniach Ŝyciowych Zakład ubezpieczeniowy pobiera za ubezpieczenia składkę brutto, składającą się ze składki netto
LIII Egzamin dla Aktuariuszy z 31 maja 2010 r.
 Komisja Egzaminacyjna dla Aktuariuszy LIII Egzamin dla Aktuariuszy z 31 maja 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LIII Egzamin dla Aktuariuszy z 31 maja 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
MODELE MATEMATYCZNE W UBEZPIECZENIACH
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 1: UWAGI WSTĘPNE. PROCENT SKŁADANY 1. Uwagi wstępne Ryzyko jest związane z niealże każdy rodzaje działalności człowieka: przy planowaniu urlopu ryzyko słabej
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 1: UWAGI WSTĘPNE. PROCENT SKŁADANY 1. Uwagi wstępne Ryzyko jest związane z niealże każdy rodzaje działalności człowieka: przy planowaniu urlopu ryzyko słabej
= = a na podstawie zadania 6 po p. 3.6 wiemy, że. b 1. a 2 ab b 2
 64 III. Zienne losowe jednowyiarowe D Ponieważ D (A) < D (B), więc należy wybrać partię A. Przykład 3.4. Obliczyć wariancję rozkładu jednostajnego. Ponieważ a na podstawie zadania 6 po p. 3.6 wiey, że
64 III. Zienne losowe jednowyiarowe D Ponieważ D (A) < D (B), więc należy wybrać partię A. Przykład 3.4. Obliczyć wariancję rozkładu jednostajnego. Ponieważ a na podstawie zadania 6 po p. 3.6 wiey, że
LIV Egzamin dla Aktuariuszy z 4 października 2010 r.
 Komisja Egzaminacyjna dla Aktuariuszy LIV Egzamin dla Aktuariuszy z 4 października 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:...klucz odpowiedzi... Czas egzaminu:
Komisja Egzaminacyjna dla Aktuariuszy LIV Egzamin dla Aktuariuszy z 4 października 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:...klucz odpowiedzi... Czas egzaminu:
Matematyka ubezpieczeń życiowych 17 marca 2008 r.
 1. Niech oznacza przeciętne dalsze trwanie życia w ciągu najbliższego roku obliczone przy założeniu hipotezy interpolacyjnej o stałym natężeniu wymierania między wiekami całkowitymi. Podobnie niech oznacza
1. Niech oznacza przeciętne dalsze trwanie życia w ciągu najbliższego roku obliczone przy założeniu hipotezy interpolacyjnej o stałym natężeniu wymierania między wiekami całkowitymi. Podobnie niech oznacza
Ubezpieczenia majątkowe
 Funkcje użyteczności a składki Uniwersytet Przyrodniczy we Wrocławiu Instytut Nauk Ekonomicznych i Społecznych 2016/2017 Funkcja użyteczności Niech ω wielkość majątku decydenta wyrażona w j.p., u (ω) stopień
Funkcje użyteczności a składki Uniwersytet Przyrodniczy we Wrocławiu Instytut Nauk Ekonomicznych i Społecznych 2016/2017 Funkcja użyteczności Niech ω wielkość majątku decydenta wyrażona w j.p., u (ω) stopień
LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r.
 Koisja Egzainacyjna dla Aktuariuszy LV Egzain dla Aktuariuszy z 13 grudnia 2010 r. Część II Mateatyka ubezpieczeń życiowych Iię i nazwisko osoby egzainowanej:... Czas egzainu: 100 inut Warszawa, 13 grudnia
Koisja Egzainacyjna dla Aktuariuszy LV Egzain dla Aktuariuszy z 13 grudnia 2010 r. Część II Mateatyka ubezpieczeń życiowych Iię i nazwisko osoby egzainowanej:... Czas egzainu: 100 inut Warszawa, 13 grudnia
LXVIII Egzamin dla Aktuariuszy z 29 września 2014 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXVIII Egzamin dla Aktuariuszy z 29 września 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXVIII Egzamin dla Aktuariuszy z 29 września 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Arytmetyka finansowa Wykład z dnia 30.04.2013
 Arytmetyka fnansowa Wykła z na 30042013 Wesław Krakowak W tym rozzale bęzemy baać wartość aktualną rent pewnych, W szczególnośc, wartość obecną renty, a równeż wartość końcową Do wartośc końcowej renty
Arytmetyka fnansowa Wykła z na 30042013 Wesław Krakowak W tym rozzale bęzemy baać wartość aktualną rent pewnych, W szczególnośc, wartość obecną renty, a równeż wartość końcową Do wartośc końcowej renty
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
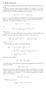 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
1.5. ZWIĄZKI KONSTYTUTYWNE STRONA FIZYCZNA
 .5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowazenie Wyprowazone w rozziałach.3 (strona statyczna i.4 (strona geoetryczna równania (.3.36 i (.4. są niezależne o rozaju ciała aterialnego, które oże
.5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowazenie Wyprowazone w rozziałach.3 (strona statyczna i.4 (strona geoetryczna równania (.3.36 i (.4. są niezależne o rozaju ciała aterialnego, które oże
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
XXXVI Egzamin dla Aktuariuszy z 10 października 2005 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXVI Egzamin dla Aktuariuszy z 10 października 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXVI Egzamin dla Aktuariuszy z 10 października 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXI Egzamin dla Aktuariuszy z 1 października 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
XXXVII Egzamin dla Aktuariuszy z 5 grudniaa 2005 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXVII Egzamin dla Aktuariuszy z 5 grudniaa 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XXXVII Egzamin dla Aktuariuszy z 5 grudniaa 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
LXXV Egzamin dla Aktuariuszy z 5 grudnia 2016 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXV Egzamin dla Aktuariuszy z 5 grudnia 2016 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXXV Egzamin dla Aktuariuszy z 5 grudnia 2016 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
LXX Egzamin dla Aktuariuszy z 23 marca 2015 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
Wyk lad 3 Grupy cykliczne
 Wyk la 3 Grupy cykliczne Definicja 3.1. Niech a bezie elementem grupy (G,, e). Jeżeli istnieje liczba naturalna k taka, że a k = e, to najmniejsza taka liczbe naturalna k nazywamy rzeem elementu a. W przeciwnym
Wyk la 3 Grupy cykliczne Definicja 3.1. Niech a bezie elementem grupy (G,, e). Jeżeli istnieje liczba naturalna k taka, że a k = e, to najmniejsza taka liczbe naturalna k nazywamy rzeem elementu a. W przeciwnym
XXXIII Egzamin dla Aktuariuszy z 17 stycznia 2005 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy z 17 stycznia 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy z 17 stycznia 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
LIII Egzamin dla Aktuariuszy z 31 maja 2010 r.
 Komisja Egzaminacyjna dla Aktuariuszy LIII Egzamin dla Aktuariuszy z 31 maja 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:. Czas egzaminu: 100 minut Warszawa, 31
Komisja Egzaminacyjna dla Aktuariuszy LIII Egzamin dla Aktuariuszy z 31 maja 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:. Czas egzaminu: 100 minut Warszawa, 31
UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI. Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH
 UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH WPROWADZENIE Opcje są instrumentem pochonym, zatem takim, którego cena zależy o ceny instrumentu
UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH WPROWADZENIE Opcje są instrumentem pochonym, zatem takim, którego cena zależy o ceny instrumentu
LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
1. Pięciu osobników pochodzi z populacji, w której pojedyncze życie podlega ryzyku śmierci
 1. Pięciu osobników pochodzi z populacji, w której pojedyncze życie podlega ryzyku śmierci + t µ + t A + B 2. Wyznacz prawdopodobieństwo, że z grupy tej nikt nie umrze w ciągu najbliższych 5 lat, jeśli
1. Pięciu osobników pochodzi z populacji, w której pojedyncze życie podlega ryzyku śmierci + t µ + t A + B 2. Wyznacz prawdopodobieństwo, że z grupy tej nikt nie umrze w ciągu najbliższych 5 lat, jeśli
Elementy teorii przeżywalności
 Elementy teorii przeżywalności Zadanie 1.1 Zapisz 1. Prawdopodobieństwo, że noworodek umrze nie później niż w wieku 8 lat 2. P-two, że noworodek umrze nie później niż w wieku 3 lat 3. P-two, że noworodek
Elementy teorii przeżywalności Zadanie 1.1 Zapisz 1. Prawdopodobieństwo, że noworodek umrze nie później niż w wieku 8 lat 2. P-two, że noworodek umrze nie później niż w wieku 3 lat 3. P-two, że noworodek
Aktuariat i matematyka finansowa. Metody kalkulacji składki w ubezpieczeniach typu non - life
 Aktuariat i matematyka finansowa Metody kalkulacji składki w ubezpieczeniach typu non - life Budowa składki ubezpieczeniowej Składka ubezpieczeniowa cena jaką ubezpieczający płaci za ochronę ubezpieczeniowa
Aktuariat i matematyka finansowa Metody kalkulacji składki w ubezpieczeniach typu non - life Budowa składki ubezpieczeniowej Składka ubezpieczeniowa cena jaką ubezpieczający płaci za ochronę ubezpieczeniowa
Ubez piecz enie ersalne saln D am a en e t n ow o a a S t S rat ra eg e i g a
 Ubezpieczenie Uniwersalne Diamentowa Strategia 17 październik 2012 Diamentowa Strategia pozwoli Ci zabezpieczyć finansowo rodzinę przed utratą głównych dochodów w przypadku: inwalidztwa, poważnego zachorowania,
Ubezpieczenie Uniwersalne Diamentowa Strategia 17 październik 2012 Diamentowa Strategia pozwoli Ci zabezpieczyć finansowo rodzinę przed utratą głównych dochodów w przypadku: inwalidztwa, poważnego zachorowania,
Politechnika Krakowska im. Tadeusza Kościuszki. Karta przedmiotu. obowiązuje studentów rozpoczynających studia w roku akademickim 2017/2018
 Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu obowiązuje studentów rozpoczynających studia w roku akademickim 2017/2018 Wydział Fizyki, Matematyki i Informatyki Kierunek studiów: Matematyka
Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu obowiązuje studentów rozpoczynających studia w roku akademickim 2017/2018 Wydział Fizyki, Matematyki i Informatyki Kierunek studiów: Matematyka
40:5. 40:5 = 500000υ5 5p 40, 40:5 = 500000 5p 40.
 Portfele polis Poieważ składka jest ustalaa jako wartość oczekiwaa rzeczywistego, losowego kosztu ubezpieczeia, więc jest tym bliższa średiej wydatków im większa jest liczba ubezpieczoych Polisy grupuje
Portfele polis Poieważ składka jest ustalaa jako wartość oczekiwaa rzeczywistego, losowego kosztu ubezpieczeia, więc jest tym bliższa średiej wydatków im większa jest liczba ubezpieczoych Polisy grupuje
1. Niech g(t) oznacza gęstość wymierania, od momentu narodzin, pewnej populacji mężczyzn. Demografowie zauważyli, że po drobnej modyfikacji: =
 . Niech g(t) oznacza gęstość wymierania, od momentu narodzin, pewnej populacji mężczyzn. Demografowie zauważyli, że po drobnej modyfikacji: ~ 0,9g( t) 0 t < 50 g ( t) =,2 g( t) 50 t. opisuje ona śmiertelność
. Niech g(t) oznacza gęstość wymierania, od momentu narodzin, pewnej populacji mężczyzn. Demografowie zauważyli, że po drobnej modyfikacji: ~ 0,9g( t) 0 t < 50 g ( t) =,2 g( t) 50 t. opisuje ona śmiertelność
UBEZPIECZ SIĘ, NAJLEPIEJ U MATEMATYKA
 KARIERA MATEMATYKĄ KREŚLONA UBEZPIECZ SIĘ, NAJLEPIEJ U MATEMATYKA Ryzyko i ubezpieczenie Możliwość zajścia niechcianego zdarzenia nazywamy ryzykiem. Ryzyko prawie zawsze wiąże się ze stratą. Ryzyko i ubezpieczenie
KARIERA MATEMATYKĄ KREŚLONA UBEZPIECZ SIĘ, NAJLEPIEJ U MATEMATYKA Ryzyko i ubezpieczenie Możliwość zajścia niechcianego zdarzenia nazywamy ryzykiem. Ryzyko prawie zawsze wiąże się ze stratą. Ryzyko i ubezpieczenie
LX Egzamin dla Aktuariuszy z 28 maja 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LX Egzamin dla Aktuariuszy z 28 maja 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa, 28
Komisja Egzaminacyjna dla Aktuariuszy LX Egzamin dla Aktuariuszy z 28 maja 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa, 28
Elementy matematyki finansowej
 ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
Matematyka ubezpieczeń życiowych r.
 . W populacji, w której śmiertelnością rządzi prawo de Moivre a z wiekiem granicznym ω = 50, dzieckiem jest się do wieku d. W wieku d rozpoczyna się pracę i pracuje się do wieku p.w wieku p przechodzi
. W populacji, w której śmiertelnością rządzi prawo de Moivre a z wiekiem granicznym ω = 50, dzieckiem jest się do wieku d. W wieku d rozpoczyna się pracę i pracuje się do wieku p.w wieku p przechodzi
Aktuariat i matematyka finansowa. Rezerwy techniczno ubezpieczeniowe i metody ich tworzenia
 Aktuariat i matematyka finansowa Rezerwy techniczno ubezpieczeniowe i metody ich tworzenia Tworzenie rezerw i ich wysokość wpływa na Obliczanie zysku dla potrzeb podatkowych, Sprawozdawczość dla udziałowców,
Aktuariat i matematyka finansowa Rezerwy techniczno ubezpieczeniowe i metody ich tworzenia Tworzenie rezerw i ich wysokość wpływa na Obliczanie zysku dla potrzeb podatkowych, Sprawozdawczość dla udziałowców,
Matematyka bankowa 2
 1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
1. Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki Uniwersytet Łódzki 2. Instytut Nauk Ekonomicznych i Informatyki Państwowa Wyższa Szkoła Zawodowa w Płocku Matematyka bankowa 2 średnio- i
1. Oblicz prawdopodobieństwo zdarzenia, że noworodek wybrany z populacji, w której śmiertelnością rządzi prawo Gompertza
 1. Oblicz prawdopodobieństwo zdarzenia, że noworodek wybrany z populacji, w której śmiertelnością rządzi prawo Gompertza x µ x = 06e. dożyje wieku największej śmiertelności (tzn. takiego wieku, w którym
1. Oblicz prawdopodobieństwo zdarzenia, że noworodek wybrany z populacji, w której śmiertelnością rządzi prawo Gompertza x µ x = 06e. dożyje wieku największej śmiertelności (tzn. takiego wieku, w którym
XXXX Egzamin dla Aktuariuszy z 9 października 2006 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXX Egzamin dla Aktuariuszy z 9 października 2006 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XXXX Egzamin dla Aktuariuszy z 9 października 2006 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Metody aktuarialne - opis przedmiotu
 Metody aktuarialne - opis przedmiotu Informacje ogólne Nazwa przedmiotu Metody aktuarialne Kod przedmiotu 11.5-WK-MATP-MA-W-S14_pNadGenEJ6TV Wydział Kierunek Wydział Matematyki, Informatyki i Ekonometrii
Metody aktuarialne - opis przedmiotu Informacje ogólne Nazwa przedmiotu Metody aktuarialne Kod przedmiotu 11.5-WK-MATP-MA-W-S14_pNadGenEJ6TV Wydział Kierunek Wydział Matematyki, Informatyki i Ekonometrii
LXXIV Egzamin dla Aktuariuszy z 23 maja 2016 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXIV Egzamin dla Aktuariuszy z 23 maja 2016 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXXIV Egzamin dla Aktuariuszy z 23 maja 2016 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
XXXV Egzamin dla Aktuariuszy z 16 maja 2005 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut Warszawa, 6
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 2005 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut Warszawa, 6
LXXII Egzamin dla Aktuariuszy z 28 września 2015 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXII Egzamin dla Aktuariuszy z 28 września 2015 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXXII Egzamin dla Aktuariuszy z 28 września 2015 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Tablice trwania życia
 ROZDZIAŁ 3 Tablice trwania życia 1 Przyszły czas życia Osobę, która ukończyła x lat życia, będziemy nazywać x-latkiem i oznaczać symbolem x Jej przyszły czas życia, tzn od chwili x do chwili śmierci, będziemy
ROZDZIAŁ 3 Tablice trwania życia 1 Przyszły czas życia Osobę, która ukończyła x lat życia, będziemy nazywać x-latkiem i oznaczać symbolem x Jej przyszły czas życia, tzn od chwili x do chwili śmierci, będziemy
LXV Egzamin dla Aktuariuszy z 30 września 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXIX Egzamin dla Aktuariuszy z 8 grudnia 2014 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
UOGÓLNIONA MIARA DOPASOWANIA W MODELU LINIOWYM
 UOGÓLNIONA MIARA DOPASOWANIA W MODELU LINIOWYM Wojciech Zieliński Katedra Ekonoetrii i Statystyki, SGGW Nowoursynowska 159, PL-0-767 Warszawa wojtekzielinski@statystykainfo Streszczenie: W odelu regresji
UOGÓLNIONA MIARA DOPASOWANIA W MODELU LINIOWYM Wojciech Zieliński Katedra Ekonoetrii i Statystyki, SGGW Nowoursynowska 159, PL-0-767 Warszawa wojtekzielinski@statystykainfo Streszczenie: W odelu regresji
Komisja Egzaminacyjna dla Aktuariuszy. XXXIX Egzamin dla Aktuariuszy z 5 czerwca 2006 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXIX Egzamin dla Aktuariuszy z 5 czerwca 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Inwestor dokonuje
Komisja Egzaminacyjna dla Aktuariuszy XXXIX Egzamin dla Aktuariuszy z 5 czerwca 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Inwestor dokonuje
OGŁOSZENIE O ZMIANACH STATUTU MM PRIME AKCJI FIZ
 Warszawa, nia 18 września 2014 r. OGŁOSZENIE O ZMIANACH STATUTU MM PRIME AKCJI FIZ Niniejszym MM Prime Towarzystwo Funuszy Inwestycyjnych Spółka Akcyjna z siezibą w Warszawie ogłasza poniższe zmiany statutu
Warszawa, nia 18 września 2014 r. OGŁOSZENIE O ZMIANACH STATUTU MM PRIME AKCJI FIZ Niniejszym MM Prime Towarzystwo Funuszy Inwestycyjnych Spółka Akcyjna z siezibą w Warszawie ogłasza poniższe zmiany statutu
zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min.
 zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min. Imię nazwisko:... numer indeksu:... nr zadania zad.1 zad.2 zad.3 zad.4 zad.5 zad.6 zad.7
zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min. Imię nazwisko:... numer indeksu:... nr zadania zad.1 zad.2 zad.3 zad.4 zad.5 zad.6 zad.7
LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
O nauczaniu oceny niepewności standardowej
 8 O nauczaniu oceny niepewności stanarowej Henryk Szyłowski Wyział Fizyki UAM, Poznań PROBLEM O lat 90. ubiegłego wieku istnieją mięzynaroowe normy oceny niepewności pomiarowych [, ], zawierające jenolitą
8 O nauczaniu oceny niepewności stanarowej Henryk Szyłowski Wyział Fizyki UAM, Poznań PROBLEM O lat 90. ubiegłego wieku istnieją mięzynaroowe normy oceny niepewności pomiarowych [, ], zawierające jenolitą
Karta Produktu UBEZPIECZENIE NA ŻYCIE DLA KREDYTOBIORCÓW RAIFFEISEN BANK POLSKA S.A. R-BEZPIECZNA SPŁATA. Ubezpieczający: Ubezpieczony:
 Karta Produktu UBEZPIECZENIE NA ŻYCIE DLA KREDYTOBIORCÓW RAIFFEISEN BANK POLSKA S.A. R-BEZPIECZNA SPŁATA Ubezpieczający: Osoba fizyczna, prowadząca działalność gospodarczą na podstawie wpisu do ewidencji
Karta Produktu UBEZPIECZENIE NA ŻYCIE DLA KREDYTOBIORCÓW RAIFFEISEN BANK POLSKA S.A. R-BEZPIECZNA SPŁATA Ubezpieczający: Osoba fizyczna, prowadząca działalność gospodarczą na podstawie wpisu do ewidencji
Regulamin Opcje na stopy procentowe
 Regulamin Opcje na stopy procentowe Warszawa, Listopa 2013 mank.pl Spis treści: Rozział I Postanowienia ogólne...3 Rozział II Warunki transakcji sprzeaży opcji na stopy procentowe...4 Rozział III Zasay
Regulamin Opcje na stopy procentowe Warszawa, Listopa 2013 mank.pl Spis treści: Rozział I Postanowienia ogólne...3 Rozział II Warunki transakcji sprzeaży opcji na stopy procentowe...4 Rozział III Zasay
Art Zakład ubezpieczeń udziela ochrony ubezpieczeniowej na podstawie umowy ubezpieczenia zawartej z ubezpieczającym. 2. Umowa ubezpieczenia
 UMOWA UBEZPIECZENIA Art. 15. 1. Zakład ubezpieczeń udziela ochrony ubezpieczeniowej na podstawie umowy ubezpieczenia zawartej z ubezpieczającym. 2. Umowa ubezpieczenia ma charakter dobrowolny, z zastrzeżeniem
UMOWA UBEZPIECZENIA Art. 15. 1. Zakład ubezpieczeń udziela ochrony ubezpieczeniowej na podstawie umowy ubezpieczenia zawartej z ubezpieczającym. 2. Umowa ubezpieczenia ma charakter dobrowolny, z zastrzeżeniem
XLIII Egzamin dla Aktuariuszy z 8 października 2007 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIII Egzamin dla Aktuariuszy z 8 października 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XLIII Egzamin dla Aktuariuszy z 8 października 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
1. Przyszła długość życia x-latka
 Przyszła długość życia x-latka Rozważmy osobę mającą x lat; oznaczenie: (x) Jej przyszłą długość życia oznaczymy T (x), lub krótko T Zatem x+t oznacza całkowitą długość życia T jest zmienną losową, której
Przyszła długość życia x-latka Rozważmy osobę mającą x lat; oznaczenie: (x) Jej przyszłą długość życia oznaczymy T (x), lub krótko T Zatem x+t oznacza całkowitą długość życia T jest zmienną losową, której
0 Rachunek czasu. Informacje pierwotne: początkowa i końcowa data inwestycji.
 0 Rachunek czasu Inforacje pierwotne: początkowa i końcowa data inwestycji. Konwencja: nie naliczay odsetek za początkowy dzień trwania inwestycji, naliczay za końcowy. Liczba dni trwania inwestycji liczba
0 Rachunek czasu Inforacje pierwotne: początkowa i końcowa data inwestycji. Konwencja: nie naliczay odsetek za początkowy dzień trwania inwestycji, naliczay za końcowy. Liczba dni trwania inwestycji liczba
Matematyka finansowa 04.04.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Zabezpieczenie społeczne
 Zabezpieczenie społeczne Zabezpieczenie społeczne - jako idea i przedmiot polityki Zabezpieczenie społeczne to całokształt środków i działań publicznych, za pomocą których społeczeństwo stara się chronić
Zabezpieczenie społeczne Zabezpieczenie społeczne - jako idea i przedmiot polityki Zabezpieczenie społeczne to całokształt środków i działań publicznych, za pomocą których społeczeństwo stara się chronić
UMOWA UBEZPIECZENIA OSOBOWEGO
 UMOWA UBEZPIECZENIA OSOBOWEGO zawarta w dniu... w..., pomiędzy: 1....... zwanym dalej Ubezpieczycielem a, 2....... zwanym dalej Ubezpieczającym, w dalszej części łącznie nazywani Stronami o następującej
UMOWA UBEZPIECZENIA OSOBOWEGO zawarta w dniu... w..., pomiędzy: 1....... zwanym dalej Ubezpieczycielem a, 2....... zwanym dalej Ubezpieczającym, w dalszej części łącznie nazywani Stronami o następującej
Matematyka ubezpieczeń życiowych r.
 1. W danej populacji intensywność śmiertelności zmienia się skokowo w rocznicę narodzin i jest stała aż do następnych urodzin. Jaka jest oczekiwana liczba osób z kohorty miliona 60-latków, które umrą po
1. W danej populacji intensywność śmiertelności zmienia się skokowo w rocznicę narodzin i jest stała aż do następnych urodzin. Jaka jest oczekiwana liczba osób z kohorty miliona 60-latków, które umrą po
Karta produktu Indywidualne Ubezpieczenie Uniwersalne DIAMENTOWA STRATEGIA
 Karta produktu Indywidualne Ubezpieczenie Uniwersalne DIAMENTOWA STRATEGIA 1. Opis i charakter produktu Ubezpieczenie bezterminowe o charakterze ochronno-inwestycyjnym łączące szeroki zakres ochrony ubezpieczeniowej
Karta produktu Indywidualne Ubezpieczenie Uniwersalne DIAMENTOWA STRATEGIA 1. Opis i charakter produktu Ubezpieczenie bezterminowe o charakterze ochronno-inwestycyjnym łączące szeroki zakres ochrony ubezpieczeniowej
2,00 % 5,00 % 0,00 % 3,01 % 2,58 % 3,12 % ZAKUP podsumowanie najlepszych ofert. Strona 1 z ,29 zł 205,12 zł 203,83 zł. 0,00 zł 0,00 zł 0,00 zł
 Jakub Misiewicz email: jakubmisiewicz@homebrokerpl telefon: Oferta przygotowana dnia: 06122015 (23:00) ZAKUP podsumowanie najlepszych ofert Parametry: Waluta: PLN, Kwota: 300 000, Wartość nieruchomości:
Jakub Misiewicz email: jakubmisiewicz@homebrokerpl telefon: Oferta przygotowana dnia: 06122015 (23:00) ZAKUP podsumowanie najlepszych ofert Parametry: Waluta: PLN, Kwota: 300 000, Wartość nieruchomości:
Ubezpieczenie na Życie POLISA DLA CIEBIE. Materiały szkoleniowe. Do użytku wewnętrznego
 Ubezpieczenie na Życie POLISA DLA CIEBIE Atuty Dożywotnia ochrona na życie ze stałą składką Brak badań lekarskich Prosta forma zawarcia umowy Atrakcyjna prowizja dla Agenta Możliwość gromadzenia środków
Ubezpieczenie na Życie POLISA DLA CIEBIE Atuty Dożywotnia ochrona na życie ze stałą składką Brak badań lekarskich Prosta forma zawarcia umowy Atrakcyjna prowizja dla Agenta Możliwość gromadzenia środków
9 Funkcje Użyteczności
 9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
Równania trygonometryczne z parametrem- inne spojrzenie
 Agnieszka Zielińska aga7ziel@wppl Nauczyciel ateatyki w III Liceu Ogólnokształcący w Zaościu Równania trygonoetryczne z paraetre- inne spojrzenie Cele tego reeratu jest zapoznanie państwa z oii etodai
Agnieszka Zielińska aga7ziel@wppl Nauczyciel ateatyki w III Liceu Ogólnokształcący w Zaościu Równania trygonoetryczne z paraetre- inne spojrzenie Cele tego reeratu jest zapoznanie państwa z oii etodai
Karta Produktu. Indywidualne Ubezpieczenie Następstw Nieszczęśliwych Wypadków - SPOKOJNY SEN dla Klientów Raiffeisen Bank Polska S.A.
 Karta Produktu Indywidualne Ubezpieczenie Następstw Nieszczęśliwych Wypadków - SPOKOJNY SEN dla Klientów Raiffeisen Bank Polska S.A. Ubezpieczający : osoba fizyczna, która zawarła z Bankiem umowę o Produkt
Karta Produktu Indywidualne Ubezpieczenie Następstw Nieszczęśliwych Wypadków - SPOKOJNY SEN dla Klientów Raiffeisen Bank Polska S.A. Ubezpieczający : osoba fizyczna, która zawarła z Bankiem umowę o Produkt
MUMIO Lab 6 (składki, kontrakt stop-loss)
 MUMIO Lab 6 (składki, kontrakt stop-loss) 1. (6p.) Niech X oznacza ryzyko (zmienn a losow a o własności P (X 0) = 1), a H( ) niech oznacza formułȩ kalkulacji składki (przyporz adkowuj ac a każdemu ryzyku
MUMIO Lab 6 (składki, kontrakt stop-loss) 1. (6p.) Niech X oznacza ryzyko (zmienn a losow a o własności P (X 0) = 1), a H( ) niech oznacza formułȩ kalkulacji składki (przyporz adkowuj ac a każdemu ryzyku
ĆWICZENIE 4. WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kraków, 2016
 Krystyna Gronostaj Maria Nowotny-Różańska Zakła Fizyki, Uniwersytet Rolniczy o użytku wewnętrznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kraków, 016 Spis treści:
Krystyna Gronostaj Maria Nowotny-Różańska Zakła Fizyki, Uniwersytet Rolniczy o użytku wewnętrznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kraków, 016 Spis treści:
ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 6 Kalkulacja sk ladki netto II. Funkcje komutacyjne.
 Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 6 Kalkulacja sk ladki netto II. Funkcje komutacyjne. 1 Przypomnienie Umowa ubezpieczenia zawiera informacje o: Przedmiocie ubezpieczenia Czasie
Wst ep do matematyki aktuarialnej Micha l Jasiczak Wyk lad 6 Kalkulacja sk ladki netto II. Funkcje komutacyjne. 1 Przypomnienie Umowa ubezpieczenia zawiera informacje o: Przedmiocie ubezpieczenia Czasie
Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych
 Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych Elżbieta Krajewska Instytut Matematyki Politechnika Łódzka Elżbieta Krajewska Immunizacja ubezpieczycieli życiowych 1/22 Plan prezentacji
Immunizacja ryzyka stopy procentowej ubezpieczycieli życiowych Elżbieta Krajewska Instytut Matematyki Politechnika Łódzka Elżbieta Krajewska Immunizacja ubezpieczycieli życiowych 1/22 Plan prezentacji
z przedziału 0,1 liczb dodatnich. Rozważmy dwie zmienne losowe:... ma złożony rozkład dwumianowy o parametrach 1,q i, gdzie X, wszystkie składniki X
 Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami:
 Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami: Pr(X 1 = 0) = 6/10, Pr(X 1 = 1) = 1/10, i gęstością: f(x) = 3/10 na przedziale (0, 1). Wobec tego Pr(X 1 + X 2 5/3) wynosi:
Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami: Pr(X 1 = 0) = 6/10, Pr(X 1 = 1) = 1/10, i gęstością: f(x) = 3/10 na przedziale (0, 1). Wobec tego Pr(X 1 + X 2 5/3) wynosi:

