Zadania ze Wstępu do Analizy Stochastycznej 1. = 0 p.n.
|
|
|
- Danuta Majewska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Zadania ze Wstępu do Analizy Stochastycznej 1 1. Znajdź rozkład zmiennej 5W 1 W 3 + W Dla jakich parametrów a i b, zmienne aw 1 W 2 oraz W 3 + bw 5 są niezależne? 3. Znajdź rozkład wektora losowego (W t1, W t2,..., W tn ) dla < t 1 < t 2 <... < t n. 4. Udowodnij, że lim t W t t = p.n. 5. Udowodnij, że następujące procesy też są procesami Wienera a) X t = W t (odbicie) b) Y t = c 1/2 W ct, c > (przeskalowanie czasu) c) Z t = tw 1/t dla t > oraz Z = (inwersja czasu) d) U t = W T +t W T, T e) V t = W t dla t T, V t = 2W T W t dla t > T, gdzie T. 6. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Wienera są nieograniczone. 7. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Wienera nie są jednostajnie ciągłe na R Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1 <... < t (n) k n = b będzie ciągiem podziałów odcinka [a, b] oraz π n := max k t (n) k t (n) k 1 oznacza średnicę π n. Udowodnij, że S n := k n k=1 W t (n) k W (n) t 2 b a w L 2 (Ω, F, P ) przy n, k 1 jeśli π n oraz S n b a p.n., jeśli n π n <. 9. Udowodnij, że prawie wszystkie trajektorie procesu Wienera mają nieskończone wahanie na każdym przedziale. 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Wienera są funkcjami nieróżniczkowalnymi w żadnym punkcie przedziału [, ). Wskazówki: a) Jeśli funkcja f jest rózniczkowalna w jakimś punkcie przedziału [, 1], to istnieje liczba M < taka, że dla odpowiednio dużych n istnieje j n 3 taka, że f((j+1)/n) f(j/n) M/n, f((j+2)/n) f((j+1)/n) M/n oraz f((j + 3)/n) f((j + 2)/n) M/n. b) Wykaż, że P( W (j+1)/n W j/n M/n, W (j+2)/n W (j+1)/n M/n, W (j+3)/n W (j+2)/n M/n) CMn 3/2 i wywioskuj stąd nieróżniczkowalność trajektorii na przedziale [, 1]. 1
2 Zadania ze Wstępu do Analizy Stochastycznej 2 1. Udowodnij, że jeśli zbiór A B(R T ), to istnieje zbiór przeliczalny T T taki, że jeśli x, y R T oraz x(t) = y(t) dla t T to x A y A. 2. Niech T = [a, b] a < t < b, wykaż, że następujące zbiory nie należą do B(R T ). i) A 1 = {x R T : sup t [a,b] x t 1}; ii) A 2 = {x R T : t x t ciągłe na [a,b] }; iii) A 3 = {x R T : lim t t x t = }: iv) A 4 = {x R T : t x t ciągłe w t }. Wykaż mierzalność tych zbiorów przy założeniu ciągłości (prawostronnej ciągłości) trajektorii tzn. wykaż, że wszystkie te zbiory po przecięciu z C(T ) (RC(T ) odp.) należą do B(R T ) C(T ) (B(R T ) RC(T ) odp.). 3. Niech T = [a, b]. Wykaż, że F = {A C(T ): A B(R T )} jest σ-ciałem zbiorów borelowskich (w metryce supremum) na C(T ). 4. Wykaż, że istnieje proces (X t ) t o przyrostach niezależnych, startujący z taki, że X t X s ma rozkład Cauchy ego z parametrem t s (proces taki nazywamy procesem Cauchy ego, bądź procesem 1-stabilnym). 5. Proces X jest modyfikacją procesu Wienera. Które z następujących własności są spełnione dla procesu X: a) niezależność przyrostów, b) stacjonarność przyrostów, c) ciągłość trajektorii, d) lim t X t t e) lim t X t t = p.n. = według prawdopodobieństwa? 6. Rozpatrzmy następujące 3 własności procesów: a) ciągłość trajektorii; b) stochastyczną ciągłość (tzn. X t P Xs gdy t s); c) ciągłość wg p-tego momentu (tzn. E X t X s p gdy t s). Jakie implikacje zachodzą między powyższymi własnościami? 2
3 Zadania ze Wstępu do Analizy Stochastycznej 3 1. Wykaż, że trajektorie procesu Wienera nie są lokalnie 1/2-hölderowskie. 2. Scentrowany proces gaussowski nazywamy ułamkowym ruchem Browna, jeśli E X t X s 2 = t s 2α (można wykazać, że taki proces istnieje dla < α < 1). Udowodnij, że ułamkowy ruch Browna ma ciągłą modyfikację. Co można powiedzieć o hölderowskości jej trajektorii? 3. Załóżmy, że T jest przedziałem i określmy: F t+ := ( F s, F t := σ F s ). s>t a) Wykaż, że filtracja F t+ jest prawostronnie ciągła, tzn. F t++ = F t+. b) Udowodnij, że jeśli F t = Ft X jest filtracją generowaną przez proces X o lewostronnie ciągłych trajektoriach, to F t = F t. c) Niech T = [, ), A F oraz X t = (t 1) + I A. Znajdź Ft X. d) Dla X jak w punkcie c) określmy τ := inf{t: X t > }. Wykaż, że τ nie jest momentem zatrzymania względem Ft X ale jest momentem zatrzymania względem Ft+. X 4. Załóżmy, że T jest przedziałem, wykaż, że: a) jeśli τ jest momentem zatrzymania, to {τ < t} F t dla wszystkich t b) jeśli {τ < t} F t dla wszystkich t, to τ jest momentem zatrzymania względem F t+. 5. Niech T = [, ), a τ będzie momentem zatrzymania, które ze zmiennych τ + 1, τ 2, (τ 1) + muszą być momentami zatrzymania? 6. Niech T = [, ), a X t procesem F t -adaptowalnym o ciągłych trajektoriach. Wykaż, że dla A otwartego τ A := inf{t: X t A} jest momentem zatrzymania względem F t+. 7. Wykaż, że jeśli τ i σ są momentami zatrzymania, to τ σ jest momentem zatrzymania, F τ σ = F τ F σ oraz zdarzenia {τ < σ}, {τ = σ} i {τ σ} należą do F τ, F σ i F τ σ. 8. Wykaż, że jeśli τ jest momentem zatrzymania, to proces X t := I [,τ) (t) jest progresywnie mierzalny. 9. Niech τ będzie momentem zatrzymania względem (F t ) t T, a (X t ) będzie procesem F t -adaptowalnym. Wykaż, że a) τ jest F τ -mierzalne b) Jeśli τ przyjmuje przeliczalnie wiele wartości, to X τ jest F τ mierzalny na zbiorze τ <. 1. Wykaż, że jeśli σ jest momentem zatrzymania, τ σ oraz τ jest F σ mierzalny, to τ jest momentem zatrzymania. 11. Wykaż, że jeśli proces X t ma niezależne przyrosty i prawostronnie ciągłe trajektorie, to dla s < t zmienna X t X s jest niezależna od F X s+. s<t 3
4 Zadania ze Wstępu do Analizy Stochastycznej 4 1. Załóżmy, że N t jest procesem Poissona, tzn. procesem o prawostronnie ciągłych trajektoriach takim, że N =, N ma przyrosty niezależne, oraz N t N s Poiss(t s) dala t > s. Wykaż, że (N t λt) t oraz ((N t λt) 2 λt) t są martyngałami względem (Ft N ) t 2. Wykaż, że (exp(λw t λ2 t 2 ), F W t ) t jest martyngałem dla dowolnego λ R. 3. Niech W t będzie n-wymiarowym procesem Wienera, a f funkcją harmoniczną na R n taką, że E f(w t ) < dla wszystkich t. Wykaż, że (f(w t ), Ft W ) t jest martyngałem. 4. (Prawo iterowanego logarytmu dla procesu Wienera) Wykaż, że a) lim sup 2t W t t ln ln t = 1 p.n. W b) lim inf t t 2t ln ln t = 1 p.n. Wskazówki: i) Niech C > 1 oraz u > C 1/2. Wykaż, że ( P sup W t u ) 2C n ln ln C n < C n t C n+1 n i wywnioskuj stąd, że lim sup t W t 2t ln ln t u p.n. ii) Wykaż, że lim sup 2t W t W t ln ln t 1 p.n. oraz lim inf t t 2t ln ln t 1 p.n. iii) Udowodnij, że dla g N (, 1) i t >, 1 ( 1 2π t 1 ) t 3 e t2 /2 P(g t) 1 e t2 /2. 2πt iv) Wykaż, że dla C > 1 i u < 1 P(WC n W C n 1 u 1 1/C 2C n ln ln C n ) = i wywnioskuj stąd i z ii), że lim sup 2t W t t ln ln t u(1 1/C) 1/2 C 1/2 p.n. 5. Udowodnij, że a) lim sup t + W t 2t ln ln(1/t) = 1 p.n. W b) lim inf t t + = 1 p.n. 2t ln ln(1/t) 4
5 Zadania ze Wstępu do Analizy Stochastycznej 5 1. Które z podanych niżej warunków implikują jednostajną całkowalność ciągu X n : a) sup n E X n <, b) sup n E X n 2 <, c) E sup n X n <, d) zbieżność X n w L 1, e) zbieżność X n p.n.? 2. Wykaż, że martyngał M t = exp(λw t λ 2 t/2) jest zbieżny p.n. i znajdź jego granicę. Czy jest on zbieżny w L 1? 3. Niech W t = (W 1 t,..., W d t ) będzie d wymiarowym procesem Wienera, a x R d oraz d > 2. a) Wykaż, że W t x 2 d jest nieujemnym nadmartyngałem. b) Udowodnij, że W t x 2 d zbiega przy t do według prawdopodobieństwa i p.n. i wywnioskuj stąd, że lim t W t = p.n.. c) Wykaż, że dla prawostronnie ciągłego nadmartyngału (X t ) t a zachodzi λ> λp(sup t a d) Wykaż, że P( t> W t = x ) =. X t λ) sup EXt + EX a. t 4. Niech τ będzie momentem zatrzymania względem F W t. a) Wykaż, że (W τ n, F τ n ) n=1 jest martyngałem. b) Udowodnij, że jeśli Eτ <, to E sup n W 2 τ n <. c) Wykaż, że jeśli Eτ <, to EW 2 τ = Eτ i EW τ =. 5. Niech W t będzie jednowymiarowym procesem Wienera oraz τ a := inf{t > : W t = a}, τ a := inf{t > : W t = a}. Rozpatrując martyngały W t i Wt 2 t wykaż, że a) τ a < p.n. dla wszystkich a R, b) P(τ a < τ b ) = b a+b dla a, b >, c) E τ a = a 2 dla a, d) Eτ a τ b = ab dla a, b >, e) Eτ a = dla wszystkich a. 6. Rozpatrując martyngały Mt λ = exp(λw t λ 2 t/2) oraz Nt λ = (Mt λ + Mt λ )/2 wykaż, że przy oznaczeniach poprzedniego zadania, dla wszystkich a, λ, a) Ee λτa = e a 2λ, b) Ee λ τa = (cosh(a 2λ)) 1. 5
6 7. Załóżmy, że h jest niemalejącą funkcją ciągłą na przedziale [a, b]. Udowodnij, że a) Jeśli g ma wahanie skończone, to g h też ma wahanie skończone b) Jeśli h(b) fdg istnieje, to h(a) b a f(h(t))dg(h(t)) = h(b) h(a) f(s)dg(s). 8. Załóżmy, że f, g, h: [a, b] R, przy czym f i g są ciągłe, a h ma wahanie skończone. Udowodnij, że a) H(x) = x g(t)dh(t) ma wahanie skończone na [a, b]. a b) b a fdh = b a fgdh. 9. Wykaż, że dla dowolnej funkcji ciągłej f o wahaniu skończonym na [a, b] zachodzi b a f(s)df(s) = 1 2 (f 2 (b) f 2 (a)). 1. Oblicz granice w L 2 (Ω) przy n a) n 1 k= W tk/n(w t(k+1)/n W tk/n ) b) n 1 k= W t(k+1)/n(w t(k+1)/n W tk/n ). 6
7 Zadania ze Wstępu do Analizy Stochastycznej 6 1. Oblicz Cov( s h 1(t)dW t, s h 2(t)dW t ) dla h 1, h 2 L 2 ([, s]). 2. Niech C p := (E W 1 p ) 1/p. Wykaż, że dla < p <, przekształcenie h Cp 1 h(t)dw t jest izometrycznym włożeniem L 2 ([, T ]) w L p (Ω). T 3. Wykaż, że dla u < t i h L 2 ([, t]) zachodzi u h(s)dw s = 4. Wykaż, że dla h C 1 [, t] zachodzi 5. Wykaż, że proces h(s)dw s = h(t)w t h1 [,u] (s)dw s p.n. h (s)w s ds p.n. { (1 t) 1 Y t = 1 s dw s t < 1 t = 1 ma takie same rozkłady skończenie wymiarowe co proces Z t = W t tw 1 (most Browna). 7
8 Zadania ze Wstępu do Analizy Stochastycznej 7 1. Wykaż, że jeśli X L 2 T, t s T oraz ξ jest ograniczoną zmienną losową F t mierzalną to ξxi (t,s] L 2 T oraz s t ξxdw = ξ s XdW (Uwaga: t s t XdW definiujemy jako T 1 (s,t]xdw ). 2. Wykaż, że jeśli < t 1 <... < t m < T oraz ξ k są zmiennymi losowymi w L 2 (Ω), F tk mierzalnymi to proces X := m 1 k=1 ξ k1 (tk,t k+1 ] należy do L 2 T oraz XdW = m 1 k=1 ξ k(w tk+1 t W tk t). 3. Załóżmy, że X jest procesem prognozowalnym, ciągłym w L 2 (tzn. t X t jest ciągła z [, T ] w L 2 (Ω)). Wykaż, że wówczas X L 2 T oraz dla dowolnego ciągu podziałów = t (n) t (n) 1... t (n) k n = T o średnicy zbiegającej do zera zachodzi dla t T k n 1 k= w L 2 (Ω) przy n. 4. Oblicz W sdw s. X (n) t (W (n) k t k+1 T W (n) t ) XdW k 5. Niech τ będzie momentem zatrzymania takim, że Eτ <. Wykaż, że 1 [,τ] L 2 oraz 1 [,τ] (s)dw s = W τ. Wywnioskuj stąd, że EW τ = oraz EWτ 2 = Eτ. 6. Dla a, b > określmy τ := inf{t : W t = a b + t}. Wykaż, że τ < p.n. oraz Eτ < wtedy i tylko wtedy gdy a < 1. Ponadto dla a < 1, Eτ = a2 b 1 a 2. 7* Niech ξ będzie zmienną losową o skończonej wariancji taką, że Eξ =. Wykaż, że istnieje moment zatrzymania τ taki, że W τ ma ten sam rozkład co ξ oraz Eτ = Eξ Załóżmy, że M jest adaptowalnym, prawostronnie ciągłym procesem takim, że M = i dla wszystkich t, E M t <. Wykaż, że M jest martyngałem wtedy i tylko wtedy gdy EM τ = dla wszystkich ograniczonych momentów zatrzymania τ. 8
9 Zadania ze Wstępu do Analizy Stochastycznej 8 1. Niech A będzie pewną klasą procesów adaptowalnych na [, T ) taką, że jeśli X A to X τ A dla dowolnego momentu zatrzymania τ. Przez A loc oznaczamy wówczas klasę tych procesów adaptowalnych na [, T ) dla których istnieje rosnący ciąg momentów zatrzymania τ n taki, że τ n T oraz X τn A dla wszystkich n. a) Wykaż, że jeśli X A loc to X τ A loc dla dowolnego momentu zatrzymania τ b) Wykaż, że (A loc ) loc = A loc c) Wykaż, że jeśli A jest liniowa to A loc też jest liniowa. 2. Wykaż, że M M M c loc wtedy i tylko wtedy, gdy M M M 2,c loc. 3. a) Wykaż, że każdy ograniczony ciągły martyngał lokalny jest martyngałem. b) Wykaż, że każdy nieujemny całkowalny ciągły martyngał lokalny jest nadmartyngałem. c*) Podaj przykład nieujemnego całkowalnego ciągłego martyngału lokalnego, który nie jest martyngałem. 4. Niech X Λ 2 T, t < s T oraz ξ będzie zmienną losową F t 1 mierzalną (niekoniecznie ograniczoną). Wykaż, że ξx1 (t,s] Λ 2 T oraz s t ξxdw = ξ s t XdW. 5. Niech M M 2,c loc oraz X Λ2 T (M). Wykaż, że dla dowolnego momentu zatrzymania τ zachodzi ( XdM) τ = XdM τ = X1 [,τ] dm = X1 [,τ] dm τ. W szczególności jeśli procesy X i Y pokrywają się na przedziale [, τ], to ( XdM) τ = ( Y dm) τ. 6. Niech X będzie martyngałem lokalnym takim, że X t Y dla wszystkich t oraz EY <. Wykaż, że X jest martyngałem. 7. Wykaż, że każdy ciągły martyngał lokalny M = (M t ) t<t, którego trajektorie mają skończone wahanie na każdym przedziale [, t] jest stale równy M. 9
10 Zadania ze Wstępu do Analizy Stochastycznej 9 1. Niech M = Wt 2 dw t. Oblicz EMs 2. Jak wygląda przestrzeń L 2 T (M)? Czy należy do tej przestrzeni? W 1 t 2. Oblicz W 1, W 2, gdzie W 1, W 2 są niezależnymi procesy Wienera. 3. Udowodnij, że a) M, M = M = M, b) M, N = N, M, c) M M, N = M, N N = M M, N N = M, N, d) (N, M) M, N jest przekształceniem dwuliniowym, e) M τ, N τ = M τ, N = M, N τ = M, N τ, f) Jeśli M M 2,c loc, X, Y Λ2 T (M) oraz N 1 = X dm, N 2 = Y dm, to N 1, N 2 = XY d M. g) Jeśli M 1, M 2 M 2,c loc, X Λ2 T (M 1) Λ 2 T (M 2) oraz N i = X dm i to N 1, N 2 = X 2 d M 1, M Wykaż, że a) M, N M N b) Wah [s,t] ( M, N ) 1 2 [ M t M s + N t N s ]. 5. Niech M, N M c loc oraz X Λ2 T (M) Λ2 T (N). Uzasadnij, że X Λ 2 T (am + bn) dla a, b R oraz Xd(aM + bn) = a XdM + b XdN. 1
11 1. Określamy Zadania ze Wstępu do Analizy Stochastycznej 1 S n (α) = 3n 1 k=n (k+1)/n k/n W 4 s dw s α. a) Wykaż, że ciąg S n (2) jest zbieżny w L 1 i zidentyfikuj jego granicę. b) Co można powiedzieć o zbieżności według prawdopodobieństwa ciągu S n (α) dla α 2? 2. Wykaż, że dla dowolnego procesu M M c loc, X ΛT 2 (M) oraz momentu zatrzymania τ T, E sup t<τ ( ) 2 τ X dm 4E Xs 2 d M s. 3. Załóżmy, że M M c loc, M = zaś τ jest momentem zatrzymania takim, że E M τ <. Wykaż, że M τ jest martyngałem. 4. Korzystając ze wzoru na całkowanie przez części przedstaw W 2 s dw s jako wyrażenie nie zawierające całek stochastycznych. 5. Załóżmy, że X jest procesem ciągłym i adaptowalnym, zaś Z ciągłym semimartyngałem. Wykaż, że jeśli t < T, Π n = (t (n), t(n) 1,..., t(n) k n ) jest ciągiem podziałów [, t] takim, że = t (n) t (n) 1... t (n) k n = t oraz diam(π n ), to k n 1 k= X (n) t (Z (n) k t k+1 Z (n) t ) k X s dz s według prawdopodobieństwa. 11
12 Zadania ze Wstępu do Analizy Stochastycznej Korzystając ze wzoru Itô oblicz W 2 t oraz W t, e Wt. 2. Niech f będzie funkcją klasy C 2 na R 2, korzystając z dwuwymiarowego wzoru Itô oblicz df(t, W t ) oraz df(tw t ). 3. Znajdź proces (A t ) t, którego trajektorie mają wahanie ograniczone na przedziałach skończonych taki, że A = oraz proces X t = sin(2w t 3t) A t jest martyngałem lokalnym. Wykaż, że X t jest martyngałem oraz EX 2 t 4t. 4. Niech Z t = exp(λw t λ 2 t/2). Wykaż, że dz t = λz t dw t tzn. Z t = 1 + λ Z sdw s. 5. Wykaż, że ciąg S n = 3n k=1 k n W 3 k/n (W k/n W (k 1)/n ) jest zbieżny według prawdopodobieństwa i znajdź jego granicę. 6. Niech M będzie ciągłym martyngałem lokalnym. Wykaż, że proces N t = exp(m t 1 2 M t) jest ciągłym martyngałem lokalnym oraz nadmartyngałem. Ponadto jeśli M jest ograniczony, to N jest martyngałem. 7. Niech g : R d R będzie funkcją klasy C 2, G zbiorem otwartym ograniczonym w R d oraz x G. Określmy τ := inf{t: W t + x / G}. Korzystając ze wzoru Itô wykaż, że jeśli g jest harmoniczna w G to g(w τ t +x) jest martyngałem. Pokaż, że wystarczy zakładać, iż g jest C 2 w pewnym otoczeniu domknięcia G. 8. Wykaż, że dla 3-wymiarowego ruchu Browna W t i a R 3, a proces X t = W t a 1 jest martyngałem lokalnym, ale nie jest martyngałem. Ponadto X t jest nadmartyngałem oraz zbiega do w L 1 i prawie na pewno. 9. Wykaż, że 2-wymiarowego ruchu Browna W t i a R 2, a proces X t = ln W t a jest martyngałem lokalnym. Wywnioskuj stąd, że z prawdopodobieństwem 1 proces W t omija punkt a, ale trajektoria procesu jest dowolnie bliska punktu a. 12
13 Zadania ze Wstępu do Analizy Stochastycznej Załóżmy, że W = (W (1), W (2), W (3) ) jest trójwymiarowym procesem Wienera oraz X t := sin(w (3) t )dw (1) t + Wykaż, że X jest procesem Wienera. cos(w (3) t )dw (2) t. 2. Wykaż, że dla a > proces X t = ξe bt + a eb(t s) dw s jest jedynym rozwiązaniem równania dx t = bx t dt+ adw t z warunkiem początkowym X = ξ. Jeśli b < oraz ξ ma rozkład N (, a 2b ) to X t jest procesem stacjonarnym (proces Ornsteina-Uhlenbecka) 3. i) Wykaż, że dla x, σ, b R istnieje dokładnie jeden proces X = (X t ) t taki, że X t = x + σ X s dw s + b X s ds. Ponadto sup t u EX 2 t < dla u <. ii) Oblicz EX t. iii) Znajdź stochastyczne równania różniczkowe spełnione przez X 2 + t i e X. 4. Wykaż, że rozwiązanie równania dx = e X dw 1 2 e 2X dt eksploduje w skończonym czasie. (Wsk. Rozpatrz proces Y = e X ). 5. Niech W = (W 1,..., W d ) będzie d-wymiarowym ruchem Browna, d 2 oraz R t := W t (R t jest nazywane procesem Bessela). Wykaż, że a) B t := d W (j) s j=1 R s dw s (j) jest jednowymiarowym procesem Wienera; b) R t = d 1 2R s ds + B t 6. Znajdź taką miarę probabilistyczną Q na (Ω, F W 1 ), by proces (W t+2t 4 ) t 1 był procesem Wienera względem Q. 7. Niech T <, U będzie procesem Wienera na (Ω, F, P), ( Z t = exp b(s, U s )du s 1 2 ) b 2 (s, U s )ds, W t := U t b(s, U s )ds. Stosując twierdzenie Girsanowa wykaż, że jeśli EZ T = 1 to istnieje miara probabilistyczna Q T taka, że na przestrzeni probabilistycznej (Ω, F, Q T ) para (W t ) t T jest procesem Wienera oraz du t = b(t, U t )dt + dw t, t T, U =. (1) 13
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1
 Zadania z Procesów Stochastycznych 1 Definicja Procesem Poissona z parametrem (intensywnością) λ > 0 nazywamy proces stochastyczny N = (N t ) t 0 taki, że N 0 = 0; (P0) N ma przyrosty niezależne; (P1)
Zadania z Procesów Stochastycznych 1 Definicja Procesem Poissona z parametrem (intensywnością) λ > 0 nazywamy proces stochastyczny N = (N t ) t 0 taki, że N 0 = 0; (P0) N ma przyrosty niezależne; (P1)
}, gdzie a = t (n) )(f(t(n) k. ) f(t(n) k 1 ) 1+δ = 0,
 Zadania z Procesów Stochastycznych II - 1 1. Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1
Zadania z Procesów Stochastycznych II - 1 1. Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1
Teoria ze Wstępu do analizy stochastycznej
 eoria ze Wstępu do analizy stochastycznej Marcin Szumski 22 czerwca 21 1 Definicje 1. proces stochastyczny - rodzina zmiennych losowych X = (X t ) t 2. trajektoria - funkcja (losowa) t X t (ω) f : E 3.
eoria ze Wstępu do analizy stochastycznej Marcin Szumski 22 czerwca 21 1 Definicje 1. proces stochastyczny - rodzina zmiennych losowych X = (X t ) t 2. trajektoria - funkcja (losowa) t X t (ω) f : E 3.
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
Zadania z Rachunku Prawdopodobieństwa III - 1
 Zadania z Rachunku Prawdopodobieństwa III - 1 Funkcją tworzącą momenty (transformatą Laplace a) zmiennej losowej X nazywamy funkcję M X (t) := Ee tx, t R. 1. Oblicz funkcję tworzącą momenty zmiennych o
Zadania z Rachunku Prawdopodobieństwa III - 1 Funkcją tworzącą momenty (transformatą Laplace a) zmiennej losowej X nazywamy funkcję M X (t) := Ee tx, t R. 1. Oblicz funkcję tworzącą momenty zmiennych o
Wstęp do Analizy Stochastycznej
 Matematyka stosowana Wstęp do Analizy Stochastycznej Rafał Latała R.Latala@mimuw.edu.pl http://www.mimuw.edu.pl/~rlatala Uniwersytet Warszawski, 211 Streszczenie. Ogólna teoria procesów, proces Wienera.
Matematyka stosowana Wstęp do Analizy Stochastycznej Rafał Latała R.Latala@mimuw.edu.pl http://www.mimuw.edu.pl/~rlatala Uniwersytet Warszawski, 211 Streszczenie. Ogólna teoria procesów, proces Wienera.
4 Kilka klas procesów
 Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
21 maja, Mocna własność Markowa procesu Wienera. Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Wstęp do Analizy Stochastycznej
 Wstęp do Analizy Stochastycznej Rafał Latała 6 września 21 Poniższy tekst zawiera notatki do wykładów ze Wstępu do Analizy Stochastycznej, prowadzonego w semestrze wiosennym 21 roku. Gwiazdkami oznaczono
Wstęp do Analizy Stochastycznej Rafał Latała 6 września 21 Poniższy tekst zawiera notatki do wykładów ze Wstępu do Analizy Stochastycznej, prowadzonego w semestrze wiosennym 21 roku. Gwiazdkami oznaczono
F t+ := s>t. F s = F t.
 M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω)
 PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
Zadania z Rachunku Prawdopodobieństwa II Podaj przykład rozkładów prawdopodobieństwa µ n, µ, takich, że µ n µ,
 Zadania z Rachunku Prawdopodobieństwa II -. Udowodnij, że dla dowolnych liczb x n, x, δ xn δ x wtedy i tylko wtedy, gdy x n x.. Wykaż, że n n k= δ k/n λ, gdzie λ jest miarą Lebesgue a na [, ].. Podaj przykład
Zadania z Rachunku Prawdopodobieństwa II -. Udowodnij, że dla dowolnych liczb x n, x, δ xn δ x wtedy i tylko wtedy, gdy x n x.. Wykaż, że n n k= δ k/n λ, gdzie λ jest miarą Lebesgue a na [, ].. Podaj przykład
Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik. Historia
 1 Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik Całka stochastyczna ( t ) H s dx s = H X. t Historia K. Itô (1944) konstrukcja całki stochastycznej
1 Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik Całka stochastyczna ( t ) H s dx s = H X. t Historia K. Itô (1944) konstrukcja całki stochastycznej
Ośrodkowość procesów, proces Wienera. Ośrodkowość procesów, proces Wienera Procesy Stochastyczne, wykład, T. Byczkowski,
 Procesy Stochastyczne, wykład, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 27 luty, 2012 Ośrodkowość procesów Dalej zakładamy, że (Ω, Σ, P) jest zupełną przestrzenią miarową. Definicja.
Procesy Stochastyczne, wykład, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 27 luty, 2012 Ośrodkowość procesów Dalej zakładamy, że (Ω, Σ, P) jest zupełną przestrzenią miarową. Definicja.
2. P (E) = 1. β B. TSIM W3: Sygnały stochastyczne 1/27
 SYGNAŁY STOCHASTYCZNE Przestrzeń probabilistyczna i zmienna losowa Definicja Przestrzenią probabilistyczną (doświadczeniem) nazywamy trójkę uporządkowaną (E, B, P ), gdzie: E przestrzeń zdarzeń elementarnych;
SYGNAŁY STOCHASTYCZNE Przestrzeń probabilistyczna i zmienna losowa Definicja Przestrzenią probabilistyczną (doświadczeniem) nazywamy trójkę uporządkowaną (E, B, P ), gdzie: E przestrzeń zdarzeń elementarnych;
3. Podać przykład rozkładów prawdopodobieństwa µ n, µ, takich, że µ n µ,
 Zadania z Rachunku Prawdopodobieństwa II - Mówimy, że i) ciąg miar probabilistycznych µ n zbiega słabo do miary probabilistycznej µ (ozn. µ n µ), jeśli fdµ n fdµ dla dowolnej funkcji ciągłej ograniczonej
Zadania z Rachunku Prawdopodobieństwa II - Mówimy, że i) ciąg miar probabilistycznych µ n zbiega słabo do miary probabilistycznej µ (ozn. µ n µ), jeśli fdµ n fdµ dla dowolnej funkcji ciągłej ograniczonej
Procesy stochastyczne 2.
 Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Seria 1. Zbieżność rozkładów
 Seria Zbieżność rozkładów We wszystkich poniższych zadaniach (E, ρ) jest przestrzenią metryczną Wykazać, że dla dowolnych x, x n, δ xn δ x wtedy i tylko wtedy, gdy x n x Sprawdzić, że n nk= δ k n λ, gdzie
Seria Zbieżność rozkładów We wszystkich poniższych zadaniach (E, ρ) jest przestrzenią metryczną Wykazać, że dla dowolnych x, x n, δ xn δ x wtedy i tylko wtedy, gdy x n x Sprawdzić, że n nk= δ k n λ, gdzie
Zadania z Analizy Funkcjonalnej I Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?
 Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi? a) X = R, d(x, y) = arctg x y ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i
Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi? a) X = R, d(x, y) = arctg x y ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i
Zadania z Rachunku Prawdopodobieństwa II Podać przykład rozkładów prawdopodobieństwa µ n, µ, takich, że µ n µ,
 Zadania z Rachunku Prawdopodobieństwa II -. Udowodnij, że dla dowolnych liczb x n, x, δ xn δ x wtedy i tylko wtedy, gdy x n x.. Wykaż, że n n k= δ k/n λ, gdzie λ jest miarą Lebesgue a na [, ].. Podać przykład
Zadania z Rachunku Prawdopodobieństwa II -. Udowodnij, że dla dowolnych liczb x n, x, δ xn δ x wtedy i tylko wtedy, gdy x n x.. Wykaż, że n n k= δ k/n λ, gdzie λ jest miarą Lebesgue a na [, ].. Podać przykład
Zadania z Rachunku Prawdopodobieństwa III - 1
 Zadania z Rachunku Prawdopodobieństwa III - 1 1. Oblicz funkcję tworzącą momenty zmiennych o następujących rozkładach: a) symetryczny dwupunktowy; b) dwumianowy z parametrami n, p; c) Poissona z parametrem
Zadania z Rachunku Prawdopodobieństwa III - 1 1. Oblicz funkcję tworzącą momenty zmiennych o następujących rozkładach: a) symetryczny dwupunktowy; b) dwumianowy z parametrami n, p; c) Poissona z parametrem
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
O procesie Wienera. O procesie Wienera. Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Proces Wienera. Ruch Browna. Ułamkowe ruchy Browna
 Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Ruch 1 {X t } jest martyngałem dokładnie wtedy, gdy E(X t F s ) = X s, s, t T, s t. Jeżeli EX 2 (t) < +, to E(X t F s ) jest rzutem ortogonalnym zmiennej
Procesy stochastyczne Wykład XV, 15 czerwca 2015 r. Ruch 1 {X t } jest martyngałem dokładnie wtedy, gdy E(X t F s ) = X s, s, t T, s t. Jeżeli EX 2 (t) < +, to E(X t F s ) jest rzutem ortogonalnym zmiennej
Zadania z RP 2. seria Podać przykład rozkładów prawdopodobieństwa µ n, µ, takich, że µ n
 Zadania z RP 2. seria 1. 1. Dla x R n, niech δ x oznacza miarę Diraca, skupioną w punkcie x. Wykazać, że dla dowolnego ciągu x n R n zachodzi δ xn δ x wtedy i tylko wtedy, gdy x n x. 2. Podać przykład
Zadania z RP 2. seria 1. 1. Dla x R n, niech δ x oznacza miarę Diraca, skupioną w punkcie x. Wykazać, że dla dowolnego ciągu x n R n zachodzi δ xn δ x wtedy i tylko wtedy, gdy x n x. 2. Podać przykład
Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga
 RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
Zadania z Analizy Funkcjonalnej I Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?
 Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?. a) X = R, x = arctg x ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i y i ;
Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?. a) X = R, x = arctg x ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i y i ;
Wykład 11: Martyngały: definicja, twierdzenia o zbieżności
 RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu.
 Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu. A Teoria Definicja A.1. Niech (Ω, F, P) będzie przestrzenią probabilistyczną. Zmienną losową określoną na przestrzeni Ω nazywamy dowolną
Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu. A Teoria Definicja A.1. Niech (Ω, F, P) będzie przestrzenią probabilistyczną. Zmienną losową określoną na przestrzeni Ω nazywamy dowolną
Stochastyczne równania różniczkowe, studia II stopnia
 Stochastyczne równania różniczkowe, studia II stopnia Niech W t (ewentualnie W, W (t)), t oznacza proces Wienera oraz niech W = Niech W = (W, W 2,, W n ) oznacza n-wymiarowy proces Wienera Pokazać, że
Stochastyczne równania różniczkowe, studia II stopnia Niech W t (ewentualnie W, W (t)), t oznacza proces Wienera oraz niech W = Niech W = (W, W 2,, W n ) oznacza n-wymiarowy proces Wienera Pokazać, że
Jak rzucać losowe spojrzenia na ruch Browna by w nim wszystko dojrzeć
 Jak rzucać losowe spojrzenia na ruch Browna by w nim wszystko dojrzeć Jan Ob lój Uniwersytet Warszawski Université Paris 6 Konwersatorium IMPAN, Listopad 2004 p.1/22 Plan referatu 1. Wstępne definicje
Jak rzucać losowe spojrzenia na ruch Browna by w nim wszystko dojrzeć Jan Ob lój Uniwersytet Warszawski Université Paris 6 Konwersatorium IMPAN, Listopad 2004 p.1/22 Plan referatu 1. Wstępne definicje
Zadania do Rozdziału X
 Zadania do Rozdziału X 1. 2. Znajdź wszystkie σ-ciała podzbiorów X, gdy X = (i) {1, 2}, (ii){1, 2, 3}. (b) Znajdź wszystkie elementy σ-ciała generowanego przez {{1, 2}, {2, 3}} dla X = {1, 2, 3, 4}. Wykaż,
Zadania do Rozdziału X 1. 2. Znajdź wszystkie σ-ciała podzbiorów X, gdy X = (i) {1, 2}, (ii){1, 2, 3}. (b) Znajdź wszystkie elementy σ-ciała generowanego przez {{1, 2}, {2, 3}} dla X = {1, 2, 3, 4}. Wykaż,
Przykład 1 W przypadku jednokrotnego rzutu kostką przestrzeń zdarzeń elementarnych
 Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Prawdopodobieństwo i statystyka
 Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
Literatura. Leitner R., Zacharski J., Zarys matematyki wyŝszej dla studentów, cz. III.
 Literatura Krysicki W., Bartos J., Dyczka W., Królikowska K, Wasilewski M., Rachunek Prawdopodobieństwa i Statystyka Matematyczna w Zadaniach, cz. I. Leitner R., Zacharski J., Zarys matematyki wyŝszej
Literatura Krysicki W., Bartos J., Dyczka W., Królikowska K, Wasilewski M., Rachunek Prawdopodobieństwa i Statystyka Matematyczna w Zadaniach, cz. I. Leitner R., Zacharski J., Zarys matematyki wyŝszej
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty
 WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 4 / 9 Przekształcenia zmiennej losowej X
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 4 / 9 Przekształcenia zmiennej losowej X
O pewnych klasach funkcji prawie okresowych (niekoniecznie ograniczonych)
 (niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
(niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
PEWNE FAKTY Z RACHUNKU PRAWDOPODOBIEŃSTWA
 PEWNE FAKTY Z RACHUNKU PRAWDOPODOBIEŃSTWA 1. Trójkę (Ω, F, P ), gdzie Ω, F jest σ-ciałem podzbiorów Ω, a P jest prawdopodobieństwem określonym na F, nazywamy przestrzenią probabilistyczną. 2. Rodzinę F
PEWNE FAKTY Z RACHUNKU PRAWDOPODOBIEŃSTWA 1. Trójkę (Ω, F, P ), gdzie Ω, F jest σ-ciałem podzbiorów Ω, a P jest prawdopodobieństwem określonym na F, nazywamy przestrzenią probabilistyczną. 2. Rodzinę F
Wykład 3 Jednowymiarowe zmienne losowe
 Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Jednowymiarowa zmienna losowa
 1 Jednowymiarowa zmienna losowa Przykład Doświadczenie losowe - rzut kostką do gry. Obserwujemy ilość wyrzuconych oczek. Teoretyczny model eksperymentu losowego - przestrzeń probabilistyczna (Ω, S, P ),
1 Jednowymiarowa zmienna losowa Przykład Doświadczenie losowe - rzut kostką do gry. Obserwujemy ilość wyrzuconych oczek. Teoretyczny model eksperymentu losowego - przestrzeń probabilistyczna (Ω, S, P ),
Prawdopodobieństwo i statystyka
 Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
WYKŁAD Z ANALIZY MATEMATYCZNEJ I. dr. Elżbieta Kotlicka. Centrum Nauczania Matematyki i Fizyki
 WYKŁAD Z ANALIZY MATEMATYCZNEJ I dr. Elżbieta Kotlicka Centrum Nauczania Matematyki i Fizyki http://im0.p.lodz.pl/~ekot Łódź 2006 Spis treści 1. CIĄGI LICZBOWE 2 1.1. Własności ciągów liczbowych o wyrazach
WYKŁAD Z ANALIZY MATEMATYCZNEJ I dr. Elżbieta Kotlicka Centrum Nauczania Matematyki i Fizyki http://im0.p.lodz.pl/~ekot Łódź 2006 Spis treści 1. CIĄGI LICZBOWE 2 1.1. Własności ciągów liczbowych o wyrazach
1. Struktury zbiorów 2. Miara 3. Miara zewnętrzna 4. Miara Lebesgue a 5. Funkcje mierzalne 6. Całka Lebesgue a. Analiza Rzeczywista.
 Literatura P. Billingsley, Miara i prawdopodobieństwo, PWN, Warszawa 1997, P. R. Halmos, Measure theory, Springer-Verlag, 1994, W, Kołodziej, naliza matematyczna, PWN, Warszawa 1978, S. Łojasiewicz, Wstęp
Literatura P. Billingsley, Miara i prawdopodobieństwo, PWN, Warszawa 1997, P. R. Halmos, Measure theory, Springer-Verlag, 1994, W, Kołodziej, naliza matematyczna, PWN, Warszawa 1978, S. Łojasiewicz, Wstęp
Procesy stochastyczne
 Procesy stochastyczne 1 Co to jest proces stochastyczny Będziemy zakładać w tej książce, że dana jest przestrzeń probabilistyczna (Ω, F, P ). Definicja 1.1 Procesem stochastycznym nazywamy zbiór zmiennych
Procesy stochastyczne 1 Co to jest proces stochastyczny Będziemy zakładać w tej książce, że dana jest przestrzeń probabilistyczna (Ω, F, P ). Definicja 1.1 Procesem stochastycznym nazywamy zbiór zmiennych
Rozdział 1. Wektory losowe. 1.1 Wektor losowy i jego rozkład
 Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
28 maja, Problem Dirichleta, proces Wienera. Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Zadania z Analizy Funkcjonalnej I* - 1
 Zadania z Analizy Funkcjonalnej I* - 1 1. Która z następujących przestrzeni jest przestrzenią Banacha w normie supremum: C(R); C ogr (R) przestrzeń funkcji ciągłych ograniczonych; C zw (R) przestrzeń funkcji
Zadania z Analizy Funkcjonalnej I* - 1 1. Która z następujących przestrzeni jest przestrzenią Banacha w normie supremum: C(R); C ogr (R) przestrzeń funkcji ciągłych ograniczonych; C zw (R) przestrzeń funkcji
Optymalne stałe w nierówności typu LlogL dla ciągłych martyngałów
 Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Piotr Dworczak Nr albumu: 91564 Optymalne stałe w nierówności typu LlogL dla ciągłych martyngałów Praca licencjacka na kierunku MATEMATYA
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Piotr Dworczak Nr albumu: 91564 Optymalne stałe w nierówności typu LlogL dla ciągłych martyngałów Praca licencjacka na kierunku MATEMATYA
Procesy stochastyczne
 Wykład I: Istnienie procesów stochastycznych 21 lutego 2017 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane
Wykład I: Istnienie procesów stochastycznych 21 lutego 2017 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane
jest ciągiem elementów z przestrzeni B(R, R)
 Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
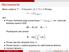 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Prawdopodobieństwo i statystyka
 Wykład V: Zmienne losowe i ich wartości oczekiwane 25 października 2017 Definicja zmiennej losowej Definicja Zmienne losowa to charakterystyka liczbowa wyniku eksperymentu losowego. Zmienne losowa na przestrzeni
Wykład V: Zmienne losowe i ich wartości oczekiwane 25 października 2017 Definicja zmiennej losowej Definicja Zmienne losowa to charakterystyka liczbowa wyniku eksperymentu losowego. Zmienne losowa na przestrzeni
Prawdopodobieństwo i statystyka
 Wykład XIII: Prognoza. 26 stycznia 2015 Wykład XIII: Prognoza. Prognoza (predykcja) Przypuśćmy, że mamy dany ciąg liczb x 1, x 2,..., x n, stanowiących wyniki pomiaru pewnej zmiennej w czasie wielkości
Wykład XIII: Prognoza. 26 stycznia 2015 Wykład XIII: Prognoza. Prognoza (predykcja) Przypuśćmy, że mamy dany ciąg liczb x 1, x 2,..., x n, stanowiących wyniki pomiaru pewnej zmiennej w czasie wielkości
Wokół nierówności Dooba
 Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Tomasz Tkocz Nr albumu: 24957 Wokół nierówności Dooba Praca licencjacka na kierunku MATEMATYKA w ramach Międzywydziałowych Indywidualnych
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Tomasz Tkocz Nr albumu: 24957 Wokół nierówności Dooba Praca licencjacka na kierunku MATEMATYKA w ramach Międzywydziałowych Indywidualnych
Rodzinę spełniającą trzeci warunek tylko dla sumy skończonej nazywamy ciałem (algebrą) w zbiorze X.
 1 σ-ciała Definicja 1.1 (σ - ciało) σ - ciałem (σ - algebrą) w danym zbiorze X (zwanym przestrzenią) nazywamy rodzinę M pewnych podzbiorów zbioru X, spełniającą trzy warunki: 1 o M; 2 o jeśli A M, to X
1 σ-ciała Definicja 1.1 (σ - ciało) σ - ciałem (σ - algebrą) w danym zbiorze X (zwanym przestrzenią) nazywamy rodzinę M pewnych podzbiorów zbioru X, spełniającą trzy warunki: 1 o M; 2 o jeśli A M, to X
Wykłady ostatnie. Rodzinę P podzbiorów przestrzeni X nazywamy σ - algebrą, jeżeli dla A, B P (2) A B P, (3) A \ B P,
 Wykłady ostatnie CAŁKA LBSGU A Zasadnicza różnica koncepcyjna między całką Riemanna i całką Lebesgue a polega na zamianie ról przestrzeni wartości i przestrzeni argumentów przy konstrukcji sum górnych
Wykłady ostatnie CAŁKA LBSGU A Zasadnicza różnica koncepcyjna między całką Riemanna i całką Lebesgue a polega na zamianie ról przestrzeni wartości i przestrzeni argumentów przy konstrukcji sum górnych
Rachunek prawdopodobieństwa i statystyka
 Rachunek prawdopodobieństwa i statystyka Momenty Zmienna losowa jest wystarczająco dokładnie opisana przez jej rozkład prawdopodobieństwa. Względy praktyczne dyktują jednak potrzebę znalezienia charakterystyk
Rachunek prawdopodobieństwa i statystyka Momenty Zmienna losowa jest wystarczająco dokładnie opisana przez jej rozkład prawdopodobieństwa. Względy praktyczne dyktują jednak potrzebę znalezienia charakterystyk
Procesy stochastyczne
 Wykład I: Istnienie procesów stochastycznych 2 marca 2015 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane są
Wykład I: Istnienie procesów stochastycznych 2 marca 2015 Forma zaliczenia przedmiotu Forma zaliczenia Literatura 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin ustny z teorii 3 Do wykładu przygotowane są
19 marzec, Łańcuchy Markowa z czasem dyskretnym. Procesy Stochastyczne, wykład 6, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136
 Procesy Stochastyczne, wykład 6, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 19 marzec, 2012 Przykłady procesów Markowa (i). P = (p ij ) - macierz stochastyczna, tzn. p ij 0, j p ij =
Procesy Stochastyczne, wykład 6, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 19 marzec, 2012 Przykłady procesów Markowa (i). P = (p ij ) - macierz stochastyczna, tzn. p ij 0, j p ij =
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA. Piotr Wiącek
 PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Piotr Wiącek ROZKŁAD PRAWDOPODOBIEŃSTWA Jest to miara probabilistyczna określona na σ-ciele podzbiorów borelowskich pewnej przestrzeni metrycznej. σ-ciało podzbiorów
PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Piotr Wiącek ROZKŁAD PRAWDOPODOBIEŃSTWA Jest to miara probabilistyczna określona na σ-ciele podzbiorów borelowskich pewnej przestrzeni metrycznej. σ-ciało podzbiorów
Analiza Funkcjonalna - Zadania
 Analiza Funkcjonalna - Zadania 1 Wprowadzamy następujące oznaczenia. K oznacza ciało liczb rzeczywistych lub zespolonych. Jeżeli T jest dowolnym zbiorem niepustym, to l (T ) = {x : E K : x funkcja ograniczona}.
Analiza Funkcjonalna - Zadania 1 Wprowadzamy następujące oznaczenia. K oznacza ciało liczb rzeczywistych lub zespolonych. Jeżeli T jest dowolnym zbiorem niepustym, to l (T ) = {x : E K : x funkcja ograniczona}.
Robert Kowalczyk. Zbiór zadań z teorii miary i całki
 Robert Kowalczyk Zbiór zadań z teorii miary i całki 2 Zadanie 1 Pokazać, że poniższe dwie definicje σ-ciała M są równoważne: (i) Rodzinę M podzbiorów przestrzeni X nazywamy σ-ciałem jeżeli zachodzą następujące
Robert Kowalczyk Zbiór zadań z teorii miary i całki 2 Zadanie 1 Pokazać, że poniższe dwie definicje σ-ciała M są równoważne: (i) Rodzinę M podzbiorów przestrzeni X nazywamy σ-ciałem jeżeli zachodzą następujące
Modelowanie zależności. Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski
 Modelowanie zależności pomiędzy zmiennymi losowymi Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski P Zmienne losowe niezależne - przypomnienie Dwie rzeczywiste zmienne losowe X i Y
Modelowanie zależności pomiędzy zmiennymi losowymi Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski P Zmienne losowe niezależne - przypomnienie Dwie rzeczywiste zmienne losowe X i Y
5 Przegląd najważniejszych rozkładów
 5 Przegląd najważniejszych rozkładów 5. Rozkład Bernoulliego W niezmieniających się warunkach wykonujemy n razy pewne doświadczenie. W wyniku każdego doświadczenia może nastąpić zdarzenie A lub A. Zakładamy,
5 Przegląd najważniejszych rozkładów 5. Rozkład Bernoulliego W niezmieniających się warunkach wykonujemy n razy pewne doświadczenie. W wyniku każdego doświadczenia może nastąpić zdarzenie A lub A. Zakładamy,
Notatki z Analizy Matematycznej 2. Jacek M. Jędrzejewski
 Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów.
 Rachunek prawdopodobieństwa MAT1332 Wydział Matematyki, Matematyka Stosowana Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów. Warunkowa
Rachunek prawdopodobieństwa MAT1332 Wydział Matematyki, Matematyka Stosowana Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów. Warunkowa
Rozdział 1. Zmienne losowe, ich rozkłady i charakterystyki. 1.1 Definicja zmiennej losowej
 Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Zbiór możliwych wyników eksperymentu będziemy nazywać przestrzenią zdarzeń elementarnych i oznaczać Ω, natomiast
Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Zbiór możliwych wyników eksperymentu będziemy nazywać przestrzenią zdarzeń elementarnych i oznaczać Ω, natomiast
Prawa wielkich liczb, centralne twierdzenia graniczne
 , centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
, centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
Nieregularne ścieżki - między determinizmem a losowością
 Nieregularne ścieżki - między determinizmem a losowością Rafał Łochowski SGH 6. Forum Matematyków Rafał Łochowski (SGH) Nieregularne ścieżki 6. Forum Matematyków 1 / 21 Problem z nieskończonym wahaniem
Nieregularne ścieżki - między determinizmem a losowością Rafał Łochowski SGH 6. Forum Matematyków Rafał Łochowski (SGH) Nieregularne ścieżki 6. Forum Matematyków 1 / 21 Problem z nieskończonym wahaniem
Metody probabilistyczne opracowane notatki 1. Zdefiniuj zmienną losową, rozkład prawdopodobieństwa. Przy jakich założeniach funkcje: F(x) = sin(x),
 Metody probabilistyczne opracowane notatki 1. Zdefiniuj zmienną losową, rozkład prawdopodobieństwa. Przy jakich założeniach funkcje: Fx sinx, Fx a e x mogą być dystrybuantami?. Podaj twierdzenie Lindeberga
Metody probabilistyczne opracowane notatki 1. Zdefiniuj zmienną losową, rozkład prawdopodobieństwa. Przy jakich założeniach funkcje: Fx sinx, Fx a e x mogą być dystrybuantami?. Podaj twierdzenie Lindeberga
Prawdopodobieństwo i statystyka
 Wykład IV: 27 października 2014 Współczynnik korelacji Brak korelacji a niezależność Definicja współczynnika korelacji Współczynnikiem korelacji całkowalnych z kwadratem zmiennych losowych X i Y nazywamy
Wykład IV: 27 października 2014 Współczynnik korelacji Brak korelacji a niezależność Definicja współczynnika korelacji Współczynnikiem korelacji całkowalnych z kwadratem zmiennych losowych X i Y nazywamy
2 Rodziny zbiorów. 2.1 Algebry i σ - algebry zbiorów. M. Beśka, Wstęp do teorii miary, rozdz. 2 11
 M. Beśka, Wstęp do teorii miary, rozdz. 2 11 2 Rodziny zbiorów 2.1 Algebry i σ - algebry zbiorów Niech X będzie niepustym zbiorem. Rodzinę indeksowaną zbiorów {A i } i I 2 X nazywamy rozbiciem zbioru X
M. Beśka, Wstęp do teorii miary, rozdz. 2 11 2 Rodziny zbiorów 2.1 Algebry i σ - algebry zbiorów Niech X będzie niepustym zbiorem. Rodzinę indeksowaną zbiorów {A i } i I 2 X nazywamy rozbiciem zbioru X
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014
 Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Informacja o przestrzeniach Hilberta
 Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Lista zadania nr 7 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie
 Lista zadania nr 7 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
Lista zadania nr 7 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Krzysztof Rykaczewski. Szeregi
 Krzysztof Rykaczewski Spis treści 1 Definicja szeregu 2 Zbieżność szeregu 3 Kryteria zbieżności szeregów 4 Iloczyn Cauchy ego szeregów 5 Bibliografia 1 / 13 Definicja szeregu Niech dany będzie ciąg (a
Krzysztof Rykaczewski Spis treści 1 Definicja szeregu 2 Zbieżność szeregu 3 Kryteria zbieżności szeregów 4 Iloczyn Cauchy ego szeregów 5 Bibliografia 1 / 13 Definicja szeregu Niech dany będzie ciąg (a
Jeśli wszystkie wartości, jakie może przyjmować zmienna można wypisać w postaci ciągu {x 1, x 2,...}, to mówimy, że jest to zmienna dyskretna.
 Wykład 4 Rozkłady i ich dystrybuanty Dwa typy zmiennych losowych Jeśli wszystkie wartości, jakie może przyjmować zmienna można wypisać w postaci ciągu {x, x 2,...}, to mówimy, że jest to zmienna dyskretna.
Wykład 4 Rozkłady i ich dystrybuanty Dwa typy zmiennych losowych Jeśli wszystkie wartości, jakie może przyjmować zmienna można wypisać w postaci ciągu {x, x 2,...}, to mówimy, że jest to zmienna dyskretna.
Modelowanie ryzyka kredytowego Zadania 1.
 1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
Szkice do zajęć z Przedmiotu Wyrównawczego
 Szkice do zajęć z Przedmiotu Wyrównawczego Matematyka Finansowa sem. letni 2011/2012 Spis treści Zajęcia 1 3 1.1 Przestrzeń probabilistyczna................................. 3 1.2 Prawdopodobieństwo warunkowe..............................
Szkice do zajęć z Przedmiotu Wyrównawczego Matematyka Finansowa sem. letni 2011/2012 Spis treści Zajęcia 1 3 1.1 Przestrzeń probabilistyczna................................. 3 1.2 Prawdopodobieństwo warunkowe..............................
Statystyka i eksploracja danych
 Projekt pn. Wzmocnienie potencjału dydaktycznego UMK w Toruniu w dziedzinach matematyczno-przyrodniczych realizowany w ramach Poddziałania 4.1.1 Programu Operacyjnego Kapitał Ludzki Statystyka i eksploracja
Projekt pn. Wzmocnienie potencjału dydaktycznego UMK w Toruniu w dziedzinach matematyczno-przyrodniczych realizowany w ramach Poddziałania 4.1.1 Programu Operacyjnego Kapitał Ludzki Statystyka i eksploracja
1 Przestrzenie metryczne
 1 Przestrzenie metryczne Definicja 1.1 (metryka) Niech będzie niepustym zbiorem. Funkcję d: R + nazywamy metryką, jeśli spełnia warunki: 1 o d(x, y) = d(y, x) (symetria) 2 o d(x, y) + d(y, z) d(x, z) (nierówność
1 Przestrzenie metryczne Definicja 1.1 (metryka) Niech będzie niepustym zbiorem. Funkcję d: R + nazywamy metryką, jeśli spełnia warunki: 1 o d(x, y) = d(y, x) (symetria) 2 o d(x, y) + d(y, z) d(x, z) (nierówność
Teoria optymalnego stopowania
 Dodatek F Teoria optymalnego stopowania F.1. Rozkład Dooba nadmartyngałów W tym paragrafie będziemy rozpatrywać nadmartyngały, podmartyngały i procesy prognozowalne względem ustalonej filtracji (F n )
Dodatek F Teoria optymalnego stopowania F.1. Rozkład Dooba nadmartyngałów W tym paragrafie będziemy rozpatrywać nadmartyngały, podmartyngały i procesy prognozowalne względem ustalonej filtracji (F n )
Wykłady... b i a i. i=1. m(d k ) inf
 Wykłady... CŁKOWNIE FUNKCJI WIELU ZMIENNYCH Zaczniemy od konstrukcji całki na przedziale domkniętym. Konstrukcja ta jest, w gruncie rzeczy, powtórzeniem definicji całki na odcinku domkniętym w R 1. Przedziałem
Wykłady... CŁKOWNIE FUNKCJI WIELU ZMIENNYCH Zaczniemy od konstrukcji całki na przedziale domkniętym. Konstrukcja ta jest, w gruncie rzeczy, powtórzeniem definicji całki na odcinku domkniętym w R 1. Przedziałem
Wariacje na temat Twierdzenia Banacha o Indykatrysie i ich zastosowanie
 Wariacje na temat Twierdzenia Banacha o Indykatrysie i ich zastosowanie Rafał M. Łochowski Wrocław 2015 Rafał M. Łochowski Twierdzenie o indykatrysie Wrocław 2015 1 / 42 Plan odczytu 1 Twierdzenie Banacha
Wariacje na temat Twierdzenia Banacha o Indykatrysie i ich zastosowanie Rafał M. Łochowski Wrocław 2015 Rafał M. Łochowski Twierdzenie o indykatrysie Wrocław 2015 1 / 42 Plan odczytu 1 Twierdzenie Banacha
Analiza I.2*, lato 2018
 Analiza I.2*, lato 218 Marcin Kotowski 14 czerwca 218 Zadanie 1. Niech x (, 1) ma rozwinięcie binarne.x 1 x 2.... Niech dla x, 1: oraz f() = f(1) =. Pokaż, że f: f(x) = lim sup n (a) przyjmuje wszystkie
Analiza I.2*, lato 218 Marcin Kotowski 14 czerwca 218 Zadanie 1. Niech x (, 1) ma rozwinięcie binarne.x 1 x 2.... Niech dla x, 1: oraz f() = f(1) =. Pokaż, że f: f(x) = lim sup n (a) przyjmuje wszystkie
Wykład 2 Zmienne losowe i ich rozkłady
 Wykład 2 Zmienne losowe i ich rozkłady Magdalena Frąszczak Wrocław, 11.10.2017r Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe Doświadczenie
Wykład 2 Zmienne losowe i ich rozkłady Magdalena Frąszczak Wrocław, 11.10.2017r Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe Doświadczenie
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 2 i 3 Zmienna losowa
 WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 2 i 3 Zmienna losowa Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 2 i 3 1 / 19 Zmienna losowa Definicja Dana jest przestrzeń probabilistyczna
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 2 i 3 Zmienna losowa Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 2 i 3 1 / 19 Zmienna losowa Definicja Dana jest przestrzeń probabilistyczna
Zadania o numerze 4 z zestawów licencjat 2014.
 Zadania o numerze 4 z zestawów licencjat 2014. W nawiasie przy zadaniu jego występowanie w numerze zestawu Spis treści (Z1, Z22, Z43) Definicja granicy ciągu. Obliczyć granicę:... 3 Definicja granicy ciągu...
Zadania o numerze 4 z zestawów licencjat 2014. W nawiasie przy zadaniu jego występowanie w numerze zestawu Spis treści (Z1, Z22, Z43) Definicja granicy ciągu. Obliczyć granicę:... 3 Definicja granicy ciągu...
Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sp. ze stałymi kosztami za transakcje
 Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sprzedaży ze stałymi kosztami za transakcje Instytut Matematyczny PAN Problem bez stałych kosztów za transakcje (Ω, F, (F t ), P) przestrzeń
Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sprzedaży ze stałymi kosztami za transakcje Instytut Matematyczny PAN Problem bez stałych kosztów za transakcje (Ω, F, (F t ), P) przestrzeń
Twierdzenia graniczne fluktuacji procesów przebywania dla układów gałazkowych
 Publiczna obrona rozprawy doktorskiej Twierdzenia graniczne fluktuacji procesów przebywania dla układów gałazkowych Piotr Miłoś Instytut Matematyczny Polskiej Akademii Nauk 23.10.2008 Warszawa Plan 1 Układy
Publiczna obrona rozprawy doktorskiej Twierdzenia graniczne fluktuacji procesów przebywania dla układów gałazkowych Piotr Miłoś Instytut Matematyczny Polskiej Akademii Nauk 23.10.2008 Warszawa Plan 1 Układy
2.7 Przestrzenie unormowane skończenie wymiarowe
 2.7 Przestrzenie unormowane skończenie wymiarowe Rozważamy teraz przestrzenie unormowane X skończenie wymiarowe. Załóżmy, że dimx = m. Niech dalej e,e 2,...,e m będzie bazą algebraiczną tej przestrzeni
2.7 Przestrzenie unormowane skończenie wymiarowe Rozważamy teraz przestrzenie unormowane X skończenie wymiarowe. Załóżmy, że dimx = m. Niech dalej e,e 2,...,e m będzie bazą algebraiczną tej przestrzeni
Wykład 21 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej
 Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Korzystając z własności metryki łatwo wykazać, że dla dowolnych x, y, z X zachodzi
 M. Beśka, Wstęp do teorii miary, Dodatek 158 10 Dodatek 10.1 Przestrzenie metryczne Niech X będzie niepustym zbiorem. Funkcję d : X X [0, ) spełniającą dla x, y, z X warunki (i) d(x, y) = 0 x = y, (ii)
M. Beśka, Wstęp do teorii miary, Dodatek 158 10 Dodatek 10.1 Przestrzenie metryczne Niech X będzie niepustym zbiorem. Funkcję d : X X [0, ) spełniającą dla x, y, z X warunki (i) d(x, y) = 0 x = y, (ii)
P(U 1 > max{u 2,..., U 1000 } U 1 = s)dp U1 (s).
 Kolokwium poszło gorzej, niż miałem nadzieję, a lepiej, niż się obawiałem. Maksymalny wynik to 74 punkty na 20), średnia to 55,6, zaś mediana to 50. Grupy były dość równe w jednej średnia to 54,5, w drugiej
Kolokwium poszło gorzej, niż miałem nadzieję, a lepiej, niż się obawiałem. Maksymalny wynik to 74 punkty na 20), średnia to 55,6, zaś mediana to 50. Grupy były dość równe w jednej średnia to 54,5, w drugiej
zadania z rachunku prawdopodobieństwa zapożyczone z egzaminów aktuarialnych
 zadania z rachunku prawdopodobieństwa zapożyczone z egzaminów aktuarialnych 1. [E.A 5.10.1996/zad.4] Funkcja gęstości dana jest wzorem { 3 x + 2xy + 1 y dla (x y) (0 1) (0 1) 4 4 P (X > 1 2 Y > 1 2 ) wynosi:
zadania z rachunku prawdopodobieństwa zapożyczone z egzaminów aktuarialnych 1. [E.A 5.10.1996/zad.4] Funkcja gęstości dana jest wzorem { 3 x + 2xy + 1 y dla (x y) (0 1) (0 1) 4 4 P (X > 1 2 Y > 1 2 ) wynosi:
