Przykładowe zadania z Analizy Matematycznej II
|
|
|
- Laura Kania
- 8 lat temu
- Przeglądów:
Transkrypt
1 Przykładowe zadania z Analizy Matematycznej II 17 marca 2016 Prośba: Gdyby okazało się, że któreś z zadań się powtarza to proszę o info na maila. 1 Mini-zadania z teorii ( 1.1 Wyznacz prostopadłą w punkcie P 0 = y = e u sin v, z = v, (u, v) R 2. e e 2, 2, π 4 ) do powierzchni zadanej parametrycznie x = e u cos v, 1.2 Wiadomo, że funkcja y s = e x jest jednym z rozwiązań zagadnienia początkowego x (y e x )+(y e x ) = 0, y (1) = e. Wyznacz przedział na jakim jest ono jednoznaczne. 1.3 Niech H będzie powierzchnią zadaną układem równań parametrycznych x (u, v) = ue v, y (u, v) = u+v, z (u, v) = u. Wyznacz równanie prostopadłej do H w punkcie (0, 1, 0). v 1.4 Niech dane będzie pole wektorowe z x ln y P (x, y, z) := z x ln z ln y, Q(x, y, x) := zx, R (x, y, z) := y xz x+1 ln y. Zbadaj czy to pole jest potencjalne. 1.5 Oblicz a) sin 4 x; b). (4+x 2 ) Oblicz potencjał pola wektorowego P (x, y, z) := e x sin yarctg (z + 1), Q (x, y, z) := e x cos yarctg (z + 1), R (x, y, z) := ex sin y 1+(z+1) Niech E R 3 będzie połową kuli o środku S = (0, 0, 1) i promieniu 1 wyznaczoną przez nierówność x 0. Całkę F (x, y, z) dydz zamień na chałkę iterowaną we współrzędnych walcowych. E 1.8 Niech E R 3 będzie połową kuli o środku S = (0, 0, 1) i promieniu 1 wyznaczoną przez nierówność x 0. Całkę F (x, y, z) dydz zamień na chałkę iterowaną we współrzędnych r, ϕ, ψ. E 1.9 Niech dane będzie pole wektorowe z x ln y P (x, y, z) := z x ln z ln y, Q(x, y, x) := zx, R (x, y, z) := y xz x+1 ln y. Zbadaj czy to pole jest potencjalne Wiadomo, że jednym z rozwiązań zagadnienia początkowego 2y = 3e x 3 y, y (0) = 1 jest funkcja y s = e 3 2 x. Zbadaj na jakim przedziale jest ono jednoznaczne. (tylko jednoznaczność! wymagane uzasadnienie) 1.11 Oblicz 1 0 x Oblicz e x sin (πx) Oblicz sin 6 x + sin 4 x Oblicz współrzędną x 0 środka ciężkości półokręgu x 2 + y 2 = x, y 0 wiedząc, że gęstość zadana 1
2 jest wzorem ρ (x, y) = x Wyznacz równanie stycznej do powierzchni H: x = cos u cos v, y = ve u, z = u w punkcie (x 0, y 0, z 0 ) = (1, 0, 0) Wiadomo, że y s = sin t cos t jest rozwiązaniem równania y sin tdy = cos t (dy cos 2 tdt), y ( π 4 ) = 1 2. Zbadaj na jakim przedziale jest ono jednoznaczne Oblicz K ye xy + xe xy dy, gdzie K jest obrysem trójkąta A = (0, 0), B = (1, 1), C = ( 1, 1) zorientowanego zgodnie z ruchem wskazówek zegara Wyznacz równanie stycznej w punkcie (1, 1, 1) do powierzchni zadanej parametrycznie x = u + 1, y = v 1, z = 1 u 2 v Wiadomo, że rozwiązaniem cos xdy = (1 y sin x), y (π) = 0 jest funkcja y 0 (x) = sin x. Na jakim przedziale jest ono jednoznaczne? 1.20 Oblicz masę krzywej K zadanej parametrycznie x = 2 sin t cos t, y = cos 2 t sin 2 t, t 0, π 4 wiedząc, że gęstość wyraża się funkcją F (x, y) = x Wypisz przewidywaną postać rozwiązania szczególnego równania y + 2y + y = x (e x + sin (2x)) Znajdź równanie przestrzeni prostopadłej do L: x := arctgt, y := arccost, z := log (x + 1) w punkcie P 0 = (0, 0, 0) Znajdź równanie stycznej do krzywej opisanej parametrycznie x (t) := ln t, y (t) := sin π 2 t, z := cos π 2 t w punkcie (x 0, y 0, z 0 ) = (0, 1, 0). ( ) 1.24 Sprawdź czy pole wektorowe P (x, y) := ycos y, Q (x, y) := y cos y cos y ln y sin y arctgx jest poten- 1+x 2 y cjalne. 2 Całki pojedyncze 2.1 Oblicz objętość bryły obrotowej powstałej przez obrót wykresu funkcji f : 2, 3 R określonej wzorem f (x) := x 4 +3x 2 2x+3 x 3 +x 2 +2x Oblicz: π 4 sin 6 x, π 4 cos 2 x 2.3 Oblicz 8 4x 4x 2 wokół osi OX. 7 2x (2x 7)( 3 7 2x x). 2.4 Niech krzywa K określona będzie układem równań parametrycznych x (t) = 6t [ 1 + 9t + 2; y (t) = t 1; t 1 2 3, 1 ]. 3 Oblicz długość krzywej K oraz wyraź całką (bez obliczania otrzymanej całki) pole obszaru znajdującego się pomiędzy krzywą K oraz osią OX. 2.5 Oblicz: π 2 π Oblicz cos 2 x, (x 2 + 3x) ln 3 x. 1+cos x x 4 +7x 2 2x+15 x 5 +x 4 +8x 3 +8x 2 +16x Niech f : [0; 1], f (x) = 1 2 x x Oblicz pole powierzchni bocznej oraz wyraź całką (bez
3 obliczania otrzymanej całki) objętość bryły powstałej przez obrót wykresu f wokół osi OX. 2.8 Oblicz 6x 4 +11x 2 +5x. x 5 2x 4 +2x 3 4x 2 +x Oblicz długość łuku krzywej zadanej układem równań parametrycznych x = t 2, y = t4 ln t łączącego 4 punkty (x 0, y 0 ) = ( 1, 4) 1 oraz (x1, y 1 ) = (4, 8 ln 2) Oblicz 2x 2 2. x 2 +6x Oblicz pole powierzchni obszaru D ograniczonego krzywymi y 3 4y 2 3y + x = 0 oraz x = Oblicz dt. 2x 7 5 2x Oblicz pole powierzchni bocznej bryły obrotowej powstałej przez obrót wykresu funkcji f (x) = cos (2x), x π 4, π 4 dookoła osi OX (6x 2 +x+1)(x 1) x x x 4 +17x x 6 +17x 4 +63x Oblicz objętość bryły otrzymanej poprzez obrót wokół osi OX wykresu funkcji f : 0, 1 3 R zadanej wzorem f (x) := x. x Oblicz pole i obwód pętli linii x = t ln 2t + 1, y = 2t + 1, t 0, Oblicz a) b) e 2x cos ( 2 x ). 1+sin x 2.19 a) sin ( 2x ) cos (ex) ; b) 7x 2 +3x+5. x 3 +x 3 Całki wielokrotne 3.1 Oblicz objętość bryły ograniczonej walcem x 2 +y 2 = x oraz powierzchniami z = 0 i z = 1 x 2 y Niech D R 2 będzie ograniczony krzywymi y = 4 2x x 2 oraz y = 3 2x x 2. Oblicz masę profilu D jeśli wiadomo, że wykonano go z materiału o gęstości ϱ (x, y) = 0, Oblicz pole płata F (x, y) := 1 2 (x2 y 2 ) wyciętego walcem y 0, x 2 + y 2 y 3.4 Niech E będzie wielościanem o wierzchołkach ( 1, 0, 0), (1, 0, 0), ( 1, 1, 0) oraz ( 1, 0, 1). Oblicz xy (z 1) dydz. E 3.5 Niech E będzie czworokątem o wierzchołkach (0, 1), (1, 3), (0, 4) oraz ( 1, 2). Oblicz E sin(2x+y) dy. x y 3.6 Oblicz pole płata F (x, y) := 1 2 (x2 y 2 ) wyciętego walcem y x, x 2 + y 2 y. 3.7 Oblicz objętość części walca y x, x 2 +y 2 2y zawartej pomiędzy płaszczyzną z = 0 a wykresem funkcji F (x, y) := 4 x 2 y Oblicz D dy (2x y) cos 2 (0,3y 0,1x) 3.9 Oblicz D zdydz gdzie D: z 0 x, z x2 + y 2 1. gdzie D to wielokąt o wierzchołkach (3, 1), (6, 2), (7, 4) oraz (4, 3) Oblicz D ln (y + 4) dy gdzie D: x + 3 y2, x 1 2y y 2 oraz x + 3 y Oblicz D zdydz gdzie D: x2 + y 2 9, y x 0, z = 0, z = 3.
4 3.12 Oblicz D x2 + y 2 dy gdzie D: x 2 + y 2 y Oblicz D zdydz gdzie D jest czworościanem o wierzchołkach (0, 0, 0), (0, 0, 1), (1, 0, 1) oraz (0, 1, 1) Oblicz objętość bryły D: z 9 x 2 y 2, z 4 x 2 y 2, z x 2 + y Oblicz masę bryły ograniczonej płaszczyznami układu współrzędnych oraz płaszczyzną 6x+4y+3z = 12 wiedząc, że gęstość wyraża się wzorem ρ (x, y, z) := 1 x+y+z Oblicz pole części płata z = x 2 y 2 zawartej wewnątrz walca x 2 + y 2 4, y x Oblicz pole części płata F (x, y) := ln x y wyciętej walcem x2 + y 2 10x, y x Oblicz objętość słupa 2 x + y π 4 ściętego powierzchniami z = 1, z = sin4 (y+2x) cos 2 (y 2x) Oblicz całkę D z 2 x 2 + y 2, x 2 + y 2 + z 2 1. x 2 +y 2 +z 2 (x 2 +y 2 ) 3/2 dydz, gdzie D jest obszarem wyznaczonym przez A 3.20 Oblicz całkę D ln (3x + y + 100) sin2 (3x y) dy gdzie D to czworokąt o wierzchołkach A = (0, 0), B = ( 1, 3), C = ( 2, 0) oraz D = ( 1, 3) Oblicz objętość bryły otrzymanej przez obrót wykresu funkcji y := e x, x 0, 1 wokół osi OX Oblicz całkę D ln (3x + y + 100) sin2 (3x y) dy gdzie D to czworokąt o wierzchołkach A = (0, 0), B = ( 1, 3), C = ( 2, 0) oraz D = ( 1, 3) Oblicz całkę D oraz z 0. e x2 +y 2 +z 2 +1 x 2 +y 2 +z 2 dydz gdzie D jest wyznaczony nierównościami: 1 x2 + y 2 + z Oblicz całkę D x2 + y 2 dydz gdzie D jest ograniczony powierzchniami x 2 + y 2 = x, z = 0 oraz z = x 2 + y 2. 4 Równania różniczkowe 4.1 Rozwiąż równanie y = 6y 9y + 18 cos (3x) z warunkiem początkowym y (0) = 5, y (0) = y + 34y = 10y + e t 6 6t + 68t Garnek z zupą o temperaturze 40 wystawiono na dwór gdzie było 0. Po 20 minutach zupa miała 5. Podać po jakim czasie temperatura wody osiągnęła y + 34y = 10y + e t 6 6t + 68t Basen odkryty napełniono wodą o temperaturze 30, przy temperaturze 20 na dworze. Temperatura wody po 20 minutach wynosiła -10. Podać po jakim temperatura wody osiągnęła yy + 3x 2 y 2 = 12x Studenci chcieli zrobić sobie basen z wodą morską, ale przesolili i wyszło im stężenie 22%, przy którym unosili się na powierzchni wody. Zaczęli więc dolewać czystej wody z prędkością 20 l/min (nadmiar mieszaniny wylewał się z tą samą prędkością). Po jakim czasie stężenie osiągnie pożądany poziom 3%? (y ) 2 y = 1 y + y.
5 4.9 W celu zbadania zachowania szczepu bakterii umieszczono próbkę zawierającą 10 6 osobników na pożywce i całość wstawiono do podgrzewacza. Po godzinie okazało się, że liczba bakterii podwoiła się. Po jakim czasie populacja osiągnie 90% stanu nasycenia, jeśli wiadomo, że dla zastosowanej pożywki wynosi on 10 7 osobników. (uwaga: nie używać wykładniczego prawa wzrostu a tego uwzględniającego stan nasycenia) 4.10 y 2 (xdy y) = x 2 (3x 2 + 1) 4.11 Pan Bogacz wybudował niewielki basen obok swojej willi. Szybko okazało się, że w dnie są nieszczelności, którymi ucieka woda. W związku z tym zamontowano system monitorujący, który automatycznie dolewał czystą wodę tak aby przez cały czas w basenie było jej dokładnie 10m 3. W konsekwencji, stopniowo malało stężenie środka bakteriobójczego. W momencie w którym osiągnęło ono poziom 0,9kg/m 3 system monitoringu informował obsługę, a ta wrzucała jego kolejną porcję do basenu. Wiedząc, że obsługa wrzucała co 3 dni (=72h) 1kg środka bakteriobójczego, oblicz z jaką prędkością uciekała woda y + 25y = 50x, y (0) = 1, y (0) = 0 = y (0) Studentka obudziwszy się ok. 3 w nocy (z twarzą na zbiorze zadań z analizy matematycznej), postanowiła zrobić sobie kolejną kawę. W tym celu wstawiła wodę. Czajnik po zagotowaniu wody wyłączył się automatycznie. 30min. później okazało się, że temperatura wody to 50C. Po jakim czasie (od zagotowania) studentka powinna była zalać kawę jeśli wiadomo, że dla idealnego efektu należy użyć wody o temperaturze 70 o C? Temperatura otoczenia to 20 o C y x+y = 2 t, y (1) = 0, y (1) = Studenci szykując się do imprezy zrobili w zamrażarce ( 20 o C) wielką bryłę lodu z zagłębieniem na butelki. Jak się okazało, już po 10min. od wyjęcia (zanim włożyli cokolwiek do środka) lód nagrzał się do temperatury 5 o C. Po jakim czasie bryła osiągnie 0 o C jeśli temperatura otoczenia to 30 o C? y sin x + y cos x = 8y 1 sin x cos 3 x 4.17 Obrotny student postanowił każdej ze swoich przyjaciółek podarować pod choinkę króliczka. W tym celu zakupił 20 osobników i zaczął je rozmnażać. W czasie gdy króliki króliczyły się w najlepsze student przeliczył swoje przyjaciółki. Miał ich dokładnie 120. W dniu z przerażeniem zauważył, że ma już dokładnie tyle króliczków ile przyjaciółek. Po namyśle, postanowił kontynuować doświadczenie i rozdzielić wszystkie otrzymane króliczki po równo. Ile króliczków dostała każda z przyjaciółek studenta? (przyjmujemy, że: - wszystkie miesiące są tej samej długości; - student jest na tyle bogaty, żeby utrzymać dowolną liczbę króliczków; - wypada obdarować kogoś ułamkową częścią króliczka) 4.18 (2x 3 + x 2 3x) y = ( 2x 2 6x + 3) y, y ( ) ( 1 2 = 1,y 1 2) = Student celem polepszenia nastrojów kolegów i koleżanek siedzących w sali wykładowej umieścił olejek pomarańczowy tak, że znajdujący się tam wentylator wdmuchuje w ciągu minuty 20m 3 powietrza zawierającego 0, 002% estrów zapachowych. Po jakim czasie studenci będą mogli czuć się odświeżeni, jeżeli odpowiednie ku temu natężenie zapachu to 0, 0004%? Po jakim czasie zaczną kichać, jeżeli dzieje się to dla stężenia 0, 001%? - Sala wykładowa ma 200m (2x 3 + x 2 3x) y = ( 2x 2 6x + 3) y.
6 4.21 y = x y + xy x Studenci po zakończeniu sesji zorganizowali w jednym z pokoi akademikowych libację alkoholową. O godzinie 22:00 postanowili przenieść imprezę do jednego z klubów. Niestety, w czasie wychodzenia z pokoju przewrócili jedną z niedopitych butelek. Jakie będzie stężenie alkoholu w znajdującym w pokoju powietrzu o godzinie 8:00 jeśli wiadomo, że: - z powstałej plamy w ciągu kwadransa wyparowuje 1g alkoholu; - w momencie przewrócenia butelki w pokoju unosiły się 3g alkoholu pochodzącego z wydychanego przez biesiadników powietrza; - kubatura pokoju to 10m 3 ; - w ciągu godziny przez otwarte okno wpada 1m 3 czystego powietrza y = 25 sin x 4 (y + y x) Na skutek awarii do 100l zbiornika z (czystą) benzyną ekstrakcyjną dostał się 1kg chlorku sodu. W celu oczyszczenia, do zbiornika podłączono filtr usuwający 10% zanieczyszczeń z przepływającej przezeń cieczy. Oblicz po jakim czasie stężenie chlorku sodu spadnie o połowę jeśli wiadomo, że w ciągu minuty przez filtr przepływa 2l mieszaniny. 5 Całki krzywoliniowe 5.1 Wyznacz potencjał pola wektorowego P, Q : R 2 R zadanego następująco: P (x, y) := 7 e sin(πy) sin(ey)+π sin(πy) cos(ey) (e 2 π 2 ) 12 7x+1( 4 7x+1 3, 7x+1) Q (x, y) := 12 ( 6 7x x ln 12 7x ) sin (πy) cos (ey). 5.2 Punkt materialny został przesunięty wzdłuż krzywej K x (t) = t 2, y (t) = 4 t 3, z (t) = 9t od A = (0, 0, 0) do B = (1, 4, 9). Oblicz pracę jaką wykonano jeśli opór towarzyszący przemieszczeniu wyraża się 2x+18 funkcją F (x, y, z) := (36+2z+9x) y Niech K będzie krzywą o końcach (0, 0) oraz ( 1 π, 1) zawartą w wykresie funkcji y = sin x. 2 a) Oblicz masę K wiedząc, że gęstość opisana jest funkcją F (x, y) := y cos x. b) Wypisz odpowiednie całki na współrzędne środka ciężkości (bez liczenia). 5.4 Niech K będzie krzywą o końcach (0, 0) oraz ( 1 2 π, 1) zawartą w wykresie funkcji y = sin x. Oblicz masę K wiedząc, że gęstość opisana jest funkcją F (x, y) := y cos x. 5.5 Niech K będzie krzywą dodatnio zorientowaną, składającą się z części osi OX oraz wykresu funkcji y = cos x znajdujących się pomiędzy punktami ( 1 2 π, 0) i ( 1 2 π, 0). Oblicz K y + e x dy. 5.6 Oblicz K x4 dl, gdzie K jest krzywą zamkniętą zawartą w y = ln x od punktu A = (1, 0) do 5.7 Oblicz K x 3 +x+1 x+1 dy gdzie K jest krzywą zawartą w xy = 1 o początku A = ( 2, 1 2) i końcu B = ( 1 2, 2). 5.8 Oblicz K y 3, gdzie K jest ujemnie zorientowanym okręgiem x 2 + y 2 = 8x. Sprawdź, że pole P (x, y) := e y cos x cos 2 y, Q (x, y) := e y sin x (cos 2 y 2 sin y cos y) jest potencjalne i wyznacz potencjał. 5.9 Oblicz pracę wykonaną przez pole P (x, y, z) = 1, Q (x, y, z) = e x z, R (x, y, z) = 1 przy przesunięciu
7 wzdłuż jednego zwoju linii śrubowej x = t, y = cos t, z = sin t Oblicz całkę arctg x sin (2x) dy, gdzie K jest obwodem trójkąta o wierzchołkach K A = (0, 0), B = ( 1, 3) oraz C = ( 1, 3) zorientowanym odwrotnie do ruchu wskazówek zegara Oblicz pracę potrzebną do przemieszczenia punktu materialnego wzdłuż paraboli 2y = 4 x 2 od punktu A = (0, 2) do B = (2, 0) jeśli wiadomo, że siła oporu wyraża się wzorem F (x, y) = x Przy użyciu całki krzywoliniowej oblicz pole obszaru D: x 2 + y & y x.
Uniwersytet Warmińsko-Mazurski w Olsztynie
 Uniwersytet Warmińsko-Mazurski w Olsztynie ZETAW II Całka podwójna.. Obliczyć całki iterowane (a 4 4 2 ( (x + y ( 2 4 ( y x y dy dx y 3 x 2 + y 2 dx dy. 2. Zmienić kolejność całkowania (a (d 2 e ( 2x x
Uniwersytet Warmińsko-Mazurski w Olsztynie ZETAW II Całka podwójna.. Obliczyć całki iterowane (a 4 4 2 ( (x + y ( 2 4 ( y x y dy dx y 3 x 2 + y 2 dx dy. 2. Zmienić kolejność całkowania (a (d 2 e ( 2x x
y(t) = y 0 + R sin t, t R. z(t) = h 2π t
 SNM - Elementy analizy wektorowej - 1 Całki krzywoliniowe Definicja (funkcja wektorowa jednej zmiennej) Funkcją wektorową jednej zmiennej nazywamy odwzorowanie r : I R 3, gdzie I oznacza przedział na prostej,
SNM - Elementy analizy wektorowej - 1 Całki krzywoliniowe Definicja (funkcja wektorowa jednej zmiennej) Funkcją wektorową jednej zmiennej nazywamy odwzorowanie r : I R 3, gdzie I oznacza przedział na prostej,
1 x + 1 dxdy, gdzie obszar D jest ograniczo-
 Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1 Zad.1 Całkę podwójną przez: a) y =, y =, = 1; b) y =, y =, y = 1; c) y =, y = 1, y = 5; d) y = ln, y = + 1, y = 1; e) y = ln, = e, y = 1;
Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1 Zad.1 Całkę podwójną przez: a) y =, y =, = 1; b) y =, y =, y = 1; c) y =, y = 1, y = 5; d) y = ln, y = + 1, y = 1; e) y = ln, = e, y = 1;
Całki krzywoliniowe. SNM - Elementy analizy wektorowej - 1
 SNM - Elementy analizy wektorowej - 1 Całki krzywoliniowe Definicja (funkcja wektorowa jednej zmiennej) Funkcją wektorową jednej zmiennej nazywamy odwzorowanie r : I R 3, gdzie I oznacza przedział na prostej,
SNM - Elementy analizy wektorowej - 1 Całki krzywoliniowe Definicja (funkcja wektorowa jednej zmiennej) Funkcją wektorową jednej zmiennej nazywamy odwzorowanie r : I R 3, gdzie I oznacza przedział na prostej,
Zadania do samodzielnego rozwiązania zestaw 11
 Zadania do samodzielnego rozwiązania zestaw 11 1 Podać definicję pochodnej funkcji w punkcie, a następnie korzystając z tej definicji obliczyć ( ) π (a) f, jeśli f(x) = cos x, (e) f (0), jeśli f(x) = 4
Zadania do samodzielnego rozwiązania zestaw 11 1 Podać definicję pochodnej funkcji w punkcie, a następnie korzystając z tej definicji obliczyć ( ) π (a) f, jeśli f(x) = cos x, (e) f (0), jeśli f(x) = 4
Niektóre zastosowania całki krzywoliniowej niezorientowanej 1.Długość l łuku zwykłego gładkiego Γ
 Niektóre zastosowania całki krzywoliniowej niezorientowanej 1.ługość l łuku zwykłego gładkiego l = 1dl = b a (x (t)) 2 + (y (t) 2 ) + (z (t)) 2 dt 2.Pole powierzchni walcowej = {(x, y, z) : (x, y), 0 z
Niektóre zastosowania całki krzywoliniowej niezorientowanej 1.ługość l łuku zwykłego gładkiego l = 1dl = b a (x (t)) 2 + (y (t) 2 ) + (z (t)) 2 dt 2.Pole powierzchni walcowej = {(x, y, z) : (x, y), 0 z
x y = 2z, + 2y f(x, y) = ln(x3y ) y x
 . Funkcje wielu zmiennych i funkcje uwikłane Zad.. Obliczyć przybliżoną wartość wyrażenia (, 4) (,), Zad.. Obliczyć przybliżoną wartość wyrażenia, 8, 5, Zad. 3. Wykazać, że każda funkcja z(x, y) = x f
. Funkcje wielu zmiennych i funkcje uwikłane Zad.. Obliczyć przybliżoną wartość wyrażenia (, 4) (,), Zad.. Obliczyć przybliżoną wartość wyrażenia, 8, 5, Zad. 3. Wykazać, że każda funkcja z(x, y) = x f
Lista zadań nr 2 z Matematyki II
 Lista zadań nr 2 z Matematyki II dla studentów wydziału Architektury, kierunku Gospodarka Przestrzenna. Wyznaczyć dziedzinę funkcji f(x, y) = ln(4 x 2 y 2 ), f(x, y) = x 2 + y 2, f(x, y) = ln(4 x 2 y 2
Lista zadań nr 2 z Matematyki II dla studentów wydziału Architektury, kierunku Gospodarka Przestrzenna. Wyznaczyć dziedzinę funkcji f(x, y) = ln(4 x 2 y 2 ), f(x, y) = x 2 + y 2, f(x, y) = ln(4 x 2 y 2
x y = 2z. + 2y f(x, y) = ln(x3y ) y x
 . Funkcje wielu zmiennych i funkcje uwikłane Zad.. Obliczyć przybliżoną wartość wyrażenia (, 4) (,). Zad.. Wykazać, że każda funkcja z(x, y) = x f ( ) y x, gdzie f jest funkcją różniczkowalną jednej zmiennej,
. Funkcje wielu zmiennych i funkcje uwikłane Zad.. Obliczyć przybliżoną wartość wyrażenia (, 4) (,). Zad.. Wykazać, że każda funkcja z(x, y) = x f ( ) y x, gdzie f jest funkcją różniczkowalną jednej zmiennej,
ELEKTROTECHNIKA Semestr 2 Rok akad / ZADANIA Z MATEMATYKI Zestaw Oblicz pochodne cząstkowe rzędu drugiego funkcji:
 ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
Analiza matematyczna 2 zadania z odpowiedziami
 Analiza matematyczna zadania z odpowiedziami Maciej Burnecki strona główna Spis treści I Całki niewłaściwe pierwszego rodzaju II Całki niewłaściwe drugiego rodzaju 5 III Szeregi liczbowe 6 IV Szeregi potęgowe
Analiza matematyczna zadania z odpowiedziami Maciej Burnecki strona główna Spis treści I Całki niewłaściwe pierwszego rodzaju II Całki niewłaściwe drugiego rodzaju 5 III Szeregi liczbowe 6 IV Szeregi potęgowe
ANALIZA MATEMATYCZNA 2 zadania z odpowiedziami
 ANALIZA MATEMATYCZNA zadania z odpowiedziami Maciej Burnecki strona główna Spis treści Całki niewłaściwe pierwszego rodzaju Całki niewłaściwe drugiego rodzaju Szeregi liczbowe 4 4 Szeregi potęgowe 5 5
ANALIZA MATEMATYCZNA zadania z odpowiedziami Maciej Burnecki strona główna Spis treści Całki niewłaściwe pierwszego rodzaju Całki niewłaściwe drugiego rodzaju Szeregi liczbowe 4 4 Szeregi potęgowe 5 5
22. CAŁKA KRZYWOLINIOWA SKIEROWANA
 CAŁA RZYWOLINIOWA SIEROWANA Niech łuk o równaniach parametrycznych: x x(t), y y(t), a < t < b, będzie łukiem regularnym skierowanym, tzn łukiem w którym przyjęto punkt A(x(a), y(a)) za początek łuku, zaś
CAŁA RZYWOLINIOWA SIEROWANA Niech łuk o równaniach parametrycznych: x x(t), y y(t), a < t < b, będzie łukiem regularnym skierowanym, tzn łukiem w którym przyjęto punkt A(x(a), y(a)) za początek łuku, zaś
ANALIZA MATEMATYCZNA 2.2B (2017/18)
 ANALIZA MATEMATYCZNA.B (7/8) ANALIZA MATEMATYCZNA.A,.A LISTA. (na ćwiczenia) Całki niewłaściwe Część A. Zadania do samodzielnego rozwiązania, czyli to, co należy umieć z poprzedniego semestru... Podać
ANALIZA MATEMATYCZNA.B (7/8) ANALIZA MATEMATYCZNA.A,.A LISTA. (na ćwiczenia) Całki niewłaściwe Część A. Zadania do samodzielnego rozwiązania, czyli to, co należy umieć z poprzedniego semestru... Podać
1 Układy równań liniowych
 1 Układy równań liniowych 1. Rozwiązać układy równań liniowych metodą eliminacji Gaussa x + 2y z = 4 y 2z = 4x y + z = 0 x y + z = 0 2y + 5z = 1 6x 4y z = 1 x + y t = 1 x + y z = 0 y + z + t = 1 x + +
1 Układy równań liniowych 1. Rozwiązać układy równań liniowych metodą eliminacji Gaussa x + 2y z = 4 y 2z = 4x y + z = 0 x y + z = 0 2y + 5z = 1 6x 4y z = 1 x + y t = 1 x + y z = 0 y + z + t = 1 x + +
Analiza Matematyczna Praca domowa
 Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
FUNKCJE ZESPOLONE Lista zadań 2005/2006
 FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
Analiza Matematyczna MAEW101
 Analiza Matematyczna MAEW Wydział Elektroniki Listy zadań nr 8-4 (część II) na podstawie skryptów: M.Gewert, Z Skoczylas, Analiza Matematyczna. Przykłady i zadania, GiS, Wrocław 5 M.Gewert, Z Skoczylas,
Analiza Matematyczna MAEW Wydział Elektroniki Listy zadań nr 8-4 (część II) na podstawie skryptów: M.Gewert, Z Skoczylas, Analiza Matematyczna. Przykłady i zadania, GiS, Wrocław 5 M.Gewert, Z Skoczylas,
x y = 2z. + 2y, z 2y df
 . Funkcje wielu zmiennych i funkcje uwikłane Zadanie.. Obliczyć przybliżoną wartość wyrażenia (, ) (,). Korzystamy z przybliżenia f, y) f, y ) + x x, y ) + y y, y ), gdzie x = x x a y = y y. Przybliżenie
. Funkcje wielu zmiennych i funkcje uwikłane Zadanie.. Obliczyć przybliżoną wartość wyrażenia (, ) (,). Korzystamy z przybliżenia f, y) f, y ) + x x, y ) + y y, y ), gdzie x = x x a y = y y. Przybliżenie
(5) f(x) = ln x + x 3, (6) f(x) = 1 x. (19) f(x) = x3 +2x
 . Zadania do samodzielnego rozwiązania Zadanie. Na podstawie definicji pochodnej funkcji w punkcie obliczyć pochodną funkcji f zdefiniowanej równością () cos (2) (3) ln (4) sin 2 (5) ln + 3 (6) cos(3 )
. Zadania do samodzielnego rozwiązania Zadanie. Na podstawie definicji pochodnej funkcji w punkcie obliczyć pochodną funkcji f zdefiniowanej równością () cos (2) (3) ln (4) sin 2 (5) ln + 3 (6) cos(3 )
Matematyka 2. Elementy analizy wektorowej cz V Całka powierzchniowa zorientowana
 Matematyka 2 Elementy analizy wektorowej cz V Całka powierzchniowa zorientowana Literatura M.Gewert, Z.Skoczylas; Elementy analizy wektorowej; Oficyna Wydawnicza GiS, Wrocław, 2000 W.Żakowski, W.Kołodziej;
Matematyka 2 Elementy analizy wektorowej cz V Całka powierzchniowa zorientowana Literatura M.Gewert, Z.Skoczylas; Elementy analizy wektorowej; Oficyna Wydawnicza GiS, Wrocław, 2000 W.Żakowski, W.Kołodziej;
Zestaw zadań z Analizy Matematycznej II 18/19. Konwencja: pierwsze litery alfabetu są parametrami, do tego zazwyczaj dodatnimi
 Literatura pomocnicza Zestaw zadań z Analizy Matematycznej II 8/9 G.M. Fichtenholz - Rachunek różniczkowy i całkowy. B. Demidowicz - Zbiór zadań z analizy matematycznej. T 2,3 Krysicki, Włodarski - Analiza
Literatura pomocnicza Zestaw zadań z Analizy Matematycznej II 8/9 G.M. Fichtenholz - Rachunek różniczkowy i całkowy. B. Demidowicz - Zbiór zadań z analizy matematycznej. T 2,3 Krysicki, Włodarski - Analiza
Rachunek różniczkowy i całkowy 2016/17
 Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Analiza Matematyczna. Zastosowania Całek
 Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
MATEMATYKA II. znaleźć f(g(x)) i g(f(x)).
 MATEMATYKA II PAWEŁ ZAPAŁOWSKI Równania i nierówności Zadanie Wyznaczyć dziedziny i wzory dla f f, f g, g f, g g, gdzie () f() =, g() =, () f() = 3 + 4, g() = Zadanie Dla f() = 3 5 i g() = 8 znaleźć f(g()),
MATEMATYKA II PAWEŁ ZAPAŁOWSKI Równania i nierówności Zadanie Wyznaczyć dziedziny i wzory dla f f, f g, g f, g g, gdzie () f() =, g() =, () f() = 3 + 4, g() = Zadanie Dla f() = 3 5 i g() = 8 znaleźć f(g()),
Całki krzywoliniowe skierowane
 Całki krzywoliniowe skierowane Zamiana całki krzywoliniowej skierowanej na całkę pojedyńcza. Twierdzenie Greena. Zastosowania całki krzywoliniowej skierowanej. Małgorzata Wyrwas Katedra Matematyki Wydział
Całki krzywoliniowe skierowane Zamiana całki krzywoliniowej skierowanej na całkę pojedyńcza. Twierdzenie Greena. Zastosowania całki krzywoliniowej skierowanej. Małgorzata Wyrwas Katedra Matematyki Wydział
Całka oznaczona zastosowania (wykład 9; ) Definicja całki oznaczonej dla funkcji ciagłej
 Całka oznaczona zastosowania (wykład 9;26.11.7) Definicja całki oznaczonej dla funkcji ciagłej Definicja 1 Załózmy, że funkcja f jest ciagła na przedziale [a, b]. Całkę oznaczona z funkcji ci b a f(x)dx
Całka oznaczona zastosowania (wykład 9;26.11.7) Definicja całki oznaczonej dla funkcji ciagłej Definicja 1 Załózmy, że funkcja f jest ciagła na przedziale [a, b]. Całkę oznaczona z funkcji ci b a f(x)dx
Równania prostych i krzywych; współrzędne punktu
 Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
ZASTOSOWANIA CAŁEK OZNACZONYCH
 YH JJ, MiF UP 13 D BL PÓL FGUR PYŹ e wszystkich wzorach zakładamy, że funkcje: f (x), g(x), r(ϕ), x(t), y(t) sa cia głe w odpowiednich przedziałach oraz że r(ϕ). D BL PÓL FGUR PYŹ Pole obszaru D = {(x,
YH JJ, MiF UP 13 D BL PÓL FGUR PYŹ e wszystkich wzorach zakładamy, że funkcje: f (x), g(x), r(ϕ), x(t), y(t) sa cia głe w odpowiednich przedziałach oraz że r(ϕ). D BL PÓL FGUR PYŹ Pole obszaru D = {(x,
Analiza Matematyczna. Lista zadań 10
 Analiza Matematyczna Lista zadań 10 Zadanie 1 pole figury ograniczonej krzywymi y 2 = 2x, x + y = 1. Zadanie 2 objȩtość bryły V powstałej z obrotu wokół osi Ox powierzchni ograniczonej krzyw a o równaniu
Analiza Matematyczna Lista zadań 10 Zadanie 1 pole figury ograniczonej krzywymi y 2 = 2x, x + y = 1. Zadanie 2 objȩtość bryły V powstałej z obrotu wokół osi Ox powierzchni ograniczonej krzyw a o równaniu
ELEKTROTECHNIKA Semestr 1 Rok akad / ZADANIA Z MATEMATYKI Zestaw Przedstaw w postaci algebraicznej liczby zespolone: (3 + 2j)(5 2j),
 ELEKTROTECHNIKA Semestr Rok akad. / 5 ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na płaszczyźnie: +j
ELEKTROTECHNIKA Semestr Rok akad. / 5 ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na płaszczyźnie: +j
Opracowanie: mgr Jerzy Pietraszko
 Analiza Matematyczna Opracowanie: mgr Jerzy Pietraszko Zadanie 1. Oblicz pochodną funkcji: (a) f(x) = x xx (b) f(x) = log sin 4 x cos 4 x (c) f(x) = sin sin x log x 2(2x) (d) f(x) = ( tg ( x + π 2 (e)
Analiza Matematyczna Opracowanie: mgr Jerzy Pietraszko Zadanie 1. Oblicz pochodną funkcji: (a) f(x) = x xx (b) f(x) = log sin 4 x cos 4 x (c) f(x) = sin sin x log x 2(2x) (d) f(x) = ( tg ( x + π 2 (e)
Elementy analizy wektorowej. Listazadań
 Elementy analizy wektorowej Opracowanie: dr Marian Gewert, dr Zbigniew Skoczylas Listazadań % Całki krzywoliniowe niezorientowane 1. Obliczyć całkę krzywoliniową niezorientowaną f dl, jeżeli: 1 a)fx,y)=
Elementy analizy wektorowej Opracowanie: dr Marian Gewert, dr Zbigniew Skoczylas Listazadań % Całki krzywoliniowe niezorientowane 1. Obliczyć całkę krzywoliniową niezorientowaną f dl, jeżeli: 1 a)fx,y)=
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE - LISTA I
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE - LISTA I RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU. ROZWIĄZAĆ RÓWNANIE RÓŻNICZKOWE LUB ZAGADNIENIE POCZĄTKOWE.......6. ln ln...7..8..9. d d.... co.... in.... in co in.6..7..8.
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE - LISTA I RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU. ROZWIĄZAĆ RÓWNANIE RÓŻNICZKOWE LUB ZAGADNIENIE POCZĄTKOWE.......6. ln ln...7..8..9. d d.... co.... in.... in co in.6..7..8.
ANALIZA MATEMATYCZNA 2
 ANALIZA MATEMATYCZNA Lista zadań 3/4 Opracowanie: dr Marian Gewert, dr Zbigniew Skoczylas Lista pierwsza Zadanie. Korzystając z definicji zbadać zbieżność podanych całek niewłaściwych pierwszego rodzaju:
ANALIZA MATEMATYCZNA Lista zadań 3/4 Opracowanie: dr Marian Gewert, dr Zbigniew Skoczylas Lista pierwsza Zadanie. Korzystając z definicji zbadać zbieżność podanych całek niewłaściwych pierwszego rodzaju:
Spis treści 1. Macierze, wyznaczniki, równania liniowe 2 2. Geometria analityczna 7 3. Granice, pochodne funkcji i ich zastosowania 10 4.
 Spis treści Macierze wyznaczniki równania liniowe Geometria analityczna 7 Granice pochodne funkcji i ich zastosowania 0 4 Liczby zespolone 6 5 Całki nieoznaczone 8 6 Zastosowania geometryczne całek 0 7
Spis treści Macierze wyznaczniki równania liniowe Geometria analityczna 7 Granice pochodne funkcji i ich zastosowania 0 4 Liczby zespolone 6 5 Całki nieoznaczone 8 6 Zastosowania geometryczne całek 0 7
Analiza Matematyczna F1 dla Fizyków na WPPT Lista zadań 4, 2018/19z (zadania na ćwiczenia)
 Analiza Matematyczna F1 dla Fizyków na WPPT Lista zadań 4, 2018/19z (zadania na ćwiczenia) (Na podstawie podręcznika M. Gewert, Z. Skoczylas, Analiza Matematyczna 1. Przykłady i zadania, GiS 2008) 4 Pochodne
Analiza Matematyczna F1 dla Fizyków na WPPT Lista zadań 4, 2018/19z (zadania na ćwiczenia) (Na podstawie podręcznika M. Gewert, Z. Skoczylas, Analiza Matematyczna 1. Przykłady i zadania, GiS 2008) 4 Pochodne
Zestaw Obliczyć objętość równoległościanu zbudowanego na wektorach m, n, p jeśli wiadomo, że objętość równoległościanu zbudowanego na wektorach:
 Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
A. fałszywa dla każdej liczby x.b. prawdziwa dla C. prawdziwa dla D. prawdziwa dla
 Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
opracował Maciej Grzesiak Całki krzywoliniowe
 opracował Maciej Grzesiak Całki krzywoliniowe 1. Definicja całki krzywoliniowej nieskierowanej Rozważmy następujący problem. Dany jest przewód elektryczny na którym rozmieszczone są ładunki. Przypuśćmy,
opracował Maciej Grzesiak Całki krzywoliniowe 1. Definicja całki krzywoliniowej nieskierowanej Rozważmy następujący problem. Dany jest przewód elektryczny na którym rozmieszczone są ładunki. Przypuśćmy,
3. Operacje na zbiorach (1) Sprowadź poniższe zdania dotyczące zbiorów do postaci zdań logicznych i sprawdź ich prawdziwość.
 1. Zapis matematyczny i elementy logiki matematycznej (1) Zapisz, używając symboliki matematycznej zdania: (a) Liczby x i y mają wspólny dzielnik większy od 2. (b) Jeśli x i y różnią się o 1, to nie mają
1. Zapis matematyczny i elementy logiki matematycznej (1) Zapisz, używając symboliki matematycznej zdania: (a) Liczby x i y mają wspólny dzielnik większy od 2. (b) Jeśli x i y różnią się o 1, to nie mają
Arkusz 6. Elementy geometrii analitycznej w przestrzeni
 Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Rachunek całkowy - całka oznaczona
 SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
Spis treści 1. Liczby zespolone 2 2. Macierze, wyznaczniki, równania liniowe 4 3. Geometria analityczna 9 4. Granice, pochodne funkcji i ich
 Spis treści Liczby zespolone Macierze wyznaczniki równania liniowe 4 Geometria analityczna 9 4 Granice pochodne funkcji i ich zastosowania 5 Całki nieoznaczone 8 6 Zastosowania geometryczne całek 0 7 Pochodne
Spis treści Liczby zespolone Macierze wyznaczniki równania liniowe 4 Geometria analityczna 9 4 Granice pochodne funkcji i ich zastosowania 5 Całki nieoznaczone 8 6 Zastosowania geometryczne całek 0 7 Pochodne
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
Analiza Matematyczna MAEW101 MAP1067
 Analiza Matematyczna MAEW MAP67 Wydział Elektroniki Przykłady do Listy Zadań nr 4 Funkcje wielu zmiennych. Pochodne cząstkowe Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania 4.: Wyznaczyć
Analiza Matematyczna MAEW MAP67 Wydział Elektroniki Przykłady do Listy Zadań nr 4 Funkcje wielu zmiennych. Pochodne cząstkowe Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania 4.: Wyznaczyć
KORESPONDENCYJNY KURS PRZYGOTOWAWCZY Z MATEMATYKI
 KORESPONDENCYJNY KURS PRZYGOTOWAWCZY Z MATEMATYKI PRACA KONTROLNA nr 1 październik 1999 r 1. Stop składa się z 40% srebra próby 0,6, 30% srebra próby 0,7 oraz 1 kg srebra próby 0,8. Jaka jest waga i jaka
KORESPONDENCYJNY KURS PRZYGOTOWAWCZY Z MATEMATYKI PRACA KONTROLNA nr 1 październik 1999 r 1. Stop składa się z 40% srebra próby 0,6, 30% srebra próby 0,7 oraz 1 kg srebra próby 0,8. Jaka jest waga i jaka
Lista 1 - Funkcje elementarne
 Lista - Funkcje elementarne Naszkicuj wykresy funkcji: a) y = sgn, y = sgn ; b) y = ; c) y = 2 Przedstaw w jednym układzie współrzędnych wykresy funkcji potęgowej y = α dla: a) α =, 2, 3, 4; b) α =,, 2;
Lista - Funkcje elementarne Naszkicuj wykresy funkcji: a) y = sgn, y = sgn ; b) y = ; c) y = 2 Przedstaw w jednym układzie współrzędnych wykresy funkcji potęgowej y = α dla: a) α =, 2, 3, 4; b) α =,, 2;
1 Funkcja wykładnicza i logarytm
 1 Funkcja wykładnicza i logarytm 1. Rozwiązać równania; (a) x + 3 = 3 ; (b) x 2 + 9 = 5 ; (c) 3 x 1 = 3x 2 2. Rozwiązać nierówności : (a) 2x 1 > 2 ; (b) 3x 4 2x + 3 > x + 2 ; (c) 3 x > 1. 3. Znając wykres
1 Funkcja wykładnicza i logarytm 1. Rozwiązać równania; (a) x + 3 = 3 ; (b) x 2 + 9 = 5 ; (c) 3 x 1 = 3x 2 2. Rozwiązać nierówności : (a) 2x 1 > 2 ; (b) 3x 4 2x + 3 > x + 2 ; (c) 3 x > 1. 3. Znając wykres
ELEKTROTECHNIKA Semestr 2 Rok akad. 2015 / 2016. ZADANIA Z MATEMATYKI Zestaw 1. 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji:
 ZADANIA Z MATEMATYKI Zestaw 1 1. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y 1+x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
ZADANIA Z MATEMATYKI Zestaw 1 1. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y 1+x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
1 Funkcja wykładnicza i logarytm
 1 Funkcja wykładnicza i logarytm 1. Rozwiązać równania; (a) x + 3 = 3 ; (b) x 2 + 9 = 5 ; (c) 3 x 1 = 3x 2 2. Rozwiązać nierówności : (a) 2x 1 > 2 ; (b) 3x 4 2x + 3 > x + 2 ; (c) 3 x > 1. 3. Znając wykres
1 Funkcja wykładnicza i logarytm 1. Rozwiązać równania; (a) x + 3 = 3 ; (b) x 2 + 9 = 5 ; (c) 3 x 1 = 3x 2 2. Rozwiązać nierówności : (a) 2x 1 > 2 ; (b) 3x 4 2x + 3 > x + 2 ; (c) 3 x > 1. 3. Znając wykres
I. Funkcja kwadratowa
 Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy w roku szkolnym 2018/2019 w CKZiU nr 3 Ekonomik w Zielonej Górze KLASA III fl POZIOM PODSTAWOWY I. Funkcja kwadratowa narysować wykres funkcji
Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy w roku szkolnym 2018/2019 w CKZiU nr 3 Ekonomik w Zielonej Górze KLASA III fl POZIOM PODSTAWOWY I. Funkcja kwadratowa narysować wykres funkcji
ANALIZA MATEMATYCZNA 2
 ANALIZA MATEMATYCZNA Opracowanie Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA Kolokwia i egzaminy Wydanie dziewiąte powiększone GiS Oficyna Wydawnicza GiS Wrocław Projekt okładki: IMPRESJA Studio
ANALIZA MATEMATYCZNA Opracowanie Marian Gewert Zbigniew Skoczylas ANALIZA MATEMATYCZNA Kolokwia i egzaminy Wydanie dziewiąte powiększone GiS Oficyna Wydawnicza GiS Wrocław Projekt okładki: IMPRESJA Studio
POZIOM PODSTAWOWY - GR 1 Czas pracy 170 minut
 POZIOM PODSTAWOWY - GR 1 Czas pracy 170 minut Klasa Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.. W zadaniach
POZIOM PODSTAWOWY - GR 1 Czas pracy 170 minut Klasa Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.. W zadaniach
Całki krzywoliniowe wiadomości wstępne
 Całki krzywoliniowe wiadomości wstępne Łuk na płaszczyźnie to zbiór punktów (x, y o współrzędnych x = x(t, y = y(t, gdzie (x(t, y(t są funkcjami ciągłymi określonymi na przedziale bez punktów wielokrotnych.
Całki krzywoliniowe wiadomości wstępne Łuk na płaszczyźnie to zbiór punktów (x, y o współrzędnych x = x(t, y = y(t, gdzie (x(t, y(t są funkcjami ciągłymi określonymi na przedziale bez punktów wielokrotnych.
Repetytorium z matematyki ćwiczenia
 Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Wykłady z Matematyki stosowanej w inżynierii środowiska, II sem. 2. CAŁKA PODWÓJNA Całka podwójna po prostokącie
 Wykłady z Matematyki stosowanej w inżynierii środowiska, II sem..1. Całka podwójna po prostokącie.. CAŁKA POWÓJNA.. Całka podwójna po obszarach normalnych..3. Całka podwójna po obszarach regularnych..4.
Wykłady z Matematyki stosowanej w inżynierii środowiska, II sem..1. Całka podwójna po prostokącie.. CAŁKA POWÓJNA.. Całka podwójna po obszarach normalnych..3. Całka podwójna po obszarach regularnych..4.
Pochodna funkcji jednej zmiennej
 Pochodna funkcji jednej zmiennej Def:(pochodnej funkcji w punkcie) Jeśli funkcja f : D R, D R określona jest w pewnym otoczeniu punktu 0 D i istnieje skończona granica ilorazu różniczkowego: f f( ( 0 )
Pochodna funkcji jednej zmiennej Def:(pochodnej funkcji w punkcie) Jeśli funkcja f : D R, D R określona jest w pewnym otoczeniu punktu 0 D i istnieje skończona granica ilorazu różniczkowego: f f( ( 0 )
Wymagania na poszczególne oceny szkolne z. matematyki. dla uczniów klasy IIIa i IIIb. Gimnazjum im. Jana Pawła II w Mętowie. w roku szkolnym 2015/2016
 Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Badanie funkcji. Zad. 1: 2 3 Funkcja f jest określona wzorem f( x) = +
 Badanie funkcji Zad : Funkcja f jest określona wzorem f( ) = + a) RozwiąŜ równanie f() = 5 b) Znajdź przedziały monotoniczności funkcji f c) Oblicz największą i najmniejszą wartość funkcji f w przedziale
Badanie funkcji Zad : Funkcja f jest określona wzorem f( ) = + a) RozwiąŜ równanie f() = 5 b) Znajdź przedziały monotoniczności funkcji f c) Oblicz największą i najmniejszą wartość funkcji f w przedziale
I. Funkcja kwadratowa
 Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy dla klas III w roku szkolnym 2017/2018 w Zespole Szkół Ekonomicznych w Zielonej Górze Dla każdej klasy 3 obowiązuje taka ilość poniższego
Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy dla klas III w roku szkolnym 2017/2018 w Zespole Szkół Ekonomicznych w Zielonej Górze Dla każdej klasy 3 obowiązuje taka ilość poniższego
Blok III: Funkcje elementarne. e) y = 1 3 x. f) y = x. g) y = 2x. h) y = 3x. c) y = 3x + 2. d) y = x 3. c) y = x. d) y = x.
 Blok III: Funkcje elementarne III. Narysuj wykres funkcji: a) y = x y = x y = x y = x III. Narysuj wykres funkcji: a) y = x + y = 4 x III. Znajdź miejsca zerowe funkcji: a) y = 6 x y = x e) y = x f) y
Blok III: Funkcje elementarne III. Narysuj wykres funkcji: a) y = x y = x y = x y = x III. Narysuj wykres funkcji: a) y = x + y = 4 x III. Znajdź miejsca zerowe funkcji: a) y = 6 x y = x e) y = x f) y
Matematyka Lista 1 1. Matematyka. Lista Obliczyć lub uprościć zapis (zapisać jako potęgę):
 Matematyka Lista 1 1 Matematyka Lista 1 1. Obliczyć lub uprościć zapis (zapisać jako potęgę): 3 3 3 ( ) 1 4 2 5 8 3 100 3 2 4 1 3 4 2 4 9 1 3 3 9 3. 5 2. Rozwiązać równania i nierówności: 4 2x+1 = 8 5x
Matematyka Lista 1 1 Matematyka Lista 1 1. Obliczyć lub uprościć zapis (zapisać jako potęgę): 3 3 3 ( ) 1 4 2 5 8 3 100 3 2 4 1 3 4 2 4 9 1 3 3 9 3. 5 2. Rozwiązać równania i nierówności: 4 2x+1 = 8 5x
Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIĘTE. W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź.
 ZADANIA ZAMKNIĘTE W zadaniach -5 wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź. Zadanie. ( pkt) Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność
ZADANIA ZAMKNIĘTE W zadaniach -5 wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź. Zadanie. ( pkt) Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność
KORESPONDENCYJNY KURS Z MATEMATYKI. PRACA KONTROLNA nr 1
 KORESPONDENCYJNY KURS Z MATEMATYKI PRACA KONTROLNA nr 1 październik 000r 1. Suma wszystkich wyrazów nieskończonego ciągu geometrycznego wynosi 040. Jeśli pierwszy wyraz tego ciągu zmniejszymy o 17, a jego
KORESPONDENCYJNY KURS Z MATEMATYKI PRACA KONTROLNA nr 1 październik 000r 1. Suma wszystkich wyrazów nieskończonego ciągu geometrycznego wynosi 040. Jeśli pierwszy wyraz tego ciągu zmniejszymy o 17, a jego
Zastosowania geometryczne całek
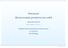 Matematyka Zastosowania geometryczne całek Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-3 Elblag Matematyka p. 1 Zastosowania geometryczne całek
Matematyka Zastosowania geometryczne całek Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-3 Elblag Matematyka p. 1 Zastosowania geometryczne całek
ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna
 Arkusz A06 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Wartość wyrażenia 1 3 + 1 + 3
Arkusz A06 2 Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNIETE W zadaniach 1-25 wybierz i zaznacz na karcie odpowiedzi poprawna odpowiedź Zadanie 1. (0-1) Wartość wyrażenia 1 3 + 1 + 3
Indukcja matematyczna
 Indukcja matematyczna Zadanie. Zapisać, używając symboli i, następujące wyrażenia (a) n!; (b) sin() + sin() sin() +... + sin() sin()... sin(n); (c) ( + )( + /)( + / + /)... ( + / + / +... + /R). Zadanie.
Indukcja matematyczna Zadanie. Zapisać, używając symboli i, następujące wyrażenia (a) n!; (b) sin() + sin() sin() +... + sin() sin()... sin(n); (c) ( + )( + /)( + / + /)... ( + / + / +... + /R). Zadanie.
ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA
 Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 2018 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz egzaminacyjny zawiera 16
Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 2018 Instrukcja dla zdającego Czas pracy: 170 minut 1. Sprawdź, czy arkusz egzaminacyjny zawiera 16
Matematyka. rok akademicki 2008/2009, semestr zimowy. Konwersatorium 1. Własności funkcji
 . Własności funkcji () Wyznaczyć dziedzinę funkcji danej wzorem: y = 2 2 + 5 y = +4 y = 2 + (2) Podać zbiór wartości funkcji: y = 2 3, [2, 5) y = 2 +, [, 4] y =, [3, 6] (3) Stwierdzić, czy dana funkcja
. Własności funkcji () Wyznaczyć dziedzinę funkcji danej wzorem: y = 2 2 + 5 y = +4 y = 2 + (2) Podać zbiór wartości funkcji: y = 2 3, [2, 5) y = 2 +, [, 4] y =, [3, 6] (3) Stwierdzić, czy dana funkcja
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne.
 Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH )
 Kujawsko-Pomorskie Centrum Edukacji Nauczycieli w Bydgoszczy PLACÓWKA AKREDYTOWANA TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH ) PAKIET ZADAŃ (zadania wybrano ze zbiorów autorów i wydawnictw: Kiełbasa, Res Polona,
Kujawsko-Pomorskie Centrum Edukacji Nauczycieli w Bydgoszczy PLACÓWKA AKREDYTOWANA TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH ) PAKIET ZADAŃ (zadania wybrano ze zbiorów autorów i wydawnictw: Kiełbasa, Res Polona,
MATEMATYKA - CYKL 5 GODZINNY. DATA : 8 czerwca 2009
 MATURA EUROPEJSKA 2009 MATEMATYKA - CYKL 5 GODZINNY DATA : 8 czerwca 2009 CZAS TRWANIA EGZAMINU: 4 godziny (240 minut) DOZWOLONE POMOCE : Europejski zestaw wzorów Kalkulator (bez grafiki, bez możliwości
MATURA EUROPEJSKA 2009 MATEMATYKA - CYKL 5 GODZINNY DATA : 8 czerwca 2009 CZAS TRWANIA EGZAMINU: 4 godziny (240 minut) DOZWOLONE POMOCE : Europejski zestaw wzorów Kalkulator (bez grafiki, bez możliwości
Tematy: zadania tematyczne
 Tematy: zadania tematyczne 1. Ciągi liczbowe zadania typu udowodnij 1) Udowodnij, Ŝe jeŝeli liczby,, tworzą ciąg arytmetyczny ), to liczby,, takŝe tworzą ciąg arytmetyczny. 2) Ciąg jest ciągiem geometrycznym.
Tematy: zadania tematyczne 1. Ciągi liczbowe zadania typu udowodnij 1) Udowodnij, Ŝe jeŝeli liczby,, tworzą ciąg arytmetyczny ), to liczby,, takŝe tworzą ciąg arytmetyczny. 2) Ciąg jest ciągiem geometrycznym.
Rachunek różniczkowy funkcji wielu zmiennych
 Wydział Matematyki Stosowanej Zestaw zadań nr 7 Akademia Górniczo-Hutnicza w Krakowie WFiIS, informatyka stosowana, I rok Elżbieta Adamus 13 grudnia 2018r. Rachunek różniczkowy funkcji wielu zmiennych
Wydział Matematyki Stosowanej Zestaw zadań nr 7 Akademia Górniczo-Hutnicza w Krakowie WFiIS, informatyka stosowana, I rok Elżbieta Adamus 13 grudnia 2018r. Rachunek różniczkowy funkcji wielu zmiennych
LISTY ZADAŃ DO KURSU ANALIZA MATEMATYCZNA 1 (MAT 1637, 1644)
 LISTY ZADAŃ DO KURSU ANALIZA MATEMATYCZNA MAT 67, 644) Zadania przeznaczone są do rozwiązywania na ćwiczeniach oraz samodzielnie. Dwie dodatkowe listy: POWTÓRKA i POWTÓRKA to przygotowanie do kolokwiów.
LISTY ZADAŃ DO KURSU ANALIZA MATEMATYCZNA MAT 67, 644) Zadania przeznaczone są do rozwiązywania na ćwiczeniach oraz samodzielnie. Dwie dodatkowe listy: POWTÓRKA i POWTÓRKA to przygotowanie do kolokwiów.
LUBELSKA PRÓBA PRZED MATURĄ
 POZIOM PODSTAWOWY GR- Czas pracy 170 minut Klasa Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.. W zadaniach od
POZIOM PODSTAWOWY GR- Czas pracy 170 minut Klasa Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym.. W zadaniach od
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 KWIETNIA 204 CZAS PRACY: 70 MINUT Zadania zamknięte ZADANIE ( PKT) Liczba 2 2 3 2 3 jest równa
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 KWIETNIA 204 CZAS PRACY: 70 MINUT Zadania zamknięte ZADANIE ( PKT) Liczba 2 2 3 2 3 jest równa
5 Równania różniczkowe zwyczajne rzędu drugiego
 5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
EGZAMIN MATURALNY OD ROKU SZKOLNEGO
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 204/205 MATEMATYKA POZIOM PODSTAWOWY PRZYKŁADOWY ZESTAW ZADAŃ (A) W czasie trwania egzaminu zdający może korzystać z zestawu wzorów matematycznych, linijki i cyrkla
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 204/205 MATEMATYKA POZIOM PODSTAWOWY PRZYKŁADOWY ZESTAW ZADAŃ (A) W czasie trwania egzaminu zdający może korzystać z zestawu wzorów matematycznych, linijki i cyrkla
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 MARZEC ROK 08 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 70 minut Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 4 stron (zadania 34). Ewentualny brak zgłoś
MARZEC ROK 08 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 70 minut Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 4 stron (zadania 34). Ewentualny brak zgłoś
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 5 MAJA Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Matematyka I. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12
 Matematyka I Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12 Egzamin Termin: 28.01, godz. 10.15-11.45, sala 309 3 pytania teoretyczne 2 zadania wybór pytań i wybór zadań
Matematyka I Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12 Egzamin Termin: 28.01, godz. 10.15-11.45, sala 309 3 pytania teoretyczne 2 zadania wybór pytań i wybór zadań
1 Funkcje dwóch zmiennych podstawowe pojęcia
 1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
Liczby zespolone. Zadanie 1. Oblicz: a) ( 3+i)( 1 3i) b) (3+i)2 (4i+1) i
 Zadanie. Oblicz: a) ( 3+i)( 3i) +i b) (3+i)2 (4i+) i (2+i) 3 Liczby zespolone Zadanie 2. Zaznacz na płaszczyźnie Gaussa zbiór: a) {z : z > 3} b) {z : z i } c) {z : 4 z + + i < 9} Zadanie 3. Wykaż, że suma
Zadanie. Oblicz: a) ( 3+i)( 3i) +i b) (3+i)2 (4i+) i (2+i) 3 Liczby zespolone Zadanie 2. Zaznacz na płaszczyźnie Gaussa zbiór: a) {z : z > 3} b) {z : z i } c) {z : 4 z + + i < 9} Zadanie 3. Wykaż, że suma
UZUPEŁNIA ZDAJĄCY miejsce na naklejkę
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 maja 017 r.
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 maja 017 r.
FUNKCJE WIELU ZMIENNYCH
 FUNKCJE WIELU ZMIENNYCH 1. Wyznaczyć i narysować dziedziny naturalne podanych funkcji: 4 x 2 y 2 ; (b) g(x, y) = e y x 2 1 ; (c) u(x, y) = arc sin xy; (d) v(x, y) = sin(x 2 + y 2 ); (e) w(x, y) = x sin
FUNKCJE WIELU ZMIENNYCH 1. Wyznaczyć i narysować dziedziny naturalne podanych funkcji: 4 x 2 y 2 ; (b) g(x, y) = e y x 2 1 ; (c) u(x, y) = arc sin xy; (d) v(x, y) = sin(x 2 + y 2 ); (e) w(x, y) = x sin
24. CAŁKA POWIERZCHNIOWA ZORIENTOWANA
 4. CAŁA POWIERZCHNIOWA ZORIENTOWANA Płat powierzchniowy gładki o równaniach parametrycznych: x = x( u, v ), y = y( u, v ), z = z( u, v ),, (u,v) w którym rozróżniamy dwie jego stron dodatnią i ujemną.
4. CAŁA POWIERZCHNIOWA ZORIENTOWANA Płat powierzchniowy gładki o równaniach parametrycznych: x = x( u, v ), y = y( u, v ), z = z( u, v ),, (u,v) w którym rozróżniamy dwie jego stron dodatnią i ujemną.
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM ROZSZERZONY 8 KWIETNIA 2017 CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Funkcja f określona
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM ROZSZERZONY 8 KWIETNIA 2017 CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Funkcja f określona
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI P-1 POZIOM PODSTAWOWY Czas pracy: 170 minut Za rozwiązanie wszystkich zadań można uzyskać łącznie 50 punktów BRUDNOPIS Zadanie 1. (1 pkt) ZADANIA ZAMKNIĘTE
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI P-1 POZIOM PODSTAWOWY Czas pracy: 170 minut Za rozwiązanie wszystkich zadań można uzyskać łącznie 50 punktów BRUDNOPIS Zadanie 1. (1 pkt) ZADANIA ZAMKNIĘTE
EGZAMIN MATURALNY Z MATEMATYKI MAJ 2013 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50 WPISUJE ZDAJĄCY
 Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 010 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem dysleksja EGZAMIN
Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 010 KOD WPISUJE ZDAJĄCY PESEL Miejsce na naklejkę z kodem dysleksja EGZAMIN
ARKUSZ II
 www.galileusz.com.pl ARKUSZ II W każdym z zadań 1.-24. wybierz i zaznacz jedną poprawną odpowiedź. Zadanie 1. (0-1 pkt) Liczba 30 to p% liczby 80, zatem A) p = 44,(4)% B) p > 44,(4)% C) p = 43,(4)% D)
www.galileusz.com.pl ARKUSZ II W każdym z zadań 1.-24. wybierz i zaznacz jedną poprawną odpowiedź. Zadanie 1. (0-1 pkt) Liczba 30 to p% liczby 80, zatem A) p = 44,(4)% B) p > 44,(4)% C) p = 43,(4)% D)
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Kurs Start plus poziom zaawansowany, materiały dla prowadzących, Marcin Kościelecki. Zajęcia 1.
 Projekt Fizyka Plus nr POKL.04.0.0-00-034/ współfinansowany przez Unię Europejską ze środków Europejskiego Funduszu Społecznego w ramach Programu Operacyjnego Kapitał Ludzki Kurs Start plus poziom zaawansowany,
Projekt Fizyka Plus nr POKL.04.0.0-00-034/ współfinansowany przez Unię Europejską ze środków Europejskiego Funduszu Społecznego w ramach Programu Operacyjnego Kapitał Ludzki Kurs Start plus poziom zaawansowany,
Całka podwójna po prostokącie
 Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
PRACA KONTROLNA nr 1
 KORESPONDENCYJNY KURS Z MATEMATYKI PRACA KONTROLNA nr 1 październik 2002r 1. Narysować wykres funkcji y = 4 + 2 x x 2. Korzystając z tego wykresu określić liczbę rozwiązań równania 4+2 x x 2 = p w zależności
KORESPONDENCYJNY KURS Z MATEMATYKI PRACA KONTROLNA nr 1 październik 2002r 1. Narysować wykres funkcji y = 4 + 2 x x 2. Korzystając z tego wykresu określić liczbę rozwiązań równania 4+2 x x 2 = p w zależności
