1. Zadanie. Określmy zbiór A = {0, 1, 2, 3, 4}. Dla x, y A definiujemy: x jest w relacji R z y (zapisujemy xry, lub (x, y) R) x + y 3
|
|
|
- Judyta Adamczyk
- 8 lat temu
- Przeglądów:
Transkrypt
1 1. Zadanie. Określmy zbiór A = {0, 1, 2, 3, 4}. Dla x, y A definiujemy: x jest w relacji R z y (zaisujemy xry, lub (x, y) R) x + y 3 (a) Ile ar (x, y) należy do relacji R? (b) Czy relacja R jest zwrotna? (c) Czy relacja R jest symetryczna? (d) Czy relacja R jest antysymetryczna? Odowiedź Nastęujące ary (0, 3), (0, 4), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 0), (3, 1), (3, 2), (3, 3), (3, 4), (4, 0), (4, 1), (4, 2), (4, 3), (4, 4) należą do R. Jest ich więc 19. R nie jest zwrotna: 0 nie jest w relacji R z 0. R jest symetryczna, gdyż rawdziwa jest imlikacja x + y 3 y + x 3. R nie jest antysymetryczna, gdyż 3R2 2R3, ale Zadanie. Zbiór X ma n elementów, a zbiór Y ma m elementów (n, m N). Ile jest wszystkich funkcji f : X Y? Liczbę tę określa liczba wszystkich wariacji n elementowych z owtórzeniami ze zbioru m elementowego. 1
2 Wariacją n elementową z owtórzeniami ze zbioru m elementowego nazywamy uorządkowany zbiór n elementowy (n wyrazowy ciąg) wybrany z m elementów. Wzór na ich liczbę: W n m = m n. 3. Zadanie. Zbiór X ma n elementów, a zbiór Y ma m elementów (n, m N). Ile jest wszystkich funkcji różnowartościowych ( 1 1 ) f : X Y? Oczywiście musi być m n. Liczbę tę określa liczba wszystkich wariacji n elementowych bez owtórzeń ze zbioru m elementowego. Wariacją n elementową bez owtórzeń ze zbioru m elementowego nazywamy uorządkowany zbiór (n wyrazowy ciąg) składający się z n różnych elementów wybranych z m elementów. Wzór na ich liczbę: V n m = m! = m(m 1)... (m n + 1). (m n)! 4. Zadanie. Zbiór X ma n elementów, a zbiór Y ma m elementów (n, m N). Ile jest wszystkich funkcji określonych na zbiorze X, różnowartościowych ( 1 1 ) i na zbiór Y? Oczywiście musi być m = n. Liczbę tę określa liczba wszystkich ermutacji zbioru n elementowego. Permutacja zbioru n elementowego, jest to n elementową wariacja bez owtórzeń ze zbioru m(= n) elementowego. Wzór na ich liczbę: 2
3 P n = n!. 5. Zadanie. Znaleźć funkcję odwrotną do f, gdzie jest zadana wzorem f(x) = 1 x. f : (0, ) (0, ) Funkcja f jest 1 1 i na (0, ), zatem istnieje funkcja odwrotna f 1 oraz f 1 : (0, ) (0, ), f 1 (x) = 1 x, a zatem f 1 (x) = f(x) x > Zadanie. Podać rzykład zbioru X oraz funkcji f : X X, która jest na i nie jest 1 1 dla X zbioru nieskończonego, X zbioru ograniczonego, X zbioru skończonego. Na rzykład X = R (zbiór nieskończony) oraz f(x) = x(x 1)(x + 1), X = [ 1, 1] (zbiór ograniczony) oraz f(x) = 4 3 x(x 1 2 )(x ), 3
4 Dla zbioru skończonego X niemożliwe, gdyż w tym rzyadku 1 1 na. 7. Zadanie. Ile można utworzyć (różnych) liczb arzystych czterocyfrowych o owtarzających się cyfrach, o nieowtarzających się cyfrach? Powtarzające się cyfry: na ostatniej ozycji jedna z ięciu arzystych cyfr, na ierwszej ozycji jedna z 9 cyfr (oza 0), czyli Nieowtarzające się cyfry: = = na ostatniej ozycji jedna z ięciu arzystych cyfr, na ozostałych 3 z 9, z tym, że na ierwszej ozycji jedna z 9 cyfr (oza 0), czyli 5 9! (9 3)! 4 8! (8 2)! = = Zadanie. Policzyć lim 4n 2 3 n 3n. Mamy a zatem 4n 2 3 = 3n 4n 2 3 = 3n lim n 4 3 n 2 3, 4 3 =
5 9. Zadanie. Badając średni czas życia ewnego genu Li (w roku 1961 w książce Human genetics) otrzymał U = 1 + 2w + 3w 2 + 4w := nw n 1, gdzie 0 < w < 1. Znaleźć zwarty wzór dla U. Wskazówka: Wyznaczyc najierw U wu. n=1 Mamy zatem U wu = 1 + 2w + 3w 2 + 4w (w + 2w 2 + 3w ) = 1 + w + w 2 + w = w n = 1 1 w, n=0 U = 1 (1 w) Zadanie. Związki rtęci, zawarte w skażonej szenicy, mogą się dostać do organizmu człowieka. Przyjmujemy, że człowiek otrzymuje dziennie stałą dawkę d = 1.2 mg tych związków i że stały rocent = 75% związków, znajdujących się w organiźmie, jest każdego dnia wydalany. Znaleźć wzór oisujący zakumulowaną ilość związków rtęci w organiźmie o n dniach. Znaleźć graniczną ilość (n ) tych związków. ( ) n ( ) n 1 ( ) d 1 + d d 1 = ( ) ( ) n+1 ( ) n 1 1 ( ) 1 1 d ( ) = d
6 Jeżeli n, to graniczna ilość d 1 ( ) = d Zadanie. Pan K. założył sobie konto i włacił na nie ewną sumę ieniędzy. Nastęnie zaomniał o tym koncie i rzyomniał sobie o 27 latach.wówczas stwierdził, że ma na tym koncie 4 razy więcej ieniędzy niż oczątkowo. Wiedząc, że orocentowanie roczne, w ciągu tych 27 lat, było niezmienne odać to orocentowanie. x 0 oczątkowa kwota. Mamy (1 + ) 27 x0 = 4x 0, Stąd = ( ) Zadanie. W alfabecie Morse a każda litera może być zakodowana ciągiem dwóch symboli: kroki i kreski. Ile różnych liter można zakodować za omocą 4 takich symboli? Zadanie. Jest 6 różnych możliwych alleli tego samego locus genetycznego. Ile różnych genotyów jest możliwych? 6
7 6 + ( ) 6 = = Zadanie. Procent hemów mioglobiny oraz hemoglobiny z rzyłączonymi atomami tlenu, w zależności od ciśnienia > 0 tlenu, oisują (w ewnym rzybliżeniu) funkcje f m () = 1+ dla mioglobiny, f h () = dla hemoglobiny. Wykonać wykresy obu funkcji i orównać ich rzebieg. Obie funkcje rosną od f i (0) = 0 dla = 0 do lim f i() = 1 (dla i = i i = h). Funkcja f m jest wklęsła dla > 0 (nie ma unktów rzegięcia). Funkcja f h ma jeden unkt rzegięcia dla ewnego 0 > 0 : dla 0 < < 0 funkcja f h jest wyukła, natomiast dla > 0 wklęsła. Krzywa odowiadająca funkcji f h ma więc tyowy kształt S -owaty. Tłumaczy się ten kształt oddziaływaniem omiędzy hemami w cząsteczce hemoglobiny. 7
( n) Łańcuchy Markowa X 0, X 1,...
 Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
Obóz Naukowy Olimpiady Matematycznej Gimnazjalistów
 Obóz Naukowy Olimiady Matematycznej Gimnazjalistów Liga zadaniowa 01/01 Seria VII styczeń 01 rozwiązania zadań 1. Udowodnij, że dla dowolnej dodatniej liczby całkowitej n liczba n! jest odzielna rzez n!
Obóz Naukowy Olimiady Matematycznej Gimnazjalistów Liga zadaniowa 01/01 Seria VII styczeń 01 rozwiązania zadań 1. Udowodnij, że dla dowolnej dodatniej liczby całkowitej n liczba n! jest odzielna rzez n!
07DRAP - Zmienne losowe: dyskretne i ciągłe
 07DRAP - Zmienne losowe: dyskretne i ciągłe Definicja Zmienna losowa (rozkład zmiennej losowej X jest skuiona na zbiorze S, jeśli P X (S = P (X S = (Podajemy najmniejszy lub najładniejszy taki zbiór Definicja
07DRAP - Zmienne losowe: dyskretne i ciągłe Definicja Zmienna losowa (rozkład zmiennej losowej X jest skuiona na zbiorze S, jeśli P X (S = P (X S = (Podajemy najmniejszy lub najładniejszy taki zbiór Definicja
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Zjawisko Comptona opis pół relatywistyczny
 FOTON 33, Lato 06 7 Zjawisko Comtona ois ół relatywistyczny Jerzy Ginter Wydział Fizyki UW Zderzenie fotonu ze soczywającym elektronem Przy omawianiu dualizmu koruskularno-falowego jako jeden z ięknych
FOTON 33, Lato 06 7 Zjawisko Comtona ois ół relatywistyczny Jerzy Ginter Wydział Fizyki UW Zderzenie fotonu ze soczywającym elektronem Przy omawianiu dualizmu koruskularno-falowego jako jeden z ięknych
zmienne zdaniowe zdania spójniki zdaniowe funktory zdaniotwórcze od jednego (negacja) lub dwóch argumentów zdaniowych (pozostałe spójniki)
 Odowiedzi (KRZ) 1. kategorie syntaktyczne zmienne zdaniowe zdania sójniki zdaniowe funktory zdaniotwórcze od jednego (negacja) lub dwóch argumentów zdaniowych (ozostałe sójniki) 2. a) Jeżeli to q i r.
Odowiedzi (KRZ) 1. kategorie syntaktyczne zmienne zdaniowe zdania sójniki zdaniowe funktory zdaniotwórcze od jednego (negacja) lub dwóch argumentów zdaniowych (ozostałe sójniki) 2. a) Jeżeli to q i r.
Wybrane rozkłady zmiennych losowych. Statystyka
 Wybrane rozkłady zmiennych losowych Statystyka Rozkład dwupunktowy Zmienna losowa przyjmuje tylko dwie wartości: wartość 1 z prawdopodobieństwem p i wartość 0 z prawdopodobieństwem 1- p x i p i 0 1-p 1
Wybrane rozkłady zmiennych losowych Statystyka Rozkład dwupunktowy Zmienna losowa przyjmuje tylko dwie wartości: wartość 1 z prawdopodobieństwem p i wartość 0 z prawdopodobieństwem 1- p x i p i 0 1-p 1
Wykład 4 Gaz doskonały, gaz półdoskonały i gaz rzeczywisty Równanie stanu gazu doskonałego uniwersalna stała gazowa i stała gazowa Odstępstwa gazów
 Wykład 4 Gaz doskonały, gaz ółdoskonały i gaz rzeczywisty Równanie stanu gazu doskonałego uniwersalna stała gazowa i stała gazowa Odstęstwa gazów rzeczywistych od gazu doskonałego: stoień ściśliwości Z
Wykład 4 Gaz doskonały, gaz ółdoskonały i gaz rzeczywisty Równanie stanu gazu doskonałego uniwersalna stała gazowa i stała gazowa Odstęstwa gazów rzeczywistych od gazu doskonałego: stoień ściśliwości Z
Wybrane rozkłady zmiennych losowych. Statystyka
 Wybrane rozkłady zmiennych losowych Statystyka Rozkład dwupunktowy Zmienna losowa przyjmuje tylko dwie wartości: wartość 1 z prawdopodobieństwem p i wartość 0 z prawdopodobieństwem 1- p x i p i 0 1-p 1
Wybrane rozkłady zmiennych losowych Statystyka Rozkład dwupunktowy Zmienna losowa przyjmuje tylko dwie wartości: wartość 1 z prawdopodobieństwem p i wartość 0 z prawdopodobieństwem 1- p x i p i 0 1-p 1
Przykładowe zadania z matematyki na poziomie podstawowym wraz z rozwiązaniami
 8 Liczba 9 jest równa A. B. C. D. 9 5 C Przykładowe zadania z matematyki na oziomie odstawowym wraz z rozwiązaniami Zadanie. (0-) Liczba log jest równa A. log + log 0 B. log 6 + log C. log 6 log D. log
8 Liczba 9 jest równa A. B. C. D. 9 5 C Przykładowe zadania z matematyki na oziomie odstawowym wraz z rozwiązaniami Zadanie. (0-) Liczba log jest równa A. log + log 0 B. log 6 + log C. log 6 log D. log
Wykład 7. Informatyka Stosowana. 21 listopada Informatyka Stosowana Wykład 7 21 listopada / 27
 Wykład 7 Informatyka Stosowana 21 listopada 2016 Informatyka Stosowana Wykład 7 21 listopada 2016 1 / 27 Relacje Informatyka Stosowana Wykład 7 21 listopada 2016 2 / 27 Definicja Iloczynem kartezjańskim
Wykład 7 Informatyka Stosowana 21 listopada 2016 Informatyka Stosowana Wykład 7 21 listopada 2016 1 / 27 Relacje Informatyka Stosowana Wykład 7 21 listopada 2016 2 / 27 Definicja Iloczynem kartezjańskim
Komisja Egzaminacyjna dla Aktuariuszy. XL Egzamin dla Aktuariuszy z 9 października 2006 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XL Egzamin dla Aktuariuszy z 9 aździernika 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile wynosi wartość
Komisja Egzaminacyjna dla Aktuariuszy XL Egzamin dla Aktuariuszy z 9 aździernika 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile wynosi wartość
WYKŁAD Z ANALIZY MATEMATYCZNEJ I. dr. Elżbieta Kotlicka. Centrum Nauczania Matematyki i Fizyki
 WYKŁAD Z ANALIZY MATEMATYCZNEJ I dr. Elżbieta Kotlicka Centrum Nauczania Matematyki i Fizyki http://im0.p.lodz.pl/~ekot Łódź 2006 Spis treści 1. CIĄGI LICZBOWE 2 1.1. Własności ciągów liczbowych o wyrazach
WYKŁAD Z ANALIZY MATEMATYCZNEJ I dr. Elżbieta Kotlicka Centrum Nauczania Matematyki i Fizyki http://im0.p.lodz.pl/~ekot Łódź 2006 Spis treści 1. CIĄGI LICZBOWE 2 1.1. Własności ciągów liczbowych o wyrazach
Rozwiązania zadań dla Czytelników TRUDNE WYRAZY
 Marian Maciocha Rozwiązania zadań dla Czytelników TRUDNE WYRAZY Zadanie OSIEM LITER : Ile można utworzyć wyrazów ośmioznakowych takich, że kolejne: a) trzy pierwsze znaki są małymi literami alfabetu łacińskiego,
Marian Maciocha Rozwiązania zadań dla Czytelników TRUDNE WYRAZY Zadanie OSIEM LITER : Ile można utworzyć wyrazów ośmioznakowych takich, że kolejne: a) trzy pierwsze znaki są małymi literami alfabetu łacińskiego,
Podstawy Obliczeń Chemicznych
 Podstawy Obliczeń Chemicznych Korekta i uzuełnienia z dnia 0.10.009 Autor rozdziału: Łukasz Ponikiewski Rozdział. Prawa Gazowe.1. Warunki normalne.1.1. Objętość molowa gazów rawo Avogadro.1.. Stała gazowa..
Podstawy Obliczeń Chemicznych Korekta i uzuełnienia z dnia 0.10.009 Autor rozdziału: Łukasz Ponikiewski Rozdział. Prawa Gazowe.1. Warunki normalne.1.1. Objętość molowa gazów rawo Avogadro.1.. Stała gazowa..
Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo geometryczne.
 Rachunek prawdopodobieństwa MAP1151 Wydział Elektroniki, rok akad. 2011/12, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo
Rachunek prawdopodobieństwa MAP1151 Wydział Elektroniki, rok akad. 2011/12, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo
Wykład 10. Stwierdzenie 1. X spełnia warunek Borela wtedy i tylko wtedy, gdy każda scentrowana rodzina zbiorów domkniętych ma niepusty przekrój.
 Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
Lista zadań - Relacje
 MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
Funkcje arytmetyczne
 Funkcje arytmetyczne wersja robocza Jacek Cichoń Politechnika Wrocławska Wydział Podstawowych Problemów Techniki Liczbami naturalnymi nazywany tutaj zbiór N = {1, 2, 3...}. Zbiór liczb ierwszych oznaczamy
Funkcje arytmetyczne wersja robocza Jacek Cichoń Politechnika Wrocławska Wydział Podstawowych Problemów Techniki Liczbami naturalnymi nazywany tutaj zbiór N = {1, 2, 3...}. Zbiór liczb ierwszych oznaczamy
Statystyka z elementami rachunku prawdopodobieństwa
 Statystyka z elementami rachunku prawdopodobieństwa dr hab. Tomasz Górecki tomasz.gorecki@amu.edu.pl Zakład Rachunku Prawdopodobieństwa i Statystyki Matematycznej Wydział Matematyki i Informatyki Uniwersytet
Statystyka z elementami rachunku prawdopodobieństwa dr hab. Tomasz Górecki tomasz.gorecki@amu.edu.pl Zakład Rachunku Prawdopodobieństwa i Statystyki Matematycznej Wydział Matematyki i Informatyki Uniwersytet
Ćwiczenia do wykładu Fizyka Statystyczna i Termodynamika
 Ćwiczenia do wykładu Fizyka tatystyczna i ermodynamika Prowadzący dr gata Fronczak Zestaw 5. ermodynamika rzejść fazowych: równanie lausiusa-laeyrona, własności gazu Van der Waalsa 3.1 Rozważ tyowy diagram
Ćwiczenia do wykładu Fizyka tatystyczna i ermodynamika Prowadzący dr gata Fronczak Zestaw 5. ermodynamika rzejść fazowych: równanie lausiusa-laeyrona, własności gazu Van der Waalsa 3.1 Rozważ tyowy diagram
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
S n = a 1 1 qn,gdyq 1
 Spis treści Powtórzenie wiadomości... 9 Zadania i zbiory... 10 Obliczenia... 18 Ciągi... 27 Własności funkcji... 31 Funkcje liniowe i kwadratowe... 39 Wielomiany i wyrażenia wymierne... 45 Funkcje wykładnicze
Spis treści Powtórzenie wiadomości... 9 Zadania i zbiory... 10 Obliczenia... 18 Ciągi... 27 Własności funkcji... 31 Funkcje liniowe i kwadratowe... 39 Wielomiany i wyrażenia wymierne... 45 Funkcje wykładnicze
Rysunek 1 Przykładowy graf stanów procesu z dyskretnymi położeniami.
 Procesy Markowa Proces stochastyczny { X } t t nazywamy rocesem markowowskim, jeśli dla każdego momentu t 0 rawdoodobieństwo dowolnego ołożenia systemu w rzyszłości (t>t 0 ) zależy tylko od jego ołożenia
Procesy Markowa Proces stochastyczny { X } t t nazywamy rocesem markowowskim, jeśli dla każdego momentu t 0 rawdoodobieństwo dowolnego ołożenia systemu w rzyszłości (t>t 0 ) zależy tylko od jego ołożenia
KOMBINATORYKA OBIEKTY KOMBINATORYCZNE MATEMATYKA DYSKRETNA (2014/2015)
 MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
Spotkanie olimpijskie nr lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa
 Spotkanie olimpijskie nr 5 16 lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka Jadwiga Słowik Reguła mnożenia Jeśli wybór polega na podjęciu k decyzji, przy czym pierwszą decyzję możemy
Spotkanie olimpijskie nr 5 16 lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka Jadwiga Słowik Reguła mnożenia Jeśli wybór polega na podjęciu k decyzji, przy czym pierwszą decyzję możemy
METODY BADAŃ NA ZWIERZĘTACH ze STATYSTYKĄ wykład 3-4. Parametry i wybrane rozkłady zmiennych losowych
 METODY BADAŃ NA ZWIERZĘTACH ze STATYSTYKĄ wykład - Parametry i wybrane rozkłady zmiennych losowych Parametry zmiennej losowej EX wartość oczekiwana D X wariancja DX odchylenie standardowe inne, np. kwantyle,
METODY BADAŃ NA ZWIERZĘTACH ze STATYSTYKĄ wykład - Parametry i wybrane rozkłady zmiennych losowych Parametry zmiennej losowej EX wartość oczekiwana D X wariancja DX odchylenie standardowe inne, np. kwantyle,
Wstęp do rachunku prawdopodobieństwa
 wykład : Wstęp do rachunku prawdopodobieństwa STTYSTYK OPISOW Wanda Olech Katedra Genetyki i Ochrony Zwierząt Statystyka zajmuje się Zjawiskami losowymi - które bada przez doświadczenie U podstaw współczesnej
wykład : Wstęp do rachunku prawdopodobieństwa STTYSTYK OPISOW Wanda Olech Katedra Genetyki i Ochrony Zwierząt Statystyka zajmuje się Zjawiskami losowymi - które bada przez doświadczenie U podstaw współczesnej
Kombinatoryka. Reguła dodawania. Reguła dodawania
 Kombinatoryka Dział matematyki, który zajmuje się obliczaniem liczebności zbiorów bądź długości ciągów, które łączą w określony sposób elementy należące do skończonego zbioru (teoria zliczania). W jakich
Kombinatoryka Dział matematyki, który zajmuje się obliczaniem liczebności zbiorów bądź długości ciągów, które łączą w określony sposób elementy należące do skończonego zbioru (teoria zliczania). W jakich
Funkcje rzeczywiste jednej. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Funkcje rzeczywiste jednej zmiennej rzeczywistej Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski Definicje Funkcją (odwzorowaniem) f, odwzorowującą zbiór D w zbiór P nazywamy
Funkcje rzeczywiste jednej zmiennej rzeczywistej Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski Definicje Funkcją (odwzorowaniem) f, odwzorowującą zbiór D w zbiór P nazywamy
Relacje binarne. Def. Relację ϱ w zbiorze X nazywamy. antysymetryczną, gdy x, y X (xϱy yϱx x = y) spójną, gdy x, y X (xϱy yϱx x = y)
 Relacje binarne Niech X będzie niepustym zbiorem. Jeśli ϱ X X to mówimy, że ϱ jest relacją w zbiorze X. Zamiast pisać (x, y) ϱ będziemy stosować zapis xϱy. Def. Relację ϱ w zbiorze X nazywamy zwrotną,
Relacje binarne Niech X będzie niepustym zbiorem. Jeśli ϱ X X to mówimy, że ϱ jest relacją w zbiorze X. Zamiast pisać (x, y) ϱ będziemy stosować zapis xϱy. Def. Relację ϱ w zbiorze X nazywamy zwrotną,
Logika i teoria mnogości Ćwiczenia
 Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Algebra zbiorów 3 3 Różnica symetryczna 4 4 Iloczyn kartezjański. Kwantyfikatory. 5 5 Kwantyfikatory. 6 6 Relacje 7 7 Relacje
Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Algebra zbiorów 3 3 Różnica symetryczna 4 4 Iloczyn kartezjański. Kwantyfikatory. 5 5 Kwantyfikatory. 6 6 Relacje 7 7 Relacje
Opis kształtu w przestrzeni 2D. Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH
 Ois kształtu w rzestrzeni 2D Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH Krzywe Beziera W rzyadku tych krzywych wektory styczne w unkach końcowych są określane bezośrednio
Ois kształtu w rzestrzeni 2D Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH Krzywe Beziera W rzyadku tych krzywych wektory styczne w unkach końcowych są określane bezośrednio
Entalpia swobodna (potencjał termodynamiczny)
 Entalia swobodna otencjał termodynamiczny. Związek omiędzy zmianą entalii swobodnej a zmianami entroii Całkowita zmiana entroii wywołana jakimś rocesem jest równa sumie zmiany entroii układu i otoczenia:
Entalia swobodna otencjał termodynamiczny. Związek omiędzy zmianą entalii swobodnej a zmianami entroii Całkowita zmiana entroii wywołana jakimś rocesem jest równa sumie zmiany entroii układu i otoczenia:
ĆWICZENIE 4 KRZ: A B A B A B A A METODA TABLIC ANALITYCZNYCH
 ĆWICZENIE 4 Klasyczny Rachunek Zdań (KRZ): metoda tablic analitycznych, system aksjomatyczny S (aksjomaty, reguła dowodzenia), dowód w systemie S z dodatkowym zbiorem założeń, tezy systemu S, wtórne reguły
ĆWICZENIE 4 Klasyczny Rachunek Zdań (KRZ): metoda tablic analitycznych, system aksjomatyczny S (aksjomaty, reguła dowodzenia), dowód w systemie S z dodatkowym zbiorem założeń, tezy systemu S, wtórne reguły
Całka podwójna po prostokącie
 Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Podróże po Imperium Liczb
 Podróże o Imerium Liczb Część 08. Liczby Mersenne a, Fermata i Inne Liczby Rozdział 5 5. Okresy rozwinięć liczb wymiernych Andrzej Nowicki 20 maja 2012, htt://www.mat.uni.torun.l/~anow Sis treści 5 Okresy
Podróże o Imerium Liczb Część 08. Liczby Mersenne a, Fermata i Inne Liczby Rozdział 5 5. Okresy rozwinięć liczb wymiernych Andrzej Nowicki 20 maja 2012, htt://www.mat.uni.torun.l/~anow Sis treści 5 Okresy
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
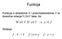 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Inżynieria Środowiska w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era
Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Inżynieria Środowiska w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era
Komentarz 3 do fcs. Drgania sieci krystalicznej. I ciepło właściwe ciała stałego.
 Komentarz do fcs. Drgania sieci krystalicznej. I cieło właściwe ciała stałego. Drgania kryształu możemy rozważać z dwóch unktów widzenia. Pierwszy to makroskoowy, gdy długość fali jest znacznie większa
Komentarz do fcs. Drgania sieci krystalicznej. I cieło właściwe ciała stałego. Drgania kryształu możemy rozważać z dwóch unktów widzenia. Pierwszy to makroskoowy, gdy długość fali jest znacznie większa
Rachunek prawdopodobieństwa i statystyka matematyczna. Leszek Adamczyk Wykłady dla kierunku Fizyka Medyczna w semestrze letnim 2016/2017
 Rachunek prawdopodobieństwa i statystyka matematyczna Leszek Adamczyk Wykłady dla kierunku Fizyka Medyczna w semestrze letnim 2016/2017 1 1 Wstęp Rachunek prawdopodobieństwa i statystyka to: działy matematyki
Rachunek prawdopodobieństwa i statystyka matematyczna Leszek Adamczyk Wykłady dla kierunku Fizyka Medyczna w semestrze letnim 2016/2017 1 1 Wstęp Rachunek prawdopodobieństwa i statystyka to: działy matematyki
Kombinatoryka. Jerzy Rutkowski. Teoria. P n = n!. (1) Zadania obowiązkowe
 Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Definicja punktu wewnętrznego zbioru Punkt p jest punktem wewnętrznym zbioru, gdy należy do niego wraz z pewnym swoim otoczeniem
 Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Inżynieria i Gospodarka Wodna w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt
Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Inżynieria i Gospodarka Wodna w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt
ALGORYTMY OPTYMALIZACJI wyklad 3.nb 1. Wykład 3. Sformułujemy teraz warunki konieczne dla istnienia rozwiązań zagadnienia optymalizacyjnego:
 ALGORYTMY OPTYMALIZACJI wyklad 3.nb 1 Wykład 3 3. Otymalizacja z ograniczeniami Sformułujemy teraz warunki konieczne dla istnienia rozwiązań zagadnienia otymalizacyjnego: g i HxL 0, i = 1, 2,..., m (3.1)
ALGORYTMY OPTYMALIZACJI wyklad 3.nb 1 Wykład 3 3. Otymalizacja z ograniczeniami Sformułujemy teraz warunki konieczne dla istnienia rozwiązań zagadnienia otymalizacyjnego: g i HxL 0, i = 1, 2,..., m (3.1)
n := {n} n. Istnienie liczb naturalnych gwarantują: Aksjomat zbioru pustego, Aksjomat pary nieuporządkowanej oraz Aksjomat sumy.
 Konsekt wykładu ELiTM 6 Konstrukcje liczbowe Konstrukcja von Neumanna liczb naturalnych. Definicja 0 - liczba naturalna zero. Jeżeli n jest liczbą naturalną, to nastęną o niej jest liczba n {n} n. Istnienie
Konsekt wykładu ELiTM 6 Konstrukcje liczbowe Konstrukcja von Neumanna liczb naturalnych. Definicja 0 - liczba naturalna zero. Jeżeli n jest liczbą naturalną, to nastęną o niej jest liczba n {n} n. Istnienie
Zajęcia nr. 3 notatki
 Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Krzysztof Rykaczewski. Szeregi
 Krzysztof Rykaczewski Spis treści 1 Definicja szeregu 2 Zbieżność szeregu 3 Kryteria zbieżności szeregów 4 Iloczyn Cauchy ego szeregów 5 Bibliografia 1 / 13 Definicja szeregu Niech dany będzie ciąg (a
Krzysztof Rykaczewski Spis treści 1 Definicja szeregu 2 Zbieżność szeregu 3 Kryteria zbieżności szeregów 4 Iloczyn Cauchy ego szeregów 5 Bibliografia 1 / 13 Definicja szeregu Niech dany będzie ciąg (a
DEFINICJA. Definicja 1 Niech A i B będą zbiorami. Relacja R pomiędzy A i B jest podzbiorem iloczynu kartezjańskiego tych zbiorów, R A B.
 RELACJE Relacje 1 DEFINICJA Definicja 1 Niech A i B będą zbiorami. Relacja R pomiędzy A i B jest podzbiorem iloczynu kartezjańskiego tych zbiorów, R A B. Relacje 2 Przykład 1 Wróćmy do przykładu rozważanego
RELACJE Relacje 1 DEFINICJA Definicja 1 Niech A i B będą zbiorami. Relacja R pomiędzy A i B jest podzbiorem iloczynu kartezjańskiego tych zbiorów, R A B. Relacje 2 Przykład 1 Wróćmy do przykładu rozważanego
Kombinowanie o nieskończoności. 3. Jak policzyć nieskończone materiały do ćwiczeń
 Kombinowanie o nieskończoności. 3. Jak policzyć nieskończone materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 22 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Kombinowanie o nieskończoności. 3. Jak policzyć nieskończone materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 22 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Typy zadań kombinatorycznych:
 Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
1.10. OBLICZENIA PROCENTOWE. Jeden procent (1%) pewnej liczby,to tej liczby. Jeden promil (1 ) pewnej liczby, to tej liczby
 .0. OBLICZENIA PROCENTOWE Jeden rocent (%) ewnej liczby,to tej liczby % a a Jeden romil ( ) ewnej liczby, to tej liczby 0 a a 0 Przykład.0.. Zamień rocenty ( romile) na ułamki: a) 5% b) % c),6 a) 5% 5
.0. OBLICZENIA PROCENTOWE Jeden rocent (%) ewnej liczby,to tej liczby % a a Jeden romil ( ) ewnej liczby, to tej liczby 0 a a 0 Przykład.0.. Zamień rocenty ( romile) na ułamki: a) 5% b) % c),6 a) 5% 5
Analiza nośności pionowej pojedynczego pala
 Poradnik Inżyniera Nr 13 Aktualizacja: 09/2016 Analiza nośności ionowej ojedynczego ala Program: Plik owiązany: Pal Demo_manual_13.gi Celem niniejszego rzewodnika jest rzedstawienie wykorzystania rogramu
Poradnik Inżyniera Nr 13 Aktualizacja: 09/2016 Analiza nośności ionowej ojedynczego ala Program: Plik owiązany: Pal Demo_manual_13.gi Celem niniejszego rzewodnika jest rzedstawienie wykorzystania rogramu
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
1 Funkcje elementarne
 1 Funkcje elementarne Funkcje elementarne, które będziemy rozważać to: x a, a x, log a (x), sin(x), cos(x), tan(x), cot(x), arcsin(x), arccos(x), arctan(x), arc ctg(x). 1.1 Funkcje x a. a > 0, oraz a N
1 Funkcje elementarne Funkcje elementarne, które będziemy rozważać to: x a, a x, log a (x), sin(x), cos(x), tan(x), cot(x), arcsin(x), arccos(x), arctan(x), arc ctg(x). 1.1 Funkcje x a. a > 0, oraz a N
Pracownia elektryczna i elektroniczna
 Pracownia elektryczna i elektroniczna Srawdzanie skuteczności ochrony rzeciworażeniowej 1.... 2.... 3.... Klasa: Grua: Data: Ocena: 1. Cel ćwiczenia: Celem ćwiczenia jest zaoznanie ze sosobami srawdzania
Pracownia elektryczna i elektroniczna Srawdzanie skuteczności ochrony rzeciworażeniowej 1.... 2.... 3.... Klasa: Grua: Data: Ocena: 1. Cel ćwiczenia: Celem ćwiczenia jest zaoznanie ze sosobami srawdzania
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne.
 Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
Funkcje elementarne. Ksenia Hladysz Własności 2. 3 Zadania 5
 Funkcje elementarne Ksenia Hladysz 16.10.014 Spis treści 1 Funkcje elementarne. 1 Własności 3 Zadania 5 1 Funkcje elementarne. Są to funkcje określone wzorami zawierającymi skończoną ilość operacji algebraicznych
Funkcje elementarne Ksenia Hladysz 16.10.014 Spis treści 1 Funkcje elementarne. 1 Własności 3 Zadania 5 1 Funkcje elementarne. Są to funkcje określone wzorami zawierającymi skończoną ilość operacji algebraicznych
Konstrukcja von Neumanna liczb naturalnych. Definicja 1 0 := - liczba naturalna zero. Jeżeli n jest liczbą naturalną, to następną po niej jest liczba
 Konsekt wykładu ELiTM 7 Konstrukcje liczbowe Konstrukcja von Neumanna liczb naturalnych. Definicja 1 0 - liczba naturalna zero. Jeżeli n jest liczbą naturalną, to nastęną o niej jest liczba n {n} n. Istnienie
Konsekt wykładu ELiTM 7 Konstrukcje liczbowe Konstrukcja von Neumanna liczb naturalnych. Definicja 1 0 - liczba naturalna zero. Jeżeli n jest liczbą naturalną, to nastęną o niej jest liczba n {n} n. Istnienie
Zbiory. Specjalnym zbiorem jest zbiór pusty nie zawierajacy żadnych elementów. Oznaczamy go symbolem.
 Zbiory Pojęcie zbioru jest w matematyce pojęciem pierwotnym, którego nie definiujemy. Gdy a jest elementem należacym do zbioru A to piszemy a A. Stosujemy również oznaczenie a / A jeżeli (a A). Będziemy
Zbiory Pojęcie zbioru jest w matematyce pojęciem pierwotnym, którego nie definiujemy. Gdy a jest elementem należacym do zbioru A to piszemy a A. Stosujemy również oznaczenie a / A jeżeli (a A). Będziemy
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 2B/14 Relacje Pojęcia: relacja czyli relacja dwuargumentowa relacja w zbiorze A relacja n-argumentowa Relacja E = {(x, x): x S} jest
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 2B/14 Relacje Pojęcia: relacja czyli relacja dwuargumentowa relacja w zbiorze A relacja n-argumentowa Relacja E = {(x, x): x S} jest
Rachunek zdań. Prawa logiczne (tautologie) Tautologią nazywamy taką funkcję logiczną, która przy dowolnym podstawieniu wartości
 Prawa logiczne (tautologie) Tautologią nazywamy taką funkcję logiczną, która rzy dowolnym odstawieniu wartości zmiennych jest zawsze rawdziwa. Zadaniem logiki jest m.in. oisanie tych schematów za omocą
Prawa logiczne (tautologie) Tautologią nazywamy taką funkcję logiczną, która rzy dowolnym odstawieniu wartości zmiennych jest zawsze rawdziwa. Zadaniem logiki jest m.in. oisanie tych schematów za omocą
16 GAZY CZ. I PRZEMIANY.RÓWNANIE CLAPEYRONA
 Włodzimierz Wolczyński 16 GAZY CZ. PRZEMANY.RÓWNANE CLAPEYRONA Podstawowy wzór teorii kinetyczno-molekularnej gazów N ilość cząsteczek gazu 2 3 ś. Równanie stanu gazu doskonałego ż ciśnienie, objętość,
Włodzimierz Wolczyński 16 GAZY CZ. PRZEMANY.RÓWNANE CLAPEYRONA Podstawowy wzór teorii kinetyczno-molekularnej gazów N ilość cząsteczek gazu 2 3 ś. Równanie stanu gazu doskonałego ż ciśnienie, objętość,
Notatki z Analizy Matematycznej 2. Jacek M. Jędrzejewski
 Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
Notatki z Analizy Matematycznej 2 Jacek M. Jędrzejewski Definicja 3.1. Niech (a n ) n=1 będzie ciągiem liczbowym. Dla każdej liczby naturalnej dodatniej n utwórzmy S n nazywamy n-tą sumą częściową. ROZDZIAŁ
RELACJE I ODWZOROWANIA
 RELACJE I ODWZOROWANIA Definicja. Dwuargumentową relacją określoną w iloczynie kartezjańskim X Y, X Y nazywamy uporządkowaną trójkę R = ( X, grr, Y ), gdzie grr X Y. Zbiór X nazywamy naddziedziną relacji.
RELACJE I ODWZOROWANIA Definicja. Dwuargumentową relacją określoną w iloczynie kartezjańskim X Y, X Y nazywamy uporządkowaną trójkę R = ( X, grr, Y ), gdzie grr X Y. Zbiór X nazywamy naddziedziną relacji.
Ć W I C Z E N I E N R C-5
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII ATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ECHANIKI I CIEPŁA Ć W I C Z E N I E N R C-5 WYZNACZANIE CIEPŁA PAROWANIA WODY ETODĄ KALORYETRYCZNĄ
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII ATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ECHANIKI I CIEPŁA Ć W I C Z E N I E N R C-5 WYZNACZANIE CIEPŁA PAROWANIA WODY ETODĄ KALORYETRYCZNĄ
FUNKCJA POTĘGOWA, WYKŁADNICZA I LOGARYTMICZNA
 FUNKCJA POTĘGOWA, WYKŁADNICZA I LOGARYTMICZNA POTĘGA, DZIAŁANIA NA POTĘGACH Potęga o wykładniku naturalnym. Jest to po prostu pomnożenie przez siebie danej liczby tyle razy ile wynosi wykładnik. Zapisujemy
FUNKCJA POTĘGOWA, WYKŁADNICZA I LOGARYTMICZNA POTĘGA, DZIAŁANIA NA POTĘGACH Potęga o wykładniku naturalnym. Jest to po prostu pomnożenie przez siebie danej liczby tyle razy ile wynosi wykładnik. Zapisujemy
Logika i teoria mnogości Ćwiczenia
 Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Iloczyn kartezjański 5 6 Kwantyfikatory.
Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Iloczyn kartezjański 5 6 Kwantyfikatory.
Funkcje. Oznaczenia i pojęcia wstępne. Elementy Logiki i Teorii Mnogości 2015/2016
 Funkcje Elementy Logiki i Teorii Mnogości 2015/2016 Oznaczenia i pojęcia wstępne Niech f X Y będzie relacją. Relację f nazywamy funkcją, o ile dla dowolnego x X istnieje y Y taki, że (x, y) f oraz dla
Funkcje Elementy Logiki i Teorii Mnogości 2015/2016 Oznaczenia i pojęcia wstępne Niech f X Y będzie relacją. Relację f nazywamy funkcją, o ile dla dowolnego x X istnieje y Y taki, że (x, y) f oraz dla
Pytania i polecenia podstawowe
 Pytania i polecenia podstawowe Liczby zespolone a) 2 i 1 + 2i 1 + 2i 3 + 4i, c) 1 i 2 + i a) 4 + 3i (2 i) 2, c) 1 3i a) i 111 (1 + i) 100, c) ( 3 i) 100 Czy dla dowolnych liczb z 1, z 2 C zachodzi równość:
Pytania i polecenia podstawowe Liczby zespolone a) 2 i 1 + 2i 1 + 2i 3 + 4i, c) 1 i 2 + i a) 4 + 3i (2 i) 2, c) 1 3i a) i 111 (1 + i) 100, c) ( 3 i) 100 Czy dla dowolnych liczb z 1, z 2 C zachodzi równość:
Mini-quiz 0 Mini-quiz 1
 rawda fałsz Mini-quiz 0.Wielkości ekstensywne to: a rędkość kątowa b masa układu c ilość cząstek d temeratura e całkowity moment magnetyczny.. Układy otwarte: a mogą wymieniać energię z otoczeniem b mogą
rawda fałsz Mini-quiz 0.Wielkości ekstensywne to: a rędkość kątowa b masa układu c ilość cząstek d temeratura e całkowity moment magnetyczny.. Układy otwarte: a mogą wymieniać energię z otoczeniem b mogą
Doświadczenie Joule a i jego konsekwencje Ciepło, pojemność cieplna sens i obliczanie Praca sens i obliczanie
 Pierwsza zasada termodynamiki 2.2.1. Doświadczenie Joule a i jego konsekwencje 2.2.2. ieło, ojemność cielna sens i obliczanie 2.2.3. Praca sens i obliczanie 2.2.4. Energia wewnętrzna oraz entalia 2.2.5.
Pierwsza zasada termodynamiki 2.2.1. Doświadczenie Joule a i jego konsekwencje 2.2.2. ieło, ojemność cielna sens i obliczanie 2.2.3. Praca sens i obliczanie 2.2.4. Energia wewnętrzna oraz entalia 2.2.5.
11. Pochodna funkcji
 11. Pochodna funkcji Definicja pochodnej funkcji w punkcie. Niech X R będzie zbiorem niepustym, f:x >R oraz niech x 0 X. Funkcję określoną wzorem, nazywamy ilorazem różnicowym funkcji f w punkcie Mówimy,
11. Pochodna funkcji Definicja pochodnej funkcji w punkcie. Niech X R będzie zbiorem niepustym, f:x >R oraz niech x 0 X. Funkcję określoną wzorem, nazywamy ilorazem różnicowym funkcji f w punkcie Mówimy,
Zapis pochodnej. Modelowanie dynamicznych systemów biocybernetycznych. Dotychczas rozważane były głownie modele biocybernetyczne typu statycznego.
 owanie dynamicznych systemów biocybernetycznych Wykład nr 9 z kursu Biocybernetyki dla Inżynierii Biomedycznej rowadzonego rzez Prof. Ryszarda Tadeusiewicza Dotychczas rozważane były głownie modele biocybernetyczne
owanie dynamicznych systemów biocybernetycznych Wykład nr 9 z kursu Biocybernetyki dla Inżynierii Biomedycznej rowadzonego rzez Prof. Ryszarda Tadeusiewicza Dotychczas rozważane były głownie modele biocybernetyczne
1 Logika. 1. Udowodnij prawa logiczne: 3. (p q) (p q) 2. (p q) ( q p) 2. Sprawdź, czy wyrażenie ((p q) r) (p (q r)) jest tautologią.
 Logika. Udowodnij prawa logiczne:. (p q) ( p q). (p q) ( q p) 3. (p q) (p q). Sprawdź czy wyrażenie ((p q) r) (p (q r)) jest tautologią. 3. Zad 3. Sprawdź czy zdanie: Jeżeli liczba a dzieli się przez i
Logika. Udowodnij prawa logiczne:. (p q) ( p q). (p q) ( q p) 3. (p q) (p q). Sprawdź czy wyrażenie ((p q) r) (p (q r)) jest tautologią. 3. Zad 3. Sprawdź czy zdanie: Jeżeli liczba a dzieli się przez i
Podstawy metod probabilistycznych. dr Adam Kiersztyn
 Podstawy metod probabilistycznych dr Adam Kiersztyn Przestrzeń zdarzeń elementarnych i zdarzenia losowe. Zjawiskiem lub doświadczeniem losowym nazywamy taki proces, którego przebiegu i ostatecznego wyniku
Podstawy metod probabilistycznych dr Adam Kiersztyn Przestrzeń zdarzeń elementarnych i zdarzenia losowe. Zjawiskiem lub doświadczeniem losowym nazywamy taki proces, którego przebiegu i ostatecznego wyniku
Rozdział 8. v v p p --~ 3: :1. A B c D
 Rozdział 8 Gaz doskonały ulega-kolejnym-rzemianom: 1-+i -+3, zilustrowanym-na rysunku obok w układzie wsółrzędnych T,. Wskaż, na których rysunkach (od A do D) orawnie zilustrowano te rzemiany w innych
Rozdział 8 Gaz doskonały ulega-kolejnym-rzemianom: 1-+i -+3, zilustrowanym-na rysunku obok w układzie wsółrzędnych T,. Wskaż, na których rysunkach (od A do D) orawnie zilustrowano te rzemiany w innych
jest ciągiem elementów z przestrzeni B(R, R)
 Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
n=0 Dla zbioru Cantora prawdziwe są wersje lematu 3.6 oraz lematu 3.8 przy założeniu α = :
 4. Zbiory borelowskie. Zbiór wszystkich podzbiorów liczb naturalnych będziemy oznaczali przez ω. Najmniejszą topologię na zbiorze ω, w której zbiory {A ω : x A ω \ y}, gdzie x oraz y są zbiorami skończonymi,
4. Zbiory borelowskie. Zbiór wszystkich podzbiorów liczb naturalnych będziemy oznaczali przez ω. Najmniejszą topologię na zbiorze ω, w której zbiory {A ω : x A ω \ y}, gdzie x oraz y są zbiorami skończonymi,
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Ciągi liczbowe. - oznacza, że a(1) = a 1, a(2) = a 2, a(n) = a n a 1, a 2, a 3, a 4,... a n a(n) a n
 Ciągi liczbowe Spis treści Ciąg liczbowy Ciąg liczbowy skończony Ciąg liczbowy nieskończony Przykłady i sposoby określania ciągu, suma n początkowych wyrazów ciągu Suma n początkowych, kolejnych wyrazów
Ciągi liczbowe Spis treści Ciąg liczbowy Ciąg liczbowy skończony Ciąg liczbowy nieskończony Przykłady i sposoby określania ciągu, suma n początkowych wyrazów ciągu Suma n początkowych, kolejnych wyrazów
ALGORYTM STRAŻAKA W WALCE Z ROZLEWAMI OLEJOWYMI
 JOLANTA MAZUREK Akademia Morska w Gdyni Katedra Matematyki ALGORYTM STRAŻAKA W WALCE Z ROZLEWAMI OLEJOWYMI W artykule rzedstawiono model wykorzystujący narzędzia matematyczne do ustalenia reguł oraz rozwiązań,
JOLANTA MAZUREK Akademia Morska w Gdyni Katedra Matematyki ALGORYTM STRAŻAKA W WALCE Z ROZLEWAMI OLEJOWYMI W artykule rzedstawiono model wykorzystujący narzędzia matematyczne do ustalenia reguł oraz rozwiązań,
1 Logika (3h) 1.1 Funkcje logiczne. 1.2 Kwantyfikatory. 1. Udowodnij prawa logiczne: 5. (p q) (p q) 6. ((p q) r) (p (q r)) 3.
 Logika (3h). Udowodnij prawa logiczne:. (p q) ( p q). (p q) ( p q) 3. (p q) ( q p) 4. (p q) ( p q) 5. (p q) (p q) 6. ((p q) r) (p (q r)) 7. (p q) r (p r) (q r) 8. (p q) (q r) (p r). Sprawdź, czy wyrażenia:.
Logika (3h). Udowodnij prawa logiczne:. (p q) ( p q). (p q) ( p q) 3. (p q) ( q p) 4. (p q) ( p q) 5. (p q) (p q) 6. ((p q) r) (p (q r)) 7. (p q) r (p r) (q r) 8. (p q) (q r) (p r). Sprawdź, czy wyrażenia:.
Zadanie 2. Obliczyć rangę dowolnego elementu zbioru uporządkowanego N 0 N 0, gdy porządek jest zdefiniowany następująco: (a, b) (c, d) (a c b d)
 Matemaryka dyskretna - zadania Zadanie 1. Opisać zbiór wszystkich elementów rangi k zbioru uporządkowanego X dla każdej liczby naturalnej k, gdy X jest rodziną podzbiorów zbioru skończonego Y. Elementem
Matemaryka dyskretna - zadania Zadanie 1. Opisać zbiór wszystkich elementów rangi k zbioru uporządkowanego X dla każdej liczby naturalnej k, gdy X jest rodziną podzbiorów zbioru skończonego Y. Elementem
Podstawy logiki i teorii mnogości Informatyka, I rok. Semestr letni 2013/14. Tomasz Połacik
 Podstawy logiki i teorii mnogości Informatyka, I rok. Semestr letni 2013/14. Tomasz Połacik 8 Funkcje 8.1 Pojęcie relacji 8.1 Definicja (Relacja). Relacją (binarną) nazywamy dowolny podzbiór produktu kartezjańskiego
Podstawy logiki i teorii mnogości Informatyka, I rok. Semestr letni 2013/14. Tomasz Połacik 8 Funkcje 8.1 Pojęcie relacji 8.1 Definicja (Relacja). Relacją (binarną) nazywamy dowolny podzbiór produktu kartezjańskiego
W pewnym mieście jeden z jej mieszkańców goli wszystkich tych i tylko tych jej mieszkańców, którzy nie golą się
 1 Logika Zdanie w sensie logicznym, to zdanie oznajmujące, o którym da się jednoznacznie powiedzieć, czy jest fałszywe, czy prawdziwe. Zmienna zdaniowa- to symbol, którym zastępujemy dowolne zdanie. Zdania
1 Logika Zdanie w sensie logicznym, to zdanie oznajmujące, o którym da się jednoznacznie powiedzieć, czy jest fałszywe, czy prawdziwe. Zmienna zdaniowa- to symbol, którym zastępujemy dowolne zdanie. Zdania
MATEMATYKA DYSKRETNA. doc. dr hab. inż. Marek Libura
 Marek Libura MATEMATYKA DYSKRETNA 1 MATEMATYKA DYSKRETNA doc. dr hab. inż. Marek Libura Instytut Badań Systemowych PAN 01-447 Warszawa, Newelska 6, pok. 324 Marek.Libura@ibspan.waw.pl tel.(48)(22)8373578
Marek Libura MATEMATYKA DYSKRETNA 1 MATEMATYKA DYSKRETNA doc. dr hab. inż. Marek Libura Instytut Badań Systemowych PAN 01-447 Warszawa, Newelska 6, pok. 324 Marek.Libura@ibspan.waw.pl tel.(48)(22)8373578
WYKŁAD 1. Witold Bednorz, Paweł Wolff. Rachunek Prawdopodobieństwa, WNE, Instytut Matematyki Uniwersytet Warszawski
 WYKŁAD 1 Witold Bednorz, Paweł Wolff Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Wprowadzenie Gry hazardowe Wprowadzenie Gry hazardowe Klasyczna definicja prawdopodobieństwa.
WYKŁAD 1 Witold Bednorz, Paweł Wolff Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Wprowadzenie Gry hazardowe Wprowadzenie Gry hazardowe Klasyczna definicja prawdopodobieństwa.
Projekt 9 Obciążenia płata nośnego i usterzenia poziomego
 Projekt 9 Obciążenia łata nośnego i usterzenia oziomego Niniejszy rojekt składa się z dwóch części:. wyznaczenie obciążeń wymiarujących skrzydło,. wyznaczenie obciążeń wymiarujących usterzenie oziome,
Projekt 9 Obciążenia łata nośnego i usterzenia oziomego Niniejszy rojekt składa się z dwóch części:. wyznaczenie obciążeń wymiarujących skrzydło,. wyznaczenie obciążeń wymiarujących usterzenie oziome,
Algorytmy tekstowe na przykładzie KMP
 Łukasz Kowalik, SD 2003 lgorytmy tekstowe na rzykładzie KMP 1 lgorytmy tekstowe na rzykładzie KMP Postawowe ojęcia Niech będzie dowolnym skończonym nieustym zbiorem symboli. Zbiór nazywamy alfabetem. Dowolny
Łukasz Kowalik, SD 2003 lgorytmy tekstowe na rzykładzie KMP 1 lgorytmy tekstowe na rzykładzie KMP Postawowe ojęcia Niech będzie dowolnym skończonym nieustym zbiorem symboli. Zbiór nazywamy alfabetem. Dowolny
Funkcja f jest ograniczona, jeśli jest ona ograniczona z
 FUNKCJE JEDNEJ ZMIENNEJ. PODSTAWOWE POJĘCIA. PODSTAWOWE FUNKCJE ELEMENTARNE R - zbiór liczb rzeczywistych, D R, P R Definicja. Jeżeli każdemu elementowi ze zbioru D jest przyporządkowany dokładnie jeden
FUNKCJE JEDNEJ ZMIENNEJ. PODSTAWOWE POJĘCIA. PODSTAWOWE FUNKCJE ELEMENTARNE R - zbiór liczb rzeczywistych, D R, P R Definicja. Jeżeli każdemu elementowi ze zbioru D jest przyporządkowany dokładnie jeden
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1
 Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Jakubowski, Sztencel:
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Jakubowski, Sztencel:
Zbiory, relacje i funkcje
 Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
KURS SZEREGI. Lekcja 10 Szeregi Fouriera ZADANIE DOMOWE. Strona 1
 KURS SZEREGI Lekcja 1 Szeregi Fouriera ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Zaznacz poprawną odpowiedź: a) Szereg Fouriera
KURS SZEREGI Lekcja 1 Szeregi Fouriera ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Zaznacz poprawną odpowiedź: a) Szereg Fouriera
Ciągi Podzbiory Symbol Newtona Zasada szufladkowa Dirichleta Zasada włączania i wyłączania. Ilość najkrótszych dróg. Kombinatoryka. Magdalena Lemańska
 Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Matematyka I. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12
 Matematyka I Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12 Egzamin Termin: 28.01, godz. 10.15-11.45, sala 309 3 pytania teoretyczne 2 zadania wybór pytań i wybór zadań
Matematyka I Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12 Egzamin Termin: 28.01, godz. 10.15-11.45, sala 309 3 pytania teoretyczne 2 zadania wybór pytań i wybór zadań
Prawa wzajemności Gaussa
 Kamil Sikorski Prawa wzajemności Gaussa Pytanie 1. Dla jakich liczb ierwszych kongruencja x 2 a() ma rozwiązanie? 1. Theorema Aureum Celem tej części jest okazanie, że x 2 q() ma rozwiązanie ma je x 2
Kamil Sikorski Prawa wzajemności Gaussa Pytanie 1. Dla jakich liczb ierwszych kongruencja x 2 a() ma rozwiązanie? 1. Theorema Aureum Celem tej części jest okazanie, że x 2 q() ma rozwiązanie ma je x 2
G. Plebanek, MIARA I CAŁKA Zadania do rozdziału 1 28
 G. Plebanek, MIARA I CAŁKA Zadania do rozdziału 1 28 1.9 Zadania 1.9.1 Niech R będzie pierścieniem zbiorów. Zauważyć, że jeśli A, B R to A B R i A B R. Sprawdzić, że (R,, ) jest także pierścieniem w sensie
G. Plebanek, MIARA I CAŁKA Zadania do rozdziału 1 28 1.9 Zadania 1.9.1 Niech R będzie pierścieniem zbiorów. Zauważyć, że jeśli A, B R to A B R i A B R. Sprawdzić, że (R,, ) jest także pierścieniem w sensie
Elastyczność popytu. Rodzaje elastyczności popytu. e p = - Pamiętajmy, że rozpatrujemy wielkości względne!!! Wzory na elastyczność cenową popytu D
 lastyczność oytu Rodzaje elastyczności oytu > lastyczność cenowa oytu - lastyczność mieszana oytu - e m = < lastyczność dochodowa oytu - e i lastyczność cenowa oytu - lastyczność cenowa oytu jest to stosunek
lastyczność oytu Rodzaje elastyczności oytu > lastyczność cenowa oytu - lastyczność mieszana oytu - e m = < lastyczność dochodowa oytu - e i lastyczność cenowa oytu - lastyczność cenowa oytu jest to stosunek
