EKSPERYMENTALNA WERYFIKACJA WYBRANYCH MODELI OBLICZENIOWYCH BALISTYKI KOŃ COWEJ
|
|
|
- Irena Wilczyńska
- 6 lat temu
- Przeglądów:
Transkrypt
1 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LII NR 4 (87) 0 Lesze Flis Mare Spersi Aadeia Marynari Wojennej EKSPERYMENTALNA WERYFIKACJA WYBRANYCH MODELI OBLICZENIOWYCH BALISTYKI KOŃ COWEJ STRESZCZENIE Na podstawie poiarów prędości pocisów alibru,7, przebijających stalowe tarcze o różnych grubościach i znanych właściwościach wytrzyałościowych, wyznaczono wartości liczbowe współczynniów występujących w równaniach ruchu pocisu opartych na ilu odiennych odelach fizycznych. Ograniczono się przy ty do odeli ciał sztywnych penetrujących odształcalne ośrodi. Przeprowadzono szereg obliczeń porównawczych ających na celu ocenę doładności badanych odeli. Rezultaty badań ogą być poocne w projetowaniu osłon balistycznych narażonych na ostrzał pocisai arabinowyi. Słowa luczowe: balistya, pancerze, etody analityczne, syulacja oputerowa, esperyent. WSTĘP Artyuł stanowi ontynuację badań prowadzonych od ilunastu lat w Instytucie Podstaw Konstrucji Maszyn przy Aadeii Marynari Wojennej w Gdyni nad budową i projetowanie osłon balistycznych chroniących wybrane obszary i poieszczenia na orętach oraz statach przed ostrzałe z broni strzeleciej. Efete tych badań było iędzy innyi: stworzenie technologicznych i teoretycznych podstaw projetowania osłon odpornych na ostrzał pocisai alibru 7,6 [9], budowa i uruchoienie stanowisa laboratoryjnego z ta zwany wahadłe balistyczny wyposażony w precyzyjną aparaturę poiarową, późniejsze przystosowanie tego stanowisa do badań nad odpornością pancerzy ostrzeliwanych pocisai o więszych średnicach [6] oraz opracowanie technologii producji stali onstrucyjnej o sybolu 0GHMBA znajdującej zastosowanie w przeyśle orętowy. 35
2 Lesze Flis, Mare Spersi Główny cele prezentowanej pracy jest przystosowanie etod obliczeniowych balistyi ońcowej pocisów aunicji strzeleciej do postaci uożliwiającej projetowanie osłon antyterrorystycznych ze wsponianej stali, odpornych na ostrzał pocisai alibru,7. Badania prowadzone od przeszło stu lat w licznych ośrodach na świecie poazały, że gdy prędości pocisów o zaostrzonych wierzchołach, wyonanych z utwardzonej stali, nie przeraczają 00 /s, dobrą zgodność z esperyentai prowadzonyi z użycie etalowych tarcz wyazują teorie, w tórych odele pocisu jest ciało sztywne, odelai tarcz zaś ośrodi odształcalne o odiennych, lecz ściśle oreślonych właściwościach [, 7, 8]. Ograniczyliśy się zate do badań etod obliczeniowych bazujących na taich założeniach. Przeprowadzone w raach pracy syulacje oputerowe, oparte na etodzie eleentów sończonych, stanowią olejny ro w ierunu bliższego poznania zjawis towarzyszących przebijaniu odształcalnego pancerza przez sztywny pocis. PRZEGLĄD MODELI OBLICZENIOWYCH Różniczowe równanie ruchu sztywnego pocisu wniającego prostopadle w etalową półprzestrzeń a postać [, 7, 8]: gdzie: t F, 0 asa pocisu; prędość; czas; d dt F, F stałe współczynnii. F F0 = F, () Pierwszy człon prawej strony równania nawiązuje do znanego z echanii płynów wzoru na wartość oporu czołowego ciała sztywnego przeieszczającego się w płynie lepi, drugi przedstawia siłę oporu tarcia ślizgowego, trzeci zaś stałą siłę zależną od właściwości wytrzyałościowych ateriału pancerza i ształtu wierzchoła pocisu. W wyniu podstawienia: = dt =, gdzie x jest drogą dx dx dt przebytą przez pocis, otrzyuje się: 36 Zeszyty Nauowe AMW
3 Esperyentalna weryfiacja wybranych odeli obliczeniowych balistyi ońcowej d dx =. () F + F + F0 Najprostsza cała tego równania [7], otrzyana przy założeniu F = F = 0, powszechnie stosowana do oceny odporności balistycznej pancerzy w drugiej połowie XIX wieu, daje wynii odbiegające od pratycznych doświadczeń [3]. Natoiast wprowadzenie do równania orety uwzględniającej zniejszenie prędości pocisu na sute wprawienia w ruch eleentów ateriału tarczy po zderzeniu prowadzi do znajdującego potwierdzenie esperyentalne wzoru [5]: π h d = 0 R τ α, (3) + gdzie: prędość pocisu po przebyciu drogi; h, d średnica pocisu; R wytrzyałość na ścinanie ateriału pancerza; α τ współczynni ształtu wierzchoła pocisu; d = ρ π h; 0 = p, 4 + przy czy: ρ gęstość ateriału tarczy; p prędość początowa pocisu. Całę równania () przy założeniu F = 0 (poinięcie oporu tarcia ślizgowego), z warunai brzegowyi: = p gdy x = 0 oraz = gdy x = h, ożna przedstawić w postaci: lub: F p + F0 ln F F + F0 h = (4a) = gdzie: e podstawa logarytu naturalnego. p F0 + e F hf F0, (4b) F 4 (87) 0 37
4 Lesze Flis, Mare Spersi Cała tego równania, przy założeniu F = 0 (poinięcie oporu czołowego), po wprowadzeniu powyższych warunów brzegowych przyjuje postać: h p F F p + F0 = ln. (5) F F F + F Rozwiązanie równania () ze wszystii współczynniai różnyi od zera przedstawia się następująco: 0 0 przy czy: Γ = h = F F ln F F arctg F Δ p + F + F p + F 0 + F 0 Γ, (6) F + p F F + F arctg Δ Δ, 0 > gdy Δ = 4 F F F 0 (ruch w ośrodu o ały oporze tarcia ślizgowego) lub: Γ = F F ln Δ gdy Δ < 0 (opór tarcia ślizgowego jest znaczny). ( F p + F Δ ) ( F + F + Δ ) ( F + + Δ )( + Δ ) p F F F Model zaproponowany pod oniec XIX wieu przez Jacoba de Marre a, oparty na założeniu, że siła działająca na pocis podczas przebijania pancerza słada się ze stałego oporu czołowego oraz stałego oporu tarcia na powierzchni bocznej pocisu, prowadzi do wzoru [3]: = p Q d gdzie: Q, n stałe współczynnii wyznaczane esperyentalnie. h d n, h, (7) Posługując się oercyjny prograe AUTODYN [0], oparty na etodzie eleentów sończonych (MES), przeprowadzono syulację oputerową procesu przebijania pancerzy o różnych grubościach przez sztywny pocis. Przyjęto, że pancerz jest zbudowany z ateriału sprężysto-plastycznego ze wzocnienie 38 Zeszyty Nauowe AMW
5 Esperyentalna weryfiacja wybranych odeli obliczeniowych balistyi ońcowej nieliniowy, zależny od prędości odształcenia opisanego w 983 rou przez Johnsona i Cooa równanie: = + n & ε σ ( A Bε ) + C ln, (8) & ε 0 gdzie: σ, ε, ε&, ε& 0 zreduowane (wg hipotezy Hubera-Misesa) naprężenia plastycznego płynięcia, zreduowane odształcenia plastyczne oraz zreduowane prędości odształcenia plastycznego; A, B, C, n stałe współczynnii. Zastosowane w prograie ryteriu zniszczenia wiąże się z potrzebą doświadczalnego oreślenia dalszych stałych ateriałowych (D, D, D 3, D 4 ) występujących we wzorze na zreduowane odształcenie niszczenia: = + D3a & ε ε f ( D De ) + D4 ln. (9) & ε 0 Bliższe szczegóły podano w pracach [, 3, 4, 0]. PORÓWNANIE REZULTATÓW OBLICZEŃ Z EKSPERYMENTEM Współczynnii (charaterystyi ateriałowe) występujące we wzorach przedstawionych w poprzedniej części wyznaczono na podstawie badań esperyentalnych przeprowadzonych w Instytucie Podstaw Konstrucji Maszyn Aadeii Marynari Wojennej w Gdyni w 009 rou [6]. Istota esperyentu sprowadzała się do poiarów prędości (, ) pocisu o asie = 4,96 0 g i średnicy d =,7 0 p przed i za przestrzeliwaną tarczą o znanej grubości. Tarcze, w forie rążów o średnicy 0 i grubościach h zieniających się (co ) od 8 do 3, wyonano ze stali o gęstości ρ = 7830g/ 3, statycznej wytrzyałości na rozciąganie R = 758,5 MPa, wytrzyałości na ścinanie R = 437, 9 MPa oraz granicy plastyczności Re = 695 MPa. Uśrednione (z więszej liczby poiarów) wynii esperyentu przedstawiono w pierwszych trzech olunach tabeli. Minialna grubość pancerza wyonanego ze stali użytej do badań, ostrzeliwanego pocisie alibru,7, z prędością zderzenia 8,7 /s, wyniosła 3. τ 4 (87) 0 39
6 Lesze Flis, Mare Spersi Podstawienie powyższych wartości liczbowych do wzoru (3) prowadzi do równania z jedną niewiadoą α. Wartość tej niewiadoej, po rozwiązaniu równania, wynosi α = 0, 63. Prędości pocisu za przestrzelonyi tarczai o grubościach niejszych niż 3, obliczone za poocą wzoru (3), przedstawiono w czwartej olunie tabeli. W celu wyznaczenia współczynniów F 0, F występujących w równaniach (4a), (4b), do równania (4b) podstawiono wartości h, p, z pierwszego i ostatniego wiersza pierwszych trzech olun tabeli. Otrzyano w ten sposób uład dwóch równań z dwiea niewiadoyi, ający rozwiązanie: F 0 = 597 N; F = 0,0665 g/. W yśl przyjętego odelu ruch badanego pocisu odbywa się zate pod wpływe dwóch sił oporu: stałej siły F 0 = 597 N oraz siły zależnej od zieniającej się prędości: F = F = Wartości siły F, w funcji drogi x przebytej przez pocis podczas przebijania pancerza o grubości 3, przedstawiono w tabeli. Średnia wartość całowitej siły oporu, obliczona z przyrównania energii inetycznej pocisu do pracy tej siły na drodze h = 3, 0 p = F h, (0) wynosi 5430 N. Prędości pocisu, po przebiciu tarcz o różnych grubościach, obliczone za poocą wzoru (4b), podano w piątej olunie tabeli. Podstawienie wartości liczbowych h, p, z pierwszego i ostatniego wiersza pierwszych trzech olun tabeli. do wzoru (5) również prowadzi do uładu dwóch równań z dwiea niewiadoyi F 0, F. Jedna w przeciwieństwie do poprzedniego przyładu, autoro nie udało się znaleźć rozwiązania tego uładu w jawnej postaci. Poszuiwanie rozwiązania etodą olejnych przybliżeń doprowadziło do wyniu: F 0 = 597 N; F = 0,99 g/s. Prędości pocisu, po przebiciu tarcz o różnych grubościach, obliczone za poocą wzoru (5), przedstawiono w szóstej olunie tabeli. Nie powiodła się również próba znalezienia ogólnego rozwiązania uładu trzech równań z niewiadoyi F 0, F, F, otrzyanego poprzez podstawienie do wzoru (6) wartości liczbowych h, p, z pierwszego, środowego i ostatniego wiersza pierwszych trzech olun tabeli. Poszuiwanie rozwiązań etodą olejnych przybliżeń poazało, że obie postacie tego uładu równań ają więcej niż po jedny rozwiązaniu. Bez trudności natoiast ożna wyznaczyć współczynnii Q, n, występujące we wzorze de Marre a (7), z uładu dwóch równań otrzyanych przez podstawienie do tego wzoru wartości liczbowych h, p, z pierwszych trzech olun 40 Zeszyty Nauowe AMW śr
7 Esperyentalna weryfiacja wybranych odeli obliczeniowych balistyi ońcowej pierwszego i ostatniego wiersza tabeli. W rozpatrywany przypadu wynoszą one: Q = 6,9858 GPa; n = 0, Prędości pocisu, po przebiciu pancerzy o różnych grubościach, obliczone za poocą wzoru (7) przy ta wyznaczonych współczynniach, przedstawiono w przedostatniej olunie tabeli. W obliczeniach przeprowadzonych przy użyciu prograu AUTODYN, opartych na etodzie eleentów sończonych, przyjęto, na podstawie przeprowadzonych esperyentów oraz dostępnej literatury [3], następujące wartości stałych ateriałowych występujących we wzorach (8), (9): A = 695 MPa, B = 50 MPa, C = 0,04; n = 0,3; D = 0,05; D = 3,44; D 3 =,; D 4 = 0,00. Rezultaty obliczeń przedstawiono w ostatniej olunie tabeli. Grubość tarczy h [] Tabela. Porównanie wyniów obliczeń prędości pocisu po przebiciu pancerza z rezultatai esperyentu Prędość początowa pocisu p [/s] Prędość ońcowa (poiar) [/s] Prędość ońcowa wzór (3) [/s] Prędość ońcowa wzór (4) [/s] Prędość ońcowa wzór (5) [/s] Prędość ońcowa wzór (7) [/s] Prędość ońcowa MES [/s] 8 85, , , , , , , , , , , , , Źródło: opracowanie własne. Tabela. Wartości siły oporu czołowego F w funcji przebytej drogi x podczas przebijania pancerza o grubości 3 według odelu (4) Źródło: opracowanie własne. x [] F [N] 33,340 30,5 7,585 4,84,534 8,47 x [] F [N] 5,57,935 0, ,393,398 4 (87) 0 4
8 Lesze Flis, Mare Spersi Rys.. Porównanie wyniów obliczeń prędości pocisów po przebiciu tarcz o różnych grubościach z poiarai uzysanyi z esperyentu Źródło: opracowanie własne. Rys.. Wynii syulacji nuerycznej przebijania odształcalnej tarczy przez sztywny pocis; rozład naprężeń zreduowanych w ateriale tarczy w wybranych chwilach czasu [s] Źródło: opracowanie własne. 4 Zeszyty Nauowe AMW
9 Esperyentalna weryfiacja wybranych odeli obliczeniowych balistyi ońcowej PODSUMOWANIE Proste odele fizyczne, stworzone do opisu wniania sztywnego pocisu w odształcalną półprzestrzeń, zastosowane do obliczeń prędości przebijania pancerzy o sończonej grubości wyazały dobrą zgodność z esperyente w przypadach, gdy grubość pancerza przeraczała półtora raza wartość średnicy pocisu. Kilunastoprocentowe rozbieżności iędzy obliczeniai a esperyente przy niejszych grubościach pancerzy ogą być spowodowane niedoładnością poiaru załócanego odłaai z przestrzeliwanej tarczy. Zadziwiającą zbieżność wyniów obliczeń wyazały dwa odele oparte na odiennych założeniach prowadzących do wzorów o odiennej postaci: odel de Marre a (wzór 7) oraz odel Newtona z siłą oporu czołowego proporcjonalną do wadratu prędości, bez uwzględnienia oporu tarcia ślizgowego (wzór 4b). Bliższa ocena wpływu siły tarcia ślizgowego (środowy człon prawej strony równania ()) na odporność balistyczną pancerzy stalowych wyaga przeprowadzenia szczegółowych analiz rozwiązań wyrażonych wzorai (6) oraz doładniejszego poparcia esperyentai. Szczególne rozwiązanie uładu równań (5), uzysane w raach prezentowanych badań, świadczy, że w rozpatrywany przypadu siła ta przybiera wartości wielorotnie niejsze od siły oporu czołowego, proporcjonalnej do wadratu prędości. Użycie prograu oputerowego AUTODYN, opartego na etodzie eleentów sończonych, uożliwiło doładniejsze prześledzenie zjawis towarzyszących przebijaniu odształcalnego pancerza przez sztywny pocis. Na rysunu., przedstawiający rozład naprężeń zreduowanych w ateriale tarczy o grubości 3, zaobserwować ożna ziany obszarów uplastycznienia ateriału w otoczeniu przeieszczającego się pocisu. W wersji aniowanej syulacja oputerowa ujawniła również efety przeieszczania i odbijania się fal sprężystych i plastycznych od ściane pancerza i czoła pocisu. Zagadnienia te będą przediote dalszych badań. Syulacja potwierdziła ponadto poprawność założeń prostszych teorii, przyjowanych nierzado za jedyną podstawę projetowania pancerzy. BIBLIOGRAFIA [] Bacan M. E, Goldsith W., The echanics of penetration of projectiles into target, International Journal of Engineering Science, 978, Vol. 6, No, pp. 99. [] Flis L., Nuerical siulation of balistic ipact on 0GHMBA steel aror, Zeszyty Nauowe AMW, 00, nr, s (87) 0 43
10 Lesze Flis, Mare Spersi [3] Flis L., Spersi M., Badania odporności balistycznej pancerzy stalowych na ostrzał pocisai arabinowyi alibru,7, Zeszyty Nauowe AMW, 0, nr, s [4] Halliquist J. O., LS-DYNA Theory Manual, LSTC 006. [5] Spersi M., Model obliczeniowy do oszacowania odporności balistycznej pancerzy stalowych, Zeszyty Nauowe AMW, 009, nr 4, s [6] Szturosi B. i inni, Charaterystyi dynaiczne do syulacji nuerycznej ateriałów stosowanych na osłony antyterrorystyczne na jednostach pływających, raport z pracy badawczej Powój, Aadeia Marynari Wojennej, Gdynia 009. [7] Szuladzinsi G., Forulas for Mechanical and Structural Shoc and Ipast, Taylor & Francis Group, 00. [8] Włodarczy E., Balistya ońcowa pocisów aunicji strzeleciej, t., Wojsowa Aadeia Techniczna, Warszawa 006. [9] Zatorsi Z., Teoretyczne i technologiczne podstawy projetowania orętowych osłon balistycznych, rozprawa habilitacyjna, Aadeia Marynari Wojennej, Gdynia 009. [0] AUTODYN Explicit Software for Nonlinear Dynaice, Theory Manual Reision 4.3, Century Dynaics, 005. EXPERIMENTAL VERIFICATION OF CALCULATION MODELS RELATED TO FINAL BALLISTICS ABSTRACT Velocity of.7 bullets, piercing steel discs with different thicnesses and of nown strength properties is used to calculate the alues of nuerical coefficients appearing in equations, related to a few different physical odels, of bullet otion. The odels considered are liited to the odels of rigid bodies penetrating deforable targets. A series of coparatie calculations is ade to assess the accuracy of the odels tested. The results ay be helpful in designing ballistic shields exposed to rifle fire. Keywords: ballistics, aror, analytical ethods, coputer siulation, experient. 44 Zeszyty Nauowe AMW
Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na okres drgań
 KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
OCENA WPŁ YWU KSZTAŁ TU WIERZCHOŁ KA POCISKU NA PROCES PRZEBIJANIA PANCERZY STALOWYCH
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIII NR (189) 01 Lesze Flis Mare Sersi Aademia Marynari Wojennej OCENA WPŁ YWU KSZTAŁ TU WIERZCHOŁ KA POCISKU NA PROCES PRZEBIJANIA PANCERZY STALOWYCH STRESZCZENIE
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIII NR (189) 01 Lesze Flis Mare Sersi Aademia Marynari Wojennej OCENA WPŁ YWU KSZTAŁ TU WIERZCHOŁ KA POCISKU NA PROCES PRZEBIJANIA PANCERZY STALOWYCH STRESZCZENIE
WYKŁAD 5 METODY OPTYMALIZACJI NIELINIOWEJ BEZ OGRANICZEŃ
 WYKŁAD 5 METODY OPTYMALIZACJI NIELINIOWEJ BEZ OGRANICZEŃ Wstęp. Za wyjątie nielicznych funcji, najczęściej w postaci wieloianów, dla tórych ożna znaleźć iniu na drodze analitycznej, pozostała więszość
WYKŁAD 5 METODY OPTYMALIZACJI NIELINIOWEJ BEZ OGRANICZEŃ Wstęp. Za wyjątie nielicznych funcji, najczęściej w postaci wieloianów, dla tórych ożna znaleźć iniu na drodze analitycznej, pozostała więszość
Temat: Prawo Hooke a. Oscylacje harmoniczne. Zagadnienia: prawa dynamiki Newtona, siła sprężysta, prawo Hooke a, oscylacje harmoniczne,
 sg M 6-1 - Teat: Prawo Hooe a. Oscylacje haroniczne. Zagadnienia: prawa dynaii Newtona, siła sprężysta, prawo Hooe a, oscylacje haroniczne, ores oscylacji. Koncepcja: Sprężyna obciążana różnyi asai wydłuża
sg M 6-1 - Teat: Prawo Hooe a. Oscylacje haroniczne. Zagadnienia: prawa dynaii Newtona, siła sprężysta, prawo Hooe a, oscylacje haroniczne, ores oscylacji. Koncepcja: Sprężyna obciążana różnyi asai wydłuża
Wyznaczenie prędkości pojazdu na podstawie długości śladów hamowania pozostawionych na drodze
 Podstawy analizy wypadów drogowych Instrucja do ćwiczenia 1 Wyznaczenie prędości pojazdu na podstawie długości śladów hamowania pozostawionych na drodze Spis treści 1. CEL ĆWICZENIA... 3. WPROWADZENIE...
Podstawy analizy wypadów drogowych Instrucja do ćwiczenia 1 Wyznaczenie prędości pojazdu na podstawie długości śladów hamowania pozostawionych na drodze Spis treści 1. CEL ĆWICZENIA... 3. WPROWADZENIE...
DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH
 Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
BADANIA ODPORNOŚ CI BALISTYCZNEJ PANCERZY ZE STALI 10GHMBA NA OSTRZAŁ POCISKAMI 12,7 mm
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LII NR 3 (186) 011 Lesze Flis Mare Sersi Aademia Marynari Wojennej BADANIA ODPORNOŚ CI BALISTYCZNEJ PANCERZY ZE STALI 10GHMBA NA OSTRZAŁ POCISKAMI 1,7 mm
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LII NR 3 (186) 011 Lesze Flis Mare Sersi Aademia Marynari Wojennej BADANIA ODPORNOŚ CI BALISTYCZNEJ PANCERZY ZE STALI 10GHMBA NA OSTRZAŁ POCISKAMI 1,7 mm
CEL PRACY ZAKRES PRACY
 CEL PRACY. Analiza energetycznych kryteriów zęczenia wieloosiowego pod względe zastosowanych ateriałów, rodzajów obciążenia, wpływu koncentratora naprężenia i zakresu stosowalności dla ałej i dużej liczby
CEL PRACY. Analiza energetycznych kryteriów zęczenia wieloosiowego pod względe zastosowanych ateriałów, rodzajów obciążenia, wpływu koncentratora naprężenia i zakresu stosowalności dla ałej i dużej liczby
OBLICZENIA W POMIARACH POŚREDNICH
 ROZDZAŁ 6 OBLCZENA W POMARACH POŚREDNCH Stefan ubisa Zachodniopoorsi niwersytet Technologiczny. Wstęp Poiar pośredni to tai w tóry wartość wielości ierzonej wielości wyjściowej ezurandu y oblicza się z
ROZDZAŁ 6 OBLCZENA W POMARACH POŚREDNCH Stefan ubisa Zachodniopoorsi niwersytet Technologiczny. Wstęp Poiar pośredni to tai w tóry wartość wielości ierzonej wielości wyjściowej ezurandu y oblicza się z
( ) + ( ) T ( ) + E IE E E. Obliczanie gradientu błędu metodą układu dołączonego
 Obliczanie gradientu błędu metodą uładu dołączonego /9 Obliczanie gradientu błędu metodą uładu dołączonego Chodzi o wyznaczenie pochodnych cząstowych funcji błędu E względem parametrów elementów uładu
Obliczanie gradientu błędu metodą uładu dołączonego /9 Obliczanie gradientu błędu metodą uładu dołączonego Chodzi o wyznaczenie pochodnych cząstowych funcji błędu E względem parametrów elementów uładu
DRGANIA MECHANICZNE. materiały uzupełniające do ćwiczeń. Wydział Samochodów i Maszyn Roboczych studia inżynierskie
 DRGANIA MECHANICZNE ateriały uzupełniające do ćwiczeń Wydział Saochodów i Maszyn Roboczych studia inżyniersie prowadzący: gr inż. Sebastian Korcza część 6 ułady dysretne o wielu stopniach swobody Poniższe
DRGANIA MECHANICZNE ateriały uzupełniające do ćwiczeń Wydział Saochodów i Maszyn Roboczych studia inżyniersie prowadzący: gr inż. Sebastian Korcza część 6 ułady dysretne o wielu stopniach swobody Poniższe
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnia Gdańsa Wydział Eletrotechnii i Autoatyi Katedra Inżynierii Systeów Sterowania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systey ciągłe budowa odeli enoenologicznych z praw zachowania Materiały poocnicze
Politechnia Gdańsa Wydział Eletrotechnii i Autoatyi Katedra Inżynierii Systeów Sterowania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systey ciągłe budowa odeli enoenologicznych z praw zachowania Materiały poocnicze
Komitet Główny Olimpiady Fizycznej; Kazimierz Rosiński: Fizyka w szkole nr 1, 1956; Czarnecki Stefan: Olimpiady Fizyczne I IV, PZWS, Warszawa 1956.
 V OLIMPIADA FIZYCZNA (955/956). Stopień wstępny, zad. doświadczalne D. Źródło: Nazwa zadania: Działy: Słowa luczowe: Koitet Główny Olipiady Fizycznej; Kaziierz Rosińsi: Fizya w szole nr, 956; Czarneci
V OLIMPIADA FIZYCZNA (955/956). Stopień wstępny, zad. doświadczalne D. Źródło: Nazwa zadania: Działy: Słowa luczowe: Koitet Główny Olipiady Fizycznej; Kaziierz Rosińsi: Fizya w szole nr, 956; Czarneci
WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII.
 ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
DRGANIA MECHANICZNE. materiały uzupełniające do ćwiczeń. Wydział Samochodów i Maszyn Roboczych studia inżynierskie
 DRGANIA MECHANICZNE ateriały uzupełniające do ćwiczeń Wydział Saochodów i Maszyn Roboczych studia inżyniersie prowadzący: gr inż. Sebastian Korcza część 5 płaszczyzna fazowa Poniższe ateriały tylo dla
DRGANIA MECHANICZNE ateriały uzupełniające do ćwiczeń Wydział Saochodów i Maszyn Roboczych studia inżyniersie prowadzący: gr inż. Sebastian Korcza część 5 płaszczyzna fazowa Poniższe ateriały tylo dla
1.5. ZWIĄZKI KONSTYTUTYWNE STRONA FIZYCZNA
 J. Wyrwał, Wykłady z echaniki ateriałów.5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowadzenie Wyprowadzone w rozdziałach.3 (strona statyczna) i.4 (strona geoetryczna) równania (.3.36) i (.4.) są niezależne
J. Wyrwał, Wykłady z echaniki ateriałów.5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowadzenie Wyprowadzone w rozdziałach.3 (strona statyczna) i.4 (strona geoetryczna) równania (.3.36) i (.4.) są niezależne
Zadania do rozdziału 5
 Zadania do rozdziału 5 Zad.5.1. Udowodnij, że stosując równię pochyłą o dającym się zmieniać ącie nachylenia α można wyznaczyć współczynni tarcia statycznego µ o. ozwiązanie: W czasie zsuwania się po równi
Zadania do rozdziału 5 Zad.5.1. Udowodnij, że stosując równię pochyłą o dającym się zmieniać ącie nachylenia α można wyznaczyć współczynni tarcia statycznego µ o. ozwiązanie: W czasie zsuwania się po równi
Układ termodynamiczny
 Uład terodynaiczny Uład terodynaiczny to ciało lub zbiór rozważanych ciał, w tóry obo wszelich innych zjawis (echanicznych, eletrycznych, agnetycznych itd.) uwzględniay zjawisa cieplne. Stan uładu charateryzuje
Uład terodynaiczny Uład terodynaiczny to ciało lub zbiór rozważanych ciał, w tóry obo wszelich innych zjawis (echanicznych, eletrycznych, agnetycznych itd.) uwzględniay zjawisa cieplne. Stan uładu charateryzuje
w stanie granicznym nośności
 Wytrzyałość ateriałów Hipotezy wytrzyałościowe 1 Podstawy wyiarowania w stanie graniczny nośności Wyiarowanie konstrukcji polega na doborze wyiarów i kształtu przekrojów eleentów. Podstawą doboru jest
Wytrzyałość ateriałów Hipotezy wytrzyałościowe 1 Podstawy wyiarowania w stanie graniczny nośności Wyiarowanie konstrukcji polega na doborze wyiarów i kształtu przekrojów eleentów. Podstawą doboru jest
Wykres linii ciśnień i linii energii (wykres Ancony)
 Wyres linii ciśnień i linii energii (wyres Ancony) W wyorzystywanej przez nas do rozwiązywania problemów inżyniersich postaci równania Bernoulliego występuje wysoość prędości (= /g), wysoość ciśnienia
Wyres linii ciśnień i linii energii (wyres Ancony) W wyorzystywanej przez nas do rozwiązywania problemów inżyniersich postaci równania Bernoulliego występuje wysoość prędości (= /g), wysoość ciśnienia
Podstawowe pojęcia wytrzymałości materiałów. Statyczna próba rozciągania metali. Warunek nośności i użytkowania. Założenia
 Wytrzymałość materiałów dział mechaniki obejmujący badania teoretyczne i doświadczalne procesów odkształceń i niszczenia ciał pod wpływem różnego rodzaju oddziaływań (obciążeń) Podstawowe pojęcia wytrzymałości
Wytrzymałość materiałów dział mechaniki obejmujący badania teoretyczne i doświadczalne procesów odkształceń i niszczenia ciał pod wpływem różnego rodzaju oddziaływań (obciążeń) Podstawowe pojęcia wytrzymałości
Napęd suwadła broni automatycznej w powylotowym okresie strzału
 BIULETYN WAT VOL. LV, NR 3, 2006 Napęd suwadła broni automatycznej w powylotowym oresie strzału STANISŁAW TORECKI, ZBIGNIEW SURMA, RYSZARD WOŹNIAK Wojsowa Aademia Techniczna, Wydział Mechatronii, Instytut
BIULETYN WAT VOL. LV, NR 3, 2006 Napęd suwadła broni automatycznej w powylotowym oresie strzału STANISŁAW TORECKI, ZBIGNIEW SURMA, RYSZARD WOŹNIAK Wojsowa Aademia Techniczna, Wydział Mechatronii, Instytut
A. Cel ćwiczenia. B. Część teoretyczna
 A. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z wsaźniami esploatacyjnymi eletronicznych systemów bezpieczeństwa oraz wyorzystaniem ich do alizacji procesu esplatacji z uwzględnieniem przeglądów
A. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z wsaźniami esploatacyjnymi eletronicznych systemów bezpieczeństwa oraz wyorzystaniem ich do alizacji procesu esplatacji z uwzględnieniem przeglądów
Modelowanie przez zjawiska przybliżone. Modelowanie poprzez zjawiska uproszczone. Modelowanie przez analogie. Modelowanie matematyczne
 Modelowanie rzeczywistości- JAK? Modelowanie przez zjawisa przybliżone Modelowanie poprzez zjawisa uproszczone Modelowanie przez analogie Modelowanie matematyczne Przyłady modelowania Modelowanie przez
Modelowanie rzeczywistości- JAK? Modelowanie przez zjawisa przybliżone Modelowanie poprzez zjawisa uproszczone Modelowanie przez analogie Modelowanie matematyczne Przyłady modelowania Modelowanie przez
Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI. Konwekcja wymuszona - 1 -
 Katedra Silniów Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Konwecja wymuszona - - Wstęp Konwecją nazywamy wymianę ciepła pomiędzy powierzchnią ciała stałego przylegającym do niej płynem, w tórym występuje
Katedra Silniów Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Konwecja wymuszona - - Wstęp Konwecją nazywamy wymianę ciepła pomiędzy powierzchnią ciała stałego przylegającym do niej płynem, w tórym występuje
Wrocław 2003 STATECZNOŚĆ. STATYKA 2 - projekt 1 zadanie 2
 Wrocław 00 STATECZNOŚĆ STATYKA - projet zadanie . Treść zadania Dla ray o scheacie statyczny ja na rysunu poniżej należy : - Sprawdzić czy uład jest statycznie niezienny - Wyznaczyć siły osiowe w prętach
Wrocław 00 STATECZNOŚĆ STATYKA - projet zadanie . Treść zadania Dla ray o scheacie statyczny ja na rysunu poniżej należy : - Sprawdzić czy uład jest statycznie niezienny - Wyznaczyć siły osiowe w prętach
LINIOWE ELEMENTY SKOŃCZONE O ZMIENNEJ SZTYWNOŚCI W MODELOWANIU PODŁOŻA GRUNTOWEGO POD BUDYNKIEM
 LINIOW LMNTY SKOŃCZON O ZMINNJ SZTYWNOŚCI W MODLOWANIU PODŁOŻA GRUNTOWGO POD BUDYNKIM Tadeusz CHYŻY, Monia MACKIWICZ Wydział Budownictwa i Inżynierii Środowisa, Politechnia Białostoca, ul. Wiejsa 45 A,
LINIOW LMNTY SKOŃCZON O ZMINNJ SZTYWNOŚCI W MODLOWANIU PODŁOŻA GRUNTOWGO POD BUDYNKIM Tadeusz CHYŻY, Monia MACKIWICZ Wydział Budownictwa i Inżynierii Środowisa, Politechnia Białostoca, ul. Wiejsa 45 A,
1. ZAGADNIENIA 2. OPIS ZAGADNIENIA
 Zad. M 09 Teat: I PRACOWNIA FIZYCZNA Instytut Fizyi US Badanie zderzeń sprężystych i nieprężystych na torze powietrzny Cel: Doświadczalne potwierdzenie zasady zachowania pędu dla zderzeń jednowyiarowych.
Zad. M 09 Teat: I PRACOWNIA FIZYCZNA Instytut Fizyi US Badanie zderzeń sprężystych i nieprężystych na torze powietrzny Cel: Doświadczalne potwierdzenie zasady zachowania pędu dla zderzeń jednowyiarowych.
Badania odporności na ostrzał pociskami kalibru 12,7 mm stali 10ghmba z wykorzystaniem wahadła balistycznego
 Bi u l e t y n WAT Vo l. LIX, Nr 4, 010 Badania odporności na ostrzał pociskami kalibru 1,7 mm stali 10ghmba z wykorzystaniem wahadła balistycznego Bogdan Szturomski Akademia Marynarki Wojennej, Wydział
Bi u l e t y n WAT Vo l. LIX, Nr 4, 010 Badania odporności na ostrzał pociskami kalibru 1,7 mm stali 10ghmba z wykorzystaniem wahadła balistycznego Bogdan Szturomski Akademia Marynarki Wojennej, Wydział
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
- obliczyć względne procentowe odchylenie otrzymanej wartości od wartości tablicowej:
 Kila uwa: - Doświadczenia przeprowadzay w rupach - osobowych (nie więszych), jedna w raach rupy ażdy suden wyonuje swoje osobne poiary i obliczenia. - Na zajęcia przychodziy z wydruowanyi wybranyi ćwiczeniai
Kila uwa: - Doświadczenia przeprowadzay w rupach - osobowych (nie więszych), jedna w raach rupy ażdy suden wyonuje swoje osobne poiary i obliczenia. - Na zajęcia przychodziy z wydruowanyi wybranyi ćwiczeniai
ANALIZA WARUNKÓW KONSOLIDACJI TORFÓW PRZECIĄŻONYCH WARSTWĄ POPIOŁÓW
 Tomasz SZCZYGIELSKI Zygmunt MEYER ANALIZA WARUNKÓW KONSOLIDACJI TORFÓW PRZECIĄŻONYCH WARSTWĄ POPIOŁÓW. Wprowadzenie Celem pracy jest analiza możliwości wyorzystania ubocznych produtów spalania nazywanych
Tomasz SZCZYGIELSKI Zygmunt MEYER ANALIZA WARUNKÓW KONSOLIDACJI TORFÓW PRZECIĄŻONYCH WARSTWĄ POPIOŁÓW. Wprowadzenie Celem pracy jest analiza możliwości wyorzystania ubocznych produtów spalania nazywanych
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwiczenia: WYZNACZANIE WSPÓŁCZYNNIKA PRZENIKANIA CIEPŁA PODCZAS SKRAPLANIA PARY
INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwiczenia: WYZNACZANIE WSPÓŁCZYNNIKA PRZENIKANIA CIEPŁA PODCZAS SKRAPLANIA PARY
STEROWANIE STRUKTUR DYNAMICZNYCH. Zastosowanie sterowania typu Sky-hook w układach redukcji drgań
 STEROWANIE STRUKTUR DYNAMICZNYCH Zastosowanie sterowania typu Sy-hoo w uładach reducji drgań gr inż. Łuasz Jastrzębsi Katedra Autoatyzacji Procesów - Aadeia Górniczo-Hutnicza Kraów, 20 LISTOPADA 2013 Plan
STEROWANIE STRUKTUR DYNAMICZNYCH Zastosowanie sterowania typu Sy-hoo w uładach reducji drgań gr inż. Łuasz Jastrzębsi Katedra Autoatyzacji Procesów - Aadeia Górniczo-Hutnicza Kraów, 20 LISTOPADA 2013 Plan
ANALIZA NUMERYCZNA DEFORMACJI WALCOWEJ PRÓBKI W ZDERZENIOWYM TEŚCIE TAYLORA
 Michał Grązka 1) ANALIZA NUMERYCZNA DEFORMACJI WALCOWEJ PRÓBKI W ZDERZENIOWYM TEŚCIE TAYLORA Streszczenie: Przedstawiony niżej artykuł jest poświęcony komputerowym badaniom deformacji próbki osiowo symetrycznej
Michał Grązka 1) ANALIZA NUMERYCZNA DEFORMACJI WALCOWEJ PRÓBKI W ZDERZENIOWYM TEŚCIE TAYLORA Streszczenie: Przedstawiony niżej artykuł jest poświęcony komputerowym badaniom deformacji próbki osiowo symetrycznej
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ
 ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
Nr 2. Laboratorium Maszyny CNC. Politechnika Poznańska Instytut Technologii Mechanicznej
 Politechnia Poznańsa Instytut Technologii Mechanicznej Laboratorium Maszyny CNC Nr 2 Badania symulacyjne napędów obrabiare sterowanych numerycznie Opracował: Dr inż. Wojciech Ptaszyńsi Poznań, 3 stycznia
Politechnia Poznańsa Instytut Technologii Mechanicznej Laboratorium Maszyny CNC Nr 2 Badania symulacyjne napędów obrabiare sterowanych numerycznie Opracował: Dr inż. Wojciech Ptaszyńsi Poznań, 3 stycznia
NUMERYCZNA SYMULACJA STOPNIOWEGO USZKADZANIA SIĘ LAMINATÓW KOMPOZYTOWYCH NUMERICAL SIMULATION OF PROGRESSIVE DAMAGE IN COMPOSITE LAMINATES
 JANUSZ GERMAN, ZBIGNIEW MIKULSKI NUMERYCZNA SYMULACJA STOPNIOWEGO USZKADZANIA SIĘ LAMINATÓW KOMPOZYTOWYCH NUMERICAL SIMULATION OF PROGRESSIVE DAMAGE IN COMPOSITE LAMINATES S t r e s z c z e n i e A b s
JANUSZ GERMAN, ZBIGNIEW MIKULSKI NUMERYCZNA SYMULACJA STOPNIOWEGO USZKADZANIA SIĘ LAMINATÓW KOMPOZYTOWYCH NUMERICAL SIMULATION OF PROGRESSIVE DAMAGE IN COMPOSITE LAMINATES S t r e s z c z e n i e A b s
Analiza nośności poziomej pojedynczego pala
 Poradni Inżyniera Nr 16 Atualizacja: 09/016 Analiza nośności poziomej pojedynczego pala Program: Pli powiązany: Pal Demo_manual_16.gpi Celem niniejszego przewodnia jest przedstawienie wyorzystania programu
Poradni Inżyniera Nr 16 Atualizacja: 09/016 Analiza nośności poziomej pojedynczego pala Program: Pli powiązany: Pal Demo_manual_16.gpi Celem niniejszego przewodnia jest przedstawienie wyorzystania programu
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie doświadczalne
 XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie doświadczalne ZADANIE D Nazwa zadania: Prędość chwilowa uli Zaproponuj metodę pomiaru prędości chwilowej stalowej uli poruszającej się po zadanym torze. Wyorzystaj
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie doświadczalne ZADANIE D Nazwa zadania: Prędość chwilowa uli Zaproponuj metodę pomiaru prędości chwilowej stalowej uli poruszającej się po zadanym torze. Wyorzystaj
Wykład 9. Fizyka 1 (Informatyka - EEIiA 2006/07)
 Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
MODELOWANIE WARSTWY POWIERZCHNIOWEJ O ZMIENNEJ TWARDOŚCI
 Dr inż. Danuta MIEDZIŃSKA, email: dmiedzinska@wat.edu.pl Dr inż. Robert PANOWICZ, email: Panowicz@wat.edu.pl Wojskowa Akademia Techniczna, Katedra Mechaniki i Informatyki Stosowanej MODELOWANIE WARSTWY
Dr inż. Danuta MIEDZIŃSKA, email: dmiedzinska@wat.edu.pl Dr inż. Robert PANOWICZ, email: Panowicz@wat.edu.pl Wojskowa Akademia Techniczna, Katedra Mechaniki i Informatyki Stosowanej MODELOWANIE WARSTWY
4.15 Badanie dyfrakcji światła laserowego na krysztale koloidalnym(o19)
 256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
Dr inż. Janusz Dębiński
 Wytrzymałość materiałów ćwiczenia projektowe 5. Projekt numer 5 przykład 5.. Temat projektu Na rysunku 5.a przedstawiono belkę swobodnie podpartą wykorzystywaną w projekcie numer 5 z wytrzymałości materiałów.
Wytrzymałość materiałów ćwiczenia projektowe 5. Projekt numer 5 przykład 5.. Temat projektu Na rysunku 5.a przedstawiono belkę swobodnie podpartą wykorzystywaną w projekcie numer 5 z wytrzymałości materiałów.
Algorytm wyznaczania krotności diagnostycznej struktury opiniowania diagnostycznego typu PMC 1
 BIULETYN INSTYTUTU AUTOMATYKI I ROBOTYKI NR 18, 2003 Algoryt wyznaczania rotności diagnostycznej strutury opiniowania diagnostycznego typu PMC 1 Artur ARCIUCH Załad Systeów Koputerowych, Instytut Teleinforatyi
BIULETYN INSTYTUTU AUTOMATYKI I ROBOTYKI NR 18, 2003 Algoryt wyznaczania rotności diagnostycznej strutury opiniowania diagnostycznego typu PMC 1 Artur ARCIUCH Załad Systeów Koputerowych, Instytut Teleinforatyi
Metoda rozwiązywania układu równań liniowych z symetryczną, nieokreśloną macierzą współczynników ( 0 )
 MATEMATYKA STOSOWANA 7, 2006 Izabella Czochralsa (Warszawa) Metoda rozwiązywania uładu równań liniowych z symetryczną, nieoreśloną macierzą współczynniów ( 0 ) Streszczenie. W pracy zaadaptowano opracowaną
MATEMATYKA STOSOWANA 7, 2006 Izabella Czochralsa (Warszawa) Metoda rozwiązywania uładu równań liniowych z symetryczną, nieoreśloną macierzą współczynniów ( 0 ) Streszczenie. W pracy zaadaptowano opracowaną
ANALIZA MOŻLIWOŚCI ZMIANY CZĘSTOTLIWOŚCI DRGAŃ WŁASNYCH KOLUMNY KIEROWNICZEJ
 MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 33, s. 49-54, Gliwice 7 ANALIZA MOŻLIWOŚCI ZMIANY CZĘSTOTLIWOŚCI DRGAŃ WŁASNYCH KOLUMNY KIEROWNICZEJ PIOTR CZUBAK Katedra Mechanii i Wiroaustyi, AGH e-ail: czua@agh.edu.pl
MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 33, s. 49-54, Gliwice 7 ANALIZA MOŻLIWOŚCI ZMIANY CZĘSTOTLIWOŚCI DRGAŃ WŁASNYCH KOLUMNY KIEROWNICZEJ PIOTR CZUBAK Katedra Mechanii i Wiroaustyi, AGH e-ail: czua@agh.edu.pl
METODA PROJEKTOWANIA REJONU ZMIANY KIERUNKU TRASY KOLEJOWEJ
 Problemy Kolejnictwa Zeszyt 5 97 Prof. dr hab. inż. Władysław Koc Politechnia Gdańsa METODA PROJEKTOWANIA REJONU ZMIANY KIERUNKU TRASY KOLEJOWEJ SPIS TREŚCI. Wprowadzenie. Ogólna ocena sytuacji geometrycznej
Problemy Kolejnictwa Zeszyt 5 97 Prof. dr hab. inż. Władysław Koc Politechnia Gdańsa METODA PROJEKTOWANIA REJONU ZMIANY KIERUNKU TRASY KOLEJOWEJ SPIS TREŚCI. Wprowadzenie. Ogólna ocena sytuacji geometrycznej
POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN ZAKŁAD MECHATRONIKI LABORATORIUM PODSTAW AUTOMATYKI INSTRUKCJA
 POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN ZAKŁAD MECHATRONIKI LABORATORIUM PODSTAW AUTOMATYKI INSTRUKCJA ĆWICZENIE LABORATORYJNE NR 4 Temat: Identyfiacja obietu regulacji
POLITECHNIKA ŚWIĘTOKRZYSKA w Kielcach WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN ZAKŁAD MECHATRONIKI LABORATORIUM PODSTAW AUTOMATYKI INSTRUKCJA ĆWICZENIE LABORATORYJNE NR 4 Temat: Identyfiacja obietu regulacji
(U.3) Podstawy formalizmu mechaniki kwantowej
 3.10.2004 24. (U.3) Podstawy formalizmu mechanii wantowej 33 Rozdział 24 (U.3) Podstawy formalizmu mechanii wantowej 24.1 Wartości oczeiwane i dyspersje dla stanu superponowanego 24.1.1 Założenia wstępne
3.10.2004 24. (U.3) Podstawy formalizmu mechanii wantowej 33 Rozdział 24 (U.3) Podstawy formalizmu mechanii wantowej 24.1 Wartości oczeiwane i dyspersje dla stanu superponowanego 24.1.1 Założenia wstępne
WSPÓŁCZYNNIK NIEPEWNOŚCI MODELU OBLICZENIOWEGO NOŚNOŚCI KONSTRUKCJI - PROPOZYCJA WYZNACZANIA
 PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK nr 3 (131) 2004 BUILDING RESEARCH INSTITUTE - QUARTERLY No 3 (131) 2004 BADANIA l STUDIA - RESEARCH AND STUDIES Bohdan Lewicki* WSPÓŁCZYNNIK NIEPEWNOŚCI
PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK nr 3 (131) 2004 BUILDING RESEARCH INSTITUTE - QUARTERLY No 3 (131) 2004 BADANIA l STUDIA - RESEARCH AND STUDIES Bohdan Lewicki* WSPÓŁCZYNNIK NIEPEWNOŚCI
ELEKTROTECHNIKA I ELEKTRONIKA
 UNIWERSYTET TECHNOLOGICZNO-PRZYRODNICZY W BYDGOSZCZY WYDZIŁ INŻYNIERII MECHNICZNEJ INSTYTUT EKSPLOTCJI MSZYN I TRNSPORTU ZKŁD STEROWNI ELEKTROTECHNIK I ELEKTRONIK ĆWICZENIE: E2 POMIRY PRĄDÓW I NPIĘĆ W
UNIWERSYTET TECHNOLOGICZNO-PRZYRODNICZY W BYDGOSZCZY WYDZIŁ INŻYNIERII MECHNICZNEJ INSTYTUT EKSPLOTCJI MSZYN I TRNSPORTU ZKŁD STEROWNI ELEKTROTECHNIK I ELEKTRONIK ĆWICZENIE: E2 POMIRY PRĄDÓW I NPIĘĆ W
PRACE ORYGINALNE ORIGINAL PAPERS
 PRACE ORYGINALNE ORIGINAL PAPERS Przegląd Nauowy Inżynieria i Kształtowanie Środowisa nr 66, 04: 37 33 (Prz. Nau. Inż. Kszt. Środ. 66, 04) Scientific Review Engineering and Environmental Sciences No 66,
PRACE ORYGINALNE ORIGINAL PAPERS Przegląd Nauowy Inżynieria i Kształtowanie Środowisa nr 66, 04: 37 33 (Prz. Nau. Inż. Kszt. Środ. 66, 04) Scientific Review Engineering and Environmental Sciences No 66,
Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie
 Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie Rozciąganie lub ściskanie Zginanie Skręcanie Ścinanie 1. Pręt rozciągany lub ściskany
Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie Rozciąganie lub ściskanie Zginanie Skręcanie Ścinanie 1. Pręt rozciągany lub ściskany
Ć w i c z e n i e K 6. Wyznaczanie stałych materiałowych przy wykorzystaniu pomiarów tensometrycznych.
 Akadeia Górniczo Hutnicza ydział Inżynierii Mechanicznej i Robotyki Katedra ytrzyałości, Zęczenia Materiałów i Konstrukcji Nazwisko i Iię: Nazwisko i Iię: ydział Górnictwa i Geoinżynierii Grupa nr: Ocena:
Akadeia Górniczo Hutnicza ydział Inżynierii Mechanicznej i Robotyki Katedra ytrzyałości, Zęczenia Materiałów i Konstrukcji Nazwisko i Iię: Nazwisko i Iię: ydział Górnictwa i Geoinżynierii Grupa nr: Ocena:
= = a na podstawie zadania 6 po p. 3.6 wiemy, że. b 1. a 2 ab b 2
 64 III. Zienne losowe jednowyiarowe D Ponieważ D (A) < D (B), więc należy wybrać partię A. Przykład 3.4. Obliczyć wariancję rozkładu jednostajnego. Ponieważ a na podstawie zadania 6 po p. 3.6 wiey, że
64 III. Zienne losowe jednowyiarowe D Ponieważ D (A) < D (B), więc należy wybrać partię A. Przykład 3.4. Obliczyć wariancję rozkładu jednostajnego. Ponieważ a na podstawie zadania 6 po p. 3.6 wiey, że
Wykład 21: Studnie i bariery cz.1.
 Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
CIAŁO CZŁOWIEKA LĄDUJĄCEGO PO ZESKOKU JAKO PRZYKŁAD UKŁADU MECHANICZNEGO ZE STABILIZUJĄCYM SPRZĘŻENIEM ZWROTNYM
 MAREK A. KSIĄŻEK, DANIEL ZIEMIAŃSKI CIAŁO CZŁOWIEKA LĄDUJĄCEGO PO ZESKOKU JAKO PRZYKŁAD UKŁADU MECHANICZNEGO ZE STABILIZUJĄCYM SPRZĘŻENIEM ZWROTNYM HUMAN BODY LANDING AFTER JUMP DOWN AS AN EXAMPLE OF A
MAREK A. KSIĄŻEK, DANIEL ZIEMIAŃSKI CIAŁO CZŁOWIEKA LĄDUJĄCEGO PO ZESKOKU JAKO PRZYKŁAD UKŁADU MECHANICZNEGO ZE STABILIZUJĄCYM SPRZĘŻENIEM ZWROTNYM HUMAN BODY LANDING AFTER JUMP DOWN AS AN EXAMPLE OF A
MODEL SYMULACYJNY MASZYNY RELUKTANCYJNEJ PRZEŁĄCZALNEJ
 Zeszyty Problemowe Maszyny Eletryczne Nr 93/2011 81 Piotr Bogusz, Mariusz Korosz, Adam Mazuriewicz, Jan Proop Politechnia Rzeszowsa MODEL SYMULACYJNY MASZYNY RELUKTANCYJNEJ PRZEŁĄCZALNEJ THE SIMULATION
Zeszyty Problemowe Maszyny Eletryczne Nr 93/2011 81 Piotr Bogusz, Mariusz Korosz, Adam Mazuriewicz, Jan Proop Politechnia Rzeszowsa MODEL SYMULACYJNY MASZYNY RELUKTANCYJNEJ PRZEŁĄCZALNEJ THE SIMULATION
Moduł stolika liniowego
 Podstawy Konstrucji Urządzeń Precyzyjnych Materiały pomocnicze do ćwiczeń projetowych część 1 Moduł stolia liniowego Presrypt opracował: dr inż. Wiesław Mościci Warszawa 2014 Materiały zawierają informacje
Podstawy Konstrucji Urządzeń Precyzyjnych Materiały pomocnicze do ćwiczeń projetowych część 1 Moduł stolia liniowego Presrypt opracował: dr inż. Wiesław Mościci Warszawa 2014 Materiały zawierają informacje
A4: Filtry aktywne rzędu II i IV
 A4: Filtry atywne rzędu II i IV Jace Grela, Radosław Strzała 3 maja 29 1 Wstęp 1.1 Wzory Poniżej zamieszczamy podstawowe wzory i definicje, tórych używaliśmy w obliczeniach: 1. Związe między stałą czasową
A4: Filtry atywne rzędu II i IV Jace Grela, Radosław Strzała 3 maja 29 1 Wstęp 1.1 Wzory Poniżej zamieszczamy podstawowe wzory i definicje, tórych używaliśmy w obliczeniach: 1. Związe między stałą czasową
Filtracja pomiarów z głowic laserowych
 dr inż. st. of. Paweł Zalewsi Filtracja pomiarów z głowic laserowych słowa luczowe: filtracja pomiaru odległości, PNDS Założenia filtracji pomiaru odległości. Problem wyznaczenia odległości i parametrów
dr inż. st. of. Paweł Zalewsi Filtracja pomiarów z głowic laserowych słowa luczowe: filtracja pomiaru odległości, PNDS Założenia filtracji pomiaru odległości. Problem wyznaczenia odległości i parametrów
Nauka o Materiałach. Wykład VIII. Odkształcenie materiałów właściwości sprężyste. Jerzy Lis
 Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
Model strefowy programu komputerowego CFAST
 Model streowy prograu oputerowego FAST (wybór z pozycji: Koneci M., Wpływ szybości wydzielania ciepła i eisji dyu na rozwój pożaru w uładzie poieszczeń, wyd. SGSP, Warszawa (007). Progra oputerowy FAST
Model streowy prograu oputerowego FAST (wybór z pozycji: Koneci M., Wpływ szybości wydzielania ciepła i eisji dyu na rozwój pożaru w uładzie poieszczeń, wyd. SGSP, Warszawa (007). Progra oputerowy FAST
1.5. ZWIĄZKI KONSTYTUTYWNE STRONA FIZYCZNA
 .5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowazenie Wyprowazone w rozziałach.3 (strona statyczna i.4 (strona geoetryczna równania (.3.36 i (.4. są niezależne o rozaju ciała aterialnego, które oże
.5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowazenie Wyprowazone w rozziałach.3 (strona statyczna i.4 (strona geoetryczna równania (.3.36 i (.4. są niezależne o rozaju ciała aterialnego, które oże
Drgania harmoniczne. Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Drgania haroniczne Projet współfinansowany przez Unię Europejsą w raach Europejsiego Funduszu Społecznego Drgania haroniczne O oscylatorze haroniczny ożey ówić wtedy, iedy siła haująca działa proporcjonalnie
Drgania haroniczne Projet współfinansowany przez Unię Europejsą w raach Europejsiego Funduszu Społecznego Drgania haroniczne O oscylatorze haroniczny ożey ówić wtedy, iedy siła haująca działa proporcjonalnie
PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
8. PODSTAWY ANALIZY NIELINIOWEJ
 8. PODSTAWY ANALIZY NIELINIOWEJ 1 8. 8. PODSTAWY ANALIZY NIELINIOWEJ 8.1. Wprowadzenie Zadania nieliniowe mają swoje zastosowanie na przykład w rozwiązywaniu cięgien. Przyczyny nieliniowości: 1) geometryczne:
8. PODSTAWY ANALIZY NIELINIOWEJ 1 8. 8. PODSTAWY ANALIZY NIELINIOWEJ 8.1. Wprowadzenie Zadania nieliniowe mają swoje zastosowanie na przykład w rozwiązywaniu cięgien. Przyczyny nieliniowości: 1) geometryczne:
SYMULACJA TŁOCZENIA ZAKRYWEK KORONKOWYCH SIMULATION OF CROWN CLOSURES FORMING
 MARIUSZ DOMAGAŁA, STANISŁAW OKOŃSKI ** SYMULACJA TŁOCZENIA ZAKRYWEK KORONKOWYCH SIMULATION OF CROWN CLOSURES FORMING S t r e s z c z e n i e A b s t r a c t W artykule podjęto próbę modelowania procesu
MARIUSZ DOMAGAŁA, STANISŁAW OKOŃSKI ** SYMULACJA TŁOCZENIA ZAKRYWEK KORONKOWYCH SIMULATION OF CROWN CLOSURES FORMING S t r e s z c z e n i e A b s t r a c t W artykule podjęto próbę modelowania procesu
MECHANIKA PŁYNÓW LABORATORIUM
 MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 7 Waga hydrostatyczna, wypór. Cele ćwiczenia jest wyznaczenie gęstości ciał stałych za poocą wagi hydrostatycznej i porównanie tej etody z etodai, w których ierzona
MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 7 Waga hydrostatyczna, wypór. Cele ćwiczenia jest wyznaczenie gęstości ciał stałych za poocą wagi hydrostatycznej i porównanie tej etody z etodai, w których ierzona
Model wnikania pocisków uderzeniowych w metalowe przeszkody. Część 2. Wnikanie prętów odkształcalnych w odkształcalne przeszkody
 PROBLEMY MECHATRONIKI. UZBROJENIE LOTNICTO INśYNIERIA BEZPIECZEŃSTA ISSN 08-589 4 3 (3) 03 39-48 Model wnikania pocisków derzeniowych w etalowe przeszkody. Część. nikanie prętów odkształcalnych w odkształcalne
PROBLEMY MECHATRONIKI. UZBROJENIE LOTNICTO INśYNIERIA BEZPIECZEŃSTA ISSN 08-589 4 3 (3) 03 39-48 Model wnikania pocisków derzeniowych w etalowe przeszkody. Część. nikanie prętów odkształcalnych w odkształcalne
MODYFIKACJA KOSZTOWA ALGORYTMU JOHNSONA DO SZEREGOWANIA ZADAŃ BUDOWLANYCH
 MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
długość całkowita: L m moment bezwładności (względem osi y): J y cm 4 moment bezwładności: J s cm 4
 .9. Stalowy ustrój niosący. Poład drewniany spoczywa na dziewięciu belach dwuteowych..., swobodnie podpartych o rozstawie... m. Beli wyonane są ze stali... Cechy geometryczne beli: długość całowita: L
.9. Stalowy ustrój niosący. Poład drewniany spoczywa na dziewięciu belach dwuteowych..., swobodnie podpartych o rozstawie... m. Beli wyonane są ze stali... Cechy geometryczne beli: długość całowita: L
Pomiar prędkości i natęŝenia przepływu za pomocą rurek spiętrzających
 Pomiar prędości i natęŝenia przepływu za pomocą rure spiętrzających Instrucja do ćwiczenia nr 8 Miernictwo energetyczne - laboratorium Opracowała: dr inŝ. ElŜbieta Wróblewsa Załad Miernictwa i Ochrony
Pomiar prędości i natęŝenia przepływu za pomocą rure spiętrzających Instrucja do ćwiczenia nr 8 Miernictwo energetyczne - laboratorium Opracowała: dr inŝ. ElŜbieta Wróblewsa Załad Miernictwa i Ochrony
EFEKTYWNOŚĆ PROCESU ROZDZIAŁU W OSADZARCE** 1. Wstęp. Marian Brożek*, Agnieszka Surowiak* Górnictwo i Geoinżynieria Rok 30 Zeszyt 3/1 2006
 Górnictwo i Geoinżynieria Ro 30 Zeszyt 3/1 006 Marian Broże*, Agniesza Surowia* EFEKTYWNOŚĆ PROCESU ROZDZIAŁU W OSADZARCE** 1. Wstęp Na stopień rozluzowania ziaren w łożu osadzari ma wpływ między innymi
Górnictwo i Geoinżynieria Ro 30 Zeszyt 3/1 006 Marian Broże*, Agniesza Surowia* EFEKTYWNOŚĆ PROCESU ROZDZIAŁU W OSADZARCE** 1. Wstęp Na stopień rozluzowania ziaren w łożu osadzari ma wpływ między innymi
Dynamika punktu materialnego nieswobodnego
 Dynaika punktu aterianego nieswobodnego dr inż. Sebastian Pakuła Wydział Inżynierii Mechanicznej i Robotyki Katedra Mechaniki i Wibroakustyki ai: spakua@agh.edu.p www: hoe.agh.edu.p/~spakua/ dr inż. Sebastian
Dynaika punktu aterianego nieswobodnego dr inż. Sebastian Pakuła Wydział Inżynierii Mechanicznej i Robotyki Katedra Mechaniki i Wibroakustyki ai: spakua@agh.edu.p www: hoe.agh.edu.p/~spakua/ dr inż. Sebastian
Powtórzenie na kolokwium nr 4. Dynamika punktu materialnego
 Powtórzenie na olowiu nr 4 Dynaia puntu aterialnego 1 zadanie dynaii: znany jest ruh, szuay siły go wywołująej. Znane funje opisująe trajetorię ruhu różnizujey i podstawiay do równań ruhu. 2 zadanie dynaii:
Powtórzenie na olowiu nr 4 Dynaia puntu aterialnego 1 zadanie dynaii: znany jest ruh, szuay siły go wywołująej. Znane funje opisująe trajetorię ruhu różnizujey i podstawiay do równań ruhu. 2 zadanie dynaii:
Kierunki racjonalizacji jednostkowego kosztu produkcji w przedsiębiorstwie górniczym
 Kieruni racjonalizacji jednostowego osztu producji w przedsiębiorstwie górniczym Roman MAGDA 1) 1) Prof dr hab inż.; AGH University of Science and Technology, Kraów, Miciewicza 30, 30-059, Poland; email:
Kieruni racjonalizacji jednostowego osztu producji w przedsiębiorstwie górniczym Roman MAGDA 1) 1) Prof dr hab inż.; AGH University of Science and Technology, Kraów, Miciewicza 30, 30-059, Poland; email:
Metody Obliczeniowe Mikrooptyki i Fotoniki. Podstawy metody różnic skończonych Podstawy metody FDTD
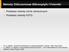 Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody różnic skończonych Podstawy etody FDTD M. N. Sadiku, Nuerical Techniques in Electroagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Coputational
Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody różnic skończonych Podstawy etody FDTD M. N. Sadiku, Nuerical Techniques in Electroagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Coputational
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
J. Szantyr Wykład nr 27 Przepływy w kanałach otwartych I
 J. Szantyr Wykład nr 7 Przepływy w kanałach otwartych Przepływy w kanałach otwartych najczęściej wymuszane są działaniem siły grawitacji. Jako wstępny uproszczony przypadek przeanalizujemy spływ warstwy
J. Szantyr Wykład nr 7 Przepływy w kanałach otwartych Przepływy w kanałach otwartych najczęściej wymuszane są działaniem siły grawitacji. Jako wstępny uproszczony przypadek przeanalizujemy spływ warstwy
WYKŁAD 15. Rozdział 8: Drgania samowzbudne
 WYKŁAD 5 Rozdział 8: Drgania samowzbudne 8.. Istota uładów i drgań samowzbudnych W tym wyładzie omówimy właściwości drgań samowzbudnych [,4], odróżniając je od poznanych wcześniej drgań swobodnych, wymuszonych
WYKŁAD 5 Rozdział 8: Drgania samowzbudne 8.. Istota uładów i drgań samowzbudnych W tym wyładzie omówimy właściwości drgań samowzbudnych [,4], odróżniając je od poznanych wcześniej drgań swobodnych, wymuszonych
Wyznaczanie ciepła topnienia lodu lub ciepła właściwego wybranego ciała
 dla specjalnośći Biofizya moleularna Wyznaczanie ciepła topnienia lodu lub ciepła właściwego wybranego ciała I. WSTĘP C 1 C 4 Ciepło jest wielością charateryzującą przepływ energii (analogiczną do pracy
dla specjalnośći Biofizya moleularna Wyznaczanie ciepła topnienia lodu lub ciepła właściwego wybranego ciała I. WSTĘP C 1 C 4 Ciepło jest wielością charateryzującą przepływ energii (analogiczną do pracy
OPŁYW PROFILU. Ciała opływane. profile lotnicze łopatki. Rys. 1. Podział ciał opływanych pod względem aerodynamicznym
 OPŁYW PROFILU Ciała opływane Nieopływowe Opływowe walec kula profile lotnicze łopatki spoilery sprężarek wentylatorów turbin Rys. 1. Podział ciał opływanych pod względem aerodynamicznym Płaski np. z blachy
OPŁYW PROFILU Ciała opływane Nieopływowe Opływowe walec kula profile lotnicze łopatki spoilery sprężarek wentylatorów turbin Rys. 1. Podział ciał opływanych pod względem aerodynamicznym Płaski np. z blachy
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW 3(89)/2012
 ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW 3(89)/2012 Jarosław Mańkowski 1, Paweł Ciężkowski 2 MODELOWANIE OSŁABIENIA MATERIAŁU NA PRZYKŁADZIE SYMULACJI PRÓBY BRAZYLIJSKIEJ 1. Wstęp Wytrzymałość na jednoosiowe
ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW 3(89)/2012 Jarosław Mańkowski 1, Paweł Ciężkowski 2 MODELOWANIE OSŁABIENIA MATERIAŁU NA PRZYKŁADZIE SYMULACJI PRÓBY BRAZYLIJSKIEJ 1. Wstęp Wytrzymałość na jednoosiowe
Zjawiska transportu 22-1
 Zjawiska transport - Zjawiska transport Zjawiska transport są zjawiskai, które występją jeżeli kład terodynaiczny nie jest w stanie równowagi: i v! const - w kładzie występje akroskopowy przepływ gaz lb
Zjawiska transport - Zjawiska transport Zjawiska transport są zjawiskai, które występją jeżeli kład terodynaiczny nie jest w stanie równowagi: i v! const - w kładzie występje akroskopowy przepływ gaz lb
9. PODSTAWY TEORII PLASTYCZNOŚCI
 9. PODSTAWY TEORII PLASTYCZNOŚCI 1 9. 9. PODSTAWY TEORII PLASTYCZNOŚCI 9.1. Pierwsze kroki Do tej pory zajmowaliśmy się w analizie ciał i konstrukcji tylko analizą sprężystą. Nie zastanawialiśmy się, co
9. PODSTAWY TEORII PLASTYCZNOŚCI 1 9. 9. PODSTAWY TEORII PLASTYCZNOŚCI 9.1. Pierwsze kroki Do tej pory zajmowaliśmy się w analizie ciał i konstrukcji tylko analizą sprężystą. Nie zastanawialiśmy się, co
Q strumień objętości, A przekrój całkowity, Przedstawiona zależność, zwana prawem filtracji, została podana przez Darcy ego w postaci równania:
 Filtracja to zjawiso przepływu płynu przez ośrode porowaty (np. wody przez grunt). W więszości przypadów przepływ odbywa się ruchem laminarnym, wyjątiem może być przepływ przez połady grubego żwiru lub
Filtracja to zjawiso przepływu płynu przez ośrode porowaty (np. wody przez grunt). W więszości przypadów przepływ odbywa się ruchem laminarnym, wyjątiem może być przepływ przez połady grubego żwiru lub
Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci
 Ćwiczenie 4 - Badanie wpływu asymetrii obciążenia na pracę sieci Strona 1/13 Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci Spis treści 1.Cel ćwiczenia...2 2.Wstęp...2 2.1.Wprowadzenie
Ćwiczenie 4 - Badanie wpływu asymetrii obciążenia na pracę sieci Strona 1/13 Ćwiczenie 4 Badanie wpływu asymetrii obciążenia na pracę sieci Spis treści 1.Cel ćwiczenia...2 2.Wstęp...2 2.1.Wprowadzenie
BLACHY TRAPEZOWE sierpień 2005
 BLACHY TRAPEZOWE sierpień 2005 Zawartość niniejszego folderu nie stanowi oferty handlowej w rozuieniu przepisów Kodeksu cywilnego. Inforacje zawarte w niniejszy opracowaniu stanowią jedynie rozwiązania
BLACHY TRAPEZOWE sierpień 2005 Zawartość niniejszego folderu nie stanowi oferty handlowej w rozuieniu przepisów Kodeksu cywilnego. Inforacje zawarte w niniejszy opracowaniu stanowią jedynie rozwiązania
PRAKTYCZNY PRZYKŁAD OCENY ŚRODOWISKOWEGO RYZYKA ZDROWOTNEGO
 PRAKTYCZNY PRZYKŁAD OCENY ŚRODOWISKOWEGO RYZYKA ZDROWOTNEGO Mgr Beata Malec, dr Mare Biesiada, dr Anicenta Buba Instytut Medycyny Pracy i Zdrowia Środowisowego, Sosnowiec Wstęp Zagrożenia zdrowotne stwarzane
PRAKTYCZNY PRZYKŁAD OCENY ŚRODOWISKOWEGO RYZYKA ZDROWOTNEGO Mgr Beata Malec, dr Mare Biesiada, dr Anicenta Buba Instytut Medycyny Pracy i Zdrowia Środowisowego, Sosnowiec Wstęp Zagrożenia zdrowotne stwarzane
MODEL NUMERYCZNY WYMIANY CIEPŁA W PROCESACH WALCOWANIA WLEWKÓW PÓŁPRZEMYSŁOWYCH W LINII LPS I WLEWKÓW CIĄGŁYCH W WALCOWNIACH BLACH I PRĘTÓW
 30 Prace IMŻ (0) Agniesza CEBO-RUDNICKA, Zbigniew MALINOWSKI, Beata HADAŁA, Andrzej GOŁDASZ AGH Aademia Górniczo-Hutnicza, Wydział Inżynierii Metali i Informatyi Przemysłowej MODEL NUMERYCZNY WYMIANY CIEPŁA
30 Prace IMŻ (0) Agniesza CEBO-RUDNICKA, Zbigniew MALINOWSKI, Beata HADAŁA, Andrzej GOŁDASZ AGH Aademia Górniczo-Hutnicza, Wydział Inżynierii Metali i Informatyi Przemysłowej MODEL NUMERYCZNY WYMIANY CIEPŁA
Pomiary napięć przemiennych
 LABORAORIUM Z MEROLOGII Ćwiczenie 7 Pomiary napięć przemiennych . Cel ćwiczenia Celem ćwiczenia jest poznanie sposobów pomiarów wielości charaterystycznych i współczynniów, stosowanych do opisu oresowych
LABORAORIUM Z MEROLOGII Ćwiczenie 7 Pomiary napięć przemiennych . Cel ćwiczenia Celem ćwiczenia jest poznanie sposobów pomiarów wielości charaterystycznych i współczynniów, stosowanych do opisu oresowych
1. RACHUNEK WEKTOROWY
 1 RACHUNEK WEKTOROWY 1 Rozstrzygnąć, czy możliwe jest y wartość sumy dwóch wetorów yła równa długości ażdego z nich 2 Dane są wetory: a i 3 j 2 ; 4 j = + = Oliczyć: a+, a, oraz a 3 Jai ąt tworzą dwa jednaowe
1 RACHUNEK WEKTOROWY 1 Rozstrzygnąć, czy możliwe jest y wartość sumy dwóch wetorów yła równa długości ażdego z nich 2 Dane są wetory: a i 3 j 2 ; 4 j = + = Oliczyć: a+, a, oraz a 3 Jai ąt tworzą dwa jednaowe
Podstawy rachunku prawdopodobieństwa (przypomnienie)
 . Zdarzenia odstawy rachunu prawdopodobieństwa (przypomnienie). rawdopodobieństwo 3. Zmienne losowe 4. rzyład rozładu zmiennej losowej. Zdarzenia (events( events) Zdarzenia elementarne Ω - zbiór zdarzeń
. Zdarzenia odstawy rachunu prawdopodobieństwa (przypomnienie). rawdopodobieństwo 3. Zmienne losowe 4. rzyład rozładu zmiennej losowej. Zdarzenia (events( events) Zdarzenia elementarne Ω - zbiór zdarzeń
MODEL OBLICZENIOWY DO OSZACOWANIA ODPORNOŚ CI BALISTYCZNEJ PANCERZY STALOWYCH
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK XLX NR 4 (79) 9 Mare Sersi Aadeia Marynari Wojennej MODEL OBLICZENIOWY DO OSZACOWANIA ODPORNOŚ CI BALISTYCZNEJ PANCERZY STALOWYCH STRESZCZENIE Przedstawiono
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK XLX NR 4 (79) 9 Mare Sersi Aadeia Marynari Wojennej MODEL OBLICZENIOWY DO OSZACOWANIA ODPORNOŚ CI BALISTYCZNEJ PANCERZY STALOWYCH STRESZCZENIE Przedstawiono
Defi f nicja n aprę r żeń
 Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
