Metody Obliczeniowe Mikrooptyki i Fotoniki. Podstawy metody różnic skończonych Podstawy metody FDTD
|
|
|
- Bogdan Żurawski
- 5 lat temu
- Przeglądów:
Transkrypt
1 Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody różnic skończonych Podstawy etody FDTD M. N. Sadiku, Nuerical Techniques in Electroagnetics 2nd Ed., CRC Press 2001 A. Taflove, S. Hagnes Coputational Electrodynaics The Finite-Difference Tie Doain Method, Artech House, 2005
2 Metoda różnic skończonych L^ Φ=0 1. Dyskretyzacja: Φ(r,t) Φ n Φ(r n,t n) 2. Zaiana równania różniczkowego na różnicowe Aproksyacja pochodnych iloraze różnicowy (lub wyrażeniai wyższego rzędu): df f x x f x x =li x 0 dx 2 x 3. Rozwiązanie równania różnicowego z uwzględnienie warunków początkowych i brzegowych
3 Klasyfikacja obszaru rozwiązań Obszar rozwiązań ożna często powiązać z podziałe równań cząstkowych drugiego rzędu na r. eliptyczne, paraboliczne i hiperboliczne
4 Klasyfikacja równań Cząstkowe równanie różniczkowe liniowe drugiego rzędu: Klasyfikacja:
5 Klasyfikacja warunków brzegowych Warunek Dirichleta: r=0 Warunek Neuanna: r =0 n Warunek ieszany: r h r r =0 n
6 Różnicowa aproksyacja pochodnych Górny iloraz różnicowy: f ' x 0 f x 0 x f x0 x Centralny iloraz różnicowy: f ' x 0 f x 0 x f x0 x 2 x Dolny iloraz różnicowy: f ' x 0 f x 0 f x 0 x x
7 Druga pochodna Z 3-krotnego zastosowania wzoru na centralny iloraz różnicowy dostajey: f ' x 0 x/ 2 f x 0 x f x0 f ' ' x 0 f ' ' x 0 f ' x 0 x/ 2 x f ' x 0 x / 2 f ' x 0 x / 2 x f x 0 x 2f x0 f x0 x x 2 f x 0 f x 0 x x
8 Dokładność aproksyacji pochodnej Rozwinięcie funkcji w szereg Taylora: n x n f x0 x= n=0 f x 0 O x N = n! 2 3 x x 3 = f x 0 x f ' x0 f ' ' x 0 f x 0 O xn 2! 3! N 1
9 Dokładność aproksyacji pochodnej Rozwinięcie funkcji w szereg Taylora: N 1 f x0 x= n=0 x n! n f n x0 O x N Przykład: rozwinięcie 2 rzędu: (I) f x0 x= f x0 x f ' x0 (II) f x0 x= f x0 x f ' x0 Wyrażenie na pierwszą pochodną: f x 0 x f x 0 x 2 x x2 2! x 2 2! f ' ' x0 O x3 f ' ' x 0 O x3 (I)-(II) : = f ' x 0 O x2 (Dokładność rozwinięcia)
10 Dokładność aproksyacji pochodnej Rozwinięcie funkcji w szereg Taylora: N 1 f x0 x= n=0 x n! n f n N x0 O x Przykład: rozwinięcie 3 rzędu: (I) f x0 x= f x0 x f ' x0 (II) f x0 x= f x0 x f ' x0 Wyrażenie na drugą pochodną: f x 0 x 2f x 0 f x 0 x x2 x2 2! x 2 2! f ' ' x0 f ' ' x 0 (I)+(II): = f ' ' x 0 O x2 (Dokładność rozwinięcia) x 3 3! x3 3! f 3 x 0 O x4 f 3 x 0 O x4
11 Ogólna etoda wyprowadzenia wyrażeń wyższego rzędu Układ N równań: i=1 N na N niewiadoych: { f N 1 n x f x0 i x = n=0 i f = A f r n! n f n 1 x0, f 2 x 0, f x 0 O i x N N x0 }
12 Dokładność aproksyacji pochodnej M. Sadiku, Nuerical Techniques in Electrodynaics CRC Press LLC 2001
13 Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy etody FDTD Algoryt FDTD w jedny wyiarze Warunki brzegowe PML w jedny wyiarze Syulacja źródła Algoryt FDTD w 3 wyiarach Wygładzanie nieciągłości przenikalności elektrycznej
14 FDTD (finite difference tie doain ethod) etoda różnic skończonych zastosowana do równań Maxwella z czase Prawa Faradaya i Apera-Maxwella posłużą do wyprowadzenia kroku iteracyjnego dla ewolucji pól w czasie: Pozostałe równania uszą być spełniane przez pole początkowe: H E= 0 t E H= E 0 t (ϵ E)=ρ (μ H )=0 (wszystkie pola rzeczywiste i zależne od czasu )
15 FDTD przypadek 1-wyiarowy H E= 0 t E H= E 0 t H z x,t, E y x,t H y x, t, E z x,t W przypadku jednowyiarowy, otrzyujey równoważne sobie niezależne równania dla dwóch polaryzacji Hz 1 E y = t 0 x ( Ey 1 Hz = ϵ ϵ σ E y 0 t x H y 1 E z = t 0 x ) Ez ( Hy 1 = σ E z + t ϵ0 ϵ x )
16 FDTD przypadek jednowyiarowy Hz 1 = ϵ ϵ σ E y 0 t x 1 E y = t 0 x n 1/ 2 n 1/ 2 n n 1/ 2 n n E y n 1 E y n 1 /2 1 /2 H z n 1 /2 x t[ t] x[ x] n 1/ 2 H zn 1 /2 H zn 1 /2 1 /2 ) 1 /2 1 /2 t ( Ey Hz x E y n 1 x 1 /2 H z n 1 /2 x
17 FDTD przypadek jednowyiarowy Hz 1 E y = t 0 x E y n =E y n x, t Dyskretyzacja H z n 1 /2 =H z n 1/ 2 x, 1/ 2 t 1 /2 n 1/ 2= n 1/2 x 1/2 1 /2 H z n 1/2 H z n 1/ 2 t 1 E y n E y n 1 = 0 n 1/ 2 x (Centralne ilorazy różnicowe) /2 1/ 2 H z 1 = H n 1 /2 z n 1/ 2 t E y n 1 E y n x 0 n 1/2
18 FDTD przypadek jednowyiarowy ( Ey Hz 1 = ϵ ϵ σ E y 0 t x ) E y n =E y n x, t H z n 1 /2 =H z n 1/ 2 x, 1/ 2 t n = n x n = n x 1 /2 Dyskretyzacja (E y ) +1 (E ) n y n δt ( =(ϵ 0 ϵn ) 1 σ n (E y ) n +1 +(E y )n 2 2 (Średnia) E y 1/ n +1 / 2 (H z ) n+1+1// 22 (H z )n 1/ 2 δx ) (Centralne ilorazy różnicowe) 1 y n E = 1 t n 0 n E y n t 1/ 2 1/ 2 3 H z n 1/ 2 H z n 1/2 O x 0 n
19 FDTD przypadek jednowyiarowy Opis układu: { 1/ 2, 3/2, N 1/ 2 } { 0, 1, N } { 0, 1, N } x, t Warunki początkowe: E, E, E { y0 y1 y N} { H 1/2 z 1/2, H z 1/3/ 22, H z 1/2 N 1/ 2 } Warunki brzegowe, np. { H 1 /2 z 1 /2 /2 =0, H z 1 N 1/ 2 =0 } E =0, E { y0 y N =0 } (PMC doskonały przewodnik agn.) (PEC doskonały przewodnik) Krok iteracyjny: /2 1/ 2 H z 1 H, E, E { n 1 /2 z n 1/ 2 y n y n 1 } 1 /2 1/ 2 E y 1 E, H, H { n y n z n 1 /2 z n 1/ 2 } n=0 N 1 n=0 N
20 Dygresja jednostki znoralizowane Układ SI: Niefizyczna przewodniość agnetyczna E= M H 0 H= E 0 H t E t t ' =ct=t / 0 0 H '= 0 H '= 0 M '= 1 M 0 0 = 0 / (ipedancja próżni) W nowy zapisie nie występują przenikalności próżni. Dodatkowo te sae jednostki ają pola E i H', obie przewodniości, a także x i t': E= M ' H ' H' = ' E E t ' H' t '
21 FDTD przypadek jednowyiarowy Ey 1 H z' = ' E y t' x H z ' 1 y n E = 1 1/ 2 n 1/ 2 1 Ey = M ' H z ' t ' x = 1 t ' n ' n H z' t ' M ' n 1/2 n 1/2 1/2 H z ' n 1 /2 t' E y n 1 E y n O 3 x n 1/ 2 t ' 1/ 2 1/2 3 E H z ' n 1/ 2 H z ' n 1 /2 O x n y n Algoryt 1-wyiarowy w tej postaci wyaga 4 nożeń / krok / koórkę. Dla sytuacji 3-wyiarowej będzie to 12 nożeń.
22 FDTD przypadek jednowyiarowy δt' ~ σ M ' =0, μ=1, E E δx 1/ 2 1/ 2 H z ' n 1/ 2 = H z ' n 1/ 2 E y n 1 E y n 1 y n E = 1 t ' n ' n An y n E t '2 2 x n H z ' 1/ 2 n 1/ 2 H z ' 1/2 n 1/2 Bn Algoryt jednowyiarowy dla ateriałów nieagnetycznych wyaga jedynie 2 nożeń / krok / koórkę!!! Ta saa operacja dla sytuacji 3-wyiarowej prowadzi do 6 nożeń.
23 Idealne sztuczne warunki brzegowe: pochłaniające i nieodbijające PEC Obszar syulacji (ϵ1,μ 1 ) (ϵ 2,μ 2 ) PEC x Brak odbić 2, 2 =? Tłuienie
24 Dygresja: dopasowanie ipedancji 1, 1 2, 2 PEC PEC x Odbicie prostopadłe (TE i TM, zapis zespolony, dla fali onochroatycznej): R= R=0 gdy n 2 / 2 n 1 / 1 T= n 2 / 2 n 1 / 1 2 n 1 / 1 n 2 / 2 n 1 / 1 n 2 / 2 =n 1 / 1 Warunkie braku odbicia od granicy ośrodków jest równość ipedancji: =
25 Dygresja: dopasowanie ipedancji = = 1 1 Wracay do zapisu rzeczywistego: t =Re exp ±i t i = i ' 0 k0 M M ' i = i 0 k0 '= 0 M '= 1 M 0 k 0 = / c
26
27 Nieodbijające warunki brzegowe 1, 1 2, 2 PEC 1 ' =0 M 1 ' =0 x L Współczynnik odbicia: r 2 =exp k 0 I n 2 2L 2 n 2 = ϵ2 μ 2= μ1 /ϵ1 (ϵ2 +i σ 2 ' / k 0 ) 2 '= ln r 2 4 L 1 / 1
28 Zadania Metoda FDTD (finite difference tie doain) Zadanie 1. Napisać funkcję opartą na etodzie FDTD w 1 wyiarze służącą do syulacji ewolucji pola elektrycznego i agnetycznego w czasie. a. Przyjąć, że obszar syulacji ograniczony jest doskonały przewodnikie. b. Przyjąć, że obszar syulacji ograniczony jest nieodbijający i stratny ateriałe (1-wyiarowy PML). c. Wprowadzić do obszaru syulacji pole początkowe odpowiadające ipulsowi d. Włączyć w obszar syulacji źródło sztywne (bądź SF/TF). Zadanie 2. Wykonać propagację ipulsu oraz fali onochroatycznej dla wybranych sytuacji, np. - dla propagacji w przestrzeni swobodnej - dla rozpraszania na granicy ośrodków - dla odbicia od ateriału z naniesioną powłoka antyodbiciową - dla rezonansowego odbicia i transisji przez płytkę FP. -przeanalizować odbicie od siatki Bragga dla długości fali spoza przerwy wzbronionej, ze środka przerwy i z brzegu przerwy -przeanalizować odbicie fali od ośrodka o ujenej przenikalności elektrycznej (etalu), a następnie rezonansową transisję przez układ dwóch etalowych zwierciadeł o wysokich współczynnikach odbicia - wykonać syulację propagacji przez ośrodek periodyczny (fale Blocha) (niekoniecznie z periodycznyi warunkai brzegowyi).
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
Metody Obliczeniowe Mikrooptyki i Fotoniki. Metoda propagacji wiązki BPM Modelowanie propagacji
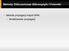 Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika. Plan: Wykład 9: Interferencja w układach warstwowych
 Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji
 Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM cd wyznaczanie modów metodą urojonej długości i korelacyjną operowanie efektywnym współczynnikiem załamania metoda FT-BPM metoda
Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM cd wyznaczanie modów metodą urojonej długości i korelacyjną operowanie efektywnym współczynnikiem załamania metoda FT-BPM metoda
y i b) metoda różnic skończonych nadal problem nieliniowy 2 go rzędu z warunkiem Dirichleta
 b) metoda różnic skończonych nadal problem nieliniowy 2 go rzędu z warunkiem Dirichleta przedział (a,b) dzielimy na siatkę, powiedzmy o stałym kroku: punkty siatki: u A y i w metodzie strzałów używamy
b) metoda różnic skończonych nadal problem nieliniowy 2 go rzędu z warunkiem Dirichleta przedział (a,b) dzielimy na siatkę, powiedzmy o stałym kroku: punkty siatki: u A y i w metodzie strzałów używamy
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Efekt naskórkowy (skin effect)
 Efekt naskórkowy (skin effect) Rozważmy cylindryczny przewód o promieniu a i o nieskończonej długości. Przez przewód płynie prąd I = I 0 cos ωt. Dla niezbyt dużych częstości ω możemy zaniedbać prąd przesunięcia,
Efekt naskórkowy (skin effect) Rozważmy cylindryczny przewód o promieniu a i o nieskończonej długości. Przez przewód płynie prąd I = I 0 cos ωt. Dla niezbyt dużych częstości ω możemy zaniedbać prąd przesunięcia,
Metody numeryczne rozwiązywania równań różniczkowych
 Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
Fotonika. Plan: Wykład 3: Polaryzacja światła
 Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Całkowanie numeryczne
 Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Metoda różnic skończonych dla
 Metoda różnic skończonych dla cząstkowych równań różniczkowych na laboratorium rozwiązywać będziemy typowe równania: dyfuzji (również przewodnictwo cieplne) paraboliczne równanie Poissona (np. pole elektrostatyczne,
Metoda różnic skończonych dla cząstkowych równań różniczkowych na laboratorium rozwiązywać będziemy typowe równania: dyfuzji (również przewodnictwo cieplne) paraboliczne równanie Poissona (np. pole elektrostatyczne,
13 Równanie struny drgającej. Równanie przewodnictwa ciepła.
 Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1
 Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
Przedmowa do wydania drugiego Konwencje i ważniejsze oznaczenia... 13
 Przedmowa do wydania drugiego... 11 Konwencje i ważniejsze oznaczenia... 13 1. Rachunek i analiza wektorowa... 17 1.1. Wielkości skalarne i wektorowe... 17 1.2. Układy współrzędnych... 20 1.2.1. Układ
Przedmowa do wydania drugiego... 11 Konwencje i ważniejsze oznaczenia... 13 1. Rachunek i analiza wektorowa... 17 1.1. Wielkości skalarne i wektorowe... 17 1.2. Układy współrzędnych... 20 1.2.1. Układ
Fale elektromagnetyczne
 Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Rachunek różniczkowy i całkowy 2016/17
 Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Spis treœci. Wstêp... 9
 Spis treœci Wstêp... 9 1. Elementy analizy wektorowej i geometrii analitycznej... 11 1.1. Podstawowe pojêcia rachunku wektorowego... 11 1.2. Dodawanie i mno enie wektorów... 14 1.3. Uk³ady wspó³rzêdnych
Spis treœci Wstêp... 9 1. Elementy analizy wektorowej i geometrii analitycznej... 11 1.1. Podstawowe pojêcia rachunku wektorowego... 11 1.2. Dodawanie i mno enie wektorów... 14 1.3. Uk³ady wspó³rzêdnych
Metoda rozdzielania zmiennych
 Rozdział 12 Metoda rozdzielania zmiennych W tym rozdziale zajmiemy się metodą rozdzielania zmiennych, którą można zastosować, aby wyrazić jawnymi wzorami rozwiązania pewnych konkretnych równań różniczkowych
Rozdział 12 Metoda rozdzielania zmiennych W tym rozdziale zajmiemy się metodą rozdzielania zmiennych, którą można zastosować, aby wyrazić jawnymi wzorami rozwiązania pewnych konkretnych równań różniczkowych
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki Kod USOS: 1103-4Fot4 Wykład (30h): R. Kotyński Wtorki 9:15-11:00, s.1.38 lub B4.17(ul. Pasteura 5) Ćwiczenia (45h): Wtorki, w godz. 14.15-16.30, s.1.7 lub B4.17
Metody Obliczeniowe Mikrooptyki i Fotoniki Kod USOS: 1103-4Fot4 Wykład (30h): R. Kotyński Wtorki 9:15-11:00, s.1.38 lub B4.17(ul. Pasteura 5) Ćwiczenia (45h): Wtorki, w godz. 14.15-16.30, s.1.7 lub B4.17
Interpolacja. Interpolacja wykorzystująca wielomian Newtona
 Interpolacja Funkcja y = f(x) jest dana w postaci dyskretnej: (1) y 1 = f(x 1 ), y 2 = f(x 2 ), y 3 = f(x 3 ), y n = f(x n ), y n +1 = f(x n +1 ), to znaczy, że w pewny przedziale x 1 ; x 2 Ú ziennej niezależnej
Interpolacja Funkcja y = f(x) jest dana w postaci dyskretnej: (1) y 1 = f(x 1 ), y 2 = f(x 2 ), y 3 = f(x 3 ), y n = f(x n ), y n +1 = f(x n +1 ), to znaczy, że w pewny przedziale x 1 ; x 2 Ú ziennej niezależnej
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Elektrodynamika Część 6 Elektrodynamika Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 6 Elektrodynamika Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 7 Elektrodynamika 3 7.1 Siła elektromotoryczna................ 3 7.2
Elektrodynamika Część 6 Elektrodynamika Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 7 Elektrodynamika 3 7.1 Siła elektromotoryczna................ 3 7.2
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy programu Meep (interfejs pythonowy i scheme) Metoda FDTD c.d. - nieciągłości przenikalności elektrycznej, dyspersja M. N. Sadiku, Numerical Techniques
Metody Obliczeniowe Mikrooptyki i Fotoniki Podstawy programu Meep (interfejs pythonowy i scheme) Metoda FDTD c.d. - nieciągłości przenikalności elektrycznej, dyspersja M. N. Sadiku, Numerical Techniques
Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional
 Fotonika Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional Plan: Jednowymiarowe kryształy fotoniczne Fale Blocha, fotoniczna struktura
Fotonika Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional Plan: Jednowymiarowe kryształy fotoniczne Fale Blocha, fotoniczna struktura
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
x y
 Przykłady pytań na egzamin końcowy: (Uwaga! Skreślone pytania nie obowiązują w tym roku.). Oblicz wartość interpolacji funkcjami sklejanymi (przypadek (case) a), dla danych i =[- 4 5], y i =[0 4 -]. Jaka
Przykłady pytań na egzamin końcowy: (Uwaga! Skreślone pytania nie obowiązują w tym roku.). Oblicz wartość interpolacji funkcjami sklejanymi (przypadek (case) a), dla danych i =[- 4 5], y i =[0 4 -]. Jaka
Elektrodynamika. Część 6. Elektrodynamika. Ryszard Tanaś. Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 6 Elektrodynamika Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 7 Elektrodynamika 3 7.1 Siła elektromotoryczna.................. 3
Elektrodynamika Część 6 Elektrodynamika Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 7 Elektrodynamika 3 7.1 Siła elektromotoryczna.................. 3
Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału
 Fizyka 2 Wykład 4 1 Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału Niezależne od czasu równanie Schödingera ma postać: 2 d ( x)
Fizyka 2 Wykład 4 1 Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału Niezależne od czasu równanie Schödingera ma postać: 2 d ( x)
Projekt 6: Równanie Poissona - rozwiązanie metodą algebraiczną.
 Projekt 6: Równanie Poissona - rozwiązanie metodą algebraiczną. Tomasz Chwiej 9 sierpnia 18 1 Wstęp 1.1 Dyskretyzacja n y V V 1 V 3 1 j= i= 1 V 4 n x Rysunek 1: Geometria układu i schemat siatki obliczeniowej
Projekt 6: Równanie Poissona - rozwiązanie metodą algebraiczną. Tomasz Chwiej 9 sierpnia 18 1 Wstęp 1.1 Dyskretyzacja n y V V 1 V 3 1 j= i= 1 V 4 n x Rysunek 1: Geometria układu i schemat siatki obliczeniowej
Analiza matematyczna dla informatyków 3 Zajęcia 14
 Analiza matematyczna dla informatyków 3 Zajęcia 14 Metoda rozwiązywania (Jednorodne równanie różniczkowe liniowe rzędu n o stałych współczynnikach). gdzie a 0,..., a n 1 C. Wielomian charakterystyczny:
Analiza matematyczna dla informatyków 3 Zajęcia 14 Metoda rozwiązywania (Jednorodne równanie różniczkowe liniowe rzędu n o stałych współczynnikach). gdzie a 0,..., a n 1 C. Wielomian charakterystyczny:
Promieniowanie dipolowe
 Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Definicja punktu wewnętrznego zbioru Punkt p jest punktem wewnętrznym zbioru, gdy należy do niego wraz z pewnym swoim otoczeniem
 Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
Definicja kuli w R n ulą o promieniu r>0 r R i o środku w punkcie p R n nazywamy zbiór {x R n : ρ(xp)
Optyka. Optyka falowa (fizyczna) Optyka geometryczna Optyka nieliniowa Koherencja światła
 Optyka Optyka falowa (fizyczna) Optyka geometryczna Optyka nieliniowa Koherencja światła 1 Optyka falowa Opis i zastosowania fal elektromagnetycznych w zakresie widzialnym i bliskim widzialnemu Podstawowe
Optyka Optyka falowa (fizyczna) Optyka geometryczna Optyka nieliniowa Koherencja światła 1 Optyka falowa Opis i zastosowania fal elektromagnetycznych w zakresie widzialnym i bliskim widzialnemu Podstawowe
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018
 Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018 Tomasz Chwiej 22 stycznia 2019 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018 Tomasz Chwiej 22 stycznia 2019 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów
Równania Maxwella redukują się w przypadku statycznego pola elektrycznego do postaci: D= E
 Elektrostatyka Równania Maxwella redukują się w przypadku statycznego pola elektrycznego do postaci: D=ϱ E=0 D= E Źródłem pola elektrycznego są ładunki, które mogą być: punktowe q [C] liniowe [C/m] powierzchniowe
Elektrostatyka Równania Maxwella redukują się w przypadku statycznego pola elektrycznego do postaci: D=ϱ E=0 D= E Źródłem pola elektrycznego są ładunki, które mogą być: punktowe q [C] liniowe [C/m] powierzchniowe
Spis treści. Wykaz ważniejszych oznaczeń. Przedmowa 15. Wprowadzenie Ruch falowy w ośrodku płynnym Pola akustyczne źródeł rzeczywistych
 Spis treści Wykaz ważniejszych oznaczeń u Przedmowa 15 Wprowadzenie 17 1. Ruch falowy w ośrodku płynnym 23 1.1. Dźwięk jako drgania ośrodka sprężystego 1.2. Fale i liczba falowa 1.3. Przestrzeń liczb falowych
Spis treści Wykaz ważniejszych oznaczeń u Przedmowa 15 Wprowadzenie 17 1. Ruch falowy w ośrodku płynnym 23 1.1. Dźwięk jako drgania ośrodka sprężystego 1.2. Fale i liczba falowa 1.3. Przestrzeń liczb falowych
MODELOWANIE POLA TEMPERATURY MOSTKÓW CIEPLNYCH PRZY WYKORZYSTANIU METODY ELEMENTÓW BRZEGOWYCH. Piotr RYNKOWSKI, Tomasz Janusz TELESZEWSKI
 ODEOWANIE POA TEPERATURY OSTKÓW CIEPNYCH PRZY WYKORZYSTANIU ETODY EEENTÓW BRZEGOWYCH Piotr RYNKOWSKI, Tomasz Janusz TEESZEWSKI Wydział Budownictwa i Inżynierii Środowiska, Politechnika Białostocka, ul.
ODEOWANIE POA TEPERATURY OSTKÓW CIEPNYCH PRZY WYKORZYSTANIU ETODY EEENTÓW BRZEGOWYCH Piotr RYNKOWSKI, Tomasz Janusz TEESZEWSKI Wydział Budownictwa i Inżynierii Środowiska, Politechnika Białostocka, ul.
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne.
 Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
Motywacja Podstawy. Historia Teoria 2D PhC Podsumowanie. Szymon Lis Photonics Group szymon.lis@pwr.wroc.pl C-2 p.305. Motywacja.
 Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
Informatyka i komputerowe wspomaganie prac inżynierskich
 Informatyka i komputerowe wspomaganie prac inżynierskich Dr Zbigniew Kozioł - wykład Dr Grzegorz Górski - laboratorium Wykład III Numeryczne rozwiązywanie równań różniczkowych. MES, Metoda Elementów Skończonych
Informatyka i komputerowe wspomaganie prac inżynierskich Dr Zbigniew Kozioł - wykład Dr Grzegorz Górski - laboratorium Wykład III Numeryczne rozwiązywanie równań różniczkowych. MES, Metoda Elementów Skończonych
Metody Obliczeniowe w Nauce i Technice
 23. Rozwiązywanie równań różniczkowych cząstkowych Marian Bubak Department of Computer Science AGH University of Science and Technology Krakow, Poland bubak@agh.edu.pl dice.cyfronet.pl Contributors Magdalena
23. Rozwiązywanie równań różniczkowych cząstkowych Marian Bubak Department of Computer Science AGH University of Science and Technology Krakow, Poland bubak@agh.edu.pl dice.cyfronet.pl Contributors Magdalena
KATEDRA TELEKOMUNIKACJI I FOTONIKI
 ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
Podstawy Automatyki. wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak. Politechnika Wrocławska. Instytut Technologii Maszyn i Automatyzacji (I-24)
 Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Fale elektromagnetyczne. Gradient pola. Gradient pola... Gradient pola... Notatki. Notatki. Notatki. Notatki. dr inż. Ireneusz Owczarek 2013/14
 dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
Elektrostatyka, cz. 1
 Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
- Strumień mocy, który wpływa do obszaru ograniczonego powierzchnią A ( z minusem wpływa z plusem wypływa)
 37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
Model oscylatorów tłumionych
 Inna nazwa: model klasyczny, Lorentza Założenia: - ośrodek jest zbiorem naładowanych oscylatorów oddziałujących z falą elektromagnetyczną - wszystkie występujące siły są izotropowe - wartość siły tłumienia
Inna nazwa: model klasyczny, Lorentza Założenia: - ośrodek jest zbiorem naładowanych oscylatorów oddziałujących z falą elektromagnetyczną - wszystkie występujące siły są izotropowe - wartość siły tłumienia
Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki
 Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki Spis treści Przedmowa... 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce?... 13 1. Analiza wektorowa... 19 1.1. Algebra
Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki Spis treści Przedmowa... 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce?... 13 1. Analiza wektorowa... 19 1.1. Algebra
Symulacja przepływu ciepła dla wybranych warunków badanego układu
 Symulacja przepływu ciepła dla wybranych warunków badanego układu I. Część teoretyczna Ciepło jest formą przekazywana energii, która jest spowodowana różnicą temperatur (inną formą przekazywania energii
Symulacja przepływu ciepła dla wybranych warunków badanego układu I. Część teoretyczna Ciepło jest formą przekazywana energii, która jest spowodowana różnicą temperatur (inną formą przekazywania energii
Informacja o przestrzeniach Sobolewa
 Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Fale elektromagnetyczne. Obrazy.
 Fale elektroagnetyczne. Obrazy. Wykład 7 1 Wrocław University of Technology 28-4-212 Tęcza Maxwella 2 1 Tęcza Maxwella 3 ( kx t) ( kx t) E = E sin ω = sin ω Prędkość rozchodzenia się fali: 1 8 c = = 3.
Fale elektroagnetyczne. Obrazy. Wykład 7 1 Wrocław University of Technology 28-4-212 Tęcza Maxwella 2 1 Tęcza Maxwella 3 ( kx t) ( kx t) E = E sin ω = sin ω Prędkość rozchodzenia się fali: 1 8 c = = 3.
Fotonika kurs magisterski grupa R41 semestr VII Specjalność: Inżynieria fotoniczna. Egzamin ustny: trzy zagadnienia do objaśnienia
 Dr inż. Tomasz Kozacki Prof. dr hab.inż. Romuald Jóźwicki Zakład Techniki Optycznej Instytut Mikromechaniki i Fotoniki pokój 513a ogłoszenia na tablicach V-tego piętra kurs magisterski grupa R41 semestr
Dr inż. Tomasz Kozacki Prof. dr hab.inż. Romuald Jóźwicki Zakład Techniki Optycznej Instytut Mikromechaniki i Fotoniki pokój 513a ogłoszenia na tablicach V-tego piętra kurs magisterski grupa R41 semestr
Fale elektromagnetyczne
 Podstawy elektromagnetyzmu Wykład 11 Fale elektromagnetyczne Równania Maxwella H=J D t E= B t D= B=0 D= E J= E B= H Ruch ładunku jest źródłem pola magnetycznego Zmiana pola magnetycznego w czasie jest
Podstawy elektromagnetyzmu Wykład 11 Fale elektromagnetyczne Równania Maxwella H=J D t E= B t D= B=0 D= E J= E B= H Ruch ładunku jest źródłem pola magnetycznego Zmiana pola magnetycznego w czasie jest
RÓWNANIA MAXWELLA. Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego?
 RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
Fala EM w izotropowym ośrodku absorbującym
 Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Równania różniczkowe zwyczajne: problem brzegowy [1D]
![Równania różniczkowe zwyczajne: problem brzegowy [1D] Równania różniczkowe zwyczajne: problem brzegowy [1D]](/thumbs/92/110705513.jpg) Równania różniczkowe zwyczajne: problem brzegowy [1D] 1) Równania różniczkowe zwyczajne jako szczególny przypadek problemów opisywanych przez eliptyczne równania cząstkowe 2) Problem brzegowy a problem
Równania różniczkowe zwyczajne: problem brzegowy [1D] 1) Równania różniczkowe zwyczajne jako szczególny przypadek problemów opisywanych przez eliptyczne równania cząstkowe 2) Problem brzegowy a problem
Metody numeryczne. materiały do ćwiczeń dla studentów. 1. Teoria błędów, notacja O
 Metody nueryczne ateriały do ćwiczeń dla studentów 1. Teoria błędów, notacja O 1.1. Błąd bezwzględny, błąd względny 1.2. Ogólna postać błędu 1.3. Proble odwrotny teorii błędów - zasada równego wpływu -
Metody nueryczne ateriały do ćwiczeń dla studentów 1. Teoria błędów, notacja O 1.1. Błąd bezwzględny, błąd względny 1.2. Ogólna postać błędu 1.3. Proble odwrotny teorii błędów - zasada równego wpływu -
region bezwzględnej stabilności dla ogólnej niejawnej metody RK R(z) 1 może być nieograniczony niejawna 1 stopniowa
 region bezwzględnej stabilności dla ogólnej niejawnej metody RK u =λu u=λu, z=λδt dla metod niejawnych: ij nie można ż obciąć bićrozwinięcia i i Taylora, bo A pełnał współczynnik wzmocnienia nie jest wielomianem,
region bezwzględnej stabilności dla ogólnej niejawnej metody RK u =λu u=λu, z=λδt dla metod niejawnych: ij nie można ż obciąć bićrozwinięcia i i Taylora, bo A pełnał współczynnik wzmocnienia nie jest wielomianem,
Modelowanie pola akustycznego. Opracowała: prof. dr hab. inż. Bożena Kostek
 Modelowanie pola akustycznego Opracowała: prof. dr hab. inż. Bożena Kostek Klasyfikacje modeli do badania pola akustycznego Modele i metody wykorzystywane do badania pola akustycznego MODELE FIZYCZNE MODELE
Modelowanie pola akustycznego Opracowała: prof. dr hab. inż. Bożena Kostek Klasyfikacje modeli do badania pola akustycznego Modele i metody wykorzystywane do badania pola akustycznego MODELE FIZYCZNE MODELE
Pole elektrostatyczne
 Termodynamika 1. Układ termodynamiczny 5 2. Proces termodynamiczny 5 3. Bilans cieplny 5 4. Pierwsza zasada termodynamiki 7 4.1 Pierwsza zasada termodynamiki w postaci różniczkowej 7 5. Praca w procesie
Termodynamika 1. Układ termodynamiczny 5 2. Proces termodynamiczny 5 3. Bilans cieplny 5 4. Pierwsza zasada termodynamiki 7 4.1 Pierwsza zasada termodynamiki w postaci różniczkowej 7 5. Praca w procesie
Skład i wilgotność betonu komórkowego jako czynniki wpływające na skuteczność systemów komunikacji bezprzewodowej w budynkach
 Skład i wilgotność betonu komórkowego jako czynniki wpływające na skuteczność systemów komunikacji bezprzewodowej w budynkach Agnieszka Choroszucho, Adam Steckiewicz Wprowadzenie Obecna polityka energetyczna
Skład i wilgotność betonu komórkowego jako czynniki wpływające na skuteczność systemów komunikacji bezprzewodowej w budynkach Agnieszka Choroszucho, Adam Steckiewicz Wprowadzenie Obecna polityka energetyczna
Lista zadań nr 2 z Matematyki II
 Lista zadań nr 2 z Matematyki II dla studentów wydziału Architektury, kierunku Gospodarka Przestrzenna. Wyznaczyć dziedzinę funkcji f(x, y) = ln(4 x 2 y 2 ), f(x, y) = x 2 + y 2, f(x, y) = ln(4 x 2 y 2
Lista zadań nr 2 z Matematyki II dla studentów wydziału Architektury, kierunku Gospodarka Przestrzenna. Wyznaczyć dziedzinę funkcji f(x, y) = ln(4 x 2 y 2 ), f(x, y) = x 2 + y 2, f(x, y) = ln(4 x 2 y 2
Fala elektromagnetyczna o określonej częstotliwości ma inną długość fali w ośrodku niż w próżni. Jako przykłady policzmy:
 Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
Równania różniczkowe cząstkowe. Wojciech Szewczuk
 Równania różniczkowe cząstkowe Równania różniczkowe cząstkowe - wstęp u x = lim x u(x + x, y) u(x, y) x u u(x, y + y) u(x, y) y = lim y y () (2) 2 u x 2 + 2xy 2 u y 2 + u = 3 u x 2 y + x 2 u + 8u = 5y
Równania różniczkowe cząstkowe Równania różniczkowe cząstkowe - wstęp u x = lim x u(x + x, y) u(x, y) x u u(x, y + y) u(x, y) y = lim y y () (2) 2 u x 2 + 2xy 2 u y 2 + u = 3 u x 2 y + x 2 u + 8u = 5y
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
1.5. ZWIĄZKI KONSTYTUTYWNE STRONA FIZYCZNA
 J. Wyrwał, Wykłady z echaniki ateriałów.5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowadzenie Wyprowadzone w rozdziałach.3 (strona statyczna) i.4 (strona geoetryczna) równania (.3.36) i (.4.) są niezależne
J. Wyrwał, Wykłady z echaniki ateriałów.5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowadzenie Wyprowadzone w rozdziałach.3 (strona statyczna) i.4 (strona geoetryczna) równania (.3.36) i (.4.) są niezależne
ELEKTROTECHNIKA Semestr 2 Rok akad / ZADANIA Z MATEMATYKI Zestaw Oblicz pochodne cząstkowe rzędu drugiego funkcji:
 ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
y f x 0 f x 0 x x 0 x 0 lim 0 h f x 0 lim x x0 - o ile ta granica właściwa istnieje. f x x2 Definicja pochodnych jednostronnych 1.5 0.
 Matematyka ZLic - 3 Pochodne i różniczki funkcji jednej zmiennej Definicja Pochodną funkcji f w punkcie x, nazwiemy liczbę oznaczaną symbolem f x lub df x dx, równą granicy właściwej f x lim h - o ile
Matematyka ZLic - 3 Pochodne i różniczki funkcji jednej zmiennej Definicja Pochodną funkcji f w punkcie x, nazwiemy liczbę oznaczaną symbolem f x lub df x dx, równą granicy właściwej f x lim h - o ile
Termodynamika. Część 12. Procesy transportu. Janusz Brzychczyk, Instytut Fizyki UJ
 Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
równania funkcyjne opisujące relacje spełniane przez pochodne nieznanej (poszukiwanej) funkcji
 Równania różniczkowe: równania funkcyjne opisujące relacje spełniane przez pochodne nieznanej (poszukiwanej) funkcji cząstkowe: funkcja więcej niż jednej zmienna, np.: czas i położenie np. wychylenie u(x,t)
Równania różniczkowe: równania funkcyjne opisujące relacje spełniane przez pochodne nieznanej (poszukiwanej) funkcji cząstkowe: funkcja więcej niż jednej zmienna, np.: czas i położenie np. wychylenie u(x,t)
) I = dq. Obwody RC. I II prawo Kirchhoffa: t = RC (stała czasowa) IR V C. ! E d! l = 0 IR +V C. R dq dt + Q C V 0 = 0. C 1 e dt = V 0.
 Obwody RC t = 0, V C = 0 V 0 IR 0 V C C I II prawo Kirchhoffa: " po całym obwodzie zamkniętym E d l = 0 IR +V C V 0 = 0 R dq dt + Q C V 0 = 0 V 0 R t = RC (stała czasowa) Czas, po którym prąd spadnie do
Obwody RC t = 0, V C = 0 V 0 IR 0 V C C I II prawo Kirchhoffa: " po całym obwodzie zamkniętym E d l = 0 IR +V C V 0 = 0 R dq dt + Q C V 0 = 0 V 0 R t = RC (stała czasowa) Czas, po którym prąd spadnie do
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
5. Analiza dyskryminacyjna: FLD, LDA, QDA
 Algorytmy rozpoznawania obrazów 5. Analiza dyskryminacyjna: FLD, LDA, QDA dr inż. Urszula Libal Politechnika Wrocławska 2015 1 1. Liniowe funkcje dyskryminacyjne Liniowe funkcje dyskryminacyjne mają ogólną
Algorytmy rozpoznawania obrazów 5. Analiza dyskryminacyjna: FLD, LDA, QDA dr inż. Urszula Libal Politechnika Wrocławska 2015 1 1. Liniowe funkcje dyskryminacyjne Liniowe funkcje dyskryminacyjne mają ogólną
Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.
![Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość. Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.](/thumbs/102/155632743.jpg) Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Równania różniczkowe zwyczajne analityczne metody rozwiazywania
 Równania różniczkowe zwyczajne analityczne meto rozwiazywania Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 8 Plan Określenia podstawowe 1 Wstęp Określenia podstawowe
Równania różniczkowe zwyczajne analityczne meto rozwiazywania Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 8 Plan Określenia podstawowe 1 Wstęp Określenia podstawowe
Wykład 8 ELEKTROMAGNETYZM
 Wykład 8 ELEKTROMAGNETYZM Równania Maxwella dive = ρ εε 0 prawo Gaussa dla pola elektrycznego divb = 0 rote = db dt prawo Gaussa dla pola magnetycznego prawo indukcji Faradaya rotb = μμ 0 j + εε 0 μμ 0
Wykład 8 ELEKTROMAGNETYZM Równania Maxwella dive = ρ εε 0 prawo Gaussa dla pola elektrycznego divb = 0 rote = db dt prawo Gaussa dla pola magnetycznego prawo indukcji Faradaya rotb = μμ 0 j + εε 0 μμ 0
Spektroskopia modulacyjna
 Spektroskopia modulacyjna pozwala na otrzymanie energii przejść optycznych w strukturze z bardzo dużą dokładnością. Charakteryzuje się również wysoką czułością, co pozwala na obserwację słabych przejść,
Spektroskopia modulacyjna pozwala na otrzymanie energii przejść optycznych w strukturze z bardzo dużą dokładnością. Charakteryzuje się również wysoką czułością, co pozwala na obserwację słabych przejść,
Metody numeryczne równań różniczkowych zwyczajnych
 Metody numeryczne równań różniczkowych zwyczajnych Marcin Jenczmyk m.jenczmyk@knm.katowice.pl 9 maja 2015 M. Jenczmyk XXX Sesja KNM Metody numeryczne R.R.Z. 1 / 18 Omawiany problem dotyczyć będzie numerycznego
Metody numeryczne równań różniczkowych zwyczajnych Marcin Jenczmyk m.jenczmyk@knm.katowice.pl 9 maja 2015 M. Jenczmyk XXX Sesja KNM Metody numeryczne R.R.Z. 1 / 18 Omawiany problem dotyczyć będzie numerycznego
Metoda różnic skończonych dla
 Metoda różnic skończonych dla cząstkowych równań różniczkowych na laboratorium rozwiązywać będziemy typowe równania: dyfuzji (również przewodnictwo cieplne) paraboliczne równanie Poissona (np. pole elektrostatyczne,
Metoda różnic skończonych dla cząstkowych równań różniczkowych na laboratorium rozwiązywać będziemy typowe równania: dyfuzji (również przewodnictwo cieplne) paraboliczne równanie Poissona (np. pole elektrostatyczne,
Równanie przewodnictwa cieplnego (II)
 Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
Optyka. Optyka geometryczna Optyka falowa (fizyczna) Interferencja i dyfrakcja Koherencja światła Optyka nieliniowa
 Optyka Optyka geometryczna Optyka falowa (fizyczna) Interferencja i dyfrakcja Koherencja światła Optyka nieliniowa 1 Optyka falowa Opis i zastosowania fal elektromagnetycznych w zakresie widzialnym i bliskim
Optyka Optyka geometryczna Optyka falowa (fizyczna) Interferencja i dyfrakcja Koherencja światła Optyka nieliniowa 1 Optyka falowa Opis i zastosowania fal elektromagnetycznych w zakresie widzialnym i bliskim
Aerodynamika I. wykład 2: 2: Skośne fale uderzeniowe iifale rozrzedzeniowe. POLITECHNIKA WARSZAWSKA - wydz. Mechaniczny Energetyki i Lotnictwa
 Aerodynamika I Skośne fale uderzeniowe i fale rozrzedzeniowe naddźwiękowy przepływ w kanale dla M = 2 (rozkład liczby Macha) 19 maja 2014 Linie Macha Do tej pory, rozważaliśmy problemy dynamiki gazu, które
Aerodynamika I Skośne fale uderzeniowe i fale rozrzedzeniowe naddźwiękowy przepływ w kanale dla M = 2 (rozkład liczby Macha) 19 maja 2014 Linie Macha Do tej pory, rozważaliśmy problemy dynamiki gazu, które
Różniczkowanie numeryczne
 Różniczkowanie numeryczne Przyjmijmy, że funkcja ciągła y = f(x) = 4sin(3x)e -x/2, gdzie x 0,2π, dana jest w postaci dyskretnej jako ciąg wartości y odpowiadających zmiennej niezależnej x, również danej
Różniczkowanie numeryczne Przyjmijmy, że funkcja ciągła y = f(x) = 4sin(3x)e -x/2, gdzie x 0,2π, dana jest w postaci dyskretnej jako ciąg wartości y odpowiadających zmiennej niezależnej x, również danej
WYZNACZANIE NIEPEWNOŚCI OBLICZEŃ W PRZYPADKU MODELI NIELINIOWO ZALEŻNYCH OD PARAMETRÓW
 WYZNACZANIE NIEPEWNOŚCI OBLICZEŃ W PRZYPADKU MODELI NIELINIOWO ZALEŻNYCH OD PARAMETRÓW TOMASZ PUSTY 1, JERZY WICHER 2 Automotive Industry Institute (PIMOT) Streszczenie W artykule podjęto problem określenia
WYZNACZANIE NIEPEWNOŚCI OBLICZEŃ W PRZYPADKU MODELI NIELINIOWO ZALEŻNYCH OD PARAMETRÓW TOMASZ PUSTY 1, JERZY WICHER 2 Automotive Industry Institute (PIMOT) Streszczenie W artykule podjęto problem określenia
ANALIZA MATEMATYCZNA
 ANALIZA MATEMATYCZNA TABLICE Spis treści: 1.) Pochodne wzory 2 2.) Całki wzory 3 3.) Kryteria zbieżności szeregów 4 4.) Przybliżona wartość wyrażenia 5 5.) Równanie płaszczyzny stycznej i prostej normalnej
ANALIZA MATEMATYCZNA TABLICE Spis treści: 1.) Pochodne wzory 2 2.) Całki wzory 3 3.) Kryteria zbieżności szeregów 4 4.) Przybliżona wartość wyrażenia 5 5.) Równanie płaszczyzny stycznej i prostej normalnej
Tydzień nr 9-10 (16 maja - 29 maja), Równania różniczkowe, wartości własne, funkcja wykładnicza od operatora - Matematyka II 2010/2011L
 Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Metoda Różnic Skończonych (MRS)
 Metoda Różnic Skończonych (MRS) METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek () Równania różniczkowe zwyczajne
Metoda Różnic Skończonych (MRS) METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek () Równania różniczkowe zwyczajne
Janusz Adamowski METODY OBLICZENIOWE FIZYKI Kwantowa wariacyjna metoda Monte Carlo. Problem własny dla stanu podstawowego układu N cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
BŁĘDY OBLICZEŃ NUMERYCZNYCH
 BŁĘDY OBLICZEŃ NUMERYCZNYCH błędy zaokrągleń skończona liczba cyfr (bitów) w reprezentacji numerycznej błędy obcięcia rozwinięcia w szeregi i procesy iteracyjne - w praktyce muszą być skończone błędy metody
BŁĘDY OBLICZEŃ NUMERYCZNYCH błędy zaokrągleń skończona liczba cyfr (bitów) w reprezentacji numerycznej błędy obcięcia rozwinięcia w szeregi i procesy iteracyjne - w praktyce muszą być skończone błędy metody
Układy równań nieliniowych (wielowymiarowa metoda Newtona-Raphsona) f(x) = 0, gdzie. dla n=2 np.
 Układy równań nieliniowych (wielowymiarowa metoda Newtona-Raphsona f(x 0, f ( f, f,..., f n gdzie 2 x ( x, x 2,..., x n dla n2 np. f ( x, y 0 g( x, y 0 dla każdej wielowymiarowej rozwinięcie w szereg Taylora
Układy równań nieliniowych (wielowymiarowa metoda Newtona-Raphsona f(x 0, f ( f, f,..., f n gdzie 2 x ( x, x 2,..., x n dla n2 np. f ( x, y 0 g( x, y 0 dla każdej wielowymiarowej rozwinięcie w szereg Taylora
