TEORIA CIAŁA STAŁEGO (cz. II)
|
|
|
- Elżbieta Muszyńska
- 6 lat temu
- Przeglądów:
Transkrypt
1 TORIA CIAŁA STAŁGO (cz. II TWIRDZNI BLOCHA W idealnym rysztale m i V ( r ( r ( r V (r - periodyczny, V (r+r = V (r, R wetor sieci prostej T R - operator translacji o wetor sieci Bravais, R; [H,T R ] = T R ( r ( r R ale musi być też funcją własną T R, przy translacji o elementarny wetor sieci np. a złożenie T a i T -a musi dać, =, = exp(i a jeśli R = l a + l a + l 3 a 3 to w ogólności = exp { i (l a + l a + l 3 3 a 3 } definiując = b + b + b 3 3 { b i } wetory bazowe sieci odwrotnej mamy T (l + l + l 3 3 = R, a ( r ( r
2 gdyż b i a i = π, a exp(iπ=, zatem ( ir ( r R e ( r e ir - to wartości własne operatora translacji o wetor R to definiuje wetor falowy, numeruje wartości własne T, a zatem wartości własne H ( jest jedną z postaci tw. Blocha Funcja o postaci ( gdzie r ( r e i u ( r U (r jest funcją o periodyczności sieci spełnia warune (; ( jest inną postacią tw. Blocha Periodyczne waruni brzegowe (waruni brzegowe Borna-Karmana zamiast niesończonego ryształu postulujemy jego sończoną (ale marosopową objętość V = ( N a, N a, N 3 a 3 = ( L, L, L 3 dla sieci regularnej i żądamy warunu ( r N a ( r z postaci Blochowsiej ( mamy iniai ( r N a e ( r i i i i
3 exp (iniai = zatem i Ni ai = i n i π, zatem i = π ni / (Ni ai (3 definiuje możliwe wartości wetora falowego, dysretyzując ciągłe widmo w przypadu sieci D swobodny eletron, fala płasa,. ψ(x = L eix, ψ(x + L = ψ(x e il =, L = nπ, n = n π L = n π Na najmniejsza wartość to /Na, i so wartości też o /Na; strefy Brillouina dla > b (b wetor bazowy sieci odwrotnej = b +, czynni fazowy w równaiu ( [tw. Blocha] gdyż br = π l e i(b+ R = e i R e ibr = e i R energia stanu o danym zależy jednoznacznie od wszystie wartości z przedziału (3 definiują IBZ, a odp. wartości energii tworzą pasmo energii wetory spoza IBZ można sprowadzić do IBZ IBZ to omóra Wignera-Seitza w sieci odwrotnej olejne strefy tworzy się w analogiczny sposób dla V =, pasma odpowiadające olejnym BZ stanowią ontynuacje olejnych pasm onstrucja stref Brillouina D, łańcuch
4 D, sieć wadratowa (prostoątna 3D -analogicznie IBZ dla fcc - objętość ażdej strefy jest taa sama
5 - fragmenty wyższych stref sładają się na IBZ ( -> Model eletronu swobodnego V(r = -> u(r = const. (, φ = /( / e ir Paraboliczna zależność ( dla ażdego m Powierzchnie Fermiego: D punty, D oręgi, 3D sfery
6 Gęstość stanów : nergia zależy tylo od długości wetora falowego ; ( d ( d Ilość stanów (dla eletronów x - spin przedziale [, +d ] d - objętość zawierająca wszystie stany (wszystie o tej samej energii 3D sfera o promieniu ; ( = / m 3/ / /( ħ 3 D orąg o promieniu ; ( = m /( ħ D punty (, -; ( = -3/ m / -/ /( ħ natomiast gęstość gazu eletronów swobodnych: n = N / N = ( objętość w przestrzeni do F / (swobodne nieoddziałujące eletrony - gaz jednorodny, gęstość stała, ale zależna od tego ile stanów jest obsadzonych 3D : n = F 3 / (3 D : n = F / ( D : n = F / Model prawie swobodnych eletronów Do obrazu eletronów swobodnych wprowadzamy słabe zaburzenie w postaci słabego periodycznego potencjału V(r. Model NF dobrze opisuje ułady zawierające słabo związane eletrony (metale Z doładnością do II rzędu RZ
7 V ' ( V funcja falowa jest dalej ombinacją liniową fal płasich (przypomnijmy, że dla stanu o najniższej energii, poprawa w II-gim rzędzie jest ujemna potencjał, jao funcję periodyczną r można rozwinąć Fourierowso w bazie fal płasich opartych o wetory sieci odwrotnej (3a V ( r g V g e igr (problem: trzeba znać V g lub umieć je przybliżyć zatem ' ' V ' Vg g dre i( ' g r tylo dla ( = g więc ( V g V g g ale dla, dla tórych mamy degenerację trzeba stosować pierwszy rząd RZ dla stanów zdegenerowanych mianowni energetyczny znia... sytuacja taa ma miejsce dla na granicach stref, np. = ½ G i = - ½ G, G = π / a (dla i -, innych niż granice strefy nie ma degeneracji w II-gim rzędzie bo i - nie różnią się o G
8 wówczas dla bliso granicy strefy przybliżamy (4 r G G r ( i i e a e a działanie H φ = φ, mnożenie z lewej przez exp(... i scałowanie da uład równań algebr. na współczynnii a, a -G (5 ( ( G G G G a a V V ( położyłem V = nietrywialne rozwiązanie gsy znia wyznaczni 4 ( ( ( G G G V dla bardzo blisich ½ G ( G G V ciągłe pasmo (continuum dla swobodnych eletronów ulega rozczłonowaniu na szereg pasm rozdzielonych przerwami
9 ze względu na tw. Blocha jednej wartości odpowiada niesończenie wiele rozwiązań: numerujemy je n (pasma - zmienia się tylo u (r -> u n (r atomowy charater funcji w pobliżu węzłów decyduje o charaterze u(r Rozwiązanie ( - daje a = /sqrt( a = /sqrt( ( + a = /sqrt( a = -/sqrt( z (4 mamy cos( Gr, i sin( Gr dla prostej sieci z jednym atomem w centrum omóri elementarnej φ - φ + oncentruje gęstość na węzłach atomowych, tam gdzie V jest najbardziej przyciągający oncentruje gęstość między węzłami atomowymi, zauważmy ponadto, że dla ażdego, z powodu periodyczności u, φ możemy przedstawić jao (6 ( r e ir g a G e igr (6 jest funcją własną H. W rzeczywistości, w pobliżu jąder φ ma charater funcji atomowej, co wymaga w pratyce bardzo długich sum w (6 zawierających szybozmienne funcje
10 Modelowe potencjały periodyczne w metodzie NF Ściśle zawsze można zapisać: V ( r g V g e igr. D, tylo g =, V = const, => model swobodnych eletronów. D, g = - / a,, / a, V V V cos( x / a D naprzemienne pasma i przerwy D, 3D - charater n ( w pasmie, może różnić się dla różnych ierunów D lub 3D mogą nie istnieć bezwzględne przerwy jednoeletronowe stany w pasmach należy obsadzić eletronami poziom Fermiego np.: w D: atom w omórce elementarnej, n eletronów w atomie => przy N omórach n*n eletronów, w pasmie mamy *N /spin/ stanów o różnych wart. n*n eletronami obsadzamy olejne stany w olejnych pasmach parzysta liczba eletronów => półprzewodni / izolator nieparzysta => metal ( w D lub 3D nieoniecznie metale, izolatory, półprzewodnii Powierzchnie stałej energii, powierzchnia Fermiego D - punty (pary puntów w ; w funcji : najpierw wadratowo się rozrzedzają, a następnie zagęszczają
11 D - sieć wadratowa I BZ - wadrat; Bliso = oręgi; w pobliżu granicy strefy pochodna ( jest blisa dla prostop. do granicy; na granicach stref nieciągłości (przerwy energetyczne! swobodne eletrony; NFG; NFG FCC 3D sieć regularna ubiczna Bliso = sfery; W pobliżu granicy strefy pochodna ( jest blisa dla prostop. do granicy; Na granicach stref nieciągłości (przerwy energetyczne! const podobne do const dla sieci wadratowej, ale trójwymiarowe (w schemacie rozszerzonych stref BZ coraz mniejsze wypełnienie obszaru olejnych stref
12 Koncepcja masy efetywnej (tensora odwrotności masy efetywnej przy omawianiu metody p; Zauważmy: swobodne eletrony ( (, m m rzywizna ( oreśla masę cząste eletrony prawie swobodne - na dnie pasma masa jest dodatnia (nieoniecznie = m - w szczycie pasma masa jest < - w puncie przegięcia ( masa może być nieoreślona Koncepcja dziury wstęp - wewnątrz pasma energie stanów jednoeletronowych rosną zgodnie z rosnącymi wartościami od N - w olejnym pasmie od N - w sytuacji zapełnione pasmo + jeden obsadzony stan w olejnym pasmie, wzbudzenia uładu można z dobrym przybliżeniem opisywać jao wzbudzenia N+ go eletronu tzn. jednego eletronu (* - w sytuacji pasma zapełnionego do N- stanu jednoeletronowego, wzbudzenia (w ramach danego pasma odpowiadają wzbudzeniom wieloeletronowym z nieobsadzonym stanem n < N - energie stanów wzbudzonych (uładu N- eletronowego, w ramach pasma rosną, chociaż: - energia nieobsadzonego stanu jednoeletronowego przy taich wzbudzeniach maleje - masa eletronu w szczycie pasma jest ujemna
13 zatem - wzbudzenia uładu N- eletronów odpowiadają więc: (wzbudzeniu jednocząstowemu cząsti o ujemnej masie efetywnej, tórej energie są coraz mniejsze (bardziej ujemne; ujemne licząc od zera szczytu pasma popatrzmy na równanie Schroedingera, dla taiej cząsti p ev * m ( mnożąc przez - dostaniemy p m * ev a to odpowiada cząstce o przeciwnym ładunu (+e i dodatniej masie - taą cząstę (pseudo-cząstę nazywamy dziurą, jej energia rośnie z olejnymi wzbudzeniami uładu N- eletronowego (w danym pasmie - jeśli w zapełnionym pasmie N-ty eletron ma spin s, to spin odpowiadającej dziury jest -s podobna analogia istnieje dla pasma o N-n eletronach = n dziurach MTODA CIASNGO WIĄZANIA Założenie: funcja falowa jest ombinacją liniową orbitali
14 (atomowych zloalizowanych na węzłach sieci załadamy, że obecność sieci (sąsiednich atomów nieznacznie modyfiuje stany eletronów w izolowanych atomach funcja musi spełniać warune Blocha załóżmy, że na ażdym węźle (i mamy P orbitali o różnej symetrii (np. ns, np, nd,... załóżmy też dla uproszczenia jeden atom w omórce elementarnej R i - wetory sieci Bravais; ( r Ri utwórzmy funcje i ( r e ( r R ir, i N i UWAGA indes spełniające warune Blocha (tzw. sumy Blocha, - orbitale o charaterze zdeloalizowanym - stanowią one bazę, w tórej rozwijamy funcję falową (* (gdyż ze wzgl. na symetrię rystaliczną, nie jest już dobrą liczbą wantową! ( r c, ( r dla więcej niż jednego atomu w omórce elementarnej, tworzymy sumy Blocha dla ażdego atomu (indes τ i ostatnie sumowanie przebiega dwa indesy ( i τ jeśli poziomy atomowe są dobrze energetycznie odseparowane, możemy w sumie (* ograniczyć się do jednego wyrazu podstawiając (* do równania H = (**, mnożąc z lewej strony przez olejne * i całując po, dostaniemy macierzowe równanie (** ( H S C = w bazie funcji c c C... c P
15 elementy macierzowe H, (*** H i( R j Ri H e N S - całi narywania S * ( r Ri H ( r ij i( R j Ri * N e ( r Ri ( r ij ( oczywiście funcja i elementy macierzowe zależą od ; dla silnie zloalizowanych orbitali można założyć S ab = ab (załadając ortogonalność orbitali na węzłach i pomiędzy węzłami; albo można pracować w orbitalach nie-ściśle-atomowych, ale ortogonalnych R j R j dr dr Przybliżenie najbliższych sąsiadów Ponieważ potencjał w hamiltonianie H jest periodyczny to możemy założyć, że w sumie w H istotnie różne od zera będą tylo całi :. zawierające orbitale na danym węźle. zawierające orbitale z sąsiednich (identycznych! węzłów w rezultacie N taich samych wyrazów węzłowych i N taich samych par wyrazów międzywęzłowych elementy macierzowe pomiędzy różnymi orbitalami z tego samego węzła możemy z dobrym przybliżeniem uznać za = (orbitale atomowe są f. własnymi H at, a V per mało różni się od V at w pobliżu węzłów atomowych ażdą różną całę tratujemy jao parametr metody Ogólnie: dla M atomów w omórce elementarnej wymiar zagadnienia macierzowego jest D = (P*M, a różnych parametrów masymalnie M*P + P*P przyłady:
16 a D, atom / omórę, orbital / atom, D=, il.param = b 3D, atom / omórę, orbital / atom, D=, il.param = c D, atom / omórę, orbitale / atom, D=, il.param = 5 d D, ident. at. / om., orbital / atom, D=, il.param = (grafit, przybliżenie -eletronowe e 3D, różne.at. / om., 4 orbitale / atom (s, p x, p y, p z + symetria D=8, il.param = 9 (blenda cynowa, fcc z bazą -atomową ad. a ina ( r e ( x na N n H, H ~ energia orbitalna, - cała rezonansowa w pot. cryst. ( hopping parameter uwaga: <, oraz * * * d { T Vper( r} dr { T Vat( r U( r} dr U( r r U( r V ( r V ( r per at - energia orbitalna, - mała poprawa Udr
17 w rezultacie ( w D r -> x (A - można tratować jao jeden parametr strefa Brillouina ( -/a, /a ( cos( a ( tylo przesuwa salę energii dla =, a = (w odpowiednich jednostavh, jedno pasmo regularna sieć ubiczna, atom / węzeł, orbital typu s na atom (model metalu alalicznego w efecie ażdy węzeł ma teraz 6-ciu sąsiadów ( a,,, ( a,,, (, a,, (, a,, (,, a, (,, a (jedno pasmo ( cos( a cos( a cos( a x y z w objętości mamy N węzłów, na ażdym po eletronie walencyjnym s, i N funcji Blocha, ale N stanow (spin, zatem pasmo jest wypełnione do polowy metal!
18 sieć D, różne atomy w om.el., orbital na atom ( r c ( r τ,,, teraz macierz H ma wymiar (dwa różne atomy w om.el., ale ażdy węzeł ma dwóch taich samych sąsiadów, H ( e id id ( e d - odległość między omórami (dla taich samych atomów mamy ( ze wzoru (A sieć D, atom w om.el., orbitale (s, p H ss ss' cos a sp' cos a sp' cos a pp pp' cos a ss = ε + α, ss = -γ grafen - przybliżenie -eletronowe
19 sześcioątna sieć grafitu to sieć rombowa Bravais z dwoma ( atomami (taimi samymi węgla w bazie C s, s p eletrony powłoi n= biorą udział w wiązaniu hybrydyzacja sp - 3 orbitale zhybrydyzowane ( o + jeden orbital p z - (orbital p z prostopadły do płaszczyzny rysunu eletrony obsadzające ten orbital decydują o własnościach fizycznych i chemicznych grafitu (najwyższe energetycznie najsłabiej związane z jądrami najbardziej zewnętrzne elementarne wetory sieci prostej (definiujące om. element. (w bazie artezjańsiej X,Y a 3 a a,, a 3 a a,
20 a = a i = a c-c (3 / R [ a / 3,], R [ a /( 3, a / ], R3 najbliżsi sąsiedzi dla danego atomu to: element macierzowy hamiltonianu pomiędzy orbitalami p z na sąsiednich atomach oznaczmy jao t, element węzłowy oznaczymy jao ( H = S (B [ a /( 3, a / ] H t f * ( t f (, S s f * ( s f ( = ( x, y, s cała narywania pomiędzy sąsied. orbitalami f ( e i a / x 3 e i a /( x 3 cos( y a / rozwiązując zagadnienie własne (B dostajemy ( t w( s w( gdzie w( f ( zaniedbując s, ( s= i ładąc = (salowanie energii 4cos( 3 a / cos( a / 4cos ( / / ( t a x y y
21 a z S różnym od zera: mamy teraz pasma ( +/- łatwo zauważyć, że w 6-ciu puntach K IBZ, przerwa wynosi, - ażdy atom dostarcza eletron na orbitalu p z - eletrony na omórę elementarną - zatem, ze względu na spin, tylo dolne pasmo jest zapełnione, zatem grafit to semimetal (półmetal sieci uładów złożonych. supersieci półprzewodniowe. nanoruri węglowe postępowanie: - definiujemy superomurę SC - węzły wewnątrz SC wiążemy całami rezonansowymi t - węzły z jednej granicy SC wiążemy z węzłami z naprzeciwległej granicy SC przez t exp(id, gdzie d rozmiar SC
22 przyład łancuch tai ja w (A (ładąc = d = a H t( e id t( e id zatem = t [+exp(-id] *[+exp(id] = ± t cos(a pamiętając, że teraz IBZ jest x mniejsza = [ - π /(a, + π /(a ] dwa styające się pasma, o łącznej szeroości taiej samej ja dla przypadu (A a =
na dnie (lub w szczycie) pasma pasmo jest paraboliczne, ale masa wyznaczona z krzywizny niekoniecznie = m 0
 Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
1. Struktura pasmowa from bonds to bands
 . Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
. Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
Wykład 21: Studnie i bariery cz.1.
 Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
jednoznacznie wyznaczają wymiary wszystkich reprezentacji grup punktowych, a związki ortogonalności jednoznacznie wyznaczają ich charaktery
 Reprezentacje grup puntowych związi pomiędzy h i n a jednoznacznie wyznaczają wymiary wszystich reprezentacji grup puntowych, a związi ortogonalności jednoznacznie wyznaczają ich charatery oznaczenia:
Reprezentacje grup puntowych związi pomiędzy h i n a jednoznacznie wyznaczają wymiary wszystich reprezentacji grup puntowych, a związi ortogonalności jednoznacznie wyznaczają ich charatery oznaczenia:
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową. Metody wytwarzania
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
S. Baran - Podstawy fizyki materii skondensowanej Pasma energetyczne. Pasma energetyczne
 Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
np. dla elektronów w kryształach; V(x+d) = V(x), d - okres periodyczności = wielkość komórki elementarnej kryształu
 Potencjały eriodyczne n. dla elektronów w kryształach; V(x+d) V(x), d - okres eriodyczności wielkość komórki elementarnej kryształu rzyadek kryształu jednowymiarowego sieci z bazą gdy w komórce elementarnej
Potencjały eriodyczne n. dla elektronów w kryształach; V(x+d) V(x), d - okres eriodyczności wielkość komórki elementarnej kryształu rzyadek kryształu jednowymiarowego sieci z bazą gdy w komórce elementarnej
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
4.15 Badanie dyfrakcji światła laserowego na krysztale koloidalnym(o19)
 256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ
 ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
C h można przedstawić w bazie wektorów bazowych grafenu (*) (**) Nanorurki węglowe (jednościenne)
 Nanorurki węglowe (jednościenne) zwinięte paski arkusza grafenu (wstęgi grafenowej) (węzły sieciowe Bravais i węzły podsieci) wstęgi: chiralna fotelowa zykzak komórka elementarna jednoznacznie definiuje
Nanorurki węglowe (jednościenne) zwinięte paski arkusza grafenu (wstęgi grafenowej) (węzły sieciowe Bravais i węzły podsieci) wstęgi: chiralna fotelowa zykzak komórka elementarna jednoznacznie definiuje
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO.
 GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
Wykład 8. Stany elektronowe molekuł dwuatomowych
 Wyład 8 Stany eletronowe moleuł dwuatomowych Całowita energia cząsteczi: E t E e E V E r E e energia eletronowa, E v energia oscylacji, E r energia rotacji Zares fal eletromagnetycznych obserwowanych przy
Wyład 8 Stany eletronowe moleuł dwuatomowych Całowita energia cząsteczi: E t E e E V E r E e energia eletronowa, E v energia oscylacji, E r energia rotacji Zares fal eletromagnetycznych obserwowanych przy
MATERIA. = m i liczby całkowite. ciała stałe. - kryształy - ciała bezpostaciowe (amorficzne) - ciecze KRYSZTAŁY. Periodyczność
 MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Matematyka dyskretna. Wykład 2: Kombinatoryka. Gniewomir Sarbicki
 Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały
 WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
Wykład Budowa atomu 3
 Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Zad Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji.
 Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Wykład V Wiązanie kowalencyjne. Półprzewodniki
 Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Orbitale typu σ i typu π
 Orbitale typu σ i typu π Dwa odpowiadające sobie orbitale sąsiednich atomów tworzą kombinacje: wiążącą i antywiążącą. W rezultacie mogą powstać orbitale o rozkładzie przestrzennym dwojakiego typu: σ -
Orbitale typu σ i typu π Dwa odpowiadające sobie orbitale sąsiednich atomów tworzą kombinacje: wiążącą i antywiążącą. W rezultacie mogą powstać orbitale o rozkładzie przestrzennym dwojakiego typu: σ -
Zaburzenia periodyczności sieci krystalicznej
 Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH
 Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Dr inż. Zbigniew Szklarski
 Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
że w wyniku pomiaru zmiennej dynamicznej A, której odpowiada operator αˆ otrzymana zostanie wartość 2.41?
 TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
3. Struktura pasmowa
 3. Strutura pasmowa Funcja Blocha Quasi-pęd, sić odwrotna Przybliżni prawi swobodngo ltronu Dziura w paśmi walncyjnym Masa ftywna Strutura pasmowa (), przyłady Półprzwodnii miszan ltron w rysztal sformułowani
3. Strutura pasmowa Funcja Blocha Quasi-pęd, sić odwrotna Przybliżni prawi swobodngo ltronu Dziura w paśmi walncyjnym Masa ftywna Strutura pasmowa (), przyłady Półprzwodnii miszan ltron w rysztal sformułowani
Podstawy chemii obliczeniowej
 Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Zadania treningowe na kolokwium
 Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
WEKTORY I WARTOŚCI WŁASNE MACIERZY. = λ c (*) problem przybliżonego rozwiązania zagadnienia własnego dla operatorów w mechanice kwantowej
 WEKTORY I WARTOŚCI WŁASNE MACIERZY Ac λ c (*) ( A λi) c nietrywialne rozwiązanie gdy det A λi problem przybliżonego rozwiązania zagadnienia własnego dla operatorów w mechanice kwantowej A - macierzowa
WEKTORY I WARTOŚCI WŁASNE MACIERZY Ac λ c (*) ( A λi) c nietrywialne rozwiązanie gdy det A λi problem przybliżonego rozwiązania zagadnienia własnego dla operatorów w mechanice kwantowej A - macierzowa
WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII.
 ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
Liczby kwantowe n, l, m l = 0 l =1 l = 2 l = 3
 Liczby kwantowe Rozwiązaniem równania Schrödingera są pewne funkcje własne, które można scharakteryzować przy pomocy zestawu trzech liczb kwantowych n, l, m. Liczby kwantowe nie mogą być dowolne, muszą
Liczby kwantowe Rozwiązaniem równania Schrödingera są pewne funkcje własne, które można scharakteryzować przy pomocy zestawu trzech liczb kwantowych n, l, m. Liczby kwantowe nie mogą być dowolne, muszą
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
Budowa atomów. Atomy wieloelektronowe Układ okresowy pierwiastków
 Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Struktura energetyczna ciał stałych. Fizyka II dla EiT oraz E, lato
 Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Fizyka 3.3 WYKŁAD II
 Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Układy równań liniowych
 Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Model uogólniony jądra atomowego
 Model uogólniony jądra atomowego Jądro traktowane jako chmura nukleonów krążąca w średnim potencjale Średni potencjał może być sferyczny ale także trwale zdeformowany lub może zależeć od czasu (wibracje)
Model uogólniony jądra atomowego Jądro traktowane jako chmura nukleonów krążąca w średnim potencjale Średni potencjał może być sferyczny ale także trwale zdeformowany lub może zależeć od czasu (wibracje)
Aby opisać strukturę krystaliczną, konieczne jest określenie jej części składowych: sieci przestrzennej oraz bazy atomowej.
 2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
Wiązania chemiczne. Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych. 5 typów wiązań
 Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
Atomy wieloelektronowe
 Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
c) prawdopodobieństwo znalezienia cząstki między x=1.0 a x=1.5 jest równe
 TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
KOLOKWIUM Z ALGEBRY I R
 Instrucje: Każde zadanie jest za 4 puntów. Rozwi azanie ażdego zadania musi znajdować siȩ na osobnej artce oraz być napisane starannie i czytelnie. W nag lówu ażdego rozwi azania musz a znajdować siȩ dane
Instrucje: Każde zadanie jest za 4 puntów. Rozwi azanie ażdego zadania musi znajdować siȩ na osobnej artce oraz być napisane starannie i czytelnie. W nag lówu ażdego rozwi azania musz a znajdować siȩ dane
Przejścia kwantowe w półprzewodnikach (kryształach)
 Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn x 1 x 2... x m ...
 Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
STRUKTURA KRYSTALICZNA
 PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
3 1 + i 1 i i 1 2i 2. Wyznaczyć macierze spełniające własność komutacji: [A, X] = B
![3 1 + i 1 i i 1 2i 2. Wyznaczyć macierze spełniające własność komutacji: [A, X] = B 3 1 + i 1 i i 1 2i 2. Wyznaczyć macierze spełniające własność komutacji: [A, X] = B](/thumbs/73/69286698.jpg) 1. Dla macierzy a) A = b) A = c) A = d) A = 3 1 + i 1 i i i 0 i i 0 1 + i 1 i 0 0 0 0 1 0 1 0 1 + i 1 i Wyznaczyć macierze spełniające własność komutacji: A, X = B. Obliczyć pierwiaski z macierzy: A =
1. Dla macierzy a) A = b) A = c) A = d) A = 3 1 + i 1 i i i 0 i i 0 1 + i 1 i 0 0 0 0 1 0 1 0 1 + i 1 i Wyznaczyć macierze spełniające własność komutacji: A, X = B. Obliczyć pierwiaski z macierzy: A =
"Bieda przeczy matematyce; gdy się ją podzieli na więcej ludzi, nie staje się mniejsza." Gabriel Laub
 "Bieda przeczy matematyce; gdy się ją podzieli na więcej ludzi, nie staje się mniejsza." Gabriel Laub Def. Macierzą odwrotną do macierzy A M(n) i deta nazywamy macierz A - M(n) taką, że A A - A - A Tw.
"Bieda przeczy matematyce; gdy się ją podzieli na więcej ludzi, nie staje się mniejsza." Gabriel Laub Def. Macierzą odwrotną do macierzy A M(n) i deta nazywamy macierz A - M(n) taką, że A A - A - A Tw.
CHEMIA 1. INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne kierunek lekarski, stomatologia, farmacja, analityka medyczna ATOM.
 INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne kierunek lekarski, stomatologia, farmacja, analityka medyczna tel. 0501 38 39 55 www.medicus.edu.pl CHEMIA 1 ATOM Budowa atomu - jądro, zawierające
INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne kierunek lekarski, stomatologia, farmacja, analityka medyczna tel. 0501 38 39 55 www.medicus.edu.pl CHEMIA 1 ATOM Budowa atomu - jądro, zawierające
S. Baran - Podstawy fizyki materii skondensowanej Fonony. Fonony
 Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA. Ćwiczenia. http://zcht.mfc.us.edu.pl/ mm
 CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
gęstością prawdopodobieństwa
 Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
WYKŁAD 3 CZĄSTECZKI WIELOATOMOWE ZWIĄZKI WĘGLA
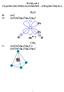 WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
2008/2009. Seweryn Kowalski IVp IF pok.424
 2008/2009 seweryn.kowalski@us.edu.pl Seweryn Kowalski IVp IF pok.424 Model powłokowy Moment kwadrupolowy w jednocząstkowym modelu powłokowym: Dla pojedynczego protonu znajdującego się na orbicie j (m j
2008/2009 seweryn.kowalski@us.edu.pl Seweryn Kowalski IVp IF pok.424 Model powłokowy Moment kwadrupolowy w jednocząstkowym modelu powłokowym: Dla pojedynczego protonu znajdującego się na orbicie j (m j
φ(x 1,..., x n ) = a i x 2 i +
 Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Koła rowerowe malują fraktale
 Koła rowerowe malują fratale Mare Berezowsi Politechnia Śląsa Rozważmy urządzenie sładającego się z n ół o różnych rozmiarach, obracających się z różnymi prędościami. Na obręczy danego oła, obracającego
Koła rowerowe malują fratale Mare Berezowsi Politechnia Śląsa Rozważmy urządzenie sładającego się z n ół o różnych rozmiarach, obracających się z różnymi prędościami. Na obręczy danego oła, obracającego
P R A C O W N I A
 P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
ef 3 (dziedzina, dziedzina naturalna) Niech f : A R, gdzie A jest podzbiorem płaszczyzny lub przestrzeni Zbiór A nazywamy dziedziną funcji f i oznacza
 FUNKCJE WÓCH I TRZECH ZMIENNYCH (było w semestrze II) ef 1 (funcja dwóch zmiennych) Funcją f dwóch zmiennych oreśloną na zbiorze A R o wartościach w R nazywamy przyporządowanie ażdemu puntowi ze zbioru
FUNKCJE WÓCH I TRZECH ZMIENNYCH (było w semestrze II) ef 1 (funcja dwóch zmiennych) Funcją f dwóch zmiennych oreśloną na zbiorze A R o wartościach w R nazywamy przyporządowanie ażdemu puntowi ze zbioru
Energia wiązania słaba rzędu 10-2 ev J. Energia cieplna 3/2 k B. T J. Energia ruchu cieplnego powoduje rozerwanie wiązań cząsteczkowych.
 Ciała stałe - o struturze rystalicznej wyazują daleo zasięgowe uporządowanie atoowe, są to onoryształy i poliryształy. - o struturze bezpostaciowej (aorficznej), wyazują bra uporządowania atoowego daleiego
Ciała stałe - o struturze rystalicznej wyazują daleo zasięgowe uporządowanie atoowe, są to onoryształy i poliryształy. - o struturze bezpostaciowej (aorficznej), wyazują bra uporządowania atoowego daleiego
Matematyka liczby zespolone. Wykład 1
 Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
Elementy teorii powierzchni metali
 Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Mechanika kwantowa. Erwin Schrödinger ( ) Werner Heisenberg
 Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
= i Ponieważ pierwiastkami stopnia 3 z 1 są (jak łatwo wyliczyć) liczby 1, 1+i 3
 ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
S. Baran - Podstawy fizyki materii skondensowanej Półprzewodniki. Półprzewodniki
 Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Modele kp wprowadzenie
 Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Półprzewodniki samoistne. Struktura krystaliczna
 Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 2003
 Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Układy równań liniowych i metody ich rozwiązywania
 Układy równań liniowych i metody ich rozwiązywania Łukasz Wojciechowski marca 00 Dany jest układ m równań o n niewiadomych postaci: a x + a x + + a n x n = b a x + a x + + a n x n = b. a m x + a m x +
Układy równań liniowych i metody ich rozwiązywania Łukasz Wojciechowski marca 00 Dany jest układ m równań o n niewiadomych postaci: a x + a x + + a n x n = b a x + a x + + a n x n = b. a m x + a m x +
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
Analiza B II zadania. cos kx = sin(n x) 2 sin x 2. cos n sin 1 n., tan x, cot x, log sin x, log tan x, 1 + x
 Analiza B II zadania Oblicz granicę n cos n n Udowodnij wzór dla mπ 3 Udowodnij że szereg + n = cos = sin(n + sin cos n sin n jest zbieżny warunowo 4 Wyprowadź wzory (sin = cos (cos = sin 5 Wyaż że funcje
Analiza B II zadania Oblicz granicę n cos n n Udowodnij wzór dla mπ 3 Udowodnij że szereg + n = cos = sin(n + sin cos n sin n jest zbieżny warunowo 4 Wyprowadź wzory (sin = cos (cos = sin 5 Wyaż że funcje
