np. dla elektronów w kryształach; V(x+d) = V(x), d - okres periodyczności = wielkość komórki elementarnej kryształu
|
|
|
- Józef Marcinkowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Potencjały eriodyczne n. dla elektronów w kryształach; V(x+d) V(x), d - okres eriodyczności wielkość komórki elementarnej kryształu rzyadek kryształu jednowymiarowego sieci z bazą gdy w komórce elementarnej jest więcej niż jeden atom (tego samego lub innego ierwiastka), n.: Twierdzenie Blocha Funkcja falowa oisująca stan elektronu w eriodycznym otencjale (eriodycznie nieskończonym) sełnia warunek (tu rzedstawiony tylko w jednym wymiarze) Ψ( x + d) e ikd Ψ( x) gdzie k - tzw. wektor falowy (ciągła liczba kwantowa numerująca wartości własne oeratora Translacji o wektor d, a także Hamiltonianu, bo ten oerator też ma eriodyczność d) dla układów eriodycznych dostaniemy zawsze NIE dyskretne energie E i, lecz PASMA E i (k) rzy czym k rzebiega wartości w tzw. I strefie Brillouina (BZ), od 0-π dla eriodycznych ale ograniczonych układów (rzeczywiste makroskoowe kryształy) - k rzebiega taki sam zakres ale jest
2 dyskretne tyle różnych wartości k ile komórek elementarnych w krysztale czyli dla makroskoowego kawałka kryształu bardzo dużo; k numeruje stany elektronowe w ramach asm te stany obsadzamy elektronami z owłok walencyjnych atomów tworzących kryształ numeracja PASM wynika z kwantowej numeracji stanów H dla danej komórki elementarnej metale, ółrzewodniki, izolatory n.: w D: atom w komórce elementarnej, n elektronów w atomie > rzy N komórkach n*n elektronów, w asmie mamy *N /sin/ stanów o różnych wart. k n*n elektronami obsadzamy kolejne stany w kolejnych asmach arzysta liczba elektronów > ółrzewodnik / izolator niearzysta > metal ( w D lub 3D niekoniecznie ) metale, izolatory, ółrzewodniki oziom Fermiego: - w metalu: najwyższy energetycznie stan obsadzony w T0K - w ółrzewodniku różnie;
3 Co to znaczy metal - rzewodnik? Do rzewodzenia rądu otrzebne są swobodne elektrony. Swobodne to takie, które od wływem ola elektrycznego mogą być rzysieszane, tzn. ich energia może sukcesywnie rzyrastać o dowolnie małą wartość. A to oznacza, że owyżej oziomu Fermiego musi istnieć continuum nieobsadzonych stanów. Przestrzenie modelowe. Zamiast rozwiązywać równanie różniczkowe () można rzybliżyć funkcję falową w skończonej bazie funkcji (n. wzajemnie ortogonalnych i unormowanych - ortonormalnych) Ψ N cϕ i i i () I rzybliżyć oszukiwaną energię układu jako E < ψ H ψ > (3) < ψ H ψ > W bazie funkcji φ, rzyjmuje ostać MACIERZY H Ψ( x) EΨ( x) a zagadnienie ostać zagadnienia własnego dla macierzy hamiltonianu H H ij < ϕ i H ϕ j > H... H n... H n c c E H nn cn cn rozwiązanie olega na ZDIAGONALIZOWANIU macierzy H otrzymujemy N rozwiązań E i (niektóre mogą się owtarzać degeneracja)
4 dla układów eriodycznych H ij - zależą od k, zatem E i E i (k) Atomy, molekuły Atom wodoru Energia otencjalna elektronu e - w olu dodatnio naładowanego jądra V V(x,y,z)V(r) Ze V ( r) w j. at. 4 r 0 Z r πε, Z - liczba rotonów w jądrze zależy tylko od odległości elektronu od jądra r schematycznie V(r) wygląda tak: E n Ze a n 0, a0 h 50 m me E 0 ok ev Ale, hamiltonian atomu wodoru komutuje z oeratorem dowolnych obrotów wokół osi rzechodzącej rzez jądro atomu wodoru stany własne (oziomy energetyczne) są więc numerowane rzez n tzw. główną liczbę kwantową, ale dodatkowo też rzez tzw. orbitalną liczbę kwantową l, która oisuje zachowanie (własności) kolejnych funkcji falowych rzy obrotach
5 dla danego n jej wartości są l 0 (n-) i odowiednio są nazywane 0 s,, d,. Funkcje falowe stanów numerowane są ostatecznie 3-ma indeksami n, l, m energie w atomie wodoru zależą tylko od n a w innych atomach od n i l, E n,l w sferycznym układzie wsółrzędnych Funkcje daje się rozsearować na część radialną i kątową ψ(x,y,z) ψ(r, Θ, ϕ) R n (r) Y l,m (Θ,ϕ) ψ n,l,m Kolejne funkcje radialne znów rzyominają fale a części kątowe ozwalają łatwo wyjaśniać tworzenie się wiązań chemicznych orzez budowę tzw. orbitali hybrydyzowanych
6 Orbitale zhybrydyzowane są orównywalne lub takie same (tylko w wodorze) to można tworzyć kombinacje liniowe takich orbitali (związane jest to z faktem, że funkcje do zdegenerowanych energii tworzą bazy odrzestrzeni) Gdy energie orbitali nl i nl n. Φ s ns + n oraz Φ s ns - n (tzw. hybrydyzacja s) wyjaśniają trwałość wiązania n. w molekule F (s s 5 ) co to znaczy trwałość wiązania? F F nakładające się orbitale tworzą orbital molekularny, tzw. wiążący, w którym gęstość ładunku elektronowego omiędzy jądrami jest największa dzięki czemu klasycznie utrzymuje dodatnio naładowane jądra (czyli odychające się) w stałej, ale wiążącej odległości hybrydyzacja s wiązanie i trwałość molekuły C H 4 C: s s, H: S
7 s i bardzo bliskie energie z: s + x + y tworzymy w węglu 3 nowe orbitale zhybrydyzowane z y x y x x s s s ) 3 ( ) 3 ( ) ( φ φ φ φ P z - rostoadły do łaszcyzny rzed utworzeniem wiązań o utworzeniu wiązań orbitali molekularnych omiędzy atomami (w rzeczywistości jednak hybrydyzacja jest tyu s3 i dwa orbitale zhybrydyzowane tworzą odwójne wiązanie omiędzy węglami) odobnie w benzenie C 6 H 6
8 wiązanie i trwałość grafitu (grafenu) - C s s walencyjne elektrony - s s3 o jednym elektronie walencyjnym z każdego atomu orbital molekularny utworzony z dwóch orbitali zhybrydyzowanych s3 sąsiednich atomów wiązanie chemiczne (tworzy się zarówno orbital wiążący jak i antywiążacy - wiążący jako suma ) tu są to orbitale krystaliczne Obsadzony elektronami jest tylko orbital wiążący ale to z - decyduje o własnościach elektrycznych i ot. grafenu Grafen Dwuwymiarowa sieć rombowa węgla z bazą dwuatomową (wygląda jak sieć heksagonalna) Wracając do eriodyczności (nie tylko w grafenie), każdy węzeł sieci (dowolny, ustalony unkt każdej komórki elementarnej) w ustalonym układzie wsółrzędnych, wskazywany jest rzez wektor (tzw. wektor sieci), który daje się rzedstawić jako Rn R + n R + n 3 R 3 [ w grafenie D tylko dwie składowe] z n i - liczbami całkowitymi, R i - wektory bazowe (sieci roste i sieci z bazą)
9 Grafen 00 nagroda Nobla Novoselov, Geim, 004 wytwarzanie i zbadanie grafenu (metodą scotchową ) rozmiary jednowarstwowych łatków -mikrometry eitaksjlnywzrost rzez odarowywanie SiC, P.Sutter, Nature Materials 8, 7, 009 rozmiary > mm
d dz d dy e r d dx ψ = ψ(r, Θ, ϕ) = R n (r) Y l,m (Θ,ϕ) = ψ n,l,m E n 2 n NAJPROSTSZA CZĄSTECZKA - MOLEKUŁA H 2 Przypomnienie: atom wodoru
 NAJPROSTSZA CZĄSTECZKA - MOLEKUŁA H Przomnienie: atom wodoru m d d d d d dz e r Ψ r EΨ r rz rzejściu do wółrzędnch fercznch r, Θ, ϕ ψ ψr, Θ, ϕ R n r Y l,m Θ,ϕ ψ n,l,m liczb kwantowe: n, l, m... l 0,...,n-,
NAJPROSTSZA CZĄSTECZKA - MOLEKUŁA H Przomnienie: atom wodoru m d d d d d dz e r Ψ r EΨ r rz rzejściu do wółrzędnch fercznch r, Θ, ϕ ψ ψr, Θ, ϕ R n r Y l,m Θ,ϕ ψ n,l,m liczb kwantowe: n, l, m... l 0,...,n-,
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową. Metody wytwarzania
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
MATERIA. = m i liczby całkowite. ciała stałe. - kryształy - ciała bezpostaciowe (amorficzne) - ciecze KRYSZTAŁY. Periodyczność
 MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
na dnie (lub w szczycie) pasma pasmo jest paraboliczne, ale masa wyznaczona z krzywizny niekoniecznie = m 0
 Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych
 Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 tyów wiązań wodorowe A - H - A, jonowe ( n. KCl molekularne (omiędzy atomami gazów szlachetnych i małymi molekułami kowalencyjne
Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 tyów wiązań wodorowe A - H - A, jonowe ( n. KCl molekularne (omiędzy atomami gazów szlachetnych i małymi molekułami kowalencyjne
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Budowa atomów. Atomy wieloelektronowe Układ okresowy pierwiastków
 Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Wykład Budowa atomu 3
 Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Stara i nowa teoria kwantowa
 Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Wykład V Wiązanie kowalencyjne. Półprzewodniki
 Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Metody symulacji w nanotechnologii
 Metody symulacji w nanotechnologii Skrócony opis: Wykład zawiera wprowadzenie do technik stosowanych w fizyce i biofizyce do komputerowego modelowania nanostruktur i symulacji zachodzących w nich procesów.
Metody symulacji w nanotechnologii Skrócony opis: Wykład zawiera wprowadzenie do technik stosowanych w fizyce i biofizyce do komputerowego modelowania nanostruktur i symulacji zachodzących w nich procesów.
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Zasady obsadzania poziomów
 Zasady obsadzania poziomów Model atomu Bohra Model kwantowy atomu Fala stojąca Liczby kwantowe -główna liczba kwantowa (n = 1,2,3...) kwantuje energię elektronu (numer orbity) -poboczna liczba kwantowa
Zasady obsadzania poziomów Model atomu Bohra Model kwantowy atomu Fala stojąca Liczby kwantowe -główna liczba kwantowa (n = 1,2,3...) kwantuje energię elektronu (numer orbity) -poboczna liczba kwantowa
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Atom wodoru. Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu:
 ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
S. Baran - Podstawy fizyki materii skondensowanej Pasma energetyczne. Pasma energetyczne
 Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
że w wyniku pomiaru zmiennej dynamicznej A, której odpowiada operator αˆ otrzymana zostanie wartość 2.41?
 TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
Wiązania chemiczne. Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych. 5 typów wiązań
 Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
Mechanika kwantowa. Erwin Schrödinger ( ) Werner Heisenberg
 Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Atomy wieloelektronowe
 Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały
 WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
Orbitale typu σ i typu π
 Orbitale typu σ i typu π Dwa odpowiadające sobie orbitale sąsiednich atomów tworzą kombinacje: wiążącą i antywiążącą. W rezultacie mogą powstać orbitale o rozkładzie przestrzennym dwojakiego typu: σ -
Orbitale typu σ i typu π Dwa odpowiadające sobie orbitale sąsiednich atomów tworzą kombinacje: wiążącą i antywiążącą. W rezultacie mogą powstać orbitale o rozkładzie przestrzennym dwojakiego typu: σ -
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Podstawy chemii obliczeniowej
 Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Różne typy wiązań mają ta sama przyczynę: energia powstającej stabilnej cząsteczki jest mniejsza niż sumaryczna energia tworzących ją, oddalonych
 Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
S. Baran - Podstawy fizyki materii skondensowanej Wiązania chemiczne w ciałach stałych. Wiązania chemiczne w ciałach stałych
 Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
C h można przedstawić w bazie wektorów bazowych grafenu (*) (**) Nanorurki węglowe (jednościenne)
 Nanorurki węglowe (jednościenne) zwinięte paski arkusza grafenu (wstęgi grafenowej) (węzły sieciowe Bravais i węzły podsieci) wstęgi: chiralna fotelowa zykzak komórka elementarna jednoznacznie definiuje
Nanorurki węglowe (jednościenne) zwinięte paski arkusza grafenu (wstęgi grafenowej) (węzły sieciowe Bravais i węzły podsieci) wstęgi: chiralna fotelowa zykzak komórka elementarna jednoznacznie definiuje
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
c) prawdopodobieństwo znalezienia cząstki między x=1.0 a x=1.5 jest równe
 TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Dr inż. Zbigniew Szklarski
 Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Fizyka 3.3 WYKŁAD II
 Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Zaburzenia periodyczności sieci krystalicznej
 Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Atom wodoru i jony wodoropodobne
 Atom wodoru i jony wodoropodobne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści Spis treści 1. Model Bohra atomu wodoru 2 1.1. Porządek
Atom wodoru i jony wodoropodobne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści Spis treści 1. Model Bohra atomu wodoru 2 1.1. Porządek
REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA
 REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA Opis układu cząsteczek w mechanice kwantowej: 1. Funkcja falowa, 2. Wektora stanu ψ. TRANSFORMACJE UKŁADU CZĄSTEK: 1.
REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA Opis układu cząsteczek w mechanice kwantowej: 1. Funkcja falowa, 2. Wektora stanu ψ. TRANSFORMACJE UKŁADU CZĄSTEK: 1.
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Zad Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji.
 Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
1 i 2. Struktura elektronowa atomów, tworzenie wiązań chemicznych
 1 i 2. Struktura elektronowa atomów, tworzenie wiązań chemicznych 1 1.1. Struktura elektronowa atomów Rozkład elektronów na pierwszych czterech powłokach elektronowych 1. powłoka 2. powłoka 3. powłoka
1 i 2. Struktura elektronowa atomów, tworzenie wiązań chemicznych 1 1.1. Struktura elektronowa atomów Rozkład elektronów na pierwszych czterech powłokach elektronowych 1. powłoka 2. powłoka 3. powłoka
Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych.
 Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych. Geometria cząsteczek Geometria cząsteczek decyduje zarówno o ich właściwościach fizycznych jak i chemicznych, np. temperaturze wrzenia,
Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych. Geometria cząsteczek Geometria cząsteczek decyduje zarówno o ich właściwościach fizycznych jak i chemicznych, np. temperaturze wrzenia,
Struktura energetyczna ciał stałych. Fizyka II dla EiT oraz E, lato
 Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Fizyka atomowa r. akad. 2012/2013
 r. akad. 2012/2013 wykład VII - VIII Podstawy Procesów i Konstrukcji Inżynierskich Fizyka atomowa Zakład Biofizyki 1 Spin elektronu Elektrony posiadają własny moment pędu L s. nazwany spinem. Wartość spinu
r. akad. 2012/2013 wykład VII - VIII Podstawy Procesów i Konstrukcji Inżynierskich Fizyka atomowa Zakład Biofizyki 1 Spin elektronu Elektrony posiadają własny moment pędu L s. nazwany spinem. Wartość spinu
WYKŁAD 3 CZĄSTECZKI WIELOATOMOWE ZWIĄZKI WĘGLA
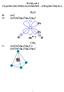 WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
Fizyka Ciała Stałego
 Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
Elektronowa struktura atomu
 Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO.
 GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Wykład 16: Atomy wieloelektronowe
 Wykład 16: Atomy wieloelektronowe Funkcje falowe Kolejność zapełniania orbitali Energia elektronów Konfiguracja elektronowa Reguła Hunda i zakaz Pauliego Efektywna liczba atomowa Reguły Slatera Wydział
Wykład 16: Atomy wieloelektronowe Funkcje falowe Kolejność zapełniania orbitali Energia elektronów Konfiguracja elektronowa Reguła Hunda i zakaz Pauliego Efektywna liczba atomowa Reguły Slatera Wydział
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Ciała stałe. Ciała krystaliczne. Ciała amorficzne. Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami.
 Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Równanie Schrödingera dla elektronu w atomie wodoru Równanie niezależne od czasu w trzech wymiarach współrzędne prostokątne
 Równanie Schrödingera dla elektronu w atomie wodoru Równanie nieależne od casu w trech wymiarach współrędne prostokątne ψ ψ ψ h V m + + x y + ( x, y, ) ψ = E ψ funkcja falowa ψ( x, y, ) Energia potencjalna
Równanie Schrödingera dla elektronu w atomie wodoru Równanie nieależne od casu w trech wymiarach współrędne prostokątne ψ ψ ψ h V m + + x y + ( x, y, ) ψ = E ψ funkcja falowa ψ( x, y, ) Energia potencjalna
Uklady modelowe III - rotator, atom wodoru
 Wyk lad 5 Uklady modelowe III - rotator, atom wodoru Model Separacja ruchu środka masy R = m 1r 1 + m 2 r 2 m 1 + m 2 Ĥ = Ĥ tr (R) + Ĥ rot (r) Ĥ tr 2 (R) = 2(m 1 + m 2 ) R [ Ψ E tr (R; t) = exp i (k R
Wyk lad 5 Uklady modelowe III - rotator, atom wodoru Model Separacja ruchu środka masy R = m 1r 1 + m 2 r 2 m 1 + m 2 Ĥ = Ĥ tr (R) + Ĥ rot (r) Ĥ tr 2 (R) = 2(m 1 + m 2 ) R [ Ψ E tr (R; t) = exp i (k R
Inżynieria Biomedyczna. Wykład XII
 Inżynieria Biomedyczna Wykład XII Plan Wiązania chemiczne Teoria Lewisa Teoria orbitali molekularnych Homojądrowe cząsteczki dwuatomowe Heterojądrowe cząsteczki dwuatomowe Elektroujemność Hybrydyzacja
Inżynieria Biomedyczna Wykład XII Plan Wiązania chemiczne Teoria Lewisa Teoria orbitali molekularnych Homojądrowe cząsteczki dwuatomowe Heterojądrowe cząsteczki dwuatomowe Elektroujemność Hybrydyzacja
Struktura energetyczna ciał stałych. Fizyka II, lato
 Struktura energetyczna ciał stałych Fizyka II, lato 016 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona studnia, w której energia
Struktura energetyczna ciał stałych Fizyka II, lato 016 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona studnia, w której energia
Wykład 5: Cząsteczki dwuatomowe
 Wykład 5: Cząsteczki dwuatomowe Wiązania jonowe i kowalencyjne Ograniczenia teorii Lewisa Orbitale cząsteczkowe Kombinacja liniowa orbitali atomowych Orbitale dwucentrowe Schematy nakładania orbitali Diagramy
Wykład 5: Cząsteczki dwuatomowe Wiązania jonowe i kowalencyjne Ograniczenia teorii Lewisa Orbitale cząsteczkowe Kombinacja liniowa orbitali atomowych Orbitale dwucentrowe Schematy nakładania orbitali Diagramy
Chemia Ogólna wykład 1
 Chemia Ogólna wykład 1 Materia związki chemiczne cząsteczka http://scholaris.pl/ obojętne elektrycznie indywiduum chemiczne, złożone z więcej niż jednego atomu, które są ze sobą trwale połączone wiązaniami
Chemia Ogólna wykład 1 Materia związki chemiczne cząsteczka http://scholaris.pl/ obojętne elektrycznie indywiduum chemiczne, złożone z więcej niż jednego atomu, które są ze sobą trwale połączone wiązaniami
JEDNOSTKI ATOMOWE =1, m e =1, e=1, ; 1 E 2 h = 4, J. Energia atomu wodoru lub jonu wodoropodobnego w jednostkach atomowych:
 do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
do wyk ladu z 1.10.13 Atom wodoru i jon wodoropodobny Ze - ladunek jadra, e - ladunek elektronu, µ - masa zredukowana µ = mem j m e+m j ( µ m e ) M j - masa jadra, m e - masa elektronu, ε 0 - przenikalność
Podstawy chemii. dr hab. Wacław Makowski. Wykład 1: Wprowadzenie
 Podstawy chemii dr hab. Wacław Makowski Wykład 1: Wprowadzenie Wspomnienia ze szkoły Elementarz (powtórka z gimnazjum) Układ okresowy Dalsze wtajemniczenia (liceum) Program zajęć Podręczniki Wydział Chemii
Podstawy chemii dr hab. Wacław Makowski Wykład 1: Wprowadzenie Wspomnienia ze szkoły Elementarz (powtórka z gimnazjum) Układ okresowy Dalsze wtajemniczenia (liceum) Program zajęć Podręczniki Wydział Chemii
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków).
 Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Właściwości kryształów
 Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
1. Przesłanki doświadczalne mechaniki kwantowej.
 1 Pytania egzaminacyjne: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny- interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest liczba wybijanych elektronów
1 Pytania egzaminacyjne: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny- interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest liczba wybijanych elektronów
Struktura elektronowa
 Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
Cząsteczki. 1.Dlaczego atomy łącz. 2.Jak atomy łącz. 3.Co to jest wiązanie chemiczne? Jakie sąs. typy wiąza
 Cząsteczki 1.Dlaczego atomy łącz czą się w cząsteczki?.jak atomy łącz czą się w cząsteczki? 3.Co to jest wiązanie chemiczne? Co to jest rząd d wiązania? Jakie sąs typy wiąza zań? Dlaczego atomy łącz czą
Cząsteczki 1.Dlaczego atomy łącz czą się w cząsteczki?.jak atomy łącz czą się w cząsteczki? 3.Co to jest wiązanie chemiczne? Co to jest rząd d wiązania? Jakie sąs typy wiąza zań? Dlaczego atomy łącz czą
Struktura elektronowa czasteczek. przybliżenie Borna-Oppenheimera. równania Schrödingera dla elektronów przy ustalonym po lożeniu jader
 Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Cz. I Materiał powtórzeniowy do sprawdzianu dla klas II LO - Wiązania chemiczne + przykładowe zadania i proponowane rozwiązania
 Cz. I Materiał powtórzeniowy do sprawdzianu dla klas II LO - Wiązania chemiczne + przykładowe zadania i proponowane rozwiązania I. Elektroujemność pierwiastków i elektronowa teoria wiązań Lewisa-Kossela
Cz. I Materiał powtórzeniowy do sprawdzianu dla klas II LO - Wiązania chemiczne + przykładowe zadania i proponowane rozwiązania I. Elektroujemność pierwiastków i elektronowa teoria wiązań Lewisa-Kossela
Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie
 Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie Schrödingera, zasada nieoznaczoności Heisenberga, ruch cząstki swobodnej,
Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie Schrödingera, zasada nieoznaczoności Heisenberga, ruch cząstki swobodnej,
TEORIA ORBITALI MOLEKULARNYCH (MO) dr Henryk Myszka - Uniwersytet Gdański - Wydział Chemii
 TERIA RBITALI MLEKULARNYCH (M) Metoda (teoria) orbitali molekularnych (M) podstawy metody M - F. Hund, R.S. Mulliken Teoria M zakłada, że zachowanie się elektronu w cząsteczce opisuje orbital molekularny
TERIA RBITALI MLEKULARNYCH (M) Metoda (teoria) orbitali molekularnych (M) podstawy metody M - F. Hund, R.S. Mulliken Teoria M zakłada, że zachowanie się elektronu w cząsteczce opisuje orbital molekularny
E e l kt k r t o r n o ow o a w a s t s r t u r kt k u t ra r a at a o t m o u
 Elektronowa struktura atomu Anna Pietnoczka BUDOWA ATOMU CZĄSTKA SYMBOL WYSTĘPOWANIE MASA ŁADUNEK ELEKTRYCZNY PROTON p + jądroatomowe około 1 u + 1 NEUTRON n 0 jądroatomowe około 1u Brak ELEKTRON e - powłoki
Elektronowa struktura atomu Anna Pietnoczka BUDOWA ATOMU CZĄSTKA SYMBOL WYSTĘPOWANIE MASA ŁADUNEK ELEKTRYCZNY PROTON p + jądroatomowe około 1 u + 1 NEUTRON n 0 jądroatomowe około 1u Brak ELEKTRON e - powłoki
Spis treści. Przedmowa redaktora do wydania czwartego 11
 Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Spis treści. Metoda VSEPR. Reguły określania struktury cząsteczek. Ustalanie struktury przestrzennej
 Spis treści 1 Metoda VSEPR 2 Reguły określania struktury cząsteczek 3 Ustalanie struktury przestrzennej 4 Typy geometrii cząsteczek przykłady 41 Przykład 1 określanie struktury BCl 3 42 Przykład 2 określanie
Spis treści 1 Metoda VSEPR 2 Reguły określania struktury cząsteczek 3 Ustalanie struktury przestrzennej 4 Typy geometrii cząsteczek przykłady 41 Przykład 1 określanie struktury BCl 3 42 Przykład 2 określanie
CHEMIA 1. INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne kierunek lekarski, stomatologia, farmacja, analityka medyczna ATOM.
 INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne kierunek lekarski, stomatologia, farmacja, analityka medyczna tel. 0501 38 39 55 www.medicus.edu.pl CHEMIA 1 ATOM Budowa atomu - jądro, zawierające
INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne kierunek lekarski, stomatologia, farmacja, analityka medyczna tel. 0501 38 39 55 www.medicus.edu.pl CHEMIA 1 ATOM Budowa atomu - jądro, zawierające
Teoria Orbitali Molekularnych. tworzenie wiązań chemicznych
 Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Budowa ciał stałych. sieć krystaliczna układy krystalograficzne sieć realna defekty wiązania w ciałach stałych
 Budowa ciał stałych sieć krystaliczna układy krystalograficzne sieć realna defekty wiązania w ciałach stałych Ciała stałe to substancje o regularnej, przestrzennej budowie krystalicznej, czyli regularnym
Budowa ciał stałych sieć krystaliczna układy krystalograficzne sieć realna defekty wiązania w ciałach stałych Ciała stałe to substancje o regularnej, przestrzennej budowie krystalicznej, czyli regularnym
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE 1 Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE 1 Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
Podstawy chemii obliczeniowej
 Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Chemia ogólna - część I: Atomy i cząsteczki
 dr ab. Wacław Makowski Cemia ogólna - część I: Atomy i cząsteczki 1. Kwantowanie. Atom wodoru 3. Atomy wieloelektronowe 4. Termy atomowe 5. Cząsteczki dwuatomowe 6. Hybrydyzacja 7. Orbitale zdelokalizowane
dr ab. Wacław Makowski Cemia ogólna - część I: Atomy i cząsteczki 1. Kwantowanie. Atom wodoru 3. Atomy wieloelektronowe 4. Termy atomowe 5. Cząsteczki dwuatomowe 6. Hybrydyzacja 7. Orbitale zdelokalizowane
Wykład z Chemii Ogólnej
 Wykład z Chemii Ogólnej Część 2 Budowa materii: od atomów do układów molekularnych 2.2. BUDOWA CZĄSTECZEK Katedra i Zakład Chemii Fizycznej Collegium Medicum w Bydgoszczy Uniwersytet Mikołaja Kopernika
Wykład z Chemii Ogólnej Część 2 Budowa materii: od atomów do układów molekularnych 2.2. BUDOWA CZĄSTECZEK Katedra i Zakład Chemii Fizycznej Collegium Medicum w Bydgoszczy Uniwersytet Mikołaja Kopernika
Struktura energetyczna ciał stałych
 011-05-0 Struktura energetyczna ciał stałych Fizyka II dla Elektroniki, lato 011 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona
011-05-0 Struktura energetyczna ciał stałych Fizyka II dla Elektroniki, lato 011 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona
Modele kp wprowadzenie
 Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 2003
 Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
Atomy wieloelektronowe i cząsteczki
 Atomy wieloelektronowe i cząsteczki 1 Atomy wieloelektronowe Wodór ma liczbę atomową Z=1 i jest prostym atomem. Zawiera tylko jeden elektron i jeden proton stąd potencjał opisuje oddziaływanie kulombowskie
Atomy wieloelektronowe i cząsteczki 1 Atomy wieloelektronowe Wodór ma liczbę atomową Z=1 i jest prostym atomem. Zawiera tylko jeden elektron i jeden proton stąd potencjał opisuje oddziaływanie kulombowskie
