Symulacja w Badaniach i Rozwoju Vol. 9, No. 1-2/2018. Romuald HOFFMANN
|
|
|
- Michalina Jabłońska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Symulacja w Badaniach i Rozwoju Vol. 9, No. -/8 Romuald HOFFMANN Wojskowa Akadmia Tchniczna, Wydział Cybrntyki, Instytut Systmów Informatycznych ul. gn. Witolda Urbanowicza, -98 Warszawa 46 romuald.hoffmann@wat.du.pl Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo Wprowadzni Mtoda dynamiki systmowj (ang. systm dynamics) jst mtodą budowy modli symulacji ciągłj, która umożliwia modlowani struktury oraz dynamiki złożonych systmów i procsów w nich zachodzących. Została zaproponowana w latach 6. XX wiku przz Jaya Forrstra, który opracował jj podstawow zasady i przdstawił j w licznych publikacjach, np. [6], [7], [8] (Forstr 96, 969, 975). Mtoda dynamiki systmowj jst przznaczona do modlowania złożonych systmów, w których występują sprzężnia zwrotn opisując zalżności przyczynowo-skutkow pomiędzy lmntami systmu [9] (Hoffmann, Protasowicki 3). W modlach matmatycznych zbudowanych z wykorzystanim mtody dynamiki systmowj wyróżniamy równania: poziomów (opisan równaniami różniczkowymi pirwszgo rzędu), przpływów (dan równaniami algbraicznymi) i zminnych pomocniczych (okrślon jako równania algbraiczn). Z równań tych otrzymujmy układ równań różniczkowo-algbraicznych, stanowiący opis matmatyczny związków przyczynowo-skutkowych występujących w modlowanym systmi. W mtodzi dynamiki systmowj stosowan są równania różniczkow zwyczajn pirwszgo rzędu wyprowadzon z ogólnj postaci zagadninia Cauchy go [] (Kasprska 5). Bardzo dobrym wprowadznim do dynamiki systmowj jst praca Strmana [8]. Przykłady zastosowania dynamiki systmowj do modlowania procsów walki w oparciu o podjści Lanchstra zostały przdstawion w pracy [] (Hoffmann, Protasowicki 3). Lanchstr (96) [9], [] analizując dynamikę walk powitrznych podczas I wojny światowj, zastosował do modlowania ilościowgo procsu walki dwóch przciwników parę liniowych zwyczajnych równań różniczkowych. Od tamtgo czasu modl Lanchstra był inspiracją dla wilu badaczy, którzy przyczynili się do szrgu publikacji, a których ni sposób wyczrpująco wyminić w tym mijscu. Warto jdnak zwrócić uwagę na prac: [4] (Mors, Kimball 95), [3], [4] (Brackn i inni 995), [3] (Washburn, Krss 9), [7] (Krss ), [9] (Tolk ). Prawi całość dostępnych publikacji dotyczy modli dynamiki walki dwóch stron. Cikawsz modl, jakimi są modl walki trzch lub więcj stron, można odnalźć tylko w nilicznych pracach najnowsz to: [] (Lin, MacKay 4), [8] (Krss i inni 8). 7
2 Romuald HOFFMANN Murray (988) [5] jako pirwszy zasugrował związk pomiędzy pidmiologią a wirusami komputrowymi, zauważając, ż wirusy komputrow są pwną analogią wirusa biologiczngo. Kphart i Whit (99, 993) [4], [5] byli pirwszymi autorami, którzy zaproponowali przyjęci modlu SIS (ang. suscptibl, infctd, suscptibl) jako modlu rozprzstrzniania się wirusów komputrowych. Od tgo czasu modl pidmiologiczn są szroko stosowan do modlowania dynamiki rozprzstrznia się wirusów komputrowych. Modl pidmii (rozprzstrzniania się) kodu złośliwgo można podzilić na dwi katgori modl dtrministyczn, opart na równaniach różniczkowych, i modl stochastyczn, wykorzystując w większości przypadków łańcuchy Markowa, procsy gałązkow i procsy dyfuzji. W ninijszj pracy bazujmy na dtrministycznych modlach pidmii. Porównani dtrministycznych oraz stochastycznych modli SIS i SIR (ang. suscptibl, infctd, rcovrd) można znalźć w wybranych publikacjach: [] (Alln, Burgin ), [] (Alln 8), [3] (Kling, Ross 8), [5] (Britton ). Nalży tutaj zaznaczyć, ż zarówno dtrministyczn, jak i stochastyczn modl odgrywają znaczącą rolę w modlowaniu dynamiki zjawisk pidmii. Wskazuj na to istnijąca bogata litratura, w większości dotycząca dtrministycznych modli pidmiologicznych rozprzstrzniania się wirusów komputrowych. Oprócz klasycznych modli SIS i SIR, bazujących na modlu Krmacka i McKndricka (97) [6], w ostatnich latach zostało sformułowanych wil nowych. Hoffmann i Protasowicki (7) [] przdstawili w ujęciu dynamiki systmowj dtrministyczn modl podstawow SIS, SIR, SIRS, a takż modl SAI (ang. suscptibl, antidotal, infctd) jako uproszczoną wrsję modlu SIRA (ang. suscptibl, infctd, rmovd, antidotal) opracowango przz Piquira i Araujo (9) [6]. Nizaprzczalni współczsny rozwój tchnologii informatycznych umożliwił prowadzni opracji militarnych równiż w cybrprzstrzni. W tj sytuacji oprogramowani złośliw stało się bronią umożliwiającą prowadzni opracji cybrntycznych, samodzilnych lub wspirających działania kintyczn. Sam modl pidmiologiczn do modlowania skutków opracji cybrntycznych wydają się już niwystarczając. Stąd obicującym kirunkim badań nad modlami dynamiki walki z wykorzystanim kodu złośliwgo wydaj się połączni podjścia Lanchstra i modli pidmiologicznych. Tutaj warto zwrócić uwagę na pracę Schramma i Gavra (3) [7], którzy modlując prowadzni opracji cybrntycznj poprzz propagację kodu złośliwgo (np. wirusów, robaków) w systmach przciwnika w połączniu z działaniami kintycznymi, przdstawili podjści połącznia klasyczngo modlu walki bzpośrdnij Lanchstra (ang. aimd fir) z modlm rozprzstrzniania się kodu złośliwgo SIR (ang. suscptibl, infctd, rmovd). W tym kontkści modl SAI w ujęciu dynamiki systmowj [] (Hoffmann, Protasowicki 7) zostani wykorzystany w ninijszj pracy i w połączniu z klasycznym modlm Lanchstra stanowić będzi przdmiot dalszych rozważań. tzn. opracj militarn, z którymi bzpośrdnio wiążą się straty ludzi i/lub uzbrojnia jak do tj pory jdyną 8
3 Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo Klasyczn modl walki Lanchstra w ujęciu dynamiki systmowj W pracy podstawą modlowania matmatyczngo dynamiki walki są modl W.F. Lanchstra ujęt w konwncji klasycznj dynamiki systmowj. Przypomnę, ż liczn modl ogólni zwan modlami Lanchstra objmują w większości rodzinę modli matmatycznych wykorzystujących równania różniczkow, zarówno liniow, jak i niliniow. Właśni ta własność umożliwia prost przdstawini modli dynamiki walki w języku klasycznj dynamiki systmowj. Gnralni modl Lanchstra opisującgo dynamikę walki dwóch stron Blu i można przdstawić następująco: #() A (), () B() = C D () z warunkami początkowymi: #()=# >, B()=B >, gdzi funkcj #(),B() opisują stan liczbny stron walczących w chwili odpowidnio: Blu,, A (),C D () są funkcjami opisującymi intnsywność zadawania strat stronom przciwnym. W modlowaniu walki układ () jst snsowny dla takigo przdziału czasu [,], ż dla każdgo [,] funkcj #()> i B()>. Przykładowy matmatyczny modl walki bzpośrdnij Lanchstra w języku dynamiki systmowj opisany układm równań () przdstawia rysunk. Natomiast wyniki przykładowj symulacji przdstawia na rysunk. W przykładzi przyjęto, A ()=@ B() oraz C D ()=C #(), gdzi są stał. B Blu ρ β ρ () FINAL TIME = 5 () INITIAL TIME = (3) B = (4) R = (5) β =. (6) ρ =.5 (7) Blu = INTEG (-ρ, B) (8) = INTEG (-β Blu, R) (9) β Blu = MAX( MIN(, β*blu ), ) () ρ = MAX( MIN( Blu, ρ* ), ) β Blu R Rys.. Przykładowy modl Lanchstra opisany układm równań () w ujęciu dynamiki systmowj Fig.. An xampl of th Lanchstr combat modl dscribd by th systm of quations () in trms of systm dynamics 9
4 Romuald HOFFMANN Blu, 75, Blu : ρ=,3; β=, Blu : ρ=,5; β=, : ρ=,3; β=, : ρ=,5; β=, Rys.. Przykładow wyniki symulacji modlu Lanchstra z rysunku Fig.. Sampl rsults of simulation of Lanchstr combat modl from Figur W tym mijscu równiż warto sformułować w konwncji dynamiki systmowj modl opisującgo dynamikę walki trzch wzajmni wrogich stron: Blu, i Grn. Zakładając dla uproszcznia, ż każda z stron niszczy zasoby przciwników z taką samą skutcznością, modl matmatyczny Lanchstra przyjmuj postać: #() A () I J (), B() = C D () I J (), () K() A () C D () z warunkami początkowymi: #()=# >, B()=B >, gdzi funkcj #(),B(),K() opisują stan liczbny stron walczących w chwili odpowidnio: Blu,, Grn, natomiast C D (),@ A (),I J () są funkcjami opisującymi intnsywność zadawania strat stronom przciwnym. Układ równań () ma sns w modlowaniu walki, gdy dla każdgo [,] funkcj #()> i B()>. Przykładowy matmatyczny modl Lanchstra walki bzpośrdnij trzch stron w języku dynamiki systmowj opisany układm równań () przdstawia rysunk 3. W przykładzi przyjęto, ż C D ()=C A () =@ B() oraz I J ()=I K(), gdzi współczynniki C,@,I są stał.
5 Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo B B() R Blu #LM() B() I KNO(), KNO() B() C #LM() γ () B = ρ () R= (3) G = (4) β=. ρ γ Grn (5) γ =.5 (6) ρ =.5 <ρ> <β> (7) Blu = INTEG ( -ρ γ Grn, B) (8) Grn= INTEG ( -β Blu ρ, G) (9) = INTEG ( -β Blu γ Grn, R) Grn () β Blu γ Grn = MAX( MIN(, β Blu ρ β*blu + γ*grn), ) G () β Blu ρ = MAX( MIN( Grn, β*blu + ρ*), ) () ρ γ Grn = MAX( MIN( Blu, β Blu γ Grn ρ* + γ*grn), ) = C #LM() I KNO(), Rys. 3. Przykładowy modl Lanchstra dla trzch stron w ujęciu dynamiki systmowj Fig. 3. An xampl of th Lanchstr modl for thr-way combat in trms of systm dynamics 3 Modl SAI rozprzstrzniania się kodu złośliwgo Rozważę modl SAI (ang. suscptibl, antidotal, infctd), który w konwncji dynamiki systmowj [] (Hoffmann, Protasowicki 3) zostani wykorzystany w dalszj części pracy w połączniu z klasycznym modlm dynamiki walki bzpośrdnij Lanchstra. W modlu przyjęto założni, ż rozprzstrzniani się kodu złośliwgo prowadzi do podziału populacji komputrów na trzy grupy urządzń: podatn (+(),t ) taki, któr mogą zostać zainfkowan, zainfkowan ((),t ) oraz β <γ> uodpornion ((),t ) w wyniku usunięcia podatności i aktualizacji oprogramowania. Modl SAI jst opisany następującym układm równań różniczkowych [6] (Piquira, Araujo 8): dt +()= R +() () T +() (), ()=R +() () U () (), (3) ()=T +() ()+U () () z wymaganymi warunkami początkowymi: +()=+ >, ()= >, ()= >. Paramtr R> oznacza współczynnik (tmpo) rozprzstrzniania się wirusa komputrowgo, U > jst współczynnikim (tmpm) usuwania kodu złośliwgo, natomiast paramtr δ> oznacza współczynnik skutczności usunięcia podatności lub aktualizacji oprogramowania. Założni stałj wilkości populacji
6 Romuald HOFFMANN komputrów jst już wbudowan w układ równań (3), tzn. +() + () + () = const=\. Modl SAI w ujęciu dynamiki systmowj [] (Hoffmann, Protasowicki 7) przdstawia rysunk 4. W modlu tym przyjęto R = ] \ >, U= >, T =M \. Wyniki przykładowj symulacji modlu SAI zostały przdstawion na rysunku 5. <N> Częstotliwość aktualizacji u Skutczność aktualizacji k B dltasa R Początkowa liczba odpornych Ao S A Początkowa liczba zarażonych Io R I B + asi R B + bia - Częstotliwość kontaktu c N Zarażalność i <N> Śrdni czas trwania infkcji d Rys. 4. Modl SAI opisany układm równań (3) w ujęciu dynamiki systmowj Fig. 4. Th SAI modl dscribd by th systm of quations (3) in trms of systm dynamics Slctd Variabls Slctd Variabls, 4, 7,5 3, Host 5, Host/Day,,5, A : currnt I : currnt S : currnt asi : currnt bia : currnt dltasa : currnt Rys. 5. Przykładow wyniki symulacji modlu SAI z rys. 4 (liczba komputrów N = ; czas symulacji 3; c = 6; d = ; i =,5; u = ; k =,65; I = ; A = ) Fig. 5. Sampl rsults of th simulation of SAI modl from Fig. 4. (numbr of computrs N = ; simulation tim 3; c = 6; d = ; i =,5; u = ; k =,65; I = ; A =
7 Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo 4 Modl dynamiki walki z użycim kodu złośliwgo przz stronę Przytoczę dalj modl Schramma i Gavra (3) [7], którzy modlując prowadzni opracji kintycznych w połączniu z opracją cybrntyczną poprzz propagację 3 kodu złośliwgo w systmach przciwnika, wykorzystali modl walki bzpośrdnij Lanchstra oraz zmodyfikowany modl SIR. Założono, ż siły stron wykorzystują systmy komputrow w walc i liminacja kintyczna członka strony przciwnj liminuj z walki równiż wyposażni komputrow. Dodatkowo przyjęto założni, ż strona w przciwiństwi do strony Blu jst nipodatna na ataki komputrow oraz wprowadziła kod złośliwy do systmów przciwnika. Chociaż założni to wydawać się moż niraln, to jdnak odpowiada na przykład przypadkowi, kidy strona posiada systmy wykonan w odminnj tchnologii, nipodatnj na ataki cybrntyczn, i posiada zdolność wczśnijszgo wprowadznia kodu złośliwgo do systmów tgoż przciwnika. W tym mijscu warto zauważyć, ż zmodyfikowany modl SIR użyty przz Schramma i Gavra [7] jst w swj istoci modlm różniącym się od modlu SAI założnim, ż intnsywność aktualizacji komputrów podatnych różni się od intnsywności usuwania kodu złośliwgo (połączongo z aktualizacją). Zatm na potrzby artykułu zostani przyjęty modl SAI i w konskwncji używan będą oznacznia z modlu SAI dotycząc funkcji opisujących liczbę w czasi komputrów podatnych +(), zainfkowanych () i uodpornionych (). Liczbność stron w czasi opisują funkcj B(), #()=+()+()+() odpowidnio stron:, Blu. Zatm pirwotny modl Schramma i Gavra [7] z wymaganymi warunkami początkowymi: ()=B >, +()=+ >, ()= >, ()= > można przdstawić następującym układm równań różniczkowych: B()= C _ S()+() C. (), dt +()= b +() () : +() () ρ B() +() #(), () ()=b +() () : () () ρ B() #(), ()=: +() ()+: () () ρ B() () #(), #()=+()+()+(). Paramtr b > oznacza współczynnik (tmpo) rozprzstrzniania się wirusa komputrowgo; : > jst współczynnikim (tmpm) zarówno usunięcia podatności (aktualizacji) oprogramowania, jak i usuwania kodu złośliwgo; ρ> oznacza współczynnik skutczności (fktywność) rażnia kintyczngo sił Blu przz stronę. Natomiast współczynniki C _, C. (C _ > C. ) oznaczają skutczności (fktywności) rażnia kintyczngo sił przz stronę Blu, gdzi C _ dotyczy wykorzystania do walki kintycznj systmów komputrowych zarówno podatnych (4) 3 wczśnij wprowadzongo 3
8 Romuald HOFFMANN i odpornych, C. zainfkowanych. Wartości :, b, C., C _ są stał. Układ (4) jst słuszny dla takigo przdziału czasu [,], ż dla każdgo [,] funkcj B()>, S()>, ()> oraz ()>. Przykładowy modl w języku dynamiki systmowj opisany układm równań (4) przdstawia rysunk 6, a wyniki przykładowj symulacji zostały podan na rysunku 7. ρ <Blu> R β.blu βd ρ..s <S> β <A> <I> A βu <ρ> ηsa S A ρ..a B η ξ I <η> Blu <> I ξsi ηia <S> <I> ρ..i <ρ> <Blu> <> Rys. 6. Przykładowy modl walki Schramma i Gavra opisany układm równań (4) w ujęciu dynamiki systmowj Fig. 6. An xampl of Schramm & Gavr s combat modl dscribd by th systm of quations (4) in trms of systm dynamics 4
9 Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo, Blu, Host Blu : ρ=,5 Blu : ρ=, : ρ=,5 : ρ=,8 6 I 6 A Host 3 Host I : ρ=,5 I : ρ=,8 Rys. 7. Przykładow wyniki symulacji modlu dynamiki z rys. 6 Fig. 7. Sampl rsults of simulation of th combat modl from Fig. 6 5 Modl dynamiki walki z użycim kodu złośliwgo przz obi strony Rozpatrzę wczśnij przytoczony modl Schramma i Gavra [7], przy dodatkowym założniu, ż strona posiada systmy podatn na atak kodm złośliwym. Oznacza to, ż w tym przypadku każda z stron jst podatna na atak cybrntyczny. Oczywiści, utrzymam założni wczśnijszj infkcji systmów, w tym przypadku obu stron. Ponadto przyjmuję założni, ż siły przciwnych stron wykorzystują systmy komputrow w walc i liminacja kintyczna członka strony przciwnj liminuj z walki równiż wyposażni komputrow. Przd zdfiniowanim układu równań różniczkowych przyjmuję następującą konwncję oznaczń. Indksm ] =, oznaczać będzi się paramtry modlu odpowiadając A : ρ=,5 A : ρ=,8 5
10 Romuald HOFFMANN stronom konfliktu, odpowidnio Blu przz ]= oraz przz ] =. Dla ] =, paramtry b d >, oznaczają współczynniki tmpa rozprzstrzniania się wirusa komputrowgo; : d > są współczynnikami tmpa zarówno usunięcia podatności (aktualizacji) oprogramowania, jak i usuwania kodu złośliwgo; ρ > oznaczają współczynniki skutczności (fktywność) wzajmngo rażnia kintyczngo sił odpowidnio Blu przz stronę, przz Blu, Natomiast współczynniki C _, C. (C _ > C. ) oznaczają skutczności (fktywności) rażnia kintyczngo sił przz stronę Blu, gdzi C _ dotyczy wykorzystania do walki kintycznj systmów komputrowych zarówno podatnych, jak i odpornych, C. zainfkowanych. Natomiast _ ) odpowidnio odnoszą się do skutczności rażnia kintyczngo sił Blu przz stronę. Ponadto przyjmuję dla strony Blu (] =) oraz (] =) oznacznia funkcji opisujących liczbę w czasi komputrów: podatnych + d (), zainfkowanych d () i uodpornionych d (). Liczbność stron w czasi opisują funkcj B()=+ ()+ ()+ (), #()=+ ()+ ()+ () odpowidnio stron:, Blu. Zatm modl z wymaganymi warunkami początkowymi dla + d ()>, d ()>, d ()> (] =,) można przdstawić w postaci układu równań różniczkowych: _ + ()+ (), B()= C _ S ()+ () C. () ; + dt ()= b + () () : + () ()+ B() f - ( ) D( ) ()=b + () () : () ()+ B(). - ( ) D( ) ()=: + () ()+: () ()+ B() g - ( ) ; D( ) + dt ()= b + () () : + () ()+ #() f / ( ) A( ) ()=b + () () : () ()+ #(). / ( ) A( ) ()=: + () ()+: () ()+ #() g / ( ) ; A( ),,,, (5) #()=+ ()+ ()+ (), B()=+ ()+ ()+ (). Wartości współczynników :, :, b, b,c _, są stał. Układ równań różniczkowych (5) ma sns w modlowaniu walki dla takigo przdziału czasu [,], ż dla każdgo [,] oraz funkcj + d ()>, d ()> oraz d ()> (] =,). Przykładowy modl w języku dynamiki systmowj opisany układm równań (5) przdstawia rysunk 8, a wyniki przykładowj symulacji zostały przdstawion na rysunku 9. 6
11 Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo β.blu R βd ρ.blu.s β βu <S> <A> <I> Poczatkowa liczba odpornych A S <R> ξ η ηsa Poczatkowa liczba zarazonych I <η> A ρ.blu.a <> <β> ξsi I ηia ρ.blu.i <> <β> Blu ρ. B ρd ρ..s ρ ρu <S> <A> <I> Poczatkowa liczba odpornych A ηsa S <B> η A ρ..a BLu ξ Poczatkowa liczba zarazonych I <η> <Blu> <ρ> ξsi I ηia ρ..i <ρ> <Blu> Rys. 8. Przykładowy modl walki opisany układm równań (5) w ujęciu dynamiki systmowj Fig. 8. An xampl of th combat modl dscribd by th systm of quations (5) in trms of systm dynamics 7
12 Romuald HOFFMANN, Blu, Blu : Io=; Io= Blu : Io=; Io= : Io=; Io= : Io=; Io= A A Host A : Io=; Io= A : Io=; Io= Host A : Io=; Io= A : Io=; Io= Rys. 9. Przykładow wyniki symulacji modlu dynamiki z rys. 8 Fig. 9. Sampl rsults of simulation of th combat modl from Fig. 8 6 Podsumowani Jak już wspomniano na wstępi, faktm jst to, ż współczsny rozwój tchnologii informatycznych umożliwił prowadzni opracji militarnych równiż w cybrprzstrzni, poprzz wykorzystani oprogramowania złośliwgo. Okazuj się, ż modl walki Lanchstra w połączniu z modlami rozprzstrzniania się kodu złośliwgo można zastosować do modlowania dynamiki walki z wsparcim opracji cybrntycznych wykorzystujących propagację kodu złośliwgo w systmach przciwnika. Najczęścij wykorzystywanymi modlami rozprzstrznia się oprogramowania złośliwgo w systmach informatycznych są modl bazując na klasycznych modlach pidmiologicznych SIS, SIR czy SIRS i ich modyfikacji, jakim jst np. modl SAI użyty w ninijszym artykul. Przntowana w artykul mtoda dynamiki systmowj ni stanowi przszkody zastosowania innych modli, takich np. jak: SEIRS (Mishra, Saini 7) [3], SEIQRS (Mishra, Jha ) [] i SIRA (Piquira i Araujo 9) [6]. Przyjęta w artykul symulacyjna mtoda dynamiki systmowj pozwala modlować w ujęciu Lanchstra dynamikę działań kintycznych z wsparcim opracji rozprzstrzninia się kodu złośliwgo w systmach przciwnika, uwzględniając przy tym występując liczn sprzężnia zwrotn. Zdanim autora, dzięki łącznmu rozpatrywaniu działań kintycznych i cybrntycznych, jako spójnj całości w kontkści jgo dynamiki systmowj, stworzon modl symulacyjn umożliwiają łatw odwzorowani i zrozumini skomplikowanych rlacji o charaktrz niliniowym. Chociaż istnijąc w litraturz współczsn modl symulacji procsów walki stanowią złożon modl stochastyczn, któr dają wyniki lpsz niż modl Lanchstra, to jdnak główną zaltą zaprzntowanych modli jst ich prostota i łatwość rozwiązywania 8
13 Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo układów zwyczajnych równań różniczkowych i w tym przypadku wykorzystania dynamiki systmowj do łatwgo uzyskania wyników symulacji. Nalży w tym mijscu zaznaczyć, ż liczbność walczących stron i współczynniki strat stanowią najważnijsz czynniki mając wpływ na odwzorowani przbigu walki w ujęciu Lanchstra. W tym kontkści przdstawion w ninijszym artykul przykładow modl dynamiki walki Lanchstra w połączniu z modlm SAI, pomimo licznych uproszczń, pozwalają na osiągnięci zadowalających wyników symulacji. Na zakończni nalży zaznaczyć, ż w przdstawionym ujęciu połączon modl walki Lanchstra z modlami rozprzstrzniania się kodu złośliwgo, za każdym razm zapisanymi jako układy równań różniczkowych, stanowią przykład transformowania zapisu formalizmu matmatyczngo do graficzngo języka dynamiki systmowj symulacji numrycznj. Oczywiści, w praktyc można budować modl przyrostowo bz uprzdnigo formalngo i płngo zdfiniowania układu równań różniczkowych, a opisy poziomów, przpływów i zminnych mogą przyjmować formę samodokumntującą, znaczni odbigającą od zapisu symboliczngo. Zatm budowa rozbudowanych i skomplikowanych modli oraz symulacja praktyczni ni sprawia większych problmów. Przdstawian w artykul modl zostały zbudowan z wykorzystanim pakitu symulacyjngo dynamiki systmowj Vnsim vr. 5. Litratura. Alln L.J.S., Burgin A.M.: Comparison of dtrministic and stochastic SIS modls in discrt tim. Mathmatical Bioscincs, vol. 63, s. 33,. Alln L.J.S.: An introduction to stochastic pidmic modls. Lctur Nots in Mathmatics, t. 945, Springr, Brlin, s Brackn J.: Lanchstr modls of th Ardnns campaign. Naval Rsarch Logistics (NRL), Vol.4, Issu 4, s , Jun Brackn J., Krss M., Rosnthal R.E. (rd.): Warfar modling. John Wily & Sons, Inc., Britton T.: Stochastic pidmic modls: a survy. Mathmatical Bioscincs, vol. 5, s. 4 35, 6. Forstr J.W.: Industrial Dynamics. MIT Prss Cambridg, Forrstr J.W.: Urban Dynamics. MIT Prss Cambridg, Forrstr J.W.: Th collctd paprs of Jay W. Forrstr. Wright-Alln Prss, Hoffmann R., Protasowicki T.: Mtoda dynamiki systmowj w modlowaniu złożonych systmów i procsów. Biultyn Instytutu Systmów Informatycznych, vol., s.9-8, 3. Hoffmann R., Protasowicki T., Modlowani pola walki z zastosowanim koncpcji dynamiki systmowj. Biultyn Instytutu Systmów Informatycznych, vol., s. 9 34, 3. Hoffmann R., Protasowicki T.: Klasyczn modl rozprzstrzniania się wirusów komputrowych w ujęciu dynamiki systmowj. Roczniki Kolgium Analiz Ekonomicznych nr 45, 7, s Szkoła Główna Handlowa, 7. Kasprska E., Dynamika systmowa. Symulacja i optymalizacja. Wydawnictwo Politchniki Śląskij Gliwic, 5 9
14 Romuald HOFFMANN 3. Kling M.J., Ross J.V.: On mthods for studying stochastic disas dynamics, Journal of Royal Socity Intrfac, vol. 5, s. 7 8, 8 4. Kphart J.O, Whit S.R., Dirctd-graph pidmiological modls of computr viruss. Procdings of IEEE Computr Socity Symposium on Rsarch in Scurity and Privacy, s , Kphart J.O, Whit S.R., Masuring and modling computr virus prvalnc. Procdings of IEEE Computr Socity Symposium on Rsarch in Scurity and Privacy, s. 5, Krmack W.O., McKndrick A.G.: A Contribution to th Mathmatical Thory of Epidmics. Procdings of Th Royal Socity, vol. 5, s. 7 7, Krss M: Modling armd conflicts. Scinc, 336 (683), s , 8. Krss M., Caulkins J.P., Fichtingr G., Grass D., Sidl A.: Lanchstr modl for thr-way combat. Europan Journal of Oprational Rsarch, Vol. 64, Issu, s , 8 9. Lanchstr F.W.: Aircraft in warfar: Th dawn of th fourth Arm. Applton Nw York, 96. Lanchstr F.W.: Th Principl of Concntration. Th "N-Squar" Law. Rprint w Nwman J.R. (rd.): Volum Four of Th World of Mathmatics, s , Simon and Schustr, Nw York 956. Lin K.Y., MacKay N.J.: Th optimal policy for th on-against-many htrognous Lanchstr modl. Oprations Rsarch Lttrs, 4 (6 7), s , 4. Mishra B.K., Jha N.: SEIQRS modl for th transmission of malicious objcts in computr ntwork. Applid Mathmatical Modlling, vol. 34, s. 7 75, 3. Mishra B.K., Saini D.K.: SEIRS pidmic modl with dlay for transmission of malicious objcts in computr ntwork. Applid Mathmatics and Computation, vol. 88, s , 7 4. Mors, P., Kimball, G.: Mthods of oprations rsarch. Chapman and Hall Ltd Murray W.H., Th application of pidmiology to computr viruss. Computr and Scurity, vol. 7, s , Piquira J.R.C., Araujo V.O.: A modifid pidmiological modl for computr viruss. Applid Mathmatics and Computation, vol. 3, s , 9 7. Schramm H.C., Gavr D.P.: Lanchstr for cybr: Th mixd pidmic combat modl. Naval Rsarch Logistics (NRL) Vol.6, Issu7, s , Octobr 3 8. Strman J.D.: Businss Dynamics. Systms Thinking and Modling for a Complx World. McGraw-Hill, 9. Tolk A.: Modling ffcts. w: Tolk A. (rd.): Enginring principls of combat modling and distributd simulation. Hobokn, JohnWily & Sons, Inc. s. 45-7, 3. Washburn A., Krss M.: Combat modling. Springr-Vrlag 9 3
15 Modlowani w języku dynamiki systmowj opracji cybrntycznych z wykorzystanim modli walki łączonych z modlami rozprzstrzniania się kodu złośliwgo Strszczni Współczsny rozwój tchnologii informatycznych umożliwił prowadzni opracji militarnych w cybrprzstrzni z wykorzystanim oprogramowania złośliwgo. Okazuj się, ż modl walki Lanchstra w połączniu z modlami rozprzstrzniania się kodu złośliwgo można zastosować do ilościowgo modlowania opracji kintycznych wspartych opracjami propagacji kodu złośliwgo w systmach przciwnika. W pracy przdstawiono w ujęciu dynamiki systmowj dwa modl walki z użycim kodu złośliwgo oraz przykładow wyniki ich symulacji. Modl w języku dynamiki systmowj bazują na klasycznym modlu dynamiki walki bzpośrdnij Lanchstra oraz modlu propagacji kodu złośliwgo w systmach komputrowych SAI (ang. suscptibl, antidotal, infctd). Słowa kluczow: dynamika systmowa, modl dynamiki walki, modl Lanchstra, modl propagacji kodu złośliwgo, SAI Modling in th languag of systm dynamics of cybr oprations using combat modls combind with modls of sprading malicious cod Summary Modrn information tchnologis hav nabld to carry out military oprations in cybrspac with using malwar. It turns out that Lanchstr combat modls in conjunction with th modls of malicious cod propagation in IT systms can b usd for quantitativ modling of kintic oprations supportd by cybr oprations with malwar propagation in opposing forcs IT systms. This papr prsnts in trms of systm dynamics two combat modls with using propagation of malwar cods and th sampl rsults of thir simulation. Th systm dynamics combat modls ar basd on th Lanchstr classical dirct fir combat modl and SAI (suscptibl, antidotal, infctd) modl of malicious cod propagation in computr systms. Kywords: systm dynamics, combat modl, Lanchstr modl, malicious cod propagation modl, SAI 3
16 Symulacja w Badaniach i Rozwoju Vol. 9, No. -/8 3
ZASTOSOWANIE METODY GRAFÓW WIĄZAŃ DO MODELOWANIA PRACY ZESPOŁU PRĄDOTWÓRCZEGO W SIŁOWNI OKRĘTOWEJ
 Chybowski L. Grzbiniak R. Matuszak Z. Maritim Acadmy zczcin Poland ZATOOWANIE METODY GRAFÓW WIĄZAŃ DO MODELOWANIA PRACY ZEPOŁU PRĄDOTWÓRCZEGO W IŁOWNI OKRĘTOWEJ ummary: Papr prsnts issus of application
Chybowski L. Grzbiniak R. Matuszak Z. Maritim Acadmy zczcin Poland ZATOOWANIE METODY GRAFÓW WIĄZAŃ DO MODELOWANIA PRACY ZEPOŁU PRĄDOTWÓRCZEGO W IŁOWNI OKRĘTOWEJ ummary: Papr prsnts issus of application
Szeregowy obwód RC - model matematyczny układu
 Akadmia Morska w Gdyni Katdra Automatyki Okrętowj Toria strowania Mirosław Tomra Na przykładzi szrgowgo obwodu lktryczngo składającgo się z dwóch lmntów pasywnych: rzystora R i kondnsatora C przdstawiony
Akadmia Morska w Gdyni Katdra Automatyki Okrętowj Toria strowania Mirosław Tomra Na przykładzi szrgowgo obwodu lktryczngo składającgo się z dwóch lmntów pasywnych: rzystora R i kondnsatora C przdstawiony
ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO OKREŚLENIA PRAWDOPODOBIEŃSTWA SPRZEDAŻY ZASOBU MIESZKANIOWEGO
 ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO OKREŚLENIA PRAWDOPODOBIEŃSTWA SPRZEDAŻY ZASOBU MIESZKANIOWEGO Łukasz MACH Strszczni: W artykul przdstawiono procs budowy modlu rgrsji logistycznj, którgo clm jst wspomagani
ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO OKREŚLENIA PRAWDOPODOBIEŃSTWA SPRZEDAŻY ZASOBU MIESZKANIOWEGO Łukasz MACH Strszczni: W artykul przdstawiono procs budowy modlu rgrsji logistycznj, którgo clm jst wspomagani
DYNAMICZNA ELIMINACJA DRGAŃ MECHANICZNYCH
 LABORATORIUM DYNAMIKI MASZYN Wydział Budowy Maszyn i Zarządzania Instytut Mchaniki Stosowanj Zakład Wibroakustyki i Bio-Dynamiki Systmów Ćwiczni nr 3 Cl ćwicznia: DYNAMICZNA ELIMINACJA DRGAŃ MECHANICZNYCH
LABORATORIUM DYNAMIKI MASZYN Wydział Budowy Maszyn i Zarządzania Instytut Mchaniki Stosowanj Zakład Wibroakustyki i Bio-Dynamiki Systmów Ćwiczni nr 3 Cl ćwicznia: DYNAMICZNA ELIMINACJA DRGAŃ MECHANICZNYCH
Sieci neuronowe - uczenie
 Sici nuronow - uczni http://zajcia.jakubw.pl/nai/ Prcptron - przypomnini x x x n w w w n wi xi θ y w p. p. y Uczni prcptronu Przykład: rozpoznawani znaków 36 wjść Wyjści:, jśli na wjściu pojawia się litra
Sici nuronow - uczni http://zajcia.jakubw.pl/nai/ Prcptron - przypomnini x x x n w w w n wi xi θ y w p. p. y Uczni prcptronu Przykład: rozpoznawani znaków 36 wjść Wyjści:, jśli na wjściu pojawia się litra
Elektroniczne systemy bezpieczeństwa mogą występować w trzech rodzajach struktur. Są to struktury typu: - skupionego, - rozproszonego, - mieszanego.
 A. Cl ćwicznia Clm ćwicznia jst zapoznani się z wskaźnikami nizawodnościowymi lktronicznych systmów bzpiczństwa oraz wykorzystanim ich do optymalizacji struktury nizawodnościowj systmu.. Część tortyczna
A. Cl ćwicznia Clm ćwicznia jst zapoznani się z wskaźnikami nizawodnościowymi lktronicznych systmów bzpiczństwa oraz wykorzystanim ich do optymalizacji struktury nizawodnościowj systmu.. Część tortyczna
Uogólnione wektory własne
 Uogólnion wktory własn m Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
Uogólnion wktory własn m Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
Laboratorium Półprzewodniki Dielektryki Magnetyki Ćwiczenie nr 11 Badanie materiałów ferromagnetycznych
 Laboratorium Półprzwodniki Dilktryki Magntyki Ćwiczni nr Badani matriałów frromagntycznych I. Zagadninia do przygotowania:. Podstawow wilkości charaktryzując matriały magntyczn. Związki pomiędzy B, H i
Laboratorium Półprzwodniki Dilktryki Magntyki Ćwiczni nr Badani matriałów frromagntycznych I. Zagadninia do przygotowania:. Podstawow wilkości charaktryzując matriały magntyczn. Związki pomiędzy B, H i
Farmakokinetyka furaginy jako przykład procesu pierwszego rzędu w modelu jednokompartmentowym zawierającym sztuczną nerkę jako układ eliminujący lek
 1 Matriał tortyczny do ćwicznia dostępny jst w oddzilnym dokumnci, jak równiż w książc: Hrmann T., Farmakokintyka. Toria i praktyka. Wydawnictwa Lkarski PZWL, Warszawa 2002, s. 13-74 Ćwiczni 6: Farmakokintyka
1 Matriał tortyczny do ćwicznia dostępny jst w oddzilnym dokumnci, jak równiż w książc: Hrmann T., Farmakokintyka. Toria i praktyka. Wydawnictwa Lkarski PZWL, Warszawa 2002, s. 13-74 Ćwiczni 6: Farmakokintyka
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 760 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 59 2013
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 760 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 59 2013 KAROL MAREK KLIMCZAK SYMULACJA FINANSOWA SPÓŁKI ZA POMOCĄ MODELU ZYSKU REZYDUALNEGO Słowa kluczow:
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 760 FINANSE, RYNKI FINANSOWE, UBEZPIECZENIA NR 59 2013 KAROL MAREK KLIMCZAK SYMULACJA FINANSOWA SPÓŁKI ZA POMOCĄ MODELU ZYSKU REZYDUALNEGO Słowa kluczow:
ADAPTACYJNA ANALIZA POWŁOK ZDOMINOWANYCH GIĘTNIE O ZŁOŻONYM OPISIE MECHANICZNYM
 Mgr inż. Magdalna ZIELIŃSKA DOI: 10.17814/mchanik.2015.7.320 Uniwrsytt Warmińsko-Mazurski w Olsztyni, Wydział Nauk Tchnicznych Dr hab. inż. Grzgorz ZBOIŃSKI Instytut Maszyn Przpływowych PAN w Gdańsku ADAPTACYJNA
Mgr inż. Magdalna ZIELIŃSKA DOI: 10.17814/mchanik.2015.7.320 Uniwrsytt Warmińsko-Mazurski w Olsztyni, Wydział Nauk Tchnicznych Dr hab. inż. Grzgorz ZBOIŃSKI Instytut Maszyn Przpływowych PAN w Gdańsku ADAPTACYJNA
CHARAKTERYSTYKA OBCIĄŻENIOWA
 Opracowani: dr inż. Ewa Fudalj-Kostrzwa CHARAKTERYSTYKA OBCIĄŻENIOWA Charaktrystyki obciążniow są wyznaczan w ramach klasycznych statycznych badań silników zarówno dla silników o zapłoni iskrowym jak i
Opracowani: dr inż. Ewa Fudalj-Kostrzwa CHARAKTERYSTYKA OBCIĄŻENIOWA Charaktrystyki obciążniow są wyznaczan w ramach klasycznych statycznych badań silników zarówno dla silników o zapłoni iskrowym jak i
Definicja: Wektor nazywamy uogólnionym wektorem własnym rzędu m macierzy A
 Uogólnion wktory własnw Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A m do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
Uogólnion wktory własnw Dfinicja: Wktor nazywamy uogólnionym wktorm własnym rzędu m macirzy A m do wartości własnj λ jśli ( A - I) m m- λ al ( A - λ I) Przykład: Znajdź uogólniony wktor własny rzędu do
Optymalizacja reguł przejścia systemu bonus-malus
 Optymalizaca rguł przścia systmu onus-malus Dr Marcin Topolwski Dr Michał Brnardlli Instytut Ekonomtrii Szkoła Główna Handlowa w Warszawi Plan: Inspiraca, motywaca, cl i zakrs adania Ryzyko Systm onus-malus
Optymalizaca rguł przścia systmu onus-malus Dr Marcin Topolwski Dr Michał Brnardlli Instytut Ekonomtrii Szkoła Główna Handlowa w Warszawi Plan: Inspiraca, motywaca, cl i zakrs adania Ryzyko Systm onus-malus
2. Architektury sztucznych sieci neuronowych
 - 8-2. Architktury sztucznych sici nuronowych 2.. Matmatyczny modl nuronu i prostj sici nuronowj Sztuczn sici nuronow są modlami inspirowanymi przz strukturę i zachowani prawdziwych nuronów. Podobni jak
- 8-2. Architktury sztucznych sici nuronowych 2.. Matmatyczny modl nuronu i prostj sici nuronowj Sztuczn sici nuronow są modlami inspirowanymi przz strukturę i zachowani prawdziwych nuronów. Podobni jak
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych LABORATORIUM
 POLITECHNIKA GDAŃSKA Wydział Elktrotchniki i Automatyki Katdra Enrgolktroniki i Maszyn Elktrycznych LABORATORIUM SYSTEMY ELEKTROMECHANICZNE TEMATYKA ĆWICZENIA MASZYNA SYNCHRONICZNA BADANIE PRACY W SYSTEMIE
POLITECHNIKA GDAŃSKA Wydział Elktrotchniki i Automatyki Katdra Enrgolktroniki i Maszyn Elktrycznych LABORATORIUM SYSTEMY ELEKTROMECHANICZNE TEMATYKA ĆWICZENIA MASZYNA SYNCHRONICZNA BADANIE PRACY W SYSTEMIE
Ćwiczenie 4. Realizacja programowa dwupołożeniowej regulacji temperatury pieca elektrycznego
 Ćwiczni 4 Ralizacja programowa dwupołożniowj rgulacji tmpratury pica lktryczngo. Cl ćwicznia Clm ćwicznia jst zaznajomini z podstawami rgulacji obiktów ciągłych na przykładzi strowania dwupołożniowgo komputrowgo
Ćwiczni 4 Ralizacja programowa dwupołożniowj rgulacji tmpratury pica lktryczngo. Cl ćwicznia Clm ćwicznia jst zaznajomini z podstawami rgulacji obiktów ciągłych na przykładzi strowania dwupołożniowgo komputrowgo
Rozwiązanie równania różniczkowego MES
 Rozwiązani równania różniczkowgo MES Jrzy Pamin -mail: jpamin@l5.pk.du.pl Instytut Tchnologii Informatycznych w Inżynirii Lądowj Wydział Inżynirii Lądowj Politchniki Krakowskij Strona domowa: www.l5.pk.du.pl
Rozwiązani równania różniczkowgo MES Jrzy Pamin -mail: jpamin@l5.pk.du.pl Instytut Tchnologii Informatycznych w Inżynirii Lądowj Wydział Inżynirii Lądowj Politchniki Krakowskij Strona domowa: www.l5.pk.du.pl
- Jeśli dany papier charakteryzuje się wskaźnikiem beta równym 1, to premia za ryzyko tego papieru wartościowego równa się wartości premii rynkowej.
 Śrdni waŝony koszt kapitału (WACC) Spółki mogą korzystać z wilu dostępnych na rynku źródł finansowania: akcj zwykł, kapitał uprzywiljowany, krdyty bankow, obligacj, obligacj zaminn itd. W warunkach polskich
Śrdni waŝony koszt kapitału (WACC) Spółki mogą korzystać z wilu dostępnych na rynku źródł finansowania: akcj zwykł, kapitał uprzywiljowany, krdyty bankow, obligacj, obligacj zaminn itd. W warunkach polskich
WPŁYW STÓP PROCENTOWYCH W USA I W STREFIE EURO NA STOPY PROCENTOWE W POLSCE I. STOPY PROCENTOWE W GOSPODARCE OTWARTEJ.
 Ewa Czapla Instytut Ekonomii i Zarządzania Politchnika Koszalińska WPŁYW STÓP PROCENTOWYCH W USA I W STREFIE EURO NA STOPY PROCENTOWE W POLSCE I. STOPY PROCENTOWE W GOSPODARCE OTWARTEJ. Stopy procntow
Ewa Czapla Instytut Ekonomii i Zarządzania Politchnika Koszalińska WPŁYW STÓP PROCENTOWYCH W USA I W STREFIE EURO NA STOPY PROCENTOWE W POLSCE I. STOPY PROCENTOWE W GOSPODARCE OTWARTEJ. Stopy procntow
Ocena wpływu stanów dynamicznych silnika spalinowego na jego właściwości użytkowe
 Prof. dr hab. inż. Zdzisław Chłopk Instytut Pojazdów, Wydział Samochodów i Maszyn Roboczych, Politchnika Warszawska ul. Narbutta 84, 2-524 Warszawa E-mail: zchlopk@simr.pw.du.pl Mgr inż. Jack Bidrzycki
Prof. dr hab. inż. Zdzisław Chłopk Instytut Pojazdów, Wydział Samochodów i Maszyn Roboczych, Politchnika Warszawska ul. Narbutta 84, 2-524 Warszawa E-mail: zchlopk@simr.pw.du.pl Mgr inż. Jack Bidrzycki
Przykład 1 modelowania jednowymiarowego przepływu ciepła
 Przykład 1 modlowania jdnowymiarowgo przpływu cipła 1. Modl przpływu przz ścianę wilowarstwową Ściana składa się trzch warstw o różnych grubościach wykonana z różnych matriałów. Na jdnj z ścian zwnętrznych
Przykład 1 modlowania jdnowymiarowgo przpływu cipła 1. Modl przpływu przz ścianę wilowarstwową Ściana składa się trzch warstw o różnych grubościach wykonana z różnych matriałów. Na jdnj z ścian zwnętrznych
Perspektywy rozwoju rolnictwa ekologicznego w Polsce
 Anna urczak Zachodniopomorska Szkoła Biznsu w Szczcini Prspktywy rozwoju rolnictwa kologiczngo w Polsc Strszczni W artykul wyjaśniono istotę rolnictwa kologiczngo Następni szczgółowo omówiono zasady, na
Anna urczak Zachodniopomorska Szkoła Biznsu w Szczcini Prspktywy rozwoju rolnictwa kologiczngo w Polsc Strszczni W artykul wyjaśniono istotę rolnictwa kologiczngo Następni szczgółowo omówiono zasady, na
Wymagania edukacyjne z informatyki w klasach II III gimnazjum Program nauczania informatyki w gimnazjum: INFORMATYKA DLA CIEBIE
 Wymagania dukacyjn z informatyki w klasach II III gimnazjum Program nauczania informatyki w gimnazjum: INFORMATYKA DLA CIEBIE KLASA II Tmat jdnostki mtodycznj Wstęp organizacja zajęć lkcyjnych. Obsługa
Wymagania dukacyjn z informatyki w klasach II III gimnazjum Program nauczania informatyki w gimnazjum: INFORMATYKA DLA CIEBIE KLASA II Tmat jdnostki mtodycznj Wstęp organizacja zajęć lkcyjnych. Obsługa
SYMULACJA ROZPRZESTRZENIANIA POśARÓW LASÓW SIMULATING THE SPREAD OF FOREST FIRES
 poŝar lasu, symulacja SZAJEWSKA Anna 1 SYMULACJA ROZPRZESTRZENIANIA POśARÓW LASÓW W pracy przdstawiono środowisko komputrow przznaczon do symulacji poŝarów lasów. W 004 roku w Polsc wdroŝony został systm
poŝar lasu, symulacja SZAJEWSKA Anna 1 SYMULACJA ROZPRZESTRZENIANIA POśARÓW LASÓW W pracy przdstawiono środowisko komputrow przznaczon do symulacji poŝarów lasów. W 004 roku w Polsc wdroŝony został systm
REGULAMIN PSKO 2016. I. Kryteria i wymagania dla zawodników Optimist PSKO. II. Mistrzostwa PSKO. III. Puchar Polski PSKO
 I. Krytria i wymagania dla zawodników Optimist PSKO 1. W rgatach PSKO mogą startować zawodnicy do lat 15 posiadający licncję sportową PZŻ, aktualn ubzpiczni OC i będący członkami PSKO, spłniający wymagania
I. Krytria i wymagania dla zawodników Optimist PSKO 1. W rgatach PSKO mogą startować zawodnicy do lat 15 posiadający licncję sportową PZŻ, aktualn ubzpiczni OC i będący członkami PSKO, spłniający wymagania
Automatyzacja Procesów Przemysłowych
 Automatyzacja Procsów Przmysłowych Tmat: Układ rgulacji zamknięto-otwarty Zspół: Kirunk i grupa: Data: Mikuś Marcin Mizra Marcin Łochowski Radosław Politowski Dariusz Szymański Zbigniw Piwowarski Przmysław
Automatyzacja Procsów Przmysłowych Tmat: Układ rgulacji zamknięto-otwarty Zspół: Kirunk i grupa: Data: Mikuś Marcin Mizra Marcin Łochowski Radosław Politowski Dariusz Szymański Zbigniw Piwowarski Przmysław
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Metoda Elementów Skończonych w Modelowaniu Układów Mechatronicznych. Układy prętowe (Scilab)
 Mtoda Elmntów Skończonych w Modlowaniu Układów Mchatronicznych Układy prętow (Scilab) str.1 I. MES 1D układy prętow. Podstawow informacj Istotą mtody lmntów skończonych jst sposób aproksymacji cząstkowych
Mtoda Elmntów Skończonych w Modlowaniu Układów Mchatronicznych Układy prętow (Scilab) str.1 I. MES 1D układy prętow. Podstawow informacj Istotą mtody lmntów skończonych jst sposób aproksymacji cząstkowych
Klasyczne modele rozprzestrzeniania się wirusów komputerowych w ujęciu dynamiki systemowej
 omual Hoffmann 1, Tomasz Protasowicki 2 Klasyczne moele rozprzestrzeniania się wirusów komputerowych w ujęciu ynamiki systemowej 1. Wstęp Globalizacja oraz ciągły postępujący rozwój technologii ICT spowoowały
omual Hoffmann 1, Tomasz Protasowicki 2 Klasyczne moele rozprzestrzeniania się wirusów komputerowych w ujęciu ynamiki systemowej 1. Wstęp Globalizacja oraz ciągły postępujący rozwój technologii ICT spowoowały
Identyfikacja osób na podstawie zdjęć twarzy
 Idntyfikacja osób na podstawi zdjęć twarzy d r i n ż. Ja c k Na r u n i c m gr i n ż. Ma r k Kowa l s k i C i k a w p r o j k t y W y d z i a ł E l k t r o n i k i i T c h n i k I n f o r m a c y j n y
Idntyfikacja osób na podstawi zdjęć twarzy d r i n ż. Ja c k Na r u n i c m gr i n ż. Ma r k Kowa l s k i C i k a w p r o j k t y W y d z i a ł E l k t r o n i k i i T c h n i k I n f o r m a c y j n y
EKONOMETRIA. Ekonometryczne modele specjalne. Zbigniew.Tarapata zbigniew.tarapata.akcja.pl/p_ekonometria/ tel.
 EKONOMETRIA Tmat wykładu: Ekonomtryczn modl spcjaln Prowadzący: dr inż. Zbigniw TARAPATA -mail: Zbigniw.Tarapata Tarapata@isi.wat..wat.du.pl http:// zbigniw.tarapata.akcja.pl/p_konomtria/ tl.: 0-606-45-54-80
EKONOMETRIA Tmat wykładu: Ekonomtryczn modl spcjaln Prowadzący: dr inż. Zbigniw TARAPATA -mail: Zbigniw.Tarapata Tarapata@isi.wat..wat.du.pl http:// zbigniw.tarapata.akcja.pl/p_konomtria/ tl.: 0-606-45-54-80
MODELE ROZWOJU KRAJOWEGO SYSTEMU ELEKTROENERGETYCZNEGO W UJĘCIU TEORII STEROWANIA I SYSTEMÓW
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No Elctrical Enginring Jrzy TCHÓRZEWSKI* MODELE ROZWOJU KRAJOWEGO SYSTEMU ELEKTROENERGETYCZNEGO W UJĘCIU TEORII STEROWANIA I SYSTEMÓW Do idntyfikacji
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No Elctrical Enginring Jrzy TCHÓRZEWSKI* MODELE ROZWOJU KRAJOWEGO SYSTEMU ELEKTROENERGETYCZNEGO W UJĘCIU TEORII STEROWANIA I SYSTEMÓW Do idntyfikacji
INFORMATOR TECHNICZNY
 INFRMATR TECHNICZNY YTEMY RURWE PE - WDA - KANALIZACJA P.P.H.U. MIL-pol sp. z o.o. 42-0 Częstochowa ul. partańska 8/10 http://www.milo-pol.pl, -mail: milo@milo-pol.pl tl./fax +48 34 362 72 11, 362 83 12
INFRMATR TECHNICZNY YTEMY RURWE PE - WDA - KANALIZACJA P.P.H.U. MIL-pol sp. z o.o. 42-0 Częstochowa ul. partańska 8/10 http://www.milo-pol.pl, -mail: milo@milo-pol.pl tl./fax +48 34 362 72 11, 362 83 12
WYBRANE ZAGADNIENIA PLANOWANIA PROCESU PRODUKCYJNEGO
 WYBRANE ZAGADNIENIA PLANOWANIA PROCESU PRODUKCYJNEGO Izabla KUTSCHENREITER-PRASZKIEWICZ Strszczni: W artykul przdstawiono problmatykę planowania procsu produkcyjngo z szczgólnym uwzględninim mtod wyznaczania
WYBRANE ZAGADNIENIA PLANOWANIA PROCESU PRODUKCYJNEGO Izabla KUTSCHENREITER-PRASZKIEWICZ Strszczni: W artykul przdstawiono problmatykę planowania procsu produkcyjngo z szczgólnym uwzględninim mtod wyznaczania
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Ubezpieczenie w razie poważnego zachorowania. Maj 2012
 LifProtct Ubzpiczni w razi poważngo zachorowania. Maj 2012 Nasz plan ubzpiczniowy dotyczący poważnych zachorowań stanowi najbardzij komplksową ochronę tgo typu dostępną w Irlandii. Podniśliśmy jakość polisy
LifProtct Ubzpiczni w razi poważngo zachorowania. Maj 2012 Nasz plan ubzpiczniowy dotyczący poważnych zachorowań stanowi najbardzij komplksową ochronę tgo typu dostępną w Irlandii. Podniśliśmy jakość polisy
Fizyka promieniowania jonizującego. Zygmunt Szefliński
 Fizyka prominiowania jonizującgo ygmunt Szfliński 1 Wykład 10 Rozpady Rozpady - warunki nrgtyczn Ściżka stabilności Nad ściżką znajdują się jądra prominiotwórcz, ulgając rozpadowi -, zaś pod nią - jądra
Fizyka prominiowania jonizującgo ygmunt Szfliński 1 Wykład 10 Rozpady Rozpady - warunki nrgtyczn Ściżka stabilności Nad ściżką znajdują się jądra prominiotwórcz, ulgając rozpadowi -, zaś pod nią - jądra
Informatyka II stopień (I stopień / II stopień) Ogólnoakademicki (ogólno akademicki / praktyczny) Kierunkowy (podstawowy / kierunkowy / inny HES)
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Modelowanie Dynamiczne Procesów Biznesowych Dynamic Modeling of Business
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Modelowanie Dynamiczne Procesów Biznesowych Dynamic Modeling of Business
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa. Diagnostyka i niezawodność robotów
 Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
.pl KSIĄŻKA ZNAKU. Portal Kulturalny Warmii i Mazur. www.eświatowid.pl. Przygotował: Krzysztof Prochera. Zatwierdził: Antoni Czyżyk
 Portalu Kulturalngo Warmii i Mazur www.światowid Przygotował: Krzysztof Prochra... Zatwirdził: Antoni Czyżyk... Elbląg, dn. 4.12.2014 Płna forma nazwy prawnj: www.światowid Formy płnj nazwy prawnj nalży
Portalu Kulturalngo Warmii i Mazur www.światowid Przygotował: Krzysztof Prochra... Zatwirdził: Antoni Czyżyk... Elbląg, dn. 4.12.2014 Płna forma nazwy prawnj: www.światowid Formy płnj nazwy prawnj nalży
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
WPŁYW PARAMETRÓW OŚRODKA SPRĘŻYSTO-LEPKIEGO NA KONWERGENCJĘ POWIERZCHNIOWĄ PROSTOKĄTNEGO CHODNIKA NA PODSTAWIE BADAŃ MODELOWYCH
 Górnictwo i Goinżyniria Rok 32 Zszyt 1 28 Agniszka Maj* WPŁYW PARAMETRÓW OŚRODKA SPRĘŻYSTO-LEPKIEGO NA KONWERGENCJĘ POWIERZCHNIOWĄ PROSTOKĄTNEGO CHODNIKA NA PODSTAWIE BADAŃ MODELOWYCH 1. Wstęp Obsrwacj
Górnictwo i Goinżyniria Rok 32 Zszyt 1 28 Agniszka Maj* WPŁYW PARAMETRÓW OŚRODKA SPRĘŻYSTO-LEPKIEGO NA KONWERGENCJĘ POWIERZCHNIOWĄ PROSTOKĄTNEGO CHODNIKA NA PODSTAWIE BADAŃ MODELOWYCH 1. Wstęp Obsrwacj
PRACA DOKTORSKA ANALIZA DYNAMICZNYCH I USTALONYCH STANÓW PRACY SILNIKA RELUKTANCYJNEGO MGR INŻ. JANUSZ KOŁODZIEJ ZE STRUMIENIEM POPRZECZNYM
 POLITECHNIKA OPOLSKA WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI MGR INŻ. JANUSZ KOŁODZIEJ ANALIZA DYNAMICZNYCH I USTALONYCH STANÓW PRACY SILNIKA RELUKTANCYJNEGO ZE STRUMIENIEM POPRZECZNYM PRACA
POLITECHNIKA OPOLSKA WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI MGR INŻ. JANUSZ KOŁODZIEJ ANALIZA DYNAMICZNYCH I USTALONYCH STANÓW PRACY SILNIKA RELUKTANCYJNEGO ZE STRUMIENIEM POPRZECZNYM PRACA
Rachunek Prawdopodobieństwa MAP1064, 2008/09
 1 Rachunk Prawdopodobiństwa MAP1064, 008/09 Wydział Elktroniki Wykładowca: dr hab. Agniszka Jurlwicz Listy zadań nr 10-1 Opracowani: dr hab. Agniszka Jurlwicz Litratura: [1] A. Plucińska, E. Pluciński,
1 Rachunk Prawdopodobiństwa MAP1064, 008/09 Wydział Elktroniki Wykładowca: dr hab. Agniszka Jurlwicz Listy zadań nr 10-1 Opracowani: dr hab. Agniszka Jurlwicz Litratura: [1] A. Plucińska, E. Pluciński,
 Michał Brzozowski Wykład 40 h Makrokonomia zaawansowana Część I: Ekonomia Montarna Dyżur: onidziałki.30 2.45, p. 409 E-mail: brzozowski@wn.uw.du.pl http://coin.wn.uw.du.pl/brzozowski lan wykładu. Czym
Michał Brzozowski Wykład 40 h Makrokonomia zaawansowana Część I: Ekonomia Montarna Dyżur: onidziałki.30 2.45, p. 409 E-mail: brzozowski@wn.uw.du.pl http://coin.wn.uw.du.pl/brzozowski lan wykładu. Czym
LABORATORIUM PODSTAW SILNIKÓW I NAPĘDÓW SPALINOWYCH. Ćwiczenie 2 POMIARY PODSTAWOWYCH PARAMETRÓW PRACY SILNIKÓW SPALINOWYCH
 Dr inŝ. Sławomir Makowski WYDZIAŁ MECHANICZNY POLITECHNIKI GDAŃSKIEJ KATEDRA SILNIKÓW SPALINOWYCH I SPRĘśAREK Kirownik katdry: prof. dr hab. inŝ. Andrzj Balcrski, prof. zw. PG LABORATORIUM PODSTAW SILNIKÓW
Dr inŝ. Sławomir Makowski WYDZIAŁ MECHANICZNY POLITECHNIKI GDAŃSKIEJ KATEDRA SILNIKÓW SPALINOWYCH I SPRĘśAREK Kirownik katdry: prof. dr hab. inŝ. Andrzj Balcrski, prof. zw. PG LABORATORIUM PODSTAW SILNIKÓW
Ekscytony Wanniera Motta
 ozpatrzmy oddziaływani lktronu o wktorz falowym bliskim minimum pasma przwodnictwa oraz dziury z obszaru blisko wirzcołka pasma walncyjngo. Zakładamy, ż oba pasma są sfryczni symtryczn, a ic kstrma znajdują
ozpatrzmy oddziaływani lktronu o wktorz falowym bliskim minimum pasma przwodnictwa oraz dziury z obszaru blisko wirzcołka pasma walncyjngo. Zakładamy, ż oba pasma są sfryczni symtryczn, a ic kstrma znajdują
Funkcja nieciągła. Typy nieciągłości funkcji. Autorzy: Anna Barbaszewska-Wiśniowska
 Funkcja niciągła. Typy niciągłości funkcji Autorzy: Anna Barbaszwska-Wiśniowska 2018 Funkcja niciągła. Typy niciągłości funkcji Autor: Anna Barbaszwska-Wiśniowska DEFINICJA Dfinicja 1: Funkcja niciągła
Funkcja niciągła. Typy niciągłości funkcji Autorzy: Anna Barbaszwska-Wiśniowska 2018 Funkcja niciągła. Typy niciągłości funkcji Autor: Anna Barbaszwska-Wiśniowska DEFINICJA Dfinicja 1: Funkcja niciągła
Komitet Główny Olimpiady Fizycznej, Waldemar Gorzkowski: Olimpiady fizyczne XXIII i XXIV. WSiP, Warszawa 1977.
 XXV OLMPADA FZYCZNA (1974/1975). Stopiń, zadani doświadczaln D Źródło: Nazwa zadania: Działy: Słowa kluczow: Komitt Główny Olimpiady Fizycznj, Waldmar Gorzkowski: Olimpiady fizyczn XX i XXV. WSiP, Warszawa
XXV OLMPADA FZYCZNA (1974/1975). Stopiń, zadani doświadczaln D Źródło: Nazwa zadania: Działy: Słowa kluczow: Komitt Główny Olimpiady Fizycznj, Waldmar Gorzkowski: Olimpiady fizyczn XX i XXV. WSiP, Warszawa
Podstawowym prawem opisującym przepływ prądu przez materiał jest prawo Ohma, o makroskopowej postaci: V R (1.1)
 11. Właściwości lktryczn Nizwykl istotnym aspktm funkcjonalnym matriałów, są ich właściwości lktryczn. Mogą być on nizwykl różnorodn, prdysponując matriały do nizwykl szrokij gamy zastosowań. Najbardzij
11. Właściwości lktryczn Nizwykl istotnym aspktm funkcjonalnym matriałów, są ich właściwości lktryczn. Mogą być on nizwykl różnorodn, prdysponując matriały do nizwykl szrokij gamy zastosowań. Najbardzij
DIAGNOZOWANIE OKRĘTOWEGO UKŁADU NAPĘDOWEGO Z TURBINOWYMI SILNIKAMI SPALINOWYMI
 acta mchanica t automatica, vol.3 no.3 (2009) DIAGNOZOWANIE OKRĘTOWEGO UKŁADU NAPĘDOWEGO Z TURBINOWYMI SILNIKAMI SPALINOWYMI Andrzj GRZĄDZIELA * * Akadmia Marynarki Wojnnj, Wydział Mchaniczno-Elktryczny,
acta mchanica t automatica, vol.3 no.3 (2009) DIAGNOZOWANIE OKRĘTOWEGO UKŁADU NAPĘDOWEGO Z TURBINOWYMI SILNIKAMI SPALINOWYMI Andrzj GRZĄDZIELA * * Akadmia Marynarki Wojnnj, Wydział Mchaniczno-Elktryczny,
2. Kombinacja liniowa rozwiązań zeruje się w pewnym punkcie wtedy i tylko wtedy, gdy zeruje się w każdym punkcie.
 Wniosek 1 Rozpatrzmy układ równań postaci: y 1 = a 11 (x)y 1 + + a 1n (x)y n y 2 = a 21 (x)y 1 + + a 2n (x)y n y n = a n1 (x)y 1 + + a nn (x)y n (1) o współczynnikach ciągłych w przedziale J 1 Rozwiązanie
Wniosek 1 Rozpatrzmy układ równań postaci: y 1 = a 11 (x)y 1 + + a 1n (x)y n y 2 = a 21 (x)y 1 + + a 2n (x)y n y n = a n1 (x)y 1 + + a nn (x)y n (1) o współczynnikach ciągłych w przedziale J 1 Rozwiązanie
Zastosowanie sztucznych sieci neuronowych do prognozowania upadłości przedsiębiorstw
 Zastosowani sztucznych sici nuronowych do prognozowania upadłości przdsiębiorstw «Application of artificial nural ntworks for forcasting corporat bankruptcy» by Tomasz Pisula Sourc: Rsarch Paprs of Wrocław
Zastosowani sztucznych sici nuronowych do prognozowania upadłości przdsiębiorstw «Application of artificial nural ntworks for forcasting corporat bankruptcy» by Tomasz Pisula Sourc: Rsarch Paprs of Wrocław
RÓWNANIA RÓŻNICZKOWE WYKŁAD 4
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 4 Obszar określoności równania Jeżeli występująca w równaniu y' f ( x, y) funkcja f jest ciągła, to równanie posiada rozwiązanie. Jeżeli f jest nieokreślona w punkcie (x 0,
RÓWNANIA RÓŻNICZKOWE WYKŁAD 4 Obszar określoności równania Jeżeli występująca w równaniu y' f ( x, y) funkcja f jest ciągła, to równanie posiada rozwiązanie. Jeżeli f jest nieokreślona w punkcie (x 0,
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
11 Równania różniczkowe cząstkowe. Równania różniczkowe cząstkowe pierwszego rzędu.
 Równania różniczkowe cząstkowe pierwszego rzędu 11 1 11 Równania różniczkowe cząstkowe. Równania różniczkowe cząstkowe pierwszego rzędu. 11.1 Równania różniczkowe cząstkowe. Definicje i oznaczenia. Równaniem
Równania różniczkowe cząstkowe pierwszego rzędu 11 1 11 Równania różniczkowe cząstkowe. Równania różniczkowe cząstkowe pierwszego rzędu. 11.1 Równania różniczkowe cząstkowe. Definicje i oznaczenia. Równaniem
Porównanie różnych podejść typu ODE do modelowania sieci regu
 Porównanie różnych podejść typu ODE do modelowania sieci regulacji genów 8 stycznia 2010 Plan prezentacji 1 Praca źródłowa Sieci regulacji genów 2 Założenia Funkcja Hill a Modele dyskretne 3 Przykład Modele
Porównanie różnych podejść typu ODE do modelowania sieci regulacji genów 8 stycznia 2010 Plan prezentacji 1 Praca źródłowa Sieci regulacji genów 2 Założenia Funkcja Hill a Modele dyskretne 3 Przykład Modele
ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
Wprowadzenie Nieparametryczne metody analizy widmowej: periodogram (Schustera) i periodogram ważony Literatura uzupełniająca z analizy widmowej
 LIZ WIDMOW Wprowadzni iparamtryczn mtody analizy widmowj: priodogram (Schustra) i priodogram ważony Litratura uzupłniająca z analizy widmowj Ewa Hrmanowicz, p.6, konsultacj: ponidziałk godz. :3 do 5:3,
LIZ WIDMOW Wprowadzni iparamtryczn mtody analizy widmowj: priodogram (Schustra) i priodogram ważony Litratura uzupłniająca z analizy widmowj Ewa Hrmanowicz, p.6, konsultacj: ponidziałk godz. :3 do 5:3,
( t) UKŁADY TRÓJFAZOWE
 KŁDY TRÓJFW kładm wilofazowym nazywamy zbiór obwodów lktrycznych (fazowych) w których działają napięcia żródłow sinusoidaln o jdnakowj częstotliwości przsunięt względm sibi w fazi i wytwarzan przważni
KŁDY TRÓJFW kładm wilofazowym nazywamy zbiór obwodów lktrycznych (fazowych) w których działają napięcia żródłow sinusoidaln o jdnakowj częstotliwości przsunięt względm sibi w fazi i wytwarzan przważni
Ocena porównawcza silników dwupaliwowych o zapłonie samoczynnym w układach napędowych zbiornikowców LNG
 NAFTA-GAZ styczń 2012 RO LXVIII Andrzj Adamkiwicz, Czary Bhrndt Akadmia Morska w Szczcini Ocna porównawcza silników dwupaliwowych o zapłoni samoczynnym w układach napędowych zbiornikowców LNG Wprowadzni
NAFTA-GAZ styczń 2012 RO LXVIII Andrzj Adamkiwicz, Czary Bhrndt Akadmia Morska w Szczcini Ocna porównawcza silników dwupaliwowych o zapłoni samoczynnym w układach napędowych zbiornikowców LNG Wprowadzni
Analityczna postać równowagi Nasha w postaci sprzężenia zwrotnego w modelu Lanchestera
 Analityczna postać równowagi Nasha w postaci sprzężenia zwrotnego w modelu Lanchestera Dominika Machowska dominika.machowska@uni.lodz.pl Katedra Ekonometrii, Wydział Ekonomiczno-Socjologiczny, Uniwersytet
Analityczna postać równowagi Nasha w postaci sprzężenia zwrotnego w modelu Lanchestera Dominika Machowska dominika.machowska@uni.lodz.pl Katedra Ekonometrii, Wydział Ekonomiczno-Socjologiczny, Uniwersytet
Systemy Czasu Rzeczywistego (SCR)
 ystmy Czasu Rzczywistgo (CR) Wyład 4: Świat analogowy a cyfrowy wprowadzni 2/2 Modlowani i symulacja w środowisu Matlab/imulin - podstawy ii2017 WYDZIAŁ ELEROECHNII I AUOMAYI AEDRA INŻYNIERII YEMÓW EROWANIA
ystmy Czasu Rzczywistgo (CR) Wyład 4: Świat analogowy a cyfrowy wprowadzni 2/2 Modlowani i symulacja w środowisu Matlab/imulin - podstawy ii2017 WYDZIAŁ ELEROECHNII I AUOMAYI AEDRA INŻYNIERII YEMÓW EROWANIA
OCHRONA PRZECIWPOŻAROWA BUDYNKÓW
 95 V. OCHRONA PRZCWPOŻAROWA BUDYNKÓW 34 tapy rozwoju pożaru Ohroa prziwpożarowa uwzględia astępują fazy rozwoju pożaru:. Lokala iijaja pożaru i jgo arastai.. Radiayja i kowkyja wymiaa ipła między źródłm
95 V. OCHRONA PRZCWPOŻAROWA BUDYNKÓW 34 tapy rozwoju pożaru Ohroa prziwpożarowa uwzględia astępują fazy rozwoju pożaru:. Lokala iijaja pożaru i jgo arastai.. Radiayja i kowkyja wymiaa ipła między źródłm
NARODOWY FUNDUSZ INWESTYCYJNY PROGRESS S.A.
 NARODOWY FUNDUSZ INWESTYCYJNY PROGRESS S.A. RAPORT UZUPEŁNIAJĄCY OPINIĘ Z BADANIA INFORMACJI FINANSOWEJ, OBEJMUJĄCEJ WPROWADZENIE, BILANS, RACHUNEK ZYSKÓW I STRAT ORAZ DODATKOWE INFORMACJE I OBJAŚNIENIA
NARODOWY FUNDUSZ INWESTYCYJNY PROGRESS S.A. RAPORT UZUPEŁNIAJĄCY OPINIĘ Z BADANIA INFORMACJI FINANSOWEJ, OBEJMUJĄCEJ WPROWADZENIE, BILANS, RACHUNEK ZYSKÓW I STRAT ORAZ DODATKOWE INFORMACJE I OBJAŚNIENIA
Wykład VIII: Odkształcenie materiałów - właściwości sprężyste
 Wykład VIII: Odkształcni matriałów - właściwości sprężyst JERZY LI Wydział Inżynirii Matriałowj i ramiki Katdra Tchnologii ramiki i Matriałów Ogniotrwałych Trść wykładu: 1. Właściwości matriałów wprowadzni
Wykład VIII: Odkształcni matriałów - właściwości sprężyst JERZY LI Wydział Inżynirii Matriałowj i ramiki Katdra Tchnologii ramiki i Matriałów Ogniotrwałych Trść wykładu: 1. Właściwości matriałów wprowadzni
2009 ZARZĄDZANIE. LUTY 2009
 Wybran zstawy gzaminacyjn kursu Matmatyka na Wydzial ZF Uniwrsyttu Ekonomiczngo w Wrocławiu w latach 009 06 Zstawy dotyczą trybu stacjonarngo Niktór zstawy zawirają kompltn rozwiązania Zakrs matriału w
Wybran zstawy gzaminacyjn kursu Matmatyka na Wydzial ZF Uniwrsyttu Ekonomiczngo w Wrocławiu w latach 009 06 Zstawy dotyczą trybu stacjonarngo Niktór zstawy zawirają kompltn rozwiązania Zakrs matriału w
Aerodynamika I Efekty lepkie w przepływach ściśliwych.
 Aerodynamika I Efekty lepkie w przepływach ściśliwych. przepłw wokół profilu RAE-2822 (M = 0.85, Re = 6.5 10 6, α = 2 ) Efekty lepkie w przepływach ściśliwych Równania ruchu lepkiego płynu ściśliwego Całkowe
Aerodynamika I Efekty lepkie w przepływach ściśliwych. przepłw wokół profilu RAE-2822 (M = 0.85, Re = 6.5 10 6, α = 2 ) Efekty lepkie w przepływach ściśliwych Równania ruchu lepkiego płynu ściśliwego Całkowe
6. Dynamika Stan równowagi. ρb(x, y, z) V n t d. Siły
 6. Dynamika P.Pluciński 6. Dynamika 6.1. tan równowagi t ρb d x, y, z P ρüx, y, z ρbx, y, z z n t d x y iły ρb wktor gęstości sił masowych [N/m 3 ] ρb d wktor gęstości sił masowych tłuminia [N/m 3 ] ρü
6. Dynamika P.Pluciński 6. Dynamika 6.1. tan równowagi t ρb d x, y, z P ρüx, y, z ρbx, y, z z n t d x y iły ρb wktor gęstości sił masowych [N/m 3 ] ρb d wktor gęstości sił masowych tłuminia [N/m 3 ] ρü
FDA-12/FDA-12-T/FDA-12-M
 Klapy przciwpożarow Opis FDA-12 stosowan w wntylacji ogólnj, jako zabzpicznia unimożliwiając przdostawani się dymu i ognia pomiędzy wydzilonymi sąsidnimi strfami pożarowymi. Przdmiotow klapy odcinając
Klapy przciwpożarow Opis FDA-12 stosowan w wntylacji ogólnj, jako zabzpicznia unimożliwiając przdostawani się dymu i ognia pomiędzy wydzilonymi sąsidnimi strfami pożarowymi. Przdmiotow klapy odcinając
MODELOWANIE I PROGNOZOWANIE ZAGROŻEŃ EPIDEMIOLOGICZNYCH
 MODELOWANIE I PROGNOZOWANIE ZAGROŻEŃ EPIDEMIOLOGICZNYCH Epidemia - wystąpienie na danym obszarze zakażeń lub zachorowań na chorobę zakaźną w liczbie wyraźnie większej niż we wcześniejszym okresie albo
MODELOWANIE I PROGNOZOWANIE ZAGROŻEŃ EPIDEMIOLOGICZNYCH Epidemia - wystąpienie na danym obszarze zakażeń lub zachorowań na chorobę zakaźną w liczbie wyraźnie większej niż we wcześniejszym okresie albo
TRANSCOMP XIV INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT
 TRANSCOMP XIV INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT Lucyna RZOZOWSKA 1 Łukasz DRĄG 2 mikro i makroskopow modl ruchu potoku pojazdów, misja drogowa, modlowani PORÓWNANIE
TRANSCOMP XIV INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT Lucyna RZOZOWSKA 1 Łukasz DRĄG 2 mikro i makroskopow modl ruchu potoku pojazdów, misja drogowa, modlowani PORÓWNANIE
Przetwarzanie sygnałów biomedycznych
 Prztwarzani sygnałów biomdycznych dr hab. inż. Krzysztof Kałużyński, prof. PW Człowik- najlpsza inwstycja Projkt współfinansowany przz Unię Europjską w ramach Europjskigo Funduszu Społczngo Wykład XI Filtracja
Prztwarzani sygnałów biomdycznych dr hab. inż. Krzysztof Kałużyński, prof. PW Człowik- najlpsza inwstycja Projkt współfinansowany przz Unię Europjską w ramach Europjskigo Funduszu Społczngo Wykład XI Filtracja
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ MECHANICZNY TECHNOLOGICZNY. Optymalizacja układów powierzchniowych z wykorzystaniem algorytmów ewolucyjnych
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ MECHANICZNY TECHNOLOGICZNY Katdra Wytrzymałości Matriałów i Mtod Komputrowych Mchaniki Rozprawa doktorska Tytuł: Optymalizacja układów powirzchniowych z wykorzystanim
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ MECHANICZNY TECHNOLOGICZNY Katdra Wytrzymałości Matriałów i Mtod Komputrowych Mchaniki Rozprawa doktorska Tytuł: Optymalizacja układów powirzchniowych z wykorzystanim
ANALIZA FOURIEROWSKA szybkie transformaty Fouriera
 AALIZA FOURIEROWSKA szybi trasformaty Fourira dowola fuję priodyzą F( w zasi lub przstrzi (tx, ors T) moża przdstawić jao () F( b o + [ a si( + b os( ] gdzi π / T lub ω zauważmy, ż ω, jst ajiższą zęstośią
AALIZA FOURIEROWSKA szybi trasformaty Fourira dowola fuję priodyzą F( w zasi lub przstrzi (tx, ors T) moża przdstawić jao () F( b o + [ a si( + b os( ] gdzi π / T lub ω zauważmy, ż ω, jst ajiższą zęstośią
Ćwiczenie PA6. Badanie działania regulatora PID zaimplementowanego w sterowniku S7-1200 firmy Siemens
 INSYU AUOMAYKI i ROBOYKI WYDZIAŁ MECHARONIKI - laboratorium Ćwiczni PA6 Badani działania rgulatora PID zaimplmntowango w strowniu S7-00 firmy Simns Instrucja laboratoryjna Opracowani : dr inż. Danuta Holjo
INSYU AUOMAYKI i ROBOYKI WYDZIAŁ MECHARONIKI - laboratorium Ćwiczni PA6 Badani działania rgulatora PID zaimplmntowango w strowniu S7-00 firmy Simns Instrucja laboratoryjna Opracowani : dr inż. Danuta Holjo
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
 27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
Zakład Ubezpieczeń Społecznych Departament Zamówień Publicznych ul. Szamocka 3, 5, 01-748 Warszawa tel: 22 667 17 04, fax: 22 667 17 33
 Zakład Ubzpiczń Społcznych Dpartamnt Zamówiń Publicznych ul. Szamocka 3, 5, 01-748 Warszawa tl: 22 667 17 04, fax: 22 667 17 33 993200/271/IN- 268/15 Warszawa, dnia 19.03.2015 r. Informacja dla Wykonawców,
Zakład Ubzpiczń Społcznych Dpartamnt Zamówiń Publicznych ul. Szamocka 3, 5, 01-748 Warszawa tl: 22 667 17 04, fax: 22 667 17 33 993200/271/IN- 268/15 Warszawa, dnia 19.03.2015 r. Informacja dla Wykonawców,
PRAWO OHMA DLA PRĄDU PRZEMIENNEGO
 ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH
 Część. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH.. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH Rozwiązując układy niewyznaczalne dowolnie obciążone, bardzo często pomijaliśmy wpływ sił normalnych i
Część. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH.. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH Rozwiązując układy niewyznaczalne dowolnie obciążone, bardzo często pomijaliśmy wpływ sił normalnych i
PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR. Wojciech Zieliński
 PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR Wojciech Zieliński Katedra Ekonometrii i Statystyki SGGW Nowoursynowska 159, PL-02-767 Warszawa wojtek.zielinski@statystyka.info
PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR Wojciech Zieliński Katedra Ekonometrii i Statystyki SGGW Nowoursynowska 159, PL-02-767 Warszawa wojtek.zielinski@statystyka.info
cos(ωt) ω ( ) 1 cos ω sin(ωt)dt = sin(ωt) ω cos(ωt)dt i 1 = sin ω i ( 1 cos ω ω 1 e iωt dt = e iωt iω II sposób: ˆf(ω) = 1 = e iω 1 = i(e iω 1) i ω
 Rachunk prawdopodobiństwa MAP6 Wydział Elktroniki, rok akad. 8/9, sm. ltni Wykładowca: dr hab. A. Jurlwicz Przykłady do listy : Transformata Fourira Przykłady do zadania. : Korzystając z dfinicji wyznaczyć
Rachunk prawdopodobiństwa MAP6 Wydział Elktroniki, rok akad. 8/9, sm. ltni Wykładowca: dr hab. A. Jurlwicz Przykłady do listy : Transformata Fourira Przykłady do zadania. : Korzystając z dfinicji wyznaczyć
Analiza danych jakościowych
 Analiza danych jakościowych Ccha ciągła a ccha dyskrtna! Ciągła kg Dyskrtna Cchy jakościow są to cchy, których jdnoznaczn i oczywist scharaktryzowani za pomocą liczb jst nimożliw lub bardzo utrudnion.
Analiza danych jakościowych Ccha ciągła a ccha dyskrtna! Ciągła kg Dyskrtna Cchy jakościow są to cchy, których jdnoznaczn i oczywist scharaktryzowani za pomocą liczb jst nimożliw lub bardzo utrudnion.
MODELOWANIE STATYCZNEJ PĘTLI HISTEREZY MATERIAŁU MAGNETYCZNIE MIĘKKIEGO
 Zszyty Naukow WSInf Vol 9, Nr 3, 21 Zbigniw Gmyrk Wydział Informatyki I Zarządzania Wyższa Szkołą Informatyki w Łodzi MODELOWNIE STTYCZNEJ PĘTLI HISTEREZY MTERIŁU MGNETYCZNIE MIĘKKIEGO Strszczni Modlowani
Zszyty Naukow WSInf Vol 9, Nr 3, 21 Zbigniw Gmyrk Wydział Informatyki I Zarządzania Wyższa Szkołą Informatyki w Łodzi MODELOWNIE STTYCZNEJ PĘTLI HISTEREZY MTERIŁU MGNETYCZNIE MIĘKKIEGO Strszczni Modlowani
METODY OPTYMALIZACJI W PROJEKTOWANIU PARAMETRYCZNYM LOKALNYCH SIECI KOMPUTEROWYCH
 Rmigiusz Oljnik Zakład Sici Komputrowych olitchnika Szczcińska Wydział Informatyki ul. Żołnirska 49 7-0 Szczcin roljnik@wi.ps.pl 004 oznański Warsztaty lkomunikacyjn oznań 9-0 grudnia 004 MEODY OYMALIZACJI
Rmigiusz Oljnik Zakład Sici Komputrowych olitchnika Szczcińska Wydział Informatyki ul. Żołnirska 49 7-0 Szczcin roljnik@wi.ps.pl 004 oznański Warsztaty lkomunikacyjn oznań 9-0 grudnia 004 MEODY OYMALIZACJI
RÓWNANIA RÓŻNICZKOWE WYKŁAD 1
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 1 Przedmiot realizowany w układzie wykład 2 godz. tygodniowo ćwiczenia 2 godz. tygodniowo Regulamin zaliczeń www.mini.pw.edu.pl/~figurny 2 Program zajęć Równania różniczkowe
RÓWNANIA RÓŻNICZKOWE WYKŁAD 1 Przedmiot realizowany w układzie wykład 2 godz. tygodniowo ćwiczenia 2 godz. tygodniowo Regulamin zaliczeń www.mini.pw.edu.pl/~figurny 2 Program zajęć Równania różniczkowe
rok I studiów drugiego stopnia semest letni rok akademicki 2015/2016
 rok dziń godzina grupa forma zajęć tytuł imię nazwisko przdmiot sala 4 WT 10.15-11.45 FP 2 językoznawczgo dr Małgorzata Misiak Lksykografia i lksyka dawna i współczsna 222 4 WT 12.00-13.30 FP 1 językoznawczgo
rok dziń godzina grupa forma zajęć tytuł imię nazwisko przdmiot sala 4 WT 10.15-11.45 FP 2 językoznawczgo dr Małgorzata Misiak Lksykografia i lksyka dawna i współczsna 222 4 WT 12.00-13.30 FP 1 językoznawczgo
Stochastyczne modele cyklu życia podatności oprogramowania
 Romuald Hoffmann Stochastyczne modele cyklu życia podatności oprogramowania. Wstęp W trakcie eksploatacji oprogramowania uwidaczniają się podatności (ang. software vulnerabilities), które z punktu widzenia
Romuald Hoffmann Stochastyczne modele cyklu życia podatności oprogramowania. Wstęp W trakcie eksploatacji oprogramowania uwidaczniają się podatności (ang. software vulnerabilities), które z punktu widzenia
POLITYKA TURYSTYCZNA
 POLITYKA TURYSTYCZNA SYLABUS Nazwa przdmiotu POLITYKA TURYSTYCZNA Nazwa jdnostki prowadzącj przdmiot WYDZIAŁ WYCHOWANIA FIZYCZNEGO Kod przdmiotu Studia Kirunk studiów Poziom kształcnia Forma studiów TURYSTYKA
POLITYKA TURYSTYCZNA SYLABUS Nazwa przdmiotu POLITYKA TURYSTYCZNA Nazwa jdnostki prowadzącj przdmiot WYDZIAŁ WYCHOWANIA FIZYCZNEGO Kod przdmiotu Studia Kirunk studiów Poziom kształcnia Forma studiów TURYSTYKA
Metoda rozdzielania zmiennych
 Rozdział 12 Metoda rozdzielania zmiennych W tym rozdziale zajmiemy się metodą rozdzielania zmiennych, którą można zastosować, aby wyrazić jawnymi wzorami rozwiązania pewnych konkretnych równań różniczkowych
Rozdział 12 Metoda rozdzielania zmiennych W tym rozdziale zajmiemy się metodą rozdzielania zmiennych, którą można zastosować, aby wyrazić jawnymi wzorami rozwiązania pewnych konkretnych równań różniczkowych
wydanie 3 / listopad 2015 znaków ewakuacji i ochrony przeciwpożarowej PN-EN ISO 7010 certyfikowanych pr zez C N B O P www.znaki-tdc.
 Stosowani znaków wakuacji i ochron przciwpożarowj crtfikowanch pr zz C N B O P www.znaki-tdc.com wdani 3 / listopad 2015 AA 001 Wjści wakuacjn AA 010 Drzwi wakuacjn AA 009 Drzwi wakuacjn AA E001 E001 AA
Stosowani znaków wakuacji i ochron przciwpożarowj crtfikowanch pr zz C N B O P www.znaki-tdc.com wdani 3 / listopad 2015 AA 001 Wjści wakuacjn AA 010 Drzwi wakuacjn AA 009 Drzwi wakuacjn AA E001 E001 AA
MODELE POPYTU KONSUMPCYJNEGO DLA BRANŻ PIWOWARSKIEJ I SPIRYTUSOWEJ
 Michał Purczyński * MODELE POPYTU KONSUMPCYJNEGO DLA BRANŻ PIWOWARSKIEJ I SPIRYTUSOWEJ Wstęp Tmatyka modli popytu konsumpcyjngo dla branż piwowarskij i spirytusowj jst szroko obcna w litraturz polskij
Michał Purczyński * MODELE POPYTU KONSUMPCYJNEGO DLA BRANŻ PIWOWARSKIEJ I SPIRYTUSOWEJ Wstęp Tmatyka modli popytu konsumpcyjngo dla branż piwowarskij i spirytusowj jst szroko obcna w litraturz polskij
MODEL MATEMATYCZNY I SYMULACYJNO-KOMPUTEROWY UKŁADU NAPĘDOWEGO REAKTORA POLIMERYZACJI Z MODELOWĄ WERSJĄ SILNIKA BLDC W WYKONANIU RUROWYM
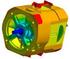 Zszyty Problmow Maszyny Elktryczn Nr 2/2013 (99) 265 Marcjan Nowak Politchnika Częstochowska, Częstochowa MODEL MATEMATYCZNY I SYMULACYJNO-KOMPUTEROWY UKŁADU NAPĘDOWEGO REAKTORA POLIMERYZACJI Z MODELOWĄ
Zszyty Problmow Maszyny Elktryczn Nr 2/2013 (99) 265 Marcjan Nowak Politchnika Częstochowska, Częstochowa MODEL MATEMATYCZNY I SYMULACYJNO-KOMPUTEROWY UKŁADU NAPĘDOWEGO REAKTORA POLIMERYZACJI Z MODELOWĄ
Układ RLC z diodą. Zadanie: Nazwisko i imię: Nr. albumu: Grzegorz Graczyk. Nazwisko i imię: Nr. albumu:
 Politechnika Łódzka TIMS Kierunek: Informatyka rok akademicki: 2009/2010 sem. 3. grupa II Zadanie: Układ z diodą Termin: 5 I 2010 Nr. albumu: 150875 Nazwisko i imię: Grzegorz Graczyk Nr. albumu: 151021
Politechnika Łódzka TIMS Kierunek: Informatyka rok akademicki: 2009/2010 sem. 3. grupa II Zadanie: Układ z diodą Termin: 5 I 2010 Nr. albumu: 150875 Nazwisko i imię: Grzegorz Graczyk Nr. albumu: 151021
ZASTOSOWANIE METODY REDUKCJI OBSZARU OBLICZENIOWEGO W DYNAMICZNYCH ZAGADNIENIACH INTERAKCJI KONSTRUKCJI Z PODŁOŻEM
 ANDRZEJ TRUTY * ZASTOSOWANIE METODY REDUKCJI OBSZARU OBLICZENIOWEGO W DYNAMICZNYCH ZAGADNIENIACH INTERAKCJI KONSTRUKCJI Z PODŁOŻEM APPLICATION OF DOMAIN REDUCTION METHOD IN DYNAMIC PROBLEMS OF SOIL-STRUCTURE
ANDRZEJ TRUTY * ZASTOSOWANIE METODY REDUKCJI OBSZARU OBLICZENIOWEGO W DYNAMICZNYCH ZAGADNIENIACH INTERAKCJI KONSTRUKCJI Z PODŁOŻEM APPLICATION OF DOMAIN REDUCTION METHOD IN DYNAMIC PROBLEMS OF SOIL-STRUCTURE
KATALOG TECHNICZNY. www.rurgaz.pl. RC MULTIsafe Rury z polietylenu PE 100RC do układania bez obsypki piaskowej i do renowacji rurociągów
 KATALOG TECHNICZNY Dz Dz Di RC MULTIsaf Rury z politylnu PE 100RC do układania bz obsypki piaskowj i do rnowacji rurociągów RC MAXIprotct PE/PP-d Rury z politylnu PE 100RC z dodatkowym płaszczm z PE lub
KATALOG TECHNICZNY Dz Dz Di RC MULTIsaf Rury z politylnu PE 100RC do układania bz obsypki piaskowj i do rnowacji rurociągów RC MAXIprotct PE/PP-d Rury z politylnu PE 100RC z dodatkowym płaszczm z PE lub
c - częstość narodzin drapieżników lub współczynnik przyrostu drapieżników,
 SIMULINK 3 Zawartość Równanie Lotki-Volterry dwa słowa wstępu... 1 Potrzebne elementy... 2 Kosmetyka 1... 3 Łączenie elementów... 3 Kosmetyka 2... 6 Symulacja... 8 Do pobrania... 10 Równanie Lotki-Volterry
SIMULINK 3 Zawartość Równanie Lotki-Volterry dwa słowa wstępu... 1 Potrzebne elementy... 2 Kosmetyka 1... 3 Łączenie elementów... 3 Kosmetyka 2... 6 Symulacja... 8 Do pobrania... 10 Równanie Lotki-Volterry
