Badania ab initio własności strukturalnych nanoukładów atomowych

Transkrypt

1 Badania ab initio własności strukturalnych nanoukładów atomowych Paweł Scharoch (dokument w opracowaniu) 1 Wstęp. Określenie nanoukłady atomowe jest bardzo szerokie i ogranicza klasę układów będących przedmiotem zainteresowania raczej ze względu na potencjalne zastosowania techniczne niż ze względu na ich rozmiary (od kilku do kilkudziesięciu tysięcy atomów). Tak więc w klasie tej znajdzie się zarówno lity kryształ (będący często np. podłożem w zastosowaniach technicznych), jak i granica faz (stała-próżnia, stała-ciekła, stała-stała), a także obiekty zlokalizowane w kryształach i na granicach faz (domieszki czy defekty strukturalne). Tematyka obejmuje zatem np. zagadnienia struktur równowagowych i przejść fazowych w kryształach litych, czystą powierzchnię kryształu z całym bogactwem zjawisk strukturalnych (rekonstrukcja), zjawiska adsorpcji i dyfuzji powierzchniowej, zagadnienia wzrostu kryształów i cienkich warstw i wiele innych. Struktury typowe dla nanontechnologii to cienkie warstwy, druty kwantowe, kropki kwantowe oraz kombinacje tych struktur. W kontekście zastosowań technicznych wyłaniają się dwie grupy problemów. Pierwszy to technologia wytwarzania takich struktur i drugi ich własności fizyczne (struktura geometryczna i elektronowa, wpływ różnych czynników np. temperatury, ciśnienia, pola elektrycznego czy magnetycznego na ich własności, problem stabilności itp.) Rozwijające się od ok. 20 lat metody obliczeniowe ab initio w coraz większym stopniu okazują się być nieocenionym narzędziem na etapie projektowania struktur oraz projektowania technologii ich wytwarzania. Wykorzystując jedynie fundamentalne teorie fizyczne (mechanika kwantowa, elektrodynamika, mechanika klasyczna) i przy minimalnych założeniach modelowych pozwalają one na wyznaczenie energii całkowitej oddziałujących atomów jako funkcji parametrów geometrycznych układu. Funkcja ta nazywana jest powierzchnią energii potencjalnej (PES - Potential Energy Surface ) lub powierzchnią energii całkowiltej lub powierzchnią Borna-Oppenheimera, choć to ostatnie określenie ma nieco inny odcień znaczeniowy gdyż odnosi się tylko do energii układu elektronowego (bez oddziaływania jon-jon). Znajomość tej funkcji oraz jej dwóch kolejnych gradientów względem parametrów geometrycznych okazuje się być kluczowa przy badaniu własności strukturalnych układów atomowych. Oprócz tego jako wynik obliczeń uzyskuje się gęstość elektronową stanu podstawowego, mierzalną wielkość fizyczną, będącą podstawową wielkością w teorii funkcjonału gęstości (DFT - Density Functional Theory), teorii wyjściowej dla metod ab initio. Znajomość gęstości elektronowej oraz zmian tej gęstości pod wpływem różnych czynników fizycznych pozwala wniknąć w naturę wiązań w układach i szukać uzasadnienia zjawisk strukturalnych. W ostatnich latach prowadzone też są intensywne poszukiwania teoretyczne efektywnych metod badania elektrono- 1

2 2 2 Powierzchnia energii potencjalnej (PES). wych stanów wzbudzonych w ramach DFT. Opracowanie takich pozwoliłoby na wejście metod ab initio na obszar całej fizyki układów atomowych. 2 Powierzchnia energii potencjalnej (PES). 2.1 Równanie Schrödingera układu wieloatomowego. Analizę rozpoczniemy od podania pełnego hamiltonianu układu wieloatomowego: Ĥ = ˆT e + ˆT j + ˆV ee + ˆV ej + ˆV jj (1) w którym operatory po prawej stronie równania reprezentują kolejno: energię kinetyczną elektronów, energię kinetyczną jonów, oraz oddziaływania kulombowskie elektron-elektron, elektron-jon i jon-jon. W równianiu Schrödingera: ĤΨ = E tot Ψ (2) E tot jest energią całkowitą układu, a Ψ(r, R) wielociałową funkcją falową, gdzie r i R oznaczają symbolicznie elektronowe i jonowe stopnie swobody. 2.2 Przybliżenie Borna-Oppenheimera. Pierwszym przybliżeniem jakie się stosuje jest przybliżenie Borna-Oppenheimera (adiabatyczne) wykorzystujące fakt dużej różnicy między masą jądra atomowego a masą elektronu (od 3 do 5 rzędów wielkości). W ramach tego przybliżenia równanie Schrödingera (2) separuje się na dwa równania, które mogą być rozwiązywane niezależnie (choć sprzężone są poprzez jonowe stopnie swobody). Są to: Ĥ e ψ(r) = E(R)ψ(r), (3) równanie dla układu elektronowego, w którym jonowe stopnie swobody (R) pełnią rolę parametrów, oraz Ĥ BO φ(r) = E tot φ(r), (4) równanie dla układu jonów. W powyższych równaniach Ĥe jest hamiltonianem układu elektronowego: a ĤBO hamiltonianem układu jonów: Ĥ e = ˆT e + ˆV ee + ˆV ej (5) Ĥ BO = ˆT j + ˆV jj + E(R), (6) do którego, jak widać, wchodzi zależna od R energia układu elektronowego. Elektronowa i jonowa funkcje falowe to odpowiednio ψ(r) i φ(r). Opisana wyżej procedura formalnie polega na przedstawieniu funkcji Ψ w równaniu (2) w postaci iloczynu funkcji ψ(r) i φ(r) oraz pominięciu małych (w sensie wartości oczekiwanej) składowych energii całkowitej układu. Fizycznie

3 2.3 Powierzchnia energii potencjalnej. 3 przybliżenie to oznacza, że układ elektronowy dopasowuje się w sposób natychmiastowy do konfiguracji jonów. Konsekwencją tego przybliżenia jest w szczególności ograniczenie możliwości uwzględniania pobudzeń zewnętrznych tylko do niskich częstości (porównywalnych z częstościami charakterystycznymi dla układu jonów) oraz wysokich częstości (przy których układ jonowy nie reaguje na pobudzenie). 2.3 Powierzchnia energii potencjalnej. Zagadnienie dynamiki układu jonowego można z bardzo dobrym przybliżeniem rozwiązywać klasycznie, rozwiązując np. równania Newtona. Rolę energii potencjalnej pełnią: energia oddziaływania jon-jon oraz sparametryzowana położeniami jonów energia układu elektronowego (patrz równie 6). Jest to jednocześnie energia całkowita układu E tot w wyrażeniach (2) i (4), w sytuacji statycznej (unieruchomionych jonów). Tak określona energia potencjalna jest więc w ogólności funkcją jonowych stopni swobody. Na poziomie mikroskopowym będą to współrzędne jonów, istnieje jednak możliwość przesunięcia części stopni swobody układu na poziom mezoskopowy (i makroskopowy) w postaci np. objętości, pola powierzchni, zmiennych strukturalnych (definiujących komórkę elementarną w krysztale), czy składowych tensora odkształceń. Funkcja ta nazywana jest powierzchnią energii potencjalnej (PES) i stanowi kluczową charakterystykę układu z punktu widzenia własności strukturalnych i materiałowych. Ważne są także dwa kolejne gradienty PES ze względu na jonowe stopnie swobody reprezentujące uogólnione siły oraz uogólnione stałe elastyczne. I tak, na poziomie mikroskopowym: F i = Etot (R) R i (7) to siły działające na jony (index i identyfikuje jednocześnie jon i współrzędną, np. kartezjańską). Drugi gradient: F i = 2 E tot (R) (8) R j R i R j określa w tym wypadku macierz stałych siłowych, wykorzystywaną w przybliżeniu harmonicznym (patrz rozdział 8.3). Na poziomie mezoskopowym, np. przy objętości traktowanej jako stopień swobody, otrzymujemy ciśnienie i moduł sprężystości objętościowej ( bulk modulus ): P = Etot (V ) V (9) B = V P (V ) V = V 2 E tot (V ) V 2 (10) Jeśli stopniem swobody będzie pole powierzchni (lub wymiar liniowy) wówczas kolejne pochodne to napięcie powierzchniowe (liniowe) i moduł sprężystości powierzchniowej (liniowej). Z kolei jako wynik kolejnych pochodnych energii całkowitej po składowych tensora odkształceń otrzymamy tensor naprężeń oraz tensor sprężystości.

4 4 3 Podstawy teoretyczne obliczeń it ab initio. 2.4 Stany równowagi statycznej. Minima lokalne lub globalne PES wyznaczają stany równowagi układów zwane równowagą statyczną ( static equilibrium ). Nie jest to do końca stan odpowiadający temperaturze zera bezwzględnego gdyż nie uwzględnia się tu drgań zerowych atomów. W przykładach podanych w poprzednim podrozdziale stan równowagi statycznej określa np. położenia atomów, na poziomie mikroskopowym. Na wyższych poziomach będzie to np. objętość równowagowa, równowagowa struktura krystaliczna. Jeśli minimum PES ma charakter lokalny wówczas mamy doczynienia ze stanem metastabilnym a więc możliwe jest przejście układu do minimum globalnego, aktywowane np. temperaturą. Warunkiem równoważnym minimum PES jest warunek zerowania się sił lub sił uogólnionych (zerowanie pierwszych pochodnych). Zerowanie się drugich pochodnych oznacza brak dobrze określonego minimum PES, co może oznaczać brak stabilności układu. Interesującym przypadkiem PES na poziomie mikroskopowym jest atom adsorbatu na powierzchni kryształu. Jeśli płaszczyzna XY kartezjańskiego układu współrzędnych pokrywa się z płaszczyzną powierzchni wówczas PES jest dwuwymiarową funkcją współrzędnych x i y atomu (zakłada się, że atom zawsze pozostaje w minimum PES ze względu na trzeci stopień swobody, współrzędną z). Wyznaczona w ten sposób PES pozwala na określanie położeń stabilnych i metastabilnych atomów na powierzchni, określanie prawdopodobieństw przejść z jednych położeń do drugich oraz na analizę dyfuzji powierzchniowej. 2.5 Włączanie temperatury. Temperatura jak wiadomo ma bardzo istotny wpływ na własności strukturalne i materiałowe układów atomowych. Jej uwzględnienie wymaga analizy termodynamiki układów. Na poziomie makro i mezoskopowym oraz w pewnych szczególnych przypadkach na poziomie mikroskopowym możliwe wydaje się uogólnienie koncepcji powierzchni energii potencjalnej na koncepcję powierzchni energii swobodnej (FES - Free Energy Surface ). Zagadnieniu temu będzie poświęcony jeden z kolejnych rozdziałów. 3 Podstawy teoretyczne obliczeń it ab initio. 3.1 Zagadnienie niejednorodnego gazu elektronów, teoria funkcjonału gęstości (DFT). Jak pokazano w poprzednim rozdziale, w badaniach teoretycznych własności strukturalnych układów atomowych kluczową rolę odgrywa powierzchnia energii potencjalnej (PES) definiowana jako energia całkowita układu przy zamrożonych jonowych stopniach swobody: E tot = V jj + E(R) (11) Obliczenia numeryczne pierwszego składnika w tym wyrażeniu (energii kulombowskiego oddziaływania jonów) są proste od strony ideowej. Trudności techniczne związane z faktem, że oddziaływanie kulombowskie jest dalekozasięgowe pokonuje się stosując technikę Ewalda (Ref). Drugi składnik to energia całkowita układu elektronowego. Jest to znane w mechanice kwantowej zagadnienie układu cząstek identycznych, samo w sobie złożone i będące obiektem

5 3.2 Twierdzenie Hohenberga-Kohna. 5 oddzielnej dziedziny badań teoretycznych. W przypadku układów atomowych mówimy o niejednorodnym gazie elektronów (fermionów). Podstawy teoretyczne analizy fizyki takich układów były znane już w końcu lat 20 XX wieku (Ref), jednak rozwiązanie równań okazało się technicznie niemożliwe (warto przypomnieć, że nawet klasyczny układ tylko trzech cząstek jest w ogólności nierozwiązywalny analitycznie). W latach 50 rozpoczęła się rewolucja w dziedzinie technik obliczeniowych, która trwa do dzisiaj i wydaje się, że jej końca ciągle nie widać. Jednak i przy obecnym stanie rozwoju komputerów, przecież imponującym, numeryczne rozwiązanie równania Schrödingera nawet dla układu 10 elektronów (np. atom neonu) jest niemożliwe. Na przykład pamięć potrzebna na zapisanie funkcji falowej takiego układu w reprezentacji położeniowej, na siatce 10-punktowej, jest rzędu 4x10 30 bytów. Gdyby więc chcieć zapisać taką funkcję na płytkach CD o pojemności 1Gb każda to potrzeba by takich płytek. Zakładając, że jedna płytka waży 10 gramów potrzebujemy ton płytek, a to dopiero początek układu okresowego i każdy następny atom to o 3 rzędy wielkości więcej pamięci! Sytuacja wydaje się beznadziejna, jednak z pomocą przychodzi teoria funkcjonału gęstości (DFT - Density Functional Theory ), której podstawy zostały sformułowane w latach 60 poprzedniego stulecia (Ref). Teoria ta pozwala efektywnie rozwiązywać zagadnienie układu identycznych cząstek kwantowych poprzez rozwiązywanie jednocząstkowego równania typu Schrödingera, a centralnym problemem teorii jest adekwatna reprezentacja kwantowego oddziaływania korelacji-wymiany. 3.2 Twierdzenie Hohenberga-Kohna. Podstawą opisu układu cząstek identycznych w zewnętrznym potencjale V ext (niejednorodnego gazu cząstek) w teorii funkcjonału gęstości jest ich gęstość: n(r) = N ψ(r 1,..., r N ) 2 dr 2... dr N (12) normowana do liczby cząstek: N = n(r)dr (13) Jest to funkcja rzeczywista współrzędnej przestrzennej (3 zmiennych) zatem znacznie prostsza od funkcji falowej. Punktem wyjścia teorii jest, sformułowane w 1964 roku, twierdzenie Hohenberga- Kohna (Ref): Energia układu kwantowych cząstek cząstek identycznych jest funkcjonałem gęstości: E[n] = F [n] + n(r)v ext (r)dr, (14) gdzie F [n] = ψ ˆT + Ŵ ψ, (15) a Ŵ jest energią kulombowskiego oddziaływania cząstek

6 6 3 Podstawy teoretyczne obliczeń it ab initio. gęstość stanu podstawowego n G minimalizuje funkcjonał (14): E G [n G ] = min E[n] δe = 0, (16) n n G δn n=ng co jest oczywistą konsekwencją zasady wariacyjnej Rayleigha-Ritza Z twierdzenia tego wynika w szczególności, że funkcjonał F [n] jest uniwersalny, to znaczy, że nie zależy od potencjału zewnętrznego. Wynika z niego także, że nie jest możliwe aby dwa nietrywialnie różne potencjały (różniące się bardziej niż o stałą) produkowały taką samą gęstość stanu podstawowego. W takim sensie potencjał zewnętrzny jest także funkcjonałem gęstości. Własność ta została wykorzystana przy konstrukcji równań Kohna-Shama, opisanej w kolejnym rozdziale. 3.3 Równania Kohna-Shama. Twierdzenie Hohenberga-Kohna nie dostarcza recepty na znajdowanie gęstości n(r). Nie jest bowiem znana jawna postać funkcjonału F [n] (a nawet są kłopoty ze zdefiniowaniem dziedziny tego funkcjonału, czyli fizycznie akceptowalnych gęstości (Ref)). Trudności te zostały w znacznym stopniu przezwyciężone w konstrukcji Kohna-Shama polegającej na mapowaniu realnego układu cząstek na pomocniczy układ cząstek nieoddziałujących, w taki sposób aby gęstości stanu podstawowego obu układów były identyczne. Zabieg polega na konstrukcji zewnętrznego potencjału lokalnego dla układu cząstek nieoddziałujących (na mocy tw. Hohenberga-Kohna istnieje jeden i tylko jeden taki potencjał). Korzyść płynąca z takiego mapowania wiąże się z faktem, że równanie Schrödingera układu cząstek nieoddziałujących separuje się na równania jednocząstkowe. Funkcjonał uniwersalny F [n] układu oddziałującego zapiszemy w postaci: F [n] = T 0 [n] + e2 2 n(r)n(r ) drdr + E xc [n], (17) r r gdzie T 0 [n] to energia kinetyczna układu cząstek nieoddziałujących, a E xc [n] jest tzw. energią korelacji-wymiany, zdefiniowaną przez powyższe równanie. Przekształcenie funkcjonału F [n] ma charakter tożsamościowy (dodanie i odjęcie T 0 [n])), pozwala jednak na ulokowanie nieznanej analitycznie części tego funkcjonału w członie E xc [n] mającym charakter energii typowo kwantowych oddziaływań korelacji i wymiany. Wariacja funkcjonału energii ze względu na gęstość n[r], z warunkiem ubocznym zachowania liczny cząstek, prowadzi formalnie do takiego samego równania jakie otrzymalibyśmy w przypadku cząstek nieoddziałujacych: ( h2 2 ) 2m r 2 + V SCF (r) ψ n (r) = ɛ n ψ n (r) (18) z potencjałem efektywnym V SCF ( Self Consistent Field ): V SCF (r) = V ext (r) + e 2 n(r ) r r dr + v xc(r) (19) gdzie

7 3.4 Twierdzenie Janaka 7 v xc (r) = δe xc[n] δn(r) (20) to potencjał lokalny nazwany potencjałem korelacji-wymiany ( exchange- Correlation ). Gęstość stanu podstawowego n(r) (będąca gęstością zarówno układu prawdziwego jak i pomocniczego) oraz energia kinetyczna układu nieoddziałującego T 0 [n] wyrażają się poprzez obsadzone przez cząstki orbitale Kohna-Shama, ψ n (r): T 0 [n] = 2 h2 2m N/2 n(r) = 2 ψ n (r) 2 (21) n=1 N/2 n=1 ψ n(r) 2 ψ n (r) r 2 dr (22) przy czym zakładamy, że układ jest niemagnetyczny i dla elektronów ma miejsce dwukrotna degeneracja ze względu na spin. Energię całkowitą układu można obliczać albo z wyrażeń (14) i (17) albo korzystając z energii własnych Kohna-Shama: n/2 E[n] = 2 ɛ n e2 2 n=1 n(r)n(r ) r r drdr + E xc [n] n(r)v xc drdr (23) Warto w tym miejscu jeszcze raz zaznaczyć, że choć równania Kohna-Shama są równaniami typu jednocząstkowego, to ich rozwiązania nie są stanami w sensie przybliżenia jednocząstkowego. W szczególności, jak widać w powyższym wyrażeniu, energia układu nie jest sumą energii stanów obsadzonych. Jedynym odniesieniem równań Kohna-Shama do układu rzeczywistego jest uzyskiwana poprzez ich rozwiązanie gęstość stanu podstawowego. Równanie (18) ma charakter nieliniowego równania Schrödingera, w tym sensie, że występujący w równaniu potencjał zależy od jego rozwiązań. Dlatego równie Kohna-Shama rozwiązuje się w sposób samouzgodniony. Od strony formalnej jest to równanie jednocząstkowe co stanowi ogromne uproszczenie w stosunku do równania wielocząstkowego. Metoda pozwala efektywnie znajdować gęstość i energię stanu podstawowego układu identycznych cząstek kwantowych, pod warunkiem, że znany jest potencjał korelacji wymiany v xc. Analityczna postać tego potencjału nie jest znana dlatego stosuje się przybliżenia opisane krótko w kolejnym podrozdziale. 3.4 Twierdzenie Janaka Istnieje możliwość rozwiązania zagadnienia wariacyjnego (16) w konstrukcji Kohna-Shama przy dowolnym wektorze obsadzeń λ. Postać równań Kohna- Shama (18) nie ulega zmianie, jednak ich rozwiązania (energie i funkcje własne, energia całkowita) stają się funkcjami wektora obsadzeń (ɛ n (λ),ψ n (λ, r),e(λ)), ponieważ od tegoż wektora zależy gęstość (a zatem i potencjał samouzgodniony V SCF ):

8 8 3 Podstawy teoretyczne obliczeń it ab initio. n(r) = λ n ψ n (r) 2 (24) n=1 gdzie λ n przyjmują wartości z zakresu 0, 2, oraz: N = λ n, (25) n=1 gdzie N jest liczbą cząstek. Twierdzenie Janaka pokazuje związek pomiędzy energiami własnymi Kohna- Shama przy zadanym wektorze obsadzeń λ o a pochodną cząstkową energii całkowitej ze względu na obsadzenia poziomów: 3.5 Stany wzbudzone ( ) E(λ) ɛ n (λ o ) = (26) λ n λ=λ o Analiza stanów wzbudzonych w ramach DFT to obszerna dziedzina współczesnych badań teoretycznych (przybliżenie GW, TDDFT - Time Dependent Density Functional Theory ). Teoria zaprezentowana w tym opracowaniu dotyczy przede wszystkim stanu podstawowego niejednorodnego układu identycznych cząstek kwantowych. Możliwa jest jednak prosta analiza energii wzbudzeń układu (przynajmniej niektórych) opierająca się na hipotezie, że stanom wzbudzonym odpowiadają całkowite obsadzenia orbitali Kohna-Shama (λ n = 1, 2). Jeśli oznaczymy przez λ g wektor obsadzeń stanu podstawowego (λ n = 2, dla n = 1,..., N/2), a przez λ e wektor obsadzeń pewnego stanu wzbudzonego, wówczas energia wzbudzenia: E = E(λ e ) E(λ g ) (27) W szczególności, wzbudzenie jednocząstkowe polegające na inwersji obsadzeń stanów n < N/2 i m > N/2, reprezentowane przez wektor obsadzeń λ mn : ( E) mn = E(λ mn ) E(λ g ) (28) Korzystając z twierdzenia Janaka energię takiego wzbudzenia można obliczyć w inny sposób: ( E ( E) mn = de = dλ n + E ) dλ m (29) λ n λ m = 1 0 = [ ɛn (λ)d(1 λ m ) + ɛ m (λ)dλ m ] 1 0 [ ɛm (λ) ɛ n (λ) ] dλ m Ostatni wzór jest użyteczny w sytuacji, gdy różnica energii całkowitych jest mniejsza niż dokładność reprezentacji numerycznej energii całkowitej, czyli w dużych układach.

9 3.6 Przybliżenia energii korelacji-wymiany: LDA i GGA Przybliżenia energii korelacji-wymiany: LDA i GGA. Historycznie pierwszym i powszechnie stosowanym przybliżeniem energii korelacjiwymiany jest przybliżenie lokalnej gęstości (LDA - Local Density Approximation ). Przyjmuje się, że energia korelacji-wymiany w układzie niejednorodnym jest lokalnie równa energii korelacji-wymiany układu jednorodnego, i wyraża się wzorem: E xc [n] = ɛ xc (n) n=n(r)n(r)dr, (30) gdzie ɛ xc (n) jest energią korelacji wymiany na jedną cząstkę w układzie jednorodnym. Potencjał korelacji wymiany przyjmuje wówczas postać: ( v xc [n](r) = ɛ xc (n) + n dɛ ) xc(n) (31) dn n=n(r) Energię ɛ xc (n) można podzielić na część korelacyjną i wymienną: ɛ xc (n) = ɛ x (n) + ɛ c (n). (32) Znana jest dokładna analityczna postać energii wymiany w układzie jednorodnym: ɛ x (n) = 3 4π (3π2 n) 1/3, (33) a formuły opisujące energię korelacji ɛ c (n) mają charakter przybliżony i opierają się na parametryzacjach wyników symulacji Monte Carlo (Ref). Przybliżenie LDA jest najlepsze w granicach dużych gęstości lub gęstości wolno zmiennej przestrzennie. W praktyce okazało się, że z sukcesem opisuje bardzo szeroką klasę układów, od pojedynczego atomu do rozmaitych układów wieloatomowych. Znane są obecnie charakterystyczne błędy wyników uzyskiwanych w ramach przybliżenia LDA: znacznie większe ( 20%) energie kohezji w kryształach oraz energie wiązań zły opis układów silnie skorelowanych, takich jak tlenki metali przejściowych mniejsze ( 1%) stałe sieci w kryształach i równowagowe długości wiązań w cząsteczkach większe ( 20%) wielkości związane z własnościami sprężystymi (np. moduły sprężystości objętościowej w kryształach) większe ( 5%) częstości oscylacji) Inne przybliżenie energii korelacji-wymiany to przybliżenie uogólnionych gradientów (GGA - Generalized Gradient Approximation ): E xc [n] = ɛ xc (n, n(r) ) n=n(r)n(r)dr, (34) w którym zakłada się zależność lokalnej energii korelacji-wymiany ɛ xc od gęstości i jej gradientu. Charakterystyczne błędy obserwowane w przybliżeniu GGA to:

10 10 4 Algorytmy. mniejsze od eksperymentalnych ( 10%) energie kohezji w kryształach oraz energie wiązań ( 10%) większe ( 1%) stałe sieci w kryształach i równowagowe długości wiązań w cząsteczkach większe ( 5%) wielkości związane z własnościami sprężystymi (moduły sprężystości) 4 Algorytmy. 4.1 Metoda dynamiki molekularnej Car-Parinello (w opracowaniu) 4.2 Metoda najszybszego spadku ( Steepest descent ) (w opracowaniu) 4.3 Metoda gradientów sprzężonych (w opracowaniu) 4.4 Algorytmy dynamiki molekularnej (w opracowaniu) 4.5 Metoda specjalnych punktów k Monkhorsta-Packa Metoda specjalnych punktów k Monkhorsta-Packa jest metodą całkowania funkcji posiadającej periodyczność nieskończonej sieci po komórce elementarnej. W obliczeniach ab initio stosuje się ją do znajdowania gęstości elektronowej w układach periodycznych. Wyznaczanie gęstosci wymaga całkowania po I strefie Brillouina kwadratów modułów obsadzonych stanów Kohna-Shama (oraz sumowania po pasmach energetycznych). Rozważamy sieć zdefiniowaną poprzez prymitywne translacje: R = R 1 a 1 + R 2 a 2 + R 3 a 3 (35) Odpowiadająca jej sieć odwrotna rozpięta jest na wektorach: b1 = 2π Ω a 2 a 3, b2 = 2π Ω a 3 a 1, b3 = 2π Ω a 1 a 2 (36) gdzie jest objętością komórki elementarnej. Definiujemy ciąg liczb: Ω = a 1 ( a 2 a 3 ) (37) u r = 2r q 1 2q r = 1, 2, 3,..., q (38)

11 4.5 Metoda specjalnych punktów k Monkhorsta-Packa 11 gdzie q (naturalne) będzie determinowało liczbę specjalnych punktów k. Wyjściowy zbiór punktów k definiujemy następująco: kprs = u p b1 + u p r 2 + u p s 3 (39) Otrzymuje się w ten sposów q 3 różnych punktów k, rozmieszczonych równomiernie w strefie Brillouina. Definiujemy także: A m ( k) = N 1 2 m R =C m e i k R (40) gdzie sumowanie przebiega po wektorach sieci należących do tej samej gwiazdy (przechodzących w siebie poprzez operacje symetrii grupy punktowej kryształu), C m oznacza długość wektorów z danej gwiazdy i zmienia się w sposów rosnący od C 1 = 0, a N m oznacza liczbę wektorów należących do danej gwiazdy. Należy zauważyć, że A m (k) są niezmiennicze względem operacji symetrii grupy punktowej kryształu. Stanowią one także ortogonalną bazę w przestrzeni k: d ka m( k)a n( k = 8π3 Ω δ mn (41) BZ Tak, że dowolną funkcję f( k), posiadającą symetrię sieci odwrotnej można przedstawić w bazie A m ( k): f( k) = f m A m ( k) (42) m=1 gdzie f m = Ω 8π 3 d ka m( k)f( k) (43) BZ Rozważmy następującą wielkość: S mn (q) = 1 q 3 q p,r,s=1 A m( k prs )A n( k prs ) (44) Po podstawieniu do powyższego wyrażenia definicji (??) można je przekształcić do postaci: N m N n 3 S mn (q) = (N m N n ) 1 2 Wj ab (q) (45) gdzie: Wj ab (q) = 1 q a=1 b=1 j=1 q e ( π q )(2r q 1)(Rb j Ra j ) (46) r=1 We wzorze (45) sumowanie po a i b odbywa się po wszystkich wektorach należących do gwiazd odpowiednio m i n. Wyrażenie Wj ab może przyjmować następujące wartości: 1 dla R Wj ab j b Ra j = 0, 2q, 4q,... (q) = ( 1) q+1 dla Rj b Ra j = q, 3q, 5q,... (47) 0 dla Rj b Ra j inne

12 12 4 Algorytmy. Należy pamiętać, że q oraz Rj a to liczby całkowite. Nałożymy następnie ograniczenie: Rj a < q 2, Rb j < q, j = 1, 2, 3 (48) 2 Co prowadzi do: a z zależności (45): W ab j (q) = δ(r a j, R b j) (49) S mn = δ mn (50) Oznacza to, że wszystkie funkcje A m ( k), które spełniają warunek (48) są ortonormalne na dyskretnym zbiorze punktów k prs w I strefie Brillouina. Liczba tych funkcji jest tym większa im większa jest liczba q. Wykorzystanie symetrii punktowej sieci prowadzi do znacznego zredukowania sumy we wzorze (44): S mn (q) = 1 P (q) q 3 j=1 w j A m( k j )A n ( k j ) (51) gdzie P (q) jest zależną od symetrii liczbą punktów k j, ze zbioru {k prs } znajdujących się w nieredukowalnej części strefy Brillouina, a w j jest współczynnikiem wagowym równym stosunkowi rzędu pełnej grupy symetrii do rzędu grupy wektora falowego k j. Inaczej mówiąc, ponieważ operacje symetrii punktowej nie zmieniają wartości wyrazów w szeregu (44), sumowanie po wektorach ze zbioru {k prs }, różnych lecz związanych operacjami symetrii punktowej, można zastąpić mnożeniem przez czynnik w j. Przypuśćmy, że chcemy całkować pewną funkcję f( k), która jest całkowicie symetryczna i periodyczna w przestrzeni k. Jak pokazano już wcześniej może ona być formalnie rozwinięta w bazie A m ( k): f( k) = f m A m ( k) (52) m=1 gdzie, z powodu ortogonalności A m ( k) w strefie Brillouina, f m = Ω 8π 3 d ka m( k)f( k) (53) BZ Całka f( k) po całej strefie Brillouina jest związana z pierwszym współczynnikiem rozwinięcia: d ka mf( k) = 8π3 Ω f 1 (54) BZ Jeśli rozwinięcie (52) ograniczymy do gwiazd spełniających warunek (48), czyli reprezentację funkcji f( k) ograniczymy do jej rzutu na przestrzeń rozpietą na gwiazdach spełniających warunek (48), to wartości współczynników f m dane są znacznie prostszą zależnością: f m = 1 q P (q) j=1 w j f( k j )A m ( k j ) (55)

13 13 Współczynniki te oczywiście różnią się od dokładnych, z powodu ograniczenia przestrzeni. Otrzymujemy w ten sposób przybliżoną reprezentację funkcji f( k): f( k) = N G m=1 f m A m ( k) (56) gdzie N G jest liczbą gwiazd spełniających warunek (48). Całkowanie po I strefie Brillouina funkcji f( k), jak w (54), z wykorzystaniem reprezentacji (56) będzie obarczone błędem: ε BZ = d k[f( k) f( k)] = f m N 1 2 m S m1 (q) (57) m>1 BZ gdzie S m1 (q) = { ( 1) q 1 q (R1+R2+R3) R dla 1 R 3 q 0 dla innych = integer (58) 5 Pseudopotencjały zachowujące normę. (W opracowaniu) 6 Reprezentacja równań Kohna-Shama. Układy periodyczne, baza fal płaskich. (W opracowaniu) 7 Przykład: atom. Atom jest podstawową cegiełką w układach wieloatomowych i jednocześnie najprostszym realnym obiektem fizycznym poddającym się analizie aparatem teoretycznym opisanym w zarysie w poprzednim rozdziale. Jednocześnie, jego własności fizyczne mają w sposób oczywisty kluczowe wpływ na własności układów złożonych. Bardzo ważny jest więc dobry opis teoretyczny atomu i dlatego warto poświęcić temu obiektowi nieco uwagi, choć od strony formalnej aparat zaprezentowany w tym rozdziale ma w dużej części charakter podręcznikowy. Rozwiązanie numeryczne równań Kohna-Shama dla atomów jest stosunkowo proste. Przy założeniu symetrii sferycznej układu równania redukują się do jednego wymiaru (promienia we współrzędnych sferycznych) i mogą być rozwiązywane w reprezentacji położeniowej, poprzez dyskretyzację na siatce radialnej. Poniżej przedstawiony jest sposób rozwiązania dla nierelatywistycznego równania Schrödingera. Rozwiązuje się także równanie Schrödingera relatywistyczneskalarne (istotne w przypadku ciężkich atomów) oraz relatywistyczne-wektorowe (istotne w przypadku atomów, w których istotne jest oddziaływanie spin-orbita). W układzie jednostek Hartree (masa elektronu m e = 1 i stała diraca h = 1) równanie Kohna-Shama ma postać: [ ] V SCF (r) ϕ(r) = εϕ(r) (59)

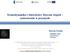
14 14 7 Przykład: atom. Jest to zagadnienie własne, którego rozwiązaniem jest zbiór: {ϕ i, ε i }, a gęstość elektronową znajdujemy z sumy: n(r) = Σ i λ i ϕ i (r) 2, (60) gdzie liczby obsadzeń {λ i = 1, dla i = 1,..., N; λ i = 0, dla i > N}, a N jest liczbą elektronów w atomie (uwzględniamy dwuktrotną degenerację stanów ze względu na spin). Przy założeniu symetrii sferycznej potencjału samouzgodnionego V SCF (r) równanie (59) można przedstawić we współrzędnych sferycznych: [ 1 ( ( 2r 2 r 2 ) ) ] + r r ˆL 2 + V SCF (r) ϕ = εϕ, (61) gdzie ˆL jest operatorem momentu pędu, zależnym tylko od współrzędnych kątowych, a więc komutującym z Hamiltonianem. Funkcja falowa ϕ jest iloczynem harmoniki sferycznej Y lm (ˆr) (gdzie ˆr jest kierunkiem w przestrzeni r) będącej funkcją własną operatora momentu pędu, oraz funkcji radialnej R ( r), będącej rozwiązaniem zagadnienia własnego: [ 1 ( d 2r 2 r 2 d ) ] l(l + 1) + dr dr r 2 + V SCF (r) R(r) = εr(r) (62) Harmoniki sferyczne indeksowane są liczbami kwantowymi: l - orbitalną, wskazującą na wartość momentu pędu, oraz m - magnetyczną, określającą rzut momentu pędu na wybraną oś. Równanie (62) ulega dalszemu uproszczeniu po dokonaniu podstawienia: R(r) = u(r)/r. Przyjmuje wówczas postać: [ 1 d 2 l(l + 1) + 2 dr2 r 2 ] + V SCF (r) u(r) = εu(r) (63) Jest to formalnie równanie Schrödingera dla cząstki poruszającej się w jednym wymiarze w potencjale efektywnym: l(l + 1)/r 2 + V SCF (r). Nietrudno także pokazać, że z warunku unormowania funkcji ϕ(r) wynika fakt unormowania funkcji u(r). Rozwiązania równania (63): {u nl, ε nl } (a więc także {R nl, ε nl }), indeksowane są liczbami kwantowymi: n - główną, określającą energię własną Kohna-Shama, oraz orbitalną (l), ponieważ od niej zależy efektywny hamiltonian. Jak widać występuje degeneracja poziomów Kohna-Shama ze względu na liczbę kwantową m. Zakresy zmienności liczb kwantowych n, l, m podlegają znanym regułom: n = 1, 2,... ; l = 0,..., (n 1) ; l m l. Liczby kwantowe l nazywa się zwyczajowo, kolejno s, p, d, f,... Równanie (63) rozwiązuje się numerycznie, poprzez dyskretyzację na siatce radialnej (zwykle kilkaset punktów), oraz zastosowanie jednego ze znanych algorytmów rekurencyjnych, z warunkami brzegowymi u(0) = 0 i R( ) = 0. Kryterium odnalezienia funkcji i wartości własnej jest równość pochodnych logarytmicznych rozwiązań uzyskiwanych poprzez całkowanie rekurencyjne od lewej (u ) i od prawej (u + ) strony, w wybranym punkcie r m zwanym punktem dopasowania (ang. matching point): d ln(u ) dr r=rm = d ln(u +) r=rm (64) dr

15 Radial Wavefunctions K 15:58:44 Feb scharoch r (bohr) 4s 3p 3s 2p 2s 1s u(r) (arbitrary scale) Fig. 1: Radialne funkcje falowe u lm (r) dla potasu, obliczone programem fhipp Warunek ten zapewnia gładkie zszycie funkcji u i u + w punkcie r m, tzn. równość wartość funkcji oraz ich pierwszych pochodnych. Rozwiązanie numeryczne równania (59) odbywa się w sposób samouzgodniony, ponieważ V SCF jest funkcjonałem gęstości. Tzn. po każdym rozwiązaniu zagadnienia własnego (59), według opisanego wyżej schematu, obliczana jest gęstość (60), nowy potencjał V SCF, itd., aż do ustabilizowania się energii całkowitej. Rysunek 7 pokazuje wyniki obliczeń radialnych funkcji u(r) dla potasu, wykonane programem fhipp. 8 Dynamika układów atomowych. W rozdziale 2.3 przedstawiono koncepcję powierzchni energii swobodnej. Jest to energia całkowita układu jako funkcja wybranych geometrycznych stopni swobody. Minima tej funkcji odpowiadają stanom równowagi statycznej, stabilnym (minimum globalne) lub matastabilnym (minimum lokalne). Jest to podstawowy krok w określeniu możliwych konfiguracji równowagowych. Jednak sytuacja

16 16 8 Dynamika układów atomowych. może się zmienić jeśli uwzględni się temperaturę układu. Jak wiadomo układ minimalizuje wówczas energię swobodną. Potrzena jest zatem analiza termodynamiki, a ta z kolei musi być poprzedzona analizą dynamiki na poziomie mikro czyli dynamiki atomów. W przybliżeniu adiabatycznym atomy poruszają się w polu PES, a zatem wyznaczanie sił sprowadza się do obliczania gradientów PES. Wykorzystuje się przy tym twierdzenie Hellmanna-Feynmana. 8.1 Twierdzenie Hellmanna-Fenmana Twierdzenie Hellmanna-Feynmana mówi, że jeśli energia E λ jest wartością oczekiwaną pewnego hamiltonianu H λ, zależnego od parametru λ, to pochodna tej energii po parametrze λ jest równa wartości oczekiwanej pochodnej hamiltonianu H λ po tym parametrze: Stąd siła F i działająca na atom (69): i ostatecznie: F i = Etot (R) R i F i = E λ λ = ψ λ H λ λ ψ λ (65) = ψ(r) HBO (R) R i ψ(r), (66) n(r, R) V ej (r, R) dr V jj (R), (67) R i R i gdzie n, V ej, V jj to odpowiednio: gęstość elektronowa, energia oddziaływania elektron-jon i energia oddziaływania jon-jon, jak w rozdziale Dynamika Molekularna Znajomość sił pozwala na symulację dynamiki molekularnej (MD - Molecular Dynamics ) poprzez numeryczne rozwiązanie zagadnienia wartości początkowej, i obserwację ewolucji trajektorii atomów w przestrzeni fazowej. Choć od strony ideowej proste, są to obliczenia wymagające bardzo dużych mocy obliczeniowych. Alternatywą jest opisane dalej przybliżenie harmoniczne. 8.3 Przybliżenie harmoniczne W przybliżeniu harmonicznym zakłada się, że siły są liniowymi funkcjami wychyleń atomów z położeń równowagi. Dynamika układu w takim przybliżeniu jest zawsze superpozycją niezależnych oscylacji harmonicznych (modów normalnych). Wektory polaryzacji oraz odpowiadające im częstości tych oscylacji {A n, ω n } znajduje się z rozwiązania zagadnienia własnego: ˆΦA = ω 2 A (68) gdzie [ ] 1 ˆΦ 2 E tot (R) = [Φ ij ] = Mi M j R i R j (69)

17 17 jest macierzą dynamiczną układu. Liczba modów normalnych jest równa 3 N A, gdzie N A jest liczbą atomów w układzie. W przypadku układów periodycznych, jak kryształ, macierz dynamiczna redukuje się, dzięki symetrii translacyjnej, do wymiaru 3x liczba atomów w komórce elementarnej, jednak elementy macierzy (a także jej wektory i wartości własne) są funkcjami wektora falowego k z I strefy Brillouina (BZ - Brillouin Zone ). Mody normalne w takim przypadku są falami płaskimi charakteryzowanymi przez związki dyspersyjne ω(k). Wykorzystując twierdzenie Hellmanna-Feynmana uzyskuje się formułę na drugie pochodne cząstkowe energii całkowitej, potrzebne do konstrukcji macierzy dynamicznej: 2 E tot (R) R i R j + = F i n(r, R) V ej (r, R) = (70) R j R j R i n(r, R) 2 V ej (r, R) dr + 2 V jj (R) R i R j R i R j W formule tej występuje pochodna cząstkowa gęstości elektronowej po współrzędnej atomu n(r, R)/ R j, której obliczanie już nie jest niestety tak łatwe jak obliczanie sił. Do jej wyznaczania w ramach DFT stosuje się teorię liniowej odpowiedzi lub rachunku zaburzeń. Istnieje też inna metoda wyznaczania macierzy dynamicznej ˆΦ, wykorzystująca fakt, że macierz ta wiąże siły działające na atomy z wychyleniami: F i = j 2 E tot (R) (R j ) = R i R j j Mi M j Φ ij (R j ) (71) Wykonując obliczenia ab initio sił działających na atomy dla odpowiedniego zestawu wychyleń i wykorzystując powyższy związek można zbudować układ równań, w którym niewiadomymi będą elementy macierzy dynamicznej. Uwzględnienie symetrii zwykle znacznie redukuje liczbę różnych elementów tej macierzy i tak np. dla kryształów o symetrii kubicznej potrzebne jest tylko jedno wychylenie atomu w wybranym kierunku. Metoda zwana jest metodą bezpośrednią (Ref). 9 Termodynamika układów atomowych. 9.1 Termodynamika w skali nano Rozważania prowadzone w tym rozdziale oparte będą na koncepcji zespołu kanonicznego. W ramach tej koncepcji układ będący w równowadze termicznej z termostatem realizuje mikrostany z prawdopodobieństwem P zależnym tylko od ich energii: P exp( βe) (72) gdzie β = 1/(k B T ), k B jest stałą Boltzmana a T temperaturą układu (i termostatu). Czynnikiem normującym prawdopodobieństwa jest 1/Z, gdzie Z = E exp( βe) (73)

18 18 9 Termodynamika układów atomowych. to tzw. funkcja rozdziału (lub suma statystyczna). Jest to podstawowa wielkość w termodynamice statystycznej. Korzystając z relacji: F = ln(z) β (74) (75) gdzie F jest energią układu, poprzez związki termodynamiczne można wyznaczyć wszystkie inne charakterystyki. Można także obliczać wartości średnie pewnych parametrów zależnych od energii (x(e)), jako wartości oczekiwane (ˆx), uzyskując w ten sposób ich zależności temperaturowe (uśrednianie po zespole kanonicznym): ˆx(T ) = x = 1 x(e) exp( βe) (76) Z E Często mamy doczynienia z sytuacją gdy z różnych powodów energię w wyrażeniu (73) można rozseparować, tzn. przedstawić jako sumę pewnych niezależnych składowych. Energię można rozseparować np. ze względu na stopnie swobody, np.: pędowe i konfiguracyjne stopnie swobody w układach klasycznych, translacyjne oraz rotacyjne i oscylacyjne stopnie swobody w cząsteczkach, oscylacyjne mody normalne w układach wieloatomowych w przybliżeniu harmonicznym, w sytuacji, gdy potencjał jest superpozycją potencjału, np. dla 3 kierunków kartezjańskich. Szczególnym przypadkiem jest sytuacja, gdy układ można podzielić na słabo oddziałujące podukłady, tzn. gdy ich energia oddziaływania jest mała w porównaniu z energią wzbudzeń samych podukładów. Przykładem jest tu gaz doskonały, który jest układem słabo oddziałujących identycznych podukładów. Do dalszych rozważań przyjmiemy, że energia separuje się na pewien składnik E i i resztę E r : Wówczas funkcja rozdziału staje się iloczynem: E = E i + E r (77) gdzie Z = Z i Zr (78) Z i = E i exp( βe i ) (79) Z r = E r exp( βe r ) (80)

19 9.2 Koncepcja powierzchni energii swobodnej (FES). 19 oraz, definiując F i(r) = ln(z i(r)) β,: F = F i + F r (81) Nietrudno pokazać, że jeśli jakiś parametr układu zależy tylko od energii E i wówczas uśrednianie po całym zespole kanonicznym upraszcza się do uśredniania po składowej energii E i : ˆx i (T ) = 1 Z i E i x i (E) exp( βe i ) (82) W takim sensie możemy mówić o termodynamice pojedynczej cząstki w gazie doskonałym (np. o rozszerzalności cieplnej pojedynczego dimera gazu doskonałego) lub termodynamice pewnego, wybranego stopnia swobody (np. zależności temperaturowej amplitudy wybranego modu normalnego w krysztale). W takim też sensie można mówić o termodynamice układów atomowych o rozmiarach rzędu nanometrów, istotnych w nanotechnologiach. Im mniejszy jest układ, którego termodynamikę w wyżej opisanym sensie chcemy badać, tym istotniejsze są fluktuacje czyli odchylenia od wartości średniej. Jedną z możliwych miar fluktuacji jest odchylenie standardowe: δ(ˆx) = [ (x x ) 2 ] 1/2 (83) W przypadku układów atomowych w nanoskali fluktuacje mają szczególnie istotne znaczenie. 9.2 Koncepcja powierzchni energii swobodnej (FES). W rozdziale 2.3 opisano koncepcję powierzchni energii potencjalnej (PES) jako funkcji pewnych wybranych geometrycznych stopni swobody, zawierającej informację o stanach równowagi statycznej a także dynamice układu. Uwzględnienie temperatury może istotnie zmienić własności strukturalne i termodynamiczne układów. Energia swobodna jest wielkością, którą układ minimalizuje przy braku fizycznych więzów geometrycznych, a także jest punktem wyjścia w obliczeniach charakterystyk termodynamicznych. Ta funkcja powinna więc być punktem wyjścia wszelkich badań. Wydaje się możliwe uogólnienie koncepcji PES na powierzchnię energii swobodnej (FES - Free Energy Surface ). Przypuśćmy, że wektor X charakteryzuje uogólnione współrzędne pewnego zestawu zamrożonych (zewnętrznych, usztywnionych, związanych, unieruchomionych) stopni swobody układu. Mogą to być np.: zmienne strukturalne w krysztale (np. długości wektorów prymitywnych i kąty pomiędzy nimi) składowe tensora odkształceń wybrane współrzędne atomów, np. kartezjańskie lub wzdłuż wektora polaryzacji wybranego modu normalnego wybrane odległości międzyatomowe na powierzchni współrzędne planarne atomu adsorbatu na powierzchni

20 20 9 Termodynamika układów atomowych. odległości pomiędzy wybranymi atomami w złożonej cząsteczce przy czym założymy, że liczba zamrożonych stopni swobody jest znacznie mniejsza od liczby wszystkich stopni swobody. Energia układu jest sumą energii statycznej E s (X), czyli energii na powierzchni PES oraz energii związanej z dynamiką względem uwolnionych stopni swobody E d (X): Funkcja rozdziału przyjmie postać: E = E s (X) + E d (X). (84) Z = E d exp( β[e s + E d )] = exp( βe s )Z d, (85) w której wydzielono wkład dynamiczny do funkcji rozdziału Z d. Energia swobodna, oprócz tego, że jest funkcją temperatury, staje się też funkcją uogólnionych współrzędnych X: F (T, X) = E s (X) 1 β ln[z d(t, X)], (86) którą nazwiemy powierzchnią energii swobodnej (FES). Dwa kolejne gradienty FES względem współrzędnych uogólnionych X: oraz P i (T, X) = F (T, X) X i (87) K ij (T, X) = 2 F (T, X) X i X j (88) mają sens odpowiednio uogólnionych sił (naprężeń) oraz stałych sprężystości. Powierzchnia energii swobodnej wyznaczona z zasad pierwszych może być podstawowym źródłem informacji o układach z punktu widzenia ich własności strukturalnych. Jej minima wyznaczają (zależne od temperatury) stany równowagi układów, znikanie drugich pochodnych może wskazywać na przemianę fazową (utrata stabilności). Możliwa jest taka sytuacja, że występuje fizyczna przyczyna zamrożenia pewnego stopnia swobody w układzie, np. powierzchnia kryształu lub cienka warstwa może być naprężona przez podłoże (kryształ lity). W takim przypadku w stanie równowagi układ minimalizuje energią swobodną Gibbsa, którą w przypadku uogólnionych współrzędnych X można zdefiniować jako: G = F i X i P i (89) 9.3 Metody obliczania funkcji rozdziału. Znanych jest kilka metod obliczania funkcji rozdziału ab initio lub z wykorzystaniem potencjałów empirycznych. Są to: dynamika molekularna - termostat Nosé-Hoovera metoda Monte Carlo (całkowanie po konfiguracyjnych stopniach swobody)

21 9.4 Przykłady zastosowania koncepcji PES i FES 21 przybliżenie harmoniczne W przybliżeniu harmonicznym układ wieloatomowy jest termodynamicznie równoważny układowi niezależnych oscylatorów harmonicznych, tzn. funkcja rozdziału jest iloczynem funkcji rozdziału pojedynczego oscylatora: Z = i Z i (90) gdzie Z i dla oscylatora kwantowego ma postać: Z i = exp( β hω i/2) 1 exp( β hω i ) (91) a energia swobodna jest sumą energii pojedynczych oscylatorów i energii statycznej całego kryształu. F = i F i + E s (92) 9.4 Przykłady zastosowania koncepcji PES i FES A. Kryształ. Najprostszym i znanym przypadkiem zastosowania koncepcji powierzchni energii swobodnej jest przybliżenie kwaziharmoniczne dla kryształu, w którym związanym stopniem swobody jest objętość, a dynamika i termodynamika układu traktowana jest w przybliżeniu harmonicznym. Ciśnienie jest uogólnioną siłą a moduł sprężystości objętościowej uogólnioną stałą sprężystości. Położenie minimum FES zależy od temperatury i opisuje rozszerzalność termiczną kryształu. Z kolei znikanie drugiej pochodnej po objętości (moduł sprężystości objętościowej dążący do zera) oznacza utratę stabilności mechanicznej (przegrzanie, stan bliski topnieniu). B. Powierzchnia. Przykłady PES. C. Atom adsorbatu. Dyskusja.