O spl ataniu kwantowym s lów kilka
|
|
|
- Aleksander Kaczor
- 9 lat temu
- Przeglądów:
Transkrypt
1 O spl ataniu kwantowym s lów kilka Krzysztof Byczuk Instytut Fizyki Teoretycznej, Uniwersytet Warszawski 30 styczeń 2006
2 Rozważania Einsteina, Podolskiego i Rosena Einstein, Podolsky, Rosen (1935) H = H + H Ψ = [ + + ]/ 2 liniowa superpozycja e 0 + π e π 0 e + + e S tot = 0 and S z = 0 - kwantowomechaniczny singlet (Bohm 1954) Ortodoksyjny (kopenhadzki) punkt widzenia: żadna z cz astek nie mia la spinu w górȩ lub w dó l do czasu pomiaru: pomiar dla e spowodowa l kolaps funkcji falowej, i natychmiast wytworzy l spin e + oddalonego 20 l.ś. EPR - Ψ nie może być zupe lnym opisem fizycznej rzeczywistości z zasad a lokalności spooky action at a distance, hidden variable, ghost field,..., aby uratować lokalność teorii
3 Twierdzenie EPR dzisiaj H = H + H locality Ψ EPR = [ + + ]/ 2 QM Verschränkung - entanglement (Schrödinger 1935) reality completness QM jest nielokalna e 0 + π e korelacje na odleg lość wyniki niezależnych pomiarów s a skorelowane (pozostaj a we wzajemnej zależności) nie ma mowy o ponadświetlnym przesy laniu informacji, energii, etc. przyroda jest fundamentalnie nielokalna, co siȩ wyraża w subtelnych korelacjach pomiȩdzy dwiema listami przypadkowych wyników pomiaru spinu
4 Spl atanie dwóch uk ladów w stanie czystym Niech { i A j B } H = H A H B oraz A i B s a rozróżnialne. Dowolny stan Ψ = X ij γ ij i A j B, który nie może być przedstawiony jako iloczyn dwóch stanów nazywany jest stanem spl atanym. spl atanie kwantowe jest konsekwencj a zasady superpozycji i nie ma klasycznego odpowiednika spl atania kwantowe s a kwantowymi korelacjami żaden stan spl atany nie może być wytworzony ze stanu iloczynowego za pomoc a operacji lokalnych i klasycznej komunikacji (LOCC)
5 Ważny przyk lad: stany spl atane Bell a klasyczny uk lad dwupoziomowy (0 lub 1) koduje jeden bit informacji w QM uk lad dwupoziomowy może być jednocześnie w 0 i 1 (spin, polaryzacja, wir) w ogólności nazywamy taki uk lad kwantowym bitem czyli qubit (czytaj: qiubit) - Schumacher (1995) Stany Bell a - maksymalnie spleciony stan dwóch qubitów Ψ = 1 2 [ ] Ψ + = 1 2 [ ] Φ = 1 2 [ ] Φ + = 1 2 [ ]
6 Kwantowa teleportacja Bennett et al. (1993), photons ( ), atoms (2004) Alice i Bob dziel a jeden stan spl atany, np. Φ + = 1 2 [ ]. Alice chce wys lać do Boba wszystkie informacje o nieznanym stanie Φ = a 0 + b 1, który aktualnie posiada, tak aby Bob móg l go odtworzyć u siebie używaj ac cz astek ze swojego laboratorium. To nazywamy kwantow a teleportacj a. Stan kwantowy, który ma Alice bȩdzie zniszczony. Co bȩdzie ze wspólnym stanem spl atanym? Φ Φ + [ Φ + (a 0 + b 1 ) + Φ (a 0 b 1 ) + Ψ + (a 1 + b 0 ) + Ψ (a 1 b 0 )] A: wykonuje rzutowy pomiar na swoich 2 qubitach - LO A: informuje Boba o wyniku (jeden z 4) - CC B: w zależności od wyniku A, B wykonuje 1 lub σ x lub/i σ z - LO koszt: jeden stan Bella jest zjedzony!
7 Stan mieszany operator gȩstości ˆρ = P n p n Ψn Ψn opisuje uk lad sprzȩżony do innego uk ladu, do którego nie mamy dostȩpu stan czysty - maksymalna wiedza ˆρ 2 = ˆρ stan mieszany - statystyczna wiedza, mieszanie różnych stanów czystych może dawać ten sam operator gȩstości, czyli ten sam stan mieszany stany z różnych zespo lów maj ace ten sam operator gȩstości s a eksperymentalnie nierozróżnialne gdy uk lad czysty jest spl atany wtedy każdy z poduk ladów jest w stanie mieszanym, np. Ψ = α 00 + β 11 zredukowany operator gȩstości ˆρA = TrBˆρ = TrB Ψ Ψ = α β Definicja pozytywna: Dwa uk lady w stanie czystym s a spl atane gdy z punktu widzenia każdego z nich z osobna s a one w stanie mieszanym
8 Spl atanie dwóch uk ladów w stanie mieszanym Stan mieszany nie jest spl atany jeśli istnieje wypuk ly rozk lad opertatora gȩstości w stany iloczynowe, t.j. ˆρ = X n p n Ψ n Ψ n z dla każdego n. Ψ n = Ψ A n ΨB n ˆρ sep = X n p nˆρ A ˆρ B mieszanina stanów separowalnych jest zawsze separowalna mieszanina stanów spl atanych nie musi być stanem spl atanym (przyk lad)
9 Mieszanina stanów Bell a ˆρ = 1 2 Φ+ Φ Φ Φ = = 1 2 [ 0 0 A 0 0 B A 1 1 B ] ten separowalny stan mieszany może być otrzymany przez zmieszanie maksymalnie spl atanych stanów Bella mieszanie niszczy spl atanie Przyk lad: Stan Werner a jest spl atany gdy λ > 1/3. ˆρ = 1 (1 λ) Id ˆ + λ Ψ Ψ 4
10 Spl atany stan GHZ Greenberger-Horne-Zeilinger (GHZ) Ψabc = 1 2 ( 0a0b0c + 1a1b1c ) oczywiście jest spl atany ale ˆρbc = Tra Ψabc Ψabc = 1 2 ( 0 b0c 0b0c + 1b1c 1b1c ) b i c nie s a spl atane! (to samo dotyczy par ac i ab) Jeśli a wykona pomiar na stan ± = ( 0 ± 1 )/ 2 wtedy Ψ ± bc = 1 2 ( 0b0c ± 1b1c ) jest stanem spl atanym; a musi poinformować o pomiarze b i c za pomoc a CC!
11 Spl atanie i III zasada termodynamiki spl atanie w uk ladzie wielu cz astek Tw. Nernsta (III zasada termodynamiki) S(T) S 0 = const, lub równoważnie C V (T) = T( S(T)/ T) V 0 gdy T 0. Twierdzenie (Wiesniak et al. (2005)): Tylko gdy spl atanie jest obecne w niskich temperaturach, twierdzenie Nernsta może być spe lnione. dowód (szkic): a.a. stan separowalny daje ograniczenie E B na energiȩ stanu podstawowego U(T = 0) E B i dlatego dla stanów separowalnych (średnie pole) C = U(T) T = T 0 γ U(T) E 0 T γ E B E 0 T 1(2) gdzie mamy 1 dla uk ladów bez szczliny energetycznej, i 2 dla uk ladów ze szczelin a. Tylko gdy E B = E 0 może zachodzić C(T) 0 W ogólności C(T) dla stanów separowalnych.
12 Spl atanie wokó l nas Niech E(ˆρ) bȩdzie miar a (ilości a) spl atania w uk ladzie wielocz astkowym podatność magnetyczna zależy od E(ˆρ) χ = 2 ln Z B 2, χ sep χ = 2 E(ˆρ) B 2 + β 2 H MF H H B 2 LiHo 0,045 Y 0,955 F 4 magnetyczna sól (Nature 03) - bez pola magnetycznego uk lad nieuporz adkowany - w polu magnetycznym uporz adkowanie wiȩksze niż przewidywania średniego pola kwantowe korelacje - spl atanie obecne w niskich T
13 Zakończenie Spl atanie - koncepcja opisuj aca korelacje kwantowe Spl atanie jest źród lem (resource) dla pewnych operacji, klasycznie niemożliwych (kwantowa teleportacja, przerzucanie spl atania, obliczenia kwantowe, kwantowa kryptografia, itd.) Materia makroskopowa jest pe lna kwantowego spl atania Jak je wykorzystać??? Podane przyk lady stanów spl atanych mog lyby znaleźć siȩ w materiale Mechaniki kwantowej I Wiele jest nadal problemów do rozwi azania: miara spl atania, uk lady identycznych cz astek,... Literatura: 1. M. Wiesniak et al., quant-ph/ S. Glish at al., Nature 425, 48 (2003) 3. A. Einstein et al., Phys. Rev. 41, 777 (1935) 4. M.B. Plenio et al., Cont. Phys. 39, 431 (1998)
Miary splątania kwantowego
 kwantowego Michał Kotowski michal.kotowski1@gmail.com K MISMaP, Uniwersystet Warszawski Studenckie Koło Fizyki UW (SKFiz UW) 24 kwietnia 2010 kwantowego Spis treści 1 2 Stany czyste i mieszane Matematyczny
kwantowego Michał Kotowski michal.kotowski1@gmail.com K MISMaP, Uniwersystet Warszawski Studenckie Koło Fizyki UW (SKFiz UW) 24 kwietnia 2010 kwantowego Spis treści 1 2 Stany czyste i mieszane Matematyczny
interpretacje mechaniki kwantowej fotony i splątanie
 mechaniki kwantowej fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Twierdzenie o nieklonowaniu Jak sklonować stan kwantowy? klonowanie
mechaniki kwantowej fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Twierdzenie o nieklonowaniu Jak sklonować stan kwantowy? klonowanie
fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW
 fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW wektory pojedyncze fotony paradoks EPR Wielkości wektorowe w fizyce punkt zaczepienia
fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW wektory pojedyncze fotony paradoks EPR Wielkości wektorowe w fizyce punkt zaczepienia
Kwantowe stany splątane w układach wielocząstkowych. Karol Życzkowski (UJ / CFT PAN) 44 Zjazd PTF Wrocław, 12 września 2017
 Kwantowe stany splątane w układach wielocząstkowych Karol Życzkowski (UJ / CFT PAN) 44 Zjazd PTF Wrocław, 12 września 2017 Otton Nikodym oraz Stefan Banach rozmawiają na ławce na krakowskich plantach
Kwantowe stany splątane w układach wielocząstkowych Karol Życzkowski (UJ / CFT PAN) 44 Zjazd PTF Wrocław, 12 września 2017 Otton Nikodym oraz Stefan Banach rozmawiają na ławce na krakowskich plantach
Kwantowe stany splątane. Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017
 B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
Splątanie a przesyłanie informacji
 Splątanie a przesyłanie informacji Jarosław A. Miszczak 21 marca 2003 roku Plan referatu Stany splątane Co to jest splątanie? Gęste kodowanie Teleportacja Przeprowadzone eksperymenty Możliwości wykorzystania
Splątanie a przesyłanie informacji Jarosław A. Miszczak 21 marca 2003 roku Plan referatu Stany splątane Co to jest splątanie? Gęste kodowanie Teleportacja Przeprowadzone eksperymenty Możliwości wykorzystania
Protokół teleportacji kwantowej
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 9 stycznia 008 Teleportacja kwantowa 1993 Propozycja teoretyczna protokołu teleportacji
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 9 stycznia 008 Teleportacja kwantowa 1993 Propozycja teoretyczna protokołu teleportacji
Wykłady z Mechaniki Kwantowej
 Wykłady z Mechaniki Kwantowej Mechanika Kwantowa, Relatywistyczna Mechanika Kwantowa Wykład dla doktorantów (2017) Wykład 7 Jesteśmy uczniami w szkole natury i kształtujemy nasze pojęcia z lekcji na lekcję.
Wykłady z Mechaniki Kwantowej Mechanika Kwantowa, Relatywistyczna Mechanika Kwantowa Wykład dla doktorantów (2017) Wykład 7 Jesteśmy uczniami w szkole natury i kształtujemy nasze pojęcia z lekcji na lekcję.
W5. Komputer kwantowy
 W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
Kwantowa kooperacja. Robert Nowotniak. Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 17 maja 2007 Materiały źródłowe Prezentacja oparta jest na publikacjach: Johann Summhammer,
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 17 maja 2007 Materiały źródłowe Prezentacja oparta jest na publikacjach: Johann Summhammer,
Spl tanie i inne korelacje kwantowe w ukªadach zªo»onych
 Spl tanie i inne korelacje kwantowe w ukªadach zªo»onych Lech Jakóbczyk Instytut Fizyki Teoretycznej Uniwersytet Wrocªawski 1 / 17 Spl tanie stanów czystych Formalna denicja spl tania Ukªad zªo»ony: Hilberta
Spl tanie i inne korelacje kwantowe w ukªadach zªo»onych Lech Jakóbczyk Instytut Fizyki Teoretycznej Uniwersytet Wrocªawski 1 / 17 Spl tanie stanów czystych Formalna denicja spl tania Ukªad zªo»ony: Hilberta
Seminarium: Efekty kwantowe w informatyce
 Seminarium: Efekty kwantowe w informatyce Aleksander Mądry Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Każdy kto będzie
Seminarium: Efekty kwantowe w informatyce Aleksander Mądry Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Każdy kto będzie
STYSTYSTYKA dla ZOM II dr inż Krzysztof Bryś Wykad 1
 1 STYSTYSTYKA dla ZOM II dr inż Krzysztof Bryś Wykad 1 Klasyczny Rachunek Prawdopodobieństwa. 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany. Posiadamy
1 STYSTYSTYKA dla ZOM II dr inż Krzysztof Bryś Wykad 1 Klasyczny Rachunek Prawdopodobieństwa. 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany. Posiadamy
Świat klasyczny i kwantowy por. WYKŁAD nr 2. Splątane stany - EPR. por. WYKŁAD nr 2. Kwantowa kryptografia i teleportacja. Splątanie kwantowe
 Kwantowa kryptografia i teleportacja. Splątanie kwantowe Świat klasyczny i kwantowy por. WYKŁAD nr a. Poplątane stany. i. Eksperyment EPR. ii. Eksperyment Bella b. Star-Trec, czyli teleportujcie mnie!
Kwantowa kryptografia i teleportacja. Splątanie kwantowe Świat klasyczny i kwantowy por. WYKŁAD nr a. Poplątane stany. i. Eksperyment EPR. ii. Eksperyment Bella b. Star-Trec, czyli teleportujcie mnie!
Funkcje wielu zmiennych
 Funkcje wielu zmiennych 13 Zbiory w przestrzeni Definicja Przestrzeni a trójwymiarow a (przestrzeni a) nazywamy zbiór wszystkich trójek uporz adkowanych (x y z) gdzie x y z R. Przestrzeń tȩ oznaczamy symbolem
Funkcje wielu zmiennych 13 Zbiory w przestrzeni Definicja Przestrzeni a trójwymiarow a (przestrzeni a) nazywamy zbiór wszystkich trójek uporz adkowanych (x y z) gdzie x y z R. Przestrzeń tȩ oznaczamy symbolem
Świat klasyczny i kwantowy
 Kwantowa kryptografia i teleportacja. Splątanie kwantowe Prawo Moore a Jacek.Szczytko@fuw.edu.pl http://www.fuw.edu.pl/~szczytko/nt.4. Prace zaliczeniowe! Zadania Studenckie Do zaliczenia wykładu wymagana
Kwantowa kryptografia i teleportacja. Splątanie kwantowe Prawo Moore a Jacek.Szczytko@fuw.edu.pl http://www.fuw.edu.pl/~szczytko/nt.4. Prace zaliczeniowe! Zadania Studenckie Do zaliczenia wykładu wymagana
bity kwantowe zastosowania stanów splątanych
 bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit kwantowy zawiera więcej informacji niż bit klasyczny
bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit kwantowy zawiera więcej informacji niż bit klasyczny
Informatyka kwantowa. Karol Bartkiewicz
 Informatyka kwantowa Karol Bartkiewicz Informacja = Wielkość fizyczna Jednostka informacji: Zasada Landauera: I A =log 2 k B T ln 2 1 P A R. Landauer, Fundamental Physical Limitations of the Computational
Informatyka kwantowa Karol Bartkiewicz Informacja = Wielkość fizyczna Jednostka informacji: Zasada Landauera: I A =log 2 k B T ln 2 1 P A R. Landauer, Fundamental Physical Limitations of the Computational
kondensat Bosego-Einsteina
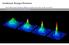 kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
WYKŁAD 15. Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego
 WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
bity kwantowe zastosowania stanów splątanych
 bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit jest jednostką informacji tzn. jest "najmniejszą możliwą
bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit jest jednostką informacji tzn. jest "najmniejszą możliwą
Paradoksy mechaniki kwantowej
 Wykład XX Paradoksy mechaniki kwantowej Chociaż przewidywania mechaniki kwantowej są w doskonałej zgodności z eksperymentem, interpretacyjna strona teorii budzi poważne spory. Przebieg zjawisk w świecie
Wykład XX Paradoksy mechaniki kwantowej Chociaż przewidywania mechaniki kwantowej są w doskonałej zgodności z eksperymentem, interpretacyjna strona teorii budzi poważne spory. Przebieg zjawisk w świecie
Modelowanie Preferencji a Ryzyko. Dlaczego w dylemat więźnia warto grać kwantowo?
 Modelowanie Preferencji a Ryzyko Dlaczego w dylemat więźnia warto grać kwantowo? Marek Szopa U n iwe r s y t e t Ś l ą s k i INSTYTUT FIZYKI im. Augusta Chełkowskiego Zakład Fizyki Teoretycznej Klasyczny
Modelowanie Preferencji a Ryzyko Dlaczego w dylemat więźnia warto grać kwantowo? Marek Szopa U n iwe r s y t e t Ś l ą s k i INSTYTUT FIZYKI im. Augusta Chełkowskiego Zakład Fizyki Teoretycznej Klasyczny
Komputery Kwantowe. Sprawy organizacyjne Literatura Plan. Komputery Kwantowe. Ravindra W. Chhajlany. 27 listopada 2006
 Sprawy organizacyjne Literatura Plan Ravindra W. Chhajlany 27 listopada 2006 Ogólne Sprawy organizacyjne Literatura Plan Współrzędne: Pokój 207, Zakład Elektroniki Kwantowej. Telefon: (0-61)-8295005 Email:
Sprawy organizacyjne Literatura Plan Ravindra W. Chhajlany 27 listopada 2006 Ogólne Sprawy organizacyjne Literatura Plan Współrzędne: Pokój 207, Zakład Elektroniki Kwantowej. Telefon: (0-61)-8295005 Email:
Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera
 Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera Określenie podpierścienia Definicja 9.. Podpierścieniem pierścienia (P, +,, 0, ) nazywamy taki podzbiór A P, który jest pierścieniem ze wzgledu
Wyk lad 9 Podpierścienie, elementy odwracalne, dzielniki zera Określenie podpierścienia Definicja 9.. Podpierścieniem pierścienia (P, +,, 0, ) nazywamy taki podzbiór A P, który jest pierścieniem ze wzgledu
Kondensat Bosego-Einsteina okiem teoretyka
 Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
W poszukiwaniu kszta ltów kulistych
 W poszukiwaniu kszta ltów kulistych Piotr Mankiewicz April 4, 2005 Konwersatorium dla doktorantów Notacje 1 Cia lo wypuk le - wypuk ly, domkniȩty podzbiór ograniczony w R n. Odleg lość geometryczna dwóch
W poszukiwaniu kszta ltów kulistych Piotr Mankiewicz April 4, 2005 Konwersatorium dla doktorantów Notacje 1 Cia lo wypuk le - wypuk ly, domkniȩty podzbiór ograniczony w R n. Odleg lość geometryczna dwóch
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 12 - Algorytmy i protokoły kwantowe Jarosław Miszczak IITiS PAN Gliwice 19/05/2016 1 / 39 1 Motywacja rozwoju informatyki kwantowej. 2 Stany kwantowe. 3 Notacja Diraca.
Obliczenia inspirowane Naturą Wykład 12 - Algorytmy i protokoły kwantowe Jarosław Miszczak IITiS PAN Gliwice 19/05/2016 1 / 39 1 Motywacja rozwoju informatyki kwantowej. 2 Stany kwantowe. 3 Notacja Diraca.
po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x)
 Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Wprowadzenie do teorii komputerów kwantowych
 Wprowadzenie do teorii komputerów kwantowych mgr inż. Olga Siedlecka olga@icis.pcz.pl Instytut Informatyki Teoretycznej i Stosowanej Wprowadzenie do teorii komputerów kwantowych p.1/35 Plan seminarium
Wprowadzenie do teorii komputerów kwantowych mgr inż. Olga Siedlecka olga@icis.pcz.pl Instytut Informatyki Teoretycznej i Stosowanej Wprowadzenie do teorii komputerów kwantowych p.1/35 Plan seminarium
Stany atomu wieloelektronowego o określonej energii. być przypisywane elektrony w tym stanie atomu.
 Notatki do wyk ladu VI Stany atomu wieloelektronowego o określonej energii. Konfiguracja elektronowa atomu - zbiór spinorbitali, wykorzystywanych do konstrukcji funkcji falowej dla danego stanu atomu;
Notatki do wyk ladu VI Stany atomu wieloelektronowego o określonej energii. Konfiguracja elektronowa atomu - zbiór spinorbitali, wykorzystywanych do konstrukcji funkcji falowej dla danego stanu atomu;
Sterowalność liniowych uk ladów sterowania
 Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Różne oblicza splątania kwantowego
 Różne oblicza splątania kwantowego Ryszard Horodecki Krajowe Centrum Informatyki Kwantowej, Zakład Optyki i Informacji Kwantowej Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański Various
Różne oblicza splątania kwantowego Ryszard Horodecki Krajowe Centrum Informatyki Kwantowej, Zakład Optyki i Informacji Kwantowej Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański Various
VIII. TELEPORTACJA KWANTOWA Janusz Adamowski
 VIII. TELEPORTACJA KWANTOWA Janusz Adamowski 1 1 Wprowadzenie Teleportacja kwantowa polega na przesyłaniu stanów cząstek kwantowych na odległość od nadawcy do odbiorcy. Przesyłane stany nie są znane nadawcy
VIII. TELEPORTACJA KWANTOWA Janusz Adamowski 1 1 Wprowadzenie Teleportacja kwantowa polega na przesyłaniu stanów cząstek kwantowych na odległość od nadawcy do odbiorcy. Przesyłane stany nie są znane nadawcy
Wyk lad 4 Dzia lania na macierzach. Określenie wyznacznika
 Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Rozdzia l 2. Najważniejsze typy algebr stosowane w logice
 Rozdzia l 2. Najważniejsze typy algebr stosowane w logice 1. Algebry Boole a Definicja. Kratȩ dystrybutywn a z zerem i jedynk a, w której dla każdego elementu istnieje jego uzupe lnienie nazywamy algebr
Rozdzia l 2. Najważniejsze typy algebr stosowane w logice 1. Algebry Boole a Definicja. Kratȩ dystrybutywn a z zerem i jedynk a, w której dla każdego elementu istnieje jego uzupe lnienie nazywamy algebr
Informatyka kwantowa. Zaproszenie do fizyki. Zakład Optyki Nieliniowej. wykład z cyklu. Ryszard Tanaś. mailto:tanas@kielich.amu.edu.
 Zakład Optyki Nieliniowej http://zon8.physd.amu.edu.pl 1/35 Informatyka kwantowa wykład z cyklu Zaproszenie do fizyki Ryszard Tanaś Umultowska 85, 61-614 Poznań mailto:tanas@kielich.amu.edu.pl Spis treści
Zakład Optyki Nieliniowej http://zon8.physd.amu.edu.pl 1/35 Informatyka kwantowa wykład z cyklu Zaproszenie do fizyki Ryszard Tanaś Umultowska 85, 61-614 Poznań mailto:tanas@kielich.amu.edu.pl Spis treści
VI. KORELACJE KWANTOWE Janusz Adamowski
 VI. KORELACJE KWANTOWE Janusz Adamowski 1 1 Korelacje klasyczne i kwantowe Zgodnie z teorią statystyki matematycznej współczynnik korelacji definiujemy jako cov(x, y) corr(x, y) =, (1) σ x σ y gdzie x
VI. KORELACJE KWANTOWE Janusz Adamowski 1 1 Korelacje klasyczne i kwantowe Zgodnie z teorią statystyki matematycznej współczynnik korelacji definiujemy jako cov(x, y) corr(x, y) =, (1) σ x σ y gdzie x
Metody obliczeniowe chemii kwantowej oparte na funkcji falowej. Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać:
 Metody obliczeniowe chemii kwantowej oparte na funkcji falowej Równanie Schrödingera: ĤΨ = EΨ Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać: Ĥ = h 2 K α=1 1 2M α 2 α h2 2m
Metody obliczeniowe chemii kwantowej oparte na funkcji falowej Równanie Schrödingera: ĤΨ = EΨ Dla uk ladu N elektronów i K j ader atomowych hamiltonian przyjmuje postać: Ĥ = h 2 K α=1 1 2M α 2 α h2 2m
STATYSTYKA MATEMATYCZNA dla ZPM I dr inż Krzysztof Bryś wyk lad 1,2 KLASYCZNY RACHUNEK PRAWDOPODOBIEŃSTWA
 1 STATYSTYKA MATEMATYCZNA dla ZPM I dr inż Krzysztof Bryś wyk lad 1,2 KLASYCZNY RACHUNEK PRAWDOPODOBIEŃSTWA 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany.
1 STATYSTYKA MATEMATYCZNA dla ZPM I dr inż Krzysztof Bryś wyk lad 1,2 KLASYCZNY RACHUNEK PRAWDOPODOBIEŃSTWA 1. Pojȩcia wstȩpne. Doświadczeniem losowym nazywamy doświadczenie, którego wynik nie jest znany.
Postulaty mechaniki kwantowej
 3.10.2004 11. Postulaty mechaniki kwantowej 120 Rozdział 11 Postulaty mechaniki kwantowej Mechanika kwantowa, jak zresztą każda teoria fizyczna, bazuje na kilku postulatach, które przyjmujemy "na wiarę".
3.10.2004 11. Postulaty mechaniki kwantowej 120 Rozdział 11 Postulaty mechaniki kwantowej Mechanika kwantowa, jak zresztą każda teoria fizyczna, bazuje na kilku postulatach, które przyjmujemy "na wiarę".
Normy wektorów i macierzy
 Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
TEORIA FUNKCJONA LÓW. (Density Functional Theory - DFT) Monika Musia l
 TEORIA FUNKCJONA LÓW GȨSTOŚCI (Density Functional Theory - DFT) Monika Musia l PRZEDMIOT BADAŃ Uk lad N elektronów + K j ader atomowych Przybliżenie Borna-Oppenheimera Zamiast funkcji falowej Ψ(r 1,σ 1,r
TEORIA FUNKCJONA LÓW GȨSTOŚCI (Density Functional Theory - DFT) Monika Musia l PRZEDMIOT BADAŃ Uk lad N elektronów + K j ader atomowych Przybliżenie Borna-Oppenheimera Zamiast funkcji falowej Ψ(r 1,σ 1,r
Wstęp do komputerów kwantowych
 Obwody kwantowe Uniwersytet Łódzki, Wydział Fizyki i Informatyki Stosowanej 2008/2009 Obwody kwantowe Bramki kwantowe 1 Algorytmy kwantowe 2 3 4 Algorytmy kwantowe W chwili obecnej znamy dwie obszerne
Obwody kwantowe Uniwersytet Łódzki, Wydział Fizyki i Informatyki Stosowanej 2008/2009 Obwody kwantowe Bramki kwantowe 1 Algorytmy kwantowe 2 3 4 Algorytmy kwantowe W chwili obecnej znamy dwie obszerne
Magnetyczne metale i izolatory od antycznych odkryć do wspó lczesnej teorii
 Magnetyczne metale i izolatory od antycznych odkryć do wspó lczesnej teorii Krzysztof Byczuk Instytut Fizyki Teoretycznej, Uniwersytet Warszawski, Polska Instytut Fizyki, Uniwersytet Augsburski, Niemcy
Magnetyczne metale i izolatory od antycznych odkryć do wspó lczesnej teorii Krzysztof Byczuk Instytut Fizyki Teoretycznej, Uniwersytet Warszawski, Polska Instytut Fizyki, Uniwersytet Augsburski, Niemcy
Analiza zrekonstruowanych śladów w danych pp 13 TeV
 Analiza zrekonstruowanych śladów w danych pp 13 TeV Odtwarzanie rozk ladów za pomoc a danych Monte Carlo Jakub Cholewiński, pod opiek a dr hab. Krzysztofa Woźniaka 31 lipca 2015 r. Jakub Cholewiński, pod
Analiza zrekonstruowanych śladów w danych pp 13 TeV Odtwarzanie rozk ladów za pomoc a danych Monte Carlo Jakub Cholewiński, pod opiek a dr hab. Krzysztofa Woźniaka 31 lipca 2015 r. Jakub Cholewiński, pod
Zagadnienie Dualne Zadania Programowania Liniowego. Seminarium Szkoleniowe Edyta Mrówka
 Zagadnienie Dualne Zadania Programowania Liniowego Seminarium Szkoleniowe Edyta Mrówka Ogólne zagadnienie PL Znajdź taki wektor X = (x 1, x 2,..., x n ), który minimalizuje kombinacje liniow a przy ograniczeniach
Zagadnienie Dualne Zadania Programowania Liniowego Seminarium Szkoleniowe Edyta Mrówka Ogólne zagadnienie PL Znajdź taki wektor X = (x 1, x 2,..., x n ), który minimalizuje kombinacje liniow a przy ograniczeniach
Algebra i jej zastosowania konspekt wyk ladu, czȩść druga
 Algebra i jej zastosowania konspekt wyk ladu, czȩść druga Anna Romanowska January 29, 2016 4 Kraty i algebry Boole a 41 Kraty zupe lne Definicja 411 Zbiór uporza dkowany (P, ) nazywamy krata zupe lna,
Algebra i jej zastosowania konspekt wyk ladu, czȩść druga Anna Romanowska January 29, 2016 4 Kraty i algebry Boole a 41 Kraty zupe lne Definicja 411 Zbiór uporza dkowany (P, ) nazywamy krata zupe lna,
Jacek Jurkowski. Korelacje nieklasyczne Kwantowe splątanie i dyskord
 Jacek Jurkowski Korelacje nieklasyczne Kwantowe splątanie i dyskord Toruń, 2014 Recenzenci: dr hab. Andrzej Jamiołkowski, prof. UMK prof. dr hab. Ryszard Horodecki Projekt okładki: Tomasz Jaroszewski c
Jacek Jurkowski Korelacje nieklasyczne Kwantowe splątanie i dyskord Toruń, 2014 Recenzenci: dr hab. Andrzej Jamiołkowski, prof. UMK prof. dr hab. Ryszard Horodecki Projekt okładki: Tomasz Jaroszewski c
Wyk lad 6 Podprzestrzenie przestrzeni liniowych
 Wyk lad 6 Podprzestrzenie przestrzeni liniowych 1 Określenie podprzestrzeni Definicja 6.1. Niepusty podzbiór V 1 V nazywamy podprzestrzeni przestrzeni liniowej V, jeśli ma on nastepuj ace w lasności: (I)
Wyk lad 6 Podprzestrzenie przestrzeni liniowych 1 Określenie podprzestrzeni Definicja 6.1. Niepusty podzbiór V 1 V nazywamy podprzestrzeni przestrzeni liniowej V, jeśli ma on nastepuj ace w lasności: (I)
1. Matematyka Fizyki Kwantowej: Cześć Druga
 . Matematyka Fizyki Kwantowej: Cześć Druga Piotr Szańkowski I. PRZESTRZEŃ WEKTOROWA Kolejnym punktem naszej jest ogólna struktura matematyczna mechaniki kwantowej, która jest strukturą przestrzeni wektorowej
. Matematyka Fizyki Kwantowej: Cześć Druga Piotr Szańkowski I. PRZESTRZEŃ WEKTOROWA Kolejnym punktem naszej jest ogólna struktura matematyczna mechaniki kwantowej, która jest strukturą przestrzeni wektorowej
Wyk lad 5 W lasności wyznaczników. Macierz odwrotna
 Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera
 Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
O symetrycznej rozszerzalności stanów kwantowych i jej zastosowaniach
 Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Katedra Fizyki Teoretycznej i Informatyki Kwantowej Streszczenie rozprawy doktorskiej O symetrycznej rozszerzalności stanów kwantowych
Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Katedra Fizyki Teoretycznej i Informatyki Kwantowej Streszczenie rozprawy doktorskiej O symetrycznej rozszerzalności stanów kwantowych
Wyk lad 7 Metoda eliminacji Gaussa. Wzory Cramera
 Wyk lad 7 Metoda eliminacji Gaussa Wzory Cramera Metoda eliminacji Gaussa Metoda eliminacji Gaussa polega na znalezieniu dla danego uk ladu a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
Wyk lad 7 Metoda eliminacji Gaussa Wzory Cramera Metoda eliminacji Gaussa Metoda eliminacji Gaussa polega na znalezieniu dla danego uk ladu a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
Układy statystyczne. Jacek Jurkowski, Fizyka Statystyczna. Instytut Fizyki
 Instytut Fizyki 2015 Stany mikroskopowe i makroskopowe w układzie wielopoziomowym Stany mikroskopowe i makroskopowe w układzie wielopoziomowym N rozróżnialnych cząstek, z których każda może mieć energię
Instytut Fizyki 2015 Stany mikroskopowe i makroskopowe w układzie wielopoziomowym Stany mikroskopowe i makroskopowe w układzie wielopoziomowym N rozróżnialnych cząstek, z których każda może mieć energię
Rozdzia l 10. Najważniejsze normalne logiki modalne
 Rozdzia l 10. Najważniejsze normalne logiki modalne 1. Logiki modalne normalne Definicja. Inwariantny zbiór formu l X jȩzyka modalnego L = (L,,,,, ) nazywamy logik a modaln a zbazowan a na logice klasycznej
Rozdzia l 10. Najważniejsze normalne logiki modalne 1. Logiki modalne normalne Definicja. Inwariantny zbiór formu l X jȩzyka modalnego L = (L,,,,, ) nazywamy logik a modaln a zbazowan a na logice klasycznej
Wyk lad 12. (ii) najstarszy wspó lczynnik wielomianu f jest elementem odwracalnym w P. Dowód. Niech st(f) = n i niech a bedzie
 1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
Monika Musia l. METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe)
 Monika Musia l METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe) ĤΨ i = E i Ψ i W metodzie mieszania konfiguracji wariacyjna funkcja falowa, jest liniow a kombinacj a
Monika Musia l METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe) ĤΨ i = E i Ψ i W metodzie mieszania konfiguracji wariacyjna funkcja falowa, jest liniow a kombinacj a
Metody obliczeniowe chemii teoretycznej
 Metody obliczeniowe chemii teoretycznej mechanika kwantowa mechanika klasyczna ւ ց WFT DFT MM FFM metody bazuj ace na metody bazuj ace na Mechanika Molekularna funkcji falowej gȩstości elektronowej Wave
Metody obliczeniowe chemii teoretycznej mechanika kwantowa mechanika klasyczna ւ ց WFT DFT MM FFM metody bazuj ace na metody bazuj ace na Mechanika Molekularna funkcji falowej gȩstości elektronowej Wave
Matematyka A, klasówka, 24 maja zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le. rozwia
 Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
Matematyka A, klasówka, 4 maja 5 Na prośbe jednej ze studentek podaje zania zadań z kolokwium z matematyki A w nadziei, że pope lni lem wielu b le dów Podać definicje wektora w lasnego i wartości w lasnej
Rozdział 8 Paradoksy i zastosowania Mechaniki Kwantowej
 Rozdział 8 Paradoksy i zastosowania Mechaniki Kwantowej 8.1: Interpretacja Kopenhaska 8.2: Paradoks Einsteina- Podolskiego-Rosena 8.3: Stany splątane 8.4: Konsekwencje EPR 8.5: Ukryte założenia: lokalność
Rozdział 8 Paradoksy i zastosowania Mechaniki Kwantowej 8.1: Interpretacja Kopenhaska 8.2: Paradoks Einsteina- Podolskiego-Rosena 8.3: Stany splątane 8.4: Konsekwencje EPR 8.5: Ukryte założenia: lokalność
TELEPORTACJA NIEZNANEGO STANU KWANTOWEGO
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 04 Seria: ORGANIZACJA I ZARZĄDZANIE z. 68 Nr kol. 905 Marcin SOBOTA Politechnika Śląska Wydział Organizacji i Zarządzania TELEPORTACJA NIEZNANEGO STANU KWANTOWEGO
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 04 Seria: ORGANIZACJA I ZARZĄDZANIE z. 68 Nr kol. 905 Marcin SOBOTA Politechnika Śląska Wydział Organizacji i Zarządzania TELEPORTACJA NIEZNANEGO STANU KWANTOWEGO
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania
 Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x)
 Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
Stan czastki określa funkcja falowa Ψ zależna od wspó lrzȩdnych określaj acych po lożenie cz astki i od czasu (t). Dla cz astki, która może poruszać siȩ tylko w jednym wymiarze (tu x) Wartości funkcji
ANALIZA II 15 marca 2014 Semestr letni. Ćwiczenie 1. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la?
 Ci ag lość i norma Ćwiczenie. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la? f (x, y) = x2 y 2 x 2 + y 2, f 2(x, y) = x2 y x 2 + y 2 f 3 (x, y) = x2 y
Ci ag lość i norma Ćwiczenie. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la? f (x, y) = x2 y 2 x 2 + y 2, f 2(x, y) = x2 y x 2 + y 2 f 3 (x, y) = x2 y
Radosław Chrapkiewicz, Piotr Migdał (SKFiz UW) Optyczny wzmacniacz parametryczny jako źródło splątanych par fotonów
 Optyczny wzmacniacz parametryczny jako źródło splątanych par fotonów Radosław Chrapkiewicz, Piotr Migdał (SKFiz UW) VII OSKNF 8 XI 2008 Plan Po co nam optyka kwantowa? Czerwony + Czerwony = Niebieski?
Optyczny wzmacniacz parametryczny jako źródło splątanych par fotonów Radosław Chrapkiewicz, Piotr Migdał (SKFiz UW) VII OSKNF 8 XI 2008 Plan Po co nam optyka kwantowa? Czerwony + Czerwony = Niebieski?
Optyka kwantowa wprowadzenie. Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej
 Optyka kwantowa wprowadzenie Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej Krótka (pre-)historia fotonu (1900-1923) Własności światła i jego oddziaływania
Optyka kwantowa wprowadzenie Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej Krótka (pre-)historia fotonu (1900-1923) Własności światła i jego oddziaływania
h 2 h p Mechanika falowa podstawy pˆ 2
 Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Suma i przeciȩcie podprzestrzeń, suma prosta, przestrzeń ilorazowa Javier de Lucas
 Suma i przeciȩcie podprzestrzeń suma prosta przestrzeń ilorazowa Javier de Lucas Ćwiczenie 1 W zależności od wartości parametru p podaj wymiar przestrzeni W = v 1 v v 3 gdzie p 0 v 1 = 1 + p 3 v = 5 3
Suma i przeciȩcie podprzestrzeń suma prosta przestrzeń ilorazowa Javier de Lucas Ćwiczenie 1 W zależności od wartości parametru p podaj wymiar przestrzeni W = v 1 v v 3 gdzie p 0 v 1 = 1 + p 3 v = 5 3
Niezwykłe cechy informacji kwantowej
 Niezwykłe cechy informacji kwantowej Michał Horodecki Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański 1. Wstęp Koncepcja informacji kwantowej zrodziła się na pograniczu dwóch dziedzin:
Niezwykłe cechy informacji kwantowej Michał Horodecki Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański 1. Wstęp Koncepcja informacji kwantowej zrodziła się na pograniczu dwóch dziedzin:
Matematyka dyskretna Oznaczenia
 Matematyka dyskretna Oznaczenia Andrzej Szepietowski W tym rozdziale przedstawimy podstawowe oznacznia. oznacza kwantyfikator ogólny dla każdego. oznacza kwantyfikator szczegó lowy istnieje. 1 Sumy i iloczyny
Matematyka dyskretna Oznaczenia Andrzej Szepietowski W tym rozdziale przedstawimy podstawowe oznacznia. oznacza kwantyfikator ogólny dla każdego. oznacza kwantyfikator szczegó lowy istnieje. 1 Sumy i iloczyny
Oddzia lywania miedzycz. jony molekularne lub atomy. edzy A i B:
 Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
Wyk lad 3 Wyznaczniki
 1 Określenie wyznacznika Wyk lad 3 Wyznaczniki Niech A bedzie macierza kwadratowa stopnia n > 1 i niech i, j bed a liczbami naturalnymi n Symbolem A ij oznaczać bedziemy macierz kwadratowa stopnia n 1
1 Określenie wyznacznika Wyk lad 3 Wyznaczniki Niech A bedzie macierza kwadratowa stopnia n > 1 i niech i, j bed a liczbami naturalnymi n Symbolem A ij oznaczać bedziemy macierz kwadratowa stopnia n 1
Wyk lad 9 Baza i wymiar przestrzeni liniowej
 Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Zadania. kwiecień 2009. Ćwiczenia III. Zadanie 1. Uk lad A o energii E A skontaktowano termicznie z uk ladem B o energii E B.
 kwiecień 009 Ćwiczenia III Zadania Zadanie 1 Uk lad A o energii E A skontaktowano termicznie z uk ladem B o energii E B Udowodnić że jeżeli ln Ω A (E A < ln Ω B(E B E A E B to energia przep lynie z uk
kwiecień 009 Ćwiczenia III Zadania Zadanie 1 Uk lad A o energii E A skontaktowano termicznie z uk ladem B o energii E B Udowodnić że jeżeli ln Ω A (E A < ln Ω B(E B E A E B to energia przep lynie z uk
Postulaty mechaniki kwantowej
 Wyk lad 2 Postulaty mechaniki kwantowej 1 wymiar Postulat Stan czastki określa funkcja falowa Ψ = Ψ(x, t) zależna od po lożenia czastki x oraz czasu t. Interpretacje fizyczna ma jedynie kwadrat modu lu
Wyk lad 2 Postulaty mechaniki kwantowej 1 wymiar Postulat Stan czastki określa funkcja falowa Ψ = Ψ(x, t) zależna od po lożenia czastki x oraz czasu t. Interpretacje fizyczna ma jedynie kwadrat modu lu
Czastka swobodna Bariera potencja lu Pud lo jednowymiarowe FEMO Pud la wielowymiarowe. Wyk lad 3. Uk lady modelowe I
 Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Wyk lad 3 Uk lady modelowe I Hamiltonian, równania Schrödingera hamiltonian Ĥ(x) = ˆT (x) = 2 d 2 2m dx 2 równanie Schrödingera zależne od czasu stany stacjonarne 2 2 Ψ(x, t) Ψ(x, t) 2m x 2 = i t dψ E
Strategie kwantowe w teorii gier
 Uniwersytet Jagielloński adam.wyrzykowski@uj.edu.pl 18 stycznia 2015 Plan prezentacji 1 Gra w odwracanie monety (PQ penny flip) 2 Wojna płci Definicje i pojęcia Równowagi Nasha w Wojnie płci 3 Kwantowanie
Uniwersytet Jagielloński adam.wyrzykowski@uj.edu.pl 18 stycznia 2015 Plan prezentacji 1 Gra w odwracanie monety (PQ penny flip) 2 Wojna płci Definicje i pojęcia Równowagi Nasha w Wojnie płci 3 Kwantowanie
Fizyka dla wszystkich
 Fizyka dla wszystkich Wykład popularny dla młodzieży szkół średnich Splątane kubity czyli rzecz o informatyce kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 21 kwietnia 2004 Spis treści 1
Fizyka dla wszystkich Wykład popularny dla młodzieży szkół średnich Splątane kubity czyli rzecz o informatyce kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 21 kwietnia 2004 Spis treści 1
Liczba 2, to jest jedyna najmniejsza liczba parzysta i pierwsza. Oś liczbowa. Liczba 1, to nie jest liczba pierwsza
 1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 3 Liczba 2, to jest jedyna najmniejsza liczba parzysta i pierwsza 2 1 0 1 2 3 x Oś liczbowa. Liczba 1, to nie jest liczba pierwsza MATEMATYKA
1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 3 Liczba 2, to jest jedyna najmniejsza liczba parzysta i pierwsza 2 1 0 1 2 3 x Oś liczbowa. Liczba 1, to nie jest liczba pierwsza MATEMATYKA
Elementy analizy funkcjonalnej PRZESTRZENIE LINIOWE
 Elementy analizy funkcjonalnej PRZESTRZENIE LINIOWE Niech K = R lub K = C oraz X - dowolny zbiór. Określmy dwa dzia lania: dodawanie + : X X X i mnożenie przez liczbȩ : K X X, spe lniaj ace nastȩpuj ace
Elementy analizy funkcjonalnej PRZESTRZENIE LINIOWE Niech K = R lub K = C oraz X - dowolny zbiór. Określmy dwa dzia lania: dodawanie + : X X X i mnożenie przez liczbȩ : K X X, spe lniaj ace nastȩpuj ace
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman ( ) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd.
 Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
Funkcje wielu zmiennych
 Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Podstawy informatyki kwantowej
 Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Algebra i jej zastosowania ćwiczenia
 Algebra i jej zastosowania ćwiczenia 14 stycznia 2013 1 Kraty 1. Pokazać, że każda klasa kongruencji kraty (K, +, ) jest podkrata kraty (K, +, ). 2. Znaleźć wszystkie kongruencje kraty 2 3, gdzie 2 jest
Algebra i jej zastosowania ćwiczenia 14 stycznia 2013 1 Kraty 1. Pokazać, że każda klasa kongruencji kraty (K, +, ) jest podkrata kraty (K, +, ). 2. Znaleźć wszystkie kongruencje kraty 2 3, gdzie 2 jest
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina.
 Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych W podstawowym problemie sterowania optymalnego minimalizacji
Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych W podstawowym problemie sterowania optymalnego minimalizacji
Testowanie hipotez statystycznych
 Testowanie hipotez statystycznych Wyk lad 8 Natalia Nehrebecka Stanis law Cichocki 29 listopada 2015 Plan zajeć 1 Rozk lad estymatora b Rozk lad sumy kwadratów reszt 2 Hipotezy proste - test t Badanie
Testowanie hipotez statystycznych Wyk lad 8 Natalia Nehrebecka Stanis law Cichocki 29 listopada 2015 Plan zajeć 1 Rozk lad estymatora b Rozk lad sumy kwadratów reszt 2 Hipotezy proste - test t Badanie
Rachunek zdań - semantyka. Wartościowanie. ezyków formalnych. Semantyka j. Logika obliczeniowa. Joanna Józefowska. Poznań, rok akademicki 2009/2010
 Logika obliczeniowa Instytut Informatyki Poznań, rok akademicki 2009/2010 1 formu l rachunku zdań Wartościowanie i sta le logiczne Logiczna równoważność 2 Model formu ly Formu la spe lniona Formu la spe
Logika obliczeniowa Instytut Informatyki Poznań, rok akademicki 2009/2010 1 formu l rachunku zdań Wartościowanie i sta le logiczne Logiczna równoważność 2 Model formu ly Formu la spe lniona Formu la spe
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
TEORIE KWANTOWE JAKO PODSTAWA NOWOCZESNEJ KRYPTOGRAFII QUANTUM TEORIIES AS MODERN CRYPTOGRAPHY BASIS
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ Seria: ORGANIZACJA I ZARZĄDZANIE z. XX XXXX Nr kol. XXXX Marcin SOBOTA Politechnika Śląska Wydział Organizacji i Zarządzania Instytut Ekonometrii i Informatyki TEORIE
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ Seria: ORGANIZACJA I ZARZĄDZANIE z. XX XXXX Nr kol. XXXX Marcin SOBOTA Politechnika Śląska Wydział Organizacji i Zarządzania Instytut Ekonometrii i Informatyki TEORIE
Lewitron TM - prosta zabawka fizyczna o wyrafinowanej teorii dzia lania
 Lewitron TM - prosta zabawka fizyczna o wyrafinowanej teorii dzia lania Krzysztof Byczuk Instytut Fizyki Teoretycznej, Uniwersytet Warszawski http://www.physik.uni-augsburg.de/theo3/kbyczuk/index.html
Lewitron TM - prosta zabawka fizyczna o wyrafinowanej teorii dzia lania Krzysztof Byczuk Instytut Fizyki Teoretycznej, Uniwersytet Warszawski http://www.physik.uni-augsburg.de/theo3/kbyczuk/index.html
Rozdzia l 11. Przestrzenie Euklidesowe Definicja, iloczyn skalarny i norma. iloczynem skalarnym.
 Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
Testowanie hipotez statystycznych
 round Testowanie hipotez statystycznych Wyk lad 9 Natalia Nehrebecka Stanis law Cichocki 13 grudnia 2014 Plan zajeć 1 Rozk lad estymatora b Rozk lad sumy kwadratów reszt 2 Hipotezy proste - test t Badanie
round Testowanie hipotez statystycznych Wyk lad 9 Natalia Nehrebecka Stanis law Cichocki 13 grudnia 2014 Plan zajeć 1 Rozk lad estymatora b Rozk lad sumy kwadratów reszt 2 Hipotezy proste - test t Badanie
Wyk lad 7 Baza i wymiar przestrzeni liniowej
 Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
Testowanie hipotez statystycznych
 Testowanie hipotez statystycznych Wyk lad 9 Natalia Nehrebecka Stanis law Cichocki 28 listopada 2018 Plan zaj eć 1 Rozk lad estymatora b 2 3 dla parametrów 4 Hipotezy l aczne - test F 5 Dodatkowe za lożenie
Testowanie hipotez statystycznych Wyk lad 9 Natalia Nehrebecka Stanis law Cichocki 28 listopada 2018 Plan zaj eć 1 Rozk lad estymatora b 2 3 dla parametrów 4 Hipotezy l aczne - test F 5 Dodatkowe za lożenie
Fizyka statystyczna Teoria Ginzburga-Landaua w średnim polu. P. F. Góra
 Fizyka statystyczna Teoria Ginzburga-Landaua w średnim polu P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Parametr porzadku W niskich temperaturach układy występuja w fazach, które łamia symetrię
Fizyka statystyczna Teoria Ginzburga-Landaua w średnim polu P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Parametr porzadku W niskich temperaturach układy występuja w fazach, które łamia symetrię
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA. Ćwiczenia. http://zcht.mfc.us.edu.pl/ mm
 CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
Szum w urzadzeniu półprzewodnikowym przeszkoda czy szansa?
 Szum w urzadzeniu półprzewodnikowym przeszkoda czy szansa? szczegółowe zastosowania kwantowego szumu śrutowego J. Tworzydło Instytut Fizyki Teoretycznej Uniwersytet Warszawski Sympozjum Instytutu Fizyki
Szum w urzadzeniu półprzewodnikowym przeszkoda czy szansa? szczegółowe zastosowania kwantowego szumu śrutowego J. Tworzydło Instytut Fizyki Teoretycznej Uniwersytet Warszawski Sympozjum Instytutu Fizyki
