Sterowanie napędów maszyn i robotów
|
|
|
- Anna Świątek
- 6 lat temu
- Przeglądów:
Transkrypt
1 Wykład 7 - układy sterowania zwykłego Instytut Automatyki i Robotyki Warszawa, 2014
2 Kryteria oceny jakości sterowania Kryteria oceny jakości sterowania Standardowe miary jakości sterowania Modyfikacje standardowych miar jakości sterowania Niestandardowe kryteria i wskaźniki oceny Wskaźniki sumowe (całkowe) Wskaźniki sumowe modyfikowane
3 Kryteria oceny jakości sterowania Miary jakości sterowania współczesnych napędów opierają się na kryteriach oceny bezpośredniej przebiegu w czasie odpowiedzi na skokową zmianę wartości sygnału zadającego - podstawą wyboru są trzy (standardowe) kryteria
4 Kryteria oceny jakości sterowania minimalizacja ustalonej (statycznej) odchyłki procesu sterowania (e su ): I esu = α es s(k u ) s o min (1) minimalizacja maksymalnej odchyłki przejściowej (dynamiczna: przeregulowania lub nadwyżki) e sp o kierunku przeciwnym do odchyłki początkowej, określanej w procedurze o schemacie: { } I esp = α esp max 0, max [(s(k) s o )sgn(s o s pocz )] min (2) 0<k<k u minimalizacja czasu zakończenia (traktowanego alternatywnie jako czas ustalania, pozycjonowania lub doregulowania) procesu pozycjonowania wyrażony przez czas dyskretny k konc lub (w praktyce wygodniejsze) przez czas ciągły t = k konc T p : I t = α t k konc T p min (3) gdzie: α es, α esp i α t są wagami oceny, s o i s pocz położeniem zadanym i początkowym ocenianego procesu.
5 Kryteria oceny jakości sterowania W praktyce oceny prowadzone są według opcjonalnych w stosunku do podanych zależności, dodatkowych warunków i żądań np. w sterowaniu pozycyjnym, dla zadania przestawiania: dla odchyłki ustalonej e su z warunkami zatrzymania ruchu lub osiągnięcia czasu oceny I esu dla ˆv(k u ) â(k u ) = 0 lub gdy k k oc, z reguły k oc < k u (4) dla przeregulowania nadwyżki e sp : nieprzekroczenia określonej krotności odchyłki ustalonej, w praktyce κ < 2, 5 > e sw /e su κe sdop (5)
6 Kryteria oceny jakości sterowania dla czasu zakończenia procesu pozycjonowania k konc traktowanego jako: czas ustalania k u(t u, I tu) - z warunkiem zatrzymania ruchu (jak poprzednio) czas pozycjonowania k p(t p, I tp) z warunkiem osiągnięcia dopuszczalnej wartości odchyłki położenia, e s e sdop czas doregulowania k ur (t ur, I tur ) z warunkiem postoju w strefie dopuszczalnej I tur gdy [ˆv(k u) â(k u) = 0] [ e s e sdop ] (6) i oceną w czasie k oc, 0 < k u, k p, k ur k oc, ograniczonym przez długość taktu pracy napędzanego urządzenia.
7 Kryteria oceny jakości sterowania Ocena jakości w oparciu o wymienione wskaźniki, jest łatwa w praktycznej realizacji, najczęściej nie prowadzi jednak do oczekiwanych wyników optymalizacji sterowania pojawiają się następujące problemy: wzajemna sprzeczność kryteriów w odniesieniu do zadań sterowania - np. żądanie większej dokładności (zmniejszenie e sdop ) prowadzi do wydłużenia czasu ustalania (t u ). obecność przeregulowania w warunkach przemysłowych e sp : w części zadań pozycjonowania wykluczone jest pojawienie się tej odchyłki i to bez względu na pogorszenie innych wskaźników (ruchy robocze), w innych zadaniach, celowość skrócenia czasu ruchu pozwala na duże przekroczenia wartości zadanej (ruchy dobiegowe)
8 Kryteria oceny jakości sterowania Rysunek : Ilustracja niejednoznaczności oceny jakości i optymalizacji sterowania pozycyjnego pneumatycznego napędu dławieniowego na przykładzie zależności: a) czas ustalania t u od dopuszczalnej wartości odchyłki ustalonej e sdop i obciążenia masowego m obc, b) liczba przełączeń rozdzielacza u rprze od wartości odchyłki e sdop.
9 Kryteria oceny jakości sterowania przeregulowanie, będące następstwem oscylacyjności słabo tłumionego układu napędowego, może być wykorzystane w trakcie uruchomieniowego (startowego), iteracyjnego strojenia nastaw, zróżnicowane wymagania odnośnie pracy układu napędowego w urządzeniach automatyki i robotyki - do wymagań wymienionych można dołączyć: żądania o charakterze ogólnym, na przykład: określonej powtarzalności zachowań dokładnościowych i czasowych - w warunkach zmieniających się obciążeń masowych, siłowych itd. likwidacji pełzania - stabilizacji położenia po (chwilowym) ustaniu ruchu zadanej podatności obciążeniowej statycznej i dynamicznej minimalizacji wpływu zmieniających się obciążeń na odchyłkę sterowania w warunkach postoju i ruchu żądania o charakterze funkcjonalnym, związane ze specyfiką realizacji w konkretnej technice napędowej zadań pozycyjnych (przestawianie, nadążania), siłowych, momentowych, przyspieszeniowych itp.
10 Niestandardowe kryteria i wskaźniki oceny W opisanej sytuacji różnorodności uniwersalnych kryteriów oceny jakości układu pozycyjnego, warto rozważyć zastosowanie kryteriów niestandardowych - uwzględniające specyfikę układu. Np. dla pneumatycznego dławieniowego układu pozycyjnego można stosować wskaźniki jakości pozycjonowania rozszerzone o liczbę przełączeń rozdzielacza proporcjonalnego.
11 Niestandardowe kryteria i wskaźniki oceny Wskaźniki sumowe (całkowe) ITAE (Integral of Time Multipled with Absolute Error) k oc I ITAE = k e s (k) min (7) k=0 ITSE (Integral of Time with Square Error) k oc I ITSE = [kes 2 (k)] min (8) k=0
12 Niestandardowe kryteria i wskaźniki oceny Cechą wspólną wskaźników ITAE i ITSE, oprócz pożądanego uwzględnienia podstawowych parametrów procesu sterowania napędu, tzn. czasu i odchyłki, jest bardzo silne dowartościowanie początkowej fazy procesu, w której wartość odchyłki jest zbliżona do wartości zadanej - prowadzi to do oceny końcowej niekorzystnej w stosunku do najbardziej istotnej dla przebiegu procesu fazy zbliżania się do wartości zadanej. W zakresie pracy liniowej (modelu) układu napędowego znalezienie minimum obu funkcjonałów nie nastręcza trudności i wartościom tym odpowiada też spełnienie innych kryteriów (odchyłki ustalonej, maksymalnej odchyłki przejściowej, czasu zakończenia), jednak w przypadku pracy nieliniowej rzeczywistego napędu związek wartości wskaźników ITAE i ITSE z minimalizacją wartości parametrów czasowych i dokładnościowych sterowania przestaje być oczywisty.
13 Niestandardowe kryteria i wskaźniki oceny Rysunek : Optymalizacja układu pozycyjnego z wykorzystaniem wskaźników sumowych (na przykładzie sterowania pozycyjnego pneumatycznego napędu dławieniowego).
14 Niestandardowe kryteria i wskaźniki oceny Wskaźniki sumowe modyfikowane zmodyfikowany wskaźnik I ITAE mod1 I ITAE mod1 = k oc mod k=0 k s(k) + k oc mod k=k oc mod k e s (k) min (9) Czas podziału k oc mod jest wyliczany ze wzmocnienia w torze głównym układu sterowania pozycyjnego: k oc mod = 1/(k s C m ) (k s = k x1 w przypadku sterowania ze sprzężeniem zwrotnym od zmiennych stanu) zmodyfikowany wskaźnik I ITAE mod2 I ITAE mod2 = k oc mod k=k oc mod (k k oc mod ) 2 e s (k) min (10) Z całkowitym wycięciem fazy początkowej przebiegu i liczeniem wartości wskaźnika wg przyjętego funkcjonału dopiero po czasie k oc mod (k oc mod < k oc ) osiągnięcia przez odpowiedź skokową układu pozycyjnego maksymalnej wartości przemieszczenia (s o + e sp max )
15 Niestandardowe kryteria i wskaźniki oceny Pierwszy wskaźnik I ITAE mod1 sprawdza się tylko w przypadku obiektów o dużym czasie opóźnienia i silnie aperiodycznym zachowaniu. Drugi wskaźnik I ITAE mod2 ograniczony jest do przypadku słabo tłumionych zachowań układu napędowego i wyraźnym przeregulowaniu, będącym warunkiem rozpoczęcia liczenia (mija się z wymaganiami praktycznymi).
16 Niestandardowe kryteria i wskaźniki oceny Wskaźniki sumowe - nowe modyfikacje wskaźnik jednokryterialny I IAED - w postaci różnicy wartości odpowiedzi układu regulowanego (zamkniętego) i układu nieregulowanego (otwartego) e s(o z) (k) - dla początkowej fazy przebiegu procesu sterowana, tzn. aż do czasu k oc otw określonego osiągnięciem wartości zadanej (np. przemieszczenia s o ) przez odpowiedź układu napędowego przy pełnym wysterowaniu k oc otw : s otw s o = 0 (11) i następnie - aż do czasu oceny k oc - przez wskaźnik I IAED = k oc otw k=0 k e s(o z) (k) + k oc k=k oc otw k e s (k) min (12)
17 Niestandardowe kryteria i wskaźniki oceny Rysunek : Ilustracja oceny jakości układu pozycyjnego z wykorzystaniem wskaźnika I IAED (na przykładzie sterowania pozycyjnego pneumatycznego napędu dławieniowego).
18 Niestandardowe kryteria i wskaźniki oceny Istotą kryterium IAED (ang. Integral of Absolute Real and Standard Error Difference) jest ocena zachowania zamkniętego układu pozycyjnego względem standaryzowanego - przez ograniczenie jego przemieszczenia do wartości zadanej so - zachowania układu otwartego (odniesienia); kryterium spełnia podstawowe wymagania praktyczne dotyczące oceny jakości sterowania pozycyjnego układów napędowych : pozwala oceniać zachowanie regulowanego układu napędowego względem równoważnego napędu standardowego (przełączalnego), uwzględnia ograniczenia energetyczne wykorzystywanego napędu i prowadzi do optymalnego - w danej realizacji - działania układu pozycyjnego, różnicuje oceny jakości dla różnych wariantów i nastaw sterowania, przebieg odniesienia (zachowanie układu nieregulowanego, otwartego) może być tworzony zarówno analitycznie (symulacyjnie), jak i poprzez eksperyment uruchomieniowy.
19 Niestandardowe kryteria i wskaźniki oceny Wskaźniki sumowe - nowe modyfikacje wskaźnik wielokryterialny I SETOC - w postaci ważonej sumy wskaźników (np. (odchyłki ustalonej, maksymalnej odchyłki przejściowej, czasu zakończenia) z ewentualnymi funkcjonalnymi wskaźnikami uzupełniającymi charakterystycznymi dla danego napędu, np. dla napędu pneumatycznego I SETOC = α esu I esu + α esp I esp + α tu I tu + α ur prze I ur prze min (13) Zapewnia to proporcjonalny, zróżnicowany przez poszczególne współczynniki wagowe, wpływ poszczególnych kryteriów na końcową ocenę; wymaga doboru wartości wag, np. dla napędu pneumatycznego pomyślne wyniki optymalizacji uzyskano po przyjęciu wartości wag: α esu = 1, 0/µm, α esp = 0, 2/µm, α tu = 0, 1/ms oraz α ur prze = 2, 0.
20 Realizacje układów sterowania zwykłego Realizacje układów sterowania zwykłego Układy jednoobwodowe Układy kaskadowe Układy wieloobwodowe ze sprzężeniem od zmiennych stanu: fizykalnych lub fazowych
21 Realizacje układów sterowania zwykłego Układy jednoobwodowe Z konwencjonalnym działaniem typu P, PD, PI, PID i działaniami zmodyfikowanymi w wersji dyskretnej: pozycyjna (wersja rzadko stosowana) 1 k 1 e s (k) e s (k 1) u(k) = α P k P e s (k) + α P [e s (i)t p ] + α D T D T I T p i=1 (14) Wymagającej pamiętania informacji o odchyłce e s (k) od początku sterowania, aż do chwili bieżącej i = k.
22 Realizacje układów sterowania zwykłego przyrostowa u(k) u(k 1) = k P [ w wersji rekursywnej gdzie: Układy jednoobwodowe ] e s(k) e s(k 1) + Tp e s(k) 2e s(k 1) + e s(k 2) e s(k 1) + T D T I T p (15) u(k) = u(k 1) + q 0 e s (k) + q 1 e s (k 1) + q 2 e s (k 2) (16) q 0 = k p [ 1 + T D T p ] [, q 1 = k p 1 T D + 2T ] D T D, q 2 = k p (17) T p T p T p Transmitancję dyskretną działania regulacyjnego opisuje zależność G PID (z) = u(z) e s (z) = q 0 + q 1 z 1 + q 2 z 2 1 z 1 (18)
23 Realizacje układów sterowania zwykłego Układy jednoobwodowe - UWAGI w wersji dyskretnej inaczej niż w ciągłej można wprowadzić różniczkowanie quasi-idealne przez zastąpienie go operatorem różnicy, którego wartości są skończone nawet w przypadku skokowej zmiany wartości zadanej s 0 (k) dla doboru nastaw mozna stosować różne podejścia, w praktyce np. wymuszanie przy pomocy sterowania proporcjonalnego k P drgań niegasnących układu napędowego o okresie T kr (k P = k kr ) i dobór nastaw na podstawie oferowanych tablic (np. Ziegler, Nichols, 1942) lub zależności [ k p = 0.6k kr 1 T ] p ; T p T kr T I = 1, 2 k kr T p k p T kr ; T D T p = 0.08 k kr T kr k p T p (19)
24 Realizacje układów sterowania zwykłego Układy kaskadowe Stosowane powszechnie w układach napędowych osi ruchu maszyn i robotów przemysłowych w postaci obwodów sterowania: położenia (P), prędkości obrotowej (PI), prądu (PI),
25 Realizacje układów sterowania zwykłego Przyczyny powszechności zastosowań układów kaskadowych dobór nastaw regulatorów i optymalizacja są bardzo proste - od wewnątrz na zewnątrz kaskady, ograniczona liczba nastaw podstawowym parametrem jest współczynnik wzmocnienia prędkościowego k v, obliczany z warunku: dla ruchu postępowego k v = v s ruch ustalony (20) dla ruchu obrotowego k v = ω ϖ ruch ustalony (21) tzn. żądanego stosunku prędkości (rzeczywistej) do odchyłki położenia w ruchu ustalonym (odchyłki nadążania, śledzenia), prosta i tania realizacja sprzętowa i/lub programowa.
26 Realizacje układów sterowania zwykłego Układy wieloobwodowe ze sprzężeniem od zmiennych stanu: fizykalnych lub fazowych w przypadku zadania przestawiania u(k) = k x1 [s o s(k)] k x2ˆv(k) k x3 â(k) (22) W postaci modalnej równania sterowania, wymuszającej przez liniowe sprzężenie zwrotne k x = [k x1 k x2 k x3 ] przejście procesu ruchu od stanu początkowego x = [0 0 0] T do końcowego x = [s o 0 0]T
27 Realizacje układów sterowania zwykłego Układy wieloobwodowe ze sprzężeniem od zmiennych stanu: fizykalnych lub fazowych w przypadku zadania nadążania { vcnc (k) = k CNC [s o s(k)], k CNC = kx1 k x2 u(k) = k x2 [v CNC ˆv(k)] k 3 â(k) (23) W postaci dostosowanej do układów o strukturze kaskadowej stosowanej w handlowych sterownikach typu CNC (ang. Computer Numerical Control) maszyn i robotów przemysłowych; w sterownikach CNC nadrzędna część układu realizując zadanie sterowania pozycyjnego o działaniu proporcjonalnym k CNC wytwarza z odchyłki śledzenia [s(k) s o (k)] sygnał wirtualnej prędkości zadanej v CNC dla podporządkowanej części układu realizującej sterowanie prędkością.
28 Realizacje układów sterowania zwykłego Rysunek : Wieloobwodowy układ regulacji, ze sprzężeniem od zmiennych stanu - zadanie przestawiania
29 Realizacje układów sterowania zwykłego Rysunek : Wieloobwodowy układ regulacji, ze sprzężeniem od zmiennych stanu - zadanie nadążania, w postaci dostosowanej do układów o strukturze kaskadowej stosowanej w handlowych sterownikach typu CNC
30 Kompensacja nieliniowości charakterystyk procesu Kompensacja nieliniowości charakterystyk procesu
31 Kompensacja nieliniowości charakterystyk procesu Ograniczeniem kształtowania właściwości dynamicznych układu sterowania napędu (np. pozycyjnego) przez dobór macierzy sprzężeń zwrotnych k x są nieliniowości zachowań procesu (ruchu,...) realizowanego przez układ napędowy; uwzględnienie nieliniowości może być prowadzone: bezpośrednio, przez składnik korekcyjny w równaniu sterowania metodą: przez bezpośredni pomiar w procedurze uruchomieniowej, przez szacowanie współczynników wybranej postaci funkcji opisującej charakterystykę prędkościową: rozszerza to zadanie identyfikacji o dodatkowe współczynniki (szacowanie to może być niepotrzebne - np. dla napędu pneumatycznego, przy założeniu stacjonarności charakterystyki przepływowej zaworu proporcjonalnego (główna przyczyna nieliniowości), charakterystyka prędkościowa może być traktowana jako czasowo i parametrycznie inwariantna - dla konkretnego układu napędowego i jego obciążenia masowego m obc. pośrednio, przez wprowadzenie dodatkowych elementów nieliniowości do modeli procesu
32 Kompensacja nieliniowości charakterystyk procesu Rysunek : Nieliniowości nastawnika napędu na przykładzie rozdzielaczy proporcjonalnych napędów pneumatycznych: a) przepływowy, b) ciśnieniowy
33 Kompensacja nieliniowości charakterystyk procesu Rysunek : Nieliniowości charakterystyk napędu na przykładzie siłownikowych napędów pneumatycznych: a) przepływowa, b) ciśnieniowa, c) tarciowa, d) prędkościowa
34 Kompensacja nieliniowości charakterystyk procesu W nowej metodzie określenia nieliniowości charakterystyki prędkościowej napędu (rys. d) wprowadzono jako wielkość pomocniczą - opisującą zachowania nieliniowe charakterystyki prędkościowej v(u) - efektywność hamowania h e (u) { ah (u) a h (u 0) a h e (u) = h (u min) a h (u gdy u < u 0) min, 0) a h (u) a h (u 0) a h (u max) a h (u gdy u (0, u (24) 0) max > Jest ona zdefiniowana jako różnica opóźnień hamowania przy danym a h (u) i zerowym wysterowaniu a h (u 0 ), normowaną przy użyciu różnicy opóźnień hamowania dla minimalnego / maksymalnego (u min, u max ) oraz zerowego wysterowania (u 0 ), gdzie opóźnienie hamowania a h (u) a h (u) = v(t pocz) v(t konc ) a h (t pocz t konc (25) jest określone względem stałych wartości prędkości: początkowej (dobranej doświadczalnie jako v pocz = 0, 3m/s) i końcowej (v konc = 0m/s) oraz chwil czasowych: t pocz przekroczenia wartości v pocz i t konc zatrzymania; wartość efektywności h e (u) jest określana w eksperymencie uruchomieniowym dla wybranych wartości wysterowania.
35 Kompensacja nieliniowości charakterystyk procesu Następnie, odwrócenie ciągu wartości h e (u i ) z zastosowaniem interpolacji liniowej przebiegu pomiędzy kolejnymi punktami podporowymi tworzy ciągłą charakterystykę korekcji nieliniowości charakterystyki prędkościowej. c k (u) = c k (u i )+ u u i [c k (u i+1 ) c k (u i )] dla u < u i, u i+1 >, i = n,.., n u i+1 u i (26) gdzie: n oznacza liczbę punktów podporowych gałęzi charakterystyki. Rysunek : Kompensacja nieliniowości charakterystyki sterowania prędkościowego pneumatycznego napędu dławieniowego przez wyznaczenie charakterystyki efektywności hamowania h e(u) i jej charakterystyki korekcyjnej
36 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie kwadratowego wskaźnika jakości Dobór nastaw na podstawie zadanych wartości własnych Dobór nastaw na podstawie przyjętych wartości wzmocnienia, pulsacji drgań swobodnych i współczynnika tłumienia modelu i układu zamkniętego Dobór nastaw na podstawie poszukiwania minimalnych wartości wskaźników oceny jakości sterowania i optymalnych zachowań napędu
37 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie kwadratowego wskaźnika jakości Ze względu na zbliżenie postaci funkcjonału do wskaźników całkowych o wyraźnym sensie fizycznym, metoda uważana za najbardziej zbliżoną do wymagań praktycznych w porównaniu z innymi metodami analitycznymi; przyjmując wskaźnik kwadratowy w postaci k oc I S = p[e s (k)] 2 + q[u(k)] 2 min (27) k=0 gdzie: p i q to stałe i dodatnie współczynniki wag. Oraz godząc się na rozwiązanie suboptymalne odpowiadające nieograniczonemu czasowi oceny k oc (w praktyce aż do osiągnięcia stanu ustalonego: k oc = k u ), macierz sprzężenia zwrotnego (macierz wzmocnień sterowania) k x określa zależność k x = q 1 B T mdr md (28) gdzie: macierz R md o wymiarze n n (np. n = 3) jest rozwiązaniem algebraicznego równania Riccatiego.
38 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie kwadratowego wskaźnika jakości Równanie Ricattiego R md A md A T mdr md + q 1 R md B md B T mdr md p = 0 (29) Próby przeniesienia koncepcji doboru nastaw (na podstawie kwadratowego wskaźnika jakości) na układy napędowe zakończyły się niepowodzeniem - zmiana współczynnika wag we wskaźniku, np. kosztu sterowania q (przy koszcie odchyłki p = 1) bardzo słabo optymalizuje zachowanie się układu pozycyjnego: dla dużych wartości q prowadzi do zachowań aperiodycznych, dalece nieoptymalnych ( słabe sterowanie), dla małych wartości q do zachowania zbliżonego do pożądanego, ale obarczonego silną periodycznością ( silne sterowanie).
39 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie kwadratowego wskaźnika jakości Rysunek : Typowe przebiegi sterowania pozycyjnego, w przypadku doboru nastaw na podstawie wskaźnika jakości I s - gdzie: p = 1, q zmienne, współczynnik k ω = ω oz/ω oo określa dynamikę zachowań napędu w układzie zamkniętym względem układu otwartego
40 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie zadanych wartości własnych metoda uważana jest za trudną ze względu na brak przekonujących - w stosunku do wymagań jakościowych sterowania - przesłanek wyboru tych wartości, które sprowadzają się do znanego, werbalnego warunku wyboru - np. wartości bezwzględnych s i - odpowiednio większych od wartości bezwzględnych części rzeczywistych dominujących wartości własnych układu otwartego; Korzystając ze znanych macierzy A mc, B mc i C mc modelu i narzucając n pierwiastków s 1, s 2,..., s n równania charakterystycznego układu zamkniętego, macierz wzmocnień (sprzężenia zwrotnego) k x określa tu równanie det(si A mc + B mc k x ) = (s s 1 )(s s 2 )...(s s n ) (30) z warunkiem Res i < 0, i = 1, 2,..., n (31)
41 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie zadanych wartości własnych Analogiczne warunki i zależności mogą być podane dla układu dyskretnego z n narzuconymi wartościami własnymi z i, i = 1,..., n; problemem pozostaje konkretyzacja wyboru wartości własnych. W technice napędowej zaleca się podejście opierające się na dwóch przesłankach odnoszących się do zamkniętego układu pozycyjnego: zachowań dynamicznych pulsacji drgań swobodnych ω oz układu, narzucenia dwóch, granicznych stosunków wartości sąsiadujących ze sobą współczynników równania charakterystycznego a i /a i+1 a i = ω oz a i oraz = ω oz, i = 1,..., n (32) a i+1 3 (3/2) i a i+1 2 (3/2) i
42 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie zadanych wartości własnych Zaletą metody jest prosta implementacja; przyjmując, że wartość pulsacji ω oz układu zamkniętego - w stosunku do ω oo otwartego układu napędowego (np. pozycyjnego; w praktyce ω om modelu układu) została dobrana realistycznie, tzn. ich stosunek k ω np. dla napędu pneumatycznego zawiera się w obszarze k ω (1, 5) (ograniczeniem są tu zachowania dynamiczne konkretnego napędu, przede wszystkim jego wydajność energetyczna). Podczas badań sterowania pneumatycznego napędu dławieniowego jakość przebiegów sterowania nie odbiega jednak - od doboru nastaw na podstawie kwadratowego wskaźnika jakości - problemem pozostaje oczywiście realistyczny wybór wartości ω oz.
43 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie przyjętych wartości wzmocnienia, pulsacji drgań swobodnych i współczynnika tłumienia modelu i układu zamkniętego Metoda ta jest rozwinięciem metody opartej na narzuceniu wartości pulsacji ω oz przez przyjęcie wartości dwóch pozostałych parametrów zachowań układu zamkniętego, tzn. wzmocnienia układowego C z i tłumienia D z. Metoda, uwzględniając wymagania praktyki przemysłowej, niewiele różni się od konieczności bezpośredniego poszukiwania nastaw; nawet ograniczając zakres wartości narzucanych parametrów np. poprawne zachowania układu pozycyjnego dla typowych napędów, warunków pracy i przeciętnych wartości parametrów modelu (np. napędu pneumatycznego) C m < 0, 15, 1, 5 > m/sv, ω om < 10, 60 > rd/s, D m < 0, 1, 1, 5 > (33) charakteryzują wartości zawierające się w obszarach C z (0, 15ω oz, 0, 35ω oz ), ω oz (ω om, 5ω om )rd/s, D z (0, 7, 0, 9) (34)
44 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie poszukiwania minimalnych wartości wskaźników oceny jakości sterowania i optymalnych zachowań napędu Akceptowalna jakość sterowania przy eksperymentalnym wyznaczeniu nastaw i trudności analitycznego doboru, są argumentami (prób) stosowania wybranych metod optymalizacji sterowania. Z wielu gotowych rozwiązań z tego zakresu najbardziej przydatne okazały się statyczne, zdeterminowane, bezgradientowe i gradientowe metody poszukiwania minimum istotą jest iteracyjne przeszukiwanie przestrzeni utworzonej z obszaru przewidywalnej zmienności dwóch lub trzech elementów macierzy wzmocnień (sprzężenia zwrotnego k x ), celem jest znalezienie minimum wybranego wskaźnika jakości sterowania, operatorem układ napędowy (np. pozycyjny) z rzeczywistym napędem lub jego modelem zbudowanym w oparciu o zależności bilansowe, wynikiem dobór macierzy wzmocnień (sprzężenia zwrotnego k x ).
45 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie poszukiwania minimalnych wartości wskaźników oceny jakości sterowania i optymalnych zachowań napędu Schemat postępowania optymalizacyjnego polega ogólnie na: odwzorowaniu wartości wybranego wskaźnika jakości I (k x ) z zachowań operatora Ω(k x ) I (k x, i) = {Ω[k x (i)] : k x (i) = k x (i 1) + τ k x, τ T } (35) poszukiwaniu w ciągu i N, {I (k x, i)} N i=1, minimalnej wartości funkcjonału wskaźnika wskazującej na znalezienie optymalnej wartości macierzy k xopt I (k xopt, i) = min I (k x, i), k xopt = lim(k x, i) (36) k x K kx i N gdzie τ, T są wektorem i zbiorem optymalnych wektorów współczynników kroku, k x macierzą wartości kroku.
46 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie poszukiwania minimalnych wartości wskaźników oceny jakości sterowania i optymalnych zachowań napędu Rysunek : Dobór nastaw sterowania pozycyjnego pneumatycznego napędu dławieniowego, b1) - idealne, b2-3) niedoregulowanie, b4-b5) przeregulowanie
47 Koncepcje doboru nastaw sterowania oraz ocena ich przydatności praktycznej Dobór nastaw na podstawie poszukiwania minimalnych wartości wskaźników oceny jakości sterowania i optymalnych zachowań napędu Głównym problemem metody jest jej czasochłonność i pracochłonność. Iteracja z kilkoma - kilkudziesięcioma cyklami pozycjonowania wyklucza zastosowania jej w trakcie normalnej pracy, w praktyce ograniczając się do przypadku cyklicznej pracy napędu). Powyższy problem dotyczy także rozruchu uruchomieniowego.
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Sterowanie napędów maszyn i robotów
 Wykład 7 - Układy sterowania. Ocena jakości układów sterowania. Instytut Automatyki i Robotyki Warszawa, 2016 Realizacje układów sterowania zwykłego Realizacje układów sterowania zwykłego układy jednoobwodowe,
Wykład 7 - Układy sterowania. Ocena jakości układów sterowania. Instytut Automatyki i Robotyki Warszawa, 2016 Realizacje układów sterowania zwykłego Realizacje układów sterowania zwykłego układy jednoobwodowe,
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Ćwiczenie 1. Badanie aktuatora elektrohydraulicznego. Sterowanie Napędów Maszyn i Robotów Przemysłowych - laboratorium. Instrukcja laboratoryjna
 Sterowanie Napędów Maszyn i Robotów Przemysłowych - laboratorium Ćwiczenie 1 Badanie aktuatora elektrohydraulicznego Instrukcja laboratoryjna Opracował : mgr inż. Arkadiusz Winnicki Warszawa 2010 Badanie
Sterowanie Napędów Maszyn i Robotów Przemysłowych - laboratorium Ćwiczenie 1 Badanie aktuatora elektrohydraulicznego Instrukcja laboratoryjna Opracował : mgr inż. Arkadiusz Winnicki Warszawa 2010 Badanie
Sterowanie Napędów Maszyn i Robotów
 Wykład 3 - Metodyka projektowania sterowania. Opis bilansowy Instytut Automatyki i Robotyki Warszawa, 2015 Metodyka projektowania sterowania Zrozumienie obiektu, możliwości, ograniczeń zapoznanie się z
Wykład 3 - Metodyka projektowania sterowania. Opis bilansowy Instytut Automatyki i Robotyki Warszawa, 2015 Metodyka projektowania sterowania Zrozumienie obiektu, możliwości, ograniczeń zapoznanie się z
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Sterowanie napędów maszyn i robotów
 Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 3 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 3 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Sterowanie mechanizmów wieloczłonowych
 Wykład 6 - Modelowanie napędów złączy Instytut Automatyki i Robotyki Warszawa, 2019 Modelowanie napędu złączy - silniki DC Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Wykład 6 - Modelowanie napędów złączy Instytut Automatyki i Robotyki Warszawa, 2019 Modelowanie napędu złączy - silniki DC Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
11. Dobór rodzaju, algorytmu i nastaw regulatora
 205 11. Dobór rodzaju, algorytmu i nastaw regulatora 11.1 Wybór rodzaju i algorytmu regulatora Poprawny wybór rodzaju regulatora i jego algorytmu uzależniony jest od znajomości (choćby przybliżonej) właściwości
205 11. Dobór rodzaju, algorytmu i nastaw regulatora 11.1 Wybór rodzaju i algorytmu regulatora Poprawny wybór rodzaju regulatora i jego algorytmu uzależniony jest od znajomości (choćby przybliżonej) właściwości
Sterowanie napędów maszyn i robotów
 Wykład 8 - zaawansowane układy sterowania Instytut Automatyki i Robotyki Warszawa, 2014 adaptacyjne (ang. adaptive control) z dostosowaniem się do aktualnych warunków pracy napędu - koncepcje: ze wstępnie
Wykład 8 - zaawansowane układy sterowania Instytut Automatyki i Robotyki Warszawa, 2014 adaptacyjne (ang. adaptive control) z dostosowaniem się do aktualnych warunków pracy napędu - koncepcje: ze wstępnie
Podstawy Automatyki. Wykład 6 - Miejsce i rola regulatora w układzie regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Sterowanie napędów maszyn i robotów
 Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 1 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
Sterowanie napędów maszyn i robotów dr inż. Jakub Możaryn Wykład 1 Instytut Automatyki i Robotyki Wydział Mechatroniki Politechnika Warszawska, 2014 Projekt współfinansowany przez Unię Europejską w ramach
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ. T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
 REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
Automatyka i sterowanie w gazownictwie. Regulatory w układach regulacji
 Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena LABORATORIUM 4. PODSTAW 5. AUTOMATYKI
 Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
Sterowanie Napędów Maszyn i Robotów
 Wykład 4 - Model w przestrzeni stanów Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Do zaprojektowania układu regulacji pozycji siłownika pneumatycznego, poszukiwany jest model dynamiki układu w
Wykład 4 - Model w przestrzeni stanów Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Do zaprojektowania układu regulacji pozycji siłownika pneumatycznego, poszukiwany jest model dynamiki układu w
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
Automatyka i robotyka
 Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Kryterium miejsca geometrycznego pierwiastków
 7.5.3. Kryterium miejsca geometrycznego pierwiastków Wprowadzenie Miejsce geometryczne pierwiastków równania charakterystycznego układu zamkniętego (mgp) umożliwia między innymi wyznaczenie wymaganego
7.5.3. Kryterium miejsca geometrycznego pierwiastków Wprowadzenie Miejsce geometryczne pierwiastków równania charakterystycznego układu zamkniętego (mgp) umożliwia między innymi wyznaczenie wymaganego
14.9. Regulatory specjalne
 14.9. Regulatory specjalne Weźmy pod uwagę względną stałą czasową obiektu regulacji T w Tz Jeżeli względna stała czasowa jest duża, czyli gdy T w >= 1, to można stosować regulatory konwencjonalne, np.
14.9. Regulatory specjalne Weźmy pod uwagę względną stałą czasową obiektu regulacji T w Tz Jeżeli względna stała czasowa jest duża, czyli gdy T w >= 1, to można stosować regulatory konwencjonalne, np.
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa.
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Dla naszego obiektu ciągłego: przy czasie próbkowania T p =2.
 1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
WYDZIAŁ ELEKTRYCZNY KATEDRA AUTOMATYKI I ELEKTRONIKI. Badanie układu regulacji dwustawnej
 POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Temat /6/: DYNAMIKA UKŁADÓW HYDRAULICZNYCH. WIADOMOŚCI PODSTAWOWE.
 1 Temat /6/: DYNAMIKA UKŁADÓW HYDRAULICZNYCH. WIADOMOŚCI PODSTAWOWE. Celem ćwiczenia jest doświadczalne określenie wskaźników charakteryzujących właściwości dynamiczne hydraulicznych układów sterujących
1 Temat /6/: DYNAMIKA UKŁADÓW HYDRAULICZNYCH. WIADOMOŚCI PODSTAWOWE. Celem ćwiczenia jest doświadczalne określenie wskaźników charakteryzujących właściwości dynamiczne hydraulicznych układów sterujących
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
Rys. 1 Otwarty układ regulacji
 Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Korekcja układów regulacji
 Korekcja układów regulacji Powszechnym sposobem wpływania na jakość procesów regulacji jest wprowadzenie urządzeń (członów) korekcyjnych. W przeważającej większości przypadków niezbędne jest umieszczenie
Korekcja układów regulacji Powszechnym sposobem wpływania na jakość procesów regulacji jest wprowadzenie urządzeń (członów) korekcyjnych. W przeważającej większości przypadków niezbędne jest umieszczenie
SILNIK KROKOWY. w ploterach i małych obrabiarkach CNC.
 SILNIK KROKOWY Silniki krokowe umożliwiają łatwe sterowanie drogi i prędkości obrotowej w zakresie do kilkuset obrotów na minutę, zależnie od parametrów silnika i sterownika. Charakterystyczną cechą silnika
SILNIK KROKOWY Silniki krokowe umożliwiają łatwe sterowanie drogi i prędkości obrotowej w zakresie do kilkuset obrotów na minutę, zależnie od parametrów silnika i sterownika. Charakterystyczną cechą silnika
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
UKŁAD AUTOMATYCZNEJ REGULACJI SILNIKA SZEREGOWEGO PRĄDU STAŁEGO KONFIGUROWANY GRAFICZNIE
 UKŁAD AUOMAYCZNEJ REGULACJI SILNIKA SZEREGOWEGO PRĄDU SAŁEGO KONFIGUROWANY GRAFICZNIE Konrad Jopek (IV rok) Opiekun naukowy referatu: dr inż. omasz Drabek Streszczenie: W pracy przedstawiono układ regulacji
UKŁAD AUOMAYCZNEJ REGULACJI SILNIKA SZEREGOWEGO PRĄDU SAŁEGO KONFIGUROWANY GRAFICZNIE Konrad Jopek (IV rok) Opiekun naukowy referatu: dr inż. omasz Drabek Streszczenie: W pracy przedstawiono układ regulacji
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku
 Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
UWAGA 2. Wszystkie wyniki zapisywać na dysku Dane E: (dotyczy symulacji i pomiarów rzeczywistych)
 Cel ćwiczenia: Zapoznanie się z budową i zasadą działania regulatorów ciągłych oraz ocena jakości regulacji ciągłej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
Cel ćwiczenia: Zapoznanie się z budową i zasadą działania regulatorów ciągłych oraz ocena jakości regulacji ciągłej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
7.2.2 Zadania rozwiązane
 7.2.2 Zadania rozwiązane PRZYKŁAD 1 (DOBÓR REGULATORA) Do poniŝszego układu (rys.1) dobrać odpowiedni regulator tak, aby realizował poniŝsze załoŝenia: -likwidacja błędu statycznego, -zmniejszenie przeregulowania
7.2.2 Zadania rozwiązane PRZYKŁAD 1 (DOBÓR REGULATORA) Do poniŝszego układu (rys.1) dobrać odpowiedni regulator tak, aby realizował poniŝsze załoŝenia: -likwidacja błędu statycznego, -zmniejszenie przeregulowania
Instrukcja do ćwiczeń laboratoryjnych Napęd hydrauliczny
 Instrukcja do ćwiczeń laboratoryjnych Napęd hydrauliczny Sterowanie układem hydraulicznym z proporcjonalnym zaworem przelewowym Opracowanie: Z. Kudźma, P. Osiński, M. Stosiak 1 Proporcjonalne elementy
Instrukcja do ćwiczeń laboratoryjnych Napęd hydrauliczny Sterowanie układem hydraulicznym z proporcjonalnym zaworem przelewowym Opracowanie: Z. Kudźma, P. Osiński, M. Stosiak 1 Proporcjonalne elementy
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Automatyka i sterowania
 Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Automatyka w inżynierii środowiska. Wykład 1
 Automatyka w inżynierii środowiska Wykład 1 Wstępne informacje Podstawa zaliczenia wykładu: kolokwium 21.01.2012 Obecność na wykładach: zalecana. Zakres tematyczny przedmiotu: (10 godzin wykładów) Standardowe
Automatyka w inżynierii środowiska Wykład 1 Wstępne informacje Podstawa zaliczenia wykładu: kolokwium 21.01.2012 Obecność na wykładach: zalecana. Zakres tematyczny przedmiotu: (10 godzin wykładów) Standardowe
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu
 Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sterowanie napędów maszyn i robotów
 Wykład 6 - odtwarzanie zmiennych stanu przez obserwację Instytut Automatyki i Robotyki Warszawa, 2014 Odtwarzanie zmiennych stanu Wykorzystanie układów sterowania od zmiennych stanu wymaga uzyskania dodatkowych
Wykład 6 - odtwarzanie zmiennych stanu przez obserwację Instytut Automatyki i Robotyki Warszawa, 2014 Odtwarzanie zmiennych stanu Wykorzystanie układów sterowania od zmiennych stanu wymaga uzyskania dodatkowych
Dobór parametrów regulatora - symulacja komputerowa. Najprostszy układ automatycznej regulacji można przedstawić za pomocą
 Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7
 Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi zastosowaniami wzmacniacza operacyjnego, poznanie jego charakterystyki przejściowej
Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi zastosowaniami wzmacniacza operacyjnego, poznanie jego charakterystyki przejściowej
Napędy urządzeń mechatronicznych - projektowanie. Ćwiczenie 1 Dobór mikrosilnika prądu stałego z przekładnią do pracy w warunkach ustalonych
 Napędy urządzeń mechatronicznych - projektowanie Dobór mikrosilnika prądu stałego z przekładnią do pracy w warunkach ustalonych Miniaturowy siłownik liniowy (Oleksiuk, Nitu 1999) Śrubowy mechanizm zamiany
Napędy urządzeń mechatronicznych - projektowanie Dobór mikrosilnika prądu stałego z przekładnią do pracy w warunkach ustalonych Miniaturowy siłownik liniowy (Oleksiuk, Nitu 1999) Śrubowy mechanizm zamiany
Zespół Placówek Kształcenia Zawodowego w Nowym Sączu
 Zespół Placówek Kształcenia Zawodowego w Nowym Sączu Laboratorium układów automatyki Temat ćwiczenia: Optymalizacja regulatora na podstawie krytycznego nastawienia regulatora wg Zieglera i Nicholsa. Symbol
Zespół Placówek Kształcenia Zawodowego w Nowym Sączu Laboratorium układów automatyki Temat ćwiczenia: Optymalizacja regulatora na podstawie krytycznego nastawienia regulatora wg Zieglera i Nicholsa. Symbol
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
PODSTAWY AUTOMATYKI. Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
2. Wyznaczenie parametrów dynamicznych obiektu na podstawie odpowiedzi na skok jednostkowy, przy wykorzystaniu metody Küpfmüllera.
 1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
REGULATOR PI W SIŁOWNIKU 2XI
 REGULATOR PI W SIŁOWNIKU 2XI Wydanie 1 lipiec 2012 r. 1 1. Regulator wbudowany PI Oprogramowanie sterownika Servocont-03 zawiera wbudowany algorytm regulacji PI (opcja). Włącza się go poprzez odpowiedni
REGULATOR PI W SIŁOWNIKU 2XI Wydanie 1 lipiec 2012 r. 1 1. Regulator wbudowany PI Oprogramowanie sterownika Servocont-03 zawiera wbudowany algorytm regulacji PI (opcja). Włącza się go poprzez odpowiedni
Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter)
 Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter) 1. WSTĘP W wielu złożonych układach mechanicznych elementy występują połączenia elastyczne (długi
Eliminacja drgań w układach o słabym tłumieniu przy zastosowaniu filtru wejściowego (Input Shaping Filter) 1. WSTĘP W wielu złożonych układach mechanicznych elementy występują połączenia elastyczne (długi
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Karta (sylabus) przedmiotu
 WM Karta (sylabus) przedmiotu Mechanika i Budowa Maszyn Studia I stopnia o profilu: A P Przedmiot: Podstawy automatyki Kod przedmiotu Status przedmiotu: MBM N 0 3 39-0_0 Język wykładowy: polski Rok: II
WM Karta (sylabus) przedmiotu Mechanika i Budowa Maszyn Studia I stopnia o profilu: A P Przedmiot: Podstawy automatyki Kod przedmiotu Status przedmiotu: MBM N 0 3 39-0_0 Język wykładowy: polski Rok: II
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Podstawy automatyki i robotyki AREW001 Wykład 2 Układy regulacji i regulatory
 Podstawy automatyki i robotyki AREW001 Wykład 2 Układy regulacji i regulatory Dr inż. Zbigniew Zajda Katedra Automatyki, Mechatroniki i Systemów Sterowania Wydział Elektroniki Politechniki Wrocławskiej
Podstawy automatyki i robotyki AREW001 Wykład 2 Układy regulacji i regulatory Dr inż. Zbigniew Zajda Katedra Automatyki, Mechatroniki i Systemów Sterowania Wydział Elektroniki Politechniki Wrocławskiej
Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników
 Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników 1. Podstawowe pojęcia związane z niewyważeniem Stan niewyważenia stan wirnika określony takim rozkładem masy, który w czasie wirowania wywołuje
Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników 1. Podstawowe pojęcia związane z niewyważeniem Stan niewyważenia stan wirnika określony takim rozkładem masy, który w czasie wirowania wywołuje
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Laboratorium Mechaniki Technicznej
 Laboratorium Mechaniki Technicznej Ćwiczenie nr 5 Badanie drgań liniowych układu o jednym stopniu swobody Katedra Automatyki, Biomechaniki i Mechatroniki 90-924 Łódź, ul. Stefanowskiego 1/15, budynek A22
Laboratorium Mechaniki Technicznej Ćwiczenie nr 5 Badanie drgań liniowych układu o jednym stopniu swobody Katedra Automatyki, Biomechaniki i Mechatroniki 90-924 Łódź, ul. Stefanowskiego 1/15, budynek A22
DYNAMIKA KONSTRUKCJI BUDOWLANYCH
 DYNAMIKA KONSTRUKCJI BUDOWLANYCH Roman Lewandowski Wydawnictwo Politechniki Poznańskiej, Poznań 2006 Książka jest przeznaczona dla studentów wydziałów budownictwa oraz inżynierów budowlanych zainteresowanych
DYNAMIKA KONSTRUKCJI BUDOWLANYCH Roman Lewandowski Wydawnictwo Politechniki Poznańskiej, Poznań 2006 Książka jest przeznaczona dla studentów wydziałów budownictwa oraz inżynierów budowlanych zainteresowanych
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Z-ZIP-103z Podstawy automatyzacji Basics of automation
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 01/013 Z-ZIP-103z Podstawy automatyzacji Basics of automation A. USYTUOWANIE MODUŁU
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 01/013 Z-ZIP-103z Podstawy automatyzacji Basics of automation A. USYTUOWANIE MODUŁU
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
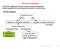 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Serwomechanizmy sterowanie
 Serwomechanizmy sterowanie Tryby pracy serwonapędu: - point-to-point, - śledzenie trajektorii (często znanej), - regulacja prędkości. Wymagania: - odpowiedź aperiodyczna, - możliwość ograniczania przyspieszenia
Serwomechanizmy sterowanie Tryby pracy serwonapędu: - point-to-point, - śledzenie trajektorii (często znanej), - regulacja prędkości. Wymagania: - odpowiedź aperiodyczna, - możliwość ograniczania przyspieszenia
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Sterowanie optymalne
 Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Sterowanie Napędów Maszyn i Robotów
 Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Sterowanie Napędów Maszyn i Robotów
 Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
Wykład 4 - Model silnika elektrycznego prądu stałego z magnesem trwałym Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Silniki elektryczne prądu stałego są bardzo często stosowanymi elementami wykonawczymi
3. WRAŻLIWOŚĆ I BŁĄD USTALONY. Podstawowe wzory. Wrażliwość Wrażliwość transmitancji względem parametru. parametry nominalne
 3. WRAŻLIWOŚĆ I BŁĄD USTALONY Podstawowe wzory Wrażliwość Wrażliwość transmitancji względem parametru (3.1a) parametry nominalne (3.1b) Wrażliwość układu zamkniętego (3.2a) (3.2b) Uwaga. Dla Zmiana odpowiedzi
3. WRAŻLIWOŚĆ I BŁĄD USTALONY Podstawowe wzory Wrażliwość Wrażliwość transmitancji względem parametru (3.1a) parametry nominalne (3.1b) Wrażliwość układu zamkniętego (3.2a) (3.2b) Uwaga. Dla Zmiana odpowiedzi
Ćwiczenie nr 6 Charakterystyki częstotliwościowe
 Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Metody optymalizacji Metody poszukiwania ekstremum funkcji jednej zmiennej Materiały pomocnicze do ćwiczeń
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Metody optymalizacji Metody poszukiwania ekstremum funkcji jednej zmiennej Materiały pomocnicze do ćwiczeń
Liniowe układy scalone w technice cyfrowej
 Liniowe układy scalone w technice cyfrowej Wykład 6 Zastosowania wzmacniaczy operacyjnych: konwertery prąd-napięcie i napięcie-prąd, źródła prądowe i napięciowe, przesuwnik fazowy Konwerter prąd-napięcie
Liniowe układy scalone w technice cyfrowej Wykład 6 Zastosowania wzmacniaczy operacyjnych: konwertery prąd-napięcie i napięcie-prąd, źródła prądowe i napięciowe, przesuwnik fazowy Konwerter prąd-napięcie
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4
 Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Spis treści. Dzień 1. I Elementy układu automatycznej regulacji (wersja 1109) II Rodzaje regulatorów i struktur regulacji (wersja 1109)
 Spis treści Dzień 1 I Elementy układu automatycznej regulacji (wersja 1109) I-3 Podstawowy problem sterowania I-4 Przykładowy obiekt regulacji I-5 Schemat blokowy układu automatycznej regulacji I-6 Klasyfikacja
Spis treści Dzień 1 I Elementy układu automatycznej regulacji (wersja 1109) I-3 Podstawowy problem sterowania I-4 Przykładowy obiekt regulacji I-5 Schemat blokowy układu automatycznej regulacji I-6 Klasyfikacja
Podstawy Elektrotechniki i Elektroniki. Opracował: Mgr inż. Marek Staude
 Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym Przypomnienie ostatniego wykładu Prąd i napięcie Podstawowe
Podstawy Elektrotechniki i Elektroniki Opracował: Mgr inż. Marek Staude Część 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym Przypomnienie ostatniego wykładu Prąd i napięcie Podstawowe
