4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
|
|
|
- Marian Skiba
- 8 lat temu
- Przeglądów:
Transkrypt
1 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź skokowa aperiodyczna aperiodyczna krytyczna (4.2) oscylacyjna Przeregulowanie (4.3) 51
2 Czas regulacji ustalanie z dokładnością 2% (4.4). Jeżeli ma reprezentować czas potrzebny na ustalanie z dokładnością 5% lub 1%, to w liczniku zamiast 4 należy wstawić odpowiednio 3 lub 4.6 Reguły upraszczania transmitancji 1. Odrzucane bieguny i zera powinny być przynajmniej 3 4 razy większe co do modułu od dominującego bieguna (najmniejszego). 2. Zero licznika i biegun mianownika można zredukować wówczas, jeżeli nie różnią się bardziej niż o 15 2%. 3. Odrzucanie i redukcja polegają na wstawieniu do odpowiednich czynników w liczniku i mianowniku celem zachowania wzmocnienia statycznego. Kryterium stabilności Hurwitza Wielomian charakterystyczny Wyznacznik Hurwitza (4.5) 52
3 Warunek stabilności Podwyznaczniki Układ III rzędu powinny być dodatnie. iloczyn wyrazów środkowych ma być większy od iloczynu wyrazów skrajnych. (4.6) Kryterium stabilności Routha Tablica Routha (4.7) Warunek stabilności W pierwszej kolumnie powinny znajdować się dodatnie elementy, tzn. itd. Jeżeli w pierwszej kolumnie występują elementy ujemne (wielomian niestabilny), to liczba zmian znaku określa liczbę pierwiastków w prawej półpłaszczyźnie. Pierwszy element zerowy Jeżeli wiersz poza zerem na początku ma przynajmniej jeden niezerowy składnik, to zero w pierwszej kolumnie zastępuje się przez małą dodatnią liczbę i kontynuuje budowę tablicy. Na końcu lub na bieżąco analizuje się znaki przy. 53
4 Zerowy wiersz Jeżeli wiersz zawiera same zera, to korzystamy z wyrazów w poprzednim wierszu budując wielomian pomocniczy odpowiedniego stopnia. Następnie różniczkujemy ten wielomian, współczynniki pochodnej wpisujemy zamiast zerowego wiersza i kontynuujemy procedurę. Wielomian pomocniczy jest podzielnikiem wielomianu głównego, zatem jego pierwiastki są pierwiastkami wielomianu głównego i na ogół można je obliczyć. Wielomian główny nie jest stabilny (niestabilny lub na granicy stabilności). Przykłady Z 4.1. Układ sterowania ma postać jak na rysunku. a) Czy można jednocześnie uzyskać przeregulowanie 1% i czas regulacji mniejszy niż 1 sekunda? b) Jeżeli nie, to podaj wartość K, która czyni zadość pierwszemu warunkowi (1%). Jaki będzie teraz czas regulacji? W jakim momencie wystąpi przeregulowanie? a) wymaganie pochodzące od wymaganie pochodzące od i Nie można jednocześnie uzyskać. 54
5 b) Matlab L=2*1.44; M=[1 2 2*1.44]; t=:.1:7; y=step(l,m,t); plot(t,y);grid Z 4.2. Dany jest serwomechanizm z silnikiem sterowanym napięciowo. a) Sprzężenie tachometryczne zostało odłączone, tzn.. Ile wyniesie przeregulowanie i czas regulacji? Jaki będzie błąd ustalony dla wymuszenia liniowego? b) Sprzężenie tachometryczne dołączono ustawiając. Jak teraz wyglądają? c) Dobierz tak, aby współczynnik tłumienia wzrósł do.6. Ile wyniosą? a) 1.5 Matlab L = 12; M = [1 1 12]; t=:.1:1;
6 y=step(l,m,t); plot(t,y),grid b) c) 56
7 Z 4.3. Dla układu pokazanego obok wyznaczyć obszar stabilności na płaszczyźnie ( ). Warunek Hurwitza Matlab kp=:.1:1; Ti=1*kp./(1+2*kp); plot(kp,ti),grid; xlabel( kp ); ylabel( Ti ); stabilny niestabilny Z 4.4. Zbadać stabilność wielomianu Tablica Routha
8 W pierwszej kolumnie przy występują dwie zmiany znaku, zatem wielomian jest niestabilny, a jego dwa pierwiastki leżą w prawej półpłaszczyźnie. Matlab Uwaga. Po wstawieniu do tablicy Routha następne elementy wystarczy ograniczyć do dominujących składników, jak to pokazano wyżej po prawej stronie. Skraca to zapis i upraszcza obliczenia. roots([ ]) Z 4.5. Wyznacz zakres wzmocnienia składowej całkującej regulatora, aby układ pokazany na rysunku był stabilny. Tablica Routha 58 :
9 : Warunek stabilności: Ostatecznie Matlab kontrola odpowiedzi dla ki=1; L=[ 3 ki]; M=[ ki]; roots(l+m) t=:.1:2; y=step(l,l+m,t); plot(t,y);grid Z 4.6. Zbadać stabilność wielomianu pierwiastki? Tablica Routha Jakie są jego W pierwszej kolumnie przy występują dwie zmiany znaku, zatem wielomian jest niestabilny, a jego dwa pierwiastki leżą w prawej półpłaszczyźnie. 59
10 Pierwiastki W tym szczególnym przypadku wielomian pomocniczy jest równy wielomianowi głównemu. Pierwiastek z liczby zespolonej: 1) 2) Pary sprzężone:. Z 4.7. Zaaproksymować transmitancję transmitancją niższego rzędu. Porównać odpowiedzi skokowe. L=[1 9 2]; roots(l) M=[ ]; roots(m), abs(-3+3i) 6
11 Dominującym biegunem jest. Przyjmując, że odrzuca się pierwiastki przynajmniej 3-krotnie większe co do modułu od dominującego bieguna mamy t=:.1:1 y=step(l,m,t); ya=step(1/27, [1 3 2],t); plot(t,y,t,ya, -- ), grid Zadania domowe D 4.1. Dla układu sterowania ramieniem robota skierowanym najpierw w dół, a potem w górę, dobrać nastawy k, α tak, aby uzyskać przebiegi aperiodyczne krytyczne ( ) z czasem regulacji.5 sekundy. D 4.2. Dobrać wzmocnienie k regulatora całkującego, który sterując obiektem ( czysto opóźniającym) zapewni przeregulowanie 4.3%. Jakiego czasu regulacji można się spodziewać? Jak wygląda odpowiedź skokowa? Wskazówki. Projektowanie: (Padé rząd 1) 61
12 Symulacja: aproksymacja Padé rząd D 4.3. W układzie regulacji zero regulatora z dobiera się eliminując biegun obiektu (czyli 3). Wyznaczyć k, p tak, aby przeregulowanie wynosiło 5%, a czas regulacji sekundy. D 4.4. Czy w układzie sterowania można dla wymuszenia jednocześnie uzyskać błąd ustalony oraz przeregulowanie? nie D 4.5. Jeden z układów sterowania pocisku manewrującego ma schemat jak na rysunku. Wyznaczyć parametry tak, aby częstotliwość naturalna wynosiła 1 rd/s, a współczynnik tłumienia był równy.5. Jaki będzie wtedy czas regulacji i przeregulowanie? D 4.6. Dla układu sterowania wyznacz obszar stabilności na płaszczyźnie ( ). Warunek stabilności określ zarówno w oparciu o kryterium Hurwitza jak i Routha. D 4.7. Jaki warunek powinny spełniać nastawy k, z regulatora PID, aby układ 62
13 był stabilny? Ile wynoszą bieguny układu dla?, bieguny D 4.8. Ile pierwiastków wielomianu leży w lewej, a ile w prawej półpłaszczyźnie? Jakie są te pierwiastki? Trzy pierwiastki w lewej, dwa w prawej D 4.9. Co można powiedzieć o stabilności i pierwiastkach wielomianów a) b) a) granica stabilności: b) granica stabilności: D 4.1. Wyznaczyć przedział wzmocnienia k, w którym układ sterowania jest stabilny. Ile wynoszą bieguny dla? D Dla jakich wartości wzmocnienia k układ sterowania jest stabilny? Ile wynoszą bieguny dla? 63
Badanie stabilności liniowych układów sterowania
 Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
pierwiastkowymi r(:,i) i-ta kolumna tablicy r z wartościami w II ćwiartce płaszczyzny (Re s, Im s) odpowiadająca linii
 5. PROJEKTOWANIE METODĄ LINII PIERWIASTKOWYCH Regulator P Problem dane: szukane: Tok projektowania Linie pierwiastkowe dla Spośród nich wybiera się linię przecinającą prostą nachyloną pod kątem (do ujemnej
5. PROJEKTOWANIE METODĄ LINII PIERWIASTKOWYCH Regulator P Problem dane: szukane: Tok projektowania Linie pierwiastkowe dla Spośród nich wybiera się linię przecinającą prostą nachyloną pod kątem (do ujemnej
3. WRAŻLIWOŚĆ I BŁĄD USTALONY. Podstawowe wzory. Wrażliwość Wrażliwość transmitancji względem parametru. parametry nominalne
 3. WRAŻLIWOŚĆ I BŁĄD USTALONY Podstawowe wzory Wrażliwość Wrażliwość transmitancji względem parametru (3.1a) parametry nominalne (3.1b) Wrażliwość układu zamkniętego (3.2a) (3.2b) Uwaga. Dla Zmiana odpowiedzi
3. WRAŻLIWOŚĆ I BŁĄD USTALONY Podstawowe wzory Wrażliwość Wrażliwość transmitancji względem parametru (3.1a) parametry nominalne (3.1b) Wrażliwość układu zamkniętego (3.2a) (3.2b) Uwaga. Dla Zmiana odpowiedzi
Stabilność. Krzysztof Patan
 Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
1. Transformata Laplace a przypomnienie
 Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
KRYTERIA ALGEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH
 KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
PAiTM. materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż.
 PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
układu otwartego na płaszczyźnie zmiennej zespolonej. Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:
 Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
Podstawowe człony dynamiczne
 . Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
. Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ. T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
 REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa.
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
analogowego regulatora PID doboru jego nastaw i przetransformowanie go na cyfrowy regulator PID, postępując według następujących podpunktów:
 Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Projektowanie układów regulacji w dziedzinie częstotliwości. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
Ćwiczenie nr 6 Charakterystyki częstotliwościowe
 Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
, (2.1) A powierzchnia przekroju zbiornika, Równanie bilansu masy cieczy w zbiorniku ma postać. , gdzie: q i dopływ,
 2. MODELE OBIEKTÓW STEROWANIA Równania bilansowe Bilans masy Bilans ten dotyczy wszelkich obiektów z przepływem cieczy, gazów, par, materiałów sypkich, takich jak zbiorniki, mieszalniki, kotły, reaktory
2. MODELE OBIEKTÓW STEROWANIA Równania bilansowe Bilans masy Bilans ten dotyczy wszelkich obiektów z przepływem cieczy, gazów, par, materiałów sypkich, takich jak zbiorniki, mieszalniki, kotły, reaktory
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
Inżynieria Systemów Dynamicznych (5)
 Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Zaliczenie - zagadnienia (aktualizacja )
 Tomasz Żabiński Ocena 3.0 Zaliczenie - zagadnienia (aktualizacja 23.01.2017) 1. Podaj na jakie dwie główne grupy dzieli się układy przełączające. 2. Scharakteryzuj układy kombinacyjne. 3. Scharakteryzuj
Tomasz Żabiński Ocena 3.0 Zaliczenie - zagadnienia (aktualizacja 23.01.2017) 1. Podaj na jakie dwie główne grupy dzieli się układy przełączające. 2. Scharakteryzuj układy kombinacyjne. 3. Scharakteryzuj
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
( 1+ s 1)( 1+ s 2)( 1+ s 3)
 Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Automatyka i Regulacja Automatyczna, PRz, r.a. 2011/2012, Żabiński Tomasz
 Wykład 8 Transformata Laplace a - przypomnienie, transmitancja operatorowa, scematy bloko, wprowadzenie do pakietu Matlab/Scilab, regulatory PID - transmitancja, modele matematyczne wybranyc obiektów regulacji,
Wykład 8 Transformata Laplace a - przypomnienie, transmitancja operatorowa, scematy bloko, wprowadzenie do pakietu Matlab/Scilab, regulatory PID - transmitancja, modele matematyczne wybranyc obiektów regulacji,
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
WYDZIAŁ ELEKTRYCZNY KATEDRA AUTOMATYKI I ELEKTRONIKI. Badanie układu regulacji dwustawnej
 POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
Ćw. S-III.3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR
 Dr inż Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw S-III3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem
Dr inż Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw S-III3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
7.2.2 Zadania rozwiązane
 7.2.2 Zadania rozwiązane PRZYKŁAD 1 (DOBÓR REGULATORA) Do poniŝszego układu (rys.1) dobrać odpowiedni regulator tak, aby realizował poniŝsze załoŝenia: -likwidacja błędu statycznego, -zmniejszenie przeregulowania
7.2.2 Zadania rozwiązane PRZYKŁAD 1 (DOBÓR REGULATORA) Do poniŝszego układu (rys.1) dobrać odpowiedni regulator tak, aby realizował poniŝsze załoŝenia: -likwidacja błędu statycznego, -zmniejszenie przeregulowania
Metody numeryczne I Równania nieliniowe
 Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
Kompensator PID. 1 sω z 1 ω. G cm. aby nie zmienić częstotliwości odcięcia f L. =G c0. s =G cm. G c. f c. /10=500 Hz aby nie zmniejszyć zapasu fazy
 Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu
 Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
Automatyka i robotyka
 Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Podstawy inżynierii sterowania Ćwiczenia laboratoryjne
 Podstawy inżynierii sterowania Ćwiczenia laboratoryjne Laboratorium nr 4: Układ sterowania silnika obcowzbudnego prądu stałego z regulatorem PID 1. Wprowadzenie Przedmiotem rozważań jest układ automatycznej
Podstawy inżynierii sterowania Ćwiczenia laboratoryjne Laboratorium nr 4: Układ sterowania silnika obcowzbudnego prądu stałego z regulatorem PID 1. Wprowadzenie Przedmiotem rozważań jest układ automatycznej
PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa
 Rok akademicki 2015/2016 Semestr letni PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa Wstęp teoretyczny: W układzie regulacji określa
Rok akademicki 2015/2016 Semestr letni PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa Wstęp teoretyczny: W układzie regulacji określa
Języki Modelowania i Symulacji
 Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
SYNTEZA obwodów. Zbigniew Leonowicz
 SYNTEZA obwodów Zbigniew Leonowicz Literatura: [1]. S. Bolkowski Elektrotechnika teoretyczna. Tom I. WNT Warszawa 1982 (s.420-439) [2]. A. Cichocki, K.Mikołajuk, S. Osowski, Z. Trzaska: Zbiór zadań z elektrotechniki
SYNTEZA obwodów Zbigniew Leonowicz Literatura: [1]. S. Bolkowski Elektrotechnika teoretyczna. Tom I. WNT Warszawa 1982 (s.420-439) [2]. A. Cichocki, K.Mikołajuk, S. Osowski, Z. Trzaska: Zbiór zadań z elektrotechniki
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
2. Wyznaczenie parametrów dynamicznych obiektu na podstawie odpowiedzi na skok jednostkowy, przy wykorzystaniu metody Küpfmüllera.
 1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
LINIOWE UKŁADY DYSKRETNE
 LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
Funkcja kwadratowa. f(x) = ax 2 + bx + c,
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Elementy metod numerycznych
 Wykład nr 5 i jej modyfikacje. i zera wielomianów Założenia metody Newtona Niech będzie dane równanie f (x) = 0 oraz przedział a, b taki, że w jego wnętrzu znajduje się dokładnie jeden pierwiastek α badanego
Wykład nr 5 i jej modyfikacje. i zera wielomianów Założenia metody Newtona Niech będzie dane równanie f (x) = 0 oraz przedział a, b taki, że w jego wnętrzu znajduje się dokładnie jeden pierwiastek α badanego
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Wstęp do analizy matematycznej
 Wstęp do analizy matematycznej Andrzej Marciniak Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych i ich zastosowań w
Wstęp do analizy matematycznej Andrzej Marciniak Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych i ich zastosowań w
PODSTAWY AUTOMATYKI. MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
Automatyka i sterowanie w gazownictwie. Regulatory w układach regulacji
 Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
Ćw. S-III.4 ELEMENTY ANALIZY I SYNTEZY UAR (Dobór nastaw regulatora)
 Dr inż. Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw. S-III.4 ELEMENTY ANALIZY I SYNTEZY UAR (Dobór nastaw regulatora) Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem "syntezy
Dr inż. Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw. S-III.4 ELEMENTY ANALIZY I SYNTEZY UAR (Dobór nastaw regulatora) Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem "syntezy
Metoda eliminacji Gaussa
 Metoda eliminacji Gaussa Rysunek 3. Rysunek 4. Rozpoczynamy od pierwszego wiersza macierzy opisującej nasz układ równań (patrz Rys.3). Zakładając, że element a 11 jest niezerowy (jeśli jest, to niezbędny
Metoda eliminacji Gaussa Rysunek 3. Rysunek 4. Rozpoczynamy od pierwszego wiersza macierzy opisującej nasz układ równań (patrz Rys.3). Zakładając, że element a 11 jest niezerowy (jeśli jest, to niezbędny
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Automatyzacja. Ćwiczenie 9. Transformata Laplace a sygnałów w układach automatycznej regulacji
 Automatyzacja Ćwiczenie 9 Transformata Laplace a sygnałów w układach automatycznej regulacji Rodzaje elementów w układach automatyki Blok: prostokąt ze strzałkami reprezentującymi jego sygnał wejściowy
Automatyzacja Ćwiczenie 9 Transformata Laplace a sygnałów w układach automatycznej regulacji Rodzaje elementów w układach automatyki Blok: prostokąt ze strzałkami reprezentującymi jego sygnał wejściowy
PODSTAWY AUTOMATYKI. Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
Automatyka i Sterowanie Laboratorium Zagadnienia kolokwium zaliczeniowe
 Tomasz Żabiński Automatyka i Sterowanie Laboratorium Zagadnienia kolokwium zaliczeniowe 1. Wyjaśnij terminy: identyfikacja, samostrojenie, adaptacja. 2. Wyjaśnij pojęcia komunikacji pionowej i poziomej
Tomasz Żabiński Automatyka i Sterowanie Laboratorium Zagadnienia kolokwium zaliczeniowe 1. Wyjaśnij terminy: identyfikacja, samostrojenie, adaptacja. 2. Wyjaśnij pojęcia komunikacji pionowej i poziomej
Funkcja kwadratowa. f(x) = ax 2 + bx + c = a
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Analiza ustalonego punktu pracy dla układu zamkniętego
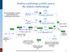 Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM
 ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
( ) Arkusz I Zadanie 1. Wartość bezwzględna Rozwiąż równanie. Naszkicujmy wykresy funkcji f ( x) = x + 3 oraz g ( x) 2x
 Arkusz I Zadanie. Wartość bezwzględna Rozwiąż równanie x + 3 x 4 x 7. Naszkicujmy wykresy funkcji f ( x) x + 3 oraz g ( x) x 4 uwzględniając tylko ich miejsca zerowe i monotoniczność w ten sposób znajdziemy
Arkusz I Zadanie. Wartość bezwzględna Rozwiąż równanie x + 3 x 4 x 7. Naszkicujmy wykresy funkcji f ( x) x + 3 oraz g ( x) x 4 uwzględniając tylko ich miejsca zerowe i monotoniczność w ten sposób znajdziemy
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
Kompensacja wyprzedzająca i opóźniająca fazę. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Własności wyznacznika
 Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji
 Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
Równania poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie = Rozwiąż układ równań: (( + 1 ( + 2 = = 1
 Równania poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/). Rozwiąż układ równań: (( + ( + 2 = 3 = 4. http://www.zadania.info/d38/2287 2. Rozwiąż układ równań: ( + 2 (
Równania poziom podstawowy (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/). Rozwiąż układ równań: (( + ( + 2 = 3 = 4. http://www.zadania.info/d38/2287 2. Rozwiąż układ równań: ( + 2 (
Wstęp do metod numerycznych Rozwiazywanie równań algebraicznych. P. F. Góra
 Wstęp do metod numerycznych Rozwiazywanie równań algebraicznych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2010 Co to znaczy rozwiazać równanie? Przypuśmy, że postawiono przed nami problem rozwiazania
Wstęp do metod numerycznych Rozwiazywanie równań algebraicznych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2010 Co to znaczy rozwiazać równanie? Przypuśmy, że postawiono przed nami problem rozwiazania
O MACIERZACH I UKŁADACH RÓWNAŃ
 O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, , tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Rozwiązanie:
 Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
jest rozwiązaniem równania jednorodnego oraz dla pewnego to jest toŝsamościowo równe zeru.
 Układy liniowe Układ liniowy pierwszego rzędu, niejednorodny. gdzie Jeśli to układ nazywamy jednorodnym Pamiętamy, Ŝe kaŝde równanie liniowe rzędu m moŝe zostać sprowadzone do układu n równań liniowych
Układy liniowe Układ liniowy pierwszego rzędu, niejednorodny. gdzie Jeśli to układ nazywamy jednorodnym Pamiętamy, Ŝe kaŝde równanie liniowe rzędu m moŝe zostać sprowadzone do układu n równań liniowych
LABORATORIUM 5: Sterowanie rzeczywistym serwomechanizmem z modułem przemieszczenia liniowego
 LABORATORIUM 5: Sterowanie rzeczywistym serwomechanizmem z modułem przemieszczenia liniowego Uwagi (pominąć, jeśli nie ma problemów z wykonywaniem ćwiczenia) 1. Jeśli pojawiają się błędy przy próbie symulacji:
LABORATORIUM 5: Sterowanie rzeczywistym serwomechanizmem z modułem przemieszczenia liniowego Uwagi (pominąć, jeśli nie ma problemów z wykonywaniem ćwiczenia) 1. Jeśli pojawiają się błędy przy próbie symulacji:
Regulator P (proporcjonalny)
 Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Inżynieria Systemów Dynamicznych (4)
 Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
1 Dana jest funkcja logiczna f(x 3, x 2, x 1, x 0 )= (1, 3, 5, 7, 12, 13, 15 (4, 6, 9))*.
 EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 0/0 Odpowiedzi do zadań dla grupy elektronicznej na zawody II stopnia (okręgowe) Dana jest funkcja logiczna f(x 3, x,
EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 0/0 Odpowiedzi do zadań dla grupy elektronicznej na zawody II stopnia (okręgowe) Dana jest funkcja logiczna f(x 3, x,
