Matematyka dyskretna
|
|
|
- Eleonora Czajkowska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Lista 1 Zadaie1.Wyzaczwszystkieparywrelacjiρ X Y,gdzie (a)x={1,2,3},y={6,7,8}iρ={(x,y):x y}, (b)x=y= Niρ={(x,y):x 2 +y 2 10}. Zadaie 2. Które z własości, tz. zwrotość, symetrię, atysymetrię, przechodiość, posiadarelacjaρ X X? (a)x=zbiórprostychapłaszczyźie,ρ={(x,y):x y}, (b)x=zbiórprostychapłaszczyźie,ρ={(x,y):x y}, (c)x=zbiórprostychapłaszczyźie,ρ={(x,y):x y }, (d)x=zbiórprostychapłaszczyźie,ρ={(x,y): x y =1}, (e)x=zbiórsłów,ρ={(x,y):słowoxmatęsamądługośćcosłowoy}, (f)x=zbiórsłów,ρ={(x,y):słowoxmawspóląprzyajmiejjedąliteręzesłowemy}, (g)x= R,ρ={(x,y):x y}, (h)x= R,ρ={(x,y):x<y}, (i)x= R,ρ={(x,y):0 xy}. Zadaie 3. Które z podstawowych własości spełiają astępujące relacje? (a)xρy x y,dlax,y N 0, (d)xρy x < y dlax,y R, (b)xρy 2 (x+y)dlax,y N, (c)xρy 3 (x y)dlax,y N, (e)xρy x+y=1dlax,y R, (f)xρy 1 x+ydlax,y R. Zadaie4.Ograiczającrelacje(a),(b),(c)zzadaia2dozbioru{1,2,...,8}sporządzić tabelki tych relacji. Zadaie 5. Które z podstawowych własości ma relacja określoa a zbiorze X formułą aρb wd(a,b)=1. Jak zmiei się ta relacja(i jej własości), gdy przyjmiemy: (a)x={2,3,4,...}, (b) X = zbiór liczb parzystych, (c) X = zbiór liczb pierwszych. Zadaie 6. Które z relacji opisaych w zadaiach 2, 3 są relacjami rówoważości? Dla takich relacji wyzaczyć klasy abstrakcji.
2 Zadaie 7. Na zbiorze liczb całkowitych Z określamy astępującą relację: xρy x 2 =y 2. Uzasadij, że to relacja rówoważości i wyzacz jej klasy abstrakcji. Zadaie8.NiechX ={1,2,3,4,5}iiechρbędzierelacjąwrodziie2 X wszystkich podzbiorów zbioru X określoą w astępujący sposób: AρB A = B, gdzie C ozacza ilość elemetów zbioru C. Sprawdzić, że relacja ρ jest relacją rówoważości. Podać klasę rówoważości tej relacji o reprezetacie{1, 2}. Zadaie9.Czyazbiorze{x R:0 x 2}istiejerelacjarówoważości,którejklasamiabstrakcjisązbiory:{x R:0 x 3 2 }oraz{x R:1<x 2}. Zadaie 10. Wykazać, że każda z poiższych relacji jest relacją rówoważości i wyzaczyć jej klasy abstrakcji: (a)xρy x = y dlax,y R, (b)kρ kmatylesamocyfrco,dlak, N, (c)(m 1, 1 )ρ(m 2, 2 ) m =m dla(m 1, 1 ),(m 2, 2 ) N 2, (d)(x 1,y 1 )ρ(x 2,y 2 ) x 1 3y 1 =x 2 3y 2 dla(x 1,y 1 ),(x 2,y 2 ) R 2. Zadaie11.Określićrelacjęrówoważościapłaszczyźie R 2,takabyklasamiabstrakcji tej relacji były: (a)prostepostaciy=3x+b,b R, (b)okręgiośrodkuwpukcie(0,0)ipromieiachr 0. Zadaie 12. Niech l będzie ustaloą prostą a płaszczyźie Π. Określamy relację ρ a zbiorze wszystkich prostych a płaszczyźie Π w astępujący sposób Czy relacja ρ jest relacją rówoważości? kρm k l oraz m l.
3 Lista 2 Zadaie 1. Które z relacji określoych a poprzediej liście są fukcjami? Zadaie2.Którazpoiższychrelacjiρ {1,2,3,4,5} {a,b,c,d,e}jestfukcją?dla każdej z takich relacji wyzaczyć relację odwrotą. Która z ich jest fukcją? (a)ρ={(1,b),(1,c),(3,d),(2,a)}, (b)ρ={(1,c),(2,d),(4,e),(3,a),(5,b)}, (c)ρ={(2,b),(4,c),(2,a)}, (d)ρ={(1,d),(2,d),(5,e),(3,a),(4,e)}. Zadaie 3. Która z astępujących fukcji jest surjekcją, która iiekcją, a która bijekcją? Dla bijekcji wyzaczyć fukcje odwrote. (a)f: R R, f(x)=x 3, (b)f: R R, f(x)= x + x 1, (c)f:[1, ) [1, ), f(x)= x + x 1, (d)f:(0, ) R, f(x)=log 2 x, (e)f:[1, ) R, f(x)=x 2 2x, (f)f:[1, ) [ 1, ), f(x)=x 2 2x. Zadaie 4. Wykazać, że złożeie surjekcji(iiekcji) jest surjekcją(iiekcją). Zadaie5.Daajestfukcjaf: R RorazzbioryAiB.Zaleźćzbioryf(A)if 1 (B), gdy (a)f(x)= x 2 4,A=[0,1],B=[2,4], (b)f(x)= x 2 2x,A=( 1,1),B=(0, 3 4 ), (c)f(x)=2 x,a=[1,3),b=[3,5).
4 Lista 3 Zadaie 1. Wykazać, że relacja rówoliczości zbiorów jest rówoważością. Zadaie 2. Czy astępujące zbiory są rówolicze? (a)a={a,b,1,2},b={α,β,γ,δ}, (b)a={x R:x 2 2x+1=0},B=, (c)a=n,b={ N:=3kdlapewegok N}, (d)a={ N:10<},B= N, (e)a=n,b= Z, (f)a=(0,1),b=(1, ), (g)a=(,0],b=[0, ), (h)a=(0, ),B=(a, ), (i)a=(0,1),b= R, Zadaie 3. Wykazać rówoliczość zbioru puktów we wętrzu i brzegu kwadratu ze zbiorempuktówajedymzjegoboków. Zadaie 4. Wykazać rówoliczość zbiorów puktów dwóch okręgów. Zadaie 5. Czy zbiór, którego każdy podzbiór właściwy jest przeliczaly, jest zbiorem przeliczalym? Zadaie 6. Zbadać moc zbioru wszystkich okręgów a płaszczyźie o środku w pukcie (0,0)ipromieiubędącymcałkowitąwielokrotością 2.
5 Lista 4 Zadaie 1. Sprawdzić, że (a) (2 1)= 2, (b) = (+1), 2 (c) = (+1)(2+1), 6 (d) (3 1)= 32 +, 2 (e) =( ) 2, (f)( ) 2 = 2 (+1) 2, 4 (g) (2 1) 2 = (2 1)(2+1), 3 (h) (2 1) 3 = 2 (2 2 1), (i) (4 3)=(2 1). Zadaie2.Dlajakich Nzachodzi 2 <2? Zadaie3.Dlajakich Nzachodzi6+6<2? Zadaie4.Dlajakich Nzachodzi<2? Zadaie5.Zajdźzbiórliczbaturalych,dlaktórychzachodziierówość Zadaie 6. Udowodij, że dla dowolej liczby aturalej > 0, (a)8 11 3, (b) , (c)5 5, (d)2 2 +, (e)19 ( ), (f)30 5, (g)6 3, (h)6 3 +5, (i) ,
6 Zadaie7.Wykaż,żedla 2liczbapostaci2 2 maakońcuwzapisiedziesiętym cyfrę 6. Zadaie8.NiechA={ N: 2 3+3jestparzysta}.Pokaż,żejeśli Atoi +1 A.JakieliczbyależąwięcdoA? Zadaie 9. Pokaż, że dla dowolej liczby N zachodzi astępująca rówość: (a) (b) (c) (d) (e) (6 5) (6+1) = 6+1, (3 1)(3+2) = 2(3+2), (+1) = +1, (2 1)(2+1) = 2+1, (3 2)(3+1) = 3+1.
7 Lista 5 Zadaie1.Oblicza 4,gdywiadomo,że (a)a 0 =1,a 1 = 1,a +1 =a 2 +a 1dla 1, (b)a 0 =1,a 1 = 1,a +1 =2 a dla 1, { 3a, gdy2, (c)a 0 =1,a 1 = 1,a +1 = 3a, gdy2, dla 1. Zadaie2.Dayjestciągarytmetyczy:2,5,8,11,14,...Podajwzórrekurecyjytego ciągu. Zadaie3.Dayjestciąggeometryczy:8,4,2,1,...Podajwzórrekurecyjytegociągu. Zadaie4.Podajrekurecyjądefiicjęciągua,wktóreja jestwyrażoeprzypomocy a 1.Pamiętajowarukachpoczątkowych. (a)a =10 dla 0, (b)a =5dla 1, (c)a = 3dla 0. Zadaie 5. Zajdź wzór jawy ciągu. Poprawość wzoru uzasadij idukcyjie. (a)a 1 =3,a 2 = 1,a =2a 1 a 2 dla 3, (b)a 0 = 2,a +1 = 1 2a dla 0, (c)a 1 =1,a =2a 1 dla 1, (d)a 0 =2,a 1 =5,a =5a 1 6a 2 dla 2, (e)a 0 =1,a 1 =2,a = a2 1 a 2 dla 2, (f)a 0 =1,a 1 =1,a =10a 1 25a 2 dla 2, (g)a 0 =1,a 1 =1,a = 14a 1 49a 2 dla 2, (h)a 1 =1,a =2a 1 +1dla 1. Zadaie6.Niecha ozacza(a)sumę,(b)sumękwadratów,(c)sumęsześciaów,pierwszychliczbaturalych.podajrekurecyjądefiicjęciągua. Zadaie 7. W pewym mieście jede człowiek zachorował a grypę. Załóżmy, że każda chora osoba zaraża codzieie 4 zdrowe osoby. Ilu będzie chorych po upływie di? Podaj rozwiązaie w postaci jawej i rekurecyjej.
8 Lista 6 Zadaie 1. Piotrek ma w szufladzie 200 białych skarpetek i 300 czarych. Lewe skarpetki są zupełie ieodróżiale od prawych. Niestety Piotr jest daltoistą i ie potrafi też odróżiać awet białego i czarego koloru. Ile skarpetek musi o zabrać, aby mieć pewość, że choć dwie będą tego samego koloru? Ile skarpetek musi o zabrać, aby mieć pewość, że choć 10 będzie tego samego koloru? Zadaie 2. Uzasadij, że wśród wszystkich mieszkańców Wila są co ajmiej dwie osoby, które mają tyle samo włosów a głowie. Zadaie 3. W szufladzie jest 20 sztućców, to zaczy łyżek, oży i widelców. Udowodij, żezajdziemytam7łyżek,lub10oży,lub5widelców. Zadaie4.Kabeldługości100cmtiemydowoliea6częścitak,żedługośćkażdejz tych części wyraża się całkowitą liczbą cetymetrów. Uzasadić, że zawsze któraś z części będzie miała przyajmiej 17cm. Czy zawsze musi powstać część dłuższa iż 17cm? Zadaie 5. Pokazać, że wsród 25 studetów zdających egzami zawsze zajdziemy pięciu, którzyotrzymalitesamąoceęprzyskalioce:2,3,3+,4,4+,5. Zadaie 6. Uzasadij, że wśród pięciu puktów wybraych wewątrz kwadratu wielkości 2 2zawszesądwapuktyodległeoiewięcejiż 2. Zadaie 7. Uzasadij, że wsród dowolych 14 liczb aturalych zajdziemy dwie, które przy dzieleiu przez 13 dają tę samą resztę.
9 Lista 7 Zadaie1.Ilejestliczbaturalychod1do100iepodzielychaiprzez2,aiprzez3? Zadaie2.Ilejestliczbaturalychod1do100iepodzielychaiprzez2,aiprzez3, aiprzez5? Zadaie 3. Zbadao 50 samochodów wykoując testy a poziom zawartości trzech grup zaieczyszczeń: NO, HC i CO. 1 samochód ie spełia żadej z trzech orm, 3 samochody przekroczyły poziom NO i HC, 2 samochody przekroczyły poziom NO i CO, 1 samochód przekroczyłpoziomhcico,6samochodówmazbytwysokipoziomno,4samochody majązbytwysokipoziomhc,a3samochodymajązbytwysokipoziomco.ilesamochodów spełia wszystkie testowae ormy? Zadaie4.Ilejestciągówdługości,gdzie>3,złożoychzcyfr0,1,...,9takich,w którychiewystępującyfry1,2,3. Zadaie5.Nailesposobówztalii52kartmożawybrać1asa?Nailesposobówmoża wybrać1asai1króla?nailesposobówmożawybrać1asa,1królai1damę?aaile sposobówmożawybrać4kartytakabybył1as,1króli1dama? Zadaie 6. Ile jest PIN-ów, czyli cztero-elemetowych słów złożoych z cyfr dziesiętych, takich że żada cyfra się ie powtarza? Zadaie 7. Na kurs tańca uczęszcza pięciu chłopaków i pięć dziewcząt. Kroki taecze ćwiczy się parami. Na ile sposobów może być wykoay jede taiec? Zadaie miu uczestikom pewej koferecji iformatyczej przygotowao kota komputerowe, gdzie ID są 8-zakowe i utworzoe wyłączie z liter a, b. Przydzieloo je późiej losowo. Na ile sposobów było to możliwe? Zadaie 9. Na ile sposobów moża rozstawić 8 wież a poumerowaych polach szachowicy8 8wtakisposób,byżadedwieiezajdowałysięwpoluwzajemegorażeia? Zadaie 10. Mamy 9 białych i 9 czarych klocków o ieodróżialych kształtach. Na ile sposobów możemy zbudować wieżę o wysokości 10 klocków? Zadaie 11. Ile jest różych relacji dwuargumetowych a zbiorze elemetowym? Ile spośród ich jest zwrotych, a ile symetryczych?
10 Lista 8 Zadaie1.Ilejestciągówdługości,>3,złożoychzcyfr0,1,...,9takich,wktórych iewystępującyfry1,2,3.ilejesttakichciągów,żekażdazcyfr1,2,3występujew każdym z ciągów co ajmiej raz? Zadaie2.Nailesposobówztalii52kartmożawybrać5karttak,abyotrzymaćco ajmiej jedego asa, co ajmiej jedego króla i co ajmiej jedą damę? Zadaie3.Ilejestparpostaci(A,B),gdzieA B X,gdy X =? Zadaie 4. Na ile sposobów moża rozmieścić 5 czerwoych kulek w 4 poumerowaych pudełkach? Zadaie 5. Ile jest sposobów rozmieszczeia idetyczych przedmiotów w k poumerowaych pudełkach? Zadaie 6. Na ile sposobów moża wybrać 10 moet mając ieograiczoy zapas po 1, 5,10i20groszy? Zadaie idetyczych listów ma być wrzucoych do 4 różych skrzyek pocztowych. Na ile sposobów moża to zrobić? Ile jest możliwych sposobów, gdy do każdej ze skrzyek muszą być wrzucoe co ajmiej 2 listy? Zadaie 8. Ile moża otrzymać różych mieszaek po 10 cukierków jeśli mamy do dyspozycji 4 rodzaje cukierków w ieograiczoej ilości? Zadaie9.Wykaż,że ( ) + 0 Zadaie 10. Wykaż, że ( )( ) m 0 k + ( ) ( )( ) m k 1 ( ) =2. ( m k )( 0 ) ( ) m+ =. k Zadaie 11. Wykaż, że ( ) ( ) ( ) 2 = ( ) 2. Rozważliczbęwyborówosóbz2-osobowejgrupyzłożoejzmężczyzikobiet.
11 Zadaie 12. Wykaż, że ( ) ( ) ( ) = Rozważ liczbę wyborów z grupy osób podzbioru z wyzaczoym w im przywódcą. Zadaie 13. Wykaż, że ( )( ) 0 k + ( )( ) 1 1 k 1 ( )( ) ( ) k + + =2 k. k 0 k Rozważ liczbę kolorowań dwoma kolorami k rozróżialych obiektów wybraych spośród obiektów.
12 Lista 9 Zadaie 1. Udowodij, że: (a)2 2, (b)6 3, (c)30 5, (d) ,dla 2. Zadaie2.Udowodij,żedlaa,b, N,jeślia,b inwd(a,b)=1,toab. Zadaie 3. Stosując algorytm Euklidesa oblicz NWD(101, 1001) oraz NWD(55, 89). Zadaie4.Któraliczbajestwiększa czy6 19? Zadaie5.Niecha= ,b= ,c= ObliczNWDiNWWdla wszystkichmożliwychparliczboraznwd(a,b,c)inww(a,b,c)? Zadaie6.Niecha= ,b= ,c= ObliczNWDiNWW dlawszystkichmożliwychparliczboraznwd(a,b,c)inww(a,b,c)? Zadaie7.ObliczNWD(24!,24 8 )oraznww(12 12,18 18 ). Zadaie8.ObliczNWD( ,10 43 ). Zadaie9.ObliczNWD( ,2 50 ). Zadaie10.Wyzaczyćwszystkieliczbyaturale>1,dlaktórychliczba 2 1jest pierwsza. Zadaie 11. Wyzaczyć wszystkie liczby pierwsze p, dla których liczba 3p + 1 jest pierwsza. Zadaie12.Wyzaczyćwszystkieliczbypierwszep,dlaktórychliczbap 2 +2jestpierwsza.
13 Lista 10 Zadaie 1. Oblicz: (a) mod8, (b) mod9, (c) mod9, (d)18 15 mod11, (e) mod12, (f) mod14. Zadaie 2. Podaj zbiór rozwiązań astępujących rówań: (a)21x 36 5, (d)3x , (g)11x 22 33, (b)4x 7 6, (c)3x 33 27, (e)2x 4 3, (f)16x (h)42x 12 78, (i)8x Zadaie3.Niechbędzieliczbącałkowitąróżąod1.Pokaż,żeiedzieli2 1. Zadaie4.Zajdźostatiącyfręliczby Zadaie5.Wyzaczdwieostatiecyfryliczby Zadaie 6. Udowodij, że liczba aturala jest podziela przez 9 wtedy i tylko wtedy, gdysumajejcyfrteżjestpodzielaprzez9.jakjestdlaliczby3? Zadaie 7. Zajdź ajmiejszą, ieujemą liczbę x, która przy dzieleiu przez 3 daje resztę2,przydzieleiuprzez5dajeresztę3,przydzieleiuprzez11dajeresztę4,aprzy dzieleiu przez 16 daje resztę 5. Zadaie 8. Zajdź ajmiejszą, ieujemą liczbę x, która przy dzieleiu przez 31 daje resztę23,przydzieleiuprzez12dajeresztę7,aprzydzieleiuprzez35dajeresztę12. Zadaie 9. Zajdź ajmiejszą, ieujemą liczbę x, która przy dzieleiu przez 3 daje resztę2,przydzieleiuprzez13dajeresztę12,przydzieleiuprzez11dajeresztę10,a przy dzieleiu przez 7 daje resztę 1. Zadaie 10. Zajdź ajmiejszą, ieujemą liczbę x, która jest podziela przez 2, przy dzieleiuprzez12dajeresztę7,aprzydzieleiuprzez15dajeresztę2.
14 Lista 11 Zadaie1.Przedstawzapomocąmacierzyicydecjigraf G= V,E wktórym Narysuj te graf V=1,2,3,4 i E= { {1,2},{2,3},{3,4},{1,3},{2,4} }. Zadaie 2. Czy graf(ieskieroway) o 7 wierzchołkach, w którym suma stopi wierzchołków wyosi 30 może być iespójy? Zadaie3.Czygraf G= V,E wktórym V=1,2,3,4,5,6 i E= { {1,4},{1,5},{1,6},{2,4},{2,5},{2,6},{3,5},{3,6} } jest plaary? Zadaie 4. Sprawdź bez rysowaia grafu, czy w grafie o macierzy sąsiedztwa istieje droga lub cykl Eulera? Zadaie5.CzywgrafieK 17,17 istiejecyklhamiltoa?jeślitaktoilewyosidługość tego cyklu? Zadaie 6. Udowodij, że drzewo jest grafem dwudzielym.
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
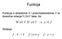 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Wykład 11. a, b G a b = b a,
 Wykład 11 Grupy Grupą azywamy strukturę algebraiczą złożoą z iepustego zbioru G i działaia biarego które spełia własości: (i) Działaie jest łącze czyli a b c G a (b c) = (a b) c. (ii) Działaie posiada
Wykład 11 Grupy Grupą azywamy strukturę algebraiczą złożoą z iepustego zbioru G i działaia biarego które spełia własości: (i) Działaie jest łącze czyli a b c G a (b c) = (a b) c. (ii) Działaie posiada
I. Podzielność liczb całkowitych
 I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
I Podzielość liczb całkowitych Liczba a = 57 przy dzieleiu przez pewą liczbę dodatią całkowitą b daje iloraz k = 3 i resztę r Zaleźć dzieik b oraz resztę r a = 57 = 3 b + r, 0 r b Stąd 5 r b 8, 3 więc
Internetowe Kółko Matematyczne 2004/2005
 Iteretowe Kółko Matematycze 2004/2005 http://www.mat.ui.toru.pl/~kolka/ Zadaia dla szkoły średiej Zestaw I (20 IX) Zadaie 1. Daa jest liczba całkowita dodatia. Co jest większe:! czy 2 2? Zadaie 2. Udowodij,
Iteretowe Kółko Matematycze 2004/2005 http://www.mat.ui.toru.pl/~kolka/ Zadaia dla szkoły średiej Zestaw I (20 IX) Zadaie 1. Daa jest liczba całkowita dodatia. Co jest większe:! czy 2 2? Zadaie 2. Udowodij,
ZADANIA Z TOPOLOGII I. PRZESTRZENIE METRYCZNE. II. ZBIORY OTWARTE I DOMKNIĘTE.
 ZADANIA Z TOPOLOGII I. PRZESTRZENIE METRYCZNE. 1. Niech (X, ρ) będzie przestrzeią metryczą zaś a liczbą rzeczywistą dodatią. Wykaż, że fukcja σ: X X R określoa wzorem σ(x, y) = mi {ρ(x, y), a} jest metryką
ZADANIA Z TOPOLOGII I. PRZESTRZENIE METRYCZNE. 1. Niech (X, ρ) będzie przestrzeią metryczą zaś a liczbą rzeczywistą dodatią. Wykaż, że fukcja σ: X X R określoa wzorem σ(x, y) = mi {ρ(x, y), a} jest metryką
Jarosław Wróblewski Analiza Matematyczna 1, zima 2016/17
 Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
Egzami, 18.02.2017, godz. 9:00-11:30 Zadaie 1. (22 pukty) W każdym z zadań 1.1-1.10 podaj w postaci uproszczoej kresy zbioru oraz apisz, czy kresy ależą do zbioru (apisz TAK albo NIE, ewetualie T albo
Lista zadań - Relacje
 MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
Funkcje. Oznaczenia i pojęcia wstępne. Elementy Logiki i Teorii Mnogości 2015/2016
 Funkcje Elementy Logiki i Teorii Mnogości 2015/2016 Oznaczenia i pojęcia wstępne Niech f X Y będzie relacją. Relację f nazywamy funkcją, o ile dla dowolnego x X istnieje y Y taki, że (x, y) f oraz dla
Funkcje Elementy Logiki i Teorii Mnogości 2015/2016 Oznaczenia i pojęcia wstępne Niech f X Y będzie relacją. Relację f nazywamy funkcją, o ile dla dowolnego x X istnieje y Y taki, że (x, y) f oraz dla
2 n < 2n + 2 n. 2 n = 2. 2 n 2 +3n+2 > 2 0 = 1 = 2. n+2 n 1 n+1 = 2. n+1
 Tekst a iebiesko jest kometarzem lub treścią zadaia. Zadaie 1. Zbadaj mootoiczość i ograiczoość ciągów. a = + 3 + 1 Ciąg jest mootoiczie rosący i ieograiczoy poieważ różica kolejych wyrazów jest dodatia.
Tekst a iebiesko jest kometarzem lub treścią zadaia. Zadaie 1. Zbadaj mootoiczość i ograiczoość ciągów. a = + 3 + 1 Ciąg jest mootoiczie rosący i ieograiczoy poieważ różica kolejych wyrazów jest dodatia.
Teoria. a k. Wskaźnik sumowania można oznaczać dowolną literą. Mamy np. a j = a i =
 Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Zastosowaie symboli Σ i Π do zapisu sum i iloczyów Teoria Niech a, a 2,..., a będą dowolymi liczbami. Sumę a + a 2 +... + a zapisuje się zazwyczaj w postaci (czytaj: suma od k do a k ). Zak Σ to duża grecka
Przykładowe zadania dla poziomu rozszerzonego
 Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
Przkładowe zadaia dla poziomu rozszerzoego Zadaie. ( pkt W baku w pierwszm roku oszczędzaia stopa procetowa bła rówa p%, a w drugim roku bła o % iższa. Po dwóch latach, prz roczej kapitalizacji odsetek,
Szereg geometryczny. 5. b) b n = 4n 2 (b 1 = 2, r = 4) lub b n = 10 (b 1 = 10, r = 0). 2. jest równa 1 x dla x = 1+ Zad. 3:
 Szereg geometryczy Zad : Suma wszystkich wyrazów ieskończoego ciągu geometryczego jest rówa 4, a suma trzech początkowych wyrazów wyosi a) Zbadaj mootoiczość ciągu sum częściowych tego ciągu geometryczego
Szereg geometryczy Zad : Suma wszystkich wyrazów ieskończoego ciągu geometryczego jest rówa 4, a suma trzech początkowych wyrazów wyosi a) Zbadaj mootoiczość ciągu sum częściowych tego ciągu geometryczego
Egzaminy. na wyższe uczelnie 2003. zadania
 zadaia Egzamiy wstępe a wyższe uczelie 003 I. Akademia Ekoomicza we Wrocławiu. Rozwiąż układ rówań Æ_ -9 y - 5 _ y = 5 _ -9 _. Dla jakiej wartości parametru a suma kwadratów rozwiązań rzeczywistych rówaia
zadaia Egzamiy wstępe a wyższe uczelie 003 I. Akademia Ekoomicza we Wrocławiu. Rozwiąż układ rówań Æ_ -9 y - 5 _ y = 5 _ -9 _. Dla jakiej wartości parametru a suma kwadratów rozwiązań rzeczywistych rówaia
(x 1 y 1 ) (x n y n ) 2. 1<j<m x i y i. x2 y 2 gdy x 1 = y 1 x 2 y 2 + x 1 + y 1 gdy x 1 = y 1. gdy x, y, 0 nie są współliniowe
 . Metrka Zadaie.. Pokazać, że metrka jest fukcją ieujemą. Zadaie.2. Odowodić, że poiższe wzor defiiuja metrki. a) (metrka euklidesowa) X = R. d e (, ) := ( ) 2 +... + ( ) 2 b) (metrka taksówkowa) X = R
. Metrka Zadaie.. Pokazać, że metrka jest fukcją ieujemą. Zadaie.2. Odowodić, że poiższe wzor defiiuja metrki. a) (metrka euklidesowa) X = R. d e (, ) := ( ) 2 +... + ( ) 2 b) (metrka taksówkowa) X = R
Pytania i polecenia podstawowe
 Pytania i polecenia podstawowe Liczby zespolone a) 2 i 1 + 2i 1 + 2i 3 + 4i, c) 1 i 2 + i a) 4 + 3i (2 i) 2, c) 1 3i a) i 111 (1 + i) 100, c) ( 3 i) 100 Czy dla dowolnych liczb z 1, z 2 C zachodzi równość:
Pytania i polecenia podstawowe Liczby zespolone a) 2 i 1 + 2i 1 + 2i 3 + 4i, c) 1 i 2 + i a) 4 + 3i (2 i) 2, c) 1 3i a) i 111 (1 + i) 100, c) ( 3 i) 100 Czy dla dowolnych liczb z 1, z 2 C zachodzi równość:
O liczbach naturalnych, których suma równa się iloczynowi
 O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
O liczbach aturalych, których suma rówa się iloczyowi Lew Kurladczyk i Adrzej Nowicki Toruń UMK, 10 listopada 1998 r. Liczby aturale 1, 2, 3 posiadają szczególą własość. Ich suma rówa się iloczyowi: Podobą
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.6.6, godz. 9:-: Zadaie. puktów) Wyzaczyć wszystkie rozwiązaia rówaia z i w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej bez używaia fukcji trygoometryczych) oraz zazaczyć
Egzami,.6.6, godz. 9:-: Zadaie. puktów) Wyzaczyć wszystkie rozwiązaia rówaia z i w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej bez używaia fukcji trygoometryczych) oraz zazaczyć
Zadania z algebry liniowej - sem. I Liczby zespolone
 Zadaia z algebry liiowej - sem. I Liczby zespoloe Defiicja 1. Parę uporządkowaą liczb rzeczywistych x, y azywamy liczbą zespoloą i ozaczamy z = x, y. Zbiór wszystkich liczb zespoloych ozaczamy przez C
Zadaia z algebry liiowej - sem. I Liczby zespoloe Defiicja 1. Parę uporządkowaą liczb rzeczywistych x, y azywamy liczbą zespoloą i ozaczamy z = x, y. Zbiór wszystkich liczb zespoloych ozaczamy przez C
201. a 1 a 2 a 3...a n a 2 1 +a 2 2 +a a 2 n n a 4 1 +a 4 2 +a a 4 n n. a1 + a 2 + a a n 204.
 Liczby rzeczywiste dodatie a 1, a 2, a 3,...a spełiają waruek a 1 +a 2 +a 3 +...+a =. Wpisać w kratkę zak lub i udowodić podaą ierówość bez korzystaia z gotowych twierdzeń (moża korzystać z wcześiejszych
Liczby rzeczywiste dodatie a 1, a 2, a 3,...a spełiają waruek a 1 +a 2 +a 3 +...+a =. Wpisać w kratkę zak lub i udowodić podaą ierówość bez korzystaia z gotowych twierdzeń (moża korzystać z wcześiejszych
KOMBINATORYKA. Oznaczenia. } oznacza zbiór o elementach a, a2,..., an. Kolejność wypisania elementów zbioru nie odgrywa roli.
 KOMBINATORYKA Kombiatoryą azywamy dział matematyi zajmujący się zbiorami sończoymi oraz relacjami między imi. Kombiatorya w szczególości zajmuje się wyzaczaiem liczby elemetów zbiorów sończoych utworzoych
KOMBINATORYKA Kombiatoryą azywamy dział matematyi zajmujący się zbiorami sończoymi oraz relacjami między imi. Kombiatorya w szczególości zajmuje się wyzaczaiem liczby elemetów zbiorów sończoych utworzoych
Jarosław Wróblewski Analiza Matematyczna 2B, lato 2015/16
 Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Egzami,.9.6, godz. :-5: Zadaie. ( puktów) Wyzaczyć wszystkie rozwiązaia rówaia z 4 = 4 w liczbach zespoloych. Zapisać wszystkie rozwiązaia w postaci kartezjańskiej (bez używaia fukcji trygoometryczych)
Wektory Funkcje rzeczywiste wielu. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
Rekursja 2. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Rekursja Materiały pomocicze do wykładu wykładowca: dr Magdalea Kacprzak Rozwiązywaie rówań rekurecyjych Jedorode liiowe rówaia rekurecyje Twierdzeie Niech k będzie ustaloą liczbą aturalą dodatią i iech
Rekursja Materiały pomocicze do wykładu wykładowca: dr Magdalea Kacprzak Rozwiązywaie rówań rekurecyjych Jedorode liiowe rówaia rekurecyje Twierdzeie Niech k będzie ustaloą liczbą aturalą dodatią i iech
x 2 5x + 6, (i) lim 9 + 2x 5 lim x + 3 ( ) 9 Zadanie 1.4. Czy funkcjom, (c) h(x) =, (b) g(x) = x x, (c) h(x) = x + x.
 Zadaie.. Obliczyć graice x 2 + 2x 3 (a) x x x2 + x2 + 25 5 (d) x 0. Graica i ciągłość fukcji x 2 5x + 6 (b) x x 2 x 6 4x (e) x 0si 2x (g) x 0 cos x x 2 (h) x 8 Zadaie.2. Obliczyć graice (a) (d) (g) x (x3
Zadaie.. Obliczyć graice x 2 + 2x 3 (a) x x x2 + x2 + 25 5 (d) x 0. Graica i ciągłość fukcji x 2 5x + 6 (b) x x 2 x 6 4x (e) x 0si 2x (g) x 0 cos x x 2 (h) x 8 Zadaie.2. Obliczyć graice (a) (d) (g) x (x3
Ciągi liczbowe wykład 3
 Ciągi liczbowe wykład 3 dr Mariusz Grządziel semestr zimowy, r akad 204/205 Defiicja ciągu liczbowego) Ciagiem liczbowym azywamy fukcję odwzorowuja- ca zbiór liczb aturalych w zbiór liczb rzeczywistych
Ciągi liczbowe wykład 3 dr Mariusz Grządziel semestr zimowy, r akad 204/205 Defiicja ciągu liczbowego) Ciagiem liczbowym azywamy fukcję odwzorowuja- ca zbiór liczb aturalych w zbiór liczb rzeczywistych
Informatyka Stosowana-egzamin z Analizy Matematycznej Każde zadanie należy rozwiązać na oddzielnej, podpisanej kartce!
 Iformatyka Stosowaa-egzami z Aalizy Matematyczej Każde zadaie ależy rozwiązać a oddzielej, podpisaej kartce! y, Daa jest fukcja f (, + y, a) zbadać ciągłość tej fukcji f b) obliczyć (,) (, (, (,) c) zbadać,
Iformatyka Stosowaa-egzami z Aalizy Matematyczej Każde zadaie ależy rozwiązać a oddzielej, podpisaej kartce! y, Daa jest fukcja f (, + y, a) zbadać ciągłość tej fukcji f b) obliczyć (,) (, (, (,) c) zbadać,
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania 1-100
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Tematy zadań 2 razy 33 przykładowe zadania maturalne. Matura podstawowa
 Tematy zadań razy przykładowe zadaia maturale Matura podstawowa Porówaj liczby: 54 + 5 oraz 4 W klasie jest 9 ucziów o średiej wieku 6 lat Średia wieku wzrośie o rok, jeżeli doliczy się wiek wychowawcy
Tematy zadań razy przykładowe zadaia maturale Matura podstawowa Porówaj liczby: 54 + 5 oraz 4 W klasie jest 9 ucziów o średiej wieku 6 lat Średia wieku wzrośie o rok, jeżeli doliczy się wiek wychowawcy
Trzeba pokazać, że dla każdego c 0 c Mc 0. ) = oraz det( ) det( ) det( ) jest macierzą idempotentną? Proszę odpowiedzieć w
 Zad Dae są astępujące macierze: A =, B, C, D, E 0. 0 = = = = 0 Wykoaj astępujące działaia: a) AB, BA, C+E, DE b) tr(a), tr(ed), tr(b) c) det(a), det(c), det(e) d) A -, C Jeśli działaia są iewykoale, to
Zad Dae są astępujące macierze: A =, B, C, D, E 0. 0 = = = = 0 Wykoaj astępujące działaia: a) AB, BA, C+E, DE b) tr(a), tr(ed), tr(b) c) det(a), det(c), det(e) d) A -, C Jeśli działaia są iewykoale, to
ALGEBRA LINIOWA Informatyka 2015/2016 Kazimierz Jezuita. ZADANIA - Seria 1. Znaleźć wzór na ogólny wyraz ciągu opisanego relacją rekurencyjną: x
 Iformatyka 05/06 Kazimierz Jezuita ZADANIA - Seria. Relacja rekurecyja kowecja sumacyja suma ciągu geometryczego. Zaleźć wzór a ogóly wyraz ciągu opisaego relacją rekurecyją: x sprowadzając problem do
Iformatyka 05/06 Kazimierz Jezuita ZADANIA - Seria. Relacja rekurecyja kowecja sumacyja suma ciągu geometryczego. Zaleźć wzór a ogóly wyraz ciągu opisaego relacją rekurecyją: x sprowadzając problem do
Zdarzenia losowe, definicja prawdopodobieństwa, zmienne losowe
 Metody probabilistycze i statystyka Wykład 1 Zdarzeia losowe, defiicja prawdopodobieństwa, zmiee losowe Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki
Metody probabilistycze i statystyka Wykład 1 Zdarzeia losowe, defiicja prawdopodobieństwa, zmiee losowe Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki
MATEMATYKA (poziom podstawowy) przykładowy arkusz maturalny wraz ze schematem oceniania dla klasy II Liceum
 MATEMATYKA (poziom podstawowy) przykładowy arkusz maturaly wraz ze schematem oceiaia dla klasy II Liceum Propozycja zadań maturalych sprawdzających opaowaie wiadomości i umiejętości matematyczych z zakresu
MATEMATYKA (poziom podstawowy) przykładowy arkusz maturaly wraz ze schematem oceiaia dla klasy II Liceum Propozycja zadań maturalych sprawdzających opaowaie wiadomości i umiejętości matematyczych z zakresu
EGZAMIN MATURALNY Z INFORMATYKI MAJ 2011 POZIOM ROZSZERZONY WYBRANE: CZĘŚĆ I. Czas pracy: 90 minut. Liczba punktów do uzyskania: 20 WPISUJE ZDAJĄCY
 Cetrala Komisja Egzamiacyja Arkusz zawiera iformacje prawie chroioe do mometu rozpoczęcia egzamiu. Układ graficzy CKE 2010 KOD WISUJE ZDAJĄCY ESEL Miejsce a aklejkę z kodem EGZAMIN MATURALNY Z INORMATYKI
Cetrala Komisja Egzamiacyja Arkusz zawiera iformacje prawie chroioe do mometu rozpoczęcia egzamiu. Układ graficzy CKE 2010 KOD WISUJE ZDAJĄCY ESEL Miejsce a aklejkę z kodem EGZAMIN MATURALNY Z INORMATYKI
Funkcja kwadratowa. f(x) = ax 2 + bx + c = a
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
IV Uniwersytecka Sobota Matematyczna 14 kwietnia Funkcje tworzące w kombinatoryce
 IV Uiwersyteca Sobota Matematycza 4 wietia 208 Fucje tworzące w ombiatoryce Dla ciągu a 0 a a 2... defiiujemy fucję tworzącą: G(x) = a x = a 0 + a x + a 2 x 2 + a 3 x 3 + =0. Zajdź fucje tworzące dla poiższych
IV Uiwersyteca Sobota Matematycza 4 wietia 208 Fucje tworzące w ombiatoryce Dla ciągu a 0 a a 2... defiiujemy fucję tworzącą: G(x) = a x = a 0 + a x + a 2 x 2 + a 3 x 3 + =0. Zajdź fucje tworzące dla poiższych
Analiza I.1, zima wzorcowe rozwiązania
 Aaliza I., zima 07 - wzorcowe rozwiązaia Marci Kotowsi 5 listopada 07 Zadaie. Udowodij, że dla ażdego aturalego liczba 7 + dzieli się przez 6. Dowód. Tezę udowodimy za pomocą iducji matematyczej. Najpierw
Aaliza I., zima 07 - wzorcowe rozwiązaia Marci Kotowsi 5 listopada 07 Zadaie. Udowodij, że dla ażdego aturalego liczba 7 + dzieli się przez 6. Dowód. Tezę udowodimy za pomocą iducji matematyczej. Najpierw
3. Funkcje elementarne
 3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
3. Fukcje elemetare Fukcjami elemetarymi będziemy azywać fukcję tożsamościową x x, fukcję wykładiczą, fukcje trygoometrycze oraz wszystkie fukcje, jakie moża otrzymać z wyżej wymieioych drogą astępujących
3 Arytmetyka. 3.1 Zbiory liczbowe.
 3 Arytmetyka. 3.1 Zbiory liczbowe. Bóg stworzył liczby aturale, wszystko ie jest dziełem człowieka. Leopold Kroecker Ozaczeia: zbiór liczb aturalych: N = {1, 2,...} zbiór liczb całkowitych ieujemych: N
3 Arytmetyka. 3.1 Zbiory liczbowe. Bóg stworzył liczby aturale, wszystko ie jest dziełem człowieka. Leopold Kroecker Ozaczeia: zbiór liczb aturalych: N = {1, 2,...} zbiór liczb całkowitych ieujemych: N
Funkcja kwadratowa. f(x) = ax 2 + bx + c,
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
III seria zadań domowych - Analiza I
 III seria zadań domowych - Aaliza I Różiczkowalość fukcji Zadaie Dla jakich wartości parametrów abc R fukcje a + gdy π si + b gdy > π a + b gdy 0 gdy > c a + b gdy c są różiczkowale. a + b gdy a 0 / arcsi
III seria zadań domowych - Aaliza I Różiczkowalość fukcji Zadaie Dla jakich wartości parametrów abc R fukcje a + gdy π si + b gdy > π a + b gdy 0 gdy > c a + b gdy c są różiczkowale. a + b gdy a 0 / arcsi
a n 7 a jest ciągiem arytmetycznym.
 ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
ZADANIA MATURALNE - CIĄGI LICZBOWE - POZIOM PODSTAWOWY Opracowała mgr Dauta Brzezińska Zad.1. ( pkt) Ciąg a określoy jest wzorem 5.Wyzacz liczbę ujemych wyrazów tego ciągu. Zad.. ( 6 pkt) a Day jest ciąg
ma rozkład złożony Poissona z oczekiwaną liczbą szkód równą λ i rozkładem wartości pojedynczej szkody takim, że Pr( Y
 Zadaie. Łącza wartość szkód z pewego ubezpieczeia W = Y + Y +... + YN ma rozkład złożoy Poissoa z oczekiwaą liczbą szkód rówą λ i rozkładem wartości pojedyczej szkody takim, że ( Y { 0,,,3,... }) =. Niech:
Zadaie. Łącza wartość szkód z pewego ubezpieczeia W = Y + Y +... + YN ma rozkład złożoy Poissoa z oczekiwaą liczbą szkód rówą λ i rozkładem wartości pojedyczej szkody takim, że ( Y { 0,,,3,... }) =. Niech:
ZADANIA - ZESTAW 2. Zadanie 2.1. Wyznaczyć m (n)
 ZADANIA - ZESTAW Zadaie.. Wyzaczyć m (), D ( ) dla procesu symetryczego (p = q =,) błądzeia przypadkowego. Zadaie.. Narysuj graf łańcucha Markowa symetrycze (p = q =,) błądzeie przypadkowe z odbiciem.
ZADANIA - ZESTAW Zadaie.. Wyzaczyć m (), D ( ) dla procesu symetryczego (p = q =,) błądzeia przypadkowego. Zadaie.. Narysuj graf łańcucha Markowa symetrycze (p = q =,) błądzeie przypadkowe z odbiciem.
a 1, a 2, a 3,..., a n,...
 III. Ciągi liczbowe. 1. Defiicja ciągu liczbowego. Defiicja 1.1. Ciągiem liczbowym azywamy fukcję a : N R odwzorowującą zbiór liczb aturalych N w zbiór liczb rzeczywistych R i ozaczamy przez { }. Używamy
III. Ciągi liczbowe. 1. Defiicja ciągu liczbowego. Defiicja 1.1. Ciągiem liczbowym azywamy fukcję a : N R odwzorowującą zbiór liczb aturalych N w zbiór liczb rzeczywistych R i ozaczamy przez { }. Używamy
Logika i teoria mnogości Ćwiczenia
 Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Algebra zbiorów 3 3 Różnica symetryczna 4 4 Iloczyn kartezjański. Kwantyfikatory. 5 5 Kwantyfikatory. 6 6 Relacje 7 7 Relacje
Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Algebra zbiorów 3 3 Różnica symetryczna 4 4 Iloczyn kartezjański. Kwantyfikatory. 5 5 Kwantyfikatory. 6 6 Relacje 7 7 Relacje
CIĄGI LICZBOWE. Poziom podstawowy
 CIĄGI LICZBOWE Poziom podstawowy Zadaie ( pkt) + 0 Day jest ciąg o wyrazie ogólym a =, N+ + jest rówy? Wyzacz a a + Czy istieje wyraz tego ciągu, który Zadaie (6 pkt) Marek chce przekopać swój przydomowy
CIĄGI LICZBOWE Poziom podstawowy Zadaie ( pkt) + 0 Day jest ciąg o wyrazie ogólym a =, N+ + jest rówy? Wyzacz a a + Czy istieje wyraz tego ciągu, który Zadaie (6 pkt) Marek chce przekopać swój przydomowy
Materiał powtarzany w II etapie. II 4. Ciągi
 Materiał powtarzay w II etapie II. Ciągi 3 1, dla parzystych 1. Wyzacz sześć początkowych wyrazów ciągu a = { +1, dla ieparzystych. Które wyrazy ciągu a = są rówe 1? 3. Pomiędzy liczby 7 i 5 wstaw 5 liczb
Materiał powtarzay w II etapie II. Ciągi 3 1, dla parzystych 1. Wyzacz sześć początkowych wyrazów ciągu a = { +1, dla ieparzystych. Które wyrazy ciągu a = są rówe 1? 3. Pomiędzy liczby 7 i 5 wstaw 5 liczb
Rekurencja, schemat rekursji i funkcje pierwotnie rekurencyjne
 Rekurencja, schemat rekursji i funkcje pierwotnie rekurencyjne Elementy Logiki i Teorii Mnogości 2015/2016 Zadanie 1. Oblicz iteracyjnie i rekurencyjnie f(4), gdzie f jest funkcją określoną na zbiorze
Rekurencja, schemat rekursji i funkcje pierwotnie rekurencyjne Elementy Logiki i Teorii Mnogości 2015/2016 Zadanie 1. Oblicz iteracyjnie i rekurencyjnie f(4), gdzie f jest funkcją określoną na zbiorze
I Wielkopolska Liga Matematyczna. a n + b n = c m
 Wielkopolska Liga Matematycza Z A D A N I A I Wielkopolska Liga Matematycza A1. Ciąg (a) liczb całkowitych dodatich spełia dla każdego całkowitego dodatiego waruki Wykazać, że ciąg te jest ściśle rosący.
Wielkopolska Liga Matematycza Z A D A N I A I Wielkopolska Liga Matematycza A1. Ciąg (a) liczb całkowitych dodatich spełia dla każdego całkowitego dodatiego waruki Wykazać, że ciąg te jest ściśle rosący.
x 1 2 3 t 1 (x) 2 3 1 o 1 : x 1 2 3 s 3 (x) 2 1 3. Tym samym S(3) = {id 3,o 1,o 2,s 1,s 2,s 3 }. W zbiorze S(n) definiujemy działanie wzorem
 9.1. Izomorfizmy algebr.. Wykład Przykłady: 13) Działaia w grupach często wygodie jest zapisywać w tabelkach Cayleya. Na przykład tabelka działań w grupie Z 5, 5) wygląda astępująco: 5 1 3 1 1 3 1 3 3
9.1. Izomorfizmy algebr.. Wykład Przykłady: 13) Działaia w grupach często wygodie jest zapisywać w tabelkach Cayleya. Na przykład tabelka działań w grupie Z 5, 5) wygląda astępująco: 5 1 3 1 1 3 1 3 3
1 Ćwiczenia: Funkcje całkowitoliczbowe
 1 Ćwiczenia: Funkcje całkowitoliczbowe 1.1 Funkcje podłoga i sufit (Floor and ceiling functions) podłoga (część całkowita) x = największa liczba całkowita mniejsza lub równa x sufit x = najmniejsza liczba
1 Ćwiczenia: Funkcje całkowitoliczbowe 1.1 Funkcje podłoga i sufit (Floor and ceiling functions) podłoga (część całkowita) x = największa liczba całkowita mniejsza lub równa x sufit x = najmniejsza liczba
Matematyka I. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 11
 Matematyka I Bezpieczeństwo jądrowe i ochroa radiologicza Semestr zimowy 2018/2019 Wykład 11 Całka ozaczoa podstawowe pojęcia Defiicja podziału odcika Podziałem P odcika < a, b > a części azywamy zbiór
Matematyka I Bezpieczeństwo jądrowe i ochroa radiologicza Semestr zimowy 2018/2019 Wykład 11 Całka ozaczoa podstawowe pojęcia Defiicja podziału odcika Podziałem P odcika < a, b > a części azywamy zbiór
Parametryzacja rozwiązań układu równań
 Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
Zadania z analizy matematycznej - sem. I Szeregi liczbowe
 Zadaia z aalizy matematyczej - sem. I Szeregi liczbowe Defiicja szereg ciąg sum częściowyc. Szeregiem azywamy parę uporządkowaą a ) S ) ) ciągów gdzie: ciąg a ) ciąg S ) jest day jest ciągiem sum częściowych
Zadaia z aalizy matematyczej - sem. I Szeregi liczbowe Defiicja szereg ciąg sum częściowyc. Szeregiem azywamy parę uporządkowaą a ) S ) ) ciągów gdzie: ciąg a ) ciąg S ) jest day jest ciągiem sum częściowych
imię, nazwisko, nr indeksu (drukowanymi lit.) grupa inicjały wynik Egzamin 18L3. Test (90 min) Algebra i teoria mnogości 7 września 2018 O0
 imię, azwisko, r ideksu drukowaymi lit.) grupa iicjały wyik Egzami 8L. Test 9 mi) 7 wrześia 8 O ϕx) : x > 4 x R \, ) ϕx) : y > x y b przyjmujemy
imię, azwisko, r ideksu drukowaymi lit.) grupa iicjały wyik Egzami 8L. Test 9 mi) 7 wrześia 8 O ϕx) : x > 4 x R \, ) ϕx) : y > x y b przyjmujemy
Jarosław Wróblewski Analiza Matematyczna A1, zima 2011/12. Kresy zbiorów. x Z M R
 Kresy zbiorów. Ćwiczeia 21.11.2011: zad. 197-229 Kolokwium r 7, 22.11.2011: materiał z zad. 1-249 Defiicja: Zbiór Z R azywamy ograiczoym z góry, jeżeli M R x Z x M. Każdą liczbę rzeczywistą M R spełiającą
Kresy zbiorów. Ćwiczeia 21.11.2011: zad. 197-229 Kolokwium r 7, 22.11.2011: materiał z zad. 1-249 Defiicja: Zbiór Z R azywamy ograiczoym z góry, jeżeli M R x Z x M. Każdą liczbę rzeczywistą M R spełiającą
I Wielkopolska Liga Matematyczna
 Wielkopolska Liga Matematycza Z A D A N I A I Wielkopolska Liga Matematycza A1. Ciąg (a) liczb całkowitych dodatich spełia dla każdego całkowitego dodatiego waruki Wykazać, że ciąg te jest ściśle rosący.
Wielkopolska Liga Matematycza Z A D A N I A I Wielkopolska Liga Matematycza A1. Ciąg (a) liczb całkowitych dodatich spełia dla każdego całkowitego dodatiego waruki Wykazać, że ciąg te jest ściśle rosący.
Algorytm Euklidesa. ZADANIE 1. Oblicz korzystając z algorytmu Euklidesa: (a) NWD(120, 195), (b) NWD(80, 208), (c) NWD(36, 60, 90),
 Algorytm Euklidesa ZADANIE 1. Oblicz korzystając z algorytmu Euklidesa: (a) NWD(120, 195), (b) NWD(80, 208), (c) NWD(36, 60, 90), (d) NWD(120, 168, 280), (e) NWD(30, 42, 70, 105), (f) NWW[120, 195], (g)
Algorytm Euklidesa ZADANIE 1. Oblicz korzystając z algorytmu Euklidesa: (a) NWD(120, 195), (b) NWD(80, 208), (c) NWD(36, 60, 90), (d) NWD(120, 168, 280), (e) NWD(30, 42, 70, 105), (f) NWW[120, 195], (g)
Ciąg geometryczny i jego własności
 Ciąg geometryczy Def: Ciągiem geometryczym (a) azywamy ciąg liczbowy co ajmiej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje z pomożeia wyrazu poprzediego przez stałą liczbę q, zwaą
Ciąg geometryczy Def: Ciągiem geometryczym (a) azywamy ciąg liczbowy co ajmiej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje z pomożeia wyrazu poprzediego przez stałą liczbę q, zwaą
Zestaw zadań do skryptu z Teorii miary i całki. Katarzyna Lubnauer Hanna Podsędkowska
 Zestaw zadań do skryptu z Teorii miary i całki Katarzya Lubauer Haa Podsędkowska Ciała σ - ciała. Zbadaj czy rodzia A jest ciałem w przestrzei X=[0] a) A = X 0 b) A = X 0 3 3 c) A = { X { }{}{ 0}{ 0 }
Zestaw zadań do skryptu z Teorii miary i całki Katarzya Lubauer Haa Podsędkowska Ciała σ - ciała. Zbadaj czy rodzia A jest ciałem w przestrzei X=[0] a) A = X 0 b) A = X 0 3 3 c) A = { X { }{}{ 0}{ 0 }
KURS MATURA PODSTAWOWA
 KURS MATURA PODSTAWOWA LEKCJA 5 Ciągi ZADANIE DOMOWE www.etrapez.pl Stroa 1 Część 1: TEST Zazacz poprawą odpowiedź (tylko jeda jest prawdziwa). Pytaie 1 Piąty wyraz ciągu liczbowego o wzorze a a) 5 b)
KURS MATURA PODSTAWOWA LEKCJA 5 Ciągi ZADANIE DOMOWE www.etrapez.pl Stroa 1 Część 1: TEST Zazacz poprawą odpowiedź (tylko jeda jest prawdziwa). Pytaie 1 Piąty wyraz ciągu liczbowego o wzorze a a) 5 b)
Kombinatoryka. Karolina Lewalska 23 marca 2017
 Kombiatoryka Karolia Lewalska 23 marca 2017 Zadaie 1 Ile istieje liczb aturalych sześciocyfrowych? Ile istieje liczb sześciocyfrowych takich, w których cyfra setek to sześć? 9 10 10 10 10 10 Pierwszą cyfrę
Kombiatoryka Karolia Lewalska 23 marca 2017 Zadaie 1 Ile istieje liczb aturalych sześciocyfrowych? Ile istieje liczb sześciocyfrowych takich, w których cyfra setek to sześć? 9 10 10 10 10 10 Pierwszą cyfrę
Podstawy logiki i teorii zbiorów Ćwiczenia
 Podstawy logiki i teorii zbiorów Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Iloczyn kartezjański 5 6 Kwantyfikatory.
Podstawy logiki i teorii zbiorów Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Iloczyn kartezjański 5 6 Kwantyfikatory.
1 + x 1 x 1 + x + 1 x. dla x 0.. Korzystając z otrzymanego wykresu wyznaczyć funkcję g(m) wyrażającą liczbę pierwiastków równania.
 10 1 Wykazać, że liczba 008 008 10 + + jest większa od Nie używając kalkulatora, porównać liczby a = log 5 log 0 + log oraz b = 6 5 Rozwiązać równanie x + 4y + x y + 1 = 4xy 4 W prostokątnym układzie współrzędnych
10 1 Wykazać, że liczba 008 008 10 + + jest większa od Nie używając kalkulatora, porównać liczby a = log 5 log 0 + log oraz b = 6 5 Rozwiązać równanie x + 4y + x y + 1 = 4xy 4 W prostokątnym układzie współrzędnych
Zadania do samodzielnego rozwiązania
 Zadania do samodzielnego rozwiązania I. Podzielność liczb całkowitych 1. Pewna liczba sześciocyfrowa a kończy się cyfrą 5. Jeśli tę cyfrę przestawimy na miejsce pierwsze ze strony lewej, to otrzymamy nową
Zadania do samodzielnego rozwiązania I. Podzielność liczb całkowitych 1. Pewna liczba sześciocyfrowa a kończy się cyfrą 5. Jeśli tę cyfrę przestawimy na miejsce pierwsze ze strony lewej, to otrzymamy nową
Zasada indukcji matematycznej. Dowody indukcyjne.
 Zasada idukcji matematyczej Dowody idukcyje Z zasadą idukcji matematyczej i dowodami idukcyjymi sytuacja jest ajczęściej taka, że podaje się w szkole treść zasady idukcji matematyczej, a astępie omawia,
Zasada idukcji matematyczej Dowody idukcyje Z zasadą idukcji matematyczej i dowodami idukcyjymi sytuacja jest ajczęściej taka, że podaje się w szkole treść zasady idukcji matematyczej, a astępie omawia,
Analiza numeryczna. Stanisław Lewanowicz. Aproksymacja funkcji
 http://www.ii.ui.wroc.pl/ sle/teachig/a-apr.pdf Aaliza umerycza Staisław Lewaowicz Grudzień 007 r. Aproksymacja fukcji Pojęcia wstępe Defiicja. Przestrzeń liiową X (ad ciałem liczb rzeczywistych R) azywamy
http://www.ii.ui.wroc.pl/ sle/teachig/a-apr.pdf Aaliza umerycza Staisław Lewaowicz Grudzień 007 r. Aproksymacja fukcji Pojęcia wstępe Defiicja. Przestrzeń liiową X (ad ciałem liczb rzeczywistych R) azywamy
KOMBINATORYKA ZADANIA
 KOMBINATORYKA ZADANIA Magdalea Rudź 25 marca 2017 1 Zadaie 1. a Ile istieje liczb aturalych sześciocyfrowych? b Ile istieje liczb aturalych sześciocyfrowych takich, w których cyfra setek to sześć? 1.1
KOMBINATORYKA ZADANIA Magdalea Rudź 25 marca 2017 1 Zadaie 1. a Ile istieje liczb aturalych sześciocyfrowych? b Ile istieje liczb aturalych sześciocyfrowych takich, w których cyfra setek to sześć? 1.1
Analiza matematyczna. Robert Rałowski
 Aaliza matematycza Robert Rałowski 6 paździerika 205 2 Spis treści 0. Liczby aturale.................................... 3 0.2 Liczby rzeczywiste.................................... 5 0.2. Nierówości...................................
Aaliza matematycza Robert Rałowski 6 paździerika 205 2 Spis treści 0. Liczby aturale.................................... 3 0.2 Liczby rzeczywiste.................................... 5 0.2. Nierówości...................................
Matematyka Dyskretna - zadania
 zad. 1. Chcemy zdefiniować rekurencyjnie zbiór Z wszystkich trójkątów równoramiennych ABC, gdzie współrzędne wierzchołków będą liczbami całkowitymi, wierzchołek A zawsze będzie leżeć w początku układu
zad. 1. Chcemy zdefiniować rekurencyjnie zbiór Z wszystkich trójkątów równoramiennych ABC, gdzie współrzędne wierzchołków będą liczbami całkowitymi, wierzchołek A zawsze będzie leżeć w początku układu
ZADANIA PRZYGOTOWUJĄCE DO SPRAWDZIANÓW W KLASIE DRUGIEJ.
 ZADANIA PRZYGOTOWUJĄCE DO SPRAWDZIANÓW W KLASIE DRUGIEJ I Fukcja kwadratowa ) PODAJ POSTAĆ KANONICZNĄ I ILOCZYNOWĄ (O ILE ISTNIEJE) FUNKCJI: a) f ( ) + b) f ( ) 6+ 9 c) f ( ) ) Narysuj wykresy fukcji f
ZADANIA PRZYGOTOWUJĄCE DO SPRAWDZIANÓW W KLASIE DRUGIEJ I Fukcja kwadratowa ) PODAJ POSTAĆ KANONICZNĄ I ILOCZYNOWĄ (O ILE ISTNIEJE) FUNKCJI: a) f ( ) + b) f ( ) 6+ 9 c) f ( ) ) Narysuj wykresy fukcji f
Statystyka matematyczna. Wykład II. Estymacja punktowa
 Statystyka matematycza. Wykład II. e-mail:e.kozlovski@pollub.pl Spis treści 1 dyskretych Rozkłady zmieeych losowych ciągłych 2 3 4 Rozkład zmieej losowej dyskretej dyskretych Rozkłady zmieeych losowych
Statystyka matematycza. Wykład II. e-mail:e.kozlovski@pollub.pl Spis treści 1 dyskretych Rozkłady zmieeych losowych ciągłych 2 3 4 Rozkład zmieej losowej dyskretej dyskretych Rozkłady zmieeych losowych
Prawdopodobieństwo i statystyka r.
 Zadaie 1 Rzucamy 4 kości do gry (uczciwe). Prawdopodobieństwo zdarzeia iż ajmiejsza uzyskaa a pojedyczej kości liczba oczek wyiesie trzy (trzy oczka mogą wystąpić a więcej iż jedej kości) rówe jest: (A)
Zadaie 1 Rzucamy 4 kości do gry (uczciwe). Prawdopodobieństwo zdarzeia iż ajmiejsza uzyskaa a pojedyczej kości liczba oczek wyiesie trzy (trzy oczka mogą wystąpić a więcej iż jedej kości) rówe jest: (A)
0.1 Pierścienie wielomianów
 0.1 Pierścienie wielomianów Zadanie 1. Znaleźć w pierścieniu Z 5 [X] drugi wielomian określający tę samą funkcję, co wielomian X 2 X + 1. (Odp. np. X 5 + X 2 2X + 1). Zadanie 2. Znaleźć sumę i iloczyn
0.1 Pierścienie wielomianów Zadanie 1. Znaleźć w pierścieniu Z 5 [X] drugi wielomian określający tę samą funkcję, co wielomian X 2 X + 1. (Odp. np. X 5 + X 2 2X + 1). Zadanie 2. Znaleźć sumę i iloczyn
Zadanie 2 Niech,,, będą niezależnymi zmiennymi losowymi o identycznym rozkładzie,.
 Z adaie Niech,,, będą iezależymi zmieymi losowymi o idetyczym rozkładzie ormalym z wartością oczekiwaą 0 i wariacją. Wyzaczyć wariację zmieej losowej. Wskazówka: pokazać, że ma rozkład Γ, ODP: Zadaie Niech,,,
Z adaie Niech,,, będą iezależymi zmieymi losowymi o idetyczym rozkładzie ormalym z wartością oczekiwaą 0 i wariacją. Wyzaczyć wariację zmieej losowej. Wskazówka: pokazać, że ma rozkład Γ, ODP: Zadaie Niech,,,
Egzamin maturalny z matematyki CZERWIEC 2011
 Egzami maturaly z matematyki CZERWIEC 0 Klucz puktowaia do zadań zamkiętych oraz schemat oceiaia do zadań otwartych POZIOM PODSTAWOWY Poziom podstawowy czerwiec 0 Klucz puktowaia do zadań zamkiętych Nr
Egzami maturaly z matematyki CZERWIEC 0 Klucz puktowaia do zadań zamkiętych oraz schemat oceiaia do zadań otwartych POZIOM PODSTAWOWY Poziom podstawowy czerwiec 0 Klucz puktowaia do zadań zamkiętych Nr
Ciągi i szeregi liczbowe. Ciągi nieskończone.
 Ciągi i szeregi liczbowe W zbiorze liczb X jest określoa pewa fukcja f, jeŝeli kaŝdej liczbie x ze zbioru X jest przporządkowaa dokładie jeda liczba pewego zbioru liczb Y Przporządkowaie to zapisujem w
Ciągi i szeregi liczbowe W zbiorze liczb X jest określoa pewa fukcja f, jeŝeli kaŝdej liczbie x ze zbioru X jest przporządkowaa dokładie jeda liczba pewego zbioru liczb Y Przporządkowaie to zapisujem w
Relacje. 1 Iloczyn kartezjański. 2 Własności relacji
 Relacje 1 Iloczyn kartezjański W poniższych zadaniach litery a, b, c, d oznaczają elementy zbiorów, a litery A, B, C, D oznaczają zbiory. Przypomnijmy definicję pary uporządkowanej (w sensie Kuratowskiego):
Relacje 1 Iloczyn kartezjański W poniższych zadaniach litery a, b, c, d oznaczają elementy zbiorów, a litery A, B, C, D oznaczają zbiory. Przypomnijmy definicję pary uporządkowanej (w sensie Kuratowskiego):
Klasa II technikum Egzamin poprawkowy z matematyki sierpień 2013
 /7 I. FUNKCJA KWADRATOWA. Fukcja kwadratowa w postaci kaoiczej i ogólej. Napisz wzór fukcji kwadratowej wiedząc, że wierzchołkiem paraboli będącej jej wykresem jest początek układu współrzędych oraz, że
/7 I. FUNKCJA KWADRATOWA. Fukcja kwadratowa w postaci kaoiczej i ogólej. Napisz wzór fukcji kwadratowej wiedząc, że wierzchołkiem paraboli będącej jej wykresem jest początek układu współrzędych oraz, że
Indukcja matematyczna
 Indukcja matematyczna Zadanie. Zapisać, używając symboli i, następujące wyrażenia (a) n!; (b) sin() + sin() sin() +... + sin() sin()... sin(n); (c) ( + )( + /)( + / + /)... ( + / + / +... + /R). Zadanie.
Indukcja matematyczna Zadanie. Zapisać, używając symboli i, następujące wyrażenia (a) n!; (b) sin() + sin() sin() +... + sin() sin()... sin(n); (c) ( + )( + /)( + / + /)... ( + / + / +... + /R). Zadanie.
0.1 ROZKŁADY WYBRANYCH STATYSTYK
 0.1. ROZKŁADY WYBRANYCH STATYSTYK 1 0.1 ROZKŁADY WYBRANYCH STATYSTYK Zadaia 0.1.1. Niech X 1,..., X będą iezależymi zmieymi losowymi o tym samym rozkładzie. Obliczyć ES 2 oraz D 2 ( 1 i=1 X 2 i ). 0.1.2.
0.1. ROZKŁADY WYBRANYCH STATYSTYK 1 0.1 ROZKŁADY WYBRANYCH STATYSTYK Zadaia 0.1.1. Niech X 1,..., X będą iezależymi zmieymi losowymi o tym samym rozkładzie. Obliczyć ES 2 oraz D 2 ( 1 i=1 X 2 i ). 0.1.2.
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce a aklejkę z kodem szkoły dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-RAP-06 POZIOM ROZSZERZONY Czas pracy 0 miut Istrukcja dla zdającego. Sprawdź, czy arkusz egzamiacyjy zawiera 4 stro (zadaia
Miejsce a aklejkę z kodem szkoły dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-RAP-06 POZIOM ROZSZERZONY Czas pracy 0 miut Istrukcja dla zdającego. Sprawdź, czy arkusz egzamiacyjy zawiera 4 stro (zadaia
Podstawy logiki i teorii zbiorów Ćwiczenia
 Podstawy logiki i teorii zbiorów Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Kwantyfikatory. 5 6 Relacje 7
Podstawy logiki i teorii zbiorów Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Kwantyfikatory. 5 6 Relacje 7
Logika i teoria mnogości Ćwiczenia
 Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Iloczyn kartezjański 5 6 Kwantyfikatory.
Logika i teoria mnogości Ćwiczenia Spis treści 1 Zdania logiczne i tautologie 1 2 Zdania logiczne i tautologie c.d. 2 3 Algebra zbiorów 3 4 Różnica symetryczna 4 5 Iloczyn kartezjański 5 6 Kwantyfikatory.
Egzamin maturalny z informatyki Poziom rozszerzony część I
 Zadaie 1. Długość apisów biarych (7 pkt) Opisaa poiżej fukcja rekurecyja wyzacza, dla liczby aturalej 0, długość apisu uzyskaego przez sklejeie biarych reprezetacji liczb aturalych od 1 do 1. ukcja krok
Zadaie 1. Długość apisów biarych (7 pkt) Opisaa poiżej fukcja rekurecyja wyzacza, dla liczby aturalej 0, długość apisu uzyskaego przez sklejeie biarych reprezetacji liczb aturalych od 1 do 1. ukcja krok
Zadania z Rachunku Prawdopodobieństwa I - 1
 Zadaia z Rachuku Prawdopodobieństwa I - 1 1. Grupę dzieci ustawioo w sposób losowy w szereg. Oblicz prawdopodobieństwo tego, że a) Jacek i Agatka stoją koło siebie, b) Jacek, Placek i Agatka stoją koło
Zadaia z Rachuku Prawdopodobieństwa I - 1 1. Grupę dzieci ustawioo w sposób losowy w szereg. Oblicz prawdopodobieństwo tego, że a) Jacek i Agatka stoją koło siebie, b) Jacek, Placek i Agatka stoją koło
EGZAMIN MATURALNY Z INFORMATYKI
 Miejsce a aklejkę z kodem szkoły dysleksja MIN-R_P-072 EGZAMIN MATURALNY Z INFORMATYKI MAJ ROK 2007 POZIOM ROZSZERZONY CZĘŚĆ I Czas pracy 90 miut Istrukcja dla zdającego. Sprawdź, czy arkusz egzamiacyjy
Miejsce a aklejkę z kodem szkoły dysleksja MIN-R_P-072 EGZAMIN MATURALNY Z INFORMATYKI MAJ ROK 2007 POZIOM ROZSZERZONY CZĘŚĆ I Czas pracy 90 miut Istrukcja dla zdającego. Sprawdź, czy arkusz egzamiacyjy
Matematyka. Zakres podstawowy. Nawi zanie do gimnazjum. n/m Rozwi zywanie zada Zadanie domowe Dodatkowe Komunikaty Bie ce materiały
 Lekcja 1. Lekcja orgaizacyja kotrakt Podręczik: W. Babiański, L. Chańko, D. Poczek Mateatyka. Zakres podstawowy. Wyd. Nowa Era. Zakres ateriału: Liczby rzeczywiste Wyrażeia algebraicze Rówaia i ierówości
Lekcja 1. Lekcja orgaizacyja kotrakt Podręczik: W. Babiański, L. Chańko, D. Poczek Mateatyka. Zakres podstawowy. Wyd. Nowa Era. Zakres ateriału: Liczby rzeczywiste Wyrażeia algebraicze Rówaia i ierówości
O pewnych zastosowaniach rachunku różniczkowego funkcji dwóch zmiennych w ekonomii
 O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
O pewych zastosowaiach rachuku różiczkowego fukcji dwóch zmieych w ekoomii 1 Wielkość wytwarzaego dochodu arodowego D zależa jest od wielkości produkcyjego majątku trwałego M i akładów pracy żywej Z Fukcję
O trzech elementarnych nierównościach i ich zastosowaniach przy dowodzeniu innych nierówności
 Edward Stachowski O trzech elemetarych ierówościach i ich zastosowaiach przy dowodzeiu iych ierówości Przy dowodzeiu ierówości stosujemy elemetare przejścia rówoważe, przeprowadzamy rozumowaie typu: jeżeli
Edward Stachowski O trzech elemetarych ierówościach i ich zastosowaiach przy dowodzeiu iych ierówości Przy dowodzeiu ierówości stosujemy elemetare przejścia rówoważe, przeprowadzamy rozumowaie typu: jeżeli
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne. Temat ćwiczenia: Problemy transportowe cd, Problem komiwojażera
 Istrukcja do ćwiczeń laboratoryjych z przedmiotu: Badaia operacyje Temat ćwiczeia: Problemy trasportowe cd Problem komiwojażera Zachodiopomorski Uiwersytet Techologiczy Wydział Iżyierii Mechaiczej i Mechatroiki
Istrukcja do ćwiczeń laboratoryjych z przedmiotu: Badaia operacyje Temat ćwiczeia: Problemy trasportowe cd Problem komiwojażera Zachodiopomorski Uiwersytet Techologiczy Wydział Iżyierii Mechaiczej i Mechatroiki
1 Układy równań liniowych
 Katarzya Borkowska, Wykłady dla EIT, UTP Układy rówań liiowych Defiicja.. Układem U m rówań liiowych o iewiadomych azywamy układ postaci: U: a x + a 2 x 2 +... + a x =b, a 2 x + a 22 x 2 +... + a 2 x =b
Katarzya Borkowska, Wykłady dla EIT, UTP Układy rówań liiowych Defiicja.. Układem U m rówań liiowych o iewiadomych azywamy układ postaci: U: a x + a 2 x 2 +... + a x =b, a 2 x + a 22 x 2 +... + a 2 x =b
1 Zbiory. 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =.
 1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
Pierwiastki z liczby zespolonej. Autorzy: Agnieszka Kowalik
 Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
Pierwiastki z liczby zespoloej Autorzy: Agieszka Kowalik 09 Pierwiastki z liczby zespoloej Autor: Agieszka Kowalik DEFINICJA Defiicja : Pierwiastek z liczby zespoloej Niech będzie liczbą aturalą. Pierwiastkiem
dna szeregu. ; m., k N ; ó. ; u. x 2n 1 ; e. n n! jest, że
 KILKA ZADAŃ O SZEREGACH Zbadać zbieżość i zbieżość bezwzgle da = a, jeśli a = a!! ; a + + ; c + ; ć! ; d +/ + 3 ; e! e 3 3+ ; f ; + g 000+ ; h ; + i! ; j k ; l 5 + l + 7 0 +3 6 0 + ; +3 ; ; m 3 + 3 ; +a
KILKA ZADAŃ O SZEREGACH Zbadać zbieżość i zbieżość bezwzgle da = a, jeśli a = a!! ; a + + ; c + ; ć! ; d +/ + 3 ; e! e 3 3+ ; f ; + g 000+ ; h ; + i! ; j k ; l 5 + l + 7 0 +3 6 0 + ; +3 ; ; m 3 + 3 ; +a
Lista 6. Estymacja punktowa
 Estymacja puktowa Lista 6 Model metoda mometów, rozkład ciągły. Zadaie. Metodą mometów zaleźć estymator iezaego parametru a w populacji jedostajej a odciku [a, a +. Czy jest to estymator ieobciążoy i zgody?
Estymacja puktowa Lista 6 Model metoda mometów, rozkład ciągły. Zadaie. Metodą mometów zaleźć estymator iezaego parametru a w populacji jedostajej a odciku [a, a +. Czy jest to estymator ieobciążoy i zgody?
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA
 Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
I kolokwium z Analizy Matematycznej
 I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
I kolokwium z Aalizy Matematyczej 4 XI 0 Grupa A. Korzystając z zasady idukcji matematyczej udowodić ierówość dla wszystkich N. Rozwiązaie:... 4 < + Nierówość zachodzi dla, bo 4
1.3. Największa liczba naturalna (bez znaku) zapisana w dwóch bajtach to a) b) 210 c) d) 32767
 Egzami maturaly z iformatyki Zadaie. (0 pkt) Każdy z puktów tego zadaia zawiera stwierdzeie lub pytaie. Zazacz (otaczając odpowiedią literę kółkiem) właściwą kotyuację zdaia lub poprawą odpowiedź. W każdym
Egzami maturaly z iformatyki Zadaie. (0 pkt) Każdy z puktów tego zadaia zawiera stwierdzeie lub pytaie. Zazacz (otaczając odpowiedią literę kółkiem) właściwą kotyuację zdaia lub poprawą odpowiedź. W każdym
a jest równa S 2 2 n 1 kn, był rosnący ), gdzie an ... , x4
 I Ciągi stroa k Oblicz sumę: k Ciąg a określoy jest w astępujący sposób: a a a wzór a -ty wyraz tego ciągu i wykaż jego prawdziwość idukcyjie Suma początkowych wyrazów ciągu a a * a dla N a jest rówa S
I Ciągi stroa k Oblicz sumę: k Ciąg a określoy jest w astępujący sposób: a a a wzór a -ty wyraz tego ciągu i wykaż jego prawdziwość idukcyjie Suma początkowych wyrazów ciągu a a * a dla N a jest rówa S
