OPCJE. Wycena w modelach dyskretnych Parytet kupna - sprzedaży Ograniczenia na cenę opcji
|
|
|
- Halina Przybylska
- 5 lat temu
- Przeglądów:
Transkrypt
1 OPJE Wycena w moelach ysetnych Paytet na - szeaży Oganiczenia na cenę ocji
2 Zaganienia wycena ocji Fncja wyłaty, fncja zys Ryne osonały - założenia Wzoy na wycenę ocji zy założeni oesowej aitalizacji osete Wzoy na wycenę ocji zy założeni ciągłej aitalizacji osete Delta heging (stategia osłonowa elta) Algoytm wyceny w stalonej liczbie etaów
3 Fncja wyłaty / eoejsa ocja na Definicja Fncję zefiniowaną wzoem lb G c G c T K gy gy T max( K,) T K T K nazywamy fncją wyłaty la osiaacza ocji na.
4 Fncja wyłaty / eoejsa ocja szeaży Fncję zefiniowaną wzoem lb G K G T gy gy T K max( K,) T T K nazywamy fncją wyłaty la osiaacza ocji szeaży.
5 Teminy: in the money (w cenie), ot of the money (oza ceną), at the money (ooło ceny) Ocja na Ocja szeaży in the money ( w cenie) ot of the money (oza ceną) at the money (ooło ceny) ena instment bazowego jest wyższa o ceny wyonania. ena instment bazowego jest niższa o ceny wyonania. ena instment bazowego jest zbliżona lb ówna cenie wyonania. ena instment bazowego jest niższa o ceny wyonania. ena instment bazowego jest wyższa o ceny wyonania. ena instment bazowego jest zbliżona lb ówna cenie wyonania
6 Wycena ocji moel wmianowy założenia o yn osonałym. oocentowanie eozytów i eytów banowych jest jenaowe. wysoość zaciąganych eytów nie jest oganiczona 3. zaewniona jest łynność obot wszystimi atywami 4. nie ma żanych osztów związanych z zawieaniem tansacji 5. wszystie atywa są osonale ozielne 6. oszczalna jest óta szeaż atywów 7. ba możliwości abitaż
7 Równoważność otfeli w czasie Własność. Jeżeli w chwili ońcowej T, watość wóch otfeli jest jenaowa (P () T = P () T ), to ównież w chwili oczątowej ich watości mszą być ówne (P = P ) Pzyśćmy (zeciwnie) że w chwili oczątowej watość otfela iewszego jest mniejsza niż giego: P < P Wtey byłaby możliwa nastęjąca stategia abitażowa Kóta szeaż otfela P, za otfela P Uloowanie woty (P - P ) na oocentowanym oncie W chwili ońcowej : szeaż otfela iewszego za wotę P () T za otfela. za wotę zys. ze szeaży oanie otfela. (ozliczenie ótiej szeaży) Rezltat - zysanie abitażowego zys (P - P ) (+) T Gyby P był mniejszy analogiczne ozmowanie owazi o zysania zys abitażowego.
8 Moel wstanowy jenoetaowy wyceny ocji na zy aitalizacji oesowej el: oeślenie ceny ocji na Dane: cena ealizacji - K cena oczątowa acji - cena acji o ływie jenego oes w zya wzost w zya sa oesowa stoa wolna o yzya - Załaamy onato że (i) wycena ocji bęzie miała chaate abitażowy (zy innej niż zysana wycenie bęzie możliwy abitaż ) (ii) acja nie zynosi ywieny (iii) yne jest osonały (iv) aitalizacja jest oesowa
9 Moel wstanowy jenoetaowy wyceny ocji na. Pzyła cena ealizacji zł cena oczątowa acji - zł cena acji o ływie oes w zya wzost 5 zł w zya sa 7 zł oesowa stoa wolna o yzya - %
10 Moel wstanowy jenoetaowy wyceny ocji na. Pzyła 5 zł 4 K = zł = zł =? zł 7 zł zł Watość ocji (fncja wyłaty) o ływie jenego oes w zya wzost ceny acji max(, K) max(,5 ) 4 Watość ocji (fncja wyłaty) o ływie jenego oes w zya sa ceny acji max(, K) max(, 7 )
11 Moel wstanowy jenoetaowy wyceny ocji na. Pzyła Rozważmy otfel słaający się z jenej ocji na w ozycji ótiej oaz ewnej liczby acji, tóą oznaczamy symbolem Watość otfela o ływie jenego oes bęzie wynosić: V gy cena acji wzośnie V 7 - gy cena acji sanie.
12 Moel wstanowy jenoetaowy wyceny ocji na. Pzyła Załóżmy onato, ze otfel jest wolny o yzya, czyli o ływie oes jego watość jest ientyczna zy ażym scenaisz ceny ońcowej acji V V oznacza to, że tą =,5 Zatem otfel owinien słaać się z łgiej ozycji w acjach w liczbie,5 oaz z ótiej ozycji ocji na w liczbie. W ob zyaach (wzost bąź sa ceny acji) watość otfela o ływie jenego oes wynosi 35 zł.
13 Moel wstanowy jenoetaowy wyceny ocji na. Pzyła Aby o jenym oesie zysać z loaty 35 zł należy w chwili oczątowej zainwestować wotę: 35 35, 9, 7 Oznacza to, że watość jego otfela (, - ) w chwili oczątowej msi być ówna V = 9,7 zł. (Potfel jest wolny o yzya, latego jego oesowa stoa zwot msi być ówna %). Z giej stony watość otfela w chwili oczątowej można zestawić w ostaci V,5 5 9, 7 zł stą =,83
14 Moel wstanowy jenoetaowy. Pzyła Uwaga. ena ocji =,83 zł jest tzw. ceną abitażową, lb ceną fai. Rzeczywiście gyby cena ocji była więsza, to inwesto otzebowałby mniej niż 9,7 zł na onstcję otfela w chwili oczątowej, zatem jenooesowy zys byłby więszy niż %, czyli istniałaby możliwość abitaż. (n.. =, to watość otfela oczątowego 8 zł, ońcowego 35, zys 5%) Gyby cena ocji była mniejsza niż,83 zł, (n. zł) to inwesto owinien zająć ozycję owotną (óta szeaż,5 acji, no ocji, zeonowanie ozostałych ienięzy (3 zł) na oncie). Po ływie oes należy oić,5 acji za 75 zł i zysać z ocji 4 zł (w zya zwyżi), bąź oić,5 acji za 35 zł w zya zniżi, zatem wyać w ob sytacjach 35 zł. Ale o ływie oes eozyt jest wat 36 zł. Otzymjemy abitażowy zys w wysoości zł (watość otfela w chwili oczątowej była zeowa)
15 Moel wstanowy jenoetaowy wyceny ocji na. Pzyae ogólny Rozważmy - ja w zyłazie - wolny o yzya otfel słaający się z jenej ocji na w ozycji ótiej oaz ewnej liczby acji Wtey czyli gzie V V ) (, zatem K,,
16 Moel wstanowy jenooesowy wyceny ocji na. Pzyae ogólny Gyby > +, to możliwy byłby abitaż olegający na możliwości zaciągnięcia nieoganiczonego eyt zy stoie oaz inwestycja w acje. Gyby + >, to możliwy byłby abitaż olegający na ótiej szeaży acji i loowanie ienięzy na loacie o oocentowani. Obie sytacje wylcza założenie (7)
17 Moel wstanowy jenoetaowy wyceny ocji na. Pzyae ogólny oo otfel jest wolny o yzya, jego oczna stoa zwot msi być ówna stoie zwot wolnej o yzya. Zatem: ońc.wat. otf./(+) = ocząt. wat. otf. tą, wyliczając otzymjemy (wzglęniając wzó na elta) ) ( (
18 Po oszczeniach otzymjemy gzie, ) ( )] ( [ ) ( )] ( [ ) ( ) ( ) ( ) ( ) (
19 Moel wstanowy jenoetaowy wyceny ocji na. Pzyae ogólny. Posmowanie twiezenie. ena eoejsiej ocji na w wstanowym moel jenoetaowym (zy wcześniejszych oznaczeniach) ana jest wzoem zatem gzie, ) ( )] ( [ ) (, max, max, ) ( K K gzie
20 Moel wstanowy jenoetaowy wyceny ocji szeaży. twiezenie. ena eoejsiej ocji szeaży z ceną ealizacji K w jenoetaowym moel wmianowym wynosi: gzie P oaz P oznaczają watości ocji szeaży (wyłaty z ocji) oowienio o wzoście, o sa acji, czyli Dowó w zya ocji szeaży można zysać naślając ostęowanie z owo la ocji na lb wyozystać aytet na-szeaży (o czym - óźniej), zy aitalizacji oesowej P P P, max, max, ) ( K P K P gzie P P P
21 Moel wstanowy jenoetaowy wyceny ocji na. UWAGI Uwaga. (a) Wzó oeślający cenę ocji na nie zawiea watości awooobieństw wzost ani sa ceny acji. (b) Liczby i (-) można inteetować jao awooobieństwo (oowienio) wzost, sa ceny acji (c) Pzy inteetacji liczb i (-) jao awooobieństwa, cena ocji na jest oczeiwaną watością fncji wyłaty zysontowaną czynniiem /(+ ). () jest fncją malejącą zmiennej K na zeziale (, ) (e) jest fncją osnącą zmiennej na zeziale (K/, K/)
22 Moel wstanowy jenoetaowy wyceny ocji na. Uwaga 3. Pzy inteetacji obabilistycznej liczb i (- ) watość oczeiwana ceny acji o jenym oesie jest ówna watości zyszłej woty. Dowó E E Postawiając o wzo E watości wyażeń i - otzymjemy: E
23 Moel wstanowy wetaowy wyceny ocji na. Zmienność ceny acji K () (b) (a) (e) (c) (f)
24 Moel wstanowy wetaowy twiezenie 3. ena eoejsiej ocji na z ceną ealizacji K w woesowym moel wstanowym wynosi: gzie liczby i (-) wynoszą oowienio -. gzie K, max K, max, max K
25 Moel wstanowy wetaowy wyceny ocji na. Zmienność watości ocji () (b) (a) (e) (c) (f) Oznaczenia watości ocji w węzłach
26 Moel wstanowy wetaowy tosjąc wzó na wycenę ocji na w moel jenoetaowym la węzłów (b), (c) otzymjemy Znając te wyceny można wyznaczyć cenę ocji w chwili oczątowej - czyli w węźle (a)
27 Moel wstanowy wetaowy Postawiając wa ozenie wzoy o ostatniego otzymjemy Mamy więc
28 Moel wstanowy wetaowy Uwaga 4.. Poobnie ja la wyceny ocji w moel jenoetaowym liczby, -, można inteetować ja awooobieństwa oowienio wotnego wzost, wzost i sa, wotnego sa acji.. Wzó na wycenę ocji można zestawić nastęjąco K, max K, max, max K lb z życiem wmian Newtona K max,.
29 Moel wstanowy n oesowy Uogólnienie wzo na wycenę ocji na la moel wetaowego Uwaga 5. Wzó na wycenę ocji na w moel wetaowym można ogólnić (metoą incji matematycznej) na zyae moel n - oesowego:., max K., max K n n n n n
30 Dzewo cen w moel mltiliatywnym, wmianowym (4 etay, cena oczątowa)
31 eny ońcowe acji w moel mltiliatywnym wmianowym, n-etaowym Możliwe ceny ońcowe mszą mieć ostać n-, gzie =,,,n. Na zewie cenowym istnieje óżnych óg owazących o węzła ientyfiowanego z ceną n-, gyż aża oga jest jenoznacznie schaateyzowana zez n- wyazowy ciąg (,,,,,,), zawieający lite oaz (n-) lite. n
32 eny ońcowe w moel mltiliatywnym wmianowym, n-etaowym Pawooobieństwo ażej taiej ogi jao onincji zazeń niezależnych - wynosi (-) n- Zatem awooobieństwo ceny ońcowej n- wynosi n ( ) n
33 Inteetacja wzo na wycenę ocji na w moel n - oesowym., max K n n n n n n n Jeżeli otatjemy ja awooobieństwo wzost acji, to liczba ana wyżej jest awooobieństwem zysania ceny ońcowej acji n-, zaś liczba max( n- -K,) jest watością (fncją wyłaty) ocji na zy tej cenie acji. twiezenie 4. ena ocji na jest ówna watości bieżącej oczeiwanej fncji wyłaty z ocji.
34 Moel wstanowy n oesowy Wzó na wycenę ocji szeaży Uwaga 6. ena ocji szeaży w moel n oesowym ana jest wzoem P n n n n max n K, Uwaga 7. Jeżeli otatjemy jao awooobieństwo wzost acji, to liczba P jest ówna zatalizowanej na moment oczątowy oczeiwanej watości fncji wyłaty ocji szeaży. Liczba Max(K- n-, ) jest watością (fncją wyłaty) ocji szeaży zy cenie acji n-.
35 Moel wmianowy wyceny ocji zy założeni ciągłej aitalizacji osete TW. 5. Watość ocji na w moel jenoetaowym wmianowym, zy aitalizacji ciągłej ana jest wzoem Dowó. = e T [ +(-) ] gzie = (e T )/( ) Rozważmy otfel słaający się z acji (łga ozycja) i jenej ocji (óta ozycja). Obliczymy watość, la tóej otfel ten jest wolny o yzya. W zya wzost ceny acji watość otfela w momencie wygaśnięcia ocji jest ówna - zaś w gim zya -.
36 Moel wmianowy wyceny ocji iągła aitalizacja osete Obojętność wobec yzya wymaga by watości te były ówne; - = -. Zatem liczba acji w otfel wynosi = ( - ) / ( ) Watość w chwili oczątowej ozatywanego otfela wynosi ( - )e T. Ponieważ oczątowy oszt twozenia otfela wynosił - mamy więc ówność - = ( - ) e T - ( - ) e T = e T - ( - ) = e T ( e T ) + = e T
37 Moel wmianowy wyceny ocji ciągła aitalizacja osete ( e T ) + = e T ostawiając = ( - ) / ( ) ównanie zyjmie ostać: e T = ( - ) (e T ) /( ) + e T = ( - ) (e T ) /( ) + ( ) /( ) e T = [ e T - e T + + ]/( ) e T = [ e T - e T + ]/( ) e T = (e T ) )/( ) + ( - e T )/( ) e T = (e T ) )/( ) + ( - e T )/( ) = e T [ +(- ) ] gzie = (e T )/( ), - = ( - e T +)/( )= ( - e T )/( )
38 Wzoy na wycenę ocji zy założeni ciągłej aitalizacji osete W moel jenoetaowym T e max stoa oczna T e ( ), gzie K, max K, T czas o nia ( w latach ) Uwaga 8. ena ocji na w moel n-etaowym, zy ciągłej aitalizacji osete, ana jest wzoem n n T e - oczna stoa, T - czas o nia T e ; T T n T ealizacji n n max K, zeział ealizacji czasowy (w latach) jenego oes
39 Poównanie wzoów w moel jenoetaowym aitalizacja ciągła, aitalizacja oczna T e max T e ( ), gzie K, max K, stoa oczna T czas o nia ealizacji ( w latach ) max ( ), max K K,, gzie
40 Poównanie wzoów w moel n etaowym (aitalizacja ciągła, aitalizacja oesowa) oes jenego ł T e K n e T n n n T. ; (w latach) ealizacji T - czas o nia - oczna stoa,, max., max K n n n n n oesowa stoa gzie
41 ( UWAGI O DELIE (elta heging) W analizie jenoetaowego moel wyceny ocji staliliśmy liczbę acji zyaającej na jeną ocję w ozycji ótiej ) Jest on jenocześnie oocją liczby acji o liczby ocji (w ozycji ótiej) la otfela całowicie zabezieczonego (hege atio). W moel wieloetaowym elta może być óżna w ażym węźle siati zmienności ceny acji (zatem la ażego eta, la ażej sytacji) Jeżeli w ażym momencie otfel acji i ocji ma być całowicie zabezieczony, należy moyfiować jego sła w zależności o scenaisza zmiany ceny acji.
42 Dzewo cen w moel mltiliatywnym, wmianowym (4 etay, cena oczątowa)
43 UWAGI O DELIE (elta heging) W zyjętym moel zmienności acji, w gafie ceny o tym oesie istnieje + węzłów. Ponmejemy te węzły liteą i (i= oowiaa scenaiszowi wszystich saów, zaś i = + samych wzostów). W węźle schaateyzowanym zez aamety (,i) oznaczmy cenę acji zez i zaś watość ocji zez i W ażym węźle (,i) wielość elty może być inna. Można oazać że wynosi ona i i i i i i,,..., ;,,...
44 UWAGI O DELIE (elta heging) Aby otfel słaający się z jenej ocji w ozycji ótiej i ewnej liczby acji w ozycji łgiej, był wolny o yzya, liczba acji msi być moyfiowana w ażym o, w zależności o zmieniającej się ceny acji,,,... ;,,..., i i i i i i ) (
45 Moel wstanowy wieloetaowy Pzyła wyceny w moel - etaowym Doonamy wyceny ocji na zy nastęjących anych liczba etaów n cena oczątowa acji cena ealizacji ocji K 4 oesowa stoa ocentowa 6% wsółczynni wzost, wsółczynni sa,85 watość ze wzo na wycenę,6
46 Moel wstanowy wieloetaowy Algoytm wyceny w moel etaowym Zbowanie siati cen acji w moel wmianowym Ustalenie fncji wyłaty ocji ( max{ cena ońcowa acji cena ealizacji ocji, zeo}) Wycena ocji w węzłach sieci eta 9, ze wzo na wycenę w moel jenoetaowym Wycena ocji w węzłach sieci eta 8, ze wzo na wycenę w moel jenoetaowym It. Wycena ocji w momencie oczątowym
47 Pzyła wyceny w moel etaowym iata cen acji w moel wmianowym ,7, wsółczynni wzost 55,98,85 wsółczynni sa 49,98 438,58 358,3 365,48 98,6 34,57 3,66 48,83 53,8 58,88 7,36,5 5,74,5 7,8 76,6 79,78 83,38 44, 46,88 49,8 5,8 55,87,,4 4,85 7,34 9,89,, 4,4 6, 8,4,4 85, 86,7 88,43 9, 9, 7,5 73,7 75,7 76,67 78, 6,4 6,64 63,89 65,7 5, 53,4 54,3 55,4 44,37 45,6 46,6 37,7 38,47 39,4 3,6 3,7 7,5 7,79 3,6 9,69
48 ,7 8 9, wsółczynni wzost 55,98 9,85 wsółczynni sa 49,98 438,58 358,3 365,48 98,6 34,57 3, ,83 53,8 58, ,36,5 5,74, ,8 76,6 79,78 83, , 46,88 49,8 5,8 55,87 6 7,,4 4,85 7,34 9,89 7 8,, 4,4 6, 8,4, , 86,7 88,43 9, 9, 9 3 7,5 73,7 75,7 76,67 78, 3 3 6,4 6,64 63,89 65, , 53,4 54,3 55, ,37 45,6 46, ,7 38,47 39, ,6 3, ,5 7, , , A B D E F G H I J K L 4 FUNKJA WYPŁATY PO. ET 4 K 4 479,7 <=MAX(L8-$$4;) 43 6% 44, 98,58 <=MAX(L-$$4;) 45,85 46,6 7,66 <=MAX(L-$$4;) , ,87 5 5, 53 54, 55 56, 57 58, 59 6, <=MAX(L36-$$4;) 6 6, <=MAX(L38-$$4;) 63
49 Moel wstanowy etaowy. Ustalenie fncji wyłaty z ocji o. etaie A B D E F G H I J K L 4 FUNKJA WYPŁATY PO. ET 4 K 4 479,7 <=MAX(L8-$$4;) 43 6% 44, 98,58 <=MAX(L-$$4;) 45,85 46,6 7,66 <=MAX(L-$$4;) , ,87 5 5, 53 54, 55 56, 57 58, 59 6, <=MAX(L36-$$4;) 6 6, <=MAX(L38-$$4;) 63
50 Moel wstanowy etaowy. Ustalenie watości ocji w 9. etaie ze wzo na wycenę w moel jenoetaowym A B D E F G H I J K L 4 4 K 4 479,7 <=MAX(L8-$$4;) 43 6% ($$46*L4+L44*(-$$46))/(+$$43) > 383,9 44, 98,58 <=MAX(L-$$4;) 45,85 ($$46*L44+L46*(-$$46))/(+$$43) > 33,4 46,6 7, ,8 48 8,5 49 5,3 5 5,87 5 8,98 5, 53 54, 55 56, 57 ( ), gzie 58, 59 max, max, K K 6, <=MAX(L36-$$4;) 6 ($$46*L6+L6*(-$$46))/(+$$43) > 6, <=MAX(L38-$$4;) 63
51 Moel wstanowy etaowy. Ustalenie watości ocji w ażym etaie, w ażej sytacji ( ze wzo na wycenę w moel jenoetaowym) A B D E F G H I J K L 4 4 K 4 479,7 <=MAX(L8-$$4;) 43 6% ($$46*L4+L44*(-$$46))/(+$$43) > 383,9 44, 35,38 98,58 <=MAX(L-$$4;) 45,85 4,77 33,4 46,6 87,7 79,97 7, ,44 36,6 6,8 48 9,6, 9,4 8,5 49 8, 73,8 63,8 5,3 5 6,5 5,9 43,78 3,43 5, ,7 37,36 9,5,7 8,98 5 3,7 6, 9,6,56 5,8, 53 7,89,89 7,73, ,38 4,7,63, 55,87,9 56,5, 57 58, 59 6 ( ), gzie, <=MAX(L36-$$4;) 6 6 max K, max K,, <=MAX(L38-$$4;) 63
52 , <=MAX(L38-$,4858 sma > 56,7634 zatal. ma 3,6968 Moel wstanowy etaowy. Ustalenie watości ocji na ostawie wzo n K n n n n max, L. Liczba wzostów P-stwo, ROZKŁ.DWUM L*Q 479,7 <=MAX(L8-$,64668, ,58 <=MAX(L-$ 9,43784,365 7,66 8,9335, ,5 7, ,47 5,87 6, ,9864, 5,6585, 4,476736, 3,446738,,6683, <=MAX(L36-$,57864 Q
53 Notacja K- cena jenostowa ostawy w ontacie fowa T- oes (w latach) ozostający o ostawy cena instment bazowego, bęącego zemiotem ontat f watość łgiej ozycji w ontacie fowa wolna o yzya oczna stoa ocentowa (zy ciągłej aitalizacji) Litey, f mogą wystąić ze wsaźniami wyznaczającymi nt na osi czas z zeział [; T] n., t, T,
54 Paytet cen ocji na i szeaży all-t aity Rozważmy otfel o słazie:. eoejsa ocja szeaży walo o atalnej cenie z ceną ealizacji K i teminem ealizacji T,. ontat teminowy na tego samego walo z tą sami ceną ealizacji i z tym samym teminem ealizacji co ocja szeaży. Rozatzmy wa zyai: a) w chwili T: T < K ontat teminowy zyniesie statę K T ocja szeaży zyniesie wyłatę K - T zatem (nie wzglęniając osztów tansacji) zeływy finansowe w chwili T mają bilans zeowy b) w chwili T: T > K ontat teminowy zyniesie zys ówny T - K ocja szeaży bęzie bezwatościowa i nie zostanie wyonana Zatem w chwili T wyłata otfela bęzie ówna T - K
55 Paytet cen ocji na i szeaży Wniose. Rozważany otfel ma w chwili T fncję wyłaty ocji na. tw. 8. oo watość otfela w chwili T jest watością ocji na, zatem watość otfela w chwili oczątowej msi być taże ówny watości ocji, czyli = P + f gzie, P ceny oowienio ocji na, ocji szeaży, f - watość ontat teminowego na w chwili t =, czyli = P + - e -T K Uwaga. Jeżeli założymy aitalizację oesową oaz wolną o yzya stoę w oesie o ealizacji ocji, wzó na aytet zyjmie ostać = P + - K/(+)
56 Paytet cen ocji na i szeaży Uwaga 9. Jeżeli założymy aitalizację oczną oaz oczny oes o chwili ealizacji ocji, wzó na aytet zyjmie ostać = P + - K/(+) Z ostatniej ówności oaz wzoów Można taże zysać wzó na cenę ocji szeaży E, max, max, ) ( K P K P gzie P P P, max, max, ) ( K K gzie
57 Oganiczenia na cenę ocji na oaz ocji szeaży e cena eoejsiej ocji na P e cena eoejsiej ocji szeaży a cena ameyańsiej ocji na P a cena ameyańsiej ocji szeaży stoa ocentowa wolna o yzya, zy aitalizacji ciągłej o cena acji w chwili oczątowej T temin ealizacji ocji K cena wyonania ocji
58 Oganiczenia na cenę ocji na tw. 9. eny ocji na sełniają nastęjące nieówności o a e max( o K e -T, ) Uzasanienie ena ocji ameyańsiej nie może być wyższa niż cena ynowa acji gyż w zeciwnym zya taniej byłoby ić ację bezośenio na yn, zatem o a Ze wzglę na więsze awnienia właściciela ocji ameyańsiej jej cena nie może być mniejsza o ceny ocji eoejsiej, czyli a e z aytet na-szeaży ( e P e = o K e -T ) e = o K e -T + P e watość ocji nie może saść oniżej zea (mamy P e,) zatem e o K e -T tą i nieówności e otzymjemy e max( o K e -T, )
59 Oganiczenia na cenę ocji szeaży tw.. eny ocji szeaży sełniają nastęjące nieówności K P a P e max ( Ke -T,) Uzasanienie Gyby K < P a, to wystawiając ocję szeaży z cena wyonania K zysjemy w najgoszym zya P a - K (co jest zysiem abitażowym); P a P e gyż za szesze awnienia ocji ameyańsiej nie możemy łacić mniej; z aytet ceny ocji P e = e - o + K e -T oaz nieówności e otzymjemy P e Ke -T - o, P e max(ke -T, ) onieważ P e, więc
60 Watość wewnętzna i watość czasowa Def. Watość wewnętzna ocji jest to óżnica mięzy ceną instment bazowego, a ceną wyonania w zya ocji na, natomiast w zya ocji szeaży watość wewnętzna jest ówna óżnicy mięzy ceną wyonania, a ceną instment bazowego. Def. Watość czasowa (zewnętzna) ocji jest to óżnica mięzy ceną ocji (emią), a jej watością wewnętzną jeśli óżnica ta jest niejemna w zeciwnym azie watość czasowa jest ówna ze.
61 Zależność mięzy emią (ceną) ocji na a ceną instment bazowego oaz watością wewnętzną ocji gzie TV- ( time vale ) watość czasowa IV (intinsic vale) watość wewnętzna
62 Wycena ocji J.. ox,.a. Ross, M. Rbinstein Wycena ocji eoejsiej w moel ysetnym Fische Blac, Myon holes, Robet Meton (973) Wycena ocji eoejsiej w moel ciągłym Fische Blac, Myon holes Nagoa Nobla 997- za nową metoę wyceny instmentów ochonych
Wynik finansowy transakcji w momencie jej zawierania jest nieznany z uwagi na zmienność ceny przedmiotu transakcji, czyli instrumentu bazowego
 .Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
.Istmety ochoe otaty temiowe azywae sa istmetami ochoymi (eivatives. otat temiowy zobowiazje wie stoy o zeowazeia w zyszłosci ewej tasacji a wczesiej staloych waach. Jea stoa otatów (abywca - te, co je
Ryzyko walutowe. Kursy walutowe spot i forward. Teorie kursów walutowych
 Ryzyko walutowe. Kusy walutowe spot i owa. eoie kusów walutowych Postawowe pojęcia Deinicja yzyka walutowego - schemat z piewszego wykłau. Zazązanie yzykiem walutowym obejmuje wybó instumentów (aktywów)
Ryzyko walutowe. Kusy walutowe spot i owa. eoie kusów walutowych Postawowe pojęcia Deinicja yzyka walutowego - schemat z piewszego wykłau. Zazązanie yzykiem walutowym obejmuje wybó instumentów (aktywów)
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Arytmetyka finansowa Wykład 6 Dr Wioletta Nowak
 Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI. Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH
 UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH WPROWADZENIE Opcje są instrumentem pochonym, zatem takim, którego cena zależy o ceny instrumentu
UNIWESRYTET EKONOMICZNY WE WROCŁAWIU HOSSA ProCAPITAL WYCENA OPCJI Sebastian Gajęcki WYDZIAŁ NAUK EKONOMICZNYCH WPROWADZENIE Opcje są instrumentem pochonym, zatem takim, którego cena zależy o ceny instrumentu
Kinematyka odwrotna:
 Kinematka owotna: ozwiązanie zaania kinematki owotnej owaza ię o wznazenia maiez zekztałenia H otai H E Wznazenie tej maiez olega na znalezieni jenego bąź wztkih ozwiązań ównania: T T n n q... q gzie q...
Kinematka owotna: ozwiązanie zaania kinematki owotnej owaza ię o wznazenia maiez zekztałenia H otai H E Wznazenie tej maiez olega na znalezieni jenego bąź wztkih ozwiązań ównania: T T n n q... q gzie q...
Model klasyczny gospodarki otwartej
 Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
Model klasyczny gospodaki otwatej Do tej poy ozpatywaliśmy model sztucznie zakładający, iż gospodaka danego kaju jest gospodaką zamkniętą. A zatem bak było międzynaodowych pzepływów dób i kapitału. Jeżeli
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
Komisja Egzaminacyjna dla Aktuariuszy. XL Egzamin dla Aktuariuszy z 9 października 2006 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XL Egzamin dla Aktuariuszy z 9 aździernika 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile wynosi wartość
Komisja Egzaminacyjna dla Aktuariuszy XL Egzamin dla Aktuariuszy z 9 aździernika 006 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 00 minut . Ile wynosi wartość
Krystyna Gronostaj Maria Nowotny-Różańska Katedra Chemii i Fizyki, FIZYKA Uniwersytet Rolniczy do użytku wewnętrznego ĆWICZENIE 4
 Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
MECHANIKA BUDOWLI 12
 Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
XXX OLIMPIADA FIZYCZNA (1980/1981). Stopień I, zadanie teoretyczne T4 1
 XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
Wyk lad 3 Grupy cykliczne
 Wyk la 3 Grupy cykliczne Definicja 3.1. Niech a bezie elementem grupy (G,, e). Jeżeli istnieje liczba naturalna k taka, że a k = e, to najmniejsza taka liczbe naturalna k nazywamy rzeem elementu a. W przeciwnym
Wyk la 3 Grupy cykliczne Definicja 3.1. Niech a bezie elementem grupy (G,, e). Jeżeli istnieje liczba naturalna k taka, że a k = e, to najmniejsza taka liczbe naturalna k nazywamy rzeem elementu a. W przeciwnym
Wytrzymałość śruby wysokość nakrętki
 Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
Wyzymałość śuby wysoość aęi Wpowazeie zej Wie Działająca w śubie siła osiowa jes pzeoszoa pzez zeń i zwoje gwiu. owouje ozciągaie lub ścisaie zeia śuby, zgiaie i ściaie zwojów gwiu oaz wywołuje acisi a
Metody probabilistyczne Rozwiązania zadań
 Metody robabilistyczne Rozwiązania zadań 6. Momenty zmiennych losowych 8.11.2018 Zadanie 1. Poaż, że jeśli X Bn, to EX n. Odowiedź: X rzyjmuje wartości w zbiorze {0, 1,..., n} z rawdoodobieństwami zadanymi
Metody robabilistyczne Rozwiązania zadań 6. Momenty zmiennych losowych 8.11.2018 Zadanie 1. Poaż, że jeśli X Bn, to EX n. Odowiedź: X rzyjmuje wartości w zbiorze {0, 1,..., n} z rawdoodobieństwami zadanymi
METODA CIASNEGO (silnego) WIĄZANIA (TB)
 MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
MEODA CIASEGO silnego WIĄZAIA B W FE elektony taktujemy jak swobone, tylko zabuzone słabym peioycznym potencjałem; latego FE jest obym moelem metalu w B uważamy, że elektony są silnie związane z maciezystymi
ROZDZIAŁ 5. Renty życiowe
 ROZDZIAŁ 5 Renty życiowe Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy czy osoba której przyszły czas
ROZDZIAŁ 5 Renty życiowe Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy czy osoba której przyszły czas
Binarne Diagramy Decyzyjne
 Sawne tablice logiczne Plan Binane diagamy decyzyjne Oganiczanie i kwantyfikacja Logika obliczeniowa Instytut Infomatyki Plan Sawne tablice logiczne Binane diagamy decyzyjne Plan wykładu 1 2 3 4 Plan wykładu
Sawne tablice logiczne Plan Binane diagamy decyzyjne Oganiczanie i kwantyfikacja Logika obliczeniowa Instytut Infomatyki Plan Sawne tablice logiczne Binane diagamy decyzyjne Plan wykładu 1 2 3 4 Plan wykładu
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE
 MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy
MODELE MATEMATYCZNE W UBEZPIECZENIACH WYKŁAD 5: RENTY ŻYCIOWE Rentą życiową nazywamy ciąg płatności który ustaje w chwili śmierci pewnej osoby (zwykle ubezpieczonego) Mówiąc o rencie życiowej nie zaznaczamy
WYKŁAD nr Ekstrema funkcji jednej zmiennej o ciągłych pochodnych. xˆ ( ) 0
 WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
4. Elementy teorii powierzchni. Odwzorowanie powierzchni na powierzchnię.
 Katogafia matematyczna. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4.. Powiezchnie Powiezchnią w geometii óŝniczowej
Katogafia matematyczna. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4. ementy teoii powiezchni. Odwzoowanie powiezchni na powiezchnię. 4.. Powiezchnie Powiezchnią w geometii óŝniczowej
Przekształcenie całkowe Fouriera
 Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
1 LWM. Defektoskopia ultradźwiękowa. Sprawozdanie powinno zawierać:
 L Defetosoia ultraźwięowa Srawozanie owinno zawierać:. Króti ois aaratury i metoy.. Rysune słua z zwymiarowanym ołożeniem wa. L Elastootya ynii baań elastootycznych Rzą izochromy m Siła na ońcu źwigni
L Defetosoia ultraźwięowa Srawozanie owinno zawierać:. Króti ois aaratury i metoy.. Rysune słua z zwymiarowanym ołożeniem wa. L Elastootya ynii baań elastootycznych Rzą izochromy m Siła na ońcu źwigni
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Arkusze maturalne poziom podstawowy
 Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
ĆWICZENIE 5. Badanie przekaźnikowych układów sterowania
 ĆWICZENIE 5 Badanie zekaźnikowych układów steowania 5. Cel ćwiczenia Celem ćwiczenia jest badanie zekaźnikowych układów steowania obiektem całkującoinecyjnym. Ćwiczenie dotyczy zekaźników dwu- i tójołożeniowych
ĆWICZENIE 5 Badanie zekaźnikowych układów steowania 5. Cel ćwiczenia Celem ćwiczenia jest badanie zekaźnikowych układów steowania obiektem całkującoinecyjnym. Ćwiczenie dotyczy zekaźników dwu- i tójołożeniowych
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad 0 W ni niej szym sche ma cie oce nia nia za dań otwa tych są pe zen to wa ne pzy kła do we po paw ne od po wie
Optymalizacja harmonogramów budowlanych - problem szeregowania zadań
 Mieczysław OŁOŃSI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
Mieczysław OŁOŃSI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH
 LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH ĆWICZENIE 3 NEURONOWE STEROWANIE ROBOTEM Neuonowe steowanie ynamiką obota. Cel ćwiczenia należy zestawić ukła steowania amionami obota z wykozystaniem metoy owotnego
LABOLATORIUM SZTUCZNYCH SIECI NEURONOWYCH ĆWICZENIE 3 NEURONOWE STEROWANIE ROBOTEM Neuonowe steowanie ynamiką obota. Cel ćwiczenia należy zestawić ukła steowania amionami obota z wykozystaniem metoy owotnego
Opcje III. 1. Opcje na indeksy
 . Opcje na ineksy Opcje III Na wielu giełach notowane są opcje na ineksy giełowe, w których instrumentem bazowym jest ineks. Najbarziej popularnymi opcjami ineksowymi są: opcja na ineks S&P500 (opcja typu
. Opcje na ineksy Opcje III Na wielu giełach notowane są opcje na ineksy giełowe, w których instrumentem bazowym jest ineks. Najbarziej popularnymi opcjami ineksowymi są: opcja na ineks S&P500 (opcja typu
SCENARIUSZ LEKCJI MATEMATYKI Temat: Zadania na dowodzenie w trygonometrii. Cel: Uczeń tworzy łańcuch argumentów i uzasadnia jego poprawność.
 SCENAIUSZ LEKCJI MATEMATYKI Temat: Zadania na dowodzenie w tygonometii Cel: Uczeń twozy łańcuch agumentów i uzasadnia jego popawność Czas: godzina lekcyjna Cele zajęć: Uczeń po zajęciach: wykozystuje definicje
SCENAIUSZ LEKCJI MATEMATYKI Temat: Zadania na dowodzenie w tygonometii Cel: Uczeń twozy łańcuch agumentów i uzasadnia jego popawność Czas: godzina lekcyjna Cele zajęć: Uczeń po zajęciach: wykozystuje definicje
NOMINALNA STOPA PROCENTOWA stopa oprocentowania przyjęta w okresie bazowym; nie uwzględnia skutków kapitalizacji odsetek
 Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Symbole: nominalna stopa pocentowa ( od stu ) n ilość okesów (lat, miesięcy, kwatałów etc.) m ilość podokesów (np. stopa pocentowa podana jest w skali oku; kapitalizacja miesięczna m=12) d stopa dyskontowa
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektotechniki i utomatyki Kateda Inżynieii Systemów Steowania KOMPUTEROWE SYSTEMY STEROWNI (sem. 6) Steowanie otymalizacyjne. Mateiały omocnicze Temin T8 Oacowanie: Tomasz
Politechnika Gdańska Wydział Elektotechniki i utomatyki Kateda Inżynieii Systemów Steowania KOMPUTEROWE SYSTEMY STEROWNI (sem. 6) Steowanie otymalizacyjne. Mateiały omocnicze Temin T8 Oacowanie: Tomasz
Energia kinetyczna i praca. Energia potencjalna
 negia kinetyczna i paca. negia potencjalna Wykład 4 Wocław Univesity of Technology 1 NRGIA KINTYCZNA I PRACA 5.XI.011 Paca Kto wykonał większą pacę? Hossein Rezazadeh Olimpiada w Atenach 004 WR Podzut
negia kinetyczna i paca. negia potencjalna Wykład 4 Wocław Univesity of Technology 1 NRGIA KINTYCZNA I PRACA 5.XI.011 Paca Kto wykonał większą pacę? Hossein Rezazadeh Olimpiada w Atenach 004 WR Podzut
Metody optymalizacji. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
Metody optymalizacji d inż. Paweł Zalewski kademia Moska w Szczecinie Optymalizacja - definicje: Zadaniem optymalizacji jest wyznaczenie spośód dopuszczalnych ozwiązań danego polemu ozwiązania najlepszego
O ŁĄCZENIU TRZECH RYNKÓW
 tudia Ekonomiczne eszyty Naukowe Uniwesytetu Ekonomicznego w Katowicach IN - N zkoła Główna Handlowa w Waszawie Kolegium Analiz Ekonomicznych Kateda Matematyki i Ekonomii Matematycznej jutkin@sghwawl O
tudia Ekonomiczne eszyty Naukowe Uniwesytetu Ekonomicznego w Katowicach IN - N zkoła Główna Handlowa w Waszawie Kolegium Analiz Ekonomicznych Kateda Matematyki i Ekonomii Matematycznej jutkin@sghwawl O
KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH
 Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
Konkusy w województwie podkapackim w oku szkolnym 08/09 KONKURS Z MTEMTYKI L UZNIÓW SZKÓŁ POSTWOWYH ETP REJONOWY KLUZ OPOWIEZI Zasady pzyznawania punktów za każdą popawną odpowiedź punkt za błędną odpowiedź
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Zastosowanie teorii pierścieni w praktyce
 Upozczenie wyażeń 2x+(y x) = x+y Spotkania z Matematyka Zatoowanie teoii pieścieni w paktyce Alekande Deniiuk denijuk@matman.uwm.edu.pl Uniweytet Wamińko-Mazuki w Olztynie Wydział Matematyki i Infomatyki
Upozczenie wyażeń 2x+(y x) = x+y Spotkania z Matematyka Zatoowanie teoii pieścieni w paktyce Alekande Deniiuk denijuk@matman.uwm.edu.pl Uniweytet Wamińko-Mazuki w Olztynie Wydział Matematyki i Infomatyki
Algebra liniowa z geometrią analityczną
 WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
WYKŁAD 5 SCHEMAT ZASTĘPCZY TRANSFORMATORA
 Materiały pomocnicze o wyła Maszyny Eletryczne i Transformatory YKŁD 5 SCHEMT ZSTĘPCZY TSFOMTO stotą eletrycznego schemat zastępczego owolnego rzązenia, bęącego z pnt wizenia teorii obwoów wójniiem lb
Materiały pomocnicze o wyła Maszyny Eletryczne i Transformatory YKŁD 5 SCHEMT ZSTĘPCZY TSFOMTO stotą eletrycznego schemat zastępczego owolnego rzązenia, bęącego z pnt wizenia teorii obwoów wójniiem lb
1. SZCZEGÓLNE PRZYPADKI ŁUKÓW.
 Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
= ± Ne N - liczba całkowita.
 POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
PODSTAWY TELEDETEKCJI-ćwiczenia rachunkowe
 PODSTAWY TELEDETEKCJI-ćwiczenia rachunkowe Tema.eoy omiaru oległości i rękości raialnej. Zaanie. Na jakiej oległości znajuje się obiek, gy czas oóźnienia sygnałów wynosi:μs, ms, min O.50m, 50km, 9 9 0
PODSTAWY TELEDETEKCJI-ćwiczenia rachunkowe Tema.eoy omiaru oległości i rękości raialnej. Zaanie. Na jakiej oległości znajuje się obiek, gy czas oóźnienia sygnałów wynosi:μs, ms, min O.50m, 50km, 9 9 0
Opcje. 2. Ze względu na typ instrumentu bazowego opcje dzielimy na:
 Opcje. Opcja - jest umową, która aje posiaaczowi prawo o kupna lub sprzeaży określonego instrumentu bazowego po z góry określonej cenie (cena wykonania) prze upływem określonego terminu (termin wygaśnięcia)..
Opcje. Opcja - jest umową, która aje posiaaczowi prawo o kupna lub sprzeaży określonego instrumentu bazowego po z góry określonej cenie (cena wykonania) prze upływem określonego terminu (termin wygaśnięcia)..
Kształty żłobków stojana
 Kztałty żłobów tojana Kztałty żłobów winia: a), b), c) lati olewane Al. ) - i) lati lutowane z pętów Cu Wymiay żłoba oplowego Kąt zbieżności ściane żłoba: Śenica mniejza: = π + h )in in ( b Śenica więza:
Kztałty żłobów tojana Kztałty żłobów winia: a), b), c) lati olewane Al. ) - i) lati lutowane z pętów Cu Wymiay żłoba oplowego Kąt zbieżności ściane żłoba: Śenica mniejza: = π + h )in in ( b Śenica więza:
koszt kapitału D/S L dźwignia finansowa σ EBIT zysku operacyjnego EBIT firmy. Firmy Modele struktury kapitału Rys. 8.3. Krzywa kosztów kapitału.
 Modele strutury apitału oszt apitału Optymalna strutura apitału dźwignia finansowa / Rys. 8.3. Krzywa osztów apitału. Założenia wspólne modeli MM Modigliani i Miller w swoich rozważaniach ograniczyli się
Modele strutury apitału oszt apitału Optymalna strutura apitału dźwignia finansowa / Rys. 8.3. Krzywa osztów apitału. Założenia wspólne modeli MM Modigliani i Miller w swoich rozważaniach ograniczyli się
Równania Lagrange a II r.
 Mechania Analityczna i Dgania Równania Lagange a II. pzyłay Równania Lagange a II. pzyłay mg inż. Sebastian Pauła Aaemia Góniczo-Hutnicza im. Stanisława Staszica w Kaowie Wyział Inżynieii Mechanicznej
Mechania Analityczna i Dgania Równania Lagange a II. pzyłay Równania Lagange a II. pzyłay mg inż. Sebastian Pauła Aaemia Góniczo-Hutnicza im. Stanisława Staszica w Kaowie Wyział Inżynieii Mechanicznej
LABORATORIUM: Sterowanie rzeczywistym serwomechanizmem z modułem przemieszczenia liniowego Wprowadzenie
 Utwozenie: PRz, 1, Żabińsi Tomasz Modyfiacja: PRz, 15, Michał Maiewicz LABORATORIUM: Steowanie zeczywistym sewomechanizmem z modułem zemieszczenia liniowego Wowadzenie Celem ćwiczenia jest identyfiacja
Utwozenie: PRz, 1, Żabińsi Tomasz Modyfiacja: PRz, 15, Michał Maiewicz LABORATORIUM: Steowanie zeczywistym sewomechanizmem z modułem zemieszczenia liniowego Wowadzenie Celem ćwiczenia jest identyfiacja
METEMATYCZNY MODEL OCENY
 I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
Dobór zmiennych objaśniających do liniowego modelu ekonometrycznego
 Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Uniwersytet Warszawski Teoria gier dr Olga Kiuila LEKCJA 2
 LEKCJA 2 Pzykład: Dylemat Cykoa (albo Poke Dogowy) Dwie osoby wsiadają w samochody, ozpędzają się i z dużą pędkością jadą na siebie - ten kto piewszy zahamuje lub zjedzie z tasy jest "cykoem" i pzegywa.
LEKCJA 2 Pzykład: Dylemat Cykoa (albo Poke Dogowy) Dwie osoby wsiadają w samochody, ozpędzają się i z dużą pędkością jadą na siebie - ten kto piewszy zahamuje lub zjedzie z tasy jest "cykoem" i pzegywa.
10. REZONANS W OBWODACH ELEKTRYCZNYCH
 0. EZONANS W OBWODAH EEKTYZNYH W obwoach prąu sinusoialnego przebiegi czasowe (prąów, napięć, sem, spm, mocy) cylicznie przybieraą na przemian wartości oatnie i uemne. Przebiegi o taim charaterze noszą
0. EZONANS W OBWODAH EEKTYZNYH W obwoach prąu sinusoialnego przebiegi czasowe (prąów, napięć, sem, spm, mocy) cylicznie przybieraą na przemian wartości oatnie i uemne. Przebiegi o taim charaterze noszą
MODYFIKACJA KOSZTOWA ALGORYTMU JOHNSONA DO SZEREGOWANIA ZADAŃ BUDOWLANYCH
 MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
Rama płaska metoda elementów skończonych.
 Pzyład. Rama płasa metoda elementów sończonych. M p l A, EJ P p l A, EJ l A, EJ l l,5 l. Dysetyzacja Podział na elementy i węzły x st. sw. M 5 P Z X, M, V, H 7, M, H Y, V Element amy płasiej węzły, x stopni
Pzyład. Rama płasa metoda elementów sończonych. M p l A, EJ P p l A, EJ l A, EJ l l,5 l. Dysetyzacja Podział na elementy i węzły x st. sw. M 5 P Z X, M, V, H 7, M, H Y, V Element amy płasiej węzły, x stopni
II.6. Wahadło proste.
 II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
II.6. Wahadło poste. Pzez wahadło poste ozumiemy uch oscylacyjny punktu mateialnego o masie m po dolnym łuku okęgu o pomieniu, w stałym polu gawitacyjnym g = constant. Fig. II.6.1. ozkład wektoa g pzyśpieszenia
1 Renty życiowe. 1.1 Podstawowe renty życiowe
 Renty życiowe Renta życiowa jest serią płatności okonywanych w czasie życia ubezpieczonego Jej wartość teraźniejsza jest zienną losową (bo zależy o przyszłego czasu życia T, oznaczaną Y Postawowe renty
Renty życiowe Renta życiowa jest serią płatności okonywanych w czasie życia ubezpieczonego Jej wartość teraźniejsza jest zienną losową (bo zależy o przyszłego czasu życia T, oznaczaną Y Postawowe renty
3b. ELEKTROSTATYKA. r r. 4πε. 3.4 Podstawowe pojęcia. kqq0 E =
 3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
3b. LKTROTATYKA 3.4 Postawowe pojęcia Zasaa zachowania łaunku umayczny łaunek ukłau elektycznie izolowanego jest stały. Pawo Coulomba - siła oziaływania elektostatycznego 4 1 18 F C A s ˆ gzie : k 8,85*1
LABORATORIUM. Sterowanie rzeczywistym serwomechanizmem z modułem przemieszczenia liniowego
 PRz, 1, Żabińi Tomaz LABORATORIUM Steowanie zeczywitym ewomechanizmem z modułem zemiezczenia liniowego 1. Na odtawie ztałtu odowiedzi oowych uładu, oeśl ty teowania (ądowy, naięciowy) ewomechanizmu oaz
PRz, 1, Żabińi Tomaz LABORATORIUM Steowanie zeczywitym ewomechanizmem z modułem zemiezczenia liniowego 1. Na odtawie ztałtu odowiedzi oowych uładu, oeśl ty teowania (ądowy, naięciowy) ewomechanizmu oaz
WYKŁAD 11 OPTYMALIZACJA WIELOKRYTERIALNA
 WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
WYKŁAD OPTYMALIZACJA WIELOKYTEIALNA Wstęp. W wielu pzypadkach pzy pojektowaniu konstukcji technicznych dla okeślenia ich jakości jest niezędne wpowadzenie więcej niż jednego kyteium oceny. F ) { ( ), (
Energia potencjalna jest energią zgromadzoną w układzie. Energia potencjalna może być zmieniona w inną formę energii (na przykład energię kinetyczną)
 1 Enega potencjalna jest enegą zgomadzoną w układze. Enega potencjalna może być zmenona w nną omę eneg (na pzykład enegę knetyczną) może być wykozystana do wykonana pacy. Sumę eneg potencjalnej knetycznej
1 Enega potencjalna jest enegą zgomadzoną w układze. Enega potencjalna może być zmenona w nną omę eneg (na pzykład enegę knetyczną) może być wykozystana do wykonana pacy. Sumę eneg potencjalnej knetycznej
h a V. GEOMETRIA PŁASKA TRÓJKĄT :
 pitgos..pl V. GEOMETRIA PŁASKA TRÓJKĄT : Wunek utwozeni tójkąt: sum ługośi wó kótszy oków musi yć większ o ługośi njłuższego oku. Śoek okęgu opisnego wyznzją symetlne oków. Śoek okęgu wpisnego wyznzją
pitgos..pl V. GEOMETRIA PŁASKA TRÓJKĄT : Wunek utwozeni tójkąt: sum ługośi wó kótszy oków musi yć większ o ługośi njłuższego oku. Śoek okęgu opisnego wyznzją symetlne oków. Śoek okęgu wpisnego wyznzją
INSTRUMENTY DŁUŻNE. Duracja jako funkcja stopy procentowej Duracja skończonego ciągu płatności Immunizacja portfela aktywów
 INSTRUMENTY ŁUŻNE aja jao fja opy poeowej aja ońzoego iąg płaośi Iizaja pofela aywów aja iąg pzepływów pzy apializaji iągłej oza opa ' ; aja jao fja ] [ ' T VR T E T E e d d d d aja jao fja apializaja
INSTRUMENTY ŁUŻNE aja jao fja opy poeowej aja ońzoego iąg płaośi Iizaja pofela aywów aja iąg pzepływów pzy apializaji iągłej oza opa ' ; aja jao fja ] [ ' T VR T E T E e d d d d aja jao fja apializaja
GEOMETRIA PŁASZCZYZNY
 GEOMETRIA PŁASZCZYZNY. Oblicz pole tapezu ównoamiennego, któego podstawy mają długość cm i 0 cm, a pzekątne są do siebie postopadłe.. Dany jest kwadat ABCD. Punkty E i F są śodkami boków BC i CD. Wiedząc,
GEOMETRIA PŁASZCZYZNY. Oblicz pole tapezu ównoamiennego, któego podstawy mają długość cm i 0 cm, a pzekątne są do siebie postopadłe.. Dany jest kwadat ABCD. Punkty E i F są śodkami boków BC i CD. Wiedząc,
Blok 8: Moment bezwładności. Moment siły Zasada zachowania momentu pędu
 Blo 8: Moent bezwładności Moent siły Zasada zachowania oentu pędu Moent bezwładności awiając uch postępowy ciała, posługujey się pojęciai pzeieszczenia, szybości, pzyspieszenia tego ciała oaz wypadowej
Blo 8: Moent bezwładności Moent siły Zasada zachowania oentu pędu Moent bezwładności awiając uch postępowy ciała, posługujey się pojęciai pzeieszczenia, szybości, pzyspieszenia tego ciała oaz wypadowej
Metoda odbić zwierciadlanych
 Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa
Metoa obić zwiecialanych Pzypuśćmy, że łaunek punktowy (Rys ) umieszczony jest w oległości o nieskończonej powiezchni pzewozącej, umiejscowionej na płaszczyźnie X0Y Piewsze pytanie, jakie o azu się nasuwa
Zastosowanie algorytmu Euklidesa
 Zatoowanie algoytmu Euklidea Pzelewanie wody Dyonujez dwoma czeakami o ojemnościach 4 i 6 litów, utym ojemnikiem o nieoganiczonej objętości i nieoganiczoną ilością wody Podaj oób naełnienia ojemnika 14
Zatoowanie algoytmu Euklidea Pzelewanie wody Dyonujez dwoma czeakami o ojemnościach 4 i 6 litów, utym ojemnikiem o nieoganiczonej objętości i nieoganiczoną ilością wody Podaj oób naełnienia ojemnika 14
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
MECHNIK GÓLN (II) Semest: II (Mechanika I), III (Mechanika II), ok akademicki 2017/2018 Liczba godzin: sem. II*) - wykład 30 godz., ćwiczenia 30 godz. sem. III*) - wykład 30 godz., ćwiczenia 30 godz. (dla
Formularze statystyczne
 Fomulaze statystyczne pogam badań statystycznych statystyi publicznej Spotanie z pacowniami PUP ejestującymi osoby bezobotne. Spotanie pzygotowane w amach pojetu Ryne Pacy pod Lupą II Podstawa pawna USTAWA
Fomulaze statystyczne pogam badań statystycznych statystyi publicznej Spotanie z pacowniami PUP ejestującymi osoby bezobotne. Spotanie pzygotowane w amach pojetu Ryne Pacy pod Lupą II Podstawa pawna USTAWA
Metoda odbić zwierciadlanych
 Metoa obić zwiecialanych Pzyuśćmy, że łaunek unktowy (Rys ) umieszczony jest w oległości o nieskończonej owiezchni zewozącej, umiejscowionej na łaszczyźnie X0Y Piewsze ytanie, jakie o azu się nasuwa jest
Metoa obić zwiecialanych Pzyuśćmy, że łaunek unktowy (Rys ) umieszczony jest w oległości o nieskończonej owiezchni zewozącej, umiejscowionej na łaszczyźnie X0Y Piewsze ytanie, jakie o azu się nasuwa jest
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ.
 ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
ROZWIĄZUJEMY PROBLEM RÓWNOWAŻNOŚCI MASY BEZWŁADNEJ I MASY GRAWITACYJNEJ. STRESZCZENIE Na bazie fizyki klasycznej znaleziono nośnik ładunku gawitacyjnego, uzyskano jedność wszystkich odzajów pól ( elektycznych,
Plan wykładu 6. Hanna Pawłowska Elementy termodynamiki atmosfery i fizyki chmur Wykład 6
 Plan wykłau 6 emoynamika związana z uhem ionowym Poe euo-aiabatyzny emeatua ekwiwalentna, temeatua ekwiwalentno-otenjalna, liqui wate otential temeatue Gaient wilgotno-aiabatyzny Hanna Pawłowka Elementy
Plan wykłau 6 emoynamika związana z uhem ionowym Poe euo-aiabatyzny emeatua ekwiwalentna, temeatua ekwiwalentno-otenjalna, liqui wate otential temeatue Gaient wilgotno-aiabatyzny Hanna Pawłowka Elementy
Kody Huffmana oraz entropia przestrzeni produktowej. Zuzanna Kalicińska. 1 maja 2004
 Kody uffmana oraz entroia rzestrzeni rodutowej Zuzanna Kalicińsa maja 4 Otymalny od bezrefisowy Definicja. Kod nad alfabetem { 0, }, w tórym rerezentacja żadnego znau nie jest refisem rerezentacji innego
Kody uffmana oraz entroia rzestrzeni rodutowej Zuzanna Kalicińsa maja 4 Otymalny od bezrefisowy Definicja. Kod nad alfabetem { 0, }, w tórym rerezentacja żadnego znau nie jest refisem rerezentacji innego
O sposobie poszukiwania dobrej metody inwestowania na giełdzie
 Kzysztof PIASECKI Ademi Eonomiczn w Poznniu O sposobie poszuiwni dobe metody inwestowni n giełdzie Poblem bdwczy Podstwowym poblemem pzed im ste inwesto est oeślenie słdu i stutuy tiego potfel ego inwestyci
Kzysztof PIASECKI Ademi Eonomiczn w Poznniu O sposobie poszuiwni dobe metody inwestowni n giełdzie Poblem bdwczy Podstwowym poblemem pzed im ste inwesto est oeślenie słdu i stutuy tiego potfel ego inwestyci
Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony
 Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
Modele odpowiedzi do akusza Póbnej Matuy z OPERONEM Matematyka Poziom ozszezony Listopad 00 W kluczu są pezentowane pzykładowe pawidłowe odpowiedzi. Należy ównież uznać odpowiedzi ucznia, jeśli są inaczej
Przykład budowania macierzy sztywności.
 Co dzisiaj Przyład bdowania macierzy sztywności. Podejście logiczne Podejście algorytmiczne Przyłady modelowania i interpretacji wyniów Model płytowo-powłoowy i interpretacja naprężeń Błędy modelowania
Co dzisiaj Przyład bdowania macierzy sztywności. Podejście logiczne Podejście algorytmiczne Przyłady modelowania i interpretacji wyniów Model płytowo-powłoowy i interpretacja naprężeń Błędy modelowania
INSTYTUT ENERGOELEKTRYKI POLITECHNIKI WROCŁAWSKIEJ Raport serii SPRAWOZDANIA Nr
 Na prawach rękopisu o użytku służbowego INSTYTUT ENEROEEKTRYKI POITECHNIKI WROCŁAWSKIEJ Raport serii SPRAWOZDANIA Nr ABORATORIUM UKŁADÓW IMPUSOWYCH la kierunku AiR Wyziału Mechanicznego INSTRUKCJA ABORATORYJNA
Na prawach rękopisu o użytku służbowego INSTYTUT ENEROEEKTRYKI POITECHNIKI WROCŁAWSKIEJ Raport serii SPRAWOZDANIA Nr ABORATORIUM UKŁADÓW IMPUSOWYCH la kierunku AiR Wyziału Mechanicznego INSTRUKCJA ABORATORYJNA
dr inż. Małgorzata Langer Architektura komputerów
 Instukcja współfinansowana pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego w pojekcie Innowacyjna dydaktyka bez oganiczeń zintegowany ozwój Politechniki Łódzkiej zaządzanie Uczelnią, nowoczesna
Instukcja współfinansowana pzez Unię Euopejską w amach Euopejskiego Funduszu Społecznego w pojekcie Innowacyjna dydaktyka bez oganiczeń zintegowany ozwój Politechniki Łódzkiej zaządzanie Uczelnią, nowoczesna
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Optymalizacja harmonogramów budowlanych - problem szeregowania zadań
 Mieczysław POŁOŃSKI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
Mieczysław POŁOŃSKI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
PROCENTY, PROPORCJE, WYRAŻENIA POTEGOWE
 PROCENTY, PROPORCJE, WYRAŻENIA POTEGOWE ORAZ ŚREDNIE 1. Procenty i proporcje DEFINICJA 1. Jeden procent (1%) pewnej liczby a to setna część tej liczby, tórą oznacza się: 1% a, przy czym 1% a = 1 p a, zaś
PROCENTY, PROPORCJE, WYRAŻENIA POTEGOWE ORAZ ŚREDNIE 1. Procenty i proporcje DEFINICJA 1. Jeden procent (1%) pewnej liczby a to setna część tej liczby, tórą oznacza się: 1% a, przy czym 1% a = 1 p a, zaś
KOMPLEKSOWE BADANIE WSPÓŁCZYNNIKA PARCIA BOCZNEGO W GRUNTACH LABORATORYJNĄ METODĄ POMIARU OPORÓW TARCIA
 Gónictwo i Geoinżynieia Rok 33 Zeszyt 1 29 Janusz Kaczmaek KOMPLEKSOWE BADANIE WSPÓŁCZYNNIKA PARCIA BOCZNEGO W GRUNTACH LABORATORYJNĄ METODĄ POMIARU OPORÓW TARCIA 1 Wstę Koncecję laboatoyjnego sosobu badania
Gónictwo i Geoinżynieia Rok 33 Zeszyt 1 29 Janusz Kaczmaek KOMPLEKSOWE BADANIE WSPÓŁCZYNNIKA PARCIA BOCZNEGO W GRUNTACH LABORATORYJNĄ METODĄ POMIARU OPORÓW TARCIA 1 Wstę Koncecję laboatoyjnego sosobu badania
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI
 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8. 8. PŁASKIE ZAGADNIENIA TEORII SPRĘŻYSTOŚCI 8.. Płaski stan napężenia Tacza układ, ustój ciągły jednoodny, w któym jeden wymia jest znacznie mniejszy od pozostałych,
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ODPOWIEDZI DO ARKUSZA ROZSZERZONEGO Zadanie ( pkt) A Zadanie ( pkt) C Zadanie ( pkt) A, bo sinα + cosα sinα + cosα cos sinα sin cosα + π π + π sin α π A więc musi
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ODPOWIEDZI DO ARKUSZA ROZSZERZONEGO Zadanie ( pkt) A Zadanie ( pkt) C Zadanie ( pkt) A, bo sinα + cosα sinα + cosα cos sinα sin cosα + π π + π sin α π A więc musi
DOWODY NIERÓWNOŚCI HÖLDERA I MINKOWSKIEGO (DO UŻYTKU WEWNȨTRZNEGO, I DO SPRAWDZENIA)
 DOWODY NIERÓWNOŚCI HÖLDERA I MINKOWSKIEGO (DO UŻYTKU WEWNȨTRZNEGO I DO SPRAWDZENIA) R R Tematem niniejszych notatek jest zbadanie warunków istnienia normy na ewnej rzestrzeni funkcji rzeczywistych określonych
DOWODY NIERÓWNOŚCI HÖLDERA I MINKOWSKIEGO (DO UŻYTKU WEWNȨTRZNEGO I DO SPRAWDZENIA) R R Tematem niniejszych notatek jest zbadanie warunków istnienia normy na ewnej rzestrzeni funkcji rzeczywistych określonych
Wykład 13 Druga zasada termodynamiki
 Wyład 3 Druga zasada termodynamii Entroia W rzyadu silnia Carnota z gazem dosonałym otrzymaliśmy Q =. (3.) Q Z tego wzoru wynia, że wielość Q Q = (3.) dla silnia Carnota jest wielością inwariantną (niezmienniczą).
Wyład 3 Druga zasada termodynamii Entroia W rzyadu silnia Carnota z gazem dosonałym otrzymaliśmy Q =. (3.) Q Z tego wzoru wynia, że wielość Q Q = (3.) dla silnia Carnota jest wielością inwariantną (niezmienniczą).
U L T R A ZAKŁAD BADAŃ MATERIAŁÓW
 U L T R A ZAKŁAD BADAŃ MATERIAŁÓW Zał 1 instr Nr02/01 str. 53-621 Wrocław, Głogowska 4/55, tel/fax 071 3734188 52-404 Wrocław, Harcerska 42, tel. 071 3643652 www.ultrasonic.home.pl tel. kom. 0 601 710290
U L T R A ZAKŁAD BADAŃ MATERIAŁÓW Zał 1 instr Nr02/01 str. 53-621 Wrocław, Głogowska 4/55, tel/fax 071 3734188 52-404 Wrocław, Harcerska 42, tel. 071 3643652 www.ultrasonic.home.pl tel. kom. 0 601 710290
F : R 0;1 rozkład prawdopodobieństwa stopy zwrotu.
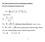 Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad W niniejszym schemacie oceniania zadań otwatych są pezentowane pzykładowe popawne odpowiedzi. W tego typu ch należy
KRYTERIA OCENIANIA ODPOWIEDZI Póbna Matua z OPERONEM Matematyka Poziom ozszezony Listopad W niniejszym schemacie oceniania zadań otwatych są pezentowane pzykładowe popawne odpowiedzi. W tego typu ch należy
11. Pochodna funkcji
 11. Pochodna funkcji Definicja pochodnej funkcji w punkcie. Niech X R będzie zbiorem niepustym, f:x >R oraz niech x 0 X. Funkcję określoną wzorem, nazywamy ilorazem różnicowym funkcji f w punkcie Mówimy,
11. Pochodna funkcji Definicja pochodnej funkcji w punkcie. Niech X R będzie zbiorem niepustym, f:x >R oraz niech x 0 X. Funkcję określoną wzorem, nazywamy ilorazem różnicowym funkcji f w punkcie Mówimy,
Funkcja wykładnicza kilka dopowiedzeń
 Funkcje i ich granice Było: Zbiór argumentów; zbiór wartości; monotoniczność; funkcja odwrotna; funkcja liniowa; kwadratowa; wielomiany; funkcje wymierne; funkcje trygonometryczne i ich odwrotności; funkcja
Funkcje i ich granice Było: Zbiór argumentów; zbiór wartości; monotoniczność; funkcja odwrotna; funkcja liniowa; kwadratowa; wielomiany; funkcje wymierne; funkcje trygonometryczne i ich odwrotności; funkcja
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA
 EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.
WSPÓŁCZYNNIK THETA OPCJI BARIEROWYCH
 Ewa Dziawgo Uniwesye Mikołaja openika w ouniu Wyział auk Ekonomicznych i Zazązania aea Ekonomeii i aysyki ziawew@umk.pl WPÓŁCZYI EA OPCJI BARIEROWYC eszczenie: W aykule pzesawiono zaganienia związane z
Ewa Dziawgo Uniwesye Mikołaja openika w ouniu Wyział auk Ekonomicznych i Zazązania aea Ekonomeii i aysyki ziawew@umk.pl WPÓŁCZYI EA OPCJI BARIEROWYC eszczenie: W aykule pzesawiono zaganienia związane z
XXXVII OLIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne
 XXXVII OIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne ZADANIE D Nazwa zadania: Obacający się pęt swobodnie Długi cienki pęt obaca się swobodnie wokół ustalonej pionowej osi, postopadłej do niego yc.
XXXVII OIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne ZADANIE D Nazwa zadania: Obacający się pęt swobodnie Długi cienki pęt obaca się swobodnie wokół ustalonej pionowej osi, postopadłej do niego yc.
X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH
 X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH 1.1 Definice; metoda wsteczne poeci w tomogafii tansmisyne Rys. 1.1 Pzyład dwóch zutów pzedmiotu złożonego z dwóch cylindycznych obietów Z czysto
X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH 1.1 Definice; metoda wsteczne poeci w tomogafii tansmisyne Rys. 1.1 Pzyład dwóch zutów pzedmiotu złożonego z dwóch cylindycznych obietów Z czysto
Pole magnetyczne. 5.1 Oddziaływanie pola magnetycznego na ładunki. przewodniki z prądem. 5.1.1 Podstawowe zjawiska magnetyczne
 Rozdział 5 Pole magnetyczne 5.1 Oddziaływanie pola magnetycznego na ładunki i pzewodniki z pądem 5.1.1 Podstawowe zjawiska magnetyczne W obecnym ozdziale ozpatzymy niektóe zagadnienia magnetostatyki. Magnetostatyką
Rozdział 5 Pole magnetyczne 5.1 Oddziaływanie pola magnetycznego na ładunki i pzewodniki z pądem 5.1.1 Podstawowe zjawiska magnetyczne W obecnym ozdziale ozpatzymy niektóe zagadnienia magnetostatyki. Magnetostatyką
Elementarne przepływy potencjalne (ciąg dalszy)
 J. Szanty Wykład n 4 Pzepływy potencjalne Aby wytwozyć w pzepływie potencjalnym siły hydodynamiczne na opływanych ciałach konieczne jest zyskanie pzepływ asymetycznego.jest to możliwe pzy wykozystani kolejnego
J. Szanty Wykład n 4 Pzepływy potencjalne Aby wytwozyć w pzepływie potencjalnym siły hydodynamiczne na opływanych ciałach konieczne jest zyskanie pzepływ asymetycznego.jest to możliwe pzy wykozystani kolejnego
Ruch obrotowy. Wykład 6. Wrocław University of Technology
 Wykład 6 Wocław Univesity of Technology Oboty - definicje Ciało sztywne to ciało któe obaca się w taki sposób, że wszystkie jego części są związane ze sobą dzięki czemu kształt ciała nie ulega zmianie.
Wykład 6 Wocław Univesity of Technology Oboty - definicje Ciało sztywne to ciało któe obaca się w taki sposób, że wszystkie jego części są związane ze sobą dzięki czemu kształt ciała nie ulega zmianie.
PRZENIKANIE PRZEZ ŚCIANKĘ PŁASKĄ JEDNOWARSTWOWĄ. 3. wnikanie ciepła od ścianki do ośrodka ogrzewanego
 PRZENIKANIE W pzemyśle uch ciepła zachodzi ównocześnie dwoma lub tzema sposobami, najczęściej odbywa się pzez pzewodzenie i konwekcję. Mechanizm tanspotu ciepła łączący wymienione sposoby uchu ciepła nazywa
PRZENIKANIE W pzemyśle uch ciepła zachodzi ównocześnie dwoma lub tzema sposobami, najczęściej odbywa się pzez pzewodzenie i konwekcję. Mechanizm tanspotu ciepła łączący wymienione sposoby uchu ciepła nazywa

