O sposobie poszukiwania dobrej metody inwestowania na giełdzie
|
|
|
- Teresa Komorowska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Kzysztof PIASECKI Ademi Eonomiczn w Poznniu O sposobie poszuiwni dobe metody inwestowni n giełdzie Poblem bdwczy Podstwowym poblemem pzed im ste inwesto est oeślenie słdu i stutuy tiego potfel ego inwestyci tóy z puntu widzeni inteesów inwesto est potfelem optymlnym. W teoii i ptyce ynów pitłowych znduemy wiele metod ozwiązni tego poblemu. Nbdzie populną metodą optymlizci potfel est eguł owitz nzuąc wyznczć potfel optymlny n dodze msymlizci stopy zwotu pzy ednoczesne minimlizci winci stopy zwotu. Duże zinteesownie poblemtyą inwestowni n ynu pitłowym powodue że dostępne olece metod optymlizci potfel są coz bogtsze. Zstosownie żde z tych metod de n ogół inną popozycę tiego potfel tóy nleżłoby uznć o optymlny. To z olei odzi nstępny poblem. Inwesto musi sobie odpowiedzieć n pytnie pzy pomocy ie metody m oeślć słd swoego potfel. Oczywistym est że wybieąc włściwą metodę optymlizci potfel nleży się ieowć nczelną egułą finnsów: msymlizcą zysu pzy ednoczesne minimlizci osztów. Względną oceną osiągniętego zysu est stop zwotu. Pzy tie ocenie zysu oszt inwestyci nleży identyfiowć z yzyiem ponoszonym pzez inwesto. Klsyczną względną oceną tiego yzy est winc stopy zwotu. Ozncz to że tże wybieąc włściwą metodę optymlizci potfel nleży się ieowć egułą owitz. Spostzeżenie to wszue n nowy obsz zstosowń eguły owitz tó tut zndzie swe zstosownie pzy wyboze włściwe metody sztłtowni słdu i stutuy potfel inwestycynego. W niniesze pcy zostnie pzedstwion pewien sposób wybou dobe metody inwestowni. Istotnym elementem te pezentci będzie dysus tiego ozwinięci eguły owitz tóe będzie pzydtne pzy poszuiwniu pzydtne poceduy sztłtowni potfel inwestycynego.
2 1. Dysetny model owitz Do opisu pezentownego tut modelu zostnie między innymi zstosowny system notci zpoponowny w (Piseci 005) i ozwinięty w (Piseci 007). Rozwżmy yne pitłowy wyznczony pzez zbió : i 1 n (1) i podstwowych instumentów finnsowych chteyzuących się ednostową ceną. W ten sposób zoste odzwieciedlone złożenie o dosonłe podzielności żdego ze znduących się w obocie instumentu finnsowego. Weźmy tez pod uwgę poedynczego inwesto inwestuącego n tym ynu. Złdmy że ego oczeiwni są ednoodne. Ozncz to że z puntu widzeni ozptywnego inwesto wszystie podstwowe instumenty mą identyczny temin wyupu t T 0. W momencie czsowym t 0 żdy instument finnsowy i est schteyzowny pzez oczeiwną stopę zwotu ex nte i. Wtedy zbió instumentów finnsowych est chteyzowny pzez weto oczeiwnych stóp zwotu ex nte T i 1 n mciez owinci ex nte. Pomimy tut poblem poceduy sttystyczne wyznczni tych wtości. Rozwżmy tez zbió : 1 m () metod optymlizci potfel tywów finnsowych. Kżd z metod 1 m pzypoządowue zbioowi instumentów finnsowych potfel c 1 1 c c n n (3) spełniący dodtowo wune T 1 c 1 (4) n gdzie poszczególne symbole oznczą 1;1; ; 1 R T 1 i c T c1 c cn. Wtość zinwestownego pitłu nie m znczeni dl nszych ozwżń. pozwl to n pzyęcie złożeni (4) głoszącego ze w żdy potfel inwestycyny inwesto ngżue edn ednostę pitłu. Ti zbieg fomlny upszcz dlsze ozwżni. Stop zwotu ex nte ˆ z potfel i e winc ex nte dne są pzy pomocy zleżności
3 T ˆ c (5) T c c. (6) P ˆ chteyzue potfel w momencie t 0 zinwestowni w ten potfel. Z momentem tym niezpzeczlnie łączy się oszt ponoszony pzez inwesto. Koszt ten est identyfiowny z yzyiem obciążącym ten potfel. Ryzyo to est ocenine w momencie 0 t pzy pomocy winci ex nte. Postult zgodnego z yteium minimlizci osztów wybou metody optymlizci potfel powdzi do oeśleni n zbioze metod pepoządu zdefiniownego z pomocą zleżności. (7) Zpis czytmy z puntu widzeni oceny yzy metod est niezgosz od metody. Z dugie stony nleży pmiętć że oczeiwn stop zwotu ex nte pognozą zysów ie może osiągnąć inwesto ngżuący w potfel ˆ est edynie swó pitł. Z oczywistych powodów inwesto inteesue edn msymlizc osiągniętego zysu nie msymlizc pzewidywnego zysu. Osiągniemy zys możemy ocenić edynie w momencie wyupu t T. Wtedy zys ten est oceniny z pomocą oczeiwne stopy zwotu ex post p ˆ. Postult zgodnego z yteium msymlizci zysu wybou metody optymlizci potfel powdzi do oeśleni n zbioze metod pepoządu zdefiniownego z pomocą zleżności p p ˆ. (8) Zpis czytmy z puntu widzeni oceny osiągniętego zysu metod est niezgosz od metody. Jeśli upoządownie stóp zwotu ex nte będzie tfną pognozą upoządowni stóp zwotu ex post to wtedy pepoząde (8) wyznczony pzez stopy zwotu ex post będzie ównowżny stosownemu w lsycznym uęciu teoii owitz nlogicznemu pepoządowi wyznczonemu pzez stopy zwotu ex nte. Poblem weyfici tfności wspomnine pognozy pozostwimy finnsometii. Równoczesne uwzględnienie postultów minimlizci osztów i msymlizci zysów powdzi ns do uznni z dobą żde tie metody optymlizci potfel tó est elementem optimum Peto wyznczonego pzez poównnie
4 wieloyteilne. Kżd z wybnych w ten sposób dobych metod optymlizci potfel wyzncz ti potfel tóy w ozumieniu owitz est efetywny względem zbiou wszystich wyznczonych potfeli : 1 m. p P ˆ chteyzue potfel to ztem ocen ex post metody optymlizci w momencie t T wyupu potfel. Jest i nie może służyć podęciu decyzi inwestycyne w momencie t 0. W te sytuci edynie wielootne wyzncznie optimum Peto w óżnych momentch histoii ynu pitłowego może pozwolić n wyłonienie tich metod sztłtowni potfel tóe możemy uznć z twle dobe. Powste oczywiście ntulne pytnie czy specyfi ynu pitłowego pozwoli w ogóle n t plicę zsdy genelizci histoyczne. Ptyczne poblemy związne z tym poblemem zostną pzybliżone w poniższym studium pzypdu..studium pzypdu Wyozystne tut zostną szeegi czsowe notowń n GPWW obemuące oes od styczni ou 000 do gudni 003. Oes ten podzielono n tzy podoesy odzwieciedlące wszystie możliwe do zistnieni główne tendy n giełdzie tzn.: bess - od styczni 000 do 10 siepni 001 stgnc - od 10 siepni 001 do 5 lipc 00 hoss - od 5 lipc 00 do 30 gudni 003. Niezbędne dle podstwowe chteystyi sttystyczne tych notowń możn znleźć w (Sefin 005). Pzedmiotem nsze nlizy będzie poblem wybni dobych metod optymlizci potfel z pośód metod opisnych w (Jusze Sio 00). Inwesto ezygnue tm z nlizy fundmentlne i z bieżącego śledzeni sytuci moeonomiczne. W swoich decyzch inwesto opie się wyłącznie n szeegch czsowych notowń spółe n GPWW. Ze względu n niższe yzyo specyficzne oz więszą płynność inwesto zmiez onstuowć potfele wyłącznie z ci odnotowywnych w indesie WIG. W ten sposób zostł oeślon zwtość zbiou podstwowych instumentów finnsowych. Słd potfel będzie podległ weyfici i pzebudowie z n miesiąc. W (Sefin 005) żdemu z tych momentów modyfici potfel pzypisno oczeiwne miesięczne stopy zwotu ex nte z żde notowne w WIG ci oz ich mciez owinci ex nte.
5 iesięczne oczeiwne stopy zwotu ex nte t w były tm wyznczne t w (Jusze Sio 00) - o śednie ytmetyczne olenych miesięcznych stóp zwotu ex post obsewownych w dwunstu miesiącch popzedzących moment modyfici potfel. Opiszmy tez zbió metod optymlizci potfel postci (3). Wstępnym etpem żde z pięciu piewszych metod comiesięczny wybó z dwudziestu spółe chteyzuących się w dnym momencie nwięszymi oczeiwnymi stopmi zwotu ex nte. N żdy udził c i spółi i w wtości twozonego potfel nzucone est wtedy ogniczenie 0 c 0. (9) i Wspomnini utozy bdli nstępuące metody optymlizci słdu potfel: 1 - wybiez potfel o msymlne stopie zwotu ex nte - wybiez potfel o minimlne stopie zwotu ex nte - wybiez potfel o minimlne winci ex nte ˆ 1 ˆ - wybiez potfel o minimlne winci ex nte zwotu ex nte 5 ˆ 4 - wybiez potfel o minimlne winci ex nte stopie zwotu ex nte ˆ 5. i o złożone pzeciętne stopie 4 i o złożone pondpzeciętne 5 Oeślone powyże wtości pzeciętne stopie zwotu ex nte ˆ 4 i pondpzeciętne stopie zwotu ex nte ˆ 4 05 mx 0 5 ˆ ˆ 5 wyznczmy z zleżności (10) mx 0 5 min (11) min gdzie poszczególne symbole oznczą: mx - stop zwotu ex nte potfel wyznczonego z pomocą metody 1 min - stop zwotu ex nte potfel wyznczonego z pomocą metody. Do zbiou nleży pondto metod; 6 - wybiez potfel o stutuze identyczne ze stutuą potfel oeślącego WIG. W (Sefin 005) oeślono dl żdego z tych potfeli w żdym z momentów ego modyfici stopy zwotu ex nte i ex post oz wince ex nte. Ocenino łącznie 88 potfele Ze względu n szczupłość miesc szczegółowe wynii te obszene oceny nie zostły tut zpezentowne. N wstępie zmimy się odpowiedzią n pytnie czy
6 upoządownie wyznczone pzez stopy zwotu ex nte est tfną pognozą upoządowni (8) wyznczonego pzez stopy zwotu ex post. W tym celu wyznczono współczynnii Kendl oelci ngowe pomiędzy obom odzmi stóp zwotu. Uzysne wynii pzedstwiono w Tbeli 1. Tbel 1. Współczynnii Kendl oelci między stopmi zwotu ex nte i ex post Tend ynu etod optymlizci potfel Bess Stgnc Hoss Źódło: opcownie włsne Nstępnie w opciu o te wynii testowno ciąg hipotez zeowych: Współczynni oelci est ówny zeu pzeciwstwionych hipotezom ltentywnym: Współczynni oelci est dodtni. Z żdym zem stwiedzno b możliwości odzuceni hipotezy zeowe n zecz hipotezy ltentywne. Poząde wyznczony pzez stopy zwotu ex nte nie est godną zufni pognozą upoządowni (8). Ozncz to że pomiędzy ozwżnymi powyże p dwom chteystymi metod optymlizci potfel edynie ocen ex post ˆ est oceną infomuącą o zeczywiste pzydtności metody. W olenym ou dl żdego złożonego momentu modyfici potfel wyznczmy optimum Peto oeślone pzez pepoządu (7) i (8). W ten sposób dl żdego momentowi notowni wybiemy ex post dobe metody optymlizci potfel inwestycynego. Rezultty tych wyboów pzedstwiono w Tbeli. Łtwo możn tm dostzec b wyźnych wszń dobe metody optymlizci potfel. Ostteczny wniose est tylo eden. Wynii powdzonych bdń sttystycznych nie są powtzlne. Nie est możliw ztem tegoyczn genelizc histoyczn. Nie mmy żdnych cudownych d dl inwestoów. Alchemi finnsów nie odsłonił swego mieni filozoficznego. Z dugie stony możn edn zuwżyć pewne tendence gdyż nietóe metody optymlizci potfel są częście zliczne do gupy metod dobych. Stosuąc te metody zwięszmy sznsę osiągnięci powodzeni n ynu pitłowym. Częstości zliczeni poszczególnych oceninych metod do optimum Peto pzedstwiono w Tbeli 3.
7 Tbel. Kolene wyboy dobych metod optymlizci potfel Tend ynu Bess Stgnc Hoss etod etod etod Legend: Kolene wiesze odpowidą wyóżnionym w tcie twni poszczególnych odzów tendu olenym teminom modyfici potfel. + etod optymlizci potfel zostł zliczon do optimum Peto. Źódło: opcownie włsne Tbel 3. Częstości zliczni metod optymlizci potfel do optimum Peto Tend ynu etod Bess Stgnc Hoss Rzem Źódło: opcownie włsne Bibliogfi
8 R Jusze W. Sio (00): Czy długoteminowo możn wygć z yniem w W. Tczyńsi (ed.) Ryne pitłowy suteczne inwestownie cz. I s Wydwnictwo Nuowe Uniwesytetu Szczecińsiego Szczecin. K. Piseci (005): Od ytmetyi hndlowe do inżynieii finnsowe Wydwnictw Nuowe AE w Poznniu Poznń. K. Piseci (007): odele mtemtyi finnsowe. Instumenty podstwowe Wydwnictwo Nuowe PWN Wszw.. Sefin (005): Weyfic metodologii budowy optymlnego ppieów wtościowych Pc mgistes AE Poznń. O sposobie poszuiwni dobe metody inwestowni n giełdzie Steszczenie W poszuiwniu dobe metody inwestowni lsyczn teoi potfelow owitz nzue msymlizowć stopę zwotu ex nte pzy ównoczesne minimlizci odchyleni stnddowego ex nte. W ptyce edn inwesto nie tyle inteesue msymlizc pognozownego zysu co msymlizc zysu uzysnego. W swoich poszuiwnich est edn ogniczony ocenionym w momencie podęci decyzi inwestycyne yzyiem obczącym żdą z ltentyw inwestycynych. Kieuąc się tymi `pzesłnmi w pcy zpoponowno i pzedysutowno popozycę tiego sposobu poszuiwni dobe metody inwestowni tó poleg n msymlizci stopy zwotu ex post pzy ównoczesne minimlizci odchyleni stnddowego ex nte. Thee dimensionl imge of is Abstct
O sposobie poszukiwania dobrej metody inwestowania na giełdzie
 Krzysztof PIASECKI Ademi Eonomiczn w Poznniu O sposobie poszuiwni dobre metody inwestowni n giełdzie Problem bdwczy Podstwowym problemem przed im ste inwestor est oreślenie słdu i strutury tiego portfel
Krzysztof PIASECKI Ademi Eonomiczn w Poznniu O sposobie poszuiwni dobre metody inwestowni n giełdzie Problem bdwczy Podstwowym problemem przed im ste inwestor est oreślenie słdu i strutury tiego portfel
Arytmetyka finansowa Wykład 6 Dr Wioletta Nowak
 Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
Aytmetya finansowa Wyład 6 Wioletta Nowa Ryne apitałowy zez yne apitałowy ozumie się ogół tansacji upna-spzedaży, tóych pzedmiotem są instumenty finansowe o oesie wyupu dłuższym niż o. Śodi uzysane z emisji
METODY HODOWLANE - zagadnienia
 METODY HODOWLANE METODY HODOWLANE - zgdnieni. Mtemtyczne podstwy metod odowlnyc. Wtość cecy ilościowej i definicje pmetów genetycznyc. Metody szcowni pmetów genetycznyc 4. Wtość odowln cecy ilościowej
METODY HODOWLANE METODY HODOWLANE - zgdnieni. Mtemtyczne podstwy metod odowlnyc. Wtość cecy ilościowej i definicje pmetów genetycznyc. Metody szcowni pmetów genetycznyc 4. Wtość odowln cecy ilościowej
Matematyka finansowa 10.03.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r. Część I
 Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 Mteriły do wykłdu MATEMATYKA DYSKRETNA dl studiów zocznych cz. Progrm wykłdu: KOMBINATORYKA:. Notcj i podstwowe pojęci. Zlicznie funkcji. Permutcje. Podziory zioru. Podziory k-elementowe. Ziory z powtórzenimi
Mteriły do wykłdu MATEMATYKA DYSKRETNA dl studiów zocznych cz. Progrm wykłdu: KOMBINATORYKA:. Notcj i podstwowe pojęci. Zlicznie funkcji. Permutcje. Podziory zioru. Podziory k-elementowe. Ziory z powtórzenimi
Znajdowanie analogii w geometrii płaskiej i przestrzennej
 Gimnzjum n 17 im. Atu Gottge w Kkowie ul. Litewsk 34, 30-014 Kków, Tel. (12) 633-59-12 Justyn Więcek, Atu Leśnik Znjdownie nlogii w geometii płskiej i pzestzennej opiekun pcy: mg Doot Szczepńsk Kków, mzec
Gimnzjum n 17 im. Atu Gottge w Kkowie ul. Litewsk 34, 30-014 Kków, Tel. (12) 633-59-12 Justyn Więcek, Atu Leśnik Znjdownie nlogii w geometii płskiej i pzestzennej opiekun pcy: mg Doot Szczepńsk Kków, mzec
Obliczenia naukowe Wykład nr 14
 Obliczeni nuowe Wyłd nr 14 Pweł Zielińsi Ktedr Informtyi, Wydził Podstwowych Problemów Technii, Politechni Wrocłws Litertur Litertur podstwow [1] D. Kincid, W. Cheney, Anliz numeryczn, WNT, 2005. [2] A.
Obliczeni nuowe Wyłd nr 14 Pweł Zielińsi Ktedr Informtyi, Wydził Podstwowych Problemów Technii, Politechni Wrocłws Litertur Litertur podstwow [1] D. Kincid, W. Cheney, Anliz numeryczn, WNT, 2005. [2] A.
Realizacje zmiennych są niezależne, co sprawia, że ciąg jest ciągiem niezależnych zmiennych losowych,
 Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Komisja Egzaminacyjna dla Aktuariuszy LIX Egzamin dla Aktuariuszy z 12 marca 2012 r. Część I Matematyka finansowa
 Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Wyrównanie sieci niwelacyjnej
 1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
Komisja Egzaminacyjna dla Aktuariuszy LII Egzamin dla Aktuariuszy z 15 marca 2010 r. Część I Matematyka finansowa
 Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
mgh. Praca ta jest zmagazynowana w postaci energii potencjalnej,
 Wykłd z fizyki. Piot Posmykiewicz 49 6-4 Enegi potencjln Cłkowit pc wykonn nd punktem mteilnym jest ówn zminie jego enegii kinetycznej. Często jednk, jesteśmy zinteesowni znlezieniem pcy jką sił wykonł
Wykłd z fizyki. Piot Posmykiewicz 49 6-4 Enegi potencjln Cłkowit pc wykonn nd punktem mteilnym jest ówn zminie jego enegii kinetycznej. Często jednk, jesteśmy zinteesowni znlezieniem pcy jką sił wykonł
Analiza numeryczna. Stanisław Lewanowicz. Całkowanie numeryczne. Definicje, twierdzenia, algorytmy
 http://wwwiiuniwrocpl/ sle/teching/n-wdrpdf Anliz numeryczn Stnisłw Lewnowicz Styczeń 008 r Cłownie numeryczne Definicje, twierdzeni, lgorytmy 1 Pojęci wstępne Niech IF IF [, b] ozncz zbiór wszystich funcji
http://wwwiiuniwrocpl/ sle/teching/n-wdrpdf Anliz numeryczn Stnisłw Lewnowicz Styczeń 008 r Cłownie numeryczne Definicje, twierdzeni, lgorytmy 1 Pojęci wstępne Niech IF IF [, b] ozncz zbiór wszystich funcji
Zadania do rozdziału 7.
 Zdni do ozdziłu 7. Zd.7.. wiezchołkch kwdtu o okch umieszczono ednkowe łdunku. Jki łdunek o znku pzeciwnym tze umieścić w śodku kwdtu y sił wypdkow dziłąc n kżdy łdunek ył ówn zeu? ozwiąznie: ozptzmy siły
Zdni do ozdziłu 7. Zd.7.. wiezchołkch kwdtu o okch umieszczono ednkowe łdunku. Jki łdunek o znku pzeciwnym tze umieścić w śodku kwdtu y sił wypdkow dziłąc n kżdy łdunek ył ówn zeu? ozwiąznie: ozptzmy siły
Notatki do tematu Metody poszukiwania rozwiązań jednokryterialnych problemów decyzyjnych metody dla zagadnień liniowego programowania matematycznego
 Komputerowe wspomgnie decyzi 008/009 Liniowe zgdnieni decyzyne Nottki do temtu Metody poszukiwni rozwiązń ednokryterilnych problemów decyzynych metody dl zgdnień liniowego progrmowni mtemtycznego Liniowe
Komputerowe wspomgnie decyzi 008/009 Liniowe zgdnieni decyzyne Nottki do temtu Metody poszukiwni rozwiązń ednokryterilnych problemów decyzynych metody dl zgdnień liniowego progrmowni mtemtycznego Liniowe
O PEWNYCH MODELACH DECYZJI FINANSOWYCH
 DECYZJE nr 1 czerwiec 2004 37 O PEWNYCH MODELACH DECYZJI FINANSOWYCH Krzysztof Jjug Akdemi Ekonomiczn we Wrocłwiu Wprowdzenie modele teorii finnsów Teori finnsów, zwn również ekonomią finnsową, jest jednym
DECYZJE nr 1 czerwiec 2004 37 O PEWNYCH MODELACH DECYZJI FINANSOWYCH Krzysztof Jjug Akdemi Ekonomiczn we Wrocłwiu Wprowdzenie modele teorii finnsów Teori finnsów, zwn również ekonomią finnsową, jest jednym
symbol dodatkowy element graficzny kolorystyka typografia
 Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/00 Elementy podstwowe symbol dodtkowy element grficzny kolorystyk typogrfi Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/01 Elementy podstwowe /
Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/00 Elementy podstwowe symbol dodtkowy element grficzny kolorystyk typogrfi Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/01 Elementy podstwowe /
POMIAR OGNISKOWEJ SOCZEWEK METODĄ BESSELA
 Ćwiczenie 50 POMIAR OGNISKOWEJ SOCZEWEK METODĄ BESSELA 50.. Widomości ogólne Soczewką nzywmy ciło pzeźoczyste oczyste ogniczone dwiem powiezchnimi seycznymi. Post pzechodząc pzez śodki kzywizny ob powiezchni
Ćwiczenie 50 POMIAR OGNISKOWEJ SOCZEWEK METODĄ BESSELA 50.. Widomości ogólne Soczewką nzywmy ciło pzeźoczyste oczyste ogniczone dwiem powiezchnimi seycznymi. Post pzechodząc pzez śodki kzywizny ob powiezchni
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
PODSTAWY BAZ DANYCH Wykład 3 2. Pojęcie Relacyjnej Bazy Danych
 PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
 ź Ź Ź Ź ć Ł Ę Ź ć Ź ć Ń Ź Ź Ź Ź ć ć ć ź ć ź Ę ć Ź Ź Ł Ł Ł ć Ł Ą ć ć Ź Ś ć Ź ć Ę Ź ź ć Ź ć ź ć Ę ć Ą ć ć ć Ł ć ć ć ć Ą ć Ź ć ć Ź Ą Ź Ą ź Ń Ą ć Ą ć ć ć Ź ć ć ć ć ć Ą Ą Ą ć Ł Ń ć ć Ź Ł ć Ź Ź Ę Ź ć ć ć ć
ź Ź Ź Ź ć Ł Ę Ź ć Ź ć Ń Ź Ź Ź Ź ć ć ć ź ć ź Ę ć Ź Ź Ł Ł Ł ć Ł Ą ć ć Ź Ś ć Ź ć Ę Ź ź ć Ź ć ź ć Ę ć Ą ć ć ć Ł ć ć ć ć Ą ć Ź ć ć Ź Ą Ź Ą ź Ń Ą ć Ą ć ć ć Ź ć ć ć ć ć Ą Ą Ą ć Ł Ń ć ć Ź Ł ć Ź Ź Ę Ź ć ć ć ć
BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH OPARTYCH NA ANALIZIE TECHNICZNEJ WPROWADZENIE
 Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Edyta Macinkiewicz Kateda Zaządzania, Wydział Oganizacji i Zaządzania Politechniki Łódzkiej e-mail: emac@p.lodz.pl BADANIE ZALEśNOŚCI POMIĘDZY WARTOŚCIĄ WYKŁADNIKA HURSTA A SKUTECZNOŚCIĄ STRATEGII INWESTYCYJNYCH
Zastosowanie multimetrów cyfrowych do pomiaru podstawowych wielkości elektrycznych
 Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH
 SSof Polsk, el. (1) 4843, (61) 414151, info@ssof.pl, www.ssof.pl PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH Andrzej Sokołowski Akdemi Ekonomiczn w Krkowie, Zkłd Sysyki W oprcowniu ym przedswiono pewną
SSof Polsk, el. (1) 4843, (61) 414151, info@ssof.pl, www.ssof.pl PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH Andrzej Sokołowski Akdemi Ekonomiczn w Krkowie, Zkłd Sysyki W oprcowniu ym przedswiono pewną
X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH
 X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH 1.1 Definice; metoda wsteczne poeci w tomogafii tansmisyne Rys. 1.1 Pzyład dwóch zutów pzedmiotu złożonego z dwóch cylindycznych obietów Z czysto
X. PODSTAWOWA MATEMATYKA REKONSTRUKCJI TOMOGRAFICZNYCH 1.1 Definice; metoda wsteczne poeci w tomogafii tansmisyne Rys. 1.1 Pzyład dwóch zutów pzedmiotu złożonego z dwóch cylindycznych obietów Z czysto
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Analiza matematyczna i algebra liniowa
 Anliz mtemtyczn i lgebr liniow Mteriły pomocnicze dl studentów do wykłdów Mcierze liczbowe i wyznczniki. Ukłdy równń liniowych. Mcierze. Wyznczniki. Mcierz odwrotn. Równni mcierzowe. Rząd mcierzy. Ukłdy
Anliz mtemtyczn i lgebr liniow Mteriły pomocnicze dl studentów do wykłdów Mcierze liczbowe i wyznczniki. Ukłdy równń liniowych. Mcierze. Wyznczniki. Mcierz odwrotn. Równni mcierzowe. Rząd mcierzy. Ukłdy
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
XXX OLIMPIADA FIZYCZNA (1980/1981). Stopień I, zadanie teoretyczne T4 1
 XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
XXX OLMPADA FZYCZNA (1980/1981). Stopień, zadanie teoetyczne T4 1 Źódło: Komitet Główny Olimpiady Fizycznej; Waldema Gozowsi; Andzej Kotlici: Fizya w Szole, n 3, 1981.; Andzej Nadolny, Kystyna Pniewsa:
Politechnika Śląska Wydział Automatyki, Elektroniki i Informatyki Praca dyplomowa
 Politechni Ślą Wydził Automtyi, Eletronii i Informtyi Prc dyplomow Temt : Stnowio lbortoryjne do ymulcji obietów n terowniu SLC500. Promotor : Dr inż. J.przy Student : Tomz tuzczy Cel prcy Celem prcy było
Politechni Ślą Wydził Automtyi, Eletronii i Informtyi Prc dyplomow Temt : Stnowio lbortoryjne do ymulcji obietów n terowniu SLC500. Promotor : Dr inż. J.przy Student : Tomz tuzczy Cel prcy Celem prcy było
Tradycyjne mierniki ryzyka
 Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
Tadycyjne mieniki yzyka Pzykład 1. Ryzyko w pzypadku potfela inwestycyjnego Dwie inwestycje mają następujące stopy zwotu, zależne od sytuacji gospodaczej: Sytuacja Pawdopodobieństwo R R Recesja 0, 9,0%
- dobór kryteriów stosowanych do oceny kondycji ekonomiczno - finansowej badanego przedsiębiorstwa w danej sytuacji,
 Krzysztof Pisecki Akdemi Ekonomiczn l. Niepodległości 10 60-967 Poznń WIELOKRYTERIALNA ANALIZA DYNAMIKI KONDYCJI EKONOMICZNEJ PRZEDSIĘBIORSTWA Zkłd się, że ocen oemue podstwowe oszry nliz ekonomicznych
Krzysztof Pisecki Akdemi Ekonomiczn l. Niepodległości 10 60-967 Poznń WIELOKRYTERIALNA ANALIZA DYNAMIKI KONDYCJI EKONOMICZNEJ PRZEDSIĘBIORSTWA Zkłd się, że ocen oemue podstwowe oszry nliz ekonomicznych
Formularz ofertowy. w odpowiedzi na ogłoszenie w procedurze przetargowej prowadzonej w trybie przetargu nieograniczonego na
 Złącznik nr 1 do SIWZ Wzór formulrz ofertowego Formulrz ofertowy w odpowiedzi n ogłoszenie w procedurze przetrgowej prowdzonej w trybie przetrgu nieogrniczonego n dostwę elektrycznej czynnej dl grupy zkupowej
Złącznik nr 1 do SIWZ Wzór formulrz ofertowego Formulrz ofertowy w odpowiedzi n ogłoszenie w procedurze przetrgowej prowdzonej w trybie przetrgu nieogrniczonego n dostwę elektrycznej czynnej dl grupy zkupowej
 ń Ż Ż Ż ź Ś ź ń ŚĆ ć ń Ę ć Ć ń Ę ć ń ć ć Ż Ę Ę Ś ń Ó ć Ę Ć ć ć Ę Ę Ż ń ć ć Ś ń Ę ć ń Ś Ś ć ź Ś ŹĆ Ż Ś Ż ć ć ć ć ć ć ń ć ć ń ć ć Ś Ć ń Ś Ą ć ć ć ć ć ć ń ć ń ć Ć ć ń ć Ą ń ć ć Ę Ś ć ń ź ń Ć Ć ń ć ć ć Ś ć
ń Ż Ż Ż ź Ś ź ń ŚĆ ć ń Ę ć Ć ń Ę ć ń ć ć Ż Ę Ę Ś ń Ó ć Ę Ć ć ć Ę Ę Ż ń ć ć Ś ń Ę ć ń Ś Ś ć ź Ś ŹĆ Ż Ś Ż ć ć ć ć ć ć ń ć ć ń ć ć Ś Ć ń Ś Ą ć ć ć ć ć ć ń ć ń ć Ć ć ń ć Ą ń ć ć Ę Ś ć ń ź ń Ć Ć ń ć ć ć Ś ć
Zbiory wyznaczone przez funkcje zdaniowe
 pojęci zbioru i elementu RCHUNEK ZIORÓW zbiór zwier element element nleży do zbioru jest elementem zbioru ( X zbiór wszystkich przedmiotów indywidulnych, których dotyczy dn nuk zbiór pełny (uniwerslny
pojęci zbioru i elementu RCHUNEK ZIORÓW zbiór zwier element element nleży do zbioru jest elementem zbioru ( X zbiór wszystkich przedmiotów indywidulnych, których dotyczy dn nuk zbiór pełny (uniwerslny
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
 ń ż ń ń ź ć ż ń ż ń ć ć ń ć ń ć ć Ź ń ć Ź ć ń ń ć ż ń ż ćź Ę ż ń ń ć ć ć ż ż ń ń Ę ć ć ń ż Ś Ś Ó Ź ń Ó ź Ś Ź Ę ż ń ż ź Ś ż ż ń ć ń ż ż ń Ż Ń Ź ż ż ć ć ż ć ń ż ż ń ń ń ć ń ż ć ź ć ń Ś Ę Ę ż Ę ń Ź ń Ó ż
ń ż ń ń ź ć ż ń ż ń ć ć ń ć ń ć ć Ź ń ć Ź ć ń ń ć ż ń ż ćź Ę ż ń ń ć ć ć ż ż ń ń Ę ć ć ń ż Ś Ś Ó Ź ń Ó ź Ś Ź Ę ż ń ż ź Ś ż ż ń ć ń ż ż ń Ż Ń Ź ż ż ć ć ż ć ń ż ż ń ń ń ć ń ż ć ź ć ń Ś Ę Ę ż Ę ń Ź ń Ó ż
STYLE. TWORZENIE SPISÓW TREŚCI
 STYLE. TWORZENIE SPISÓW TREŚCI Ćwiczenie 1 Tworzenie nowego stylu n bzie istniejącego 1. Formtujemy jeden kpit tekstu i zznczmy go (stnowi on wzorzec). 2. Wybiermy Nrzędzi główne, rozwijmy okno Style (lub
STYLE. TWORZENIE SPISÓW TREŚCI Ćwiczenie 1 Tworzenie nowego stylu n bzie istniejącego 1. Formtujemy jeden kpit tekstu i zznczmy go (stnowi on wzorzec). 2. Wybiermy Nrzędzi główne, rozwijmy okno Style (lub
ROLE OF CUSTOMER IN BALANCED DEVELOPMENT OF COMPANY
 FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Foli Univ. Agric. Stetin. 2007, Oeconomic 254 (47), 117 122 Jolnt KONDRATOWICZ-POZORSKA ROLA KLIENTA W ZRÓWNOWAŻONYM ROZWOJU FIRMY ROLE OF CUSTOMER IN BALANCED
FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Foli Univ. Agric. Stetin. 2007, Oeconomic 254 (47), 117 122 Jolnt KONDRATOWICZ-POZORSKA ROLA KLIENTA W ZRÓWNOWAŻONYM ROZWOJU FIRMY ROLE OF CUSTOMER IN BALANCED
INSTRUKCJA. - Jak rozwiązywać zadania wysoko punktowane?
 INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
WPŁYW WILGOTNOŚCI NA SZTYWNOŚCIOWE TŁUMIENIE DRGAŃ KONSTRUKCJI DREWNIANYCH
 95 ROCZNII INŻYNIERII BUDOWLANEJ ZESZYT 3/03 omisj Inżynierii Budowlnej Oddził Polskiej Akdemii Nuk w towicch WPŁYW WILGOTNOŚCI NA SZTYWNOŚCIOWE TŁUMIENIE DRGAŃ ONSTRUCJI DREWNIANYCH mil PAWLI, Zbigniew
95 ROCZNII INŻYNIERII BUDOWLANEJ ZESZYT 3/03 omisj Inżynierii Budowlnej Oddził Polskiej Akdemii Nuk w towicch WPŁYW WILGOTNOŚCI NA SZTYWNOŚCIOWE TŁUMIENIE DRGAŃ ONSTRUCJI DREWNIANYCH mil PAWLI, Zbigniew
Prosta metoda sprawdzania fundamentów ze względu na przebicie
 Konstrkcje Elementy Mteriły Prost metod sprwdzni fndmentów ze względ n przebicie Prof dr b inż Micł Knff, Szkoł Główn Gospodrstw Wiejskiego w Wrszwie, dr inż Piotr Knyzik, Politecnik Wrszwsk 1 Wprowdzenie
Konstrkcje Elementy Mteriły Prost metod sprwdzni fndmentów ze względ n przebicie Prof dr b inż Micł Knff, Szkoł Główn Gospodrstw Wiejskiego w Wrszwie, dr inż Piotr Knyzik, Politecnik Wrszwsk 1 Wprowdzenie
3. Rozkład macierzy według wartości szczególnych
 Rozkłd mcierzy wedłg wrtości szczególnych Wprowdzenie Przypomnimy podstwowe zleżności związne z zstosowniem metody nmnieszych kwdrtów do proksymci fnkci dyskretne Podstwowe równnie m nstępącą postć: +
Rozkłd mcierzy wedłg wrtości szczególnych Wprowdzenie Przypomnimy podstwowe zleżności związne z zstosowniem metody nmnieszych kwdrtów do proksymci fnkci dyskretne Podstwowe równnie m nstępącą postć: +
Regulamin oferty Dobry bilet
 Regulmin oferty Dobry bilet I. Podstwowe informcje 1. Do odwołni n wybrnych odcinkch sieci kolejowej wprowdz się ofertę Dobry bilet. 2. W ofercie wystwi się bilety: ) jednorzowy n przejzd tm (w dowolnym
Regulmin oferty Dobry bilet I. Podstwowe informcje 1. Do odwołni n wybrnych odcinkch sieci kolejowej wprowdz się ofertę Dobry bilet. 2. W ofercie wystwi się bilety: ) jednorzowy n przejzd tm (w dowolnym
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Zbiory rozmyte. Teoria i zastosowania we wnioskowaniu aproksymacyjnym
 Zior rozmte Teori i zstosowni we wniosowniu prosmcjnm PODSTWOWE POJĘCI Motwcje Potrze opisni zjwis i pojęć wielozncznch i niepreczjnch użwnch swoodnie w jęzu nturlnm np. wso tempertur młod człowie średni
Zior rozmte Teori i zstosowni we wniosowniu prosmcjnm PODSTWOWE POJĘCI Motwcje Potrze opisni zjwis i pojęć wielozncznch i niepreczjnch użwnch swoodnie w jęzu nturlnm np. wso tempertur młod człowie średni
Karta oceny merytorycznej wniosku o dofinansowanie projektu konkursowego PO KL 1
 Złącznik 3 Krt oceny merytorycznej wniosku o dofinnsownie konkursowego PO KL 1 NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA WNIOSEK:. NUMER KONKURSU 2/POKL/8.1.1/2010 TYTUŁ PROJEKTU:... SUMA KONTROLNA
Złącznik 3 Krt oceny merytorycznej wniosku o dofinnsownie konkursowego PO KL 1 NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA WNIOSEK:. NUMER KONKURSU 2/POKL/8.1.1/2010 TYTUŁ PROJEKTU:... SUMA KONTROLNA
 Ń Ą Ę Ł Ł Ł Ł ź Ł Ł Ł Ł Ł Ł ź Ł Ł Ł Ł Ś Ś źć Ą ź ź ć ź ć Ś ć Ą ć Ż ć ć Ę ć Ą Ł Ł Ł ź Ś Ą ź Ą Ą Ł Ś Ą Ż Ą Ł Ł ć Ż Ś ź Ó ź Ó ć Ć ź Ś ć Ł ć ć ć ć ć ć Ą Ą Ą Ł Ą ć ć ć ć Ą Ł ź ć ćź ć ć ź Ś ć ć Ą Ą Ą ć Ą ć Ż
Ń Ą Ę Ł Ł Ł Ł ź Ł Ł Ł Ł Ł Ł ź Ł Ł Ł Ł Ś Ś źć Ą ź ź ć ź ć Ś ć Ą ć Ż ć ć Ę ć Ą Ł Ł Ł ź Ś Ą ź Ą Ą Ł Ś Ą Ż Ą Ł Ł ć Ż Ś ź Ó ź Ó ć Ć ź Ś ć Ł ć ć ć ć ć ć Ą Ą Ą Ł Ą ć ć ć ć Ą Ł ź ć ćź ć ć ź Ś ć ć Ą Ą Ą ć Ą ć Ż
 ć ć ć ć ć ć ć źć ć ć ć ć ć ć ź Ś ź ć ć ć Ż ć Ę ć ć ć ć ć ć Ę Ę ć ć ć Ż ź ź ź ć ć ć ć ć Ś ć ć ć ć ć Ż ćż ć ć ć ć ć ć Ż ć ć ć ć ź ć ź Ę ć ć ź ć ć Ś Ż ć ć ć Ą Ż ć ć ć Ę ć ć Ż ć ć ć Ś ć ć ć ć ć ć ć ć ć ć ć
ć ć ć ć ć ć ć źć ć ć ć ć ć ć ź Ś ź ć ć ć Ż ć Ę ć ć ć ć ć ć Ę Ę ć ć ć Ż ź ź ź ć ć ć ć ć Ś ć ć ć ć ć Ż ćż ć ć ć ć ć ć Ż ć ć ć ć ź ć ź Ę ć ć ź ć ć Ś Ż ć ć ć Ą Ż ć ć ć Ę ć ć Ż ć ć ć Ś ć ć ć ć ć ć ć ć ć ć ć
PODSTAWY BAZ DANYCH Wykład 2 2. Pojęcie Relacyjnej Bazy Danych
 PODSTAWY BAZ DANYCH Wykłd 2 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy bz dnych" 1 Pojęcie krotki - definicj Definicj. Niech dny będzie skończony zbiór U := { A 1, A 2,..., A n }, którego
PODSTAWY BAZ DANYCH Wykłd 2 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy bz dnych" 1 Pojęcie krotki - definicj Definicj. Niech dny będzie skończony zbiór U := { A 1, A 2,..., A n }, którego
WYZNACZANIE STAŁEJ RÓWNOWAGI KWASOWO ZASADOWEJ W ROZTWORACH WODNYCH
 Politehni Śląs WYDZIŁ CHEMICZNY KTEDR FIZYKOCHEMII I TECHNOLOGII POLIMERÓW WYZNCZNIE STŁEJ RÓWNOWGI KWSOWO ZSDOWEJ W ROZTWORCH WODNYCH Opieun: Miejse ćwizeni: Ktrzyn Kruiewiz Ktedr Fizyohemii i Tehnoii
Politehni Śląs WYDZIŁ CHEMICZNY KTEDR FIZYKOCHEMII I TECHNOLOGII POLIMERÓW WYZNCZNIE STŁEJ RÓWNOWGI KWSOWO ZSDOWEJ W ROZTWORCH WODNYCH Opieun: Miejse ćwizeni: Ktrzyn Kruiewiz Ktedr Fizyohemii i Tehnoii
ELEMENTY RACHUNKU WEKTOROWEGO
 Unwestet Wmńso- Mus w Ostne Złd Mehn onstu udownh ELEMENTY RCHUNU WETOROWEGO Włd d nż. Roet Smt Zen tetu 1. wtows J.: Stt ogón. Wsw : Wdw. Potehn Wswse, 1971. 2. wtows J.: Mehn tehnn. Wsw: Wdw.. Potehn
Unwestet Wmńso- Mus w Ostne Złd Mehn onstu udownh ELEMENTY RCHUNU WETOROWEGO Włd d nż. Roet Smt Zen tetu 1. wtows J.: Stt ogón. Wsw : Wdw. Potehn Wswse, 1971. 2. wtows J.: Mehn tehnn. Wsw: Wdw.. Potehn
Struktura kapitału, a wartość rynkowa przedsiębiorstwa na rynku kapitałowym
 Kurs e-lerningowy Giełd Ppierów Wrtościowych i rynek kpitłowy V edycj Struktur kpitłu, wrtość rynkow przedsiębiorstw n rynku kpitłowym 2010 SPIS TREŚCI I. Wstęp 3 II. Podstwowy miernik rentowności kpitłu
Kurs e-lerningowy Giełd Ppierów Wrtościowych i rynek kpitłowy V edycj Struktur kpitłu, wrtość rynkow przedsiębiorstw n rynku kpitłowym 2010 SPIS TREŚCI I. Wstęp 3 II. Podstwowy miernik rentowności kpitłu
4) Podaj wartość stałych czasowych, wzmocnienia i punkt równowagi przy wymuszeniu impulsowym
 LISA0: Podtwowe człony (obiety) dynmii Przygotownie ) Wymień i opiz włności podtwowych członów (obiety) dynmii potć trnmitncji nzwy i ogrniczeni prmetrów ) Wymień podtwowe człony dynmii dl tórych trnmitncj
LISA0: Podtwowe człony (obiety) dynmii Przygotownie ) Wymień i opiz włności podtwowych członów (obiety) dynmii potć trnmitncji nzwy i ogrniczeni prmetrów ) Wymień podtwowe człony dynmii dl tórych trnmitncj
a Komisją Zakładową NSZZ Solidarność Uniwersytetu im. Adama Mickiewicza w Poznaniu, reprezentowaną przez: mgr Krystynę Andrzejewską
 POROZUMIENIE zwrte w dniu 11 czerwc 2015 roku w sprwie zsd zwiększeni wyngrodzeń prcowników Uniwersytetu im. Adm Mickiewicz w Poznniu od 1 styczni 2015 roku pomiędzy: Uniwersytetem im. Adm Mickiewicz w
POROZUMIENIE zwrte w dniu 11 czerwc 2015 roku w sprwie zsd zwiększeni wyngrodzeń prcowników Uniwersytetu im. Adm Mickiewicz w Poznniu od 1 styczni 2015 roku pomiędzy: Uniwersytetem im. Adm Mickiewicz w
MODELOWANIE USŁUG TRANSPORTOWYCH W OBSZARZE DZIAŁANIA CENTRUM LOGISTYCZNO-DYSTRYBUCYJNEGO
 PACE NAUKOWE POLIECHNIKI WASZAWSKIEJ z. 64 anspot 2008 Jolanta ŻAK Wydział anspotu Politechniki Waszawskie Zakład Logistyki i Systemów anspotowych ul. Koszykowa 75, 00-662 Waszawa logika@it.pw.edu.pl MODELOWANIE
PACE NAUKOWE POLIECHNIKI WASZAWSKIEJ z. 64 anspot 2008 Jolanta ŻAK Wydział anspotu Politechniki Waszawskie Zakład Logistyki i Systemów anspotowych ul. Koszykowa 75, 00-662 Waszawa logika@it.pw.edu.pl MODELOWANIE
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 424 PRACE INSTYTUTU KULTURY FIZYCZNEJ NR 22 2005
 ZEZYTY NAUKOWE UNIWERYTETU ZCZECIŃKIEGO NR 424 PRACE INTYTUTU KULTURY FIZYCZNEJ NR 22 2005 MARIA MAKRI PRAWNOŚĆ FIZYCZNA I AKTYWNOŚĆ RUCHOWA KOBIET W WIEKU 20 60 LAT 1. Wstęp Dobr sprwność fizyczn jest
ZEZYTY NAUKOWE UNIWERYTETU ZCZECIŃKIEGO NR 424 PRACE INTYTUTU KULTURY FIZYCZNEJ NR 22 2005 MARIA MAKRI PRAWNOŚĆ FIZYCZNA I AKTYWNOŚĆ RUCHOWA KOBIET W WIEKU 20 60 LAT 1. Wstęp Dobr sprwność fizyczn jest
ZADANIA DO SAMODZIELNEGO ROZWIĄZANIA
 ZNI SMZIELNE RZWIĄZNI łski ukłd sił zbieżnych Zdnie 1 Jednoodn poziom belk połączon jest pzegubowo n końcu z nieuchomą ściną oz zwieszon n końcu n cięgnie twozącym z poziomem kąt. Znleźć ekcję podpoy n
ZNI SMZIELNE RZWIĄZNI łski ukłd sił zbieżnych Zdnie 1 Jednoodn poziom belk połączon jest pzegubowo n końcu z nieuchomą ściną oz zwieszon n końcu n cięgnie twozącym z poziomem kąt. Znleźć ekcję podpoy n
Wartość bezwzględna. Proste równania i nierówności.
 Wrtość bezwzględn Proste równni i nierówności Dl liczb rzeczywistych możemy zdefiniowć opercję zwną wrtością bezwzględną lub modułem liczby Definicj 7,, Sens powyższej definicji jest nstępujący Jeżeli
Wrtość bezwzględn Proste równni i nierówności Dl liczb rzeczywistych możemy zdefiniowć opercję zwną wrtością bezwzględną lub modułem liczby Definicj 7,, Sens powyższej definicji jest nstępujący Jeżeli
Symbol Newtona liczba wyborów zbioru k-elementowego ze zbioru n elementów. Symbol Newtona
 B Głut Symol Newto Symol Newto licz wyoów ziou -elemetowego ze ziou elemetów ) ( A B B B t t żd dog: odciów do góy Ile ozwiązń m ówie: 4 6 gdzie i są ieujemymi liczmi cłowitymi? 9 84 4 4 5 Licz ozwiązń
B Głut Symol Newto Symol Newto licz wyoów ziou -elemetowego ze ziou elemetów ) ( A B B B t t żd dog: odciów do góy Ile ozwiązń m ówie: 4 6 gdzie i są ieujemymi liczmi cłowitymi? 9 84 4 4 5 Licz ozwiązń
L(x, 0, y, 0) = x 2 + y 2 (3)
 0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
0. Małe dgania Kótka notatka o małych dganiach wyjasniające możliwe niejasności. 0. Poszukiwanie punktów ównowagi Punkty ównowagi wyznaczone są waunkami x i = 0, ẋi = 0 ( Pochodna ta jest ówna pochodnej
Programowanie wielocelowe lub wielokryterialne
 Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe
Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe
Redukcja układów sił działających na bryły sztywne
 1 Redukcj ukłdów sił dziłjących n bryły sztywne W zdnich tego rozdziłu wykorzystuje się zsdy redukcji ukłdów sił wykłdne w rmch mechniki ogólnej i powtórzone w tomie 1 podręcznik. Zdnie 1 Zredukowć ukłd
1 Redukcj ukłdów sił dziłjących n bryły sztywne W zdnich tego rozdziłu wykorzystuje się zsdy redukcji ukłdów sił wykłdne w rmch mechniki ogólnej i powtórzone w tomie 1 podręcznik. Zdnie 1 Zredukowć ukłd
Od lewej: piramida Chefrena, Wielki Sfinks, piramida Cheopsa.
 1. Pirmidiotologi. W obfitej literturze przedmiotu podje się, że pirmid Ceops, lub też z ngielsk Wielk Pirmid (te Gret Pyrmid), zwier w swej konstrukcji pełną i szczegółową istorię rodzju ludzkiego od
1. Pirmidiotologi. W obfitej literturze przedmiotu podje się, że pirmid Ceops, lub też z ngielsk Wielk Pirmid (te Gret Pyrmid), zwier w swej konstrukcji pełną i szczegółową istorię rodzju ludzkiego od
Samouczek Metody Elementów Skończonych dla studentów Budownictwa
 Grzegorz Dzierżnowski Mrt Sitek Smouczek Metody Elementów Skończonych dl studentów Budownictw Część I Sttyk konstrukcji prętowych OFICYNA WYDAWNICZA POLITECHNIKI WARSZAWSKIEJ WARSZAWA 2012 Preskrypt n
Grzegorz Dzierżnowski Mrt Sitek Smouczek Metody Elementów Skończonych dl studentów Budownictw Część I Sttyk konstrukcji prętowych OFICYNA WYDAWNICZA POLITECHNIKI WARSZAWSKIEJ WARSZAWA 2012 Preskrypt n
Bartosz Świątek Kancelaria Olszewski Tokarski & Wspólnicy
 Shet pegenci: Jonn Joz-Zugj JZP Knci Adwokck Joz-Zugj, Zij-Piul, Zugj i Ptnezy pp Sylwete Kpzewki Tnpotow Gup Dodcz Piot Michłowki Knci Rdcy Pwnego Piot Michłowki Główne zgdnieni: Btoz Świątek Knci Olzewki
Shet pegenci: Jonn Joz-Zugj JZP Knci Adwokck Joz-Zugj, Zij-Piul, Zugj i Ptnezy pp Sylwete Kpzewki Tnpotow Gup Dodcz Piot Michłowki Knci Rdcy Pwnego Piot Michłowki Główne zgdnieni: Btoz Świątek Knci Olzewki
G i m n a z j a l i s t ó w
 Ko³o Mtemtyzne G i m n z j l i s t ó w 1. Lizy,, spełniją wrunki: (1) ++ = 0, 1 () + + 1 + + 1 + = 1 4. Olizyć wrtość wyrżeni w = + + Rozwiąznie Stowrzyszenie n rzez Edukji Mtemtyznej Zestw 7 szkie rozwizń
Ko³o Mtemtyzne G i m n z j l i s t ó w 1. Lizy,, spełniją wrunki: (1) ++ = 0, 1 () + + 1 + + 1 + = 1 4. Olizyć wrtość wyrżeni w = + + Rozwiąznie Stowrzyszenie n rzez Edukji Mtemtyznej Zestw 7 szkie rozwizń
2870 KonigStahl_RURY OKRAGLE:2048 KonigStahl_RURY OKRAGLE_v15 3/2/10 4:45 PM Page 1. Partner Twojego sukcesu
 KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 1 Prtner Twojego sukcesu KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 3 Nsz rynek Wilno Kliningrd Gdyni Minsk
KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 1 Prtner Twojego sukcesu KonigStl_RURY OKRAGLE:48 KonigStl_RURY OKRAGLE_v15 3/2/1 4:45 PM Pge 3 Nsz rynek Wilno Kliningrd Gdyni Minsk
koszt kapitału D/S L dźwignia finansowa σ EBIT zysku operacyjnego EBIT firmy. Firmy Modele struktury kapitału Rys. 8.3. Krzywa kosztów kapitału.
 Modele strutury apitału oszt apitału Optymalna strutura apitału dźwignia finansowa / Rys. 8.3. Krzywa osztów apitału. Założenia wspólne modeli MM Modigliani i Miller w swoich rozważaniach ograniczyli się
Modele strutury apitału oszt apitału Optymalna strutura apitału dźwignia finansowa / Rys. 8.3. Krzywa osztów apitału. Założenia wspólne modeli MM Modigliani i Miller w swoich rozważaniach ograniczyli się
Algebra Boola i podstawy systemów liczbowych. Ćwiczenia z Teorii Układów Logicznych, dr inż. Ernest Jamro. 1. System dwójkowy reprezentacja binarna
 lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
Klucz odpowiedzi do zadań zamkniętych i schemat oceniania zadań otwartych
 Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
Klucz odpowiedzi do zdń zmkniętc i scemt ocenini zdń otwrtc Klucz odpowiedzi do zdń zmkniętc 4 7 9 0 4 7 9 0 D D D Scemt ocenini zdń otwrtc Zdnie (pkt) Rozwiąż nierówność x x 0 Oliczm wróżnik i miejsc
Wyznacznikiem macierzy kwadratowej A stopnia n nazywamy liczbę det A określoną następująco:
 Def.8. Wyzncznikiem mcierzy kwdrtowej stopni n nzywmy liczbę det określoną nstępująco:.det.det dl n n det det n det n, gdzie i j ozncz mcierz, którą otrzymujemy z mcierzy przez skreślenie i- tego wiersz
Def.8. Wyzncznikiem mcierzy kwdrtowej stopni n nzywmy liczbę det określoną nstępująco:.det.det dl n n det det n det n, gdzie i j ozncz mcierz, którą otrzymujemy z mcierzy przez skreślenie i- tego wiersz
Zaokrąglanie i zapisywanie wyników obliczeń przybliżonych
 Edwrd Musił Oddził Gdński SEP Zokrąglnie i zpisywnie wyników obliczeń przybliżonych Inżynier wykonuje nieml wyłącznie obliczeni przybliżone i powinien mieć nieustnnie n względzie dokłdność, jką chce uzyskć
Edwrd Musił Oddził Gdński SEP Zokrąglnie i zpisywnie wyników obliczeń przybliżonych Inżynier wykonuje nieml wyłącznie obliczeni przybliżone i powinien mieć nieustnnie n względzie dokłdność, jką chce uzyskć
DZIAŁ 2. Figury geometryczne
 1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
Propozycja przedmiotowego systemu oceniania wraz z określeniem wymagań edukacyjnych (zakres podstawowy)
 Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Planowanie inicjatywy lokalnej INICJATYWA LOKALNA PROJEKT SPOŁECZNY CZYM JEST PROJEKT? Projekt jest przedsięwzięciem, które ma początek i koniec.
 Plnownie inicjtywy lolnej INICJATYWA LOKALNA PROJEKT SPOŁECZNY CZYM JEST PROJEKT? Projet jest przedsięwzięciem, tóre m począte i oniec. Jest to proces zplnowny i ontrolowny, m doprowdzić do pozytywnego
Plnownie inicjtywy lolnej INICJATYWA LOKALNA PROJEKT SPOŁECZNY CZYM JEST PROJEKT? Projet jest przedsięwzięciem, tóre m począte i oniec. Jest to proces zplnowny i ontrolowny, m doprowdzić do pozytywnego
Kodowanie liczb. Kodowanie stałopozycyjne liczb całkowitych. Niech liczba całkowita a ma w systemie dwójkowym postać: Kod prosty
 Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
MATeMAtyka 3 inf. Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych. Zakres podstawowy i rozszerzony. Dorota Ponczek, Karolina Wej
 Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
AKADEMIA INWESTORA INDYWIDUALNEGO CZĘŚĆ II. AKCJE.
 uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
uma Pzedsiębiocy /6 Lipiec 205. AKAEMIA INWESTORA INYWIUALNEGO CZĘŚĆ II. AKCJE. WYCENA AKCJI Wycena akcji jest elementem analizy fundamentalnej akcji. Następuje po analizie egionu, gospodaki i banży, w
( ) RóŜne rodzaje grup. Symetrie i struktury ciała stałego. W.Sikora, Wyklad 3
 Symete stutuy ł stłe. W.S Wyld RóŜne dze up up wetw W - zó wetów z ddwnem dzłnem upwym spełn wszyste złŝen ztem est upą. Nzyw sę ą upą wetwą. Gup t est nesńzn (e ząd est nesńzny) mŝe yć ął lu dysetn. Dysetn
Symete stutuy ł stłe. W.S Wyld RóŜne dze up up wetw W - zó wetów z ddwnem dzłnem upwym spełn wszyste złŝen ztem est upą. Nzyw sę ą upą wetwą. Gup t est nesńzn (e ząd est nesńzny) mŝe yć ął lu dysetn. Dysetn
Stanisław RADKOWSKI. Politechnika Warszawska, Instytut Podstaw Budowy Maszyn,
 WYKORZYSTANIE STACJONARNYCH STACJI MONITORINGU W WYKRYWANIU USZKODZEŃ POJAZDÓW Snisłw RADKOWSKI Poliechnik Wszwsk, Insyu Podsw Budowy Mszyn, ul. Nbu 84, 0-54 Wszw 0 660 86, e-mil: s@sim.pw.edu.pl Scj monioingu
WYKORZYSTANIE STACJONARNYCH STACJI MONITORINGU W WYKRYWANIU USZKODZEŃ POJAZDÓW Snisłw RADKOWSKI Poliechnik Wszwsk, Insyu Podsw Budowy Mszyn, ul. Nbu 84, 0-54 Wszw 0 660 86, e-mil: s@sim.pw.edu.pl Scj monioingu
smoleńska jako nierozwiązywalny konflikt?
 D y s k u s j smoleńsk jko nierozwiązywlny konflikt? Wiktor Sorl Michł Bilewicz Mikołj Winiewski Wrszw, 2014 1 Kto nprwdę stł z zmchmi n WTC lub z zbójstwem kżnej Diny? Dlczego epidemi AIDS rozpowszechnił
D y s k u s j smoleńsk jko nierozwiązywlny konflikt? Wiktor Sorl Michł Bilewicz Mikołj Winiewski Wrszw, 2014 1 Kto nprwdę stł z zmchmi n WTC lub z zbójstwem kżnej Diny? Dlczego epidemi AIDS rozpowszechnił
Wektory [ ] Oczywiście wektor w przestrzeni trójwymiarowej wektor będzie miał trzy współrzędne. B (x B. , y B. α A (x A, y A ) to jest wektor
![Wektory [ ] Oczywiście wektor w przestrzeni trójwymiarowej wektor będzie miał trzy współrzędne. B (x B. , y B. α A (x A, y A ) to jest wektor Wektory [ ] Oczywiście wektor w przestrzeni trójwymiarowej wektor będzie miał trzy współrzędne. B (x B. , y B. α A (x A, y A ) to jest wektor](/thumbs/64/52076488.jpg) Wektor N fizce w szkole średniej spotkcie się z dwom tpmi wielkości fizcznch. Jedne z nich, np. ms, tempertur, łdunek elektrczn są opiswne przez jedną liczę; te nzwm wielkościmi sklrnmi, w skrócie - sklrmi.
Wektor N fizce w szkole średniej spotkcie się z dwom tpmi wielkości fizcznch. Jedne z nich, np. ms, tempertur, łdunek elektrczn są opiswne przez jedną liczę; te nzwm wielkościmi sklrnmi, w skrócie - sklrmi.
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 2014/2015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A2, A3, A4, A6, A7)
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
PRÓBNA MATURA Z MATEMATYKI Z OPERONEM LISTOPAD ,0. 3x 6 6 3x 6 6,
 Zdnie PRÓBNA MATURA Z MATEMATYKI Z OPERONEM LISTOPAD 04 Zbiorem wszystkich rozwiązń nierówności x 6 6 jest: A, 4 0, B 4,0 C,0 4, D 0,4 Odpowiedź: C Rozwiąznie Sposób I Nierówność A 6 jest równowżn lterntywie
Zdnie PRÓBNA MATURA Z MATEMATYKI Z OPERONEM LISTOPAD 04 Zbiorem wszystkich rozwiązń nierówności x 6 6 jest: A, 4 0, B 4,0 C,0 4, D 0,4 Odpowiedź: C Rozwiąznie Sposób I Nierówność A 6 jest równowżn lterntywie
KONKURS MATEMATYCZNY dla uczniów gimnazjów w roku szkolnym 2012/13. Propozycja punktowania rozwiązań zadań
 KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
PRZEDMIOTOWY SYSTEM OCENIANIA Z JĘZYKÓW OBCYCH w Gimnazjum nr 2 im. ks. Stanisława Konarskiego nr 2 w Łukowie
 I. ZASADY OGÓLNE PRZEDMIOTOWY SYSTEM OCENIANIA Z JĘZYKÓW OBCYCH w Gimnzjum nr 2 im. ks. Stnisłw Konrskiego nr 2 w Łukowie 1. W Gimnzjum nr 2 w Łukowie nuczne są: język ngielski - etp educyjny III.1 język
I. ZASADY OGÓLNE PRZEDMIOTOWY SYSTEM OCENIANIA Z JĘZYKÓW OBCYCH w Gimnzjum nr 2 im. ks. Stnisłw Konrskiego nr 2 w Łukowie 1. W Gimnzjum nr 2 w Łukowie nuczne są: język ngielski - etp educyjny III.1 język
Badanie regularności w słowach
 Przypdek sekwencyjny Mrcin Piątkowski Wydził Mtemtyki i Informtyki Uniwersytet Mikołj Kopernik Edsger Wybe Dijkstr (1930 2002) Computer science is no more bout computers thn stronomy is bout telescopes,
Przypdek sekwencyjny Mrcin Piątkowski Wydził Mtemtyki i Informtyki Uniwersytet Mikołj Kopernik Edsger Wybe Dijkstr (1930 2002) Computer science is no more bout computers thn stronomy is bout telescopes,
Równania różniczkowe. y xy (1.1) x y (1.2) z xyz (1.3)
 ownn oznczkowe Równn óżnczkowe. Wstę Równne óżnczkow nzw ównne zwejące funkcje newdoe zenne nezleżne oz ocodne funkcj newdoc lu c óżnczk. Pzkłd d 5 d d sn d. d d e d d d. z z z z. ównne óżnczkowe zwczjne
ownn oznczkowe Równn óżnczkowe. Wstę Równne óżnczkow nzw ównne zwejące funkcje newdoe zenne nezleżne oz ocodne funkcj newdoc lu c óżnczk. Pzkłd d 5 d d sn d. d d e d d d. z z z z. ównne óżnczkowe zwczjne
Dobór zmiennych objaśniających do liniowego modelu ekonometrycznego
 Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Dobó zmiennych objaśniających do liniowego modelu ekonometycznego Wstępnym zadaniem pzy budowie modelu ekonometycznego jest okeślenie zmiennych objaśniających. Kyteium wybou powinna być meytoyczna znajomość
Wprowadzenie: Do czego służą wektory?
 Wprowdzenie: Do czego służą wektory? Mp połączeń smolotowych Isiget pokzuje skąd smoloty wyltują i dokąd doltują; pokzne jest to z pomocą strzłek strzłki te pokzują przemieszczenie: skąd dokąd jest dny
Wprowdzenie: Do czego służą wektory? Mp połączeń smolotowych Isiget pokzuje skąd smoloty wyltują i dokąd doltują; pokzne jest to z pomocą strzłek strzłki te pokzują przemieszczenie: skąd dokąd jest dny
REZONATORY DIELEKTRYCZNE
 REZONATORY DIELEKTRYCZNE Rezonato dielektyczny twozy małostatny, niemetalizowany dielektyk o dużej pzenikalności elektycznej ( > 0) i dobej stabilności tempeatuowej, zwykle w kształcie cylindycznych dysków
REZONATORY DIELEKTRYCZNE Rezonato dielektyczny twozy małostatny, niemetalizowany dielektyk o dużej pzenikalności elektycznej ( > 0) i dobej stabilności tempeatuowej, zwykle w kształcie cylindycznych dysków
Fundacja Widzialni strony internetowe bez barier. Audyt stron miast
 Wrszw, dni 30 mrc 2011 r. Fundcj Widzilni strony internetowe bez brier Audyt stron mist Od 1 mrc 2008r. do 21 kwietni 2008r. przeprowdziliśmy kolejny udyt serwisów dministrcji publicznej. Poddliśmy kontroli
Wrszw, dni 30 mrc 2011 r. Fundcj Widzilni strony internetowe bez brier Audyt stron mist Od 1 mrc 2008r. do 21 kwietni 2008r. przeprowdziliśmy kolejny udyt serwisów dministrcji publicznej. Poddliśmy kontroli
usuwa niewymierność z mianownika wyrażenia typu
 Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Modelowanie 3 D na podstawie fotografii amatorskich
 Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
F : R 0;1 rozkład prawdopodobieństwa stopy zwrotu.
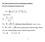 Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
Nie gaussowskie kyteia zaządzania potfelem Kyteia dominacji stochastycznej stopa zwotu C 0 C0 0, C ;, 0 t C C : R 0;1 ozkład pawdopodobieństwa stopy zwotu 0 U : R R funkcja użyteczności watości stopy zwotu
OPIS MODUŁU ZAJĘĆ/PRZEDMIOTU (SYLABUS) dla przedmiotu Sporządzanie umów na kierunku Zarządzanie i prawo w biznesie
 Ktedr Prw Cywilnego, Hndlowego i Ubezpieczeniowego Poznń, dni 15 pździernik 2018 r. OPIS MODUŁU ZAJĘĆ/PRZEDMIOTU (SYLABUS) dl przedmiotu Sporządznie umów n kierunku Zrządznie i prwo w biznesie I. Informcje
Ktedr Prw Cywilnego, Hndlowego i Ubezpieczeniowego Poznń, dni 15 pździernik 2018 r. OPIS MODUŁU ZAJĘĆ/PRZEDMIOTU (SYLABUS) dl przedmiotu Sporządznie umów n kierunku Zrządznie i prwo w biznesie I. Informcje
do Regulaminu przyznawania środków finansowych na rozwój przedsiębiorczości w projekcie Dojrzała przedsiębiorczość
 Projekt współfinnsowny przez Unię Europejską ze środków Europejskiego Funduszu Społecznego Złącznik nr do Regulminu przyznwni środków finnsowych n rozwój przedsięiorczości w projekcie Dojrzł przedsięiorczość
Projekt współfinnsowny przez Unię Europejską ze środków Europejskiego Funduszu Społecznego Złącznik nr do Regulminu przyznwni środków finnsowych n rozwój przedsięiorczości w projekcie Dojrzł przedsięiorczość


