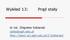
Ćwiczenie 403. Wyznaczanie prędkości dźwięku w powietrzu metodą rezonansu akustycznego. f [m/s] Wyznaczanie długości fali dźwiękowej o częstotliwości
|
|
|
- Józef Borkowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 azwsko... Imę.... Daa... r na lśce... Wydzał... Dzeń yg... Godzna... Ćwczene 403 Wyznaczane prędkośc dźwęku w powerzu meodą rezonansu akusycznego Wyznaczane długośc fal dźwękowej o częsolwośc f... Hz r pomaru Położene łoka podczas rezonansu L, [m] Długość fal 2, [m] L Średna długość fal:, [m] Uwaga: Pomar zerowy oznacza odczy podczas perwszego rezonansu. Oblczene prędkość dźwęku w powerzu Temperaura powerza T [K] Prędkość dźwęku w powerzu f [m/s] Teoreyczna warość prędkośc dźwęku 0 TT0 [m/s] Błąd względny wzgl. warośc eoreycznej Bp 100% [%] Błąd średn kwadraowy [m] Błąd względny z rachunku błędów 100% [%]
2 2 Ćwczene 403: Wyznaczane prędkośc dźwęku w powerzu meodą rezonansu akusycznego POTRZEBE WYPOSAŻEIE Termomer CEL Rura rezonansowa z generaorem Mernk unwersalny Dwa przewody elekryczne Celem ego ćwczena jes wyznaczene długośc fal dźwękowej. Do pomaru wykorzysamy zjawsko rezonansu akusycznego w rurze, w kórej rozchodz sę fala o określonej częsolwośc. Uzyskane dane pozwalają oblczyć prędkość dźwęku w powerzu. TEORIA Powsawane fal mechancznych Jeżel przemeścmy jakś fragmen ośrodka sprężysego z jego położena równowag, o będze on wykonywał drgana wokół ego położena. Te drgana, dzęk właścwoścom sprężysym ośrodka, są przekazywane na kolejne cząseczk ośrodka, kóre równeż zaczynają drgać. W en sposób zaburzene przechodz przez cały ośrodek. Ruchem falowym nazywamy rozchodzene sę zaburzena w ośrodku. Fale powsające rozchodzące sę w ośrodkach sprężysych nazywamy falam mechancznym. Fala dobegająca do danego punku ośrodka wprawa go w ruch drgający przekazując mu energę, kóra jes dosarczana przez źródło drgań. Energa fal o energa kneyczna poencjalna drgań cząsek ośrodka. Za pomocą fal można przekazywać energę na duże odległośc. Przenoszene energ bez przenoszena subsancj, czyl masy, nazywamy ransporem energ. Ze względu na kerunek drgań cząsek ośrodka względem kerunku rozchodzena sę fal rozróżnamy fale poprzeczne fale podłużne. Fala jes poprzeczna, gdy kerunek drgań cząsek ośrodka jes prosopadły do kerunku rozchodzena sę fal zarazem kerunku ransporu energ. Przykładem mogą u być drgana naprężonego sznura, kórego końcem poruszamy cyklczne w górę w dół. Fala jes podłużna, gdy kerunek drgań cząsek ośrodka jes równoległy do kerunku rozchodzena sę fal zarazem kerunku ransporu energ. Przykładem są u fale dźwękowe w powerzu. Falę charakeryzują nasępujące, podsawowe welkośc: Ampluda fal A jes równa bezwzględnej warośc maksymalnego przemeszczena elemenu ośrodka względem położena równowag; Faza fal określa warość przemeszczena w punkce x w czase ; Okres drgań T cząseczek ośrodka, przez, kóry przechodz fala jes o czas, w kórym cząseczka wykona jes jedno pełne drgane. Częsolwość fal f oznacza lczbę drgań elemenu ośrodka w jednosce czasu. Okres częsolwość zwązane są zależnoścą: f 1 T. Jednoską częsolwośc jes herc (Hz). Przy częsolwośc 1 Hz cząseczka wykonuje 1 drgane w czase 1 s. Drogę, jaką przebędze fala w czase jednego okresu drgańt nazywamy długoścą fal. Prędkość fal jes, węc równa: T f (1)
3 Prędkość fal jes równa loczynow długośc fal częsolwośc drgań. Gdy fala przejdze drogę, o cząseczka w punkce począkowym wykona 1 pełne drgane, węc będze w akej samej faze jak cząska, do kórej fala właśne doarła. y 0 3 y=a Zaem długość fal jes równa odległośc pomędzy najblższym punkam o jednakowym wychylenu kerunku ruchu. Fale dźwękowe Szczególnym rodzajem fal mechancznych są fale dźwękowe. Falą dźwękową nazywamy dowolną mechanczną falę podłużną. Wrażene dźwęku jes u człoweka wywołane przez fale o częsolwoścach meszczących sę w przedzale od 20 Hz do Hz. Zarówno górna jak dolna granca odberanych częsolwośc może być ndywdualną cechą człoweka. Falę dźwękową w powerzu sanową rozchodzące sę zaburzena polegające na cyklcznym zgęszczenu rozrzedzenu powerza (cyklcznej zmane cśnena gęsośc). Te obszary zagęszczena rozrzedzena przesuwają sę z prędkoścą dźwęku w pewnym kerunku, mogą wpaść do czyjegoś ucha wywołać w nm wrażene dźwęku. Dźwęk o częsolwośc wększej od 20 khz nazywamy ulradźwękam. Słyszą je nekóre zwerzęa jak psy (do 35 khz), neoperze (do 100 khz) delfny (200 khz). Dźwęk o częsolwoścach ponżej 20 Hz noszą nazwę nfradźwęków. Do kaegor nfradźwęków należą fale sejsmczne, rozchodzące sę we wnęrzu Zem. W sałych warunkach prędkośc dźwęku w różnych ośrodkach są w marę sablne określone. Prędkość dźwęku zależy od gęsośc ośrodka, jego własnośc sprężysych (w przypadku cał sałych), ścślwośc emperaury (w przypadku płynów). Prędkość dźwęku w powerzu zależy od emperaury (w kelwnach) według zależnośc: TT (2) 0 0 T, 0C gdze 0 331,5 m s prędkość dźwęku w powerzu w emperaurze 0 273,15 K Zmana emperaury powerza o 10C powoduje zmanę prędkośc dźwęku o około 6 m/s, (z emperaurą zmena sę gęsość powerza). Rezonans akusyczny Gdy membrana głośnka drga w poblżu rury, przy pewnych częsolwoścach dźwęku rura rezonuje w rurze powsaje wedy fala sojąca. Fala sojąca powsaje w rurze, gdy fala odba od końca rury nerferuje z falą wysyłaną ze źródła. Inerferencją fal nazywamy nakładane sę fal o ej samej częsolwośc, powodujące wzmocnene lub osłabene naężena fal wypadkowej. W rzeczywsośc fala dźwękowa w rurze ulega klkukronemu odbcu w ę z powroem pomędzy końcam rury. a ogół kolejno odbjane fale ne są zgodne w faze ampluda fal wypadkowej będze mała. Przy pewnych częsolwoścach drgań, wszyske odbe fale są zgodne w faze dają dużą ampludę fal sojącej. Te częsolwośc są zwane częsolwoścam rezonansowym przy ych częsolwoścach ma mejsce maksymalny ransfer energ pomędzy głośnkem rurą o danej długośc. A A x.
4 Sojąca fala dźwękowa w powerzu ma węzły srzałk. Węzłem w sojącej fal dźwękowej jes punk, w kórym prawe ne ma wbracj powerza. Srzałką jes punk, w kórym ruch powerza jes maksymalny. Odległośc mędzy kolejnym węzłam lub srzałkam są równe połowe długośc fal,. A 4 W S W S W S W fala padająca fala odba Fala sojąca jako wynk nerferencj fal padającej odbej. W węzeł, S srzałka. Odbce fal dźwękowej może zachodzć zarówno na owarych, jak zamknęych końcach rury. Jeżel konec rury jes zamknęy, cząseczk powerza ne mogą drgać poza płaszczyznę zamknęca przy końcu rury wysępuje węzeł. W przypadku odbca fal na końcu owarym, wysępuje am srzałka. Warunk dla rezonansu ławej zrozumeć posługując sę pojęcem długośc fal. Sformułujemy je dla rury zamknęej z jednego końca. Jeśl rura jes zamknęa z jednej srony (owara ylko po srone głośnka) rezonans wysępuje, gdy długość rury L jes równa neparzysej welokronośc ćwark długośc fal. x S S W W W Rura zamknęa: n =1 n = 3 L n ; n 1, 3, 5, 7,... 4 Dla rury zamknęej z jednej srony warunek rezonansowy na długość fal jes, węc nasępujący: 4L ; n 1, 3, 5, 7,... (3) n Korzysając z zależnośc (1) (3) możemy oblczyć, przy jakej długośc rury L wysąp rezonans dźwęku o danej częsolwośc f. Dla rury zamknęej jednosronne dosajemy: n L ; n 1, 3, 5, 7,... (4) 4 f Pomar długośc fal W ćwczenu badany będze rezonans dźwęku o sałej częsolwośc f w rurze zamknęej z jednego końca. Rura zamknęa jes łoczkem, kóry może być przesuwany wzdłuż rury. Odległość powerzchn czołowej łoczka od końca rury, przy kórym zamocowany jes głośnk, jes marą fakycznej długośc L rury rezonansowej. Gdy odległość a umożlwa powsane w rurze fal sojącej powsaje rezonans z rury dochodz dźwęk o dużym naężenu, co oznacza, że długośc L jes dokładne równa neparzysej welokronośc ćwark długośc fal. W marę oddalana łoczka od końca rury z głośnkem, zn. wydłużana odległośc L, rezonans zanka, a gdy przyros długośc rury jes równy połowe długośc fal, rezonans wysępuje ponowne: L n 2 4 f 4 2 ( n różnca sąsednch lczb neparzysych). Odczy dwóch sąsednch położeń łoczka (współrzędnych), przy kórych wysępuje rezonans umożlwa oblczene warośc połowy długośc fal dźwękowej rozchodzącej sę w rurze. S
5 5 Po wyznaczenu długośc fal z zależnośc (1) oblczamy prędkość dźwęku w powerzu w emperaurze pokojowej. WYKOAIE ĆWICZEIA Głośnk, podłączony do generaora częsolwośc akusycznych, wywołuje drgana powerza w rurze rezonansowej. Generaor sygnału może wyworzyć klka warośc częsolwośc napęca przekazywanego do głośnka. Mkrofon, zamonowany u wylou rury rezonansowej (obok głośnka), wywarza napęce sałe o warośc odpowadającej głośnośc dźwęku. Sygnał rejesrowany przez mkrofon może być odczyany na wolomerzu podłączonym do mkrofonu. Czynnośc pomarowe 1. Przysuń łoczek w rurze rezonansowej blsko generaora. 2. Podłącz kabel generaora częsolwośc do gnazdka napęca 230 V pokręłem częsolwośc wyberz jedną z sedmu możlwych warośc częsolwośc. 3. Mernk unwersalny usaw na pomar częsolwośc podłącz go do gnazd w generaorze oznaczonych Częsolwość, Hz. 4. Włącz generaor odczyaj oraz zapsz warość wybranej częsolwośc (w dalszej częśc ćwczena ne zmenaj już częsolwośc generaora). 5. Wyłącz generaor odłącz mulmer. 6. Przesaw pokręło mulmeru na pomar napęca sałego podłącz go do gnazd w generaorze oznaczonych Głośność, V DC. 7. Włącz ponowne generaor zacznj powol oddalać łoczek od głośnka. Gdy głośność dźwęku jes maksymalna usaw precyzyjne położne łoczka obserwując wskazana wolomerza. Maksymalna warość napęca oznacza dokładne położene rezonansowe (maksymalna warość napęca może być dla każdego rezonansu rochę nna). 8. Wpsz w abelę współrzędną położena łoczka (z dokładnoścą do 1mm). 9. Ponowne oddalaj łoczek usal współrzędną odpowadającą kolejnemu położenu rezonansowemu. Pomary powarzamy aż do uzyskana od pęcu do sześcu odczyów. 10. Wyłącz generaor mulmer, odczyaj zapsz emperaurę powerza. Analza danych 1. Oblcz różncę sąsednch odczyów L dla kolejnych rezonansów określ dla każdej różncy długośc fal: 2 L. 2. Oblcz średną długość fal prędkość dźwęku w powerzu, f. 3. Oblcz eoreyczną prędkość dźwęku na podsawe przyblżonego wzoru (2) opsującego zależność prędkośc dźwęku w powerzu od emperaury (emperaura w kelwnach!). 4. Oblcz błąd względny wyznaczonej warośc względem warośc eoreycznej : B p 100%.
6 6 Rachunek błędów. W ćwczenu mamy do czynena z pomarem powórzonym klkakrone. Oznaczmy kolejne wynk pomaru przez, gdze ndeks oznacza numer pomaru ( 1,..., ). Średna arymeyczna z wynków pomarów jes dobrym oszacowanem warośc długośc fal dźwękowej: Za marę nepewnośc pomarowej średnej arymeycznej warośc przyjmujemy błąd średn kwadraowy (zw. odchylene sandardowe warośc średnej): Uznajemy, że błąd wyznaczonej warośc wynos, co możemy zapsać w posac. Błąd względny wyznaczena prędkośc dźwęku w powerzu, oblczonej na podsawe wzoru f, jes równy sume błędu względnego błędu względnego pomaru częsolwośc f mernkem cyfrowym: f f. f f W przypadku mernków cyfrowych wykorzysywanych w ćwczenu należy przyjąć dokładność (błąd względny) pomaru częsolwośc równą 0,3 %. Wynk oblczeń błędu pomaru pownen być zaokrąglony w górę. a zakończene należy we wnoskach porównać błąd względny prędkośc dźwęku uzyskany z rachunku błędów z błędem względnym względem warośc eoreycznej.
Wyznaczanie współczynnika sztywności zastępczej układu sprężyn
 Wyznaczane zastępczej sprężyn Ćwczene nr 10 Wprowadzene W przypadku klku sprężyn ze sobą połączonych, można mu przypsać tzw. współczynnk zastępczej k z. W skrajnych przypadkach sprężyny mogą być ze sobą
Wyznaczane zastępczej sprężyn Ćwczene nr 10 Wprowadzene W przypadku klku sprężyn ze sobą połączonych, można mu przypsać tzw. współczynnk zastępczej k z. W skrajnych przypadkach sprężyny mogą być ze sobą
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ STOKESA
 WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ STOKESA. Ops teoretyczny do ćwczena zameszczony jest na strone www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE.. Ops układu pomarowego
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ STOKESA. Ops teoretyczny do ćwczena zameszczony jest na strone www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE.. Ops układu pomarowego
Wyznaczanie długości fali światła metodą pierścieni Newtona
 013 Katedra Fzyk SGGW Ćwczene 368 Nazwsko... Data... Nr na lśce... Imę... Wydzał... Dzeń tyg.... Ćwczene 368: Godzna.... Wyznaczane długośc fal śwatła metodą perścen Newtona Cechowane podzałk okularu pomarowego
013 Katedra Fzyk SGGW Ćwczene 368 Nazwsko... Data... Nr na lśce... Imę... Wydzał... Dzeń tyg.... Ćwczene 368: Godzna.... Wyznaczane długośc fal śwatła metodą perścen Newtona Cechowane podzałk okularu pomarowego
Ćwiczenie 133. Interferencja fal akustycznych - dudnienia. Wyznaczanie częstotliwości dudnień. Teoretyczna częstotliwość dudnienia dla danego pomiaru
 Kaedra Fizyki SGGW Nazwisko... Daa... Nr na liście... Imię... Wydział... Dzień yg.... Godzina... Ćwiczenie 33 Inererencja al akusycznych - dudnienia Tabela I. Wyznaczanie częsoliwości dudnień Pomiar Czas,
Kaedra Fizyki SGGW Nazwisko... Daa... Nr na liście... Imię... Wydział... Dzień yg.... Godzina... Ćwiczenie 33 Inererencja al akusycznych - dudnienia Tabela I. Wyznaczanie częsoliwości dudnień Pomiar Czas,
Prąd sinusoidalny. najogólniejszy prąd sinusoidalny ma postać. gdzie: wartości i(t) zmieniają się w czasie sinusoidalnie
 Opracował: mgr nż. Marcn Weczorek www.marwe.ne.pl Prąd snsodalny najogólnejszy prąd snsodalny ma posać ( ) m sn(2π α) gdze: warość chwlowa, m warość maksymalna (amplda), T okres, α ką fazowy. T m α m T
Opracował: mgr nż. Marcn Weczorek www.marwe.ne.pl Prąd snsodalny najogólnejszy prąd snsodalny ma posać ( ) m sn(2π α) gdze: warość chwlowa, m warość maksymalna (amplda), T okres, α ką fazowy. T m α m T
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Pomiary parametrów akustycznych wnętrz.
 Pomary parametrów akustycznych wnętrz. Ocena obektywna wnętrz pod względem akustycznym dokonywana jest na podstawe wartośc następujących parametrów: czasu pogłosu, wczesnego czasu pogłosu ED, wskaźnków
Pomary parametrów akustycznych wnętrz. Ocena obektywna wnętrz pod względem akustycznym dokonywana jest na podstawe wartośc następujących parametrów: czasu pogłosu, wczesnego czasu pogłosu ED, wskaźnków
PARAMETRY ELEKTRYCZNE CYFROWYCH ELEMENTÓW PÓŁPRZEWODNIKOWYCH
 ARAMETRY ELEKTRYZNE YFROWYH ELEMENTÓW ÓŁRZEWODNIKOWYH SZYBKOŚĆ DZIAŁANIA wyrażona maksymalną częsolwoścą racy max MO OBIERANA WSÓŁZYNNIK DOBROI D OBIĄŻALNOŚĆ ELEMENTÓW N MAKSYMALNA LIZBA WEJŚĆ M ODORNOŚĆ
ARAMETRY ELEKTRYZNE YFROWYH ELEMENTÓW ÓŁRZEWODNIKOWYH SZYBKOŚĆ DZIAŁANIA wyrażona maksymalną częsolwoścą racy max MO OBIERANA WSÓŁZYNNIK DOBROI D OBIĄŻALNOŚĆ ELEMENTÓW N MAKSYMALNA LIZBA WEJŚĆ M ODORNOŚĆ
Sprawozdanie powinno zawierać:
 Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
W tym module rozpoczniemy poznawanie właściwości fal powstających w ośrodkach sprężystych (takich jak fale dźwiękowe),
 Fale mechaniczne Autorzy: Zbigniew Kąkol, Bartek Wiendlocha Ruch falowy jest bardzo rozpowszechniony w przyrodzie. Na co dzień doświadczamy obecności fal dźwiękowych i fal świetlnych. Powszechnie też wykorzystujemy
Fale mechaniczne Autorzy: Zbigniew Kąkol, Bartek Wiendlocha Ruch falowy jest bardzo rozpowszechniony w przyrodzie. Na co dzień doświadczamy obecności fal dźwiękowych i fal świetlnych. Powszechnie też wykorzystujemy
Laboratorium Akustyki Architektonicznej Ćw. 4
 Laboratorum Akustyk Archtektoncznej Ćw. 4 POMARY ZOLACYJNOŚC AKUSTYCZNEJ PRZEGRODY BUDOWLANEJ. Cel ćwczena Celem ćwczena jest zapoznane sę z metodą pomaru zolacyjnośc akustycznej przegród budowlanych.
Laboratorum Akustyk Archtektoncznej Ćw. 4 POMARY ZOLACYJNOŚC AKUSTYCZNEJ PRZEGRODY BUDOWLANEJ. Cel ćwczena Celem ćwczena jest zapoznane sę z metodą pomaru zolacyjnośc akustycznej przegród budowlanych.
Pomiar mocy i energii
 Zakład Napędów Weloźródłowych Instytut Maszyn Roboczych CęŜkch PW Laboratorum Elektrotechnk Elektronk Ćwczene P3 - protokół Pomar mocy energ Data wykonana ćwczena... Zespół wykonujący ćwczene: Nazwsko
Zakład Napędów Weloźródłowych Instytut Maszyn Roboczych CęŜkch PW Laboratorum Elektrotechnk Elektronk Ćwczene P3 - protokół Pomar mocy energ Data wykonana ćwczena... Zespół wykonujący ćwczene: Nazwsko
RUCH OBROTOWY Można opisać ruch obrotowy ze stałym przyspieszeniem ε poprzez analogię do ruchu postępowego jednostajnie zmiennego.
 RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
Teoria niepewności pomiaru (Rachunek niepewności pomiaru) Rodzaje błędów pomiaru
 Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Fal podłużna. Polaryzacja fali podłużnej
 Fala dźwiękowa Podział fal Fala oznacza energię wypełniającą pewien obszar w przestrzeni. Wyróżniamy trzy główne rodzaje fal: Mechaniczne najbardziej znane, typowe przykłady to fale na wodzie czy fale
Fala dźwiękowa Podział fal Fala oznacza energię wypełniającą pewien obszar w przestrzeni. Wyróżniamy trzy główne rodzaje fal: Mechaniczne najbardziej znane, typowe przykłady to fale na wodzie czy fale
WYDZIAŁ EKOLOGII LABORATORIUM FIZYCZNE
 W S E i Z W WARSZAWIE WYDZIAŁ EKOLOGII LABORATORIUM FIZYCZNE Ćwiczenie Nr 2 Temat: WYZNACZNIE CZĘSTOŚCI DRGAŃ WIDEŁEK STROIKOWYCH METODĄ REZONANSU Warszawa 2009 1 WYZNACZANIE PRĘDKOŚCI DŹWIĘKU ZA POMOCĄ
W S E i Z W WARSZAWIE WYDZIAŁ EKOLOGII LABORATORIUM FIZYCZNE Ćwiczenie Nr 2 Temat: WYZNACZNIE CZĘSTOŚCI DRGAŃ WIDEŁEK STROIKOWYCH METODĄ REZONANSU Warszawa 2009 1 WYZNACZANIE PRĘDKOŚCI DŹWIĘKU ZA POMOCĄ
XXX OLIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne
 XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
LABORATORIUM PODSTAW ELEKTROTECHNIKI Badanie obwodów prądu sinusoidalnie zmiennego
 Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Część teoretyczna IZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD
 Część teoretyczna ZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD Energa dźwęku padającego na przegrodę będze częścowo odbta, częścowo pochłonęta, a ch stosunek będze zależał od stosunku mpedancj akustycznej materału
Część teoretyczna ZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD Energa dźwęku padającego na przegrodę będze częścowo odbta, częścowo pochłonęta, a ch stosunek będze zależał od stosunku mpedancj akustycznej materału
SPRAWDZANIE PRAWA MALUSA
 INSTYTUT ELEKTRONIKI I SYSTEMÓW STEROWANIA WYDZIAŁ ELEKTRYCZNY POLITECHNIKA CZĘSTOCHOWSKA LABORATORIUM FIZYKI ĆWICZENIE NR O- SPRAWDZANIE PRAWA MALUSA I. Zagadnena do przestudowana 1. Fala elektromagnetyczna,
INSTYTUT ELEKTRONIKI I SYSTEMÓW STEROWANIA WYDZIAŁ ELEKTRYCZNY POLITECHNIKA CZĘSTOCHOWSKA LABORATORIUM FIZYKI ĆWICZENIE NR O- SPRAWDZANIE PRAWA MALUSA I. Zagadnena do przestudowana 1. Fala elektromagnetyczna,
WYZNACZENIE CHARAKTERYSTYK DYNAMICZNYCH PRZETWORNIKÓW POMIAROWYCH
 Zakład Metrolog Systemów Pomarowych P o l t e c h n k a P o z n ańska ul. Jana Pawła II 6-965 POZNAŃ (budynek Centrum Mechatronk, Bomechank Nanonżyner) www.zmsp.mt.put.poznan.pl tel. +8 6 665 35 7 fa +8
Zakład Metrolog Systemów Pomarowych P o l t e c h n k a P o z n ańska ul. Jana Pawła II 6-965 POZNAŃ (budynek Centrum Mechatronk, Bomechank Nanonżyner) www.zmsp.mt.put.poznan.pl tel. +8 6 665 35 7 fa +8
Ćwiczenie nr 1 WAHADŁO MATEMATYCZNE Instrukcja dla studenta
 Analza nepewnośc pomarowych w eksperymentach fzycznych dla specjalnośc Bofzyka molekularna Ćwczene nr WAHADŁO MATEMATYCZE Instrukcja dla studenta I. WSTĘP Celem ćwczena jest ukazane początkującemu eksperymentatorow
Analza nepewnośc pomarowych w eksperymentach fzycznych dla specjalnośc Bofzyka molekularna Ćwczene nr WAHADŁO MATEMATYCZE Instrukcja dla studenta I. WSTĘP Celem ćwczena jest ukazane początkującemu eksperymentatorow
III. Przetwornice napięcia stałego
 III. Przewornce napęca sałego III.1. Wsęp Przewornce: dosarczane pożądanej warośc napęca sałego koszem energ ze źródła napęca G. Możlwość zmnejszana, zwększana, odwracana polaryzacj lb kszałowane pożądanego
III. Przewornce napęca sałego III.1. Wsęp Przewornce: dosarczane pożądanej warośc napęca sałego koszem energ ze źródła napęca G. Możlwość zmnejszana, zwększana, odwracana polaryzacj lb kszałowane pożądanego
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO
 I PRACOWNIA FIZYCZNA, INSYU FIZYKI UMK, ORUŃ Instrukca do ćwczena nr WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO 1. Cel ćwczena Celem ćwczena est poznane ruchu harmonczneo eo praw,
I PRACOWNIA FIZYCZNA, INSYU FIZYKI UMK, ORUŃ Instrukca do ćwczena nr WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO 1. Cel ćwczena Celem ćwczena est poznane ruchu harmonczneo eo praw,
3. ŁUK ELEKTRYCZNY PRĄDU STAŁEGO I PRZEMIENNEGO
 3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
Tensorowe. Wielkości fizyczne. Wielkości i Jednostki UŜywane w Elektryce Wielkość Fizyczna to właściwość fizyczna zjawisk lub obiektów,
 Welkośc Jednosk UŜywane w Elekryce Welkość Fzyczna o właścwość fzyczna zjawsk lub obeków, Przykłady: W. f.: kórą moŝna zmerzyć. czas, długość, naęŝene pola elekrycznego, przenkalność elekryczna kryszałów.
Welkośc Jednosk UŜywane w Elekryce Welkość Fzyczna o właścwość fzyczna zjawsk lub obeków, Przykłady: W. f.: kórą moŝna zmerzyć. czas, długość, naęŝene pola elekrycznego, przenkalność elekryczna kryszałów.
ĆWICZENIE 7 WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA. Wprowadzenie
 ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
Hipotezy o istotności oszacowao parametrów zmiennych objaśniających ˆ ) ˆ
 WERYFIKACJA HIPOTEZY O ISTOTNOŚCI OCEN PARAMETRÓW STRUKTURALNYCH MODELU Hpoezy o sonośc oszacowao paramerów zmennych objaśnających Tesowane sonośc paramerów zmennych objaśnających sprowadza sę do nasępującego
WERYFIKACJA HIPOTEZY O ISTOTNOŚCI OCEN PARAMETRÓW STRUKTURALNYCH MODELU Hpoezy o sonośc oszacowao paramerów zmennych objaśnających Tesowane sonośc paramerów zmennych objaśnających sprowadza sę do nasępującego
BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH
 INSTYTUT KLIMATYZACJI I OGRZEWNICTWA ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH 1. WSTĘP Stanowsko laboratoryjne pośwęcone badanu
INSTYTUT KLIMATYZACJI I OGRZEWNICTWA ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH 1. WSTĘP Stanowsko laboratoryjne pośwęcone badanu
Kwantowa natura promieniowania elektromagnetycznego
 Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
tor ruchu ruch prostoliniowy ruch krzywoliniowy
 KINEMATYKA Klasyfkacja ruchów Ruch jednosajny prosolnowy Ruch jednosajne zmenny Spadek swobodny Rzu ponowy w dół w órę Rzu pozomy rzu ukośny Ruch jednosajny po okręu Welkośc kąowe Polechnka Opolska Opole
KINEMATYKA Klasyfkacja ruchów Ruch jednosajny prosolnowy Ruch jednosajne zmenny Spadek swobodny Rzu ponowy w dół w órę Rzu pozomy rzu ukośny Ruch jednosajny po okręu Welkośc kąowe Polechnka Opolska Opole
5.1. Powstawanie i rozchodzenie się fal mechanicznych.
 5. Fale mechaniczne 5.1. Powstawanie i rozchodzenie się fal mechanicznych. Ruch falowy jest zjawiskiem bardzo rozpowszechnionym w przyrodzie. Spotkałeś się z pewnością w życiu codziennym z takimi pojęciami
5. Fale mechaniczne 5.1. Powstawanie i rozchodzenie się fal mechanicznych. Ruch falowy jest zjawiskiem bardzo rozpowszechnionym w przyrodzie. Spotkałeś się z pewnością w życiu codziennym z takimi pojęciami
Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE
 Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale mechaniczne i akustyczne
 Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
Kier. MTR Programowanie w MATLABie Laboratorium
 Ker. MTR Programowane w MATLABe Laboraorum Ćw. Zasosowane bbloecznych funkcj MATLABa do numerycznego rozwązywana równań różnczkowych. Wprowadzene Układy równań różnczkowych zwyczajnych perwszego rzędu
Ker. MTR Programowane w MATLABe Laboraorum Ćw. Zasosowane bbloecznych funkcj MATLABa do numerycznego rozwązywana równań różnczkowych. Wprowadzene Układy równań różnczkowych zwyczajnych perwszego rzędu
Teoria niepewności pomiaru (Rachunek niepewności pomiaru) Rodzaje błędów pomiaru
 Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
Projekt Inżynier mechanik zawód z przyszłością współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia wyrównawcze z izyki -Zestaw 13 -eoria Drgania i ale. Ruch drgający harmoniczny, równanie ali płaskiej, eekt Dopplera, ale stojące. Siła harmoniczna, ruch drgający harmoniczny Siłą harmoniczną (sprężystości)
Zajęcia wyrównawcze z izyki -Zestaw 13 -eoria Drgania i ale. Ruch drgający harmoniczny, równanie ali płaskiej, eekt Dopplera, ale stojące. Siła harmoniczna, ruch drgający harmoniczny Siłą harmoniczną (sprężystości)
± Δ. Podstawowe pojęcia procesu pomiarowego. x rzeczywiste. Określenie jakości poznania rzeczywistości
 Podstawowe pojęca procesu pomarowego kreślene jakośc poznana rzeczywstośc Δ zmerzone rzeczywste 17 9 Zalety stosowana elektrycznych przyrządów 1/ 1. możlwość budowy czujnków zamenających werne każdą welkość
Podstawowe pojęca procesu pomarowego kreślene jakośc poznana rzeczywstośc Δ zmerzone rzeczywste 17 9 Zalety stosowana elektrycznych przyrządów 1/ 1. możlwość budowy czujnków zamenających werne każdą welkość
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
XI Konferencja Naukowa WZEE Rzeszów - Czarna, wrzesień 2013 r.
 XI Konferencja Naukowa WZEE 203 Rzeszów - Czarna, 27-30 wrzeseń 203 r. XI Konferencja Naukowa WZEE 203 Rzeszów - Czarna, 27-30 wrzeseń 203 r. CYFROWE PRZEWARZANIE IMPULSOWEGO SYGNAŁU CZĘSOLIWOŚCIOWEGO
XI Konferencja Naukowa WZEE 203 Rzeszów - Czarna, 27-30 wrzeseń 203 r. XI Konferencja Naukowa WZEE 203 Rzeszów - Czarna, 27-30 wrzeseń 203 r. CYFROWE PRZEWARZANIE IMPULSOWEGO SYGNAŁU CZĘSOLIWOŚCIOWEGO
I. Elementy analizy matematycznej
 WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch
![Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch](/thumbs/25/5046464.jpg) Za: Stansław Latoś, Nwelacja trygonometryczna, [w:] Ćwczena z geodezj II [red.] J. eluch 6.1. Ogólne zasady nwelacj trygonometrycznej. Wprowadzene Nwelacja trygonometryczna, zwana równeż trygonometrycznym
Za: Stansław Latoś, Nwelacja trygonometryczna, [w:] Ćwczena z geodezj II [red.] J. eluch 6.1. Ogólne zasady nwelacj trygonometrycznej. Wprowadzene Nwelacja trygonometryczna, zwana równeż trygonometrycznym
STATYSTYCZNA ANALIZA WYNIKÓW POMIARÓW
 Zakład Metrolog Systemów Pomarowych P o l t e c h n k a P o z n ańska ul. Jana Pawła II 4 60-965 POZAŃ (budynek Centrum Mechatronk, Bomechank anonżyner) www.zmsp.mt.put.poznan.pl tel. +48 61 665 5 70 fax
Zakład Metrolog Systemów Pomarowych P o l t e c h n k a P o z n ańska ul. Jana Pawła II 4 60-965 POZAŃ (budynek Centrum Mechatronk, Bomechank anonżyner) www.zmsp.mt.put.poznan.pl tel. +48 61 665 5 70 fax
Przedmiotowy system nauczania z fizyki dla klasy II gimnazjum
 Przedmioowy sysem nauczania z fizyki dla klasy II gimnazjum 7. Przemiany energii w zjawiskach cieplnych 7.1. Energia wewnęrzna i jej zmiany przez wykonanie pracy 7.2. Cieplny przepływ energii. Rola izolacji
Przedmioowy sysem nauczania z fizyki dla klasy II gimnazjum 7. Przemiany energii w zjawiskach cieplnych 7.1. Energia wewnęrzna i jej zmiany przez wykonanie pracy 7.2. Cieplny przepływ energii. Rola izolacji
Wykład Turbina parowa kondensacyjna
 Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
AUTOMATYKA I STEROWANIE W CHŁODNICTWIE, KLIMATYZACJI I OGRZEWNICTWIE L3 STEROWANIE INWERTEROWYM URZĄDZENIEM CHŁODNICZYM W TRYBIE PD ORAZ PID
 ĆWICZENIE LABORAORYJNE AUOMAYKA I SEROWANIE W CHŁODNICWIE, KLIMAYZACJI I OGRZEWNICWIE L3 SEROWANIE INWEREROWYM URZĄDZENIEM CHŁODNICZYM W RYBIE PD ORAZ PID Wersja: 03-09-30 -- 3.. Cel ćwczena Celem ćwczena
ĆWICZENIE LABORAORYJNE AUOMAYKA I SEROWANIE W CHŁODNICWIE, KLIMAYZACJI I OGRZEWNICWIE L3 SEROWANIE INWEREROWYM URZĄDZENIEM CHŁODNICZYM W RYBIE PD ORAZ PID Wersja: 03-09-30 -- 3.. Cel ćwczena Celem ćwczena
Systemy Ochrony Powietrza Ćwiczenia Laboratoryjne
 ś POLITECHNIKA POZNAŃSKA INSTYTUT INŻYNIERII ŚRODOWISKA PROWADZĄCY: mgr nż. Łukasz Amanowcz Systemy Ochrony Powetrza Ćwczena Laboratoryjne 2 TEMAT ĆWICZENIA: Oznaczane lczbowego rozkładu lnowych projekcyjnych
ś POLITECHNIKA POZNAŃSKA INSTYTUT INŻYNIERII ŚRODOWISKA PROWADZĄCY: mgr nż. Łukasz Amanowcz Systemy Ochrony Powetrza Ćwczena Laboratoryjne 2 TEMAT ĆWICZENIA: Oznaczane lczbowego rozkładu lnowych projekcyjnych
Siła jest przyczyną przyspieszenia. Siła jest wektorem. Siła wypadkowa jest sumą wektorową działających sił.
 1 Sła jest przyczyną przyspeszena. Sła jest wektorem. Sła wypadkowa jest sumą wektorową dzałających sł. Sr Isaac Newton (164-177) Jeśl na cało ne dzała żadna sła lub sły dzałające równoważą sę, to cało
1 Sła jest przyczyną przyspeszena. Sła jest wektorem. Sła wypadkowa jest sumą wektorową dzałających sł. Sr Isaac Newton (164-177) Jeśl na cało ne dzała żadna sła lub sły dzałające równoważą sę, to cało
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne
 XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadane teoretyczne Rozwąż dowolne rzez sebe wybrane dwa sośród odanych nże zadań: ZADANIE T Nazwa zadana: Protony antyrotony A. Cząstk o mase równe mase rotonu, ale
XLI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadane teoretyczne Rozwąż dowolne rzez sebe wybrane dwa sośród odanych nże zadań: ZADANIE T Nazwa zadana: Protony antyrotony A. Cząstk o mase równe mase rotonu, ale
Pneumatyczne pomiary długości
 Wrocław, dna Metrologa Welkośc Geometrycznych Ćwczene Rok kerunek... Grupa (dzeń godzna rozpoczęca zajęć) Pneumatyczne pomary długośc A. Wyznaczene charakterystyk statycznej czujnka pneumatycznego. Identyfkacja
Wrocław, dna Metrologa Welkośc Geometrycznych Ćwczene Rok kerunek... Grupa (dzeń godzna rozpoczęca zajęć) Pneumatyczne pomary długośc A. Wyznaczene charakterystyk statycznej czujnka pneumatycznego. Identyfkacja
( 3 ) Kondensator o pojemności C naładowany do różnicy potencjałów U posiada ładunek: q = C U. ( 4 ) Eliminując U z równania (3) i (4) otrzymamy: =
 ROZŁADOWANIE KONDENSATORA I. el ćwiczenia: wyznaczenie zależności napięcia (i/lub prądu I ) rozładowania kondensaora w funkcji czasu : = (), wyznaczanie sałej czasowej τ =. II. Przyrządy: III. Lieraura:
ROZŁADOWANIE KONDENSATORA I. el ćwiczenia: wyznaczenie zależności napięcia (i/lub prądu I ) rozładowania kondensaora w funkcji czasu : = (), wyznaczanie sałej czasowej τ =. II. Przyrządy: III. Lieraura:
Fizyka dla Informatyki Stosowanej
 Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
dr inż. Zbigniew Szklarski
 Wykład 13: Prąd sały dr nż. Zbgnew Szklarsk szkla@agh.edu.pl hp://layer.uc.agh.edu.pl/z.szklarsk/ Prąd elekryczny naężene prądu C A s j ds gęsość prądu j S A m V u l S U W przewodnku o objęośc V S l znajduje
Wykład 13: Prąd sały dr nż. Zbgnew Szklarsk szkla@agh.edu.pl hp://layer.uc.agh.edu.pl/z.szklarsk/ Prąd elekryczny naężene prądu C A s j ds gęsość prądu j S A m V u l S U W przewodnku o objęośc V S l znajduje
Matematyka ubezpieczeń majątkowych r.
 Maemayka ubezpeczeń mająkowych 7.05.00 r. Zadane. Pewne ryzyko generuje jedną szkodę z prawdopodobeńswem q, zaś zero szkód z prawdopodobeńswem ( q). Ubezpeczycel pokrywa nadwyżkę szkody ponad udzał własny
Maemayka ubezpeczeń mająkowych 7.05.00 r. Zadane. Pewne ryzyko generuje jedną szkodę z prawdopodobeńswem q, zaś zero szkód z prawdopodobeńswem ( q). Ubezpeczycel pokrywa nadwyżkę szkody ponad udzał własny
1. Jeśli częstotliwość drgań ciała wynosi 10 Hz, to jego okres jest równy: 20 s, 10 s, 5 s, 0,1 s.
 1. Jeśli częstotliwość drgań ciała wynosi 10 Hz, to jego okres jest równy: 20 s, 10 s, 5 s, 0,1 s. 2. Dwie kulki, zawieszone na niciach o jednakowej długości, wychylono o niewielkie kąty tak, jak pokazuje
1. Jeśli częstotliwość drgań ciała wynosi 10 Hz, to jego okres jest równy: 20 s, 10 s, 5 s, 0,1 s. 2. Dwie kulki, zawieszone na niciach o jednakowej długości, wychylono o niewielkie kąty tak, jak pokazuje
Ćw. 5. Wyznaczanie współczynnika sprężystości przy pomocy wahadła sprężynowego
 5 KATEDRA FIZYKI STOSOWANEJ PRACOWNIA FIZYKI Ćw. 5. Wyznaczane współczynna sprężystośc przy pomocy wahadła sprężynowego Wprowadzene Ruch drgający należy do najbardzej rozpowszechnonych ruchów w przyrodze.
5 KATEDRA FIZYKI STOSOWANEJ PRACOWNIA FIZYKI Ćw. 5. Wyznaczane współczynna sprężystośc przy pomocy wahadła sprężynowego Wprowadzene Ruch drgający należy do najbardzej rozpowszechnonych ruchów w przyrodze.
Refraktometria. sin β sin β
 efraktometra Prędkość rozchodzena sę promen śwetlnych zależy od gęstośc optycznej ośrodka oraz od długośc fal promenena. Promene śwetlne padając pod pewnym kątem na płaszczyznę granczących ze sobą dwóch
efraktometra Prędkość rozchodzena sę promen śwetlnych zależy od gęstośc optycznej ośrodka oraz od długośc fal promenena. Promene śwetlne padając pod pewnym kątem na płaszczyznę granczących ze sobą dwóch
4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)
 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2)185 4.3 Wyznaczanie prędkości dźwięku w powietrzu metodą fali biegnącej(f2) Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu
Ćwiczenie 2. Parametry statyczne tranzystorów bipolarnych
 Ćwczene arametry statyczne tranzystorów bpolarnych el ćwczena odstawowym celem ćwczena jest poznane statycznych charakterystyk tranzystorów bpolarnych oraz metod dentyfkacj parametrów odpowadających m
Ćwczene arametry statyczne tranzystorów bpolarnych el ćwczena odstawowym celem ćwczena jest poznane statycznych charakterystyk tranzystorów bpolarnych oraz metod dentyfkacj parametrów odpowadających m
Praca domowa nr 1. Metodologia Fizyki. Grupa 1. Szacowanie wartości wielkości fizycznych Zad Stoisz na brzegu oceanu, pogoda jest idealna,
 Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORYJNE Z FIZYKI. SPRAWOZDANIE Z PRACY LABORATORYJNEJ nr 0. Badanie rozkładu rzutu śnieżkami do celu
 WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząca(y)... grupa... podgrupa... zespół... semestr roku akademckego... student(ka)... SPRAWOZDANIE
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząca(y)... grupa... podgrupa... zespół... semestr roku akademckego... student(ka)... SPRAWOZDANIE
Energia potencjalna jest energią zgromadzoną w układzie. Energia potencjalna może być zmieniona w inną formę energii (na przykład energię kinetyczną)
 1 Enega potencjalna jest enegą zgomadzoną w układze. Enega potencjalna może być zmenona w nną omę eneg (na pzykład enegę knetyczną) może być wykozystana do wykonana pacy. Sumę eneg potencjalnej knetycznej
1 Enega potencjalna jest enegą zgomadzoną w układze. Enega potencjalna może być zmenona w nną omę eneg (na pzykład enegę knetyczną) może być wykozystana do wykonana pacy. Sumę eneg potencjalnej knetycznej
Wykład FIZYKA I. 2. Kinematyka punktu materialnego. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORYJNE Z FIZYKI. SPRAWOZDANIE Z PRACY LABORATORYJNEJ nr 0. Badanie rozkładu rzutu śnieżkami do celu
 WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząc(a/y)... grupa... podgrupa... zespół... semestr... roku akademckego... student(ka)... SPRAWOZDANIE
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząc(a/y)... grupa... podgrupa... zespół... semestr... roku akademckego... student(ka)... SPRAWOZDANIE
W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące
 Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
1. Po upływie jakiego czasu ciało drgające ruchem harmonicznym o okresie T = 8 s przebędzie drogę równą: a) całej amplitudzie b) czterem amplitudom?
 1. Po upływie jakiego czasu ciało drgające ruchem harmonicznym o okresie T = 8 s przebędzie drogę równą: a) całej amplitudzie b) czterem amplitudom? 2. Ciało wykonujące drgania harmoniczne o amplitudzie
1. Po upływie jakiego czasu ciało drgające ruchem harmonicznym o okresie T = 8 s przebędzie drogę równą: a) całej amplitudzie b) czterem amplitudom? 2. Ciało wykonujące drgania harmoniczne o amplitudzie
DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH
 Franciszek SPYRA ZPBE Energopomiar Elekryka, Gliwice Marian URBAŃCZYK Insyu Fizyki Poliechnika Śląska, Gliwice DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH. Wsęp Zagadnienie poprawnego
Franciszek SPYRA ZPBE Energopomiar Elekryka, Gliwice Marian URBAŃCZYK Insyu Fizyki Poliechnika Śląska, Gliwice DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH. Wsęp Zagadnienie poprawnego
 Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwczena: BADANIE POPRAWNOŚCI OPISU STANU TERMICZNEGO POWIETRZA PRZEZ RÓWNANIE
INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwczena: BADANIE POPRAWNOŚCI OPISU STANU TERMICZNEGO POWIETRZA PRZEZ RÓWNANIE
Grupa: Elektrotechnika, wersja z dn Studia stacjonarne, II stopień, sem.1 Laboratorium Techniki Świetlnej
 ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, wersja z dn. 29.03.2016 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Badane parametrów fotometrycznych
ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, wersja z dn. 29.03.2016 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Badane parametrów fotometrycznych
Krzysztof Łapsa Wyznaczenie prędkości fal ultradźwiękowych metodami interferencyjnymi
 Krzysztof Łapsa Wyznaczenie prędkości fal ultradźwiękowych metodami interferencyjnymi Cele ćwiczenia Praktyczne zapoznanie się ze zjawiskiem interferencji fal akustycznych Wyznaczenie prędkości fal ultradźwiękowych
Krzysztof Łapsa Wyznaczenie prędkości fal ultradźwiękowych metodami interferencyjnymi Cele ćwiczenia Praktyczne zapoznanie się ze zjawiskiem interferencji fal akustycznych Wyznaczenie prędkości fal ultradźwiękowych
Podstawy elektrotechniki
 Wydzał Mechanczno-Energeyczny Podsawy elekroechnk Prof. dr hab. nż. Jlsz B. Gajewsk, prof. zw. PWr Wybrzeże S. Wyspańskego 7, 50-370 Wrocław Bd. A4 Sara kołowna, pokój 359 Tel.: 7 30 30 Fax: 7 38 38 E-al:
Wydzał Mechanczno-Energeyczny Podsawy elekroechnk Prof. dr hab. nż. Jlsz B. Gajewsk, prof. zw. PWr Wybrzeże S. Wyspańskego 7, 50-370 Wrocław Bd. A4 Sara kołowna, pokój 359 Tel.: 7 30 30 Fax: 7 38 38 E-al:
ELEKTROCHEMIA. ( i = i ) Wykład II b. Nadnapięcie Równanie Buttlera-Volmera Równania Tafela. Wykład II. Równowaga dynamiczna i prąd wymiany
 Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
Systemy nawigacji satelitarnej. Przemysław Bartczak
 Sysemy nawgacj saelarnej Przemysław Barczak Częsolwość nośna Wszyske saely GPS emują neprzerwane sygnały na dwóch częsolwoścach nośnych L1 L2 z pograncza mkrofalowych fal L S, kóre z punku wdzena nazemnego
Sysemy nawgacj saelarnej Przemysław Barczak Częsolwość nośna Wszyske saely GPS emują neprzerwane sygnały na dwóch częsolwoścach nośnych L1 L2 z pograncza mkrofalowych fal L S, kóre z punku wdzena nazemnego
W praktyce często zdarza się, że wyniki obu prób możemy traktować jako. wyniki pomiarów na tym samym elemencie populacji np.
 Wykład 7 Uwaga: W praktyce często zdarza sę, że wynk obu prób możemy traktować jako wynk pomarów na tym samym elemence populacj np. wynk x przed wynk y po operacj dla tego samego osobnka. Należy wówczas
Wykład 7 Uwaga: W praktyce często zdarza sę, że wynk obu prób możemy traktować jako wynk pomarów na tym samym elemence populacj np. wynk x przed wynk y po operacj dla tego samego osobnka. Należy wówczas
Drgania i fale sprężyste. 1/24
 Drgania i fale sprężyste. 1/24 Ruch drgający Każdy z tych ruchów: - Zachodzi tam i z powrotem po tym samym torze. - Powtarza się w równych odstępach czasu. 2/24 Ruch drgający W rzeczywistości: - Jest coraz
Drgania i fale sprężyste. 1/24 Ruch drgający Każdy z tych ruchów: - Zachodzi tam i z powrotem po tym samym torze. - Powtarza się w równych odstępach czasu. 2/24 Ruch drgający W rzeczywistości: - Jest coraz
) będą niezależnymi zmiennymi losowymi o tym samym rozkładzie normalnym z następującymi parametrami: nieznaną wartością 1 4
 Zadane. Nech ( X, Y ),( X, Y ), K,( X, Y n n ) będą nezależnym zmennym losowym o tym samym rozkładze normalnym z następującym parametram: neznaną wartoścą oczekwaną EX = EY = m, warancją VarX = VarY =
Zadane. Nech ( X, Y ),( X, Y ), K,( X, Y n n ) będą nezależnym zmennym losowym o tym samym rozkładze normalnym z następującym parametram: neznaną wartoścą oczekwaną EX = EY = m, warancją VarX = VarY =
Podstawy fizyki wykład 7
 Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
SCENARIUSZ LEKCJI Z FIZYKI DLA KLASY III GIMNAZJUM. Temat lekcji: Co wiemy o drganiach i falach mechanicznych powtórzenie wiadomości.
 SCENARIUSZ LEKCJI Z FIZYKI DLA KLASY III GIMNAZJUM Temat lekcji: Co wiemy o drganiach i falach mechanicznych powtórzenie wiadomości. Prowadzący: mgr Iwona Rucińska nauczyciel fizyki, INFORMACJE OGÓLNE
SCENARIUSZ LEKCJI Z FIZYKI DLA KLASY III GIMNAZJUM Temat lekcji: Co wiemy o drganiach i falach mechanicznych powtórzenie wiadomości. Prowadzący: mgr Iwona Rucińska nauczyciel fizyki, INFORMACJE OGÓLNE
termodynamika fenomenologiczna p, VT V, teoria kinetyczno-molekularna <v 2 > termodynamika statystyczna n(v) to jest długi czas, zachodzi
 fzka statstczna stan makroskopow układ - skończon obszar przestrzenn (w szczególnośc zolowan) termodnamka fenomenologczna p, VT V, teora knetczno-molekularna termodnamka statstczna n(v) stan makroskopow
fzka statstczna stan makroskopow układ - skończon obszar przestrzenn (w szczególnośc zolowan) termodnamka fenomenologczna p, VT V, teora knetczno-molekularna termodnamka statstczna n(v) stan makroskopow
Badanie efektu Dopplera metodą fali ultradźwiękowej
 Badanie efektu Dopplera metodą fali ultradźwiękowej Cele eksperymentu 1. Pomiar zmiany częstotliwości postrzeganej przez obserwatora w spoczynku w funkcji prędkości v źródła fali ultradźwiękowej. 2. Potwierdzenie
Badanie efektu Dopplera metodą fali ultradźwiękowej Cele eksperymentu 1. Pomiar zmiany częstotliwości postrzeganej przez obserwatora w spoczynku w funkcji prędkości v źródła fali ultradźwiękowej. 2. Potwierdzenie
Energia w ruchu harmonicznym
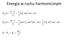 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Aby nie uszkodzić głowicy dźwiękowej, nie wolno stosować amplitudy większej niż 2000 mv.
 Tematy powiązane Fale poprzeczne i podłużne, długość fali, amplituda, częstotliwość, przesunięcie fazowe, interferencja, prędkość dźwięku w powietrzu, głośność, prawo Webera-Fechnera. Podstawy Jeśli fala
Tematy powiązane Fale poprzeczne i podłużne, długość fali, amplituda, częstotliwość, przesunięcie fazowe, interferencja, prędkość dźwięku w powietrzu, głośność, prawo Webera-Fechnera. Podstawy Jeśli fala
BADANIA OPERACYJNE. Podejmowanie decyzji w warunkach niepewności. dr Adam Sojda
 BADANIA OPERACYJNE Podejmowane decyzj w warunkach nepewnośc dr Adam Sojda Teora podejmowana decyzj gry z naturą Wynk dzałana zależy ne tylko od tego, jaką podejmujemy decyzję, ale równeż od tego, jak wystąp
BADANIA OPERACYJNE Podejmowane decyzj w warunkach nepewnośc dr Adam Sojda Teora podejmowana decyzj gry z naturą Wynk dzałana zależy ne tylko od tego, jaką podejmujemy decyzję, ale równeż od tego, jak wystąp
TRANZYSTOR BIPOLARNY CHARAKTERYSTYKI STATYCZNE
 POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
Układy sekwencyjne asynchroniczne Zadania projektowe
 Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
Studia stacjonarne, II stopień, sem.1 Laboratorium Techniki Świetlnej
 60-965 Poznań ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, Studa stacjonarne, II stopeń, sem.1 Laboratorum Technk Śwetlnej wersja z dn. 08.05.017 Ćwczene nr 6 Temat: Porównane parametrów
60-965 Poznań ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, Studa stacjonarne, II stopeń, sem.1 Laboratorum Technk Śwetlnej wersja z dn. 08.05.017 Ćwczene nr 6 Temat: Porównane parametrów
Ćwiczenie nr 25: Interferencja fal akustycznych
 Wydział PRACOWNIA FIZYCZNA WFiIS AGH Imię i nazwisko 1. 2. Temat: Rok Grupa Zespół Nr ćwiczenia Data wykonania Data oddania Zwrot do popr. Data oddania Data zaliczenia OCENA Ćwiczenie nr 25: Interferencja
Wydział PRACOWNIA FIZYCZNA WFiIS AGH Imię i nazwisko 1. 2. Temat: Rok Grupa Zespół Nr ćwiczenia Data wykonania Data oddania Zwrot do popr. Data oddania Data zaliczenia OCENA Ćwiczenie nr 25: Interferencja
WYZNACZANIE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ
 Grupa: Elektrotechnka, sem 3., wersja z dn. 14.1.015 Podstawy Technk Śwetlnej Laboratorum Ćwczene nr 5 Temat: WYZNACZANE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ Opracowane wykonano na podstawe następującej
Grupa: Elektrotechnka, sem 3., wersja z dn. 14.1.015 Podstawy Technk Śwetlnej Laboratorum Ćwczene nr 5 Temat: WYZNACZANE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ Opracowane wykonano na podstawe następującej
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego
 Katedra Chem Fzycznej Unwersytetu Łódzkego Wyznaczane współczynnka podzału Nernsta w układze: woda aceton chloroform metodą refraktometryczną opracowała dr hab. Małgorzata Jóźwak ćwczene nr 0 Zakres zagadneń
Katedra Chem Fzycznej Unwersytetu Łódzkego Wyznaczane współczynnka podzału Nernsta w układze: woda aceton chloroform metodą refraktometryczną opracowała dr hab. Małgorzata Jóźwak ćwczene nr 0 Zakres zagadneń
Stanisław Cichocki Natalia Nehrebecka. Wykład 2
 Sansław Cchock Naala Nehrebecka Wykład 2 1 1. Szereg czasowy 2. Sezonowość 3. Zmenne sacjonarne 4. Zmenne znegrowane 2 1. Szereg czasowy 2. Sezonowość 3. Zmenne sacjonarne 4. Zmenne znegrowane 3 Szereg
Sansław Cchock Naala Nehrebecka Wykład 2 1 1. Szereg czasowy 2. Sezonowość 3. Zmenne sacjonarne 4. Zmenne znegrowane 2 1. Szereg czasowy 2. Sezonowość 3. Zmenne sacjonarne 4. Zmenne znegrowane 3 Szereg
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Podstawowe algorytmy indeksów giełdowych
 Podsawowe algorymy ndeksów gełdowych Wersja 1.1 San na 25-11-13 Podsawowe algorymy ndeksów gełdowych Wersja 1.1 San na 2013-11-25 Sps reśc I. Algorymy oblczana warośc ndeksów gełdowych...3 1. Warość beżąca
Podsawowe algorymy ndeksów gełdowych Wersja 1.1 San na 25-11-13 Podsawowe algorymy ndeksów gełdowych Wersja 1.1 San na 2013-11-25 Sps reśc I. Algorymy oblczana warośc ndeksów gełdowych...3 1. Warość beżąca
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy
 Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
PRZEDMIOTOWY SYSTEM OCENIANIA Z FIZYKI WYMAGANIA EDUKACYJNE DLA UCZNIÓW KLAS I
 PRZEDMIOTOWY SYSTEM OCENIANIA Z FIZYKI WYMAGANIA EDUKACYJNE DLA UCZNIÓW KLAS I Wymagania konieczne ocena dopuszczająca wie że długość i odległość mierzymy w milimerach cenymerach merach lub kilomerach
PRZEDMIOTOWY SYSTEM OCENIANIA Z FIZYKI WYMAGANIA EDUKACYJNE DLA UCZNIÓW KLAS I Wymagania konieczne ocena dopuszczająca wie że długość i odległość mierzymy w milimerach cenymerach merach lub kilomerach
Laboratorium ochrony danych
 Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
