Układy z regulatorami P, PI oraz PID
|
|
|
- Arkadiusz Kucharski
- 6 lat temu
- Przeglądów:
Transkrypt
1 Układy z regulatorami P, PI oraz PID Sterowanie Procesami Ciągłymi 2016
2 Układ automatycznej regulacji y0( t) + _ ε () t ut () K R (s) yt () KO () s yt () y 0 (t) = 1(t)
3 Postulaty, kryteria oceny jakości regulacji stabilność wartość uchybu w stanie ustalonym ε ust = lim t ε(t) czas regulacji czas po którym zagwarantowane jest zredukowanie uchybu do 5% wartości początkowej t r : ε(t) ε ust δ, t t r, δ = 5% ε(0) ε ust, całka kwadratu uchybu Q = 0 ε 2 (t)dt
4 Postulaty, kryteria oceny jakości regulacji przeregulowanie κ = ε 2 ε %
5 Postulaty, kryteria oceny jakości regulacji szybkość regulacji rząd (numer) pierwszej niezerowej pochodnej λ UAR (t) na starcie, tzn. dla t = 0 zapas amplitudy i zapas fazy
6 Regulacja typu P Uchyb w stanie ustalonym K R (s) = k p K otw (s) = k p K O (s) = k p L O (s) M O (s) E (s) = 1 s K E (s) ε ust = lim t ε(t) = lim s 0 se (s) = np. K O (s) = 1 s + 1 K E (s) = K otw (s) k p K 0 (0) = 0 ε ust = k p
7 Regulacja typu P Oscylacje, kwestia stabilnośći, linie pierwiastkowe Przykład K O (s) = 1 (s + 1) 3, K otw (s) = k p (s + 1) 3, K UAR (s) = k p (s + 1) 3 + k p
8 Regulacja typu P Szybkość regulacji K 0 (s) = b ls l b 0 a m s m a 0 p = m l 0 b K otw (s) = l s l b 0 k p a m s m a 0 k p (b K UAR (s) = l s l b 0 ) a m s m a 0 + k p (b l s l b 0 ) lim t 0 λ(i) UAR (t) = lim s s si 1 s K UAR (s) Przykłady K O (s) = K O (s) = = 0, dla i = 0, 1,..., p 1 = 0, dla i = p 1 λ UAR (0) = 0, λ UAR (0) = 0 s (s + 1) 2 λ UAR (0) = 0, λ UAR (0) = 0, λ UAR (0) =
9 Regulacja typu I Uchyb w stanie ustalonym K R (s) = k i s K otw (s) = k i s K O (s) = k i s E (s) = 1 s K E (s) L O (s) M O (s) ε ust = lim t ε(t) = lim s 0 se (s) = K E (s) = k i s K 0(0) = K otw (s)
10 Regulacja typu I Szybkość regulacji K 0 (s) = b ls l b 0 a m s m p = m l a 0 K otw (s) = k i b l s l b 0 s a m s m a 0 k i (b K UAR (s) = l s l b 0 ) s (a m s m a 0 ) + k i (b l s l b 0 ) lim t 0 λ(i) UAR (t) = lim s s si 1 s K UAR (s) = 0, dla i = 0, 1,..., p = 0, dla i = p + 1 Przykład K O (s) = 1 s + 1 λ UAR (0) = 0, λ UAR (0) = 0, λ UAR (0) = 0
11 Regulacja typu I Przykład. Analityczna analiza wpływu wartości nastawy na kryterium całkowe a K O (s) = s + b, a, b > 0 K R (s) = k i s K otw (s) = k i a 1 (s + b) s K E (s) = = s s + b 1 + K otw (s) s 2 + bs + k i a s + b E (s) = s 2 + bs + k i a Q(k i ) = ε 2 (t)dt = k i a + b 2 0 2k i ab Q(k i ) = 2k i a 2 ( b 2ab ki a + b 2) k i (2k i ab) 2 = 2ab3 (2k i ab) 2 k i
12 Regulacja typu PI Uchyb w stanie ustalonym K R (s) = k p + k i s = k ps + k i s K otw (s) = k ps + k i s K E (s) = K otw (s) E (s) = 1 s K E (s) K O (s) = k ps + k i s ε ust = lim t ε(t) = lim s 0 se (s) = L O (s) M O (s) s s + (k p s + k i ) K 0 (0) = 0
13 Regulacja typu PI Szybkość regulacji K 0 (s) = b ls l b 0 a m s m p = m l a 0 K otw (s) = k ps + k i b l s l b 0 s a m s m a 0 (k p s + k i ) (b K UAR (s) = l s l b 0 ) s (a m s m a 0 ) + (k p s + k i ) (b l s l b 0 ) lim t 0 λ(i) UAR (t) = lim s s si 1 s K UAR (s) = 0, dla i = 0, 1,..., p 1 = 0, dla i = p
14 Regulacja typu PID Szybkość regulacji K R (s) = k p + k i s + k d s = k d s 2 + k p s + k i s K otw (s) = k d s 2 + k p s + k i b l s l b 0 s a m s m a ( 0 kd s 2 ) + k p s + k i (bl s l b 0 ) K UAR (s) = s (a m s m a 0 ) + (k d s 2 + k p s + k i ) (b l s l b 0 ) lim t 0 λ(i) UAR (t) = lim s s si 1 s K UAR (s) = 0, dla i = 0, 1,..., p 2 = 0, dla i = p 1
15 Podsumowanie ε ust... λ (p 1) (0) λ (p) (0) λ (p+1) (0) P = 0 0 = 0 I = 0 PI 0 0 = 0 PID 0 = 0
16 Pierwsza metoda Zieglera-Nicolsa Aproksymacja obiektu stabilnego Uwaga! Nie znamy K O (s), dokonujemy aproksymacji K (1) approx (s) = ke sτ T Z s + 1
17 Pierwsza metoda Zieglera-Nicolsa Aproksymacja obiektu całkującego K (2) approx (s) = ke sτ s
18 Pierwsza metoda Zieglera-Nicolsa Rekomendowane ustawienia Typ regulatora k p 1 k i k d P 1/a PI 0, 9/a 3τ PID 1, 2/a 2τ τ/2 Żuchowski A., Metoda doboru nastaw regulatora PID uwzgledniaj aca postulowany zapas stabilno sci modułu i fazy, Pomiary Automatyka Kontrola, str , Nr 1/2004.
19 Druga metoda Zieglera-Nicolsa Możliwa do zastosowania dla obiektów stabilnych wyższych rzędów Nie trzeba aproksymować Doprowadzamy UAR z regulatorem typu P do granicy stabilność (zwiększając k p ) Typ regulatora k p T i T d P 0, 5k P,kryt 0 PI 0, 45k P,kryt T osc /1, 2 0 PID 0, 6k P,kryt T osc /2 T osc /8
20 Metoda funkcji opisującej Przyblizona analiza układów z elementami nieliniowymi y(t) = a 0 + u(t) = A sin ωt k=0 (b k sin kωt + c k cos kωt), pierwsze harmoniczne y 1 (t) = b 1 sin ωt + c 1 cos ωt y(t) funkcja opisująca (transmitancja przybliżająca) J(s) = Y 1(s) U(s) = b 1 + jc 1. A
21 Przykładowe elementy nieliniowe Charakterystyka f (x) max {kx, B} { B, dla x 0 B, dla x < 0 0, dla x < a B, dla x a B, dla x < a Funkcja opisująca dla x(t) = A sin ωt ( ( J(A) = 2k π arcsin B Ak + B Ak 1 ( ) B 2 ) 1 ) 2 Ak J(A) = 4B πa ( J(A) = 4B πa 1 ( ) ) 1 a 2 2 A
22 Nadążność UAR y 0 (t) = A 0 + A 1 t + A 2 t A r t r K otw (s) = L otw(s) M otw (s) = L otw(s) s h N otw (s), lim t ε(t) = 0, gdy h > r lim t ε(t) = ε ust = 0, gdy h = r lim t ε(t) =, gdy h < r h rząd astatyzmu
23 Regulacja dyskretna
24 Realizacja regulatora PID w MATLAB
25 Realizacja regulatora PID w MATLAB Uwaga! K par PID (s) = k p + k i s + k d Ns s + N = k p + k i s + k d ( KPID ideal (s) = k p 1 + k i s + k Ns d s + N ) 1 1 N s + 1s
26 Sterowanie dyskretne układem z czasem ciągłym Ingerujemy w sterowanie jedynie w dyskretnych chwilach czasu t = 0, T, 2T, 3T,..., nt,... t = nt, n = 0, 1, 2... Okres dyskretyzacji (próbkowania) T jest z góry określony (znany) Nie mylić dyskretyzacji z kwantyzacją!!! Dwie koncepcje: x(nt ) R sterowanie impulsowe: w chwilach 0, T, 2T,... generujemy odpowiednio zmodulowane impulsy Diraca, a pomiędzy tymi chwilami sterowanie jest zerowe sterowanie odcinkami stałe: wartość sterowania u(nt ) obowiązuje aż do chwili t = (n + 1)T
27 Impulsator jeżeli wejściem impulsatora jest u(t) to jego wyjściem jest u (t) = u(nt )δ(t nt ) n=0 u (t) jest ciągiem modulowanych impulsów Diraca: u(0)δ(t), u(t )δ(t T ), u(2t )δ(t 2T ),...
28 Ekstrapolator jego wejściem jest ciąg impulsów Diraca u (t), a wyjściem funkcja u(t) odcinkami stała u(t) = u(nt ), dla t [nt, (n + 1)T ) U(s) = 1 s u(t) = u(nt ) [1(t nt ) 1(t (n + 1)T )] n=0 u(nt ) [e ] nst e (n+1)st = 1 e st n=0 s a ponieważ n=0 u(nt )e nst = U (s), to U(s) = 1 e st s U (s) u(nt )e nst n=0
29 Obiekt ciągły z dwoma impulsatorami synchronicznymi U() s U * () s Ks () Y() s Y * () s Oznaczmy y (t) = y(nt )δ(t nt ) n=0 u n = u(nt ) y n = y(nt ) Wyznaczamy transmitancję systemu (dyskretnego), który przekształca ciąg {u n } w ciąg {y n } y(t) = Y (s) = K (s)u (s), y(t) = t 0 k(t τ)u (τ)dτ n nt n u(it ) k(nt τ)δ(τ it )dτ = k ((n i)t ) u(it ) i=0 0 i=0
30 Obiekt ciągły z dwoma impulsatorami synchronicznymi System dyskretny ma zatem odpowiedź impulsową k n = k(nt ) i odpowiednio transmitancję dyskretną K (z) = Z {k(nt )} Schemat postępowania K (s) k(t) k(nt ) Z {k(nt )} = K (z)
31 Obiekt ciągły sterowany przez impulsator z ekstrapolatorem U() s U * () s E U() s Ks () Y() s Y * () s Y (s) = K (s)u(s) = H(s)U (s), gdzie H(s) = 1 e st K (s) s { } { } 1 1 L 1 {H(s)} = L 1 s K (s) L 1 s K (s)e st = λ(t) λ(t T ) po zastosowaniu reguły o splocie można pokazać, że y n = n (λ n i λ n 1 i ) u i i=0
32 Obiekt ciągły sterowany przez impulsator z ekstrapolatorem Odpowiadający system dyskretny ma zatem transmitancję K (z) = Z(λ n λ n 1 ) = Z(λ n ) z 1 Z(λ n ) = z 1 Z {λ(nt )} z Schemat postępowania 1 s z 1 K (s) λ(t) λ(nt ) Z {λ(nt )} = K (z) z
33 Przykład Wzmacniacz K (s) = c k(t) = cδ(t) k(nt ) = cδ(nt ) K (z) = cz {δ(nt )} = c λ(t) = c1(t) λ(nt ) = c K (z) = z 1 z cz {1 n } = c z 1 z z z 1 = c
34 Przykład Element całkujący K (s) = 1 s k(t) = 1(t) k(nt ) = 1 n K (z) = Z {1 n } = z z 1 λ(t) = t λ(nt ) = nt K (z) = z 1 z T Z {n} = z 1 T z z (z 1) 2 = T z 1
35 Przykład Obiekt inercyjny I-rzędu K (s) = 1 s+1 k(t) = e t k(nt ) = e nt K (z) = Z { e nt } = z z e T λ(t) = 1 e t λ(nt ) = 1 n ( e T ) n K (z) = z 1 z np. dla T = 1 mamy K (z) z ( ) z z 1 z z e T = 1 e T z e T
36 Wstęp de regulacji predykcyjnej i adaptacyjnej PROGRAMOWANIE NASTAW w(t) (tzw. zmienna wiodąca) y ( ) 0 t REGULATOR OBIEKT y(t) Adaptacja na podstawie zmiennej wiodącej
37 Wstęp de regulacji predykcyjnej i adaptacyjnej cel sterowania WYZNACZANIE OPTYMALNYCH NASTAW REGULATORA IDENTYFIKACJA OBIEKTU w(t) y ( ) 0 t REGULATOR OBIEKT y(t) Pośrednia regulacja adaptacyjna
38 Wstęp de regulacji predykcyjnej i adaptacyjnej cel sterowania IDENTYFIKACJA OPTYMALNYCH PARAMETRÓW REGULATORA w(t) y ( ) 0 t REGULATOR OBIEKT y(t) Bezpośrednia regulacja adaptacyjna
39 Identyfikacja Liniowy obiekt statyczny (1) (1) x (2) x * a z y a = a 1 a 2. a s ( s) x Figure: Liniowy obiekt statyczny typu MISO X N = x T 1 x T 2. x T N = Założenia: Ez = 0, varz < x (i), z niezależne x (1) 1 x (2) 1.. x (s) 1 x (1) 2 x (2) 2.. x (s) x (1) N x (2) N.. x (s) N
40 Identyfikacja Liniowy obiekt statyczny (2) y 1 y 2 Y N =., Z N = y N Równanie pomiarów Model Y N = X N a + Z N Y N (a) = X N a z 1 z 2. z N Istota metody najmniejszych kwadratów Y N Y N (a) 2 2 min a Równania normalne X T N X N a = X T N Y N Warunek jednoznaczności rozwiązania Estymator NK rankx N = s ( ) 1 â N = X T N X N X T N Y N = X + N Y N â N p.1 a, gdy N
41 Identyfikacja iniowy obiekt dynamiczny typu MA(s) (1) L ε k uk B( q 1 ) vk y k Figure: Model MA v k = b0u k bs u k s y k = v k + ε k y k = b0u k bs u k s + z k z k = ε k
42 Identyfikacja iniowy obiekt dynamiczny typu MA(s) (2) L u k uk 1 * b z k y k b = b 0 b 1. b s uk s Φ N = Figure: Model MA φ T 1 φ T 2. φ T N u 1 u 0.. u 1 s u 2 u 1.. u 2 s Założenia: Ez = 0, varz < {u k }, {z k } niezależne =.... u N u N 1.. u N s ( ) 1
43 Identyfikacja Liniowy obiekt dynamiczny typu ARMA(s,p) (1) 1 u B k ( q ) 1 Aq ( ) v k ε k y k Figure: Model ARMA v k = b0u k bs u k s + a1v k apv k p y k = v k + ε k y k = b0u k bs u k s + a1y k apy k p + z k z k = ε k a1ε k 1... apε k p
44 Identyfikacja Liniowy obiekt dynamiczny typu ARMA(s,p) (2) u k uk 1 uk s yk 1 yk p * θ z k y k θ = b 0 b 1. b s a 1 a 2. a p Figure: Model ARMA Ez = 0, varz < u k i, z k niezależne y k i, z k zależne, gdy {z k } jest procesem skorelowanym
45 Identyfikacja Liniowy obiekt dynamiczny typu ARMA(s,p) (3) φ T 1 φ T 2 Φ N =. = φ T N u 1 u 0 u 1 s y 0 y 1 y 1 p u 2 u 1 u 2 s y 1 y 0 y 2 p u N u N 1 u N s y N 1 y N 2 y N p ( ) 1 Y N = Φ N θ + Z N θ N = Φ T N Φ N Φ T N Y N
46 Wersja rekurencyjna θ k = θ k 1 + P k φ k (y k φ T k θ k 1 ) P k = P k 1 P k 1φ k φ T k P k φ T k P k 1φ k wszystkie pomiary {φ k, y k } mają takie same znaczenie (taką samą wagę) a co jeśli prawdziwe szukane θ zmienia się w czasie? "stare" pomiary są mniej godne zaufania
47 Śledzenie parametrów θ = arg min θ y k = θ + z k, N k=1 α k (y k θ) 2, (1) α k wagi reprezentujące stopień ważności pomiaru y k θ N k=1 α k (y k θ) 2 = 2 θ N k=1 α k = N k=1 N y k α k k=1 (θα k y k α k ), gdy α = const θ = N k=1 y k α k N k=1 α k, (2) to θ = α N k=1 y k Nα = 1 N N y k. k=1
48 Wagi, przykłady α k = λ N k, with 0 < λ < 1 (3) α k+1 = 1 λ α k. α k = k=1 α k = k=1 λ N k < { 1, as N n < k N 0, as k N n.
49 Strojenie θ (N ) n = 1 n N y k k=n n+1 w chwili N: skok parametru z wartości θ na θ + błąd średniokwadratowy horyzoncie H Q(n) = Hσ2 z n Hσ2 z n Q(n) = + 2 n n, N +H ( var θ (i) n i=n +1 n 1 j 2 = Hσ2 z j=1 n ) + bias 2 θ (i) n, + 2 n 2 n opt. = arg min Q(n) n ( ) n(n + 1)(2n + 1) n 2 6
50 Składniki kryterium jakości Q(n) 1,2 1 0,8 var ˆ ( k ) n 10 0,6 0,4 bias ˆ ( k ) n 10 bias ˆ ( k ) n 50 0, var ˆ ( k ) n k Figure:
51 Sumaryczny błąd w funkcji n (długości zapamiętywanej historii) Q n Figure:
52 Ilustracja działania 1,6 1,4 1, ,8 0,6 0, ,2 0-0, ,4-0,6 Figure:
Automatyka i robotyka ETP2005L. Laboratorium semestr zimowy
 Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
x x 1. Przedmiot identyfikacji System x (1) x (2) : x (s) a 1 a 2 : a s mierzone, a = zestaw współczynników konkretyzujacych F ()
 . Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
. Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
LINIOWE UKŁADY DYSKRETNE
 LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Automatyka i sterowanie w gazownictwie. Regulatory w układach regulacji
 Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Sterowanie optymalne
 Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
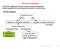 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
INTELIGENTNE SYSTEMY STEROWANIA OPRACOWANIE
 Arkadiusz Kwiatkowski INTELIGENTNE SYSTEMY STEROWANIA OPRACOWANIE Nie biorę odpowiedzialności za skutki błędów zawartych w opracowaniu. 1. Schemat inteligentnego sensora inteligentny sensor zintegrowany
Arkadiusz Kwiatkowski INTELIGENTNE SYSTEMY STEROWANIA OPRACOWANIE Nie biorę odpowiedzialności za skutki błędów zawartych w opracowaniu. 1. Schemat inteligentnego sensora inteligentny sensor zintegrowany
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa.
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Praktyka inżynierska korzystamy z tego co mamy. regulator. zespół wykonawczy. obiekt (model) Konfiguracja regulatora
 raktyka inżynierska korzystamy z tego co mamy Urządzenia realizujące: - blok funkcyjny D w sterowniku LC - moduł D w sterowniku LC - regulator wielofunkcyjny - prosty regulator cyfrowy zadajnik S e CV
raktyka inżynierska korzystamy z tego co mamy Urządzenia realizujące: - blok funkcyjny D w sterowniku LC - moduł D w sterowniku LC - regulator wielofunkcyjny - prosty regulator cyfrowy zadajnik S e CV
Automatyka i robotyka
 Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Inżynieria Systemów Dynamicznych (3)
 Inżynieria Systemów Dynamicznych (3) Charakterystyki podstawowych członów dynamicznych Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili?
Inżynieria Systemów Dynamicznych (3) Charakterystyki podstawowych członów dynamicznych Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili?
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ. T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
 REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
PAiTM. materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż.
 PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Systemy. Krzysztof Patan
 Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych
 XXXVIII MIĘDZYUCZELNIANIA KONFERENCJA METROLOGÓW MKM 06 Warszawa Białobrzegi, 4-6 września 2006 r. Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych Eligiusz PAWŁOWSKI Politechnika
XXXVIII MIĘDZYUCZELNIANIA KONFERENCJA METROLOGÓW MKM 06 Warszawa Białobrzegi, 4-6 września 2006 r. Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych Eligiusz PAWŁOWSKI Politechnika
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Właściwości sygnałów i splot. Krzysztof Patan
 Właściwości sygnałów i splot Krzysztof Patan Właściwości sygnałów Dla sygnału ciągłego x(t) można zdefiniować wielkości liczbowe charakteryzujące ten sygnał wartość średnia energia sygnału x sr = lim τ
Właściwości sygnałów i splot Krzysztof Patan Właściwości sygnałów Dla sygnału ciągłego x(t) można zdefiniować wielkości liczbowe charakteryzujące ten sygnał wartość średnia energia sygnału x sr = lim τ
Rok akademicki: 2016/2017 Kod: EEL s Punkty ECTS: 6. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Teoria sterowania i technika regulacji Rok akademicki: 2016/2017 Kod: EEL-1-406-s Punkty ECTS: 6 Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Elektrotechnika
Nazwa modułu: Teoria sterowania i technika regulacji Rok akademicki: 2016/2017 Kod: EEL-1-406-s Punkty ECTS: 6 Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Elektrotechnika
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
(Wszystkie wyniki zapisywać na dysku Dane E:)
 Cel ćwiczenia: Zapoznanie się z budową i zasadą działania PID oraz ocena jakości regulacji ciągłej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. UWAGA Temperatura mikrotermostatu
Cel ćwiczenia: Zapoznanie się z budową i zasadą działania PID oraz ocena jakości regulacji ciągłej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. UWAGA Temperatura mikrotermostatu
Spis treści. Dzień 1. I Elementy układu automatycznej regulacji (wersja 1109) II Rodzaje regulatorów i struktur regulacji (wersja 1109)
 Spis treści Dzień 1 I Elementy układu automatycznej regulacji (wersja 1109) I-3 Podstawowy problem sterowania I-4 Przykładowy obiekt regulacji I-5 Schemat blokowy układu automatycznej regulacji I-6 Klasyfikacja
Spis treści Dzień 1 I Elementy układu automatycznej regulacji (wersja 1109) I-3 Podstawowy problem sterowania I-4 Przykładowy obiekt regulacji I-5 Schemat blokowy układu automatycznej regulacji I-6 Klasyfikacja
Model Predictive Control
 Model Predictive Control podstawy Politechnika Gdańska Wydział Elektrotechniki i Automatyki Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania 2014/2015 1 Plan wykładu Część I:
Model Predictive Control podstawy Politechnika Gdańska Wydział Elektrotechniki i Automatyki Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania 2014/2015 1 Plan wykładu Część I:
AiR_TR2_5/9 Teoria Regulacji II Control Theory II. Automatyka i Robotyka I stopień ogólno akademicki studia niestacjonarne
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU AiR_TR2_5/9 Teoria Regulacji II Control Theory II Kod modułu Nazwa modułu Nazwa modułu w języku angielskim
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU AiR_TR2_5/9 Teoria Regulacji II Control Theory II Kod modułu Nazwa modułu Nazwa modułu w języku angielskim
analogowego regulatora PID doboru jego nastaw i przetransformowanie go na cyfrowy regulator PID, postępując według następujących podpunktów:
 Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Analiza Matematyczna część 5
 [wersja z 14 V 6] Analiza Matematyczna część 5 Konspekt wykładu dla studentów fizyki/informatyki Akademia Świętokrzyska 5/6 Wojciech Broniowski 1 Równania różniczkowe Definicje, klasyfikacja Równanie różniczkowe
[wersja z 14 V 6] Analiza Matematyczna część 5 Konspekt wykładu dla studentów fizyki/informatyki Akademia Świętokrzyska 5/6 Wojciech Broniowski 1 Równania różniczkowe Definicje, klasyfikacja Równanie różniczkowe
Automatyka i robotyka
 Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
Analityczne metody detekcji uszkodzeń
 Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Badanie wpływu parametrów korektora na własności dynamiczne układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Automatyzacji
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Badanie wpływu parametrów korektora na własności dynamiczne układu regulacji Ćwiczenia Laboratoryjne Podstawy Automatyki i Automatyzacji mgr inż.
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Badanie wpływu parametrów korektora na własności dynamiczne układu regulacji Ćwiczenia Laboratoryjne Podstawy Automatyki i Automatyzacji mgr inż.
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Inżynieria Systemów Dynamicznych (4)
 Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
#09. Systemy o złożonej strukturze
 #09 Systemy o złożonej strukturze system składa się z wielu elementów, obiekty (podsystemy) wchodzące w skład systemu są ze sobą połączone i wzajemnie od siebie zależne mogą wystąpić ograniczenia w dostępności
#09 Systemy o złożonej strukturze system składa się z wielu elementów, obiekty (podsystemy) wchodzące w skład systemu są ze sobą połączone i wzajemnie od siebie zależne mogą wystąpić ograniczenia w dostępności
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Podstawy Automatyki. wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak. Politechnika Wrocławska. Instytut Technologii Maszyn i Automatyzacji (I-24)
 Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie. Sterowanie ciągłe. Teoria sterowania układów jednowymiarowych
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Laboratorium Mechaniki Technicznej
 Laboratorium Mechaniki Technicznej Ćwiczenie nr 5 Badanie drgań liniowych układu o jednym stopniu swobody Katedra Automatyki, Biomechaniki i Mechatroniki 90-924 Łódź, ul. Stefanowskiego 1/15, budynek A22
Laboratorium Mechaniki Technicznej Ćwiczenie nr 5 Badanie drgań liniowych układu o jednym stopniu swobody Katedra Automatyki, Biomechaniki i Mechatroniki 90-924 Łódź, ul. Stefanowskiego 1/15, budynek A22
(Wszystkie wyniki zapisywać na dysku Dane E:)
 Cel ćwiczenia: Zapoznanie się z budową i zasadą działania PID oraz ocena jakości regulacji ciągłej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. UWAGA Temperatura mikrotermostatu
Cel ćwiczenia: Zapoznanie się z budową i zasadą działania PID oraz ocena jakości regulacji ciągłej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. UWAGA Temperatura mikrotermostatu
Opis systemów dynamicznych w przestrzeni stanu. Wojciech Kurek , Gdańsk
 Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Inżynieria Systemów Dynamicznych (5)
 Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Inżynieria Systemów Dynamicznych (5) Dokładność Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 DOKŁAD 2 Uchyb Podstawowy strukturalny
Podstawy Automatyki. Wykład 2 - matematyczne modelowanie układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - matematyczne modelowanie układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - matematyczne modelowanie układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
WYDZIAŁ PPT / KATEDRA INŻYNIERII BIOMEDYCZNE D-1 LABORATORIUM Z MIERNICTWA I AUTOMATYKI Ćwiczenie nr 10. Pomiary w warunkach dynamicznych.
 Cel ćwiczenia: Poznanie budowy i zasady działania oraz parametrów charakterystycznych dla stykowych czujników temperatury. Zapoznanie się z metodami pomiaru temperatur czujnikami stykowymi oraz sposobami
Cel ćwiczenia: Poznanie budowy i zasady działania oraz parametrów charakterystycznych dla stykowych czujników temperatury. Zapoznanie się z metodami pomiaru temperatur czujnikami stykowymi oraz sposobami
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego Dobór typu regulatora i jego nastaw w procesie syntezy układu regulacji automatycznej Ćwiczenia Laboratoryjne Podstawy Automatyki i Robotyki mgr
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie. Sterowanie ciągłe. Teoria sterowania układów jednowymiarowych
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Dobór parametrów regulatora - symulacja komputerowa. Najprostszy układ automatycznej regulacji można przedstawić za pomocą
 Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Laboratorium Metod i Algorytmów Sterowania Cyfrowego
 Laboratorium Metod i Algorytmów Sterowania Cyfrowego Ćwiczenie 3 Dobór nastaw cyfrowych regulatorów rzemysłowych PID I. Cel ćwiczenia 1. Poznanie zasad doboru nastaw cyfrowych regulatorów rzemysłowych..
Laboratorium Metod i Algorytmów Sterowania Cyfrowego Ćwiczenie 3 Dobór nastaw cyfrowych regulatorów rzemysłowych PID I. Cel ćwiczenia 1. Poznanie zasad doboru nastaw cyfrowych regulatorów rzemysłowych..
INTERPOLACJA I APROKSYMACJA FUNKCJI
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Wprowadzenie Na czym polega interpolacja? Interpolacja polega
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Wprowadzenie Na czym polega interpolacja? Interpolacja polega
Kompensacja wyprzedzająca i opóźniająca fazę. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Przetwarzanie sygnałów z czasem ciągłym
 Przetwarzanie sygnałów z czasem ciągłym Model systemowy układu p( t ) r ( t) wejście Układ wyjście p( t ) pobudzenie r ( t) reakcja Układ wykonuje pewną operację { i } na sygnale wejściowym p t (pobudzeniu),
Przetwarzanie sygnałów z czasem ciągłym Model systemowy układu p( t ) r ( t) wejście Układ wyjście p( t ) pobudzenie r ( t) reakcja Układ wykonuje pewną operację { i } na sygnale wejściowym p t (pobudzeniu),
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Plan wykładu. Własności statyczne i dynamiczne elementów automatyki:
 Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena LABORATORIUM 4. PODSTAW 5. AUTOMATYKI
 Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Akwizycja i przetwarzanie sygnałów cyfrowych
 Akwizycja i przetwarzanie sygnałów cyfrowych Instytut Teleinformatyki ITI PK Kraków 21 luty 2011 Plan na dziś 1 Przedstawienie przedmiotu i zakresu wykładu polecanej iteratury zasad zaliczenia 2 Wyklad
Akwizycja i przetwarzanie sygnałów cyfrowych Instytut Teleinformatyki ITI PK Kraków 21 luty 2011 Plan na dziś 1 Przedstawienie przedmiotu i zakresu wykładu polecanej iteratury zasad zaliczenia 2 Wyklad
Modelowanie wybranych. urządzeń mechatronicznych
 Modelowanie wybranych elementów torów pomiarowych urządzeń mechatronicznych Pomiary - element sterowania napędem mechatronicznym Układ napędowy - Zintegrowane czujniki Zewnetrzne sygnały sterujące Sprzężenia
Modelowanie wybranych elementów torów pomiarowych urządzeń mechatronicznych Pomiary - element sterowania napędem mechatronicznym Układ napędowy - Zintegrowane czujniki Zewnetrzne sygnały sterujące Sprzężenia
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów
 Laboratorium Metod Optymalizacji 216 Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów 1. Za pomocą funkcji lsqcurvefit dobrać parametry a i b funkcji: Posiadając następujące dane pomiarowe:
Laboratorium Metod Optymalizacji 216 Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów 1. Za pomocą funkcji lsqcurvefit dobrać parametry a i b funkcji: Posiadając następujące dane pomiarowe:
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
ZAJĘCIA VII. Zastosowanie estymatora LS do identyfikacji obiektów dynamicznych
 ZAJĘCIA VII Zastosowanie estymatora LS do identyfikacji obiektów dynamicznych Równanie różniczkowe a metoda LS Czas dyskretny a czas ciągły Obciążenie estymatora LS w przypadku dynamicznym Estymacja parametrów
ZAJĘCIA VII Zastosowanie estymatora LS do identyfikacji obiektów dynamicznych Równanie różniczkowe a metoda LS Czas dyskretny a czas ciągły Obciążenie estymatora LS w przypadku dynamicznym Estymacja parametrów
Rys. 1 Otwarty układ regulacji
 Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
Podstawy Automatyki. Wykład 3 - Charakterystyki częstotliwościowe, podstawowe człony dynamiczne. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 3 -, podstawowe człony dynamiczne Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp określają zachowanie się elementu (układu) pod wpływem ciągłych sinusoidalnych sygnałów wejściowych. W analizie
Wykład 3 -, podstawowe człony dynamiczne Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp określają zachowanie się elementu (układu) pod wpływem ciągłych sinusoidalnych sygnałów wejściowych. W analizie
