Stabilność. Krzysztof Patan
|
|
|
- Janina Urban
- 10 lat temu
- Przeglądów:
Transkrypt
1 Stabilność Krzysztof Patan
2 Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu jakiegoś czasu obiekt znowu znajdzie się w położeniu początkowym to mówimy, że jest stabilny Jeżeli obiekt nie powraca do stanu początkowego mówimy o obiekcie niestabilnym (a) (b) F F
3 Warunki stabilności systemów czasu ciągłego System liniowy ciągły będziemy nazywali stabilnym ze względu na wymuszenie, jeżeli dowolny ograniczony sygnał wejściowy sup x(t) η n [o, ) powoduje powstanie ograniczonego sygnału wyjściowego sup y(t) η n [o, ) Stabilność systemu ciągłego Warunkiem koniecznym i dostatecznym na to, aby przyczynowy system czasu ciągłego był stabilny jest, aby wszystkie bieguny jego transmitancji H(s) leżały w lewej półpłaszczyźnie zmiennej zespolonej s (Re(s) < 0), a stopień licznika transmitancji był nie większy od stopnia mianownika
4 Kryterium Hurwitza W roku 1895 Adolf Hurwitz podał warunki jakie musi spełniać wielomian, aby jego pierwiastki leżały w lewej półpłaszczyźnie zmiennej zespolonej s Rozpatrzmy wielomian a m s m + a m 1 s m a 1 s + a 0, a m > 0. (1) Wielomian (1) nazywamy wielomianem Hurwitza, albo wielomianem stabilnym, jeśli jego pierwiastki leżą w lewej półpłaszczyźnie zmiennej zespolonej s Tw.1. Warunek konieczny stabilności Jeżeli wielomian (1) jest wielomianem Hurwitza, to wszystkie jego współczynniki są dodatnie, tzn a j > 0, j = 1, 2,..., m
5 Twierdzenie 1 pozwala proste wskazanie, który wielomian nie jest wielomianem Hurwitza Przykład 1 Sprawadzić które z podanych wielomianów to wielomiany Hurwitza (a) s 2 s + 1, (b) s 2 + 1, (c) s 3 + s 2 + 4s + 30 Przykład 2 Wyznaczyć bieguny wielomianu s 3 + s 2 + 4s + 30 Twierdzenie 1 określa warunek konieczny, ale jak pokazuje przykład 2 nie jest to warunek dostateczny Należy podać mocniejsze twierdzenie podające warunki konieczny i dostateczny stabilności
6 Zdefiniujmy macierz Hurwitza a m 1 a m a m 3 a m 2 am 1 a m... H m = a m 5 a m 4 am 3 a m a 0 (2) Wprowadźmy minory główne 1 = a m 1, 2 = 3 = a m 1 a m 0 a m 3 a m 2 a m 1 a m 5 a m 4 a m 3 a m 1 a m 3 a m a m 2, m = det(h m )
7 Tw.2. Warunek stabilności Hurwitza Wielomian (1) jest wielomianem stabilnym wtedy i tylko wtedy, gdy wszystkie jego minory główne są dodatnie, tzn. 1 > 0, 2 > 0,..., m > 0 stosowanie twierdzenia 2 wymaga obliczenia m 1 wyznaczników można złagodzić wymagania obliczeniowe stosując modyfikację twierdzenia Hurwitza modyfikacja nosi nazwę twierdzenia Hurwitza-Lienarda
8 Przykład 3 Za pomocą kryterium Hurwitza sprawdzić stabilność wielomianu z przykładu 2 Wielomian s 3 + s 2 + 4s + 30 ma wszystkie współczynniki dodatnie Obliczamy wyznaczniki 1 = 1 > = = = 26 < System jest niestabilny Wynik można zweryfikować z wynikami uzyskanymi w przykładzie 2
9 Przykład 3 Za pomocą kryterium Hurwitza sprawdzić stabilność wielomianu s 4 + 2s 3 + ks 2 + 4s + 5 współczynniki powinny być dodatnie, więc k > 0 Obliczamy wyznaczniki 1 = 2 > = 4 k = 2k 4 > 0 k > = 4 k 2 = 8k 36 > 0 k > 4,
10 Kryterium Routha Klasyczne kryterium Hurwitza wymaga obliczania m 1 wyznaczników stopnia od 1 do m 1 włącznie Obliczenie wartości wyznacznika stopnia k-tego wymaga nakładu obliczeniowego rzędu k 2 Kryterium Hurwitza jest niedogodne dla większych wartości m (dla wielomianów wysokiego stopnia) Wymienionych wyżej wad nie posiada kryterium Routha, które wymaga sprawdzenia większej liczby wyznaczników, ale wyłącznie stopnia drugiego Aby zabadać stabilność systemu metodą Routha należy skonstruować tzw. tablicę Routha
11 Tablica Routha gdzie b m 2 = a m 1a m 2 a ma m 3 a m 1 a m a m 2 a m 4... a m 1 a m 3 a m 5... b m 2 b m 4 b m 6... c m 3 c m 5 c m d 2 d e f c m 3 = b m 2a m 3 a m 1 b m 4 b m 2 b m 4 = a m 1a m 4 a ma m 5 a m 1 b m 6 = a m 1a m 6 a ma m 7 a m 1 c m 5 = b m 2a m 5 a m 1 b m 6 b m 2 c m 7 = b m 2a m 7 a m 1 b m 8 b m 2
12 Liczba wierszy tablicy jest równa m + 1, liczba kolumn jest równa m m (dla m parzystego) lub 2 (dla m nieparzystego) Łatwo zauważyć, że liczniki wyrażeń c i d i itd. są wyznacznikami drugiego stopnia ze znakiem minus Kolejne elementy tablicy Routha są wyliczane w sposób analogiczny Wartość ostatniego niezerowego elementu każdej kolumny jest równa a 0 (sposób na sprawdzenie poprawności obliczeń) Tw. 3. Kryterium Routha Wielomian (1) jest stabilny wtedy i tylko wtedy, gdy wszystkie elementy pierwszej kolumny tablicy Routha tego wielomianu są dodatnie, tzn. a m > 0, a m 1 > 0, b m 2 > 0, c m 3 > 0,..., e 1 > 0, f 0 > 0
13 Przykład 4 Sprawdzić stabilność wielomianu s 3 + s 2 + 4s + 30 Tablica Routha ma 4 wiersze i 2 kolumny a 3 a 1 a 2 a 0 b 1 0 c 0 0 Ostatecznie b 1 0 c 0 0 System jest niestabilny b 1 = a 2a 1 a 3 a 0 a 2 = = 26 c 0 = b b 1 =
14 Przykład 4 Sprawdzić stabilność wielomianu s 3 + s 2 + 4s + 30 Tablica Routha ma 4 wiersze i 2 kolumny a 3 a 1 a 2 a 0 b 1 0 c 0 0 Ostatecznie b 1 0 c 0 0 System jest niestabilny b 1 = a 2a 1 a 3 a 0 a 2 = = 26 c 0 = b b 1 =
15 Przykład 4 Sprawdzić stabilność wielomianu s 3 + s 2 + 4s + 30 Tablica Routha ma 4 wiersze i 2 kolumny a 3 a 1 a 2 a 0 b 1 0 c 0 0 Ostatecznie b 1 0 c 0 0 System jest niestabilny b 1 = a 2a 1 a 3 a 0 a 2 = = 26 c 0 = b b 1 =
16 Przykład 4 Sprawdzić stabilność wielomianu s 3 + s 2 + 4s + 30 Tablica Routha ma 4 wiersze i 2 kolumny a 3 a 1 a 2 a 0 b 1 0 c 0 0 Ostatecznie b 1 0 c 0 0 System jest niestabilny b 1 = a 2a 1 a 3 a 0 a 2 = = 26 c 0 = b b 1 =
17 Kryterium Nyquista Kryterium Nyquista należy do grupy kryteriów częstotliwościowych Jest stosowane do systemów ze sprzężeniem zwrotnym Kryterium Hurwitza czy Routha wymaga znajomości postaci analitycznej wielomianu mianownika transmitancji Kryterium Nyquista oferuje większe możliwości, gdyż wymaga znajomości odpowiednich charakterystyk częstotliwościowych, które można zmierzyć Kryterium Nyquista pozwala na sprawdzenie stabilności układu zamkniętego na podstawie badania układu otwartego W przypadku otwarcia pętli sprzężenia zwrotnego transmitancja zastępcza przyjmuje postać H 0 (s) = H 1 (s)h 2 (s)
18 Tw. 4. Kryterium Nyquista System czasu ciągłego z ujemnym sprzężeniem zwrotnym jest stabilny wtedy i tylko wtedy, gdy wykres charakterystyki amplitudowo-fazowej (charakterystyki Nyquista) systemu otwartego H 0 (jω), ω (, ) okrąża punkt s = ( 1, j0) dokładnie m razy w kierunku przeciwnym do ruchu wskazówek zegara, gdzie m jest liczbą biegunów funkcji H 0 (s) położonych w prawej półpłaszczyźnie Re(s) > 0 Badanie układu zamkniętego metodą Nyquista, w przypadku gdy układ otwarty jest niestabilny jest niepraktyczne Wymagane jest ustalenie liczby biegunów niestabilnych Można to ustalić na drodze analitycznej przy znajomości transmitancji układu Ale w takich przypadkach wygodniej jest użyć kryterium Hurwitza lub Routha
19 Najważniejszym przypadkiem z praktycznego punktu widzenia jest sytuacja, gdy układ otwarty jest stabilny W takim przypadku kryterium Nyquista przybiera postać Tw. 5. Kryterium Nyquista Gdy system otwarty jest stabilny (m = 0) to system ze sprzężeniem zwrotnym jest stabilny wtedy i tylko wtedy, gdy wykres Nyquista nie zawiera punktu s = ( 1, j0)
20 Przykład 5 Zbadać stabilność układu zamkniętego o transmitancji G z (s) = za pomocą kryterium Nyquista. G 1 (s) 1+G 1 (s)g 2 (s) G 1 (s) = 10 3s 3 + 2s 2 + s + 1 G 2 (s) = 1, 9s + 1 Transmitancja układu otwartego G o (s) = 10(1, 9s + 1) 3s 3 + 2s 2 + s + 1 Układ otwarty jest niestabilny: s 1 = 0, 7839, s 2 = 0, j0.6495, s 3 = 0, 0586 j0.6495
21 Nyquist Diagram Imaginary Axis Real Axis
22 Przykład 6 Zbadać stabilność układu zamkniętego na podstawie transmitancji układu otwartego postaci G o (s) = 1 s 3 + 2s 2 + s + 1 Układ otwarty jest stabilny: s 1 = 1, 7549, s 2 = 0, j0.7449, s 3 = 0, 1226 j0.7449
23 Nyquist Diagram Imaginary Axis Real Axis
24 Zapas stabilności Kryterium Nyquista opiera się o zasadę przyrostu fazy Cauchy ego, która analizuje funkcję X(s) poprzez obieganie bieguna s względem środka układu współrzędnych Kryterium Nyquista analizuje stabilność układu zamkniętego postaci: G z (s) = G 1(s) 1 + G o (s) czyli analizowana jest transmitancja X(s) = 1 + G o (s) Jeżeli analizujemy układ poprzez rozważanie układu otwartego, więc G o = X(s) 1 i środek układu współrzędnych przesuwany jest do punktu s = ( 1, j0) W punkcie s = ( 1, j0) moduł amplitudy M = 1 i przesunięcie fazowe ϕ = 180 o
25 Interpretacja zapasu stabilności charakterystyka Nyquista Nyquist Diagram Imaginary Axis ϕ M d Real Axis zapas wzmocnienia k = 1 d, zapas modułu λ = 20 log k
26 Interpretacja zapasu stabilności charakterystyki Bodego Bode Diagram Gm = 4.44 db (at 1.73 rad/sec), Pm = 33.4 deg (at 1.32 rad/sec) 50 Magnitude (db) Phase (deg) Frequency (rad/sec)
27 Interpretacja zapasu stabilności charakterystyka Nicholsa Nichols Chart 20 0 λ ϕ Open Loop Gain (db) Open Loop Phase (deg)
28 Warunki stabilności dla układów dyskretnych System liniowy dyskretny będziemy nazywali stabilnym ze względu na wymuszenie, jeżeli dowolny ograniczony sygnał wejściowy sup x[n] η n [o, ) powoduje powstanie ograniczonego sygnału wyjściowego sup y[n] η n [o, ) Stabilność systemu dyskretnego Warunkiem koniecznym i dostatecznym stabilności przyczynowego systemu czasu dyskretnego jest, aby wszystkie bieguny z i, i = 1,..., m jego transmitancji H(z) leżały wewnątrz koła jednostkowego, tzn. z i < 1, i, 1,..., m
29 Kryterium Jury Do zbadania stabilności systemu dyskretnego potrzebna jest informacja czy wszystkie bieguny leżą wewnątrz koła jednostkowego Wielomian a 0 z m + a 1 z m a m 1 z + a m (3) o współczynnikach rzeczywistych nazywamy wielomianem Schura, jeśli wszystkie jego pierwiastki mają moduł mniejszy od jedności Tw. 5. Warunek konieczny stabilności systemu dyskretnego Jeżeli wielomian (3) w postaci znormalizowanej (a 0 = 1) jest wielomianem Schura, to jego współczynniki spełniają następujące nierówności ( ) m a j <, j = 1, 2,..., m j
30 Przykład 6 Zbadać warunki konieczne dla wielomianu z 4 + a 1 z 3 + a 2 z 2 + a 3 z + a 4 Aby wielomian W (z) był wielomianem Schura muszą być spełnione warunki a 1 < 4, a 2 < 6, a 3 < 4, a 4 < 1 Zatem wielomian W 1 (z) = z 4 + 5z 3 + 5z 2 + 2z + 0, 8 nie jest wielomianem Schura Natomiast wielomian W 2 (z) = z 4 2z 3 + 5z 2 + 2z + 0, 8 spełnia warunki konieczne, aby być wielomianem Schura
31 Przykład 6 Zbadać warunki konieczne dla wielomianu z 4 + a 1 z 3 + a 2 z 2 + a 3 z + a 4 Aby wielomian W (z) był wielomianem Schura muszą być spełnione warunki a 1 < 4, a 2 < 6, a 3 < 4, a 4 < 1 Zatem wielomian W 1 (z) = z 4 + 5z 3 + 5z 2 + 2z + 0, 8 nie jest wielomianem Schura Natomiast wielomian W 2 (z) = z 4 2z 3 + 5z 2 + 2z + 0, 8 spełnia warunki konieczne, aby być wielomianem Schura
32 Przykład 6 Zbadać warunki konieczne dla wielomianu z 4 + a 1 z 3 + a 2 z 2 + a 3 z + a 4 Aby wielomian W (z) był wielomianem Schura muszą być spełnione warunki a 1 < 4, a 2 < 6, a 3 < 4, a 4 < 1 Zatem wielomian W 1 (z) = z 4 + 5z 3 + 5z 2 + 2z + 0, 8 nie jest wielomianem Schura Natomiast wielomian W 2 (z) = z 4 2z 3 + 5z 2 + 2z + 0, 8 spełnia warunki konieczne, aby być wielomianem Schura
33 Tablica Jury a 0 a 1 a 2... a m 2 a m 1 a m a m a m 1 a m 2... a 2 a 1 a 0 b 0 b 1 b 2... b m 2 b m 1 b m 1 b m 2 b m 3... b 1 b 0 c 0 c 1 c 2... c m 2 c m 2 c m 3 c m 4... c d 0 d 1 d 2 d 3 d 3 d 2 d 1 d 0 e 0 e 1 e 2 e 2 e 1 e 0 f 0 f 1 f 1 f 0 g 0.
34 Wyliczenie elementów tablicy Jury b i = a 0a i a m a m i a 0, i = 0, 1,..., m 1 c i = b 0b i b m 1 b m 1 i b 0, i = 0, 1,..., m 2 Liczba wierszy tablicy Jury jest równa 2m + 1 Tw.6. Kryterium Jury Wielomian (3) o współczynniku a 0 > 0 jest wielomianem Schura wtedy i tylko wtedy, gdy współczynniki pierwszej kolumny w wierszach o numerach nieparzystych tablicy Jury są dodatnie (tzn. współczynniki a 0, b 0, c 0, itd.)
35 Przykład 7 Sprawdzić stabilność wielomianu W 2 (z) z przykładu 6 Tworzymy tablicę Jury , 8 0, , 36 3, 6 1 3, 6 3, 6 1 3, 6 0, 36 35, 64 c 0 < 0 wielomian niestabilny, nie jest to wielomian Schura dalszych współczynników nie trzeba liczyć
36 Przykład 7 Sprawdzić stabilność wielomianu W 2 (z) z przykładu 6 Tworzymy tablicę Jury , 8 0, , 36 3, 6 1 3, 6 3, 6 1 3, 6 0, 36 35, 64 c 0 < 0 wielomian niestabilny, nie jest to wielomian Schura dalszych współczynników nie trzeba liczyć
37 Przykład 7 Sprawdzić stabilność wielomianu W 2 (z) z przykładu 6 Tworzymy tablicę Jury , 8 0, , 36 3, 6 1 3, 6 3, 6 1 3, 6 0, 36 35, 64 c 0 < 0 wielomian niestabilny, nie jest to wielomian Schura dalszych współczynników nie trzeba liczyć
38 Metoda transformacji zmiennych Badanie stabilności systemu czasu dyskretnego można zredukować do badania stabilności systemu czasu ciągłego poprzez zastosowanie odpowiedniej transformacji zmiennych Wiadomo, że z powiązań pomiędzy transformatą Laplace a, a transformatą Z wynikają zależności oś urojona s = jω rzutowana jest na okrąg jednostkowy z = 1 półpłaszczyzna Re(s) > 0 rzutowana jest na zewnątrz koła jednostkowego z > 1 półpłaszczyzna Re(s) < 0 rzutowana jest na wnętrze koła jednostkowego z < 1
39 Przykłady przekształceń z = e sts z = s + 1 s 1 Po przekształceniu stosuje się kryteria opracowane dla systemów ciągłych, np. kryterium Hurwitza albo Routha
Badanie stabilności liniowych układów sterowania
 Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 6. Badanie
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 6. Badanie
układu otwartego na płaszczyźnie zmiennej zespolonej. Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:
 Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Projektowanie układów regulacji w dziedzinie częstotliwości. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
( 1+ s 1)( 1+ s 2)( 1+ s 3)
 Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Transmitancje i charakterystyki częstotliwościowe. Krzysztof Patan
 Transmitancje i charakterystyki częstotliwościowe Krzysztof Patan Transmitancja systemu czasu ciągłego Przekształcenie Laplace a systemu czasu ciągłego jest superpozycją składowych pochodzących od wymuszenia
Transmitancje i charakterystyki częstotliwościowe Krzysztof Patan Transmitancja systemu czasu ciągłego Przekształcenie Laplace a systemu czasu ciągłego jest superpozycją składowych pochodzących od wymuszenia
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
Technika regulacji automatycznej Wykład 3 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 32 Plan wykładu Wprowadzenie Układ pierwszego rzędu Układ drugiego
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka
 Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Kompensacja wyprzedzająca i opóźniająca fazę. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
Kompensacja wyprzedzająca i opóźniająca fazę dr hab. inż. Krzysztof Patan, prof. PWSZ Kształtowanie charakterystyki częstotliwościowej Kształtujemy charakterystykę układu otwartego aby uzyskać: pożądane
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
PAiTM. materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż.
 PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
KRYTERIA ALGEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH
 KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
KRYTERIA ALEBRAICZNE STABILNOŚCI UKŁADÓW LINIOWYCH Zadie 1 Problem: Zbadać stabilność układu zamkniętego przedstawionego na schemacie według kryterium Hurwitza. 1 (s) (s) Rys 1. Schemat układu regulacji
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Podstawowe człony dynamiczne. dr hab. inż. Krzysztof Patan
 Podstawowe człony dynamiczne dr hab. inż. Krzysztof Patan Człon proporcjonalny Równanie w dziedzinie czasu Transmitancja y(t) = Ku(t) Y (s) = KU(s) G(s) = Y (s) U(S) = K Transmiancja widmowa G(s) = K G(jω)
Podstawowe człony dynamiczne dr hab. inż. Krzysztof Patan Człon proporcjonalny Równanie w dziedzinie czasu Transmitancja y(t) = Ku(t) Y (s) = KU(s) G(s) = Y (s) U(S) = K Transmiancja widmowa G(s) = K G(jω)
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
Technika regulacji automatycznej Wykład 5 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 38 Plan wykładu Kompensator wyprzedzający Kompensator opóźniający
Ćwiczenie nr 6 Charakterystyki częstotliwościowe
 Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Systemy. Krzysztof Patan
 Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Języki Modelowania i Symulacji
 Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
Przekształcenie Z. Krzysztof Patan
 Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
Przekształcenie Z Krzysztof Patan Wprowadzenie Przekształcenie Laplace a można stosować do sygnałów i systemów czasu ciągłego W przypadku sygnałów czy systemów czasu dyskretnego do wyznaczenia transmitancji
analogowego regulatora PID doboru jego nastaw i przetransformowanie go na cyfrowy regulator PID, postępując według następujących podpunktów:
 Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Automatyka i robotyka
 Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Automatyka i robotyka Wykład 8 - Regulator PID Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 29 Plan wykładu regulator PID 2 z 29 Kompensator wyprzedzająco-opóźniający
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki Stabilność systemów sterowania kryterium Nyquist a Materiały pomocnicze do ćwiczeń termin
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki Stabilność systemów sterowania kryterium Nyquist a Materiały pomocnicze do ćwiczeń termin
Podstawowe człony dynamiczne
 . Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
. Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
Inżynieria Systemów Dynamicznych (4)
 Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Kompensator PID. 1 sω z 1 ω. G cm. aby nie zmienić częstotliwości odcięcia f L. =G c0. s =G cm. G c. f c. /10=500 Hz aby nie zmniejszyć zapasu fazy
 Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
Kompensator PID G c s =G cm sω z ω L s s ω p G cm =G c0 aby nie zmienić częstotliwości odcięcia f L f c /0=500 Hz aby nie zmniejszyć zapasu fazy Łukasz Starzak, Sterowanie przekształtników elektronicznych,
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Laboratorium nr 3. Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka
 Laboratorium nr 3. Cele ćwiczenia Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka poznanie sposobów tworzenia liniowych modeli układów automatyki, zmiana postaci modeli, tworzenie
Laboratorium nr 3. Cele ćwiczenia Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka poznanie sposobów tworzenia liniowych modeli układów automatyki, zmiana postaci modeli, tworzenie
Ćw. S-III.3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR
 Dr inż Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw S-III3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem
Dr inż Michał Chłędowski PODSTAWY AUTOMATYKI I ROBOTYKI LABORATORIUM Ćw S-III3 ELEMENTY ANALIZY I SYNTEZY UAR Badanie stabilności liniowego UAR Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z pojęciem
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów
 ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
Otrzymaliśmy w ten sposób ograniczenie na wartości parametru m.
 Dla jakich wartości parametru m dziedziną funkcji f ( x) = x + mx + m 1 jest zbiór liczb rzeczywistych? We wzorze funkcji f(x) pojawia się funkcja kwadratowa, jednak znajduje się ona pod pierwiastkiem.
Dla jakich wartości parametru m dziedziną funkcji f ( x) = x + mx + m 1 jest zbiór liczb rzeczywistych? We wzorze funkcji f(x) pojawia się funkcja kwadratowa, jednak znajduje się ona pod pierwiastkiem.
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
PRZEMYSŁOWE UKŁADY STEROWANIA PID. Wykład 5 i 6. Michał Grochowski, dr inż. Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki PRZEMYSŁOWE UKŁADY STEROWANIA PID Wykład 5 i 6 Michał Grochowski, dr inż. Studia I stopnia inżynierskie, Semestr IV Charakterystyki częstotliwościowe
Politechnika Gdańska Wydział Elektrotechniki i Automatyki PRZEMYSŁOWE UKŁADY STEROWANIA PID Wykład 5 i 6 Michał Grochowski, dr inż. Studia I stopnia inżynierskie, Semestr IV Charakterystyki częstotliwościowe
ZASTOSOWANIA PRZEKSZTAŁCENIA ZET
 CPS - - ZASTOSOWANIA PRZEKSZTAŁCENIA ZET Rozwiązywanie równań różnicowych Dyskretny system liniowy-stacjonarny można opisać równaniem różnicowym w postaci ogólnej N M aky[ n k] bkx[ n k] k k Przekształcenie
CPS - - ZASTOSOWANIA PRZEKSZTAŁCENIA ZET Rozwiązywanie równań różnicowych Dyskretny system liniowy-stacjonarny można opisać równaniem różnicowym w postaci ogólnej N M aky[ n k] bkx[ n k] k k Przekształcenie
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne.
 Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
LINIOWE UKŁADY DYSKRETNE
 LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
LINIOWE UKŁADY DYSKRETNE Współczesne układy regulacji automatycznej wyposażone są w regulatory cyfrowe, co narzuca konieczność stosowania w ich analizie i syntezie odpowiednich równań dynamiki, opisujących
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Przeksztacenie Laplace a. Krzysztof Patan
 Przeksztacenie Laplace a Krzysztof Patan Wprowadzenie Transformata Fouriera popularna metoda opisu systemów w dziedzinie częstotliwości Transformata Fouriera umożliwia wykonanie wielu użytecznych czynności:
Przeksztacenie Laplace a Krzysztof Patan Wprowadzenie Transformata Fouriera popularna metoda opisu systemów w dziedzinie częstotliwości Transformata Fouriera umożliwia wykonanie wielu użytecznych czynności:
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Transformata Laplace a to przekształcenie całkowe funkcji f(t) opisane następującym wzorem:
 PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM
 ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
ELEKTRONIKA W EKSPERYMENCIE FIZYCZNYM D. B. Tefelski Zakład VI Badań Wysokociśnieniowych Wydział Fizyki Politechnika Warszawska, Koszykowa 75, 00-662 Warszawa, PL 28 lutego 2011 Stany nieustalone, stabilność
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transform
 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. March 20, 2013 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. Sygnał i system Sygnał jest opisem
Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. March 20, 2013 Dyskretne układy liniowe. Funkcja splotu. Równania różnicowe. Transformata Z. Sygnał i system Sygnał jest opisem
1. Transformata Laplace a przypomnienie
 Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
Podstawy środowiska Matlab
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ. T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
 REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
REGULATORY W UKŁADACH REGULACJI AUTOMATYCZNEJ Y o (s) - E(s) B(s) /T I s K p U(s) Z(s) G o (s) Y(s) T I - czas zdwojenia (całkowania) T D - czas wyprzedzenia (różniczkowania) K p współczynnik wzmocnienia
Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC.
 Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC. Spis treści 1 Cel ćwiczenia 2 2 Podstawy teoretyczne 2 2.1 Charakterystyki częstotliwościowe..........................
Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC. Spis treści 1 Cel ćwiczenia 2 2 Podstawy teoretyczne 2 2.1 Charakterystyki częstotliwościowe..........................
Równania różniczkowe liniowe II rzędu
 Równania różniczkowe liniowe II rzędu Definicja równania różniczkowego liniowego II rzędu Warunki początkowe dla równania różniczkowego II rzędu Równania różniczkowe liniowe II rzędu jednorodne (krótko
Równania różniczkowe liniowe II rzędu Definicja równania różniczkowego liniowego II rzędu Warunki początkowe dla równania różniczkowego II rzędu Równania różniczkowe liniowe II rzędu jednorodne (krótko
Liczby zespolone. x + 2 = 0.
 Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Rozwiązaniem jest zbiór (, ] (5, )
![Rozwiązaniem jest zbiór (, ] (5, ) Rozwiązaniem jest zbiór (, ] (5, )](/thumbs/62/48086093.jpg) FUNKCJE WYMIERNE Definicja Miech L() i M() będą niezerowymi wielomianami i niech D { R : M( ) 0 } Funkcję (*) D F : D R określoną wzorem F( ) L( ) M( ) nazywamy funkcją wymierną Funkcja wymierna, to iloraz
FUNKCJE WYMIERNE Definicja Miech L() i M() będą niezerowymi wielomianami i niech D { R : M( ) 0 } Funkcję (*) D F : D R określoną wzorem F( ) L( ) M( ) nazywamy funkcją wymierną Funkcja wymierna, to iloraz
Analiza ustalonego punktu pracy dla układu zamkniętego
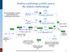 Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
Analiza ustalonego punktu pracy dla układu zamkniętego W tym przypadku oznacza stałą odchyłkę od ustalonego punktu pracy element SUM element DIFF napięcie odniesienia V ref napięcie uchybu V e V ref HV
Zastosowania liniowe wzmacniaczy operacyjnych
 UKŁADY ELEKTRONICZNE Instrukcja do ćwiczeń laboratoryjnych Zastosowania liniowe wzmacniaczy operacyjnych Laboratorium Układów Elektronicznych Poznań 2008 1. Cel i zakres ćwiczenia Celem ćwiczenia jest
UKŁADY ELEKTRONICZNE Instrukcja do ćwiczeń laboratoryjnych Zastosowania liniowe wzmacniaczy operacyjnych Laboratorium Układów Elektronicznych Poznań 2008 1. Cel i zakres ćwiczenia Celem ćwiczenia jest
Automatyka i sterowanie w gazownictwie. Regulatory w układach regulacji
 Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Rok akademicki: 2016/2017 Kod: EEL s Punkty ECTS: 6. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Teoria sterowania i technika regulacji Rok akademicki: 2016/2017 Kod: EEL-1-406-s Punkty ECTS: 6 Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Elektrotechnika
Nazwa modułu: Teoria sterowania i technika regulacji Rok akademicki: 2016/2017 Kod: EEL-1-406-s Punkty ECTS: 6 Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Elektrotechnika
Wstęp do analizy matematycznej
 Wstęp do analizy matematycznej Andrzej Marciniak Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych i ich zastosowań w
Wstęp do analizy matematycznej Andrzej Marciniak Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych i ich zastosowań w
Metody numeryczne I Równania nieliniowe
 Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
Rozdział 2. Liczby zespolone
 Rozdział Liczby zespolone Zbiór C = R z działaniami + oraz określonymi poniżej: x 1, y 1 ) + x, y ) := x 1 + x, y 1 + y ), 1) x 1, y 1 ) x, y ) := x 1 x y 1 y, x 1 y + x y 1 ) ) jest ciałem zob rozdział
Rozdział Liczby zespolone Zbiór C = R z działaniami + oraz określonymi poniżej: x 1, y 1 ) + x, y ) := x 1 + x, y 1 + y ), 1) x 1, y 1 ) x, y ) := x 1 x y 1 y, x 1 y + x y 1 ) ) jest ciałem zob rozdział
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Reakcja Bielousowa-Żabotyńskiego
 Reakcja Bielousowa-Żabotyńskiego 1 Kryteria pomocne przy badaniu stabilności punktów stacjonarnych Często badamy układy dynamiczne w pobliżu punktów stacjonarnych. Rozważamy wtedy ich postać zlinearyzowaną:
Reakcja Bielousowa-Żabotyńskiego 1 Kryteria pomocne przy badaniu stabilności punktów stacjonarnych Często badamy układy dynamiczne w pobliżu punktów stacjonarnych. Rozważamy wtedy ich postać zlinearyzowaną:
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Plan wykładu. Własności statyczne i dynamiczne elementów automatyki:
 Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Formy kwadratowe. Mirosław Sobolewski. Wydział Matematyki, Informatyki i Mechaniki UW. 14. wykład z algebry liniowej Warszawa, styczeń 2017
 Formy kwadratowe Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 14. wykład z algebry liniowej Warszawa, styczeń 2017 Mirosław Sobolewski (UW) Warszawa, 2017 1 / 10 Definicja Funkcja
Formy kwadratowe Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 14. wykład z algebry liniowej Warszawa, styczeń 2017 Mirosław Sobolewski (UW) Warszawa, 2017 1 / 10 Definicja Funkcja
Własności wyznacznika
 Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Filtracja. Krzysztof Patan
 Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
Filtracja Krzysztof Patan Wprowadzenie Działanie systemu polega na przetwarzaniu sygnału wejściowego x(t) na sygnał wyjściowy y(t) Równoważnie, system przetwarza widmo sygnału wejściowego X(jω) na widmo
A-2. Filtry bierne. wersja
 wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
wersja 04 2014 1. Zakres ćwiczenia Celem ćwiczenia jest zrozumienie propagacji sygnałów zmiennych w czasie przez układy filtracji oparte na elementach rezystancyjno-pojemnościowych. Wyznaczenie doświadczalne
Lepkosprężystość. Metody pomiarów właściwości lepkosprężystych materii
 Metody pomiarów właściwości lepkosprężystych materii Pomiarów dokonuje się w dwóch dziedzinach: czasowej lub częstotliwościowej i nie zależy to od rodzaju przyłożonych naprężeń (normalnych lub stycznych).
Metody pomiarów właściwości lepkosprężystych materii Pomiarów dokonuje się w dwóch dziedzinach: czasowej lub częstotliwościowej i nie zależy to od rodzaju przyłożonych naprężeń (normalnych lub stycznych).
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
Podstawy Automatyki. Wykład 2 - modelowanie matematyczne układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
Lista. Algebra z Geometrią Analityczną. Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami:
 Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji
 Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
TEORIA STEROWANIA I, w 5. dr inż. Adam Woźniak ZTMiR MEiL PW
 TEORIA STEROWANIA I, w 5 dr inż. Adam Woźniak ZTMiR MEiL PW Układy LTI- SISO Stacjonarne, przyczynowe liniowe układy z jednym wyjściem i jednym wejściem najczęściej modeluje się przy pomocy właściwej transmitancji
TEORIA STEROWANIA I, w 5 dr inż. Adam Woźniak ZTMiR MEiL PW Układy LTI- SISO Stacjonarne, przyczynowe liniowe układy z jednym wyjściem i jednym wejściem najczęściej modeluje się przy pomocy właściwej transmitancji
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych
 Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Przetwarzanie sygnałów dyskretnych
 Przetwarzanie sygnałów dyskretnych System dyskretny p[ n ] r[ n] Przykłady: [ ] = [ ] + [ ] r n a p n a p n [ ] r n = 2 [ + ] + p[ n ] p n 2 r[ n] = a p[ n] + b n [ ] = [ ] r n a p n n [ ] = [ + ] r n
Przetwarzanie sygnałów dyskretnych System dyskretny p[ n ] r[ n] Przykłady: [ ] = [ ] + [ ] r n a p n a p n [ ] r n = 2 [ + ] + p[ n ] p n 2 r[ n] = a p[ n] + b n [ ] = [ ] r n a p n n [ ] = [ + ] r n
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
